Abstract
Background:
Adaptive radiation treatment (ART) for locally advanced pancreatic cancer (LAPC) requires consistently accurate segmentation of the extremely mobile gastrointestinal (GI) organs at risk (OAR) including the stomach, duodenum, large and small bowel. Also, due to lack of sufficiently accurate and fast deformable image registration (DIR), accumulated dose to the GI OARs is currently only approximated, further limiting the ability to more precisely adapt treatments.
Purpose:
Develop a 3-D Progressively refined joint Registration-Segmentation (ProRSeg) deep network to deformably align and segment treatment fraction magnetic resonance images (MRI)s, then evaluate segmentation accuracy, registration consistency, and feasibility for OAR dose accumulation.
Method:
ProRSeg was trained using 5-fold cross-validation with 110 T2-weighted MRI acquired at 5 treatment fractions from 10 different patients, taking care that same patient scans were not placed in training and testing folds. Segmentation accuracy was measured using Dice similarity coefficient (DSC) and Hausdorff distance at 95th percentile (HD95). Registration consistency was measured using coefficient of variation (CV) in displacement of OARs. Statistical comparison to other deep learning and iterative registration methods were done using the Kruskal-Wallis test, followed by pair-wise comparisons with Bonferroni correction applied for multiple testing. Ablation tests and accuracy comparisons against multiple methods were done. Finally, applicability of ProRSeg to segment cone-beam CT (CBCT) scans was evaluated on a publicly available dataset of 80 scans using 5-fold cross-validation.
Results:
ProRSeg processed 3D volumes (128 × 192 × 128) in 3 secs on a NVIDIA Tesla V100 GPU. It’s segmentations were significantly more accurate (p < 0.001) than compared methods, achieving a DSC of 0.94±0.02 for liver, 0.88±0.04 for large bowel, 0.78±0.03 for small bowel and 0.82±0.04 for stomach-duodenum from MRI. ProRSeg achieved a DSC of 0.72±0.01 for small bowel and 0.76±0.03 for stomach-duodenum from public CBCT dataset. ProRSeg registrations resulted in the lowest CV in displacement (stomach-duodenum , , and ; small bowel , , and ; large bowel , , and ). ProRSeg based dose accumulation accounting for intra-fraction (pre-treatment to post-treatment MRI scan) and inter-fraction motion showed that the organ dose constraints were violated in 4 patients for stomach-duodenum and for 3 patients for small bowel. Study limitations include lack of independent testing and ground truth phantom datasets to measure dose accumulation accuracy.
Conclusions:
ProRSeg produced more accurate and consistent GI OARs segmentation and DIR of MRI and CBCTs compared to multiple methods. Preliminary results indicates feasibility for OAR dose accumulation using ProRSeg.
Keywords: Recurrent deep networks, GI organs, segmentation, registration, MRI, CBCT
I. Introduction
MR-guided adaptive radiation therapy (MRgART) is a new treatment that allows for radiative dose escalation of locally advanced pancreatic cancers (LAPC) with higher precision than conventionally used cone-beam CTs (CBCT) due to improved soft-tissue visualization on MRI. MR-LINAC treatments also allow daily treatment adaptation and replanning to account for the changing anatomy. Anatomy changes result from day-to-day variations in organ shape and configuration as well as motion due to peristalsis and breathing, all of which introduce large geometric uncertainties to the delivery of radiation. However, widespread adoption of MRgART is hampered by the need for manual contouring and plan re-optimization, which together can take 40 to 70 mins1,2 daily. Hence, there is a clinical need for consistently accurate and fast auto-segmentation of the gastrointestinal (GI) organs at risk (OARs) including the stomach, duodenum, small and large bowel.
Highly accurate segmentation, measured as a Dice similarity coefficient (DSC) exceeding 0.8 of abdominal organs such as the liver, kidneys, spleen, as well as the stomach (excluding duodenum) has been reported by using off-the-shelf deep learning (DL) architectures including nnUnet3 and Unet4, as well as customized dense V-Nets5 and new transformer based methods6,7 applied to CT images. Slice-wise priors provided as manual segmentations8, multi-view methods using inter-slice information from several slices and dense connections6 as well as self-supervised learning of transformers9 have shown the ability to segment the more challenging GI OARs such as large and small bowel and duodenum from MRI. However, the need for manual editing8 and large number of adjacent slices6 required to provide priors may reduce the number of available training sets and the practicality (due to need for manual editing) of such methods.
Besides segmentation, reliable deformable image registration (DIR) is also needed for voxel-wise OAR dose accumulation in order to ensure that the prescription dose was delivered to the targets while sparing organs of unnecessary radiation. DIR based contour propagation10,11,12 is a convenient option that is commonly available in commercial software to solve both deformable dose accumulation and contour propagation. However, commonly available DIR methods often use small deformation frameworks based on parameterizing a displacement field added to an identity transform, which cannot preserve topology13 for large organ displacements. Deep learning image registration (DLIR) methods14,15,16,17 are often faster than iterative registration methods because they directly compute the diffeomorphic transformation between images in a single step instead of solving a non-linear optimization to align every image pair. DLIR methods often use stationary velocity field (SVF) for faster training by reducing the search space to a set of diffeomorphisms that are within a Lie structure. However, this assumption limits their flexibility to handle large and complex deformations18. Also these methods minimize an energy function composed of global similarity and global smoothness regularization, which ignores local abrupt and large motion occurring at the organ boundaries19.
Compositional DIR strategies such as used for non-sliding and sliding organs19, adaptive anisotropic filtering of the incrementally refined deformation vector field (DVF)20 as well as cascaded network formulations13,21,22 increase robustness by using a staged approach for refining registrations. However, such methods are limited by the memory requirements and often require sequential training of individual networks, which increases training time and does not guarantee the preservation of deformations already captured in the previous stages. Recurrent registration method (R2N2) that computes local parameterized Gaussian deformations23 has demonstrated ability to model large anatomic deformations occurring in a respiratory cycle. However, the use of local parametrization restricts its flexibility to handle large and continuous deformations such as for tumors24. Our approach improves on these works to compute topology preserving (quantified by non-negative Jacobian determinant) diffeomorphic deformations and multi-organ segmentations by using a progressive joint registration-segmentation (ProRSeg) approach, wherein deformation flow computed at a given step is conditioned on the prior step using a 3D convolutional long short term memory network (CLSTM)25. ProRSeg is optimized using a multi-tasked learning of a registration and segmentation network, which allows it to leverage the implicit backpropagated errors from the two networks. Multi-tasked networks have previously shown to produce more accurate normal tissue segmentation than individually trained DL networks14,15,16,26.
One approach to robustly handle large deformations is to use regularization constraints such as rigidity penalty27 and geometry matching constraints used for successfully aligning images exhibiting large anatomic deformations such as upper gastrointestinal organs27 and female reproductive organs such as the uterus and cervix28. A recent DLIR method by Han et.al29 have also shown that using geometry constraints can benefit handling large anatomic differences inherent in organs like the small and large bowel when aligning CBCT images with CT images. Our proposed method also uses geometry matching losses during training to better regularize the registration and segmentation sub-networks with a key difference that such losses are used also as deep supervision losses to optimize the incremental deformations computed by the network. However, unlike Han et.al29, our method uses the entire image volume for computing the DIR instead of a prespecified region of interest and is thus directly applicable to clinical settings. Finally, our approach uses recurrent network formulation to compute a progressive sequence of deformations instead of estimating the momentum and velocity parameters to drive LDDMM, thus providing a single step approach to compute DIR between pairs of images.
ProRSeg is most similar to a prior registration-segmentation method that we developed for tracking lung tumor response to radiation therapy24 from cone-beam CT (CBCT) images. However, ProRSeg accounts for both respiratory and large organ shape variations, while our prior work was only concerned with tracking linearly shrinking tumors during radiation treatment. ProRSeg computes a smooth interpolated sequence of dense deformation by implementing 3D CLSTM networks in all the encoder layers of both registration and segmentation networks. This approach explicitly enforces consistency of the computed deformations for the registration and progressively refined geometry priors used to refine segmentation. Hence, the segmentation network avails progressively refined information about the organs and their geometry from a prior treatment fraction, which increases robustness to arbitrary variations occurring in the GI organs. In contrast, prior works14,16 used a weaker regularizing constraint to ensure that the outputs of registration and segmentation networks matched as additional losses during training. Finally, the segmentation consistency loss enforces similarity of segmentations generated by registration-based propagation, segmentation network, and the manual delineations, which improves accuracy of both networks.
Our contributions are: (i) a simultaneous registration-segmentation approach for segmenting GI OARs from MRI while computing voxel-wise deformable dose accumulation, (ii) use of registration derived spatially aligned appearance and geometry priors to constrain segmentation that increases accuracy, (iii) use of a 3D CLSTM implemented in the encoders of both registration and segmentation networks that increases robustness to arbitrary organ deformations by modeling such deformations as a progressively varying dense flow field. (iv) We also evaluated ProRSeg for segmenting GI organs (stomach-duodenum and small bowel) from treatment CBCTs using a publicly available longitudinal CT-CBCT dataset provided by Hong et.al30. (v) Finally, we show that the registration-segmentation network allows to incorporate organs such as whole pancreas and pancreatic tumors that were never used in the network’s training using a subset analysis.
II. Materials and Method
II.A. Pancreas MRI dataset for MR-MR registration-segmentation
The retrospective analysis was approved by the institutional internal review board. One hundred and ten 3D T2-weighted MRIs acquired from on treatment MRIs from 10 patients undergoing five fraction MR-guided SBRT to a total dose of 50 Gy were analyzed. A pneumatic compression belt set according to the patient convenience was used to minimize gross tumor volume (GTV) and GI organs motion occurring within 5mm of the GTV31. The dose constraints to GI organs were defined as or and . for large bowel was ≤ 30 Gy. In each treatment fraction, three 3D T2-weighted MRI (TR/TE of 1300/87 ms, voxel size of 1 × 1 × 2 mm3, FOV of 400 × 450 × 250 mm3) were acquired at pre-treatment, verification (before beam on), and at post-treatment. Six patients had pre-treatment, verification, and post-treatment MRI with segmentation on all five fractions with the remaining 4 containing only pre-treatment MRI for all fractions. Additional details of treatment planning are in prior study27,31.
Expert contouring details:
Stomach-duodenum, large bowel, and small bowel, as well as liver were contoured on all the available treatment fraction MRIs by an expert medical student and verified by radiation oncologists, and represented the ground truth for verifying the ProSeg segmentations and deformable image registration (DIR).
II.B. Pancreas dataset for pCT-CBCT registration-segmentation
ProRSeg was additionally evaluated using a publicly available dataset30 of 80 CBCTs acquired from 40 LAPC patients treated with hypofractionated RT on a regular linac. This dataset consists of a planning CT (pCT) and 2 CBCT scans acquired on different days in a deep inspiration breath hold (DIBH) state using an external respiratory monitor (Real-time Position Monitor, Varian Medical Systems). pCT scans were acquired in DIBH with a diagnostic quality scanner (Brilliance Big Bore, Phillips Health Systems; or DiscoveryST, GE Healthcare). The kilovoltage CBCT scans were acquired with 200-degree gantry rotation. The CBCT reconstruction diameter was 25 cm and length was 17.8 cm.
Expert contouring details:
Radiation oncologist delineated the OARs within a volume of interest defined as 1 cm expansion on the 3D volume including the high and ultra-high dose planning target volume on the pCT and CBCT scans29.
II.C. Image preprocessing details
Rigid registration, MRI preprocessing (N4 bias field correction and histogram standardization) used methods available in open source CERR software32. MRIs were aligned with prior treatment fraction MRI while CBCTs were aligned to pCT scans. Only the body region of the images were used for analysis by subjecting them to intensity thresholding, hole filling, followed by largest connected region extraction as a preprocessing step.
II.D. ProRSeg: Progressively refined joint registration segmentation
II.D.1. Approach Overview:
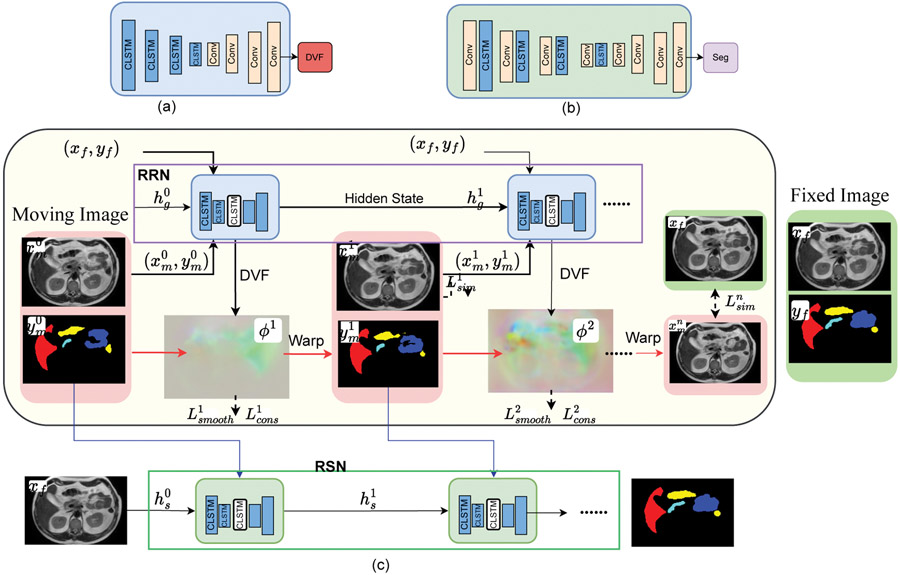
ProRSeg is implemented using 3D convolutional recurrent registration or RRN () and recurrent segmentation networks or RSN (). RRN uses a pair of source and target images and computes a dense deformation flow field to warp the source image into target () image’s spatial coordinates (or ) by using a progressive sequence of deformations , where is the number of 3D CLSTM steps. The 3D CLSTM is implemented into all the encoder layers of RRN and RSN. The RSN generates a segmentation for by combining with progressively warped moving images and contours produced by the RRN as inputs to each CLSTM step (Figure 1).
Figure 1:
(a) Schematic of recurrent Registration Network (RRN), where convolutional (Conv) layers in the encoder are combined with 3D-CLSTM. (b) Recurrent Segmentation Network (RSN) uses a Unet-3D backbone with 3D-CLSTM placed after convolutional blocks in the encoder layers. (c) ProRSeg combines RRN and RSN. The unrolled representation showing CLSTM in the encoder layers for progressively refining the registration and segmentation are shown. RSN combines with the progressively aligned images and segmentations produced by RRN as inputs to its CLSTMs to generate segmentation in N steps.
II.D.2. Convolutional long short term memory network (CLSTM):
CLSTM is a type of recurrent neural network, which maintains long term contextual information about the state at step by using gating filters called forget gate and memory cells , implemented using sigmoid activation function and a multiplicative term (Eqn 1). CLSTM improves upon long-short term memory network by using convolutional filters to maintain the state information using a dense encoding of the spatial neighborhood or the whole image. The CLSTM components including the state, forget gate, memory cells, hidden state , input state , and output gate are updated as below:
| (1) |
where, is the sigmoid activation function, the convolution operator, the Hadamard product, and the weight matrix.
II.D.3. Recurrent registration network:
A schematic of the RRN architecture is depicted in Figure 1 (a). RRN deforms an image into , expressed as by computing a sequence of progressive deformation vector fields (DVF) using CLSTM steps: . , where I is the identity and is the DVF. The input to the first layer is a channel-wise concatenated pair of source and target images () and the hidden state initialized to 0. Subsequent layers use the progressively deformed source and the hidden state output from the prior CLSTM step together with the target image as inputs to the current CLSTM step . Images are channel-wise concatenated () for use in the CLSTM step. A CLSTM step computes a warped image and contour () as:
| (2) |
Note that the contour is not used as an input to constrain the RRN network.
RRN is optimized without any ground truth DVFs. Deep image similarity and deep smoothness losses are used to regularize the warped image and the DVF of each CLSTM step. A supervised segmentation consistency loss comparing the warped contour produced after CLSTM steps of the RRN with the expert delineation was computed by measuring contour overlaps using Dice similarity coefficient (DSC):
| (3) |
is computed by comparing the warped images in each CLSTM step with the fixed images by using mean square error (MSE) loss for the MR to MR registration. In the case of pCT-CBCT registration experiment, was computed using normalized Cross-Correlation (NCC) computed locally using window of 5×5×5 centered on each voxel to improve robustness to CT and CBCT intensity differences17. This can be expressed as:
| (4) |
The NCC loss at each CLSTM step is an average of all the local NCC calculations, thereby ensuring robustness to local variations.
was used to regularize the incremental deformation flow from each CLSTM step by averaging the flow field gradient within each voxel as:
| (5) |
The total registration loss is then computed as:
| (6) |
where and are tradeoff parameters.
Implementation details:
RRN was constructed by modifying the Voxelmorph (a 3D-Unet backbone)17 such that the convolutional filters in the encoder were replaced with 3D-CLSTM. Because the CLSTM extracts features by keeping track of prior state information, it computes features that capture both the temporal context and the dense spatial context (from the convolutional filters used to implement CLSTM). Each CLSTM block was composed of encoders implemented with CLSTM, a decoder to convert the features into a velocity field, which then was followed by a spatial transformation function based on spatial transform networks33 to convert the stationary displacement field into DVF. Diffeomorphic deformation from each CLSTM block at time step was ensured using a integration of the stationary velocity field over [1, 7] to obtain the registration field and implemented using scaling and squaring transforms to provide efficient numerical integration34. The resampled moving image after each step was obtained as , which then was input to the subsequent RRN CLSTM step to compute the deformation field . More details of specific RRN network layers are in Supplemental Table 1. Eight 3D CLSTM steps were used for RRN as done in a different work applied to lung tumor segmentation from CBCT24.
II.D.4. Recurrent segmentation network:
Schematic of the RSN network is shown in Figure 1(b). RSN progressively refines the multiclass segmentation of a given target image using CLSTM steps. RSN uses one additional CLSTM than the RRN because the first CLSTM step uses the undeformed moving image and it’s segmentation with the target image as channel-wise concatenated input. The remaining CLSTM steps use channel-wise concatenated input where and are produced by the RRN CLSTM step . Segmentation from each one of the RSN CLSTM steps are computed as , where is the hidden state of the RSN CLSTM step , (Eqn. 2).
The RSN is optimized by computing a deep supervision segmentation loss comparing the segmentations produced after each CLSTM step with expert segmentation. This loss is computed using cross-entropy as:
| (7) |
The losses, provide deep supervision to train RSN.
Implementation details:
RSN is implemented with a 3D Unet backbone with CLSTM steps implemented into the encoder layers. The standard 3DUnet was improved by replacing the first convolutional layer with a CLSTM before the max pooling layer. Each convolutional block was composed of two convolution units, ReLU activation, and max-pooling layer. This resulted in feature sizes of 32,64,128,256, and 512. Nine CLSTM steps were used to implement the RSN and GPU memory limitation was addressed using truncated backpropagation as used for RRN. The detailed network architecture for RRN and RSN are in Supplementary Table 1 and Supplementary Table 2.
II.E. Training details
Both RRN and RSN are trained end-to-end and optimized jointly to use the losses computed from both networks for optimizing the networks parameters. The networks were implemented using Pytorch library and trained on Nvidia GTX V100 with 16 GB memory. The networks were optimized using ADAM algorithm with an initial learning rate of 2e-4 for the first 30 epochs and then decayed to 0 in the next 30 epochs and a batch size of 1. The was set to 20 and to 1 experimentally.
ProRSeg was trained separately for MR-to-MR and pCT-CBCT registration using five-fold cross-validation taking care that the same patient scans were not used in the training and corresponding validation folds. In order to increase the number of training examples, all possible pairs of images for each patient arising from different treatment fractions were used. In addition, online data augmentation using image rotation and translation was implemented to increase data diversity for training.
II.F. Metrics and statistical analysis:
Segmentation accuracy was measured using the Dice similarity coefficient (DSC) and Hausdorff distance at 95th percentile (HD95) on the validation set (validation data not used for training in each cross-validation fold). Statistical accuracy comparison of all the analyzed methods was performed by measuring the differences in the average DSC and HD95 metrics using non-parametric Kruskal-Wallis test, followed by individual pairwise comparisons (36 for all fractions and 49 when including ProRSeg++ for 4 and 5th fractions) using paired, two-sided Wilcoxon-signed rank tests at 95% confidence level with Bonferroni correction applied for multiple comparisons. Non-parametric tests were used as they do not assume normality of distribution of the data. Only p values < 0.05 were considered significant.
Segmentation consistency was computed by using coefficient of variation (), where is the standard deviation of the DSC per patient and is the population mean DSC. Variability in segmentation accuracy across treatment fractions was analyzed by measuring statistical differences in DSC and HD95 for the GI OARs extracted at 5 different treatment fractions for MRI using paired and two-sided Kruskal-Wallis tests at 95% significance levels.
Registration smoothness was measured using standard deviation of Jacobian determinant () and the folding fraction . Finally, consistency of registration to variations in anatomy was measured using percentage coefficient of variation (CV) in the median displacement for each GI OAR at patient level, by varying the source images (different treatment fractions) aligned to each treatment fraction MRI (as target). CV for each patient was evaluated in all three displacement directions as , where is the standard deviation and is the mean displacement.
II.G. Experiments configuration
II.G.1. Comparative experiments
We evaluated our method against baseline methods that were most similar to ours, including joint registration-segmentation using the UResNet16 and a deep registration only method called VoxelMorph17 and two segmentation only methods, namely 3DUnet4 and nnUnet3. Finally, a non deep learning iterative registration method from the open-source Elastix35 was also included for comparison. Image pairs were pre-aligned using rigid registration in order to bring them into similar spatial coordinates prior to application of the DIR methods. The CBCT OAR segmentation results by Han et.al29 using the same public dataset30 are included for comparison.
II.H. Ablation experiments
Ablation experiments were done using the MRI dataset. Experiments were performed to study differences in accuracy when using RRN based segmentation versus when using RSN that combines information from RRN to compute the segmentation. The impact of spatially aligned appearance and shape prior provided by RRN to RSN and segmentation consistency loss on the segmentation accuracy were also measured. The impact of number of CLSTM steps (1 to 8) on segmentation accuracy produced by RRN and RSN were analyzed. Accuracy differences due to the use of Dice vs. cross entropy loss to optimize the segmentation sub-network as well as the hyperparameter selection and experiments were done.
III. Results
III.A. GI OAR segmentation accuracy from MRI
Table 1 shows the segmentation accuracies produced by the evaluated methods when aligning all consecutive treatment fractions. ProRSeg produced the highest average DSC of 0.85 and the lowest average HD95 of 8.23 mm compared to all other baseline methods. Kruskal-Wallis test showed significant difference in the DSC (p < 0.001) and HD95 (p < 0.001) accuracy between the various methods. Pairwise comparison followed by Bonferroni correction showed that ProRSeg was significantly more accurate (p < 0.001) than UNet3D (average DSC of 0.85 vs. 0.77, average HD95 of 8.23 mm vs. 20.06 mm), the nnUnet (average DSC of 0.79, average HD95 of 16.12 mm), and the joint registration-segmentation method, UResNet16 (average DSC of 0.763, average HD95 of 12.365 mm). UResNet was less accurate than the nnUnet when using the DSC metric but more accurate with the HD95 metric, with significant difference observed for large bowel (p=0.03 with DSC, p<0.001 with HD95) and the stomach-duodenum (p<0.001 with HD95) metrics. Supplemental Table 3 shows the p values measuring the differences between various methods with respect to ProRSeg after Bonferroni correction.
Table 1:
Segmentation accuracy (mean and standard deviation) of various methods applied to T2-w MRI. LG bowel: Large bowel, SM bowel: small bowel, Sto-Duo: stomach-duodenum.
†: Segmentations generated for treatment fraction 4 and 5 using majority voting of segmentations produced by using 1, 2, and 3 treatment fraction MRI.
°: p < 0.05, *: p < 0.01, **: p < 0.001.
| Method | DSC ↑ | HD95 mm ↓ | ||||||
|---|---|---|---|---|---|---|---|---|
| Liver | LG Bowel | SM Bowel | Sto-Duo | Liver | LG Bowel | SM Bowel | Sto-Duo | |
| SyN35 | 0.89±0.04** | 0.59±0.13** | 0.61±0.09** | 0.66±0.08** | 9.17±3.55** | 20.04±8.55** | 20.74±7.36** | 13.08±5.08** |
| Voxelmorph17 | 0.91±0.06** | 0.74±0.18** | 0.67±0.10** | 0.75±0.09** | 7.85±3.85** | 14.52±9.81** | 19.26±7.97** | 13.35±13.21** |
| Unet3D | 0.92±0.02** | 0.79±0.11** | 0.68±0.11** | 0.68±0.10** | 13.57±15.72** | 20.63±13.90** | 26.11±9.68** | 19.95±11.33** |
| nnUnet3 | 0.93±0.02* | 0.81±0.10** | 0.72±0.09** | 0.70±0.10** | 8.22±3.14** | 18.00±13.43** | 18.95±6.19** | 19.33±8.48** |
| UResNet16 | 0.91±0.04** | 0.72±0.15** | 0.67±0.07** | 0.75±0.08** | 6.80±2.76** | 11.92±9.18** | 18.56±8.53** | 12.18±12.87** |
| ProRSeg | 0.94±0.02 | 0.86±0.08 | 0.78±0.07 | 0.82±0.05 | 5.69±1.72 | 7.00±5.14 | 12.11±5.30 | 8.11±3.54 |
| ProRSeg++† | 0.95±0.01** | 0.91±0.02 | 0.83±0.02° | 0.85±0.04 | 5.52±0.85 | 6.49±3.91 | 10.70±1.20° | 7.35±2.50 |
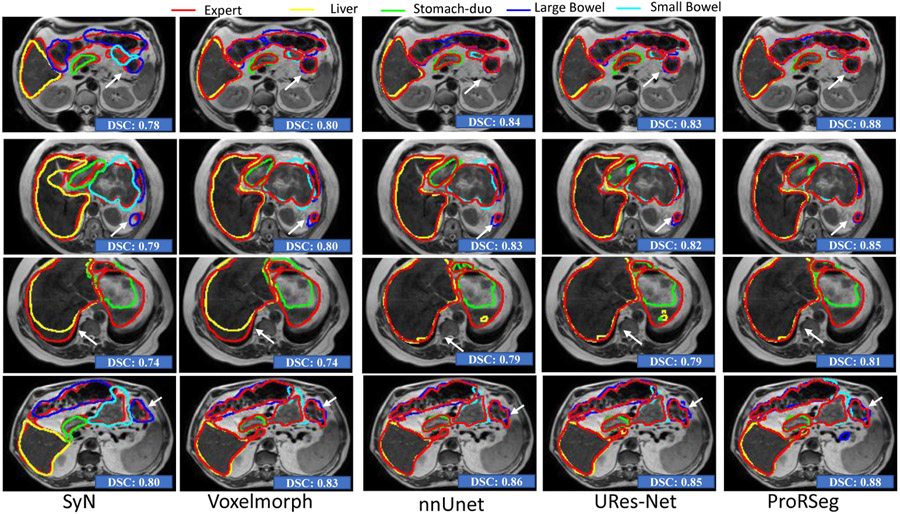
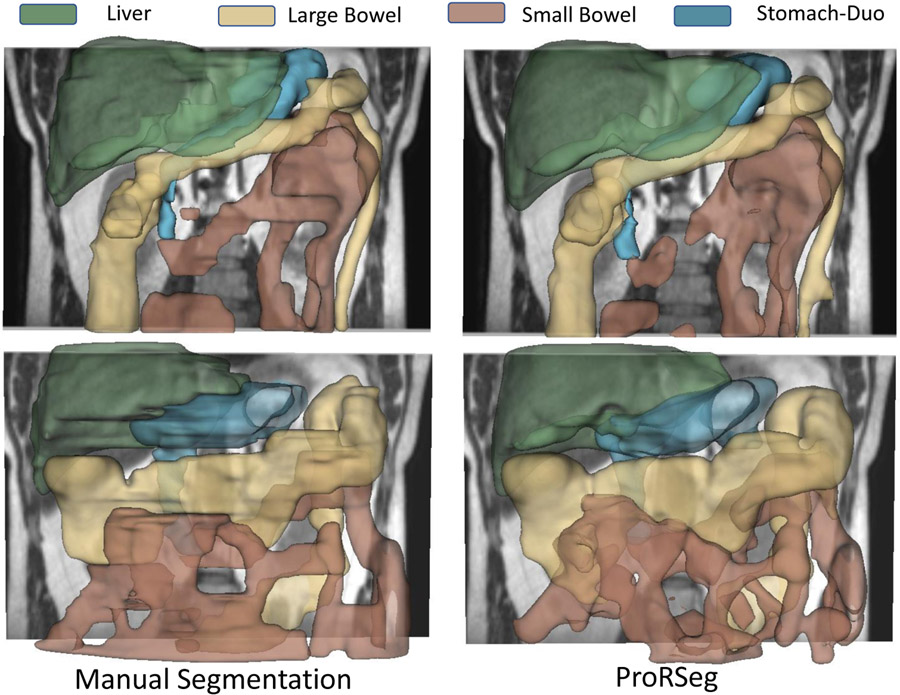
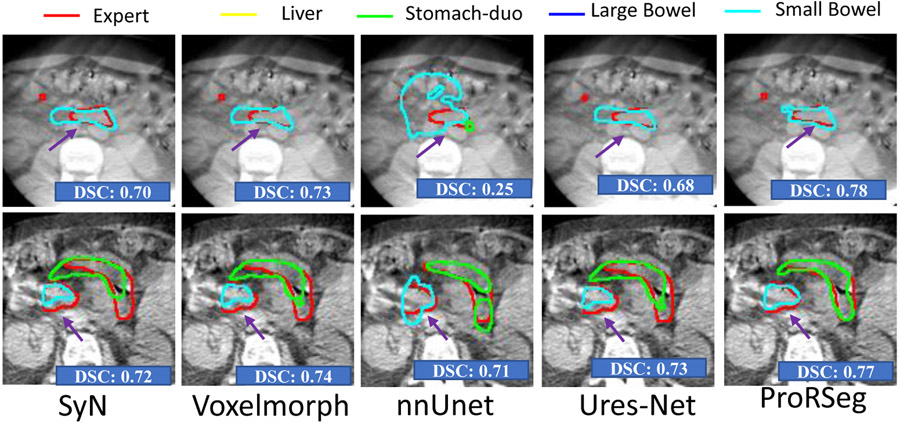
Figure. 2 shows segmentation contours produced by the analyzed methods together with the expert delineations (in red) on representative examples. The overall DSC accuracy is also shown for all the cases and methods. As seen, ProRseg most closely matched the expert delineations even for hard to segment small bowel (Figure. 2 row 1, 2 and 4) and stomach-duodenum (Figure. 2 row 1, 2, 4). On the other hand, iterative registration35 resulted in poor segmentations even for large organs such as the liver, indicating the difficulty of aligning images using intensity based information alone. Similarly, Voxelmorph17, a deep learning registration based segmentation method was unable to match the expert contours as closely as either the UResNet16 or ProRSeg. nnUnet, UResNet, and ProRSeg showed higher accuracy for the presented cases, except when large differences in organ shape and appearance occurred between treatment fractions. An example case with poor segmentation of the stomach occurring as a result of filled stomach aligned to empty stomach occurring in the prior treatment fraction is shown in Figure. 2, row 3. Figure 3 shows 3D rendering of two examples, the best case with an overall DSC of 0.88 and the worst case with an overall DSC of 0.81. As shown, for the best case example, ProRSeg closely matched the expert delineation of intra-peritoneal small bowel, and achieving a high DSC of 0.81 for small bowel. Reduction in overall accuracy in the second case occurred due to lower accuracy in segmenting the intra-peritoneal small bowel loops (DSC of 0.72). In comparison, the DSC for other OARs were high, stomach-duodenum DSC of 0.85 and large bowel DSC of 0.93.
Figure 2:
Comparison of OAR segmentations generated by multiple methods from MRI on representative examples.
Figure 3:
Three dimensional rendering of volumetric segmentations produced by expert (first column) and ProRSeg (second column) for best case (top row) and worst case (bottom row) patients.
Motivated by a prior study for MRI-based upper GI organs segmentation12 that fused DIR based segmentations from multiple prior fraction MRIs, ensemble segmentations were computed for the treatment fractions 4 and 5 by performing decision level fusion using simple majority voting of the segmentations produced by using multiple prior fraction MRIs (first to third fraction for treatment fraction 4, and first to fourth fraction for treatment fraction 5) as prior images for the registration-segmentation. The ProRSeg ensemble called ProRSeg++ applied only to the 4 and 5 fractions, increased the segmentation accuracy for large bowel (0.91 ±0.02 vs. 0.90 ± 0.04), small bowel (0.83±0.02 vs. 0.80 ±0.05), and the stomach-duodenum (0.85±0.04 vs. 0.80±0.07). ProRSeg++ was not applied to the first three fractions because at least three preceding treatment fraction MRIs are required to create the ensemble segmentation. Kruskal-Wallis test performed to compare the various methods including ProRSeg showed significant difference in both DSC (p < 0.001) and HD95 (p < 0.001). Pairwise comparisons followed by Bonferroni correction showed that ProRSeg++ remained significantly more accurate than all baseline methods (p < 0.001) for both accuracy metrics. It was also more accurate than ProSeg for liver using the DSC metric (p = 0.0007) as well as for the small bowel using both DSC (p = 0.016) suggesting that combining information from prior treatment fractions as an ensemble improves accuracy for some of the organs. Significance test results after Bonferroni corrections are shown in Supplementary Table 7.
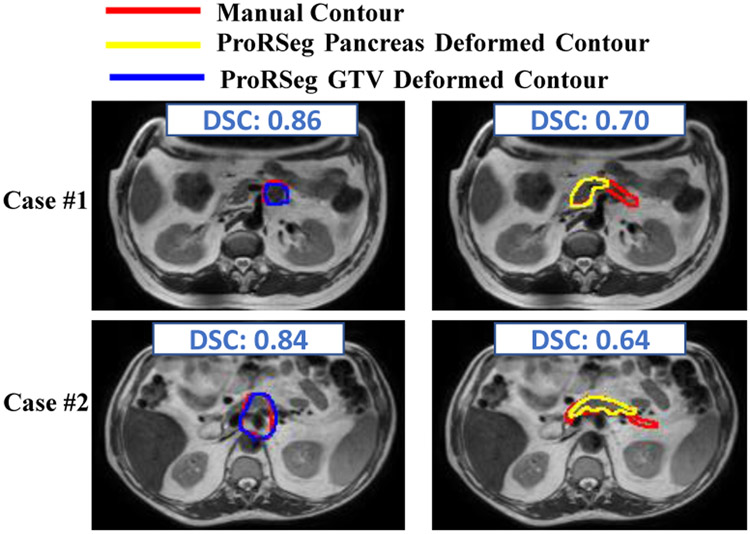
Finally, the ability of the registration subnetwork (RRN) of ProRSeg to produce segmentations of structures not included in the training of the segmentation subnetwork was evaluated by applying registration based segmentation propagation for whole pancreas and the gross tumor volume on a subset of 5 patients. RRN segmentations were compared against rigidly propagated segmentation. RRN segmentations improved the accuracy of rigidly propagated GTV from 0.64 ± 0.23 to 0.73 ± 0.16 and for the whole pancreas from 0.66 ± 0.15 to 0.70 ± 0.07, indicating ability of ProRSeg to generate segmentations even for structures never used in the network training. Figure 4 shows two representative examples with RRN propagated segmentations and manual delineations. RRN propagated the segmentations for GTV with reasonable accuracy as well as for the pancreatic head but resulted in a worse accuracy for narrower sections and tail regions of the pancreas. Equivalence test was performed to compare the accuracies of pancreas and GTV segmentations using two independent one-sided test method with unequal variances36 to determine if the accuracies were within a DSC of 0.1. Analysis was performed using two one-sided null hypothesis t-tests, which showed that the results were equivalent (p = 0.035). Furthermore, a two-sided t-test of comparing the means also showed no significant difference in accuracies (p = 0.32).
Figure 4:
RRN propagated segmentations for GTV and pancreas on two representative cases.
III.B. Segmentation consistency with varying organ configurations
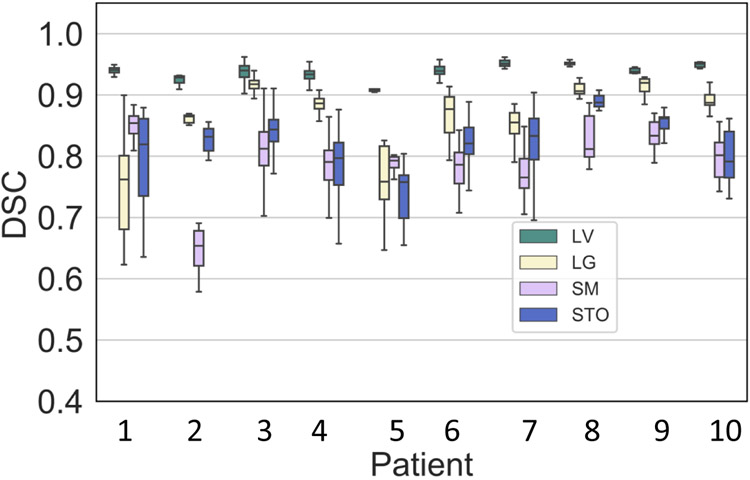
Figure 5 shows the DSC variability for each patient when using all possible combination of treatment fraction MRIs as target and moving image pairs, instead of just aligning consecutive treatment fraction MRIs. This test was performed to evaluate the robustness of segmentation to anatomic configuration of the prior moving image. The median was under 6% for all organs with lowest observed for the liver (median of 0.45%, inter-quartile range [IQR] of 0.31% to 0.63%) and the highest observed for small bowel (median of 4.54%, IQR of 3.77% to 5.26%). Stomach-duodenum (median of 4.04%, IQR of 3.77% to 5.26%) had the second highest and large bowel had relatively smaller variation (median of 1.39%, IQR of 0.61% to 2.66%) than both small bowel and stomach-duodenum. The highest overall variation for all organs (combined average of 6.60% was observed for patient P4 (see Supplemental Table 4) due to large variability in the segmentation of stomach-duodenum ( of 11.02%). This specific patient MRI depicted appearance variability due to differences in stomach filling in one of the treatment fractions (3rd row of Figure 2). All the remaining patients were treated on empty stomach. Four patients had a exceeding 5% for small bowel and stomach-duodenum, 2 such patients for large bowel, and none for liver.
Figure 5:
Segmentation consistency for all analyzed patients measured using all possible patient-specific pairs (any prior treatment fraction to a current fraction for a given patient) for producing GI OAR segmentations.
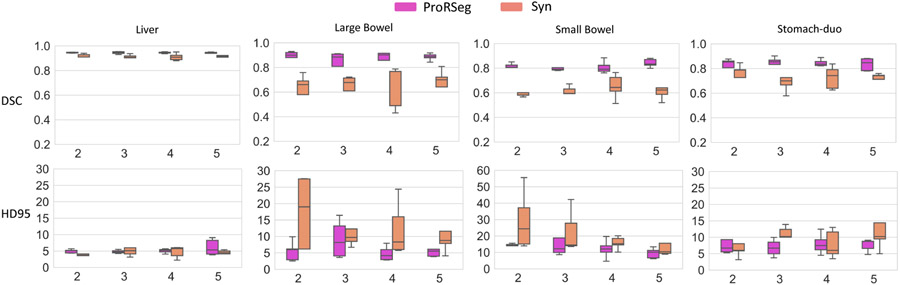
Figure 6 depicts the variability in segmentation accuracies measured using DSC and HD95 across the treatment fractions for the GI OARs. Results produced by iterative deformable image registration using SyN35 is also shown for comparison purposes. As shown, ProRSeg shows smaller variability in the segmentation accuracies across the treatment fractions for the analyzed patients compared to the SyN method. Kruskal-Wallis tests of the segmentation accuracies computed across the different fractions showed no difference in DSC (liver: p=0.23, large bowel: p=0.88, small bowel: p = 0.18, stomach: p = 0.46) and HD95 (liver: p = 0.45, large bowel: p = 0.83, small bowel: p = 0.67, stomach: p = 0.65) with ProRSeg method. These results show that ProRSeg generates consistent GI OAR segmentations across the treatment fractions.
Figure 6:
Longitudinal variability of segmentation accuracy (DSC and HD95) for ProRSeg and SyN when applied for sequential alignment of treatment fractions as used in the clinic.
III.C. Consistency and smoothness of MR-MR DIR
ProRSeg produced smooth deformations, which were within the accepted range of 1% of the folding fraction21,22 (Table 2). Higher values of and the folding fraction compared to SyN35 and Voxelmorph17 are expected because ProRSeg allows for more deformation needed to better align the GI organs. The coefficient of variation for the displacement in three directions (x, y, and z) for small bowel, large bowel, and the stomach-duodenum are shown in Table 2. Liver was excluded in this analysis because only stomach-duodenum, small and large bowel exhibit large deformations and appearance changes. As shown, ProRSeg resulted in the least coefficient of variation in the measured displacements for all three organs, which indicates its ability to produce more consistent registrations. The organ displacements measured in all three directions using ProRSeg and other methods are shown in Supplementary Table 5 and Supplementary Figure 1. ProRSeg measured displacement was the largest for small bowel (x median of 4.92 mm, inter-quartile range [IQR] of 2.31 mm to 8.80 mm; y median of 3.21 mm, IQR of 1.58 mm to 5.48 mm; z median of 4.06 mm, IQR of 2.67 mm to 5.57 mm).
Table 2:
Mean and standard deviation of MR-MR DIR smoothness ( and ) and consistency (CV of displacement). CV per patient is ratio of standard deviation in displacements to the mean displacements for each patient.
| Method | LG Bowel (CV %) | SM Bowel (CV %) | Stomach-Duo (CV %) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SyN35 | 0.04 | 0.00 | 1.52 | 1.16 | 1.37 | 1.37 | 1.29 | 1.56 | 1.30 | 1.32 | 1.29 |
| 0.01 | 0.25 | 0.06 | 0.13 | 0.10 | 0.11 | 0.22 | 0.18 | 0.20 | 0.12 | ||
| Voxelmorph17 | 0.06 | 0.00 | 0.94 | 0.89 | 1.00 | 0.84 | 0.85 | 0.92 | 0.78 | 0.78 | 0.92 |
| 0.01 | 0.05 | 0.14 | 0.42 | 0.17 | 0.06 | 0.42 | 0.10 | 0.18 | 0.51 | ||
| UResNet16 | 0.09 | 0.00 | 0.81 | 0.80 | 0.81 | 0.83 | 0.80 | 0.75 | 0.76 | 0.77 | 0.83 |
| 0.03 | 0.21 | 0.16 | 0.30 | 0.11 | 0.17 | 0.29 | 0.14 | 0.19 | 0.38 | ||
| ProRSeg | 0.18 | 0.071 | 0.71 | 0.81 | 0.75 | 0.80 | 0.80 | 0.68 | 0.75 | 0.73 | 0.81 |
| 0.03 | 0.20 | 0.15 | 0.29 | 0.03 | 0.13 | 0.27 | 0.04 | 0.16 | 0.36 | ||
III.D. Ablation experiments:
Accuracies computed by combination of the losses and network design are shown in Table 4. As shown, RRN segmentations were less accurate than RSN, clearly indicating that a registration-segmentation network increases accuracy. The importance of multi-tasked network optimization is shown by the reduced accuracy when removing the segmentation consistency loss. Similarly, joint optimization of the networks using RRN provided spatial prior with segmentation loss applied to RSN increased accuracy for hard to segment small and large bowel and stomach-duodenum. However, the segmentation loss applied to RSN was more critical than RRN provided spatially aligned priors. Finally, removing the CLSTM from RSN lowered accuracy for all analyzed organs. Similarly, the use of RRN without CLSTM (row 2 of Table 3), resulted in the largest drop in accuracy.
Table 4:
Ablation experiments performed using MRI for GI OAR segmentation.
| Method | Liver | LG Bowel | SM Bowel | Stomach | |||
|---|---|---|---|---|---|---|---|
| Seg consistency | Spatial prior | Reg-based seg | CLSTM | ||||
| × | ✓ | ✓ | ✓ | 0.91±0.03 | 0.75±0.13 | 0.69±0.06 | 0.76±0.08 |
| ✓ | ✓ | ✓ | × | 0.90±0.03 | 0.74±0.13 | 0.68±0.06 | 0.75±0.08 |
| ✓ | ✓ | ✓ | ✓ | 0.91±0.03 | 0.78±0.11 | 0.70±0.08 | 0.78±0.06 |
| × | ✓ | × | ✓ | 0.93±0.02 | 0.82±0.08 | 0.74±0.08 | 0.78±0.11 |
| ✓ | ✓ | × | × | 0.93±0.02 | 0.83±0.08 | 0.75±0.08 | 0.79±0.11 |
| ✓ | × | × | ✓ | 0.93±0.02 | 0.84±0.08 | 0.76±0.07 | 0.79±0.11 |
| × | × | × | ✓ | 0.91±0.04 | 0.74±0.11 | 0.67±0.08 | 0.74±0.16 |
| ✓ | ✓ | × | ✓ | 0.94±0.02 | 0.86±0.08 | 0.78±0.07 | 0.82±0.05 |
Table 3:
Segmentation accuracy (mean and standard deviation) of ProRSeg trained using cross-entropy loss(default) and DSC loss applied to T2-w MRI. LG bowel: Large bowel, SM bowel: small bowel, Sto-Duo: stomach-duodenum.
*: p < 0.05, +: p < 0.01, ‡: p < 0.001.
| Method | DSC ↑ | HD95 mm ↓ | ||||||
|---|---|---|---|---|---|---|---|---|
| Liver | LG Bowel | SM Bowel | Sto-Duo | Liver | LG Bowel | SM Bowel | Sto-Duo | |
| ProRSeg Dice | 0.94±0.02 | 0.87±0.06 | 0.77±0.07 | 0.81±0.06 | 5.85±1.10 | 6.84±5.14 | 12.00±3.64 | 8.65±3.40 |
| ProRSeg | 0.94±0.02 | 0.86±0.08 | 0.78±0.07 | 0.82±0.05 | 5.69±1.72 | 7.00±5.14 | 12.11±5.30 | 8.11±3.54 |
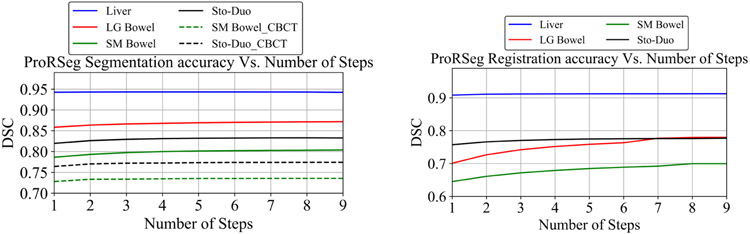
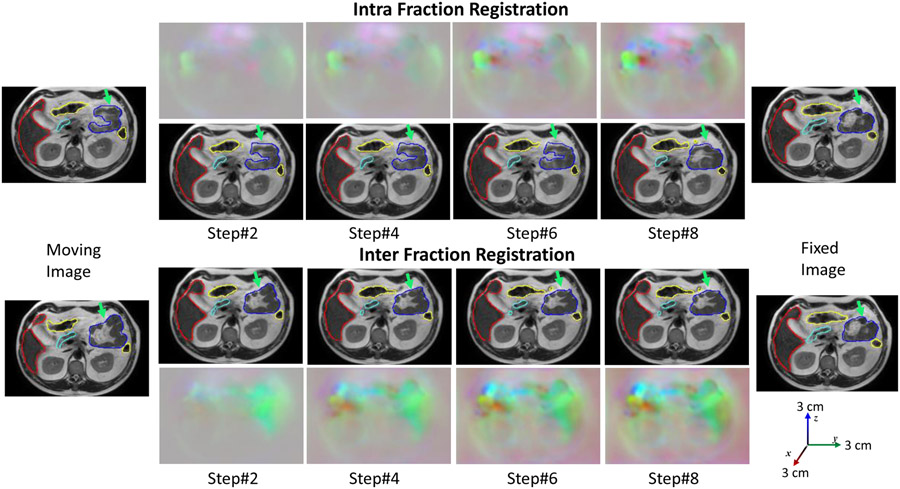
Figure 7 shows the segmentation accuracy changes due to increasing number of CLSTM steps used in the RRN and RSN networks. As shown, when using RRN to generate segmentations, there was no benefit in increasing the number of CLSTM steps beyond 4. On the other hand, increasing the CLSTM steps in the RSN continued to improve segmentation accuracy for small and large bowel. Figure 8 shows segmentations produced with increasing number of CLSTM steps for a representative case in both the intra-fraction and inter-fraction registration scenario. As seen, the displacements or DVF are progressively refined with marked displacements occurring during at different steps for the various organs.
Figure 7:
Impact of number of CLSTM steps used for RRN and RSN on segmentation accuracy.
Figure 8:
Progressive deformation with segmentations produced with ProRSeg shown for aligning intra-fraction (pre-treatment and post-treatment MRI after fraction 1) and inter-fraction (pre-treatment. fraction 1 to pre-treatment fraction 2) for a representative patient.
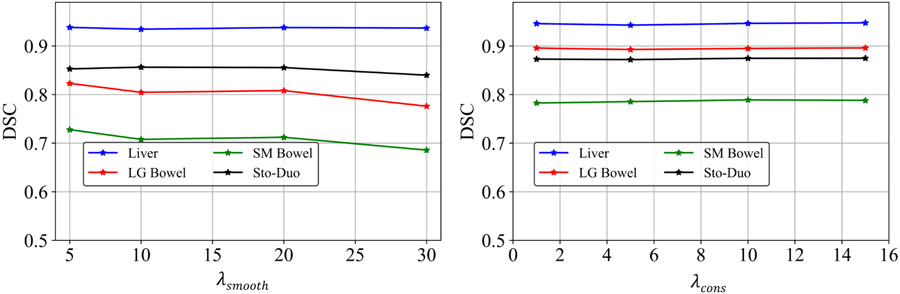
Figure. 9 shows the validation accuracy for the analyzed four organs at risk using a subset of 3 patients with 5 daily treatment MRIs, with the range of analyzed hyperparameters for optimizing the network, namely and . As shown, the accuracies were stable with and showed a small variation for . Specifically, small resulted in highly unrealistic deformations, whereas increasing values reduced the amount of deformations. Accuracy decreased beyond of 20, and hence, it was selected for the analysis.Finally, the accuracies for the various organs were similar for ProRSeg optimized using cross-entropy and Dice loss, indicating that either one of these losses were a good choice for optimizing the segmentation sub-network (Table 3).
Figure 9:
The accuracy with different and . We used the in all the experiments.
III.E. ProRSeg applied to registration (planning CT to CBCT) based CBCT segmentation
We next evaluated whether ProRSeg was able to generate segmentation of stomach-duodenum and small bowel from CBCT images. Table 5 shows a comparison of segmentation accuracies against the SyN35, Voxelmorph17, and a previously published method using this same dataset37 and which combined deep learning to learn the momentum parameters to drive the LDDMM. Kruskal-Wallis test showed a significant difference in both DSC and HD95 (p < 0.001) for all analyzed methods for both organs. Pairwise comparisons followed by Bonferroni correction showed that ProRSeg was significantly more accurate than SyN for both organs (p < 0.001 for DSC and HD95), Voxelmorph (stomach duodenum p< 0.001 for DSC and p=0.019 for HD95, small bowel p< 0.001 for DSC and p=0.031 for HD95), nnUnet for both organs (p < 0.001 for DSC and HD95), and UResNet for both organs (p < 0.001 for DSC , but not significantly different for HD95). The analysis with CBCT clearly shows that using deep learning registration increases accuracy over segmentation only nnUnet method3 as seen for both analyzed organs using both metrics with UResNet (p< 0.001), and Voxelmorph (p< 0.001). On the other hand, iterative registration based SyN significantly outperformed nnUnet with one of the two metrics but not both (stomach duodenum p= 0.25 for DSC, p< 0.001 for HD95, small bowel p= 0.005 for DSC, p= 0.25 for HD95). Representative examples from two patients showing segmentations produced by the various methods are in Figure 10. As shown, ProRSeg closely followed expert delineation compared to SyN35 and Voxelmorph17. nnUnet3 resulted in over segmentation for the small bowel and under segmentation for the stomach duodenum in both cases.
Table 5:
Segmentation accuracy of various methods applied to CBCT scans. SM Bowel: Small bowel; Stomach-Duo: Stomach duodenum. □ HD95 results were not reported. °: p < 0.05, *: p < 0.01, **: p < 0.001.
| Method | DSC ↑ | HD95 mm ↓ | ||
|---|---|---|---|---|
| SM Bowel | Stomach-Duo | SM Bowel | Stomach-Duo | |
| SyN35 | 0.55±0.04** | 0.67±0.03** | 15.87±2.63** | 19.52±8.82** |
| Voxelmorph17 | 0.65±0.04** | 0.73±0.03** | 11.43±3.03* | 13.35±1.81* |
| Han et.al 37 □ | 0.71±0.11 | 0.76±0.11 | NA | NA |
| nnUnet3 | 0.49±0.06** | 0.59±0.10** | 26.97±3.97** | 22.04±4.65** |
| UResNet16 | 0.68±0.03** | 0.74±0.03** | 12.79±1.75 | 10.97±3.10 |
| ProRSeg | 0.74±0.02 | 0.77±0.03 | 10.05±2.67 | 9.68±2.67 |
Figure 10:
Segmentations from CBCT produced on two representative patients using the various methods.
III.F. Proof of principle application of ProRSeg to compute accumulated dose to GI OARs
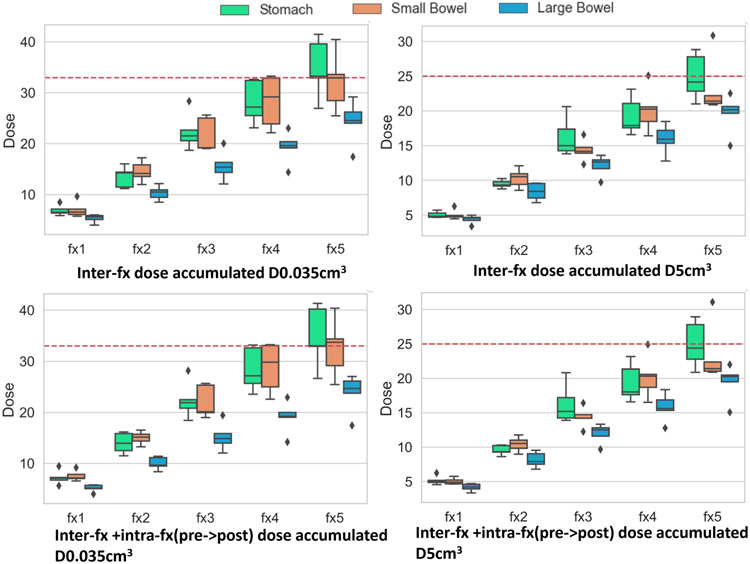
Figure 11 shows the accumulated dose over the course of 5 fractions to the GI OARs without and with intra-fraction dose accumulation. Dose accumulation was performed by sequential alignment of the treatment fraction images and daily fraction doses (scaled to 5 fractions). DVF after each deformation was used to interfractionally accumulate doses for 5 patients who had daily dose maps available from online replanning. Intra-fraction dose accumulation was accomplished by aligning the pre-treatment MRI with the post-treatment MRI taken after completion of treatment on the same day. The adaptive plan generated on the pre-treatment MRI in each fraction was copied to the post-treatment MRI and the doses were recalculated, which was then used to compute the intrafraction accumulated doses.
Figure 11:
Box plots showing accumulated dose metrics D0.035cm3(left) and D5cm3 (right) for stomach duodenum, small bowel and large bowel from interfraction (top row) and inter + intrafraction (bottom row) accumulated dose of all patients for all 5 fractions. Dotted horizontal line represents the instituitional constraint of 33 Gy (left) for D0.035cm3 and 25 Gy (right) for D5cm3.
The institutional dose constraint or and are also shown (dotted red lines) in Figure 11. Accumulated dose showed dose violation for stomach-duodenum in four out of 5 patients (Supplemental Table 6). Two patients exceeded both dose constraints for (, ; , ). Three out of the five patients also violated dose constraints for the small bowel at fraction 5. However, despite the violation of dose constraints, treatment was well-tolerated in these patients with only one patient (P1) experiencing Grade 1 (mild abdominal pain) acute and late abdominal toxicity38. Comparison of the accumulated doses for the same patients with LDDMM method used in our prior study38 showed that our method produced a higher estimate of the accumulated doses in general. However, it is difficult to verify the dosimetric accuracy of the individual methods at a voxel-level due to lack of known landmarks to measure target registration error. Also, the prior study38 uses manual segmentations of the OARs in both moving and target images for alignment, which makes comparison of the two methods using volume overlap measures such as DSC and HD95 meaningless.
IV. Discussion
In this study, we developed and evaluated a multi-task deep registration and segmentation network called ProRSeg to simultaneously segment and deformably align MRI scans longitudinally during radiation treatment course. ProRSeg performs progressive alignment of images as well as refines segmentations progressively by computing dense pixel-level inference using 3D CLSTM implemented into the encoders of registration and segmentation networks. Our approach shows clear accuracy gains compared to segmentation only 3DUnet4, nnUnet3, registration-based segmentation using iterative35 and deep learning17, and a current simultaneous registration-segmentation method16. ProRSeg was also applicable to segmenting the more challenging CBCT scans and showed a slightly better accuracy than a current deep learning based LDDMM method37 using the same dataset. Ability of ProRSeg to segment on both MRI and CBCT broadens its applicability for radiation treatment planning. Significance testing after adjusting for multiple comparisons showed that ProRSeg significantly outperformed segmentation network nnUnet3, which is inline with prior works that showed improved accuracy when using multi-tasked registration-segmentation networks compared to single task networks14,16,39. The need for using registration is most evident for CBCT, where all the deep registration methods outperformed nnUnet3. On the other hand, iterative registration using SyN35 showed mixed improvement based on the choice of the metric, indicating that a deep learning segmentation is a reasonable approach than iterative registration based segmentation methods.
Additionally, training as a registration-segmentation method allows the method to incorporate organs never used in the training by directly using the registration-subnetwork for propagating segmentations, as shown for the whole pancreas and pancreatic tumor segmentation in a subset of cases. The segmentation accuracy for the pancreatic GTV by contour propagation of 0.73 ± 0.13 achieved by our approach is similar to the previously reported accuracy for pancreatic GTV segmentation from MRI40. As no further refinement following registration propagation was done, the segmentation at the head of pancreas was reasonable but worsened at the narrower sections of the pancreas. Although the GTV segmentation accuracy appeared to be slightly better than pancreas, equivalence tests indicate similar accuracy. One prior work applied to CT-based segmentation reported higher accuracy for pancreas and much lower accuracy for the tumor using a multi-staged and multi-scale segmentation approach41 using CT scans from patients who underwent screening for pancreatic cancers as well as patients with kidney cancers. Their results are thus not directly comparable with ours due to differences in the modality used (CT vs. MRI), registration-based propagation applied to these structures as opposed to segmentation method, and importantly the analysis of LAPC patients who underwent radiation treatment.
ProRSeg also produced consistent segmentations and registrations as shown by low and low coefficient of variation in the computed displacements for organs compared to other methods. Patient-specific analysis of segmentation accuracy variations due to differences in the anatomical configuration of the prior (or moving images) showed that ProRSeg produced variations within a maximum of 10%. The larger variations were observed for more complex organs such as the small bowel and stomach-duodenum. At least one patient exhibited differences in stomach volume and appearance due to stomach contents between treatment fractions. In this regard, appearance and anatomic variabilities not encountered in training were difficult to handle in the testing.
Our analysis showed that ProRSeg produced reasonably accurate GI OAR segmentations exceeding a DSC of 0.80 even for challenging organs such as the small bowel. ProRSeg accuracies are better or comparable to prior published studies applied to different datasets used for MR-Linac treatments8,12,19. It is notable that these published methods required ensembling of segmentations12 from prior treatment fractions or user editing to drive semi-automated semgentations8. ProRSeg does not require user editing or ensembling. Nevertheless, given differences in datasets, number of training and testing sets, and the way in which the organs were segmented, it’s hard to make a head to head comparison of these methods. For example, study by Fu et.al19 separated stomach and duodenum into two distinct structures but combined small and large bowel into one structure, whereas we combined stomach and duodenum as one structure but separated the small and large bowels into two distinct structures, consistent with the treatment planning requirements at our institution and others8,42. Consistent with the findings in a prior study by Zhang et.al12, incorporating prior knowledge from multiple preceding fractions as an ensemble segmentation improved the accuracy for all organs including the small bowel in the later treatment fractions. We will provide our model in the GitHub repository to enable side-by-side comparison by other works upon acceptance for publication. Furthermore, the CBCT analysis was performed using a publicly available dataset by Hong et.al30.
Our results are also consistent with prior multi-task methods14,15,24,43, and clearly showed that the inclusion of an additional segmentation network resulted in a higher accuracy than the registration-based segmentation alone. Furthermore, ablation tests clearly showed that spatially aligned priors provided by the registration increased accuracy of segmentation. Finally, incorporating supervised segmentation losses, which is easier to obtain than DVF as ground truths also improved accuracy.
In addition to segmentation, our method also showed the ability to deformably align images and preliminary feasibility to compute dose accumulation to organs. The computed displacements for organs showed largest median displacement exceeding 4mm for small bowel, which is far below the computed displacements of 10 mm reported using the LDDMM method when applied to a subset of the same patients in a prior study38. We believe the differences resulted from the additional number of patients included in our study as well as from the averaging of the intra and inter-fraction displacements when computing the overall median displacements. Importantly, our analysis of the dose accumulation showed that ProRSeg measured dose violations were consistent with the findings using LDDMM, albeit ProRSeg produced a higher estimate of accumulated dose for the same patients than LDDMM38 (see Supplementary Table 6). However, it is difficult to assess the voxel-level registration accuracy of either method in order to ascertain the dose accumulation accuracy due to lack of known and visible landmarks to measure target registration error, which also represents a limitation of our study. Robust estimate of TRE for these organs would potentially require synthesizing digital phantom with known landmarks, which was not in the scope of the current study. Also, the prior study38 used manual segmentations of OARs in both moving and fixed image volumes for computing the alignment, which makes comparison of these two methods using volume overlap measures meaningless.
Our study is limited by lack of set aside testing and lack of large training set for further improving and evaluating the accuracy of the method as well as by the lack of well defined landmarks for measuring target registration error to evaluate registration. Nevertheless, our analysis indicates ability to perform both consistently accurate segmentation and dose accumulation on pancreatic cancer patients using a computationally fast method, thus allowing the use of accumulated doses for potential treatment adaptation in place of the currently used conservative dose constraints.
V. Conclusion
A multi-tasked, progressive registration segmentation deep learning approach was developed for segmenting upper GI organs from MRI. Our approach showed ability to produce consistently accurate segmentations and consistent deformable image registration of longitudinal treatment MRI. It was also applicable for segmenting GI organs from cone-beam CT images.
Supplementary Material
Acknowledgments
This research was partially supported through the NIH/NCI Cancer Center Support Grant (grant number P30 CA00874) who had no involvement in the study design; the collection, analysis and interpretation of data; the writing of the report; and the decision to submit the article for publication.
VII. Reference
- 1.Glide-Hurst CK, Lee P, Yock A, Olsen J, Cao M, Siddiqui F, Parker W, Doemer A, Rong Y, Kishan A, Benedict S, Li X, Erickson B, Sohn J, Xiao Y, and Wuthrick E, “Adaptive radiation therapy (ART) strategies and technical considerations: A state of the ART review from NRG oncology,” Int J Radiat Oncol Biol Phys, vol. 109, no. 4, pp. 1054–1075, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Henke L, Kashani R, Robinson C, Curcuru A, DeWees T, Bradley J, Green O, Michalski J, Mutic S, Parikh P, and Olsen J, “Phase I trial of stereotactic MR-guided online adaptive radiation therapy (SMART) for the treatment of oligometastatic or unresectable primary malignancies of the abdomen,” Radiother Oncol, vol. 126, no. 3, pp. 519–526, 2018. [DOI] [PubMed] [Google Scholar]
- 3.Isensee F, Jaeger PF, Kohl SA, Petersen J, and Maier-Hein KH, “nnu-net: a self-configuring method for deep learning-based biomedical image segmentation,” Nature methods, vol. 18, no. 2, pp. 203–211, 2021. [DOI] [PubMed] [Google Scholar]
- 4.Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in MICCAI, 2015, pp. 234–241. [Google Scholar]
- 5.Gibson E, Giganti F, Hu Y, Bonmati E, Bandula S, Gurusamy K, Davidson B, Pereira SP, Clarkson MJ, and Barratt DC, “Automatic multi-organ segmentation on abdominal ct with dense v-networks,” IEEE Transactions on Medical Imaging, vol. 37, no. 8, pp. 1822–1834, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yuhua C, Dan R, Jiayo X, Lixia W, Bin S, Rola S, Wensha Y, Debiao L, and Zhaoyang F, “Fully automated multiorgan segmentation in abdominal magnetic resonance imaging with deep neural networks,” Med Phys, vol. 47, no. 10, pp. 4971–4982, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hatamizadeh A, Tang Y, Nath V, Yang D, Myronenko A, Landman B, Roth HR, and Xu D, “Unetr: Transformers for 3d medical image segmentation,” in IEEE/CVF Winter Conf. Applications of Computer Vision, 2022, pp. 1748–1758. [Google Scholar]
- 8.Ying Z, Ying L, Jie D, Asma A, Eric P, Ergun A, H. William A., Beth E, and Allen LX, “A prior knowledge guided deep learning based semi-automatic segmentation for complex anatomy on mri,” Intl J of Radiat Oncol, Biol, Physics, vol. 22, pp. S0360–3016, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jiang J, Tyagi N, Tringale K, Crane C, and Veeraraghavan H, “Self-supervised 3d anatomy segmentation using self-distilled masked image transformer (smit),” International Conference on Medical Image Computing and Computer-Assisted Intervention, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Velec M, Moseley J, Svenson S, Hårdemark B, Jaffary D, and Brock K, “Validation of biomechanical deformable image registration in the abdomen, thorax, and pelvis in a commercial radiotherapy treatment planning system,” Med Phys, vol. 44, no. 7, pp. 3407–3417, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Van de Lindt T, Fast M, Van Kranen S, Nowee M, Jansen E, Van der Heide U, and Sonke J, “MRI-guided mid-position liver radiotherapy: Validation of image processing and registration steps,” Radiotherapy and Oncology, vol. 138, pp. 132–140, 2019. [DOI] [PubMed] [Google Scholar]
- 12.Zhang Y, Paulson E, Lim S, Hall W, Ahunbay E, Mickevicius N, Straza M, Erickson B, and Li A, “A patient-specific autosegmentation strategy using multi-input deformable image registration for magnetic resonance imaging–guided online adaptive radiation therapy: A feasibility study,” Adv Radiat Oncol, vol. 5, no. 6, pp. 1350–1358, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ashburner J, “A fast diffeomorphic image registration algorithm,” Neuroimage, vol. 38, no. 1, pp. 95–113, 2007. [DOI] [PubMed] [Google Scholar]
- 14.Xu Z and Niethammer M, “Deepatlas: Joint semi-supervised learning of image registration and segmentation,” in MICCAI, 2019, pp. 420–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.He Y, Li T, Yang G, Kong Y, Chen Y, Shu H, Coatrieux J-L, Dillenseger J-L, and Li S, “Deep complementary joint model for complex scene registration and few-shot segmentation on medical images,” in ECCV, vol. 1, 2020. [Google Scholar]
- 16.Estienne T, Vakalopoulou M, Christodoulidis S, Battistela E, Lerousseau M, Carre A, Klausner G, Sun R, Robert C, Mougiakakou S et al. , “U-resnet: Ultimate coupling of registration and segmentation with deep nets,” in MICCAI, 2019, pp. 310–319. [Google Scholar]
- 17.Balakrishnan G, Zhao A, Sabuncu MR, Guttag J, and Dalca AV, “Voxelmorph: a learning framework for deformable medical image registration,” IEEE Trans. Med Imaging, vol. 38, no. 8, pp. 1788–1800, 2019. [DOI] [PubMed] [Google Scholar]
- 18.Mok TC and Chung A, “Fast symmetric diffeomorphic image registration with convolutional neural networks,” in IEEE CVPR, 2020, pp. 4644–4653. [Google Scholar]
- 19.Fu Y, Liu S, Li H, Li H, and Yang D, “An adaptive motion regularization technique to support sliding motion in deformable image registration,” Med Phys, vol. 45, no. 2, pp. 735–747, 2018. [DOI] [PubMed] [Google Scholar]
- 20.Papiez B, Heinrich M, Fehrenbach J, Risser L, and Schnabel J, “An implicit sliding-motion preserving regularisation via bilateral filtering for deformable image registration,” Med Image Analysis, vol. 18, no. 8, pp. 1299–1311, 2014. [DOI] [PubMed] [Google Scholar]
- 21.de Vos BD, Berendsen FF, Viergever MA, Sokooti H, Staring M, and Išgum I, “A deep learning framework for unsupervised affine and deformable image registration,” Medical Image Anal., vol. 52, pp. 128–143, 2019. [DOI] [PubMed] [Google Scholar]
- 22.Zhao S, Dong Y, Chang EI, Xu Y et al. , “Recursive cascaded networks for unsupervised medical image registration,” in CVPR, 2019, pp. 10 600–10 610. [Google Scholar]
- 23.Sandkühler R, Andermatt S, Bauman G, Nyilas S, Jud C, and Cattin PC, “Recurrent registration neural networks for deformable image registration,” NeurIPS, vol. 32, pp. 8758–8768, 2019. [Google Scholar]
- 24.Jiang J and Veeraraghavan H, “One shot PACS: Patient specific anatomic context and shape prior aware recurrent registration-segmentation of longitudinal thoracic cone beam CTs,” IEEE Trans Med Imaging, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shi X, Chen Z, Wang H, Yeung D-Y, Wong W-K, and Woo W.-c., “Convolutional LSTM network: A machine learning approach for precipitation nowcasting,” arXiv preprint arXiv:1506.04214, 2015. [Google Scholar]
- 26.Beljaards L, Elmahdy MS, Verbeek F, and Staring M, “A cross-stitch architecture for joint registration and segmentation in adaptive radiotherapy,” in Med. Imaging with Deep Learning, 2020, pp. 62–74. [Google Scholar]
- 27.Alam S, Veeraraghavan H, Tringale K, Amoateng E, Subashi E, Wu A, Crane C, and Tyagi N, “Inter- and intrafraction motion assessment and accumulated dose quantification of upper gastrointestinal organs during magnetic resonance-guided ablative radiation therapy of pancreas patients,” Phys Imaging Radiat Oncol, vol. 21, pp. 54–61, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Salehi M, Sadr A, Mahdavi S, Arabi H, Shiri I, and Reiazi R, “Deep learning-based non-rigid image registration for high-dose rate brachytherapy in inter-fraction cervical cancer,” Journal Digital Imaging, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Han X, Hong J, Reyngold M, Crane C, Cuaron J, Hajj C, Mann J, Zinovoy M, Greer H, Yorke E, Mageras G, and Neithammer M, “Deep learning based image registration and automatic segmentation of organs-at-risk in cone-beam ct scans from high-dose radiation treatment of pancreatic cancer,” Med Phys, vol. 28, no. 6, pp. 3084–3095, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hong J, Reyngold M, Crane C, Cuaron J, Hajj C, Mann J, Zinovoy M, Yorke E, LoCastro E, Apte AP et al. , “Ct and cone-beam ct of ablative radiation therapy for pancreatic cancer with expert organ-at-risk contours,” Scientific Data, vol. 9, no. 1, p. 637, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tyagi N, Liang J, Burleson S, Subhashi E, Godoy S, and Tringale K. e., “Feasibility of ablative stereotactic body radiation therapy of pancreas cancer patients on a 1.5 tesla magnetic resonance-linac system using abdominal compression,” Phys Imaging Radiat Oncol, vol. 19, pp. 53–59, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Apte A, O. J Wang Y, and Deasy J, “CERR: New tools to analyze image registration precision,” p. 3673, 2012. [DOI] [PubMed] [Google Scholar]
- 33.Jaderberg M, Simonyan K, Zisserman A, and Kavukcuoglu K, “Spatial transformer networks,” arXiv preprint arXiv:1506.02025, 2015. [Google Scholar]
- 34.Dalca AV, Balakrishnan G, Guttag J, and Sabuncu MR, “Unsupervised learning of probabilistic diffeomorphic registration for images and surfaces,” Medical Image Anal., vol. 57, pp. 226–236, 2019. [DOI] [PubMed] [Google Scholar]
- 35.Avants BB, Epstein CL, Grossman M, and Gee JC, “Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain,” Medical Image Anal., vol. 12, no. 1, pp. 26–41, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lakens D, “Equivalence tests: A practical primer for T tests, correlations, and meta-analyses,” Soc Psychol Personal Sci, vol. 8, no. 4, pp. 355–362, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Han X, Hong J, Reyngold M, Crane C, Cuaron J, Hajj C, Mann J, Zinovoy M, Greer H, Yorke E et al. , “Deep-learning-based image registration and automatic segmentation of organs-at-risk in cone-beam ct scans from high-dose radiation treatment of pancreatic cancer,” Medical Physics, vol. 48, no. 6, pp. 3084–3095, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Alam S, Zhang P, Zhang S-Y, Chen I, Rimner A, Tyagi N, Hu Y-C, Lu W, Yorke E, Deasy J, and Thor M, “Early prediction of acute esophagitis for adaptive radiation therapy,” Int J Radiat Oncol Bio Phys, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Elhmahdy MS, Jagt T, Zinkstok RT, Qiao Y, Shahzad R, Sokooti H, Yousefi S, Incrocci L, Marijnen C, Hoogeman M, and Staring M, “Robust contour propagation using deep learning and image registration for online adaptive proton therapy of prostate cancer,” Med Physics, vol. 46, no. 8, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liang Y, Schott D, Zhang Y, Wang Z, Nasief H, Paulson E, Hall W, Knechtges P, Erickson B, and Li A, “Auto-segmentation of pancreatic tumor in multi-parametric mri using deep convolutional neural networks,” Radiotherapy and Oncol, vol. 145, pp. 193–200, 2020. [DOI] [PubMed] [Google Scholar]
- 41.Zhu Z, Xia Y, Xie L, Fishman EK, and Yuille AL, “Multi-scale coarse-to-fine segmentation for screening pancreatic ductal adenocarcinoma,” in Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, Shen D, Liu T, Peters TM, Staib LH, Essert C, Zhou S, Yap P-T, and Khan A, Eds. Cham: Springer International Publishing, 2019, pp. 3–12. [Google Scholar]
- 42.Ding J, Zhang Y, Amjad A, Xu J, Thill D, and Li X, “Automatic contour refinement for deep learning auto-segmentation of complex organs in mri-guided adaptive radiation therapy,” Adv Radiat Oncol, vol. 7, no. 5, p. 100968, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhou B, Augenfeld Z, Chapiro J, Zhou SK, Liu C, and Duncan JS, “Anatomy-guided multimodal registration by learning segmentation without ground truth: Application to intraprocedural CBCT/MR liver segmentation and registration,” Medical Image Anal., vol. 71, p. 102041, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.