Modeling of Learning Processes Using Continuous-Time Markov Chain for Virtual-Reality-Based Surgical Training in Laparoscopic Surgery

Abstract

Recent usage of Virtual Reality (VR) technology in surgical training has emerged because of its cost-effectiveness, time savings, and cognition-based feedback generation. However, the quantitative evaluation of its effectiveness in training is still not studied thoroughly. This paper demonstrates the effectiveness of a VR-based surgical training simulator in laparoscopic surgery and investigates how stochastic modeling represented as Continuous-time Markov-chain (CTMC) can be used to explicit the training status of the surgeon. By comparing the training in real environments and in VR-based training simulators, the authors also explore the validity of the VR simulator in laparoscopic surgery. The study further aids in establishing learning models of surgeons, supporting continuous evaluation of training processes for the derivation of real-time feedback by CTMC-based modeling.

I. Introduction

Surgeons require practicing skills ranging from simple wound closure to highly complex diagnostic and therapeutic procedures. Thus, surgical training has been on the verge of a seismic shift in how one can give the level of surgical training expected of a modern surgeon. Surgical training has traditionally been an opportunity-based learning strategy centered on an operating room apprenticeship. This “see one, do one, teach one” approach to surgical training was commonly typified by this Halstedian method (Higgins et al., [31]). As a result of this apprenticeship model, surgical training was extended to gather enough surgical experience to reach a subjective degree of operative experience, which is time-consuming and costly (Franzese and Stringer [15]).

Surgical education has changed to overcome these limitations by adopting new technology such as virtual reality (VR). The adoption of VR has seen a surge of interest for training surgical skills both inside and outside of the operating room (Seymour [68]). Incorporating VR with the physics-level of simulations for surgical operations allows the transfer of techniques learned in a skills lab to the operating room. Moreover, artificial tissue movements and the movements of surgical tools generated in computer simulation would be accessible to trainees. In laparoscopic surgery, these technical skills often lead to a prolonged learning curve. Thus, one can investigate the advantages of using VR-based training models in laparoscopic surgery, which can provide an objective assessment of technical ability, while retaining realism, and measuring self-confidence in a controlled laboratory setting. The VR-based training system also enables generating a large set of training data, stimulating research to apply advanced statistical methods and machine learning techniques for learning model investigation as Rogers et al. studied [62].

Although VR-based training has the potential to contribute significant advantages in surgical training for new skills and procedures, quantitative evaluation of skills acquired within the simulated environment is still limited. Thus, this study aimed to investigate the learning curve of training in a real environment versus in a VR environment, identifying any competitive advantage of VR-based training. The second goal was to demonstrate the use of continuous assessments of surgical skills during training for identifying surgical skill deficiencies to provide targeted and individualized feedback. To answer our research questions, we have studied four different learning process methods: Hidden-Markov Models (HMM), learning curves, Generalized Estimating Equation (GEE), and Cumulative Sum (CUSUM). After investigating other modeling methods, the authors found the competitive advantage of using the Continuous-Time Markov Chain (CTMC) over others. Therefore, the authors proposed a new approach to model the learning process using Continuous Time Markov Chains (CTMC) by capturing learning variability, sudden accuracy drops, and simultaneous consideration of time and accuracy together. The proposed model was validated by training data for a simulated laparoscopic surgery skill.

The remainder of this paper is as follows. Section II shows the literature review results of how VR has been used in general surgery and laparoscopic surgery while summarizing the learning curve models in surgical training. Section III utilizes the traditional learning model via learning curves to compare laparoscopic surgery practices in real versus VR-based environments. Section IV proposes a new learning modeling approach using CTMC, examining its merits compared to the traditional one. Section V concludes with observations and findings from the proposed approach.

II. Literature Review

The traditional surgical training methods have supported generations of surgeons, but it is not enough due to cost effectiveness, time management, and the procedure’s safety. This forced surgeons to examine the possibility of incorporating an advanced technology like VR to tackle these challenges [28, 34, 44, 59, 65, 81]. It was also shown that patients had excellent outcomes when the surgical procedure was simulated through VR first the operation was started [33, 35, 69, 77]. Moreover, VR-based training provided efficient guidance for trainees [21, 31, 47] and revealed the group using VR training showed higher accuracy scores [17, 20, 37, 55, 68], less operating time [4, 17, 50, 80, 85], and a better understanding of procedural knowledge [22, 40, 48, 78]. Researchers also revealed that surgical platforms consisting of interactive user interface and guidance reduce complexity in getting used to VR as a training tool [8, 12, 14, 42, 82]. Table I summarizes how those benefits of VR-based training are utilized in each type of surgery.

TABLE I.

Recent Development of VR in Surgical Training

Type of Surgery	Methodology	References
General Surgery	Comparison: Experimental vs Control groups	Aggarwal et al. (2006) Gurusamy et al. (2008)
	Theoretical studies	Haluck et al. (2000)
	Machine Learning	Kim et al. (2017)
Osteotomy	Comparison: Experimental vs Control groups	Pulijala et al. (2017)
	Theoretical studies	Hsieh et al. (2002), Sayadi et al. (2019)
	Descriptive Statistics	Wilson et al. (2020)
Heart	Theoretical studies	Wang and Wu (2021), Friedl et al. (2002), Falah et al. (2002)
	Comparison: Augmented vs Virtual Reality	Silva et al. (2018)
Brain	Descriptive Statistics	Bracq et al. (2017)
	Comparison: Experimental vs Control groups	Phaneuf et al. (2014), Fried et al. (2010)
Cataract	Comparison: Experimental vs Control groups	Beauchamp et al. (2020), Thomsen et al. (2017), Thomsen et al. (2017)
	Theoretical studies	Lama et al. (2013)
Tendon repair	Comparison: Experimental vs Control groups	Mok et al. (2021)
Neuro	Machine Learning	Schwartz et al. (2019)
	Theoretical studies	Fiani et al. (2020), Alaraj et al. (2011)
Spine	Comparison: Experimental vs Control groups	Luca et al. (2020), Xin et al. (2019)
	Theoretical studies	Pfandler et al. (2017)
Arthroscopy	Theoretical studies	Muller et al. (1995)
	Descriptive Statistics	Gomoll et al. (2007), Gomoll et al. (2008), Jacobsen et al. (2015)

The authors’ literature review is three-fold. Firstly, the authors investigated the advanced role of VR in laparoscopic surgery. Secondly, learning curve approaches in a surgery application are majorly summarized. Lastly, the advanced statistical modeling, such as Hidden Markov Chain (HMM), Generalized Estimating Equation (GEE), and Cumulative Sum (CUSUM) approaches, are also summarized.

2.1. VR-based training in laparoscopic surgery

Reducing operating time and improving the accuracy are two major advantages of using VR-based simulators in laparoscopic surgery. For example, Grantcharov et al. [24–25] showed that VR-based training stimulated learning faster and improved movement scores while reducing errors, while Munz et al. [52] demonstrated that completion time was more rapid by reducing the necessary movements. Aggarwal et al. [1] showed VR shortens the learning curve as a time- and cost-effective training model. Portelli et al. [60] also concluded that VR improves efficiency in the trainee’s surgical practice and improves quality with reduced error rates and improved tissue handling. Gurusamy et al. [26–27] revealed that VR decreased time, errors, and increased accuracy, whereas Larsen et al. [43] verified that using a VR simulator aided trainees’ proficiency as their operation time was halved.

It was also studied that VR-based training could be more accurate than video-based training. Alaker et al. [3] exhibited that a VR-based simulator was more effective than video-based training, while Yiannakopoulou et al. [86] indicated VR could provide alternative means of video-based practicing while improving performance in surgery. Phe et al. [58] and Botden et al. [7] illustrated that a VR simulator could offer better realism and haptic feedback based on trainees’ skill levels. Hart et al. [30] also showed a VR as an essential part of clinical training, supporting trainees to practice surgical tools. Instead, to maximize the efficiency of VR-based training, Aggarwal et al. [2] pointed out that junior trainees were recommended to acquire pre-requisite skill levels before entering an operating room. Table II summarizes and classifies all the work based on the types of design of experiments and methodologies.

TABLE II.

VR-based Surgical Training in Laparoscopic Surgery

Design of Experiments	Methodology	References
VR vs Physical simulator	Descriptive Statistics	Taba et al. (2021)
	Comparison: Experimental vs Control groups	Gurusamy et al. (2009), Papanikolaou et al. (2019)
VR vs real	Descriptive Statistics	Larsen et al. (2009), Munz et al. (2007)
	Machine Learning Comparison: Experimental vs Control groups	Alaker et al. (2016) Grantcharov et al. (2004)
VR vs trad mentoring	Meta-analysis	Gurusamy et al. (2008)
	Meta-analysis & Descriptive Statistics	Portelli et al. (2020)
	Theoretical Studies	Yiannakopoulou et al. (2015), Harta and Karthigasua (2007)
	Descriptive Statistics	Aggarwal et al. (2007)
VR	Descriptive Statistics	Aggarwal et al. (2006)
		Jain et al. (2020)
	Experimental vs Control groups	Phé et al. (2017)
	Machine Learning	Botden et al. (2007)

2.2. Traditional learning curve modeling in surgical training

Developing learning curves requires a proper selection of independent (predictor) and dependent (response) variables to derive general causality. This subsection summarizes relevant work for developing the learning curve and its related parameters in surgical training. Feldman et al. [13] suggested two parameters called learning plateau (intercept) and learning late (slop) while assuming that the improvement of surgical proficiency over time follows an S-curve such as y = a – b/x. These smooth improvement in skill acquisition and performance over trial was also investigated by Bosse et al. [6], provided with high and low-frequency intermittent feedback. Khan et al. [39] instead considered procedural variables, including experiences and supervision levels, to develop a learning curve using logistic regression. Subramonian and Muir [73] investigated responses by measuring surgeons’ skills and techniques whereas Suguita et al. [74] evaluated their average operating time for learning curve development.

Time factors have been heavily considered for the learning curve analysis. Brunckhorst et al. [9] investigated the effect of the time factors on learning curves in VR-based training, whereas Howells et al. [32] examined the time factor affecting the learning curve by showing that even with a time delay (e.g., six months later after the trainees were exposed to the surgical procedure for the first time) in training, repeating it again can improve their proficiency. Uribe et al. [79] also proved that novices initially displayed a steeper learning curve, while Leijte et al. [45] observed a performance delay in minimal invasive surgery compared to robot-assisted surgery.

The other consideration for developing learning curves is classifying trainees into several groups based on their expertise [54]. Papachristofi et al. [53] suggested that learning curves were different based on the trainees’ prior knowledge, whereas Hardon et al. [29] investigated the expertise based on force and motion factors during surgery. Grantcharov et al. [24–25] further investigated that trainers’ proficiency differences could not be captured by changing the function parameters but by requiring different learning kernels. A comprehensive review of learning curve modeling in surgical training was performed by Chan et al. [10]. The challenge of using learning curves is the trainee-specific nature, which requires carefully selecting the curve’s kernel structure for generalization. Moreover, if more than two response variables (e.g., completion time and accuracy) are of interest, then it requires more than two learning curves per trainee. The authors explain the universality of the proposed CTMC-based model in Section 3.

2.3. Other Modeling Methods in Surgical Training

Hidden Markov Models (HMM) are widely used to model the training process in surgery when high-fidelity data is provided. Especially if surgical instrument trajectory data is given, HMM was shown to supports to detect hidden states beyond the movement [46]. The HMM approach was widely used to decompose all the surgical tasks by Rosen et al. [63], which helps to develop objective performance metrics [49]. From the analysis of high-fidelity data, HMM also supports classifying surgeons based on their surgical proficiency [64], and it helps to provide a continuous evaluation by temporal and motion-based analysis [23]. As HMM requires high-resolution data (motion and tracking data) to recognize hidden learning phases, it could be challenging to provide an intuitive and practical learning model to derive the best time to support additional feedback.

Generalized Estimating Equation (GEE) modeling is appropriate when one collects repeated training data per participant by Aggarwal et al. [2], especially the modeler is interested in investigating the covariance structure among predictors. Since GEE identifies the correlation structures in repeated trials, it also supports to demonstrate the interaction effects on proficiency achievement in laparoscopic-guided surgery [38, 87]. GEE can also be used to generate an objective surgical proficiency measure, such as a visual analog scale (VAS), as studied by Zhang et al. [87]. The recent advance in using GEE in surgical training has been studied and comprehensively summarized in the review papers by Chang et al. and Jin et al. [11, 36].

Cumulative-sum (CUSUM) can also be used to demonstrate learning processes. CUSUM was originally designed to detect the small process shift in quality control, but it is also used to magnitude the improvement over the trials [19]. The benefit of using CUSUM in modeling learning processes is to detect learning improvement when the reading in charts exceeds control limits [5, 16]. Sood et al. [72] demonstrated that the learning curve could be estimated using a CUSUM chart, aiding in determining the length of training time, whereas Smith et al. [70] claimed the CUSUM chart itself could support trainees’ learning processes. All the literature review results of different modeling approaches are summarized in Table III.

TABLE III.

Learning Models for Surgical Training

Methodology	References
Generalized Estimating Equation (GEE)	Aggarwal et al. (2007)
	Chang et al., (2020)
	Jin et al. (2021)
	Kauffman (2020)
	Portelli et al. (2020)
	Zhang et al. (2022)
Learning Curves	Chan et al. (2021)
	Feldman et al. (2009)
	Hardon et al. (2021)
	Leijte et al. (2020)
	Wong et al. (2022)
Hidden Markov Models (HMM)	Megali et al. (2006)
	Leong et al. (2006), Gorantla and Esfahani (2019), Rosen et al. (2002), Saravanan and Menold (2022).
Cumulative-Sum (CUSUM)	Fraser et al. (2005)
	Fu et al. (2020)
	Perivoliotis et al (2022)
	Sultana et al. (2019)

As shown in Fraser et al. [16], it also requires separate CUSUM analyses when looking at different criterion levels (e.g., junior, intermediate, and senior in their case). Also, trainees can show a “back and forth” pattern in learning when advancing to the next stage because the trainee requires time to get familiar with the achievement (Feldman et al. [13]). As our learning process is not linear, multiple threshold values are required and it is even possible that the threshold value (δ) itself could be a function of time (δ(t)). To address the variability shown right after the state transition in the learning process, the authors proposed a new approach based on CTMC. Because our proposed CTMC model has two levels (high-level states and sub-states), it can help to keep track of the continuous evaluation of learning processes. The details of our model are explained in Section 3.

III. Traditional Learning Curve-Based Modeling

3.1. Description of Surgical Process for Training

Table IV explains the experimental configuration. The surgical skills training task performed was the intracorporal suturing with knot tying task of the Fundamentals of Laparoscopic Surgery (FLS) curriculum. The task was performed either in a standard FLS box trainer or using the Virtual Basic Laparoscopic Skill Trainer - Suturing Simulator (VBLaST-SS(c)) following the same task procedures [71]. For the task, a Penrose drain is placed on a Velcro strip inside the trainer. The subject uses two needle drivers to feed a needle and suture through two marked targets on the Penrose drain and complete three knots intracorporeally to close a slit in the drain. The task ends after three knots have been completed and the suture has been trimmed. Task completion is limited to 10 min (600 sec). The overall performance score is based on the completion time, error in needle placement, knot security, and slit closure, following the equation published in Korndorffer et al. [41]. The proficiency time was set at 112 sec with deviation from the marked targets of less than 1 mm [66, 71]. Fifteen trainees who were pre-medical or 1^st to 3^rd year medical students participated the training and those participants completed the task for multiple repetitions over 15 days within a three-week period. The study was approved by the University at Buffalo Institutional Review Board under protocols STUDY00000750 and STUDY00004789 and all participants provided written informed consent. Two figures in Fig. 1 illustrate the practice in physical box (in a real environment) and VR-based training.

TABLE IV.

Experimental Configuration

Configuration	Experimental Settings
Number of Trainees	In a Real Environment: 7
	In a VR Environment: 8
Training Environments	Real vs Virtual-Reality (VR)
Measurements	Accuracy vs Completion Time
Analysis	Learning Curve Fitting vs CTMC

Fig. 1.

Practice in physical box trainer (top) versus VR-based training (bottom)

3.2. Learning Process using Learning Curve Fitting

Generally, surgical proficiency is expected to mature as the number of practice trials accumulates. Thus, researchers have developed the relationship between practice trials and surgical ability to demonstrate surgeons’ learning processes. Once researchers have training data with respect to surgical precision and/or time data over the number of trials, one can fit the data to a certain function using different kernels such as polynomial, Gaussian, and sigmoid functions to oblige in classifying trainees into their proficiency levels. The authors have performed polynomial fitting by taking data sets of training accuracy and time in two different surgical training settings: training in a real environment versus in a VR environment. Fig. 2 illustrates four different trainees’ scores over trials, and the red line demonstrates the best-fitted line using the maximum likelihood approach. The degree of 3 polynomial functions ($y={\beta }_3{x}^3+{\beta }_2{x}^2+{\beta }_{1}x+{\beta }_0$) were used to derive the fitted lines.

Fig. 2.

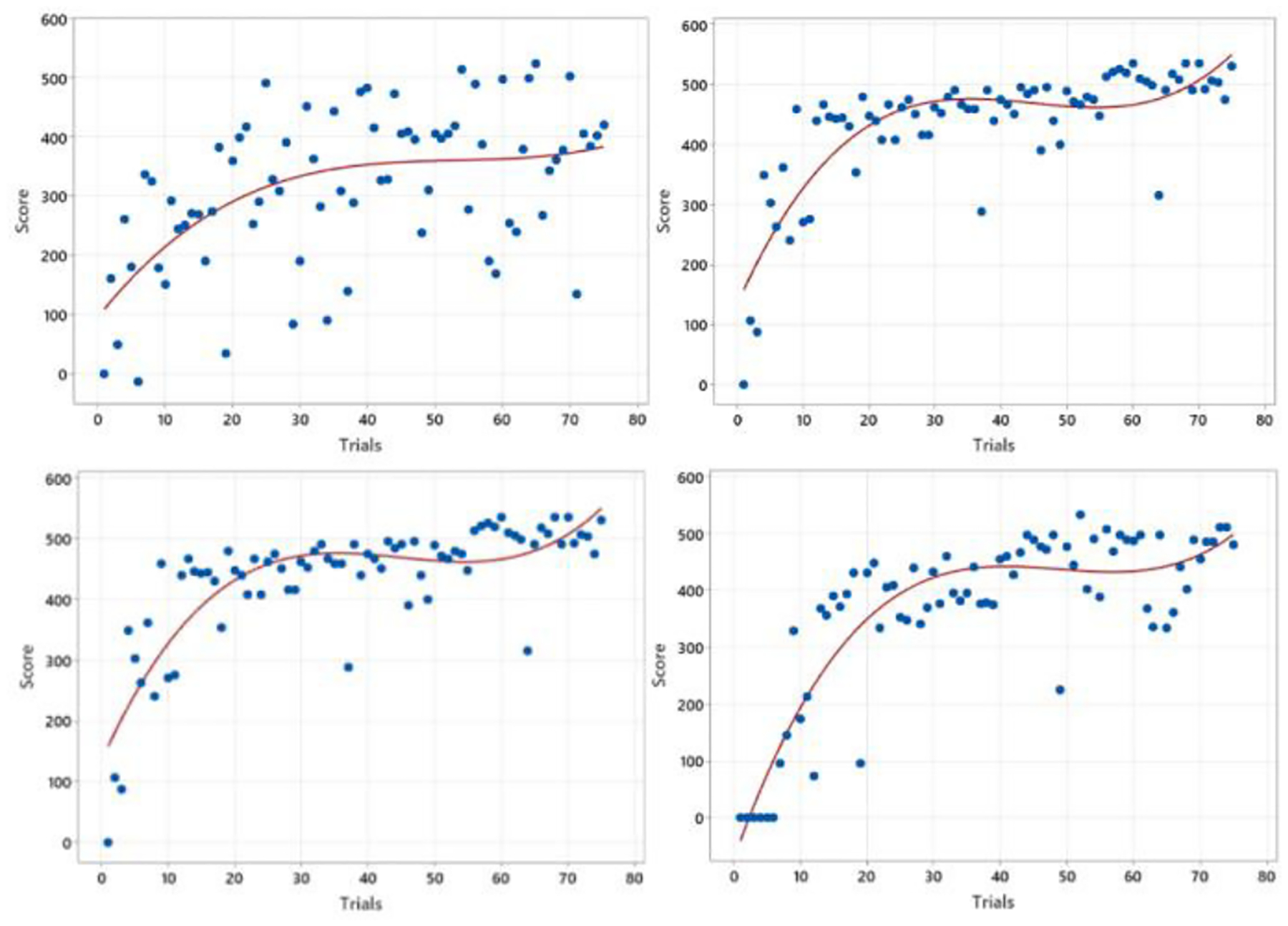
Four learning curve fitting results of accuracy scores vs training trials in real surgery practicing.

Fig. 2 displays that all four trainees’ accuracy scores have grown over the trials, revealing their learning processes. Moreover, within the first few trials, the slopes of the learning curves are more elevated than in the later trials, demonstrating a steep learning curve representing an initial learning barrier at an earlier phase. However, Fig 2 also illustrates some limitations of the learning curve approaches in modeling surgical training processes. Firstly, the fitted line still carries a considerable variability, weakening the expressiveness of the line as a representative of learning processes. For example, the top left figure exhibits an evident variability, indicating that most observations are far from the best fitting line. The other three figures also depict frequent outliers, conveying a sudden significant performance drop even at a later learning phase. Those variabilities, which the fitted line cannot capture, require an advanced analysis. Thus, further discussions will be followed at the end of this section by investigating R-squared values. Another limitation observed in Fig. 2. is the significant differences among the fitted lines of individual results, indicating the possibilities of discrepancies in function types. In specific, not just differences in the parameter values of the similar kernel (function), each result requires different kernels, preventing generalizing the learning processes across individuals. For instance, it is sufficient to use the degree of three polynomial function to find the best fit in the bottom left figure; however, a Gaussian kernel would work well to describe the learning pattern in the bottom right figure. These observations (and limitations) demonstrate the challenges of learning process generalization regardless of the trainees, supporting the need for proposing a new approach for mimicking learning processes.

Fig. 3 exhibits the completion time of one training procedure over trials. As shown in the four different figures in Fig. 3, the results by the four trainees describe that the completion time has reduced as they practiced more, which is consistent with the expectation. However, the learning curve approach has not clearly demonstrated the variability problems of training time either. Even between a few successive trials, their completion times are wildly distinct, indicating a limitation of the expressive power of the single fitted line. Compared to the performance score graph (Fig. 2), all four figures in Fig. 3 suggest that those functions are based on the same kernels; however, another limitation is observed - saturation. For example, when comparing the top-right and bottom-right figures, it is evident that the bottom figure shows a trainee’s maturity in terms of time, while the other trainee from the top figure may still need extra training due to his/her time variability. However, the fitted line cannot convey such information, leaving the time variability unconsidered.

Fig. 3.

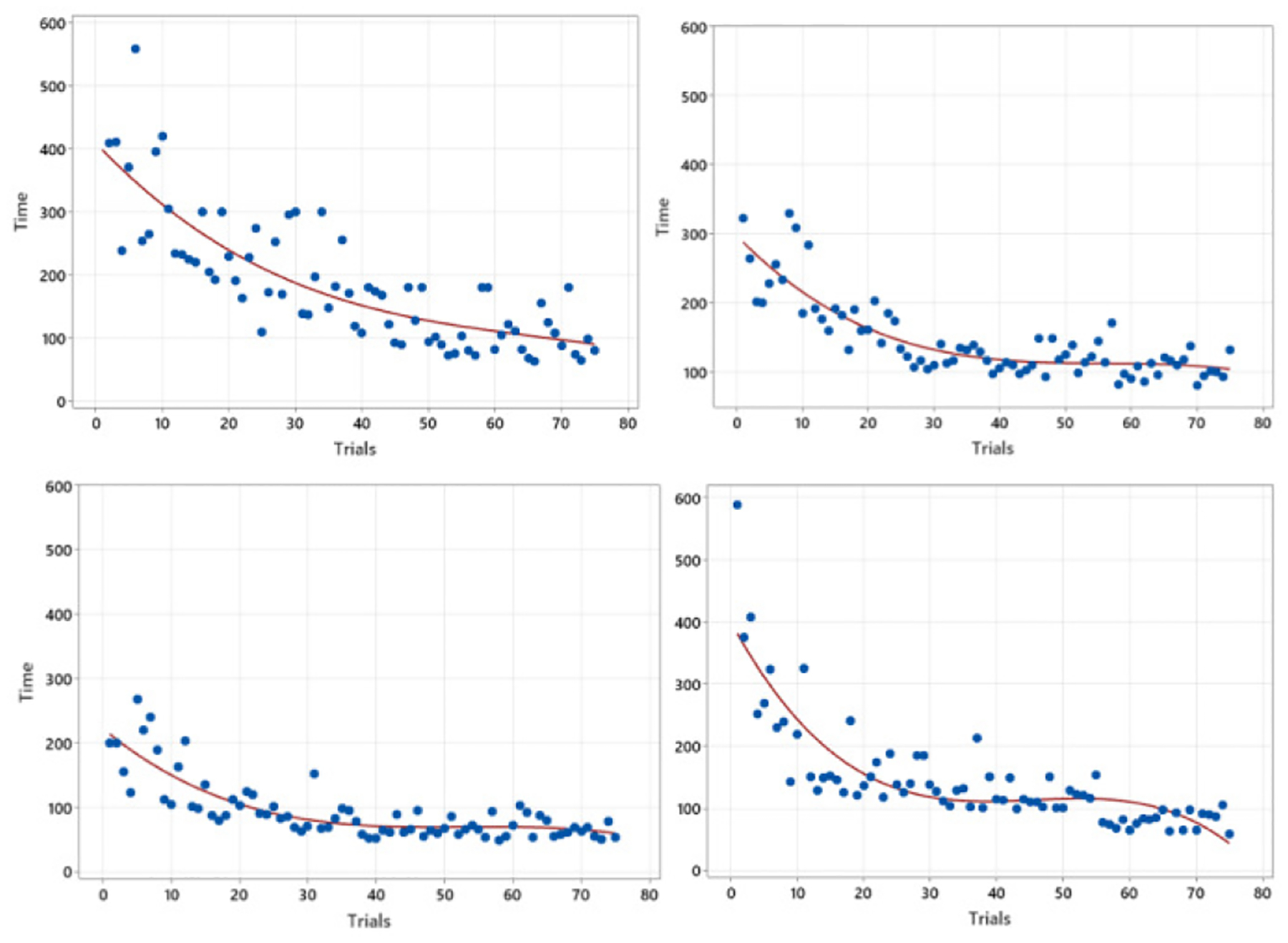
Completion time changes over practice trials in real surgical training.

As investigated in Fig. 2 and 3, two proficiency measures, including accuracy and time, were considered separately in the learning curve approaches. Thus, it is required to capture both overall performance score and time together to represent the learning processes, leading the authors to propose a new modeling approach using the CTMC. Another advantage of using CTMC is its capability for generalization. As in Fig. 2, it is possible that each trainee requires different learning kernels for modeling his/her learning process, prohibiting the generalized guidelines for trainees. However, the CTMC modeling approach allows generalizing all the trainees’ learning processes, which will be investigated at the end of this section. Finally, the learning curve approach makes it unattainable to compare two different training processes in real versus VR environments. The following Fig. 4 shows the learning curve derived in a VR-training environment to investigate the limitation of using a learning curve in comparison between real and VR-based training.

Fig. 4.

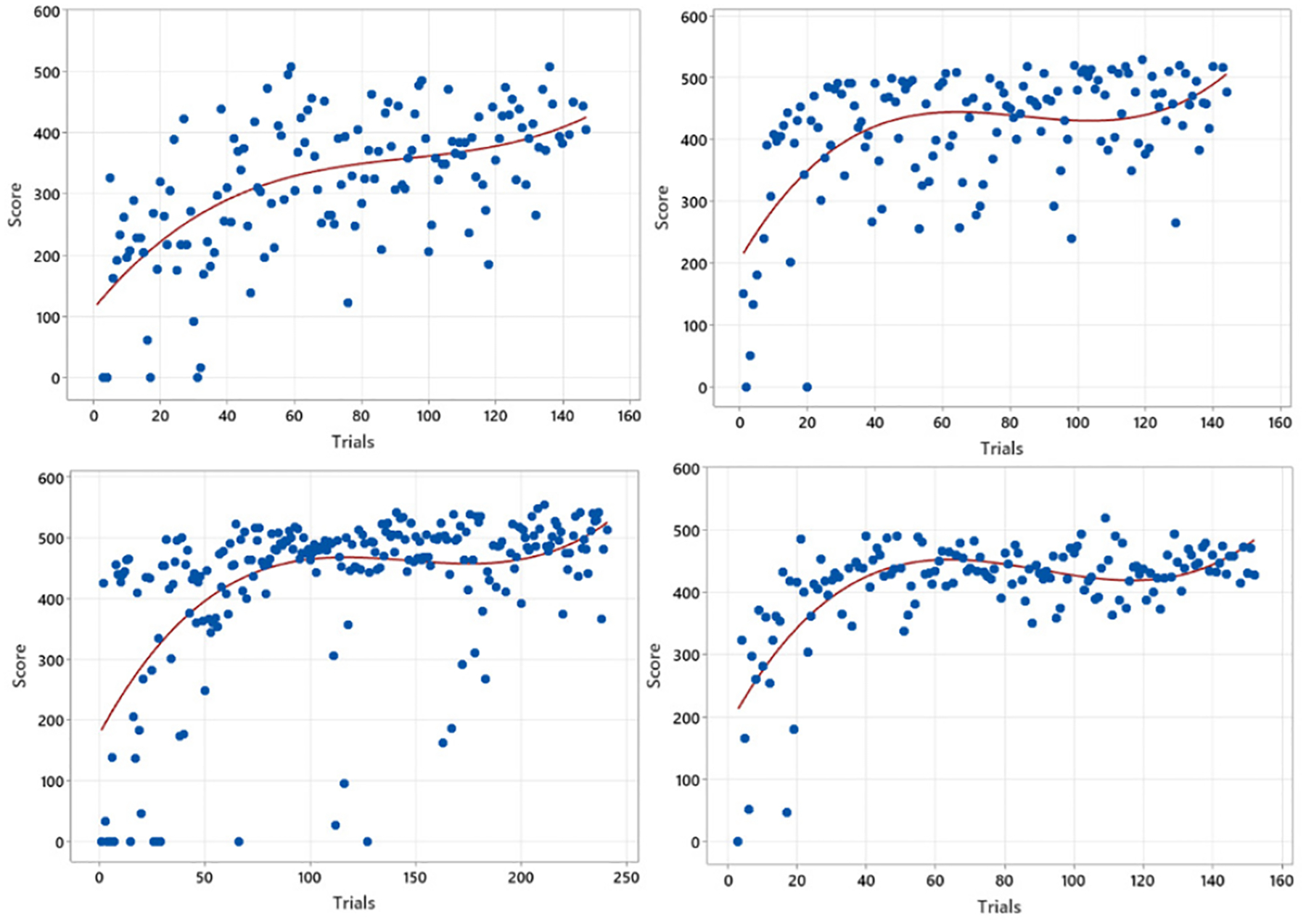
Four Learning Curve Fitting results of scores vs trials in VR-based surgery practicing.

Fig. 4 illustrates four selected trainees’ accuracy scores over practice trials in a VR environment. Trainees’ learning processes within VR show similar patterns as in a real environment, as studied in Fig. 2, presenting that trainees’ performance scores have enhanced as the number of trials accumulates. The steeper slope in an earlier learning phase also denotes an initial learning barrier in the processes. However, the figures also demonstrate the difficulty of modeling the learning process in a VR environment using a fitted line. Firstly, more observations do not lie the fitted line close enough, indicating a higher variability than a real-environment practice. Secondly, as shown in the top-left and bottom-left figures, sudden accuracy drops are marked even after numerous practice trials, weakening the fitted line’s expressiveness in the learning process in a VR environment. Finally, all the fitted lines may require different kernels as described in a real environment configuration. Fig. 4, similar to Fig. 2, suggests that the modeling of learning processes should tackle the sudden accuracy drops, which the fitted line couldn’t capture enough. The authors will demonstrate the capability of CTMC-based modeling in explaining those variabilities.

Fig. 5 shows the trainee’s completion time of one training procedure over the number of trials. As investigated in Fig. 3, one can claim that the completion time drops with practice, indicating the similarity of learning processes in real and VR training environments. However, the variability at a later training phase also diminishes faster compared to the real environment, implying that a VR-based practice can support the trainees to become familiar with the surgical procedure in a shorter amount of time. Therefore, Fig. 5 suggests the potential advantage of VR-based surgical training as a complementary learning system, supporting lower initial learning barriers as well as improving trainees’ confidence before they perform surgery in a real environment.

Fig. 5.

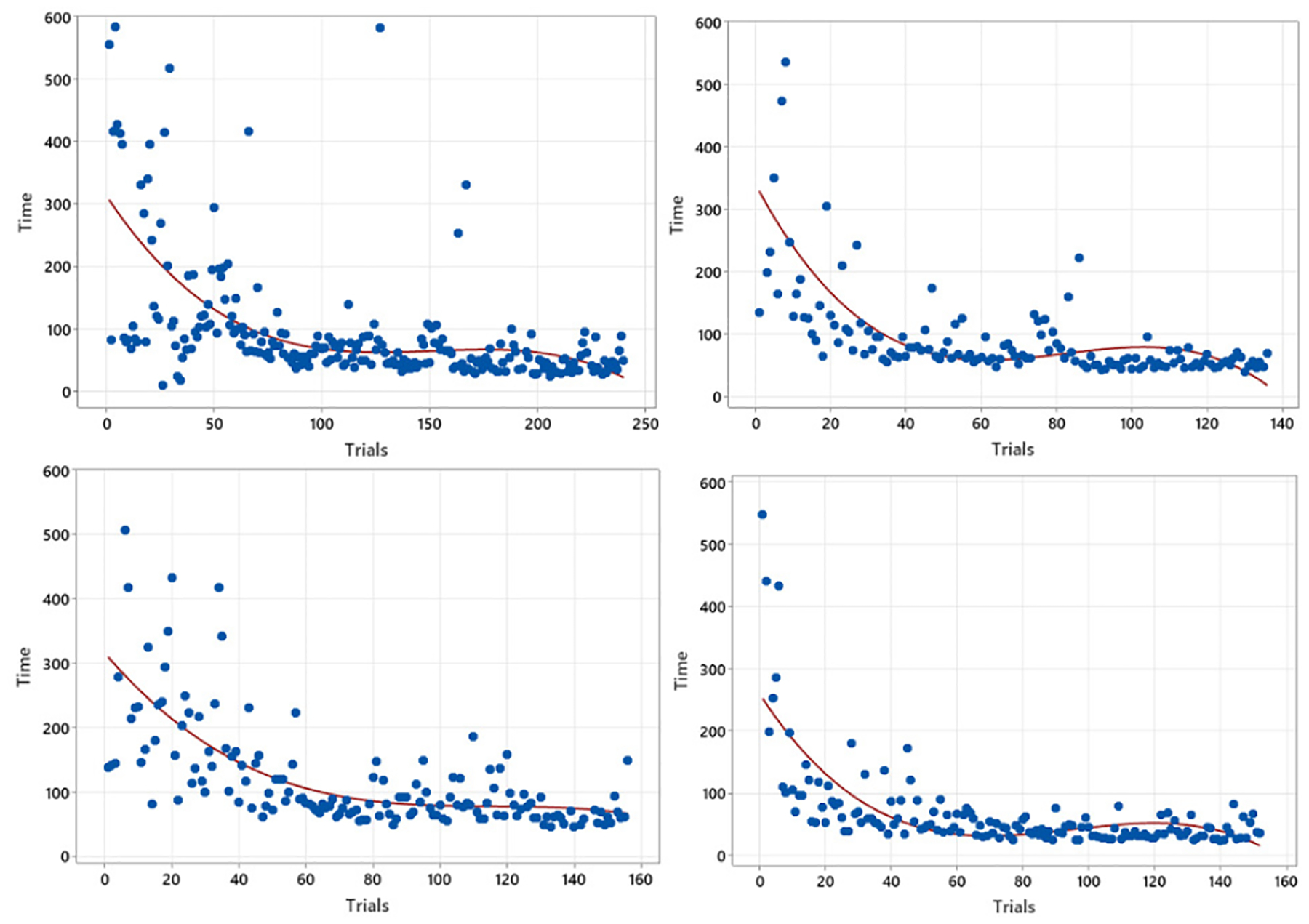
Four Learning Curve Fitting results of times vs trials in VR-based surgery practicing.

To conclude the discussions of learning curve modeling approaches, the authors studied two representative statistics of the R-square values of the fitted results. Table V summarizes the average and the standard deviation of the R-square values of all the trainee’s fitted results in a real and a VR practice environment. As shown in the table, it is evident that the R-square values of the fitted lines are higher in a real practice environment than in a VR environment in terms of both accuracy and time. The result indicates that advanced approaches are required to incorporate the variability, which the best-fitted line cannot capture. Secondly, since R-squared values are lower in training in a VR experiment, one should consider a different approach when especially analyzing the learning processes using a VR setting. Finally, a smaller standard deviation of R-square values in VR training represents that it could be easier to generalize the learning processes in a VR, requiring a new modeling technique to demonstrate all phases over trials. Therefore, the authors introduce a new modeling approach to the learning processes using the Continuous-time Markov chain (CTMC) to enrich the model’s expressiveness, capturing more variability, especially in VR-based training.

TABLE V.

Mean and Standard Deviation of R² Values

Measures	Mean	Standard Deviation
Accuracy Scores in Real	0.5514	0.2323
Accuracy Scores in VR	0.4847	0.1611
Completion Time in Real	0.6789	0.2956
Completion Time in VR	0.5215	0.1033

IV. CTMC-Based Learning Process Modeling

This section introduces the CTMC-based modeling of learning processes in surgical training by addressing the following four limitations of learning curve approaches: demonstrating learning variability, incorporating a sudden performance drop, revealing differences between learning in a real and VR environment, and considering both accuracy and time together. Within the CTMC modeling, it is required to define state sets (S), transition probabilities (T), and rates (average time staying at each state). Firstly, the authors identified four different high-level learning states based on trainees’ performance scores, named Stages 1, 2, 3, and 4. Stage 1 corresponds to the performance score range between 0 and 199, Stage 2 between 200 and 369, Stage 3 between 370 and 477, and Stage 4 over 477 [16, 41]. The Stage 4 threshold is based on the target proficiency score described above [17]. The cutoff for the top-level score 477 in CTMC was based on the proficiency requirement described in the FLS training instructions [16, 66]. According to the instructions, the ultimate proficiency is achieved with a completion time less than 112 seconds, and an accuracy within 1 mm deviation (error score of 10), for a total score of 478 [66].

As the training trial repeats, it is expected that the trainee’s stage will advance, assuming that there is no backward movement such as moving down from Stages 4 to 3, 3 to 2, or 2 to 1. Instead, the authors included low-level learning states (named “sub-states” in each stage) to represent the learning variability and a sudden accuracy drop. The following tables show both high- and low-level states within the proposed CTMC-based learning model.

As discussed, one can admit that the trainees’ skills (in terms of accuracy and time) will enhance as they practice repeatedly. Thus, the authors introduced the low-level state “Mature” in Stages 1, 2, and 3, representing the situation where the trainee hit the next level’s score for the first time, which works as an absorbing state. Since it is an absorbing state, the chain always advances to a higher stage. Once one’s learning process reaches the “Mature” state in Stages 1, 2, and 3, the chain moves to the next stage and never returns to the previous stage. At the same time, “Immature” and “In-Progress” sub-states in each stage illustrate that trainees require enough trials to progress to the next stage while demonstrating accuracy drops and fluctuation of the surgical proficiency in learning processes. For example, if one’s progress stays in an “Immature” sub-state in Stage 2, a trainee has advanced to Stage 2 by scoring the accuracy value between 200 and 369 once, but he/she scored below 200 in his latest training trial. The second column in Table VI shows all the accuracy score ranges of higher-level states (Stages), and the last column describes the corresponding accuracy score in each lower-level state.

TABLE VI.

States in Two-Stage Markov Chain Model

High-level States	Accuracy Score Range	Sub-States	Accuracy Score Range
Stage 1	[0, 199]	Immature	[0, 199]
		Mature	over 199
Stage 2	[200, 369]	Immature	[0, 199]
		In-Progress	[200, 369]
		Mature	over 369
Stage 3	[370, 477]	Immature	[0, 369]
		In-Progress	[370, 476]
		Mature	over 477
Stage 4	over 477	Immature	[0, 369]
		In-Progress	[370, 476]
		Mature	over 477

Fig. 6 shows a proposed CTMC describing training processes in a real environment by incorporating all seven participants’ practice results. Four high-level states along with nine sub-states are determined, as shown below. The transition matrix (T) demonstrating the transition probability from one state to the other is also developed by considering the likelihood of accuracy changes in two subsequent trials. Thus, the matrix dimension is nine by nine, considering the number of sub-states. Since all the “Mature” states in Stages 1, 2, and 3 are absorbing states, the transition probabilities from $S_1^M$ to $S_2^I$, from $S_2^M$ to $S_3^I$ and from $S_3^M$ to $S_4^I$ are all 1, meaning the trainee advanced to the next stage. Notations in Equation (1) represent both high- and low-level states.

Fig. 6.

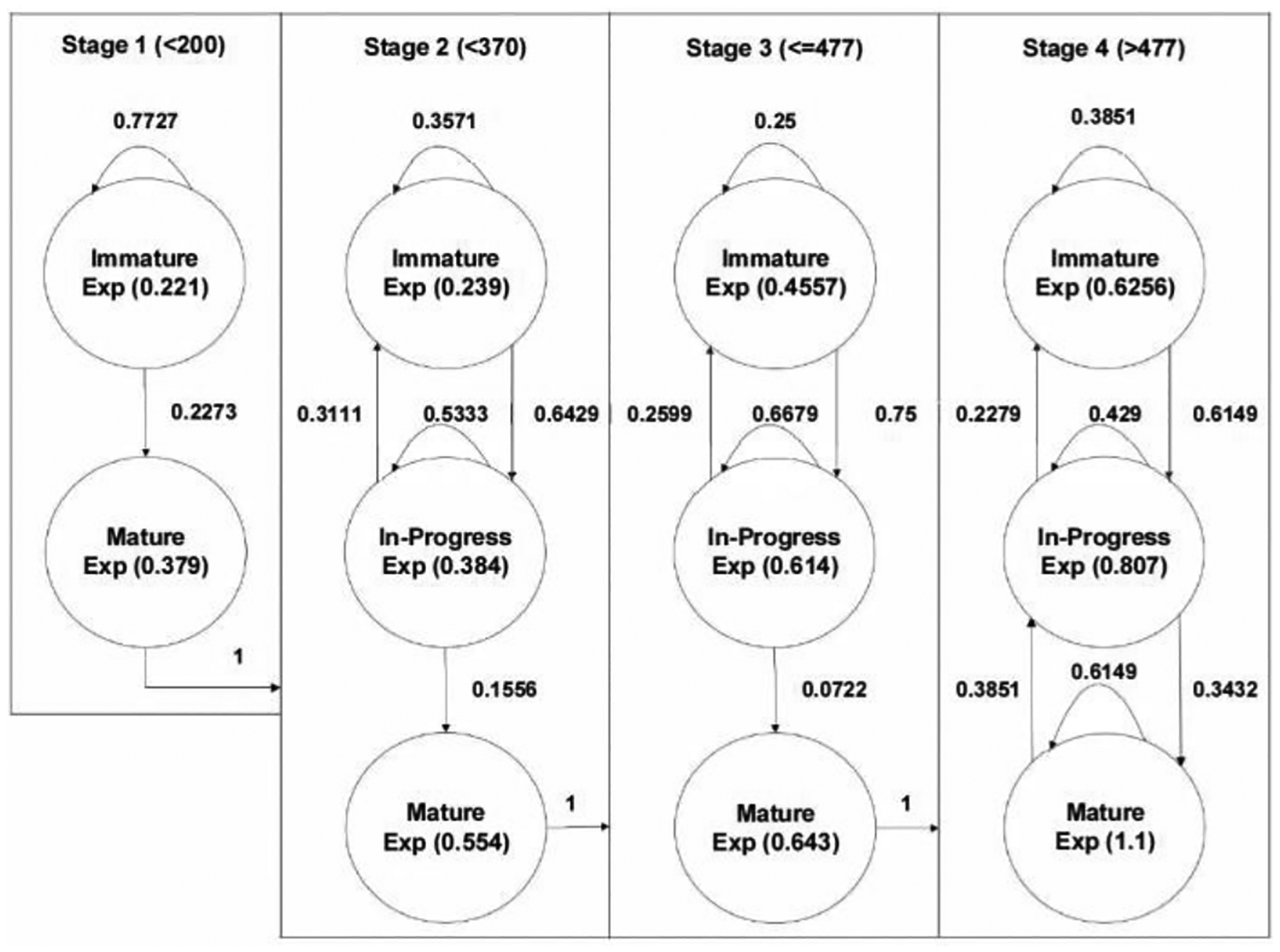
CTMC modeling results of practicing using real environment

$$\begin{gathered} \mathit{\text{S}}=\left\{{\mathit{\text{S}}}_1,{\mathit{\text{S}}}_2,{\mathit{\text{S}}}_3,{\mathit{\text{S}}}_4\right\} \\ {\mathit{\text{S}}}_1=\left\{S_1^I,S_1^M\right\},{\mathit{\text{S}}}_2=\left\{S_2^I,S_2^{IP},S_2^M\right\} \\ {\mathit{\text{S}}}_3=\left\{S_3^I,S_3^{IP},S_3^M\right\},{\mathit{\text{S}}}_4=\left\{S_4^I,S_4^{IP},S_4^M\right\} \end{gathered}$$ (1)

The corresponding transition matrix (T) is as derived below. The authors observed trainees’ subsequent attempts and calculated the occurrence of the next trials’ accuracy score to derive the transition probability.

$$\mathit{\text{T}}=\left[\begin{array}{cccccccccc}0.73& 0.23& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0.36& 0.64& 0& 0& 0& 0& 0& 0\\ 0& 0& 0.31& 0.53& 0.16& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0.25& 0.75& 0& 0& 0\\ 0& 0& 0& 0& 0& 0.26& 0.67& 0.07& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0.39& 0.61& 0\\ 0& 0& 0& 0& 0& 0& 0& 0.23& 0.43& 0.34\\ 0& 0& 0& 0& 0& 0& 0& 0& 0.39& 0.61\end{array}\right]$$

Once the learning process was modeled with the CTMC, the general Markov Chain analytics were applied to characterize the learning process. For example, it can be analytically derived based on the average number of trials to advance to the next stage (Stages 1 to 2, 2 to 3, and 3 to 4), as all the mature states are absorbing states. The transit matrices (Q) in each stage (named Q₁, Q₂, and Q₃, respectively) were also developed under the consideration of transition probabilities only between transient states, as in Equation (2).

$${\mathit{\text{Q}}}_1=[0.77],{\mathit{\text{Q}}}_2=\left[\begin{array}{ll}0.36\hfill & 0.64\hfill \\ 0.31\hfill & 0.53\hfill \end{array}\right],{\mathit{\text{Q}}}_3=\left[\begin{array}{ll}0.25\hfill & 0.75\hfill \\ 0.26\hfill & 0.67\hfill \end{array}\right]$$ (2)

Then, the average number of trials (N) required to advance to the next stage can be obtained by reading the first element of the vector derived by the following formula: $E[\mathit{\text{N}}]={(\mathit{\text{I}}-Q)}^{-1}1$, where I, Q, and 1 represent an identity matrix, a transient matrix, and vector of 1, respectively. On average, 4.35, 11.09, and 20.57 trials were required to advance to the next stage from 1 to 2, from 2 to 3, and from 3 to 4, respectively. This observation is consistent with the traditional learning theory that more additional efforts are required to advance to the next stage after the trainee passes the earlier learning phase (i.e., it is more challenging to become an expert). Moreover, one can estimate each state’s rate values by considering the completion time in each trial, as shown in Table VII. The authors have empirically proved that the rate values follow an exponential distribution, satisfying the assumption of the Markov Chain model. This will be investigated at the end of this section.

TABLE VII.

Rate Values in a Real Environment

High-level States	Sub-States	Rate (× 10−2)	Average Completion Time (sec)
Stage 1	Immature	0.221	451.74
	Mature	0.379	263.80
Stage 2	Immature	0.239	418.41
	In-Progress	0.384	260.42
	Mature	0.554	180.51
Stage 3	Immature	0.456	219.30
	In-Progress	0.614	162.87
	Mature	0.643	155.52
Stage 4	Immature	0.626	159.74
	In-Progress	0.807	123.92
	Mature	1.1	90.91

The trainee took in each training state. Rate values were estimated by taking the reciprocal values of the average practice time, implying how fast a trainee completes a trial in each learning state. As shown in the table, it is evident that a trainee spends less time as she advances to a higher level, indicating her progress in learning. Moreover, even if she is at a higher level, it is also possible that she could produce a sudden proficiency drop, resulting in an increased completion time in the same stage. The table also shows that regardless of Stages where the trainee is in, the completion time drops (the rate values increase) as she moves from “Immature” to “In-Progress” and from “In-Progress” to “Mature, demonstrating the trainee’s performance improves in each Stage.

Now, the same analogy can be applied to the VR-based training data. The authors have developed the CTMC model along with a transition matrix to mimic the learning process in a VR training environment. The transition matrix (T) was also derived in the same way as before.

$$\mathit{\text{T}}=\left[\begin{array}{cccccccccc}0.68& 0.32& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0.33& 0.67& 0& 0& 0& 0& 0& 0\\ 0& 0& 0.31& 0.46& 0.23& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0.68& 0.32& 0& 0& 0\\ 0& 0& 0& 0& 0& 0.36& 0.56& 0.08& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0.24& 0.76& 0\\ 0& 0& 0& 0& 0& 0& 0& 0.21& 0.48& 0.31\\ 0& 0& 0& 0& 0& 0& 0& 0& 0.5& 0.5\end{array}\right]$$

Fig. 7 shows CTMC modeling results in a VR training environment by incorporating all eight participants’ practice results. Corresponding transient matrices are as follows: ${\mathit{\text{Q}}}_1=[0.68],{\mathit{\text{Q}}}_2=\left[\begin{array}{ll}0.33\hfill & 0.67\hfill \\ 0.46\hfill & 0.31\hfill \end{array}\right],{\mathit{\text{Q}}}_3=\left[\begin{array}{ll}0.68\hfill & 0.32\hfill \\ 0.56\hfill & 0.36\hfill \end{array}\right]$ One can use the same formula, $E[\mathit{\text{N}}]={(\mathit{\text{I}}-Q)}^{-1}1$ to find the expected number of trials to advance the next stages by checking its first element, as discussed before. On average, 3.1, 8.83, and 29.68 trials are required to advance to Stages 2, 3, and 4, respectively.

Fig. 7.

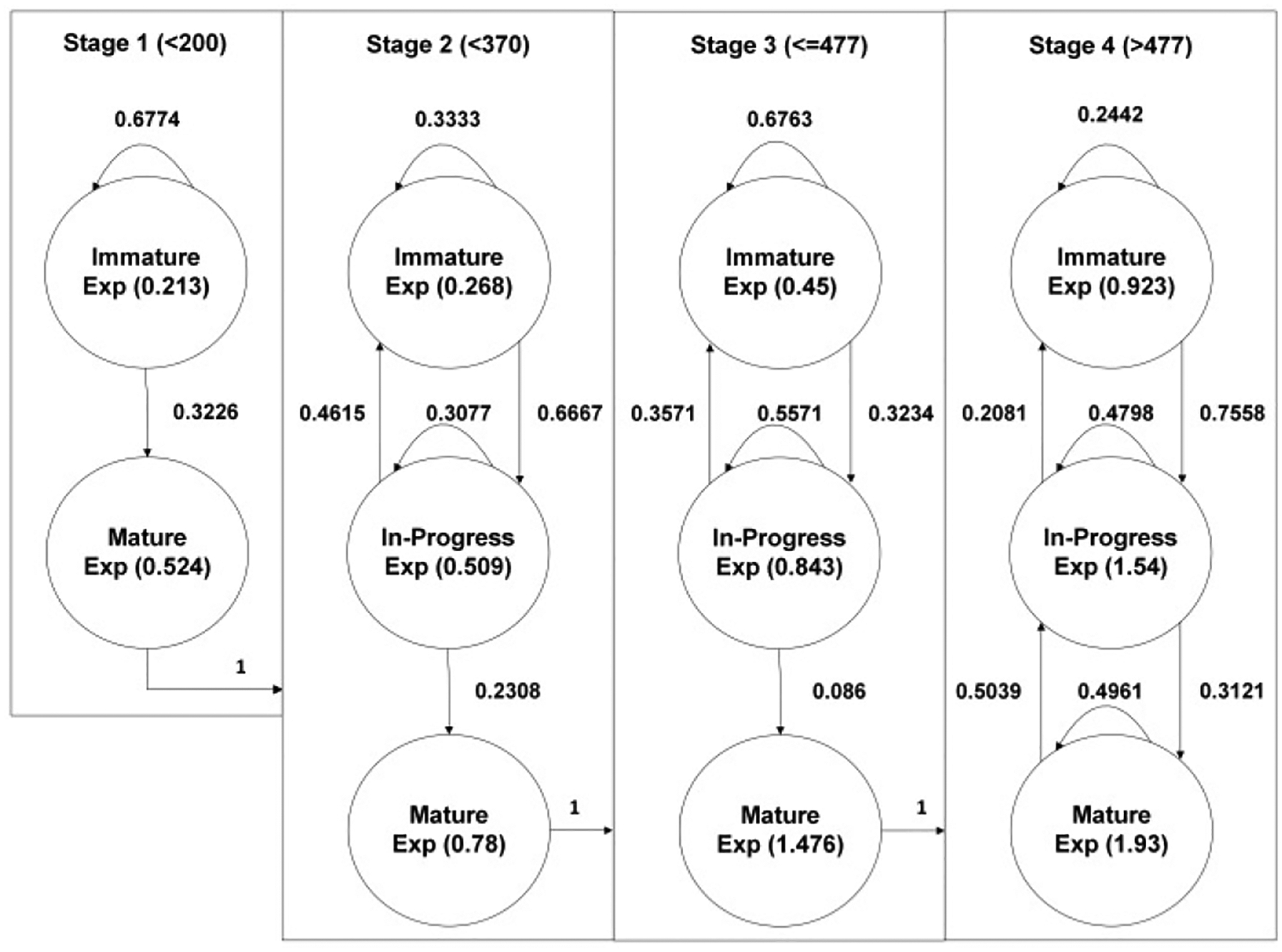
CTMC modeling results of practicing in a VR environment

Table VIII summarizes the average number of trials to advance to the next stage in real- and VR-based training environments. Compared to the learning process in a real environment, it requires fewer trials to reach Stages 2 and 3, as shown in Table VIII, representing that the VR-based training aided in bending the initial learning barriers. However, after the practitioners reach Stage 3, it requires more trials of experiments to reach Stage 4, meaning that a trainee has to practice more in a VR environment to score more than 477. This result indicates that even though the VR-based training model helps you reduce the initial barrier in surgical training, it becomes less effective for trainees at a later learning phase (who have already overcome the initial learning barrier) to become fully trained. It also implies that a higher level of resolution and complexity of the training model is required to support the trainees with advanced skills.

TABLE VIII.

Average Number of Trials for Advancing

From	To	Average # of Trials in Real Env.	Average # of Trials in VR Env.
Stage 1	Stage 2	4.35	3.1
Stage 2	Stage 3	8.83	11.09
Stage 3	Stage 4	20.57	29.68

Table IX shows the average completion time and the rate values at each state in VR-based training. Compared to training in a real environment, the “Immature” state in Stage 1 is more prolonged, indicating that trainees take more time to become familiar with the VR setting. After the trainee advances to Stage 2, the rate value increases as the sub-state moves forward, indicating sequential improvement in learning in each stage. Overall, compared to Table VIII, one can observe that VR experiments result in less completion per trial, indicating that VR could assist better for trainees to mature faster compared to training in a real environment.

TABLE IX.

Rate Values in a VR Environment

High-level States	Sub-States	Rate (× 10−2)	Average Completion Time (sec)
Stage 1	Immature	0.213	469.48
	Mature	0.524	190.84
Stage 2	Immature	0.268	373.13
	In-Progress	0.509	196.46
	Mature	0.78	128.21
Stage 3	Immature	0.45	222.22
	In-Progress	0.843	118.62
	Mature	1.476	67.75
Stage 4	Immature	0.923	108.34
	In-Progress	1.54	64.94
	Mature	1.93	51.81

The authors checked whether the proposed model satisfies the major assumption of CTMC that all the rate values in the proposed CTMC model should follow Exponential distribution. The distribution fitting was carried out using rate values in all states through the goodness-of-fit (GOF). The authors selected six representative continuous distributions, including Normal, Lognormal, Exponential, Weibull, Gamma, and Exponential distributions, and fitted the completion time data into each distribution. Then, both Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) values were derived to find the best distribution representing the rate values. Tables IX and X present both AIC and BIC values of each distribution’s fitting results in real and VR environments, respectively.

TABLE X.

AIC and BIC Values in a Real Environment

$S_1^I$	Exp	Uniform	Normal	Gamma	Weibull	Log. N.
AIC	388.20	367.41	362.70	362.70	361.46	360.7
BIC	389.50	370.00	365.29	365.29	364.05	363.3
$S_2^I$	Exp	Normal	Uniform	Gamma	Weibull	Log. N.
AIC	154.27	151.30	150.28	149.75	149.53	149.53
BIC	154.67	152.10	151.07	150.54	150.32	150.32
$S_2^{IP}$	Exp	Gamma	Log. N.	Normal	Weibull	Uniform
AIC	290.92	257.91	256.12	254.30	253.55	250.62
BIC	292.05	260.18	258.39	256.57	255.82	252.89
$S_3^I$	Uniform	Exp	Normal	Gamma	Log.N.	Weibull
AIC	1052.63	1026.57	1010.59	995.5	988.15	991.58
BIC	1057.39	1028.95	1015.35	1000.26	992.91	996.34
$S_3^{IP}$	Uniform	Exp	Normal	Weibull	Log.N.	Gamma
AIC	707.3	637.35	639.42	607.84	576.9	553.22
BIC	711.31	639.36	643.43	611.85	580.92	557.24
$S_3^M$	Exp	Gamma	Log.N.	Normal	Weibull	Uniform
AIC	85.45	64.92	64.26	63.09	61.15	60.89
BIC	85.53	65.08	64.42	63.25	61.31	61.04
$S_4^I$	Exp	Normal	Uniform	Weibull	Log.N.	Gamma
AIC	1790.99	1645.08	1605.23	1564.87	1541.3	1513.78
BIC	1796.88	1650.98	1608.18	1570.77	1547.19	1519.68
$S_4^{IP}$	Exp	Uniform	Normal	Weibull	Log.N.	Gamma
AIC	5382.53	5295.1	4879.54	4843.24	4771.06	4753.92
BIC	5386.79	5303.61	4888.05	4851.75	4779.57	4762.43
$S_4^M$	Exp	Uniform	Weibull	Normal	Gamma	Log.N.
AIC	3127.56	2689.05	2583.29	2576.16	2566.32	2562.29
BIC	3131.32	2696.56	2590.81	2583.67	2573.83	2569.8

Both Tables X and XI are displayed in decreasing order of AIC & BIC values from left to right. Table X observes that the highest AIC & BIC values are produced when fitting to Exponential distribution in most of the cases. Only two states show that the Uniform distribution fits better; however, uniform distribution works far worse in all the other states, indicating that exponential would be the best distribution to represent the randomness of rate values in each state. On the other hand, in a VR environment, the exponential distribution beats all the other distributions, as shown in Table XI. Both AIC and BIC values are highest in the case of exponential distributions in all the states. Therefore, one can conclude that the exponential distribution is the best distribution to represent the variability of the rate values (average completion time) in states within the proposed CTMC model. It is confirmed that the proposed model satisfies the basic assumption of CTMC.

TABLE XI.

AIC and BIC Values in a VR Environment

$S_1^I$	Exp	Gamma	Log.N.	Normal	Weibull	Uniform
AIC	329.2	297.22	295.47	293.26	291.81	273.86
BIC	330.34	299.49	297.74	295.53	294.08	276.13
$S_2^I$	Exp	Weibull	Gamma	Normal	Log.N.	Uniform
AIC	157.27	130.72	130.47	130.42	130.37	126.17
BIC	157.67	131.52	131.26	131.22	131.16	126.96
$S_2^{IP}$	Exp	Uniform	Gamma	Weibull	Log.N.	Normal
AIC	500.81	430.32	418.46	416.96	416.7	415.52
BIC	502.45	433.6	421.73	420.23	419.97	418.8
$S_3^I$	Exp	Gamma	Log.N.	Normal	Weibull	Uniform
AIC	138.28	104.6	104.4	104.11	103.42	97.15
BIC	138.68	105.39	105.2	104.90	104.21	97.95
$S_3^{IP}$	Exp	Gamma	Log.N.	Normal	Weibull	Uniform
AIC	295.99	266.65	264.98	263.58	262.83	256.68
BIC	297.12	268.92	267.25	265.85	265.1	258.95
$S_3^M$	Exp	Weibull	Normal	Log.N.	Gamma	Uniform
AIC	586.87	476.28	473.72	471.58	471.13	463.6
BIC	588.74	480.02	477.47	475.32	474.87	467.34
$S_4^I$	Exp	Uniform	Normal	Weibull	Log.N.	Gamma
AIC	500.08	452.38	450.97	450.11	444.87	444.15
BIC	501.79	455.81	454.4	453.54	448.3	447.58
$S_4^{IP}$	Exp	Uniform	Weibull	Gamma	Normal	Log.N.
AIC	1154.23	986.64	954.24	952.55	950.86	950.16
BIC	1156.83	991.83	959.43	957.74	956.05	955.35
$S_4^M$	Exp	Log.N.	Gamma	Normal	Wi.	Uniform
AIC	1257.02	990.35	995.23	984.02	978.11	969.38
BIC	1259.76	995.83	1000.70	989.49	983.58	974.85

V. Conclusion

This work proposes a new modeling framework to depict the learning procedures in surgical training. The proposed CTMC-based model of the learning processes captures learning variability induced by trainees and a sudden performance drop at the later learning phase, which supports to find the best time to provide additional feedback in the learning process. Secondly, our proposed model helps to identify a “stagnation” phase by relying on the advanced analytics of CTMC. One can compare the expected number of trials for a trainee to advance to the next stage analytically. Thus, if a trainee performs more than the average number of trials and remains in the same stage, we can provide any additional feedback to facilitate their training process. Thirdly, through CTMC, we can identify differences in the surgical learning processes in a real versus VR environment, which could be used to identify additional aids to support trainees at a later learning phase by investigating the rate and transition probabilities. Finally, CTMC can represent three different measures, including accuracy scores, trials, and completion time, together in one graph, which is simple and intuitive compared to the other learning methods we described. The competitive advantages of the proposed CTMC-model demonstrate the validity of the VR-based training model.

Biographies

Seunghan Lee is an assistant professor in the Industrial and Systems Engineering Department at Mississippi State University.

His research encompasses modeling and analysis of data-driven systems under uncertainty using simulation and stochastics. Major application areas include disaster relief and mitigation efforts, smart city and homeland security, and healthcare operations.

Dr. Lee received the Institute of Industrial and Systems Engineering (IISE) Annual Meetings Best Paper Awards in the Service & Work Systems Track and the Security Engineering Track in 2016 and 2018, respectively. He is also a member of IISE and the Institute of Operation Research and Management Sciences (INFORMS).

Amar Sadanand Shetty received the bachelor’s degree in Mechanical Engineering from University of Mumbai, Mumbai, India, in 2018 and currently pursuing Master of Science in Industrial and Systems Engineering (Operations Research specialization) from University at Buffalo, The State University of New York.

Mr. Shetty’s research interest includes process optimization using mathematical modelling, statistical data analysis, system analysis using stochastics process, mechanical process like thermodynamic system. The research applies to areas like Supply Chain Planning, Warehousing, Temperature-controlled system. In 2015, Mr. Shetty was awarded with Academic Award for Engineering Drawing Exam by University of Mumbai. He is a member of IISE.

Lora A. Cavuoto received her B.S. degree in Biomedical Engineering and M.S. in Occupational Ergonomics and Safety from the University of Miami, Coral Gables, FL, USA, in 2006 and 2008, respectively. She received M.S. and Ph.D. degrees in Industrial and Systems Engineering from Virginia Tech, Blacksburg, VA, USA, in 2009 and 2012, respectively.

She is currently an Associate Professor of Industrial and Systems Engineering at the University at Buffalo, Buffalo, NY, USA. She is the author of more than 60 journal papers. Her research interests include surgical training, motor skills development, occupational ergonomics, fatigue, and wearable sensor applications in industry. She serves as a scientific editor for Applied Ergonomics and an associate editor for Human Factors and Ergonomics in Manufacturing & Service Industries.