Improving the walktrap algorithm using K-means clustering

Abstract

The walktrap algorithm is one of the most popular community-detection methods in psychological research. Several simulation studies have shown that it is often effective at determining the correct number of communities and assigning items to their proper community. Nevertheless, it is important to recognize that the walktrap algorithm relies on hierarchical clustering because it was originally developed for networks much larger than those encountered in psychological research. In this paper, we present and demonstrate a computational alternative to the hierarchical algorithm that is conceptually easier to understand. More importantly, we show that better solutions to the sum-of-squares optimization problem that is heuristically tackled by hierarchical clustering in the walktrap algorithm can often be obtained using exact or approximate methods for K-means clustering. Three simulation studies and analyses of empirical networks were completed to assess the impact of better sum-of-squares solutions.

Introduction

There are a variety of different types of networks that arise in psychological applications. For example, social networks are relevant to applications in organizational psychology (Brass et al., 2012), developmental psychology (Neal, 2020), and social psychology (Brusco & Steinley, 2010). A recent survey of social network applications in psychology is provided by Broda et al. (2021). Networks have also received considerable attention in the identification of neural components that exhibit high levels of connectivity within the context of fMRI data (Mumford et al., 2010; Rubinov & Sporns, 2010, 2011) and the depiction of the relations among features of psychopathology in clinical psychology (Borsboom et al., 2021). During the past 10–15 years, the burgeoning area of network psychometrics has seen the modeling of symptoms, beliefs, and attitudes as vertices of a network (Borsboom et al., 2021; Epskamp, Maris et al., 2018; Epskamp, Waldorp et al., 2018). Once the network edges and their weights have been collected or estimated, it is not uncommon to partition the vertices into communities (or clusters).

The walktrap algorithm (Pons & Latapy, 2006) is a very popular community-detection method and applications of it abound in the psychological literature (Briganti et al., 2018; Choi et al., 2017; Christensen, 2018; Fried, 2016; Golino & Demetriou, 2017; Hevey, 2018; Jones et al., 2018; Kendler et al., 2018; McCormick et al., 2019; McElroy & Patalay, 2019; Price et al., 2017). The walktrap algorithm produces communities by applying Ward’s (1963) hierarchical clustering algorithm based on degree-weighted distances between rows of a t-step transition probability matrix. In their presentation of the algorithm, Pons and Latapy (2006) describe distances between pairs of vertices, between vertices and communities, and between pairs of communities using formulas that incorporate both transition probabilities and degree centralities. Brusco, Steinley, et al. (2022a) have recently described a simplified data matrix, which leads to the same matrix of distances between pairs of vertices that subsequently affords easy computation of community distances.

The walktrap algorithm has performed well in several simulation-based comparisons of community-detection methods in the psychological literature. Gates et al. (2016) evaluated a variety of community-detection methods across several different types of data structures (sparse count matrices, correlation matrices, and Euclidean distance matrices ranging in size from 25 to 1000 vertices) that might be common in psychological applications such as the analysis of fMRI data. Based on their results, they concluded that the walktrap algorithm was one of the two most reliable methods. Hoffman et al. (2018) introduced a new community-detection method based on Cohen’s Kappa (Cohen, 1960) and compared its performance to a variety of other algorithms within the context of unweighted networks. Although their proposed method was the top performer, the walktrap algorithm was a close second in many instances.

More recently, Christensen et al. (2021) evaluated community-detection algorithms within the framework of exploratory graph analysis (Golino & Epskamp, 2017; Golino et al., 2020, 2021) with networks ranging in size from 4 to 48 vertices divided into one, two, or four communities. They found that the walktrap algorithm was one of the top three performing methods, with fast modularity (Newman, 2004a) and the Louvain method (Blondel et al., 2008) being the other two. Also, Brusco, Steinley et al. (2022a) compared the walktrap algorithm to spectral clustering (von Luxburg, 2017) for 24- and 48-vertex networks generated based on the Gaussian graphical model. Although spectral clustering tended to perform better when the number of communities was prespecified, the walktrap algorithm performed better when the number of communities was assumed unknown and estimated from the data. Finally, Brusco, Steinley et al. (2022b) compared the walktrap algorithm to fast modularity, the Louvain method, and an integer programming approach to maximize modularity (Aloise et al., 2010). Relative to its three modularity-based competitors, the results of the Brusco, Steinley et al. (2022b) studies revealed the robustness of the walktrap algorithm for conditions of unequal community sizes.

In this paper, we rationalize the original computational scheme proposed by Pons and Latapy (2006) with the one recently offered by Brusco, Steinley et al. (2022a) and propose that the computational scheme described by Brusco, Steinley et al. (2022a) is easier to understand. More importantly, despite the popularity and success of the walktrap algorithm, its performance might be improved (Brusco, Steinley et al., 2022a). There are several avenues that could be pursued in search of improvement, including the development of better approaches for: (i) specifying the weights for loops (self-edges) of the network, (ii) choosing the step size parameter for the transition matrix, and (iii) selecting the number of communities. In this paper, however, we focus on the opportunity to improve the walktrap algorithm by replacing Ward’s method with methods for K-means clustering.

Both Ward’s method and K-means clustering seek to minimize the sum (across all vertices in all communities) of the squared Euclidean distance between the vertex and the centroid of the community for which that vertex is a member. Hereafter, we refer to the sum of the squared Euclidean distances as SSE. For a given number of communities, K, Ward’s method might not produce a partition of the vertices that minimizes SSE and, therefore, is only an approximate or heuristic method for this problem. Most K-means clustering methods are also heuristic methods; however, they tend to produce better SSE values than Ward’s method (Steinley, 2003; Steinley & Brusco, 2007). Moreover, there are also exact methods for K-means clustering that are guaranteed to find partitions that minimize SSE (Aloise et al., 2012; Brusco, 2006; Diehr, 1985; Koontz et al., 1975). These methods will often be scalable for networks of the sizes commonly encountered in the psychological literature.

The proposition that Ward’s method should be replaced by better methods for minimum SSE clustering should not be misinterpreted as a criticism of the walktrap algorithm as originally proposed by Pons and Latapy (2006), as they were focusing on the design of an efficient method for very large networks.¹ Instead, our proposition is that, for the much smaller networks encountered in most psychological applications, the performance of the walktrap algorithm can often be improved by replacing the suboptimal hierarchical clustering component with K-means clustering methods. Our recommendations would apply to the use of the walktrap algorithm in any of the application areas mentioned previously: (i) unweighted networks (Hoffman et al., 2018), (ii) fMRI networks (Gates et al., 2016), and (iii) exploratory graph analysis (Christensen et al., 2021; Golino & Epskamp, 2017).

Our contribution builds on recent research pertaining to the walktrap algorithm in several respects. First, using a small illustrative example we formally demonstrate the equivalence of the computational scheme proposed by Brusco, Steinley et al. (2022a) to the one described by Pons and Latapy (2006). Second, this same example is used to demonstrate precisely how the implementation of the walktrap algorithm using Ward’s method can fail to yield partitions that minimize SSE. Third, we examine the frequency and the severity of the suboptimality of Ward’s hierarchical clustering method with respect to the SSE measure when applying the walktrap algorithm to a diverse group of empirical networks from the literature. Fourth, via a series of simulation experiments, we examine the extent to which differences in SSE translate into differences in the partitions of vertices into communities.

In the next section, we describe the walktrap algorithm and the underlying optimization problem that is tackled using Ward’s method. Alternative approaches based on exact and approximate K-means clustering are then described. This is followed by a small, illustrative example that clearly indicates the pitfalls of hierarchical clustering and how they are rectified by K-means clustering. Three simulation studies were conducted to assess the SSE suboptimality of Ward’s method and its implications for the recovery of underlying community structure. Next, the potential suboptimality of Ward’s method and improvements using K-means are examined using actual networks from the literature. The paper concludes with a brief summary and suggestions for future research.

The walktrap algorithm

The walktrap algorithm assumes an undirected graph, $G(V,E)$, with vertex set $V=\{1,\dots ,p\}$ and edge set $E:\{i,j\}\in E$. In psychological applications, the vertices correspond to items such as symptoms, beliefs, or attitudes and the edges represent ties or relationships between pairs of items without any implication of direction from one item to another in any pair. The graph is assumed to contain self-edges (or loops) for vertices, such that $\{i,i\}\in E$ for all $1\le i\le p$. The walktrap algorithm was originally described within the framework of unweighted graphs but is readily extensible to graphs with positive edge weights that measure the strength of the tie between pairs of items. For weighted undirected graphs that do not have loops, we assume that the loop edge weight for each vertex is specified as the largest edge weight that vertex shares with another vertex. As noted by Brusco, Steinley et al. (2022a), this assumption is consistent with setting the loop edge weight to one for an unweighted network and is also justifiable based on the notion that a self-tie for a vertex would be at least as large as a tie it shares with some other vertex.

We denote the $p\times p$ nonnegative symmetric adjacency matrix containing the edge weights as $\mathbf{\text{A}}=[a_{ij}]$, such that $a_{ij}=a_{ji}$ is the edge weight for all vertex pairs $\{i,j\}\in E$ and $a_{ij}=a_{ji}=0$ if $\{i,j\}\notin E$. In a psychological context, the positive elements of $\mathbf{\text{A}}$ represent the strength of ties between pairs of items and elements equal to zero indicate absence of a tie between pairs of items. The $p\times p$ diagonal matrix, $\mathbf{\text{D}}$, contains main diagonal elements ($d_{ii}$ for $1\le i\le p$) equal to the degree centralities for the vertices, which are computed as the sum of the edge weights in each row of $\mathbf{\text{A}}\mathbf{:}$

$$d_{ii}={\sum }_{j=1}^p{a}_{ij}\text{for}1\le i\le p.$$ (1)

The walktrap algorithm is grounded in the principles of random walks and Markov chains. To illustrate, suppose that a ‘walker’ is positioned at a particular vertex at a particular point in time. As time is incremented, the walker takes a random step to one of its neighboring vertices based on a probability distribution. This is a random walk with a length of $t=1$. The transition matrix, $\mathbf{\text{P}}={\mathbf{\text{D}}}^{-1}\mathbf{\text{A}}$, has elements [$p_{ij}$] that correspond to the probability of a transition from vertex $i$ to vertex $j$ for a walk of length one. For a random walk of length greater than one, a sequence of vertices will be visited and this constitutes a Markov chain. For a walk of length $t>1$, the $t$-step transition matrix is computed as ${\mathbf{\text{P}}}^t=[p_{ij}^t]$ where the elements $p_{ij}^t$ correspond to the probability of a transition from vertex $i$ to vertex $j$ in t steps. Two properties of the $p_{ij}^t$ values are:

1. Stationary distribution: $\underset{t\to \infty }{\lim }{p}_{ij}^t=\frac{d_{jj}}{{\sum }_{h=1}^p{d}_{hh}}$ for all $1\le i\le p$, and

2. Reversibility: $d_{ii}{p}_{ij}^t=d_{jj}{p}_{ji}^t$ for all $1\le i\le p$ and $1\le j\le p$.

The stationary condition means that the transition probabilities for each row approach the ratio of the degree of the column vertex to the sum of the edge weights as $t$ increases. The reversibility condition shows that the $p_{ij}^t$ to $p_{ji}^t$ ratios depend only on the degree centralities of vertices $i$ and $j$.

The next step is to establish distances between pairs of vertices based on information gleaned from random walks in the graph. A step length of $t=1$ is likely not sufficient to afford much information regarding the topological structure of the graph, whereas too many steps can lead to convergence to the stationary condition described above. A common range is $2\le t\le 5$. Pons and Latapy (2006) defined a measure of squared Euclidean distance between the probability distributions associated with rows $i$ and $j$ of the $t$-step transition matrix as follows:

$$r_{ij}^2(t)={\sum }_{h=1}^p\frac{{\left(p_{ih}^t-p_{jh}^t\right)}^2}{d_{hh}}\text{for all}1\le i\le p\text{and}1\le j\le p.$$ (2)

Brusco, Steinley et al. (2022a) have observed that another way to compute the $r_{ij}^2(t)$ distances is to define a $p\times p$ data matrix, ${\mathbf{\text{X}}}^t=[x_{ij}^t$] with elements $x_{ij}^t=\frac{1}{\sqrt{d_{jj}}}\left(p_{ij}^t\right)$ for all $1\le i\le p$ and $1\le j\le p$ and calculate the squared Euclidean distances accordingly:

$$r_{ij}^2(t)={\sum }_{h=1}^p{\left(x_{ih}^t-x_{jh}^t\right)}^2\text{for all}1\le i\le p\text{and}1\le j\le p.$$ (3)

Pons and Latapy (2006) also establish distances between communities of vertices. To illustrate, we define $\pi =\{C_1,\dots ,C_K\}$ as a $K$-community partition of $V$, where $C_k$ is the subset of vertices in $V$ assigned to community $C_k$. The probability of a transition from some community $C$ to vertex $j$ in $t$ steps is computed as follows:

$$p_{Cj}^t(t)=\frac{1}{\left|C\right|}{\sum }_{i\in C}{p}_{ij}^t$$ (4)

The distance between two communities, say $C_1$ and $C_2$, is then computed as follows:

$$r_{C_1{C}_2}^2(t)={\sum }_{h=1}^p\frac{{\left(p_{C_{1}h}^t-p_{C_{2}h}^t\right)}^2}{d_{hh}}$$ (5)

Another very important measure is the increase in the SSE that stems from the merger of $C_1$ and $C_2$ to create a new community:

$$∆SSE\left(C_1,C_2\right)=\left(\frac{\left|C_1\right|\left|C_2\right|}{\left(\left|C_1\right|+\left|C_2\right|\right)}\right)r_{C_1{C}_2}^2(t)$$ (6)

Ward’s (1963) agglomerative hierarchical clustering procedure is the engine of the walktrap algorithm. The algorithm begins with each vertex in its own community and successively merges pairs of communities until all vertices are in one community. At each stage, the merger that minimizes the increase in SSE is selected. More formally, Ward’s method begins with $K=p$, such that $\pi =\{C_1,\dots ,C_K\}$ where $C_k=\left\{k\right\}$ for all $1\le k\le K$. Because each vertex is its own community, there is no ‘error’ associated with any community and SSE = 0. Next, all $\left(\begin{array}{c}p\\ 2\end{array}\right)$ mergers of communities are evaluated using Equation 6 and the merger yielding the smallest value of $∆SSE\left(C_k,C_l\right)$ across all pairs of communities $k$ and l is accepted and SSE is increased accordingly. This merger reduces the number of communities to $K=p-1$. The process is repeated via evaluation of all $\left(\begin{array}{c}p-1\\ 2\end{array}\right)$ mergers, and so on, until finally all $p$ vertices are in K = 1 community. Upon completion of the hierarchical clustering algorithm, there are $p$ partitions of the vertices for each number of communities ($K$) on the interval $1\le K\le p$, and there is an SSE associated for each of these partitions that we will refer to as SSE(K).

A natural question is: For each value of $K$, is the partition of $V$ into $K$ vertices obtained by the hierarchical algorithm providing the minimum (best) possible value of SSE(K)? In most instances, the answer to this question is “no”. The reason is that, although Ward’s method greedily selects the merger minimizing $∆SSE\left(C_k,C_l\right)$ at each stage, it is not guaranteed to produce the best SSE(K) for one or more values of $K$ because some other path of mergers (not all greedy ones) might lead to a better SSE(K). Thus, it is an approximate as opposed to exact procedure.

The problem of finding a $K$-community partition that minimizes SSE(K) is formidable. The number of possible partitions of $p$ vertices into $K$ communities, $S(p,K)$ is a Stirling number of the second kind (see Brusco, 2006) and is computed as follows:

$$S\left(p,K\right)=\frac{1}{K!}{\sum }_{k=0}^K{\left(-1\right)}^k\left(\begin{array}{c}K\\ k\end{array}\right){(K-k)}^p.$$ (7)

So, for example, the number of ways to partition $p$ = 30 vertices into K = 5 communities is just over 7.713 × 10¹⁸. Finding a partition that minimizes SSE via exhaustive evaluation of such an enormous number of partitions is impossible; however, there are exact solution methods that can often achieve this goal even when $S(p,K)$ is very large. Examples of exact solution methods include branch-and-bound programming (Brusco, 2006; Brusco & Stahl, 2005, Ch. 5; Diehr, 1985; Koontz et al., 1975) and mixed-integer nonlinear programming (Aloise et al., 2012). We have implemented the branch-and-bound algorithm described by Brusco (2006) in MATLAB and use it to obtain globally-optimal $K$-means partitions in our simulation experiments.

Because exact methods have the potential for lengthy computation times and might require mathematical programming software, heuristic (approximate) approaches for minimizing SSE are more common. Ward’s hierarchical clustering is one possible heuristic approach; however $K$-means clustering algorithms (Forgy, 1965; MacQueen, 1967; Steinhaus, 1956; Steinley, 2003, 2006) are much more effective. These methods begin with an assignment (often a random assignment) of the $p$ vertices into $K$ communities. The centroids (variable means) for each community are computed and each vertex is re-assigned to the community associated with the centroid to which it is nearest. This process is repeated until no vertices change membership or there is no further reduction in SSE, at which point the best-found partition is returned. The partition returned by the $K$-means algorithm is sensitive to the initial partition that was entered and is not guaranteed to be the one that minimizes SSE. To mitigate this problem, it is common to restart the $K$-means algorithm thousands of times using different random initial partitions (Steinley, 2003; Steinley & Brusco, 2007) and adopt the best result obtained across the restarts. Although this multistart approach does not guarantee that the optimal partition will be found, it typically will for networks of the size encountered in network psychometrics. We use a multistart implementation of a $K$-means clustering heuristic for some of the larger empirical networks where the branch-and-bound algorithm is not scalable.

An illustrative example

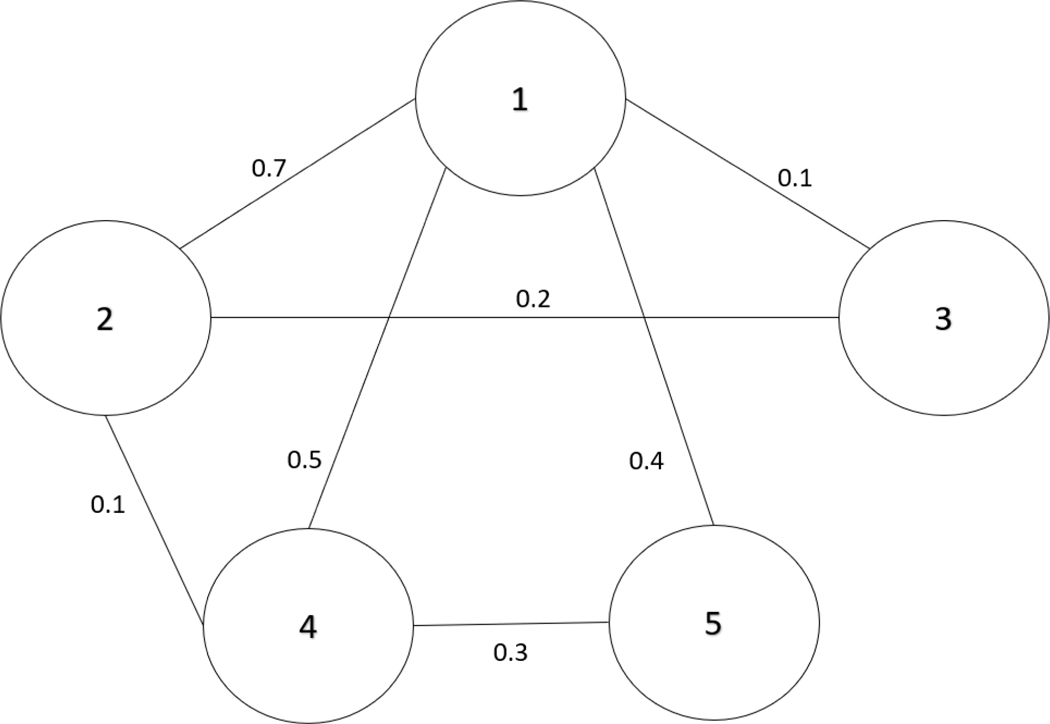
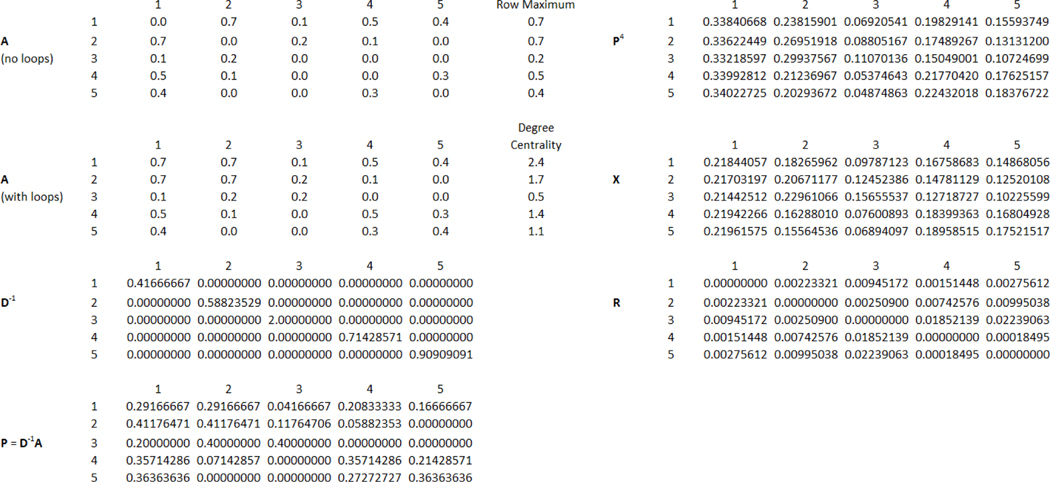
We consider the undirected five-vertex network in Figure 1. The original adjacency matrix, adjacency matrix after adding loop edge weights based on row maximums ($\mathbf{\text{A}}$), diagonal matrix containing the degree centrality inverses (${\mathbf{\text{D}}}^{-1}$), the transition probability matrix ($\mathbf{\text{P}}={\mathbf{\text{D}}}^{-1}\mathbf{\text{A}}$), the four-step ($t=4$) transition matrix (${\mathbf{\text{P}}}^4$), the data matrix ($\mathbf{\text{X}}$) with elements $x_{ij}^t=\frac{1}{\sqrt{d_{jj}}}\left(p_{ij}^t\right)$, and the matrix of squared Euclidean distance between pairs of vertices ($\mathbf{\text{R}}=[r_{ij}^2(t)]$) are shown in Figure 2.

Figure 1. The 5-Vertex Network Used for the Illustrative Example.

Note. The lines indicate undirected edges between pairs of the five vertices and the numerical values adjacent to the lines are the edge weights.

Figure 2. Relevant Input Matrices for the Illustrative Example.

Note. The figure provides the adjacency matrix ($\mathbf{\text{A}}$) both with and without loop edge weights, the degree centrality ($d_{jj}$) for each vertex, the diagonal matrix containing the inverse of the degree centralities (${\mathbf{\text{D}}}^{-1}$), the transition probability matrix ($\mathbf{\text{P}}={\mathbf{\text{D}}}^{-1}\mathbf{\text{A}}$), the four-step ($t=4$) transition matrix (${\mathbf{\text{P}}}^4$), the data matrix ($\mathbf{\text{X}}$) with elements $x_{ij}^t=\frac{1}{\sqrt{d_{jj}}}\left(p_{ij}^t\right)$, and the matrix of squared Euclidean distance between pairs of vertices ($\mathbf{\text{R}}=[r_{ij}^2(t)]$).

The elements of $\mathbf{\text{R}}$ can be computed using ${\mathbf{\text{P}}}^4$ and $d_{jj}$ (for $1\le j\le 5$) via the Pons and Latapy (2006) formula, which we provided in Equation 2 above. For example, the squared Euclidean distance between objects 1 and 3 is as follows:

$$r_{13}^2\left(t\right)=\frac{{\left(0.33840668-0.33218597\right)}^2}{2.4}+\frac{{\left(0.23815901-0.29937567\right)}^2}{1.7}+\frac{{\left(0.06920541-0.11070136\right)}^2}{0.5}+\frac{{\left(0.19829141-0.15049001\right)}^2}{1.4}+\frac{{\left(0.15593749-0.10724699\right)}^2}{1.1}=0.00945172$$

The same result can be obtained more directly from $\mathbf{\text{X}}$ using the formula from Brusco, Steinley et al. (2022a), which we provided in Equation 3 above, as follows:

$$r_{13}^2\left(t\right)=\mathrm{ }{\left(0.21844057-0.21442512\right)}^2+{\left(0.18265962-0.22961066\right)}^2+{\left(0.09787123-0.15655537\right)}^2+{\left(0.16758683-0.12718727\right)}^2+{\left(0.14868056-0.10225599\right)}^2=0.00945172$$

Figure 3 presents detailed results pertaining to the implementation of Ward’s method using the process described by Pons and Latapy (2006) and accomplished using Equations 5 and 6. Figure 4 reports a summary table from SPSS after using Ward’s method to cluster the data matrix, $\mathbf{\text{X}}$. We begin by rationalizing the results in the two Figures.

Figure 3. The Steps of Ward’s Hierarchical Clustering Method for the Example.

Note. The four-step transition matrix (P⁴) and degree centralities (d_jj) are shown at the top because they are used for computation of the ΔSSE values. At each stage, the ΔSSE values are computed for each possible merger of communities and the merger with the smallest ΔSSE value (identified by the rows in bold font) is selected. The total SSE value and corresponding partition after each stage are reported, respectively, in the last two columns.

Figure 4. SPSS Results for the Example After Applying Ward’s Method Directly to X.

Note. The SSE column is actually labeled ‘Coefficient’ in the SPSS output because it is the agglomeration coefficient on which Ward’s method is based. Also, the ΔSSE column is not part of the SPSS output. We added this column, which contains values equal the SSE value for the current row minus the SSE value for the previous row, to facilitate comparison to Figure 3.

Ward’s method begins with all vertices in their own individual community and SSE = 0. Next, at Stage 1, all possible $\left(\begin{array}{c}5\\ 2\end{array}\right)=10$ mergers of communities are evaluated and the one yielding the smallest value of ΔSSE is selected. For this example, the best merger is vertices {4} and {5}, with ΔSSE({4},{5}) computed using Equations 5 and 6 as follows:

$$\frac{(1)(1)}{(1+1)}\left(\frac{{\left(0.33992812-0.34022725\right)}^2}{2.4}+\frac{{\left(0.21236967-0.20293672\right)}^2}{1.7}+\frac{{\left(0.05374643-0.04874863\right)}^2}{0.5}+\frac{{\left(0.21770420-0.22432018\right)}^2}{1.4}+\frac{{\left(0.17625157-0.18376722\right)}^2}{1.1}\right)=0.00009247$$

After merging vertices {4} and {5}, the new value of SSE is SSE = 0 + 0.00009247 = 0.00009247. This number is displayed in the SSE column of Figure 4 for the first merger and is referred to as the agglomeration ‘coefficient’ by SPSS. It is important to recognize that the SSE can be computed efficiently using $\mathbf{\text{R}}$ via the following formula:

$$SSE={\sum }_{k=1}^K\frac{1}{\left|C_k\right|}{\sum }_{\left\{i<j\right\}\in C_k}{r}_{ij}^2(t).$$ (8)

Here, K = 4, with the communities {1}, {2}, {3}, and {4, 5}. The first three of these contribute nothing to SSE because there is no distance between a single vertex and itself. The contribution from the {4, 5} community is (1/2)(.00018495) = 0.00009247, which is the total SSE value.

At Stage 2, all possible $\left(\begin{array}{c}4\\ 2\end{array}\right)=6$ mergers of communities are evaluated and the one yielding the smallest value of ΔSSE is selected. For this example, the best merger is vertices {2} and {3}, with ΔSSE({1},{2}) = 0.00111661 computed using Equations 5 and 6. This brings total SSE to 0.00009247 + 0.00111661 = 0.00120908, which is the value found in the SSE column of the Stage 2 row of the SPSS output. The K = 3 community partition is {1, 2}, {3}, {4, 5}.

At Stage 3, all possible $\left(\begin{array}{c}3\\ 2\end{array}\right)=3$ mergers of communities are evaluated and the one yielding the smallest value of ΔSSE is selected. For this example, the best merger is community {1, 2} and {3}, with ΔSSE({1,2},{3}) = 0.00361470. To make this computation using the method as described by Pons and Latapy (2006), we need to use Equation 4 in addition to Equations 5 and 6 because community {1, 2} has more than a single vertex. Specifically, in Equation 4, the computation of $p_{C=\left\{\mathrm{1,2}\right\},j}^t(t)=\frac{1}{2}{\sum }_{i\in C}{p}_{ij}^t$ for all 1 ≤ $j$ ≤ 5 is required. For example, as shown in Figure 3, $p_{C=\left\{\mathrm{1,2}\right\},4}^t(t)$ = (1/2)(0.19829141 + 0.17489267) = 0.18659204. Once the $p_{Cj}^t(t)$ values are in place, Equation 5 is used to compute $r_{\left\{\mathrm{1,2}\right\},\left\{3\right\}}^2(t)$ as follows:

$$r_{\left\{\mathrm{1,2}\right\},\left\{3\right\}}^2\left(t\right)=\frac{{\left(0.33731558-0.33218597\right)}^2}{2.4}+\frac{{\left(0.25383909-0.29937567\right)}^2}{1.7}+\frac{{\left(0.07862854-0.11070136\right)}^2}{0.5}+\frac{{\left(0.18659204-0.15049001\right)}^2}{1.4}+\frac{{\left(0.14362474-0.10724699\right)}^2}{1.1}=0.00542205$$

Equation 6 is then used to compute ΔSSE({1,2},{3}) = $\frac{\left(2\right)\left(1\right)}{\left(2+1\right)}\left(0.00542205\right)=0.00361470.$ The new value of SSE for the K = 2-community partition {1, 2, 3}, {4, 5} is obtained by adding this increase to the SSE value (0.00120908) from the previous stage: 0.00120908 + 0.00361470 = 0.00482378, which is the value shown in the SSE column of the Stage 3 row of the SPSS output in Figure 4. Once again, in our estimation, it is much easier to get this SSE value directly using Equation 8 and then work backwards to get ΔSSE if desired. The computation for this two-community partition is simply:

$$SSE=\frac{1}{3}\left(0.00223321+0.00945172+0.00250900\right)+\frac{1}{2}\left(0.00018495\right)=0.00482378$$

The first term in this SSE computation is the sum of the squared distances between pairs of vertices in the community {1, 2, 3} divided by the number of vertices in that community (i.e., 3). The second term is the sum of the squared distances between pairs of vertices in the community {4, 5}, which in this case is just the distance between 4 and 5 (0.00018495), divided by the number of vertices in that community (i.e., 2).

At Stage 4, there is only $\left(\begin{array}{c}2\\ 2\end{array}\right)=1$ possible merger of communities. Specifically, {1, 2, 3} and {4, 5} to obtain {1, 2, 3, 4, 5}. Using Equation 8, the SSE for this partition is obtained easily by adding up all the elements below (or above) the main diagonal of $\mathbf{\text{R}}$ in Figure 3 and dividing by the number of vertices in {1, 2, 3, 4, 5}, which is 5. This will result in SSE = 0.01538753 as shown in the SSE column of the Stage 4 row in the SPSS output in Figure 4. If ΔSSE is desired, then it can be obtained by subtracting the SSE value at Stage 3 from the SSE value at Stage 4: ΔSSE = 0.01538753 – 0.00482378 = 0.01056374.

The failure of Ward’s method

We return to the Stage 3 solution of Ward’s method, which corresponds to the two-community partition: $C_1=\{1,2,3\}$, $C_2=\{4,5\}$, and SSE = 0.00482378. Is this the two-community partition that provides the minimum value of SSE? The answer is “no”. Consider the following (optimal) two-community partition: $C_1=\{1,4,5\}$, $C_2=\{2,3\}$. Using Equation 8, the SSE for this partition is:

$$SSE=\frac{1}{3}\left(0.00151448+0.00275612+0.00018495\right)+\frac{1}{2}\left(0.00250900\right)=0.00273968$$

Thus, the SSE associated with the two-community partition obtained by Ward’s method is more than 76% greater than the SSE corresponding to the optimal two-community partition.

The explanation for the failure of Ward’s method can be discerned by examining its stages. At Stage 1, vertices {4} and {5} are merged. This does not present a problem because these two vertices are in the same community in the optimal two-community partition. At Stage 2, vertices {1} and {2} are merged into a community. Although this is the best SSE move at this particular stage, it has ramifications for later stages that cannot be undone. In other words, once vertices {1} and {2} are placed in the same community, it becomes impossible for Ward’s method to find the optimal two-community partition because these two vertices are not in the same community in the optimal partition, which is $C_1=\{1,4,5\}$, $C_2=\{2,3\}$.

Our proposed remedy for this problem is straightforward. Specifically, whenever possible, replace Ward’s method with an exact method for K-means clustering for small values of K that are of interest (e.g., 2 ≤ K ≤ 6). When this is not possible, Ward’s method should be replaced with a multistart implementation of a heuristic method for K-means clustering. The severity of the suboptimality problem of Ward’s method is apt to vary from one network to the next. In some instances, Ward’s method will obtain the minimum SSE partition for one or more values of K. In other instances, Ward’s method will fail to find the minimum SSE partition and the potential difference from the optimal partition might be severe. In the next sections, we explore the suboptimality issues for Ward’s method using both simulation experiments (with synthetic networks) and actual networks from the literature.

Simulation studies

We conducted three simulation studies to evaluate the suboptimality of Ward’s method and its potential implications for the recovery of community structure. The MATLAB (MATLAB, 2020) files for implementing both the Ward’s and K-means versions of the walktrap algorithm and reproducing the results of the simulation studies are available from the public repository: https://figshare.com/articles/software/Walktrap_Using_Kmeans_Clustering/21183454

The maximum network size in all three simulation studies was $p$ = 24 vertices, which assured that partitions with the global minimum value of SSE for all test problems could be obtained using a branch-and-bound programming algorithm (Brusco, 2006; Brusco & Stahl, 2005). The three studies are differentiated by the manner in which the ‘true’ network structures were generated. We felt this was important to provide some assurance that the conclusions from the experiments were not simply an artifact of the network generation process. In the first study, we generated networks based on the Girvan and Newman (2002) procedure, whereby within-community and between-community edges were randomly-selected along with their edge weights (see Brusco, Steinley et al., 2022b). In the second experiment, we generated networks by sampling from the Gaussian Graphical Model (Epskamp, Waldorp et al., 2018; Lauritzen, 1996) for different sample sizes. In the third experiment, networks were generated based on factor models (Christensen et al., 2021; Golino et al., 2020).

Simulation 1

The first simulation study is based on the experimental design from Brusco, Steinley et al. (2022b). Four problem-design features were considered: (i) number of communities, (ii) distribution of vertices across communities, (iii) within-community cohesion, and (iv) overlap between communities. The number of communities was evaluated at five levels: K = 2, K = 3, K = 4, K = 5, and K = 6. The distribution of vertices across communities was tested at two levels: equal community sizes and unequal community sizes. Within-community cohesion, which is the probability of an edge between two vertices in the same community, was evaluated at three levels: 0.9 (high), 0.8 (medium), and 0.7 (low). Edge weights were drawn from a uniform distribution on the interval [0.4, 1.0] for the selected within-community edges. Community overlap, which is the probability of an edge connecting two vertices in different communities, was tested at three levels: 0.1 (low), 0.2 (medium), and 0.3 (high). Edge weights were drawn from a uniform distribution on the interval [0.0, 0.6] for the selected between-community edges. The experimental design consisted of 5 × 2 × 3 × 3 = 90 cells and we used 100 replications per cell, resulting in a total of 9000 test problems for the simulation experiment.

Two versions of the walktrap algorithm were applied to each of the 9000 problems assuming the correct number of communities was known. The first version was the standard algorithm using Ward’s hierarchical clustering method, whereas the second version used a branch-and-bound algorithm (Brusco, 2006) to obtain the guaranteed minimum SSE. For each cell, data were collected with respect to the following performance measures: (a) percentage of test problems for which the Ward’s method implementation yielded a suboptimal SSE, (b) the percentage of test problems for which the adjusted Rand index (ARI: Hubert & Arabie, 1985) measure of partition agreement for the Ward’s method implementation provided a better/worse ARI than the branch-and-bound implementation, and (c) the average ARI for each method. The ARI realizes a value of one for perfect agreement and is near zero for agreement expected by chance. Steinley (2004) provided the following thresholds for ARI: ‘excellent’ – ARI ≥ 0.9, ‘good’ – ARI ≥ 0.8, ‘fair’ – ARI ≥ 0.65, ‘poor’ – ARI < 0.65. The results for Simulation 1 are provided in Table 1.

Table 1.

Simulation 1 –Cell Means for Proportion of Suboptimal Walktrap SSE’s, ARIs, Proportion of Test Problems for Which Each Method Yielded a Better ARI, and ARI.

				Proportion	Proportion with better ARI		Mean ARI
Dist	K	Cohesion	Overlap	Ward’s SSE > K-means SSEs	Ward’s	K-means	Ward’s	K-means
Equal	2	0.9	0.1	0.00	0.00	0.00	0.9900	0.9900
Equal	2	0.9	0.2	0.00	0.00	0.00	0.9900	0.9900
Equal	2	0.9	0.3	0.00	0.00	0.00	0.9900	0.9900
Equal	2	0.8	0.1	0.00	0.00	0.00	1.0000	1.0000
Equal	2	0.8	0.2	0.00	0.00	0.00	1.0000	1.0000
Equal	2	0.8	0.3	0.00	0.00	0.00	1.0000	1.0000
Equal	2	0.7	0.1	0.00	0.00	0.00	0.9983	0.9983
Equal	2	0.7	0.2	0.00	0.00	0.00	1.0000	1.0000
Equal	2	0.7	0.3	0.00	0.00	0.00	1.0000	1.0000
Equal	3	0.9	0.1	0.00	0.00	0.00	1.0000	1.0000
Equal	3	0.9	0.2	0.00	0.00	0.00	1.0000	1.0000
Equal	3	0.9	0.3	0.00	0.00	0.00	1.0000	1.0000
Equal	3	0.8	0.1	0.00	0.00	0.00	1.0000	1.0000
Equal	3	0.8	0.2	0.01	0.00	0.01	1.0000	0.9987
Equal	3	0.8	0.3	0.05	0.04	0.01	0.9863	0.9910
Equal	3	0.7	0.1	0.03	0.01	0.02	0.9974	0.9962
Equal	3	0.7	0.2	0.07	0.06	0.01	0.9768	0.9852
Equal	3	0.7	0.3	0.18	0.12	0.04	0.9493	0.9590
Equal	4	0.9	0.1	0.00	0.00	0.00	0.9988	0.9988
Equal	4	0.9	0.2	0.01	0.01	0.00	0.9977	0.9988
Equal	4	0.9	0.3	0.04	0.03	0.01	0.9865	0.9896
Equal	4	0.8	0.1	0.01	0.01	0.00	0.9956	0.9968
Equal	4	0.8	0.2	0.10	0.08	0.02	0.9663	0.9748
Equal	4	0.8	0.3	0.22	0.13	0.06	0.9346	0.9481
Equal	4	0.7	0.1	0.11	0.06	0.05	0.9730	0.9730
Equal	4	0.7	0.2	0.33	0.19	0.13	0.8830	0.8912
Equal	4	0.7	0.3	0.58	0.36	0.19	0.7864	0.8166
Equal	5	0.9	0.1	0.03	0.02	0.01	0.9905	0.9916
Equal	5	0.9	0.2	0.11	0.08	0.03	0.9756	0.9808
Equal	5	0.9	0.3	0.19	0.12	0.07	0.9445	0.9530
Equal	5	0.8	0.1	0.11	0.06	0.05	0.9653	0.9714
Equal	5	0.8	0.2	0.18	0.09	0.09	0.9194	0.9173
Equal	5	0.8	0.3	0.37	0.19	0.14	0.8227	0.8354
Equal	5	0.7	0.1	0.26	0.12	0.14	0.8982	0.8947
Equal	5	0.7	0.2	0.42	0.18	0.20	0.8037	0.8004
Equal	5	0.7	0.3	0.55	0.33	0.19	0.6738	0.6878
Equal	6	0.9	0.1	0.08	0.03	0.03	0.9777	0.9794
Equal	6	0.9	0.2	0.17	0.05	0.10	0.9454	0.9392
Equal	6	0.9	0.3	0.31	0.22	0.09	0.8585	0.8800
Equal	6	0.8	0.1	0.09	0.05	0.03	0.9226	0.9217
Equal	6	0.8	0.2	0.43	0.19	0.23	0.8168	0.8150
Equal	6	0.8	0.3	0.51	0.28	0.20	0.7242	0.7306
Equal	6	0.7	0.1	0.37	0.18	0.17	0.8280	0.8285
Equal	6	0.7	0.2	0.68	0.37	0.29	0.6769	0.6942
Equal	6	0.7	0.3	0.69	0.43	0.25	0.5830	0.6032
Unequal	2	0.9	0.1	0.01	0.00	0.01	0.9900	0.9865
Unequal	2	0.9	0.2	0.01	0.00	0.01	0.9900	0.9882
Unequal	2	0.9	0.3	0.02	0.00	0.02	0.9846	0.9811
Unequal	2	0.8	0.1	0.00	0.00	0.00	0.9982	0.9982
Unequal	2	0.8	0.2	0.00	0.00	0.00	0.9930	0.9930
Unequal	2	0.8	0.3	0.02	0.01	0.01	0.9822	0.9821
Unequal	2	0.7	0.1	0.01	0.00	0.01	0.9928	0.9911
Unequal	2	0.7	0.2	0.08	0.01	0.07	0.9876	0.9734
Unequal	2	0.7	0.3	0.12	0.03	0.09	0.9529	0.9454
Unequal	3	0.9	0.1	0.00	0.00	0.00	0.9967	0.9967
Unequal	3	0.9	0.2	0.02	0.00	0.02	0.9947	0.9927
Unequal	3	0.9	0.3	0.04	0.02	0.02	0.9891	0.9896
Unequal	3	0.8	0.1	0.01	0.01	0.00	0.9926	0.9936
Unequal	3	0.8	0.2	0.05	0.00	0.05	0.9950	0.9897
Unequal	3	0.8	0.3	0.10	0.03	0.07	0.9687	0.9649
Unequal	3	0.7	0.1	0.05	0.03	0.02	0.9804	0.9804
Unequal	3	0.7	0.2	0.12	0.07	0.05	0.9609	0.9613
Unequal	3	0.7	0.3	0.28	0.15	0.13	0.9359	0.9355
Unequal	4	0.9	0.1	0.03	0.01	0.02	0.9962	0.9954
Unequal	4	0.9	0.2	0.02	0.02	0.00	0.9889	0.9905
Unequal	4	0.9	0.3	0.08	0.04	0.04	0.9739	0.9762
Unequal	4	0.8	0.1	0.05	0.03	0.02	0.9824	0.9839
Unequal	4	0.8	0.2	0.06	0.02	0.04	0.9658	0.9632
Unequal	4	0.8	0.3	0.17	0.12	0.05	0.9436	0.9508
Unequal	4	0.7	0.1	0.08	0.03	0.04	0.9789	0.9775
Unequal	4	0.7	0.2	0.31	0.17	0.13	0.9256	0.9287
Unequal	4	0.7	0.3	0.41	0.18	0.23	0.8468	0.8485
Unequal	5	0.9	0.1	0.02	0.01	0.01	0.9917	0.9916
Unequal	5	0.9	0.2	0.15	0.06	0.09	0.9569	0.9540
Unequal	5	0.9	0.3	0.19	0.11	0.07	0.9307	0.9336
Unequal	5	0.8	0.1	0.11	0.05	0.06	0.9657	0.9645
Unequal	5	0.8	0.2	0.20	0.14	0.06	0.9173	0.9245
Unequal	5	0.8	0.3	0.36	0.22	0.13	0.8527	0.8609
Unequal	5	0.7	0.1	0.27	0.12	0.15	0.9217	0.9202
Unequal	5	0.7	0.2	0.45	0.21	0.23	0.8582	0.8597
Unequal	5	0.7	0.3	0.50	0.26	0.23	0.7510	0.7578
Unequal	6	0.9	0.1	0.09	0.04	0.04	0.9732	0.9717
Unequal	6	0.9	0.2	0.24	0.15	0.07	0.9267	0.9331
Unequal	6	0.9	0.3	0.22	0.15	0.05	0.8832	0.8916
Unequal	6	0.8	0.1	0.12	0.02	0.09	0.9460	0.9387
Unequal	6	0.8	0.2	0.32	0.13	0.17	0.8808	0.8780
Unequal	6	0.8	0.3	0.46	0.23	0.23	0.8090	0.8122
Unequal	6	0.7	0.1	0.21	0.11	0.10	0.9280	0.9291
Unequal	6	0.7	0.2	0.40	0.24	0.15	0.8376	0.8450
Unequal	6	0.7	0.3	0.49	0.22	0.27	0.7300	0.7317

Note. The first four columns correspond to the cells of the experimental design: the distribution of vertices across communities, the number of communities, cohesion, and overlap, respectively. The fifth column is the proportion of cell replicates for which the Ward’s method SSE exceeded the K-means SSE. The sixth and seventh columns for which Ward’s method and K-means partitions, respectively, yielded better agreement with the true partition. The eighth and ninth columns correspond to the cell average ARI values for the Ward’s and K-means implementations, respectively.

The walktrap algorithm using Ward’s method failed to match the optimal SSE identified by the implementation using the branch-and-bound algorithm for 1424 (15.8%) of the 9000 test problems. The proportion of test problems for which Ward’s method failed to minimize SSE increased monotonically as a function of the number of communities, with proportions of 0.015, 0.056, 0.145, 0.248, and 0.327 for K = 2, 3, 4, 5, and 6, respectively. The suboptimality of Ward’s method was also profoundly affected by the strength of the community structure. Under conditions of high cohesion (0.9) and low overlap (0.1), the proportion of test problems for which Ward’s method failed to minimize SSE was 0.026; however, under conditions of low cohesion (0.7) and high overlap (0.3), the corresponding proportion was 0.380.

Interestingly, a better (smaller) SSE did not necessarily translate into a better (larger) ARI. For the 1424 test problems where K-means provided a smaller SSE than Ward’s method, there were 754 (52.9%) instances where the K-means partition had stronger agreement with the true partition but 621 (43.6%) instances where the Ward’s method partition had stronger agreement.² Similarly, the differences in the average ARIs for the two methods were generally modest. Across all 9000 test problems, the average ARI for the Ward’s and K-means implementations of the walktrap algorithm were 0.9348 and 0.9370, respectively. The K-means implementation had a larger average ARI than the Ward’s implementation for 42 cells, the Ward’s implementation had a larger average ARI for 31 cells, and the two methods had the same average ARI for 17 cells.

With respect to both average ARI and the proportion of problems with larger ARI, the average performances of the Ward’s and K-means implementations were extremely similar when the number of communities was unequally-sized. For example, across all test problems with unequally-sized communities, the average ARIs for the Ward’s and K-means implementations were 0.9417 and 0.9419, respectively.

Simulation 2

The second experimental design was based on one recently used by Brusco, Steinley et al. (2022a). Three problem-design features were manipulated: (ii) the number of communities (K), (iii) the distribution of items across communities, and (iii) sample size (n). The number of communities was tested at the same five levels considered in Simulation 1: K = 2, K = 3, K = 4, K = 5, and K = 6. Likewise, the two levels for the distribution of items across communities were also analogous to those in Simulation 1: (i) an equal distribution of vertices across communities, and (ii) an unequal distribution of vertices across communities. The third design feature was tested at three levels: n = 1,000, n = 2,000, and n = 4,000. The experimental design consisted of 5 × 2 × 3 = 30 cells and we used 100 replications per cell, resulting in a total of 3000 test problems for the simulation experiment.

The test problems were generated using the Gaussian graphical model (GGM: Lauritzen, 1996). A population inverse covariance matrix, ${\mathbf{\text{Σ}}}^{-1}$, also known as a precision matrix, was established for each combination of K and distribution of vertices across communities. Consistent with other simulation studies (Barber & Drton, 2015; Ravikumar et al., 2010), precision matrix elements of σ⁻¹(i,j) = σ⁻¹(j,i) = −0.50 were used for all couplings of vertices in the same community and off-diagonal elements pertaining to elements not in the same community were set to zero. To assure a positive definite covariance matrix, a constant of 10 was used for the main diagonal elements. Samples of size n were subsequently simulated from the covariance to produce an n × p data matrix. The inverse sample covariance matrix, ${\mathbf{\text{S}}}^{-1}=[s_{ij}^{-1}]$, was computed from the sample data matrix. Finally, the adjacency matrix ($\mathbf{\text{A}}$) elements, which are measures of partial correlation, are computed as follows:

$$a_{ij}=\frac{{-s}_{ij}^{-1}}{\sqrt{s_{ii}^{-1}{s}_{jj}^{-1}}}\text{for}1\le i\le p\text{and}1\le j\le p$$ (9)

The same two versions of the walktrap algorithm evaluated in Simulation 1 were applied to each of the 3000 test problems. The same performance measures from Simulation 1 were computed for each cell of the experimental design. The results for Simulation 2 are displayed in Table 2.

Table 2.

Simulation 2 –Cell Means for Proportion of Suboptimal Walktrap SSE’s, ARIs, Proportion of Test Problems for Which Each Method Yielded a Better ARI, and ARI.

			Proportion	Proportion with better ARI		Mean ARI
Dist	K	n	Ward’s SEE > K-means SSEs	Ward’s	K-means	Ward’s	K-means
Equal	2	1000	0.12	0.09	0.03	0.9668	0.9768
Equal	2	2000	0.00	0.00	0.00	1.0000	1.0000
Equal	2	4000	0.00	0.00	0.00	1.0000	1.0000
Equal	3	1000	0.68	0.38	0.28	0.7104	0.7500
Equal	3	2000	0.03	0.03	0.00	0.9910	0.9949
Equal	3	4000	0.00	0.00	0.00	1.0000	1.0000
Equal	4	1000	0.76	0.52	0.24	0.4580	0.5055
Equal	4	2000	0.22	0.17	0.05	0.9348	0.9418
Equal	4	4000	0.00	0.00	0.00	1.0000	1.0000
Equal	5	1000	0.77	0.43	0.32	0.3446	0.3595
Equal	5	2000	0.52	0.36	0.15	0.7517	0.7852
Equal	5	4000	0.05	0.04	0.01	0.9883	0.9947
Equal	6	1000	0.87	0.50	0.37	0.2534	0.2678
Equal	6	2000	0.66	0.37	0.27	0.6150	0.6272
Equal	6	4000	0.09	0.05	0.02	0.9585	0.9652
Unequal	2	1000	0.18	0.13	0.05	0.9110	0.9282
Unequal	2	2000	0.02	0.00	0.02	0.9982	0.9946
Unequal	2	4000	0.00	0.00	0.00	1.0000	1.0000
Unequal	3	1000	0.67	0.36	0.31	0.7269	0.7227
Unequal	3	2000	0.15	0.10	0.05	0.9635	0.9699
Unequal	3	4000	0.01	0.01	0.00	0.9980	0.9991
Unequal	4	1000	0.68	0.39	0.29	0.5183	0.5294
Unequal	4	2000	0.38	0.21	0.17	0.8902	0.8877
Unequal	4	4000	0.04	0.00	0.04	0.9915	0.9888
Unequal	5	1000	0.76	0.38	0.38	0.3794	0.3856
Unequal	5	2000	0.45	0.19	0.26	0.7933	0.7816
Unequal	5	4000	0.11	0.07	0.04	0.9616	0.9619
Unequal	6	1000	0.80	0.43	0.35	0.3083	0.3097
Unequal	6	2000	0.64	0.26	0.33	0.6501	0.6413
Unequal	6	4000	0.30	0.18	0.10	0.8950	0.9019

Note. The first three columns correspond to the cells of the experimental design: the distribution of vertices across communities, the number of communities, and the sample size, respectively. The fourth column is the proportion of cell replicates for which the Ward’s method SSE exceeded the K-means SSE. The fifth and sixth columns for which Ward’s method and K-means partitions, respectively, yielded better agreement with the true partition. The seventh and eight columns correspond to the cell average ARI values for the Ward’s and K-means implementations, respectively.

On average, the SSE optimization problems in Simulation 2 seemed to be more challenging than those in Simulation 1 as the Ward’s implementation failed to attain the globally-optimal SSE for a larger percentage of test problems. The walktrap algorithm using Ward’s method failed to match the optimal SSE identified by the implementation using the branch-and-bound algorithm for 996 (33.2%) of the 3000 test problems. Once again, the proportion of test problems for which Ward’s method failed to minimize SSE increased monotonically as a function of the number of communities, with proportions of 0.053, 0.257, 0.347, 0.443, and 0.560 for K = 2, 3, 4, 5, and 6, respectively. The suboptimality of Ward’s method was also affected by the strength of the community structure, as measured by sample size. The proportions of test problems for which Ward’s method failed to minimize SSE were 0.629, 0.307, and 0.060 for the n = 1000, n = 2000, and n = 4000 conditions, respectively.

Like Simulation 1, the results in Simulation 2 revealed that a better (smaller) SSE frequently did not translate into a better (larger) ARI. For the 996 test problems where K-means provided a smaller SSE than Ward’s method, there were 565 (56.7%) instances where the K-means partition had stronger agreement with the true partition but 413 (41.5%) instances where the Ward’s method had stronger agreement.³ Moreover, like Simulation 1, the differences in the average ARIs for the two methods were modest. Across all 3000 test problems in Simulation 2, the average ARI for the Ward’s and K-means implementations of the walktrap algorithm were 0.7986 and 0.8057, respectively. The K-means implementation had a larger average ARI than the Ward’s implementation for 20 cells, the Ward’s implementation had a larger average ARI for 4 cells, and the two methods had the same average ARI for 6 cells.

Also like Simulation 2, with respect to both average ARI and the proportion of problems with larger ARI than the K-means implementation, the average performances of the Ward’s and K-means implementations were more similar when the number of communities was unequally-sized. For example, across all test problems with unequally-sized communities, the average ARIs for the Ward’s and K-means implementations were 0.7990 and 0.8002, respectively.

Simulation 3

For Simulation 3, data were generated based on a factor model and estimation of the association matrix was accomplished based on the Gaussian graphical model. Five experimental design features were manipulated in the experimental study and the guidelines for the selection of their levels were largely based on the work of Golino et al. (2020) and Christensen et al. (2021): (a) the strength of the factor loadings, (b) the number of factors, (c) the number variables per factor, (d) the correlation between the factors, and (e) the sample size. The factor loading levels were λ* = 0.7 and λ* = 0.55, which correspond, respectively, to excellent and moderate loading strength (Golino et al., 2020; Comrey & Lee, 2016). The number of factors⁴ was tested at levels of g = 2 and g = 4, whereby g represents the ‘true’ dimensionality of the data. The levels for the number of variables (or items) per factor were v = 4 and v = 6. Four items is slightly above the threshold of three necessary for factor identification (Anderson & Rubin, 1958), whereas six items is modestly stronger. Together, the settings of g and v will produce networks ranging from p = gv = 8 to p = 24 variables and networks in the network psychometrics literature commonly fall within this size range. The correlation between factors was tested at levels of ϕ = 0.0 and ϕ = 0.5, which correspond, respectively, to orthogonal factors and large correlation between factors (Cohen, 1988; Golino et al., 2020). Finally, sample size was tested at levels of n = 500 and n = 1000, which correspond , respectively, to low-to-medium and large sample sizes (Li, 2016).

The five design features each with two levels produce 2⁵ = 32 experimental cells and 100 replications were completed for each cell, resulting in 3200 test problems. The generation of the test problems in MATLAB was accomplished by producing a p × g matrix of factor loadings for the selected loading strength, $\mathbf{\text{Λ}}$, and a g × g factor correlation matrix $\mathbf{\text{Φ}}$. Following Golino et al. (2020), the elements of $\mathbf{\text{Λ}}=[{\text{λ}}_{iq}]$ are randomly drawn from a uniform distribution on the interval [λ* - 0.1, λ* + 0.1] if variable $i$ is a member of factor $q$; otherwise, ${\text{ω}}_{iq}$ is randomly drawn from a normal distribution with a mean of zero and standard deviation of 0.05. The $p\times p$ population correlation matrix, $\mathbf{\text{Γ}}$, is obtained by setting $\mathbf{\text{Γ}}=\mathbf{\text{ΛΦ}}{\mathbf{\text{Λ}}}^{\prime }$ and then re-setting the main diagonal elements to unity.⁵ A Cholesky decomposition is performed on $\mathbf{\text{Γ}}$, $\mathbf{\text{Γ}}={\mathbf{\text{U}}}^{\prime }\mathbf{\text{U}}$, where $\mathbf{\text{U}}$ is a $p\times p$ upper triangular matrix. Finally, the $n\times p$ data matrix, $\mathbf{\text{Y}}$, is obtained via $\mathbf{\text{Y}}=\mathbf{\text{ZU}}$, where $\mathbf{\text{Z}}$ is an $n\times p$ matrix generated from a multivariate normal distribution.

The estimation of the association matrix, $\mathbf{\text{A}}$, from $\mathbf{\text{Y}}$ is based on the Gaussian graphical model (Epskamp & Fried, 2018; Lauritzen, 1996). There are several types estimation procedures that can be used, which include non-regularized methods (Williams et al, 2019; Williams & Rast, 2020), global l₁-regularized estimation procedures (Friedman et al., 2008, 2014), nodewise l₁-regularized estimation procedures (Meinshausen & Buhlmann, 2006), and nodewise best subsets regression (Brusco, Watts et al. 2022). Although the method selected could potentially have an effect on the recovery of network structure, all of these methods are well-established and our focus is not on evaluation of estimation methods. Because it is readily available in MATLAB, we use nodewise, l₁-regularized estimation herein. With this approach, each variable is taken in turn and all other variables are used as predictors. Model selection for each variable is accomplished by evaluating a large range of lasso penalty parameters and the extended Bayesian information criterion (EBIC; Chen & Chen, 2008) is used for selection. Finally, because nodewise selection results in an asymmetric association matrix such that $a_{ij}\ne a_{ji}$, the elements are coerced to symmetric using the ‘AND’ rule (Wainwright et al., 2007), whereby $a_{ij}=a_{ji}=(a_{ij}+a_{ji})/2$ if $a_{ij}\ne 0$ and $a_{ji}\ne 0$; otherwise, $a_{ij}=a_{ji}=0$.

Unlike Simulations 1 and 2, the true (or correct) number of communities was not prespecified in Simulation 3. For each of the 3200 test problems, the walktrap algorithm using Ward’s method was applied and the walktrap algorithm using the branch-and-bound algorithm for K-means clustering was applied for 2 ≤ K ≤ 6 communities. Because it is the default index (see Csardi & Nepusz, 2006) used to choose the number of communities for the R implementation of the walktrap algorithm, we use the modularity score (Fan et al., 2007; Newman, 2004a; Newman, 2004b; Newman & Girvan, 2004) to select the number of communities for the Ward’s and K-means partitions. The modularity scores requires the sum of the network edge weights⁶:

$$E=\frac{1}{2}{\sum }_{i=1}^p{\sum }_{j=1}^p{a}_{ij}.$$ (10)

It also requires the Kronecker delta, $\text{δ}(c_i$, $c_j)$, where $c_i$ and $c_j$ denote the community memberships of vertices $i$ and $j$, respectively. The Kronecker delta is $\text{δ}(c_i,c_j)=1$ if $c_i=c_j$ and $\text{δ}(c_i,c_j)=0$ if $c_i\ne c_j$. The modularity score for a partition of the vertices is computed as such:

$$Q=\frac{1}{2E}{\sum }_{i=1}^p{\sum }_{j=1}^p\left[a_{ij}-\frac{d_{ii}{d}_{jj}}{2E}\right]\delta \left(c_i,c_j\right)$$ (11)

For unweighted networks, Q is an estimate of the sum, across all communities, of the deviations between actual and expected proportions of edges within the communities based on the assumption that the vertices have the same degrees, while the edges are randomly assigned (Aloise et al., 2010; Newman & Girvan, 2004). Values of Q near zero (one) reflect weak (strong) community structure. For both the Ward’s and K-means implementations of the walktrap algorithm, the modularity scores were computed for all K-community partitions on the interval 2 ≤ K ≤ 6 and the partition (and its corresponding number of communities) with the largest modularity score was selected. For each method and test problem, results were stored for the number of communities, the SSE, and the ARI.

For 3138 of the 3200 test problems, the Ward’s method and K-means implementations of the walktrap algorithm resulted in the selection of the same number of communities. Across these 3138 test problems, the K-means SSE was smaller than the Ward’s method SSE in only 74 instances. Thus, relative to Simulations 1 and 2, Ward’s method was far more likely to match the globally-optimal SSE in Simulation 3. Table 3 reveals that the Ward’s method and K-means implementations of the walktrap algorithm resulted in the selection of the true number of communities for the vast majority of the test problems. For 21 of the 32 cells of the experimental design, the two methods yielded the same proportions of correct identifications of the true number of communities. In 19 of these 21 instances, correct identification was established by both methods for all 100 cell replicates. In the 11 cells where the two methods yielded different proportions, the K-means implementation yielded a larger proportion of correct identifications for eight cells, whereas the Ward’s method implementation had a larger proportion for three.

Table 3.

Simulation 3 Results

					Proportion correct K		Average ARI
Loadings (λ)	Factors (g)	Variables (v)	Correlation (ϕ)	Sample size (n)	Ward’s	K-means	Ward’s	K-means
0.7	2	4	0	500	1.00	1.00	1.0000	1.0000
0.7	2	4	0	1000	1.00	1.00	1.0000	1.0000
0.7	2	4	0.5	500	1.00	1.00	1.0000	1.0000
0.7	2	4	0.5	1000	1.00	1.00	1.0000	1.0000
0.7	2	6	0	500	1.00	1.00	1.0000	1.0000
0.7	2	6	0	1000	1.00	1.00	1.0000	1.0000
0.7	2	6	0.5	500	0.98	1.00	0.9910	0.9933
0.7	2	6	0.5	1000	1.00	1.00	1.0000	1.0000
0.7	4	4	0	500	1.00	1.00	1.0000	1.0000
0.7	4	4	0	1000	1.00	1.00	1.0000	1.0000
0.7	4	4	0.5	500	0.98	0.99	0.9939	0.9938
0.7	4	4	0.5	1000	1.00	1.00	1.0000	1.0000
0.7	4	6	0	500	1.00	1.00	1.0000	1.0000
0.7	4	6	0	1000	1.00	1.00	1.0000	1.0000
0.7	4	6	0.5	500	0.92	0.97	0.9742	0.9711
0.7	4	6	0.5	1000	0.99	1.00	0.9988	0.9988
0.55	2	4	0	500	1.00	1.00	1.0000	1.0000
0.55	2	4	0	1000	1.00	1.00	1.0000	1.0000
0.55	2	4	0.5	500	0.92	0.91	0.9443	0.9516
0.55	2	4	0.5	1000	0.98	0.99	0.9931	0.9927
0.55	2	6	0	500	1.00	1.00	1.0000	1.0000
0.55	2	6	0	1000	1.00	1.00	1.0000	1.0000
0.55	2	6	0.5	500	0.92	0.91	0.9609	0.9721
0.55	2	6	0.5	1000	1.00	1.00	1.0000	1.0000
0.55	4	4	0	500	0.99	0.99	0.9992	0.9992
0.55	4	4	0	1000	1.00	1.00	1.0000	1.0000
0.55	4	4	0.5	500	0.64	0.59	0.8680	0.8552
0.55	4	4	0.5	1000	0.90	0.94	0.9668	0.9708
0.55	4	6	0	500	0.98	0.98	0.9977	0.9989
0.55	4	6	0	1000	1.00	1.00	1.0000	1.0000
0.55	4	6	0.5	500	0.53	0.59	0.8524	0.8498
0.55	4	6	0.5	1000	0.94	0.97	0.9841	0.9828

Note. The first five columns correspond to the cells of the experimental design: the strength of the factor loadings, the number of factors/communities, items per factor, correlation between factors, and sample size, respectively. The sixth and seventh columns indicate the proportion of problems in the cell for which Ward’s method and K-means led to the identification of the correct/true number of factors/communities. The eighth and eight ninth columns correspond to the cell average ARI values for the Ward’s and K-means implementations, respectively.

Table 3 also provides the average ARI for each method for each of the 32 cells of the experimental design. The two methods yielded the same average ARI for 21 of the 32 cells and, in 19 of these 21 instances, both methods provided perfect recovery of the true community structure for all 100 test problems in the cell (i.e., average ARI = 1.0). In the 11 instances where the two methods had different average ARIs, the Ward’s method average was larger for six cells and the K-means average larger for five. Moreover, like Simulations 1 and 2, the differences in the average ARIs for the two methods were modest. As expected, the worst average recovery performances for the two methods occurred for weaker structures associated with smaller loadings (0.55), higher factor correlation (0.5), and lower sample size (n = 500).

Evaluation of Ward’s method on empirical networks

In the simulation study conducted by Brusco, Steinley et al. (2022a), when provided with the correct number of communities, Ward’s method and multistart K-means implementations of the walktrap algorithm produced the same SSE value for 55.6% of the 8000 test problems and multistart K-means provided a better SSE for the remainder of the test problems. The two algorithms were much more likely to produce the same SSE value for well-structured networks based on larger sample sizes. For example, for the most well-structured networks based on a sample size of n = 8000, Ward’s method and multistart K-means yielded the same SSE value for 94.2% of the networks. However, for the least-structured networks based on a sample size of n = 1000, Ward’s method and multistart K-means yielded the same SSE value for only 20.1% of the networks. Here, we compare the SSE values obtained by Ward’s and multistart K-means implementations of the walktrap algorithm across empirical networks from the literature. All analyses were completed using MATLAB (MATLAB, 2020).

Unweighted networks

Table 1 provides a comparison of SSE values for four empirical unweighted networks of the type studied by Hoffman et al. (2018). The four networks are: (i) Zachary’s (1977) Karate Club network, p = 34; (ii) the Dolphins social interaction network (Lusseau et al., 2003), p = 62; (iii) Krebs (unpublished) political books (PolBooks) network, p = 105; and (iv) Girvan and Newman’s (2002) Football schedule network, p = 115. Table 4 contains the SSE values for Ward’s method and multistart K-means, as well as the SSE difference and the percentage by which the Ward’s method SSE value exceeds the K-means SSE value. It is evident that SSE decreases monotonically as K increases and, therefore, SSE alone cannot be used to select K. For this reason, the modularity score (Q) is also reported in Table 4.

Table 4.

SSE Comparisons for Unweighted Networks

		SSE Results				Modularity
Network	K	Ward	K-means	Difference	% Difference	Ward	K-means
Karate	2	0.06947375	0.06862876	0.00084499	1.23%	0.3715	0.3560
	3	0.03061119	0.03061119	0.00000000	0.00%	0.3991	0.3991
	4	0.01969391	0.01969391	0.00000000	0.00%	0.4112	0.4112
	5	0.01591384	0.01521854	0.00069530	4.57%	0.3860	0.4000
Dolphins	2	0.24947190	0.24363008	0.00584182	2.40%	0.3899	0.3787
	3	0.20515727	0.20032330	0.00483397	2.41%	0.3852	0.3732
	4	0.17515406	0.16947426	0.00567980	3.35%	0.4774	0.4778
	5	0.14807816	0.14350780	0.00457036	3.18%	0.4735	0.4749
	6	0.12256497	0.11808402	0.00448095	3.79%	0.4725	0.4639
	7	0.10576203	0.10278764	0.00297439	2.89%	0.4591	0.4981
	8	0.09294599	0.09156716	0.00137883	1.51%	0.4872	0.4948
PolBooks	2	0.12664194	0.12649827	0.00014367	0.11%	0.4569	0.4544
	3	0.08680631	0.08669552	0.00011079	0.13%	0.4986	0.4946
	4	0.06909158	0.06898079	0.00011079	0.16%	0.5262	0.5222
	5	0.05585446	0.05567723	0.00017723	0.32%	0.5202	0.5192
	6	0.04334890	0.04281414	0.00053476	1.25%	0.5154	0.5165
Football	2	0.07537154	0.07531854	0.00005300	0.07%	0.3846	0.3865
	3	0.05886640	0.05884744	0.00001896	0.03%	0.5084	0.5051
	4	0.04863588	0.04778899	0.00084689	1.77%	0.5483	0.5418
	5	0.03848163	0.03746888	0.00101275	2.70%	0.5687	0.5708
	6	0.03077726	0.03046479	0.00031247	1.03%	0.5901	0.5773
	7	0.02429795	0.02416722	0.00013073	0.54%	0.5979	0.5930
	8	0.01800223	0.01789957	0.00010266	0.57%	0.6032	0.5998
	9	0.01317048	0.01304179	0.00012869	0.99%	0.6043	0.5954
	10	0.00849672	0.00849672	0.00000000	0.00%	0.6044	0.6044

Note. The SSE results obtained using the walktrap algorithm with both Ward’s method and a multistart K-means clustering heuristic are reported, as is the difference in the SSE values (Ward minus K-means) and the percentage difference. Modularity scores associated with the Ward’s method and K-means clustering are also reported.

The results in Table 4 reveal that Ward’s method generally yields an SSE value that exceeds the SSE value obtained by multistart K-means clustering. Two of the three instances where the Ward’s method matched the K-means result occurred for Karate network. The percentage deviations for the PolBooks network were quite small for most values of K. Contrastingly, the percentage deviations for the Dolphins network were mostly in the 2–3% range. The percentage deviations for the Football network ranged from 0% to 2.7%.

The results in Table 4 also show that there is often discordance between SSE and Q. That is, smaller (better) values of SSE do not necessarily translate to larger (better) values of Q. This finding was recently observed by Brusco, Steinley et al. (2022b) and, moreover, it should be recognized that methods that attempt to minimize SSE (including Ward’s method and K-means) generally do not find partitions that maximize Q. It is encouraging to note that, for three of the four networks in Table 4, the selection of K based on largest Q would be the same regardless of whether Ward’s method or K-means is used. The exception is the Dolphins network, where Ward’s method results in the selection of K = 8 (based on Q = 0.4872) and K-means results in the selection of K = 7 (based on Q = 0.4981). As noted by Aloise et al. (2010) and Brusco, Steinley et al. (2022b), the maximum value of Q = 0.5285 actually corresponds to a K = 5-community partition.

Weighted (partial correlation) networks

Table 5 provides a comparison of SSE values for four empirical weighted networks of the type commonly studied in the network psychometrics literature. The four networks are: (i) the Obama beliefs and attitudes network (Dalege et al., 2017) p = 10; (ii) the Han Chinese women depression network (Kendler et al., 2018), p = 19; (iii) the Empathy network (Briganti et al., 2018), p = 28; and (iv) the Emotion network (Lange & Zickfeld, 2021; Weidman & Tracy, 2020), p = 56. Table 5 contains the SSE values for Ward’s method and K-means, as well as the SSE difference, the percentage by which the Ward’s method SSE value exceeds the K-means SSE value, and the modularity scores. For the three smaller networks, branch-and-bound programming was used to obtain guaranteed optimal SSE values for the K-means solution, whereas the multistart K-means heuristic was necessary for the larger Emotion network.

Table 5.

SSE Comparisons for Weighted Networks

		SSE Results				Modularity
Network	K	Ward	K-means	Difference	% Difference	Ward	K-means
Obama	2	0.00063952	0.00063952	0.00000000	0.00%	0.0887	0.0887
	3	0.00025376	0.00025376	0.00000000	0.00%	0.1475	0.1475
	4	0.00005760	0.00005760	0.00000000	0.00%	0.1342	0.1342
	5	0.00003550	0.00003550	0.00000000	0.00%	0.0768	0.0768
Han	2	0.01897008	0.01897008	0.00000000	0.00%	0.2738	0.2738
	3	0.00788391	0.00788391	0.00000000	0.00%	0.3019	0.3019
	4	0.00621154	0.00598555	0.00022599	3.78%	0.2457	0.2667
	5	0.00471093	0.00448496	0.00022597	5.04%	0.2022	0.2231
Empathy	2	0.12560777	0.12560777	0.00000000	0.00%	0.2390	0.2390
	3	0.07100972	0.07100972	0.00000000	0.00%	0.3833	0.3833
	4	0.04466778	0.03951395	0.00515383	13.04%	0.4163	0.4005
	5	0.03497292	0.02981909	0.00515383	17.28%	0.4092	0.3933
	6	0.02585761	0.02271613	0.00314148	13.83%	0.3762	0.3558
Emotion	2	0.08683991	0.08229943	0.00454048	5.52%	0.0866	0.1873
	3	0.05786092	0.05521453	0.00264639	4.79%	0.2216	0.2616
	4	0.04044612	0.03838701	0.00205911	5.36%	0.2735	0.2907
	5	0.03339145	0.03147526	0.00191619	6.09%	0.2855	0.2985
	6	0.02689232	0.02622428	0.00066804	2.55%	0.3035	0.2934
	7	0.02304063	0.02152170	0.00151893	7.06%	0.3240	0.3105
	8	0.01996470	0.01844577	0.00151893	8.23%	0.3022	0.2887

Note. The SSE results obtained using the walktrap algorithm with both Ward’s method and a multistart K-means clustering are reported, as is the difference in the SSE values (Ward minus K-means) and the percentage difference. Modularity scores associated with the Ward’s method and K-means clustering are also reported. For the Obama, Han, and Empathy networks, branch-and-bound was used to obtain globally-optimal K-means partitions. For the Emotion network, the multistart K-means heuristic was used.

For the two smaller networks (Obama and Han), Ward’s method frequently matched the optimal SSE value obtained using the branch-and-bound algorithm for K-means. For the Han depression network at K = 4 and K = 5, the SSE value for Ward’s method exceeded the optimal SSE by 3.78% and 5.04%, respectively. For the Empathy network, Ward’s method matched the optimal SSE for K ≤ 3 but yielded an appreciably larger SSE when K ≥ 4, ranging from 13.04% to 17.28% greater than the optimal SSE. The 13.04% deviation at K = 4 is especially significant because four communities would be selected based on modularity for both Ward’s method and K-means. Finally, for the Emotion network, Ward’s method did not match the multistart K-means SSE for any value of K and the percentage differences ranged from 2.55% to 8.23%. The modularity score indicates a seven-community solution for both the Ward’s and K-means algorithms; however, the SSE for the seven-community Ward’s method solution is 7.06% greater than that of the K-means solution. Moreover, as noted by Brusco, Steinley et al. (2022a), the agreement between these two partitions as measured by the adjusted Rand index (ARI; Hubert & Arabie, 1985) is only ARI = 0.6692, which is at the low end of the range for ‘fair’ agreement based on the scale provided by Steinley (2004).

fMRI networks

Next, we turned our attention to 36 empirical functional connectivity matrices from the fMRI literature (Rieck et al., 2021a, 2021b)⁷. The matrices correspond to functional connectivity (measured by time series correlations) for two subjects, measured for six different tasks, using three different brain atlases (2 × 6 × 3 = 36). The six tasks were inhibition, initiation, shifting, and working memory at three loads (0-back, 1-back, and 2-back). The three brain atlases were: Schaefer 100 parcel 17 network atlas (Schaefer et al., 2018; Yeo et al., 2011), and Schaefer 200 parcel 17 network atlas (Schaefer et al., 2018; Yeo et al., 2011), and Power 229 node 10 network atlas (Power et al., 2011).

Our analyses of the fMRI networks was completed in two phases. In the first phase, we applied the walktrap algorithm using Ward’s method and the walktrap algorithm using multistart K-means separately, allowing each method to choose the number of communities based on maximum modularity. Accordingly, the two methods did not necessarily result in the selection of the same number of communities. For each of the 36 functional connectivity matrices, Table 6 provides the number of communities selected for each method. The two methods selected the same number of communities for only 18 of the 36 matrices. The Ward’s method implementation selected more communities than multistart K-means for 12 of the 18 matrices and had a larger average number of communities selected (3.14 for Ward’s vs. 2.86 for multistart K-means).

Table 6.

Number of Communities and SSE Results for Functional Connectivity Matrices

	# of communities (K)		SSE
Functional connectivity matrix	Ward’s	K-means	Ward’s	K-means	ARI
Schaefer100_17_sub-001_gng_inhibition	4	2	0.00551865	0.01558034	0.4367
Schaefer100_17_sub-001_gng_initiation	3	2	0.04659361	0.06408007	0.5257
Schaefer100_17_sub-001_nbk_0back	2	2	0.06951225	0.06872225	0.9600
Schaefer100_17_sub-001_nbk_1back	2	2	0.02078832	0.02065508	0.8824
Schaefer100_17_sub-001_nbk_2back	4	5	0.02352271	0.01644922	0.8323
Schaefer100_17_sub-001_tsw_shifting	2	3	0.04464777	0.01923589	0.7009
Schaefer200_17_sub-001_gng_inhibition	2	2	0.01672525	0.01578580	0.5893
Schaefer200_17_sub-001_gng_initiation	4	2	0.01368322	0.02312299	0.4044
Schaefer200_17_sub-001_nbk_0back	2	2	0.02748137	0.02668606	0.7383
Schaefer200_17_sub-001_nbk_1back	2	2	0.01520388	0.01450658	0.8091
Schaefer200_17_sub-001_nbk_2back	4	5	0.00828381	0.00598431	0.6667
Schaefer200_17_sub-001_tsw_shifting	4	3	0.00718619	0.00870851	0.3847
Power229_10_sub-001_gng_inhibition	3	2	0.01357558	0.02678875	0.3185
Power229_10_sub-001_gng_initiation	3	4	0.00684126	0.00541662	0.4146
Power229_10_sub-001_nbk_0back	5	4	0.01042447	0.01098515	0.4795
Power229_10_sub-001_nbk_1back	3	2	0.00886022	0.01509397	0.4474
Power229_10_sub-001_nbk_2back	3	3	0.00874520	0.00771644	0.6757
Power229_10_sub-001_tsw_shifting	2	2	0.03854919	0.03406566	0.5428
Schaefer100_17_sub-002_gng_inhibition	3	3	0.20265374	0.17856246	0.6673
Schaefer100_17_sub-002_gng_initiation	3	3	0.06450903	0.06170384	0.6507
Schaefer100_17_sub-002_nbk_0back	3	3	0.17659350	0.12949262	0.3495
Schaefer100_17_sub-002_nbk_1back	2	2	0.09835984	0.09049773	0.8448
Schaefer100_17_sub-002_nbk_2back	4	3	0.03479563	0.04252043	0.4466
Schaefer100_17_sub-002_tsw_shifting	3	4	0.01670888	0.01162490	0.7080
Schaefer200_17_sub-002_gng_inhibition	5	3	0.03529750	0.04944566	0.5071
Schaefer200_17_sub-002_gng_initiation	5	5	0.01023696	0.00931474	0.7047
Schaefer200_17_sub-002_nbk_0back	4	3	0.01839637	0.02228965	0.5933
Schaefer200_17_sub-002_nbk_1back	2	2	0.02426733	0.02388012	0.9212
Schaefer200_17_sub-002_nbk_2back	3	3	0.01599856	0.01528689	0.8182
Schaefer200_17_sub-002_tsw_shifting	4	3	0.00718619	0.00870851	0.3847
Power229_10_sub-002_gng_inhibition	3	3	0.02236710	0.01900347	0.5747
Power229_10_sub-002_gng_initiation	4	2	0.00515824	0.00837468	0.3702
Power229_10_sub-002_nbk_0back	3	3	0.00842898	0.00791738	0.7372
Power229_10_sub-002_nbk_1back	3	3	0.00820437	0.00786124	0.7418
Power229_10_sub-002_nbk_2back	3	3	0.00672173	0.00617936	0.5242
Power229_10_sub-002_tsw_shifting	2	3	0.02003771	0.01267962	0.3657

Note. The number of communities (K) selected based on the modularity index are reported for both the walktrap algorithm using Ward’s method and the walktrap algorithm using multistart K-means. The SSE results (after multiplication by 10⁴ to improve readability) are also reported for the two methods but the values are only comparable when K is the same for both methods. The adjusted Rand index (ARI) measure of agreement between the Ward’s method and K-means partitions is reported in the last column.

Although Table 6 reports the SSE values for both the Ward’s method and multistart K-means implementations of the walktrap algorithm, these numbers are only directly comparable when the two methods use the same number of communities. In all 18 instances where the two methods used the same number of communities, the multistart K-means SSE was smaller (better) than the Ward’s method SSE.

The partition agreement results are valid for all 36 matrices because computation of the ARI does not require an equal number of communities. The agreement between the Ward’s method and multistart K-means partitions was generally weak. The average ARI across the 36 test problems was only 0.6033, which is below the 0.65 threshold for fair agreement. Moreover, poor agreement (ARI < 0.65) was observed for 19 problems. The ARI exceeds the threshold of 0.8 for ‘good’ agreement for only seven of the 36 problems (in two of these seven instances, the ARI exceeded the threshold of 0.9 for ‘excellent’ agreement).

In the second phase of the analysis, we ran the walktrap algorithm using multistart K-means for the same number of communities selected using Ward’s method. This facilitates a fair SSE comparison of Ward’s method and multistart K-means for the full set of 36 functional connectivity network matrices. The results are shown in Table 7.

Table 7.

Fixed K Results for Functional Connectivity Matrices

Functional connectivity matrix	Ward’s K	SSE Ward’s – SSE K-means	% Difference	ARI
Schaefer100_17_sub-001_gng_inhibition	4	0.00059521	12.09%	0.6914
Schaefer100_17_sub-001_gng_initiation	3	0.00074619	1.63%	0.7227
Schaefer100_17_sub-001_nbk_0back	2	0.00079000	1.15%	0.9600
Schaefer100_17_sub-001_nbk_1back	2	0.00013324	0.65%	0.8824
Schaefer100_17_sub-001_nbk_2back	4	0.00234554	11.08%	0.7707
Schaefer100_17_sub-001_tsw_shifting	2	0.00776123	21.04%	0.3073
Schaefer200_17_sub-001_gng_inhibition	2	0.00093945	5.95%	0.5893
Schaefer200_17_sub-001_gng_initiation	4	0.00066151	5.08%	0.8113
Schaefer200_17_sub-001_nbk_0back	2	0.00079530	2.98%	0.7383
Schaefer200_17_sub-001_nbk_1back	2	0.00069729	4.81%	0.8091
Schaefer200_17_sub-001_nbk_2back	4	0.00024676	3.07%	0.5033
Schaefer200_17_sub-001_tsw_shifting	4	0.00078530	12.27%	0.6829
Power229_10_sub-001_gng_inhibition	3	0.00038341	2.91%	0.8035
Power229_10_sub-001_gng_initiation	3	0.00044213	6.91%	0.4589
Power229_10_sub-001_nbk_0back	5	0.00093608	9.87%	0.5387
Power229_10_sub-001_nbk_1back	3	0.00046089	5.49%	0.7103
Power229_10_sub-001_nbk_2back	3	0.00102876	13.33%	0.6757
Power229_10_sub-001_tsw_shifting	2	0.00448353	13.16%	0.5428
Schaefer100_17_sub-002_gng_inhibition	3	0.02409128	13.49%	0.6673
Schaefer100_17_sub-002_gng_initiation	3	0.00280519	4.55%	0.6507
Schaefer100_17_sub-002_nbk_0back	3	0.04710088	36.37%	0.3495
Schaefer100_17_sub-002_nbk_1back	2	0.00786211	8.69%	0.8448
Schaefer100_17_sub-002_nbk_2back	4	0.00391188	12.67%	0.7464
Schaefer100_17_sub-002_tsw_shifting	3	0.00090796	5.75%	0.9053
Schaefer200_17_sub-002_gng_inhibition	5	0.00621493	21.37%	0.5474
Schaefer200_17_sub-002_gng_initiation	5	0.00092222	9.90%	0.7047
Schaefer200_17_sub-002_nbk_0back	4	0.00161890	9.65%	0.7545
Schaefer200_17_sub-002_nbk_1back	2	0.00038721	1.62%	0.9212
Schaefer200_17_sub-002_nbk_2back	3	0.00071167	4.66%	0.8182
Schaefer200_17_sub-002_tsw_shifting	4	0.00078530	12.27%	0.6829
Power229_10_sub-002_gng_inhibition	3	0.00336363	17.70%	0.5747
Power229_10_sub-002_gng_initiation	4	0.00028062	5.75%	0.6859
Power229_10_sub-002_nbk_0back	3	0.00051160	6.46%	0.7372
Power229_10_sub-002_nbk_1back	3	0.00034313	4.36%	0.7418
Power229_10_sub-002_nbk_2back	3	0.00054237	8.78%	0.5242
Power229_10_sub-002_tsw_shifting	2	0.00029968	1.52%	0.8965

Note. The values in column K are the number of communities selected when using the walktrap algorithm with Ward’s method. For the given number of communities, the next column reports the amount (after multiplication by 10⁴ to improve readability) by which the SSE using Ward’s method exceeds the SSE using multistart K-means. The percentage difference in the SSE values (Ward minus K-means)/K-means is also provided. The adjusted Rand index (ARI) measure of agreement between the Ward’s method and K-means partitions is reported in the last column.

For each of the 36 functional connectivity matrices, Table 7 provides the number of communities selected using the walktrap algorithm with Ward’s method, as well as the SSE difference when the implementations using Ward’s method and multistart K-means use this same number of communities. Ward’s method did not match the SSE obtained using multistart K-means for any of the 36 test problems. The SSE associated with Ward’s method ranged from 0.65% to 36.37% greater than the multistart K-means SSE with an average of 8.86%. Perhaps more importantly, the agreement between the Ward’s method and multistart K-means partitions remained fairly weak even when the two methods were constrained to the same prescribed number of communities. The average ARI across the 36 test problems was only 0.6931 and poor agreement (ARI < 0.65) was observed for 10 problems. The ARI exceeds the threshold of 0.8 for ‘good’ agreement for 10 of the 36 problems (in three of these 10 instances, the ARI exceeded the threshold of 0.9 for ‘excellent’ agreement).

Discussion

Summary and conclusions

The walktrap algorithm (Pons & Latapy, 2006) has a prominent position as a community-detection method in psychological research because of its performance in simulation studies (Brusco, Steinley et al., 2022a, 2022b; Christensen et al., 2021; Gates et al., 2016; Golino et al., 2020, 2021; Hoffman et al., 2018) and its use in applied research (Dalege et al., 2017; Kendler et al., 2018; McCormick et al., 2019; Price et al., 2017). One of our goals in this paper has been to meticulously illustrate that the computational aspects of the walktrap algorithm can be greatly simplified by working with a data matrix of degree-adjusted transition probabilities and its corresponding matrix of squared Euclidean distances. Using a small example, we rationalize the computational descriptions provided by Pons and Latapy (2006) with this simpler scheme.

More importantly, we used the small example to demonstrate the potential suboptimality of Ward’s hierarchical clustering algorithm, which is the key algorithmic engine of the walktrap algorithm. We then evaluated how common it was for Ward’s method to yield a partition with a suboptimal SSE value and the possible implications of this suboptimality for the recovery of community structure. To do so, we used three simulation studies and analysis of empirical networks of several different types.

The three simulation studies used very different processes for network generation. Nevertheless, it was encouraging to find that the results of the three experiments were similar. The standard implementation of the walktrap algorithm using Ward’s method frequently failed to find the partition with minimum SSE in the first two simulation studies. Surprisingly, however, this did not lead to a severe degradation in the recovery of community structure. Although the optimal K-means implementation tended to yield slightly better recovery in most instances, there were still many test problems where the suboptimal Ward’s partition led to better recovery. What this finding indicates is that there is not always a perfect relationship between minimization of SSE and maximization of ARI, which has been noted previously observed in the cluster analysis literature (Brusco & Steinley, 2007).

The results reported for empirical networks from the literature also showed that suboptimality is not a rare occurrence. The results for the fMRI networks, in particular, reveal that Ward’s method and multistart K-means often result in the selection of a different number of communities and markedly different assignments of vertices to communities.

Overall, the results suggest that the importance of replacing Ward’s method with K-means clustering when implementing the walktrap algorithm might be largely dependent on the nature of the network application. We recommend that Ward’s method should be replaced with K-means clustering when applying the walktrap algorithm to larger psychological networks, such as those encountered in fMRI research, because the SSE differences and the partition differences can be profound. For smaller networks that tend to be well-structured, such as those encountered in exploratory graph analysis, the need for replacing Ward’s method with K-means is less essential. However, the use of either Ward’s or K-means suggests that minimization of SSE is the appropriate criterion and, in the absence of any justifiable reason, it seems logical to go with the latter method because it tends to provide the better SSE. When available and feasible, exact methods for finding a partition that minimizes SSE can be used. Otherwise, multistart implementations of a K-means clustering heuristic should be implemented, as these are known to perform extremely well (Brusco & Steinley, 2007; Steinley, 2003; Steinley & Brusco, 2007).

Limitations and extensions

Although the inferior performance of Ward’s hierarchal clustering (relative to exact or multistart K-means clustering) with respect to minimization of SSE is an indisputable fact, two important caveats should be recognized: (i) There is no guarantee that a partition with a smaller SSE is better from a substantive standpoint than one with a larger SSE; and (2) The clustering algorithm is not the only aspect of the walktrap method that is of critical importance.

Minimization of SSE is a well-recognized criterion in cluster analysis (and statistics in general). If it is the selected objective criterion for optimization, then, arguably, superior methods for minimizing SSE should be preferable to inferior ones. However, as our simulation experiments revealed, there is not necessarily a one-to-one correspondence between minimization of SSE and maximization of the recovery of true community structure. Moreover, in a practical application where ‘true’ structure is unknown, it is possible that an applied researcher might prefer a partition with a larger SSE to one with a smaller SSE based on substantive interpretation. What this suggests is that SSE, like the modularity score and other measures, is not a foolproof measure of the quality of a partition.

There are a variety of other hierarchical clustering and partitioning methods that are viable alternatives to the SSE-based methods. Among the popular hierarchical approaches are single-linkage, complete-linkage, and average-linkage clustering. Brusco and Steinley (2014) have described the relationship between complete-linkage hierarchical clustering and minimum-diameter partitioning, which is analogous in some respects to the relationship between Ward’s method and K-means clustering. Another possible partitioning approach that we are currently investigating is p-median clustering (see Köhn et al., 2010 for a psychologically-oriented tutorial), which has the advantages of flexibility and the provision of community exemplars.

Other essential decisions regarding the implementation of the walktrap algorithm include: (a) the specification of the edge weights for the loops, (b) the selection of the step parameter, t, and (c) the criterion for choosing the number of communities. Using the maximum edge weight that a vertex shares with other vertices as the loop edge weight has performed well in recent simulation studies (Brusco, Steinley et al., 2022a, 2022b) but better options might be available. Likewise, the step size parameter setting of t = 4 seems remarkably robust. Nevertheless, it is doubtful that it is the ideal choice for all networks and the development of approaches for selecting t are worthwhile. Finally, regarding the selection of the number of communities, Pons and Latapy (2006) suggest that ratios of changes in SSE can be used as an alternative to the modularity score. A host of other criteria for choosing the number of communities are also available.

Data availability

The MATLAB files for implementing both the Ward’s and K-means versions of the walktrap algorithm and reproducing the result of Simulations 1, 2, and 3 are available from: https://figshare.com/articles/software/Walktrap_Using_Kmeans_Clustering/21183454

Rieck et al. (2021a) describe the functional connectivity matrices analyzed herein and provide a direct URL to obtain them: https://osf.io/m5crs/