Abstract
Flowering time and plant height are two critical determinants of yield potential in barley (Hordeum vulgare). Despite their role in plant physiological regulation, a complete overview of the genetic complexity of flowering time and plant height regulation in barley is still lacking. Using a double round-robin population originated from the crossings of 23 diverse parental inbred lines, we aimed to determine the variance components in the regulation of flowering time and plant height in barley as well as to identify new genetic variants by single and multi-population QTL analyses and allele mining. Despite similar genotypic variance, we observed higher environmental variance components for plant height than flowering time. Furthermore, we detected new QTLs for flowering time and plant height. Finally, we identified a new functional allelic variant of the main regulatory gene Ppd-H1. Our results show that the genetic architecture of flowering time and plant height might be more complex than reported earlier and that a number of undetected, small effect, or low-frequency genetic variants underlie the control of these two traits.
Keywords: Allele mining, barley, flowering time, plant height, QTL, variance components, WGCNA
Using 45 interconnected sub-populations, the genetic architecture of flowering time and plant height were dissected in barley. QTL analyses revealed new genomic variants associated with the control of these traits.
Introduction
The increase in world population, the reduction of available arable land, and climate change represent some of the greatest challenges that humanity faces now and in the near future (Vyas et al., 2022). One answer to these challenges is to reduce the influence of biotic and abiotic stress factors and that way increase crop productivity (Khush, 2013). Of particular importance are yield increases of cereals (Araus et al., 2008), crops that are essential for human nutrition as they alone contribute about 44.5% of the calorie uptake of the world population (FAO, 2019). In addition, they are important for animal feed and beverage production (FAO, 2020).
Flowering time is a critical determinant of yield potential in cereals (Hill and Li, 2016). Indeed, after flowering, grain filling starts (Cockram et al., 2007), and this process has maximal efficiency if it coincides with optimal environmental conditions (Wiegmann et al., 2019). Therefore, plants and farmers have adopted several strategies to synchronize the phenological stages to environmental conditions (Anderson and Song, 2020).
Barley (Hordeum vulgare L.) is ranked fourth among the most cultivated cereals worldwide (FAO, 2020). This species is characterized by great environmental plasticity that allows it to be cultivated at different latitudes, with extremely dissimilar temperature and photoperiod conditions (Dawson et al., 2015). The adaptive success of barley is also due to the selection of favorable allelic variants at the main genes determining the transition from the vegetative to the reproductive phase (Turner et al., 2005; Comadran et al., 2012; Göransson et al., 2019). Three types of genes have been identified as being responsible for the modulation of flowering time in barley: genes that act under the influence of photoperiod, genes that act under the influence of temperature, and genes, called earliness per se that act independently of environmental variables (Fernández-Calleja et al., 2021).
The main genes whose expression is influenced by the photoperiod are Ppd-H1 (Turner et al., 2005) and Ppd-H2 (Kikuchi and Handa, 2009). Ppd-H1, which is located on chromosome 2H, is the major determinant of the response to long-day conditions in barley, acting jointly with HvCO1 and HvCO2 (Campoli et al., 2012). At the same time, Ppd-H1 indirectly influences the response to vernalization by promoting the expression of Vrn-H3 (Mulki and von Korff, 2016). Ppd-H2 is the second main driver of the photoperiod response in barley, but unlike Ppd-H1 it acts in short-day conditions. The non-functional allelic variant of Ppd-H2 allowed the expansion of the cultivation area of barley at higher latitudes (Casao et al., 2011).
The major determinants of the response to temperature are genes involved in the vernalization process. Vrn-H1, located on chromosome 5H, promotes flowering after the plant has satisfied its vernalization requirement (Yan et al., 2003). Furthermore, Vrn-H1 inhibits the expression of Vrn-H2, which is located on chromosome 4H. Vrn-H2 delays flowering, allowing the plant to fulfill its cold needs (Yan et al., 2004; Deng et al., 2015). Therefore, the interaction between Vrn-H1 and Vrn-H2 is one of the main mechanisms that allow the control of flowering time in winter or facultative barley varieties (Yan et al., 2004). The third vernalization gene is Vrn-H3, on chromosome 7H (Yan et al., 2006). Vrn-H3, when not repressed by Vrn-H2, promotes flowering by allowing the transition from the vegetative to the reproductive phase in long-day conditions (Hemming et al., 2008).
Within the earliness per se genes group, the major determinant is HvCEN, located on chromosome 2H. Because its expression is not directly influenced by environmental variables, the allelic variants of HvCEN allowed the adaptation of barley to new areas through the regulation of flowering time (Comadran et al., 2012). In addition, three other genes have been described as circadian clock-related earliness per se genes which, although not directly influencing flowering, alter the expression of Ppd-H1: HvELF3 (Faure et al., 2012), on chromosome 1H, HvLUX1 (Campoli et al., 2013), on chromosome 3H, and HvPHYC (eam5) (Nishida et al., 2013), on chromosome 5H. Furthermore, mutations in HvELF3 can affect the expression of HvGI (Dunford et al., 2005), causing earlier flowering (Zakhrabekova et al., 2012). Finally, other genes initially reported to control other quantitative traits have also been described as having an influence on flowering time or flower development: HvAP2 (Shoesmith et al., 2021), on chromosome 2H, and Hv20ox2 (sdw1/denso) (Bezant et al., 1996; Jia et al., 2009), on chromosome 3H.
Another key trait responsible for determining production performance in cereals is plant height (Mikołajczak et al., 2017). An adequate height allows the plant to obtain a lower exposure to lodging and a higher harvest index, but on the other side, it is essential to keep the spikes far from the soil to reduce the risk of yield losses caused by infectious diseases (Vidal et al., 2018). Plant height and flowering time are two inter-related traits. This is because flowering is possible when the meristem has switched from the vegetative to the reproductive phase. For this reason, many of the genes controlling flowering time, such as Ppd-H1 (Turner et al., 2005), Vrn-H1 (Wiegmann et al., 2019), Vrn-H2 (Rollins et al., 2013), Vrn-H3 (Arifuzzaman et al., 2016), Hv20ox2 (Jia et al., 2009), HvCEN (Bi et al., 2019), and HvAP2 (Patil et al., 2019), have a pleiotropic effect on plant height. In addition to these genes, other genes involved in the biosynthesis of brassinosteroids, such as HvBRD on chromosome 2H, HvBRI1 (uzu) on chromosome 3H, HvDWF4 on chromosome 4H, HvCPD and HvDEP1 on chromosome 5H, and HvDIM on chromosome 7H (Dockter et al., 2014; Wendt et al., 2016), have been described as being involved in plant height regulation of barley.
Some of the above-mentioned genes, such as HvAP2 and the genes regulating brassinosteroid biosynthesis, have been identified based on mutant approaches (Dockter et al., 2014; Shoesmith et al., 2021). Natural variation was also exploited through screening of germplasm collections (Comadran et al., 2012) and bi-parental (Von Korff et al., 2006; Schmalenbach et al., 2009; Rollins et al., 2013; Arifuzzaman et al., 2014) or nested association mapping populations (Maurer et al., 2015; Nice et al., 2017). When multi-parental populations were examined instead, the experiments included a restricted number of inbred lines (Cuesta-Marcos et al., 2008) and/or the selected parental inbreds were from a restricted geographical range (Cuesta-Marcos et al., 2008; Afsharyan et al., 2020). All these factors reduce the likelihood of identifying genes and allelic variants with low population frequency (Yu et al., 2006). Therefore, the utilization of segregating populations derived from genetic resources with high genotypic and phenotypic diversity could allow the identification of further genes that are involved in flowering time and plant height regulation. This has the potential to facilitate and speed up breeding and provide new targets for genetic modification through, for example, CRISPR platforms. In turn, this could help to extend the cultivation area of barley by allowing its adaptation to new environmental conditions. Furthermore, the knowledge gained in barley has a high potential for transfer to other cereal species that are genetically close but have a polyploid chromosomal structure, such as tetraploid (Triticum turgidum var. durum) and hexaploid (Triticum aestivum) wheat (Langridge, 2018).
In this study, a multi-parent population was used to explore the genetic landscape of flowering time and plant height in barley with the objectives of: (i) determining the genetic variance components in the regulation of flowering time and plant height, (ii) obtaining a comprehensive understanding of the genetic complexity of flowering time and plant height in barley by single and multi-population QTL analyses, and (iii) identifying candidate genes for the detected QTLs regulating flowering time and plant height and detecting new allelic variants of genes responsible for the control of these two traits.
Materials and methods
Plant material and genotypic evaluation
The plant material used in this study consisted of a population designated as HvDRR (Hordeum vulgare Double Round-Robin).
The population originated from the crossings of 23 parental inbred lines, including 11 cultivars and 12 landraces (Shrestha et al., 2022), in a double round-robin scheme (Stich, 2009) (Supplementary Table S1). The parental inbred lines were chosen from a diversity panel of 224 spring barley accessions selected from the Barley Core Collection (BCC) (Pasam et al., 2012) to maximize the combined genotypic and phenotypic richness index (Weisweiler et al., 2019).
Starting from the 45 F1s, a single seed descent strategy was applied to develop between 39 and 145 recombinant inbred lines (RILs) for each of the 45 sub-populations, totaling 4065 RILs (Casale et al., 2022). For flowering time (FT), 3972 RILs were phenotyped, while for plant height (PH) 4025 RILs have been characterized. The plants were phenotyped at generations F5 to F7. The RILs were genotyped as individual plants at the F4 generation using a 50K single nucleotide polymorphism (SNP) genotyping array (Bayer et al., 2017).
Phenotyping
FT evaluation was carried out in Cologne (50.960188 N, 6.860009 E) from 2017 to 2019, Mechernich (50.601335 N, 6.645622 E) from 2018 to 2019, and Quedlinburg (51.787661 N, 11.205353 E) from 2018 to 2019. PH was evaluated in the same environments except for Quedlinburg, totaling five environments. All the experimental fields were located in Germany. At the Cologne and Mechernich environments, 33 seeds were sown in single rows of 1.6 m length. In Quedlinburg, double rows of the same length were sown. The inter-row distance was 20 cm. Fertilization and plant protection followed local practices. In each environment, an augmented design was used. RILs of the HvDRR population and the inbreds of the diversity panel were planted in single rows with one replicate and only the parental inbreds of the HvDRR population were replicated 15–20 times per environment. The percentage of parental inbreds sown in the field, in relation to the total number of plants of the HvDRR population (parental inbreds included), ranged from 8.73% (Cologne, 2019) to 9.97% (Cologne, 2017 and Quedlinburg, 2018).
FT was recorded as days after sowing when 50% of the plants within the (double) row were flowering. PH was measured as the mean across all emergent plants within a row as height in cm from the ground to the top of the spike (without measuring the awns) when the plant was fully developed.
Statistical analyses
The collected phenotypic data were subject to statistical analysis using the following linear mixed model:
| (1) |
where Yijk indicated the observed phenotypic value for the ith genotype in the jth environment within the kth replication, μ the general mean of the trait, Gi the effect of the ith genotype, Ej the effect of the jth environment, and eijk the random error. For the calculation of adjusted entry means, the genotypic effect was considered fixed, while the environmental effect was considered random.
The broad sense heritability (h2) was calculated as:
| (2) |
where Vg represented the genotypic variance and the mean of the standard errors of the contrasts among all pairs of genotypes (Piepho and Möhring, 2007). For the calculation of the genotypic variance (Vg), model 1 was used, but all effects were considered random. In addition, we calculated h2, when applying for each environment a correction based on the augmented design considering different grid sizes, and then estimating Vg and across the environments.
In order to quantify the interaction between genotype and environment, we used a second linear mixed model:
| (3) |
where (G:E)ij represented the interaction between the ith genotype in the jth environment, which was fitted to the data of the parental inbreds.
QTL analyses
Two different QTL analyses were performed in this study on the HvDRR population: multi-parent population (MPP) and single population (SP) analyses.
The estimation of genetic maps necessary for the SP analysis, as well as that of the consensus map used in the MPP analysis, have been described by Casale et al. (2022).
For each sub-population and each trait, an SP QTL analysis was performed, based on the adjusted entry means for each RIL calculated with model 1, using the following scheme. First, standard interval mapping using the Haley–Knott regression algorithm (Knott and Haley, 1992) was applied, followed by forward selection in order to determine the number of QTLs to include in the model. Then a forward and backward selection algorithm was applied to perform multiple QTL mapping. Model selection was based on the highest penalized logarithm of odds (LOD) score with penalties determined through 4000 permutations. A two-dimensional genome-wide scan was performed to detect epistatic interactions between all pairs of loci in the genome. The SP analyses were carried out with the R package ‘qtl’ (Broman et al., 2003).
Confidence intervals for the QTLs detected via SP were calculated using a 1.5 LOD drop method (Manichaikul et al., 2006).
The MPP analyses were performed by jointly analysing all sub-populations using an ancestral model that took into account the degree of relatedness among the parental inbreds (Garin et al., 2017). The degree of relatedness was calculated by clustering the haplotypes. The haplotype window size was chosen as the consensus genetic map distance for which the linkage disequilibrium, measured as r², was 0.2 (Giraud et al., 2014) (Supplementary Table S2). The MPP analysis was performed using the R package ‘mppR’ (Garin et al., 2015).
To exclude potential effects created by using the consensus map, we performed an association mapping analysis across the entire HvDRR population. A mixed model approach was used, where the known pedigree of the individual RILs was used to calculate a pedigree-based kinship matrix that modeled the covariance among RILs.
Genomic prediction
Genomic predictions of FT and PH in the HvDRR population were performed by genomic best linear unbiased prediction (GBLUP) using the following model (VanRaden, 2008):
| (4) |
where y was the vector of the adjusted entry means of the considered trait (FT or PH), 1 was a unit vector, μ the general mean, Z the design matrix that assigned the random effects to the genotypes, and u the vector of genotypic effects that were assumed to be normally distributed with N (0, K ), in which K denotes the realized kinship matrix between inbreds and the genetic variance of the GBLUP model. In addition, ε is the vector of residuals following a normal distribution . The prediction ability of the GBLUP model was evaluated by Pearson’s correlation coefficient (r) between observed and predicted phenotypes.
To assess the model performance, 5-fold cross-validation with 20 replications was performed. In that case, the prediction ability was defined as the median of the prediction abilities across the 20 runs of each 5-fold cross-validation.
Candidate gene analysis and allele mining
The candidate gene analysis was performed for those QTLs from the SP analysis that did not carry inside their confidence intervals previously reported genes controlling the corresponding trait, explained ≥15% of the phenotypic variance, and had a confidence interval ≤30 cM. For the QTLs that fulfilled these criteria, all the genes within the confidence interval were extracted using the Morex v3 reference sequence (Mascher et al., 2021). Next, variant calling data of SNPs, causing tolerated and deleterious mutations, insertion and deletions (INDELs), and predicted structural variants, obtained as described by Weisweiler et al. (2022), were used to identify genes that were polymorphic between the two parental inbreds of the sub-population in which the QTL was detected. For each gene, we took into account all the polymorphisms inside the coding, non-coding, and, for structural variants, potential regulatory regions of the gene within 5 kb up- and downstream of the gene. Subsequently, we performed a weighted gene co-expression network analysis (WGCNA) to identify modules of co-expressed genes that were associated with the phenotypic variability of the traits. The mRNA sequencing experiment of leaf samples of 21 parental inbred lines, described by Weisweiler et al. (2019), was the basis for this analysis. The selected soft thresholding power was 2, based on the scale-free topology criterion (Zhang and Horvath, 2005). We predicted the gene networks for the three modules with the highest and the three lowest correlations for both traits. In order to obtain a comprehensive understanding of the networks, we selected genes with a gene-module membership P<0.01 and, within them, the top 30% of gene–gene interactions based on the weight of the interactions. Because of the high number of gene–gene interactions in the module ‘turquoise’, we selected the top 5% of interactions with the highest weight. For the ‘lightyellow’ and ‘tan’ modules, we did not filter the interactions based on weight. Furthermore, for the ‘black’ module we selected the genes with a gene-module membership P<0.05. In the next step, the results of the WGCNA and SP QTL analyses were combined: we further filtered the polymorphic genes within the confidence intervals based on their membership of a module (Wei et al., 2022). The genes within the three modules with the highest and the three with the lowest correlation with the trait under consideration were evaluated for their functional annotation. We selected as candidate genes those with an annotation similar to that of genes previously reported to control the trait under consideration in barley and those for which functional annotation has been described to be involved in plant vegetative or reproductive development. All the analyses for the calculation of the weighted gene co-expression networks were performed with the R package ‘WGCNA’ (Langfelder and Horvath, 2008).
To confirm the accuracy of the whole genome sequencing data, we performed Sanger sequencing of the 23 parental inbreds for Ppd-H1. To predict if amino acid substitution appearing at a conserved position had a potential effect on the protein function, the SIFT algorithm was used (Vaser et al., 2016). In addition, we performed PCR, as described in Karsai et al. (2005), to check the presence/absence of the three Vrn-H2 genes.
Fine mapping of QTLs by association genetics
We used association genetics in the diversity panel of Pasam et al. (2012) to fine-map the QTLs that did not carry within their confidence intervals genes reported to control the corresponding trait, explained ≥15% of the phenotipic variance, and had a confidence interval ≤30 cM. We used the phenotypic data of the 224 inbreds collected in our field trials and the genotypic information available from Milner et al. (2019). To construct the kinship matrix among the 224 inbreds, we used all the SNPs in the SNP matrix. Association analysis was performed using only polymorphisms from QTLs fulfilling the above-mentioned criteria. For association analysis, we used a mixed model approach, implemented for the variance component (Kang et al., 2010), with the R package ‘statgenGWAS’ (van Rossum et al., 2022).
Results
Phenotypic variation and covariation
FT and PH were evaluated for each RIL across seven and five environments, respectively. For both traits, the environmental variance (E) was about two to three times higher than the genotypic variance (G) (Table 1). Furthermore, for FT, the variance of the interaction between genotype and environment (G:E) was, in the parental inbreds, about half of G, while, for PH, G:E was about 87% of G. The values of broad-sense heritability, for the whole HvDRR population, on an entry means basis were high to very high, ranging from 0.76 for PH to 0.86 for FT (Table 1).
Table 1.
Variance components of the multi-environment linear mixed model and heritability values for flowering time and plant height
| Trait and group | Variance | h² |
|---|---|---|
| Flowering time | ||
| G | 41.33 | 0.86 |
| E | 77.12 | |
| G:E | 22.31 | |
| e | 17.02 | |
| Plant height | ||
| G | 41.46 | 0.76 |
| E | 128.55 | |
| G:E | 36.32 | |
| e | 56.04 | |
G represents the genetic variance, E the environmental variance, G:E the variance explained by the interaction between G and E for the parental inbreds, e the residual error, and h² the heritability of the trait, which was calculated for the whole HvDRR population.
To take into account possible intra-environmental variation, the phenotypic values were adjusted using moving grids of three different sizes, exploiting the possibilities of an augmented design. Because of the lack of considerable field effects, the resulting heritability values across all environments and for all three examined grid sizes were reduced compared with the analysis without adjustment. Therefore, we decided to discuss in the following only results from analyses where intra-environmental variation was not corrected for.
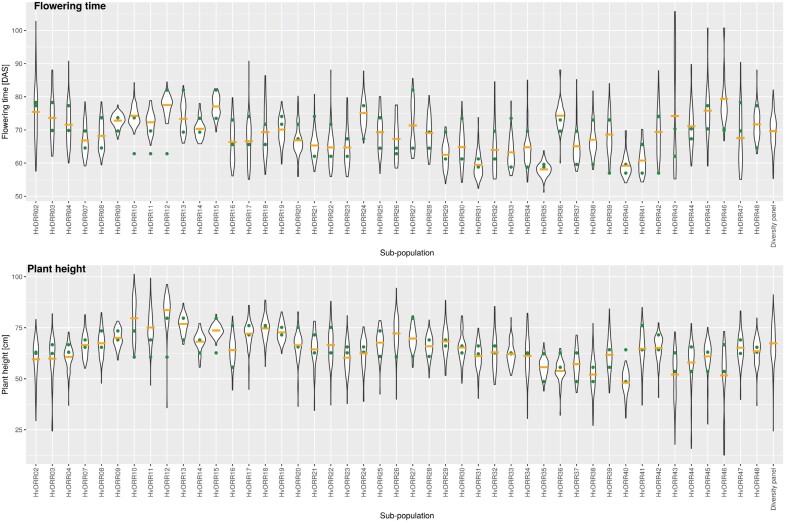
Across all environments, the first sub-population to flower was HvDRR35, where RILs flowered on average 58 d after sowing. In contrast, the latest sub-population to flower was HvDRR46 for which, on average, RILs flowered 79 d after sowing (Fig. 1; Supplementary Table S3). HvDRR46 was also the sub-population with the smallest plants, with a mean height of 48 cm. In contrast, HvDRR12 was, with a mean of 87 cm, the sub-population with the tallest plants (Fig. 1; Supplementary Table S3). HvDRR09 was the sub-population with the lowest coefficient of variation (CoV) value for FT (2.73 d), while the highest CoV was observed for HvDRR43 (23.31 d) (Supplementary Table S3). Regarding PH, the sub-population with the smallest variability was HvDRR15 (CoV=3.83 cm), while the highest CoV, 30.53 cm, was observed for HvDRR46 (Supplementary Table S3). The CoV was, for the diversity panel across the same environments, 7.35 d for FT and 14.01 cm for PH (Supplementary Table S3).
Fig. 1.
Violin plots for adjusted entry means for flowering time and plant height of each HvDRR sub-population and for the 224 inbreds of the diversity panel. DAS, days after sowing. The green circles represent the adjusted entry means of the parental inbreds of the sub-population. The orange lines represent the mean of the adjusted entry means of the recombinant inbred lines of the respective sub-population.
The differences between the mean of the parental inbreds and the mean of the sub-populations were also examined as these were an indicator for the presence of epistasis. For FT, the differences between the means of the parental inbred lines and the respective sub-populations were statistically significant (P<0.05) in 22 cases. Among them, the highest differences were observed for sub-populations HvDRR43, with 7.2 d, and HvDRR46, with 10.5 d. For PH the differences of the means of the sub-populations and the parental inbreds were significant (P<0.05) in 14 cases. The strongest differences between the parental inbreds and the progeny mean were observed for sub-populations HvDRR10, with 9.62 cm, HvDRR12, with 9.88 cm, and HvDRR11, with 10.60 cm. All these sub-populations had Sanalta as common parental inbred (Fig. 1; Supplementary Table S1).
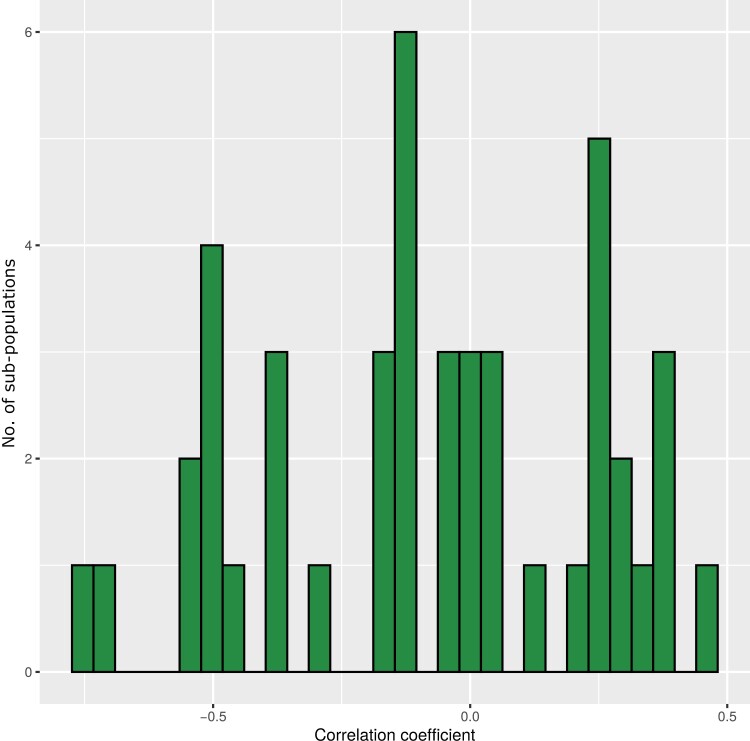
Across all sub-populations, the correlation coefficient of FT and PH was −0.012 (Supplementary Fig. S1). However, considerable differences were observed for the single sub-populations (Fig. 2). HvDRR28 was the sub-population with the highest correlation coefficient (0.44), while the sub-population where the two traits were most negatively correlated was HvDRR43 (−0.77) (Supplementary Fig. S2).
Fig. 2.
Distribution of correlation coefficients between flowering time and plant height calculated for the HvDRR sub-populations.
Multi-parent population analysis
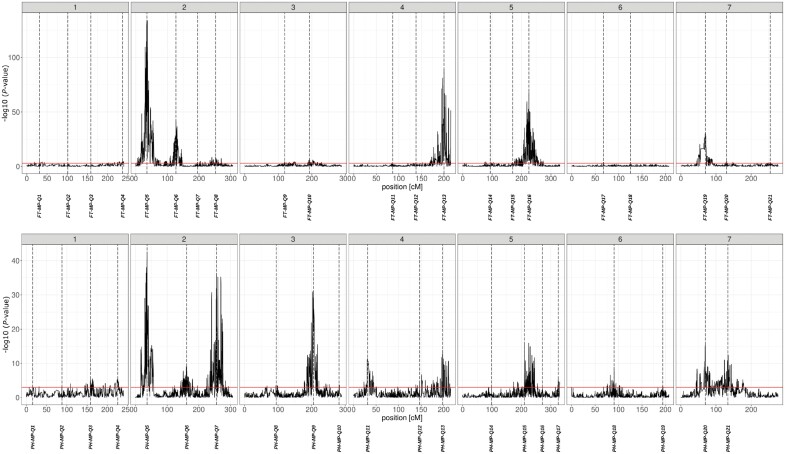
The MPP identified 21 QTLs each for FT and PH, distributed across all seven chromosomes (Fig. 3). The analysis was performed using the genetic haplotype window sizes estimated from the extent of linkage disequilibrium (Supplementary Table S2). The percentage of phenotypic variance explained by all the QTLs detected in the MPP analysis was 39.1% and 24.9% for FT and PH, respectively. For FT, the confidence interval of 17 QTLs overlapped with the interval of at least one QTL identified in the SP analysis (Supplementary Tables S4, S5). Out of 21 QTLs identified for PH, 16 overlapped with one or more QTLs detected in SP analysis (Supplementary Tables S4–S6). Among the QTLs detected for both traits, the intervals of two pairs of QTLs overlapped: FT-MP-Q3 with PH-MP-Q3 and FT-MP-Q19 with PH-MP-Q20.
Fig. 3.
Negative decadic logarithm of the P-value of the multi-parent population analysis for flowering time (top) and plant height (bottom) using an ancestral model. On the x-axis, the position on the consensus genetic map is reported. Each dashed line indicates the peak position of the corresponding QTL.
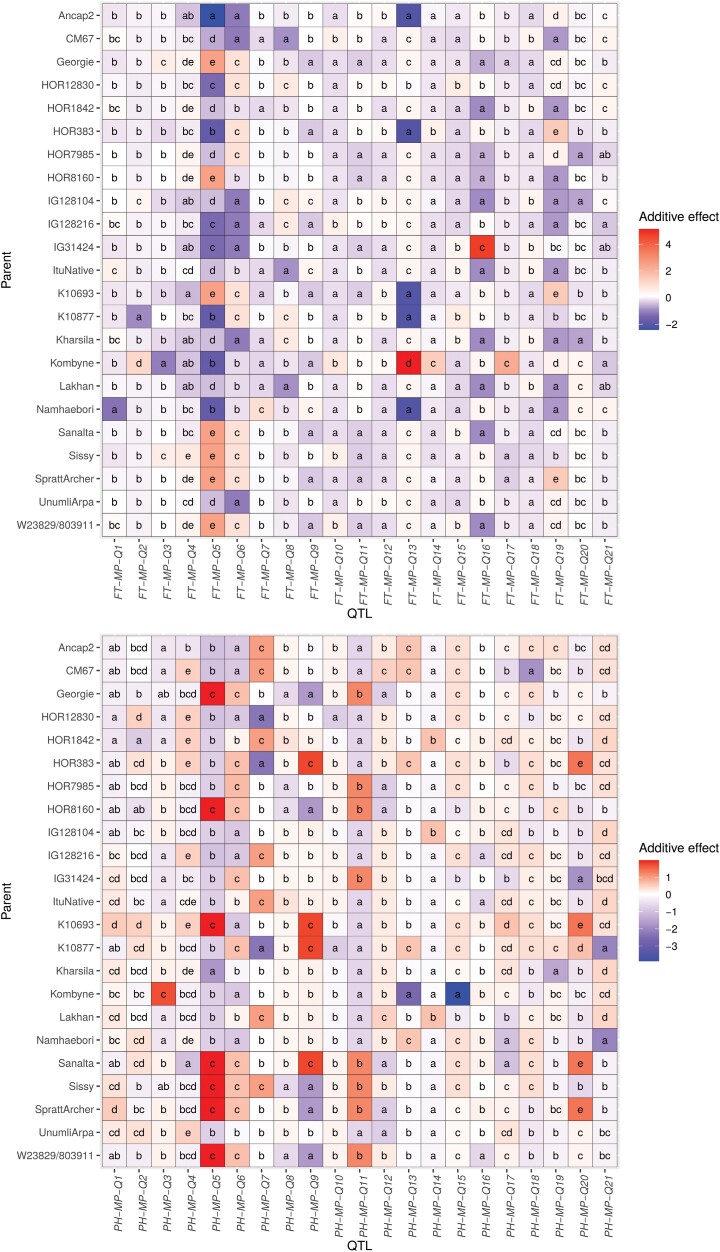
The additive effect of the 23 parental inbreds for the 21 QTLs for FT ranged from −2.42 d, observed for Ancap2 at FT-MP-Q5, to 5.14 d, for Kombyne at FT-MP-Q13 (Fig. 4). However, in about 92% of cases, the additive effect for FT was between −1 and 1 d (Supplementary Fig. S3). For PH, the effect ranged from −3.88 cm for Kombyne at PH-MP-Q15, to a maximum of 1.99 cm at PH-MP-Q5, for seven parental inbreds (Fig. 4). Also in this case more than 90% of the additive effects had a value between −1 and 1 cm (Supplementary Fig. S3). Among the allele effects detected for FT, 20 were conferred exclusively by landraces (nine negative and 11 positive additive effects) and 27 exclusively by cultivars (10 negative and 17 positive additive effects). For PH, the allele effects derived from landraces were 18 (12 negative and six positive additive effects), while the effects inherited exclusively from cultivars were 16 (10 negative and six positive additive effects). The crossing design underlying our population allows estimation of the number of alleles at each QTL. The QTLs with the highest number of significantly different allele effects and thereby with presumably alleles were for FT, FT-MP-Q4 and FT-MP-Q19, with six significantly different effects each, and for PH, PH-MP-Q2 and PH-MP-Q4, with seven different effects each (Fig. 4). To verify the consistency of the consensus genetic map, we performed association mapping with a GWAS-type mixed model approach. Overall, four QTLs for FT and seven for PH, from the MPP, contained in their interval significant markers detected with GWAS: FT-MP-Q5, FT-MP-Q6, FT-MP-Q16, FT-MP-Q19, PH-MP-Q5, PH-MP-Q6, PH-MP-Q7, PH-MP-Q9, PH-MP-Q11, PH-MP-Q17, and PH-MP-Q20 (Supplementary Fig. S4).
Fig. 4.
Heat map of the effects of the parental inbreds at the QTLs detected through multi-parent population analysis for flowering time (top, in days after sowing) and for plant height (bottom, in cm). Indexed letters indicate the significance of the difference (P<0.05) between the effects of the same QTL.
Genomic prediction ability
The prediction abilities of the GBLUP model across the HvDRR population were high with values of 0.89 and 0.87 for FT and PH, respectively (Supplementary Table S7). To compare the prediction performance of the GBLUP model with those of the detected QTLs, we used the squared prediction abilities. The coefficient of determination (r²) obtained by genomic prediction without cross-validation was 0.79 for FT and 0.76 for PH. The cross-validated prediction abilities were 0.77 for both FT and PH.
Single population QTL analysis
Through SP, 89 QTLs were identified for FT and 80 for PH (Figs 5, 6; Supplementary Tables S5, S6). The percentages of explained variance by the individual QTLs detected for FT ranged from 1.02%, for qHvDRR47-FT-7.1, to 77.75%, for qHvDRR27-FT-2.1 (Supplementary Table S5), while for PH the values ranged from 2.52%, for qHvDRR11-PH-2.2, to 63.62%, for qHvDRR10-PH-3.1 (Supplementary Table S6). For FT, HvDRR27 was the sub-population with the highest values of explained variance (77.75%), while for PH the sub-population with the highest percentage of explained variance was HvDRR22 (78.54%). The lowest percentages of explained variance by the detected QTLs were observed for FT in HvDRR23 (16.91%) and for PH in HvDRR04 (10.27%) (Supplementary Tables S5, S6).
Fig. 5.
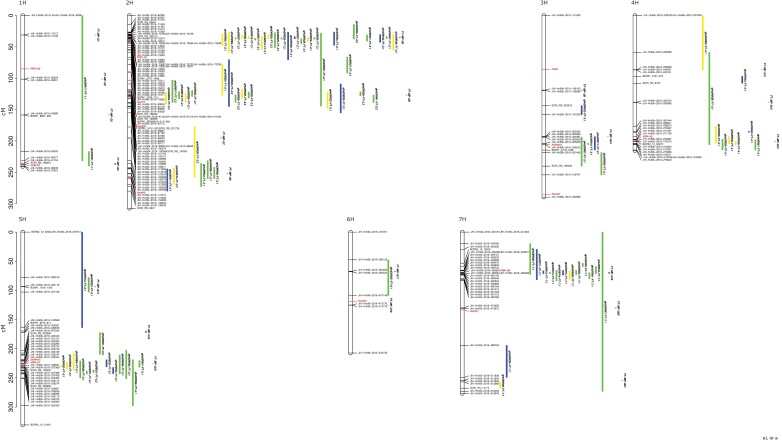
Genetic position of the QTL detected in single population analyses for flowering time projected to the consensus map. The position of the QTL confidence intervals is represented as a vertical bar parallel to the right of the chromosome. The color of the bar indicates if the sub-population was obtained by crossing two landraces (yellow), two cultivars (blue), or a landrace and a cultivar (green). The position of the QTL confidence intervals detected through multi-parent population analysis is represented by purple bars. The genetic positions of the known genes regulating flowering time in barley are shown in red. The positions of the markers that flank each QTL are also reported.
Fig. 6.
Genetic position of the QTL detected in single population analysis for plant height projected to the consensus map. The position of the QTL confidence intervals is shown as a vertical bar to the right of the chromosome. The color of the bar indicates if the sub-population was obtained by crossing two landraces (yellow), two cultivars (blue), or a landrace and a cultivar (green). The position of the QTL confidence intervals detected through multi-parent population analysis is represented by purple bars. The known regulatory genes previously described as being responsible for plant height regulation and their genetic position are reported in red. The positions of the markers at the borders of each QTL are also reported.
Out of 89 QTLs identified in the SP analysis for FT, 43 mapped to chromosome 2H (Fig. 5). A cluster comprising 21 QTLs was located at the beginning of chromosome 2H. The region covered by the confidence interval of these QTLs included Ppd-H1. Also for other major effect genes, QTL clusters were identified: six QTLs at the end of chromosome 4H, whose confidence intervals included Vrn-H2, 10 QTLs on the long arm of chromosome 5H, a region in which Vrn-H1 and HvPHYC were positioned, and 11 QTLs at the beginning of chromosome 7H, in which Vrn-H3 was located. Other QTLs included additional genes within their confidence intervals such as HvELF3, HvCEN, Hv20ox2 (sdw1/denso), HvFT4 (Pieper et al., 2021), and HvAP2 (Supplementary Table S5).
Single population analysis for PH identified 80 QTLs, where these QTLs were characterized by wider confidence intervals compared with those detected for FT (Fig. 6; Supplementary Table S6). As for FT, the chromosome with the highest number of QTLs was 2H. A cluster, including 14 QTLs, included within its confidence interval Ppd-H1. Other clusters of QTLs included in their confidence intervals HvAP2, Hv20ox2 (sdw1/denso), Vrn-H1, and Vrn-H3 (Supplementary Table S6).
However, we identified 16 QTLs for FT and 31 QTLs for PH where no genes previously described for the control of the trait were present within their confidence interval (Supplementary Tables S5, S6), although the confidence intervals of most of these QTLs overlapped with previously reported QTLs. Among the 16 QTLs detected for FT, the QTLs with the lowest number of genes in the confidence interval were qHvDRR02-FT-5.1 and qHvDRR31-FT-5.2. The QTLs included 52 and 71 genes, respectively, which reduced to 35 and 45 when neglecting the low-confidence genes. qHvDRR31-FT-5.2 was, with 3.4 cM, the QTL with the shortest genetic confidence interval. For PH, qHvDRR48-PH-4.1 was the QTL with the lowest number of genes in its confidence interval (115 low- and high-confidence or 79 high-confidence genes). The QTL with the shortest confidence interval was qHvDRR22-PH-7.1 with 3.9 cM.
Eight sub-populations showed significant epistatic interactions between loci on a genome-wide scale. In total, 10 significant epistatic interactions were detected, nine for PH and one for FT. Two epistatic interactions each were observed for sub-populations HvDRR34 and HvDRR44 (Supplementary Table S8).
Allele mining
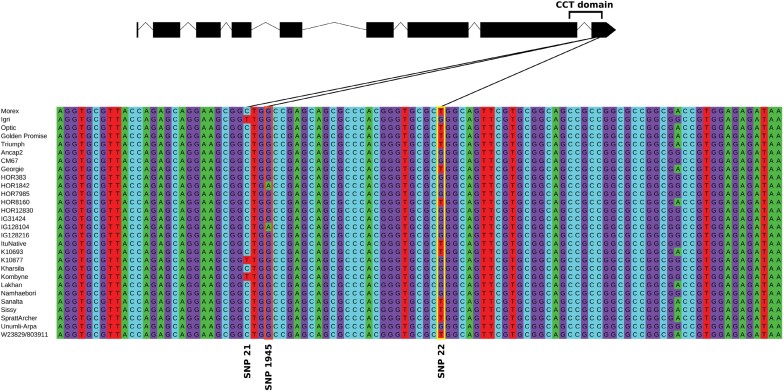
For FT, 21 sub-populations showed a QTL co-localizing with Ppd-H1. For 14 of these, a QTL that included Ppd-H1 was also identified for PH. Sixteen of the 21 sub-populations were polymorphic for the causal SNP 22 of Ppd-H1 (Turner et al., 2005). However, five sub-populations (HvDRR02, HvDRR04, HvDRR20, HvDRR23, and HvDRR48), for which the QTL confidence intervals included Ppd-H1, did not segregate for this polymorphism. All non-polymorphic sub-populations for SNP 22 had HOR1842 or IG128104 as parental inbred lines (Supplementary Table S1). Through Sanger sequencing, we identified the presence of a unique SNP in HOR1842 and IG128104 in the CCT domain of Ppd-H1 (Fig. 7). The primers used to amplify Ppd-H1 are listed in Supplementary Table S9. Based on the SNP position on the Ppd-H1 coding sequence of Morex, we refer to it as SNP 1945. SNP 1945 determines the synthesis of a threonine instead of an alanine (Supplementary Fig. S5). The SIFT algorithm predicted that the amino acid substitution caused by SNP 1945 affected a conserved position and, thus, might negatively affect the protein function. All the parental inbreds of the above-mentioned sub-populations carried a guanine (SNP 22 early allele), in correspondence with SNP 22 but the RILs that inherited SNP1945 from HOR1842 or IG128104 (adenine), tended to have later flowering compared with RILs that carried a thymine in correspondence of SNP 1945.
Fig. 7.
Genomic sequence of the last exon of Ppd-H1 of Morex, Igri, Optic, Golden Promise, Triumph, and the 23 parental inbreds of the HvDRR population. SNP 22 is highlighted in yellow, SNP 1945 in orange. At the top, the gene structure of Ppd-H1 is given. Lines indicate the positions of SNP 21, SNP 22 (Turner et al, 2005), and SNP 1945 within the last exon.
At the Vrn-H2 locus, an FT QTL was detected in six sub-populations. We evaluated by PCR, as described in Karsai et al. (2005) (Supplementary Table S9), the presence/absence of the three causal Vrn-H2 genes. Out of six sub-populations, five were polymorphic for the genes regulating the Vrn-H2 locus. In HvDRR29, both parental inbred lines, HOR8160 and IG128216, had the complete set of genes (Supplementary Fig. S6).
We did not detect new functional polymorphisms for Vrn-H1 and HvPHYC. However, we identified a significant number of RILs that were recombinant for these two genes which might be a valid resource for future functional studies (Supplementary Table S10).
Candidate gene analysis
The candidate gene analysis was performed for the QTLs detected in the SP analysis that did not carry in their confidence interval previously reported genes controlling the trait under consideration, explained ≥15% of the phenotypic variance, and had a confidence interval ≤30 cM. For these QTLs, we combined the results of QTL mapping with variant calling data and results from WGCNA. Through WGCNA, 27 different gene modules were detected across all the expressed genes in the barley genome (Supplementary Fig. S7). The correlation of the gene expression of modules and the adjusted entry means ranged from −0.52 to 0.49 for FT and from −0.54 to 0.47 for PH. Interestingly, the module with the highest correlation was the same for both traits. After selecting genes within the QTL range and that were included in one of the three modules with the highest or the lowest correlation (Supplementary Fig. S8), we searched for candidate genes. The most represented class of genes for the two traits was that of receptor-like kinase, followed by genes involved in the ethylene pathways, and genes coding for F-box proteins (Supplementary Table S11).
In addition to the function-based candidate gene analysis, we used association genetics in the diversity panel to fine-map the selected QTLs using the genome-wide genotyping-by-sequencing data of Milner et al. (2019). For FT, none of the polymorphisms in the QTL confidence intervals was significantly associated with the phenotype. For PH, we identified four significant SNPs associated with the phenotype (Supplementary Fig. S9).
Discussion
With this study, we aimed to obtain a comprehensive overview of the environmental and genotypic contributions to the regulation of FT and PH in barley. We performed MPP and SP analysis to elucidate the genetic complexity underlying the control of FT and PH. Finally, we identified candidate genes and new allelic variants using additional approaches such as WGCNA and association genetics.
The double round-robin population shows high variability of flowering time and plant height
We observed, with a range of adjusted entry means of 51.2–105.7 d as well as 12.6–101.2 cm for FT and PH, respectively, a higher phenotypic diversity among the RILs of the HvDRR population (Fig. 1) compared with previous studies (Cuesta-Marcos et al., 2008; Maurer et al., 2015; Arifuzzaman et al., 2016; Nice et al., 2017; Afsharyan et al., 2020). Also, the standard deviation of the adjusted entry means of the RILs was higher for both traits than that described in previous studies (Pauli et al., 2014; Wang et al., 2014) (Supplementary Table S3). These observations might be due to the higher number of RILs and the selection of the 23 parental inbreds with maximal genotypic and phenotypic richness.
In addition, the variation observed for FT and PH in the diversity panel of 224 spring barley inbreds (Pasam et al., 2012) was similar to that observed in individual sub-populations. However, it was considerably smaller (FT) and more influenced by a few outliers (PH) compared with the diversity observed in the entire HvDRR population (Fig. 1).
We observed that relative to the genotypic variance the variance components of environment and genotype–environment interaction were higher for PH than FT (Table 1). This finding was in discordance with a previous study where the variance component of the genotype–environment interaction was higher for FT than for PH (Rodriguez et al., 2008). This result might be explained by the higher variability of edaphic and meteorological variables (e.g. precipitation and temperature) of our study, which influenced PH more strongly than FT (Li et al., 2003), but also the lower difference in latitude among the environmental locations in our study compared with that of Rodriguez et al. (2008).
The high phenotypic variability and heritability values, combined with high-quality genotypic data, suggest that the HvDRR population is a valuable tool for detecting new genetic variants controlling agronomic traits in barley.
QTL analyses uncovered the role of genetic background in determining the correlation between FT and PH
The correlation between FT and PH differed across the HvDRR sub-populations (Fig. 2; Supplementary Fig. S2). These results were in agreement with those of previous studies that have detected positive and negative correlations between FT and PH (Von Korff et al., 2006; Schmalenbach et al., 2009; Maurer et al., 2016; Nice et al., 2017). The high variability of the correlation coefficients could be due to the great genotypic diversity of the parental inbreds used in our study. To understand this aspect better, we considered in detail the co-located QTLs for FT and PH in the SP analysis.
For the sub-populations with the most negative correlation between FT and PH (HvDRR10, HvDRR11, and HvDRR43), all QTLs detected for FT were also detected for PH, although additional QTLs were observed for PH (Supplementary Tables S5, S6). For four of the five FT/PH QTL pairs, the parental inbred line conferring a positive additive effect for PH revealed a negative additive effect for FT and vice versa (Supplementary Tables S5, S6; Supplementary Fig. S2). In addition, the three sub-populations with the highest correlation coefficient (HvDRR19, HvDRR28, and HvDRR29) also had QTLs falling within the same interval for the two traits (Figs 5, 6). In this case, for the three overlapping QTL pairs, the positive additive effect was given by the same parental inbred for both traits (Supplementary Tables S5, S6; Supplementary Fig. S2).
To increase the resolution of the dissection of the genetic origin of the correlation between FT and PH, we exploited MPP analysis. For each of the two traits, we identified 21 QTLs (Fig. 3). The QTL profiles obtained through MPP analysis for both traits had peaks falling within neighboring regions for the main genes previously reported to control FT and PH, such as Ppd-H1 and the vernalization genes. The diversity of the parental inbreds and the large number of sub-populations as well as the total RILs resulted in a high mapping resolution that led to narrow confidence intervals. We observed a pleiotropic effect only for two QTL pairs (FT-MP-Q3/PH-MP-Q3 and FT-MP-Q19/PH-MP-Q20). FT-MP-Q3/PH-MP-Q3 included in their interval HORVU.MOREX.r3.1HG0075860, which was functionally annotated as a transcription factor, while FT-MP-Q19/PH-MP-Q20 included in their intervals Vrn-H3. Therewith, our results suggested that FT and PH variations, with the exception of two QTLs, may be caused by independent genetic factors (Figs 3, 5, 6; Supplementary Tables S4–S6).
Multi-parent and single population analyses revealed new genome regions as well as genomic variants involved in the control of flowering time and plant height
The number of QTLs identified through MPP analysis (Fig. 3; Supplementary Table S4) was, with 21 each, higher than the number of QTLs detected in earlier studies using bi- and multi-parental populations of barley (Von Korff et al., 2006; Cuesta-Marcos et al., 2008; Schmalenbach et al., 2009; Rollins et al., 2013; Arifuzzaman et al., 2014; Pauli et al., 2014; Maurer et al., 2015; Nice et al., 2017). In the study of Hemshrot et al. (2019), a total of 23 QTLs were identified for FT. However, QTLs with the same genetic position were detected, which reduced the number of non-overlapping QTLs to 13. The reasons for the higher number of QTLs detected in our study compared with earlier studies were most probably the greater number of RILs and environments as well as the selection of very diverse parental inbreds (Stich, 2009; Weisweiler et al., 2019). We compared the physical positions of the QTLs with previous studies (Laurie et al., 1994; Druka et al., 2011; Pauli et al., 2014; Maurer et al., 2015; Nice et al., 2017; Hemshrot et al., 2019; Afsharyan et al., 2020) and did not find any previously reported QTLs co-localizing with FT-MP-Q1, FT-MP-Q2, FT-MP-Q3, FT-MP-Q10, FT-MP-Q11, FT-MP-Q17, FT-MP-Q18, PH-MP-Q6, PH-MP-Q10, and PH-MP-Q19.
The use of a consensus map for our analyses could have led to these observations. This is because structural variants have the potential to lead to inconsistencies in such maps. However, the peaks detected by a GWAS approach, in which the physical order of the markers was used, were in very good accordance with the results of the MPP analysis and, thus, we consider the discrepancies introduced by the consensus map to be of minor importance (Supplementary Fig. S4).
Our observations suggested that the genetic complexity of FT and PH is higher than initially reported. Furthermore, for both traits, the percentage of explained variance by a genomic prediction model was about twice the percentage of variance explained by the QTLs detected in the MPP analysis (Supplementary Table S7). This result suggested that many small effect QTLs remain undetected.
The difference between the percentage of variance explained by a genomic prediction model and that explained by the QTLs detected in the MPP analysis was greater for PH compared with FT (Supplementary Table S7). This observation suggests that PH is more influenced by small effect (and undetected) QTLs than FT. In addition, the total proportion of variance explained by the detected QTLs was lower for PH (25.7%) than for FT (37.4%). This trend was in agreement with the observation that epistatic interactions played a bigger role for PH than for FT (Supplementary Table S8).
The SP QTL analyses detected 89 QTLs for FT and 80 for PH (Figs 5, 6; Supplementary Tables S5, S6). We compared the physical position of QTLs reported in earlier studies (Laurie et al., 1994; Druka et al., 2011; Pauli et al., 2014; Maurer et al., 2015; Nice et al., 2017; Hemshrot et al., 2019; Afsharyan et al., 2020), wherever possible, with those of the QTLs detected in our study. We observed for 166 QTLs a co-localization with previously reported QTLs. However, three QTLs, one for FT and two for PH, did not overlap with other previously reported QTLs. The novel QTLs detected by SP were qHvDRR30-FT-3.1, qHvDRR24-PH-3.1, and qHvDRR48-PH-4.1. The percentage of variance explained by these QTLs was relatively low for qHvDRR30-FT-3.1 (4.3%) but higher for qHvDRR24-PH-3.1 (26.2%) and qHvDRR48-PH-4.1 (19.5%). Therefore, qHvDRR24-PH-3.1 was selected for fine-mapping, as well as qHvDRR28-FT-2.2, qHvDRR41-FT-2.2, qHvDRR42-FT-3.1, qHvDRR22-PH-7.1, qHvDRR29-PH-2.1, and qHvDRR47-PH-2.1.
For 21 sub-populations, an FT QTL co-localized with the Ppd-H1 locus. Five of these sub-populations (HvDRR02, HvDRR04, HvDRR20, HvDRR23, and HvDRR48) were not polymorphic for SNP 22 (Fig. 7; Supplementary Table S1). SNP 22 is located within the CCT domain of Ppd-H1 (Turner et al., 2005) and was described as the only functional polymorphism of Ppd-H1 (Turner et al., 2005). Another polymorphism of Ppd-H1, SNP 48 (Jones et al., 2008), had previously been associated with FT variation. However, the study of Sharma et al. (2020, Preprint) did not observe hints that SNP 48 was the causal SNP of the Ppd-H1 mutation. In addition, in none of the above-mentioned five sub-populations was SNP 48 segregating. All five sub-populations had HOR1842 or IG128104 as parental inbreds (Supplementary Table S1). From the whole genome sequencing data of the parental inbreds (Weisweiler et al., 2022), followed by Sanger sequencing, we identified a not previously reported polymorphism, SNP 1945, that is unique to HOR1842 and IG128104 (Fig. 7). SNP 1945 is located within the CCT domain of Ppd-H1 and it causes the synthesis of threonine instead of alanine (Supplementary Fig. S5). In the sub-population HvDRR24, whose parental inbreds were HOR1842 and IG128104, we did not detect a QTL for either FT or PH in the genome region of Ppd-H1. In addition, HOR1842 and IG128104 originated from the same geographical region (south-central Asia). Furthermore, we observed that the additive effect for the FT QTL co-localizing with Ppd-H1 was, with about 3.5 d, higher in sub-populations segregating for SNP 22 compared with about 2.3 d for the five sub-populations that did not segregate for SNP 22 (Supplementary Table S5). For the latter sub-populations, the additive effect assumed a positive value for the RILs that inherited the Ppd-H1 allele from HOR1842 or IG128104. These observations support the hypothesis that HOR1842 and IG128104 carry the same causal polymorphism and that SNP 1945 is the causal polymorphism for the QTL in those sub-populations that were monomorphic for SNP 22 as well as a new functional allelic variant of Ppd-H1.
A similar observation was made for the QTL co-localizing with Vrn-H2. The Vrn-H2 locus has been described as one of the main loci responsible for the difference between winter and spring barley varieties (Distelfeld et al., 2009). This difference is caused by the total deletion of a complex of three genes (ZCCT-Ha, ZCCT-Hb, and ZCCT-Hc) in spring barley or, in facultative barley, of a partial deletion (Karsai et al., 2005; Fernández-Calleja et al., 2021). Surprisingly, we observed for four of the HvDRR parental inbreds the complete set of Vrn-H2 causal genes in spring barley varieties (Supplementary Fig. S6). This observation suggested that the role of Vrn-H2 in the vernalization requirement may be more complex than previously assumed and not merely based on the presence/absence of the Vrn-H2 genes. In addition, for HvDRR29, both parental inbreds, HOR8160 and IG128126, carried the three Vrn-H2 causal genes (Supplementary Fig. S6). Similarly to Ppd-H1, it could be hypothesized that HOR8160 or IG128216 carried a new functional allelic variant of Vrn-H2 or that an additional gene, acting on the phenotype in a similar way to ZCCT-Ha:c, was present within the same QTL confidence interval. However, although HOR8160 and IG128126 have been classified as spring barley varieties (Pasam et al., 2012), it cannot be excluded that they originated from winter or intermediate genotypes.
These two examples suggest that the genetic complexity of the studied traits might be higher than anticipated from the simple comparison of co-localizing QTLs and can now be resolved using multiple segregating populations together with next-generation sequencing of the parental inbreds. Finally, cloning of the underlying genes will complement our understanding of the regulatory mechanisms of FT and PH.
Candidate gene analysis for a subset of the QTLs
We first extracted the polymorphic genes among the parental inbred lines within the confidence interval of the QTLs that explained ≥15% of the phenotypic variance, had a confidence interval ≤30 cM, and did not carry in their confidence interval any previously reported gene controlling the trait under consideration. Then, we combined this screening with the results of the WGCNA, selecting the three modules that showed each the lowest and highest correlation with FT and PH (Supplementary Fig. S7).
Among the FT QTLs fulfilling the above-mentioned criteria, qHvDRR28-FT-2.2 had the highest percentage of explained variance and the shortest genetic confidence interval. Two candidate genes identified for this QTL encoded the pseudo-response regulator 3 (PRR3) HORVU.MOREX.r3.2HG0170150 and the ethylene-responsive transcription factor HORVU.MOREX.r3.2HG0170460 (Supplementary Table S11).
Pseudo-response regulator is the same class of genes as Ppd-H1. The role of these genes is critical for the regulation of the plant circadian clock (Eriksson and Millar, 2003; Mizuno and Nakamichi, 2005) which is involved in the control of flowering time (Hayama and Coupland, 2004). Five different sub-groups belonging to this class of genes have been reported: PRR1, PRR3, PRR5, PRR7 (to which Ppd-H1 belongs), and PRR9 (Matsushika et al., 2000). Phylogenetic analyses grouped the five sub-groups into three main clusters: PRR1, PRR5–PRR9, and PRR3–PRR7 (Nakamichi et al., 2020). Although genes belonging to all three clusters have been described as controlling FT or being influenced by the photoperiod, the only cluster containing genes from grass species described as being dependent on the photoperiod and at the same time controlling FT was PRR3–PRR7 (Nakamichi et al., 2020). Therewith this gene is an interesting target for further functional studies.
Genes responsible for ethylene biosynthesis are involved in a multitude of developmental processes throughout the plant life cycle (Bleecker and Kende, 2000). The concentration of ethylene also influences gene networks that regulate flowering to optimize the timing of the transition from the vegetative to the reproductive stage in relation to endogenous and external stimuli (Iqbal et al., 2017). Although further studies are needed to identify the ethylene pathways in barley, in rice, overexpression of an ethylene receptor (ETR2) was associated with delayed flowering (Hada et al., 2009). The delay was linked with an up-regulation of a homologous gene of GIGANTEA and TERMINAL FLOWER 1/CENTRORADIALIS (Hada et al., 2009); both of these classes of genes are involved in barley in the control of flowering since HvGI (Dunford et al., 2005) and HvCEN (Comadran et al., 2012) belong to them. Ethylene is also involved in plant growth (Dubois et al., 2018), and its role in vegetative development has been described in barley (Patil et al., 2019). In addition to the one found in qHvDRR28-FT-2.2, we identified two ethylene-responsive transcription factors (HORVU.MOREX.r3.7HG0685230 and HORVU.MOREX.r3.2HG0182430) in qHvDRR22-PH-7.1 and qHvDRR29-PH-2.1 (Supplementary Table S11). Besides being an ethylene-responsive transcription factor, HORVU.MOREX.r3.2HG0182430 also belongs to the same class of genes as HvAP2.
In addition to functional data, we used association genetics to fine-map the detected QTLs using the diversity panel that was evaluated in the same set of environments as the HvDRR population. For FT, none of the polymorphisms from Milner et al. (2019) that were located in the QTL confidence intervals were significantly associated (P<0.05) with FT variation. The reason for this discrepancy was most probably that association mapping panels have a low power to detect marker-trait associations in the case of low-frequency alleles (Myles et al., 2009), which is overcome by using segregating populations as in the HvDRR population. For PH, low-significance marker-trait associations have been detected. However, one of the polymorphisms was in proximity (<150 kbp) to HORVU.MOREX.r3.3HG0222500, a candidate gene detected for qHvDRR24-PH-3.1 through the WGCNA approach (Supplementary Table S11; Supplementary Fig. S9).
These results suggest that the integration of QTL analyses with other omics datasets supports the detection of candidate genes regulating traits of agronomic interest.
Conclusions
The great phenotypic variability observed for FT and PH in the HvDRR population suggests that this population will be a powerful genetic resource to detect new regulatory mechanisms that could allow the extension of the barley cultivation area or its adaptation in changing environmental conditions. Furthermore, it was observed that environmental variables affected these traits and that the environmental component had a greater influence on PH compared with FT. In addition, our study provides a comprehensive summary of the genetic architecture of FT and PH and forms the basis for future QTL cloning studies. Finally, the detection of novel QTLs, but also the observation that additional alleles or genes segregate at known loci like Ppd-H1 and Vrn-H2, suggests that the studied traits are genetically more complex than previously reported.
Supplementary data
Supplementary data are available at JXB online.
Fig. S1. Histogram and correlation plot between flowering time and plant height across all 45 HvDRR sub-populations.
Fig. S2. Histograms and correlation plots between flowering time and plant height, for each of the 45 HvDRR sub-populations.
Fig. S3. Effect size of the QTL detected through multi-parent population analysis for flowering time and plant height for each of the parental lines.
Fig. S4. GWAS-type mixed model approach for flowering time (FT) and plant height (PH) of the HvDRR population.
Fig. S5. Amino acid sequence of the terminal region of Ppd-H1 of Morex, Igri, Optic, Golden Promise, Triumph, and the 23 parental inbreds of the HvDRR population.
Fig. S6. Gel pictures of PCRs performed to detect the presence/absence of ZCCT-Ha:b and ZCCT-Hc as described in Karsai et al. (2005).
Fig. S7. Heat map of the module-trait relationships for plant height and flowering time.
Fig. S8. Network predictions for modules ‘orange’, ‘black’, ‘darkgreen’, ‘purple’, ‘tan’, ‘lightyellow’, ‘green’, ‘blue’, and ‘turquoise’.
Fig. S9. Negative decadic logarithm of the P-value for association tests of sequence variants in QTL without previously reported genes for the control of the trait within their interval, explaining ≥15% variance, and with interval ≤30 cM for flowering time and plant height.
Table S1. Crossing scheme of the 45 HvDRR sub-populations and number of RILs for each sub-population.
Table S2. Genetic and physical distances for which the linkage disequilibrium measured r² reached a value of 0.2.
Table S3. Average of the adjusted entry means, standard deviations, and coefficients of variation across all 45 sub-populations and the diversity panel for flowering time and plant height.
Table S4. Summary of the results of the multi-parent population analysis for flowering time and plant height.
Table S5. Summary of the results of the single population analysis for flowering time.
Table S6. Summary of the results of the single population analysis for plant height.
Table S7. Prediction ability of the genomic SNP marker data for flowering time and plant height without cross-validation and with 5-fold cross-validation across all sub-populations.
Table S8. Genome-wide epistatic loci detected in the HvDRR population.
Table S9: Lists of primers used to amplify Ppd-H1 and Vrn-H2.
Table S10. Recombinant RILs between Vrn-H1 and HvPHYC for sub-populations having a QTL in the Vrn-H1 and eam5 genomic region.
Table S11. List of candidate genes in the confidence interval of selected QTL that carried a polymorphism among the parental lines.
Acknowledgements
We would like to thank our former colleagues George Alskief and Florian Esser for their technical support and for organizing and managing the field trials of the HvDRR population in the Cologne and Eifel locations. We acknowledge Muenteha Yilmaz and Srinivasa Reddy Mothukuri for their contribution to data collection and analyses. We thank the team of Saatzucht Breun for running the field trials in Quedlinburg. Computational infrastructure and support were provided by the Centre for Information and Media Technology at Heinrich Heine University, Düsseldorf. We appreciate the helpful comments of two reviewers on an earlier version of the manuscript.
Glossary
Abbreviations
- CoV
coefficient of variation
- FT
flowering time
- GBLUP
genomic best linear unbiased prediction
- HvDRR
Hordeum vulgare double round-robin
- INDEL
insertion and deletion
- LOD
logarithm of odds
- MPP
multi-parent population
- PH
plant height
- RIL
recombinant inbred line
- SNP
single nucleotide polymorphism
- SP
single population
- WGCNA
weighted gene co-expression network analysis
Contributor Information
Francesco Cosenza, Institute for Quantitative Genetics and Genomics of Plants, Heinrich Heine University, 40225 Düsseldorf, Germany.
Asis Shrestha, Institute for Quantitative Genetics and Genomics of Plants, Heinrich Heine University, 40225 Düsseldorf, Germany.
Delphine Van Inghelandt, Institute for Quantitative Genetics and Genomics of Plants, Heinrich Heine University, 40225 Düsseldorf, Germany.
Federico A Casale, Institute for Quantitative Genetics and Genomics of Plants, Heinrich Heine University, 40225 Düsseldorf, Germany.
Po-Ya Wu, Institute for Quantitative Genetics and Genomics of Plants, Heinrich Heine University, 40225 Düsseldorf, Germany.
Marius Weisweiler, Institute for Quantitative Genetics and Genomics of Plants, Heinrich Heine University, 40225 Düsseldorf, Germany.
Jinquan Li, Max Planck Institute for Plant Breeding Research, 50829 Köln, Germany.
Franziska Wespel, Saatzucht Josef Breun GmbH Co. KG, Amselweg 1, 91074 Herzogenaurach, Germany.
Benjamin Stich, Institute for Quantitative Genetics and Genomics of Plants, Heinrich Heine University, 40225 Düsseldorf, Germany; Max Planck Institute for Plant Breeding Research, 50829 Köln, Germany; Cluster of Excellence on Plant Sciences (CEPLAS), Heinrich Heine University, 40225 Düsseldorf, Germany.
Susanne Dreisigacker, CIMMYT, Mexico.
Author contributions
FCo, AS, and BS: conceptualization; FCo, AS, DVI, FCa, PW, MW, and BS: data analysis; FCo and BS: investigation; JL, FW, and BS: resources; BS: funding acquisition; FCo and BS: writing.
Conflict of interest
The authors declare no conflict of interest.
Funding
This research is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) in the frame of GRK 2466: Netzwerk-, Austausch und Trainingsprogramm zum Verständnis von Ressourcenallokation in Pflanzen (Project ID: 391465903).
Data availability
The codes used for the calculation of the adjusted entry means, the single and multi-parent population QTL analyses, the epistatic QTL models, the WGCNA analysis, as well as the datasets of the adjusted entry means of the HvDRR population, the genetic haplotypes used to build the ancestral model, and the genotypic and phenotypic data used in the QTL analyses are available at GitHub: https://github.com/cosenzaf/HvDRR_FT_PH. The data for membership of genes to gene modules used in the WGCNA are available at Zenodo repository: https://zenodo.org/record/7525604#.Y7_VgxXMLIW (Cosenza, 2023). Genetic maps and variant calling data can be obtained from Casale et al. (2022) and Weisweiler et al. (2022). Seeds of the RILs of the HvDRR population can be requested from the corresponding author.
References
- Afsharyan NP, Sannemann W, Léon J, Ballvora A.. 2020. Effect of epistasis and environment on flowering time in barley reveals a novel flowering-delaying QTL allele. Journal of Experimental Botany 71, 893–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson JT, Song BH.. 2020. Plant adaptation to climate change—where are we? Journal of Systematics and Evolution 58, 533–545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Araus JL, Slafer GA, Royo C, Serret MD.. 2008. Breeding for yield potential and stress adaptation in cereals. Critical Reviews in Plant Sciences 27, 377–412. [Google Scholar]
- Arifuzzaman M, Günal S, Bungartz A, Muzammil S, Afsharyan NP, Léon J, Naz AA.. 2016. Genetic mapping reveals broader role of Vrn-h3 gene in root and shoot development beyond heading in barley. PLoS One 11, e0158718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arifuzzaman M, Sayed MA, Muzammil S, Pillen K, Schumann H, Naz AA, Léon J.. 2014. Detection and validation of novel QTL for shoot and root traits in barley (Hordeum vulgare L.). Molecular Breeding 34, 1373–1387. [Google Scholar]
- Bayer MM, Rapazote-Flores P, Ganal M, et al. 2017. Development and evaluation of a barley 50k iSelect SNP array. Frontiers in Plant Science 8, 1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezant J, Laurie D, Pratchett N, Chojecki J, Kearsey M.. 1996. Marker regression mapping of QTL controlling flowering time and plant height in a spring barley (Hordeum vulgare L.) cross. Heredity 77, 64–73. [Google Scholar]
- Bi X, Esse WV, Mulki MA, Kirschner G, Zhong J, Simon R, Korff MV.. 2019. CENTRORADIALIS interacts with FLOWERING LOCUS T-like genes to control floret development and grain number. Plant Physiology 180, 1013–1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bleecker AB, Kende H.. 2000. Ethylene: A gaseous signal molecule in plant. Annual Review of Cell and Developmental Biology 16, 1–18. [DOI] [PubMed] [Google Scholar]
- Broman KW, Wu H, Sen S, Churchill GA.. 2003. R/qtl: QTL mapping in experimental crosses. Bioinformatics 19, 889–890. [DOI] [PubMed] [Google Scholar]
- Campoli C, Drosse B, Searle I, Coupland G, Von Korff M.. 2012. Functional characterisation of HvCO1, the barley (Hordeum vulgare) flowering time ortholog of CONSTANS. The Plant Journal 69, 868–880. [DOI] [PubMed] [Google Scholar]
- Campoli C, Pankin A, Drosse B, Casao CM, Davis SJ, Von Korff M.. 2013. HvLUX1 is a candidate gene underlying the early maturity 10 locus in barley: phylogeny, diversity, and interactions with the circadian clock and photoperiodic pathways. New Phytologist 199, 1045–1059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casale F, Van Inghelandt D, Weisweiler M, Li J, Stich B.. 2022. Genomic prediction of the recombination rate variation in barley – a route to highly recombinogenic genotypes. Plant Biotechnology Journal 20, 676–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casao MC, Karsai I, Igartua E, Gracia MP, Veisz O, Casas AM.. 2011. Adaptation of barley to mild winters: a role for PPDH2. BMC Plant Biology 11, 164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockram J, Jones H, Leigh FJ, O’Sullivan D, Powell W, Laurie DA, Greenland AJ.. 2007. Control of flowering time in temperate cereals: genes, domestication, and sustainable productivity. Journal of Experimental Botany 58, 1231–1244. [DOI] [PubMed] [Google Scholar]
- Comadran J, Kilian B, Russell J, et al. 2012. Natural variation in a homolog of Antirrhinum CENTRORADIALIS contributed to spring growth habit and environmental adaptation in cultivated barley. Nature Genetics 44, 1388–1392. [DOI] [PubMed] [Google Scholar]
- Cosenza F. 2023. Data from: Genetic mapping reveals new loci and alleles for flowering time and plant height using the double round-robin population of barley. [Dataset]. Zenodo. 10.5281/zenodo.7525604 [DOI] [PMC free article] [PubMed]
- Cuesta-Marcos A, Casas AM, Yahiaoui S, Gracia MP, Lasa JM, Igartua E.. 2008. Joint analysis for heading date QTL in small interconnected barley populations. Molecular Breeding 21, 383–399. [Google Scholar]
- Dawson IK, Russell J, Powell W, Steffenson B, Thomas WTB, Waugh R.. 2015. Barley: a translational model for adaptation to climate change. New Phytologist 206, 913–931. [DOI] [PubMed] [Google Scholar]
- Deng W, Casao MC, Wang P, Sato K, Hayes PM, Finnegan EJ, Trevaskis B.. 2015. Direct links between the vernalization response and other key traits of cereal crops. Nature Communications 6, 5882. [DOI] [PubMed] [Google Scholar]
- Distelfeld A, Li C, Dubcovsky J.. 2009. Regulation of flowering in temperate cereals. Current Opinion in Plant Biology 12, 178–184. [DOI] [PubMed] [Google Scholar]
- Dockter C, Gruszka D, Braumann I, et al. 2014. Induced variations in brassinosteroid genes define barley height and sturdiness, and expand the green revolution genetic toolkit. Plant Physiology 166, 1912–1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Druka A, Franckowiak J, Lundqvist U, et al. 2011. Genetic dissection of barley morphology and development. Plant Physiology 155, 617–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubois M, Van den Broeck L, Inzé D.. 2018. The pivotal role of ethylene in plant growth. Trends in Plant Science 23, 311–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunford RP, Griffiths S, Christodoulou V, Laurie DA.. 2005. Characterisation of a barley (Hordeum vulgare L.) homologue of the Arabidopsis flowering time regulator GIGANTEA. Theoretical and Applied Genetics 110, 925–931. [DOI] [PubMed] [Google Scholar]
- Eriksson ME, Millar AJ.. 2003. The circadian clock. A plant’s best friend in a spinning world. Plant Physiology 132, 732–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faure S, Turner AS, Gruszka D, Christodoulou V, Davis SJ, Von Korff M, Laurie DA.. 2012. Mutation at the circadian clock gene EARLY MATURITY 8 adapts domesticated barley (Hordeum vulgare) to short growing seasons. Proceedings of the National Academy of Sciences, USA 109, 8328–8333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández-Calleja M, Casas AM, Igartua E.. 2021. Major flowering time genes of barley: allelic diversity, effects, and comparison with wheat. Theoretical and Applied Genetics 134, 1867–1897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FAO. 2019. FAOSTAT statistical database. Rome: Food and Agriculture Organization of the United Nations. [Google Scholar]
- FAO. 2020. FAOSTAT statistical database. Rome: Food and Agriculture Organization of the United Nations. [Google Scholar]
- Garin V, Wimmer V, Malosetti M.. 2015. mppR: an R package for QTL analysis in multi-parent populations using linear mixed models. https://cran.r-hub.io/web/packages/mppR/vignettes/mppR_vignette.pdf
- Garin V, Wimmer V, Mezmouk S, Malosetti M, van Eeuwijk F.. 2017. How do the type of QTL effect and the form of the residual term influence QTL detection in multi-parent populations? A case study in the maize EU-NAM population. Theoretical and Applied Genetics 130, 1753–1764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giraud H, Lehermeier C, Bauer E, et al. 2014. Linkage disequilibrium with linkage analysis of multiline crosses reveals different multiallelic QTL for hybrid performance in the flint and dent heterotic groups of maize. Genetics 198, 1717–1734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Göransson M, Hallsson JH, Lillemo M, et al. 2019. Identification of ideal allele combinations for the adaptation of spring barley to northern latitudes. Frontiers in Plant Science 10, 542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hada W, Bo Z, Cao WH, et al. 2009. The ethylene receptor ETR2 delays floral transition and affects starch accumulation in rice. The Plant Cell 21, 1473–1494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayama R, Coupland G.. 2004. The molecular basis of diversity in the photoperiodic flowering responses of Arabidopsis and rice. Plant Physiology 135, 677–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemming MN, Peacock WJ, Dennis ES, Trevaskis B.. 2008. Low-temperature and daylength cues are integrated to regulate FLOWERING LOCUS T in barley. Plant Physiology 147, 355–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemshrot A, Poets AM, Tyagi P, et al. 2019. Development of a multiparent population for genetic mapping and allele discovery in six-row barley. Genetics 213, 595–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill CB, Li C.. 2016. Genetic architecture of flowering phenology in cereals and opportunities for crop improvement. Frontiers in Plant Science 7, 1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iqbal N, Khan NA, Ferrante A, Trivellini A, Francini A, Khan MIR.. 2017. Ethylene role in plant growth, development and senescence: interaction with other phytohormones. Frontiers in Plant Science 8, 475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia QJ, Zhang JJ, Westcott S, Zhang XQ, Bellgard M, Lance R, Li CD.. 2009. GA-20 oxidase as a candidate for the semidwarf gene sdw1/denso in barley. Functional & Integrative Genomics 9, 255–262. [DOI] [PubMed] [Google Scholar]
- Jones H, Leigh FJ, Mackay I, et al. 2008. Population-based resequencing reveals that the flowering time adaptation of cultivated barley originated east of the Fertile Crescent. Molecular Biology and Evolution 25, 2211–2219. [DOI] [PubMed] [Google Scholar]
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong SY, Freimer NB, Sabatti C, Eskin E.. 2010. Variance component model to account for sample structure in genome-wide association studies. Nature Genetics 42, 348–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karsai I, Szucs P, Mészáros K, Filichkina T, Hayes PM, Skinner JS, Láng L, Bedő Z.. 2005. The Vrn-H2 locus is a major determinant of flowering time in a facultative × winter growth habit barley (Hordeum vulgare L.) mapping population. Theoretical and Applied Genetics 110, 1458–1466. [DOI] [PubMed] [Google Scholar]
- Khush GS. 2013. Strategies for increasing the yield potential of cereals: case of rice as an example. Plant Breeding 132, 433–436. [Google Scholar]
- Kikuchi R, Handa H.. 2009. Photoperiodic control of flowering in barley. Breeding Science 59, 546–552. [Google Scholar]
- Knott SA, Haley CS.. 1992. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69, 315–324. [DOI] [PubMed] [Google Scholar]
- Langfelder P, Horvath S.. 2008. WGCNA: An R package for weighted correlation network analysis. BMC Bioinformatics 9, 559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langridge P. 2018. Economic and academic importance of barley. In: Stein N, Muehlbauer G, eds. The barley genome. Compendium of Plant Genomes. Cham: Springer, 1–10. [Google Scholar]
- Laurie DA, Pratchett N, Bezant JH, Snape JW.. 1994. Genetic analysis of a photoperiod response gene on the short arm of chromosome 2(2H) of Hordeum vulgare (barley). Heredity 72, 619–627. [Google Scholar]
- Li ZK, Yu SB, Lafitte HR, et al. 2003. QTL × environment interactions in rice. I. Heading date and plant height. Theoretical and Applied Genetics 108, 141–153. [DOI] [PubMed] [Google Scholar]
- Manichaikul A, Dupuis J, Sen S, Broman KW.. 2006. Poor performance of bootstrap confidence intervals for the location of a quantitative trait locus. Genetics 174, 481–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mascher M, Wicker T, Jenkins J, et al. 2021. Long-read sequence assembly: a technical evaluation in barley. The Plant Cell 33, 1888–1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsushika A, Makino S, Kojima M, Mizuno T.. 2000. Circadian waves of expression of the APRR1/TOC1 family of pseudo-response regulators in Arabidopsis thaliana: Insight into the plant circadian clock. Plant and Cell Physiology 41, 1002–1012. [DOI] [PubMed] [Google Scholar]
- Maurer A, Draba V, Jiang Y, Schnaithmann F, Sharma R, Schumann E, Kilian B, Reif JC, Pillen K.. 2015. Modelling the genetic architecture of flowering time control in barley through nested association mapping. BMC Genomics 16, 290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer A, Draba V, Pillen K.. 2016. Genomic dissection of plant development and its impact on thousand grain weight in barley through nested association mapping. Journal of Experimental Botany 67, 2507–2518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikołajczak K, Kuczyńska A, Krajewski P, et al. 2017. Quantitative trait loci for plant height in Maresi × CamB barley population and their associations with yield-related traits under different water regimes. Journal of Applied Genetics 58, 23–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milner SG, Jost M, Taketa S, et al. 2019. Genebank genomics highlights the diversity of a global barley collection. Nature Genetics 51, 319–326. [DOI] [PubMed] [Google Scholar]
- Mizuno T, Nakamichi N.. 2005. Pseudo-response regulators (PRRs) or True oscillator components (TOCs). Plant and Cell Physiology 46, 677–685. [DOI] [PubMed] [Google Scholar]
- Mulki MA, von Korff M.. 2016. CONSTANS controls floral repression by up-regulating VERNALIZATION2 (VRN-H2) in barley. Plant Physiology 170, 325–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myles S, Peiffer J, Brown PJ, Ersoz ES, Zhang Z, Costich DE, Buckler E.. 2009. Association mapping: Critical considerations shift from genotyping to experimental design. The Plant Cell 21, 2194–2202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamichi N, Kudo T, Makita N, Kiba T, Kinoshita T, Sakakibara H.. 2020. Flowering time control in rice by introducing Arabidopsis clock-associated PSEUDO-RESPONSE REGULATOR 5. Bioscience, Biotechnology, and Biochemistry 84, 970–979. [DOI] [PubMed] [Google Scholar]
- Nice LM, Steffenson BJ, Blake TK, Horsley RD, Smith KP, Muehlbauer GJ.. 2017. Mapping agronomic traits in a wild barley advanced backcross–nested association mapping population. Crop Science 57, 1199–1210. [Google Scholar]
- Nishida H, Ishihara D, Ishii M, et al. 2013. Phytochrome C is a key factor controlling long-day flowering in barley. Plant Physiology 163, 804–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasam RK, Sharma R, Malosetti M, van Eeuwijk F, Haseneyer G, Kilian B, Graner A.. 2012. Genome-wide association studies for agronomical traits in a world wide spring barley collection. BMC Plant Biology 12, 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patil V, McDermott HI, McAllister T, et al. 2019. APETALA2 control of barley internode elongation. Development 146, dev170373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pauli D, Muehlbauer GJ, Smith KP, Cooper B, Hole D, Obert DE, Ullrich SE, Blake TK.. 2014. Association mapping of agronomic QTLs in US spring barley breeding germplasm. The Plant Genome 7, plantgenome2013.11.0037. [Google Scholar]
- Pieper R, Tomé F, Pankin A, Von Korff M.. 2021. FLOWERING LOCUS T4 delays flowering and decreases floret fertility in barley. Journal of Experimental Botany 72, 107–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piepho HP, Möhring J.. 2007. Computing heritability and selection response from unbalanced plant breeding trials. Genetics 177, 1881–1888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez M, Rau D, Papa R, Attene G.. 2008. Genotype by environment interactions in barley (Hordeum vulgare L.): different responses of landraces, recombinant inbred lines and varieties to Mediterranean environment. Euphytica 163, 231–247. [Google Scholar]
- Rollins JA, Drosse B, Mulki MA, Grando S, Baum M, Singh M, Ceccarelli S, Von Korff M.. 2013. Variation at the vernalisation genes Vrn-H1 and Vrn-H2 determines growth and yield stability in barley (Hordeum vulgare) grown under dryland conditions in Syria. Theoretical and Applied Genetics 126, 2803–2824. [DOI] [PubMed] [Google Scholar]
- Schmalenbach I, Léon J, Pillen K.. 2009. Identification and verification of QTLs for agronomic traits using wild barley introgression lines. Theoretical and Applied Genetics 118, 483–497. [DOI] [PubMed] [Google Scholar]
- Sharma R, Shaaf S, Neumann K, et al. 2020. On the origin of photoperiod non-responsiveness in barley. bioRxiv doi: 10.1101/2020.07.02.185488. [Preprint]. [Google Scholar]
- Shoesmith JR, Solomon CU, Yang X, et al. 2021. APETALA2 functions as a temporal factor together with BLADE-ON-PETIOLE2 and MADS29 to control flower and grain development in barley. Development 148, dev194894. [DOI] [PubMed] [Google Scholar]
- Shrestha A, Cosenza F, van Inghelandt D, Wu P-Y, Li J, Casale FA, Weisweiler M, Stich B.. 2022. The double round-robin population unravels the genetic architecture of grain size in barley. Journal of Experimental Botany 73, 7344–7361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stich B. 2009. Comparison of mating designs for establishing nested association mapping populations in maize and Arabidopsis thaliana. Genetics 183, 1525–1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner A, Beales J, Faure S, Dunford RP, Laurie DA.. 2005. The pseudo-response regulator Ppd-H1 provides adaptation to photoperiod in barley. Science 310, 1031–1034. [DOI] [PubMed] [Google Scholar]
- VanRaden PM. 2008. Efficient methods to compute genomic predictions. Journal of Dairy Science 91, 4414–4423. [DOI] [PubMed] [Google Scholar]
- van Rossum BJ, Kruijer W, van Eeuwijk F, Boer M, Malosetti M, Bustos-Korts D, Wehrens R.. 2022. Package ‘statgenGWAS’. R Package version 1. https://cran.r-project.org/web/packages/statgenGWAS/statgenGWAS.pdf
- Vaser R, Adusumalli S, Leng SN, Sikic M, Ng PC.. 2016. SIFT missense predictions for genomes. Nature Protocols 11, 1–9. [DOI] [PubMed] [Google Scholar]
- Vidal T, Gigot C, De Vallavieille-Pope C, Huber L, Saint-Jean S.. 2018. Contrasting plant height can improve the control of rain-borne diseases in wheat cultivar mixture: Modelling splash dispersal in 3-D canopies. Annals of Botany 121, 1299–1308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Korff M, Wang H, Léon J, Pillen K.. 2006. AB-QTL analysis in spring barley: II. Detection of favourable exotic alleles for agronomic traits introgressed from wild barley (H. vulgare ssp. spontaneum). Theoretical and Applied Genetics 112, 1221–1231. [DOI] [PubMed] [Google Scholar]
- Vyas S, Khatri-Chhetri A, Aggarwal P, Thornton P, Campbell BM.. 2022. Perspective: The gap between intent and climate action in agriculture. Global Food Security 32, 100612. [Google Scholar]
- Wang J, Yang J, Jia Q, Zhu J, Shang Y, Hua W, Zhou M.. 2014. A new QTL for plant height in barley (Hordeum vulgare L.) showing no negative effects on grain yield. PLoS One 9, e90144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei J, Fang Y, Jiang H, Wu X, Zuo J, Xia X, Li J, Stich B, Cao H, Liu Y.. 2022. Combining QTL mapping and gene co-expression network analysis for prediction of candidate genes and molecular network related to yield in wheat. BMC Plant Biology 22, 288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisweiler M, Arlt C, Wu P-Y, Van Inghelandt D, Hartwig T, Stich B.. 2022. Structural variants in the barley gene pool: precision and sensitivity to detect them using short-read sequencing and their association with gene expression and phenotypic variation. Theoretical and Applied Genetics 135, 3511–3529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisweiler M, Montaigu AD, Ries D, Pfeifer M, Stich B.. 2019. Transcriptomic and presence/absence variation in the barley genome assessed from multi-tissue mRNA sequencing and their power to predict phenotypic traits. BMC Genomics 20, 787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wendt T, Holme I, Dockter C, Preu A, Thomas W, Druka A, Waugh R, Hansonn M, Braumann I.. 2016. HvDep1 is a positive regulator of culm elongation and grain size in barley and impacts yield in an environment-dependent manner. PLoS One 11, e0168924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiegmann M, Maurer A, Pham A, et al. 2019. Barley yield formation under abiotic stress depends on the interplay between flowering time genes and environmental cues. Scientific Reports 9, 6397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan L, Fu D, Li C, Blechl A, Tranquilli G, Bonafede M, Sanchez A, Valarik M, Yasuda S, Dubcovskz J.. 2006. The wheat and barley vernalization gene VRN3 is an orthologue of FT. Proceedings of the National Academy of Sciences, USA 103, 19581–19586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan L, Loukoianov A, Blechl A, Tranquilli G, Ramakrishna W, SanMiguel P, Bennetzen JL, Echenique V, Dubcovsky J.. 2004. The wheat VRN2 gene is a flowering repressor down-regulated by vernalization. Science 303, 1640–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan L, Loukoianov A, Tranquilli G, Helguera M, Fahima T, Dubcovsky J.. 2003. Positional cloning of the wheat vernalization gene VRN1. Proceedings of the National Academy of Sciences, USA 100, 6263–6268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Bi IV, et al. 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nature Genetics 38, 203–208. [DOI] [PubMed] [Google Scholar]
- Zakhrabekova S, Gough SP, Braumann I, et al. 2012. Induced mutations in circadian clock regulator Mat-a facilitated short-season adaptation and range extension in cultivated barley. Proceedings of the National Academy of Sciences, USA 109, 4326–4331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, Horvath S.. 2005. A general framework for weighted gene co-expression network analysis. Statistical Applications in Genetics and Molecular Biology 4, Article17. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The codes used for the calculation of the adjusted entry means, the single and multi-parent population QTL analyses, the epistatic QTL models, the WGCNA analysis, as well as the datasets of the adjusted entry means of the HvDRR population, the genetic haplotypes used to build the ancestral model, and the genotypic and phenotypic data used in the QTL analyses are available at GitHub: https://github.com/cosenzaf/HvDRR_FT_PH. The data for membership of genes to gene modules used in the WGCNA are available at Zenodo repository: https://zenodo.org/record/7525604#.Y7_VgxXMLIW (Cosenza, 2023). Genetic maps and variant calling data can be obtained from Casale et al. (2022) and Weisweiler et al. (2022). Seeds of the RILs of the HvDRR population can be requested from the corresponding author.