Abstract
In 2015 the US federal government sponsored a dengue forecasting competition using historical case data from Iquitos, Peru and San Juan, Puerto Rico. Competitors were evaluated on several aspects of out-of-sample forecasts including the targets of peak week, peak incidence during that week, and total season incidence across each of several seasons. our team was one of the winners of that competition, outperforming other teams in multiple targets/locales. In this paper we report on our methodology, a large component of which, surprisingly, ignores the known biology of epidemics at large—for example, relationships between dengue transmission and environmental factors—and instead relies on flexible nonparametric nonlinear Gaussian process (GP) regression fits that “memorize” the trajectories of past seasons, and then “match” the dynamics of the unfolding season to past ones in real-time. Our phenomenological approach has advantages in situations where disease dynamics are less well understood, or where measurements and forecasts of ancillary covariates like precipitation are unavailable, and/or where the strength of association with cases are as yet unknown. In particular, we show that the GP approach generally outperforms a more classical generalized linear (autoregressive) model (GLM) that we developed to utilize abundant covariate information. We illustrate variations of our method(s) on the two benchmark locales alongside a full summary of results submitted by other contest competitors.
Keywords: Epidemiology, Gaussian process, heteroskedastic modeling, latent variable, generalized linear (autoregressive) model, dengue fever
1. Introduction
According to the United States Centers for Disease Control and Prevention (CDC) more than one-third of the world’s population lives at risk of infection from dengue, a viral disease transmitted by Aedes aegypti and Aedes albopictus mosquitos. In the tropics and sub-tropics dengue is one of the leading causes of mortality and morbidity among viral vector-borne diseases (http://www.cdc.gov/Dengue, December 2016). Although the first dengue vaccine was licensed in Mexico in December 2015, the World Health Organization recommends it only be used in geographic areas with high disease burden [World Health Organization (2016)], and it is not available throughout most of Latin America. As a result, prevention measures focus on avoiding mosquito bites and controlling mosquito populations. Although initial infections are often mild, subsequent infections can be very serious, leading to potentially life threatening disease manifestations such as hemorrhage and shock [World Health Organization (2009)].
Early recognition and prompt treatment of severe cases can substantially lower the risk of medical complications and death. Accurate forecasts of cases of infected individuals, or incidence, are key to planning and resource allocation. For example, knowing well in advance the numbers of cases that are expected and when they will occur allows preparation via education and community mobilization campaigns, reallocation of resources (people, insecticide, diagnostic reagents) to high-risk areas, or retraining of physicians to recognize symptoms and to treat appropriately [Degallier et al. (2010), Kuhn et al. (2005), Thomson, Garcia-Herrera and Beniston (2008)] in advance of peak transmission.
In 2015 several agencies of the US federal government (Department of Health and Human Services, Department of Defense, Department of Commerce, and the Department of Homeland Security) joined together, with the support of the Pandemic Prediction and Forecasting Science and Technology Interagency Working Group under the National Science and Technology Council, to design an infectious disease forecasting project with the aim of galvanizing efforts to predict epidemics of dengue. Details of this “Dengue Forecasting Project” are available on the web pages of the National Oceanic and Atmospheric Administration (http://dengueforecasting.noaa.gov/), and will be summarized in Section 2. The basic idea is to allow competitors to train on historical incidence data, independently at two sites (Iquitos, Peru and San Juan, Puerto Rico), and then make forecasts for the full remainder of an epidemic season as weekly incidence numbers arrive. Competitors are judged relative to one another via proper scoring rules on several predictive targets, including peak incidence, peak week, and total season incidence (described in more detail below).
Our team was one of six top performers selected to present their methods to the White House Office of Science and Technology Policy and the Federal Pandemic Prediction and Forecasting Science and Technology Working Group at an event at the White House in October 2015. Our method was consistently among the best of competitors in all three targets, although not for absolutely all weeks of every season, as we will illustrate in Section 5. Surprisingly, a substantial component of our strategy deliberately ignores known associations between incidence and environmental variables such as precipitation and temperature. Instead we preferred a more phenomenological approach that modeled relationships in the incidence data only, and developed a dynamic forecasting tool that attempted to determine, as the season unfolded, which of previous seasons the current one most resembles. The tools included data transformations, Gaussian processes, heteroskedastic components, latent variables, and Monte Carlo sampling of forecasted incidence trajectories. Below we refer to this as the hetGP (for heteroskedastic Gaussian Process) approach.
Our use of GPs toward this end is novel, although others have used GPs in epidemiological forecasting exercises in slightly different contexts. For example Farah et al. (2014) use GPs to emulate an SIR-type computer model in a forecasting framework for influenza, and Hu and Ludkovsk (2017) deploy GPs within a stochastic control framework involving a continuous time Markov process inspired by SIR models. Our hetGP predictor relies on novel extensions to the typical GP arsenal: a multitude of variance components which are learned from data to achieve the heteroskedastic effect, and a latent variable scheme that allows forecasts to adapt to emerging season dynamics. Both of these terms, heteroskedastic [e.g., Binois, Gramacy and Ludkovski (2016)] and latent variable [e.g., Bornn, Shaddick and Zidek (2012)] can be found attached to GP methodology in the literature. However again our treatment of those, with choices motivated by our application to disease forecasting are, we believe, both new.
Our team also developed, in parallel, a forecasting apparatus based on a more conventional dynamic generalized linear model (GLM) framework, utilizing lagged environmental (e.g., precipitation and temperature) and demographic (e.g., population) covariates. The GLM occasionally out-performed hetGP. Since we could only submit one comparator to the contest, we opted for a hybrid of the two as a hedge. In this paper we focus our exposition on hetGP. We showcase its forecasting prowess in isolation, as compared to the GLM alone, to our original hybridized model, and to the results reported by other contest competitors. Besides uncoupling hetGP from the GLM, the hetGP version presented here is slightly updated from our contest submission. The original hetGP worked with a different data transformation, and deployed a more crude heteroskedastic mechanism. In our exposition we are careful to delineate the original contest submission and its more recent update, and to motivate the enhancements subsequently made.
The remainder of the paper is outlined as follows. In Section 2 we review contest particulars, with details on the transmission of dengue and its relationship to environmental covariates. We also introduce the data, discuss appropriate transformations, and summarize the contest scoring metrics that impacted some of our methodological choices. Section 3 provides a description of our main modeling contribution, hetGP. Section 4 discusses implementation details, including a classical GLM strategy. In Section 5 we provide visualization of our learning and forecasting procedures over the contest seasons, and a full comparison of our results against those of other contest entrants. We conclude with a brief discussion in Section 6. A detailed appendix contains additional views into the data and results, technical details including analytic derivative expressions for the hetGP likelihood, a list of the environmental and demographic predictors that were key to the GLM setup, and an influential derived predictor based on a parameterized model of the so-called basic reproductive rate, .
2. Dengue forecasting project
Here we summarize the competition setup described in more detail on NOAA’s website (http://dengueforecasting.noaa.gov/docs/project_description.pdf). The “Dengue Forecasting Project” was announced in the first half of 2015, with training data up to 2009 made publicly available in June. For San Juan, Puerto Rico, the data go back to 1990, and for Iquitos, Peru, back to 2000. Competitors “registered” for the competition by submitting a brief report and results on the training data, treating the latter four years (2005–2009) as an out-of-sample testing set. Those successfully submitting initial results were invited to participate in the real testing exercise, which comprised data from 2009–2013. Only invited teams received these data, delivered later in August, with the understanding that it could not be shared with other parties. Forecasts on the testing data were due one week later, in early September. The quick turnaround meant that methods must be reasonably computationally efficient to be competitive.
2.1. The data
The provided data include weekly dengue incidence and linked environmental variables. The training and testing sets may be downloaded from http://predict.phiresearchlab.org/legacy/dengue/index.html. The dengue incidence portion is comprised of historical surveillance data at Iquitos, Peru and San Juan, Puerto Rico, summarized weekly. Cases in the data set include laboratory-confirmed and serotype-specific cases. The data are actual final counts, that is, reflecting the total number of cases in each week, possibly revised or estimated ex post. A breakdown of incidence into strata of four serotypes, with a fifth un-serotyped category, were also provided. However, we only trained on total_cases in the data file, that is, the same variable that we were tasked with predicting out of sample.
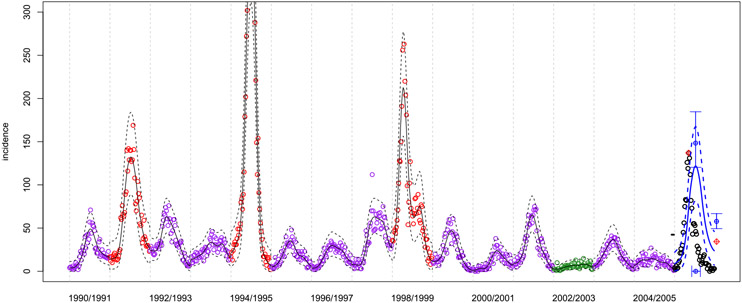
As an example of the data, in Figure 1 we show San Juan incidence over the first sixteen years of the training period. Many of the details in the figure will emerge over the course of our presentation in later sections. For now, the focus is on high-level features in weekly incidences, shown as open circles. Observe that there is a yearly cycle, although the severity and timing from one year to the next does not suggest an obvious pattern. Occasionally there are two bumps in a season. Notice that the data clearly exhibit a heteroskedastic feature, that is, in addition to having a mean response that changes over time, the dispersion of points around that mean response also varies. This is most easily seen by comparing the 1991/1992 season to the 2000/2001 season, with the former having much larger spread than the latter. Visually, dispersion is correlated with level: the larger the levels the larger the dispersion. Naturally, the dispersion is also asymmetric due to positivity.
Fig. 1.
San Juan incidence data (open circles) over most of the training period. Incidence here are the number of reported cases of dengue each week. The colors indicate a judgment of severity in data that have been observed, specifically: green = mild (< 25 cases in any week), purple=moderate (25–100 in any week), red = severe (> 100 cases in any week). Further discussion is provided in Section 3.1.2. Future, unobserved data are indicated with black open circles. Solid lines indicate the mean predictive curve and dashed lines the 2.5% and 97.5% quantiles around this mean. The black lines are the within-sample fits. The blue lines are the forecasted dynamics for the unobserved season (see Section 3). In the unobserved season, red circles indicate the true values of targets (see Section 2.2), blue open circles indicate point forecasts for the targets, and central 95% predictive intervals around those are indicated with blue error bars (see Section 4.2).
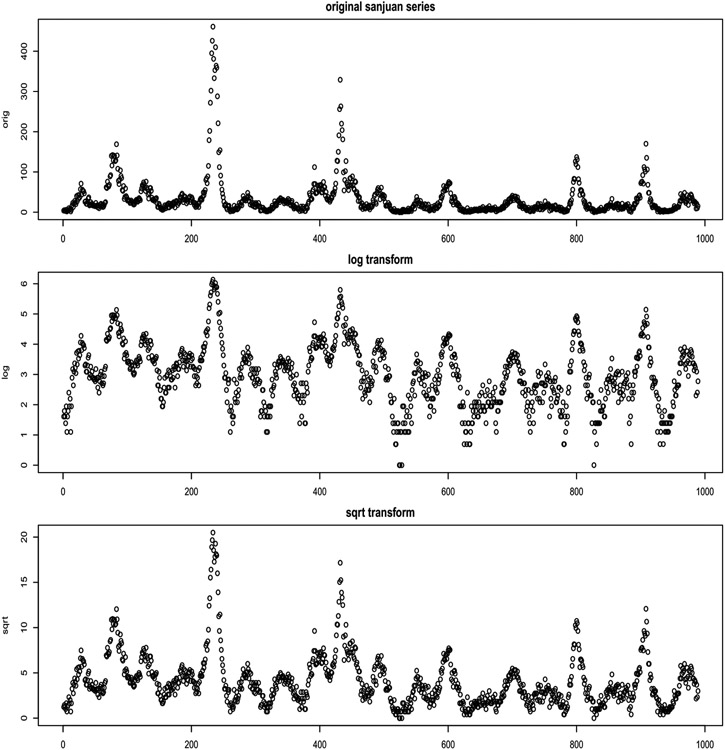
Sometimes such level-dependent variability and asymmetry can be simultaneously mitigated with a log transformation. Indeed, our originally submitted solution involved GP modeling on log (one-plus) incidence. However, the log transformation over-corrects: lower dispersions are too spaced out relative to larger ones, which are aggressively squashed (see Figure 10). A square-root transformation works much better. Since forecasts based on Gaussians may be negative, we use a modified transformation, detailed in Appendix A.1.
The contest organizers also provided environmental and demographic data as potential covariates, as it is widely known that environmental factors impact the dynamics of mosquito vectors and thus transmission [e.g., Barrera, Amador and MacKay (2011), Johansson, Cummings and Glass (2009), Lambrechts et al. (2011), Moore et al. (1978), Stewart-Ibarra et al. (2013), Xu et al. (2016)]. The data provided included weekly precipitation, temperatures (min, max, and average), habitat indices [specifically the normalized difference vegetation index (NDVI) a measure of presence of live green vegetation], and yearly population. Participants were free to augment with other social media, environmental, and demographic covariates, but were barred from using dengue incidence measures from other (e.g., nearby) locations. Previous studies have identified correlations between the Southern Oscillation Index (SOI) and other El Nino sea surface temperature indices and dengue [e.g., Gagnon, Bush and Smoyer-Tomic (2001), Johansson, Cummings and Glass (2009)]. Our team obtained current monthly SOI and sea surface temperatures [Reynolds et al. (2002)] and aligned these with the weekly case data to augment our data set.
An exploratory analysis revealed strong correlations between (lagged values) of these predictors and the total_cases response. For example, the correlations to average temperature and average squared temperature peak at around eleven weeks in the in-sample training portion of our data, and these exhibit the highest linear correlation among the covariates provided. Other previous studies indicate similar long lags between environmental covariates and incidence measures for dengue [Johansson, Cummings and Glass (2009), Xu et al. (2016), Stewart-Ibarra and Lowe (2013), Stewart-Ibarra et al. (2013)].
2.2. Forecasts and evaluation
Three predetermined forecasting targets are evaluated: peak week, peak incidence, and total incidence, revised every four weeks in each 52-week “season.” These are evaluated separately at the two sites, Iquitos and San Juan, for six targets total. Peak week refers to a forecast of the week having the highest incidence and peak incidence is the count of the number of (newly) infected individuals in that week. Total or season incidence refers to the sum of weekly incidences over all 52 weeks. Contest organizers asked for point forecasts for each target, together with a predictive distribution discretized into “buckets” for each of 13 weeks evenly spanning the season (i.e., one forecast every four weeks, starting from week zero). Competition evaluation focused on logarithmic scores over the first 24 weeks of each season in the testing set. These log scores are a variation on Example 3 from Gneiting and Raftery (2007): an aggregate of the natural logarithm of the probability pi where i is the “bucket” containing true value of each target/week. The “bucket” discretization(s) and other details are provided in the contest rules document. Log scores are intended to evaluate forecasts based on a coherent blend of their accuracy and confidence.
As an example of forecasts for the three targets, refer again to Figure 1 for San Juan. The final season segment, delineated by the vertical dashed gray bars, corresponds to (as yet unobserved) incidence in the 2005/2006 season shown as black open circles. The blue solid and dashed lines in that segment are a forecast of the incidence trajectory using only data from previous seasons, via the hetGP method described in Section 3. There are two open red circles with red crosses through them indicating the true values of the three targets. The y-coordinate of the first open red crossed circle indicates peak incidence, and the x coordinate indicates peak week. The y-value of the second open red crossed circle, drawn at the position of week “53” shows total incidence (divided by 52 so that it is on the same scale as the weekly incidence values). These are the targets for the current season, but they are unknown to the fitting and prediction method in the out-of-sample forecasting exercise(s). Predictions for these targets are shown as blue open circles with blue “I”-shaped error bars through them, representing central 95% prediction intervals. There are three of these, one each for peak incidence, peak week (on the horizontal axis), and total incidence (at the position of week 53). We describe how these point forecasts and intervals, and ultimately the full predictive distribution over these targets, are derived in Section 4.2.
It is worth remarking that our modeling efforts do not explicitly leverage the form of the targets or the log score evaluation, say to tune parameters via cross-validation. We simply model historical incidence and derive predictions for future incidence. However, our forecasting distributions for the targets, which are derived from the predictive distribution, are designed to be coherent with the evaluation scheme.
3. Gaussian process modeling
Our team’s initial approach to modeling the dengue challenge data was via the GLM described in Section 4.1; however there were several shortcomings. We found that parameters for environmental predictors lacked stability when trained on fewer than seven years of data (particularly problematic for Iquitos) and early season forecasts consistently underestimated the potential for large epidemics. We were unable to address these weaknesses with linear models despite entertaining many diverse incarnations. Moreover, obtaining accurate forecasts for environmental predictors such as weekly precipitation was particularly fraught. Note that this is necessary even when using, say, lag-11 predictors if forecasting the full remaining season’s trajectory, up to 52 weeks into the future. Obtaining useful precipitation and SOI forecasts (e.g., via a purely statistical apparatus, without sophisticated climate-modeling machinery), proved be harder than the original incidence modeling problem.
Thus we decided to explore a second approach based on Gaussian processes (GPs). This alternative strategy is simultaneously simpler (in its use of data) and far more flexible (non-parametrically estimating non-linear relationships). In fact, it uses no observed covariates other than the (square-root transformed) series of weekly incidence numbers, and therefore no environmental or other predictors required forecasting subroutines.
The basic idea behind the GP was to build a fitting mechanism that “memorized” the incidence trajectories of previous seasons, in a certain statistical sense, and thus could produce forecasts for the current season that resemble previous, similar seasons. At the start of a season, before any new data have arrived, we desired forecasts based almost entirely on an amalgam of previous seasons, with an adjustment for starting level (taken from the end of the previous season). Our contest submission involved a conservative “hedge,” biasing early season forecasts toward more extreme past seasons, but this has been revised in our updated version. As the forecasting season progresses, we desired a fitting mechanism which could be updated quickly (in light of the new data), so that predictions could be tailored to track some previous seasons more closely than others, but be flexible enough to exhibit/track novel behavior depending on what the incoming data suggested. The details follow.
3.1. A simple GP fit on derived variables
Gaussian process (GP) regression is an established nonparametric modeling apparatus originating in the spatial statistics literature, where it is also known as kriging [Cressie (1993), Matheron (1963)]. The GP has subsequently gained popularity in the computer experiments [Sacks et al. (1989)] and machine learning literatures [Rasmussen and Williams (2006)] for its ability to capture complicated nonlinear dynamics with a high degree of analytic tractability and very few tunable hyperparameters. For our purposes a GP is simply a flexible model , facilitating nonparametric regression given n example training pairs . When choosing predictors comprising the p coordinates of the it helps to think spatially, rather than linearly, as with more standard regressions (like GLMs). That is, the GP will give more similar predictions (i.e., more highly correlated) for and if and are close in the input space. Following a common default in the GP prediction literature, we model the correlation, , as a product of exponential inverse squared distances in the coordinates of via
| (1) |
a so-called product (or separable) Gaussian kernel. The characteristic lengthscale hyperparameter in each input coordinate , or weight on distances in each , can be learned from the data through the likelihood. The unknown quantities are referred to as hyperparameters, rather than ordinary parameters, due to the nonparametric nature of GP prediction and to the subtle effect their settings have on those predictions. Default values are often sufficient to get highly accurate results. We briefly digress to review some relevant GP specifics before continuing with details on how we deploy GPs for dengue incidence forecasting.
3.1.1. GP review
The model for a finite collection of -variables, observed at a row-wise collected n × p matrix of inputs in GP regression is multivariate normal (MVN), which is where the term Gaussian process comes from.5 A typical setup is
| (2) |
where is an n × n matrix constructed from pairs of rows of . The scale parameter and the so-called nugget may be estimated along with by reinterpreting (2) as a likelihood. Appendix B provides an expression for the log likelihood, a concentrated version with closed form maximum likelihood estimator (MLE) for the scale plugged in, and one for the gradient of the concentrated log likelihood comprised of partial derivatives with respect to all parameters. That discussion is tailored to our heteroskedastic (hetGP) extensions described in Section 3.3, but comments therein also address the simpler case described here. Observe that the ordinary linear model is nested within the GP framework as a special case if we take and and . Many GP modeling setups take unless one has a priori knowledge of mean dynamics. This has the effect of moving all of the modeling effort to the correlation structure.
The forecasting distribution then arises as a consequence of MVN conditioning rules. Let denote a set of predictive locations. The GP setup extends the MVN to the joint distribution of data and predictive quantities. Using and dropping from to streamline the notation,
The conditional distribution is where
| (3) |
Inference for the unknown hyperparameters (via MLE, say) and prediction (following the equations above) is fairly straightforward to code, however many libraries exist. Our contest submission implementation used the newGPsep, mleGPsep, and predGPsep functions in the laGP library [Gramacy (2014), Gramacy (2016)] for R [R Development Core Team (2008)] on the Comprehensive R Archive Network (CRAN). Those functions serve as the basis for extensions provided by our new hetGP version, implementing the new (revised) methods we describe in Section 3.3.
3.1.2. GP dengue incidence forecasting
To use this setup to forecast dengue incidence requires “divining” some x-variables to pair with the square-root-transformed y incidence values. We say “divining” because a unique, and perhaps at first somewhat puzzling, feature of our approach is that (unlike the GLM in Section 4.1) we deliberately avoid environmental and demographic predictors known to covary with dengue incidence. Our x-values are entirely determined by fixed values we create in order to encourage the dynamics we observe in the training data, and by the dengue incidence (y) values themselves. Nevertheless, through inference for hyperparameters, particularly the , the GP predictors we calculate are able to accurately track trajectories as they evolve in time by learning the appropriate “spatial” lengthscale, which acts as a similarity measure between y-values depending on the closeness of their associated x’s.
We use the four predictors described below.
: Season–time
Our first predictor is the repeated sequence 1, …, 52, corresponding to the week number of the response y-value. This causes the response y-values to be modeled as more highly correlated with one another if they come from the same or nearby weeks in the current season and other seasons.
: Sine wave
Our second predictor acknowledges periodic effects, for example, as may be driven by temperature and precipitation, but more importantly encodes that the end of all seasons should be correlated with their beginnings and the beginnings of others, and vice versa. Like this is a deterministic predictor that is repeated for all seasons.
: Starting level
Our third predictor is the value of the final y-value in the previous season. This -value is repeated for each of the 52 observations in each season, and encodes our belief that the season-dynamics are more similar (more highly correlated) to other seasons which started at similar levels. For the first season in each data set we take the first value of the season instead.
: Severity
Based on the y-values (on the original scale) this predictor takes on one of three values {−1, 0, 1} depending on the value of the largest number of cases in a week during that season. For example, for the San Juan incidence data, if there are more than 100 cases in any week in a particular season, then the value for all observations in that season is set to 1, recording a severe season. If no week has more than 25 cases it is set to −1, a mild season. Otherwise it is set to zero, indicating an intermediate level. The open circles in Figure 1 are colored by this value: −1 is green, 0 is purple, and red is +1. For Iquitos the thresholds are 25 and 10, respectively. Therefore, encodes that the dynamics of severe seasons should be more similar to one another than to intermediate or (to a lesser extent) mild ones.
Clearly is unknown as a particular season unfolds, during which time forecasts are being derived from predictive distributions. It is a so-called latent variable in this context, requiring special treatment as we describe below. Its settings, {−1, 0, 1}, are arbitrary and its relationship to the y-values in the data is deliberately weak. We chose a discretization of past severities over several incarnations of continuous alternatives, such as setting to the actual value of that season’s peak incidence (or a transformed version), because the former had a nice pooling effect. Continuous versions, rather, resulted in estimated lengthscale parameters that had the effect of spreading out past seasons, making it difficult to “classify” the severity of new seasons as they unfolded. In other settings, perhaps a higher dimensional variable, or one with more categories, or with a stronger link to y, may work as well or better. We preferred our {−1, 0, 1} choice primarily for its implementation advantages; that is, it was the simplest setup we could envision that provided the requisite flexibility, forecasting accuracy and coverage.
3.2. Forecasting, latent learning, and nonstationary dynamics
At the start of a new forecasting season, that is, at week zero, all historical observations are used to form the x and y-values that comprise the training set. Maximum likelihood is used to infer the unknown hyperparameters. Forming a predictor for the following weeks involves assembling the x-values describing those weeks, and then running them through the predictive equations as values (3). In the case of , , this is straightforward; is more challenging because the severity of the new season is an unknown quantity. (Part way through the season we may know if the maximum incidence is above, say 100, but if it is not the chances that it will be are a complicated function of the evolving dynamics and noise in the data.) To address this we treat the new-season value as a latent variable. Although the historical data values of are discrete, taking on one of {−1, 0, 1}, we allow the new season’s value to be continuous, to achieve a smoothing effect over historical regimes. The initial setting of for the new season must be chosen carefully, and then be allowed to adapt as the season unfolds. In our contest submission we hedged toward severe seasons with an initial setting of .6 Initialization details for our revised version are more nuanced and less hedged, and are provided in Section 3.3. As data arrive throughout the season we use the so-called predictive log likelihood (PLL) to optimize its setting.
Our use of the PLL involves the model’s predictive probability of observed data from the first weeks of the new season, paired with inputs , for . This is calculated following equation (3), evaluating the (log) MVN density with as and the as . To choose latents we view that log predictive probability as a function of , which in our setup is the same for all , and optimize over that value. That is, if represents a set of severity values of interest, then one solves
| (4) |
to obtain an estimate of the latent severity coordinate . In equation (4) the … refer to settings of the GP hyperparameters, for example, MLE settings. Especially early in the season we find it helpful to restrict to a small window (e.g., ±0.25) around the previous estimated from earlier weeks in the season.
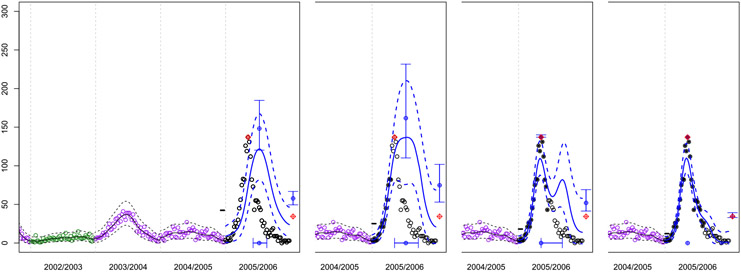
As an illustration, consider the week zero season forecasts corresponding to the setup in Figure 1. We redraw a zoomed-in version of the figure here, in the left panel of Figure 2. With a latent structure indicating moderate-to-high severity, and a low setting of the starting level , we can see (referring to Figure 1) that the week zero forecasts most resemble the mildest of the severe historical seasons (1991/1992). However the other seasons, both milder and more extreme, contribute to the forecasts via the exponentially decaying distances calculated in the GP covariance structure.
FIG. 2.
Snapshots of GP forecasts for San Juan corresponding to weeks 0, 16, 24 and 32 in the 2005/2006 season. Symbols, colors, and plotting lines are the same as in Figure 1.
As the season progresses the model fit learns that it is indeed a severe year. The second panel of Figure 2 shows the revised predictive equations after data up to week 16 are incorporated. (Incorporated weeks have their open circles filled in with solid dots.) Observed incidences are on an upward trend, and we can see from the future data that the peak is yet to come. It is perhaps not surprising then that the forecasts of potential future incidence, and the associated uncertainty, have increased substantially compared to week zero. However, eight weeks later, shown in the third panel, the observed incidences are declining, and the forecasts indicate that it is quite likely that the peak has passed. The probabilities associated with that hypothesis, and the associated error bars shown in the figure, are explained in Section 4.2. Observe that the forecasting distribution indicates the potential for a relapse of high incidence, mimicking the observed dynamics of 1998/1999. After another eight weeks, shown in the final panel, the potential for such a relapse is much diminished.
Toward the end of the season it is typical for the estimated latent value to drift away from {−1, 0, 1} values that encode in the training data . This is because each season is distinct from the previous ones, and capturing those distinct dynamics requires the new season to exhibit differences rather than similarities to the past. Moreover, it is clear from examining Figure 1, or the transformed versions in Figure 10, that the dynamics are highly nonstationary in that within-season dynamics do not have the same mean structure from one season to the next. However our Gaussian correlation structure assumes stationarity (i.e., that the correlation depends only on distance between the inputs). The introduction of a latent coordinate has recently been proposed as a remedy for adapting a stationary GP to nonstationary data [Bornn, Shaddick and Zidek (2012)]. Therefore there is a tension in the dual role we are asking to take on: indicating severity (i.e., similarly to certain past seasons with similar incidence heights) and nonstationary flexibility (i.e., dissimilarity to any previous year, whether by height or otherwise).
3.3. Heteroskedastic enhancements
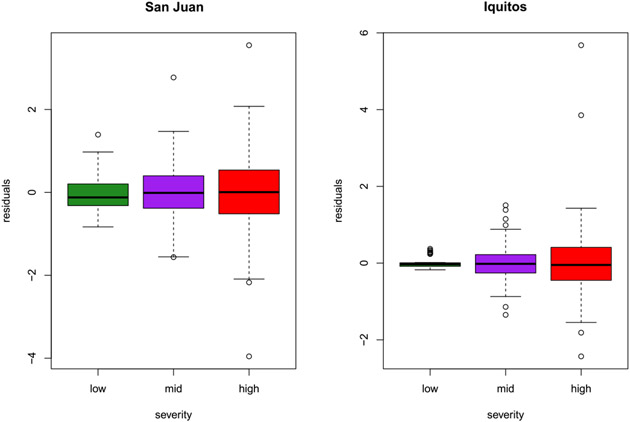
During the contest period we noticed a relationship between seasonal severity (i.e., mean weekly incidence) and the dispersion of incidences around their mean. That is, we noticed that the data were heteroskedastic, even after using the square root (and log) transformations (Appendix A.1) in an attempt to minimize such relationships. However, due to time constraints imposed by the contest deadlines we were unable to develop the methodological extensions required address this nuance for our original submitted forecasts. Figure 3 illustrates this feature of the data by plotting in-sample residuals from the weekly predicted mean fitted values obtained over the training period for San Juan and Iquitos. These results are on the scale of the square root transformed y-values. Observe that residuals for seasons classified as mild (less than 25 weekly cases for San Juan and less than 10 for Iquitos) show the lowest dispersion, whereas residuals for the highest severity seasons (more than 100 and 25, respectively) show the highest dispersion. Therefore, even after using the variable to account for dynamics differentiated by seasonal severity, there is potentially unaccounted-for variation in uncertainty that could adversely effect our forecasting distributions and the log scores that were used to judge contest participants.
Fig. 3.
Residual errors from the homoskedastic GP fit to the square root transformed data by severity level for San Juan (left) and Iquitos (right) training data.
To address this issue in our revised method we introduced an indicator variable based on , the severity input, to modulate the nugget in our covariance function (2), allowing it to differentiate by seasonal severity. In particular, we redefine the MVN covariance as where is a diagonal matrix with entries
| (5) |
The newly created three-vector hyperparameter may be inferred by MLE via extensions to the closed form derivative calculations on the log likelihood, as we detail in Appendix B. We observe very little difference in the computational demands required to infer the three-vector parameter compared to its scalar, that is, homoskedastic, counterpart in (2). There is nothing special about having three categories; should a practitioner believe there are more or less than three severities, for instance, the calculations are the same. Indeed, Appendix B’s presentation is engineered so that, for example, the scalar version clearly arises as a special case. However, a different approach may be desired for cases where severity is likely to smoothly vary with the other inputs. In that case, stochastic Kriging [SK, Ankenman, Nelson and Staum (2010)] may present an attractive alternative. However, note that SK requires replication of observations to obtain stable input dependent variance estimates. That could only be accomplished in our setup by restricting , the starting level input, to a small discrete set of values, which (in experiments not detailed herein) has deleterious effects.
The final ingredient in our hetGP scheme is to extend the latent learning strategy of Section 3.2 to the noise level utilized for new season forecasts. With only three, discrete, choices it is straightforward to evaluate the MVN PLLs under each choice by assigning all in the new season alternately to each -value. Then, rather than picking one, we weight the three sets of resulting forecasts according to those predictive probabilities within the Monte Carlo scheme outlined in Section 4.2.
There are several choices when it comes to pairing latent values with noise levels, . One is to insist that they match, as they do in the historical training data. That is, when evaluating the PLL for , set all . This works well, but optimizing over , again using the PLL, works even better. Specifically, we choose initial values (at the start of the season) that match their noise pairings, and then allow them to be optimized—three times, independently, conditional on each noise setting—via the scheme outlined in Section 3.2. Note that, in contrast to the discussion therein where an inital was used, our three-fold initial settings do not a priori bias early season forecasts toward extreme historical seasons. However, should some such bias be desired, our Monte Carlo scheme in Section 4.2 provides a simple mechanism for doing so. We show that estimated correlations between starting level, , and seasonal severity, could yield beneficial such “priors.”
4. GLM comparator and implementation details
Below we outline a somewhat more standard generalized linear model (GLM)-based comparator. We focus here on a high-level description, emphasizing a particularly useful derived predictor based on the basic reproductive rate, . We conclude the section with a description of a Monte Carlo framework for generating forecasts for both GP and GLM-based comparators, and a brief commentary on how we produce the particular summaries required for contest submission.
4.1. A GLM approach
Our preferred GLM models the total_cases response using a negative binomial family with a log link and with computation facilitated by glm.nb in the MASS library [Venables and Ripley (1994)] for R. Our predictors include a deterministic time index (to allow for a temporal trend), autoregressive components, population size, environmental variables, and deterministic sine/cosine functions to capture broad seasonal effects. Full details on the complete set of (lagged) predictors included are detailed in Appendix C.1. In addition to these covariates we included a scaled version of the basic reproductive number of the epidemic, , as a function of temperature. This measure was derived and parameterized using previously published data on how mosquito traits depend on temperature, following methods developed in Mordecai et al. (2013) and Johnson et al. (2015). Brief details are provided in Appendix C.2 and full details for the particular case of dengue are presented by Mordecai et al. (2017).
Most of the (nondeterministic) predictors were smoothed using a one-sided filter with equal weights over the preceding 10 weeks (via filter in R). Some of the covariates entertained were cumulatively derived (e.g., by summing up precip-tation over the weeks preceding forecasts) in a particular season. To initialize a suitable set of potential covariates, and in particular to identify suitable transformations and lags and to find appropriate phases for the deterministic trigonometric predictors, we performed an extensive exploratory analysis on the training data (up through the 2004/2005 season).
In each out-of-sample forecasting week we retrain the GLM. The first step involves selecting variables among the universe of deterministic, derived, accumulated, lagged and transformed predictors via Bayes information criterion (BIC), which is automated by step in R. Forecasts are then derived from the selected model. Forecasts beyond one week ahead that condition on predictors, like temperature, will necessitate forecasting subroutines. Separate Gaussian time-series models are fit for these predictors. The full historical data are used, up to the current forecasting week, but otherwise these submodels are far simpler in flavor compared to the original total_cases GLM, and favor autoregressive, trend, and trigonometric components. Note that these submodels are needed even when the total_cases GLM uses substantially lagged predictors. For example, a lag 11 predictor requires full forward propagation to be utilized twelve or more weeks into the future.
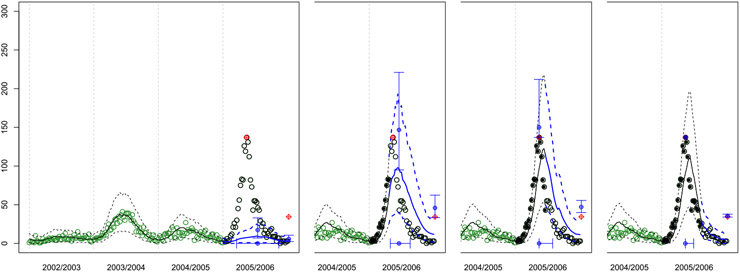
Finally, a Monte Carlo scheme, described in more detail in Section 4.2, is used to propagate uncertainty in submodeled predictors through to forecasts of total_cases in subsequent weeks. Compounding errors in the autoregressive submodel forecasts can obliterate the influence of those predictors, especially for end-of-season forecasts made early in the season. This “washing out” was one of the substantial drawbacks of the GLM approach that motivated our hetGP alternative. An example of such forecasts, mirroring Figure 2, is shown in Figure 4. Although the historical data are colored in green, as open circles, the color does not indicate severity, as unlike in the hetGP setup, there is no such (latent) indicator variable in the GLM. The predictive curves are more “jagged” owing to a higher Monte Carlo error arising from additional forward simulation of predictors. Observe the overly optimistic forecasts early in the season (first panel). The hetGP method is much better at “matching” to previous similar seasons before the current season’s dynamics begin to unfold. Later in the season the GP and GLM are more comparable, although a notable exception in this example is the lack of a (potential) second hump in the third panel compared to Figure 2.
Fig. 4.
Snapshots of GLM forecasts for San Juan. Here the colors, lines, and symbols are the same as in Figures 1 and 2, except that we do not include the severity indicator and instead the green open circles correspond to data from historical seasons.
4.2. Monte Carlo and model averaging
We deployed a Monte Carlo (MC) post-processing scheme to obtain point forecasts and distributions for the contest targets: peak incidence, peak week, and season incidence. In the case of the GP predictor this involved sampling from the MVN predictive equations (3). For the GLM it meant sampling first from from submodeled predictors (e.g., via predict.lm in R), and then conditionally from the negative binomial GLM using the associated predict method. Samples from the three targets may then be obtained via simple identification rules. For instance, the distributions of peak week and peak incidence are determined by the frequency of MC samples indicating that a particular week has the highest sampled incidence values, and the incident value at the highest week, respectively. Season incidence is simply the sum over those weekly samples.
After sample trajectories are converted into target samples, their distribution can be summarized in a variety of ways (e.g., by histogram); we show them as intervals in Figure 2, on which we offer further comment shortly. Point estimates can be derived by extracting empirical summaries of the MC samples. For example, median week, median highest observed weekly incidence, and median sum over the weeks, respectively, are appropriate under the mean-absolute error metric used for contest evaluation [Gneiting (2011)]. However, medians may not be appropriate, for example, when incidences are multimodal (see, e.g, 1998/1999 in Figure 1). In that case, reporting peak week as the week whose MC samples were most frequently largest, the optimal choice under 0–1 loss [Gneiting (2017)] could help avoid pathologies such as forecasting in the trough between two modes.
Our original contest submission involved a hybrid (homoskedastic) GP/GLM, mitigating some of the GLM limitations alluded to previously. We used MC to implement that hybrid by ignoring GLM sampled forecasts obtained from fewer than seven years of historical data, and those based only only on first three four-weekly forecasts, taking GP samples exclusively for those forecasting weeks. Otherwise, the MC sampled both methods equally.
Our new multiple-nugget hetGP version (Section 3.3) involves calculating predictive quantities under three noise hypotheses, which we also facilitate via MC. We weight draws from the MVN predictive equations, where weights are calculated according to the predictive log likelihood (PLL) under each noise regime, as in Section 3.3. At the start of the forecasting season, before any incidences during that season have been observed, we take uniform weights on the three processes, which can be interpreted as a uniform unit information prior. Carrying that prior through the forecasting season, again with unit information so that eventually the data in the form of new season incidences dominate the weight calculation via the PLL, helps guard against extreme weights from potentially spurious early season observations.
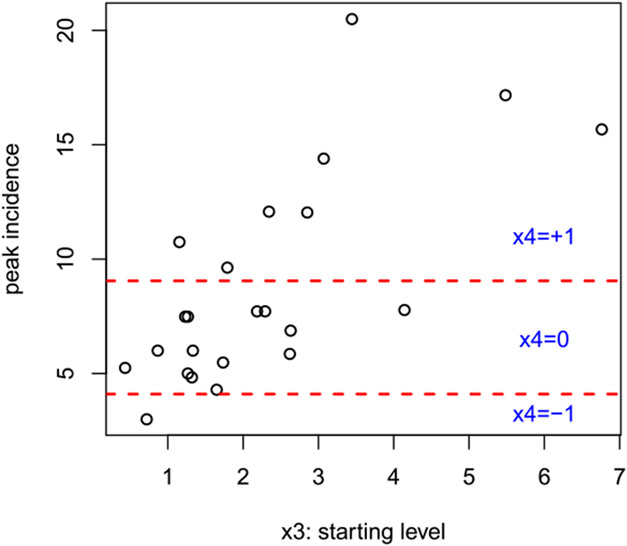
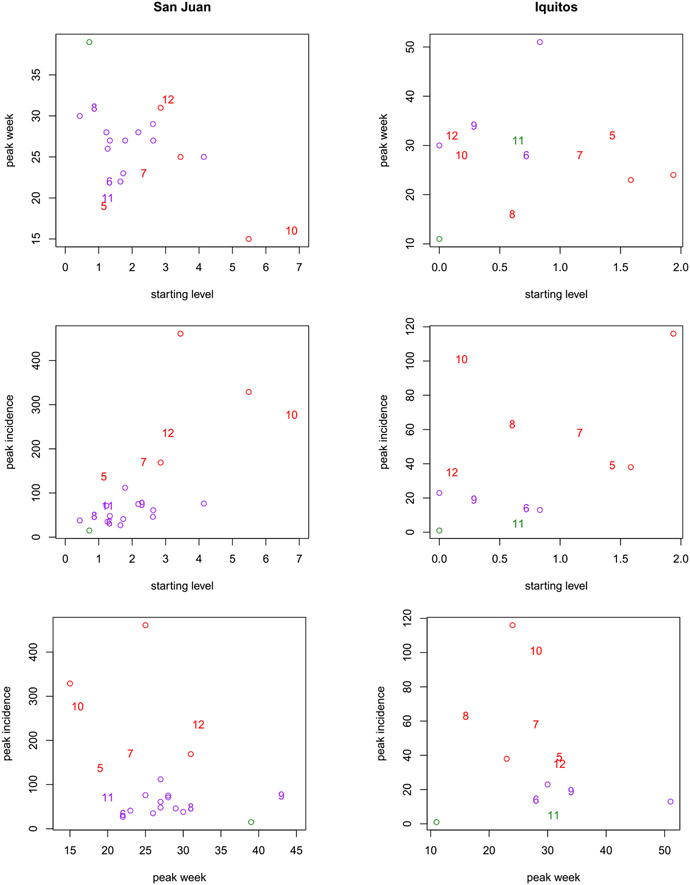
Alternatively, nonuniform weights can be developed as a means of hedging, similar to our setting in the original contest submission. For example, the low incidence category , while visually striking (see 2002/2003 in Figure 1), is exceedingly rare in the data we have seen. A sensible approach could be to down-weight this category for future forecasts. A more data-dependent setting may be inspired by the relationship between , the season’s starting level, and max y, the seasons peak incidence (both on a transformed scale), shown in Figure 5. Observe that there is a clear linear correlation between these two variables, suggesting that higher starting levels lead to higher peak incidence. This relationship has no doubt already been “learned” by the GP models, since starting level () is included as a predictor. But the figure also suggests that higher starting level leads to higher noise, which is not directly accounted for by the GP where noise level may only depend on . For the hetGP results in this paper we use a unit information prior that gives 50% weight to the regime predicted by under a linear fit to historical data like that shown in Figure 5, and splits the remaining 50% evenly among the other two regimes. However, the results are nearly identical under a uniform setting.
Fig. 5.
Scatterplot showing (transformed) peak incidence versus starting level on the San Juan training data. The horizontal lines are the transformed levels separating severe, moderate, and mild incidence seasons.
It is worth noting that, since the data are noisy, predicting peak level and timing is as much about forecasting into the future as it is about smoothing the past. Both GP and GLM setups can provide a full sample over all weeks in the season, regardless of the forecasting week (even for past weeks), in order to fully assess all uncertainties in the distribution of the targets. This is particularly relevant for forecasting the peak week target for Iquitos in 2006/2007 and 2011/2012 [see additional results in Johnson and Gramacy (2017)], where our models indicate that the true peak week actually occurs after the observed peak week, and a visual inspection agrees. In 2006/2007 an outlier is likely to blame, whereas in 2011/2012 there are actually two identically observed peak weeks several weeks apart—the true peak is likely in the middle.
However, the contest rules made it inefficient to regard “backcasts” as random variables, with observed targets standing in for true ones. That is, if the observed peak incidence so far is in week 10, then for all weeks before or after week 10 any observed incidence below the week 10 incidence should be regarded as having zero probability of being a peak week or having peak incidence, irrespective of model predictions and irrespective of the unknown true incidences underlying the noisy data. Although we believe this would be the wrong way to present target forecasts in a real-world setting, for reasons described above, we adjusted our MC scheme to replace simulated values by observed values up to the forecasting week in order to maximize our contest score.
An example of the effect of this can be seen in the third panel of Figure 2. Observe that the peak week interval is truncated on the left by the point forecast because the MC samples have been post-processed so that historical times cannot take on any other value than what was actually observed. Although the interval “contains” other observed weeks that had values less than the historical peak (red dot), this is an artifact of our display of the peak week target as a connected interval. The set of weeks with a positive probability of being a peak week may be disconnected—especially later in the season. As can be seen in the third panel, only one or two weeks in the second “hump” of the forecasting distribution have a chance of besting the historical peak week observed so far in that season.
Before turning to an exhaustive analysis of our empirical results, we make a final remark here about computational demands. Model fitting is relatively fast; it is the MC forecasting scheme that is computationally expensive. GP fitting and prediction, although typically requiring flops that are cubic in the data size, n, takes seconds (for each forecasting week) with a well-designed C implementation linking to accelerated linear algebra libraries (e.g., Intel MKL) on the data sizes we entertain (e.g., n = 520 for 10 years of historical data). GLM fitting, even with step searches, is similarly speedy. Including submodel fits for predictors, this approach requires tens of seconds for obtaining fits and forecasts. However, obtaining enough MC samples to make smooth forecasting plots (Figures 2 and 4) and thus deduce accurate target distributions, requires millions of predictive draws. For the MVNs behind hetGP (3), this is still reasonably fast because a joint sample over all season weeks can be taken at once, requiring tens of seconds for the largest n. In contrast, GLM forecasting with the nested submodel predictions is much slower because propagation must proceed step-by-step, in a Markov fashion, over the weeks of the season. The result is a scheme that requires several minutes for each forecasting week.
5. Empirical results
Below we summarize our out-of-sample results on the contest data in two views. First is an “absolute” view, illustrating our forecasts on their own merits against the six true targets. The second is a “relative” view, comparing our results to those of other contest entrants.
5.1. Absolute view
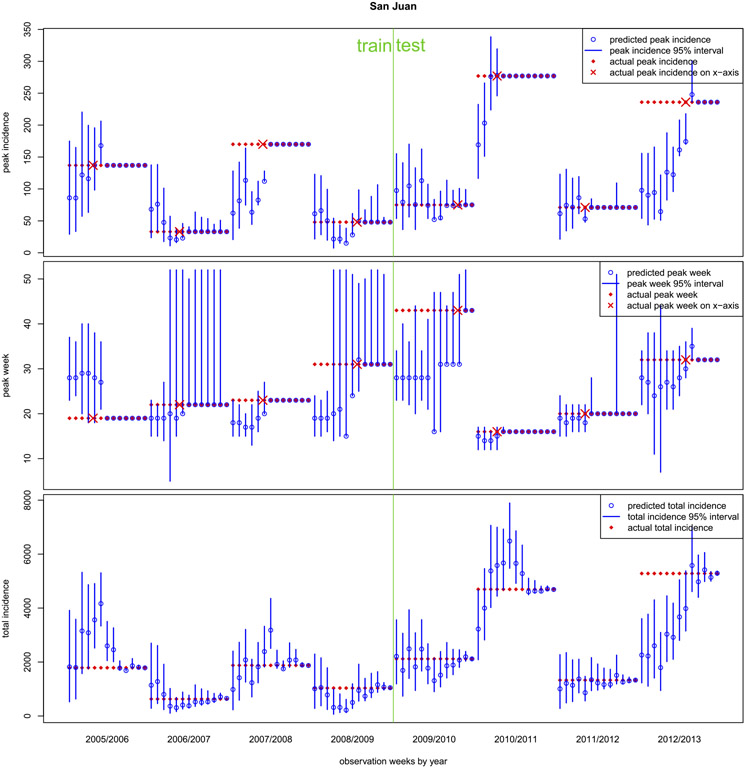
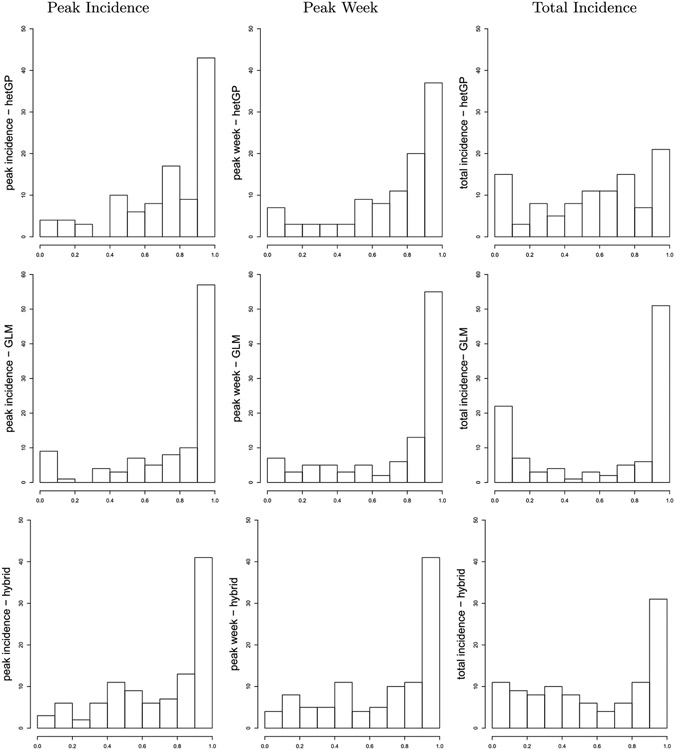
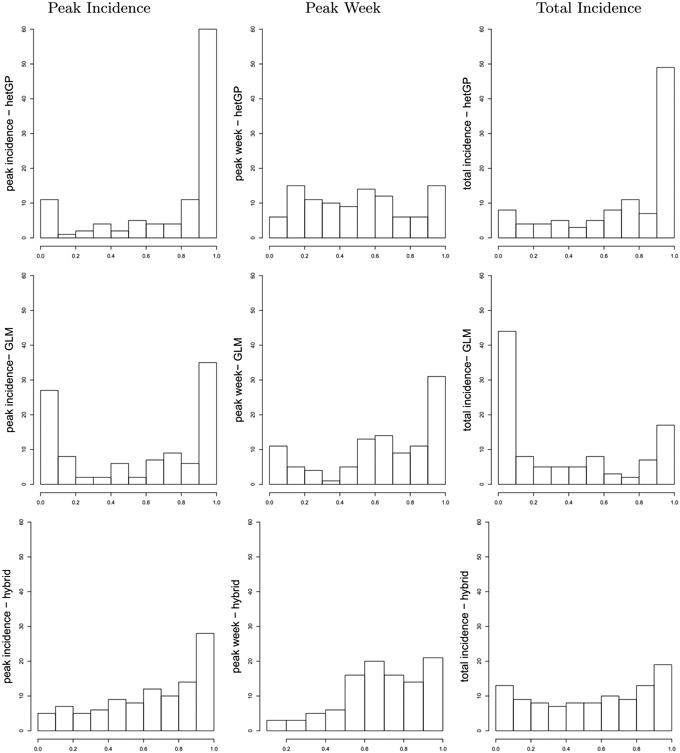
In lieu of a full suite of four-weekly panels as in Figures 6-7, requiring 208 panels across locations and training and testing phases (separately for each comparator, hetGP and GLM), we instead provide a more compact summary in terms of point forecasts and intervals.7 While intervals offer a convenient visualization, note that actual predictive uncertainty sets may be disconnected. Appendix D provides a more accurate and encompassing view of goodness-of-fit via histograms of probability integral transforms (PITs) collected over the forecasting weeks for all three of our comparators: hetGP, GLM, and hybrid. The presentation here focuses on our hetGP results.
Fig. 6.
Weekly progress of out-of-sample forecasts at San Juan, separated by the training and testing period. Top: peak incidence; Middle: peak week; Bottom: total incidence. The forecasts are in blue, showing points (open circles) and intervals. The true targets are solid diamonds in red, shown on both x (week) and y (target) axes as appropriate.
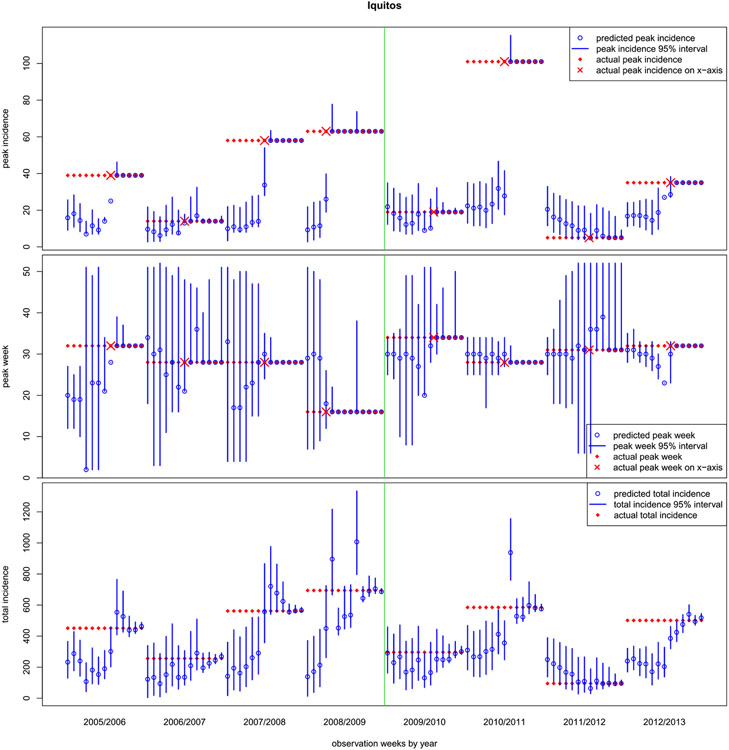
Fig. 7.
Weekly progress for Iquitos, mirroring the setup of Figure 6.
Figure 6 shows the four-weekly results for San Juan. The partition into training and testing sets corresponds to the phases of the contest, not to the nature of the data: all forecasts are out-of-sample. Notice our early season forecasts for San Juan are by no means perfect. We typically, but not always, capture the peak week and peak incidence (top two panels) within our central 95% interval several weeks before the actual observed peak week (red ×). Once the observed peak week arrives, our intervals quickly shrink to point masses around the true values. That is, we have very little backcasting error, an exception perhaps being 2011/2012 for all three targets. Our peak week predictions are nearly always in the ballpark, with the exception of 2009/2010 whose peak comes later than any previous season. We struggle with 2012/2013 (for all targets) because, as we show in the left panel of Figure 11 of Appendix A.2, it too represents an extrapolation. There is no historical data “nearby,” either in the data space (i.e., historical peak incidence or peak week), or in the predictor space (say in terms of starting level, ). Therefore we underforecast peak incidence, and thus total incidence, early in that season.
Figure 7 summarizes our results in the much more challenging Iquitos locale. On the whole, our forecasts are poorer here despite wider error-bars, in relative terms (incidence is overall lower), with both phenomena arising due to the much smaller amount of historical data. Recall that data are only available for five seasons before the first forecasting season, 2005/2006. The right panel of Figure 11 of Appendix A.2 shows that at least three of these eight forecasting seasons represent extrapolations, as there are no “nearby“ historical seasons to match on. For example, seasons 2007/2008, 2008/09, and 2010/2011 (corresponding to labels 7, 8, and 10 in Figure 11) are particularly “isolated.” These three also happen to have higher peak incidences than all but one of the previously observed seasons. As a result our early season forecasts of peak incidence well undershoot and undercover. However, as we show below, these predictions (and their corresponding log scores) compare favorably to the other contest entrants. All entrants found these seasons particularly hard to predict.
5.2. Relative view
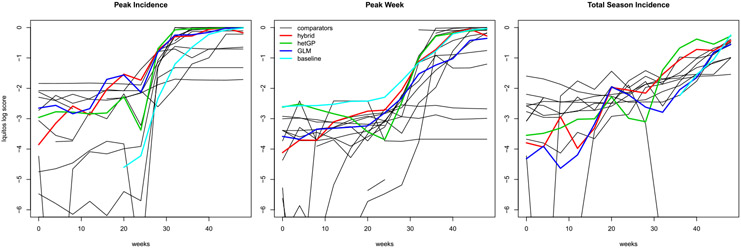
Our summary of the contest results is more inclusive than the absolute results above. We are careful to delineate between our original, somewhat rushed, hybrid GLM/GP entry, and our newer, separate results for the revamped hetGP and the pure GLM-based predictor, although those were not actually entered into the contest. The main contest evaluation metric was log score, with larger being better, and contest winners were determined by aggregate scores reported for roughly the first half of the season. Contest organizers provided us with the full suite of aggregate four-weekly scores for all entrants, and it is these results that we display, and compare here. Unfortunately, these scores have been anonymized; we do not know who participated in the development of the methods, nor the details of how the methods were comprised, with the exception of a “baseline” SARIMA (1, 0, 0)(4, 1, 0)52 model developed by the contest organizers.
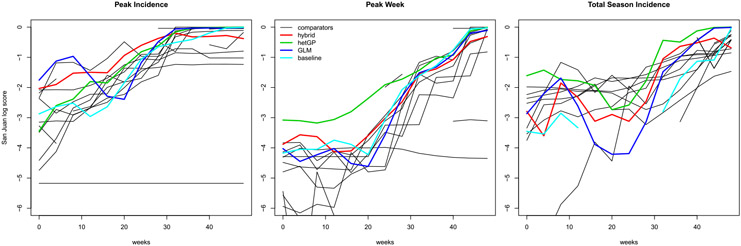
San Juan
Figure 8 shows log scores for the three targets on the San Juan data. Some of our comparator’s lines in the plots, including the “baseline,” are cut off because their log scores contained !NaN! or-Inf values. Observe that our team, via the the original hybrid GP/GLM submission (red), the GLM only (blue), or the new hetGP (green) has among the top average log scores for all three targets with the exception of a handful of weeks for total season incidence (right panel). Our best results are for the new hetGP comparator on the peak week target (middle panel), being by far highest (on average) for the first 30 weeks of the season, and competitive with the best thereafter. In the case of peak incidence our methods are in the top three for the first thirty weeks (and our GLM in blue leads for the first 8 weeks). Although our original hybrid outperforms the new hetGP comparator for the first thirty weeks, that order reverses for the latter twenty with hetGP giving the very best log scores for the peak incidence target.
Fig. 8.
San Juan contest results via four-weekly average log score. Our original hybrid GP/GLM predictor is in red; our new hetGP in green, and the GLM in blue.
Table 1 provides a numerical summary of lines in Figure 8, averaging over the weeks. The left table shows straight averages, whereas the middle table shows average ranks. Both have been negated/reversed so that lower scores and ranks are best. While averaging ranks does not lead to a “proper” aggregation of scores, it has two advantages over the raw averages: (1) it is more forgiving to extreme (poor) performance, in particular preventing an Inf from precluding any comparison based on better-behaving forecasts in others weeks; (2) ranks offer a more readily interpretable scale. The right table shows mean absolute errors, the other metric used to judge contest entrants. Lower is better here. Observe that one of our methods is in the top two by every metric, and that hetGP is in the top three in all nine columns. No other method is in the top three in more than four columns.
Table 1.
Averages of log scores (left) and averages of their ranks (middle) from San Juan predictive distributions (see Figure 8) over the forecasting weeks. These have been negated so that lower average scores (and ranks) are best. The right table shows mean absolute errors (MAE). The alphabetic labels A–P are the anonymized names from the CSV file provided by the CDC at the end of the contest period. Our hybrid GP/GLM was comparator “E” in that file. Superscripts denote the top three in each column
| San Juan Method |
Average Score | Average Ranked Score | MAE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Peak | Week | Season | Peak | Week | Season | Peak | Week | Season | |
| A | Inf | Inf | Inf | 15.08 | 16.19 | 14.15 | 221.83 | 8.15 | 4965.6 |
| B | 1.54 | 2.77 | 1.67 | 9.92 | 6.46 | 35.62 | 50.65 | 7.81 | 1009.6 |
| C | 1.24 | 3.11 | 1.69 | 5.85 | 8.00 | 6.23 | 42.96 | 6.83 | 989.6 |
| D | 1.48 | Inf | 3.29 | 5.73 | 14.73 | 9.23 | 45.42 | 9.56 | 1306.2 |
| F | Inf | Inf | Inf | 14.88 | 12.38 | 15.96 | 59.51 | 35.71 | 982.0 |
| G | 1.08 | 3.21 | 21.51 | 6.92 | 9.00 | 25.00 | 326.61 | 25.01 | 723.5 |
| H | 1.55 | 3.55 | 2.30 | 8.38 | 8.62 | 8.92 | 49.76 | 5.81 | 1117.4 |
| I | Inf | Inf | Inf | 17.15 | 15.46 | 16.85 | 42.52 | 7.29 | 949.4 |
| J | 1.34 | 3.20 | 31.59 | 8.15 | 8.69 | 5.77 | 34.48 | 5.87 | 939.1 |
| K | Inf | Inf | Inf | 11.54 | 12.85 | 14.88 | 49.06 | 6.06 | 1151.7 |
| L | Inf | Inf | Inf | 14.46 | 16.19 | 16.85 | 54.12 | 15.69 | 1361.3 |
| M | 5.17 | Inf | 7.66 | 14.31 | 16.19 | 13.69 | 86.75 | 10.25 | 1915.0 |
| N | Inf | 4.15 | 1.93 | 15.08 | 8.92 | 7.00 | 273.21 | 8.60 | 1048.5 |
| O | 1.52 | 32.56 | 1.87 | 7.23 | 34.38 | 6.00 | 124.96 | 5.89 | 2712.1 |
| P | Inf | Inf | Inf | 12.23 | 14.62 | 15.77 | 68.00 | 8.98 | 1166.0 |
| hybrid/E | 10.91 | 22.55 | 1.96 | 35.38 | 5.08 | 6.85 | 32.37 | 5.88 | 826.8 |
| hetGP | 30.94 | 11.91 | 11.38 | 14.08 | 11.92 | 13.00 | 225.86 | 14.25 | 1667.2 |
| GLM | 20.92 | 2.75 | 2.14 | 25.15 | 6.15 | 6.69 | 28.64 | 6.21 | 3803.7 |
| baseline | 1.41 | 2.54 | Inf | 8.46 | 24.15 | 11.54 | 55.45 | 6.83 | 845.0 |
Recently Yamana, Kandula and Shaman (2016) built predictive model(s) for the San Juan data, including so-called superensembles in a spirit similar to our hybrid approach. Base models include simple SIR (refit to each season separately) which they called “F1;” a curve matching approach similar in spirit to our GP called F2; and estimated distributions of each of the targets, F3. An evaluation of their models based on the MAE is provided in Table 2. Overall, any of their methods that include F2 (the curve matching approach) is competitive with our approach: hetGP performs best for peak week, but theirs comes out on top for the other two targets. It is interesting to note that although Yamana, Kandula and Shaman suggest that a superensemble approach can improve forecasting, their results imply that F2 by itself is both parsimonious and better performing across all seasons. Thus the takeaway here may be that curve matching, or history “memorizing” whether by GPs or otherwise, leads to excellent point prediction. Unfortunately, Yamana, Kandula and Shaman do not provide evaluations of their models based on log score, and their study does not include the Iquitos locale.
Table 2.
MAE results for San Juan from forecasts provided by Yamana, Kandula and Shaman, comparable to the right panel of Table 1
| San Juan Method |
Yamana, Kandula and Shaman MAE | ||
|---|---|---|---|
| Peak | Week | Season | |
| F1 | 44.61 | 7.80 | 796.4 |
| F2 | 18.98 | 5.27 | 568.4 |
| F3 | 37.60 | 6.71 | 954.4 |
| SEF12 | 21.74 | 5.70 | 630.8 |
| SEF123 | 20.76 | 6.30 | 733.1 |
Iquitos
The story is similar for Iquitos, with log scores from the contest being displayed in Figure 9. The scores are noisier due to the smaller amount of training data. Although our comparators, new and old, are bested by some of the others in early weeks, those comparators which dominate early on are actually among some of the weaker alternatives later on. Observe that although the “baseline” gives excellent early peak week forecasts, for some reason it gives invalid values for the other targets during those weeks.
Fig. 9.
Iquitos contest results on the three targets.
Table 3 offers an aggregated numerical summary. Our hetGP comparator comes in second for both peak incidence and peek week. Although hetGP is never a placed “1st,” it is in the top three positions in six out of the nine columns, which is better than any other comparator. It is the only comparator to have average ranked scores higher than 14 on all three targets. Comparators B and the “baseline,” which came in first on two targets, by all three metrics respectively, happen also to be in the bottom 40% of comparators on the third target, again by all three metrics. In other words, where one got the magnitude right, it was off in the timing, and vice versa. Therefore our second- and third-place results, here, would seem to offer some robustness. On the final target, total season incidence, our hetGP comparator was beaten out by four other teams in terms of log score (both ranked and unranked). Success on this target is bimodal, with very few ranks between 4 and 12.
Table 3.
Same as Table 1 for the Iquitos locale
| Iquitos Method |
Average Score | Average Ranked Score | MAE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Peak | Week | Season | Peak | Week | Season | Peak | Week | Season | |
| A | Inf | Inf | Inf | 15.19 | 17.73 | 12.69 | 114.29 | 20.62 | 1516.6 |
| B | 11.13 | 4.25 | 21.88 | 14.46 | 12.85 | 6.00 | 314.94 | 4.87 | 140.1 |
| C | 1.68 | 2.49 | 2.11 | 7.54 | 9.23 | 7.00 | 26.29 | 2.92 | 123.9 |
| D | 2.67 | Inf | Inf | 7.69 | 15.12 | 12.31 | 18.75 | 10.21 | 308.1 |
| f | Inf | Inf | Inf | 10.81 | 12.00 | 16.23 | 17.77 | 4.69 | 142.8 |
| G | 1.53 | 2.40 | 32.01 | 6.92 | 9.00 | 5.85 | 19.22 | 3.28 | 132.8 |
| H | 1.77 | 32.11 | 2.02 | 6.54 | 6.31 | 35.46 | 17.53 | 4.08 | 1109.1 |
| I | Inf | Inf | Inf | 11.12 | 11.85 | 16.23 | 18.08 | 5.23 | 149.5 |
| J | 1.57 | 2.51 | 2.10 | 7.77 | 10.23 | 6.85 | 17.50 | 21.96 | 3117.2 |
| K | Inf | Inf | Inf | 16.81 | 12.31 | 16.23 | 38.15 | 4.72 | 241.8 |
| L | Inf | Inf | Inf | 16.81 | 15.00 | 16.23 | 47.91 | 17.21 | 319.7 |
| M | 3.74 | 3.31 | 2.67 | 12.77 | 10.08 | 9.77 | 22.13 | 3.59 | 138.6 |
| N | Inf | 2.80 | 11.81 | 14.15 | 8.15 | 24.15 | 76.58 | 2.51 | 119.4 |
| O | 2.95 | 2.63 | 2.45 | 8.85 | 6.46 | 14.08 | 19.97 | 2.49 | 128.0 |
| P | Inf | 3.03 | Inf | 12.27 | 9.85 | 16.23 | 24.97 | 4.41 | 134.1 |
| hybrid/E | 31.49 | 32.11 | 2.20 | 6.08 | 36.00 | 6.08 | 19.24 | 7.28 | 140.2 |
| hetGP | 1.59 | 21.91 | 2.16 | 35.85 | 25.46 | 6.00 | 214.74 | 32.08 | 2116.2 |
| GLM | 21.35 | 2.32 | 2.68 | 25.62 | 9.00 | 9.08 | 114.05 | 3.35 | 124.7 |
| baseline | Inf | 11.65 | Inf | 12.77 | 13.38 | 13.54 | 32.88 | 11.72 | 138.8 |
6. Discussion
In 2015 several US governmental agencies jointly proposed a forecasting competition focused specifically on dengue, a vector borne disease endemic to tropical climates, to attract interest to the challenging and very important problem of learning to predict the observed patterns of disease occurrence and its relationship with its environment. Our team participated in the contest and our submission was chosen as one of six winners. In particular our hybrid GP/GLM forecasts were best overall for San Juan peak incidence. This hybrid submission was based more on pragmatics and a desire to hedge than it was on a belief that that hybridization was best suited to the problem at hand.
In this paper we presented an updated GP methodology. The biggest aspect of that revamp was the addition of explicit heteroskedastic errors that could vary with the severity of the season. This required new inference methodology and a bespoke implementation in code. A library called hetGP is available on GitHub as part of the vbdcast repository [Johnson and Gramacy (2017)], which includes code supporting both GLM and hetGP “runs,” diagnostics, and visualizations for the Dengue Forecasting Project. Here we have shown that hetGP compares favorably to the hybrid GP/GLM contest submission, although it does not uniformly dominate that method, which perhaps suggests that our hedge for the submission was a sensible one.
We note that a simpler alternative to our hetGP could involve separately fitting three independent GP predictors with data differentiated by the (severity) coordinate. However, one downside would be much less data for each GP fit, and once the data is partitioned by , that variable could no longer serve its dual role of encouraging nonstationary mean diversity in the spirit of Bornn, Shaddick and Zidek (2012), as described in Section 3.2. Our single GP, linking mean and nugget via , offers a parsimonious compromise between signal and noise modeling.
Our more conventional GLM alternative relied heavily on historical environmental and case data. Its forecast accuracy depends crucially on accurate submodeling of environmental components, and we used linear models. Using richer climate based submodels would almost certainly improve forecasts of the predictors and so improve predictions of incidence. However, quantifying the uncertainty in the GLM would still require significant Monte Carlo simulation. Further, climate models come with their own, sometimes daunting, computational demands. A promising way to avoid propagating submodeled forecasts, that is, taking a joint-modeling approach, may involve direct modeling of conditional distributions [e.g., Gneiting et al. (2006)]. A disadvantage here is bespoke implementation—simple lm and glm commands no longer suffice. We have been pointed to Ray et al. (2017) who are perusing a promising, related approach in a disease modeling context. Their method utilizes kernel conditional density estimation, a nonparametric method not unrelated to GPs.
Although our hetGP is by no means perfect, it is surprising how well a phenomenological nonparametric, nonlinear predictor can do with no data other than the time series of values themselves (and stylized facts gleaned from a simple visual observation of that series of values). There is clear potential for improvement, and one possible avenue may be to interject more covariate information into the GP framework, in a similar way as in the GLM. However, as with the GLM, more historical data means more to forecast forward. When such covariates are unavailable or untrustworthy, as might arise with a newly emerging/establishing disease in a part of the world without reliable instrumentation and demographic surveys, an ability to construct reliable forecasts solely from observed counts of the number of confirmed cases may prove handy indeed.
Predictions from phenomenological models have the potential to inform mechanistic modeling efforts, or serve as a baseline against which mechanistic models can be tested. For instance, our approach is likely well suited to modeling influenza cases in the US, as approached by Osthus et al. (2017) using a state-space version of an SIR model. They describe multiple years of data which could inform the “spatial” components of our approach. Applications such as cholera in Bangladesh, as described by Koepke et al. (2016), would be more challenging as only a single season of data is available. However, in both cases our hetGP could serve as a comparative predictor to assess model performance, or as a component model in a superensemble akin to Yamana, Kandula and Shaman (2016). Turning things around, hetGP-based simulated forecasts could be fed into mechanistic models of interventions and their costs, as entertained in the setups of Ludkovski and Niemi (2010), Merl et al. (2009) and Hu and Ludkovsk (2017). All three of those papers involve forward simulations that use SIR-type models to evolve dynamics and thus to calculate potential costs and benefits of interventions. It has previously been noted that uncertainty in parameter values and in model structure for SIR-type models can result in poor prediction and in suboptimal and more costly interventions [Elderd, Dukic and Dwyer (2006)]. Our methods make no such mechanistic modeling assumptions and may provide more robust predictions of cases.
Finally, we note that although our hetGP approach needs much less data than the GLM approach (a few seasons of cases vs. 5–10 seasons of cases plus environmental data) it is still very much tuned to learning about patterns of a particular disease for a particular location. Thus, we expect it will be much more useful for predicting cases and planning responses for seasonal outbreaks of established infectious diseases in specific locations as opposed to outbreaks of novel, emerging epidemics. An exception may be for new vector-borne diseases that are transmitted by the same vector as the focal infection, for example Zika which is transmitted by the same mosquitoes as dengue. This could be an area for future exploration.
Supplementary Material
Acknowledgments.
We gratefully acknowledge the agencies sponsoring the dengue forecasting challenge for collating and sharing the dengue incidence and environmental covariate data, and for producing and supplying the anonymized challenge metrics.
1Supported in part by NSF Grant DEB-1518681.
2Supported in part by NSF Grant DMS-1521702.
3Supported by NSF Grant DEB-1640780; the Stanford Center for Innovation in Global Health—Seed Grant Program; and the Stanford Woods Institute for the Environment—Environmental Ventures Program.
4Supported in part by NSF Grant EF-1241889, the National Institutes of Health grants R01GM109499 and R01TW010286-01.
APPENDIX A: DATA PROPERTIES
A.1. Variance stabilizing transformations
The original data are positive counts of the number of infected individuals in each week, which we have been calling the weekly incidence. As typical in such setups, there is a mean–variance relationship, with variance increasing as the mean increases. When modeling such data with Gaussian errors, as we describe in Section 3, it helps to deploy a variance stabilizing transformation. Figure 10 shows two such common transformations, based on the logarithm and the square root (bottom two panes; with the original series at the top). Observe that the log transformation does a good job of stabilizing the largest variances (occurring with the largest means), but overexpands the disturbances in values corresponding to the smallest means. The square root transformation (bottom) offers better balance.
Fig. 10.
Original San Jan data over the first 1000 weeks (top panel); a log transformed version (middle); and a square root (bottom).
Our original contest submission used the log. The revised version we prefer in this paper is based on the square root, modified to account for the possibility that Gaussian forecasts on the transformed scale could be negative. In that case, the axis symmetry offered by inverting with a square is inappropriate. We therefore prefer the following forward/inverse pair:
Note that the +1, and the associated −1 in the inverse is not absolutely necessary for valid square-roots. However it is required for a log transformation and we opted to keep it for the square root, in part to streamline the implementation in code.
A.2. Assessing forecastibility
To get a sense of the difficulty of forecasting the dynamics of some of the seasons, especially for Iquitos which has many fewer historical seasons for training, Figure 11 shows a view into the peak incidence and peak week targets plotted against the starting level in each season, as well as against themselves. The historical data, that is, corresponding to the plot in Figure 10 for San Juan, which does not overlap with the forecasting seasons summarized in Figures 6-7, are plotted as open circles. The numbered points correspond to the season, from left to right, shown in those figures. Observe that for San Juan, the numbered forecasting seasons are close to the historical seasons, making the prediction problem rather easier. An exception may be seasons 10 and 12, corresponding to 2010/2011 and 2012/2013, respectively. For Iquitos, those numbered forecasting seasons are rather farther from the historical seasons, indicating a much harder prediction problem. Indeed many of these forecasting seasons require extrapolations from the historical data. An exception may be season 11, corresponding to 2011/2012, which benefits from an earlier forecasting season (6: 2006/2007) being nearby.
APPENDIX B: HETEROSKEDASTIC MLE GP INFERENCE
The log likelihood for a zero-mean GP with covariance is
| (6) |
where are the free parameters in ,for example, a scalar nugget in the typical homoskedastic version outlined in Section 3.1; or () defining in the heteroskedastic generalization of Section 3.3. An MLE for may be derived as
Fig. 11.
True target levels (original scale) and starting locations (, on transformed scale) for each season. The historical data, that is, those not shown in Figures 6-7, are open circles. The numbered points correspond to the seasons in those figures where, for example, 8 indicates season 2008/2009. Colors indicate the true severity labeling.
Plugging into (6) yields the so-called concentrated log likelihood
| (7) |
Obtaining MLEs for the remaining (vectorized) parameters (, ) requires numerical techniques benefiting from a closed form gradient expression for the concentrated log likelihood (7). Two useful matrix derivative results are
Here indicates a matrix comprised of entry-wise partial derivative calculations on .
Let denote the matrix of derivatives of the correlation structure with respect to . In the case of our preferred separable Gaussian kernel (1) we have
Since depends on and not we have . Therefore,
| (8) |
In the case of the nugget, vectorized or otherwise, because does not depend on . In the case of scalar , is the identity matrix. Then we obtain
| (9) |
For a vectorized , such as the three vector {} determined by , i = 1, …, n, observe that is a zero matrix with the exception of ones in positions i where for . This yields an expression for the partial derivative of the log likelihood that resembles (8), except for :
| (10) |
However, since each is mostly zero it can be more efficient to perform calculations following the homogeneous derivative (9) on the -sized subset of the data agreeing with .
In our vbdcast Github repository, Johnson and Gramacy (2017), we provide a C implementation of likelihood and gradient for both homoskedastic and heteroskedasic versions together with an optimization wrapper that utilizes R’s C back-end for the method="l-bfgs-b" to the built-in optim function. Prediction wrapper functions in R accessing underlying C implementations of Equation (3) are also included. Examples are provided on the dengue contest data, together with optimization of latent settings, as well as stand-alone examples on toy data.
APPENDIX C: GLM DETAILS
Below we summarize some of the implementation details of our GLM-based scheme, outlined in Section 4.1. We first discuss the universe of variables searched via step and BIC; then basic reproductive rate predictor; and finally present out-of-sample forecasting results in a similar spirit to those provided in Section 5.1 for GP-based forecasts.
C.1. GLM universe of predictors
Table 4 provides a summary of the covariates entertained as a universe of potential predictors for San Juan and Iquitos dengue incidence, respectively. Separate entries are provided for each transformation, with lags indicated, and the tables are separated in smoothed (via a one-sided 10-week filter) and unsmoothed (“raw”) categories, with the latter including the deterministic predictors. These universes define the scope provided to our automated step-wise BIC selection via step in R. They were determined by an extensive exploratory analysis performed on the training data, separately for San Juan and Iquitos.
A few brief notes on Table 4 follow. The time predictor, t, is the index of the observation under study, included to capture a linear trend. Although sin and cos share an entry, both predictors (at both periods) are entertained, together comprising of four deterministic “covariates.” There were a small number of missing values in the NDVI series provided by the contest organizers. We performed a simple GP-based prediction to infill the missing values and ignored their uncertainty in our analysis. Our universe of variables was smaller for Iquitos due to the smaller amount of data, and overall lower degree of predictability, despite the smaller scale of incidence in most seasons. This is handled through a smaller number of lags (El Nino and SOI) and some averaging (NDVI) of the environmental covariates. Only yearly population figures were available for each location. Weekly populations were constructed for each site using simple linear interpolation.
Table 4.
Variables entertained for San Juan (SJ) and Iquitos (Iq) stepwise search. Lags are provided in weeks
| SJ | Iq | name | lags | description | |
|---|---|---|---|---|---|
| Raw | ✓ | ✓ | t | – | time since the first modeled response |
| ✓ | ✓ | ci | – | cumulative observed cases in previous 52 weeks | |
| ✓ | ✓ | sin + cos | – | (both included) with periods of 52 and 26 weeks | |
| Smooth | ✓ | ✓ | ly | 1 | log cases observed [i.e., an AR(1) term] |
| ✓ | ✓ | lgm | – | average of current week’s log cases over all previous seasons | |
| ✓ | lpop | 1 | log weekly population size | ||
| ✓ | ✓ | lp | 1 | log precipitation | |
| ✓ | ✓ | lp2 | 1 | squared log precipitation | |
| ✓ | ✓ | tavg | 1, 11 | average temperature | |
| ✓ | ✓ | tavg2 | 1, 11 | squared average temperature | |
| ✓ | ndvi.45 | 1, 16 | value of NDVI at location [18.45, −66.14] | ||
| ✓ | ndvi.50 | 1, 11 | value of NDVI at location [18.50, −66.14] | ||
| ✓ | ndvi.avg | 1 | average of the four NDVI (raw climatology) values provided | ||
| ✓ | ✓ | 1, 11 | average value of scaled basic reproductive rate (Appendix C.2) | ||
| ✓ | nino12 | 1, 6, 32 | value of El Niño 1/2 | ||
| ✓ | nino12 | 1 | value of El Niño 1/2 | ||
| ✓ | soi | 1, 24 | Southern Oscillation Index | ||
| ✓ | soi | 1 | Southern Oscillation Index |
As a reminder, we modeled the total_cases response with a negative binomial GLM using a log link. We also entertained a log-linear model (i.e., Poisson GLM), but a residual analysis revealed underestimated spread. The log-linear model also underperformed in a cross-validated prediction exercise on the training data (not shown).
C.2. Basic reproductive rate predictor
We deployed a derived predictor, scaled (i.e., basic reproductive rate) as a function of temperature. The basic reproductive rate is defined as the expected number of new cases of an infectious disease that will be caused by a single infected individual introduced into a naive (entirely susceptible) population. If > 1 an epidemic is expected to occur whereas if < 1 the disease will not spread. It is used as a standard, convenient measure of how easily a disease is transmitted and how hard it is to control. For vector-borne disease, the value of depends on vector (here mosquito) traits such as mortality rates, biting rates, reproduction, etc. Full details of parameterized versions of from data are given by Mordecai et al. (2017). Here we present an abbreviated description as is relevant to dengue forecasting via GLMs.
Data were collected on the viruses and mosquito vital rates from assorted laboratory studies that observed Aedes spp. mosquitoes, a dengue vector, and dengue virus prevalence at a range of constant temperatures. Although raw data were preferred, if the experimenter was unreachable then data were collected by hand from tables or figures digitized using WebPlotDigitizer. Following the methods laid out by Mordecai et al. (2013) and Johnson et al. (2015) we calculated a Bayesian posterior for parameters involved in a functional thermal response for each trait. More specifically, we fit unimodal thermal responses for each temperature sensitive portion of the mosquito/pathogen system. These posteriors were then combined together to derive a distribution of :
| (11) |
where is the density of mosquitoes, is the bite rate, is vector competence, is the mortality rate of adult mosquitoes, is the parasite development rate (1/EIP, the extrinsic incubation period of the parasite), is the human density, and is the human recovery rate. Following Mordecai et al. (2013), we take
| (12) |
where EFD is the number of eggs produced per female per day, pEA is the probability that an egg will hatch and the larvae will survive to the adult stage, and MDR is the mosquito development rate. All of the parameters that describe mosquito or parasite traits (i.e., everything except and ) area assumed to depend on temperature.
The basic reproductive rate, is also influenced by factors other than temperature, and the particular value at any location depends on the number of susceptible humans at that location and socio-economic factors that impact whether humans and mosquitoes interact. We do not have access to data as part of this challenge to estimate these values, and anyways the GLM would naturally rescale this predictor. Thus, we used the posterior mean of as a function of temperature and rescaled to lie between [0, 1] as the predictor in our model.
APPENDIX D: PROBABILITY INTEGRAL TRANSFORMS
As an absolute “view” into the performance of our methods, we present a summary of probability integral transforms (PITs), a common measure of goodness-of-fit. PITs were calculated from the Monte Carlo samples of the target distributions, separately in each four-weekly forecasting period, and for each target in each locale. Specifically, for a particular forecast we calculated the empirical CDF (from the Monte Carlo samples for that locale–target–week) using ecdf in R, and recorded the cumulative distribution evaluation of the true value for that locale–target–week triplet under that empirical distribution, a value between zero and 1. Cumulatively, there were 104 such values for each locale–target pair.
Figure 12 and 13, for San Juan and Iquitos, respectively, summarizes those 104 values via histogram, separately for each target (across the rows) and each method (columns). The more uniform the histogram the better the fit. Most of the histograms are not particularly uniform, but none are pathologically imbalanced. On the whole, our methods are overly pessimistic, as indicated by the peaks in the histograms near a PIT of one. In the case of San Juan, observe that hetGP fits the total incidence target particularly well, being more uniform on all targets, compared to the pure GLM and the hybrid GP/GLM. On Iquitos, hetGP it is quite accurate for peak week, but is perhaps not as good as the hybrid on the other two. We can see that the hybrid benefits from the GLM’s lower mode of PIT density, near zero, balancing things out somewhat. Although most of these observations are similar to ones from Section 5.1, this last one is a noteworthy exception.
Fig. 12.
Histograms of probability integral transforms (PITs) for the three San Juan targets across the rows, and our three comparators across the columns.
Fig. 13.
Histograms of probability integral transforms (PITs) for the three Iquitos targets across the rows, and our three comparators across the columns.
Compared to that analysis in Section 5.1, these PIT histograms are more crude since they aggregate over time, whereas Figures 6 and 7 show intervals separately for each forecasting week. However, we remarked that those intervals may not be an accurate representation of the actual distribution, which is at times multimodal. Therefore the PIT histograms offer a more accurate summary of goodness-of-fit.
Footnotes
SUPPLEMENTARY MATERIAL
Supplement A: Supplement to: Phenomenological forecasting of disease incidence using heteroskedastic Gaussian processes: a dengue case study: hetgp San Juan predictions (DOI: 10.1214/17-AOAS1090SUPPA; .pdf). We provide the full forecasting results for San Juan using the heteroskedastic GP methods.
Supplement B: Supplement to: Phenomenological forecasting of disease incidence using heteroskedastic Gaussian processes: a dengue case study: GLM San Juan predictions (DOI: 10.1214/17-AOAS1090SUPPB; .pdf). We provide the full forecasting results for San Juan using the GLM model.
That is, not from the choice of kernel with a Gaussian form; a GP can involve any kernel function that induces a positive semidefinite correlation structure.
Our logic here was that the contest architects wouldn’t have put so much effort into organizing the contest if the future dynamics (in data yet to be revealed during the testing phase) were not somewhat surprising, and thus hard to predict. We gambled that they were hard to predict because they were more severe than historical data indicated.
Our supplement [Johnson et al. (2018)] provides a slide-show-like rendition akin to Figures 6-7 for the interested reader.
REFERENCES
- Ankenman B, Nelson BL and Staum J (2010). Stochastic kriging for simulation meta-modeling. Oper. Res 58 371–382. MR2674803 [Google Scholar]
- Barrera R, Amador M and MacKay AJ (2011). Population dynamics of Aedes aegypti and dengue as influenced by weather and human behavior in San Juan, Puerto Rico. PLoS Negl. Trop. Dis 5 e1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binois M, Gramacy RB and Ludkovski M (2016). Practical heteroskedastic Gaussian process modeling for large simulation experiments. arXiv preprint, arXiv:1611.05902 [Google Scholar]
- Bornn L, Shaddick G and Zidek JV (2012). Modeling nonstationary processes through dimension expansion. J. Amer. Statist. Assoc 107 281–289. MR2949359 [Google Scholar]
- Cressie NAC (1993). Statistics for Spatial Data. Wiley, New York. Revised reprint of the 1991 edition. MR1239641 [Google Scholar]
- Degallier N, Favier C, Menkes C, Lengaigne M, Ramalho WM, Souza R, Servain J and Boulanger J-P (2010). Toward an early warning system for dengue prevention: Modeling climate impact on dengue transmission. Clim. Change 98 581–592. [Google Scholar]
- Elderd BD, Dukic VM and Dwyer G (2006). Uncertainty in predictions of disease spread and public health responses to bioterrorism and emerging diseases. Proc. Natl. Acad. Sci. USA 103 15693–15697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farah M, Birrell P, Conti S and De Angelis D (2014). Bayesian emulation and calibration of a dynamic epidemic model for A/H1N1 influenza. J. Amer. Statist. Assoc 109 1398–1411. MR3293599 [Google Scholar]
- Gagnon AS, Bush AB and Smoyer-Tomic KE (2001). Dengue epidemics and the El Niño southern oscillation. Clim. Res 19 35–43. [DOI] [PubMed] [Google Scholar]
- Gneiting T. (2011). Making and evaluating point forecasts. J. Amer. Statist. Assoc 106 746–762. MR2847988 [Google Scholar]
- Gneiting T. (2017). When is the mode functional the Bayes classifier? Stat 6 204–206. MR3671158 [Google Scholar]
- Gneiting T and Raftery AE (2007). Strictly proper scoring rules, prediction, and estimation. J. Amer. Statist. Assoc 102 359–378. MR2345548 [Google Scholar]
- Gneiting T, Larson K, Westrick K, Genton MG and Aldrich E (2006). Calibrated probabilistic forecasting at the Stateline wind energy center: The regime-switching space-time method. J. Amer. Statist. Assoc 101 968–979. MR2324108 [Google Scholar]
- Gramacy RB (2014). laGP: Local approximate Gaussian process regression. R package version 1.1–4. [Google Scholar]
- Gramacy RB (2016). laGP: Large-scale spatial modeling via local approximate Gaussian processes in R. J. Stat. Softw 72 1–46. [Google Scholar]
- Hu R and Ludkovsk M (2017). Sequential design for ranking response surfaces. SIAM/ASA J. Uncertain. Quantificat 5 212–239. MR3614687 [Google Scholar]
- Johansson MA, Cummings DAT and Glass GE (2009). Multiyear climate variability and dengue–El Niño southern oscillation, weather, and dengue incidence in Puerto Rico, Mexico, and Thailand: A longitudinal data analysis. PLoS Med. 6 e1000168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson LR and Gramacy RB (2017). vbdcast: Vector-borne disease forecasting. Technical report. https://github.com/lrjohnson0/vbdcast. [Google Scholar]
- Johnson LR, Ben-Horin T, Lafferty KD, McNally A, Mordecai E, Paaijmans KP, Pawar S and Ryan SJ (2015). Understanding uncertainty in temperature effects on vector-borne disease: A Bayesian approach. Ecology 96 203–213. [DOI] [PubMed] [Google Scholar]
- Johnson LR, Gramacy RB, Cohen J, Mordecai E, Murdock C, Rohr J, Ryan SJ, Stewart-Ibarra AM and Weikel D (2018). Supplement to “Phenomenological forecasting of disease incidence using heteroskedastic Gaussian processes: A dengue case study”. DOI: 10.1214/17-AOAS1090SUPPA, DOI:. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koepke AA, Longini IM Jr., Halloran ME, Wakefield J and Minin VN (2016). Predictive modeling of cholera outbreaks in Bangladesh. Ann. Appl. Stat 10 575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn K, Campbell-Lendrum D, Haines A, Cox J, Corvalán C, Anker M et al. (2005). Using climate to predict infectious disease epidemics. White Paper, World Health Organization, Geneva. www.who.int/globalchange/publications/infectdiseases/en/index.html. [Google Scholar]
- Lambrechts L, Paaijmans KP, Fansiri T, Carrington LB, Kramer LD, Thomas MB and Scott TW (2011). Impact of daily temperature fluctuations on dengue virus transmission by Aedes aegypti. Proc. Natl. Acad. Sci. USA 108 7460–7465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludkovski M and Niemi J (2010). Optimal dynamic policies for influenza management. Stat. Commun. Infec. Dis. 2 Art 5, 27. MR2764286 [Google Scholar]
- Matheron G. (1963). Principles of geostatistics. Econ. Geol 58 1246–1266. [Google Scholar]
- Merl D, Johnson LR, Gramacy RB and Mangel M (2009). A statistical framework for the adaptive management of epidemiological interventions. PLoS ONE 4 e5807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore CG, Cline BL, Ruiz-Tibén E, Lee D, Romney-Joseph H and Rivera-Correa E (1978). Aedes aegypti in Puerto Rico: Environmental determinants of larval abundance and relation to dengue virus transmission. Am. J. Trop. Med. Hyg 27 1225–1231. [DOI] [PubMed] [Google Scholar]
- Mordecai EA, Paaijmans KP, Johnson LR, Balzer C, Ben-Horin T, de Moor E, McNally A, Pawar S, Ryan SJ, Smith TC and Lafferty KD (2013). optimal temperature for malaria transmission is dramatically lower than previously predicted. Ecol. Lett 16 22–30. [DOI] [PubMed] [Google Scholar]
- Mordecai E, Cohen J, Evans MV, Gudapati P, Johnson LR, Lippi CA, Miazgowicz K, Murdock CC, Rohr j. R., Ryan S. j., Savage V, Shocket M, Stewart Ibarra A, Thomas MB and Weikel DP (2017). Detecting the impact of temperature on transmission of zika, dengue and chikungunya using mechanistic models. PLoS Negl. Trop. Dis 11 e0005568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osthus D, Hickmann KS, Caragea PC, Higdon D and Del Valle SY (2017). Forecasting seasonal influenza with a state–space SIR model. Ann. Appl. Stat 11 202–224. MR3634321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R DEVELOPMENT Core Team (2008). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3–900051-07–0. [Google Scholar]
- Rasmussen CE and Williams CKI (2006). Gaussian Processes for Machine Learning. The MIT Press. [Google Scholar]
- Ray EL, Sakrejda K, Lauer SA, Johansson MA and Reich NG (2017). Infectious disease prediction with kernel conditional density estimation. Technical report. github.com/reichlab/article-disease-pred-with-kcde. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds RW, Rayner NA, Smith TM, Stokes DC and Wang W (2002). An improved in situ and satellite SST analysis for climate. J. Climate 15 1609–1625. [Google Scholar]
- Sacks J, Welch W. j., Mitchell T. j. and Wynn HP (1989). Design and analysis of computer experiments. Statist. Sci 4 409–435. With comments and a rejoinder by the authors. MR1041765 [Google Scholar]
- Stewart-Ibarra AM and Lowe R (2013). Climate and non-climate drivers of dengue epidemics in southern coastal Ecuador. Am. J. Trop. Med. Hyg 88 971–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart-Ibarra AM, Ryan S. j., Beltrán E, Mejía R, Silva M and Muñoz Á (2013). Dengue vector dynamics (Aedes aegypti) influenced by climate and social factors in Ecuador: Implications for targeted control. PLoS ONE 8 e78263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson MC, Garcia-Herrera R and Beniston M (2008). Seasonal Forecasts, Climatic Change and Human Health. Springer. [Google Scholar]
- Venables WN and Ripley BD (1994). Modern Applied Statistics with S-Plus. Springer, New York. MR1337030 [Google Scholar]
- WORLD Health Organization (2009). Dengue: Guidelines for diagnosis, treatment, prevention and control. Special Programme for Research and Training in Tropical Diseases, Department of Control of Neglected Tropical Diseases, and Epidemic and Pandemic Alert, World Health Organization. [Google Scholar]
- WORLD Health Organization (2016). Dengue vaccine: WHO position paper—July 2016. Weekly Epidemiological Record 91 349–364.27476189 [Google Scholar]
- Xu L, Stige LC, Chan K-S, Zhou J, Yang J, Sang S, Wang M, Yang Z, Yan Z, Jiang T, Lu L, Yue Y, Liu X, Lin H, Xu J, Liu Q and Stenseth NC (2016). Climate variation drives dengue dynamics. Proc. Natl. Acad. Sci. USA 201618558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamana TK, Kandula S and Shaman J (2016). Superensemble forecasts of dengue outbreaks. J. R. Soc. Interface 13 20160410. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.