Abstract
Compression elastography allows the precise measurement of large deformations of soft tissue in vivo. From an image sequence showing tissue undergoing large deformation, an inverse problem for both the linear and nonlinear elastic moduli distributions can be solved. As part of a larger clinical study to evaluate nonlinear elastic modulus maps (NEMs) in breast cancer, we evaluate the repeatability of linear and nonlinear modulus maps from repeat measurements. Within the cohort of subjects scanned to date, 20 had repeat scans. These repeated scans were processed to evaluate NEM repeatability. In vivo data were acquired by a custom-built, digitally controlled, uniaxial compression device with force feedback from the pressure-plate. RF-data were acquired using plane-wave imaging, at a frame-rate of 200 Hz, with a ramp-and-hold compressive force of 8N, applied at 8N/sec. A 2D block-matching algorithm was used to obtain sample-level displacement fields which were then tracked at subsample resolution using 2D cross correlation. Linear and nonlinear elasticity parameters in a modified Veronda-Westmann model of tissue elasticity were estimated using an iterative optimization method. For the repeated scans, B-mode images, strain images, and linear and nonlinear elastic modulus maps are measured and compared. Results indicate that when images are acquired in the same region of tissue and sufficiently high strain is used to recover nonlinearity parameters, then the reconstructed modulus maps are consistent.
Keywords: elastography, breast cancer, inverse problem, quantitative, elastic modulus, elastic nonlinearity
I. Introduction
Breast tumors are often palpable. The alteration in elastic properties is in part a result of inflammation that usually occurs during the early stages of disease development. The extracellular matrix (ECM) of breast stroma, which provides the solid consistency of parenchymal tissues, plays an active role in cancerous tumor growth [1], [2]. Breast tumors are often stiffer than normal tissue [3] and malignant breast lesions are often stiffer than benign lesions [4], [5].
Several elasticity imaging approaches have been used for noninvasive and objective evaluation of tissue elasticity. Magnetic resonance elastography (MRE) has been used to differentiate normal and pathological tissues in some diseases and to increase diagnostic specificity [6]–[10]. MRI and MRE technology are expensive, however, and thus less likely to see wide clinical applications for a wide range of the patient population. Conventional quasi-static elastography utilizes compression and ultrasound-based motion tracking to present maps of tissue strain [11]–[16]. Vibro-acoustography is an imaging method based on acoustic response of tissue to harmonic acoustic radiation force [17]–[20]. Both conventional ultrasound elastography and vibro-acoustography have shown promising results in differentiating breast masses in patients [21]–[29]. Shear Wave Elastography (SWE) uses ultrasound radiation force to generate shear waves and then measures shear wave speed, which depends on shear elastic modulus. Results of studies using SWE [5], [30]–[37] for breast have been very promising.
Overlap in linear elasticity between benign and malignant breast masses has been reported [38]–[43]. Such overlap limits the discriminating power of elasticity imaging regardless of the accuracy of the measurement method. It should be noted that the common goal of the above-mentioned methods is to measure elasticity in the linear regime. It is known that soft tissues behave nonlinearly under high strains, however, and this opens up a new way of characterizing tissues. Results on a small sample of subjects in [44], [45] suggest that the nonlinearity parameter of elasticity can be significantly different for benign fibroadenoma (FA) and invasive ductal carcinoma (IDC). Hence evaluating elastic nonlinearity in a larger cohort of subjects is of interest.
The linear and non-linear elasticity parameters are physically independent. Accordingly, information from each of these independent parameters can improve our understanding about the lesion’s mechanical properties with respect to its pathology. The physiological reasons for this can be attributed to the changes in the morphology of the collagen fiber bundles in the ECM during tumorigenesis. It has been observed that as cancer develops an invasive phenotype, these fibers transform from a wavy state that is highly tortuous to a more straight and rod-like configuration [46]–[48]. In a tortuous configuration (benign lesions), the fibers require a significant amount of stretch before they become taut, which is subsequently associated with an increase in apparent stiffness. This shifts their nonlinear elastic behavior to strains that are greater than 20-30%. In a less tortuous configuration seen in cancerous tumors, however, significantly lower strain is required to make the fibers taut. This makes it possible to observe their nonlinear behavior within the levels of strain we have considered in the present study.
This paper presents Nonlinear Elasticity Mapping (NEM) as a generalized (i.e., linear and nonlinear) elasticity evaluation/imaging method to provide complementary and relevant information for identification and characterization of breast masses. Nonlinear tissue elasticity is measured by recording ultrasound scans of the tissue under different values of externally applied compression and processing the resulting data. To reliably recover nonlinear elastic parameters, deformations of sufficiently large strain are required so that the nonlinear tissue behavior can be observed. Tracking such large deformations in vivo can be challenging. It must be done in small increments, and even so, tissue motion out of the imaging plane is possible. For NEM imaging, therefore, an automated compression mechanism is used that can apply a quantified amount of force at a known speed to the breast. Further, imaging is performed at a high frame-rate to allow the tracking of large deformations in sufficiently small increments. Because of these potential issues, a necessary step in the development and evaluation of NEM is evaluation of repeatability, which is the focus of the present study. The goal of this study is essentially to answer the question: If the same region of tissue is imaged and measured twice, do we recover the same mechanical properties?
The remainder of this paper is organized as follows. Section II describes methods of data acquisition, subject enrollment, RF processing for displacement and strain estimation, inverse problem solution for linear and nonlinear modulus reconstructions, and metrics developed to measure the similarity of images. Section III contains the results showing correlation between nominally similar fields obtained in different acquisitions. As a control, comparisons of acquisitions between distinct subjects are also computed and presented. A discussion of the results and their interpretation is presented in Section IV, with conclusions drawn in Section V.
II. Methods
In order to evaluate the repeatability of reconstructing NEMs from in-vivo data, 20 subjects were scanned multiple times under similar conditions and the data for each acquisition were separately processed in order to obtain modulus estimates. The scans were performed using a custom built uniaxial compression device. RF-data were acquired using plane wave imaging of the tissue while a ramp-and-hold compressive force was applied. A 2D block-matching algorithm was used to obtain sample-level displacement fields which were then tracked using 2D cross correlation. Linear and nonlinear elasticity parameters in a modified Veronda-Westmann model of tissue elasticity were then estimated using an iterative optimization method. Repeatability for both B-mode images and modulus estimates were evaluated and compared. Further details for each of these steps are given below.
A. Data acquisition
The in vivo raw ultrasound in-phase and quadrature (IQ) data were acquired using a programmable Verasonics Vantage scanner (Verasonics Inc., Kirkland, WA), equipped with a 128 channel linear array L11-4 transducer (Verasonics Inc., Kirkland, WA). The automated compression device described in [49] was used to induce large strain in the breast lesions. The linear array transducer was held in the probe holder fixture and guided by the arm of the compression device, which allowed high frame-rate imaging of the breast lesion and the surrounding tissue during the compression. The physical footprint of the transducer surface was extended by a compression plate that was semi-suspended on four load cells, one mounted at each corner of the rectangular probe-holder. The compression arm consisted of an actuator that was driven by a servo motor. Upon activation, the compression arm equipped with the probe and the force sensors moved rapidly into the tissue (the ramp phase) to achieve a preset force level on the compression plate. The force data acquired from the load sensors were used as feedback for the ramp-and-hold compression. The ultrasound IQ data were acquired using plane wave imaging, at a center and sampling frequency of 6.25 MHz and 25 MHz, respectively. The imaging and the force sensor data from the compression arm were acquired synchronously for eight seconds. To minimize tissue decorrelation incurred during the large compression, a high imaging frame-rate of 200 frames/second was used.
B. In vivo Study
The in vivo study was conducted on 20 female patients, with at least one suspicious breast lesion recommended for biopsy. The study was performed in accordance with the relevant guidelines and regulations approved by the Mayo Clinic institutional review board (IRB). Informed consent was obtained from all patients prior to their participation, and documented in writing on IRB approved forms. All patients were scanned by an experienced sonographer who identified the lesion using regular B-mode imaging. Subsequently, the transducer held by the automated compression device was positioned over the lesion. To minimize initial pre-compression, a roughly 5 mm diameter bead of liquid ultrasound coupling gel was applied to the active elements of probe, allowing acoustic contact to be created before significant mechanical coupling was created. An additional thin smear of ultrasound coupling gel lubricated the compression plate. Depending on the location of the lesion, subjects were scanned in either the supine or posterior-oblique position, using using a transverse or longitudinal imaging plane. The choice was determined by that which minimized out-of-plane motion and achieved better acoustic contact under the flat compression plate between the probe and breast tissue. Finer refinement of the final plane selection was based on visual inspection of the B-mode sequence to assess and minimize out-of-plane motion. Once the final probe-orientation was determined, a scan was acquired under breath hold. For each acquisition, a ramp-and-hold force of 8N was applied at a rate of 8N per second. Additional scans were acquired from the same lesion, without repositioning the patient, bed or the probe. Subjects were instructed to lie as still as possible during the 5-7 minutes between repeat acquisitions.
C. Displacement estimation
Sequences of ultrasound RF echo signals corresponding to individual B-mode image frames were obtained as described above in multi-compression breast scans. Using these frames, we estimated the large displacements for material points in the first frame from the initial state to the last deformation step. We dynamically paired echo signal frames [50] to achieve a relatively constant frame-average strain of about either 0.3% or 0.5%. For each scan, the starting and ending frame was selected for motion tracking and a 2D companding method [51] was performed to track incremental displacements. Relatively large-scale deformation was tracked using a guided-search block matching motion tracking method based on regiongrowing [52], [53]. That large scale motion tracking is used to warp the post-deformation field into the coordinate system of the pre-deformation field followed by a phase tracking method to refine displacements [54], [55]. The incremental displacements were accumulated at all material points for all deformation steps to obtain the accumulated displacement from the first to the last step in the selected sequence.
D. Modulus reconstruction
The inverse elasticity problem is posed as a constrained optimization problem, as in [44], with slight modifications below. For a given measured axial displacement field we wish to find the distribution of a material parameter
(representing either log of the linear shear modulus, or the non-linearity parameter ) that will minimize the following cost function:
| (1) |
Here, is the predicted displacement field from a computational model of the deformation of breast tissue with material property . The material parameter is the familiar linear elastic shear modulus. The material parameter determines the exponential increase of energy with strain, and is referred to here as the “nonlinear elastic modulus” (NEM), “nonlinearity parameter” (NLP), or simply the “nonlinearity”.
The first term of the objective function (1) represents the mismatch between the measured and predicted displacement fields. Due to the high level of noise in the lateral displacements relative to the axial displacements, we match only the axial displacements. The mismatch between the measured and predicted displacements is calculated in the norm represented here by the symbol , which is defined as . Here, is the region of interest in the undeformed image.
The second term of the objective function is the regularization term. It ameliorates the ill-posed nature of the inverse problem and smooths the solution. Here is the regularization parameter. It is a weight given to the regularization term. Its value is noise dependent and is chosen through the L-Curve method, described in chapter 7.4 of [56]. For the regularization term itself, a smoothed total variation diminishing regularization was used of this form:
| (2) |
Here, c is a small constant that is used to make the regularization term smooth, so that it does not have the cusp that is inherent to the absolute value function.
The computational model for the breast tissue deformation is based on the following boundary conditions. The axial displacements on all surfaces of the boundary are prescribed to equal the measured axial displacements on the boundary. The lateral displacement is prescribed only at one point, to prevent rigid body motion. These boundary conditions correspond to the case of unconfined compression between two surfaces, where the displacement of the medium is prescribed in the axial direction but the tissue is free to slip and expand in the lateral direction. Thus, the equilibrium equation and boundary conditions are:
| (3) |
| (4) |
| (5) |
Here is the deformation gradient and is the second Piola-Kirchhoff stress tensor [57], that will be defined through a strain energy function. The traction vector on the boundary is given by [57], where represents the unit outward normal vector.
The constitutive equation for the tissue is obtained by assuming a modified Veronda-Westmann strain energy function [58] for an incompressible material. This function is:
| (6) |
Here, and represent the first and second principal invariants of the right Cauchy-Green strain tensor . The material parameter is the linear shear modulus. The material parameter determines the exponential increase of energy with strain, and will be referred to as the “nonlinearity parameter” or simply “nonlinearity”. The strain energy function (6) is equivalent to that presented in equation (14) of [58] if the nonlinearity parameter is called rather then and the two linear parameters have the values and .
Since ultrasound imaging collects data in a single plane, an assumption must be made in order to reduce the problem from 3D to 2D. There are two classical 2D models of elastic behavior, plane stress and plane strain. In plane strain, the material is constrained in the out of plane direction preventing out of plane deformations, while in plane stress the material is unconstrained in the out of plane direction and an assumption is made that there are no loads in the out of plane direction. Since the breast tissue is neither loaded nor constrained in the out of plane direction, the plane stress approximation is used. Using the strain energy function defined in (6) under plane stress conditions gives the following expression for the stress,
| (7) |
Here, I is the 2 × 2 identity tensor.
The steps to solve the inverse elasticity problem are as follows:
For a given measured displacement field and an initial (constant) guess of the material property distribution, solve the forward problem (3-5) to obtain a predicted displacement field.
Solve the adjoint problem which is driven by the mismatch in predicted and measured displacements.
Evaluate the objective function and its gradient with respect to the material parameters using the solutions to the forward and adjoint problems.
Use the objective function value and gradient to update the material parameter distribution.
Repeat steps 1-4 until convergence.
In order to reconstruct both the linear shear modulus and the nonlinearity parameter, the above process is performed twice, sequentially. First, the linear shear modulus is reconstructed at low deformation (around 2% mean axial strain), using an incompressible, plane stress, linear elasticity model. The reconstructed shear modulus is then used to reconstruct the nonlinearity at the maximum measured deformation in the image sequence using the nonlinear model described above. For a given regularization parameter, the inverse problem solution time is roughly 2 hours on a single core.
E. Repeatability evaluation
In order to compare elasticity maps of homologous regions to one another, repeat acquisitions are registered via the B-mode images. The alternative of registering elasticity images directly would be inappropriate, since it would ensure maximal similarity between material property images and thus potentially bias the outcome of the study. Therefore, the authors chose to, instead, register the corresponding B-mode images, and use this transformation directly on the material parameter images.
Therefore, the procedure followed is as follows:
Choose the B-mode image corresponding to zero strain for each acquisition.
Smooth the B-mode images using 7 × 7 pixel averaging filter.
Crop the outer 3 pixels to remove edge artifacts from the smoothing filter. After this, subtract the mean intensity to remove any overall intensity differences between the two acquisitions.
Register the smoothed B-mode images from two acquisitions to one another using rigid motion transformation (command “imregtform” in MatLab (TM).)
Apply the same transformation(s) to the corresponding material property maps.
Measure correlations between aligned B-mode images and material property maps as defined in equation (8) below.
Steps (1-4) for registering the B-mode images are illustrated in Figure 1 on subject 2.
Fig. 1:
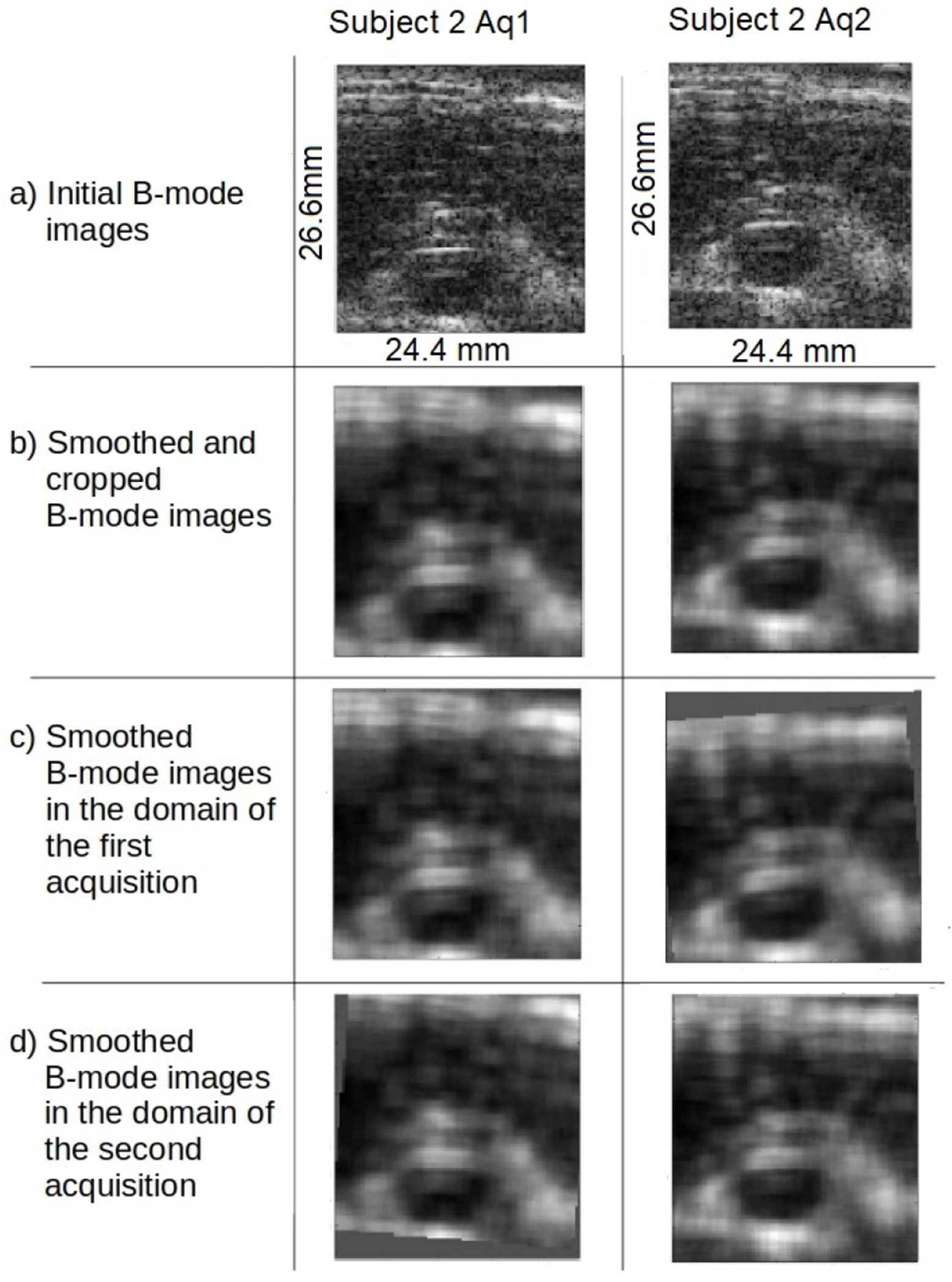
The process of registering B-mode images for acquisitions 1 and 2 of subject 2. a) The initial B-mode images for acquisitions 1 and 2 respectively. b) The initial B-mode images smoothed to avoid registering speckle noise and cropped to avoid edge artifacts from the smoothing. c) The smoothed B-mode image for acquisition 1 is reproduced from line (b); the smoothed B-mode image for acquisition 2 is shifted to be in the domain of acquisition 1. d) The smoothed B-mode image for acquisition 2 is reproduced from line (b); the smoothed B-mode image for acquisition 1 is shifted to be in the domain of acquisition 2.
The mean correlation between two fields, and is computed as:
| (8) |
Here, represents the first field in its own region of imaging, represents the second field mapped to the domain of the first field, represents the first field mapped to the domain of the second field, represents the second field in its own domain, represents the domain of the first field, while represents the domain of the second field.
For correlating B-mode images, is the smoothed B-mode image intensity used to find the registration mapping. When correlating strain, is the strain field in the sequence whose frame-average is closest to ; this is the strain field used to recover linear elastic modulus. For correlating shear moduli, , where is chosen so that has zero mean.1 When correlating nonlinearity, . All fields are computed and stored as floating point values.
III. Results
Numerical values of the correlation coefficients for all results considered are shown in Table I. These are shown on a scatter plot in Figure 2.
TABLE I:
Table of correlation values for subjects with repeat acquisitions sorted by subject ID. Some subjects, e.g. 13, were scanned more than twice, permitting more than one comparison. For example, subject 13 was scanned three times, permitting us to compare acquisitions 1 and 2, 2 and 3 , and 1 and 3, thus giving three comparisons. We obtained 6 comparisons from 4 scans of subject is the linear elastic shear modulus; is the nonlinear elastic parameter; indicates benign or malignant on pathology; indicates whether frame-average strain used to recover was . Example images are shown for those entries listed in bold font.
| ID | B-Mode Correl | Sirain Correl | Correl | Correl | B/M | Final Strain ≥ 14%? |
|---|---|---|---|---|---|---|
|
| ||||||
| 1 | 0.922 | 0.830 | 0.952 | 0.963 | B | Y |
| 2 | 0.820 | 0.709 | 0.808 | 0.910 | B | Y |
| 3 | 0.894 | 0.852 | 0.932 | 0.878 | M | Y |
| 4 | 0.709 | 0.685 | 0.791 | 0.821 | M | Y |
| 4 | 0.751 | 0.708 | 0.847 | 0.776 | M | Y |
| 4 | 0.924 | 0.812 | 0.903 | 0.945 | M | Y |
| 5 | 0.910 | 0.797 | 0.873 | 0.880 | B | Y |
| 6 | 0.927 | 0.801 | 0.950 | 0.918 | B | N |
| 7 | 0.951 | 0.877 | 0.927 | 0.702 | B | N |
| 8 | 0.865 | 0.666 | 0.761 | 0.464 | M | Y |
| 9 | 0.932 | 0.826 | 0.915 | 0.739 | B | N |
| 10 | 0.934 | 0.935 | 0.976 | 0.359 | M | N |
| 11 | 0.947 | 0.627 | 0.702 | 0.644 | M | N |
| 12 | 0.966 | 0.853 | 0.933 | 0.988 | B | Y |
| 13 | 0.0967 | 0.828 | 0.956 | 0.528 | B | N |
| 13 | 00.852 | 0.590 | 0.772 | 0.200 | B | N |
| 13 | 0.851 | 0.569 | 0.818 | 0.313 | B | N |
| 14 | 0.920 | 0.678 | 0.792 | 0.605 | M | N |
| 14 | 0.900 | 0.641 | 0.763 | 0.651 | M | N |
| 14 | 0.881 | 0.565 | 0.741 | 0.827 | M | N |
| 15 | 0.918 | 0.794 | 0.926 | 0.926 | M | N |
| 15 | 0.873 | 0.797 | 0.925 | 0.897 | M | N |
| 15 | 0.587 | 0.718 | 0.856 | 0.826 | M | N |
| 15 | 0.866 | 0.791 | 0.889 | 0.833 | M | N |
| 15 | 0.665 | 0.735 | 0.848 | 0.785 | M | N |
| 15 | 0.762 | 0.775 | 0.888 | 0.840 | M | N |
| 16 | 0.680 | 0.532 | 0.658 | 0.304 | B | Y |
| 17 | 0.753 | 0.435 | 0.488 | 0.670 | B | N |
| 18 | 0.704 | 0.259 | 0.415 | −0.155 | B | N |
| 19 | 0.915 | 0.740 | 0.827 | 0.844 | B | Y |
| 20 | 0.875 | 0.716 | 0.793 | 0.947 | B | Y |
| 20 | 0.796 | 0.672 | 0.782 | 0.852 | B | Y |
| 20 | 0.789 | 0.636 | 0.725 | 0.910 | B | Y |
| 20 | 0.785 | 0.616 | 0.768 | 0.786 | B | Y |
| 20 | 0.814 | 0.619 | 0.765 | 0.842 | B | Y |
| 20 | 0.900 | 0.741 | 0.847 | 0.914 | B | Y |
| Avg | 0.847 | 0.706 | 0.820 | 0.706 | ||
| Std | 0.095 | 0.B3 | 0.121 | 0.133 | ||
Fig. 2:
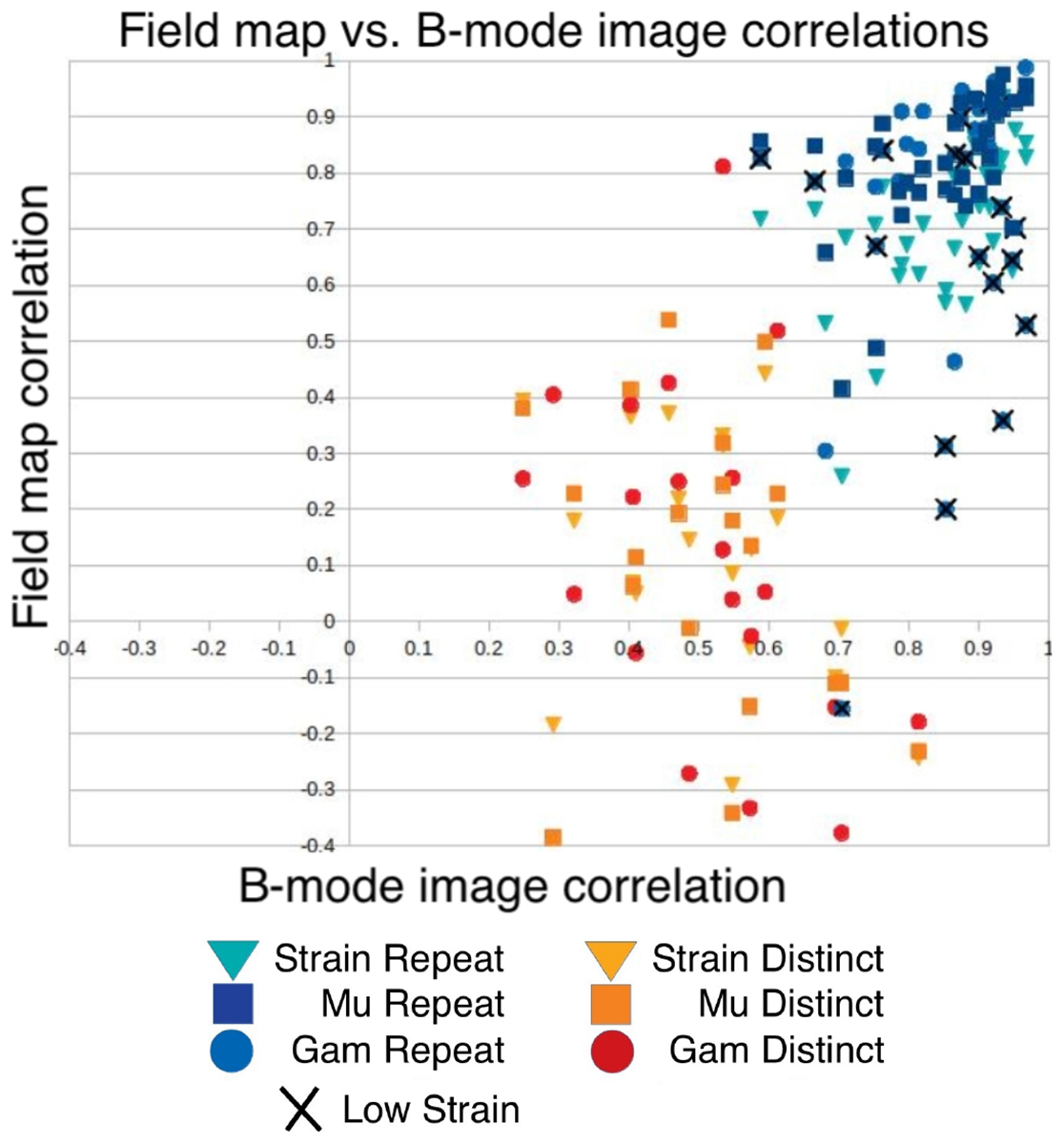
Comparison of correlations between initial B-mode images, strain fields, shear modulus maps, and elastic nonlinearity maps, for both repeat acquisitions (blue markers), and those between distinct subjects (orange markers).
Figure 2 shows the correlation between B-mode images for different acquisitions versus the correlation between strain and modulus fields. The correlation between smoothed B-mode images can be interpreted as a measure of whether the two acquisitions represent the same region of tissue. Correlations between strain fields are presented as triangles; correlations between shear modulus fields are presented with squares, and correlations between nonlinearitier are presented with circles. Correlations between nonlinearities obtained from repeat acquisitions where the average final strain was less than 14% are also marked with a cross in order to remind the reader that values of nonlinearity obtained at low strain are less trustworthy.
We might expect that the correlations between repeated acquisitions of B-mode images and repeated acquisitions of the elasticity images would be correlated. A t-test for the null-hypothesis that they are not correlated yields p-values of 0.0005, 0.001, 0.12, for strain images, shear modulus images, and nonlinearity parameter images, respectively. When excluding nonlinearity maps reconstructed from strain fields with frame-average strain less than 14%, however, the last p-value decreases from 0.12 to 0.009. In there cases, therefore, we rejrct the null-hypothesis, and conclude that the correlations between repeated acquisitions of B-mode images is statistically significantly correlated with repeated acquisitions of the elasticity images, provided the elastic nonlinearity parameter maps are recovered from strain fields of sufficiently high magnitude. We found no significant difference between these results for benign vs. malignant cases.
Correlations between reconstructed shear modulus and nonlinearity from repeated acquisitions tended to be relatively high, overall, and so the authors considered whether this might be an accident of the processing steps used2. Therefore, Figure 2 contains 2 sets of points: those representing acquisitions in the same ROI and subject (presented in blue), and those comparing acquisitions in two different subjects (shown in orange). The expectation was that comparisons of different subjects would show low correlations, while comparisons of the same ROI in the same subject would show higher correlations. This trend is evident in the figure. If the high correlation between reconstructed fields from repeated acquisitions were indeed an accident, then both the orange and the blue markers would be concentrated near the top. That is not the case.
There are dozens of images whose comparisons are summarized in Figure 2. To aid the interpretation of that figure, we now present several examples representative of different locations on the scatter plot in Figure 2.
Figure 3 shows an example with high agreement between acquisitions. It shows excellent agreement between B-mode images, which suggests that the same ROIs were well targeted in both acquisitions. The correlations between the strain, shear modulus, and elastic nonlinearity were correspondingly high. We note that the final strains used to recover the elastic nonlinearity parameters were higher than 14%, and therefore we also see high agreement between the elastic nonlinearity fields. Data points from this comparison would appear as blue points in the top right of the chart in Figure 2.
Fig. 3:
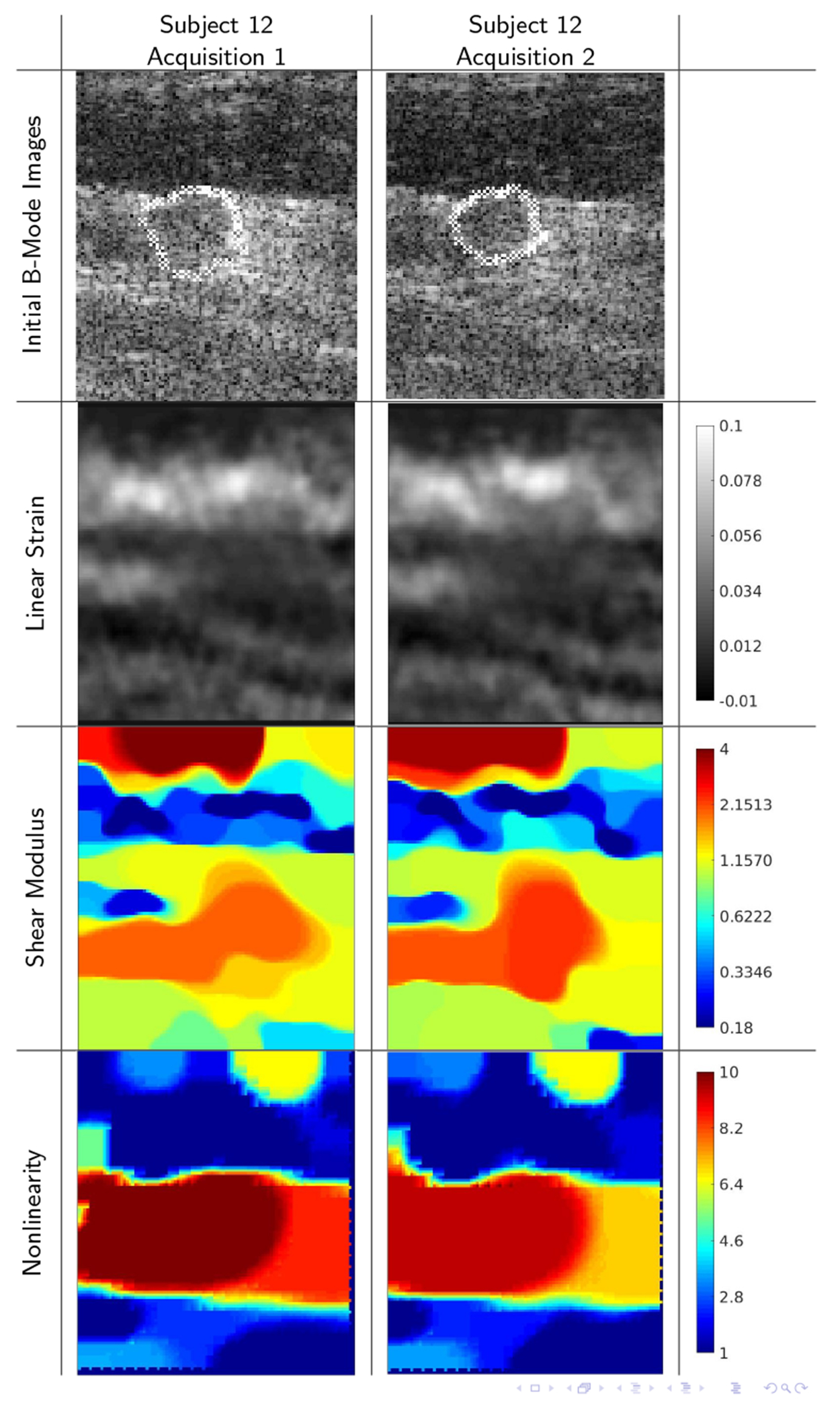
B-mode images, strain images, linear elastic shear modulus images, and elastic nonlinearity parameter images for subject 12. (ROI: 24 × 28mm) This panel shows excellent agreement between B-mode images (correlation 0.966), which suggests that the same ROIs were well targeted in both acquisitions. The correlations between the strain images (0.853) and between the shear modulus images (0.933) were correspondingly high. Furthermore sufficiently high strain (≥ 14%) was available to reliably reconstruct the elastic nonlinearity, which also shows excellent agreement (correlation 0.988). All color bars are dimensionless; strain and nonlinearity parameters are shown in absolute terms; linear shear modulus is normalized to unit geometric mean.
By comparison, Figures 4 and 5 show examples of high repeatability in ROIs, but low repeatability in the nonlinearity images. As with the previous example, the high B-mode image correlation suggests that the same ROIs were well targeted in both acquisitions. The correlations between the strain, shear modulus, are correspondingly very high (i.e. all > 0.8, most > 0.9), while the correlation between nonlinearity images is below 0.6. In these image sequences, the maximum measured frame-average strain was less than 14%. Therefore, there was insufficient strain to observe nonlinear tissue behavior, from which to infer the elastic nonlinearity parameter. These and similar points in the chart, Figure 2, are marked with an X.
Fig. 4:
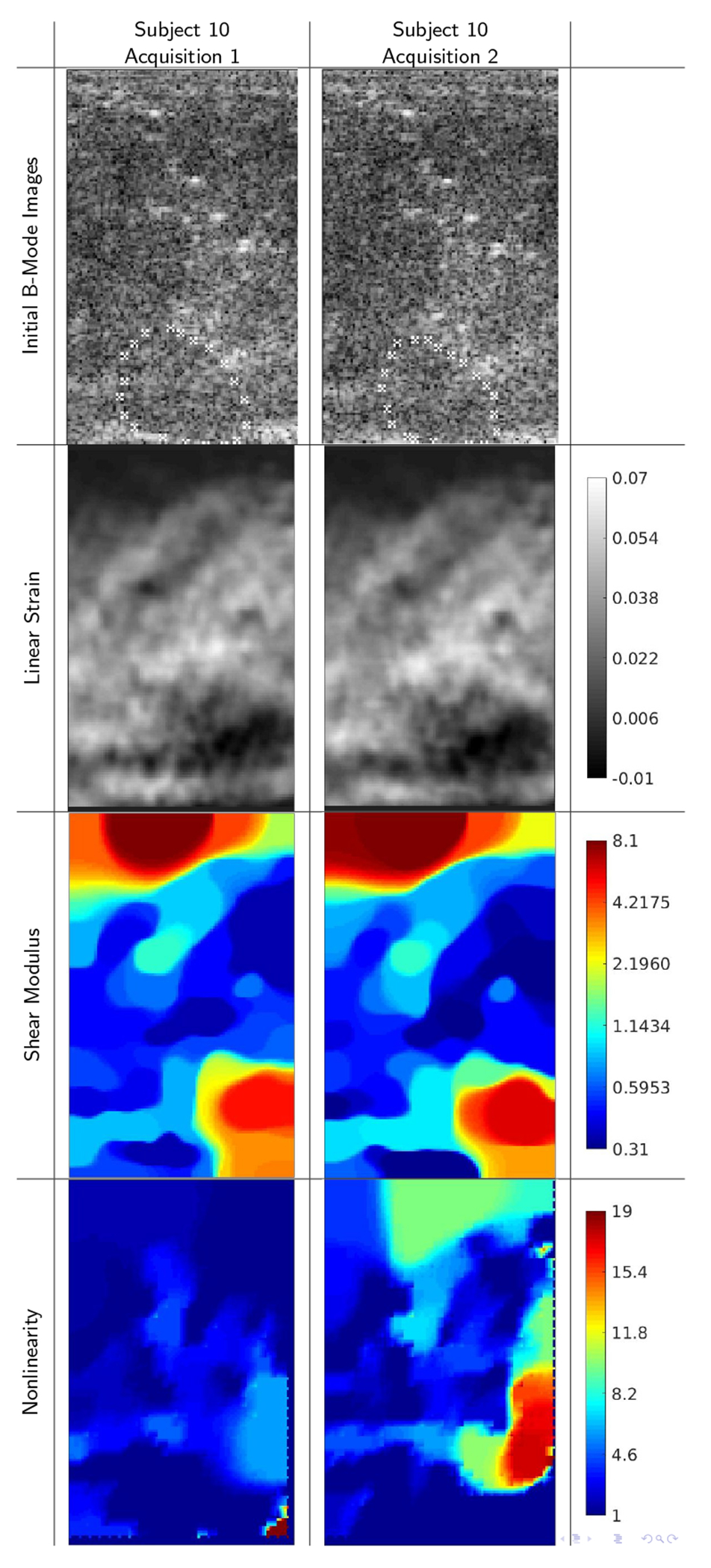
B-mode images and reconstructions for repeat acquisitions of subject 10, (ROI: 22 × 36mm) showing strong agreement between B-mode echo data acquisitions (correlation 0.934), between linear strain fields (0.935), and between linear elastic shear modulus reconstructions (0.976). A low level of maximum frame-average strain, however, gave nonlinearity parameters that were quite different (correlation 0.359).
Fig. 5:
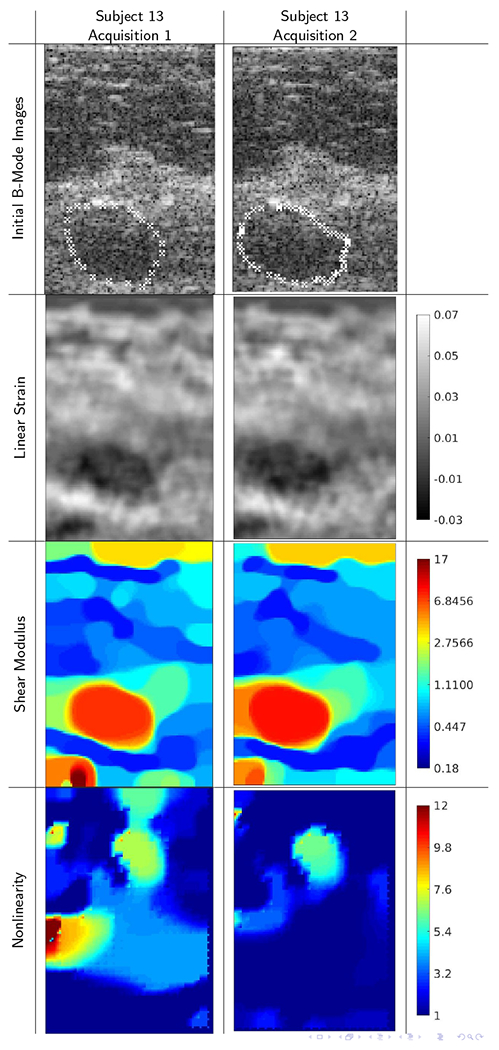
B-mode images and reconstructions for repeat acquisitions from subject 13 (ROI: 21 × 31mm) This panel shows excellent agreement between B-mode images (correlation 0.967), which suggests that the same ROIs were well targeted in both acquisitions. The correlations between the strain images (0.828) and shear modulus images (0.956) are correspondingly high. The correlation between elastic nonlinearity reconstructions, however, was relatively low (0.528), mostly likely due to an insufficiently high final strain to recover nonlinearity well.
Among the blue markers in Figure 2, Subject 15 provided three sets near the top left of that grouping. These comparisons show relatively poor correlation between the B-mode images, but moderately good correlation in the elasticity images. One example is shown in Figure 6. In none of the acquisitions with subject 15 was the final strain above our threshold of 14%.
Fig. 6:
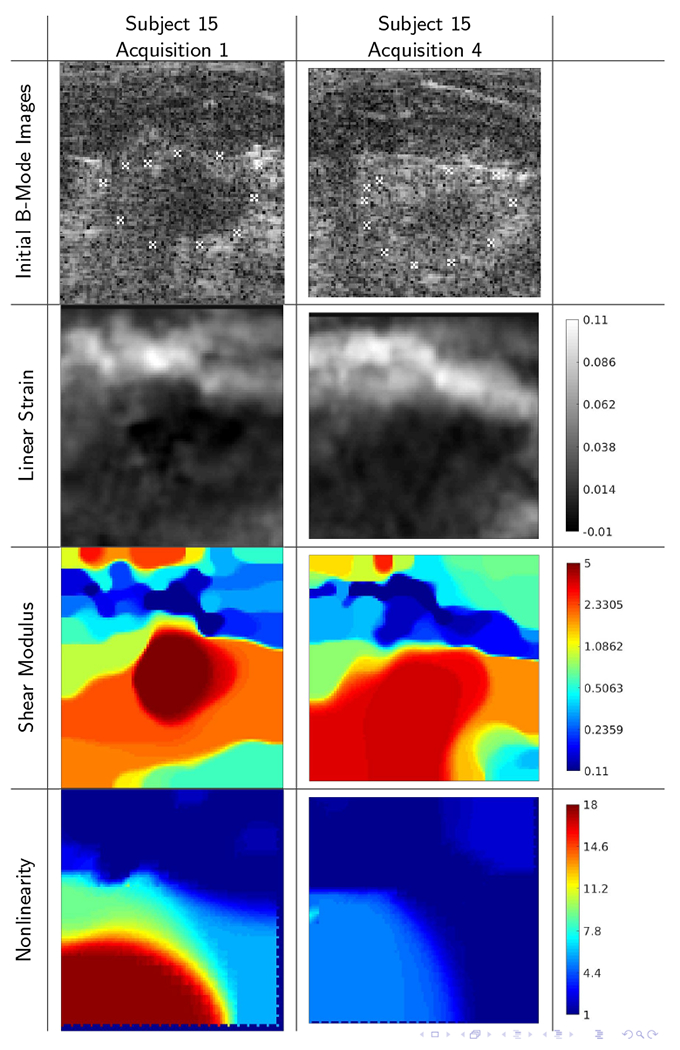
B-mode images and reconstructions for repeat acquisitions of subject 15 (ROI: 23 × 24mm) showing relatively poor agreement between the acquisitions (B-mode image correlation 0.665). The correlations for the strain (0.735), linear shear modulus (0.848), and nonlinearity parameter (0.785) images show moderately good agreement, despite a low level of maximum frame-average strain.
The images corresponding to the greatest outlier in the chart are shown in Figure 7. These data suffered from two shortcomings in the repeat acquisitions. First, the ROIs were not strongly similar between the two acquisitions, as suggested by a B-mode image correlation coefficient of only 0.70. This is a relatively low correlation for B-mode images; in some cases, the correlation between B-mode images from different subjects was higher than this value. Second, the final strain was relatively low, preventing accurate reconstruction of the nonlinearity. Nevertheless, certain similar features in the images are discernible.
Fig. 7:
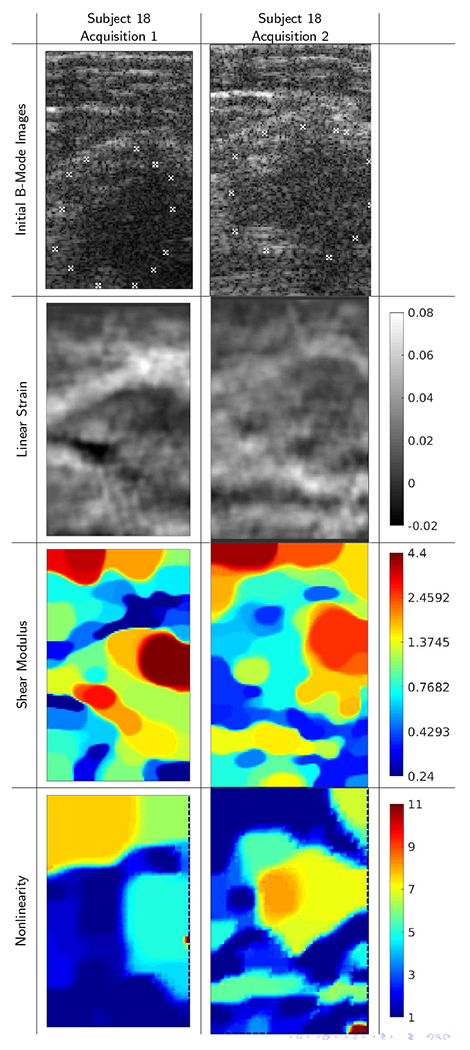
B-mode images, strain images, linear elastic shear modulus images, and elastic nonlinearity parameter images for repeat acquisitions of subject 18 showing exceptionally poor agreement between the acquisitions. In this example, the original ROI was poorly targeted in the repeat acquisition, and so all four image types show large differences. Correlations between repeat acquisitions are 0.704, 0.259, 0.415, −0.155, between repeated acquisition of B-mode images, strain images, shear modulus images, and elastic nonlinearity parameter images. We note in particular that the nonlinearity maps are negatively correlated.
IV. Discussion
The goal of this study is to answer the question: If the same region of tissue is imaged and measured twice, do we recover the same mechanical properties? By registering the B-mode images in our data sets, we sought to suppress variability in ROI targeting, so as to focus on the variability inherent in the in vivo mechanical property measurement itself.
There are several observations to be made about Figure 2. The first is that all repeat acquisitions (all the blue markers) are clustered in the upper right corner of the plot, showing a relatively high degree of correlation. It was for this reason that we asked the question whether any pair of images of two breast masses would show similarly high degrees of correlation. This question motivated computing comparisons of images of different masses, shown in orange. The general separation of these groups shows that the high correlation between repeat acquisitions is not coincidental.
The second pattern that may be noticed in Table I and in Figure 2 is that the correlation between modulus estimates from repeat acquisitions is consistently greater than the correlation between strain fields from repeat acquisitions in every subject, without exception. Hence the linear elastic modulus is a more repeatable characterization of tissue behavior. This may be due to the fact that the modulus contains extra information from the physical model that leads to greater repeatability, or it may be due to the fact that the modulus reconstruction is regularized and is thus smoother and less variable.
A third observation is that the correlations between nonlinearity distributions varied greatly. In many cases, correlations between nonlinearity were lower than those of strain and shear modulus, as might be expected as it is a noisier measurement. In some cases, however, nonlinearity correlation was higher. In those, the nonlinearity images showed little contrast and structure, and so high correlations were accidental. Finally, we note some cases where the nonlinearity correlation was very low (i.e. ≤ 0.6) despite the B-mode image correlation being quite high (≥ 0.9). All of these extreme outliers came from cases where the final measured strain was low (< 14%), and therefore are marked with an ×. In those cases, the tissue was not deformed enough to exhibit nonlinear behavior, and hence the nonlinearity parameter was not recovered accurately.
Finally, we note that Figure 2 shows that the correlation between modulus fields has a positive relationship with correlations between the respective B-mode images, with a few outliers. That is, greater similarity between the initial B-mode images leads to greater similarity between the moduli, and lower correlation between B-mode images implies lower correlation between the elastic fields. An illustration of this can be seen in Figure 3. Here the initial B-mode images are nearly identical and the reconstructed modulus distributions are also nearly identical. By contrast, Figure 7 shows an example in which the initial B-mode images are noticeably different, and consequently, the modulus reconstructions are also noticeably different. The differences in B-mode image suggest that the two acquisitions represent two slightly different regions of tissue. Consequently, the elasticity maps show properties of slightly different regions of tissue and are therefore themselves slightly different from each other. Finally, we note that there are a few cases in which B-mode images of distinct masses show relatively high correlations; we ascribe this to coincidence. The fact that the correlation between elastic fields is low in these cases demonstrates that the elastic fields show information not contained in the B-mode images. It is possible that a different image similarity metric would be able to identify the general similarities present between B-mode images of breast masses.
The present study on repeatability of NEM imaging provides a necessary step toward evaluating NEM on a larger cohort of subjects. Because imaging large deformations in vivo is much more challenging than doing so in phantoms, it was necessary to do such a repeatability study with human subjects. Finally, the results here provide some assurance that if the same region of tissue is imaged twice, the same material parameter maps will result. The NEM mapping capability used here is currently implemented at only one site, and therefore inter-site variability was not considered. Furthermore, interobserver variability was not evaluated.
The study here has a number of limitations. First, our focus is on the repeatability inherent in linear and nonlinear elasticity mapping. Thus efforts were made to diminish all other contributions to variability. For example, we neglect inter-observer variability, inter-site variability, and by registering our B-mode images, we diminish variability due to ROI targeting. Second, image correlation fails to acknowledge similarity between images that share similar features and thus be similar enough for clinical practice. Figure 7 shows an example where certain similar features are discernible, but the correlations between the corresponding images is low. Image correlation was chosen here because it is applicable independent of the features being compared, and since clinically relevant features of nonlinear elasticity images have yet to be identified.
V. Conclusions
In this study, repeatability of modulus image reconstructions was evaluated through a correlation metric. Correlation was found to be an adequate measure of repeatability as the correlation between reconstructions obtained from repeat acquisitions was consistently higher than the correlation between reconstructions from distinct subjects.
Overall with few exceptions, when the same region of tissue was imaged (defined as having a B-mode image correlation of greater than 0.9), the shear modulus reconstructions had a correlation of greater than 0.9. This shows the repeatability of the shear modulus reconstructions. The repeatability of the nonlinearity reconstructions was lower, but still typically above 0.8, provided a final strain > 14% is available in the data and used in the reconstruction. Correlation between B-mode image similarity and elasticity image similarity was statistically significant under these conditions.
We conclude that linear elastic shear modulus images may be repeatably recovered, and nonlinearity may be repeatably measured provided a final strain greater than 14% is used in the acquisition and reconstruction. Results of this study pave the way for the nonlinear elastography mapping as a modality for breast cancer applications.
Acknowledgements
The authors would like to thank Ms. C. Andrist for recruiting patients. Authors also thank Mr. Duane Meixner for scanning patients, Ms. Adriana Gregory and Mr. Jeremy Webb for assistance with data collection, and Mr. Mark Barbone for assistance with statistical analysis. This work was supported by the National Institutes of Health, grant R01 CA195527.
Footnotes
Recall that is recovered only up to a multiplicative constant. That is, in the forward model (3-5), a guess of shear modulus and a guess of shear modulus times that, , gives identical predicted displacement. Since , subtracting a constant from the is equivalent to multiplying the original shear modulus by . Furthermore, should be recognized to be a Jeffrey’s parameter [59], which is appropriately measured through its logarithm.
For example, a sufficiently high regularization will yield a homogeneous reconstructed field regardless of the data, and thus be highly “repeatable.”
Contributor Information
Daniel I. Gendin, Boston University, Boston, MA 02215 USA
Rohit Nayak, Department of Radiology, Mayo Clinic College of Medicine and Science, Rochester, MN, 55905, USA.
Yuqi Wang, University of Wisconsin, Madison, WI 53705 USA.
Mahdi Bayat, Mayo Clinic College of Medicine and Science, Rochester, MN. Currently, he is with the Department of Electrical Engineering and Computer Science, Case Western Reserve University.
Robert T. Fazzio, Department of Radiology, Mayo Clinic College of Medicine and Science, Rochester, MN, 55905, USA
Assad A. Oberai, University of Southern California, Los Angeles, CA 90089 USA
Timothy J. Hall, University of Wisconsin, Madison, WI 53705 USA.
Paul E. Barbone, Boston University, Boston, MA 02215 USA
Azra Alizad, Department of Radiology, Mayo Clinic College of Medicine and Science, Rochester, MN, 55905, USA, University of Southern California, Los Angeles, CA 90089 USA.
Mostafa Fatemi, Department of Physiology and Biomedical Engineering, Mayo Clinic College of Medicine and Science, Rochester, MN, 55905, USA.
References
- [1].Qiu Y, Sridhar M, Tsou JK, Lindfors KK, and Insana MF, “Ultrasonic viscoelasticity imaging of nonpalpable breast tumors: preliminary results,” Academic Radiology, vol. 15, no. 12, pp. 1526–1533, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Moinfar F, Man YG, Arnould L, Bratthauer GL, Ratschek M, and Tavassoli FA, “Concurrent and independent genetic alterations in the stromal and epithelial cells of mammary carcinoma: implications for tumorigenesis,” Cancer Research, vol. 60, no. 9, pp. 2562–2566, 2000. [PubMed] [Google Scholar]
- [3].Sarvazyan AP, “Elastic properties of soft tissue,” in Handbook of elastic properties of solid, liquid and gases - Vol III: Elastic properties of solids: Biological and organical materials, earth and marine sciences, Levy Bass, and Stern, Eds. New York: Academic, 2001, ch. 5. [Google Scholar]
- [4].Krouskop TA, Wheeler TM, Kallel F, Garra BS, and Hall T, “Elastic moduli of breast and prostate tissues under compression,” Ultrasonic Imaging, vol. 20, no. 4, pp. 260–274, 1998. [DOI] [PubMed] [Google Scholar]
- [5].Berg WA et al. , “Shear-wave elastography improves the specificity of breast US: the BE1 multinational study of 939 masses,” Radiology, vol. 262, no. 2, pp. 435–449, 2012. [DOI] [PubMed] [Google Scholar]
- [6].Mariappan YK, Glaser KJ, and Ehman RL, “Magnetic resonance elastography: a review,” Clinical Anatomy, vol. 23, no. 5, pp. 497–511, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Sinkus R, Lorenzen J, Schrader D, Lorenzen M, Dargatz M, and Holz D, “High-resolution tensor MR elastography for breast tumour detection,” Physics in Medicine & Biology, vol. 45, no. 6, p. 1649, 2000. [DOI] [PubMed] [Google Scholar]
- [8].McKnight AL, Kugel JL, Rossman PJ, Manduca A, Hartmann LC, and Ehman RL, “MR elastography of breast cancer: preliminary results,” American Journal of Roentgenology, vol. 178, no. 6, pp. 1411–1417, 2002. [DOI] [PubMed] [Google Scholar]
- [9].Lorenzen J, Sinkus R, and Adam G, “Elastography: Quantitative imaging modality of the elastic tissue properties,” RoFo: Fortschritte auf dem Gebiete der Rontgenstrahlen und der Nuklearmedizin, vol. 175, no. 5, pp. 623–630, 2003. [DOI] [PubMed] [Google Scholar]
- [10].Sinkus R, Siegmann K, Xydeas T, Tanter M, Claussen C, and Fink M, “MR elastography of breast lesions: understanding the solid/liquid duality can improve the specificity of contrast-enhanced MR mammography,” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1135–1144, 2007. [DOI] [PubMed] [Google Scholar]
- [11].Ginat DT, Destounis SV, Barr RG, Castaneda B, Strang JG, and Rubens DJ, “US elastography of breast and prostate lesions,” Radiographics, vol. 29, no. 7, pp. 2007–2016, 2009. [DOI] [PubMed] [Google Scholar]
- [12].Garra BS et al. , “Elastography of breast lesions: initial clinical results.” Radiology, vol. 202, no. 1, pp. 79–86, 1997. [DOI] [PubMed] [Google Scholar]
- [13].Yoon JH, Kim MH, Kim E-K, Moon HJ, Kwak JY, and Kim MJ, “Interobserver variability of ultrasound elastography: how it affects the diagnosis of breast lesions,” American Journal of Roentgenology, vol. 196, no. 3, pp. 730–736, 2011. [DOI] [PubMed] [Google Scholar]
- [14].Scaperrotta G. et al. , “Role of sonoelastography in non-palpable breast lesions,” European Radiology, vol. 18, no. 11, pp. 2381–2389, 2008. [DOI] [PubMed] [Google Scholar]
- [15].Barr RG, “Real-time ultrasound elasticity of the breast: initial clinical results,” Ultrasound Quarterly, vol. 26, no. 2, pp. 61–66, 2010. [DOI] [PubMed] [Google Scholar]
- [16].Cho N, Moon WK, Kim HY, Chang JM, Park SH, and Lyou CY, “Sonoelastographic strain index for differentiation of benign and malignant nonpalpable breast masses,” Journal of Ultrasound in Medicine, vol. 29, no. 1, pp. 1–7, 2010. [DOI] [PubMed] [Google Scholar]
- [17].Fatemi M and Greenleaf JF, “Application of radiation force in noncontact measurement of the elastic parameters,” Ultrasonic Imaging, vol. 21, no. 2, pp. 147–154, 1999. [DOI] [PubMed] [Google Scholar]
- [18].——, “Ultrasound-stimulated vibro-acoustic spectrography,” Science, vol. 280, no. 5360, pp. 82–85, 1998. [DOI] [PubMed] [Google Scholar]
- [19].Urban MW, Chalek C, Haider B, Thomenius KE, Fatemi M, and Alizad A, “A beamforming study for implementation of vibro-acoustography with a 1.75-d array transducer,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 60, no. 3, pp. 535–551, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Urban MW et al. , “Implementation of vibro-acoustography on a clinical ultrasound system,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 58, no. 6, pp. 1169–1181, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Alizad A. et al. , “Breast vibro-acoustography: initial experience in benign lesions,” BMC Medical Imaging, vol. 14, no. 1, p. 40, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Mehrmohammadi M. et al. , “Preliminary in vivo breast vibro-acoustography results with a quasi-2D array transducer: a step forward toward clinical applications,” Ultrasound in Medicine & Biology, vol. 40, no. 12, pp. 2819–2829, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Alizad A. et al. , “Breast vibro-acoustography: initial results show promise,” Breast Cancer Research, vol. 14, no. 5, p. R128, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Urban MW, Alizad A, Aquino W, Greenleaf JF, and Fatemi M, “A review of vibro-acoustography and its applications in medicine,” Current Medical Imaging Reviews, vol. 7, no. 4, pp. 350–359, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Alizad A, Whaley DH, Greenleaf JF, and Fatemi M, “Image features in medical vibro-acoustography: In vitro and in vivo results,” Ultrasonics, vol. 48, no. 6-7, pp. 559–562, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].——, “Critical issues in breast imaging by vibro-acoustography,” Ultrasonics, vol. 44, pp. e217–e220, 2006. [DOI] [PubMed] [Google Scholar]
- [27].——, “Potential applications of vibro-acoustography in breast imaging,” Technology in Cancer Research & Treatment, vol. 4, no. 2, pp. 151–157, 2005. [DOI] [PubMed] [Google Scholar]
- [28].Alizad A, Fatemi M, Wold LE, and Greenleaf JF, “Performance of vibro-acoustography in detecting microcalcifications in excised human breast tissue: A study of 74 tissue samples,” IEEE Transactions on Medical Imaging, vol. 23, no. 3, pp. 307–312, 2004. [DOI] [PubMed] [Google Scholar]
- [29].Fatemi M, Wold LE, Alizad A, and Greenleaf JF, “Vibro-acoustic tissue mammography,” IEEE Transactions on Medical Imaging, vol. 21, no. 1, pp. 1–8, 2002. [DOI] [PubMed] [Google Scholar]
- [30].Athanasiou A. et al. , “Breast lesions: quantitative elastography with supersonic shear imaging—preliminary results,” Radiology, vol. 256, no. 1, pp. 297–303, 2010. [DOI] [PubMed] [Google Scholar]
- [31].Chang JM et al. , “Clinical application of shear wave elastography (swe) in the diagnosis of benign and malignant breast diseases,” Breast Cancer Research and Treatment, vol. 129, no. 1, pp. 89–97, 2011. [DOI] [PubMed] [Google Scholar]
- [32].Cosgrove DO et al. , “Shear wave elastography for breast masses is highly reproducible,” European Radiology, vol. 22, no. 5, pp. 1023–1032, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Evans A. et al. , “Invasive breast cancer: relationship between shear-wave elastographic findings and histologic prognostic factors,” Radiology, vol. 263, no. 3, pp. 673–677, 2012. [DOI] [PubMed] [Google Scholar]
- [34].——, “Quantitative shear wave ultrasound elastography: initial experience in solid breast masses,” Breast Cancer Research, vol. 12, no. 6, p. R104, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Tanter M. et al. , “Quantitative assessment of breast lesion viscoelasticity: initial clinical results using supersonic shear imaging,” Ultrasound in Medicine & Biology, vol. 34, no. 9, pp. 1373–1386, 2008. [DOI] [PubMed] [Google Scholar]
- [36].Gweon HM, Youk JH, Son EJ, and Kim J-A, “Visually assessed colour overlay features in shear-wave elastography for breast masses: quantification and diagnostic performance,” European Radiology, vol. 23, no. 3, pp. 658–663, 2013. [DOI] [PubMed] [Google Scholar]
- [37].Evans A. et al. , “Differentiating benign from malignant solid breast masses: value of shear wave elastography according to lesion stiffness combined with greyscale ultrasound according to bi-rads classification,” British Journal of Cancer, vol. 107, no. 2, p. 224, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Barr RG, “Shear wave imaging of the breast: still on the learning curve,” Journal of Ultrasound in Medicine, vol. 31, no. 3, pp. 347–350, 2012. [DOI] [PubMed] [Google Scholar]
- [39].Barr RG and Zhang Z, “Effects of precompression on elasticity imaging of the breast: development of a clinically useful semiquantitative method of precompression assessment,” Journal of Ultrasound in Medicine, vol. 31, no. 6, pp. 895–902, 2012. [DOI] [PubMed] [Google Scholar]
- [40].Tozaki M and Fukuma E, “Pattern classification of shearwavetm elastography images for differential diagnosis between benign and malignant solid breast masses,” Acta Radiologica, vol. 52, no. 10, pp. 1069–1075, 2011. [DOI] [PubMed] [Google Scholar]
- [41].Youk JH, Gweon HM, Son EJ, Han KH, and Kim J-A, “Diagnostic value of commercially available shear-wave elastography for breast cancers: integration into bi-rads classification with subcategories of category 4,” European Radiology, vol. 23, no. 10, pp. 2695–2704, 2013. [DOI] [PubMed] [Google Scholar]
- [42].Lee SH et al. , “Differentiation of benign from malignant solid breast masses: comparison of two-dimensional and three-dimensional shearwave elastography,” European Radiology, vol. 23, no. 4, pp. 1015–1026, 2013. [DOI] [PubMed] [Google Scholar]
- [43].Lee EJ, Jung HK, Ko KH, Lee JT, and Yoon JH, “Diagnostic performances of shear wave elastography: which parameter to use in differential diagnosis of solid breast masses?” European Radiology, vol. 23, no. 7, pp. 1803–1811, 2013. [DOI] [PubMed] [Google Scholar]
- [44].Goenezen S. et al. , “Linear and nonlinear elastic modulus imaging: an application to breast cancer diagnosis,” IEEE Transactions on Medical Imaging, vol. 31, no. 8, pp. 1628–1637, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Oberai AA et al. , “Linear and nonlinear elasticity imaging of soft tissue in vivo: demonstration of feasibility,” Phys Med Biol, vol. 54, no. 5, pp. 1191–207, Mar 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Falzon G, Pearson S, and Murison R, “Analysis of collagen fibre shape changes in breast cancer,” Physics in Medicine & Biology, vol. 53, no. 23, p. 6641, 2008. [DOI] [PubMed] [Google Scholar]
- [47].Conklin MW et al. , “Aligned collagen is a prognostic signature for survival in human breast carcinoma,” The American Journal of Pathology, vol. 178, no. 3, pp. 1221–1232, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Provenzano PP et al. , “Collagen reorganization at the tumor-stromal interface facilitates local invasion,” BMC Medicine, vol. 4, no. 1, p. 38, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Nabavizadeh A. et al. , “Automated compression device for viscoelasticity imaging,” IEEE Transactions on Biomedical Engineering, vol. 64, no. 7, pp. 1535–1546, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Jiang J, Hall TJ, and Sommer AM, “A novel performance descriptor for ultrasonic strain imaging: A preliminary study,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 53, no. 6, pp. 1088–1102, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Chaturvedi P, Insana MF, and Hall TJ, “2-d companding for noise reduction in strain imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 45, no. 1, pp. 179–191, 1998. [DOI] [PubMed] [Google Scholar]
- [52].Wang Y. et al. , “Three-dimensional ultrasound elasticity imaging on an automated breast volume scanning system,” Ultrasonic Imaging, vol. 39, no. 6, pp. 369–392, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Wang Y, Jiang J, and Hall TJ, “A 3-d region-growing motion-tracking method for ultrasound elasticity imaging,” Ultrasound in Medicine & Biology, vol. 44, no. 8, pp. 1638–1653, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].O’Donnell M, Skovoroda AR, Shapo BM, and Emelianov SY, “Internal displacement and strain imaging using ultrasonic speckle tracking,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 41, no. 3, pp. 314—325, 1994. [Google Scholar]
- [55].Pesavento A, Perrey C, Krueger M, and Ermert H, “A time-efficient and accurate strain estimation concept for ultrasonic elastography using iterative phase zero estimation,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 46, no. 5, pp. 1057–1067, 1999. [DOI] [PubMed] [Google Scholar]
- [56].Vogel CR, Computational methods for inverse problems. SIAM, 2002, vol. 23. [Google Scholar]
- [57].Holzapfel G, Nonlinear Solid Mechanics: A Continuum Approach for Engineering. Wiley, 2000. [Google Scholar]
- [58].Veronda D and Westmann R, “Mechanical characterization of skin—finite deformations,” Journal of Biomechanics, vol. 3, no. 1, pp. 111–124, 1970. [DOI] [PubMed] [Google Scholar]
- [59].Tarantola A, Inverse problem theory and methods for model parameter estimation. SIAM, 2005. [Google Scholar]


