Optical coherence tomography for multicellular tumor spheroid category recognition and drug screening classification via multi-spatial-superficial-parameter and machine learning

Abstract

Optical coherence tomography (OCT) is an ideal imaging technique for noninvasive and longitudinal monitoring of multicellular tumor spheroids (MCTS). However, the internal structure features within MCTS from OCT images are still not fully utilized. In this study, we developed cross-statistical, cross-screening, and composite-hyperparameter feature processing methods in conjunction with 12 machine learning models to assess changes within the MCTS internal structure. Our results indicated that the effective features combined with supervised learning models successfully classify OVCAR-8 MCTS culturing with 5,000 and 50,000 cell numbers, MCTS with pancreatic tumor cells (Panc02-H7) culturing with the ratio of 0%, 33%, 50%, and 67% of fibroblasts, and OVCAR-4 MCTS treated by 2-methoxyestradiol, AZD1208, and R-ketorolac with concentrations of 1, 10, and 25 µM. This approach holds promise for obtaining multi-dimensional physiological and functional evaluations for using OCT and MCTS in anticancer studies.

1. Introduction

Multicellular tumor spheroids (MCTS) are widely used as an essential high-throughput and rapid in vitro research tool for cancer studies and the development of anticancer drugs. They closely simulate molecular, morphological, immunological, and functional aspects of in vivo tumors [1–3]. The study of clinical tumor characteristics and physiological gradients, including lactate accumulation, cell apoptosis, necrosis, ATP distribution, cell proliferation, glucose distribution, and oxygen gradients, has made significant progress with the development and application of MCTS [4–13]. Multiple imaging platforms, including phase-contrast, bright-field, and dark-field imaging, confocal and multiphoton microscopy, light sheet fluorescence microscopy, and fluorescence imaging, have been developed for the imaging and monitoring of MCTS [14–21]. However, limitations in these imaging modalities, such as limited penetration of fluorescence reagents and light, dye toxicity, and complex sample preparation, hinder advanced clinical studies of MCTS. Hence, optical coherence tomography (OCT) has been introduced to provide noninvasive, rapid, and real-time three-dimensional (3D) imaging for monitoring the morphology and microstructure of MCTS [22,23].

OCT can detect both microstructures and tissue distributions, and measure molecular and functional information in MCTS, therefore can provide detailed and accurate information. Previous studies have shown that OCT enables dynamic monitoring of the growth kinetics and morphology of in vivo tumors [22,24,25]. Specifically during the preclinical studies of new therapeutics, necrotic tissue formation and diffusion of drugs within spheroids can be tracked by calculating the scattered attenuation coefficient from OCT intensity images [23,24,26]. Recently, OCT has been used to calculate necrotic core, uniformity degree, and tumor tissue metabolism, enabling the monitoring of dynamic changes in spheroid morphology and internal tissues during the treatment of various drugs with different concentrations for anticancer drug screenings [25,27–29]. OCT observations of external shapes and internal tissues in MCTS can reveal real-time therapeutic effects and treatment cycles of drugs, aiding in the screening of targeted drugs. Despite the dynamic changes in spheroid morphology and tissue distribution, the differences among MCTS treated by drugs are not fully discernible through current analyses of microstructures and tissue distribution in spheroids, even though these changes provide valuable information for screening anticancer drugs. The use of OCT intensity images for extracting structural and physiological information to screen effective drugs remains limited, due to the lack of comprehensive and effective image analysis parameters, and appropriate classification methods. Therefore, the current critical need is to develop robust methods for extracting additional morphological and structural information from OCT intensity images to monitor therapeutic effects and screen anticancer drugs more effectively. Moreover, culturing MCTS with varying cell numbers and different cell types also leads to diverse internal structures and tissue distributions [2,30,31]. Noninvasive imaging modalities have not yet successfully captured these crucial differences and changes in MCTS. It is still uncertain whether OCT images can be used for noninvasive monitoring and distinguishing these internal differences.

To enhance the effectiveness of structural image analysis, various methods have been employed to extract morphological, physiological, and functional information by analyzing spatial structures and superficial distributions [32–39]. Particularly, roughness [34], morphology [36], and multiscale [37] texture analyses are commonly employed to extract superficial and spatial characteristics from intensity images for pattern recognition and image classification. This spatial and superficial information from images can reveal characteristic distributions and patterns that are not readily apparent in the original intensity structures. Spatial and surface feature analyses find broad applications in satellite and geological images, effectively extracting information on region distribution, object recognition, geological structures, and tectonics [40–47]. Due to the advantages of expanding image features through superficial and spatial parameters, some studies have showed that OCT images combined with multiple texture analyses can be used for tissue differentiation in diagnostics [48], retinal thickness classification [49], urinary bladder cancer recognition [50], ovarian tissue characterization [51], gastrointestinal tissues classification [52], oral carcinoma identification [53], skin layer segmentation and surface quantification [54,55], and inner surface assessment of dental crowns [56]. These superficial and spatial texture analyses extract additional statistical, structural, model-based, transform-based, modulation-based, and image-moments characteristic information for segmenting, classifying, and recognizing biological tissues, internal layers, and tumors [57]. Thus, we hypothesize that applying superficial and spatial parameters to OCT intensity images of MCTS can extract additional features of internal structures, allowing differentiation between cell cultures with varying cell numbers and types and facilitating the monitoring of therapeutic effects and the screening of anticancer drugs. Given the limitations of finite sample size and the extensive feature extractions required, the current challenge is to identify ideal methods for effectively screening features to classify MCTS significantly under varying cell numbers, cell types, and drug concentrations.

In this study, we scanned three categories of MCTS with varying cell numbers, cell types, and treatments using inhibitors of different concentrations, using a swept-source optical coherence tomography (SS-OCT) system. We employed a total of 27 texture and roughness parameters to extract 2484 superficial and spatial features from each OCT intensity image of MCTS. To extract effective superficial and spatial features, we employed three combined screening methods based on mathematical statistics, machine learning, and linear convolution to obtain features for MCTS classification. Using the effective superficial and spatial features, we employ six supervised classification models and six unsupervised clustering models to classify MCTS based on cell numbers, cell type mixtures, and diverse drug treatments. Our results showed an effective screening of superficial and spatial features for classifying MCTS based on cell numbers, cell type mixtures, and treatment of drugs with diverse concentrations. Our results also help identify effective machine learning models for classification in different categories of MCTS studies and enhance the highly comprehensive and accurate preclinical analysis for fast-forward and safe clinical translation of newly developed therapeutics.

2. Methods

2.1. Cell culture and drug treatment

MCTS containing mouse epithelial ovarian cancer cell line OVCAR-8, high-grade serous carcinoma cell line OVCAR-4, or pancreatic tumor cell line Panc02-H7 were cultured with different cell numbers, cell types, and diverse drug treatments. For different cell numbers, OVCAR-8 cells were cultured in round-bottom 96-well plates at 5,000 and 50,000 cells/well. Each group of cells (5,000 or 50,000) were cultured within 12 spheroids for a total of 10 days. The details of spheroid culturing and formation were described in our previous study [24]. For different cell types, tumor spheroids were formed using the ultra-low attachment technique. Briefly, round-bottom 96-well plates were treated with an anti-adherence rinsing solution and washed with basal media. Panc02-H7 and fibroblasts (3T3 cells) were then seeded with either 0%, 33% (2P:1F), 50% (1P:1F), or 67% (1P:2F) fibroblasts for a total of 5,000 cells per well in the treated microplates and centrifuged at 100 g for 3 minutes. After two days of culture, medium change was performed daily for a total of 10 days. A total of 15 spheroids per group were monitored for 10 days. For different drug treatments, OVCAR-4 cells (5,000 cells/well) were cultured in round-bottom 96-well plates and treated with either of the three FDA-approved inhibitors, 2-Methoxyestradiol (2-ME), R-ketorolac (R-ke), and the PIM inhibitor AZD1208 (AZD) at varying concentrations. There were nine treatment groups and one control group, with each group cultured 12 spheroids for a total of 10 days and treatment administered on day 5. The nine treatment groups were treated with inhibitors, including 2-ME, AZD, and R-ke, at concentrations of 1 µM, 10 µM, and 25 µM, respectively. The details of spheroid culturing, formation, and treatment were described in our previous study [25].

2.2. Swept-source optical coherence tomography scanning protocol

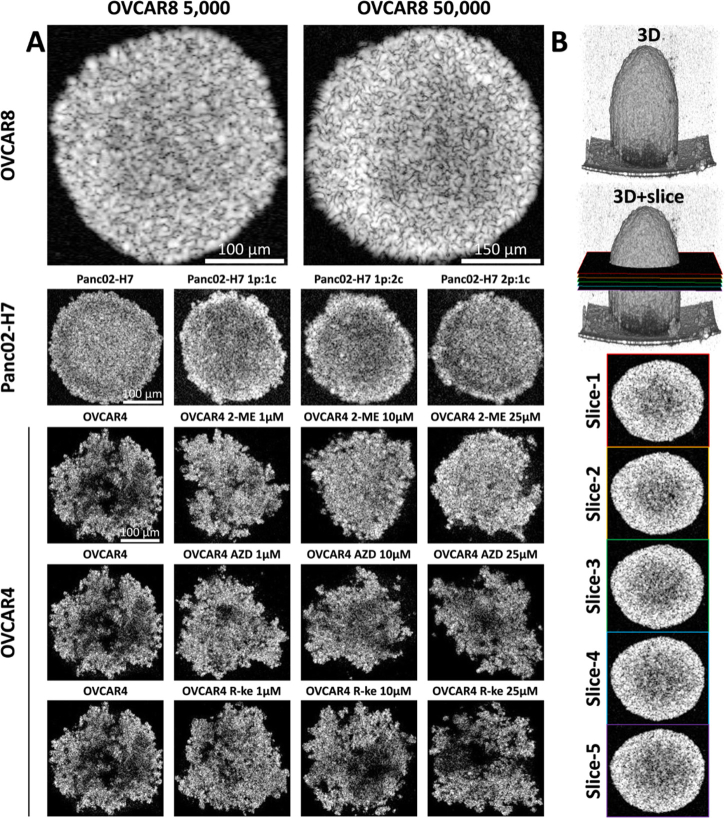
We used a swept-source optical coherence tomography (SS-OCT) system with a central wavelength of 1300 nm and a 100 nm full-width at half-maximum (FWHM) broadband spectrum to scan MCTS on day 10. The system (Fig. S1) offered an axial resolution of 14 µm and a lateral resolution of 20 µm in air, with a sensitivity of 98 dB at a wavelength-swept frequency of 200 kHz [58–60]. We used a 3 mm × 3 mm field of view (FOV) with a pixel count of 600 × 600, providing a sampling resolution of 5 µm × 5 µm, to cover the entire spheroid area. The imaging depth reached 2.6 mm with 1024 pixel counts, resulting in a sampling axial resolution of 2.5 µm. To maintain a sterile environment and prevent bacterial infections during OCT scanning, we constructed a custom-made SS-OCT scanner stage for imaging within the biosafety cabinet (Fig. S1). We selected five enface OCT intensity images at the center height of the spheroid, with a 20 µm height interval, and cropped the target area for data processing. The details and selections of OCT intensity images for different sample groups are shown in Fig. 1. In the end, we used 5 enface images of each spheroid for the following study, as shown in Fig. 1(B). We adjusted the intensity range to 30 to 90 dB to remove background noises for all OCT images before processing.

Fig. 1.

OCT images of different sample groups and the image selecting protocol. A, representative OCT intensity images of multicellular tumor spheroids culturing with different cell numbers, cell types, and treated by different drugs. B, the selection protocol of representative OCT images for data processing. 5 slices with 20 µm depth interval started at the middle height of the spheroid are selected as representative slices for data processing.

2.3. Spatial and superficial texture and roughness parameters

We used a total of 27 texture and roughness parameters, including statistical, structural, model-based, transform-based, modulation-based, and image-moments characterizations, to extract superficial and spatial features from OCT intensity images of MCTS under varying cell numbers, cell types, and different drug treatments [34,57,61–64]. With the 27 texture and roughness parameters, we extracted 2484 superficial and spatial features from each image. These parameters included: 1) Histogram (32 features), 2) Gray-Level Co-occurrence Matrix (GLCM, 28 features), 3) Local Binary Descriptors (LBP, 6 features), 4) Gray-Level Run Length Matrix (GLRLM, 10 features), 5) Histogram of Oriented Gradients (HOG, 4 features), 6) Gray Level Difference Statistics (GLDS, 5 features), 7) First-Order Statistics (FOS, 16 features), 8) Correlogram_ht (1024 features), 9) Correlogram_hd (1024 features), 10) Statistical Feature Matrices (SFM, 4 features), 11) Gray Level Size Zone Matrix (GLSZM, 14 features), 12) Shape-parameter (5 features), 13) Fractal Dimension Texture Analysis (FDTA, 6 features), 14) Gabor Pattern (GP, 4 features), 15) Wavelet Packets (WP, 126 features), 16) Discrete Wavelet Transform (DWT, 18 features), 17) Stroke Width Transform (SWT, 18 features), 18) Higher Order Spectra (HOS, 5 features), 19) Laws Texture Energy (LTE, 6 features), 20) Amplitude Modulation-Frequency Modulation (AMFM, 4 features), 21) Zero moments (25 features), 22) Hu moments (7 features), 23) Multilevel Binary Morphological Analysis (MultiBNA, 6 features), 24) Gray Scale Morphological Analysis (GSMA, 2 features), 25) thresholding adjacency statistics (TAS, 54 features), 26) multiregional (4 features), and 27) Roughness (26 features) parameters.

2.4. Feature screening and machine learning

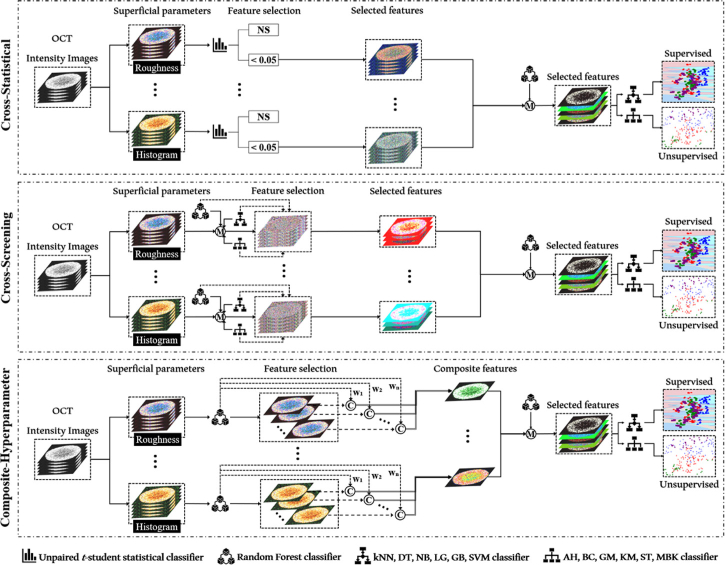
In this study, we developed three feature-processing methods (cross-statistical, cross-screening, and composite-hyperparameter) for screening effective features based on mathematical statistics, machine learning, and linear convolution. Figure 2 showed the framework of the three feature screening methods. 1) The cross-statistical method involved unpaired t-student tests among all MCTS groups to extract effective features (Fig. S2). Firstly, features from each of the 27 parameters with a p-value greater than 0.05 in the cross-statistics of all groups were considered effective features. After the first screening, the random forest model was used to determine the weight/importance of all selected features. To calculate the weight or importance of each feature, we used the entire feature dataset (100%) for training in the random forest model. We input all selected features from different categories into six supervised models (decision tree DT, k-nearest neighbor kNN, logistic regression LG, naïve Bayes NB, gradient boosting GB, and support vector machine SVM) and six unsupervised models (agglomerative AG, birch BC, Gaussian mixture GM, k-means K M, mini-batch k-means MBK, and spectral ST) to classify MCTS by group and category. In the end, we selected the features with the two largest weights to plot the two-dimensional (2D) distribution of MCTS classification and clustering. 2) In the cross-screening calculation, all features from each of the 27 parameters were input into the random forest model and 12 supervised and unsupervised models to obtain the weight/importance of each feature and assess the accuracy of classifications and clustering for different parameter categories. In the supervised models, we used 80% of the feature data for training and the remaining 20% for testing. We selected features with a weight/importance greater than 0.1 and corresponding features that achieved a prediction accuracy greater than 0.5 as the effective features (Fig. S3). Then all selected features were input into the random forest model and 12 machine learning models again to obtain their weight/importance and plot their classification and clustering distributions. 3) The composite-hyperparameter method was based on the random forest model and linear convolution to produce composite features corresponding to all texture and roughness parameters, as shown in Fig. S4. We input all superficial and spatial features into the random forest model to obtain the weight/importance of each feature. The composite feature was created through linear convolution between each feature and its corresponding weight/importance. Next, we input all composite features into the random forest model and 12 machine learning models to obtain their weight/importance and plot their classification and clustering distributions for different categories.

Fig. 2.

Overview of the cross-statistical, cross-screening, and composite-hyperparameter feature processing framework. NS, not significant. M, model prediction. C, convolution calculation. W, weight. DT, decision tree model. GB, gradient boosting model. kNN, k-nearest neighbor model. LG, logistics model. NB, naïve bayes model. SVM, support vector machine model. KM, k-means model. BC, birch model. AH, agglomerative hierarchical model. MBK, mini batch k-means model. ST, spectral model. GM, Gaussian mixture model.

2.5. Statistical analysis

We used precision, recall, F1-score, and receiver operating characteristic (ROC) curves to evaluate the supervised models’ performance. Higher values of precision, recall, and F1-score, ranging between 0 and 1, indicate a better classification performance [65]. A ROC curve closer to the top-left corner indicates better classification performance [65,66]. We utilized silhouette, homogeneity, completeness, and V-measure to assess the performance of unsupervised models. The evaluation values of silhouette, homogeneity, completeness, and V-measure range from -1 to 1, 0 to 1, 0 to 1, and 0 to 1, respectively. A value of -1 in silhouette indicates samples are assigned to the wrong clusters, a value of 0 indicates samples are close to the decision boundary, and a value of 1 indicates samples are far away from the neighboring clusters. Higher homogeneity values indicate greater similarity among samples within a cluster. Higher completeness values indicate that more similar samples are grouped together. A higher v_measure value indicates a better clustering partition of samples [67].

3. Results

3.1. Feature prescreening

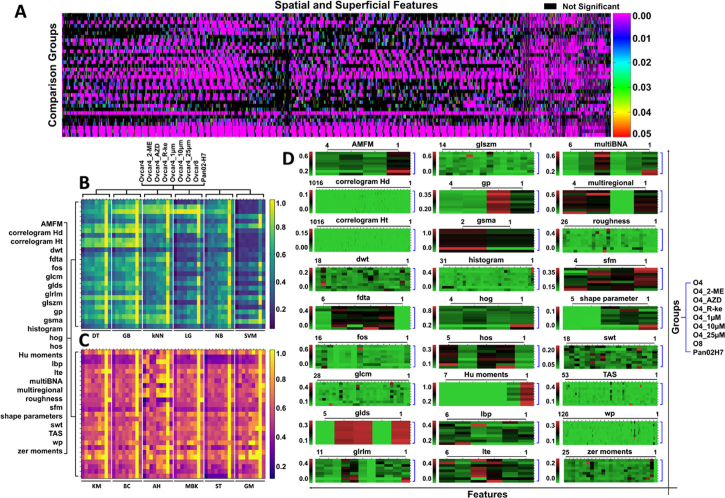
We applied mathematical statistics, machine learning, and linear convolution in superficial and spatial features of MCTS OCT images to provide the first-step feature selections for the classification of MCTS categories. For the cross-statistical method, there were 34 comparison groups in total from different MCTS categories and 2484 features were compared via the unpaired t-student test for each comparison group to obtain the p-value of each feature, the feature details were shown in Dataset 1 ^{(95.7KB, xlsx)} [68]. Figure 3(A) displays a heatmap of p-values less than 0.05 for features across various comparison groups, enabling us to assess the significance of differences in superficial and spatial features among different categories (Fig. S5). We found that most superficial and spatial features in OVCAR-8 and Panc02-H7 MCTS categories are significantly different, but the features with significant differences in different OVCAR-4 MCTS categories primarily gathered in Correlogram_hd_13_0 to Correlogram_hd_26_10 and GLDS to SWT parameters. These features with a p-value smaller than 0.05 were selected as effective features to further classify MCTS with machine learning models. For the cross-screening method, Fig. 3(B) and 3(C) showed the distribution of the classification accuracy of MCTS by six supervised models and six unsupervised models, respectively. We found that DT, GB, and kNN outperformed LG, NB, and SVM in supervised models, while AH achieved higher classification accuracy than KM, BC, MBK, ST, and GM in unsupervised models. Furthermore, all 12 machine learning models achieved high classification accuracy (>90%) for OVCAR-8 MCTS across most superficial and spatial parameters. The heatmap also revealed the performance of various parameters in MCTS classification using machine learning models. Parameters like Correlogram_hd and Correlogram_ht achieved high accuracies with GB, kNN, LG, and AH models but showed lower accuracies with SVM, KM, BC, MBK, ST, and GM models. The random forest model provided the weight/importance of each feature for classifying MCTS in each parameter, as shown in Fig. 3(D). The heatmap illustrates the distribution of feature weight/importance, indicating the performance of different features in classifying MCTS within each parameter. These filtered accuracies (>0.5, Fig. S6) and weight/importance (>0.1) were further applied to the following cross-screening algorithm to screen effective features for the classification of MCTS. For the composite-hyperparameter method, the weight/importance of each feature from the random forest model (Fig. 3(D)) was employed to multiply the corresponding feature value to gain a feature contribution value. In each superficial and spatial parameter, the sum of all feature contribution values (linear convolution) was utilized as the composite-hyperparameter value. The 27 composite-hyperparameter values of each OCT image were used for MCTS classification.

Fig. 3.

Heatmaps of texture & roughness parameters and superficial & spatial features processed by mathematical statistics and machine learning models for different MCTS categories. A, unpaired t-student statistics with p-value <0.05 of all features for the selection of effective features in the cross-statistical algorithm. The X-axis shows 2484 superficial and spatial features from 27 parameters. The specific feature orders and names are listed in Fig. S5 (order is from left to right) and Data File 1 (Ref. [68]). The Y-axis shows 34 groups of MCTS comparisons in cell number, cell type, and different drug treatment categories. The specific comparison among different groups in different categories is listed in Fig. S5. B, the accuracy of supervised models for MCTS classifications by superficial and spatial parameters. C, the accuracy of unsupervised models for MCTS classifications by superficial and spatial parameters. Six supervised and six unsupervised models are used to classify nine MCTS categories by 27 texture and roughness parameters. The filtered heatmap (accuracy >0.5) in Fig. S6 illustrates the texture and roughness parameters contributing to the effective classification of MCTS categories across the 12 machine learning models. D, the weight/importance of features in superficial and spatial parameters for the cross-screening and composite-hyperparameter algorithms. The X-axis indicates the features within the parameters and the details are listed in Fig. S5 (order is from right to left). DT, decision tree model. GB, gradient boosting model. kNN, k-nearest neighbor model. LG, logistics model. NB, naïve bayes model. SVM, support vector machine model. KM, k-means model. BC, birch model. AH, agglomerative hierarchical model. MBK, mini batch k-means model. ST, spectral model. GM, Gaussian mixture model. O4, OVCAR-4 MCTS. O4_2-ME, OVCAR-4 MCTS treated by 2-ME with 1 µM, 10 µM, and 25 µM concentrations. O4_AZD, OVCAR-4 MCTS treated by AZD with 1 µM, 10 µM, and 25 µM concentrations. O4_R-ke, OVCAR-4 MCTS treated by R-ke with 1 µM, 10 µM, and 25 µM concentrations. O4_1 µM, OVCAR-4 MCTS treated with 1 µM 2-ME, AZD, and R-ke drugs. O4_10 µM, OVCAR-4 MCTS treated with 10 µM 2-ME, AZD, and R-ke drugs. O4_25 µM, OVCAR-4 MCTS treated with 25 µM 2-ME, AZD, and R-ke drugs. O8, OVCAR-8 MCTS with 5,000 and 50,000 cell numbers. Pan02H7, Panc02-H7 MCTS with different ratio mixtures of fibroblasts.

3.2. Varying cell numbers MCTS classification

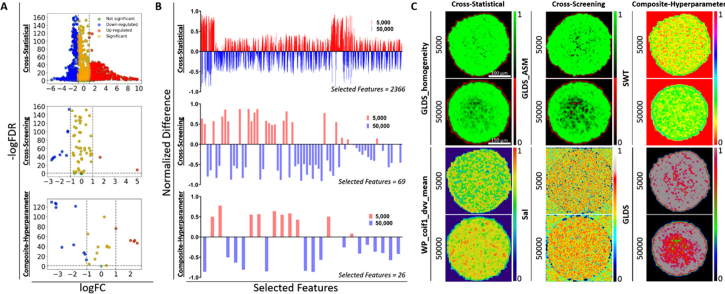
We initially applied three feature-processing methods to classify tissue properties within OVCAR-8 tumor spheroids cultured with varying cell numbers. Figure 4(A) showed the classification accuracy of all machine learning models (supervised + unsupervised) using the three feature-processing methods. We observed that all models achieved 100% accuracy except for NB and ST in the cross-statistical. We further provided the feature distribution map for each machine learning model and the ROC curve for supervised models to exhibit the classification performance, as shown in Fig. 4(B)–4(D). In the cross-statistical, cross-screening, and composite-hyperparameter approaches, all machine learning models except for the ST model successfully distinguished between tumor spheroids with 5,000 and 50,000 cell numbers using selected features, achieving a ROC value of 1.00 for each supervised model. Table 1 showed the performance evaluation of machine learning models. Only NB and ST models in cross-statistical have not completely classified samples. Among the three feature processing methods, the composite-hyperparameter was the most effective in ensuring that samples were far away from neighboring clusters, as indicated by the silhouette score. We exhibited the difference distribution of superficial and spatial features and Fig. 5 showed the representative feature figures. We employed volcano plots to assess the significance and magnitude of differences (Fig. 5(A)). Most features in the three processing methods exhibited significant differences, with some displaying large magnitudes of difference. Figure 5(B) depicted the relative differences in selected features after normalization, providing a visualization of the feature distinctions between 5,000 and 50,000 OVCAR-8 MCTS. 5,000 MCTS exhibited higher values in more selected superficial features compared to 50,000 MCTS in the cross-statistical. In the cross-screening and composite-hyperparameter, 50,000 MCTS exhibited higher values at more selected features compared to 5,000 MCTS. Figure 5(C) displayed the representative top two weighted features within the three feature processing methods. In the cross-statistical, 5,000 MCTS showed higher GLDS_homogeneity but lower WP_coif1_dvv_mean compared to 50,000 MCTS. In the cross-screening, 5,000 MCTS was higher in the GLDS_ASM but lower Sal than that of 50,000 MCTS. 5,000 MCTS exhibited lower SWT but higher GLDS compared to 50,000 MCTS in the composite-hyperparameter.

Fig. 4.

Performance of machine learning models in OVCAR-8 MCTS classifications. A, histogram of the accuracy of machine learning models. B, model evaluation and classification performance of the cross-statistical. C, model evaluation and classification performance of the cross-screening. D, model evaluation and classification performance of the composite-hyperparameter. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

Table 1. Performance of machine learning models in OVCAR-8 MCTS classifications. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	1.00	1.00	1.00	1.00	0.93	1.00	1.00	1.00	1.00	1.00	1.00	0.52
Precision	1.00	1.00	1.00	1.00	0.94	1.00	/	/	/	/	/	/
Recall	1.00	1.00	1.00	1.00	0.93	1.00	/	/	/	/	/	/
F1-score	1.00	1.00	1.00	1.00	0.93	1.00	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.44	0.44	0.44	0.44	0.44	0.05
Homogeneity	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	0.03
Completeness	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	0.15
V_meaure	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	0.04
Cross_Screening
Accuracy	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Precision	1.00	1.00	1.00	1.00	1.00	1.00	/	/	/	/	/	/
Recall	1.00	1.00	1.00	1.00	1.00	1.00	/	/	/	/	/	/
F1-score	1.00	1.00	1.00	1.00	1.00	1.00	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.70	0.70	0.70	0.70	0.70	0.70
Homogeneity	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	1.00
Completeness	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	1.00
V_meaure	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	1.00
Composite_Hyperparameter
Accuracy	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Precision	1.00	1.00	1.00	1.00	1.00	1.00	/	/	/	/	/	/
Recall	1.00	1.00	1.00	1.00	1.00	1.00	/	/	/	/	/	/
F1-score	1.00	1.00	1.00	1.00	1.00	1.00	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.72	0.72	0.72	0.72	0.72	0.72
Homogeneity	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	1.00
Completeness	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	1.00
V_meaure	/	/	/	/	/	/	1.00	1.00	1.00	1.00	1.00	1.00

Fig. 5.

The statistics and difference of superficial and spatial features in OVCAR-8 MCTS. A, volcano plot of the difference among selected features. B, the normalized difference of selected features in the cross-statistical, cross-screening, and composite-hyperparameter. C, the representative images of the first two highest weight features of OVCAR-8 MCTS with different cell numbers in the cross-statistical, cross-screening, and composite-hyperparameter.

3.3. Varying cell types mix-culture MCTS classification

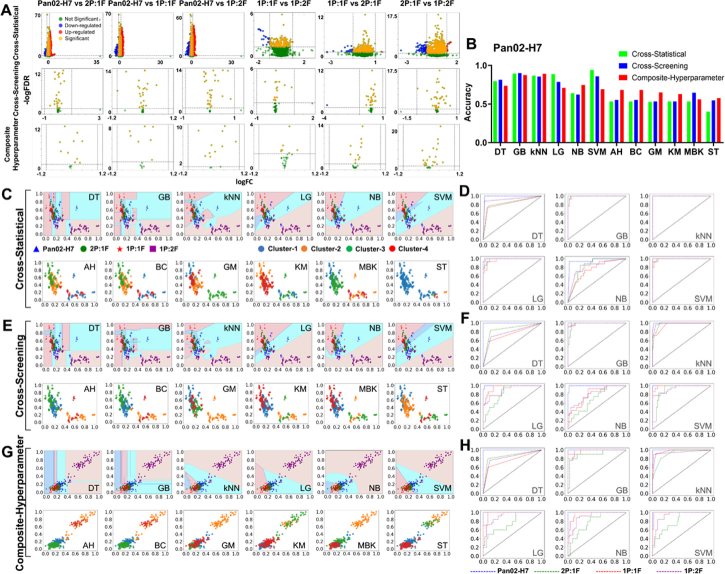
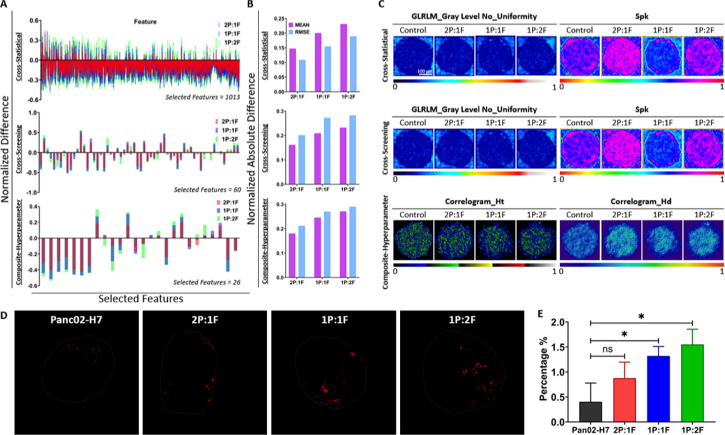
To explore the internal characterization of mix-culture MCTS of tumor cells and fibroblasts, we cultured MCTS using various mixture ratios of these cells and applied superficial features and machine learning to observe their properties. We mixed Panc02-H7 cells with fibroblasts at various ratios (0%, 33% 2P:1F, 50% 1P:1F, 67% 1P:2F) to culture spheroids with a total of 5,000 cells. Figure 6(A) showed the classification results among different mixing ratios of MCTS. In the cross-statistical, cross-screening, and composite-hyperparameter, most superficial and spatial features in mixing MCTS exhibited significant differences from those in Panc02-H7 MCTS. Some features also exhibited a large difference magnitude between mixing MCTS and Panc02-H7 MCTS. However, among different mixing groups, fewer features exhibited significant differences, and the differences were smaller in magnitude. Figure 6(B) and Table 2 showed the accuracy and performance evaluation of machine learning models for MCTS classification. We noticed that supervised models achieved higher classification accuracies than unsupervised models. Particularly, SVM, GB, and kNN achieved the highest classification accuracies (> 62%) in the cross-statistical, cross-screening, and composite-hyperparameter, respectively. Among unsupervised models, the composite-hyperparameter feature processing yielded the highest classification accuracies (> 56%), except for the MBK model. Figure 6(C)–6 H showed the model evaluation and classification of machine learning models with the ROC curves of corresponding supervised models. We observed significant classification differences between mixing MCTS with 1P:1F and 1P:2F ratios and Panc02-H7 MCTS using machine learning models. Additionally, Panc02-H7 MCTS without fibroblasts achieved the highest classification performance among all machine learning models, as evident from the ROC curves in the cross-statistical, cross-screening, and composite-hyperparameter. Figure 6(D), 6(F), and 6 H showed that GB and kNN models were the most stable and robust models for classifying Panc02-H7 MCTS in the cross-statistical, cross-screening, and composite-hyperparameter analyses. While SVM achieved the highest accuracy in the cross-statistical analysis, its classification accuracy and ROC values in the cross-screening and composite-hyperparameter analyses were lower. Additionally, we calculated the normalization difference between Panc02-H7 MCTS and the mixing MCTS with diverse ratios. Figure 7(A)–7(B) and Fig. S7 exhibited that increasing the ratio of fibroblasts within MCTS results in larger feature differences. The MEAN and RMSE values indicated that a higher fibroblast ratio within MCTS leads to larger absolute differences compared to Panc02-H7 MCTS. We provided representative images of the top two highest-weighted features in the three feature processing methods, as shown in Fig. 7(C). GLRLM_Gray Level No_Uniformity and Spk were the two features with the highest weights for classifying MCTS with different drug treatments in the cross-statistical and cross-screening. In the Spk images, we found that MCTS with 33% and 67% fibroblasts showed higher Spk values but MCTS with 50% fibroblasts showed lower Spk values. In the composite-hyperparameter, Correlogram_Ht and Correlogram_Hd were the first two weights of selected features and exhibited obvious changes compared to Panc02-H7 MCTS. Particularly, MCTS with 33% and 67% fibroblasts showed higher feature values than that of 50% fibroblasts MCTS. The confocal auto-fluorescence imaging of Panc02-H7 MCTS revealed an increased collagen formation due to the presence of fibroblasts, as depicted in Fig. 7(D). In the case of a lower fibroblast ratio (2P:1F), collagen predominantly accumulated at the outer layer of MCTS, whereas with a higher fibroblast ratio (1P:2F), collagen was observed to form within the central region. As the ratio of fibroblasts within MCTS increased, a greater amount of collagen was produced within MCTS (Fig. 7(E)). In contrast to the control Panc02-H7 MCTS, the mixed-culture MCTS with fibroblasts exhibited significantly higher collagen levels at the 50% and 67% ratios.

Fig. 6.

Performance of machine learning models in Panc02-H7 MCTS classifications. A, volcano plot of the difference among selected features. B, histogram of the accuracy of machine learning models. C&D, model evaluation and classification performance of the cross-statistical. E&F, model evaluation and classification performance of the cross-screening. G&H, model evaluation and classification performance of the composite-hyperparameter. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral. 2P:1F, 67% Panc02-H7 cells and 33% fibroblasts. 1P:1F, 50% Panc02-H7 cells and 50% fibroblasts. 1P:2F, 33% Panc02-H7 cells and 67% fibroblasts.

Table 2. Performance of machine learning models in Panc02-H7 MCTS classifications. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	0.80	0.89	0.87	0.89	0.64	0.94	0.53	0.53	0.53	0.53	0.53	0.40
Precision	0.80	0.90	0.88	0.90	0.66	0.95	/	/	/	/	/	/
Recall	0.80	0.89	0.87	0.89	0.64	0.94	/	/	/	/	/	/
F1-score	0.80	0.89	0.87	0.89	0.64	0.94	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.18	0.18	0.11	0.18	0.18	0.40
Homogeneity	/	/	/	/	/	/	0.27	0.27	0.25	0.25	0.25	0.16
Completeness	/	/	/	/	/	/	0.36	0.36	0.26	0.33	0.33	0.49
V_meaure	/	/	/	/	/	/	0.31	0.31	0.25	0.29	0.29	0.24
Cross_Screening
Accuracy	0.82	0.90	0.85	0.79	0.62	0.86	0.55	0.55	0.53	0.53	0.65	0.55
Precision	0.83	0.91	0.87	0.80	0.68	0.87	/	/	/	/	/	/
Recall	0.82	0.90	0.85	0.79	0.62	0.86	/	/	/	/	/	/
F1-score	0.82	0.90	0.85	0.79	0.62	0.86	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.23	0.23	0.23	0.24	0.20	0.22
Homogeneity	/	/	/	/	/	/	0.29	0.29	0.25	0.25	0.42	0.26
Completeness	/	/	/	/	/	/	0.38	0.38	0.32	0.33	0.42	0.34
V_meaure	/	/	/	/	/	/	0.33	0.33	0.28	0.29	0.42	0.30
Composite_Hyperparameter
Accuracy	0.77	0.87	0.89	0.71	0.75	0.77	0.68	0.68	0.65	0.63	0.56	0.58
Precision	0.79	0.88	0.88	0.72	0.77	0.78	/	/	/	/	/	/
Recall	0.77	0.87	0.89	0.71	0.75	0.77	/	/	/	/	/	/
F1-score	0.77	0.87	0.88	0.70	0.75	0.77	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.25	0.25	0.19	0.27	0.25	0.25
Homogeneity	/	/	/	/	/	/	0.52	0.52	0.46	0.46	0.35	0.32
Completeness	/	/	/	/	/	/	0.67	0.67	0.48	0.59	0.46	0.42
V_meaure	/	/	/	/	/	/	0.58	0.58	0.47	0.52	0.40	0.36

Fig. 7.

The statistics and difference of superficial and spatial features in Panc02-H7 MCTS. A, the normalized difference of selected features in the cross-statistical, cross-screening, and composite-hyperparameter. B, the absolute difference of selected features in the cross-statistical, cross-screening, and composite-hyperparameter. C, the representative images of the first two highest weight features of Panc02-H7 MCTS in the cross-statistical, cross-screening, and composite-hyperparameter. RMSE, root mean square error. D, the distribution of collagen within Panc02-H7 MCTS with different ratios of fibroblasts using confocal auto-fluorescence imaging. E, the comparison of collagen percentage within MCTS among different groups.

3.4. Varying drug treatments with diverse concentrations MCTS classification

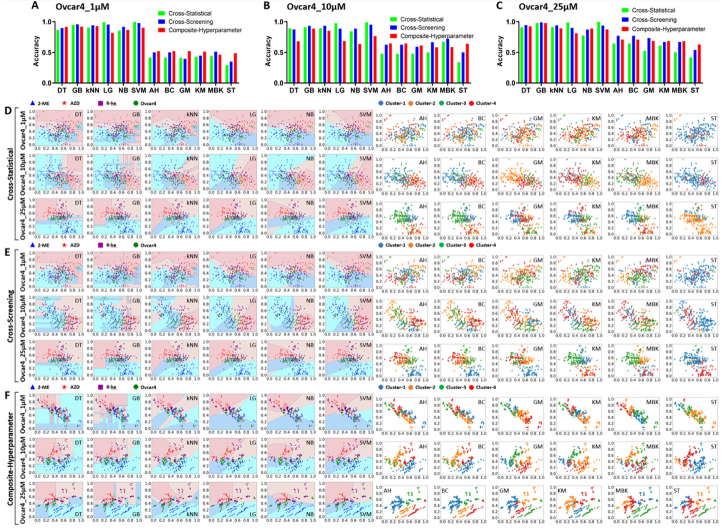
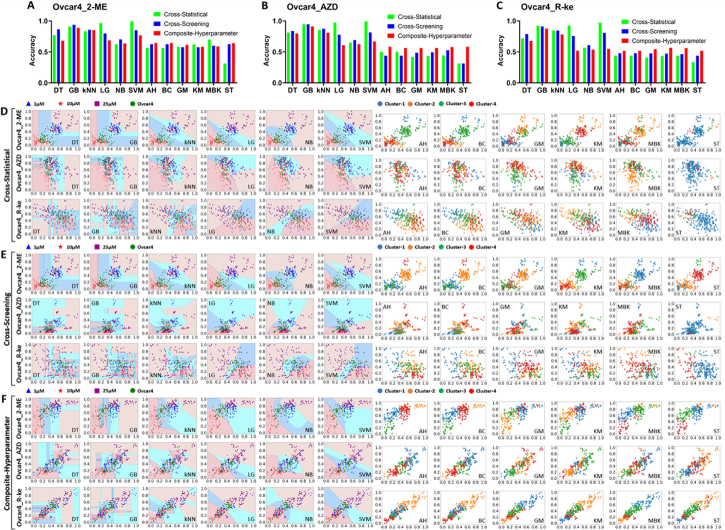
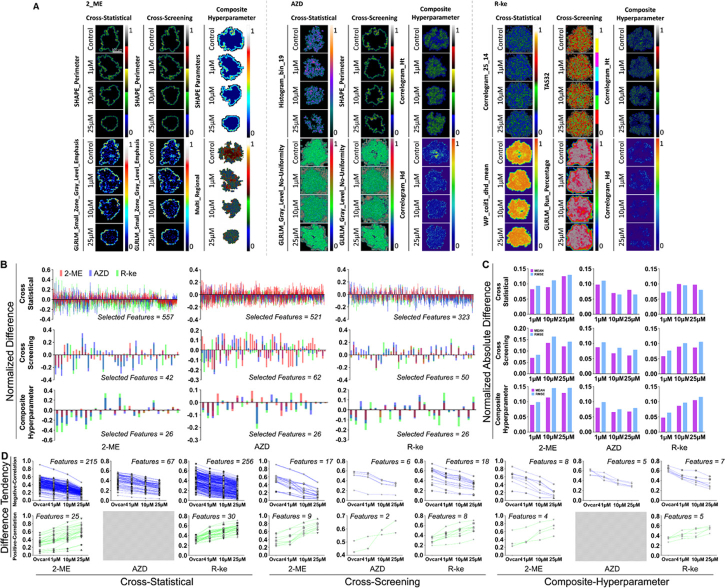
To investigate the anti-cancer therapeutic effects and repurposing potential of FDA-approved drugs, we used machine learning on superficial and spatial features from OCT intensity images to observe and classify tissue changes within OVCAR-4 MCTS after various drug treatments and concentrations. Figure 8 showed the accuracy and classification performance of machine learning models for classifying MCTS treated with drugs (2-ME, AZD, R-ke) at the same concentrations. Significance, magnitude of differences, and machine learning model performance evaluation are presented in Tables 3,4,5, Fig. S8 and Fig. S9. We found that supervised models had an overall higher accuracy than that of unsupervised models in Fig. 8(A)–8(C). LG and SVM models displayed high accuracies in the cross-statistical and cross-screening analyses with all these three concentrations, but their accuracy was relatively lower in the composite-hyperparameter analysis. GB and kNN models consistently achieved high accuracies across all three feature processing methods. Moreover, unsupervised models exhibited higher overall accuracies in the cross-screening and composite-hyperparameter analyses, with particularly noticeable improvements in accuracy for higher concentration drug treatments. Figure 8(D)–8(F) showed the classification performance of the top two highest-weighted features of machine learning models in the cross-statistical, cross-screening, and composite-hyperparameter analyses. We observed that LG and SVM models performed better in classifying OVCAR-4 MCTS treated with drugs at the same concentration. GB and kNN models demonstrated superior classification performance across all three feature processing methods, as depicted in Fig. S9. Additionally, we visualized the top two highest-weighted features for classifications (Fig. 9(A)), and SWT_bior_3.3_level_2_v_mean and TAS50 were the features used to classify MCTS treated with different drugs at a concentration of 1 µM in the cross-statistical and cross-screening analyses. TAS32 & WP_coif1_dhd_mean were the features for classifying MCTS treated with different drugs at a concentration of 10 µM in the cross-statistical analysis, while GLCM_Correlation_Range & GLRLM_Run_Percentage were used in the cross-screening. WP_coif1_daa_mean and SHAPE_Perimeter were the features used to classify MCTS treated with different drugs at a concentration of 25 µM in both the cross-statistical and cross-screening analyses. In the composite-hyperparameter analysis, GLRLM was the top-weighted feature in the classification under concentrations of 1, 10, and 25 µM. SWT was the second highest feature in the classification under the concentration of 1 µM, while Histogram held the second position in the classification under concentrations of 10 and 25 µM. Figure 9(B)–9(C) and Fig. S10 showed the normalized difference between OVCAR-4 MCTS and the different drug treatments under the same concentration. We zoomed in on the black-framed area labeled in Fig. 9(B) at a 1 µM concentration and displayed it in Fig. S8 and Fig. S9 to visualize the normalized difference of the last 20 features in the cross-statistical analysis. In the cross-statistical analysis, 1 µM AZD induced the largest difference in selected superficial and spatial features, while in the cross-screening and composite-hyperparameter analyses, 1 µM R-ke had the greatest impact on the selected features. In the cross-screening and composite-hyperparameter analyses, 2-ME induced the largest difference in selected superficial and spatial features at concentrations of 1, 10, and 25 µM.

Fig. 8.

Performance of machine learning models in OVCAR-4 MCTS with different drug treatment classifications. A, B, and C, histogram of the accuracy of machine learning models in OVCAR-4 MCTS with 1 µM, 10 µM, and 25 µM 2-ME, AZD, and R-ke. D, E, and F, classification performance of the cross-statistical, cross-screening, and composite-hyperparameter. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

Table 3. Performance of machine learning models in OVCAR-4 MCTS classifications with 1 µM drug treatments. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	0.86	0.95	0.91	0.99	0.86	1.00	0.42	0.42	0.41	0.43	0.44	0.29
Precision	0.88	0.96	0.92	0.99	0.87	1.00	/	/	/	/	/	/
Recall	0.87	0.95	0.91	0.99	0.86	1.00	/	/	/	/	/	/
F1-score	0.87	0.95	0.91	0.99	0.86	1.00	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.14	0.14	0.10	0.11	0.13	0.19
Homogeneity	/	/	/	/	/	/	0.13	0.14	0.12	0.16	0.12	0.03
Completeness	/	/	/	/	/	/	0.15	0.15	0.14	0.18	0.17	0.08
V_meaure	/	/	/	/	/	/	0.14	0.14	0.13	0.17	0.14	0.04
Cross_Screening
Accuracy	0.90	0.96	0.94	0.95	0.92	0.98	0.50	0.50	0.40	0.45	0.51	0.35
Precision	0.90	0.96	0.95	0.96	0.93	0.98	/	/	/	/	/	/
Recall	0.90	0.96	0.94	0.95	0.92	0.98	/	/	/	/	/	/
F1-score	0.90	0.96	0.94	0.95	0.92	0.98	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.11	0.11	0.14	0.14	0.10	0.18
Homogeneity	/	/	/	/	/	/	0.20	0.20	0.09	0.13	0.33	0.09
Completeness	/	/	/	/	/	/	0.26	0.26	0.13	0.16	0.42	0.27
V_meaure	/	/	/	/	/	/	0.22	0.22	0.10	0.14	0.37	0.14
Composite_Hyperparameter
Accuracy	0.89	0.93	0.92	0.88	0.85	0.93	0.52	0.52	0.52	0.51	0.46	0.49
Precision	0.90	0.94	0.93	0.89	0.87	0.94	/	/	/	/	/	/
Recall	0.89	0.93	0.92	0.88	0.85	0.93	/	/	/	/	/	/
F1-score	0.89	0.93	0.92	0.88	0.85	0.93	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.17	0.17	0.17	0.17	0.17	0.21
Homogeneity	/	/	/	/	/	/	0.32	0.32	0.28	0.26	0.15	0.33
Completeness	/	/	/	/	/	/	0.34	0.34	0.29	0.27	0.19	0.54
V_meaure	/	/	/	/	/	/	0.33	0.33	0.28	0.26	0.17	0.41

Table 4. Performance of machine learning models in OVCAR-4 MCTS classifications with 10 µM drug treatments. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	0.89	0.91	0.89	0.98	0.84	0.99	0.50	0.50	0.50	0.50	0.68	0.34
Precision	0.90	0.92	0.91	0.98	0.85	0.99	/	/	/	/	/	/
Recall	0.89	0.91	0.89	0.98	0.84	0.99	/	/	/	/	/	/
F1-score	0.89	0.91	0.89	0.98	0.84	0.99	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.13	0.13	0.14	0.14	0.10	0.07
Homogeneity	/	/	/	/	/	/	0.25	0.25	0.20	0.30	0.42	0.08
Completeness	/	/	/	/	/	/	0.36	0.35	0.42	0.42	0.43	0.20
V_meaure	/	/	/	/	/	/	0.30	0.30	0.27	0.35	0.42	0.11
Cross_Screening
Accuracy	0.88	0.93	0.93	0.89	0.89	0.95	0.63	0.63	0.59	0.67	0.72	0.50
Precision	0.89	0.94	0.94	0.90	0.90	0.96	/	/	/	/	/	/
Recall	0.88	0.93	0.93	0.89	0.89	0.95	/	/	/	/	/	/
F1-score	0.88	0.93	0.93	0.89	0.89	0.95	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.12	0.12	0.17	0.17	0.18	0.18
Homogeneity	/	/	/	/	/	/	0.41	0.40	0.44	0.47	0.54	0.35
Completeness	/	/	/	/	/	/	0.57	0.57	0.46	0.60	0.55	0.77
V_meaure	/	/	/	/	/	/	0.47	0.47	0.45	0.53	0.55	0.49
Composite_Hyperparameter
Accuracy	0.85	0.92	0.92	0.86	0.86	0.92	0.69	0.68	0.55	0.58	0.61	0.49
Precision	0.91	0.96	0.94	0.81	0.89	0.93	/	/	/	/	/	/
Recall	0.90	0.95	0.93	0.81	0.88	0.93	/	/	/	/	/	/
F1-score	0.90	0.95	0.93	0.81	0.88	0.93	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.14	0.14	0.14	0.19	0.12	0.21
Homogeneity	/	/	/	/	/	/	0.53	0.53	0.33	0.41	0.38	0.27
Completeness	/	/	/	/	/	/	0.70	0.69	0.43	0.44	0.51	0.39
V_meaure	/	/	/	/	/	/	0.60	0.60	0.37	0.42	0.44	0.32

Table 5. Performance of machine learning models in OVCAR-4 MCTS classifications with 25 µM drug treatments. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	0.91	0.98	0.91	0.99	0.78	1.00	0.65	0.65	0.53	0.61	0.50	0.42
Precision	0.91	0.98	0.92	0.99	0.80	1.00	/	/	/	/	/	/
Recall	0.91	0.98	0.91	0.99	0.78	1.00	/	/	/	/	/	/
F1-score	0.91	0.98	0.91	0.99	0.77	1.00	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.15	0.15	0.14	0.15	0.13	0.04
Homogeneity	/	/	/	/	/	/	0.40	0.40	0.26	0.35	0.27	0.10
Completeness	/	/	/	/	/	/	0.51	0.51	0.35	0.44	0.37	0.16
V_meaure	/	/	/	/	/	/	0.45	0.45	0.30	0.39	0.31	0.12
Cross_Screening
Accuracy	0.95	0.99	0.94	0.90	0.87	0.94	0.77	0.77	0.73	0.67	0.67	0.54
Precision	0.95	0.99	0.95	0.91	0.89	0.94	/	/	/	/	/	/
Recall	0.95	0.99	0.94	0.90	0.87	0.94	/	/	/	/	/	/
F1-score	0.95	0.99	0.94	0.90	0.87	0.94	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.18	0.18	0.19	0.22	0.22	0.19
Homogeneity	/	/	/	/	/	/	0.65	0.65	0.50	0.45	0.48	0.39
Completeness	/	/	/	/	/	/	0.66	0.66	0.52	0.58	0.62	0.70
V_meaure	/	/	/	/	/	/	0.66	0.66	0.51	0.51	0.54	0.50
Composite_Hyperparameter
Accuracy	0.90	0.95	0.93	0.81	0.88	0.93	0.71	0.71	0.69	0.69	0.68	0.63
Precision	0.91	0.96	0.94	0.81	0.89	0.93	/	/	/	/	/	/
Recall	0.90	0.95	0.93	0.81	0.88	0.93	/	/	/	/	/	/
F1-score	0.90	0.95	0.93	0.81	0.88	0.93	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.26	0.26	0.23	0.23	0.19	0.21
Homogeneity	/	/	/	/	/	/	0.58	0.58	0.48	0.48	0.45	0.45
Completeness	/	/	/	/	/	/	0.78	0.78	0.62	0.62	0.46	0.48
V_meaure	/	/	/	/	/	/	0.67	0.67	0.54	0.54	0.46	0.46

Fig. 9.

The statistics and difference of superficial and spatial parameters in OVCAR-4 MCTS with different drug treatments. A, the representative images of the first two highest weight features of OVCAR-4 MCTS in the cross-statistical, cross-screening, and composite-hyperparameter. RMSE, root mean square error. B, the normalized difference of selected features in the cross-statistical, cross-screening, and composite-hyperparameter. C, the absolute difference of selected features in the cross-statistical, cross-screening, and composite-hyperparameter.

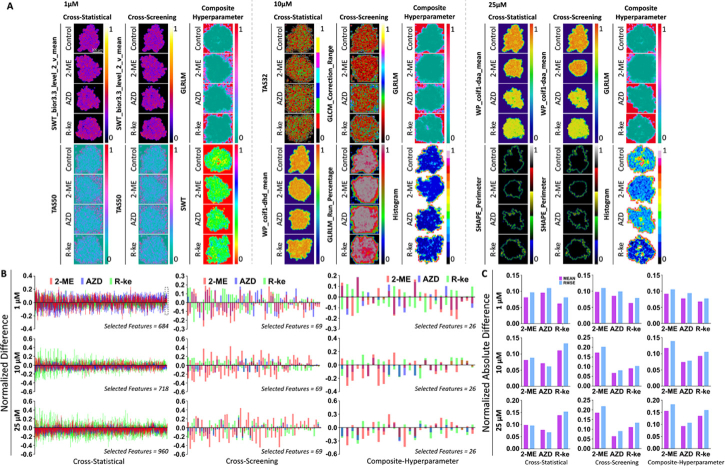
We further explored the difference of diverse concentrations (1, 10, and 25 µM) under the same drug treatment to OVCAR-4 MCTS. Fig. S11 displayed the significance and magnitude of differences at different concentrations from the same drug treatment in the cross-statistical, cross-screening, and composite-hyperparameter analyses. Figure 10(A)–10(C) and Fig. S12 showed that supervised models had overall higher accuracies of classifications than that of unsupervised models. LG and SVM models achieved high classification accuracies for different drugs at various concentrations in the cross-statistical analysis. GB and kNN models also demonstrated high classification accuracies for different drugs across all three feature processing methods. In unsupervised models, the composite-hyperparameter showed higher overall accuracies compared to the other two feature processing methods. Figure 10(D)–10(E) illustrated the classification performance of the top two highest-weighted features in the cross-statistical, cross-screening, and composite-hyperparameter analyses. With the performance evaluation of machine learning models in Table 6,7, and 8, we further confirmed that LG and SVM had high classification accuracies of OVCAR-4 MCTS with different concentration drug treatments in the cross-statistical, but GB had high classification accuracies for all three feature processing methods. In the 2-ME drug treatment, SHAPE_Perimeter and GLRLM_Small_Zone_Gray_Level_Emphasis were the top two features for classifying different concentration treatments in both the cross-statistical and cross-screening analyses. The SHAPE Parameter and Multi_Regional were the top two features for classification in the composite-hyperparameter, as depicted in Fig. 11(A). In the AZD drug treatment, Histogram_bin_19 & GLRLM_Gray_Level_No-Uniformity, SHAPE_Perimeter & GLRLM_Gray_Level_No-Uniformity, and Correlogram_Ht & Correlogram_Hd were the top two features for classification in the cross-statistical, cross-screening, and composite-hyperparameter analyses (Fig. 11(A)), respectively. In the R-ke drug treatment, Correlogram_25_14 & WP_coif1_dhd_mean, TAS32 & GLRLM_RUN_Percentage, and Correlogram_Ht & Correlogram_Hd were the top two features for classification in the cross-statistical, cross-screening, and composite-hyperparameter analyses, as depicted in Fig. 11(A). Figure 11(B)–11(C) and Fig. S13 revealed the normalized differences in selected features compared to the control MCTS. We observed that 2-ME in the cross-statistical and composite-hyperparameter analyses and R-ke in the cross-screening and composite-hyperparameter analyses resulted in larger differences at higher treatment concentrations. However, higher treatment concentrations of AZD resulted in smaller differences. Furthermore, we depicted the trend of differences with varying drug concentrations in Fig. 11(D). We selected features that showed an increasing or decreasing trend with the rising drug treatment concentration. Except for AZD in the cross-statistical and composite-hyperparameter analyses, there were features that exhibited significant increasing or decreasing trends in response to the increasing concentrations of 2-ME, AZD, and R-ke treatments.

Fig. 10.

Performance of machine learning models in OVCAR-4 MCTS with different concentration treatment classifications. A, B, and C, histogram of the accuracy of machine learning models in OVCAR-4 MCTS with 1 µM, 10 µM, and 25 µM. D, E, and F, classification performance of the cross-statistical, cross-screening, and composite-hyperparameter. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

Table 6. Performance of machine learning models in OVCAR-4 MCTS classifications with 2-ME inhibitor treatment. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	0.77	0.91	0.83	0.97	0.63	0.99	0.56	0.56	0.58	0.62	0.70	0.31
Precision	0.80	0.92	0.86	0.97	0.66	0.99	/	/	/	/	/	/
Recall	0.77	0.91	0.83	0.97	0.63	0.99	/	/	/	/	/	/
F1-score	0.77	0.91	0.84	0.97	0.61	0.99	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.11	0.11	0.15	0.15	0.14	0.22
Homogeneity	/	/	/	/	/	/	0.37	0.37	0.37	0.42	0.55	0.06
Completeness	/	/	/	/	/	/	0.51	0.51	0.42	0.45	0.56	0.33
V_meaure	/	/	/	/	/	/	0.42	0.42	0.39	0.44	0.55	0.11
Cross_Screening
Accuracy	0.86	0.94	0.86	0.80	0.70	0.85	0.63	0.63	0.58	0.58	0.60	0.63
Precision	0.87	0.94	0.88	0.81	0.73	0.86	/	/	/	/	/	/
Recall	0.86	0.94	0.86	0.80	0.70	0.85	/	/	/	/	/	/
F1-score	0.86	0.94	0.86	0.80	0.70	0.85	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.26	0.26	0.26	0.26	0.26	0.26
Homogeneity	/	/	/	/	/	/	0.55	0.55	0.51	0.45	0.48	0.51
Completeness	/	/	/	/	/	/	0.65	0.65	0.70	0.50	0.54	0.62
V_meaure	/	/	/	/	/	/	0.60	0.60	0.59	0.47	0.51	0.56
Composite_Hyperparameter
Accuracy	0.73	0.91	0.86	0.80	0.68	0.80	0.65	0.65	0.61	0.58	0.59	0.64
Precision	0.74	0.92	0.87	0.81	0.70	0.81	/	/	/	/	/	/
Recall	0.73	0.91	0.86	0.80	0.68	0.80	/	/	/	/	/	/
F1-score	0.73	0.91	0.86	0.79	0.68	0.79	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.29	0.29	0.32	0.32	.031	0.32
Homogeneity	/	/	/	/	/	/	0.50	0.50	0.50	.046	0.46	0.52
Completeness	/	/	/	/	/	/	0.54	0.54	0.55	0.50	0.50	0.61
V_meaure	/	/	/	/	/	/	0.52	0.52	0.52	0.48	0.48	0.56

Table 7. Performance of machine learning models in OVCAR-4 MCTS classifications with AZD inhibitor treatment. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	0.81	0.95	0.86	0.97	0.65	0.99	0.50	0.50	0.42	0.43	0.44	0.31
Precision	0.83	0.95	0.88	0.98	0.68	0.99	/	/	/	/	/	/
Recall	0.81	0.95	0.86	0.97	0.65	0.99	/	/	/	/	/	/
F1-score	0.81	0.95	0.86	0.97	0.64	0.99	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.10	0.10	0.10	0.10	0.14	0.20
Homogeneity	/	/	/	/	/	/	0.18	0.18	0.07	0.11	0.11	0.04
Completeness	/	/	/	/	/	/	0.18	0.18	0.10	0.12	0.15	0.14
V_meaure	/	/	/	/	/	/	0.18	0.18	0.08	0.12	0.13	0.06
Cross_Screening
Accuracy	0.84	0.95	0.87	0.78	0.69	0.81	0.44	0.44	0.49	0.49	0.53	0.31
Precision	0.85	0.95	0.89	0.80	0.71	0.83	/	/	/	/	/	/
Recall	0.84	0.95	0.87	0.78	0.69	0.81	/	/	/	/	/	/
F1-score	0.84	0.95	0.87	0.78	0.69	0.81	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.11	0.11	0.11	0.11	0.11	0.18
Homogeneity	/	/	/	/	/	/	0.21	0.21	0.23	0.24	0.25	0.06
Completeness	/	/	/	/	/	/	0.44	0.44	0.30	0.31	0.32	0.33
V_meaure	/	/	/	/	/	/	0.28	0.28	0.26	0.27	0.28	0.11
Composite_Hyperparameter
Accuracy	0.81	0.91	0.85	0.71	0.61	0.79	0.58	0.56	0.56	0.56	0.58	0.58
Precision	0.82	0.93	0.86	0.76	0.63	0.80	/	/	/	/	/	/
Recall	0.81	0.91	0.85	0.71	0.61	0.79	/	/	/	/	/	/
F1-score	0.81	0.92	0.85	0.71	0.61	0.79	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.17	0.19	0.21	0.22	0.20	0.20
Homogeneity	/	/	/	/	/	/	0.33	0.36	0.38	0.41	0.38	0.40
Completeness	/	/	/	/	/	/	0.42	0.51	0.48	0.43	0.39	0.52
V_meaure	/	/	/	/	/	/	0.37	0.42	0.43	0.42	0.38	0.45

Table 8. Performance of machine learning models in OVCAR-4 MCTS classifications with R-ke inhibitor treatment. DT, decision tree. GB, gradient boosting. kNN, k nearest neighbor. LG, logistics. NB, naïve bayes. SVM, support vector machine. AH, agglomerative hierarchical. BC, birch. GM, Gaussian mixture. KM, k means. MBK, mini batch k-means. ST, spectral.

	Supervised						Unsupervised
Models	DT	GB	kNN	LG	NB	SVM	AH	BC	GM	KM	MBK	ST
Cross_Statistical
Accuracy	0.72	0.92	0.85	0.93	0.57	0.97	0.44	0.44	0.41	0.43	0.44	0.33
Precision	0.74	0.93	0.86	0.93	0.59	0.98	/	/	/	/	/	/
Recall	0.72	0.92	0.85	0.93	0.57	0.97	/	/	/	/	/	/
F1-score	0.72	0.92	0.85	0.93	0.56	0.97	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.13	0.13	0.14	0.12	0.13	0.27
Homogeneity	/	/	/	/	/	/	0.15	0.15	0.14	0.12	0.13	0.08
Completeness	/	/	/	/	/	/	0.20	0.20	0.18	0.15	0.22	0.28
V_meaure	/	/	/	/	/	/	0.17	0.17	0.16	0.13	0.16	0.12
Cross_Screening
Accuracy	0.79	0.91	0.85	0.76	0.61	0.81	0.48	0.48	0.48	0.47	0.46	0.44
Precision	0.80	0.92	0.86	0.78	0.65	0.82	/	/	/	/	/	/
Recall	0.79	0.91	0.85	0.76	0.61	0.81	/	/	/	/	/	/
F1-score	0.79	0.91	0.85	0.76	0.60	0.81	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.11	0.11	0.18	0.18	0.18	0.20
Homogeneity	/	/	/	/	/	/	0.21	0.21	0.15	0.15	0.12	0.17
Completeness	/	/	/	/	/	/	0.28	0.28	0.21	0.20	0.13	0.36
V_meaure	/	/	/	/	/	/	0.24	0.24	0.17	0.17	0.12	0.23
Composite_Hyperparameter
Accuracy	0.72	0.87	0.80	0.58	0.52	0.67	0.52	0.52	0.54	0.57	0.56	0.52
Precision	0.74	0.88	0.83	0.62	0.56	0.70	/	/	/	/	/	/
Recall	0.72	0.87	0.80	0.58	0.52	0.67	/	/	/	/	/	/
F1-score	0.72	0.87	0.81	0.58	0.49	0.67	/	/	/	/	/	/
Silhouette	/	/	/	/	/	/	0.16	0.16	0.22	0.21	0.21	0.23
Homogeneity	/	/	/	/	/	/	0.32	0.32	0.29	0.30	0.31	0.30
Completeness	/	/	/	/	/	/	0.33	0.33	0.37	0.32	0.33	0.40
V_meaure	/	/	/	/	/	/	0.33	0.33	0.32	0.31	0.32	0.34

Fig. 11.

The statistics and difference of superficial and spatial parameters in OVCAR-4 MCTS with different concentration treatments. A, the representative images of the first two highest weight features of OVCAR-4 MCTS in the cross-statistical, cross-screening, and composite-hyperparameter. RMSE, root mean square error. B, the normalized difference of selected features in the cross-statistical, cross-screening, and composite-hyperparameter. C, the absolute difference of selected features in the cross-statistical, cross-screening, and composite-hyperparameter.

4. Discussion

In this study, we aimed to develop an image processing method for recognizing OCT imaging of different MCTS under various conditions. We introduced three feature processing methods that leverage both superficial and spatial features, in conjunction with machine learning models, to classify MCTS cultures exhibiting variations in cell numbers, cell types, and responses to distinct drug treatments. Our results illustrate that the integration of superficial and spatial parameters with machine learning unveils the internal tissue distinctions arising from the cultivation involving varying cell numbers, cell types, and diverse drug treatments. With the superficial and spatial features, we successfully quantified the internal tissue alterations brought about by the diversities in culturing and treatment diversities by utilizing the noninvasive scanning capabilities of OCT. Through the application of machine learning, we screened effective features for the classification of MCTS conditions and treatment outcomes. Reciprocally, the attained classification performance aided in the selection of suitable machine learning models for the categorization of MCTS. These selected superficial and spatial features effectively describe and predict the internal tissue changes under the cell culture by different cell numbers, blends of cell types, and diverse drug treatments.

In the OVCAR-8 MCTS, the internal tissue distribution of 5,000 and 50,000 tumor cells was distinguishable from the OCT intensity images (Fig. 1(A)). The superficial and spatial features (Data File 1) selected through the cross-statistical, cross-screening, and composite-hyperparameter yielded a remarkable 100% classification accuracy across the majority of machine learning models except for NB and ST models (Fig. 4(A)), which underscored the utility of these features in analyzing internal tissue changes with the cell culturing of diverse cell numbers. In our prior study, we showcased that 50,000 OVCAR-8 tumor cells exhibited not only a larger spheroid volume on day 10 compared to the 5,000 tumor cells, but also contained a more pronounced necrosis volume within the MCTS structure [24]. Our findings highlighted selected features that exhibited higher and lower values in the 50,000 MCTS group as opposed to the 5,000 MCTS group. These features demonstrated a positive and a negative correlation with the differences in spheroid and necrotic core volumes between the two groups, respectively (Data File 1). As MCTS formed, robust interactions emerged among cells and between cells and their environments, facilitating the establishment of physical communication channels and signaling pathways [69]. Concurrently, restricted circulation and limited oxygen and nutrient penetration led to necrotic regions forming at the center of the spheroids [2,70]. The variation in cell population numbers influenced the spatial arrangement and interspaces among cells, subsequently impacting the configuration of internal spheroid structures, similar to the clinical tumors. This effect led to the formation of distinct layers, ranging from the core to the periphery, including necrotic, quiescent, and proliferative layers [71]. These internal structures played a pivotal role in the decision of appropriate treatment, as they affect the analysis of cellular gene expression [31,72], drug resistance [73,74], and metabolism [75] — a scope previously accessible solely through conventional imaging modalities. Currently, our study demonstrated that the amalgamation of OCT intensity images with superficial and spatial features, alongside the utilization of machine learning techniques, can effectively facilitate the observation and comprehensive analysis of the intricate internal structures inherent to MCTS specimens throughout the preclinical research and provide a more accurate profile about new drugs. Of greater significance, the inherent benefits of noninvasive and noncontact scanning offered by OCT enabled the realization of longitudinal internal structure monitoring [24,25], thereby conferring substantial advantages to extended and uninterrupted investigations in the domain of anticancer research not only preclinical, but also clinical.

The co-culture of Panc02-H7 MCTS with fibroblasts more closely approximated the dynamic milieu of actual tumor microenvironment. By leveraging cross-statistical analysis, cross-screening, and composite hyperparameter selection, we judiciously identified effective features, enabling the adept classification of Panc02-H7 MCTS characterized by distinct mixing ratios using machine learning models (Fig. 6). Our findings revealed that GB and kNN emerged as dependable models for effectively categorizing Panc02-H7 MCTS with varying fibroblast mixing ratios. This conclusion stems from their notable classification accuracies and robust performance evaluations at all three feature processing methods. Fibroblasts assumed a pivotal role in cancer progression and drug resistance, constituting an integral component of genuine tumor microenvironments, and the formation of spheroids is strictly regulated by the fibroblasts [76,77]. In our results, mixing MCTS exhibited larger differences compared to Panc02-H7 MCTS with the increase of the ratio of fibroblasts (Fig. 7(A)–7(B)). Through confocal auto-fluorescence imaging of collagen within MCTS, it was evident that collagen formation increased with a higher fibroblast ratio. The normalized absolute difference among various ratio groups remained consistent with the confocal imaging of collagen, affirming the reliability of the results concerning both superficial and spatial characteristics. This effect suggested that the composition of fibroblasts within Panc02-H7 MCTS substantially altered the internal structure of spheroids and these alterations were extracted through superficial features for subsequent quantitative analysis. The distribution of cancer-associated fibroblasts within MCTS, such as clustering in the center or dispersing throughout the spheroids, was associated with the capability of tumor cell invasion [30,78–80]. We noted that the distinct distribution information of various ratios of fibroblasts within MCTS was evident in the representative Spk, Correlogram_Ht, and Correlogram_Hd features. These distribution characterizations not only validated the invasive potential of tumor cells but also facilitated the analysis of tumor proliferation, angiogenesis, and drug resistance [79–82]. We noticed that Fig. 7(C) showed there was a substantial difference in Spk feature distributions of Pancreatic MCTS with a 1:1 ratio (1P:1F). The quantity of pancreatic tumor cells correlates with the growth and alterations in fibroblasts [83]. A higher number of pancreatic tumor cells has been observed to enhance the growth of fibroblasts. Additionally, pancreatic tumor cells contribute to the elongation of fibroblast cells. However, it's noteworthy that fibroblasts, in turn, can produce the extracellular matrix, which has inhibitory effects on the growth of pancreatic cells. Consequently, the presence of a relatively higher quantity of tumor cells or fibroblasts in the mixed culture tends to exhibit characteristics akin to a single tissue. Therefore, maintaining a 1:1 ratio (1P:1F) of Pan02-H7 cells and fibroblasts may establish a balanced condition between tumor cells and fibroblasts. This equilibrium is speculated to induce a specific pattern distribution of tissues within Multicellular Tumor Spheroids (MCTS). Therefore, the superficial and spatial features selected through the cross-statistical, cross-screening, and composite-hyperparameter were potential to study tumor properties by combining machine learning and OCT intensity images. Furthermore, for the exploration of tumor invasion and resistance, the integration of machine learning models with OCT intensity images exhibited the capability to predict and classify varying degrees of tumor invasion and drug response.

According to genomic profiles collected from patients, OVCAR-4 cell line represents one of the most clinically relevant high-grade serous ovarian cancer mutations [84]. Our results showing that the supervised learning models were reliable in classifying OVCAR-4 MCTS treated by different drugs under the same concentration are extremely significant (Fig. 8(A)–8(C)). Particularly, these supervised learning models demonstrated high classification accuracy in cross-statistical feature screening, indicating significant diversity in superficial and spatial features among OVCAR-4 MCTS treated with different drugs, which is an expected behavior of a clinical cancer model. GB and kNN emerged as relatively robust models for classifying the therapeutic effects of drugs on MCTS, thanks to their consistently stable performance across cross-statistical, cross-screening, and composite hyperparameter classifications. The supervised learning models were more appropriate to be employed for classifying the drug treatments on MCTS compared to the unsupervised models. OCT has been validated for tracking the growth dynamics of spheroid volume, necrotic tissues, and tissue uniformity in OVCAR-4 MCTS treated with 2-ME, AZD, and R-ke inhibitors in our previous study [25]. 2-ME, AZD, and R-ke exhibited activity in terms of antiproliferative and apoptotic effects, as well as in regulating tumor cell adhesion and migration in anticancer treatments. [85–89]. Our previous work exhibited that high concentration 2-ME, AZD, and R-ke effectively inhibited the volume growth of OVCAR-4 MCTS and 2-ME and AZD substantially inhibited the formation of high uniform tissues within MCTS [25]. In this work, we employed superficial and spatial features to further explore the changes of internal tissues with the treatment of these drugs. We observed that 2-ME, AZD, and R-ke did not induce noticeable internal tissue alterations within MCTS at low concentrations (1 and 10 µM). However, high-concentration treatments with these three drugs resulted in significant changes in the WP and Histogram features (Fig. 9(A)). This result remained consistent with the changes in MCTS volume size during the drug treatments. R-ke with high concentrations (10 and 25 µM) induced the largest absolute differences of superficial and spatial features in the cross-statistical compared to the control. Since the cross-statistical method encompassed more superficial and spatial features, we observed larger differences in most features among MCTS treated with R-ke compared to those treated with 2-ME and AZD (Fig. 9(B)–9(C)). Nevertheless, 2-ME at all concentration levels (1, 10, and 25 µM) showed the highest absolute differences in superficial and spatial features in both cross-screening and composite-hyperparameter analyses. OCT intensity images revealed that MCTS treated with R-ke exhibited an empty core (Fig. S1C), potentially having a significant impact on the texture characterization of internal tissues within the MCTS. Since R-ke was primarily active to the inhibition of adhesion and migration of tumor cells through Ras-related C3 botulinum toxin substrate 1 (Rac1) and cell division control protein 42 (Cdc42) [88–91], we speculated that R-ke inhibitors influenced the adhesion and migration of OVCAR-4 tumor cells in the core of spheroids and thereby caused larger differences of more superficial and spatial features. Furthermore, we observed that there was an overall increase in the absolute differences of 2-Me and R-ke and an overall decrease in the absolute differences of AZD with the increase in concentrations, except for the 2-ME in the cross-screening and R-ke in the cross-statistical (Fig. 10(C)). By employing cross-statistical and cross-screening to select effective superficial and spatial features based on the statistical significance and weight/importance, there was a notable absence of non-effective feature contributions in the analysis of the overall absolute differences, which could potentially lead to variations in the change trend of absolute differences at different drug concentrations. Composite-hyperparameter, based on the weight/importance, provided a more comprehensive analysis of all features for the absolute differences than cross-statistical and cross-screening. We found that specific superficial and spatial features from all selected features in cross-statistical, cross-screening, and composite-hyperparameter exhibited consistent alteration trends with the increase of drug concentration (Fig. 11(D) and Data File 1). Previous studies demonstrated that there was a dependence relationship between the therapeutic effect and the concentration of 2-ME, AZD, and R-ke [88,92,93]. Therefore, these superficial and spatial features that exhibited the correlation with drug concentrations had the potential to be considered as biomarkers for monitoring and screening anticancer drugs.

Within the machine learning models, our findings indicated that the supervised models consistently achieved superior classification accuracies of MCTS when compared to the unsupervised models across all data sets of Panc02-H7 and OVCAR-4 MCTS in cross-statistical, cross-screening, and composite-hyperparameter. Furthermore, the incorporation of composite-hyperparameter feature processing markedly enhanced the classification performance of the unsupervised models (Fig. 4(A), Fig. 6(B), Fig. 8(A), and Fig. 10(A)). In the supervised models, GB and kNN maintained stably high classification accuracies of MCTS in cross-statistical, cross-screening, and composite-hyperparameter. SVM exhibited the highest classification accuracy of OVCAR-4 MCTS in cross-statistical, but the overall classification performance in cross-screening and composite-hyperparameter was relatively lower. In the classification of MCTS, especially in the OVCAR-4 and Pan02-H7 MCTS, we found that GB, kNN, LG, and SVM models showed high accuracies of classification. However, LG and SVM models exhibited lower stability of classification in cross-screening and composite-hyperparameter. kNN model possessed a stable performance of prediction but exhibited a relatively lower accuracy compared to GB model. Therefore, with the feature extraction and screening from cross-statistical, cross-screening, composite-hyperparameter, and random forest model, GB model can provide stable and robust classification to analyze MCTS for drug screening and development. The ex vivo culturing of tumor cells is becoming popular and widely employed in chemotherapy of cancer patients [94,95]. Our method can extract effective surface and spatial features from OCT images to analyze the therapeutic mechanism of new drugs and recommend the best combination of drug option with specific concentrations under the assistance of GB learning models. Compared with current microscopy and fluorescence techniques, OCT is label free and can provide real time imaging with high-speed and longitudinal monitoring, which can overcome the limitations such as time consuming, dye labeling, and 2D-projection-only from current imaging modalities.

In the three categories of MCTS, machine learning models achieved perfect classifications of OVCAR-8 MCTS, except for NB and ST models in the cross-statistical method. In other words, both cross-screening and composite-hyperparameter methods demonstrated robustness in classifying OVCAR-8 MCTS with different cell numbers. Moreover, unsupervised models exhibited relatively lower accuracies compared to supervised models when classifying MCTS with varying cell types and drug treatments at diverse concentrations. The classification performance of supervised models in different cell types and drug treatments was used to compare the efficacy of feature selection in this study. In Pan02-H7 MCTS, cross-statistical, cross-screening, and composite-hyperparameter methods displayed the highest accuracy in two supervised models (LG and SVM in cross-statistical, DT and GB in cross-screening, kNN and NB in composite-hyperparameter), respectively. Cross-statistical demonstrated better feasibility in classifying different cell types in Pan02-H7 MCTS, primarily due to the SVM model in the cross-statistical method achieving the highest classification accuracy. Additionally, in OVCAR-4 MCTS, the cross-screening method achieved the highest classification accuracy in three supervised models with different drugs and diverse concentrations. This indicates that the cross-screening feature selection method performed better in classifying different drug treatments with diverse concentrations in OVCAR-4 MCTS.

Deep learning models have been widely used to classify tumor spheroids and single cells [96–99] due to a high accuracy of spheroid and cell classification compared to conventional machine learning methods. However, deep learning models are black-box processing mode so we cannot track the internal characterization of images during the classification process. Moreover, deep learning faces the limitation of characteristics and quantity of inputs [100] compared to traditional image processing methods. Our study emphasizes the application of 2848 texture and roughness features on the classification of spheroids and the visualization of internal characterization of OCT images. With machine learning models, we can screen effective texture and roughness features to describe the internal alteration of spheroids cultured by different cell number and cell types and treated by different drugs with different concentrations. These selected effective features can be used to further track the therapeutic progress of drug treatment in future anticancer drug developments. Deep learning algorithms demonstrate proficient classification of spheroid types, while traditional machine learning models excel in extracting established and impactful image features. The amalgamation of conventional supervised learning models and deep learning models appears promising as an ideal approach to extracting the most effective features, integrating spatial and surface parameters to reveal alterations within the internal tissues of spheroids. Our future work will continue in this direction. These machine learning models, along with feature selection methods and texture features, are applicable to various types of cell lines. While the specific effective features selected from screening methods and the accuracy of diverse machine learning models may vary, these methods remain versatile for studying different cell line cultures and drug treatments in the future.

In this study, we used 60 images from 12 spheroids for OVCAR-8, 60 images from 12 spheroids for OVCAR-4 MCTS, and 75 images from 15 spheroids for Panc02-H7 MCTS to extract superficial and spatial features. Our experimental design adheres to the common sample size requirements for statistics in preclinical MCTS studies [22,25–29,60], which is adequate for qualifying and quantifying texture analysis for MCTS. However, it may be insufficient for machine learning models, especially the unsupervised ones that require larger datasets. Compared to supervised learning models, unsupervised learning models require larger datasets to capture classification characteristics for different groups [101]. In this study, our datasets may be limited in size, potentially contributing to lower accuracies in unsupervised learning models. This limitation could be attributed to the need for larger volumes of data. Additionally, we observed some features identified as ‘low-effective’ through the three screening methods. In contrast, supervised learning models achieve high predictive accuracy, benefiting from explicit feedback from labeled data. However, unsupervised learning models may introduce interference clustering based on these low-effective features, leading to a decline in predictive accuracy. On the other hand, the cross-screening feature processing method utilizes both the weight/importance derived from the random forest model and the accuracy obtained from machine learning models to select effective features. Either the weight/importance of > 0.1 or the accuracy of > 0.5 for feature selection might import the feature interference among different groups, which might influence the classification performances. Other factors such as culturing environments (temperature, medium concentration, genetic modification, etc.) and markers (nanoparticles) can also affect internal tissue alterations of spheroids [102–106]. It remains unknown whether these internal alterations caused by these factors can be effectively extracted from spatial and surface features and machine learning models. Our future work will continue in this direction.

5. Conclusion

We employed 27 texture and roughness parameters to extract 2484 superficial and spatial features from OCT intensity images and three feature processing methods to select effective features. Twelve machine learning models were used to classify MCTS culturing with different cell numbers, cell types, and diverse drug treatments. Our results demonstrated that the supervised learning models exhibited significantly higher classification performances compared to the unsupervised learning models. The effective features combining the supervised learning models successfully classify OVCAR-8 MCTS culturing with 5,000 and 50,000 cells, Panc02-H7 MCTS culturing with the ratio of 0%, 33%, 50%, and 67% of fibroblasts, and OVCAR-4 MCTS treated by 2-ME, AZD, R-ke with concentrations of 1, 10, and 25 µM. SVM model provided the highest classification accuracy of MCTS in cross-statistical feature processing method as well as GB and kNN offered the most stable and robust performances of MCTS classifications in cross-statistical, cross-screening, and composite-hyperparameter. There was a trend correlation between particular effective features and the treatment concentration of drugs within MCTS. In summary, we confirmed that OCT intensity images combined with machine learning models and superficial and spatial features could achieve noninvasive monitoring of internal structures within MCTS, which was promising for obtaining multi-dimensional physiological and functional evaluation of MCTS in anticancer studies.

This study represents the detailed application of various methods to establish the OCT image analysis of MCTS. Compared to monolayer cultures, MCTS better mimics the complexity of real tumors, enabling more accurate and relevant studies in various aspects of cancer research and therapy development in high-throughput in vitro preclinical studies. Thus, the identification of accurate analysis methods of the OCT images of MCTS is crucial for combining and boosting innovations and discoveries by utilizing both methods.

Funding

U.S. Department of Defense10.13039/100000005 (W81XWH-22-1-0415); Midwest Biomedical Accelerator Consortium (MBArC); Oklahoma Center for the Advancement of Science and Technology10.13039/100008569 (HR 23-069, HR23-071); University of Oklahoma Health Sciences Center10.13039/100007927 (3P30CA225520); Oklahoma Shared Clinical and Translational Resources (NIGMS U54GM104938); National Cancer Institute10.13039/100000054 (P30CA225520); National Institute of General Medical Sciences10.13039/100000057 (P20GM103639); American Cancer Society10.13039/100000048 (IRG-19-142-01); National Science Foundation10.13039/100000001 (2238648, OIA-2132161); National Institute of Health (R01CA269897, R01DK133717).

Disclosures

The authors declare no competing interests.

Data availability

Data underlying the results presented in this paper are available in Dataset 1 ^{(95.7KB, xlsx)} , Ref. [68].

Supplemental document

See Supplement 1 ^{(5.3MB, pdf)} for supporting content.