stDiff: a diffusion model for imputing spatial transcriptomics through single-cell transcriptomics

Abstract

Spatial transcriptomics (ST) has become a powerful tool for exploring the spatial organization of gene expression in tissues. Imaging-based methods, though offering superior spatial resolutions at the single-cell level, are limited in either the number of imaged genes or the sensitivity of gene detection. Existing approaches for enhancing ST rely on the similarity between ST cells and reference single-cell RNA sequencing (scRNA-seq) cells. In contrast, we introduce stDiff, which leverages relationships between gene expression abundance in scRNA-seq data to enhance ST. stDiff employs a conditional diffusion model, capturing gene expression abundance relationships in scRNA-seq data through two Markov processes: one introducing noise to transcriptomics data and the other denoising to recover them. The missing portion of ST is predicted by incorporating the original ST data into the denoising process. In our comprehensive performance evaluation across 16 datasets, utilizing multiple clustering and similarity metrics, stDiff stands out for its exceptional ability to preserve topological structures among cells, positioning itself as a robust solution for cell population identification. Moreover, stDiff’s enhancement outcomes closely mirror the actual ST data within the batch space. Across diverse spatial expression patterns, our model accurately reconstructs them, delineating distinct spatial boundaries. This highlights stDiff’s capability to unify the observed and predicted segments of ST data for subsequent analysis. We anticipate that stDiff, with its innovative approach, will contribute to advancing ST imputation methodologies.

INTRODUCTION

Single-cell RNA sequencing (scRNA-seq) is a high-throughput technique utilized to assess gene expression at the individual cell level, affording researchers a profound understanding of cellular heterogeneity. However, scRNA-seq involves a cell dissociation step, resulting in the loss of spatial context. Because of the importance of spatial information in comprehending intricate physiological processes and enhancing our understanding of disease pathology, spatial transcriptomics (ST) emerges as an advanced method for measuring gene expression in tissue or cell samples while retaining spatial location information. This technology empowers researchers to unravel the spatial distribution of gene expression in tissues, contributing to insights into cell types, functions, interactions, and critical details in developmental, disease, and biological processes.

Currently, ST technologies can be broadly classified into two main categories. The first category encompasses imaging-based technologies such as MERFISH [1], osmFISH [2] and seqFISH+ [3]. While excelling in single-cell resolution, this technology is typically limited to hundreds of preselected genes. The second category involves sequencing-based technologies using spatial barcoding, including methods like Slide-seq [4], 10x Visium and Stereo-seq [5]. Although this category can detect transcriptome-wide gene expression, it operates at a spatial resolution larger than a single cell and has a limited capture rate. Researchers are currently utilizing scRNA-seq data to enhance ST data to transcriptome-wide, or deconvolve ST data to infer the cell-type composition in a spatial spot.

In recent years, various models have been proposed to impute ST data based on reference scRNA-seq data. These models, including Tangram [6], gimVI [7], stPlus [8], SpaGE [9], uniPort [10] and SpatialScope [11], assume that scRNA-seq data and ST data share similar gene expression distributions. They identify similarities between scRNA-seq cells and ST cells by examining the expression patterns of shared genes. Then, these methods use referencing similar scRNA-seq cells to complete unmeasured portions in the ST data. Consequently, the accuracy of aligning cells from the two different -omics significantly influences imputation results.

Due to the sparsity of both scRNA-seq and ST data and the reliance on a limited number of shared gene expression abundances for calculating similarity between scRNA-seq cells and ST cells, finding precise alignments is often challenging. Moreover, batch effect between scRNA-seq data and ST data poses an additional challenge in establishing accurate alignments between cells of the two -omics through shared genes.

Furthermore, when using scRNA-seq cells as a reference for imputation, either through reconstruction via a decoder [7] or averaging over the top K similar scRNA-seq cells [8, 9], it is difficult to avoid introducing batch bias from scRNA-seq. As a result, the measured gene expression in ST and the predicted gene expression exist in different batch spaces, thereby increasing the complexity of downstream analysis tasks.

Cells serve as the fundamental units that collectively form the intricate structure of biological tissues. Within multicellular organisms, cell types differentiate through the synthesis and accumulation of distinct sets of RNA molecules. The specific combination and regulation of expressed genes within a cell contribute to its unique cell type. Gene expression patterns play a crucial role in defining and maintaining cell identity, and the coordinated regulation of genes is fundamental to establishing and preserving various cell types in biological organisms. In essence, a sophisticated control logic is embedded in the gene expression profile. ScRNA-seq data reveal the expression pattern in a cell, providing an opportunity to uncover the regulatory relationships that govern the gene expression profile. Since scRNA-seq data and ST data share the same gene expression distributions, the control rules learned from scRNA-seq data can be employed to impute the unmeasured portions in the ST data. Considering that the control rules for expression vary among different cell types, the appropriate set of rules is selected based on the measured gene of an ST cell. In summary, our enhancement strategy does not seek similarity between scRNA-seq cells and ST cells; instead, it involves learning the regulatory rules hidden in scRNA-seq data and utilizing them to impute ST data, guided by the ST cell itself. This process is analogous to treating each scRNA-seq cell as a complete image, with the ST data seen as a masked and perturbed version of that image. The imputation task for ST data is comparable to completing the masked image.

In this paper, we introduce a novel method named stDiff that employs a diffusion model to comprehend the gene expression relationships within scRNA-seq data. Its objective is to impute missing gene expressions in ST data by leveraging the learned gene expression relationships. While diffusion models [12, 13] have achieved notable success in the field of image processing and demonstrated excellence in protein generation [14], their application in genomics remains relatively limited.

We have conducted comparative experiments on 16 data sets, evaluating our model against several representative methods. The results indicate that our model yields the best clustering results and exhibits strong competitiveness in terms of the correlation between predicted and real data. This suggests that stDiff effectively preserves the global topological relationships among cells when enhancing missing gene expressions in ST data, showcasing strong capabilities in identifying cell populations. Furthermore, the enhancement results of our model closely resemble real ST data in batch space, and for various spatial expression patterns, our model accurately reconstructs them with clear spatial boundaries. This underscores that stDiff enables the integration of the measured and predicted portions of ST data for downstream analysis.

MATERIALS AND METHODS

Methods

ST data and reference scRNA-seq data, derived from the same biological tissue or organ, exhibit similar gene expression regulation relationships and profiles across identical cell types. However, the two -omics data types originate from distinct experimental platforms, introducing specific technical noise to the actual gene expression data. In light of this, we propose stDiff, a model designed to discern the relationships between genes within scRNA-seq data. Subsequently, we leverage this model to impute ST data, guided by the existing measured ST data.

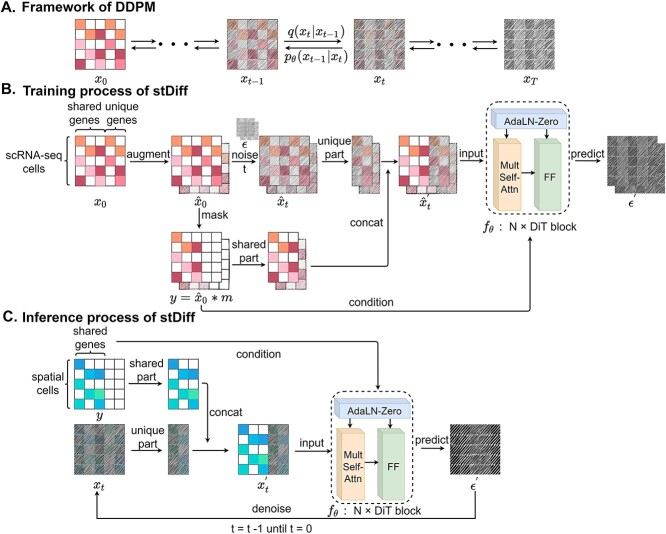
stDiff is a denoising diffusion probability model (DDPM) composed of two interconnected Markov chains [12]: forward diffusion and reverse diffusion. Illustrated in Figure 1(A), the forward diffusion process of stDiff gradually introduces random noise to the initial RNA data 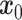, utilizing a known conditional distribution 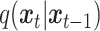. This process continues incrementally until the data distribution converges to the prior distribution (Gaussian noise), where 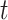denotes the time step for the gradual addition of noise. In contrast, the reverse diffusion process employs the learned denoising conditional distribution 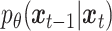to progressively recover the original data from the given prior. Specifically, starting with a noise matrix 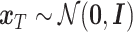, it denoises step by step to ultimately generate a target 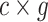two-dimensional matrix 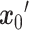, where 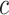represents the number of cells and 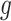represents the number of genes.

Figure 1.

Framework of stDiff. (A) Brief framework of DDPM. The forward diffusion process 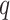(left to right) gradually introduces Gaussian noise to the target data. The reverse process 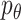(right to left) iteratively denoises the target data. (B) Training process of stDiff. ScRNA-seq data 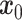undergoes noise perturbation to get 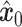. It is then introduced noise dependent on time step 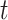, resulting in 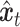. Shared part of 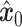and unique part of 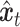are concatenated to form 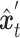. Finally, a denoising network 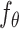is trained to predict the introduced noise. The training process is guided by the shared gene part of 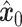. (C) Inference process of stDiff. ST data serve as condition to guide the learned denoising network 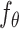to denoise step by step from a random noise. The final result after removing introduced noise is the predicted imputation for ST data.

The training phase of stDiff, as shown in Figure 1(B), involves learning the complex functional relationship between gene expression abundance during noise introduction and denoising in scRNA-seq data. To enhance the robustness of stDiff, we commence by applying perturbation to the scRNA-seq data. Considering that batch effects introduce variations in noise between ST data and reference scRNA-seq data, random noise is introduced into the scRNA-seq data (represented as 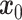). This step aims to diversify the training data while preserving gene relationships. The goal is to prevent the model from excessively focusing on the absolute values of gene expression in scRNA-seq data and instead emphasize the interrelationships between gene expressions. The augmented scRNA-seq data, denoted as 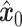, subsequently serves as the training dataset.

During each training iteration, a time step 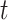is randomly sampled from a uniform distribution 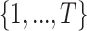. Following Equation (2), Gaussian noise 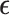is added to the scRNA-seq data at the corresponding time step 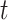, resulting in :

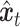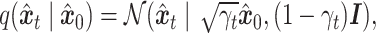(1)

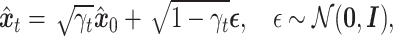(2)

where 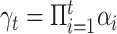, and the hyperparameters 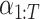are determined by the cosine function in Equation (3), ensuring .

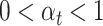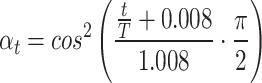(3)

These parameters control the mean and variance of the noise added at each iteration.

Subsequently, the unique gene part of 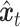and the shared gene part of 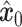are selectively extracted and combined to form the input 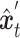. The term unique gene part’ refers to genes specific to scRNA-seq data, while shared gene part’ denotes genes measured in both scRNA-seq data and ST data. The outcome achieved by masking out the unique gene part of 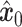is represented as the condition 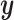. 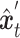and the condition 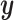are then fed into the denoising network 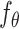to predict the added noise :

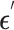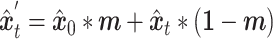(4)

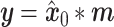(5)

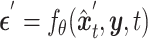(6)

where 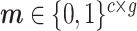, the shared gene part of 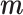is set to 1, and the unique gene part is set to 0. The symbol * denotes element-wise matrix multiplication.

The backbone network of stDiff is built upon the Diffusion Transformer (DiT) [15]. As illustrated in Figure 1(B), the DiT block primarily comprises the multi-head self-attention mechanism, the feed-forward linear layer (FF) and AdaLN-zero. The attention mechanism enhances the understanding of the relationship between known and unknown segments, surpassing traditional multi-layer neural networks. AdaLN-zero is employed to incorporate the condition 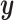. The denoising network 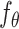is responsible for predicting the noise .

During the training process, the loss function exclusively focuses on the noise component of the unique genes that has been masked:

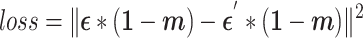(7)

The inference phase of stDiff, as depicted in Figure 1(C), utilizes the learned functional relationship from the training phase to impute missing values in the ST data. First, the ST data is expanded to condition 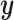, in which the unique gene part is filled with zeros. A random noise 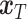is sampled at time 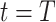. The shared gene part of condition 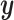(serving as condition guidance for the reverse diffusion process) and the unique gene part of 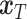, are concatenated to form the input 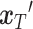, as shown in Equation (8). Subsequently, 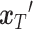and the condition 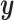are fed into the pre-trained denoising network 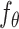to predict the noise at time 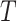, which is then used to further produce 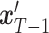at time 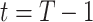, following Equation (9). This iterative process is repeated for 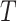steps until the final prediction is obtained when :

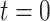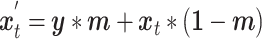(8)

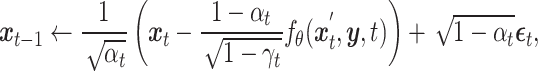(9)

where .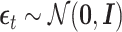

Validation data sets

We have selected 16 pairs of ST and scRNA-seq datasets for validation. These ST datasets represent a diverse range of experimental protocols, encompassing various tissue and organ types, and exhibiting significant variations in both gene and cell numbers. A detailed overview of these comprehensive datasets is presented in Table 1. Notably, the first data-set, ST cell, comes with known cell type labels, while the remaining ST data sets lack this information.

Table 1.

Summary of the 16 validation dataset pairs

		Spatial data			scRNA-seq data
Data pair	Tissue	Cell num	Gene num	Reference	Cell num	Gene num	Reference
Dataset1_MERFISH	Mop	5551	247	[16]	14 249	34 041	[17]
Dataset2_osmFISH	Somatosensory cortex	3405	33	[2]	5613	30 527	[17]
Dataset3_ExSeq	Primary visual cortex	1154	42	[18]	14 249	34 041	[17]
Dataset4_seqFISH+	Cortex	524	10 000	[3]	14 249	34 041	[17]
Dataset5_MERFISH	Osteosarcoma	645	12 903	[19]	9234	19 098	[20]
Dataset6_MERFISH	Primary visual cortex	2399	268	[21]	14 249	34 041	[17]
Dataset7_ISS	Primary visual cortex	6000	119	[21]	14 249	34 041	[17]
Dataset8_FISH	Embryo	3039	84	[22]	1297	8924	[22]
Dataset9_BARISTAseq	Primary visual cortex	11 426	80	[23]	14 249	34 041	[17]
Dataset10_seqFISH	Embryonic	175	45	[24]	9991	16 477	[25]
Dataset11_seqFish	Gastrulation	8425	351	[26]	4651	19 103	[26]
Dataset12_seqFISH+	Olfactory bulb	2050	10 000	[3]	31 217	30 593	[27]
Dataset13_MERFISH	Hypothalamic preoptic region	4975	154	[1]	31 299	18 646	[1]
Dataset14_STARmap	Visual cortex	1549	1020	[28]	14 249	34 041	[17]
Dataset15_STARmap	Prefrontal cortex	1380	166	[28]	7737	14 837	[29]
Dataset16_ISS	MTG	6000	120	[30]	15 928	48 278	[30]

Baselines

We compared the performance of stDiff with six baseline methods, including Tangram [6], gimVI [7], stPlus [8], SpaGE [9], uniPort [10], SpatialScope [11]. Data processing procedures, such as normalization and scaling, were performed following the source code of each method.

Tangram. We followed the guidelines on the Tangram GitHub repository: https://github.com/broadinstitute/Tangram. We set the parameters as modes = `clusters’, density = `rna_count_based’.

gimVI. We followed the guidelines on the gimVI’s introduction website: https://docs.scvi-tools.org/en/0.8.0/user_guide/notebooks/gimvi_tutorial.html. The spatial distribution of genes was obtained using the model.get_imputed_values function with parameter normalized = False.

SpaGE. We followed the instructions on the GitHub repository of SpaGE: https://github.com/tabdelaal/SpaGE/blob/master/SpaGE_Tutorial.ipynb. We set the parameter n_pv = gene_num / 2.

stPlus. We followed the guidelines on the stPlus GitHub repository: http://github.com/xy-chen16/stPlus. We set tmin = 5, neighbor = 50.

uniPort. We followed the instructions of official example on its website: https://uniport.readthedocs.io/en/latest/examples/MERFISH/MERFISH_impute.html.

SpatialScope. We followed the instructions on the SpatialScope GitHub repository: https://github.com/YangLabHKUST/SpatialScope. We set epoch = 5000, batch_size = 512, replicates = 5.

Evaluation metrics

We conducted a quantitative evaluation of various imputation algorithms, considering both cellular and gene perspectives. From the cellular perspective, we assessed the ability of imputed ST data to identify cell populations or maintain the consistency in the intercellular similarity relationships between the real measurement and imputed ST data. Four clustering-related metrics [31]—Adjusted Rand Index (ARI), Adjusted Mutual Information (AMI), Normalized Mutual Information (NMI) and Homogeneity(Homo) were employed to evaluate these aspects. From the gene perspective, we utilized a cross-validation approach to assess the similarity between imputed data and the real ST data at the gene level. This evaluation employed four metrics: Spearman Rank Correlation Coefficient (SPCC), Structural Similarity Index (SSIM), Root Mean Square Error (RMSE) and Jensen–Shannon Divergence (JS).

The formulas for ARI, AMI, NMI, Homo are as follows.

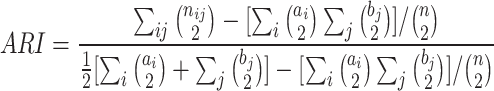(10)

where 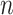is the total number of samples, 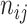is the number of samples assigned to both class 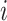and class 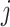, 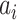is the number of samples assigned to class 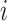, and 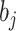is the number of samples assigned to class :

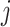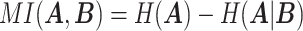(11)

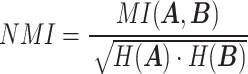(12)

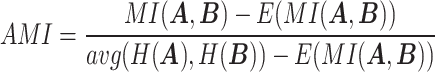(13)

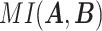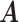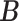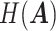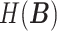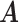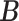where represents the mutual information between and , and represent the entropy of and , respectively, and 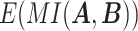represents the mutual information expectation under the stochastic model:

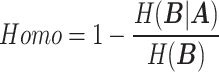(14)

where 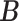represents the set of true cell categories, and represents the set of predicted cell categories.

For SSIM, RMSE, and JS, we followed the definitions outlined in [21]. In the case of these four metrics, high SPCC/SSIM values or low RMSE/JS values indicate better prediction accuracy:

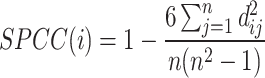(15)

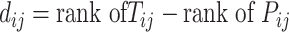(16)

where 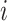represents the 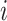th gene, 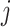represents the 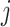th cell and 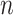represents the total number of cells. 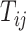is the expression value of the 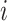th gene for the 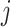th cell in the ground truth, while 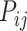is the predicted one.

Before calculating SSIM, normalization is performed:

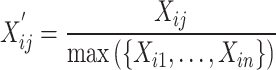(17)

where 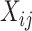represents the expression value of the 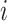th gene in the 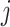th cell. SSIM is calculated after normalizing both the true and predicted values:

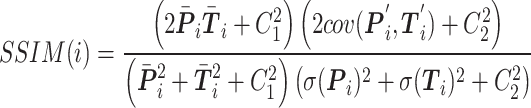(18)

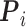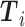where and , respectively, represent the vector corresponding to the 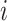th gene in the predicted values and in the ground truth. 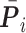, 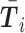denotes the mean of 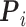, 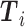. 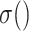denotes the process of calculating the standard deviation. 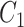and 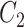are set to 0.01 and 0.03, respectively.

Before calculating RMSE, it is necessary to compute the z-score for gene 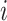across all cells. Use 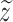to denote the z-score for the predicted values and 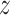for the z-score of the ground truth:

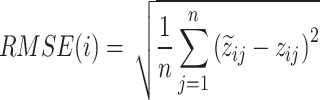(19)

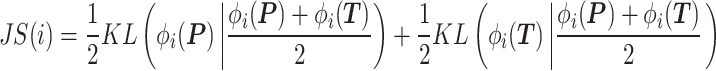(20)

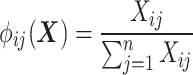(21)

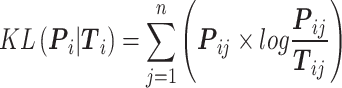(22)

where 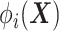computes the spatial distribution probability of gene 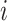across all cells in 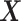, and 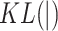calculates the KL divergence between the true gene expression values and the predicted values.

We utilized multiple metrics to evaluate the performance across various data sets. The effectiveness of each method may vary across different data sets. To present a comprehensive and consistent ranking, we employed an Accuracy Score (AS) [21]. For each evaluation metric on a data set, we ranked the performance of each method in ascending order and assigned a rank accordingly. The AS is the average rank across all evaluation metrics and datasets. A higher AS value indicates superior overall performance.

RESULTS

stDiff excels in bringing the imputed data close to the real ST data

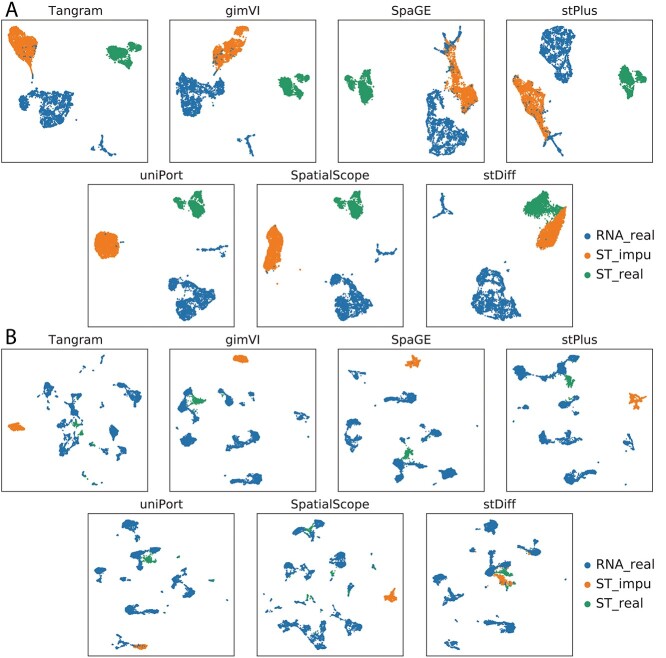
To visually illustrate the proximity between the predicted and real data, we employed a 5-fold cross-validation method with UMAP plots. Genes in the ST data were divided into five parts. Beginning with four of these parts, we predicted the expression of the remaining set of genes, repeating this process for all genes in ST cells to generate the imputed data. UMAP plots were generated for scRNA-seq data, real ST data and imputed ST data, as depicted in Figure 2.

Figure 2.

UMAP plots illustrating scRNA-seq data, real ST data and imputed ST data generated by Tangram, gimVI, stPlus, SpaGE, uniPort, SpatialScope and stDiff. (A) and (B) correspond to Dataset2_osmFISH and Dataset3_ExSeq in Table 1, respectively.

The results demonstrate that stDiff’s predictions (in orange) closely match with the real ST data (in green), while predictions from Tangram, gimVI, stPlus, SpaGE, uniPort and SpatialScope methods distinctly deviate from the real ST data. In the case of Dataset2_osmFISH shown in Figure 2(A), an interesting observation is that predictions made by Tangram, gimVI, SpaGE and stPlus methods appear to be closer to scRNA-seq data than to real ST data. It indicates that batch noises from scRNA-seq are kept in the predicted ST data. In the case of Dataset3_ExSeq shown in Figure 2(B), with only 1154 ST cells compared to 14 249 scRNA-seq cells, where the scRNA-seq cell population is more abundant, stDiff consistently and accurately predicts ST data, while predictions from other methods are significantly distant from real ST data. In comparison, stDiff demonstrates a more accurate alignment between predicted results and real data.

The imputation strategy of stDiff differs from other methods. stDiff learns mutual relationships between gene expression abundance from scRNA-seq data, effectively functioning as a predictive model. This function is then used to enhance the gene expression in ST data with the input of the real ST data. Consequently, the predicted data aligns more easily with real data in a batch space. In contrast, other methods calculate the similarity between scRNA-seq cells and ST cells based on shared gene expression levels. They employ one of the following imputation approaches: averaging the top K most similar scRNA-seq cells, reconstructing ST data using a decoder trained on scRNA-seq data, or sampling from the scRNA-seq distribution using batch-effect-removed ST data. In summary, these methods map ST data to the batch space of scRNA-seq data and enhance ST data based on the scRNA-seq data space, posing a challenge for the predicted data to align well with the correct batch space of the ST data since usually ST data resides in different batch space from scRNA-seq data.

stDiff exhibits the most significant improvement in identification of cell population

In this evaluation, we utilized the ST data set with known cell type labels, specifically Dataset1_MERFISH in Table 1. Each method was employed to enhance ST data to the whole-genome level. The imputed results encompass both the gene expression levels measured in the authentic ST data and the predicted expression levels for other genes by each method. Subsequently, Leiden clustering [32] was applied to the imputed ST data at the whole-genome level. The known cell types served as the ground truth for clustering, and four clustering metrics (AMI, ARI, Homogeneity, NMI) were employed to evaluate the predictive performance of each method. The clustering results obtained from the authentic ST data were used as the baseline for comparison.

As presented in Table 2, Tangram, gimVI, uniPort and SpatialScope do not exhibit superiority in imputed results when compared to the authentic ST data. In contrast, SpaGE, stPlus and stDiff show improvements in clustering metrics, with stDiff achieving the most favorable outcome. This suggests that stDiff stands out as the top-performing method, enhancing the capability to discover cell populations.

Table 2.

Clustering metrics for authentic ST data and imputed results at the whole-genome level using various methods

	ARI	AMI	Homo	NMI
authentic ST data	0.640	0.807	0.837	0.810
Tangram	0.674	0.794	0.821	0.797
gimVI	0.683	0.804	0.832	0.807
SpaGE	0.690	0.816	0.843	0.818
stPlus	0.702	0.829	0.859	0.832
uniPort	0.593	0.793	0.829	0.796
SpatialScope	0.613	0.783	0.777	0.787
stDiff	0.725	0.834	0.865	0.836

stDiff’s imputed results best preserve the topological structure among cells

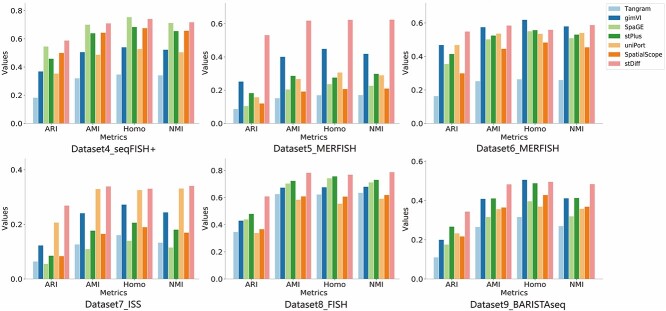
For most ST datasets lacking cell type annotations, we conducted an evaluation of the similarity in topological structure among cells between authentic and imputed datasets using a 5-fold cross-validation approach. Employing the Leiden clustering method and four clustering metrics (AMI, ARI, Homogeneity, NMI), with authentic ST data clustering results as the ground truth, this evaluation aimed to quantify the consistency between predicted and authentic data in terms of clustering outcomes, providing insights into the similarity in topological structure among cells.

For each experimental platform of the ST data, we individually selected representative datasets, and the outcomes are illustrated in Figure 3. Numeric results for all 15 datasets without cell type labels can be referenced in Supplementary Table 1.

Figure 3.

Clustering metrics (ARI, AMI, Homogeneity, NMI) demonstrating the topological consistency among cells between authentic ST data and predicted data generated by Tangram, gimVI, stPlus, SpaGE, uniPort, SpatialScope and stDiff across different platforms of ST data.

As shown in Figure 3, stDiff consistently outperforms other methods across the four clustering metrics, exhibiting the highest similarity to authentic ST data in terms of topological structure among cells. It demonstrates that stDiff’s imputed results are most conducive to discovering cell populations. In contrast, Tangram shows the poorest clustering results, while gimVI, SpaGE, stPlus, uniPort and SpatialScope demonstrate unstable performance across different datasets. Notably, stDiff’s clustering metrics often significantly surpasses other methods’ (Supplementary Table 1), highlighting stDiff’s superiority in preserving the similarity relationships among cells within authentic ST data.

From gene perspective, stDiff’s imputed data demonstrates competitive similarity to authentic data

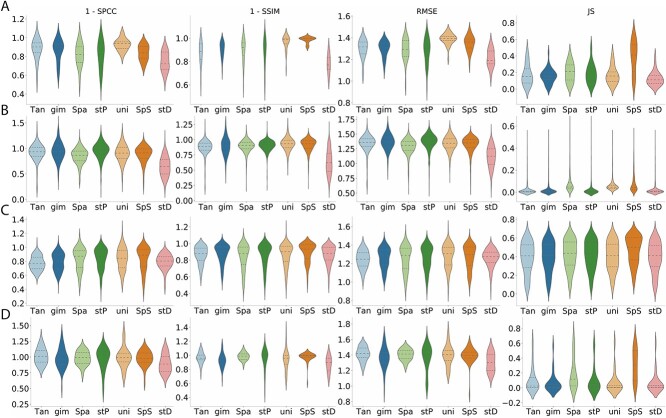
The preceding experimental results focused on assessing prediction outcomes from the cellular perspective. In this section, we evaluated imputed results from the gene standpoint using four metrics (SPCC, SSIM, RMSE, JS) after 5-fold cross-validation. Partial results are depicted in Figure 4, with complete dataset results available in Supplementary Table 2.

Figure 4.

Evaluation metrics (1-SPCC, 1-SSIM, RMSE, JS) to assess gene expression similarity between authentic ST data and predicted data generated by Tangram(Tan), gimVI(gim), SpaGE(Spa), stPlus(stP), uniPort(uni), SpatialScope(SpS) and stDiff(stD) across different platforms of ST data. (A)–(D) correspond to Dataset2_osmFISH, Dataset5_MERFISH, Dataset6_MERFISH and Dataset10_seqFISH in Table 1, respectively.

Across the four datasets in Figure 4, stDiff’s imputed data exhibits the highest similarity to authentic data. However, overall, the correlation coefficients between imputed and authentic data are relatively low, indicating room for improvement in all methods.

stDiff accurately reconstructs gene expression abundance with clear spatial patterns

In addition to quantitative assessments of gene expression similarity between authentic and predicted ST data, we visually showcased the concordance in spatial patterns in Figure 5.

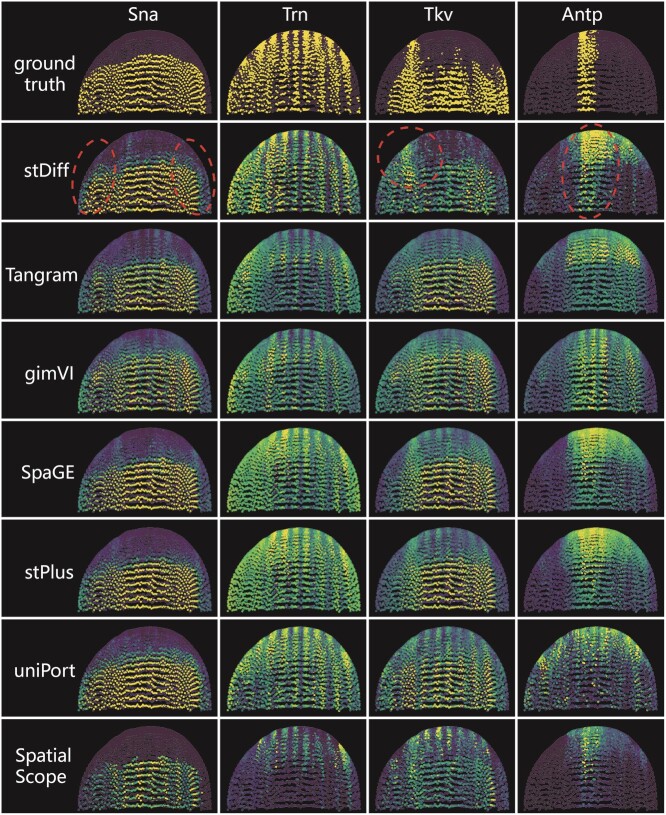
Figure 5.

The predicted expression abundance of known spatially patterned genes in Dataset8_FISH. Each column corresponds to a single gene with a clear spatial pattern. The first row from the top displays the ground truth of spatial gene expression in Dataset8_FISH, while the subsequent rows show the corresponding predicted expression patterns through 5-fold cross-validation experiments using stDiff, Tangram, gimVI, SpaGE, stPlus, uniPort and SpatialScope.

Four genes with clear spatial patterns were chosen from Dataset8_FISH embryo tissue for this illustration. The Sna gene, expressed in the lower-half region with a horizontal spatial pattern, is accurately predicted by stDiff, SpaGE, stPlus and uniPort. These methods precisely capture the lower-half region, and, notably, stDiff provides more accurate predictions on the left and right sides. In contrast, predictions from Tangram, gimVI appear somewhat messy between regions of high and low expression, and SpatialScope narrows down the highly expressed regions.

For the gene Trn with a vertical pattern, stDiff predictions exhibit clear vertical boundaries, accurately recovering each vertical contour. In contrast, predictions from other methods show less distinct spatial contours. stPlus, SpaGE and uniPort tend to favor higher expression abundance across the entire space, while predictions from Tangram, gimVI and SpatialScope lean towards an overall lower expression.

For the complex spatial pattern of the Tkv gene, stDiff predictions best match this intricate pattern. Moreover, only stDiff clearly recovers the high-expression area in the upper-left corner.

The Antp gene expression, concentrated in a narrow central region, sees stDiff’s predictions closely resembling the real scenario, while other methods except SpatialScope significantly expand the spatial expression range of this gene. The spatial boundary of SpatialScope’s predictions is not as clear as the real pattern, and for all these four genes, SpatialScope seems to underestimate the expression abundance of the marker gene.

stDiff demonstrates superior overall performance across multiple datasets.

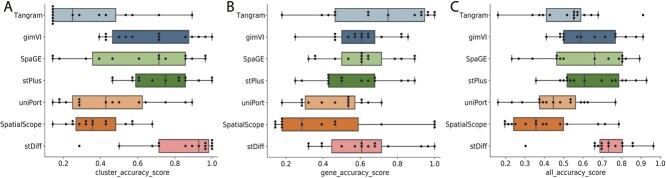
Our evaluation spanned 15 datasets, utilizing four clustering metrics and four similarity evaluation metrics. Each method displayed varying performance across datasets. To provide a comprehensive evaluation, we employed the AS index, as shown in Figure 6.

Figure 6.

Boxplots and scatter plots of the AS for the data generated by the seven methods across all 15 paired datasets. The central line represents the median, the box depicts the interquartile range, whiskers extend to 1.5 times the interquartile range, and dots represent the AS of individual datasets. (A) The AS scores for clustering metrics. (B) the AS scores for gene similarity metrics. Panel (C), The overall AS scores for all eight metrics.

Cluster results reflect the consistency between the predicted and authentic data in terms of cellular topological relationships. Figure 6(A) illustrates that stDiff achieves the best clustering results, far exceeding other methods. stDiff’s median value on the AS composite index surpasses the upper quartile values of other methods. gimVI, SpaGE and stPlus are in the second tier, with stPlus exhibiting relatively more stable performance. Surprisingly, Tangram’s clustering results lag far behind other methods, consistently ranking at the bottom in most cases.

Figure 6(B) demonstrates the similarity between predicted and authentic results at the gene level. Overall, Tangram performs the best, and stDiff, gimVI and SpaGE achieve the second position on the AS median value and shows good stability. In contrast, Tangram and SpatialScope demonstrate less stability across different datasets in terms of gene similarity.

It is important to note that this evaluation calculates the similarity between authentic and imputed data for each gene across all cells. Due to the high dimensionality caused by a large number of cells, metrics like SPCC face challenges in accurately reflecting the real similarity between imputed and authentic data.

Finally, the combined results from both cell clustering and gene similarity across 15 datasets are shown in Figure 6(C). stDiff stands out as the best-performing method, displaying the most stable outcomes. Overall, stDiff significantly outperforms other methods in maintaining cellular topological similarity and ranks in second place in gene similarity. Tangram excels in gene similarity, though all methods struggle to predict gene similarity accurately. However, Tangram’s predictions at the cell level fall far behind other methods, suggesting potential loss of original cellular similarity and limited applicability for cell population discovery. gimVI, SpaGE and stPlus perform relatively similarly. On closer inspection, stPlus shows slightly better performance in cell clustering and slightly worse performance in gene similarity, while gimVI and SpaGE exhibit better gene similarity but less stable cell clustering performance.

Time cost

To investigate the time complexity of the methods in the experimental comparison, we have selected Dataset2_osmFISH as an example and documented the time cost for each method, as presented in Table 3. Our time cost experiment is conducted on an Ubuntu server with an AMD Ryzen 9 5950X 16-Core Processor, NVIDIA GeForce RTX 3090 GPU and 125GB of memory.

Table 3.

Time cost of five cross-validations on Dataset2_osmFIsh for different methods

Methods	Time cost
Tangram	1 min
gimVI	30 min
SpaGE	30 s
stPlus	3 min
uniPort	75 min
SpatialScope	14 h
stDiff	60 min

From Table 3, it is evident that stDiff’s time cost is in a moderate position among all methods, with SpaGE being the fastest.

Model details of stDiff

The backbone of stDiff utilizes DiT [15], consisting mainly of three components: AdaLN-zero, multi-head self-attention mechanism and multi-layer perceptron (MLP). In AdaLN-zero, the guidance condition is projected to 6 times the feature dimension through the SiLU activation function and a linear layer. Subsequently, it is split into six parameters used for combining the guidance condition and input. The multi-head self-attention mechanism allows the module to focus on information from different positions in the input sequence, with num_heads’ in Table 4 meaning the number of attention heads. The MLP employs the GELU activation function to nonlinearly transform the input, enhancing the module’s ability to model complex patterns.

Table 4.

Parameter details of stDiff

Gene num	< 512	< 1024	< 2048
block num	6	6	6
hidden size	512	1024	2048
heads	16	16	16
sample_timestep	1500	1500	1500
parameter num	29M	117M	480M
learning rate	1.6e-4	1.6e-4	1.6e-4
train_step (epoch)	900	900	900
batch size	2048	512	512

The hyperparameters of stDiff are listed in Table 4, applicable to all datasets used in this study.

Since stDiff is a diffusion model, we investigated the impact of diffusion steps by varying the values of sample_timestep and train_step. The performances of stDiff are depicted in Supplementary Figure 1 and 2. Overall, stDiff exhibits robustness, although optimal hyperparameter settings may slightly differ for tasks such as cell population discovery and gene similarity across cells.

DISCUSSION

In this paper, we introduced stDiff, a novel method for imputing ST data. Methodologically, stDiff differs from existing approaches. While existing methods enhance ST cells based on the similarity between ST cells and reference scRNA-seq cells, stDiff takes a distinct approach by considering the gene expression profile as the determinant of cell populations. It enhances ST data by leveraging the correlations between gene expression abundances within a cell.

StDiff is a conditional diffusion model, where the processes of adding noise and denoising learn the relationships between gene expression abundances from scRNA-seq data. During the inference stage, the original ST data are conditionally introduced into the denoising process, facilitating the imputation of ST data. Currently, the application of diffusion models in genomics and transcriptomics data is underexplored. This paper provides valuable exploration in this field.

We conducted a comprehensive evaluation of stDiff across 16 datasets, employing multiple clustering and similarity metrics. The stDiff algorithm exhibits superior performance in preserving topological structures among cells and demonstrates competitiveness in similarity between predicted data and authentic data at the gene level, highlighting its potential for cell population discovery. Moreover, stDiff’s predictions closely match the authentic ST data in batch space, indicating that stDiff facilitates the integrated analysis of both measured and predicted segments of ST data. These findings contribute to the advancement of ST analysis and data imputation methodologies.

In the future, we could explore the possibility of integrating both methodologies, simultaneously considering the relationships between gene expression levels and the similarity between ST cells and scRNA-seq cells. This approach has the potential to significantly improve the performance of ST data imputation, potentially opening new avenues for advancements in this field.

It should be noted that when the ST data lacks marker signals, indicating that the measured gene expressions are unable to discern a cell’s identity, the effectiveness of current imputation methods, including stDiff, might be compromised. This limitation arises from the inadequacy of measured ST data to identify clear cell-type neighbors in scRNA-seq cells and to determine the underlying whole transcriptome pattern necessary for guiding the imputation process.

Key Points

• stDiff represents an innovative approach to enhance spatial transcriptomics data (ST) by utilizing correlations among gene expression levels within cells from reference scRNA-seq data. Unlike existing methods that rely on the similarity between ST cells and reference scRNA-seq cells, stDiff introduces a novel perspective.

• stDiff operates as a conditional diffusion model, contributing to the exploration of diffusion models in genomics and transcriptomics data.

• The extensive evaluation, covering 16 data sets and utilizing various clustering and similarity metrics, consistently positions stDiff as the leading and most stable imputation method across both cell and gene dimensions.

Author Biographies

Li Kongming is currently a master candidate at the School of Computer Science and Technology, Fudan University, China. His interests are machine learning and bioinformatics.

Li Jiahao is currently pursuing a master’s degree at the School of Computer Science and Technology, Fudan University. His research focuses on bioinformatics, deep learning and artificial intelligent generated content.

Tao Yuhao is currently a PhD candidate at the School of Computer Science and Technology, Fudan University, China. His research interests include deep learning, bioinformatics and computational biology.

Wang Fei is an associate Professor of Fudan University. Her research intertests include biological data analysis, systems biology and artificial intelligence.

FUNDING

This work is supported in part by funds from the National Natural Science Foundation of China (NSFC 61472086).

CODE AVAILABILITY

The implementation of stDiff is accessible through the GitHub repository at https://github.com/fdu-wangfeilab/stDiff.