Centroid precision and orientation precision of planar localization microscopy

Summary

The concept of localization precision, which is essential to localization microscopy, is formally extended from optical point sources to microscopic rigid bodies. Measurement functions are presented to calculate the planar pose and motion of microscopic rigid bodies from localization microscopy data. Physical lower bounds on the associated uncertainties – termed centroid precision and orientation precision – are derived analytically in terms of the characteristics of the optical measurement system and validated numerically by Monte Carlo simulations. The practical utility of these expressions is demonstrated experimentally by an analysis of the motion of a microelectromechanical goniometer indicated by a sparse constellation of fluorescent nanoparticles. Centroid precision and orientation precision, as developed here, are useful concepts due to the generality of the expressions and the widespread interest in localization microscopy for super-resolution imaging and particle tracking.

1. Introduction

Localization microscopy comprises a class of rapidly advancing and broadly applicable experimental and computational methods for measuring the positions and motions of small optical indicators (Deschout et al., 2014a, b; Chenouard et al., 2014). Although the resolution of optical microscopy is ordinarily limited by diffraction to the Rayleigh limit of approximately half the imaging wavelength, the position of an optical point source that is individually resolved within an image with pixels and noise can be measured with an uncertainty that is orders of magnitude smaller (Bobroff, 1986). The physical lower bound of uncertainty in estimating the position of a fluorescent point source was derived (Thompson et al., 2002) and corrected (Mortensen et al., 2010) to:

$$L_P=\sqrt{\frac{16\left({\sigma }_G^2+a^2∕12\right)}{9N}+\frac{8\pi b^2{\left({\sigma }_G^2+a^2∕12\right)}^2}{a^2{N}^2}},$$ (1)

where ${\sigma }_G$ is the standard deviation of the Gaussian approximation of the microscope point spread function, $a$ is the pixel pitch of the imaging sensor, $b^2$ is the expected number of background photons per pixel and $N$ is the total number of detected signal photons. This expression of localization precision denotes one standard deviation along a single spatial axis.

Localization precision is widely used as a metric of minimum uncertainty for designing measurements for low uncertainty and for assessing empirical uncertainties (Thompson et al., 2002; Ober et al., 2004; Betzig et al., 2006; Huang et al., 2009, 2013; Mortensen et al., 2010; Smith et al., 2010; Deschout et al., 2014b; Chenouard et al., 2014; Endesfelder & Heilemann, 2014). For a given experimental measurement or analysis, Eq. (1) can be used to predict if a target uncertainty is physically possible to achieve. Eq. (1) can also be informative of critical parameters in the design of an experimental measurement system to achieve a target uncertainty. In an analysis of experimental measurement results, if the empirical uncertainty is significantly larger than the localization precision, then experimental errors not modelled by Eq. (1), such as microscope drift (Elmokadem & Yu, 2015), vibration, or fixed pattern noise (Fox-Roberts et al., 2014; Long et al., 2014), must dominate the uncertainty in the measurement. If the empirical uncertainty is approximately equal to the localization precision, however, then it might be possible to reduce the empirical uncertainty by changing one of the experimental parameters in Eq. (1), such as increasing the number of detected signal photons emitted by an optical indicator.

Common optical indicators for localization microscopy include individual fluorophores, which are widely used in super-resolution imaging, and subresolution particles containing many fluorophores, which are frequently tracked as probes and fiducials (Ribeck & Saleh, 2008). Such fluorescent nanoparticles are better localized than individual fluorophores in two ways. An ensemble of many fluorophores with random orientations increases $N$ in Eq. (1), other things being equal, and produces approximately isotropic emission for which simple algorithms produce optimal results (Enderlein et al., 2006; Stallinga & Rieger, 2010) that otherwise require more complex methods (Stallinga & Rieger, 2012). For many practical applications, the localization precision of an individual optical indicator is on the order of 1 to 10 nm.

Many microscopic objects of interest are rigid bodies with planar motions which can be measured by localizing and tracking multiple optical indicators in or on the bodies. For such experimental systems, information from multiple optical indicators can be mathematically combined to further reduce the uncertainty of a position measurement and to enable an orientation measurement with low uncertainty. Related measurements have diverse applications in microtechnology, nanotechnology, biology, materials and metrology (Freeman, 2001; Ropp et al., 2013; Berfield et al., 2006, 2007; McGray et al., 2013; Samuel et al., 2007; Yoshida et al., 2011; Teyssieux et al., 2011; Ueno et al., 2010). Recently, constellations of fluorescent nanoparticles indicating the motion of microscopic actuators were localized and tracked, demonstrating the utility of the measurement method (McGray et al., 2013; Copeland et al., 2015). McGray et al. (2013) presented an expression for the minimum uncertainty of the centroid of a constellation of point sources of equal brightness. However, metrics comparable to localization precision have not been developed for either the centroid or the orientation of a sparse constellation of point sources of variable brightness on a microscopic rigid body. Such metrics would be useful to design measurements and assess uncertainties in these experimental systems.

In this paper, the concept of localization precision is extended to the analogous concepts of centroid precision and orientation precision. Just as localization precision provides the minimum uncertainty of localizing a point source by optical microscopy, centroid precision and orientation precision provide minimum uncertainties of the position and orientation of a sparse constellation of point sources of variable brightness on a microscopic rigid body in the image plane of an optical microscope. In Section 2, measurement functions and associated uncertainties for planar pose and motion are formally derived in terms of the localization precision and weighting of individual point sources in the constellation. This leads to the expressions for centroid precision and orientation precision that are summarized in Section 3. In Section 4, the expressions are numerically tested by Monte Carlo simulation, giving confidence in their validity. In Section 5, the expressions are applied to evaluate the experimental measurement uncertainties of the motion of a microelectromechanical goniometer labelled with fluorescent nanoparticles, providing a specific example of the type of analysis for which the expressions are useful. Future directions are indicated in Section 6, and conclusions are made in Section 7. Details of the measurement functions and associated uncertainties are presented in the Appendix.

2. Measurement functions and uncertainties for planar pose and motion

A sparse constellation of point sources in an invariant configuration can be used to measure the pose and motion of a rigid body in the imaging plane of an optical microscope by localizing and tracking the point sources, as illustrated in Figure 1. The optical indicators can be inherent to the body or applied for the purpose of the measurement. In such a measurement, an optical micrograph of a set of indicators in or on the body is captured, and the position of each point source is localized relative to the coordinate frame of the micrograph using an estimation technique, such as least squares or maximum likelihood (Mortensen et al., 2010). The images of the point sources in a micrograph captured after the body has moved are similarly localized. The full planar motion of the body can then be tracked by calculating the rigid planar transform that maps the points in the prior micrograph to the points in the subsequent micrograph. This transform can be expressed as a rotation followed by a translation.

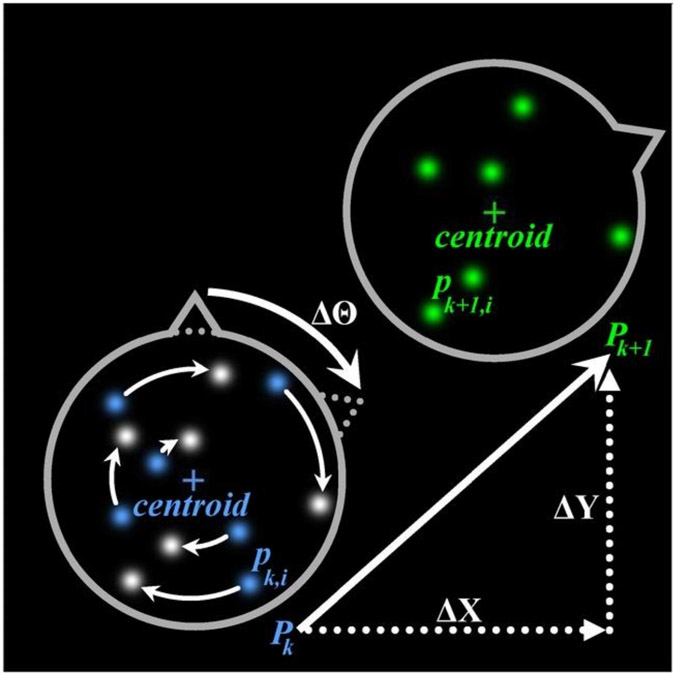
Fig. 1.

Schematic illustrating the measurement concept, in which a sparse constellation of point sources in an invariant constellation indicates the planarmotion of a microscopic rigid body. Planar motion of the body (gray) can be expressed by a rotation ($\Delta \Theta$) followed by a translation, ($\Delta X$, $\Delta Y$). The initial positions of the point sources (blue) are $P_k=\{p_{k,1},\dots ,p_{k,\eta }\}$, where $k$ is the index of a series of images, $\eta$ is the number of point sources, and $p_{i,j}$ is the position of the $j^{\text{th}}$ point source in the $i^{\text{th}}$ frame of an image sequence. After the body has moved, the final positions of the point sources (green) are $P_{k+1}=\{p_{k+1,1},\dots ,p_{k+1,\eta }\}$. Uncertainties of each of the three motion parameters are derived from the uncertainties of the positions of the point sources. The fundamental limits of uncertainty of position and orientation measurements are termed centroid precision and orientation precision, respectively. These limits are derived from the localization precision and radial position of the individual point sources in the constellation.

Let $P_k=\{p_{k,1},\dots ,p_{k,\eta }\}$ be a set of point source positions estimated from an image of a rigid body, and let ${\widehat{P}}_0=\{{\widehat{p}}_{0,1},\dots ,{\widehat{p}}_{0,\eta }\}$ be the set of true positions of those point sources when an arbitrarily defined coordinate system intrinsic to the body is aligned with the ($x$, $y$) axes of the measurement. The diacritical hat, such as appears in ${\widehat{P}}_0$, is used to denote a true value, as opposed to an estimated value. Let $T_P(\stackrel{\rightharpoonup }{v})$ be a transform over ($x$, $y$) vectors in the Cartesian plane. The pose of the body is the triple ($X$, $Y$, $\Theta$) such that $T_P(\stackrel{\rightharpoonup }{v})=\left[\begin{array}{cc}\hfill \cos \Theta \hfill & \hfill -\sin \Theta \hfill \\ \hfill \sin \Theta \hfill & \hfill \cos \Theta \hfill \end{array}\right]\stackrel{\rightharpoonup }{v}+(X,Y)$ is the transform that best maps ${\widehat{P}}_0$ onto $P$.

Similarly, if $P_k=\{p_{k,1},\dots ,p_{k,\eta }\}$ is a set of point source positions estimated prior to some planar rigid motion, and $P_{k+1}=\{p_{k+1,1},\dots ,p_{k+1,\eta }\}$ is the set of point source positions estimated subsequent to the motion, then $M_{k,k+1}(\stackrel{\rightharpoonup }{v})=T_{P_{k+1}}(\stackrel{\rightharpoonup }{v})-T_{P_k}(\stackrel{\rightharpoonup }{v})=\left[\begin{array}{cc}\hfill \cos \Delta \Theta \hfill & \hfill -\sin \Delta \Theta \hfill \\ \hfill \sin \Delta \Theta \hfill & \hfill \cos \Delta \Theta \hfill \end{array}\right]\stackrel{\rightharpoonup }{v}+(\Delta X,\Delta Y)$ is the transform characterizing the motion. Importantly, the triple ($\Delta X$, $\Delta Y$, $\Delta \Theta$) is independent of ${\widehat{P}}_0$, allowing motion measurements to be performed independently of the choice of the $\theta$ origin, which can be arbitrarily defined. The sets $P_k$ and $P_{k+1}$ may represent the positions of all point sources observed in the two images or the intersection of two different sets of point sources observed in the two images, as, for example, in the case of super-resolution imaging (Betzig et al., 2006; Hess et al., 2006; Rust et al., 2006).

The measurement functions utilized in calculating $M_{k,k+1}$ from $P_k$ and $P_{k+1}$ are best selected to minimize the uncertainty of each coordinate of the motion ($\Delta X$, $\Delta Y$, $\Delta \Theta$). In selecting these measurement functions and in calculating the associated uncertainties of motion, random and independent errors in the position estimates of point sources are assumed. The rotation and translation components of the motion can be treated separately (Arun et al., 1987). The translation, ($\Delta X$, $\Delta Y$), is considered first. Each coordinate of each position estimate of a point source, $p_{k,i}\in P_k$ or $p_{k+1,i}\in P_{k+1}$, has some associated measurement uncertainty, ${\sigma }_{x,k,i}\in S_{x,k}$, ${\sigma }_{x,k+1,i}\in S_{x,k+1}$, ${\sigma }_{y,k,i}\in S_{y,k}$, or ${\sigma }_{y,k+1,i}\in S_{y,k+1}$, which is at best the localization precision of that point source. If the uncertainties in $S_{x,k}$, $S_{y,k}$, $S_{x,k+1}$, and $S_{y,k+1}$ are all equal, then ($\Delta X$, $\Delta Y$) can be estimated with minimum uncertainty by the centroid displacement. However, in the experimentally relevant case that some of the points have lower uncertainties than others, for example due to a larger number of detected signal photons, then it is appropriate to weight the contribution of each point to the measurement, producing the following measurement function and associated uncertainty:

$$\begin{gathered} \Delta X_w=\sum _{i=1}^{\eta }{w}_{\Delta Xi}\left(x_{k+1,i}-x_{k,i}\right), \\ U(\Delta X_w)=\sqrt{\sum _{i=1}^{\eta }{w}_{\Delta Xi}^2\left({\sigma }_{x,k,i}^2+{\sigma }_{x,k+1,i}^2\right)}, \\ {w}_{\Delta Xi}^{\text{Opt}}=\frac{1}{\left(({\sigma }_{x,k,i}^2+{\sigma }_{x,k+1,i}^2)\sum _{j=1}^{\eta }\frac{1}{{\sigma }_{x,k,j}^2+{\sigma }_{x,k+1,j}^2}\right)}, \end{gathered}$$ (2)

where $\Delta X_w$ is the $x$ coordinate component of the weighted estimate of the object motion, $U(\Delta X_w)$ is the associated uncertainty, and the set $W_{\Delta X}=\{w_{\Delta Xi}:i\in 1..\eta \}$ is a set of weights applied to the point sources. Optimal choices of $W_{\Delta X}$ and $W_{\Delta Y}$ are inversely proportional to the sum of the variance, as shown in Eq. (2).

Similarly, an estimate of the minimum uncertainty of object rotation, ${\Delta \Theta }_w$, can be calculated from the optimally weighted measurement function with uncertainty $U({\Delta \Theta }_w)$ as follows:

$$\begin{gathered} \Delta {\Theta }_w=\frac{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}{r}_{k,i}{r}_{k+1,i}\left({\theta }_{k+1,i}-{\theta }_{k,i}\right)}{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}{r}_{k,i}{r}_{k+1,i}}, \\ U(\Delta {\Theta }_w)=\frac{\sqrt{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}^2\left(r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2\right)}}{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}{r}_{k,i}{r}_{k+1,i}}, \\ {w}_{\Delta \Theta i}^{\text{Opt}}=\frac{r_{k,i}{r}_{k+1,i}∕\left(r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2\right)}{\sum _{j=1}^{\eta }\frac{r_{k,j}{r}_{k+1,j}}{r_{k+1,j}^2{\sigma }_{k,j}^2+r_{k,j}^2{\sigma }_{k+1,j}^2}}, \end{gathered}$$ (3)

where ${\Delta \Theta }_w$ is the weighted estimate of the rotation of the object, ($r_{k,i}$, ${\theta }_{k,i}$) and ($r_{k+1,i}$, ${\theta }_{k+1,i}$) are the polar coordinates of the measured position of the $i^{\text{th}}$ point source with respect to the unweighted centroid of the constellation in the first and second image, respectively, $U({\Delta \Theta }_w)$ is the uncertainty of ${\Delta \Theta }_w$, $w_{\Delta \Theta i}$ is the weight applied to the $i^{\text{th}}$ point source, and $w_{\Delta \Theta i}^{\text{Opt}}$ is the value of the $i^{\text{th}}$ weight in a normalized, optimized weighting. Derivations are presented in the Appendix.

If ${\sigma }_{x,k,i}\approx {\sigma }_{x,k+1,i}\approx {\sigma }_{y,k,i}\approx {\sigma }_{y,k+1,i}$ for all $i\in \{1,\dots ,\eta \}$, then the uncertainty of each component of the motion is a factor of $\sqrt{2}$ greater than the corresponding component of the pose. The true positions ${\widehat{P}}_0$ are not ordinarily known or estimated in measurement applications, since there is no axis to which the orientation of the rigid body is absolutely registered. In such cases, rotation is a meaningful metric, but orientation is not. In contrast, the true positions, ${\widehat{P}}_0$, are typically known in simulations, such as the one reported in the Section 4.

3. Centroid precision and orientation precision

The expression of localization precision given by Eq. (1) is the minimum uncertainty of a position measurement of a point source. Analogously, the equations in Table 3 can be used to express the minimum uncertainties of position and orientation measurements of a constellation of point sources on a microscopic rigid body in the image plane of a microscope. Most notable of these expressions are the centroid precision and the orientation precision. Centroid precision and orientation precision are minimum values of the centroid uncertainty and orientation uncertainty of the constellation, respectively, as determined from optimally weighted measurements of the pose of the constellation:

$$\begin{gathered} C_{XP}=\sqrt{\frac{1}{\sum _{i=1}^{\eta }\frac{1}{{\sigma }_i^2}}},C_{YP}=\sqrt{\frac{1}{\sum _{i=1}^{\eta }\frac{1}{{\sigma }_i^2}}},O_P=\sqrt{\frac{1}{\sum _{i=1}^{\eta }{\left(\frac{r_i}{{\sigma }_i}\right)}^2}}, \\ {\sigma }_i=\frac{\sqrt{(16a^2{N}_i+72\pi b^2)\left({\sigma }_G^2+\frac{a^2}{12}\right)}}{3a{N}_i}, \end{gathered}$$ (4)

where ($C_{XP}$, $C_{YP}$) is the centroid precision, $O_p$ is the orientation precision and $N_i$ is the total number of signal photons detected from the $i^{\text{th}}$ point source. The minimum values for the associated measurements of motion are given in Table 3. These expressions have several practical implications. Both centroid precision and orientation precision can be improved by increasing the brightness of individual point sources and the number of point sources in the constellation. Orientation precision can be further improved by increasing the radius of the constellation.

Table 3.

Measurement functions and associated uncertainties.

	Pose($X$, $Y$, $\Theta$)		Motion($\Delta X$,$\Delta Y$,$\Delta \Theta$)
Measurand	Measurement	Uncertainty	Measurement	Uncertainty
$X_u$, $\Delta X_u$	$\frac{1}{\eta }\sum _{i=1}^{\eta }{x}_i$	$\frac{1}{\eta }\sqrt{\sum _{i=1}^{\eta }{\sigma }_i^2}$	$\frac{1}{\eta }\sum _{i=1}^{\eta }(x_{k+1,i}-x_{k,i})$	$\sqrt{\frac{1}{{\eta }^2}\sum _{i=1}^{\eta }({\sigma }_{k,i}^2+{\sigma }_{k+1,i}^2)}$
$X_w$, $\Delta X_w$	$\frac{\sum _{i=1}^{\eta }\frac{x_i}{{\sigma }_i^2}}{\sum _{\mathrm{i}=1}^{\eta }\frac{1}{{\sigma }_i^2}}$	$\sqrt{\frac{1}{\sum _{i=1}^{\eta }\frac{1}{{\sigma }_i^2}}}$	$\frac{\sum _{i=1}^{\eta }\frac{x_{k+1,i}-x_{k,i}}{{\sigma }_{k,i}^2+{\sigma }_{k+1,i}^2}}{\sum _{\mathrm{i}=1}^{\eta }\frac{1}{{\sigma }_{k,i}^2+{\sigma }_{k+1,i}^2}}$	$\sqrt{\frac{1}{\sum _{i=1}^{\eta }\frac{1}{{\sigma }_{k,i}^2+{\sigma }_{k+1,i}^2}}}$
${\Theta }_u$, $\Delta {\Theta }_u$	$\frac{\sum _{i=1}^{\eta }{r}_i{\widehat{s}}_i({\widehat{\gamma }}_i-{\theta }_i)}{\sum _{i=1}^{\eta }{r}_i{\widehat{s}}_i}$	$\frac{\sqrt{\sum _{i=1}^{\eta }{\sigma }_i^2{r}_i^2}}{\sum _{i=1}^{\eta }{r}_i^2}$	$\frac{\sum _{i=1}^{\eta }{r}_{k,i}{r}_{k+1,i}({\theta }_{k+1,i}-{\theta }_{k,i})}{\sum _{i=1}^{\eta }{r}_{k,i}{r}_{k+1,i}}$	$\frac{\sqrt{\sum _{i=1}^{\eta }(r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2)}}{\sum _{i=1}^{\eta }{r}_{k,i}{r}_{k+1,i}}$
${\Theta }_w$, $\Delta {\Theta }_w$	$\frac{\sum _{i=1}^{\eta }\frac{r_i{\widehat{s}}_i({\widehat{\gamma }}_i-{\theta }_i)}{{\sigma }_i^2}}{\sum _{i=1}^{\eta }\frac{r_i{\widehat{s}}_i}{{\sigma }_i^2}}$	$\sqrt{\frac{1}{\sum _{i=1}^{\eta }{(\frac{r_i}{{\sigma }_i})}^2}}$	$\frac{\sum _{i=1}^{\eta }\frac{r_{k,i}^2{r}_{k+1,i}^2({\theta }_{k+1,i}-{\theta }_{k,i})}{r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2}}{\sum _{i=1}^{\eta }\frac{r_{k,i}^2{r}_{k+1,i}^2}{r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2}}$	$\sqrt{\frac{1}{\sum _{i=1}^{\eta }\frac{r_{k,i}^2{r}_{k+1,i}^2}{r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2}}}$
Expressions for $x$-axis pose and motion are isomorphic to those for $y$-axis pose and motion.

$\eta$ is the number of point sources used in the measurement; $x_i$, $x_{k,i}$, $x_{k+1,i}$ the estimated $x$ coordinate of the ith point in the only image, image $k$, and image $k+1$; ${\sigma }_i$, ${\sigma }_{k,i}$, ${\sigma }_{k+1,i}$ the single-axis uncertainties of the $i^{\text{th}}$ point in the only image, image $k$, and image $k+1$; $r_i$, $r_{k,i}$, $r_{k+1,i}$ the estimated $r$ coordinate of the $i^{\text{th}}$ point in the only image, image $k$, and image $k+1$; ${\theta }_i$, ${\theta }_{k,i}$, ${\theta }_{k+1,i}$ the estimated $\theta$ coordinate of the $i^{\text{th}}$ point in the only image, image $k$, and image $k+1$; ${\widehat{s}}_i$, ${\widehat{\gamma }}_i$ the true centroid-offset position of the $i^{\text{th}}$ point in polar coordinates; $X_u$, $X_w$ the uniformly weighted and optimally weighted estimates of $x$-axis centroid position; ${\Theta }_u$, ${\Theta }_w$ the uniformly weighted and optimally weighted estimates of orientationl; ${\Delta X}_u$, ${\Delta X}_w$ the uniformly and optimally weighted estimates of $x$-axis centroid displacement; ${\Delta \Theta }_u$, ${\Delta \Theta }_w$ the uniformly weighted and optimally weighted estimates of rotation.

4. Numerical validation of uncertainty equations

A Monte Carlo simulation was conducted to validate the measurement uncertainties shown in Table 3. Sets of points were randomly generated, and each set of points was subjected to a randomly generated rigid planar transformation. Two images were synthesized from each set of points, one from the untransformed configuration of the set and one from the transformed configuration. In the synthetic images, each point was represented by a two-dimensional Gaussian intensity function with a randomly generated total number of photons. After adding a randomly generated uniform background photon intensity to the image, the intensity value of each pixel in the image was used as the lambda parameter for generating a value from a Poisson distribution. In this way, each image was constructed to resemble the image of a set of point sources recorded by an ideal sensor (Geist et al., 1982), and to represent isotropic emitters, as opposed to dipole emitters, for which synthetic images can be found elsewhere (Sage et al., 2015). The ranges of the parameters used and other details of the simulation are summarized in Section A5 of the Appendix.

The positions of the points in each synthetic image were estimated by regression to a bivariate Gaussian with parameters $\{x_0,y_0,\alpha ,s,C\}$, where ($x_0$, $y_0$) are the coordinates of the Gaussian peak, $\alpha \approx kN∕2\pi {\sigma }_{\mathrm{G}}^2$ is the Gaussian amplitude, $s\approx {\sigma }_{\mathrm{G}}$ is the Gaussian standard deviation, $C\approx {kb}^2∕a^2$ is an offset approximating the background intensity, and $k$ is the ratio of camera pixel intensity counts to photon counts. Poses and motions of the simulated rigid body were calculated from the estimated point positions using the measurement functions in Table 3. For simulated pose measurements, the true positions of the untransformed points were treated as ${\widehat{P}}_0$.

A set of $\tau =200$ image pairs was simulated according to the above procedure. Each pair was simulated $\omega =2500$ times for a total of 1 million images. For each of the 12 measurands, $M_i$, of Table 3, the standard deviation of the set of estimates is the simulated uncertainty of the measurement, $U_{\text{sim}}(M_i)$. The calculated uncertainty, $U_{calc}(M_i)$, is determined from the associated uncertainty equation in Table 3. For each measurand, the normalized root mean square residual is defined as $\sqrt{\frac{1}{\tau }{\sum }_{i=1}^{\tau }{(\frac{U_{\text{sim}}(M_i)-U_{\text{calc}}(M_i)}{U_{\text{calc}}(M_i)})}^2}$, the residual bias is defined as $\frac{1}{\tau }{\sum }_{i=1}^{\tau }\frac{U_{\text{sim}}(M_i)-U_{\text{calc}}(M_i)}{U_{\text{calc}}(M_i)}$, and the coefficient of determination is defined as $R^2=1-\frac{{\sum }_{i=1}^{\tau }{(U_{\text{sim}}(M_i)-U_{\text{calc}}(M_i))}^2}{{\sum }_{i=1}^{\tau }{(U_{\text{sim}}(M_i)-{\sum }_{j=1}^{\tau }{U}_{\text{sim}}(M_j)∕\tau )}^2}$. All of the normalized root mean square residuals were less than 2.5 %, the absolute values of all of the residual biases were less than 0.8 %, and the $R^2$ values of all of the measurands were greater than 0.996, indicating good agreement between the calculated and simulated uncertainties.

Normal probability plots (not shown) indicated that the residuals were normally distributed. Graphical residual analysis demonstrated good randomness in the residuals with respect to the calculated uncertainties and all model parameters except for the standard deviation of the Gaussian point spread function, ${\sigma }_{\mathrm{G}}$. A slight positive relationship between ${\sigma }_{\mathrm{G}}$ and the normalized residual of each measurand was fit to a linear regression model. For each measurand, the slope of this trend line was less than 0.5 % per pixel of ${\sigma }_{\mathrm{G}}$. This systematic difference between the analytical calculations and the Monte Carlo calculations may have been due to truncation of wide Gaussians, since the region of interest employed in calculating each point source position had a width of 30 pixels. The largest simulated Gaussians with ${\sigma }_{\mathrm{G}}=6$ were therefore truncated at $\pm 2.5{\sigma }_{\mathrm{G}}$. The systematic variation between the analytical and Monte Carlo models due to this effect was only 3% across the full domain of point spread functions tested.

5. Experimental pose and motion measurements

The utility of the derived measurement functions and associated uncertainties was demonstrated by analysis of the uncertainties from experimental measurements of the motion of a microelectromechanical system (MEMS). This particular MEMS (Oak et al., 2011) took the form of a goniometer, articulated by a chevron-type electrothermal actuator (Sinclair, 2000; Baker et al., 2004), with an indicator needle rotating around a pivot, pointing to a dial gauge with graduations at increments of 17.5 mrad (1°) for readout, as shown in Figure 2. The indicator needle was labelled with subresolution fluorescent nanoparticles, and the system was imaged using a widefield epifluorescence microscope equipped with a light emitting diode for excitation at approximately 630 nm, an objective lens with a nominal magnification of 50× and a numerical aperture of 0.55, and a complementary metal–oxide–semiconductor camera with a nominal pixel size of 6.5 μm × 6.5 μm for detection at approximately 660 nm. A region of the imaging sensor of 812 pixels × 1856 pixels was used, resulting in a field of view of 103 μm × 236 μm. Representative parameters of the experimental measurement system that are relevant to the calculation of uncertainties are given in Table 1.

Fig. 2.

(Top) Optical brightfield micrograph showing a microelectromechanical system (MEMS) in the form of a goniometer, with an electrothermal actuator linked to an indicator needle. Linear actuation of the electrothermal actuator resulted in rotary motion of the indicator needle around a pivot. Coarse measurement of rotation was enabled by a graduated dial gauge. A region of interest is indicated by a white box. (Middle) Optical fluorescence micrograph showing a constellation of fluorescent nanoparticles on the indicator needle in the region of interest. (Bottom) Optical fluorescence micrographs showing four of the nanoparticles that label the indicator needle, appearing as the point spread function of the imaging system. The nanoparticles are ordered from left to right by increasing numbers of detected signal photons ($N$), which vary due to polydispersity in nanoparticle size and heterogeneity in illumination intensity. A larger number of detected signal photons results in a lower measurement uncertainty, motivating weighting of the contributions of individual nanoparticles to the overall measurement.

Table 1.

Representative parameters of the experimental measurement system.

Parameter	Value	Units	Subsystem
$a$	127	nm	Microscope
$b^2$	228	photons per pixel	Microscope
${\sigma }_{\mathrm{G}}$	286	nm	Microscope
$N_i$	104 to 105	photons	Particles
$r_i$	10 to 100	$\mu \mathrm{m}$	Particles

To evaluate the uncertainties of position measurements of individual fluorescent nanoparticles, 2000 sequential fluorescence micrographs of the labelled indicator needle were recorded at a rate of 8 Hz in the absence of intended motion. Images were processed after the experiment at a rate of 2.5 Hz, including target detection, registration, Gaussian estimation and motion calculation. The $x$ and $y$ position of each nanoparticle was measured by least squares Gaussian estimation from the image data, which is equivalent to maximum likelihood estimation for the number of detected signal photons. The corresponding uncertainty of each coordinate of the position of each nanoparticle was determined from the root mean square displacement of the nanoparticle between successive images divided by $\sqrt{2}$, which is equivalent to a pooled standard deviation of successive image pairs (ISO Technical Advisory Group 4, 1995). The position uncertainties of individual nanoparticles were then used to calculate predicted uncertainties for motion measurements of the nominally rigid indicator needle, according to the uncertainty expressions of Table 3.

Empirical uncertainties for motion measurements of the indicator needle were then estimated from the apparent motion of the needle between each pair of successive images, due to vibration, drift, or other non-ideal behaviour, as well as photon shot noise described by Eq. (1). The motion of the indicator needle between each successive pair of images was estimated using the expressions of Table 3, after establishing a correspondence between the points in each image (Besl & McKay, 1992; Pennec & Thirion, 1997; Zitova & Flusser, 2003). The empirical uncertainty of each coordinate of this motion was calculated as the standard deviation of the set of estimates of the corresponding coordinate. The resulting empirical uncertainties are compared in Table 2 with the uncertainties predicted by the expressions of Table 3, and also with the minimum uncertainties given by the centroid and orientation precision.

Table 2.

Measurement uncertainties of the planar motion of a MEMS goniometer.

Uncertainty	Uniform $\Delta X_u$ (pixels)	Optimal $\Delta X_w$ (pixels)	Uniform $\Delta Y_u$ (pixels)	Optimal $\Delta Y_w$ (pixels)	Uniform $\Delta {\Theta }_u$ (μ-rad)	Optimal $\Delta {\Theta }_w$ (μ-rad)
Predicted	0.0093	0.0081	0.0096	0.0081	21.4	18.5
Empirical	0.0101	0.0093	0.0107	0.0097	23.4	18.9
Minimum	0.0031	0.0030	0.0031	0.0030	6.7	6.5

The predicted and empirical uncertainties agree to within 2.9–16.5%. This near equality of uncertainties validates the assumption of planar rigid motion, as violation of this assumption would lead to much higher empirical uncertainties. In contrast, the predicted and empirical uncertainties are approximately a factor of three times greater than the minimum uncertainties defined by Eq. (4). This is a useful result, indicating that the limiting factor of the experimental measurement was not one of the parameters modelled by the measurement functions.

Such factors might include vibration and drift of the microscope system, or fixed pattern noise of the complementary metal–oxide–semiconductor camera. The empirical uncertainty might therefore be improved by up to a factor of three by additional investigation and mitigation of such factors, for example, by drift correction (Lee et al., 2012; Elmokadem & Yu, 2015) or camera calibration (Huang et al., 2013) If the empirical uncertainties and predicted uncertainties were then to become approximately equal to the associated minimum uncertainties, the signal-to-noise ratio would be the limiting factor of the measurement. Only at this point would the detection of more signal photons, for example, be useful to further reduce the measurement uncertainty. Such comparison of measured to minimum uncertainties provides practical guidance for ongoing improvement of the experimental measurement system.

Once the uncertainty of the rotation measurement was established, the repeatability of the MEMS rotation was tested. The actuator was driven alternately with an applied voltage of 0 and 5 V for 1000 cycles, which repeatedly rotated the indicator needle by an angle of ±5.00 mrad (±0.287°). Fluorescence micrographs were taken after each motion, and the rotation of the indicator needle was determined using the optimally weighted and uniformly weighted estimators, ${\Delta \Theta }_w$ and ${\Delta \Theta }_u$. The rotational repeatability of the indicator needle, as determined by the standard deviation of the motion measurement, was 18.9 μrad – the same as the empirical uncertainty – indicating that the observed repeatability was dominated by measurement uncertainty. Therefore, the repeatability of the MEMS may have been even better than indicated by this measurement. This is an interesting result, considering the sliding contact in the linkage coupling the electrothermal actuator and indicator needle. The motions of such systems can be complex, as will be investigated in future studies.

6. Future directions

The measurement functions and associated uncertainties presented in this paper have expressed the physical lower bounds of uncertainty of measurements of planar pose and motion, in terms of the parameters of the experimental measurement system used to perform localization microscopy. The direct calculation of these minimum uncertainties was facilitated by the existing theoretical basis of localization precision. This is an important distinction between the mathematical expressions presented here, and many generic algorithms for image registration (Zitova & Flusser, 2003). Although measurement uncertainties derived from such algorithms are beginning to be addressed (Fitzpatrick & West, 2001; Simonson et al., 2007), a similar physical basis for uncertainty is not ordinarily available for such generic algorithms. Future work might trace the uncertainties of generic algorithms to a physical basis in the quantization of light.

The measurement functions and associated uncertainties presented in this paper apply to the broadly relevant case of the pose and motion of rigid bodies within the image plane of an optical microscope. However, in some applications of localization microscopy, microscopic rigid bodies exhibit a component of motion out of the image plane. Such motion may lead to systematic effects that are not modelled here, and would be indicated by a discrepancy between the empirical and predicted uncertainties. The effects of such motion will be addressed in future work by a generalization of the image mapping from rigid to affine transformations.

The measurement functions, associated uncertainties, and experimental analysis presented in this paper are predicated on the assumption stated in Section 2 that errors in position estimates of point sources are random and independent. However, this assumption could be invalidated by some motions of optical microscopes, such as drift and vibration, which could result in correlated errors in position estimates of multiple point sources. Related effects will be addressed in future work.

Finally, the experimental measurements in this paper were performed on a microfabricated device that implemented motion as an engineered function. The measurement functions and associated uncertainties presented in this paper are similarly applicable in different experimental contexts, for example, reference measurements of multiple point sources in a fiducial constellation for investigation and correction of errors from unintended motion of an optical microscope.

7. Conclusions

This paper has extended the concept of localization precision from optical point sources to microscopic rigid bodies in the imaging plane of a widefield microscope. This has established a firm foundation for related measurements involving localization microscopy. A complete set of measurement functions in closed form, along with the associated set of measurement uncertainties, was calculated for the planar pose and motion of rigid bodies indicated by a sparse constellation of multiple point sources of light in an invariant configuration. Physical limits on the minimum uncertainties, termed centroid precision and orientation precision, were expressed in terms of the characteristic properties of the optical measurement system. These measurement functions and uncertainties were numerically validated by Monte Carlo simulation. The utility of the expressions was demonstrated by analysis of the empirical uncertainty of motion measurements of a microelectromechanical goniometer. Because of the generality of centroid precision and orientation precision, and the widespread interest in super-resolution imaging and particle tracking, these innovations are broadly applicable to designing measurements for low uncertainty, interpreting the significance of measurement uncertainties, and identifying sources of uncertainty in measurement systems.

Appendix

Detailed descriptions of measurement functions, associated uncertainties, analytical derivations, and numerical simulations are presented in this appendix.

A1. Measurement functions for planar motion of a rigid body

If a sparse constellation of multiple point sources in an invariant configuration is located in or on a rigid body, then the planar pose of the body can be determined from the positions of the point sources. Similarly, the motion of the body can be determined from the change in the positions of the point sources resulting from the motion. Measurement functions for each coordinate of pose and motion, reflecting uniform weighting of the point sources and optimal weighting of the point sources, along with associated uncertainties for the measurements, are presented in Table 3. Derivations and discussion of the measurement functions are presented in the remainder of this section. The associated uncertainties are derived and discussed in Section A2.

A1.1. Measurement functions for planar motion of a rigid body.

Let $\widehat{P}=\{{\widehat{p}}_1,\dots ,{\widehat{p}}_{\eta }\}$ be the true positions of a set of $\eta$ point sources on a rigid body and let ${\widehat{P}}_0=\{{\widehat{p}}_{0,1},\dots ,{\widehat{p}}_{0,\eta }\}$ be the set of true positions of those point sources when an arbitrarily-defined coordinate system intrinsic to the body is aligned with the ($x$, $y$) axes of the measurement. The true pose of the body is defined by the proper rigid planar transform, ${\widehat{T}}_P(\stackrel{\rightharpoonup }{v})$ over ($x$, $y$) vectors in the Cartesian plane, that maps ${\widehat{P}}_0$ to $\widehat{P}$. The transform ${\widehat{T}}_P(\stackrel{\rightharpoonup }{v})$ can be expressed in terms of three scalar parameters as follows:

$${\widehat{T}}_P\left(\stackrel{\rightharpoonup }{v}\right)=\left[\begin{array}{cc}\hfill \cos \widehat{\Theta }\hfill & \hfill -\sin \widehat{\Theta }\hfill \\ \hfill \sin \widehat{\Theta }\hfill & \hfill \cos \widehat{\Theta }\hfill \end{array}\right]\left(\stackrel{\rightharpoonup }{v}-(\widehat{X},\widehat{Y})\right)+(\widehat{X},\widehat{Y}),$$ (A1)

where the triple, ($\widehat{X}$, $\widehat{Y}$, $\widehat{\Theta }$), is an equivalent expression of the true object pose, with $\widehat{X}$ corresponding to the $x$-axis position, $\widehat{Y}$ to the $y$-axis position, and $\widehat{\Theta }$ to the orientation.

Let $P=\{p_1,\dots ,p_{\eta }\}$ be a set of estimates of the positions in $\widehat{P}$. Estimates of the object pose can be calculated from $P$ as follows:

$$X=\sum _{i=1}^{\eta }{w}_{xi}{x}_{i}Y=\sum _{i=1}^{\eta }{w}_{yi}{y}_i\Theta =\frac{\sum _{i=1}^{\eta }{w}_{\theta i}{r}_i{\widehat{s}}_i\left({\widehat{\gamma }}_i-{\theta }_i\right)}{\sum _{i=1}^{\eta }{w}_{\theta i}{r}_i{\widehat{s}}_i}$$ (A2)

where $X$, $Y$ and $\Theta$ are estimates of $\widehat{X}$, $\widehat{Y}$ and $\widehat{\Theta }$, respectively; $x_i$ and $y_i$ are the Cartesian coordinates of $p_i$; $r_i$ and ${\theta }_i$ are the polar coordinates of $p_i$ with respect to an origin at the (weighted) centroid of $P$; ${\widehat{s}}_i$ and ${\widehat{\gamma }}_i$ are the polar coordinates of ${\widehat{p}}_{0,i}$ with respect to an origin at the (weighted) centroid of ${\widehat{P}}_0$ and the sets $W_x=\{w_{xi}:i\in 1..\eta \}$, $W_y=\{w_{yi}:i\in 1..\eta \}$ and $W_{\theta }=\{w_{\theta i}:i\in 1..\eta \}$ are weights applied to the measurements.

A1.2. Motion measurement functions.

If two images bracket a motion of a planar rigid body, then the motion can be determined from the change in the estimated positions of corresponding point sources in the two images, as determined by localization microscopy. Let ${\widehat{P}}_k=\{{\widehat{p}}_{k,1},\dots ,{\widehat{p}}_{k,\eta }\}$ be the true positions of a set of $\eta$ point sources on a rigid body prior to some motion, and let ${\widehat{P}}_{k+1}=\{{\widehat{p}}_{k+1,1},\dots ,{\widehat{p}}_{k+1,\eta }\}$ be the set of true positions of those point sources after the motion. The motion of the body is defined by the proper rigid planar transform, ${\widehat{T}}_{k,k+1}(\stackrel{\rightharpoonup }{v})$ over ($x$, $y$) vectors in the Cartesian plane, that maps ${\widehat{P}}_k$ to ${\widehat{P}}_{k+1}$. The transform ${\widehat{T}}_{k,k+1}(\stackrel{\rightharpoonup }{v})$ can be expressed in terms of three scalar parameters as follows:

$$\begin{gathered} {\widehat{T}}_{k,k+1}\left(\stackrel{\rightharpoonup }{v}\right)=\left[\begin{array}{cc}\hfill \cos \Delta \widehat{\Theta }\hfill & \hfill -\sin \Delta \widehat{\Theta }\hfill \\ \hfill \sin \Delta \widehat{\Theta }\hfill & \hfill \cos \Delta \widehat{\Theta }\hfill \end{array}\right]\left(\stackrel{\rightharpoonup }{v}-(\Delta \widehat{X},\Delta \widehat{Y})\right) \\ +(\Delta \widehat{X},\Delta \widehat{Y}), \end{gathered}$$ (A3)

where ($\Delta \widehat{X}$, $\Delta \widehat{Y}$, $\Delta \widehat{\Theta }$) is an equivalent expression of the true motion of the object, with $\Delta \widehat{X}$, $\Delta \widehat{Y}$ and $\Delta \widehat{\Theta }$ corresponding to the $x$-axis displacement, $y$-axis displacement, and rotation, respectively.

Let $P_k=\{p_{k,1},\dots ,p_{k,\eta }\}$ be a set of estimates of the positions in ${\widehat{P}}_k$, and let $P_{k+1}=\{p_{k+1,1},\dots ,p_{k+1,\eta }\}$ be a set of estimates of the positions in ${\widehat{P}}_{k+1}$. Estimates of the motion of the object can be calculated from $P_k$ and $P_{k+1}$ as follows:

$$\begin{gathered} \Delta X=\sum _{i=1}^{\eta }{w}_{\Delta Xi}\left(x_{k+1,i}-x_{k,i}\right), \\ \Delta Y=\sum _{i=1}^{\eta }{w}_{\Delta Yi}\left(y_{k+1,i}-y_{k,i}\right), \\ \Delta \Theta =\frac{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}{r}_{k+1,i}{r}_{k,i}\left({\theta }_{k,i}-{\theta }_{k+1,i}\right)}{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}{r}_{k+1,i}{r}_{k,i}}, \end{gathered}$$ (A4)

where $\Delta X$, $\Delta Y$ and $\Delta \Theta$ are estimates of $\Delta \widehat{X}$, $\Delta \widehat{Y}$ and $\Delta \widehat{\Theta }$, respectively; ($x_{k,i}$, $y_{k,i}$) and ($x_{k+1,i}$, $y_{k+1,i}$) are the Cartesian coordinates of $p_{k,i}$ and $p_{k+1,i}$; ($r_{k,i}$, ${\theta }_{k,i}$) and ($r_{k+1,i}$, ${\theta }_{k+1,i}$) are the polar coordinates of $p_{k,i}$ and $p_{k+1,i}$ with respect to origins at the (weighted) centroids of $P_k$ and $P_{k+1}$, respectively; and the sets $W_{\Delta X}=\{w_{\Delta Xi}:i\in 1..\eta \}$, $W_{\Delta Y}=\{w_{\Delta Yi}:i\in 1..\eta \}$ and $W_{\Delta \Theta }=\{w_{\Delta \Theta i}:i\in 1..\eta \}$ are weights applied to the measurements.

A1.3. Derivation of the orientation measurement function.

The expression for $\Theta$ in Eq. (A2) is derived by finding the value of $\Theta$ that minimizes the weighted sum of squared error between $P$ and $T_P({\widehat{P}}_0)$:

$$\begin{gathered} E(\alpha )=\sum _{i=1}^{\eta }{w}_{\Theta i}{\epsilon }_i^2=\sum _{i=1}^{\eta }{w}_{\Theta i}(r_i^2+{\widehat{s}}_i^2-2r_i{\widehat{s}}_i\phantom{)} \\ \phantom{(}\cos ({\widehat{\gamma }}_i-({\theta }_i+\alpha ))), \end{gathered}$$ (A5)

where ($r_i$, ${\theta }_i$) are the coordinates of the $i^{\text{th}}$ point in $P-(X,Y)$ and (${\widehat{s}}_i$, ${\widehat{\gamma }}_i$) are the coordinates of the corresponding point in ${\widehat{P}}_0$. The offset, $\alpha$, is the free variable for the optimization and represents a test rotation between the two sets of points. The error, ${\epsilon }_i$, is the distance between ${\widehat{p}}_i$ and the point found by rotating $p_i$ by $\alpha$, and $w_{\theta i}$ is the weight applied to the squared error ${\epsilon }_i^2$. The optimal choice of rotation determined by this method, $\Theta$, is found by minimizing $E$:

$$\begin{gathered} \Theta =\left[\alpha :\frac{dE}{d\alpha }=0\right] \\ =\left[\alpha :\sum _{i=1}^{\eta }(-2w_{\theta i}{r}_i{\widehat{s}}_{i}sin\left({\widehat{\gamma }}_i-({\theta }_i+\alpha )\right))=0\right] \\ =[\alpha :\sum _{i=1}^{\eta }-2w_{\theta i}{r}_i{\widehat{s}}_i(\sin ({\widehat{\gamma }}_i-{\theta }_i)\cos \alpha \phantom{)}\phantom{]} \\ \phantom{[}-\cos \left({\widehat{\gamma }}_i-{\theta }_i\right)\sin \alpha )=0]. \end{gathered}$$ (A6)

The optimal value of $\alpha$ can then be found by solving Eq. (A6), which yields:

$$\Theta =\alpha =\mathrm{atan}\frac{\sum _{i=1}^{\eta }{w}_{\theta i}{r}_i{\widehat{s}}_i\sin ({\widehat{\gamma }}_i-{\theta }_i)}{\sum _{i=1}^{\eta }{w}_{\theta i}{r}_i{\widehat{s}}_i\cos ({\widehat{\gamma }}_i-{\theta }_i)}.$$ (A7)

Alternatively, the residuals (${\widehat{\gamma }}_i-({\theta }_i+\alpha )$) in Eq. (A6) can be treated with a small angle approximation yielding the simpler expression:

$$\Theta =\alpha =\frac{\sum _{i=1}^{\eta }{w}_{\theta i}{r}_i{\widehat{s}}_i({\widehat{\gamma }}_i-{\theta }_i)}{\sum _{i=1}^{\eta }{w}_{\theta i}{r}_i{\widehat{s}}_i}=\frac{\beta }{\lambda },$$ (A8)

where the sums $\beta$ and $\lambda$ are implicitly defined by the numerator and denominator to simplify use of the expression in the next section.

A2. Uncertainties of motion measurements by localization microscopy

Given uncertainties, (${\sigma }_{xi}$, ${\sigma }_{yi}$), of the position of each point source $p_i\in P$, the combined standard uncertainty of each component of the pose of $P$ can be calculated from the associated measurement function using the law of propagation of uncertainty (ISO Technical Advisory Group 4, 1995). Here the pose and motion uncertainties are calculated for the common case in which ${\sigma }_i={\sigma }_x={\sigma }_y$ for each value of $i$.

A2.1. Position uncertainty.

The $x$-axis position uncertainty of a pose measurement by localization microscopy can be calculated from the $x$-axis position uncertainties of the individual points, $S_x=\{{\sigma }_i:i\in 1..\eta \}$, and the associated weights, $W_X$, using the law of propagation of uncertainty as follows:

$$U(X)=\sqrt{\sum _{i=1}^{\eta }\left(\frac{dX}{d{x}_i}\right){(U(x_i))}^2}=\sqrt{\sum _{i=1}^{\eta }{w}_{Xi}^2{\sigma }_i^2}.$$ (A9)

The expression for $U(Y)$ is isomorphic to $U(X)$.

A2.2. Orientation uncertainty.

With Eq. (A8) defining the measured value of $\Theta$, the measurement uncertainty associated with $\Theta$ can be calculated from the law of propagation of uncertainty (ISO Technical Advisory Group 4, 1995) as follows:

$$\begin{gathered} {(U(\Theta ))}^2=\sum _{i=1}^{\eta }({\left(\frac{d\Theta }{d{\theta }_i}U({\theta }_i)\right)}^2+{\left(\frac{d\Theta }{d{\widehat{\gamma }}_i}U({\widehat{\gamma }}_i)\right)}^2\phantom{)} \\ +\phantom{(}{\left(\frac{d\Theta }{d{r}_i}U(r_i)\right)}^2+{\left(\frac{d\Theta }{d{\widehat{s}}_i}U({\widehat{s}}_i)\right)}^2) \\ \approx \sum _{i=1}^{\eta }({\left(\frac{-w_{\Theta i}{r}_i{\widehat{s}}_i}{\lambda }U({\theta }_i)\right)}^2\phantom{)} \\ +\phantom{(}{\left(\frac{w_{\theta i}{\widehat{s}}_i({\widehat{\gamma }}_i-{\theta }_i)\lambda -w_{\Theta i}{\widehat{s}}_i\beta }{{\lambda }^2}U(r_i)\right)}^2), \end{gathered}$$ (A10)

where $U(\Theta )$ is the uncertainty of $\Theta$, $U({\theta }_i)$ is the uncertainty of ${\theta }_i$, $U(r_i)$ is the uncertainty of $r_i$, $U({\widehat{\gamma }}_i)$ is the uncertainty of ${\widehat{\gamma }}_i$, $U({\widehat{s}}_i)$ is the uncertainty of ${\widehat{s}}_i$ and $\beta$ and $\lambda$ are defined in Eq. (A8). Since ${\widehat{\gamma }}_i$ and ${\widehat{s}}_i$ are true point coordinates, $U({\widehat{\gamma }}_i)$ and $U({\widehat{s}}_i)$ are both zero.

$U({\theta }_i)$ and $U(r_i)$ can be derived from the position uncertainties, $U(x_i)=U(y_i)={\sigma }_i$, again by using the law of propagation of uncertainty:

$$U({\theta }_i)=\frac{{\sigma }_i}{r_i},U(r_i)={\sigma }_i.$$ (A11)

The uncertainty of the rotation can then be calculated as:

$${(U(\Theta ))}^2\approx \frac{1}{{\lambda }^2}\sum _{i=1}^{\eta }\left({(w_{\Theta i}{\widehat{s}}_i{\sigma }_i)}^2(1+{({\widehat{\gamma }}_i-{\theta }_i-\Theta )}^2)\right).$$ (A12)

Noting that the residuals, (${\widehat{\gamma }}_i-{\theta }_i-\Theta$), are far smaller than unity and that the centroid distance errors, ($r_i-{\widehat{s}}_i$), are far smaller than the centroid distances themselves in all but degenerate cases, the orientation uncertainty can then be approximated as:

$$U(\Theta )\approx \frac{\sqrt{\sum _{i=1}^{\eta }{(w_{\Theta i}{r}_i{\sigma }_i)}^2}}{\sum _{i=1}^{\eta }\left(w_{\Theta i}{r}_i^2\right)}.$$ (A13)

It is evident from Eq. (A13) that the orientation uncertainty depends neither on the choice of the ($x$, $y$, $\theta$) origin, nor on the orientation, $\Theta$, but only on the weight, the position uncertainty, and the distance from the centroid of each point in $P$.

A3. Minimum uncertainty weights

An optimal weighting, $W_M$, for each measurand, $M\in \{X,Y,\Theta ,\Delta X,\Delta Y,\Delta \Theta \}$, can be determined from the estimated coordinates of the individual point sources and their associated uncertainties, such that the uncertainty of the measurand is minimized. The calculations for optimally weighted measurement functions are presented below and uncertainties are presented in Table 3. The optimal weight calculations are presented in Sections A3.1-A3.3.

A3.1. Optimal weighting for position.

Weightings for measurements of the position of a rigid body are restricted to those in which the weights sum to unity, to avoid scaling the measurand. The method of Lagrange is utilized to minimize the uncertainties of the weighted position calculated in Section 2, subject to the normalization constraint.

Consider the square of the $x$-axis position uncertainty of Eq. (A9):

$$U^2(X)=\sum _1^{\eta }{w}_{Xi}^2{\sigma }_i^2.$$ (A14)

To minimize the squared uncertainty subject to the constraint ${\sum }_{i=1}^{\eta }{w}_{Xi}=1$, a Lagrangian is constructed as follows:

$$\Lambda \left(w_{X1},\dots ,w_{X\eta },\lambda \right)=\left(\sum _{i=1}^{\eta }{w}_{Xi}^2{\sigma }_i^2\right)+\lambda \left(\left(\sum _{i=1}^{\eta }{w}_{Xi}\right)-1\right),$$ (A15)

where $\Lambda$ is the Lagrangian and $\lambda$ the Lagrange multiplier. The zeros of the partial derivatives of $\Lambda$ with respect to $W_X$, coupled with the normalization constraint, provide the following system of $\eta +1$ equations:

$$w_{Xi}=\frac{-\lambda }{2{\sigma }_i^2},\sum _{i=1}^{\eta }{w}_{Xi}=1,$$ (A16)

which yields uniquely optimal weights:

$$w_{Xi}=\frac{1}{{\sigma }_i^2\sum _{j=1}^{\eta }\frac{1}{{\sigma }_j^2}}.$$ (A17)

Substituting Eq. (A17) into Eq. (A9) produces the minimum uncertainty in $x$-axis position that is achievable:

$$U(X)=\sqrt{\frac{1}{\sum _{i=1}^{\eta }\frac{1}{{\sigma }_i^2}}}$$ (A18)

The weighting for minimum uncertainty of $y$-axis position is isomorphic.

A3.2. Optimal weighting for orientation.

Since orientation is scale invariant, the method of Lagrange need not be used, and a set of weightings can be determined all of which are optimal with respect to orientation uncertainty. For simplicity, the unique normalized optimal weighting is selected.

Consider the square of the orientation uncertainty of Eq. (A13):

$$U^2(\Theta )\approx \frac{\sum _{i=1}^{\eta }{(w_{\Theta i}{r}_i{\sigma }_i)}^2}{{\left(\sum _{i=1}^{\eta }{w}_{\Theta i}{r}_i^2)\right)}^2}.$$ (A19)

Optimal weightings occur where the gradient of $U^2(\Theta )$ with respect to the set of $w_i$ is zero. Each component of the gradient can be expressed as:

$$\begin{gathered} \frac{\partial U^2(\Theta )}{\partial w_{\Theta i}}\approx \frac{\partial }{\partial w_{\Theta i}}\left[\sum _{j=1}^{\eta }{(w_{\Theta j}{r}_j{\sigma }_j)}^2{\mathrm{Z}}^{-2}\right], \\ \mathrm{Z}=\sum _{j=1}^{\eta }\left(w_{\Theta i}{r}_i^2\right). \end{gathered}$$ (A20)

The partials can then be calculated as follows:

$$\frac{\partial U^2(\Theta )}{\partial w_{\Theta i}}\approx \frac{2w_{\Theta i}{r}_i^2{\sigma }_i^2\mathrm{Z}-2r_i^2\sum _{j=1}^{\eta }{\left(w_{\Theta j}{r}_j{\sigma }_j\right)}^2}{{\mathrm{Z}}^3},$$ (A21)

which at their roots yield a unique set of optimal normalized weights:

$$w_{\Theta i}=\frac{1}{{\sigma }_i^2\sum _{j=1}^{\eta }\frac{1}{{\sigma }_j^2}}.$$ (A22)

Substituting Eq. (A22) into Eq. (A13) produces the minimum uncertainty in orientation:

$$U(\Theta )=\sqrt{\frac{1}{\sum _{i=1}^{\eta }{\left(\frac{r_i}{{\sigma }_i}\right)}^2}}.$$ (A23)

Table A1.

Parameters of the Monte Carlo simulation.

Parameter	Units	Domain	Probability distribution
${\sigma }_G$	Pixels	{${\sigma }_{\mathrm{G}}\in \mathbb{R}:1\le {\sigma }_{\mathrm{G}}\le 6$}	$f({\sigma }_{\mathrm{G}})=1∕5$
$b^2$	Photons per pixel	{$b^2\in \mathbb{Z}:1\le b^2\le 250$}	$\text{Pr}(b^2)={(b^2\text{ln}10)}^{-1}{({\log }_{10}250)}^{-1}$
$\eta$	Points	{$\eta \in \mathbb{Z}:3\le \eta \le 20$}	$\text{Pr}(\eta )=1∕18$
$N_{\mu }$	Photons	{$N_{\mu }\in \mathbb{Z}:{10}^3\le N_{\mu }\le {10}^8$}	$\text{Pr}(N_{\mu })=1∕(5N_{\mu }\text{ln}10)$
$N_S$	Photons	{$N_S\in \mathbb{Z}:-0.9N_{\mu }\le N_S\le 0.9N_{\mu }$}	$\text{Pr}(N_S)=1∕(1.8N_{\mu }+1)$
$N_i$	Photons	{$N_i\in \mathbb{Z}:N_{\mu }-\frac{1}{2}{N}_S\le N_i\le N_{\mu }+\frac{1}{2}{N}_S$}	$\text{Pr}(N_i)=1∕(N_S+1)$
${\widehat{r}}_i$	Pixels	{${\widehat{r}}_i\in \mathbb{R}:0\le {\widehat{r}}_i\le 150$}	$f({\widehat{r}}_i)=2{\widehat{r}}_i∕22,500$
${\widehat{\theta }}_i$	Radians	{${\widehat{\theta }}_i\in \mathbb{R}:0\le {\widehat{\theta }}_i\le 2\pi$}	$f({\widehat{\theta }}_i)=1∕2\pi$
$\Delta \widehat{X}$	Pixels	{$\Delta \widehat{X}\in \mathbb{R}:-50\le \Delta \widehat{X}\le 50$}	$f(\Delta \widehat{X})=1∕100$
$\Delta \widehat{Y}$	Pixels	{$\Delta \widehat{Y}\in \mathbb{R}:-50\le \Delta \widehat{Y}\le 50$}	$f(\Delta \widehat{Y})=1∕100$
$\Delta \widehat{\Theta }$	Radians	{$\Delta \widehat{\Theta }\in \mathbb{R}:0\le \Delta \widehat{\Theta }\le 2\pi$}	$f(\Delta \widehat{\Theta })=1∕2\pi$

A4. Motion uncertainty

Uncertainties of motion measurements can be calculated from the measurement functions of Eq. (A4) in the same way that uncertainties of pose measurements were calculated from Eq. (A2) in the previous section, resulting in the following expressions:

$$\begin{gathered} U(\Delta X)=\sqrt{\sum _{i=1}^{\eta }{w}_{\Delta Xi}^2\left({\sigma }_{k,i}^2+{\sigma }_{k+1,i}^2\right)}, \\ U(\Delta Y)=\sqrt{\sum _{i=1}^{\eta }{w}_{\Delta Yi}^2\left({\sigma }_{k,i}^2+{\sigma }_{k+1,i}^2\right)}, \\ U(\Delta \Theta )\approx \frac{\sqrt{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}^2\left(r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2\right)}}{\sum _{i=1}^{\eta }{w}_{\Delta \Theta i}{r}_{k,i}{r}_{k+1,i}}. \end{gathered}$$ (A24)

In cases that the uncertainties of the positions of the points in the two images are the same in the two images that bracketed the measured motion, the above motion uncertainties are simply a factor of $\sqrt{2}$ greater than the corresponding pose uncertainty.

A5. Optimal weightings for motion measurements.

Optimal weightings for motion measurements can be calculated in the same way as those for pose measurements described in Section A.3, resulting in the following expressions:

$$\begin{gathered} U(\Delta X)=U(\Delta Y)=\sqrt{\frac{1}{\sum _{i=1}^{\eta }\frac{1}{{\sigma }_{k,i}^2+{\sigma }_{k+1,i}^2}}}, \\ U(\Delta \Theta )=\frac{1}{\sum _{i=1}^{\eta }\frac{r_{k,i}^2{r}_{k+1,i}^2}{r_{k+1,i}^2{\sigma }_{k,i}^2+r_{k,i}^2{\sigma }_{k+1,i}^2}}. \end{gathered}$$ (A25)

A5. Range of simulation parameters

A total of 200 configurations were randomly generated for the Monte Carlo method described above. Each configuration consisted of set of parameters, {${\sigma }_{\mathrm{G}}$, $b^2$, $\eta$, $N$, $P$, $\Delta X$, $\Delta Y$, $\Delta \Theta$}, where ${\sigma }_{\mathrm{G}}$ is the standard deviation of the Gaussian intensity function used to approximate the image of each point source, $b^2$ is the expected number of background photons detected at each pixel, $\eta$ is the number of point sources, each $N_i$ of $N=\{N_1,\dots ,N_{\eta }\}$ is the expectation value of the number of photons detected from the $i^{\text{th}}$ point source, $P$ is the set of untransformed points, and the triple ($\Delta \widehat{X}$, $\Delta \widehat{Y}$, $\Delta \widehat{\Theta }$) denotes the true transform of the points from the first image to the second. The parameters ${\sigma }_G$, $\eta$, $\Delta \widehat{X}$, $\Delta \widehat{Y}$ and $\Delta \widehat{\Theta }$ are generated from uniform distributions, whereas the distribution from which $b^2$ is generated is logarithmically scaled. The $\eta$ points $p_i\in P$ are generated as polar coordinates $p_i=({\widehat{r}}_i,{\widehat{\theta }}_i)$, where ${\widehat{\theta }}_i$ is generated from a uniform distribution over the range 0 to $2\pi$, and ${\widehat{r}}_i$ is generated over the range 0 to 150 from a distribution that is quadratically scaled to ensure that points are distributed uniformly over a circle of diameter 300. Each of the $\eta$ photon counts in $N$ is generated from a uniform distribution over the range of scale $N_{\mathrm{S}}$ centred on a mean value, $N_{\mu }$, that is generated from a logarithmic distribution. The domain and probability distribution of each parameter are shown in Table A1.