A Conformal TOF-DOI Prism-PET Prototype Scanner For High Resolution Quantitative Neuroimaging

Abstract

Background:

Positron emission tomography (PET) has had a transformative impact on oncological and neurological applications. However, still much of PET’s potential remains untapped with limitations primarily driven by low spatial resolution which severely hampers accurate quantitative PET imaging via the partial volume effect (PVE).

Purpose:

We present experimental results of a practical and cost-effective ultra-high resolution brain-dedicated PET scanner, using our depth-encoding Prism-PET detectors arranged along a compact and conformal gantry, showing substantial reduction in PVE and accurate radiotracer uptake quantification in small regions.

Methods:

The decagon-shaped prototype scanner has a long diameter of 38.5 cm, a short diameter of 29.1 cm, and an axial field-of-view (FOV) of 25.5 mm with a single ring of 40 Prism-PET detector modules. Each module comprises a 16 × 16 array of 1.5 × 1.5 × 20 mm³ lutetium yttrium oxyorthosillicate (LYSO) scintillator crystals coupled 4-to-1 to an 8 × 8 array of silicon photomultiplier (SiPM) pixels on one end and to a prismatoid light guide array on the opposite end. The scanner’s performance was evaluated by measuring depth-of-interaction (DOI) resolution, energy resolution, timing resolution, spatial resolution, sensitivity, and image quality of ultra-micro Derenzo and three-dimensional (3D) Hoffman brain phantoms.

Results:

The full width at half maximum (FWHM) DOI, energy, and timing resolutions of the scanner are 2.85 mm, 12.6%, and 271 ps, respectively. Not considering artifacts due to mechanical misalignment of detector blocks, the intrinsic spatial resolution is 0.89 mm FWHM. Point source images reconstructed with 3D filtered back-projection (FBP) show an average spatial resolution of 1.53 mm FWHM across the entire FOV. The peak absolute sensitivity is 1.2% for an energy window of 400–650 keV. The ultra-micro Derenzo phantom study demonstrates the highest reported spatial resolution performance for a human brain PET scanner with perfect reconstruction of 1.00 mm diameter hot-rods. Reconstructed images of customized Hoffman brain phantoms prove that Prism-PET enables accurate radiotracer uptake quantification in small brain regions (2–3 mm).

Conclusions:

Prism PET will substantially strengthen the utility of quantitative PET in neurological disorders, such as early detection of neurodegenerative pathology or improved detection of metastases.

INTRODUCTION

Positron emission tomography (PET) is predominantly used for the staging of metastatic cancers with a burgeoning role in the differential diagnosis of neurodegenerative diseases, identification of a seizure focus in intractable epilepsy, and in the management of patients with brain tumors¹. PET has a tremendous potential contribution to advancing our understanding of brain physiology and pathology. Its unique ability to directly image molecular markers of neuropathology can enable early detection and tracking of neurodegenerative diseases long before the onset of clinical symptoms. Despite the availability of several highly specific FDA-approved and experimental tracers directly targeting brain pathology, much of PET’s potential remains untapped. Poor spatial resolution and partial volume effect (PVE) are the major limiting factors impacting not only image quality (for qualitative evaluation and visual identification of tracer avid regions) but also severely hampering the promise of PET to provide reliable quantitative information on biomarkers². PVE limits accurate quantification of lesions less than 2–3 times the PET system’s spatial resolution. Pathological changes in small subcortical nuclei, predominantly in the locus coeruleus (LC) of the pons, are evident in the early stages of neurodegenerative diseases such as the Alzheimer’s disease (AD)³. The LC is a bilateral structure and serves as the primary site of norepinephrine synthesis for the central nervous system, and in vivo imaging of LC can potentially be a very accurate biomarker for AD⁴. However, this small brainstem nucleus cannot be accurately imaged and quantified using current clinical PET scanners due to adverse PVE⁵.

The advent of new radiotracers has also markedly increased the role of PET in neuro-oncology in recent years. The rapid growth in this field is because, when compared to magnetic resonance imaging (MRI) for the clinical management of brain tumors, PET helps gain further insights into tumor biology for increasing the accuracy of differential diagnosis, noninvasive grading, delineation of tumor extent, surgery and radiotherapy planning, assessment of response, and post-treatment monitoring^6,7. Recent studies have shown that PET radiotracers which cross the blood-brain barrier can be complementary to MRI to enhance sensitivity and specificity. In particular, the radiolabeled amino acid tracer O-(2-[¹⁸F]-fluoroethyl)-L-tyrosine (FET) provides a high tumor-to-brain ratio (TBR) for detecting gliomas and brain metastases, and in some cases FET-PET showed considerably larger tumor volume compared to contrast-enhanced MRI for newly diagnosed glioblastoma^8,9,10. However, low spatial resolution in PET limits the ability to visualize small tumors and PVE severely degrades the accuracy of tumor volume delineation¹¹. Partial volume correction (PVC) may be used to reduce PVE, but the choice of PVC method may drastically influence PET quantification results^12,13,14 and thus reliable quantitative PET imaging necessitates improvement in spatial resolution at the scanner level.

Compared to whole-body cylindrical PET scanners, a compact and conformal design (arranging detectors close to the subject) can achieve lower cost and higher sensitivity due to a lower number of detectors and larger solid angle coverage, respectively¹⁵. In addition, a small diameter detector ring reduces the spatial blurring caused by photon acollinearity¹⁶. However, such a geometry substantially increases the parallax error (PE), an image blurring artifact due to the mispositioned lines-of-response (LORs), not only at the peripheral but also at the center of the field-of-view (FOV). Thus, depth-of-interaction (DOI) localization in the detector module is an indispensable feature to mitigate PE and achieve uniform high spatial resolution across the entire FOV¹⁷.

Although several brain-dedicated PET scanners using DOI detectors have been developed^{18,19,20,21,22}, the high-resolution research tomograph (HRRT)²³, which was designed over 20 years ago and is no longer commercially available, is still the most widely used brain PET scanner and serves as a performance benchmark for new high-resolution systems. However, HRRT’s moderate spatial resolution (from 2.4 mm at the center of FOV to 2.8 mm at 10 cm off-center), insufficient DOI resolution (double-layer discrete DOI), poor sensitivity (4.3% at the center of FOV), and the lack of time-of-flight (TOF) capability have significantly limited its quantitative accuracy for the numerous studies performed at the 17 installed sites around the world¹⁸. For example, despite having 12 times higher norepinephrine transporter (NET) density in the LC compared to the thalamus based on an autoradiographic study²⁴, the measured NET concentration in the LC was much lower than expected²⁵. In another recent serotonergic system study using HRRT, small brain regions such as the raphe nuclei (RN) were excluded from any quantitative analysis due to PVE caused by a combination of limited spatial resolution and sensitivity²⁶. Besides HRRT, hemispherical brain PET (Vrain) also has high spatial resolution and improves visualization of small nuclei such as the raphe nucleus²⁷. However, they did not evaluate the visualization capability of the LC regions which are < 3 mm in size.

Recently, we have developed a novel depth-encoding single-ended readout PET detector module that utilizes a segmented prismatoid light-guide array, hence the name Prism-PET, for enhanced and localized light sharing^28,29,30,31. The Prism-PET detectors have achieved unsurpassed spatial, DOI, and TOF resolutions when compared to other single-ended readout PET detector technologies^32,33. In this study, we have developed a one-ring prototype TOF-DOI Prism-PET brain scanner using a compact and conformal decagon geometry. We have previously simulated the performance of our high-resolution Prism-PET brain scanner and showed substantially more accurate delimitation and radiotracer uptake quantification of small brain structures such as the RN and LC when compared to the state-of-the-art whole-body Siemens Biograph Vision and total-body EXPLORER PET scanners^34,35. Here we experimentally characterize the scanner performance in terms of energy resolution, DOI resolution, spatial resolution, timing resolution, and sensitivity. Finally, we evaluate the imaging performance of Prism-PET using ultra-micro Derenzo and customized three-dimensional (3D) Hoffman brain phantoms filled with ¹⁸F-fluorodeoxyglucose (¹⁸F-FDG).

MATERIALS AND METHODS

Design of the Prism-PET prototype

The depth-encoding Prism-PET detector module developed in this study consists of a 16 × 16 array of 1.5 × 1.5 × 20 mm³ lutetium yttrium oxyorthosillicate (LYSO) scintillator crystals (X-Lum, Shanghai, China) coupled 4-to-1 to an 8 × 8 array of 3 mm silicon photomultiplier (SiPM) pixels (Hamamatsu, Japan) on one side and to a prismatoid light guide array on the opposite side (Figure 1A and 1B). The crystal pitch is 1.6 mm, and the pitch between SiPMs is 3.2 mm. The segmented light guide is made of an array of right triangular prisms with three distinct designs at the center, edge, and corner (Figure 1C), which confine inter-crystal light sharing to only the nearest neighboring SiPMs^28–29. To ensure optical isolation, Barium sulfate (BaSO₄) is placed between crystals and prisms, as the reflective material²⁸.

Figure 1.

(A) 3D schematic and (B) fabrication of the 4-to-1 coupled Prism-PET detector. (C) The unique prismatoid light guide designs at the center, edge and corner. Front (D) and side (E) views of the first prototype Prism-PET brain scanner with 40 detector modules and 25.5 mm axial coverage. The insets show the representative Prism-PET scan of a human subject and the magnified view of a customized FEM256 board made by PETsys.

The front and side views of the conformal prototype PET scanner without cover consisting of 40 Prism-PET detector modules in one ring are shown in Figure 1D and 1E. The prototype scanner conforms to the human head with a long diameter of 38.5 cm, a short diameter of 29.1 cm, and an axial FOV of 25.5 mm³⁶. Each crystal ring consists of 640 (16 × 40) crystals, and the total number of crystals in the prototype is 10,240 (16 × 16 × 40). The specification of the prototype scanner is summarized in Table 1. Data acquisition was performed using 20 TOF front-end-module (FEM) boards each comprising of 4 TOFPET2 application specific integrated circuit (ASIC) chips reading 256 channels (the inset of Figure 1E), 6 TOF FEB/D_v2 readout boards, and a Clock&Trigger module all developed and manufactured by PETsys Electronics^37,38,39. We utilized 10 cold plates with embedded copper pipes arranged in a decagon geometry to form the scanner gantry. Given that ASIC chips are the main source of heat that is generated from the scanner, they are directly coupled to the copper pipes using a thermal compound. Continuous flow of cool water circulated using a chiller removes heat from the ASICs and we have been able to maintain <0.2 °C temperature stability across all SiPM chips. Each SiPM module was read out by one ASIC with 64 channels, and the signal from each channel was fed into an analog-to-digital converter (ADC) as well as a time-to-digital converter (TDC) for obtaining both energy and timing information, respectively. Before data acquisition, all ASICs in the scanner were calibrated using the procedure provided by PETsys³⁹. All list-mode data were processed with an energy window of 460–560 keV except for the ⁶⁸Ge energy spectrum (5–800 keV). The sensitivity was measured in the energy windows of 400–650 keV and 440-580 keV. The coincidence time window was set to 15 ns and 4 ns for non-TOF and TOF reconstructed images, respectively. Each SiPM module was read out by one ASIC with 64 channels, and the signal from each channel was fed into an analog-to-digital converter (ADC) as well as a time-to-digital converter (TDC) for obtaining both energy and timing information, respectively.

Table 1.

The specifications of the conformal Prism-PET brain prototype scanner.

Detector	Scintillator crystals	LYSO
	Size of the scintillator cyrstals	1.5 × 1.5 × 20 mm3
	Size of the SiPM pixels	3.0 × 3.0 mm2
	Scintillator to SiPM ratio	4:1
	Number of crystals per detector module	16 × 16
	Crystal pitch	16 × mm × 1.6 mm (transaxial × axial)
	SiPM pixel pitch	3.2 mm × 3.2 mm (transaxial × axial)
System	Number of detector modules per ring	40
	Number of crystals per crystal ring	640
	Number of SiPMs/channels	2560
	Number of crystals	10240
	Short diameter	29.1 cm
	Long diameter	38.5 cm
	Axial FOV length	25.5 mm

Figure 6.

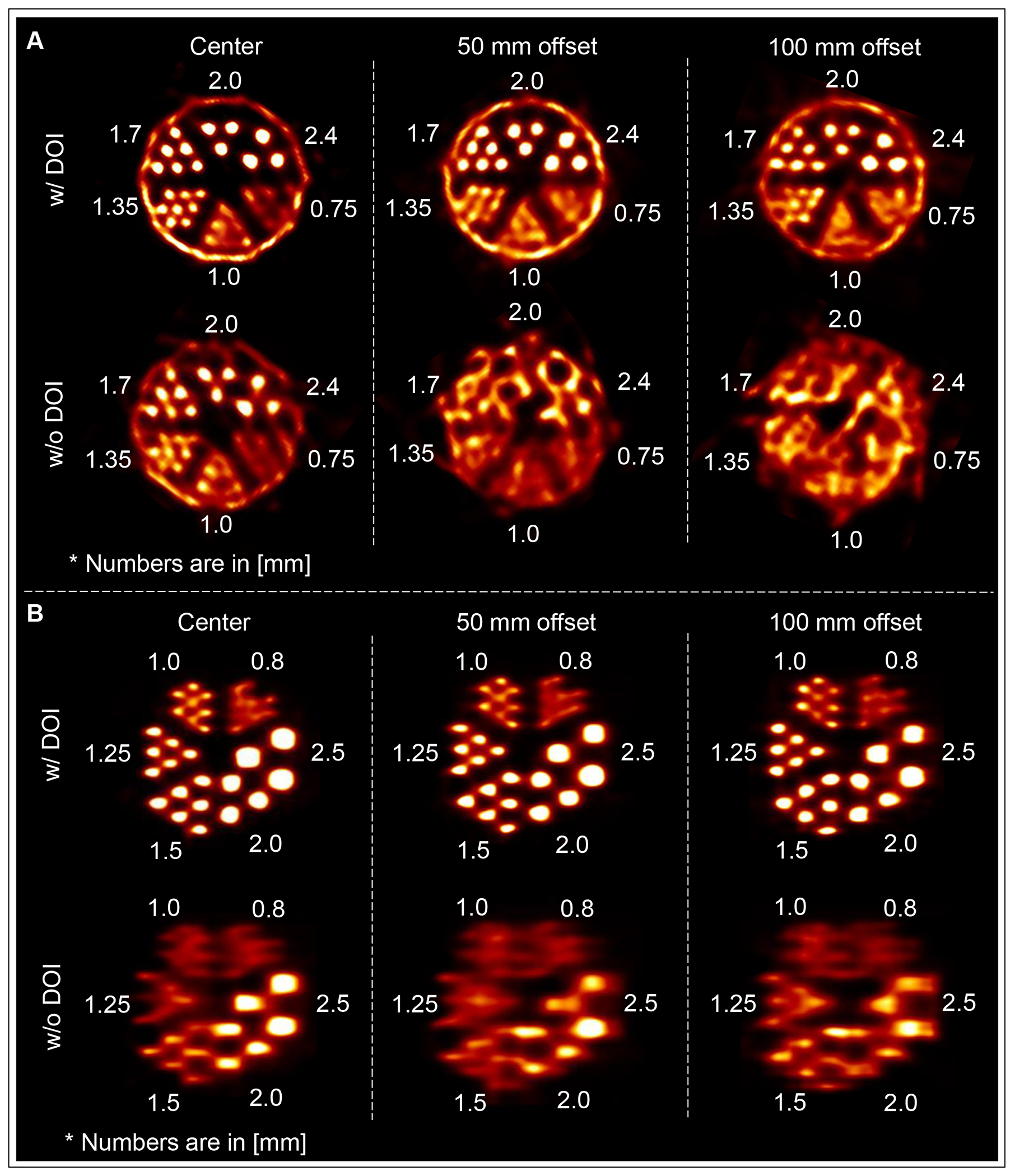
Reconstructed images of ultra-Micro Derenzo phantoms fabricated by (A) Data Spectrum and (B) Phantech with (top row) and without (bottom row) DOI rebinning at 0 mm (left column), 50 mm (middle column) and 100 mm (right column) vertical offsets from the FOV center.

Image reconstruction

The inter-crystal scatter (ICS) events were identified and rejected based on the characteristic energy pattern between the neighboring SiPMs that under the same Prismatoid mirror. We performed DOI rebinning in the list-mode to correct for the PE-caused spatial blurring³⁵. In specific, for each coincidence event, we drew the LOR between the two photon interaction sites based on the continuous DOI information, and the event was re-assigned to the pair of crystals with their gamma photon entrance surface intersecting the LOR^35,40. A cylinder phantom with 25.4 cm in diameter and 5 cm in axial, which covered the entire FOV of the prototype, was scanned to obtain the normalization data (~ 200 million events). The DOI rebinning was performed to the normalization data and the rebinned events were sorted into a LOR map that records the number of counts of all the valid LORs. The normalization factors were computed by comparing the measured data with the analytical forward projection of the uniform cylinder. For the Hoffman brain phantom experiments, a μ-map was generated using a water phantom with the same dimensions as the brain phantom. The normalization factors and μ-map were fed into the Customized and Advanced Software for Tomographic Reconstruction (CASToR)⁴¹ for the calculation of sensitivity image. The 3D LM-ordered subset expectation maximization (OSEM) with TOF and point spread function (PSF) modeling was used to reconstruct the images if not otherwise stated.

DOI and energy resolution

DOI calibration and resolution.

The DOI variable, w, is defined as w = E_max/E, where E_max is the maximum intensity signal from the primary SiPM and E is the total detected signal from the primary and light-sharing SiPMs⁴². The w-histogram for each detector was measured in singles mode by placing a ⁶⁸Ge source at the center of the FOV. To guide the linear mapping between w and DOI, we modeled the rising and falling edges of the w histogram as a pair of error functions with the mean of their Gaussian derivatives assigned to DOI = 0 mm and DOI = 20 mm, respectively (Supplemental Figure 1). The derivatives of the calibrated DOI histogram’s rising and falling edges were fitted into Gaussian functions and their FWHM values represented the crystal’s minimum and maximum DOI resolutions, respectively (with the assumption that the DOI resolution increases linearly from the minimum to the maximum value across the crystal depth). The weighted average FWHM value based on the Beer-Lambert law represented the crystal’s effective DOI resolution.

Flood histogram.

The two-dimensional (2D) coordinates of flood histograms were calculated based on the weighted average energy method from singles list-mode data obtained by placing a ⁶⁸Ge source at the center of the FOV⁴². The flood histogram was projected to the x and y axis and the maximum peaks of the projected counts were detected (solid circles shown in the 1D projections in Supplemental Figure 2A). The center locations between the 2nd-3rd, 5th-6th, 7th-8th, 9th-10th, 11th-12th, and 14th-15th peaks were used to divide the flood histogram into an array of 7 x 7 square-shaped regions (see Supplemental Figure 2A). Each region was segmented individually, for enhanced spatial identification accuracy, using K-means clustering⁴³ and the segmented masks (Supplemental Figure 2B) were saved for all detector blocks. In comparison, directly segmenting the entire histogram without localized regions provides worse performance as regions tend to have different count statistics and the global segmentation often cannot find a threshold that is suitable for the entire map. After segmentation, the center of each cluster was shifted to its corresponding equally sampled crystal region (Supplemental Figure 2C).

Energy resolution.

Crystal look-up tables (LUTs) were generated from the corrected flood histograms and used to generate energy data for each crystal which was then grouped into 8 DOI bins (i.e., bin size of 2.5 mm and a total of 81,920 DOI bins). Eight depth-localized energy histograms were calculated for each crystal and normalized individually so their photopeaks correspond to 511 keV. The normalized histograms were merged into one energy histogram and the photopeak was fitted into a Gaussian function with its full width at half maximum (FWHM) value representing the DOI-corrected energy resolution. The saturation effect was corrected using ¹⁷⁶Lu intrinsic radioactivity (202 keV and 307 keV) from LYSO crystals and a ²²Na point source (511 keV and 1.2 MeV)²¹.

Timing resolution

We expect the major variations in timing offset to arise from ASIC channel-to-channel and SiPM pixel-to-pixel variations. This offset is corrected using a moving line source to ensure that each detector channel in the scanner forms a reasonably large cone of LORs with different channels on the opposite side. An iterative algorithm was utilized to minimize the TOF difference error (ΔTOF) between the ground truth TOF (given that the source location is known) and the measured TOF (the difference of two LOR timestamps). In each iteration, a ΔTOF histogram was calculated for each cone belonging to each detector channel and fitted into a Gaussian function. The timing offset for each channel was then calculated by subtracting the peak of the Gaussian from a priori offset estimate (initially set to zero). The scanner is properly calibrated once all the cone’s delta-TOF histograms are centered about zero and the process above is iterated until this convergence criterion is satisfied⁴⁴.

The DOI-induced time bias can also be corrected by using the same iterative process described above, except that one must use the 3D channel ID instead as represented by the 2D crystal ID (radial number, axial number) and the DOI bin number. Benefiting from enhanced and localized light sharing in Prism-PET which generates a characteristic pattern of SiPM signals, the timestamp correction was also incorporated for each gamma interaction using the primary timestamp (T₁) and N_nn nearest-neighbor light-sharing timestamps (LSTS), where N_nn is 3, 2, and 1 for center, corner, and edge crystals (Figure 1C), respectively. The corrected timestamp T_c is given as:

$$T_c=\sum _{n=1}^N\left(k_n·T_n\right)$$ (1)

where N is the total number of timestamps and is equal to $N_{nn}+1$, $k_n$ is the DOI-dependent weight of the corresponding timestamp with the primary weight k₁ increasing and the remaining light sharing weights (i.e., k₂ to k_n) decreasing as gamma photons penetrate deeper into the crystal and interact closer to the crystal-SiPM interface, and T₂ to T_N are the nearest-neighbor light-sharing timestamps. To further optimize the timing resolution, a fine-tuning step was applied using the LOR-based timing offset correction. For the timing resolution measurement, a 0.25 mm ²²Na point source was positioned at the center of the FOV. The timing resolution was measured as the FWHM and full width at tenth maximum (FWTM) of the TOF histogram.

Spatial resolution

Intrinsic spatial resolution.

To evaluate the intrinsic spatial resolution, a 0.25-mm-diameter ²²Na point source with radioactivity of 1.85 MBq (50 μCi) was aligned to the center of a coincidence detector pair on the vertical cold plates and moved axially with 0.3 mm increments. The coincidence response functions of eight directly opposing crystal pairs were plotted and fitted into a Gaussian function with their FWHM values representing a range of intrinsic spatial resolutions of our Prism-PET scanner.

Reconstructed image spatial resolution.

The reconstructed image spatial resolution was measured with the same ²²Na point source positioned at vertical and horizontal offsets of 10, 25, 50, 75, and 100 mm from the center of the transaxial FOV. The measurements were performed at both 0 mm and one-quarter axial FOV (i.e., 6.4 mm) from the axial center. The scanned time was 30 min and approximately 4.5 million coincidence counts were obtained at each position. List-mode coincidence events were rebinned to a virtual cylindrical scanner with 0.5 × 0.5 mm² virtual crystals³⁵, and images of point sources were reconstructed using Software for Tomographic Image Reconstruction (STIR) using the filtered back projection 3D reprojection method (FBP3DRP) with 0.5 × 0.5 × 0.5 mm³ voxel size⁴⁵. The spatial resolution was reported as FWHM and FWTM of the point source response function in the radial, tangential, and axial directions.

Sensitivity

The sensitivity of the scanner was measured using a 2.3-MBq ²²Na point source placed at the center of the transaxial FOV and moved from end to end of the axial FOV with a 1 mm step size. The 0.906 branching ratio of ²²Na was corrected for activity, and energy windows of 400–650 and 440–580 keV were applied.

Phantom studies

The image quality was evaluated qualitatively using two ultra-micro Derenzo phantoms (Data Spectrum and Phantech) and semi-quantitatively using a customized 3D Hoffman brain phantom (Data Spectrum) with the latter including fillable regions for hippocampus (HPC), DRN, and bilateral LC. Figure 2 illustrates the synthetically generated axial digital reference object (DRO) of a representative slice of the Hoffman brain phantom and how it’s constructed (schematic of the coronal cross-section and slice photographs are also shown)⁴⁶. Each slice is 6.4 mm thick, and it simulates different uptake ratios in the gray and white matter regions by having the fillable activity region for the gray matter extend across the entire slice thickness but limiting the fillable activity region for the white matter to two symmetrical 0.8 mm thick layers spaced 1.6 mm apart. The ventricles which are void of radioactivity are also present. Figure 3 depicts the 3D schematics of the customized slices with the spiral-shaped HPC and cylindrical subcortical nuclei where the diameter of the fillable DRN and LC regions are 3 mm and 2 mm, respectively.

Figure 2.

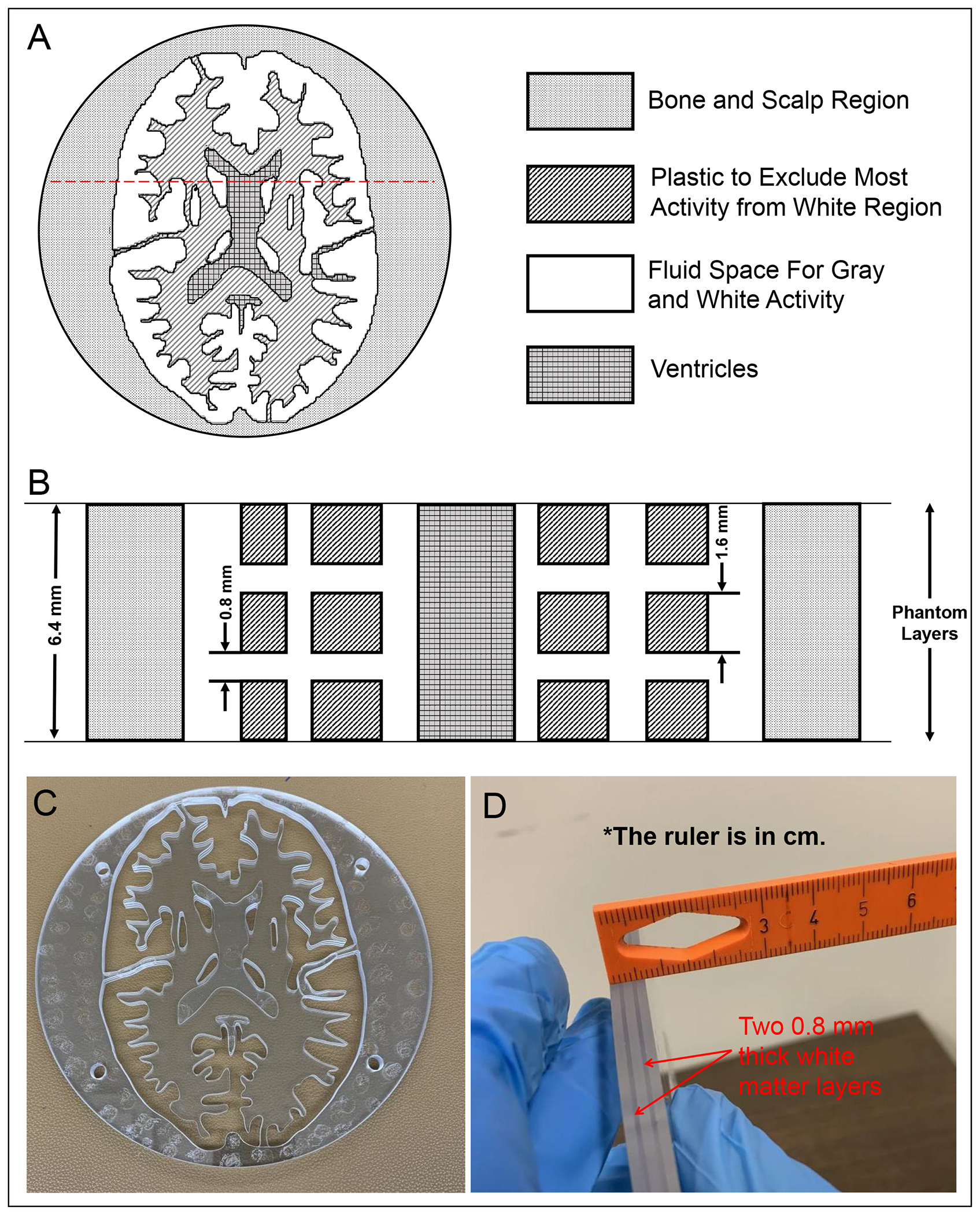
(A) One representative axial section through the 3D Hoffman brain phantom’s DRO containing two fluid regions (i.e., gray matter and white matter), which will be filled with 18F activity, and ventricles. (B) Schematic coronal cross section through the red dashed lines in A. Gray matter and ventricles extend across the entire 6.4 mm thickness of each slice whereas the two white matter layers are each 0.8 mm thick. Photographs of the representative slice in the (C) axial and (D) coronal views.

Figure 3.

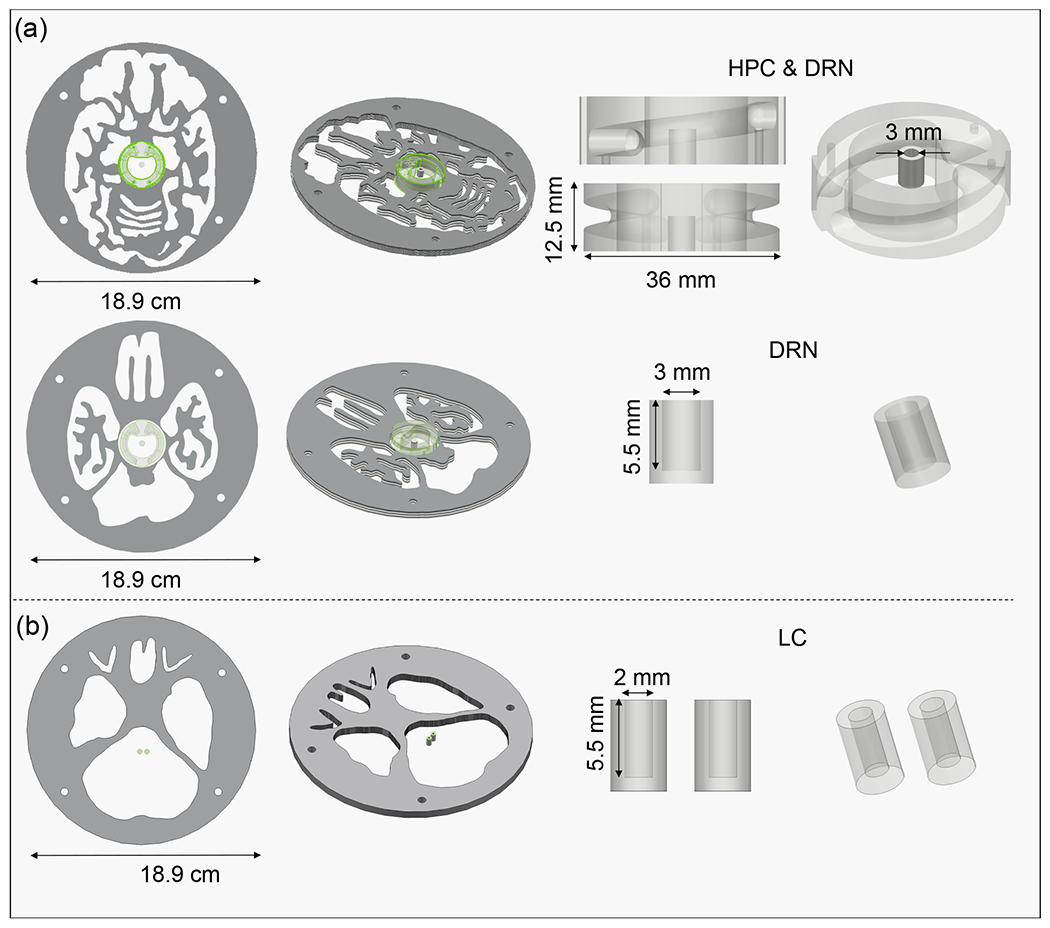
3D schematic of the customized brain phantom slices showing the spiral hippocampus (HPC) and dorsal raphe nucleus (DRN) in (A) and the bilateral locus coeruleus (LC) nuclei in (B).

Ultra-micro Derenzo phantoms.

The ultra-micro Derenzo phantom made by Data Spectrum (model ECT/HOT/UMMP) has rod diameters of 0.75, 1.00, 1.35, 1.70, 2.00, and 2.40 mm whereas the phantom made by Phantech (model D270825) comes with a smaller footprint, is much easier to fill without air bubbles, and has rod diameters of 0.80, 1.00, 1.25, 1.50, 2.00, and 2.50 mm. Both phantoms were filled with 37 MBq (1 mCi) of ¹⁸F-FDG, placed at three different vertical offsets (i.e., 0 mm, 50 mm, and 100 mm) from the center of the FOV, and scanned for 60 min by the Prism-PET scanner. Note that the hot rods in the Data Spectrum and Phantech Derenzo phantoms were positioned to be parallel with the axial axis and vertical axis of the scanner, respectively. The acquired list-mode data was post-processed to filter for ICS events and correct for PE using DOI information, and normalized to correct for varying crystal efficiencies. In total, at least 15 million counts were acquired at each position and hot-spot images were reconstructed by CASToR using 3D-LM-OSEM with 16 iterations and 12 subsets. Different voxel sizes of 0.5 × 0.5 × 0.5 mm³ for the Data Spectrum phantom and 0.25 × 0.25 × 0.25 mm³ for the Phantech phantom were selected during reconstruction.

3D Hoffman brain phantom.

The 3D Hoffman brain phantom placed at the center of the FOV (Supplemental Figure 3) was filled with 37 MBq (1 mCi) of ¹⁸F-FDG initially, and then scanned for 240 min (two phantom slices were imaged in each experiment). ICS rejection, DOI rebinning, time offset correction, normalization, and attenuation correction were employed to process the list-mode data, and brain phantom images were reconstructed by CASToR using TOF 3D-LM-OSEM with 7 iterations, 8 subsets, and 0.5 × 0.5 × 0.5 mm³ voxels. In total, at least 50 million counts were acquired for each experiment. Two representative phantom slice images were used to illustrate the substantial improvement in image quality and signal-to-noise ratio (SNR) using DOI and TOF information. The activity concentration in the gray matter, HPC, DRN, and LC were 560 kBq/mL, 1901 kBq/mL, 2516 kBq/mL, and 4653 kBq/mL, respectively. The activity concentration ratios used in different fillable regions of the HPC-DRN and LC phantoms were based on estimated 5-HT_1A receptor⁴⁷ and NET densities²⁴ using post-mortem autoradiography studies, respectively. The customized phantoms with the same activity concentrations were also imaged by Siemens Biograph Truepoint PET/CT using the manufacturer’s OSEM reconstruction with 6 iterations, 16 subsets, and voxel size of 1.03 × 1.03 × 2 mm³ (Head/Neck protocol with a zoom of 2 and a FOV diameter of 350 mm). Normalization, attenuation, random, and scatter corrections were applied. The average voxel intensity of the HPC and maximum voxel intensity of the DRN and LC regions were used to represent the uptake value of the volume of interests (VOIs). We calculated the relative uptake ratio (RUR) as the average or maximum intensity of the VOI versus that of the entire gray matter to characterize the quantitation performance of the two scanners.

RESULTS

DOI and energy resolution

DOI histograms (blue) and the derivatives of their rising and falling edges (black) for all 40 detectors in the scanner are shown in Supplemental Figure 4. Original and corrected flood histograms of one representative detector module is shown in Supplemental Figure 2A and 2C. All the center, edge, and corner crystals are well segmented throughout the entire array, indicating that the decoding error of our Prism-PET detector is negligible. The ⁶⁸Ge energy spectra of representative center, edge, and corner crystals are shown in Supplemental Figure 2C. The DOI histogram and energy spectrum of the scanner are shown in Figure 4A and 4B, respectively. The average DOI resolution across all detectors and DOI-corrected energy resolution of the scanner are 2.85 mm FWHM and 12.6% (corrected for saturation effects), respectively. Supplemental Figure 5 shows a representative crystal’s energy spectrum using ²²Na point source, which achieved an energy resolution of 11.9% at the 511 keV peak.

Figure 4.

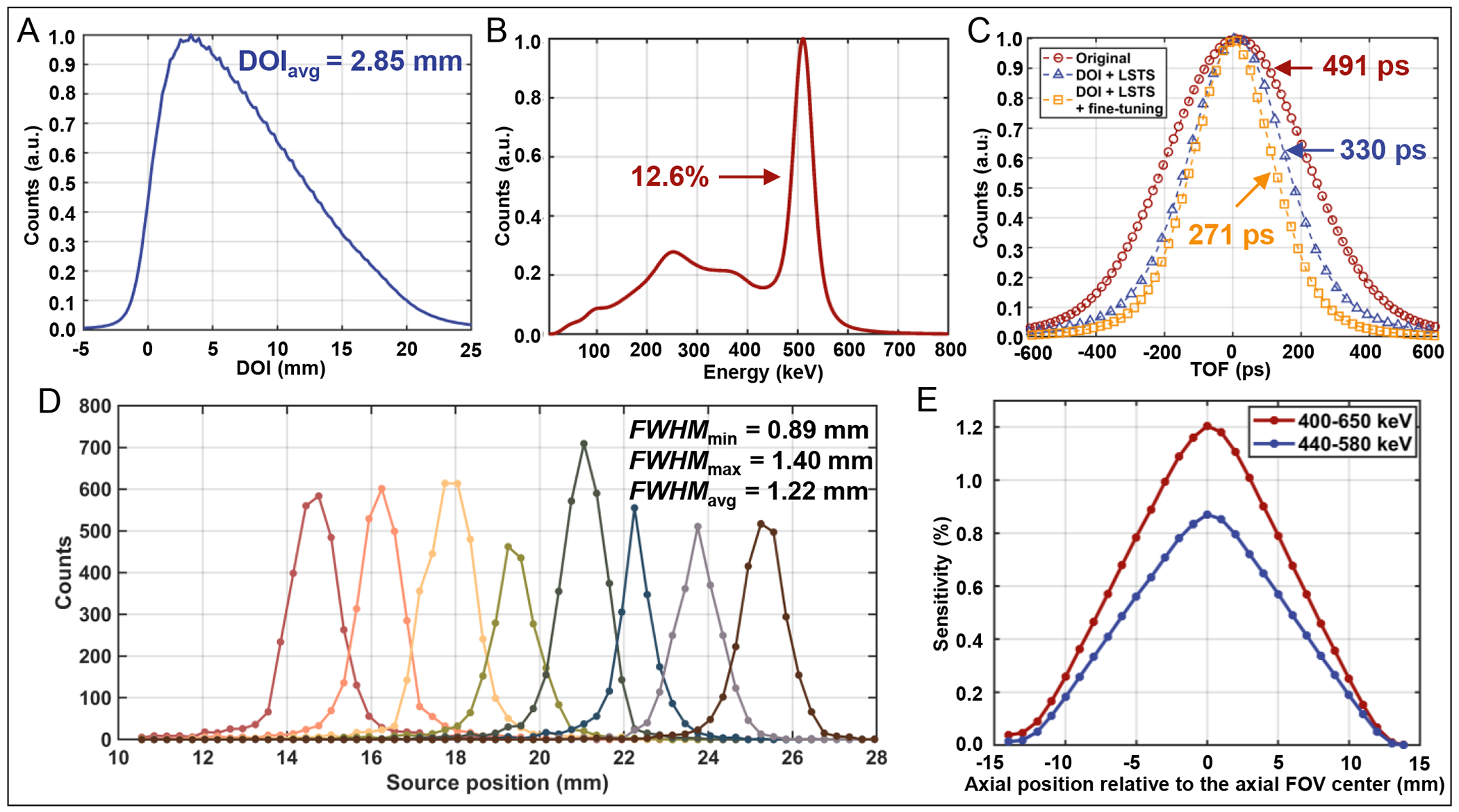
(A) DOI histogram and (B) DOI-corrected energy spectrum of the Prism-PET scanner. (C) TOF histograms of the scanner at three conditions for the ²²Na point source: (1) original (standard TOF offset calibration, red), (2) DOI and LSTS correction (blue), and (3) combining DOI and LSTS correction with fine-tuning (yellow). (D) Intrinsic spatial resolution profiles of eight representative coincidence crystal pairs in the scanner. (E) The absolute sensitivity of the scanner at various axial positions with the energy window of 400–650 keV and 440–580 keV.

Timing resolution

Figure 4C shows the TOF histograms with the ²²Na point source placed at the center of the FOV. The timing resolutions of 491 ps, 330 ps, and 271 ps FWHM are obtained using timing offset correction of 2D SiPM channels (i.e., 64 × 40 = 2,560 channels), time offset correction of crystals with 8 DOI bins (i.e., 8 × 256 × 40 = 81,920 3D channels) including timestamp correction using nearest-neighbor LSTS, and timing offset and timestamp corrections of 3D channels together with LOR-based fine-tuning, respectively.

Spatial resolution

Intrinsic spatial resolution.

The coincidence response functions of eight representative coincidence crystal pairs are shown in Figure 4D. The intrinsic spatial resolution ranges from 0.89 mm to 1.40 mm with an average value of 1.22 mm FWHM.

Reconstructed image spatial resolution.

The spatial resolutions at vertical and horizontal offsets of 10, 25, 50, 75, and 100 mm from the transaxial center at both 0 mm and one-quarter axial FOV from the center are displayed in Table 2 and Table 3, respectively. Images of point sources for the quantification of the spatial resolution were reconstructed using STIR FBP3DRP and shown in 5. The average spatial resolutions are 1.54 mm FWHM at the center of the axial FOV and 1.52 mm FWHM at the one-quarter axial FOV from the center. The average spatial resolution across the entire FOV is 1.53 mm FWHM.

Table 2.

Spatial resolution measurements of the prototype at the center of the FOV

At axial center
Distance (mm)		10		25		50		75		100
Spatial Resolution (mm)		FWHM	FWTM	FWHM	FWTM	FWHM	FWTM	FWHM	FWTM	FWHM	FWTM
Vertical	Radial	1.66	3.17	1.71	3.59	1.73	3.21	1.90	3.33	1.73	3.10
	Tangential	1.56	2.28	1.41	2.70	1.57	2.87	1.62	3.27	1.84	3.79
	Axial	1.35	2.82	1.23	2.51	1.16	2.50	1.21	2.51	1.22	2.66
Horizontal	Radial	1.37	2.78	1.49	2.85	1.44	2.81	1.56	2.77	1.55	2.92
	Tangential	1.55	2.99	1.69	3.08	1.76	3.48	1.81	3.56	1.96	3.90
	Axial	1.23	2.44	1.25	2.62	1.41	2.64	1.56	2.81	1.63	2.98

Table 3.

Spatial resolution measurements of the prototype at one-quarter axial FOV from the center

At one-quarter axial FOV from center
Distance (mm)		10		25		50		75		100
Spatial Resolution (mm)		FWHM	FWTM	FWHM	FWTM	FWHM	FWTM	FWHM	FWTM	FWHM	FWTM
Vertical	Radial	1.66	3.04	2.03	3.71	1.76	3.22	1.97	3.61	2.26	4.60
	Tangential	1.23	3.01	1.43	3.25	1.56	2.02	1.42	2.72	1.48	3.03
	Axial	0.95	2.65	0.94	2.65	0.91	2.63	1.27	2.69	1.47	2.64
Horizontal	Radial	1.25	2.62	1.38	2.78	1.46	2.76	1.62	2.90	1.74	3.26
	Tangential	1.86	3.66	2.02	4.58	2.01	4.52	2.07	4.07	2.08	4.99
	Axial	1.18	2.63	1.36	2.48	1.06	2.59	0.91	1.66	1.34	2.45

Figure 5.

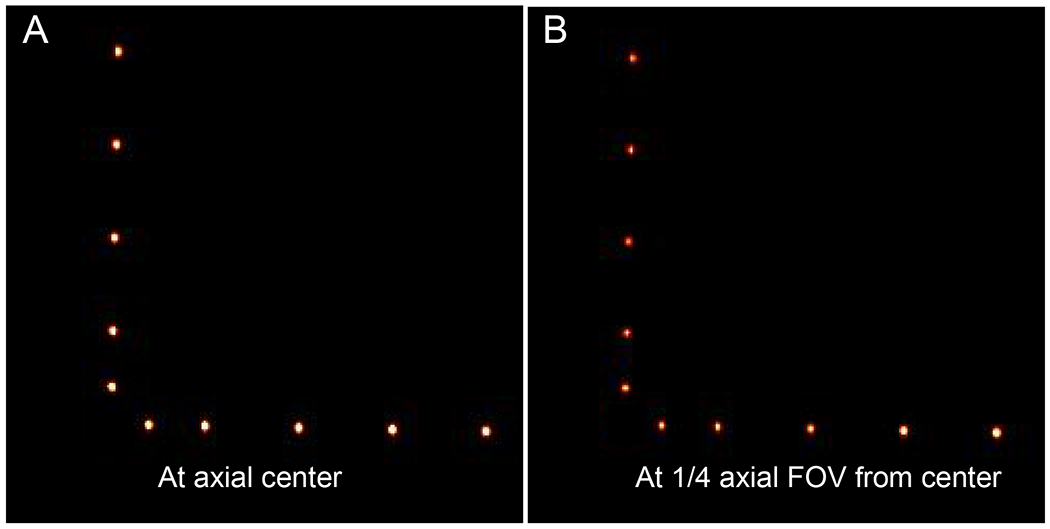
Reconstructed images of ²²Na point sources using STIR FBP3DRP at (A) 0 mm and (B) one-quarter (6.4 mm) axial FOV from the center.

Sensitivity

The absolute sensitivity profile of the Prism-PET prototype scanner at different axial locations is shown in Figure 4E. The peak absolute sensitivity is 1.2% at the center of the FOV with an energy window of 400–650 keV. One must note that this is the sensitivity of only one detector ring with 25.5 mm axial coverage and we estimate it to increase to ~ 17% once axial FOV is increased to 264 mm.

Phantom studies

Ultra-micro Derenzo phantoms.

Figure 6A and 6B show the transverse and coronal cross-sections of reconstructed images of ultra-micro Derenzo phantom fabricated by Data Spectrum and Phantech, respectively. The images are shown with and without DOI rebinning at 0, 50, and 100 mm vertical offsets from the center of the FOV. After DOI rebinning, all hot-spots with a diameter of 1.00 mm or larger can be clearly resolved across the entire FOV for the Phantech phantom.

3D Hoffman brain phantom.

Figure 7A shows the DRO for two representative axial slices of the Hoffman brain phantom where black, grey, and white represent the gray matter, white matter, and ventricles, respectively. Figure 7B and 7C show non-TOF OSEM-PSF reconstructed Prism-PET images without and with DOI rebinning, respectively. The TOF-DOI Prism-PET images of Figure 7D show enhanced characteristics associated with TOF reconstruction and the fine details of the cerebral sulci and gyri and ventricles are clearly visualized. Figure 8A shows reconstructed ultra-high resolution TOF-DOI Prism-PET images of a set of 15 upper levels of the 3D Hoffman brain phantom. Figure 8B shows the coronal view images of the two customized slices with the cut plane along the red dashed lines in Figure 8A. The DRO (top image) includes gray, white, and HPC regions, with the four 0.8 mm thick white regions having intra-slice and inter-slice pitches of 2.4 mm and 4.0 mm, respectively. Reconstructed TOF-DOI PET images of Biograph Truepoint (middle image) and Prims-PET (bottom image) view are also shown in Figure 8B. The estimated intra-slice and inter-slice pitches of the white regions using the Prism-PET image are 2.5 mm and 3.75 mm, respectively. Figure 9A shows the axial DROs for the customized brain phantom slices that include HPC, DRN, and LC regions. The reconstructed images using the Siemens Biograph TruePoint and Prism-PET scanners are depicted in Figures 9B and 9C, respectively, with the insets showing magnified views of maximum intensity projections (MIPs) for the selected regions. Figure 9D illustrates the line profiles across the DRN and LC, together with the RUR values of the HPC, DRN, left LC (LLC), and right LC (RLC) regions.

Figure 7.

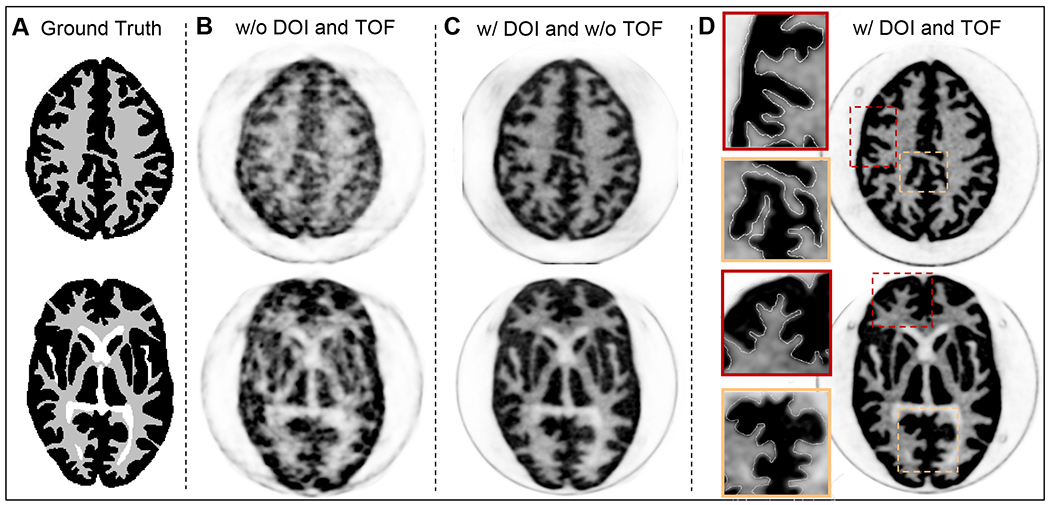
(A) Two axial slices of the Hoffman brain phantom’s DRO. Top slice: level of cingulate cortex. Bottom slice: level of basal ganglia and thalamus. (B) The reconstructed non-TOF PET images without and (C) with DOI. (D) The reconstructed TOF-DOI PET images with the zoom-in inset views.

Figure 8.

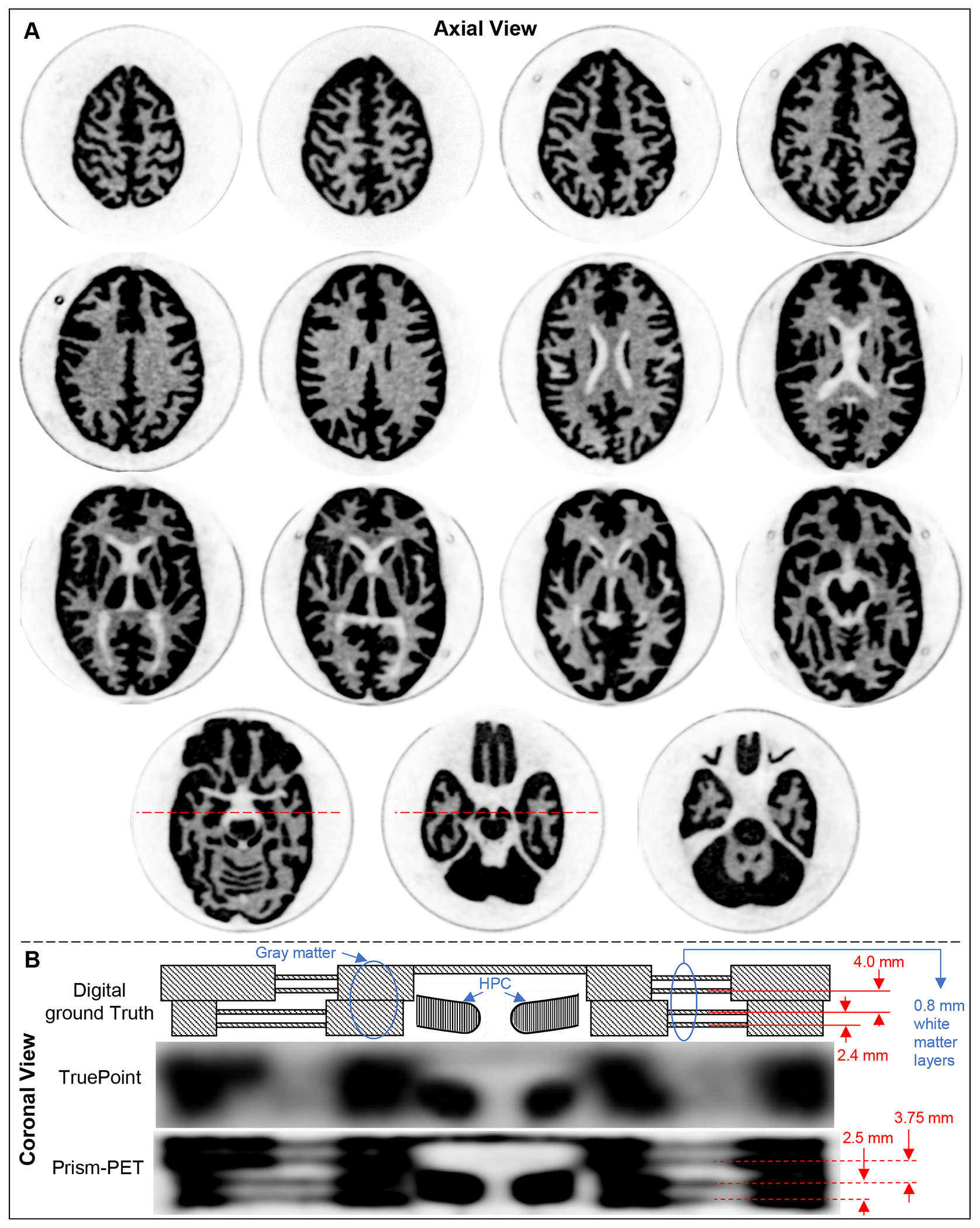
(A) Set of TOF-DOI Prism-PET axial images of 15 upper levels of the brain phantom. (B) Coronal cut plane of two slices along the red dashed lines in A. The DRO includes gray, white, and HPC regions. The four 0.8 mm thick white regions have intra-slice and inter-slice pitches of 2.4 mm and 4.0 mm, respectively. Reconstructed TOF-DOI PET images of Biograph Truepoint and Prims-PET in coronal view are also shown.

Figure 9.

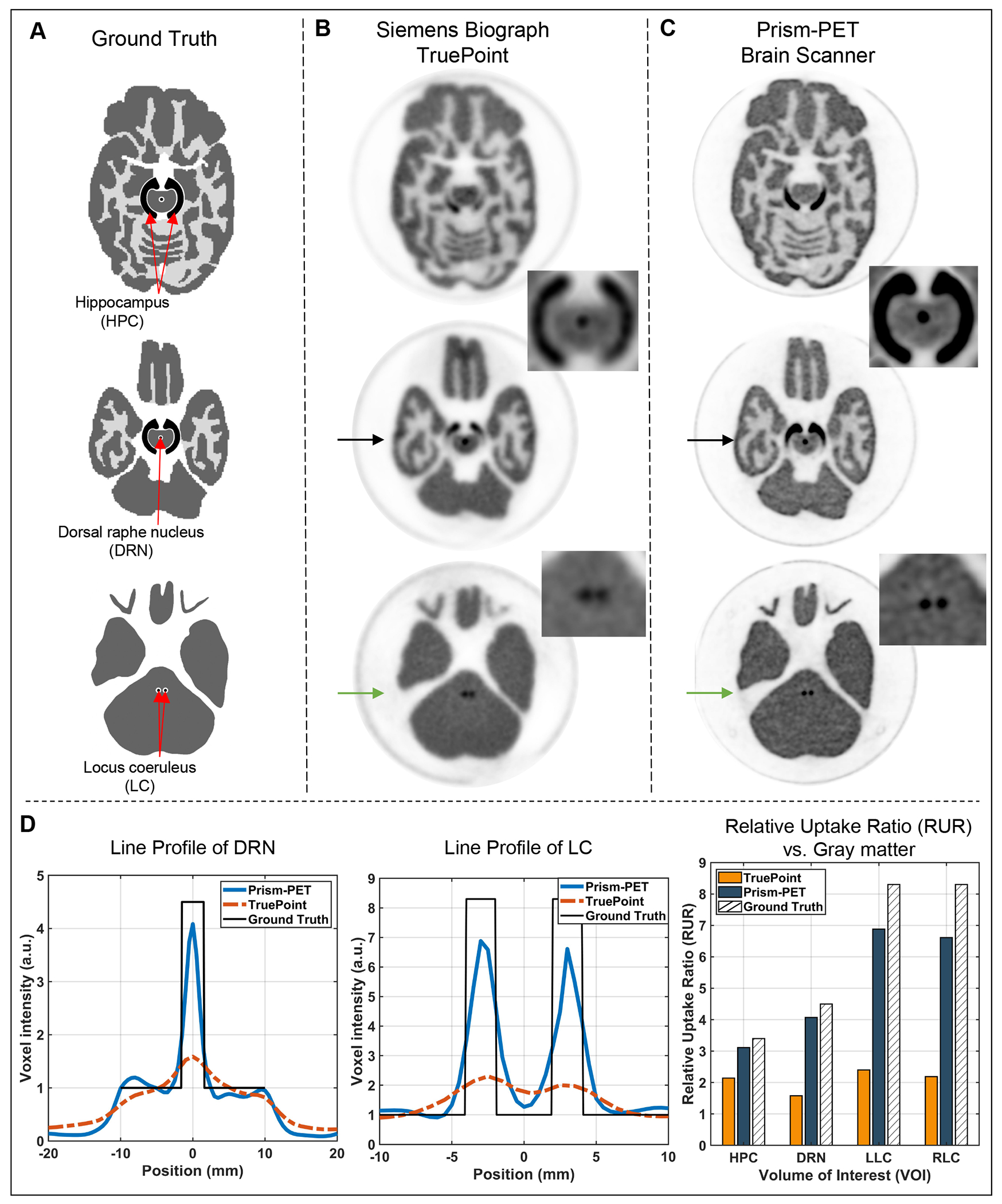
(A) The axial slices of the customized Hoffman brain phantom’s DRO with built-in HPC, DRN, and LC. The reconstructed TOF-DOI slice images of (B) the Siemens Biograph TruePoint and (C) the Prism-PET brain scanner. The black arrows and green arrows point at the cutlines of the DRN and LC, respectively. The insets in B and C show the MIP of the HPC-DRN and LC inserts for Biograph Truepoint and Prism-PET, respectively. (D) Line profiles across the DRN and LC (blue: Prism-PET; Red: Biograph TruePoint; Black: ground truth), and the RUR of HPC, DRN, LLC, and RLC vs. the gray matter.

DISCUSSION

A conformal decagon geometry was leveraged to 1) reduce the acollinearity factor to 0.85 mm¹⁶, 2) improve sensitivity by enhancing the geometric efficiency ^†, and 3) lower the cost by reducing the crystal volume ^‡. However, since this geometry increases the number of incident gamma rays that penetrate the crystal surface obliquely, the Prism-PET brain scanner suffers from PE even at the center of the scanner with severe blurring towards the edge of the FOV. The impact of PE on image quality can be substantially reduced by accurately positioning the LORs using the high resolution (i.e., 2.85 mm FWHM) and continuous DOI information offered by the Prism-PET detectors^29,31. We measured a wide range of intrinsic spatial resolutions from 0.89 mm to 1.40 mm FWHM and the average point source spatial resolutions are 1.66, 1.70, and 1.23 mm FWHM in the radial, tangential, and axial directions, respectively. This suggests submillimeter geometrical misalignment of detector positions in the radial and tangential directions which will be addressed in the construction of the next clinical Prism-PET brain scanner with full axial coverage. Benefiting from very small mechanical tolerances in the axial direction, we were able to resolve all hot-rods with a diameter of 1.00 mm across the entire FOV for the Phantech phantom with the rods aligned parallel to the vertical axis of the scanner.

Aside from reporting the highest single-ended readout DOI and spatial resolutions compared to any other whole-body or organ-specific human PET scanner, we have also measured the best timing resolution of 330 ps with 1.5 × 1.5 × 20 mm³ crystals thanks to corrections using DOI information and multiple LSTSs. Timing resolution can be improved further to 271 ps by performing an additional LOR-based fine-tuning step and creating a second LUT to store refined timing offset corrections for each channel pair. Although this involves hundreds of millions of pairs for the Prism-PET scanner with full axial coverage, each offset in this refinement step can be stored as 8-bit signed integers or one byte per channel pair which makes it practical to store the entire LUT in memory. All the reconstructed phantom images shown here, however, use the 330 ps TOF resolution without LOR-based timing offset refinement. Given that the major boost in image quality and SNR comes from DOI rebinning which substantially reduces spatial blur due to PE, adding TOF information has further enhanced image sharpness, contrast, and overall clarity.

Compton scatter of the 511 keV photons is another factor that leads to the incorrect localization of the annihilation photons, thereby degrading the spatial resolution. Discriminating the ICS events from the photoelectric events and rejecting them before the image reconstruction can improve the image quality but would significantly reduce the sensitivity as ~50% of singles are Compton scattered given the small crystal cross section (i.e., 1.5 × 1.5 mm²) used by the Prism-PET brain scanner. However for every gamma interaction, enhanced and localized light sharing in the Prism-PET detector module produces an anisotropic and deterministic pattern of primary and nearest-neighbor SiPM signals. The overlap of multiple such characteristic patterns due to multi-crystal Compton events can be very accurately decomposed to yield crystal-level energy, spatial, and DOI information of the individual interactions. This capability allows the accurate recovery of the primary interaction site which in turn enhances both spatial resolution and sensitivity (see the Supplemental section in Ref.²⁹ and Ref.⁵⁰).

The ultra-high spatial resolution of the Prism-PET brain scanner can significantly reduce PVE and thus enables accurate quantitative imaging of small brain regions. While the current clinical whole body PET scanners cannot reliably delineate and quantify radiotracer distribution in small brain nuclei due to PVE, the Prism-PET brain scanner can accurately visualize tracer avid regions when imaging the HPC-DRN and LC phantoms and obtains 2.6-3 times higher RUR values in DRN and LC nuclei when compared to the Siemens Biograph Truepoint (zoomed reconstruction using 1 × 1 × 2 mm³ voxel size). Note that the asymmetric uptake of LLC and RLC in both Biograph Truepoint and Prism-PET is due to the variation in the fabrication of the LC pockets inside the phantom. Furthermore, thanks to achieving ultra-high resolution not just at the center but across the entire FOV, Prism-PET scanner can, for the first time, distinctly visualize all 0.8 mm thick white matter layers in the axial direction along which the scanner has it’s best spatial resolution performance of ~ 1.2 mm FWHM. This result is particularly interesting because it may allow for PET-drived large scale and high resolution mapping of neurotransmitter receptor densities in very small anatomic regions, such as the cortical gray matter layers, in living subjects^51,52.

Ultra-high resolution in vivo molecular and functional imaging of the brain can lead to a better understanding of brain physiology, pathology, and pathogenesis of neurodegenerative diseases, as well as improved clinical decision making and tumor management. Research in neuroimaging suggests that degeneration of LC neurons is linked to the onset of AD pathology before cytoskeletal changes occur in the entorhinal cortex^53,54. Until now, significant PVE has hindered reliable PET imaging of LC and other small brain regions. However, our successful ultra-high resolution imaging of the HPC-DRN and LC phantoms with accurate estimation of the relative radiotracer concentration in the DRN and LC suggest that Prism-PET brain scanner has the potential to enable reliable quantitative PET neuroimaging of the subcortical nuclei and help discover imaging biomarkers of neurodegenerative diseases. In addition, observing changes in the LC and RN in response to lifestyle adjustments or medical therapy could also guide the discovery and application of new and effective treatments. Prism-PET will also be an indispensable in vivo imaging tool for generating high resolution quantitative atlases of neurotransmitter receptor distribution for better understanding of the function of normal and pathologic brain. In neuro-oncology, the ultra-high resolution PET imaging using highly specific amino acid radiotracers can be complementary to MRI to enhance sensitivity and specificity of tumor diagnosis.

CONCLUSION

We have developed, and experimentally characterized the performance of, the first compact and conformal brain-dedicated TOF-DOI Prism-PET prototype scanner. We reduced spatial blur caused by parallax effect, acollinearity and Compton-scattered photons, and achieved uniform and ultra-high spatial resolution with 4-to-1 coupling of 1.5 mm crystals to 3 mm SiPM pixels. We increased sensitivity using a compact and conformal geometry for enhanced solid angle coverage of coincidence events. We also achieved excellent energy and timing resolutions especially after applying corrections using DOI and multiple light-sharing timestamps. The ultra-micro Derenzo phantom experiments demonstrated the successful reconstruction of 1.00 mm diameter hot-rods across the entire FOV. The 3D Hoffman brain phantom experiments proved that our Prism-PET scanner (with 1.53 mm spatial resolution, 2.85 mm DOI resolution, and 271 ps timing resolution) enables accurate visualization and uptake quantification of DRN and LC by drastically reducing the PVE and enhancing the SNR. Our prototype TOF-DOI Prism-PET human brain scanner has achieved the highest resolution PET phantom images using a cost-effective and scalable design. For future work, we will extend the axial FOV to ~ 26 cm (i.e., 10 rings of detector modules) using our recently developed 4-to-1 SiPM to ASIC channel interleaved multiplexing scheme (iMUX)^55,56 and include our recently developed motion tracking and correction with sub-millimeter accuracy⁵⁷ for further clinical validation of our technology using human subject studies. The ultimate goal is to enable accurate quantitative PET imaging of small brain regions and substantially strengthen the promise of quantitative PET in neurology for early diagnosis of neurodegenerative diseases, and in neuro-oncology for improved management of both primary and metastatic brain tumors.