Charge Transport and Ion Kinetics in 1D TiS₂ Structures are Dependent on the Introduction of Selenium Extrinsic Atoms

Abstract

Improving charge insertion into intercalation hosts is essential for crucial energy and memory technologies. The layered material TiS₂ provides a promising template for study, but further development of this compound demands improvement to its ion kinetics. Here, we report the incorporation of Se atoms into TiS₂ nanobelts to address barriers related to sluggish ion motion in the material. TiS_1.8Se_0.2 nanobelts are synthesized through a solid-state method, and structural and electrochemical characterizations reveal that solid solutions based on TiS_1.8Se_0.2 nanobelts display increased interlayer spacing and electrical conductivity compared to pure TiS₂ nanobelts. Cyclic voltammetry and electrochemical impedance spectroscopy indicate that the capacitive behavior of the TiS₂ electrode is improved upon Se incorporation, particularly at low depths of discharge in the materials. The presence of Se in the structure can be directly related to an increased pseudocapacitive contribution to electrode behavior at a low Li⁺ content in the material and thus to improved ion kinetics in the TiS_1.8Se_0.2 nanobelts.

Introduction

Intercalation chemistry involving ion insertion into a host lattice has been a key developer of essential as well as emerging technologies such as energy storage,¹ neuromorphic computing,² water desalination,³ and selective ion extraction.⁴ Development in these areas hinges on one fundamental challenge: facilitating ion transport through a host material. Electrochemical ion intercalation into a solid-state material involves several distinct kinetic steps, including ion motion through an electrolyte, ion transfer across a solid-electrolyte interphase (SEI), and ion diffusion through the solid host material itself. In some cases (e.g., MoS₂,² LiCoO₂⁵), structural and morphological phase transformation of the solid-state host upon ion intercalation presents another kinetic limitation. Though ion transport has also been studied in tunnel structures (NASICON-type)⁶ and polymer chains (poly(ethylene oxide) LiAsF₆),⁷ layered van der Waals (vdW) metal chalcogenides stand out as a promising class of materials for reversible ion insertion. One of the chief advantages of vdW solids is that the interlayer distance can easily be altered upon ion intercalation/deintercalation; since vdW layers are not covalently bound, such materials tend to be well suited for ion kinetic studies.

Titanium disulfide (TiS₂) is an attractive candidate for the further development of layered vdW transition metal chalcogenides. TiS₂ crystallizes in a CdI₂-type hexagonal lattice; this structure is typified by individual TiS₂ octahedra propagating in an infinite 2D plane, while successive planes are held together purely by vdW forces. Such a layered structure allows TiS₂ to be readily exfoliated and makes it a robust intercalation compound. Given the nature of TiS₂ as an archetypal vdW solid, it became a pioneering material in the development of now-ubiquitous Li⁺-intercalation-based rechargeable batteries.¹ While past interest in TiS₂ has certainly been framed in the realm of energy storage, other applications for this material exist. Reports indicate the study of TiS₂ as an active component in such diverse realms as thermoelectrics,⁸⁻¹⁰ hydrogen storage,^11,12 optical limiting,¹³ and photoacoustic imaging devices.¹⁴

Insertion kinetics of TiS₂ are most conveniently studied with Li⁺ intercalation. The Li⁺ ion’s small size (76 pm)¹⁵ lends itself well to the study of ion kinetics, as it minimizes structural perturbations that come with the insertion of larger or multivalent ions.^16,17 Indeed, Li⁺ intercalation remains at the forefront of development in intercalation chemistry, demonstrated by recent efforts to determine Li⁺ ordering upon high degrees of lithiation.¹⁸⁻²⁰ Li⁺ intercalation into TiS₂ follows a continuous solid-solution path with no phase transformations evident with increasing Li⁺ content as per the following equation:

1

TiS₂ exhibits a constant voltage drop associated with the lattice occupancy of Li⁺ (x) in Li_xTiS₂, providing a suitable measure of Li⁺ content in the structure.²¹ The facile intercalation of Li⁺ into TiS₂ makes it a promising template material for advancing fast ion kinetics within vdW structures.

Researchers have been refining existing synthesis techniques and developing new methods to fabricate 2D layered vdW materials that were once considered thermodynamically unstable.²²⁻²⁴ These advancements include better control over growth conditions, manipulation of precursor materials, and addition of extrinsic atoms/molecules to facilitate the formation of unique 2D structures with tunable optoelectronic and electrochemical properties. These synthetic developments have laid the groundwork for modifying ion kinetics in a given material by highlighting the tunable nature of material conductivity and dimensionality in vdW compounds. Electrical properties of TiS₂ have been tailored with S vacancies²⁵ as well as intrinsic (Ti)^24,26 and extrinsic (Se)⁸ atom incorporation. Further tuning of the electrical conductivity of TiS₂ arises from the intercalation of cations such as Li⁺,²⁷ Cu⁺,²⁸ and Ag⁺.²⁹ While the tendency of TiS₂ toward nonstoichiometry has complicated past analyses of its electrical properties, the current understanding of the relationship between composition and band structure allows this versatile transition metal dichalcogenide to predictably display a variety of electronic properties.

Furthermore, reducing a material’s dimensionality leads to shorter bulk diffusion lengths and has been a principal consideration of past research into ion kinetics. Methods of reducing the morphological dimensionality of TiS₂ from 3D bulk to 2D/1D structures have been developed to help minimize diffusion lengths across particles and introduce other novel characteristics and functionalities. These methods include ball milling,³⁰ exfoliation in a solvent (benzyl alcohol),³¹ intercalation of large molecules,³² sulfurization of TiO₂ nanotubes,³³ and direct synthesis from solid-state precursors to produce nanobelts.²⁵ This prior research contends that reducing the length of the primary ion diffusion pathways in TiS₂ nanobelts allows the material to display faster ion kinetics.³⁴ A broader trend recognizing the importance of nanostructuring for improved ion kinetics is evidenced by materials such as V₂O₅,^18,35 TiO₂,³⁶ and LiCoO₂,³⁷ which all exhibit superior performance of nanostructured electrodes with respect to the bulk counterpart.

While TiS₂ is an acceptable template for fast ion kinetics, it is held back by its relatively low electrical conductivity, which can lead to a sluggish kinetic response of intercalated ions. Additionally, while its interlamellar spacing is large enough to reversibly host ions (5.69 Å), TiS₂ exhibits an interlayer expansion of 9% when fully lithiated.^38,39 Given that the analogous TiSe₂ intercalate exhibits less than 8% expansion,³⁹ increasing TiS₂ interlayer spacing through extrinsic atom incorporation would reduce its volume expansion upon lithiation and thus mitigate a kinetic barrier to ion motion in the material.

With regard to improving the electronic and intercalation properties of TiS₂, Se incorporation is a suitable option. TiSe₂ displays over an order of magnitude higher electrical conductivity (6.5 × 10⁴ S m^–1)⁴⁰ than TiS₂ (5 × 10³ S m^–1),⁴¹ as well as a larger interlayer spacing (5.99 Å for TiSe₂, 5.69 Å for TiS₂), suggesting that Se incorporation into a TiS₂ structure would impart increased lattice spacing and electrical conductivity on the TiS_2–xSe_x solid solution. TiS₂ and TiSe₂ share the same crystallographic structure (hexagonal) and space group (P3̅m1), which facilitates substitution of Se atoms into the S sites in TiS₂ without lattice destabilization.

Here, we report the incorporation of extrinsic atoms into 2D layered titanium sulfide nanobelts. Based on stoichiometry, titanium sulfides can crystallize as TiS₃ or TiS₂ structures. TiS₃ crystallizes as a monoclinic structure that is composed of 1D chains of trigonal prismatic TiS₆ units that are held by S–S vdW forces within the gaps. Similarly, TiS₂ crystallizes as a hexagonal structure where 2D slabs of edge-shared TiS₆ octahedra come together to form infinite layers perpendicular to the c-axis. Within the layers, strong covalently held TiS₆ octahedra are stacked on top of each other and separated by a vdW gap.

Both TiS₃ and TiS₂ possess a cleavage plane parallel to the crystallographic ab plane, constraining particle growth in the c direction. However, only TiS₃ possesses an additional cleavage plane parallel to the bc plane, which promotes the formation of 1D nanobelt structures in TiS₃, compared to the 2D hexagonal platelets which dominate the morphology of direct TiS₂ syntheses.⁴² While the lamellar structure of both TiS₃ and TiS₂ makes them ideal candidates for investigating intercalation processes where ion species can be inserted between the layers without disrupting the overall crystal structure, a platelet morphology is less suitable for fast ion intercalation.³⁴ For this reason, we developed a method by which we fabricated TiS₃ nanobelts. We then used these TiS₃ nanobelts as sacrificial scaffolds that are pyrolyzed to yield TiS₂ with a 1D morphology. To investigate the ion insertion properties of TiS₂, Se is incorporated into the S sites, which gives us control over the electronic properties as well as the vdW gap upon the formation of the TiS_1.8Se_0.2 nanobelts.

Here, a solid-state synthesis of nanostructured TiS_1.8Se_0.2 is developed. For electrochemical and structural comparison, TiS₂ nanobelts are also synthesized following a previously reported method by our group that utilizes a two-step synthesis with a TiS₃ intermediate.^25,43 TiS_1.8Se_0.2 nanobelts are formed through an analogous two-step synthesis that also leverages the monoclinic crystal structure of a TiS_3–xSe_x intermediate. This two-step method is visualized in Figure 1. In step 1, the synthesis of TiS_3–xSe_x (TiS₃) is performed by heating elemental Ti with excess SeS₂ (S) powder. Crucially, the nanobelt morphology of these intermediates is preserved during the pyrolysis step of the TiS_3–xSe_x (TiS₃) intermediate. S from the S₂^2– dianion is driven out of the nanobelts at a high temperature, leading to the formation of TiS_1.8Se_0.2 (TiS₂). To prevent this S from reabsorbing into the nanobelts, Ti powder is added to the ampule, separated from the nanobelt material by a glass wool plug (step 2). The synthesized TiS_1.8Se_0.2 nanobelts exhibit high phase purity and homogeneous Se concentration throughout the nanobelt structure.

Figure 1.

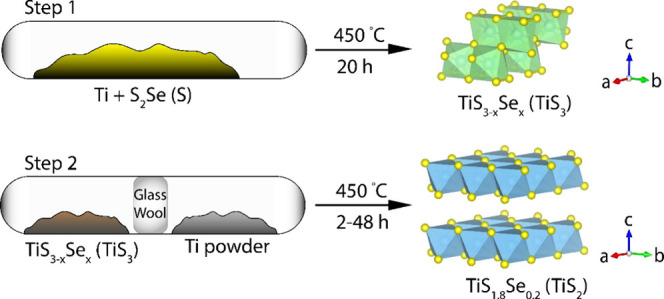
Two-step synthesis of TiS_1.8Se_0.2 and TiS₂ nanobelts. The layered structures of the intermediate TiS_3–xSe_x (TiS₃) and TiS_1.8Se_0.2 (TiS₂) products are depicted for clarity.

TiS₂ displays an increase in the interlayer spacing and electrical conductivity upon Se incorporation. The kinetics of Li⁺ ion insertion are probed in TiS₂ and TiS_1.8Se_0.2 nanobelts using rate-dependent cyclic voltammetry (CV), electrochemical impedance spectroscopy (EIS), and galvanostatic intermittent titration technique (GITT) analysis. It is found that increases in the lattice spacing and electrical conductivity imparted by the structural substitution of S by Se atoms contribute to altered ion kinetics in TiS₂. Li⁺ ion kinetics are particularly improved at low Li⁺ concentrations in the material, near the open-circuit discharge voltage. Widening of the interlayer spacing of TiS₂ upon Li⁺ insertion leads to comparable ion kinetics in both TiS₂ and TiS_1.8Se_0.2 as Li⁺ occupation approaches 1 per stoichiometric host unit. This work presents a thorough investigation of the limiting factors affecting ion kinetics in an archetypal vdW solid and lays the groundwork for further implementation of TiS₂ into applications such as neuromorphic computing, where ion transport plays a pivotal role.

Results and Discussion

As shown in Figure 1, the fabrication of TiS₂ and TiS_1.8Se_0.2 nanobelts involves two successive reaction steps: the formation of TiS_3–xSe_x (TiS₃) nanobelts, followed by the pyrolysis of the S₂^2– dianion to S^2–, for the formation of TiS_1.8Se_0.2 (TiS₂). Figure 2A shows an SEM image for as-synthesized TiS₃ sacrificial nanobelts. These TiS₃ nanobelts have an average width of 332 ± 31 nm, while the TiS_3–xSe_x nanobelts seen in Figure 2B have an average width of 367 ± 30 nm. Figure 2C,D depicts the SEM images of the products obtained upon the desulfurization of TiS_3–xSe_x (TiS₃) and pyrolysis into TiS_1.8Se_0.2 (TiS₂). Upon completion of the reaction, the nanobelts continue to dominate the morphology of both products. From statistical distributions, TiS₂ nanobelts have an average width of 371 ± 37 nm, while TiS_1.8Se_0.2 nanobelts have an average width of 357 ± 31 nm. No statistical difference in nanobelt width is observed upon desulfurization and Se incorporation. All structures demonstrate clear anisotropy, as nanobelt lengths greatly exceed the measured widths.

Figure 2.

SEM images for (A) TiS₃, (B) TiS_3–xSe_x, (C) TiS₂, and (D) TiS_1.8Se_0.2 nanobelts.

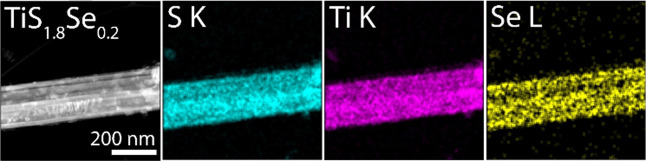
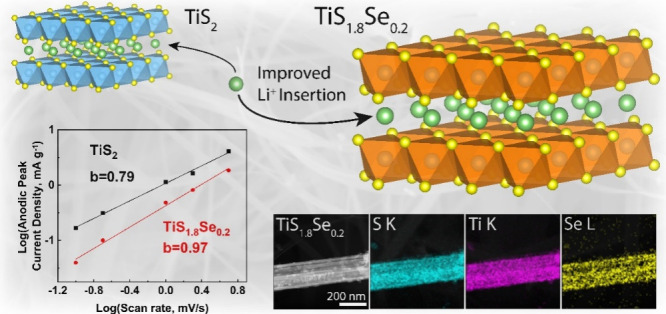
Preserving the nanobelt morphology and dimensions following desulfurization and Se incorporation allowed us to independently investigate extrinsic atom effects on the ion insertion properties of TiS_1.8Se_0.2 without finite size contributions (vide infra). To confirm the uniform incorporation of Se into the TiS₂ lattice, high-resolution energy dispersive X-ray spectroscopy (EDS) was performed on a single nanobelt of TiS_1.8Se_0.2 (Figure 3). EDS analysis indicates a homogeneous composition of Ti, S, and Se in the TiS_1.8Se_0.2 nanobelts. Compositional estimates from EDS provide evidence of a stoichiometry of TiS_1.8Se_0.2.

Figure 3.

EDS elemental distribution maps of S, Ti, and Se along the length of a TiS_1.8Se_0.2 nanobelt.

Further structural and morphological studies of individual TiS₂ and TiS_1.8Se_0.2 nanobelts were undertaken using lattice-resolved high-resolution transmission electron microscopy (HRTEM) and selected area electron diffraction (SAED). The HRTEM images acquired along the c-axis of the TiS₂ and TiS_1.8Se_0.2 nanobelts are depicted in Figure 4A,B, respectively. Imaging of the vdW gap for TiS₂ and TiS_1.8Se_0.2 indicates an increase of the (001) interlayer distance from 0.572 nm (TiS₂) to 0.582 nm (TiS_1.8Se_0.2). The observed interlayer distance expansion upon Se incorporation corresponds to an ≈1.7% increase in the c-axis of TiS₂. Additionally, Figure 4C shows lattice fringes obtained from HRTEM, where the hexagonal structure of the ab crystallographic plane of TiS_1.8Se_0.2 is evident. Lattice fringes spaced at 0.294 and 0.298 nm agree well with the spacing of the (100) and (010) planes of a hexagonal TiS_1.8Se_0.2 nanobelt. The SAED pattern presented in Figure 4D corroborates the crystalline nature of the TiS_1.8Se_0.2 nanobelt. The diffraction spots observed in the SAED pattern are associated with a nanobelt in the ab plane, and crystallographic reflections of the (110), (010), and (020) planes in the hexagonal lattice pattern of TiS_1.8Se_0.2 are indexed. The evidence of twinning of some diffraction spots is indicative of small crystallite sizes in the diffraction area. Dark field transmission electron microscopy (TEM) imaging highlights small crystallite grain sizes in the TiS_1.8Se_0.2 nanobelts, which leads to many regions of contrast across the length of the nanobelt (Figure S1). These overlapping crystallites likely give rise to SAED pattern twinning in the TiS_1.8Se_0.2 nanobelts (Figure 4D). Conversely, large grain sizes in TiS₂ nanobelts are observed, as little image contrast exists across the nanobelt length (Figure S1).

Figure 4.

HRTEM lattice fringes indicate an increase in the (001) interlayer distance from (A) TiS₂ to (B) TiS_1.8Se_0.2. (C) TiS_1.8Se_0.2 is further identified through the lattice fringes of the ab plane. (D) SAED identifies the crystalline nature of a TiS_1.8Se_0.2 nanobelt.

Structural modification upon Se incorporation was determined by using X-ray diffraction (XRD) studies. Figure 5 displays diffraction peaks of TiS₂ and TiS_1.8Se_0.2 which are indexed to lattice planes of the CdI₂-type crystal structure of TiS₂, (Joint Committee of Powder Diffraction Standards (JCPDS) 74-1141), in the P3̅m1 space group (164). As shown in the XRD pattern presented in Figure 5, an increase in interlayer spacing with Se incorporation is observed with a blue shift in the (001) diffraction peak from 15.56° 2θ (TiS₂) to 15.26° 2θ (TiS_1.8Se_0.2). This indicates an increase of the d-spacing from 0.569 nm in TiS₂ to 0.580 nm in TiS_1.8Se_0.2 and corresponds to an ≈1.9% expansion of the lithium-hosting van der Waals interlayer. The increase in lattice spacing along this axis is expected with the introduction of the larger Se^2– anion (0.191 nm) vs the S^2– anion (0.184 nm) into the CdI₂-type lattice. This finding is in good agreement with our HRTEM/SAED studies, providing further evidence for the substitutional incorporation of Se into the TiS₂ crystal structure. Additionally, the broadening of the (011) and (012) diffraction peaks of the TiS_1.8Se_0.2 sample suggests a decreased crystallite size imparted upon the substitution of S for Se. However, given the lack of broadening in the (001) diffraction peak, these smaller grain sizes in TiS_1.8Se_0.2 are seen to manifest only in the ab plane and do not affect the spacing of the vdW layer. We also note a minor oxidation peak at 2θ = 27.9°, which can be attributed to TiO₂ in the rutile (JCPDS 88-1175) phase and results from air exposure during acquisition of the XRD spectra.

Figure 5.

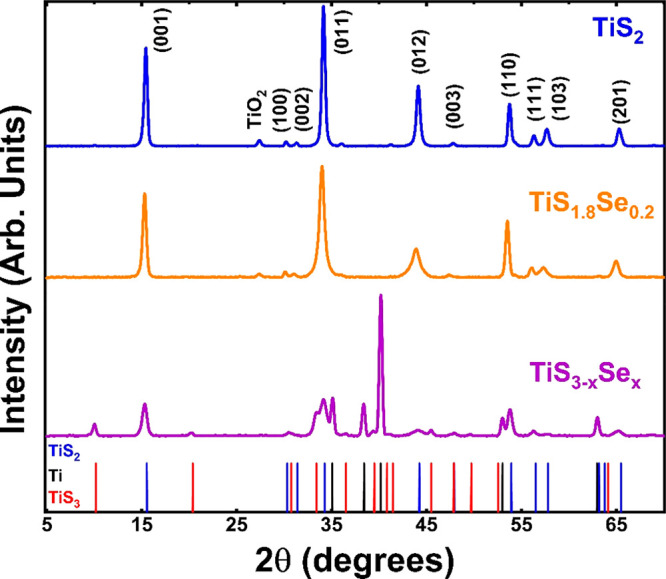
XRD patterns of TiS₂, TiS_1.8Se_0.2, and TiS_3–xSe_x nanobelts. To facilitate phase identification, standard patterns of TiS₂ (JCPDS 74-1141), Ti (JCPDS 44-1294), and TiS₃ (JCPDS 15-0783) are presented as solid vertical lines at the bottom of the graph.

The XRD pattern for the TiS_3–xSe_x sacrificial precursor (prior to desulfurization) is also presented and is in good agreement with JCPDS No. 15-0783 (TiS₃). However, as this intermediate is unstable, XRD analysis of TiS_3–xSe_x displays peaks corresponding to multiple phases. Ti precursor, TiS_1.8Se_0.2 product, and TiS_3–xSe_x intermediate can all be identified in the XRD pattern of TiS_3–xSe_x. Reference lines to the accepted JCPDS peaks for each species are presented as solid vertical lines at the bottom of Figure 5, while these peaks are modeled via the predicted diffraction intensity in Figure S2. Peaks that can be unambiguously assigned to each of these phases are at 40.17° 2θ (Ti), 15.26° 2θ (TiS_1.8Se_0.2), and 10.14° 2θ (TiS_3–xSe_x). This intermediate phase is likely unstable because, while TiS₃ is easily synthesized, TiSe₃ remains unrealized in bulk syntheses. Though pure TiS_3–xSe_x is not isolated, its monoclinic structure plays an important role in the formation of TiS_1.8Se_0.2 nanobelts.

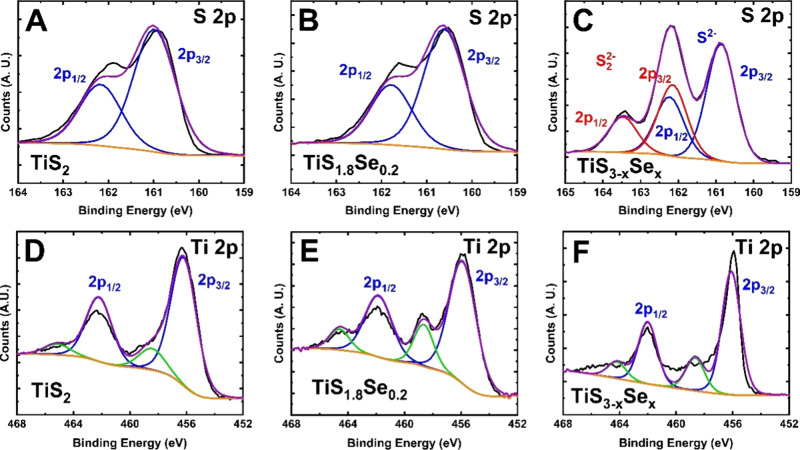
To confirm the purity and coordination environment of our samples, X-ray photoelectron spectroscopy (XPS) spectra were collected for the TiS₂, TiS_1.8Se_0.2, and TiS_3–xSe_x species in the S 2p and Ti 2p binding energy regions (Figure 6). XPS spectra are also collected in the Se 3d binding energy region, which overlaps with the Ti 3s photoelectron peak; these spectra are presented in Figure S3. The S 2p region for TiS₂ contains two peaks for the spin–orbit splitting of 2p_3/2 and 2p_1/2. The S 2p_3/2 and 2p_1/2 peaks of TiS₂ have binding energies of ≈160.9 and 161.9 eV, respectively, with a spin–orbit doublet splitting of 1.0 eV (Figure 6A). A similar spin–orbit doublet splitting of 1.1 eV is determined for TiS_1.8Se_0.2, where the S 2p_3/2 and 2p_1/2 peaks are located at binding energies of ≈160.5 and 161.6 eV, respectively (Figure 6B). Thus, within the resolution of the instrument, no shift to the S 2p peak is observed between pure TiS₂ and TiS_1.8Se_0.2. However, a noticeable difference is noted in the S 2p peak for the TiS_3–xSe_x intermediate. This region contains two sets of overlapping peaks, with maxima at ≈160.9 162.2, and 163.4 eV which correspond to S^2– and S₂^2– species. By analysis of the XPS spectrum in Figure 6C, the peak centered at ≈160.9 eV is assigned to the S^2– 2p_3/2 binding mode. The peak centered at ≈162.2 eV is a combination of the S^2– 2p_1/2 and S₂^2– 2p_3/2 binding modes. Finally, the peak centered at ≈163.4 eV can be assigned to the S₂^2– 2p_1/2 binding mode. As depicted in Figure 6A–C, the S^2– doublet for the TiS_3–xSe_x intermediate exists in a location similar to that of the TiS₂ and TiS_1.8Se_0.2 species. The additional doublet highlighted by the red fitting corresponds to the S₂^2– anion in the TiS_3–xSe_x intermediate. For a stoichiometric TiS₃ species, the ratio of S₂^2– to S^2– should be 2:1. However, given the instability of the intermediate (as evidenced through XRD), the ratio of the 2p_3/2 peak areas is 0.66:1 for S₂^2–:S^2– in TiS_3–xSe_x. Thus, rapid conversion to the TiS_1.8Se_0.2 product is confirmed.

Figure 6.

XPS spectra of TiS₂, TiS_1.8Se_0.2, and TiS_3–xSe_x nanobelts. The S 2p region is shown for (A) TiS₂, (B) TiS_1.8Se_0.2, and (C) TiS_3–xSe_x. The Ti 2p region is shown for (D) TiS₂, (E) TiS_1.8Se_0.2, and (F) TiS_3–xSe_x.

As shown in Figure 6D–F, the Ti 2p regions follow the same spin–orbit splitting pattern as that of S 2p. Each species displays a 2p doublet corresponding to bonding to the S/Se as well as an additional minor doublet (the green fitting in Figure 6D–F) corresponding to sample surface oxidation during loading into the instrument. The Ti 2p XPS region for TiS₂ features a 2p_3/2 peak at ≈456.3 eV and a 2p_1/2 peak at ≈462.4 eV (Figure 6D). The TiS_1.8Se_0.2 sample shows two prominent peaks centered at 2p_3/2 ≈ 455.9 eV and 2p_1/2 ≈ 461.9 eV (Figure 6E). With the addition of Se into the structure, it is expected that the Ti 2p doublet will shift to lower binding energies due to more covalent-type electron sharing with the Se atoms. Though this trend is demonstrated, the differences in peak position are again inside the instrument line width resolution, so the difference in peak position is not quantitative. Figure 6F shows the XPS spectra for the Ti 2p region of the TiS_3–xSe_x sacrificial scaffold, where the binding energies for the 2p_3/2 and 2p_1/2 regions (≈456.0 and 462.0, respectively) are in good agreement with the Ti bonding environments observed for pristine TiS₂ and TiS_1.8Se_0.2 nanobelts, which is to be expected considering the minor change to the coordination environment following desulfurization.

In the region of the Se 3d photoelectron peak, all samples showed the presence of the Ti 3s singlet, centered at around 60 eV. As in the Ti 2p spectrum, the Ti 3s peak for TiS_1.8Se_0.2 displays significant oxidation. As expected, the TiS₂ spectrum did not display a Se 3d photoelectron peak. The TiS_1.8Se_0.2 spectrum displays a Se 3d doublet centered at ≈53.5 eV, corresponding to a single Se oxidation state. The TiS_3–xSe_x spectrum has a small doublet also centered at ≈53.5 eV but also an additional doublet that is centered at ≈55 eV. This is a trend similar to what is observed in the S 2p photoelectron peak for TiS_3–xSe_x and indicates that Se is present as a dianion form in this intermediate state.

As discussed, it is well documented that TiS₂ can show metallic, semimetallic, or semiconducting behavior depending on the defect states within its crystal structure (e.g., S/Ti vacancies, Ti adatoms, and/or S/Se adatoms).²⁵Figure 7 shows the electrical conductivity as a function of temperature for TiS₂ and TiS_1.8Se_0.2 nanobelts. In the measured range of 150–350 K, TiS₂ nanobelts display semimetallic behavior, in agreement with previous studies.^25,44,45 It is expected that TiS_1.8Se_0.2 nanobelts will have a higher electrical conductivity than TiS₂ due to Se being less electronegative than S. The lower electronegativity of Se (relative to S) is expected to cause a partial filling of the Ti 3d conduction band and thus produce degenerate extrinsic electrical behavior. Indeed, such a trend is supported by the Hall electrical conductivity measurements presented in Figure 7. TiS_1.8Se_0.2 exhibits semimetallic behavior over the temperature range of 150–350 K, with a maximum electrical conductivity of 6.88 S cm^–1 observed at 150 K. This represents a 6-fold increase over the maximum electrical conductivity of TiS₂, which was 1.05 S cm^–1 at the same temperature. For both materials, n-type conductivity is suggested by a negative value of the Hall coefficient across the measured temperature range. This concurs with previous analysis of TiS₂ nanobelts where S vacancies are demonstrated to n-dope the materials.²⁵

Figure 7.

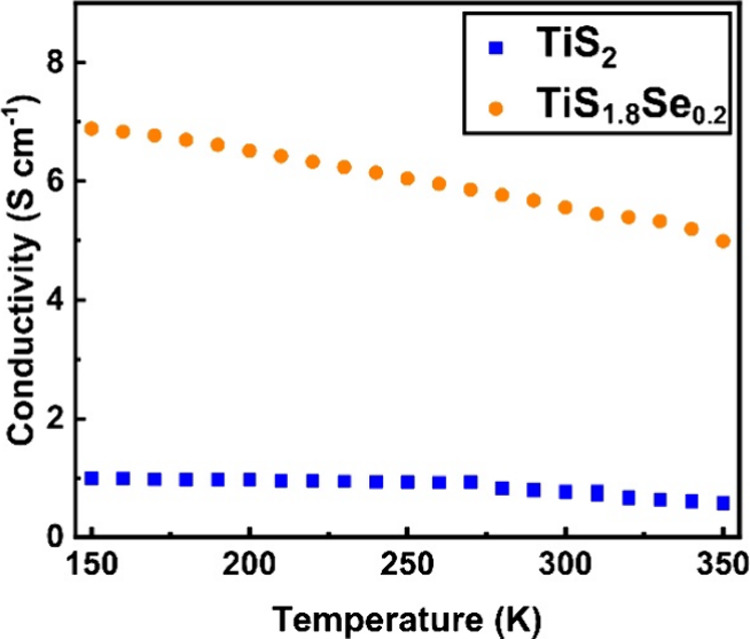
Hall electrical conductivity of TiS₂ and TiS_1.8Se_0.2 nanobelts.

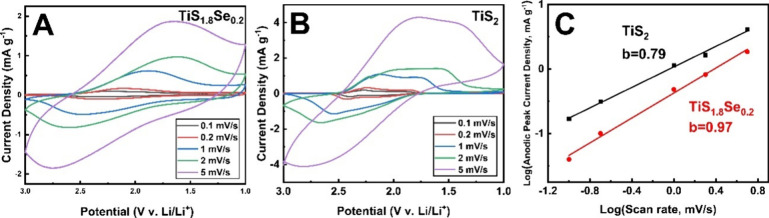
To determine the impact of Se incorporation on the kinetics of Li⁺ ion insertion within the van der Waals layers of our TiS₂ nanobelts, electrochemical studies using cyclic voltammetry (CV) were performed. CV curves were acquired within the voltage range of 1–3 V (vs Li/Li⁺) at variable scan rates (0.1–5 mVs^–1). As illustrated in Figure 8A,B, the CV curves for the Li-based half-cell for both the TiS₂ and TiS_1.8Se_0.2 electrodes display peaks corresponding to the Ti³⁺/Ti⁴⁺ couple, which is the only observable redox process in this voltage window. While TiS₂ displays small redox peaks in both the anodic and cathodic CV curves, these peaks are suppressed for the TiS_1.8Se_0.2 electrode, giving a line shape that more closely resembles a capacitive process.

Figure 8.

Rate-dependent cyclic voltammograms in the range of 0.1–5 mV/s for (A) TiS₂ and (B) TiS_1.8Se_0.2. (C) b-value analysis of intercalation kinetics for TiS₂ and TiS_1.8Se_0.2 was obtained from the anodic peak current density.

To evaluate the different limitations to ion motion in these materials, a b-value analysis of the anodic peak currents at each scan rate was used. Voltammetric response as a function of scan rate can be expressed using the following power law relation:

2

where i is the current measured at electrochemical potential V, v is the scan rate, and a and b are adjustable parameters.⁴⁶ When the logarithmic anodic peak currents (log(i)) versus the logarithmic sweep rates (log(v)) are plotted, the slope of the linear fit should lie between 0.5 (purely diffusion-limited process) and 1.0 (purely surface-limited/capacitive process).^38,47 The b-value obtained from the slope is indicative of what charge-transfer processes are rate-limiting for each material at the redox peak voltage. It is a salient point that the intercalation process of Li⁺ in TiS₂ has been previously labeled as pseudocapacitive due to the continuous potential drop with increased Li⁺ content.²¹ Intercalation pseudocapacitance describes a capacitive-type process that arises from ion insertion into a host material rather than a classical capacitive double-layer. It is anticipated that charge transfer into intercalation-type electrodes contains contributions from faradaic as well as pseudocapacitive processes.

Using the rate-dependent CV curves presented in Figure 8A,B and following eq 2, we calculated the b-values for both TiS₂ and TiS_1.8Se_0.2 (Figure 8C). The TiS₂ electrode has a b-value of 0.79, lying between a diffusive and a capacitive process. However, the TiS_1.8Se_0.2 electrode exhibits a b-value of 0.97, indicating an almost purely capacitive process at the peak discharge voltage. TiS_1.8Se_0.2 demonstrates faradaic behavior in its cyclic voltammograms and thus deviates from ideal pseudocapacitive behavior, defined as a purely capacitive response arising from properties other than the classical double layer.⁴⁸ However, the b-value analysis and a suppressed redox peak in our TiS_1.8Se_0.2 nanobelts indicate significant pseudocapacitive contributions to the charge storage mechanism, leading to fast Li⁺ ion kinetics near the open-circuit voltage

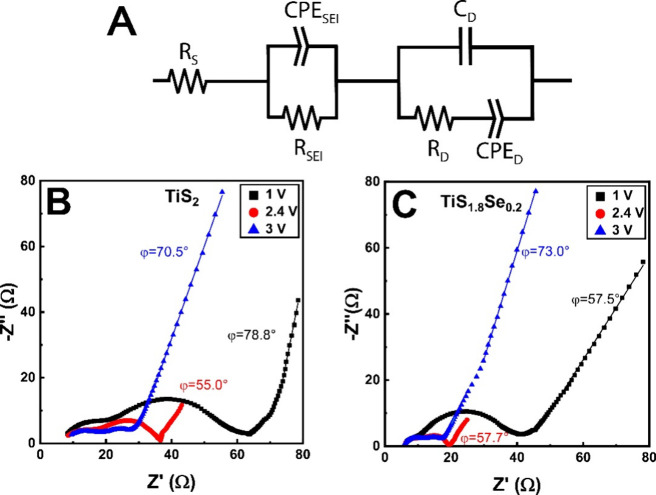
Electrochemical impedance spectroscopy (EIS) studies provide insights into the charge/ion transport, resistances, and interfacial processes in our Li-based TiS₂ and TiS_1.8Se_0.2 electrochemical systems. Moreover, EIS may resolve different factors that contribute to impedance across an electrochemical cell, considering the different time scales of each limiting process. To isolate separate charge-transfer behaviors across each electrode, EIS data was collected across a frequency range of 10^–2–10⁵ Hz. This range allows for the analysis of three charge/mass-transfer mechanisms in the electrochemical cell in three distinctive frequency regimes, which are modeled in the equivalent circuit depicted in Figure 9A. The highest frequency regime (10³–10⁵ Hz) of this circuit is dominated by the series (S) resistance of the electrochemical cell and is represented by R_S. Following this, the middle frequency regime (10⁰–10³ Hz) has contributions from charge/mass transfer from the electrolyte into the solid-state host at the solid electrolyte interphase (SEI), and it is modeled by R_SEI and CPE_SEI in parallel. Finally, in the low frequency regime (10^–2–10⁰ Hz), the Warburg impedance is the major contributor, accounting for ion diffusion (D) through the solid electrode; this region is modeled by C_D in parallel with R_D and CPE_D. Figure 9B,C displays Nyquist plots of TiS₂ and TiS_1.8Se_0.2 acquired from EIS studies. At all potentials, the series resistance of the cell is comparable for both materials with a value of R_S ≈ 4 Ω. This is to be expected considering that the electrolyte resistance should not change significantly between species. However, at all potentials, TiS₂ displays a larger mass/charge-transfer (SEI) resistance than that of TiS_1.8Se_0.2 solid solutions. The SEI resistance of TiS₂ is 28 Ω at 3 V and 23 Ω at 2.4 V and increases significantly to 58 Ω at 1 V. TiS_1.8Se_0.2 is fit to SEI resistances of 13 Ω at 3 V, 12 Ω at 2.4 Ω, and 27 Ω at 1 V. Lower resistances at this interface can be attributed to the increased electrical conductivity and lattice spacing of TiS_1.8Se_0.2. This lower R_SEI term is expected to be a significant contributor to the high capacitance of TiS_1.8Se_0.2 corroborated by the b-value analysis at the open circuit voltage. For both materials, a much larger charge-transfer resistance appears with decreased electrode polarization, evidenced graphically by the increase in the midfrequency semicircle when the cell voltage is lowered to 1 V.

Figure 9.

(A) Equivalent Randles circuit used for fitting. In this diagram, R is a resistor, C is an ideal capacitor, and the CPE is a constant phase element. Nyquist plots of (B) TiS₂ and (C) TiS_1.8Se_0.2 spanning the cycling potential range of the electrochemical cells.

The low-frequency Warburg region of the EIS spectra allows further analysis of ion motion in each species, as diffusion through the electrode happens on this time scale. Phase angle analysis is a useful probe of the electrode behavior in this region. Phase angles of |Φ|= 45° in this frequency region are considered to arise from ideally diffusion-limited processes; higher angles contain contributions from surface-limited processes to the limit of a fully capacitive process at |Φ| = 1. At 3 V, phase angle analysis from the slope in the low frequency Warburg region shows |Φ| = 70.5° for TiS₂ and |Φ| = 73.0° for TiS_1.8Se_0.2. Both materials thus show the presence of blocking electrode-type behavior at 3 V vs Li/Li⁺, which indicates that mass transfer into the electrode does not occur; instead, an electric double layer is formed by ions on the outside of the electrode. In this region, R_D for TiS₂ is 4.0 Ω, while R_D for TiS_1.8Se_0.2 is 1.4 Ω.

At the open circuit voltage of 2.4 V, the TiS_1.8Se_0.2 electrode displays a steeper phase angle in the Warburg region, indicating more capacitive behavior of TiS_1.8Se_0.2 at this voltage. Phase angles from the Nyquist plot are |Φ| = 55.0° for TiS₂ and |Φ| = 57.7° for TiS_1.8Se_0.2. Thus, in this region, a slightly greater value of |Φ| for TiS_1.8Se_0.2 indicates an incremental improvement of ion diffusion kinetics at the open-circuit voltage, in addition to the improved charge and mass transfer into the material from the low R_SEI. Analysis from the equivalent circuit indicates that R_D increases to 8.6 Ω for TiS₂, while R_D remains lower with a value of 3.1 Ω. As the voltage drops to 1 V, however, the phase angle of TiS₂ becomes |Φ| = 78.8° while the phase angle of TiS_1.8Se_0.2 remains relatively constant at |Φ| = 57.5°. Phase angle analysis suggests that Li⁺ ion kinetics in TiS_1.8Se_0.2 remain limited with a decreased cell potential, while a similar reduction in potential improves the ion kinetics of TiS₂. As with R_SEI, both electrodes display an increase in R_D with decreasing voltage, as TiS₂ displays an R_D value of 14 Ω and TiS_1.8Se_0.2 has only a slightly lower R_D of 13 Ω.

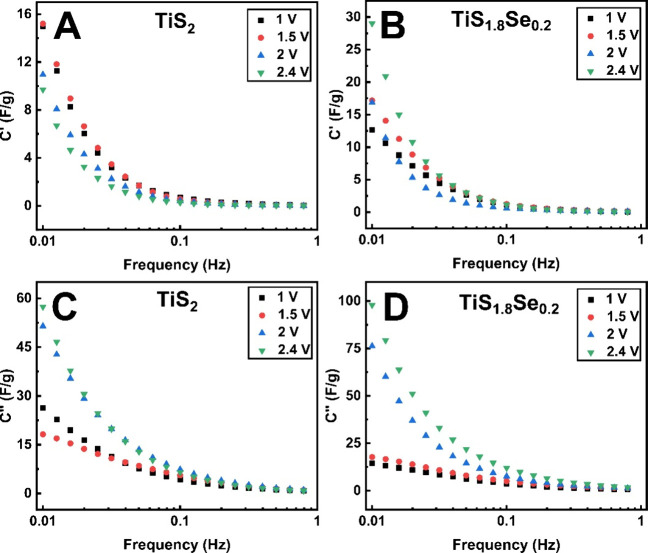
To further understand the ion kinetics of TiS_1.8Se_0.2 electrodes, capacitance in the low-frequency regime is modeled using a 2D Bode plot analysis (Figure 10). Analysis in the low-frequency regime (0.01–1 Hz) is the most relevant for ion kinetics because diffusive processes happen at this time scale. In this frequency range, the electrochemical characteristics of the cell can be simplified to a frequency-dependent resistor and capacitor in series.⁴⁹ Using this model, it is possible to isolate the real (C′(ω)) and imaginary (C″(ω)) components of the capacitance of the cell. These can be calculated from the raw impedance data as per the following equations:⁴⁹

3

4

where C′(ω) and C″(ω) are capacitance terms, ω is the angular frequency, Z′(ω) is the real component of the impedance, Z″(ω) is the imaginary component of the impedance, and |Z(ω)| is the magnitude of the impedance. These two terms provide insight into the frequency-dependent capacitive response of an electrochemical cell. C′(ω) represents the observable capacitance of the cell during discharge and arises from reversible electrochemical processes. C″(ω) is best described as accounting for energy dissipation from irreversible processes at the electrode; diffusion limitations are the key factor being evaluated here. Analysis of both C′ and C″ elucidates the effect of Se doping on ion kinetics in layered TiS₂.

Figure 10.

2D Bode plots of frequency-dependent real and imaginary capacitance of TiS₂ and TiS_1.8Se_0.2. C′ values for (A) TiS₂ and (B) TiS_1.8Se_0.2, and C″ values for (C) TiS₂ and (D) TiS_1.8Se_0.2 are shown.

Analysis of C′ for TiS₂ and TiS_1.8Se_0.2 highlights opposite trends for each material. As displayed in Figure 10A,B, TiS₂ displays an increase in C′ with lowering of the applied voltage, though C′ values are incrementally higher at 1.5 V than at the fully discharged 1 V. TiS_1.8Se_0.2, on the other hand, displays a spike in C′ around the open circuit voltage of 2.4 V, followed by a decrease in C′ at lower potentials. For both materials, C′ has minimal values above the open-circuit voltage (2.4 V), because while blocking electrode behavior gives rise to capacitive behavior, charge storage in this potential region is negligible. The TiS₂C′ response follows the expected trend from the EIS Nyquist plot phase angle analysis: greater capacitive behavior is displayed at the minimum applied voltage of 1 V. However, the maximum in C′ for TiS_1.8Se_0.2 arises near the open-circuit voltage (2.4 V) and exists where phase angle analysis suggests mostly diffusion-limited behavior. Similar anomalous behavior (a maximum in C′ corresponding with low |Φ|) has been previously observed for Nb₂O₅ and was ascribed to the subtleties of its pseudocapacitive behavior.⁵⁰ Fast Li⁺ transfer across the SEI and into the expanded interstitial layer brought about by Se incorporation is expected to be a major contributor to this observed phenomenon.

The maximum of C″ can be used to determine the time constant, τ, where the electrodes switch from displaying resistive to capacitive behavior. As observed in Figure 10C,D, C″ increases throughout the measured frequency range, without displaying any apparent maximum for any of the voltages tested. However, both electrodes appear to display a plateau in C″ around 0.01 Hz at 1 and 1.5 V, suggesting that the time constant for charge transfer at these voltages is τ ≈ 100 s. Both materials display τ > 100 s for higher potentials, suggesting that Li⁺ ion dynamics are too slow to be effectively investigated in this frequency window. These slow charge-transfer dynamics are typical of battery-like intercalation processes, meaning that pseudocapacitance is only a partial contributor to the charge-transfer process present in these electrodes. However, it is worth noting that the high C′ of TiS_1.8Se_0.2 occurs at the same high potential (2.4 V), where kinetics appear limited by C″ analysis.

Overall, C′ and Nyquist plot phase angle analysis indicate that the rate of charge transfer in TiS₂ electrodes increases with decreasing voltage; this agrees with the recently reported behavior of TiS₂ as being diffusion-limited at high voltages, while becoming more capacitive as the voltage lowers from the redox peak potential.³⁸ It is well-reported that TiS₂ interlayer spacing increases with Li⁺ occupation in its interstitial layers, with an expansion of ∼0.05 Å accompanying the full intercalation of Li⁺.^1,38 Li⁺ ion diffusion kinetics thus increase with the increased interlayer spacing of the Li_xTiS₂ solid solution. However, our C′ calculations and b-value analysis indicate a different ion kinetic behavior for TiS_1.8Se_0.2. Highly capacitive behavior is shown near the open-circuit voltage of TiS_1.8Se_0.2, contrary to what is observed for TiS₂. Fast charge transfer in this region is thus suggested. However, C′ decreases with decreasing cell potential, even as the Nyquist plot phase angle remains relatively constant for the material. Se incorporation into TiS₂ thus improves diffusion kinetics at high voltages, while the kinetic behavior of TiS_1.8Se_0.2 becomes similar to TiS₂ as the voltage is lowered.

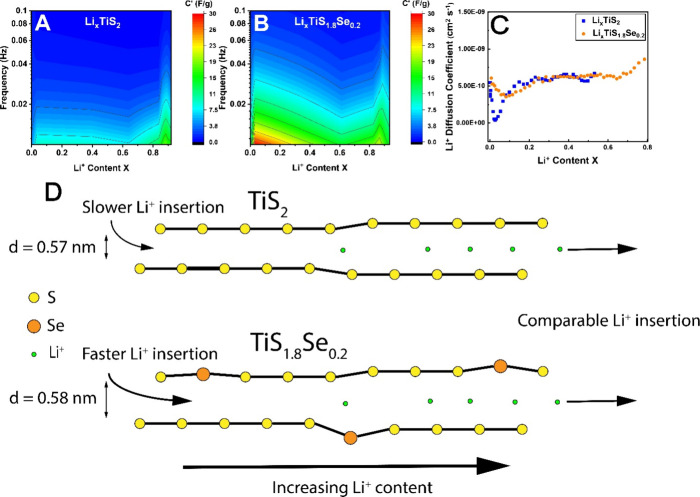
To directly correlate the material capacitance to Li⁺ content, C′ values are plotted versus the Li⁺ concentration at each respective voltage (Figure 11). Li⁺ concentrations are calculated from the theoretical specific capacity of each material, at which stoichiometric LiTiS₂ or LiTi_1.8Se_0.2 is formed. Theoretical specific capacities are 239 m Ah g^–1 for TiS₂ and 221 m Ah g^–1 for TiS_1.8Se_0.2. Specific capacities are collected at a 0.2 C rate in the second cell discharge to allow for solid-electrolyte interphase layer formation. The ratio of the experimental to theoretical specific capacity gives the Li⁺ content of the electrode at a given voltage. It is found that TiS₂ exhibits a maximum Li⁺ loading of Li_0.92TiS₂, while TiS_1.8Se_0.2 has a maximum Li⁺ loading of Li_0.93TiS_1.8Se_0.2. It is important to note that, despite the lower theoretical specific capacity of TiS_1.8Se_0.2, it can host an equivalent concentration of Li⁺ ions as stoichiometric TiS₂.

Figure 11.

3D maps highlighting C′ of (A) TiS₂ and (B) Ti_1.8Se_0.2 relative to Li⁺ content in the electrodes. (C) Li⁺ diffusion coefficients for TiS₂ and TiS_1.8Se_0.2 were determined from GITT analysis. (D) Improvements to Li⁺ insertion due to Se incorporation are most pronounced at a low Li⁺ content.

Figure 11A,B indicates that the capacitive behavior of TiS₂ is greatest when the material is almost fully lithiated, while a maximum capacitive behavior of TiS_1.8Se_0.2 occurs with low Li⁺ content in the material. As Li⁺ concentration in the material is increased, both electrodes display a minimum in C′ at [Li⁺] ≈ 0.6 per stoichiometric unit. In the region of [Li⁺] = 0.85–0.88, TiS₂ and TiS_1.8Se_0.2 and have a spike in C′ of comparable magnitude. A slight downturn in C′ is observed at full Li⁺ insertion; this decrease is likely due to the nearly full occupancy of Li⁺ ions slowing down insertion kinetics.

Additional analysis of ion motion in TiS₂ and TiS_1.8Se_0.2 is gathered through a galvanostatic intermittent titration technique (GITT) analysis. GITT analysis uses Fick’s second law of diffusion to quantify ion migration, allowing the Li⁺ ion diffusion coefficient (D_Li) to be calculated by^38,51

5

where τ is the current pulse time (600 s), m is the active material mass (excluding binder components), V_m is the molar volume, M is the molar mass, A is the electrode contact area (geometric area),³⁸ ΔE_s is the potential difference of the starting and equilibrium potential (after electrode rest), and ΔE_τ is the potential difference of the starting and pulsed potential (before electrode rest). In Figure 11C, D_Li for both TiS₂ and TiS_1.8Se_0.2 is plotted versus the Li⁺ content in the material. Both materials display an increase in D_Li with increasing Li⁺ content, though comparison of TiS₂ and TiS_1.8Se_0.2 is limited in the [Li⁺] range of 0–0.6 due to excessive noise in the TiS₂ data. Importantly, it is observed that, at low Li⁺ concentration ([Li⁺] ≈ 0.02), TiS₂ displays a dip in D_Li of over an order of magnitude. A similar dip in D_Li is observed for TiS_1.8Se_0.2, although its magnitude is significantly reduced. TiS_1.8Se_0.2 thus mitigates a limitation to Li⁺ kinetics that is clearly present for TiS₂ at a low Li⁺ content in the material, concurring with other analyses (vide supra). While GITT analysis indicates that Li⁺ kinetics of TiS_1.8Se_0.2 do improve with increasing Li⁺ content, the most drastic improvement relative to TiS₂ occurs at low Li⁺ loading in the material. At higher Li⁺ content, D_Li becomes comparable for both materials; given that both species are expected to show expanded interlayer spacing with increased Li⁺ content, this is the most likely cause of the increase in D_Li with an increase in [Li⁺].

So, what drives the unusual ion kinetics in TiS_1.8Se_0.2 electrodes? It is anticipated that the large interlayer spacing and increased electrical conductivity both play a crucial role in allowing faster charge transfer into the material at a low Li⁺ content. As the Li⁺ content in the material increases, kinetics become comparable with the TiS₂ and TiS_1.8Se_0.2 nanobelts, with the TiS₂ nanobelts in fact demonstrating superior kinetics (through EIS phase angle analysis) at the low voltage limit. Considering the morphological similarity of TiS₂ and TiS_1.8Se_0.2, differences in the electrochemical performance can be attributed to the presence of the extrinsic Se atom.

Conclusions

We developed a synthesis protocol for fabricating TiS_1.8Se_0.2 nanobelts that display wider interlayer spacing and higher electrical conductivity than their TiS₂ counterparts. Electrochemical analysis indicates that TiS₂ electrodes become more capacitive with increasing Li⁺ ion content. TiS_1.8Se_0.2 electrodes instead display almost purely capacitive behavior near the open-circuit voltage while becoming more resistive during cell discharge. It is therefore suggested that TiS_1.8Se_0.2 displays complex charge-transfer dynamics that consist of pseudocapacitive incorporation of Li⁺ into the host lattice at low Li⁺ content, as well as kinetic limitations to ion diffusion as Li⁺ approaches maximum loading. TiS_1.8Se_0.2 exhibits unusual behavior as it displays superior charge storage in a kinetically limited regime, while D_Li rises in a region of lower capacitance of the electrode. Chalcogen substitution is demonstrated to improve Li⁺ incorporation into a model vdW material and presents a crucial improvement to the development of fast ion insertion mechanisms which can be further implemented and investigated in other 1D structures for future energy storage and neuromorphic computing applications.

Methods

Synthesis

Ti powder (Alfa Aesar, ∼325 mesh, 99.5% trace metals basis), S powder (Alfa Aesar 99.5%, ∼100 mesh), and SeS₂ powder (Sigma-Aldrich, ∼100 mesh) were used without further purification. All work was done under inert conditions using a Schlenk line technique or in an Ar glovebox atmosphere to mitigate sample oxidation. To synthesize TiS_3–xSe_x, Ti and SeS₂ powder were ground in a 1:1 molar ratio using an agate mortar and pestle. The contents were placed in a borosilicate glass ampule, then evacuated to 1 × 10^–3 Torr, and backfilled with N₂ gas on a Schlenk line. Ampules were evacuated and backfilled three times, finishing under a final vacuum of 1 × 10^–3 Torr, and were flame-sealed. Ampules were heated for 20 h at 450 °C. This produced the intermediate phase TiS_3–xSe_x. TiS_3–xSe_x was then placed in a new borosilicate glass ampule. Ti powder was added to the ampule, surrounded by glass wool, and ampules were evacuated and backfilled with N₂ three times and flame-sealed. Heating for 24 h at 450 °C produced nanobelts of the desired phase and stoichiometry, TiS_1.8Se_0.2.

TiS₂ nanobelts are synthesized following a similar, previously reported synthesis.²⁵ Briefly, Ti powder and S powder were ground together in a stoichiometric ratio for the synthesis of TiS₃. The homogeneous mixture of Ti and S was placed in a borosilicate glass ampule that was evacuated to 1 × 10^–3 Torr and backfilled with N₂ thrice. Ampules were placed under a final vacuum of 1 × 10^–3 Torr and flame-sealed. Heating for 20 h at 450 °C produced TiS₃ nanobelts. These nanobelts were placed in a new ampule along with Ti powder surrounded by glass wool. Ampules were evacuated and backfilled with N₂ three times, placed under vacuum, and flame-sealed. Heating for 48 h at 500 °C produced nearly stoichiometric TiS₂.

Characterization

X-ray diffraction (XRD) was performed on a Bruker D8 Advance X-ray diffractometer using monochromated Cu Kα radiation (1.5406 Å). Operating voltage and current were 40 kV and 40 mA, respectively. A scan rate of 1.2° min^–1 was used in a 2θ range of 5–70°.

Scanning electron microscopy (SEM) was performed using a FEI Quanta 600F spectrometer. A field emission gun (FEI Nova Nano, FE-SEM 630) operated at 10 keV was used to image samples.

A JEOL JEM 2800 scanning transmission electron microscope (STEM) with a field emission gun operated at 200 keV was used to determine the crystallinity and measure the lattice parameters of the synthesized nanobelts. Selected area electron diffraction (SAED) was also performed by using this instrument. Energy dispersive X-ray spectroscopy (EDS) was gathered on the instrument by using dual SDD EDS detectors. Sample preparation was done by dispersing nanobelts in isopropyl alcohol, followed by deposition onto a 300 mesh holey carbon-coated copper grid (Ted Pella).

X-ray photoelectron spectroscopy (XPS) was gathered on a Kratos Axis Ultra DLD instrument equipped with a hemispherical analyzer. Aluminum Kα radiation (1486.6 eV) was used for spectra collection, with a pass energy of 40 eV used to collect high-resolution spectra. Measurements were taken at normal takeoff angles. All peaks acquired were normalized to the adventitious carbon peak at 284.6 eV. Data fitting was done using the CasaXPS software, where peaks were fit using a Gaussian–Lorentzian (30% Gaussian) line shape profile. A nonlinear Shirley-type background was used. Within samples, photoelectron peaks originating from the same orbital were fit with the same full width at half-maximum, which was confined between the values of 0.7–3 eV.

The electrical transport properties of pressed pellets and thin films of the synthesized materials were measured using an Ecopia 7000 Photonic Hall measurement system, following a four-point probe configuration.

Electrochemical Studies

Both TiS₂ and TiS_1.8Se_0.2 were incorporated into the Li-ion half cells. Electrodes were prepared using 80% by mass active material (TiS₂ or TiS_1.8Se_0.2), 10% poly(vinylidene fluoride) (PVDF), and 10% carbon black. Precursors were ground with n-methylpyrrolidone (NMP) in a mortar and pestle, and the resulting slurry was cast onto C–Al foil using a doctor blade. Electrodes were dried overnight in a vacuum oven at 60 °C. 1 M LiPF₆ in ethylene carbonate was used as the electrolyte and Li foil, as the anode. Celgard (2400) membrane was used to separate the electrodes, and test cells were crimped together in CR2032 coin cells in an Ar glovebox.

Cyclic voltammetry (CV) and electrochemical impedance spectroscopy (EIS) were performed using a CH Instruments 600E Electrochemical Workstation. EIS data fitting to the equivalent circuit was done using the Zfit MATLAB code.⁵²

Battery cycling was done on a Neware BT-4008 battery test station. Batteries were cycled in the range of 1–3 V vs Li/Li⁺, and variable current densities were used based on the theoretical specific capacity of each material. Galvanostatic intermittent titration technique (GITT) measurements were performed on the same instrument.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnanoscienceau.3c00059.

• (i) Dark field transmission electron micrographs for TiS₂ and TiS_1.8Se_0.2 nanobelts; (ii) Standard X-ray diffraction patterns for TiS₂, Ti, and TiS₃; (iii) X-ray photoelectron spectroscopy spectra for the Se 3d and Ti 3s regions (PDF)

Author Contributions

CRediT: Edwin J Miller conceptualization, formal analysis, visualization, writing-original draft, writing-review & editing; Kameron R Hansen formal analysis, visualization, writing-review & editing; Luisa Whittaker-Brooks conceptualization, formal analysis, funding acquisition, writing-original draft, writing-review & editing.

The authors declare no competing financial interest.

Special Issue

Published as part of ACS Nanoscience Auvirtual special issue “Advances in Energy Conversion and Storage at the Nanoscale”.