A model for positive feedback control of the transformation of fibroblasts to myofibroblasts

Abstract

The phenotypic conversion of normal fibroblasts to myofibroblasts is central to normal wound healing and to pathological fibrosis that can occur in the heart and many other tissues. The transformation occurs in two stages. The first stage is driven mainly by mechanical changes such as increased stiffness of the heart due to hypertension and cellular contractility. The second stage requires both increasing stiffness and biochemical factors such as the growth factor, TGFβ. As more and more cells convert from weakly contractile fibroblasts to strongly contractile myofibroblasts, the stiffness of the ventricular muscle increases. We propose a simple model for the establishment of non-equilibrium steady states with different compositions of fibroblasts and myofibroblasts. Under some conditions a positive feedback loop resulting from the increasing stiffness caused by increasing numbers of myofibroblasts can produce a bifurcation between steady states with low and high myofibroblast content. We illustrate the large mechanical differences between normal fibroblasts and myofibroblasts with measurements in engineered tissue constructs.

1. Introduction

1.1. Fibroblasts and fibrosis

Many organs including lung, liver, kidney, and heart can undergo fibrosis, a condition in which the deposition and remodeling of excess extracellular matrix material (ECM) causes an increased tissue stiffness that ultimately can impair organ function (Hinz, 2009). Central to this process is the transformation of normal fibroblasts (nF) and possibly other types of cells such as endothelial cells and fibrocytes (Zeisberg et al., 2007; Krenning et al., 2010) to myofibroblasts (mF), which combine properties of nFs and smooth muscle cells, including secretion of ECM components and enhanced contractility (Hinz, 2010; Wynn and Ramalingam, 2012). (We use the term “normal” fibroblasts to designate the cells that are resident in tissues under normal or baseline conditions prior to their conversion to myofibroblasts.) Myofibroblasts can have beneficial wound healing functions but also can, when insufficiently regulated, produce fibrosis that seriously distorts the structure and function of the affected organs. Activation of the transformation from nF to mF requires both mechanical signaling and soluble growth factors (Tomasek et al., 2002). We are specifically concerned with fibrosis in the heart. This can result from an acute response as in the repair of local tissue damage due to a myocardial infarction. The mFs form a “scar” that sustains the integrity of the heart muscle by replacing myocytes lost to the infarction (“reparative” fibrosis). In contrast, “reactive” fibrosis, for example, in response to hyper-tension, results from the appearance of mFs diffusely throughout the left ventricular wall. In both cases the mFs can stiffen the heart muscle, either locally or generally, due to the excessive ECM that they produce and possibly also due to their increased contractility. The increased stiffness, both that localized in the infarct scar and the more diffuse stiffening, can cause severe mechanical problems that impair heart function (Richardson et al., 2015; Weber et al., 1993). The stiffening of the heart can lead to both systolic and diastolic dysfunction. The stiffened left ventricle is less able to relax after systole and so experiences a filling defect, a diastolic dysfunction, that can lead to heart failure (Burlew and Weber, 2002). In addition the presence both of locally concentrated and of diffusely distributed myofibroblasts can distort electrical transmission among the cardiomyocytes leading to potentially fatal reentrant arrhythmias (Rohr, 2009; Ongstad and Kohl, 2016).

The function of nFs under normal conditions is to maintain homeostasis of the ECM. The cells secrete the structural proteins of the ECM, mainly types I and III collagen and also elastin and laminin. By exerting contractile forces on collagen fibrils nFs organize the ECM around themselves and establish a prestress, i.e., a tension in the matrix that can be fixed by cross-linking the matrix fibrils rendering unnecessary continued energy-requiring cellular contractile force (Krenning et al., 2010; Humphrey et al., 2014). Fibro-blasts also secrete enzymes that break down the matrix, e.g., matrix metalloproteinases (MMPs) such as collagenases and gelatinases and also inhibitors of these enzymes, tissue inhibitors of metal-loproteinases (TIMPs). The nFs respond to mechanical stimulation, e.g. stretch, to growth factors (TGFβ, PDGF) and to cytokines (TNFα, IL1β, IL6) to modulate the properties of the ECM. To preserve mechanical homeostasis cells must sense changes in the mechanical properties of the ECM and use negative feedback to restore the matrix to its homeostatic set-point (Humphrey et al., 2014). To accomplish this task the cells can sense mechanical changes, e.g. through stress-induced unfolding of focal adhesion proteins such as fibronectin and talin, and through Rho GTPases, that also respond to stretching of the ECM (Janmey et al., 2013; Mao and Schwarzbauer, 2005; Yao et al., 2014). In the short term cells can restore the matrix to the target homeostatic condition by remodeling the matrix and crosslinking its fibers. In the longer term the cells can restore the set-point by breaking down ECM components such as collagen and re-synthesizing them under the prevailing conditions (Humphrey et al., 2014). The continual breaking down and building up and remodeling of the ECM maintains mechanical homeostasis in the form of a Non-Equilibrium (or dynamic) Steady State (NESS) that is balanced to optimize the structure and function of the tissue under current conditions. One can regard this process as a continuous flux of matrix precursors into formed matrix balanced by matrix degradation that maintains matrix stability. As we shall discuss below, conversion of the homeostatic mechanical negative feedback to a positive feedback mechanism, could cause the system to undergo pathological fibrosis.

1.2. Proto-myofibroblasts

The nFs transform into fully differentiated mFs in two steps with the intervening cellular intermediate called a “proto-myofibro-blast” (pmF) (Tomasek et al., 2002). Whereas the actin microfilaments in nFs appear mainly in a relatively diffuse cortical meshwork, pmFs contain actin microfilament bundles (stress fibers). These are composed of β- and γ-cytoplasmic actin and lack β-smooth muscle actin (αSMA). The presence of αSMA is a defining property that distinguishes fully differentiated mFs from pmFs and nFs. The pmFs produce collagen and organize the ECM with relatively small traction forces (Hinz, 2010). They also display the EDA splice form of fibronectin that is essential for progression to the fully differentiated mF. Although it does not appear to be involved in the formation of pmFs, TGFβ is essential for the transformation of pmFs to mature mFs. The increased tension produced by the pmFs is instrumental in releasing and activating this growth factor (Wipff et al., 2007). PDGF is also important for the formation of pmFs but does not initiate the appearance of αSMA (Tomasek et al., 2002).

1.3. Models for nF to mF transformation

The transformation from nF to mF has been studied mainly in two kinds of “model” systems. One of these is the granulation tissue that forms during repair of a wound; the other is a collagen hydrogel lattice in which the fibroblasts are embedded to form an engineered tissue construct. One advantage of the latter system is that the initial density of the ECM and the cells, the stretching forces exerted on the construct and the contractile forces developed by the cells in the construct can readily be controlled and measured quantitatively. A problem in using this approach, however, is to obtain the nFs. Culturing fibroblasts on rigid glass or plastic surfaces, as is typically done prior to forming a collagen-based tissue construct, already transforms them at least partially into mFs. Releasing the lattice from its anchorage to the rigid substrate prevents the cells from developing force against a strong resistance and allows the tissue construct to undergo a cell driven contraction that eventually results in the disappearance of the microfilament bundles. Fibroblasts embedded in anchored collagen matrices, however, do form stress fibers and integrin-dependent attachments to the collagen lattice suggesting a transformation toward the mF phenotype (Tomasek et al., 1992, 2002; Grinnell, 2003). These observations suggest that tension generated in the cells is necessary to form and maintain stress fibers. These results also suggest that the phenotypic transformation is at least partially reversible.

Either the stiffness of the tissue in which the fibroblasts are embedded or the stress/force exerted on it internally by the cells or by an external force could be used as the independent variable to interpret the effect of mechanical change on the fibroblast phenotype. This is because stiffness, i.e., Young’s modulus, varies linearly with stress, and so the functional dependence of the phenotypic transformation is interchangeable for the two variables. It has been known for some time that the stiffness of soft biological tissues varies linearly with stress (Fung, 1993), and this stress stiffening property was analyzed in collagen-based tissue constructs (Wakatsuki et al., 2000) as well as biological hydrogels (Storm et al., 2005a).

Fibroblasts cultured in soft matrices, either polyacrylamide gels or collagen, do not display stress fibers and have only small adhesions to collagen fibers (“focal complexes”) (Hinz, 2010; Tamariz and Grinnell, 2002; Yeung et al., 2005). Stress fibers appear only after the stiffness exceeds a threshold level (Yeung et al., 2005). This suggests that for the cells to transform from nF to pmF they must exert a sufficient contractile force on their surroundings (substrate or ECM or adjacent cells). The surroundings must be stiff enough to resist cellular contraction to allow the cells to develop at least a threshold level of contractile force. When cells at high concentration interact directly with each other, they also could develop stress fibers even in a soft environment. Presumably, the forces that they exert directly on each other would be sufficient to overcome the failure of the matrix to supply sufficient resistance to their contractile force. Normal heart tissue has a Young’s modulus of approximately 10 kPa, which might be expected to trigger formation of mF (Hinz, 2009). That fibroblasts lacking stress fibers predominate in normal heart muscle could be explained by a mechanism in which the cells are shielded from stress by ECM that they have produced and remodeled under the conditions of stress that they normally experience (Tomasek et al., 2002). How, then, do nF sense the increases in stiffness or stress that trigger a transformation to pmF, for example, in response to hypertension that produces hypertrophic cardiomyopathy? (Perhaps there is a stress threshold that must be exceeded to overcome the remodeled matrix that shields the nF.) Of course, for the heart there is the additional consideration that the changes of stress and stiffness that accompany periodic contraction do not trigger the phenotypic conversion of fibroblasts. That these changes are transient suggests that the duration of stress/stiffness changes might be critical.

1.4. Transformation of pmF to mF

To progress from pmFs to fully mature mFs that contain αSMA and a greater amount of EDA fibronectin requires culture substrates even stiffer than those that trigger the transformation from nF to pmF (Hinz, 2010). The resulting mature mFs also display large super mature focal adhesions with dimensions in the range of 8–30 μm that exert stress on the substrate in the range of ~12 nN/μm² compared to conventional FAs with dimensions of 2–6 μm and one fourth the level of stress (Goffin et al., 2006). In addition to stiffer substrata activation of the TGFβ type II receptor is also required. This triggers the production of both αSMA and other components of the mF contractile machinery, the EDA splice form of fibronectin, and also collagen (Tomasek et al., 2002).

An interesting mechanical mechanism makes the active TGFβ available to pmF (Hinz, 2010; Wipff et al., 2007; Arora et al., 1999). Cell-secreted TGFβs are latent because of their binding to the latency-associated protein (LAP), which forms a complex with the latent TGFβ1 binding protein (LTBP-1). The LTBP-1 binds to the ECM and the LAP binds to integrins that connect to the intracellular contractile machinery. The TGFβs are released when LTBP-1 and LAP are mechanically pulled apart. Therefore, activation of the TGFβ type I receptor requires that the ECM be stiff enough (>5 kPa) to allow the cells to exert adequate force on LTBP-1. Alternatively, TGF can be activated by proteolytic cleavage of LAP-TGFβ (Wipff et al., 2007). A similar cooperation of mechanical stress and TGFβ1 seems also to upregulate the expression of collagen and other matrix proteins (Chiquet et al., 2003; Carver and Goldsmith, 2013). Conversely, reduction of matrix stiffness seems to establish an anti-fibrotic environment with increased production of MMPs (Carver and Goldsmith, 2013).

From observations of cells on flexible polymer substrates, Hinz summarizes a series of stiffness thresholds (Hinz, 2010): 1) nFs, no stress fibers (1 kPa), 2) pmFs, stress fibers without αSMA (3–5 kPa),3) TGFβ type II receptor activation (5–9 kPa), and mature mF stress fibers with αSMA (16–20 kPa). As the transformation from nF to pmF to mF progresses, the cells exert increasing stress on the ECM, and the structures that bind the cell to the ECM evolve from small focal complexes through mature focal adhesions and then to supermature focal adhesions (Hinz, 2010). The contractile force exerted by the cells and the tissue stiffness continue to increase. Note that threshold stress values are likely to be different for cells in 3D tissues than for cells in 2D culture.

2. Mechanical Properties of Normal Fibroblasts and myofibroblasts in 3D tissue constructs

The remodeling of ECM by fibroblasts is crucial for normal development, and myofibroblasts play a central role in both wound healing and pathological fibrosis. The stiffening of the ECM by contractile mF and pmF helps drive the transformations of nF to pmF and mF. Mechanical differences between nF and mF are readily demonstrated in 3D collagen-based tissue constructs.

These constructs are formed by embedding fibroblasts in a relatively dilute collagen matrix (~1 mg/ml) and then allowing them to compress and stiffen the matrix to form tissue rings or loops suited to mechanical measurements (Wakatsuki et al., 2000). This has been illustrated by measuring the increase in contractile force, activation of non-muscle myosin regulated by Rho ATPases, as well as the stiffness and the compression of the matrix requiring attachment of the cells to the collagen via integrins over the duration of the process (Wakatsuki and Elson, 2003). The matrix stiffens as it is compressed and its volume can shrink 10-fold within 24 h.

Measurements of contractile force and tissue viscoelasticity illustrate the mechanical differences between nFs and mFs. The nFs were prepared by isolating cardiac fibroblasts from 10-day-old chicken embryo hearts using enzymatic treatments and were enriched using their strong adhesion strength to cell culture plates (Eschenhagen et al., 1997). The mFs were prepared by culturing those freshly isolated nFs on cell culture dishes for ~1 week supplemented with 3% fetal bovine serum (FBS). We distinguished mFs from nFs by detecting αSMA expression using Western blotting analysis. Using the protocols described previously (Wakatsuki et al., 2000), the 3D tissue constructs containing nFs and mFs were readily distinguished by the following criteria (data not shown):

1. The rings containing mFs were compressed to a much smaller volume than those containing nFs.

2. The highly compressed mF constructs but not the much less compressed nF constructs showed αSMA and EDA fibronectin immuno-histochemically.

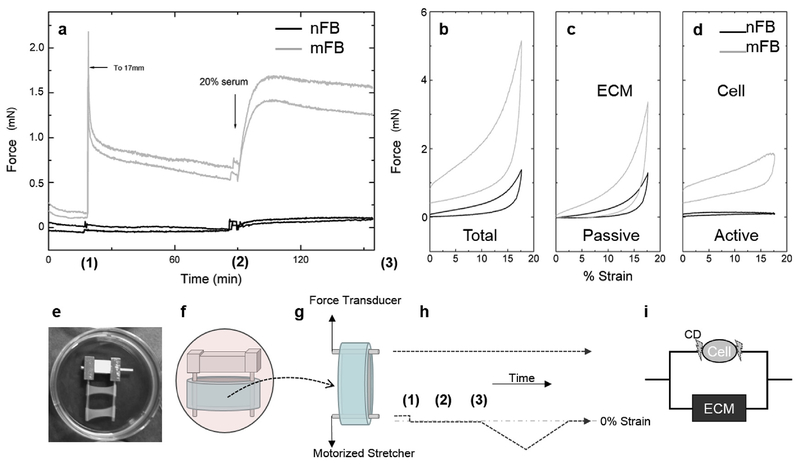
The differences in their mechanical properties and experimental protocol are illustrated in Fig. 1. Fig. 1a shows the response of tissue constructs that contain nFs or mFs to stretch and to activation by 20% calf serum (containing lysophosphatidic acid that activates the Rho ATPase pathway). When mF constructs were stretched and then held at a constant strain, they exerted a restoring force that relaxed over time to a level that was higher than the original force level (Fig. 1a), as expected for a viscoelastic material. In contrast, the nF constructs were much less stiff and barely registered an increase in force after stretch, indicating a lack of ECM compression by the nFs. Similarly, mF constructs responded sharply after 20% calf serum while there was a minimal response from the nF constructs. ‘Hysteresis” curves in Fig. 1b–d provide further evidence of the mechanical difference between nF and mF constructs. For these studies force was measured as the tissue constructs were stretched at a constant rate and then unloaded at the same rate (Wakatsuki et al., 2000). Prior to these measurements the tissue constructs had been stretched once to a strain of 20% to reduce an apparently irreversible effect of stretch on the mechanical properties of the construct (Wagenseil et al., 2003). Fig. 1b shows the plots for untreated constructs, and the difference between the loading and unloading curves defines a hysteresis area that indicates the mechanical energy dissipated due to viscosity (and possibly other effects). The resistance to stretch and the hysteresis area were much greater for the mF construct than those of nF constructs. The same constructs were treated with cytochalasin D that disrupts the actin filament cytoskeleton and effectively disconnects the cells from the ECM. Hence, they represent the hysteresis curves for the ECM as remodeled by the cells but without a direct mechanical contribution of the cells (Fig. 1c). Total and Passive curves of nFB and mFB constructs show a typical strain-stiffening behavior seen in biological tissue, natural ECM hydrogels, and some synthetic ones (Storm et al., 2005b; Jaspers et al., 2014) but not in Active curves that represent force-strain relationship of cells. As expected, the matrix remodeled by the mFs was much stiffer and had a larger hysteresis area. Subtracting Fig. 1c curves from those in Fig. 1b approximately represents the direct contribution of the cells to the measured force (Fig. 1d) (Wakatsuki et al., 2000). While the mFs contributed a substantial level of resistance to stretch, that contributed by the nFs was barely detectable.

Fig. 1. Mechanical Properties of Normal Fibroblasts (nFs) and Myofibroblasts (mFs).

(a) When mF constructs were stretched, they exerted a restoring force that relaxed over time to a level of that was higher than the original force level, as expected for a viscoelastic solid material. After the force had stabilized over an hour interval, the cells in this construct responded to 20% serum by exerting a substantial contractile force (time course traces of duplicated constructs). The tissue constructs that contain the nFs showed minimal stretch-induced resistance force and contractile response to 20% serum. Panels b-d. Loading/unloading curves for tissue constructs with nFs (black) and mFs (grey). Construct rings were stretched 3 mm over 7.5 min at a constant rate and unloaded at the same rate (Wakatsuki et al., 2000). (b) Untreated constructs. (c) Cytochalasin D-treated constructs. Without actin filaments the mechanical contributions of the cells are effectively removed from the construct. (d) Subtracting the curves in (c) from those in (b) illustrates the mechanical properties of the cells. The mFs have a much larger viscoelastic response than do the nFs. (b, c, and d show one of duplicated constructs) (e) Typical duplicated constructs in culture. A construct cultured with scaffold bars (f) is transferred to a mechanical measurement apparatus (g) which consists of a force transducer and motorized stretcher expanding the construct submerged in an organ bath (37° C and 25 mM HEPES buffed culture medium). (h) A time course of experimental steps shows (1) stretch from relaxed to 0% strain level (2) serum addition (3) stretching and recovering with a constant strain rate. (i) A schematic shows an effect of CD disconnect cells from ECM.

These and earlier measurements (Wakatsuki and Elson, 2003) demonstrate that mFs stiffen their ECM and develop a contractile force over time. The matrix stiffens due to the contractile forces exerted by the cells and due to the compression and remodeling of the matrix by the cells. As this is happening, any nFs present in the matrix would experience an ever greater matrix stiffness that, together with exposure to serum growth factors, would continually increase their propensity to convert into mFs. After 3–4 days, the nFs embedded in the construct converted to mFs and compressed the constructs to an extent comparable to that of the constructs that had been populated initially by mFs. This suggests a positive feedback mechanism for the conversion of nFs to mFs. We explore this possibility below in terms of simple kinetic models.

3. Simple kinetic models of phenotypic transformations induced by mechanical stress

Under stable physiological conditions one expects the heart muscle to be in a stable phenotypic tissue state. For example, the synthesis and remodeling of the ECM is balanced by protein degradation and disassembly to maintain a steady homeostatic optimum. Similarly, at the cellular level the production of normal fibroblasts is balanced by their loss to maintain a steady population level. Might there also be stable intermediate cellular states along the pathway to fibrosis? Are there conditions in which a balance between normal and proto-myofibroblasts is maintained leading to a stable pre-fibrotic tissue steady state, e.g., at one or more of the stiffness thresholds mentioned above? Finally, would there also be a stable state for fully mature myofibroblasts that would maintain a stable fibrotic condition subject to external constraints such as mechanical stress and the presence of soluble activators such as TGFβ1? It is helpful to frame these questions in terms of simple linear and nonlinear kinetic models that predict markedly different behavior.

In developing a model for the transformation of nF to pmF and eventually to mF one must first decide whether to treat the total fibroblast population as an open or closed system. In the former case the fibroblasts in the tissue neither gain nor lose cells from outside the system. If the transformations of nF to pmF and of pmF to mF are irreversible, then it is obvious that ultimately all the fibroblasts in the tissue become mF. If the transformations are, however, reversible, then a steady state condition among the different cells types is established. In an open system fibroblasts can be generated from non-fibroblast precursor cells and can lose cells, e.g., due to cell death. Thus there is a continual flux of cells from precursors through the fibroblast phenotypes and eventually removal from the system. Both open and closed systems eventually reach a time-independent condition. We have chosen to treat the fibroblast system as open, which, in our opinion, is the more realistic option. As we discuss below, open systems can reach time-independent steady states, but these states are not equilibrium conditions.

3.1. Simple tissue kinetic model

For simplicity let us suppose that the transformation of an individual cell from the fibroblast to the myofibroblast phenotype involves three states, as described above: normal fibroblast (nF, no stress fibers), proto-myofibroblasts (pmF, stress fibers, no αSMA), and mature myofibroblast (mF, αSM-containing stress fibers). We assume that a tissue consists of individual cells each of which undergoes the following possible transitions:

where r₀ represents a precursor cell population, and k₃ is a rate constant for an mF cell disappearing, e.g., by apoptosis. It is possible that nF and pmF are also subject to apoptosis, but a recent paper suggests that mF are particularly susceptible (Lagares et al., 2017a). Therefore, we have for the sake of simplicity presumed that only mF are removed by apoptosis. We also assume that the transitions among nF, pmF, and mF are reversible. In the following, we will mainly focus on the nF to pmF transformation. We will address the larger kinetic model in Scheme 1, including mF, in subsequent work.

3.2. General linear model

Let x_nF, x_pmF and x_mF be the fraction of cells in each of the three states in the tissue at time t. If all the cells that undergo the transitions in Scheme 1 are statistically identical and independent

Scheme 1.

Sequence of conversions that represent a linear model of the transformation of normal fibroblasts (nF) to myofibroblasts (mF). The nF are supplied from precursors (r0) and the mF are subject to apoptosis (k3).

$$r_0\stackrel{k_0}{\to }nF\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}pmF\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}mF\stackrel{k_3}{\to }\varnothing$$

individuals, then one has

$$\begin{gathered} \frac{d{x}_{nF}}{dt}=k_0{r}_0-k_1{x}_{nF}+k_{-1}{x}_{pmF} \\ \frac{d{x}_{pmF}}{dt}=k_1{x}_{nF}-\left(k_{-1}+k_2\right)x_{pmF}+k_{-2}{x}_{mF} \\ \frac{d{x}_{mF}}{dt}=k_2{x}_{pmF}-\left(k_{-2}+k_3\right)x_{mF} \end{gathered}$$ (1)

For this system to be in a NESS the rate of supply of normal fibroblasts must equal the rate of loss of mF, i.e., k₀r₀ = k₃x_mf and k₃x_mf (or k₀r₀) is the flux of cells through the system. We have taken x_mf as the fraction of the fibroblasts in the tissue volume that are mF. For our purposes the important aspect of this linear system is that the rate of flux is entirely fixed by the balance between the rate of supply of nF and elimination of mF, and so the steady state concentrations of nF, pmF and mF are unique continuously variable functions of

$$k_0{r}_0;{\left(x_{nF}\right)}_{ss}=\frac{k_0{r}_0}{k_1}\left[\frac{k_{-1}\left(k_{-1}+k_3\right)}{k_2{k}_3}+1\right];{\left(x_{pmF}\right)}_{ss}=\frac{k_0{r}_0\left(k_{-2}+k_3\right)}{k_2{k}_3};$$

${\left(x_{mF}\right)}_{ss}=\frac{k_0{r}_0}{k_3}$ As we show below, this could contrast to nonlinear kinetic systems that under certain conditions can experience a bifurcation into co-existence of two different states with faster and slower fluxes through the phenotypic transformation system.

3.3. Effects of mechanical feedback on the transformation of normal fibroblasts to proto-myofibroblasts

We consider possible effects of mechanical feedback from the contractile influence of pmF on the stiffness of the ECM. The preceding discussion and experimental results indicate that contractile force exerted by myofibroblasts stiffens the ECM in their vicinity and that increasing stiffness of the ECM enhances the transformation of nF to pmF. We explore the consequences of these observations using a simple model that, while it is inadequate for an accurate description of the actual cellular behavior, is sufficient to illustrate the principles involved. Also, in this analysis we omit consideration of the supply of nF from precursor and their removal by apoptosis to focus on the effects of mechanical feedback. Subsequently, we consider how the model could be made more realistic although more complicated.

As the basis of the model we suppose that fibroblasts are quasi-randomly distributed throughout the heart muscle and that under baseline conditions they reside as “normal” fibro-blasts that maintain the ECM in a homeostatic steady state and rarely are transformed into pmF. When the heart is exposed to hypertension, the muscle is stretched thereby increasing its stiffness. We suppose that the changes of tension and stiffness expected during the contractile cycle are too transient to affect the phenotypic state of the fibroblasts but that the long term increase in diastolic stiffness due to the hypertension, even if small relative to the effects of the contractile cycle, could slightly increase the probability of the conversion of a nF to a pmF. A single pmF by exerting increased contractile force among the surrounding nFs slightly increases the local stiffness of the matrix thereby further slightly increasing the probability that another of the nearby nFs would convert to a pmF. Alternatively, a pmF could directly exert force on a cell to which it is attached by gap junctions increasing its probability of conversion. The presence of two pmFs in this region further stiffens the local tissue thereby further slightly increasing the probability of inducing nearby nFs to convert to pmFs. At each step of this positive feedback process, there are more pmFs and their combined contractile force that stiffens the local ECM is that much greater, thereby correspondingly increasing the probability of converting nearby nFs to pmFs.

The following kinetic model described in Scheme 2 accounts for mechanical interactions among the cells. We consider within the tissue many “region(s) of interest” (ROIs) defined as volumes, which are small but nevertheless contain many (n) cells. Such a treatment is a standard approach in continuum mechanics. The state of an individual ROI is represented by an integer variable, j. There are j pmFs and n–j nFs with 0 ≤ j ≤ n The following kinetic set of steps in Scheme 2 is a probabilistic description of Markov state transitions within a single ROI:

(One might also think of this sequence steps in terms of a system of chemical reactions.) In the kinetic scheme, we have assumed that a single cell transition from the pmf state to nF state, with rate k_b, is an event of that individual pmf cell, independent of other cells and its environment. This leads to the rate of transition of an ROI from containing j + 1 pmF to j pmF being (j + 1)k_b due to simple combinatorics. The transition rate of an ROI from the state of having n – j nF cells to having n – j – 1 nF cells (increasing pmF by one), is denoted by k_j(n – j; T_j). This rate is a function of the number of nF cells (n – j) as well as of the tension, T_j, exerted by the j pmF cells in the ROI.

First we illustrate how this formalism could be applied to a linear model for the transformation. We shall assume that s is the tension exerted by each of the n identical and independent fibroblasts in the ROI. We define

$$k_j\left(n-j,T_j\right)=\left(n-j\right)k_{f}s$$

where s represents T_j. The term (n – j) is a combinatoric factor and k_f is an elementary rate constant common to all the “forward”, i.e., j→j + 1 kinetic steps. As indicated above, the “reverse”, i.e., j+1→j, is (j + 1)k_b.

We denote the probability that an ROI has j pmF cells at time t, as p_j(t). The mean number of pmF in the ROI is given as

$${\overline{n}}_{pmF}\left(t\right)={\displaystyle \sum _{j=0}^n{p}_j\left(t\right)}$$

The mean fraction of the pmFs that are in the ROI is $x=\frac{{\overline{n}}_{pmF}}{n}$ The probabilities p_j(t) are obtained using a master equation as described in the Appendix. This yields a rate equation of the form:

$$\frac{dx}{dt}=k_{f}s\left(1-x\right)-k_{b}x$$

Hence, as might be expected, the system behaves as a simple monomolecular reaction. Therefore, a binomial distribution yields the steady state number of pmF cells in the ROI as

$$p_j^{ss}=\frac{n!}{j!\left(n-j\right)!}\frac{k_f^j{k}_b^{n-j}}{{\left(k_f+k_b\right)}^n}$$

In contrast, the behavior of a nonlinear system can be much more complex.

3.4. Nonlinear model

We propose that the nF to pmF transformation is nonlinear. Among a number of possibilities we have chosen to introduce a model in which the pmF in an ROI exert force on the matrix cooperatively. We therefore define k_j(n – j, T_j) as follows:

$$k_j\left(n-j,T_j\right)=\left(n-j\right)k_f{\left(\frac{sj}{n}\right)}^j$$ (2)

where ${\left(\frac{sj}{n}\right)}^j$ represents T_j.The “simple” tension exerted by j cells is $\frac{sj}{n}$. While each cell exerts tension, s as before, cooperative exertion of force by the pmFs leads to the exponentiation by j introducing the nonlinearity.

For both the linear and nonlinear models we have also assumed that the dynamics between nF and pmF are on a faster time scale than the transition from pmF to mF. Thus, we have neglected the latter’s presence in Scheme 2 The present effort should be considered a kinetic model for the pre-transformation to the state of a tissue containing a high concentration of proto-myofibroblasts, an intermediate along the pathway to a state with a high population of fully mature myofibroblasts. We will address a more complete model that includes the transformation of pmF to mF in the future.

Scheme 2.

$$\begin{array}{c}n\left[nF\right]\underset{k_b}{\overset{k_f\left(n\right)}{\rightleftharpoons }}\left(n-1\right)\left[nF\right]+\left[pmF\right]\\ \left(n-1\right)\left[nF\right]+\left[pmF\right]\underset{2k_b}{\overset{k_1\left(n-1,T_1\right)}{\rightleftharpoons }}\left(n-2\right)\left[nF\right]+2\left[pmF\right]\\ ⋮\\ \left(n-j\right)\left[nF\right]+j\left[pmF\right]\underset{\left(j+1\right)k_b}{\overset{k_j\left(n-j,T_j\right)}{\rightleftharpoons }}\left(n-j-1\right)\left[nF\right]+\left(j+1\right)\left[pmF\right]\end{array}$$

As before, the probabilities p_j(t) are obtained using a master equation described in the Appendix. The Appendix derives the following equation for the time rate of change of x, the fraction of the cells that a pmF:

$$\frac{dx}{dt}=k_f{\left(sx\right)}^{nx}\left(1-x\right)-k_{b}x=g\left(x;s\right)$$ (3)

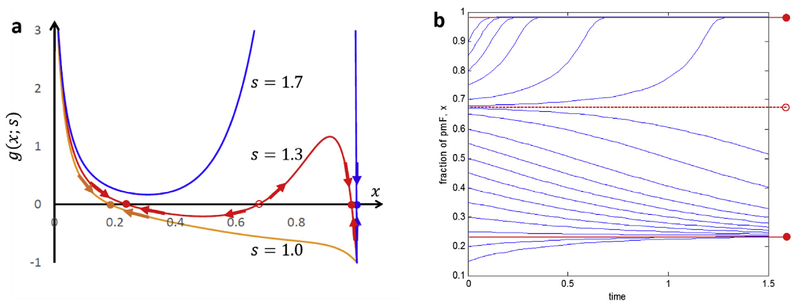
Fig. 2 shows plots of g(x; s) as a function of x, with several different values of s. The steady states occur when $\frac{dx}{dt}=0$ and so are identified as the roots of g(x; s) = 0, i.e., the values of x at which $\frac{dx}{dt}=g\left(x;s\right)=0$. We observe a saddle-node bifurcation (Strogatz, 1994) (Fig. 2A). With a low tension parameter and therefore at a low probability of converting nF to pmF [s = 1.0, orange] there is a single steady state at a low value of x (x ≅ 0.20) As the tension parameter increases [s = 1.3 (red)] the system exhibits bistability: there are three roots. The lowest root indicates a stable steady state with x ≅0.22. The highest root corresponds to a stable steady state at high x (x≅0.98). The intermediate root at (x≅0.67) corresponds to an unstable state. If the system begins at x > 0.67 it goes to the higher stable state (x≅0.98). If the system begins at x < 0.67, it goes to the lower stable state (x ≅0.22). At still higher tension parameter [s = 1.7 (blue)] the system is monostable again and has a single, steady state with a high concentration of pmF (x≅1.). Fig. 2b illustrates how under bistable conditions the system goes either to the high x (fibrotic) state or the low x (nonfibrotic) state depending on the initial value of x. For tension parameter at this intermediate level (s = 1.3), starting with x < 0.67, the concentration of pmF goes to the lower steady state (x≅0.22). Starting at x > 0.67 the concentration of pmF rises to the higher steady state concentration(x≅1). For lower tension parameter values, e.g., s = 1, a plot analogous to Fig. 2b would show only curves that, if they started at x > 0.2, decreased or if they started at x < 0.2 increased over time to the low steady state at x≅0.20. Similarly, for higher tension parameter values (s = 1.7) there would be only curves that increased time to the high concentration steady state (x≅1.).

Fig. 2. Stability analysis of profibrotic tissue using bifurcation theory.

(a) Plots of g(x; s) with different values of tension, s (1:0–1:7). With increasing tension, s, by pmF in an ROI, the nF-to-pmF transformation switches from monostability with a single steady state at low x (≅0.20; s = 1) to bistability with two coexisting steady states (x≅0.23 and 0.98;s = 1.3). With a higher value of s (s = 1.7) the system becomes more stable with a single steady state at x ≅1.0 (~all pmF). Other parameters n = 10 and k_f/k_b = 5. Solid circle: stable fixed point and open circle: unstable fixed point. (b) Bistable behavior of the pmF fraction, x, of proto-myofibroblasts in an ROI predicted by the nonlinear model (s = 1.3) in (a). For an initial value of x below the unstable fixed point (x≅0.67) the system relaxes to the steady state with a low concentration of pmF (x≅0.23). When x > 0.67, x advances to the steady state with high pmF concentration (x≅0.98).

The values of the parameters used in Fig. 2a and b were selected only to illustrate the behavior of the system. Our model is so oversimplified that it cannot be used to derive actual properties of the nF to pmF transformation. Nevertheless, the model does demonstrate how an increase of local tissue stiffness that depends in a nonlinear fashion on the increasing number of pmF could lead to an accelerating conversion of nF to pmF and therefore to bistable behavior. Recently nonlinear stress inference microscopy (NSIM) analyzed stress fields in a 3D matrix around a single cell and revealed cellular F-actin dependent stress-stiffening phenomena (Han et al., 2018). While the stress stiffening should be taken into account carefully, interrupting the feedback mechanism, e.g., by disrupting the cells’ actin cytoskeletons or inhibiting myosin contractility to reduce tissue stiffness would abate the phenotypic conversion process and decrease the development of fibrosis. It is worth noting that the reduction of tissue stiffness due to these treatments is a consequence of the strain stiffening of the collagen matrix. Strain stiffening was included implicitly in our model by the presumption that the stiffness increases as the cells exert more contractile force. This can be made more quantitative in later work.

To describe the nF to pmF transition realistically a number of oversimplifications must be addressed of which we describe a few. The current model does not account for the dependence of the stiffening of the local matrix on the distance from the pmF (or mF) exerting contractile force on the ECM. Because of this effect the embodiment of the mechanical coupling among cells in the simple constant, s, is oversimplified. Future work will take this into account. This distance dependence will depend on the viscoelastic properties of the matrix, which change as the matrix stiffens due to hypertension or to the local contractile effects of pmF. Furthermore, the current model is limited to mechanical effects. It does not account for the effects of TGFβ (and other growth factors and cytokines (Storm et al., 2005b)) that promotes the pmF to mF transformation. The dependence of the release and activation of TGFβ on stress in the tissue provides another positive feedback loop: increased stress or stiffness activates TGFβ, which then further increases stress/stiffness by promoting the pmF to mF transformation. If, among the cells that convert early to pmF some advance to mature mF, their increased contractility and secretion of TGFβ would substantially strengthen the positive feedback loop, increasing the likelihood of further nF to pmF and pmF to mF conversions. Finally, the rate of diffusion of TGFβ throughout the ROI should be taken into account. This is complicated by the binding of TGFβ to the ECM.

It is also important to emphasize that there is, as far as we know, no direct experimental evidence that a positive mechanical feedback mechanism like the one we have described does function in heart tissue. Nevertheless, we have demonstrated that this kind of mechanism based on the effects of pmF and mF on the stiffness of the ECM and also direct mechanical interactions among cells in contact is at least theoretically possible and for our very simple model could lead to a bifurcation. In our view, the possibility of this positive feedback process and its potentially important effects in regulating the transformations of normal fibroblasts to myofibro-blasts justify investigating whether or not the mechanism is present and, if so, to measure the properties of cells and tissues that make its operation possible. The practical significance for cardiac pathology arises from the possibility of finding new approaches to abating the progress of fibrosis in the heart and possibly other organs as well. Several accessible kinds of experimental measurements both in reconstituted tissue constructs and in animals would be useful for this purpose. Microrheological methods could supply measurements of the stiffness changes induced by contraction of a single nF, pmF and mF. These could be accomplished in tissue constructs, for example by tracking nanometric beads at different distances from contracting fibroblasts in a collagen matrix. Furthermore, it would be important to measure how the mechanical effects of groups of cells depend on the size of the group, both in spatial extent and number of cells. These measurements could determine the degree of cooperativity of groups containing different numbers of cells in stiffening the ECM via their contraction. For these measurements tissue constructs that allow control of cell density and ECM composition and stiffness have obvious advantages. For these studies to succeed it is also important to secure and maintain normal fibroblasts in culture conditions that do not promote their transformation to myofibroblasts. Current culture methods are not favorable to retaining fibroblasts in the normal form. It would also be useful to determine whether iPSC-derived fibroblasts adopt a normal phenotype.

It would be informative to measure the sensitivity of individual cells to the mechanical effects exerted by groups of pmF or mF in promoting the conversion of nF to pmF and of pmF to mF. The conversion could be followed by observing the formation of stress fibers either with or without αSMA at different times in groups containing different numbers of cells in engineered tissue constructs. Our model also predicts that local matrix stiffening by nearby pmF or mF promotes the release of TGFβ. Microrheological measurements of force/stiffening correlated with release of TGFβ should be possible if the local concentration of the latter could be measured, e.g., by fluorescent tagged TGFβ. These measurements could also determine the effectiveness of the released TGFβ in promoting further conversion of nF to pmF and pmF to mF thereby making clear the existence of a positive feedback loop based on TGFβ.

The positive feedback model predicts that the transformation of nF to pmF should accelerate as the fraction of pmF increases, e.g., Fig. 2b. If it occurred, this could be detectable in hearts of hyper-tensive animals. Moreover, similar experiments could be done on cells in tissue constructs. The tension in a construct can be changed by stretching to a defined strain. Viscoelastic relaxation will decrease the tension in the construct after it is stretched (Pryse et al., 2003), and so the set point of the tension after stretch will require empirical calibration. It would also be possible and perhaps preferable to carry out these kinds of experiments under isotonic conditions in which the tension on the construct is held constant. For example, this can be simply accomplished by hanging weights from the constructs.

The model that we have discussed above is deterministic. Noting that the ROI may contain a small number of fibroblasts, it may be more realistic to extend the model to account for the effects of fluctuations in the number of cells that undergo transformation (Qian et al., 2009, 2010). From this perspective it seems more plausible that, among a small pool of nFs, some might advance to mFs while other nFs remain and are subject to transformation into pmFs. This would make it more likely that the initial positive feedback loop that we have described would be further augmented by the additional positive feedback based on the activation of TGFβ and increased contractile force of mF that we have discussed above.

In summary of this section, we have presented both linear and nonlinear models for the conversion of nF to pmF. We propose that there could be positive feedback systems in which pmF exert force on the matrix, stiffening it, and thereby increasing the rate of conversion of nF to pmF. Under some conditions there could be non-equilibrium steady states at defined levels of conversion of nF to pmF. It is possible that understanding the mechanisms by which these putative steady states are regulated, e.g., by cell contractility, would open therapeutic possibilities for controlling fibrosis. At this point there is no definitive evidence that these feedback mechanisms and steady states do occur in the heart. Nevertheless, demonstrating their existence would reveal important aspects of the mechanism by which fibrosis develops. We have suggested a number of ways in which the model could be made more realistic and in which it could be experimentally tested.

4. Discussion

Normal fibroblasts convert to myofibroblasts in two stages of which the first produces an intermediate phenotype called a protomyofibroblast. The conversion to pmF is driven by responses of nF to mechanical changes in their environment. The probability or rate of conversion increases with the stiffness of the tissue in which the cells reside. The tissue stiffness, however, is strongly influenced by external stretching forces and by the contractile forces exerted on the ECM by the cells. This leads to the possibility of a positive feedback mechanism that could produce specific steady states of pmF or mF populations. pmFs exert more tension on their surrounding matrix than do the nFs. We propose that, as more nFs are converted to pmFs, the latter exert more force on the local matrix, stiffening it and thereby accelerating the phenotypic conversion. Under some conditions this positive feedback can cause the system to bifurcate into two states: one with low and one with high concentrations of pmF. We illustrate this with a simple mechanical model. Although the model is very oversimplified, it illustrates how this kind of mechanical feedback might operate in a tissue. We further suggest a number of experimental approaches to testing whether or not this mechanism does operate in a real biological tissue.

Crucial to this view of the transformation of nF to pmF is the enhanced contractility of both proto-myofibroblasts and myofibroblasts relative to normal fibroblasts and the resulting enhancement of the ability of the former cell type to stiffen the ECM in which they are embedded. We have shown a series of measurements on engineered tissue constructs that contain either normal fibroblasts or myofibroblasts. The former contribute very little to the mechanical properties of the ECM in which they are embedded. The latter substantially stiffen the constructs both by compressing the ECM and by their own stiffness and contractility, which is much greater than that of the normal fibroblasts. It is noteworthy that, as shown in Fig. 1, disconnection of the myofibroblasts from the ECM causes a substantial drop in the force measured in the hysteresis loop measurements. This seems to argue against the idea that, as the myofibroblasts remodel the matrix, they shield themselves from stress exerted on the tissue (Tomasek et al., 2002). One might expect that the detachment of stress-shielded myofibroblasts from the ECM would not cause a substantial change in the force they exert on the tissue in which they reside. These observations emphasize the strong effects of fibroblast contractility on tissue stiffness and the likelihood that this contractility makes an important contribution to fibrosis.

We suggest that future work to characterize whether or not the proposed positive feedback mechanism operates in real tissue would be worthwhile. Also, developing a more realistic mechanical model that accounts for the viscoelastic properties of the ECM and also extension of the model to include the effects of TGFβ1 and other growth factors and cytokines would allow a much better assessment of whether or not it is a feasible description of the phenotypic cellular transformations from normal to myofibroblast.

To determine whether or not there are definable steady states along the pathway from nFs to mFs is important both for basic understanding and describing of the transformation process and also could provide useful avenues for therapeutic intervention. Drug discovery is very active for anti-fibrotic cardiovascular disease therapies, including inhibitors of the renin-angiotensinaldosterone system and modulators of inflammation (Fang et al., 2017). For example, options for biologics therapy using the natural hormone, relaxin, known to regulate natural maternal vascular adaptation to pregnancy (Teichman et al., 2009) can be one promising option against cardiac fibrosis (Du et al., 2009; Martin et al., 2018). Another is inhibition of the Rho/ROCK pathway (Zhou et al., 2013). While mFs have been considered to be terminally differentiated, a recent study shows spontaneous dedifferentiation of mFs back to nFs in mouse lung (El Agha et al., 2017). As the model described above indicates, increasing the rate constant, k_b, of the transition from pmF to nF could also be a promising therapeutic target to reduce fibrosis. A useful recent review provides further information about the reversal of mF differentiation (Yang et al., 2014).

We have emphasized that the control of fibroblast phenotype by contractility and stiffness is approachable in terms of quantitative measurements and models. Mechanically induced nF to mF differentiation has been shown to increase the mFs mitochondrial priming for apoptosis and anti-fibrotic potential through pharmacological reduction of the mF’s contractility has been observed in animal model studies (Lagares et al., 2017b). In the near future, this mechano-biology could become a basis for developing anti-fibrotic treatments. Going forward, this perspective is likely to be very useful whether or not definable NESSs are confirmed. To consider this work in a broader perspective, we note that negative feedback is essential for maintenance of homeostasis, while positive feedback (possibly double negative feedback) can drive switching behavior and bi- or multi-stability that occurs in development and phenotypic switching. Positive feedback in biochemical reaction systems has been extensively studied, e.g., in regulation of the galactose operon and cell cycle of yeast (Apostu and Mackey, 2012; Chen et al., 2000). There has been less attention paid to mechanical feedback in regulation of cellular properties. We expect that more systems that display positive or negative mechanical feedback will be found to play important roles in regulation of the properties and behaviors of cells and tissues.

Abbreviations:

nF

normal fibroblasts (as distinct from protomyofibroblasts and myofibroblasts)

pmF

proto-myofibroblasts

mF

mature myofibroblasts

ECM

extra-cellular matrix

αSMA

alpha smooth muscle actin

TGFβ

transforming growth factor β

PDGF

platelet-derived growth factor

LAP

latency-associated protein; LTBP-1, latent TGFβ1 binding protein

FBS

fetal bovine serum

iPSC

induced pluripotential stem cells

Appendix

Nonlinear Model

The nonlinear model is embodied in Scheme 2 and Equation (2) in the main text. In contrast to the linear model in which the cells behave independently, the cells increase the tension that they exert on the matrix cooperatively in the nonlinear model and so have a cooperative effect on tissue stiffness. The cooperative dependence of tension on number of pmF is described in Equation (3) in the main text.

For the nonlinear model, if we use p_j(t) to denote the probability of an ROI having j number of pmF cells, then we have a master equation for the stochastic kinetics of a single ROI:

$$\frac{d{p}_0}{dt}=-{\phi }_1,\frac{d{p}_1}{dt}={\phi }_1-{\phi }_2\frac{d{p}_j}{dt}={\phi }_j-{\phi }_{j+1,\dots ,}\frac{d{p}_n}{dt}={\phi }_n$$ (A1a)

In which the net probability flux for the j^th transition,

$$\begin{gathered} {\phi }_j\left[p_{j-1},p_j\right]=k_{j-1}\left(n-j+\text{}1,T_{j-1}\right)p_{j-1}-j{k}_b{p}_j \\ =\left(n-j+1\right)k_f{\left(\frac{s\left(j-1\right)}{n}\right)}^{j-1}{p}_{j-1}-j{k}_b{p}_j \end{gathered}$$ (A1b)

The mean number of pmF in an ROI is

$${\overline{n}}_{pmF}\left(t\right)={\displaystyle \sum _{j=0}^{n}j{p}_j\left(t\right)}$$ (A2)

Whose time derivative:

$$\frac{d}{dt}{\overline{n}}_{pmF}={\displaystyle \sum _{j=0}^{n}j\left(\frac{d{p}_j\left(t\right)}{dt}\right)}={\displaystyle \sum _{j=0}^{n}j\left({\phi }_j-{\phi }_{j+1}\right)}={\displaystyle \sum _{j=1}^n{\phi }_j}$$ (A3)

That is, if we denote $x=\frac{{\overline{n}}_{pmF}}{n}$ as the fraction of pmF cells in an ROI, then

$$\begin{gathered} \frac{dx\left(t\right)}{dt}=\frac{1}{n}{\displaystyle \sum _{j=1}^n\left\{\left(n-j+1\right)k_f{\left(\frac{s\left(j-1\right)}{n}\right)}^{j-1}{p}_{j-1}-j{k}_b{p}_j\right\}} \\ ={\tilde{k}}_f\left(x\right)\left(1-x\right)-k_{b}x \end{gathered}$$ (A4)

In which an effective nF to pmF transition rate constant is

$${\tilde{k}}_f\left(x\right)=\frac{k_f{\sum }_{j=1}^n\left\{\left(n-j+1\right){\left(\frac{s\left(j-1\right)}{n}\right)}^{j-1}{p}_j-1\right\}}{{\sum }_{j=1}^n\left(n-j+1\right)p_j-1}\cong k_f{\left(sx\right)}^{nx}$$ (A5)

The ≅ is based on the assumption that (n – j)p_j is sharply peaked at j^* = nx. Therefore, the summation can be approximately replaced by the maximum term.

Nonlinear kinetics with feedback

We thus have

$$\frac{dx}{dt}=k_f{\left(sx\right)}^{nx}\left(1-x\right)-k_{b}x=g\left(x;s\right)$$ (A6)

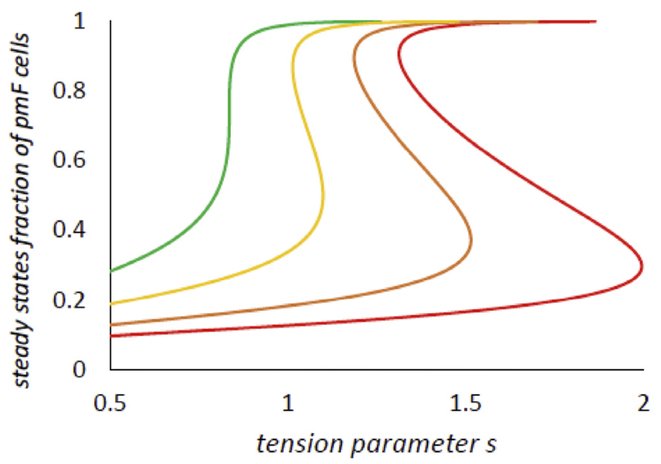
We are interested in the non-equilibrium steady states of the system. These will occur when $\frac{dx}{dt}=0$. In the main text of the paper Fig. 2A shows the right-hand side g(x; s) with several different values of s. The steady states are the roots of g(x; s) = 0. observe saddle-node bifurcation with increasing s (Strogatz, 1994). The system starts at low s. with only a single, low x steady state, progresses with increasing s to a bistable state, and, with further increase of s, to a high x steady state. In the main text Fig. 2B shows an example of the bifurcation of a bistable system. There are two stable steady states, one at higher and one at lower values of x. Fig. A1 shows the steady state(s) as a function of s with different values of $\frac{k_f}{k_b}$.

Steady state probability distribution.

The probabilistic model in (A1) allows us to solve for the steady state probability of the number of pmF in an ROI:

$$\frac{p_J^{SS}}{p_{J-1}^{SS}}=\frac{k_{j-1}}{j{k}_b},j=1,2,\dots n$$ (A7)

Thus,

$$p_J^{SS}=p_1^{SS}{\displaystyle {\prod }_{i=1}^j\frac{k_{i-1}}{i{k}_b}}=p_0^{SS}{\left(\frac{k_f}{k_b}\right)}^j\frac{n!}{j!\left(n-j\right)!}{\left(\frac{s}{n}\right)}^{\frac{\left(j-1\right)j}{2}}{\displaystyle {\prod }_{i=1}^{j-1}{i}^i}$$ (A8)

The extreme of the distribution in (A8) can be obtained by setting k_j−1≅k_j = jk_b

$$\left(n-j\right)k_f{\left(\frac{sj}{n}\right)}^j=j{k}_b$$ (A9)

Substituting j = nx, this equation becomes

$$\frac{k_f{\left(sx\right)}^{nx}\left(1-x\right)}{k_{b}x}=1$$ (A10)

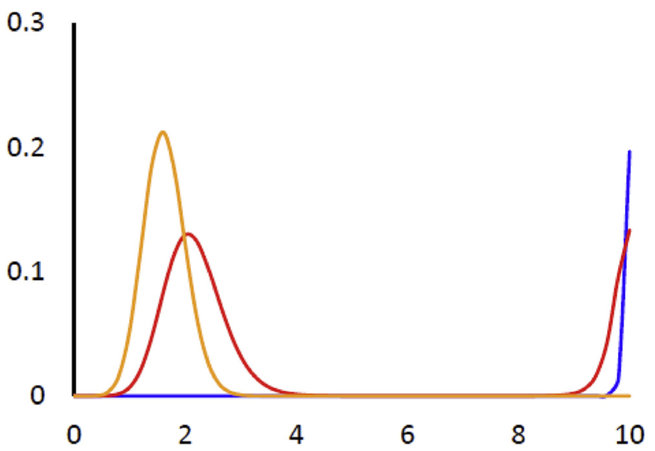
That is equivalent to g(x; s) = 0, as expected. The extrema of the probability distribution are the steady states of the nonlinear kinetics: a maximum corresponds to a stable steady state, a minimum corresponds to an unstable steady state. Fig. A2 shows the steady state probability distribution $p_j^{ss}$ for several different values of s, corresponding to those in Fig. 2 in the main text.

Fig. A1.

Steady state(s) of x, the fraction of pmF cells in an ROI

These curves were obtained from g(x; s) = 0 as a function of s. From left to right$\frac{k_f}{k_b}=100$, 20, 5, 2 and n = 10.

Fig. A2.

Steady state probability distribution p_j Orange, s = 1; Red, s = 1;345; Blue, s = 1.7

Also n = 10 and $\frac{k_f}{k_b}=5$, as in Fig. 2A in the main text.