Intracellular magnesium optimizes transmission efficiency and plasticity of hippocampal synapses by reconfiguring their connectivity

Hang Zhou; Guo-Qiang Bi; Guosong Liu

doi:10.1038/s41467-024-47571-3

. 2024 Apr 22;15:3406. doi: 10.1038/s41467-024-47571-3

Intracellular magnesium optimizes transmission efficiency and plasticity of hippocampal synapses by reconfiguring their connectivity

Hang Zhou ^1,^2,^✉, Guo-Qiang Bi ^1,^2,^3,⁴, Guosong Liu ^5,^6,^✉

PMCID: PMC11035601 PMID: 38649706

Abstract

Synapses at dendritic branches exhibit specific properties for information processing. However, how the synapses are orchestrated to dynamically modify their properties, thus optimizing information processing, remains elusive. Here, we observed at hippocampal dendritic branches diverse configurations of synaptic connectivity, two extremes of which are characterized by low transmission efficiency, high plasticity and coding capacity, or inversely. The former favors information encoding, pertinent to learning, while the latter prefers information storage, relevant to memory. Presynaptic intracellular Mg²⁺ crucially mediates the dynamic transition continuously between the two extreme configurations. Consequently, varying intracellular Mg²⁺ levels endow individual branches with diverse synaptic computations, thus modulating their ability to process information. Notably, elevating brain Mg²⁺ levels in aging animals restores synaptic configuration resembling that of young animals, coincident with improved learning and memory. These findings establish intracellular Mg²⁺ as a crucial factor reconfiguring synaptic connectivity at dendrites, thus optimizing their branch-specific properties in information processing.

Subject terms: Hippocampus, Synaptic plasticity, Synaptic transmission, Neural ageing

How synapses at dendrites are organized to optimize information processing remains elusive. Here, the authors found that intracellular magnesium optimizes transmission, plasticity, and coding capacity of synapses by reconfiguring their connectivity at dendrites.

Introduction

Modifications in synaptic connectivity play a pivotal role in information processing during learning and memory^1–6. Previous research has predominantly focused on connectivity changes in single synapses during learning and memory, proposing classical paradigms such as synaptic potentiation and depression^1,5,7–10 that contribute to strengthening and weakening of synapses, respectively. When considering a group of synapses instead of a single one, learning induces populational changes in their synaptic connectivity, reshaping the distribution pattern of synaptic strengths (or weights)³. Such distribution changes are involved in encoding information during learning^3,11; for instance, in cerebellar Purkinje cells, motor skill learning induces changes in synaptic weight distribution, which help to establish task-specific input-output associations, thus perpetuating the motor skill^3,11–13.

Despite the advancements made at the single-synapse and cellular levels, it remains elusive at the dendritic branch level how the synapses, with various presynaptic origins, are organized to generate diverse computational properties to meet varying demands of information processing. This inquiry is particularly important because dendritic branches are the basic unit for information processing in neural systems^14–28, and branch-specific reorganization of synapses is crucially involved in learning and memory^29–32. Moreover, as aging brains undergo pronounced alterations to cortical synaptic connectivity, hallmarked by both reduced synapse number and increased synaptic weight (and/or structural size)^33–37, gaining insights into this question would advance our understanding of synaptic correlates behind the progression of brain aging and might inspire new therapeutic strategies.

By examining synaptic connectivity, our study addresses an organization principle that orchestrates the synapses at hippocampal dendritic branches to generate diverse computational properties, including transmission efficiency, plasticity, and coding capacity. We reveal that the configuration of synaptic connectivity is a biomarker for branch-specific synaptic computations, and intracellular Mg²⁺ is a crucial regulator of the configuration. Finally, we show evidence in aging brains and behaving animals supporting the major findings in vitro.

Results

Diversity of synaptic configuration across dendritic branches

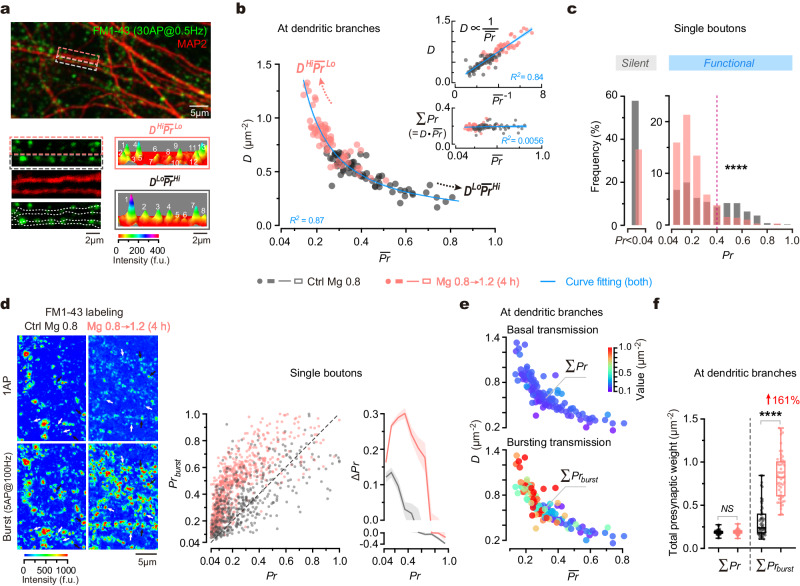
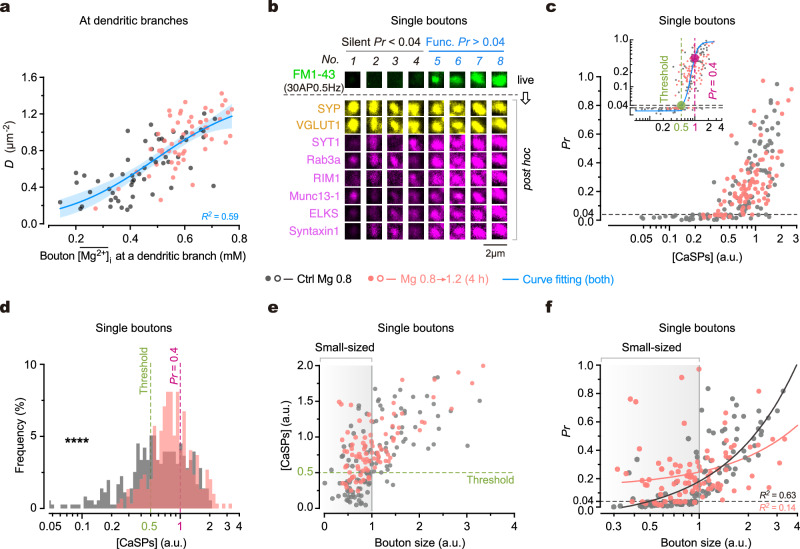
To address the organization principle of the synapses at individual dendritic branches, we initially investigated the synaptic connectivity at distal dendrites of primary cultured hippocampal neurons. To measure presynaptic weight (indicated by vesicular release probability, Pr) of individual synapses, we utilized a fluorescent indicator of vesicle turnover, FM1-43, to visualize and quantify the released vesicles from individual presynaptic boutons in response to 30 single action potentials (APs) at a frequency of 0.5 Hz (Fig. 1a, Supplementary Fig. 1a; Methods). This approach allows for measuring Pr at a minimum level of ∼ 0.04, corresponding to one released vesicle per 30 APs. At distal dendritic branches (0.62 ± 0.21 µm in diameter, mean ± SD), we observed significant variations in presynaptic weight distribution of dendritic branches, as indicated by diverse combinations of D and mean Pr ( $\bar{\Pr}$ ) (Fig. 1b). Notably, an inverse correlation between D and $\bar{\Pr}$ can be accurately described by a hyperbolic function, resulting in a linear correlation between D and 1/ $\bar{\Pr}$ (Fig. 1b). We termed the pattern of synaptic connectivity at individual branches as ‘synaptic configuration’, denoted by the D ∼ $\bar{\Pr}$ combination. Despite continuous variations in D ∼ $\bar{\Pr}$ combination among branches, for illustrative purposes, we categorized two extreme patterns as follows: high-D and low- $\bar{\Pr}$ (D^Hi $\bar{\Pr}$ ^Lo), or conversely, low-D and high- $\bar{\Pr}$ (D^Lo $\bar{\Pr}$ ^Hi), facilitating the description of the synaptic configuration.

Under diverse synaptic configurations, the total presynaptic weight per unit area of dendrites (denoted as ΣPr) remained constant (Fig. 1b, coefficient of variation of ΣPr was 0.14). To investigate whether ΣPr is always constant, we perturbed the synaptic configuration and examined its impact on ΣPr. Previously, we discovered that chronic elevation of extracellular Mg²⁺ concentration ([Mg²⁺]_o) around a physiological range (0.8–1.2 mM) increases functional synapse density³⁸. Here, we evaluated the effect of changing [Mg²⁺]_o on the synaptic configuration. By elevating [Mg²⁺]_o in the culture medium from 0.8 mM (corresponding to a typical ‘physiological Mg²⁺ condition’ in the rodent brain) to 1.2 mM (corresponding to an ‘elevated Mg²⁺ condition’ within physiological range) for 4 h (for rationales for Mg²⁺ conditions, refer to Supplementary Notes), we observed both an increase in D and a decrease in $\bar{\Pr}$ , resulting in a global shift of synaptic configurations towards the D^Hi $\bar{\Pr}$ ^Lo mode (Fig. 1b). Notably, throughout this perturbation, ΣPr remained constant across dendritic branches (Fig. 1b). These findings support the notion that the total presynaptic weight per unit area of dendrites remains constant, regardless of varying synaptic configurations.

To understand the influence of [Mg²⁺]_o on the synaptic configuration, we analyzed how the Pr distribution of synapses was affected. Analyses revealed three apparent functional states of synapses based on the shape of Pr distribution: silent (Pr < 0.04), low-Pr (0.04–0.4), and high-Pr (0.4–1.0) (Fig. 1c). Elevating [Mg²⁺]_o exerted a dual effect on the strength of vesicle release, reducing the proportion of silent presynaptic boutons (from 57.93% to 35.03%) and converting some high-Pr boutons to low-Pr ones. As a result, the percentage of low-Pr boutons increased from 24.79% to 56.62%, whereas that of high-Pr boutons decreased from 17.29% to 8.35% (Fig. 1c). These analyses suggest that during the configurational shift from D^Lo $\bar{\Pr}$ ^Hi to D^Hi $\bar{\Pr}$ ^Lo following the elevation of [Mg²⁺]_o, the increase in D was primarily attributed to the conversion of silent boutons into functional ones, while the decrease in $\bar{\Pr}$ was due to the reduction of high-Pr synapses (Fig. 1c).

In summary, the configuration of synaptic connectivity, as indicated by presynaptic weight distribution, varies across dendritic branches and can be modified by altering Mg²⁺ levels. Notably, despite the substantial diversity in synaptic configuration, the total presynaptic weight of dendritic branches remains constant.

Impact of synaptic configuration on presynaptic release at dendrites

We have shown that ΣPr remains constant during basal transmission. Given the critical role of bursting activity in synaptic computations during information processing^39–47, we further investigated how the total presynaptic weight during bursting transmission is influenced by the synaptic configuration. In the hippocampus, naturally-occurred bursts typically consist of 2–7 APs with inter-spike intervals of 1.5–6 ms under physiological conditions⁴⁸. Of particular interest are theta bursts, a specific form of bursts that induce synaptic plasticity and are relevant to multiple cognitive functions^49–51. Theta bursts typically consist of several trains of high-frequency APs occurring at a theta frequency. Here, we used 5 APs at 100 Hz (referred to as ‘5AP burst’) to represent bursting activity.

To compare basal with bursting transmission, we measured Pr and the release probability in bursting transmission (Pr_burst) in the same boutons sequentially (Fig. 1d, Methods). We observed a supralinear relationship between Pr_burst and Pr, with the largest difference (ΔPr) occurring in the middle range of Pr (∼0.1–0.4) (Fig. 1d). When comparing ΣPr with the total presynaptic weight in bursting transmission (ΣPr_burst) at the same dendritic branches, we found intriguingly that unlike the constant ΣPr, the ΣPr_burst was significantly higher under D^Hi $\bar{\Pr}$ ^Lo configuration than under D^Lo $\bar{\Pr}$ ^Hi configuration (Fig. 1e). Furthermore, trials with a 4-h elevation of [Mg²⁺]_o from 0.8 to 1.2 mM significantly enhanced ΣPr_burst by 161.19% (Fig. 1f, from 0.32 ± 0.19 to 0.83 ± 0.26), showing a strong positive effect of Mg²⁺ on presynaptic weights in bursting transmission. Similar phenomena were observed when examining other patterns of bursting activity (2–15 APs at 100 Hz per burst) (Supplementary Fig. 1b–f).

Together, synaptic configuration differentially impacts presynaptic release during basal and bursting transmission, with no effect in basal transmission but a strong regulatory effect in bursting transmission.

Impact of synaptic configuration on postsynaptic AMPAR and PSD95 distributions

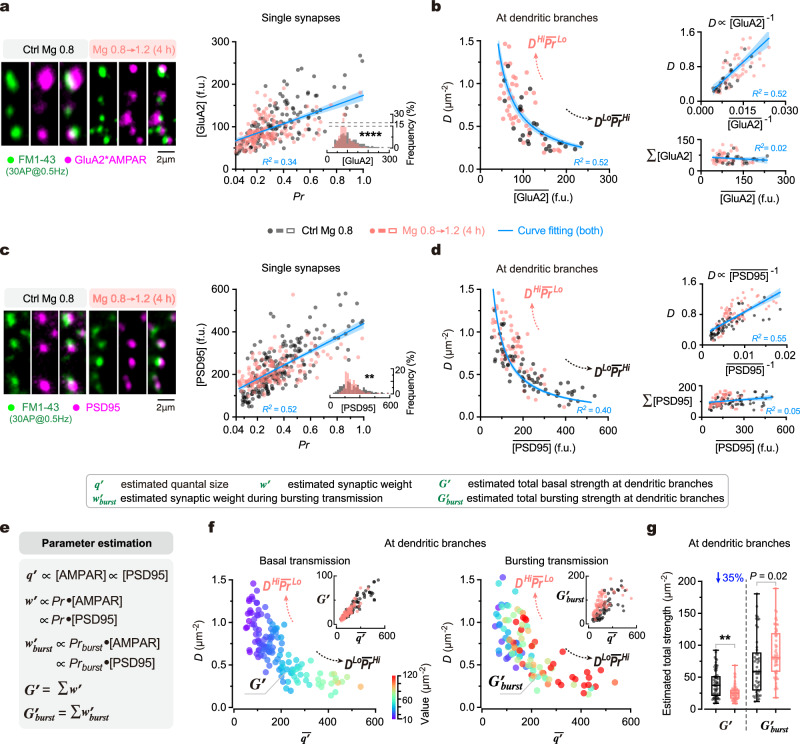
We next examined postsynaptic properties under varying synaptic configurations. During synaptic transmission, the postsynaptic weight of an excitatory synapse is primarily determined by its quantal size (q), which is influenced by three major factors: the amount of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid receptors (AMPARs) anchored to the postsynaptic density (PSD), AMPAR channel conductance, and AMPAR opening probability. Since AMPARs containing the GluA2 subunits (GluA2*AMPARs) at postsynaptic sites are crucial for maintaining and scaling basal synaptic transmission^52–55, we conducted immunostaining to detect the extracellular epitope of GluA2 and used its quantity at a postsynaptic site ([GluA2]) as an index to approximate the q. To ensure the GluA2 immunoreactive (GluA2⁺) sites from real synapses, we first labeled functional presynaptic boutons using FM1-43 (to measure their Pr) before conducting post hoc immunostaining (Methods). The GluA2⁺ sites juxtaposed with FM⁺ puncta were considered to originate from real synapses (Fig. 2a).

At the single-synapse level, we observed a weak positive correlation (R² = 0.34) between [GluA2] and Pr (Fig. 2a), demonstrating a coordination between q and its corresponding presynaptic weight. This coordination suggests that the pattern of postsynaptic q distribution would resemble the pattern of Pr distribution at dendritic branches. Indeed, when quantifying the density of juxtaposed FM1-43⁺GluA2⁺ puncta (D), which reports the density of functional synapses, we found an inverse association between D and the mean [GluA2] ( $\bar{[GluA2]}$ ) of synapses along individual branches (Fig. 2b), similar to the inverse relationship between D and $\bar{\Pr}$ at presynaptic sites (Fig. 1b). This relationship can be well fitted by a hyperbolic function, resulting consequently in a linear correlation between D and 1/ $\bar{[GluA2]}$ (Fig. 2b). Importantly, despite varying D ∼ $\bar{[GluA2]}$ combinations, the total amount of postsynaptic GluA2*AMPARs per unit area of dendrites (Σ[GluA2]) remained constant across different branches (Fig. 2b). These findings suggest that the distribution pattern of q correlates with the synaptic configuration (D ∼ $\bar{\Pr}$ combination). When using another biomarker postsynaptic density protein 95 (PSD95), a scaffolding protein closely associated with AMPARs^56–58, to estimate q alternatively, we observed similar results as those using GluA2 (Fig. 2c, d). Moreover, when changing synaptic configurations by a 4-h elevation of [Mg²⁺]_o, the distribution pattern of [GluA2] or [PSD95] was remarkably altered (Fig. 2a, c), and the combinations of D ∼ $\bar{[GluA2]}$ and D ∼ $\bar{[PSD95]}$ at dendritic branches significantly shifted, maintaining constant Σ[GluA2] and Σ[PSD95] (Fig. 2b, d).

Together, these findings suggest that synaptic configuration impacts the distribution pattern of postsynaptic proteins critical for excitatory synaptic transmission (representing q) while maintaining a pre-postsynaptic coordination.

Impact of synaptic configuration on transmission efficiency at dendrites

Next, we examined how the synaptic configuration affects the synaptic transmission efficiency of dendritic branches. In basal transmission, the synaptic transmission efficiency of an individual branch can be reported by the total strength of excitatory synaptic transmission (that is, the total AMPAR-mediated current) upon a single AP (denoted by G). To measure G, we first measured the synaptic weight of excitatory transmission (w) in an individual synapse, equal to Pr ·q. To precisely measure w of synapses distributed along dendrites, both Pr and q need to be determined in individual synapses, presently beyond the reach of current techniques. As a compromise, we directly measured Pr while indirectly estimating q by postsynaptic [GluA2] or [PSD95] in dendrites as shown above (Fig. 2a–d), then further estimated both w of each synapse and the G of all synapses within the dendritic branch, which is the sum of w per unit area of dendrites (denoted by Σw) (Fig. 2e, Supplementary Fig. 2a–d). Hereafter, q’, w’ and G’ are used to denote the estimated q, w and G, respectively. As mentioned above, the constant Σ[GluA2] and Σ[PSD95] at a dendritic branch suggests a constant Σq’ (Fig. 2a–d). However, intriguingly, unlike the constant ΣPr and Σq’, the G’ (Σw’) was lower under the “high-D and low- $\bar{q ’}$ ” pattern than the “low-D and high- $\bar{q ’}$ ” pattern, meaning that G’ was lower under D^Hi $\bar{\Pr}$ ^Lo than D^Lo $\bar{\Pr}$ ^Hi configuration (Fig. 2f, Supplementary Fig. 2b–e). The total strength of synapses in bursting transmission (G’_burst, Fig. 2e) showed a weak trend being lower under the “high-D and low- $\bar{q ’}$ ” pattern than the “low-D and high- $\bar{q ’}$ ” pattern. However, this trend was not as uniform as G’ but instead highly variable in the medium range of $\bar{q ’}$ (at 100–300) (Fig. 2f). Intriguingly, when we altered synaptic configurations by elevating [Mg²⁺]_o, the general effect was to substantially suppress the average G’ of dendritic branches by 34.73% (from 39.51 ± 21.54 to 25.79 ± 12.08) (Fig. 2g).

Collectively, these data suggest that the synaptic configuration has a substantial impact on the transmission efficiency in basal transmission at individual dendritic branches. The transition of synaptic configurations from D^Lo $\bar{\Pr}$ ^Hi to D^Hi $\bar{\Pr}$ ^Lo decreases basal transmission efficiency.

Impact of synaptic configuration on postsynaptic Ca²⁺ signals in dendrites

While the synaptic configuration affects transmission efficiency, how does it relate to synaptic plasticity at dendritic branches? To address this question, we first examined how synaptic configuration influences the distribution of postsynaptic Ca²⁺ signals that are essential for the generation of synaptic plasticity.

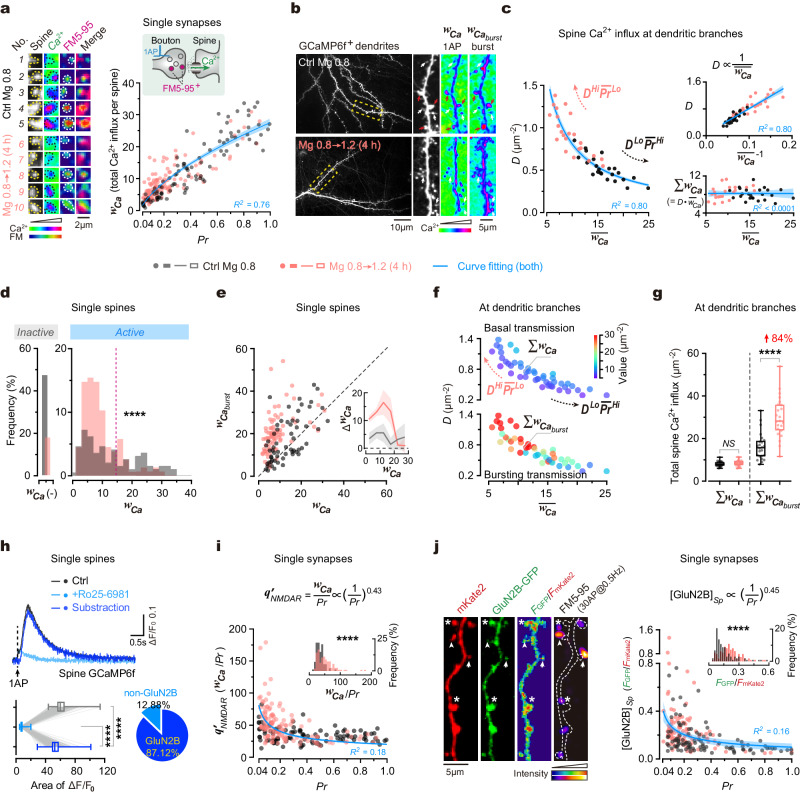
To start, using a genetically encoded Ca²⁺ indicator (GCaMP6f), we measured both Pr and spine Ca²⁺ influx during basal transmission (that is, single AP-evoked Ca²⁺ influx through spines) at the same synapses (Methods) and found that they were positively correlated (Fig. 3a). Thus, spine Ca²⁺ influx of synapses may distribute along dendritic branches in a similar pattern as the Pr. To examine this possibility, we quantified functional synapse density D and the Ca²⁺ entry through individual spines (denoted by w_Ca) (Fig. 3b). As expected, D and the mean w_Ca of spines ( $\bar{w_{Ca}}$ ) were inversely correlated, resulting in constant total w_Ca at per unit area of dendrites in basal transmission (Σw_Ca) (Fig. 3c). Thus, the distribution of w_Ca showed “high-D and low- $\bar{w_{Ca}}$ ” and “low-D and high- $\bar{w_{Ca}}$ ” patterns under the D^Hi $\bar{\Pr}$ ^Lo and D^Lo $\bar{\Pr}$ ^Hi configurations, respectively (similar to q’ distribution patterns, see Fig. 2b, d).

Fig. 3 — a Left, spine Ca²⁺ influx (GCaMP⁺) and Pr (FM5-95⁺) of synapses. Right, integrated spine Ca²⁺ (w_Ca) against Pr (n = 101, 127 synapses from 3, 3 repeats). Curve fitting, w_Ca = 31.10•Pr^0.55–3.95 (R² = 0.76). b Left, GCaMP⁺ dendrites. Right, box magnification. Pseudo-color, integrated ΔF/F₀. White/red arrows, low/high-Ca²⁺ spines. c Left, synapse density (D) against $\bar{w_{Ca}}$ in dendrites (n = 24, 23 branches from 3, 3 repeats; hyperbolic fitting, R² = 0.80). Top-right, D versus 1/ $\bar{w_{Ca}}$ (linear regression, R² = 0.81, P < 0.0001). Bottom-right, total w_Ca (Σw_Ca) versus $\bar{w_{Ca}}$ (linear regression, R² < 0.0001, P = 0.97). d Shifted w_Ca distribution (n = 193, 156 spines from 4, 3 repeats; two-sided Kolmogorov–Smirnov test, ****P < 0.0001). w_Ca(-), no Ca²⁺ influx. Dashed line, w_Ca = 15. e Integrated burst-evoked Ca²⁺ ( ${w_{Ca}}_{burst}$ ) against w_Ca in single spines (n = 59, 81 spines from 3, 3 repeats). Dashed line, bisector. Inset, Δw_Ca (= ${w_{Ca}}_{burst}$ -w_Ca) against w_Ca. Curve/error band, mean/SEM. f Relationship between D, $\bar{w_{Ca}}$ , Σw_Ca and Σ ${w_{Ca}}_{burst}$ at dendrites (n = 24, 23 branches from c). g Comparison of Σw_Ca and Σ ${w_{Ca}}_{burst}$ of individual branches (n = 24, 23 branches from f; two-sided Kolmogorov–Smirnov tests, P = 0.73, ****P < 0.0001). h Top, evoked spine Ca²⁺ before and after GluN2B blockade. Traces, averaged 30 sweeps from 441 spines. Bottom-left, integrated Ca²⁺ (n = 441 spines from 7 repeats; two-sided Kolmogorov–Smirnov tests, ****P < 0.0001). Bottom-right, percentages. i Plot of q’_NMDAR (=w_Ca/Pr) against Pr (n = 101, 127 synapses from a). Inset, distribution (two-sided Kolmogorov–Smirnov test, ****P < 0.0001). Curve fitting, w_Ca /Pr = 20.25•(1/Pr)^0.43 (R² = 0.18). j Left, juxtaposed FM5-95⁺ boutons and GluN2B-GFP⁺ spines. Arrowheads/asterisks, high-Pr–low-[GluN2B] or low-Pr–high-[GluN2B] synapses. Right, spine [GluN2B] versus Pr (n = 102, 110 synapses from 3, 3 repeats). Inset, [GluN2B]_Sp distribution (two-sided Kolmogorov–Smirnov tests, ****P < 0.0001). Curve fitting, [GluN2B]_Sp = 0.0987•(1/Pr)^0.45 (R² = 0.16). In (a, c, i, j), blue lines and error bands, fitted curves and 95% CIs. In (g, h), box borders/line, quantiles/median; whiskers, min/max. Source data are provided as a Source Data file.

Given the crucial role of bursting activity in synaptic plasticity induction, we examined how synaptic configuration influences spine Ca²⁺ influx in bursting transmission. By measuring both the 1AP- and burst-evoked Ca²⁺ influx (w_Ca and ${w_{Ca}}_{burst}$ ) in the same spines (Fig. 3b), we observed a supralinear-like association between ${w_{Ca}}_{burst}$ and w_Ca (Fig. 3e), and consequently, medium-w_Ca spines (~ 10–15 in value) showed larger Δw_Ca (that is, ${w_{Ca}}_{burst}$ - w_Ca) than others (Fig. 3e, inset), similar to the result of Pr and Pr_burst (Fig. 1d). These findings suggest that medium-w_Ca spines can better distinguish bursting activity from basal activity. At the branch levels, the total burst-induced Ca²⁺ influx (Σ ${w_{Ca}}_{burst}$ ) was higher under D^Hi $\bar{\Pr}$ ^Lo than D^Lo $\bar{\Pr}$ ^Hi configuration (Fig. 3f), alike presynaptic ΣPr_burst (Fig. 1f).

Moreover, when altering synaptic configurations by a 4-h elevation of [Mg²⁺]_o from 0.8 to 1.2 mM, we observed both increased D and decreased $\bar{w_{Ca}}$ at dendritic branches, reshaping w_Ca distribution towards the “high-D and low- $\bar{w_{Ca}}$ ” pattern while maintaining constant Σw_Ca (Fig. 3c, f, g, from 8.09 ± 1.23 to 8.44 ± 1.41). During this configurational transition, a significant portion of spines got converted from inactive (no detectable Ca²⁺ influx) to active (Fig. 3d). Notably, like the Pr redistribution (Fig. 1c), w_Ca also underwent a similar redistribution, showing a remarkable reduction of both Ca²⁺-inactive spines and large-w_Ca ones, as a result, the majority of spines became medium-w_Ca ones (within the range of 0–15) (Fig. 3d). By contrast, during bursting transmission, the Σ ${w_{Ca}}_{burst}$ of dendritic branches was significantly increased by 84.10% (Fig. 3f, g, Supplementary Fig. 3a, from 16.29 ± 6.36 to 29.99 ± 9.55), similar to the results of ΣPr and ΣPr_burst after such configurational transition (Fig. 1e, f).

Together, these results indicate that postsynaptic Ca²⁺ signals essential for synaptic plasticity induction are correlated with the synaptic configuration. The transition of synaptic configurations from D^Lo $\bar{\Pr}$ ^Hi to D^Hi $\bar{\Pr}$ ^Lo increases bursting Ca²⁺ influx in dendritic branches, suggestive of enhanced synaptic plasticity.

Impact of synaptic configuration on postsynaptic GluN2B distribution

We proceeded to investigate the molecular basis of the observed properties of postsynaptic Ca²⁺ activity. Since vesicle release-induced spine Ca²⁺ influx is primarily mediated by N-methyl-D-aspartate receptors (NMDARs)^59,60, the observed spine Ca²⁺ influx (Fig. 3a–g) may be largely induced by the opening of postsynaptic NMDARs. Indeed, utilizing GluN2B subunit-specific pharmacological inhibition with Ro25-6981, we confirmed that GluN2B-containing (GluN2B*) NMDARs accounted for 87.12 ± 3.59% of 1AP-evoked Ca²⁺ entry (Fig. 3h, Methods). For a single synapse, its postsynaptic Ca²⁺ entry in synaptic transmission (that is, w_Ca) is determined by the product of Pr and the quantal release-induced Ca²⁺ current through postsynaptic NMDARs (denoted by q_NMDAR), thus the ratio of w_Ca/Pr should quantitatively approximate q_NMDAR (denoted by q’_NMDAR). Notably, q’_NMDAR was negatively associated with Pr for individual synapses (Fig. 3i). During the configurational transition from D^Lo $\bar{\Pr}$ ^Hi to D^Hi $\bar{\Pr}$ ^Lo by elevating [Mg²⁺]_o, q’_NMDAR increased while Pr decreased in single synapses, maintaining their inverse association (Fig. 3i). Meanwhile, this transition also caused a decrease in $\bar{\Pr}$ and an increase in Σq’_NMDAR at individual dendritic branches (Supplementary Fig. 3b), suggesting higher expression levels of postsynaptic GluN2B*NMDARs.

To further verify the expression levels of GluN2B*NMDARs in dendrites, we directly examined the distribution of postsynaptic [GluN2B*NMDAR] of individual synapses along dendritic branches. To visualize postsynaptic GluN2B subunits, we transfected a green fluorescent protein-tagged GluN2B (GluN2B-GFP) vector⁶¹ in conjunction with a red fluorescent indicator (mKate2) to label spine and dendrite morphology (Fig. 3j, Methods). The fluorescence ratio of GFP against mKate2 was used to estimate the concentration of transfected GluN2B subunits in spines ([GluN2B]_Sp) (Fig. 3j), which also approximates q_NMDAR. By measuring Pr and [GluN2B]_Sp of the same synapses, we found that they were inversely associated (Fig. 3j). Moreover, when shifting synaptic configurations from D^Lo $\bar{\Pr}$ ^Hi to D^Hi $\bar{\Pr}$ ^Lo by an elevation of [Mg²⁺]_o, such an inverse association remained but [GluN2B]_Sp increased (Fig. 3j), indicating that spine GluN2B levels in dendritic branches are higher under D^Hi $\bar{\Pr}$ ^Lo than D^Lo $\bar{\Pr}$ ^Hi configuration.

These findings (Fig. 3) suggest that the synaptic configuration determines synaptic plasticity of individual dendritic branches, given the crucial role of bursting Ca²⁺ signals through postsynaptic GluN2B*NMDARs for synaptic plasticity^62–65.

Intracellular Mg²⁺ regulates synaptic configuration by inhibiting release probability

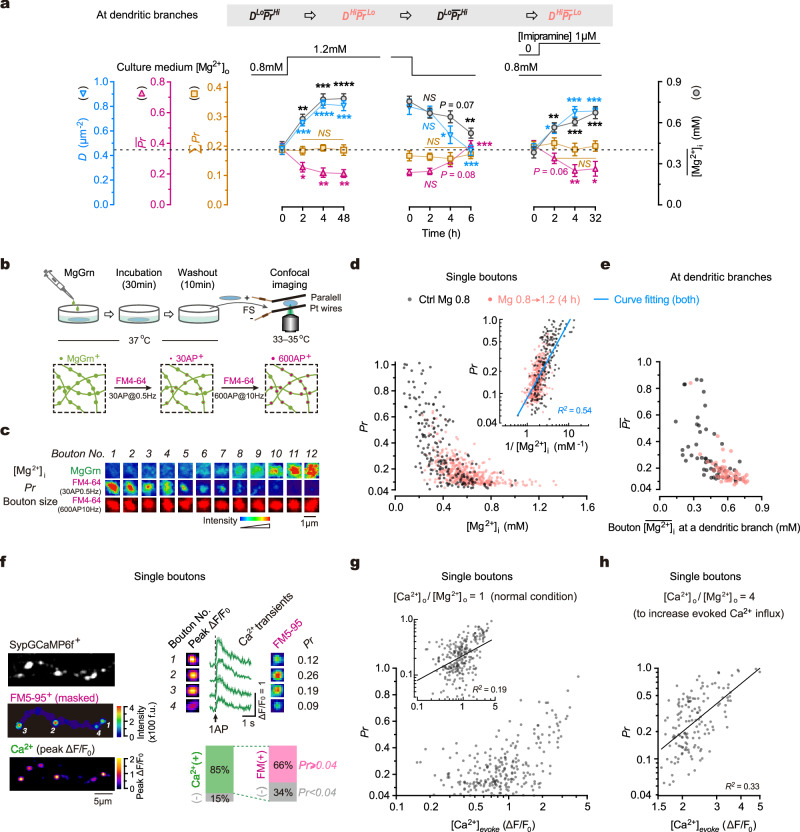
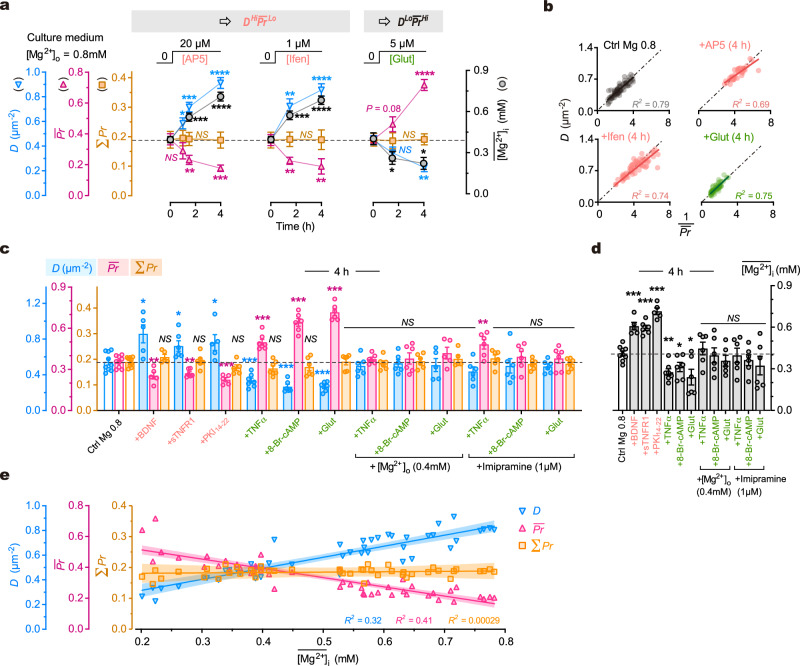
The above findings suggest that the synaptic configuration is a significant biomarker indicating the computational features of synapses at individual dendritic branches, including synaptic transmission efficiency and synaptic plasticity. Notably, chronically altering [Mg²⁺]_o can effectively modify synaptic configurations. We next explored the molecular mechanisms underlying the Mg²⁺-mediated regulation of synaptic configuration. Previously, we have shown that intracellular Mg²⁺ concentration ([Mg²⁺]_i) determines the functional synapse density³⁸, inspiring us to hypothesize that the effect of [Mg²⁺]_o on the synaptic configuration is mediated by changes in [Mg²⁺]_i. To test this hypothesis, we utilized a chemical fluorescent probe called Magnesium Green acetoxymethyl ester (MgGrn) to visualize and quantify [Mg²⁺]_i³⁸. Interestingly, altering [Mg²⁺]_o did not immediately impact the synaptic configuration; however, it was followed by significant changes in [Mg²⁺]_i after 4–6 h (Fig. 4a). The temporal correlation between [Mg²⁺]_i and the synaptic configuration suggests that [Mg²⁺]_i may be responsible for mediating the changes in configuration observed. To further investigate this, we administered imipramine, a compound known to increase [Mg²⁺]_i by regulating Na⁺/Mg²⁺ antiporters⁶⁶, allowing us to test the effect of increased [Mg²⁺]_i on synaptic configurations without altering [Mg²⁺]_o. As expected, imipramine induced changes in the synaptic configuration accompanied by an elevation of [Mg²⁺]_i (Fig. 4a). These findings suggest that [Mg²⁺]_i plays a crucial role in controlling the synaptic configuration.

Fig. 4 — a Time-courses of changes in synaptic configuration and ${\bar{[{Mg}^{2 +}]}}_{i}$ (mM) in neurites after various treatments (n = 5, 8, 10, 11, 8, 8, 7, 7, 6, 7, 9, 8 repeats for configuration, 5, 8, 9, 8, 9, 7, 7, 6, 6, 6, 6, 6 repeats for Mg²⁺). Two-sided unpaired t-tests (time 4 h vs. 0 h). For ΣPr, P = 0.4068, 0.7444, 0.7391; for D, P < 0.0001, = 0.0305, 0.0003; for $\bar{\Pr}$ , P = 0.0084, 0.0799, 0.0044; for [Mg²⁺]_i, P = 0.0001, 0.0724, 0.0009. NS, no significance, *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. b Experimental design for measuring [Mg²⁺]_i and Pr in the same boutons. c FM4-64⁺ and MgGrn⁺ signals in the same boutons. d Measurement of Pr and [Mg²⁺]_i (mM) in boutons (n = 204, 444 from 3, 4 repeats). Inset, Pr versus 1/[Mg²⁺]_i. Double logarithmic fitting, R² = 0.54, P < 0.0001. e Measurement of $\bar{\Pr}$ and ${\bar{[{Mg}^{2 +}]}}_{i}$ (mM) of the boutons at individual branches (n = 55, 56 branches from 4, 4 repeats). f–h Concurrent measurement of Pr and 1AP-evoked Ca²⁺ influx in the same boutons. f Left, images to show evoked Ca²⁺ influx (peak ΔF/F₀) and FM5-95⁺ puncta (masked by GCaMP⁺ axon morphology) in the same boutons. Top-right, peak ΔF/F₀, Ca²⁺ traces, FM5-95⁺ puncta, and Pr values in the same boutons. Bottom-right, percentage of boutons undergoing Ca²⁺ influx, referred to as Ca²⁺(+), and vesicle turnover (Pr ≥ 0.04) (n = 3 repeats). ΔF/F₀ puncta and Ca²⁺ traces were averaged from 30 repeats. Band over traces, SEM. g Plot of Pr against [Ca²⁺]_evoke (the amplitude of 1AP-evoked Ca²⁺ influx) in boutons (n = 243 boutons from 5 repeats, physiological Mg²⁺ condition). Inset, logarithmic plot. Line, double logarithmic fitting, R² = 0.19, P < 0.0001. h Similar to (g) but using working solution containing [Ca²⁺]_o 4.8 mM and [Mg²⁺]_o 1.2 mM (ratio 4:1) (n = 146 boutons from 3 repeats). Line, double logarithmic fitting, R² = 0.33, P < 0.0001. Data are mean ± SEM. Source data are provided as a Source Data file.

To elucidate how [Mg²⁺]_i regulates the synaptic configuration (that is, the D ∼ $\bar{\Pr}$ combination), we first examined the relationship between [Mg²⁺]_i and Pr in the same presynaptic boutons (Fig. 4b; Methods). Under a physiological Mg²⁺ condition ([Mg²⁺]_o 0.8 mM), [Mg²⁺]_i exhibited remarkable variations among boutons (Fig. 4c, Supplementary Fig. 4). Strikingly, Pr was inversely correlated with [Mg²⁺]_i in individual boutons (Fig. 4c, d). When elevating [Mg²⁺]_o from 0.8 to 1.2 mM for 4 h, mean [Mg²⁺]_i ( ${\bar{[{Mg}^{2 +}]}}_{i}$ ) of boutons increased from 396.34 ± 205.12 to 597.53 ± 175.41 μM (mean ± SD) and the distribution of [Mg²⁺]_i in boutons was shifted; concurrently, the Pr distribution was significantly shifted, but the inverse relationship remained (Fig. 4d). These results demonstrate a negative correlation between Pr and [Mg²⁺]_i in single boutons. In addition, we further confirmed at individual dendritic branches that $\bar{\Pr}$ and ${\bar{[{Mg}^{2 +}]}}_{i}$ of the boutons were negatively associated (Fig. 4e).

We noticed that this observation differs from what is observed in large synapses, such as neuromuscular junctions (NMJs) and the Calyx of Held synapses, where presynaptic Pr is dominantly controlled by single AP-evoked [Ca²⁺]_i (reviewed in⁶⁷). To compare, we concurrently measured Pr and single AP-evoked Ca²⁺ influx in the same boutons using synaptophysin-fused GCaMP6f (SypGCaMP6f) for detecting presynaptic Ca²⁺ activity^68,69 and FM5-95, a red fluorescence FM dye, for measuring Pr (Fig. 4f, Supplementary Fig. 5). We observed evoked Ca²⁺ events in 85% of SypGCaMP6f⁺ boutons and 66% of these boutons underwent vesicle release (Fig. 4f). Generally, there was a positive association between Pr and the amplitude of evoked Ca²⁺ influx, but this association diminished at the lower range of Ca²⁺ influx (Fig. 4g). This observation raises a possibility that the association between Pr and [Ca²⁺]_i would be stronger when AP-evoked [Ca²⁺]_i is sufficiently high. Indeed, when single AP-evoked [Ca²⁺]_i was remarkably elevated by an acute increase in the ratio of extracellular [Ca²⁺]_o/[Mg²⁺]_o from 1 to 4, the Ca²⁺ dependency of Pr became significantly improved (Fig. 4h).

Taken together, [Mg²⁺]_i exerts a significant negative effect on Pr in small hippocampal synapses.

Intracellular Mg²⁺ regulates configuration by increasing functional synapse density

Next, we investigated how intracellular Mg²⁺ regulates the other parameter of synaptic configuration, functional synapse density D. To explore this, we examined the correlation between D and the bouton ${\bar{[{Mg}^{2 +}]}}_{i}$ of synapses within individual dendritic branches. Our findings revealed a positive association between them, and a 4-h elevation of [Mg²⁺]_o concurrently increased both D and ${\bar{[{Mg}^{2 +}]}}_{i}$ (Fig. 5a). These results suggest that local [Mg²⁺]_i positively correlates with D in a branch-specific manner. To further understand the underlying molecular mechanisms, we investigated the expression levels of presynaptic Ca²⁺-sensitivity-related proteins (CaSPs)^70,71, which have been shown in our previous study to be involved in the conversion of silent boutons to functional ones through elevated [Mg²⁺]_i³⁸. We measured both Pr and the expression level of individual CaSPs within the same boutons (Fig. 5b, Supplementary Fig. 6). Consistently, we observed a positive correlation between Pr and the total expression level of CaSPs ([CaSPs], a normalized value, refer to Methods) in individual boutons (Fig. 5c). Interestingly, there seemed to be an empirical threshold of [CaSPs] for functional boutons, as most boutons remained silent when [CaSPs] was below 0.5 (Fig. 5c, inset). Importantly, increasing [Mg²⁺]_i by elevating [Mg²⁺]_o from 0.8 to 1.2 mM for 4 h significantly increased [CaSPs] in silent boutons, converting them into functional ones (Fig. 5c, d). Thus, the upregulation of D by elevated [Mg²⁺]_i is primarily attributed to the supplementation of CaSPs in originally silent boutons lacking these proteins.

Fig. 5 — a Plot of D (measured under the 30AP@0.5 Hz stimulation) against bouton ${\bar{[{Mg}^{2 +}]}}_{i}$ at dendritic branches (n = 55, 56 branches from 4, 4 repeats; the same experiment as in Fig. 4e). Logistic growth curve fitting, R² = 0.59. Blue line, fitted curve. Error band, 95% CI. b Confocal images to show FM1-43 (indicative of Pr) and *post hoc* immunostaining of various proteins in the same boutons (see also Supplementary Fig. 6). c Plot of Pr against [CaSPs] in the same boutons (n = 121, 94 boutons from 4, 3 repeats). Inset, double logarithmic plot. Boltzmann-Sigmoidal curve fitting, R² = 0.44. Dashed lines and large dots, the locations on fitted curve where Pr = 0.04 (threshold) and 0.4. d Shifted distribution of [CaSPs] in boutons (n = 345, 288 boutons from 8, 6 repeats; two-sided Kolmogorov–Smirnov test, ****P < 0.0001). Dashed lines, [CaSPs] values when Pr = 0.04 (threshold) and 0.4 based on (c inset). e Plot of [CaSPs] against estimated bouton size (estimated by median-normalized [VGLUT1]) in single boutons (n = 121, 94 boutons from 4, 3 repeats). Dashed line, threshold of [CaSPs]. Shade, small-sized boutons (size < 1). f Plot of Pr against bouton size (n = 121, 94 boutons from 4, 3 repeats). Note the marked increase in Pr of small-sized boutons after a 4-h elevation of [Mg²⁺]_o. Lines, linear regressions (R² = 0.63, 0.14). Shade, small-sized boutons (size < 1). a.u. in (c–f), arbitrary unit. Source data are provided as a Source Data file.

Considering that the abundance of presynaptic proteins is correlated with the structural size of boutons^72,73, where smaller boutons are more likely to lack CaSPs and remain silent, we used the vesicle protein VGLUT1 as a marker of bouton size (Methods) to examine its association with [CaSPs] and Pr in the same boutons. Our results demonstrated a positive association for both [CaSPs] and Pr with bouton size (Fig. 5e, f). Remarkably, increasing [Mg²⁺]_i substantially augmented the presence of CaSPs in small-sized boutons, resulting in the conversion of a significant portion of them from silent to functional (Fig. 5e, f).

Taken together (Figs. 4, 5), these findings demonstrate that intracellular Mg²⁺ plays a dual role in regulating the synaptic configuration. Firstly, it exerts an ongoing negative effect on vesicle release (to reduce Pr). Secondly, over a period of hours, elevated [Mg²⁺]_i gradually increases the concentration of presynaptic CaSPs, enabling the conversion of a substantial number of small-sized, silent boutons into functional ones (to increase D).

Multiple pathways converge on intracellular Mg²⁺ in regulating synaptic configuration

The results presented above demonstrate that intracellular Mg²⁺ plays a significant role in regulating synaptic configuration. To further understand the influence of other major signaling pathways on synaptic configuration, we investigated the impact of Ca²⁺ signaling, neurotrophic factors (such as BDNF), neuroinflammatory cytokines (such as TNF-α), and cAMP/PKA signaling. For each pathway (excluding BDNF), we first examined whether reducing the background level of signaling affected synaptic configuration. If a positive effect was observed, we then investigated whether moderately upregulating the signaling pathway caused a shift in synaptic configuration in the opposite direction. This approach ensured that each identified signaling pathway had physiological relevance.

We initially examined the influence of basal presynaptic [Ca²⁺]_i (that is, the presynaptic [Ca²⁺]_i at resting condition) on synaptic configuration, as it is known to affect Pr⁷⁴. Bath application of the NMDAR blocker AP5 (20 μM) or ifenprodil (1 μM) reduced basal [Ca²⁺]_i by ∼20% after 10 min (Supplementary Fig. 7a, b). This extent of basal [Ca²⁺]_i alteration should not affect Pr significantly⁷⁴. Indeed, the Pr was not significantly changed following 10 min of NMDAR blockade (Supplementary Fig. 7c). However, a chronic suppression of basal [Ca²⁺]_i for 4 h resulted in changes in synaptic configuration towards D^Hi $\bar{\Pr}$ ^Lo (Fig. 6a, b). Conversely, we examined the effect of bath application of glutamate, which could increase basal presynaptic [Ca²⁺]_i directly through activation of presynaptic glutamate receptors and subsequently influence Pr⁷⁵. We found that application of ambient glutamate (5 μM) increased basal presynaptic [Ca²⁺]_i by ∼20% after 10 min (Supplementary Fig. 7a, b) but this moderate increase did not change Pr acutely (Supplementary Fig. 7c). However, a 4-h administration of ambient glutamate at the same concentration significantly shifted the synaptic configuration towards D^Lo $\bar{\Pr}$ ^Hi (Fig. 6a, b). In both perturbations, ΣPr of dendrites remained constant across branches. These findings suggest that chronic alterations in basal presynaptic [Ca²⁺]_i can bidirectionally modify synaptic configurations.

Fig. 6 — a Time courses of changes in synaptic configuration and ${\bar{[{Mg}^{2 +}]}}_{i}$ (mM) after various treatments (for timepoints from left to right, n = 6, 7, 8, 8, 6, 5, 6, 5, 7, 6 repeats for configuration measurements, 8, 7, 7, 9, 6, 8, 8, 8, 8 repeats for [Mg²⁺]_i measurements). Two-sided unpaired t-tests (time 4 h vs. 0 h). For ΣPr, P = 0.8979, 0.9945, 0.9370; for D, P = 0.0334, < 0.0001, = 0.0015; for $\bar{\Pr}$ , P = 0.0003, 0.0093, < 0.0001; for [Mg²⁺]_i, P < 0.0001, < 0.0001, = 0.0109. b Plots of D against 1/ $\bar{\Pr}$ at dendritic branches 4 h after various treatments (n = 81, 42, 64, 57 branches from 7, 5, 6, 5 for control, AP5, ifenprodil and glutamate, respectively). Solid lines, linear regressions (P < 0.0001 for all). Dash-dot lines, bisectors. c, d Measurements of D, $\bar{\Pr}$ , ΣPr and ${\bar{[{Mg}^{2 +}]}}_{i}$ 4 h after various treatments (left to right, n = 9, 5, 6, 5, 7, 6, 6, 6, 6, 5, 6, 6, 6 repeats). Two-sided Mann-Whitney tests (vs. control). For D, P = 0.0190, 0.0360, 0.0420, 0.0007, 0.0004, 0.0004, 0.4559, 0.8639, 0.6993, 0.1135, 0.3277, 0.4559; for $\bar{\Pr}$ , P = 0.0070, 0.0048, 0.0010, 0.0002, 0.0004, 0.0004, 0.6070, 0.8639, 0.2977, 0.0076, 0.3277, 0.5287; for [Mg²⁺]_i, P = 0.0010, 0.0004, 0.0010, 0.0021, 0.0360, 0.0256, 0.4559, 0.7756, 0.2238, > 0.9999, 0.3277, 0.3884. e Plot of D, $\bar{\Pr}$ and ΣPr against ${\bar{[{Mg}^{2 +}]}}_{i}$ at the same timepoints after various treatments (n = 46 various conditions from a, c, d and Fig. 4a; linear regressions, P < 0.0001, < 0.0001, = 0.79). Lines, fitted curves. Error bands, 95% CIs. Data are presented as mean ± SEM. NS, no significance, *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001. Source data are provided as a Source Data file.

We next investigated the influence of TNF-α signaling on synaptic configuration. TNF-α signaling is involved in the homeostatic regulation of synaptic transmission⁷⁶, making it a potential candidate for regulating synaptic configuration. We found that chronic inhibition of basal TNF-α signaling by administering recombinant soluble TNF receptor 1 (sTNFR1, 10 pg ml^-1) shifted the synaptic configuration towards D^Hi $\bar{\Pr}$ ^Lo (Fig. 6c). In contrast, a 4-h moderate elevation of TNF-α concentration (100 pg ml^-1) shifted the synaptic configuration towards D^Lo $\bar{\Pr}$ ^Hi (Fig. 6c). In both perturbations, ΣPr of dendrites remained constant across branches. These results suggest that chronic manipulations of endogenous TNF-α signaling around the basal level can modify the synaptic configuration.

Consistent results were obtained when perturbating cAMP/PKA or BDNF signaling around basal levels. Inhibiting cAMP/PKA or increasing [BDNF] shifted synaptic configuration towards D^Hi $\bar{\Pr}$ ^Lo, while activating cAMP/PKA shifted the configuration towards D^Lo $\bar{\Pr}$ ^Hi (Fig. 6c). Overall, these pharmacological experiments demonstrate that under physiological conditions, the synaptic configuration can be regulated by multiple signaling pathways.

An intriguing observation was the concurrent influence of these pathways on the mean intracellular Mg²⁺ concentration ( ${\bar{[{Mg}^{2 +}]}}_{i}$ ) (Fig. 6a, c, d). This coincidence suggests two possibilities: either these pathways regulate synaptic configuration and [Mg²⁺]_i in parallel, or their influence on synaptic configuration is mediated by changes in [Mg²⁺]_i. Our data support the latter hypothesis, as the changes of synaptic configuration induced by perturbations of ambient glutamate, TNF-α, or 8-Br-cAMP were counteracted by preventing the decrease in ${\bar{[{Mg}^{2 +}]}}_{i}$ through the addition of [Mg²⁺]_o (+0.4 mM) or imipramine (1 μM) (Fig. 6c). Lastly, we pooled the data of synaptic configurations (D ∼ $\bar{\Pr}$ combinations) and their corresponding ${\bar{[{Mg}^{2 +}]}}_{i}$ values from various experimental conditions (from Figs. 4a, 6a, c, d) and found a linear correlation for D and $\bar{\Pr}$ with ${\bar{[{Mg}^{2 +}]}}_{i}$ (Fig. 6e). These findings collectively suggest that intracellular Mg²⁺ is a crucial regulator of synaptic configuration under physiological conditions.

Elevating brain Mg²⁺ levels modifies hippocampal synaptic configuration

The above findings demonstrate a regulatory scheme of [Mg²⁺]_i → configuration → transmission/plasticity of synapses at dendritic branches in cultured hippocampal neurons. However, it remains unclear if Mg²⁺ plays a similar role in intact animals and whether elevating brain Mg²⁺ levels can change synaptic configurations in vivo.

To address these questions, it is crucial to identify a reliable indicator for the synaptic configuration in vivo. In our in vitro research, we employed D ∼ $\bar{\Pr}$ combinations as simplified representation of diverse synaptic configurations. The configurational transition from D^Lo $\bar{\Pr}$ ^Hi to D^Hi $\bar{\Pr}$ ^Lo induced by elevated [Mg²⁺]_i involves two concurrent processes of synaptic weight redistribution: the conversion from silent to functional synapses and the shift from high-Pr to low-Pr synapses (Fig. 1c). Consequently, the distribution of synaptic weights undergoes a transition from a wide and long-tailed shape to a narrower distribution. Therefore, the changes in the shape of synaptic weight distribution can be taken as an in vivo indicator of synaptic configuration.

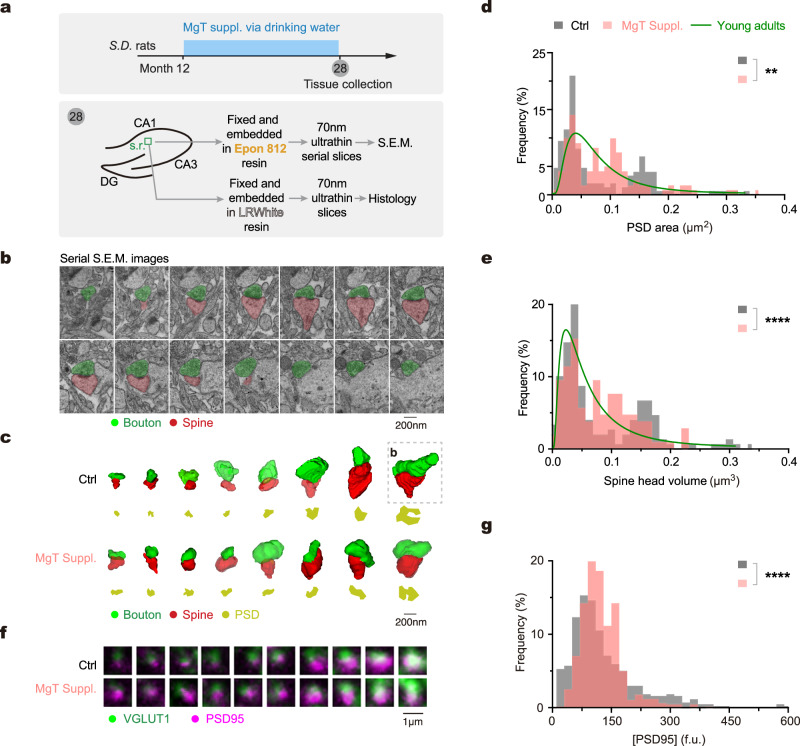
Measuring synaptic weights directly in the hippocampus of living animals is difficult due to technical limitations. As an alternative, we utilized indirect markers to infer synaptic weights. Synaptic weight strongly correlates with multiple parameters that report the structural size of individual synapses^77–82, including the presynaptic active zone (AZ) area (a robust Pr indicator), the postsynaptic density (PSD) area, and the spine head volume. Thus, both the AZ/PSD area and the spine head volume serve as reliable indicators of synaptic weights. Here, we quantified the PSD area and spine head volume to infer synaptic weight distribution in the hippocampus of animals. Notably, considering that silent and low-weight synapses are typically small in structural size (Fig. 5e, f), we expected to observe a subset of putative nonfunctional synapses with extremely small PSD area and spine head volume.

To modulate synaptic configuration in the hippocampus of living brains, we developed a Mg²⁺ compound named magnesium L-threonate (MgT), which effectively elevates brain Mg²⁺ levels through daily oral intake⁸³. We aimed to compare the distribution of synaptic weights between animals with or without MgT treatment. As a baseline, we examined the PSD area and spine head volume of randomly selected spiny synapses in the CA1 stratum radiatum (s.r.) of hippocampus in aged rats (28 months of age) (Fig. 7a). We performed 3D reconstruction of synapses using serial scanning electron microscopy images (Fig. 7b, c). Remarkably, both parameters exhibited a nonuniform and bimodal-like distribution, with synapses predominantly falling into either the large or small size categories, while medium-sized synapses were scarce (Fig. 7d, e, Supplementary Fig. 8a). Importantly, this long-tailed distribution pattern resembled the distribution pattern observed under the D^Lo $\bar{\Pr}$ ^Hi configuration in vitro (Figs. 1–3). Subsequently, we investigated the influence of elevated brain Mg²⁺ levels on the distribution of structural size of synapses. Age-matched rats were subjected to daily oral Mg²⁺ supplementation from 12 to 28 months of age by drinking water containing MgT (Fig. 7a). Interestingly, the distribution pattern of both PSD area and spine head volume significantly changed in MgT-treated animals, with a reduction in the number of both small and large synapses, and concurrently, an increase in medium-sized synapses (Fig. 7d, e). These observations suggest a significant modification of synaptic configuration in the hippocampus after elevating brain Mg²⁺ levels.

Fig. 7 — a Experimental design. Tissue samples were collected from CA1 stratum radiatum (s.r.) of the hippocampus for serial scanning electron microscopy (S.E.M.) and immunohistology. Note these animals were tested for learning and memory by water maze before tissue collection (see Supplementary Fig. 10). b An example of a spiny synapse from serial S.E.M. images at a 70-nm thickness (n = 7 rats, the same as in c–e). c Examples of 3D-reconstructed synapses from rats of control and MgT-treated. Note the difference in PSD area (yellow) and spine head volume (red) between the two groups. Box, the synapse shown in (b). d, e Distribution of PSD area (d) and spine head volume (e) (n = 165, 187 synapses from 3, 4 rats for control and MgT groups; two-sided Kolmogorov–Smirnov tests, **P = 0.0064, ****P < 0.0001). Green lines, distributions of PSD area and spine head volume in young adult animals (data from refs. ^118,119). f Examples of synapses (juxtaposed contacts) labeled by PSD95 and VGLUT1 on 70-nm ultrathin slices. VGLUT1 was used to identify presynaptic contacts. Note the difference in PSD95⁺ puncta between the two groups. g Distribution of [PSD95] in single synaptic contacts from control and MgT-treated rats (n = 438, 682 synapses from 3, 4 rats; two-sided Kolmogorov–Smirnov test, ****P < 0.0001). Source data are provided as a Source Data file.

To assess functional implications of the above ultrastructural changes, we further measured [PSD95] in individual synapses as a functional biomarker. Immunostaining on 70-nm tissue slices from the same hippocampal region of the same rats as described above (Fig. 7a) allowed us to determine the levels of [PSD95] in synapses, while VGLUT1 co-staining facilitated the identification of presynaptic contacts (Fig. 7f). Consistently, MgT treatment caused a reduced percentage of both low- and high-[PSD95] synapses, along with an increased percentage of medium-[PSD95] synapses. Consequently, these changes narrowed the distribution of [PSD95] to the medium range (Fig. 7g), aligning with the in vitro observations (Supplementary Fig. 8b–d). These findings further suggest that synaptic configuration in the hippocampus was modified following an elevation of brain Mg²⁺ levels.

The above data provide evidence for configurational changes induced by elevating brain Mg²⁺ levels, primarily based on the postsynaptic sites in dendrites. We further examined the critical presynaptic parameter, [CaSPs], that influences presynaptic functional state and consequently synaptic connectivity as shown above (Fig. 5). We observed an aging-related decline in [CaSPs] in the hippocampus and found that treatment with MgT to elevate brain Mg²⁺ levels prevented this decline (Supplementary Fig. 9). This evidence consistently supports the notion that synaptic configuration in the hippocampus can be modified by an increase in brain Mg²⁺ levels.

In addition, we also examined learning and memory of the same living animals ahead of the above post hoc experiments and confirmed that the aged animals with chronic MgT treatment showed better performance in water maze tests as compared to the control group (Supplementary Fig. 10), indicating improved learning and memory.

In summary, the above experiments support the hypothesis that elevating brain Mg²⁺ levels can modify the synaptic configuration in the hippocampus of intact animals, coincident with improved learning and memory.

Discussion

Organization principle of synapses along dendrites

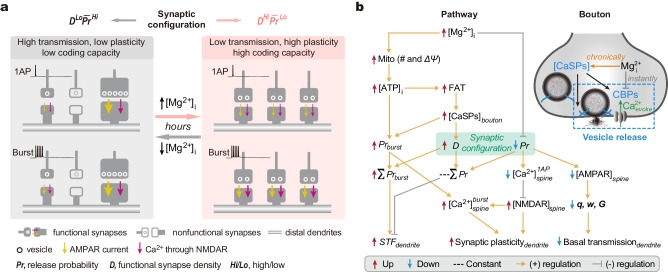
In this study, we examined the connectivity of synapses at dendritic branches and revealed that the synaptic configuration is a significant biomarker for branch-specific synaptic computations (for a schematic, Fig. 8a), which are fundamental for information processing in learning and memory. We directly measured and/or indirectly estimated multiple biophysical variables in characterizing properties of synaptic computations (for a full list and description of the variables, see Supplementary Table 1). Here, we summarized the mathematical associations between these variables to clarify the organizational principle behind.

Fig. 8 — a Schematic to show that the synaptic configuration is a biomarker for dendritic branch-specific synaptic computations. Intracellular Mg²⁺ regulates the configuration and optimizes computational properties of nearby synapses along individual branches, including transmission efficiency, plasticity, and coding capacity (see Discussion). b A [Mg²⁺]_i-mediated regulatory pathway (left, schematic pathway; top-right, regulatory scheme in a bouton). In brief, [Mg²⁺]_i exerts a dual effect on D and Pr. On the one hand, [Mg²⁺]_i enhances mitochondrion (Mito) functions by increasing Mito number and membrane potential (ΔΨ)³⁸. This leads to an increase in intracellular free ATP levels ([ATP]_i), promoting the anterograde fast axonal transport (FAT) of CaSPs³⁸. As a result, presynaptic [CaSPs] increases, converting a remarkable portion of synapses from silent to functional and increasing D. On the other hand, it has an ongoing negative effect on Pr likely by competing with intracellular Ca²⁺ on presynaptic Ca²⁺-binding proteins (CBPs) (top-right). Overall, the changes in [Mg²⁺]_i lead to varying synaptic configurations across individual dendritic branches. Notably, at presynaptic sites, the strength of vesicle release during bursting transmission is dominantly determined by both burst-induced facilitation of presynaptic Ca²⁺ influx and [CaSPs], suggesting a regulatory scheme: ↑[Mg²⁺]_i → ↑ [CaSPs] → ↑ Pr_burst. In synergy, the increase in [ATP]_i accompanied by elevated [Mg²⁺]_i can well support the high-energy demand of vesicle turnover during bursting transmission. Consequently, ↑[Mg²⁺]_i causes increases in both ΣPr_burst and short-term facilitation (***STF***, =ΣPr_burst/ΣPr) at dendritic branches. At postsynaptic sites, elevated [Mg²⁺]_i induces an increase in [GluN2B], enhancing Ca²⁺ influx via GluN2B*NMDARs in dendritic spines ([Ca²⁺]^burst_spine) during bursting transmission. Hence, both pre- and postsynaptic sites synergize burst-induced synaptic plasticity^83,111. Overall, the synaptic configuration, crucially regulated by [Mg²⁺]_i, determines branch-specific synaptic computations during information processing.

First, influence of synaptic configuration on presynaptic properties. At presynaptic sites, the total presynaptic strength per unit area of dendrites (ΣPr) during basal transmission remains constant, and functional synapse density is inversely correlated with $\bar{\Pr}$ , as per formulae (1) and (2).

D \propto \frac{1}{\bar{\Pr}}

Σ \Pr = D \cdot \bar{\Pr} = Constant

Second, influence of synaptic configuration on postsynaptic AMPAR-related properties. At postsynaptic sites, the quantal size, as approximated by GluA2*AMPAR or PSD95 expression levels, positively correlates with Pr in individual synapses. The total quantal size per unit area of dendrites (Σq), as approximated by GluA2 or PSD95 density, remains constant. Notably, the D ∼ $\bar{q}$ relationship mirrors the D ∼ $\bar{\Pr}$ combination, as per formulae (3) and (4).

D \propto \frac{1}{\bar{q}}

Σ q = D \cdot \bar{q} = Constant

Third, influence of synaptic configuration on postsynaptic NMDAR-related properties. At postsynaptic sites, the NMDAR quantal size (q_NMDAR), as approximated by the expression level of GluN2B*NMDARs, negatively correlates with Pr in individual synapses, while the total q_NMDAR per unit area of dendrites (Σq_NMDAR), as represented by the total amount of receptors, positively correlates with D, as per formula (5). Consequently, Σq_NMDAR is not constant but influenced by the synaptic configuration, as per formulae (6) and (7).

D \propto \bar{q_{NMDAR}}

Σ q_{NMDAR} = D \cdot \bar{q_{NMDAR}} \neq Constant

Σ q_{NMDAR} \propto \frac{1}{\bar{\Pr}} or D

Fourth, influence of synaptic configuration on AMPAR-mediated synaptic transmission. With above arrangements, the total transmission strength of excitatory synapses per unit area of dendrites during basal transmission (also named the basal gain, G) branch-specifically depends on the synaptic configuration. The D^Lo $\bar{\Pr}$ ^Hi configuration is more efficient in basal synaptic transmission than the D^Hi $\bar{\Pr}$ ^Lo configuration, as per formulae (8) and (9). During bursting transmission, the total strength of excitatory transmission (also named the bursting gain, G_burst) also depends on the synaptic configuration, but with larger variations, as per formula (10).

G = Σ w = Σ (\Pr \cdot q) \neq Constant

G \propto \bar{\Pr} or \frac{1}{D}

G_{burst} = Σ w_{b u r s t} = Σ (\Pr_{b u r s t} \cdot q) \neq Constant

Fifth, influence of synaptic configuration on postsynaptic NMDAR-mediated Ca²⁺ signals. During basal transmission, the total spine Ca²⁺ influx per unit area of dendrites (Σw_Ca) remains constant, independent of the synaptic configuration, as per formula (11). However, during bursting transmission, the total postsynaptic Ca²⁺ influx upon a burst is not constant, depending on the synaptic configuration, as per formulae (12) and (13).

Σ w_{Ca} = Σ (\Pr \cdot q_{NMDAR}) \neq Constant

Σ w_{{Ca}_{burst}} = Σ (\Pr_{burst} \cdot q_{NMDAR}) \neq Constant

Σ w_{{Ca}_{burst}} \propto \frac{1}{\bar{\Pr}} or D

In summary, the synaptic configuration influences the total strength of excitatory transmission and the postsynaptic NMDAR-mediated Ca²⁺ signals. The D^Lo $\bar{\Pr}$ ^Hi configuration has high basal transmission efficiency, while the D^Hi $\bar{\Pr}$ ^Lo configuration is more effective in generating high postsynaptic NMDAR-mediated Ca²⁺ influx, contributing to the induction of synaptic plasticity.

Notably, a key aspect of this organizational principle is the inverse relationship between synapse density and strength. Similar inverse relationship has been observed in different types of synapses across species^84–87. Such a relationship may hold significant implications for cognitive functions, because underlying various cognitive processes, when a single synapse or a cluster of synapses is strengthened (or enlarged), its nearby synapses within the same dendritic branch may be weakened (or eliminated), leading to changes in synaptic connectivity^{15,29,88–101}. Thus, the inverse density-strength relationship likely represents a fundamental and universal way of synaptic organization that is crucial for maintaining brain functions (see also Supplementary Notes).

Implications of synaptic configuration to information turnover

Governed by this organizational principle, the synaptic configuration is likely a significant biomarker for branch-specific information turnover (that is, information storage versus erasure) underlying learning and memory.

Firstly, the synaptic configuration of an individual branch may determine its functional state favorable for either learning or memory. Dendritic branches of D^Lo $\bar{\Pr}$ ^Hi configuration are more efficient in transmitting excitatory currents in basal transmission, suggestive of a higher efficiency in information transfer; meanwhile, their less amount of postsynaptic GluN2B*NMDARs reduces the ability of coincidence detection, thus protecting the current synaptic connectivity against perturbations induced by new learning. These features could synergistically contribute to holding the stored information, which is pertinent to memory. By contrast, dendritic branches of D^Hi $\bar{\Pr}$ ^Lo configuration present higher burst-induced postsynaptic Ca²⁺ signal (Σ ${w_{Ca}}_{burst}$ ) through larger number of GluN2B*NMDARs. Thereby, they are more sensitive in detecting coincidence and inducing synaptic plasticity to modify the current synaptic connectivity, favorable for encoding new information from learning. Therefore, varying configurations define the ability of nearby synapses in processing information during learning and memory in a branch-specific manner.

Secondly, the synaptic configuration per se may indicate the information coding capacity of an individual branch in its present state (such as before or after learning). It is widely accepted that synapses with high contrast in strength may crucially contribute to information representation. Single synapses, as the fundamental coding units, have varying capacities for information encoding. According to Shannon’s information theory¹⁰², synapses with normalized Pr values have higher information entropy than those with polarized Pr values. Our calculations of information entropy for diverse configurations within individual branches showed that the D^Hi $\bar{\Pr}$ ^Lo configuration has higher density of information entropy than the D^Lo $\bar{\Pr}$ ^Hi configuration, ranging from 0.77 to 0.10 bits μm^-2 (Supplementary Fig. 11). Therefore, the D^Hi $\bar{\Pr}$ ^Lo configuration conceptually has greater coding capacity (or less stored information) than the D^Lo $\bar{\Pr}$ ^Hi configuration, making it more favorable for encoding new information from learning.

Thirdly, alterations in synaptic configuration may represent information turnover. Learning induces branch-specific encoding of new information, such that it is reasonable to expect a configurational transition from D^Hi $\bar{\Pr}$ ^Lo to D^Lo $\bar{\Pr}$ ^Hi in relevant dendritic branches after learning. Indeed, theoretical and experimental studies have demonstrated at the cellular level such changes in the configuration of synaptic weight distribution following learning processes³. For example, after motor task learning, synaptic weights redistribute across the dendritic tree of cerebellar Purkinje cells, resulting in both an increased number of silent synapses and polarized synaptic weights in the remaining functional synapses¹³. Such a configurational transition is also evident by 3D reconstructions through electron microscopy, revealing strengthened synapses accompanied by weakened nearby synapses along the same dendrites of Purkinje cells after learning¹². This configurational change is considered crucial for encoding task-specific input-output associations after motor learning^3,13, supporting our speculation.

Taken together, we propose that the synaptic configuration is a biomarker indicating the present state of information capacity of an individual dendritic branch, while dynamic alterations to configuration contribute to branch-specific information turnover. Future studies in behaving animals are required to obtain direct evidence at the single-synapse resolution regarding the role of synaptic configuration in information turnover during learning and memory.

Intracellular Mg²⁺ crucially regulates synaptic configuration

In this study, intracellular Mg²⁺ is identified as a key regulator of synaptic configuration, revealing a Mg²⁺-mediated regulatory pathway under physiological conditions. Here, we summarized and illustrated this pathway (Fig. 8b) and briefly described it below.

Within individual boutons, intracellular Mg²⁺ levels ([Mg²⁺]_i) enhance functions of mitochondria by increasing their density and membrane potential (ΔΨ), thereby raising intracellular free ATP concentration ([ATP]_i)³⁸. The boosted energy supply accelerates anterograde fast axonal transport (FAT) of Ca²⁺-sensitivity-related proteins (CaSPs), leading to an increase in presynaptic [CaSPs] to facilitate the activation of silent boutons (and ultimately an increase in D). Concurrently, [Mg²⁺]_i exerts a pronounced inhibitory effect on Pr. The dual effect of [Mg²⁺]_i confers varying configurations for individual dendritic branches, thus branch-specifically modulating transmission efficiency, plasticity, and coding capacity of the synapses. Notably, factors other than intracellular Mg²⁺ could also regulate the synaptic configuration, as exemplified by the muscle-selective overexpression of fasciclin II at NMJs⁸⁷, the activation of presynaptic p35/p25/Cdk5 pathway in the hippocampal CA3 recurrent synapses¹⁰³, and the activation of postsynaptic CaMKII signaling¹⁰⁰. Future studies should aim to explore and identify additional endogenous configuration-regulating factors in the brain.

In this Mg²⁺-mediated regulatory pathway, an interesting finding is the substantial negative effect of intracellular Mg²⁺ on Pr in hippocampal synapses. The exact molecular mechanisms underlying this negative effect remain unclear, but several possibilities warrant further investigation. For example, physiological concentrations of [Mg²⁺]_i (that is, 1 mM) can potentially influence the conformation of the synaptotagmin-1–membrane complex via its C2 domains^104,105, which may negatively affect vesicle fusion processes. Another possibility is the peak concentration of presynaptic Ca²⁺ influx in the immediate proximity to sensor proteins might be low in a large portion of synapses; consequently, the [Ca²⁺]_i elicited by a single AP might not be sufficient to trigger vesicle fusion, making the negative effect of [Mg²⁺]_i remarkable for these synapses. Additionally, endogenous Ca²⁺ buffers have been shown to modulate Pr at central synapses¹⁰⁶, and in our case, increased [ATP]_i accompanied by high [Mg²⁺]_i³⁸ could buffer intracellular Ca²⁺ influx upon a single AP invasion, thereby reducing the sensitivity of Ca²⁺ in triggering vesicle fusion. These possibilities, among others, require further investigation in future studies.

Is intracellular Mg²⁺ a “memory molecule”?

We showed that intracellular Mg²⁺ crucially regulates the synaptic configuration at dendritic branches. This regulatory effect suggests that intracellular Mg²⁺ may serve as a molecular constituent of information turnover at dendritic branches, given the implications of synaptic configuration to information turnover as discussed above. First, the present [Mg²⁺]_i levels make the synapses within an individual branch optimal for either learning or memory. Low [Mg²⁺]_i promotes the D^Lo $\bar{\Pr}$ ^Hi configuration with the features of “high basal synaptic transmission efficiency, low plasticity and coding capacity”, favoring holding information that is critical for memory, while high [Mg²⁺]_i promotes the D^Hi $\bar{\Pr}$ ^Lo configuration exhibiting “low basal transmission efficiency, high plasticity and coding capacity”, favorable for encoding information during learning. Second, reversible fluctuation of [Mg²⁺]_i between low and high levels causes the configurational transition, which may contribute to the dynamic processes of information storing and erasing at a dendritic branch as discussed above. Therefore, intracellular Mg²⁺ may act as a modulator of branch-specific information turnover, behaving like a “memory molecule”. Notably, it takes tens-of-minutes to hours for [Mg²⁺]_i to mediate an equilibrium configurational transition. Interestingly, this timescale coincides with that of short-term or daily memory turnover, raising a speculation that intracellular Mg²⁺ might be a molecular substrate of short-term or daily memory. However, direct evidence at the branch level is required to test this hypothesis in future in vivo studies.

Translational implications

Lastly, we discussed translational implications of synaptic configuration. Aging and neurodegeneration perpetuate pronounced changes in synaptic connectivity across different brain regions in both humans and non-human primates^33–37, hallmarked by reduced synapse density and increased synaptic weight (or structural size) in the remaining synapses, consistent with our observations on hippocampal synapses in aging rodents. These long-lasting connectivity changes, resembling the D^Lo $\bar{\Pr}$ ^Hi configuration, impair the dynamic balance between D^Lo $\bar{\Pr}$ ^Hi and D^Hi $\bar{\Pr}$ ^Lo configurations, perhaps compromising the ability of information encoding relevant to learning. Such a scenario may be more detrimental in brain regions, like the hippocampus and prefrontal cortex, that require dynamic memory turnover to maintain persistent ability of learning and working/short-term memory.

To protect learning and memory against aging, reversing the synaptic configuration towards the D^Hi $\bar{\Pr}$ ^Lo mode might be a plausible approach. In support, our in vivo experiments demonstrate that the restoration of hippocampal synaptic configuration in aged animals, towards that in young animals, coincides with their improved learning and memory. Thus, targeting synaptic configuration by manipulating intracellular Mg²⁺ concentration may have a therapeutic potential for treating cognitive impairments caused by aging and neurodegenerative diseases in humans (see Supplementary Notes). Indeed, clinical studies have reported that brain Mg²⁺ supplementation by oral intake of MgT (also known as L-TAMS) improves cognitive functions of individuals with mild cognitive impairment (MCI)¹⁰⁷, patients with mild-to-moderate Alzheimer’s disease^108,109, and attention-deficit/hyperactivity disorder (ADHD)¹¹⁰.

Overall, our findings reveal that the synaptic configuration is a biomarker indicating branch-specific synaptic computations and underscore an important role of intracellular Mg²⁺, as a crucial regulator of configuration, in maintaining brain health and rejuvenating aging brains (see also Supplementary Notes). More importantly, besides intracellular Mg²⁺, these findings further suggest that any synaptic configuration-regulating factors would be potential therapeutic targets for preventing, mitigating, or perhaps reversing brain aging and neurodegeneration.

Methods

Animals

Neonatal Sprague-Dawley (S.D.) rats of both sexes were obtained from Vital River Laboratory (Beijing, China) or Anhui Medical School Animal Facility (Hefei, China). Adult male rats were also acquired from Vital River Laboratory and housed in temperature- and humidity-controlled rooms under a 12-h light-dark cycle. The rats were randomly assigned to either the control group or the magnesium L-threonate (MgT) supplement group. As previously described in our study⁸³, MgT (604 mg kg^-1 d^-1, equivalent to 50 mg kg^-1 d^-1 of elemental Mg²⁺) was administered via ad libitum water intake starting at 12 months of age. The average daily water intake was measured to be ∼ 30 ml. At 26 months of age, both control and MgT-treated animals were subjected to behavior tests for learning and memory using water maze (see ‘Water maze’). Then, at 28 months of age, these animals were anesthetized with intraperitoneal injection of chloral hydrate (400 mg kg^-1) and subsequently sacrificed for histology and electron microscopy imaging. For some experiments, separate groups of young adult rats (6 months of age), aged rats (24 months of age), and aged rats (24 months of age) supplemented with MgT (starting from 16 months of age) were sacrificed for histological comparisons. The animal protocols adhered to the guidelines and were approved by the Institutional Committees on Animal Care of Tsinghua University and USTC.

Culture of hippocampal neurons

High-density primary cultures of hippocampal CA3–CA1 pyramidal neurons obtained from neonatal S.D. rats (< 24 h) were utilized in this study, following the protocols described in our previous studies^38,111. In brief, the dissociated cells were plated and cultured on 1# coverslips (8 mm × 8 mm) in a water jacket incubator (ThermoFisher) maintained at 37 °C, 5% CO₂, and saturated humidity for a minimum of 14 days in vitro (d.i.v.) before experimentation. The culture medium contained a physiological concentration of 0.8 or 1.2 mM [Mg²⁺]_o (for rationales, see Supplementary Notes) and a constant level of 1.2 mM [Ca²⁺]_o. For experiments, cultures aged 18.69 ± 1.92 (mean ± SD) d.i.v. were utilized. In the standard working solution for imaging, both [Ca²⁺]_o and [Mg²⁺]_o were set at 1.2 mM to achieve a [Ca²⁺]_o/[Mg²⁺]_o ratio of one. However, in certain experiments, the [Ca²⁺]_o/[Mg²⁺]_o ratio was acutely increased to four by elevating [Ca²⁺]_o to 4.8 mM while maintaining [Mg²⁺]_o at 1.2 mM. This adjustment aimed to enhance the Ca²⁺ influx in triggering vesicle release during action potential (AP) propagation by mitigating the inhibitory effect of extracellular Mg²⁺ on Ca²⁺ channels. All pre-treatments were administered within the home incubator prior to transfer to the working solution for imaging. Each timepoint/condition was repeated by individual coverslips derived from a minimum of three individual batches of cultures. For all culture experiments, an individual coverslip was taken as a “biological repeat”.

Pharmacological treatments

To investigate the impact of various signaling pathways on the synaptic configuration, specific drugs were introduced into the culture medium and incubated at 37 °C, 5% CO₂, and saturated humidity for a duration ranging from 10 min to 4 h prior to imaging. The following drugs and concentrations were utilized (Supplementary Table 2): AP5 (20 μM), ifenprodil (1 μM), glutamate (5 μM), imipramine (1 μM), TNF-α (100 pg ml^-1), sTNFR1 (10 pg ml^-1), 8-Br-cAMP (10 μM), PKI_14-22 (0.25 μM), and BDNF (10 ng ml^-1). To counteract the effects of TNF-α, 8-Br-cAMP, or glutamate on synaptic configuration, concurrent administration of [Mg²⁺]_o at an extra concentration of 0.4 mM (to a final 1.2 mM in concentration) or imipramine at a concentration of 1 μM was implemented alongside each drug.

Imaging systems

Imaging experiments were conducted in a perfusion chamber (RC-27NE2; Warner) integrated into a custom-made mini-incubator, which maintained control over CO₂ levels (5%), temperature (33–35 °C), and humidity (saturated). The working solution was continuously perfused through the chamber using a peristaltic pump (Gilson) and pre-warmed to 33–35 °C using a line heater (SC-20 and TC344C; Sutter).

Three different imaging systems were employed in this study: a regular confocal system (FV300 or FV1000; Olympus), a spinning disk confocal system (Yokogawa), and an ultrafast imaging system (custom-made). The regular confocal system was utilized for imaging [Mg²⁺]_i, FM dyes, and immunofluorescence of histology. A stack of fluorescence images was captured at a resolution of 1024 × 1024 pixels, with a pixel size of 0.05754 μm and a z-step of 0.5 μm. The spinning disk confocal system was used for imaging Ca²⁺ activity at a resolution of 512 × 512 pixels, with a pixel size of 0.1151 μm and a frame rate of 36 Hz. In certain experiments, this system also captured a z-stack of FM images (0.5 μm z-step) at the same resolutions, albeit in a slower mode. The ultrafast imaging system was employed to investigate the involvement and percentage of GluN2B*NMDARs mediated Ca²⁺ influx in dendritic spines. Images were acquired at a resolution of 512 × 512 pixels, with a pixel size of 0.1151 μm and a frame rate of 2000 Hz.

For most experiments, a 60 × water-immersion objective lens (UplanSApo 60 × W N.A. 1.20; Olympus) was used. The z-stack images were subsequently projected at maximum intensity for post hoc analysis using ImageJ (NIH). Time-lapse images were registered and automatically analyzed using CaImAn¹¹², an automated pipeline specifically designed for Ca²⁺ activity analysis (see ‘Calcium imaging and analysis’).

Measurement of intracellular magnesium concentration

To measure [Mg²⁺]_i in boutons or neurites, we utilized the fluorescence of Magnesium Green-acetoxymethyl (AM) ester (MgGrn; 5 μM) (Supplementary Table 2). Prior to imaging, the cells were incubated with MgGrn for 30 min and then transferred to medium absent of MgGrn for 15 min (to wash out extracellular dye) under the aforementioned culture conditions. A stack of MgGrn images was acquired using the imaging systems described earlier and subsequently projected at maximum intensity for post hoc analysis. Importantly, MgGrn imaging was performed before any electrical stimulations were delivered to avoid potential confounds introduced by evoked Ca²⁺ responses.

Following MgGrn imaging, the release probability (Pr) of the same boutons was measured by staining with FM4-64 or FM5-95, which was elicited by a 30AP@0.5 Hz stimulation. For details on FM staining, please refer to the section ‘Detection of vesicle turnover’. To compare [Mg²⁺]_i among boutons with diverse volumes (sizes), the intensity of MgGrn fluorescence was normalized by the bouton volume. Bouton volume was estimated by quantifying the total fluorescence of FM4-64 labeled by a 600AP@10 Hz stimulation, known as the ‘maximum stimulation’ protocol¹¹³. This protocol induces vesicle release for all the releasable vesicles in individual boutons¹¹³. The measurement of FM staining with the 600AP stimulation was performed after Pr measurement. The contours of individual boutons were determined using the 600AP⁺ puncta. For the measurement of neurite [Mg²⁺]_i, the MgGrn fluorescence was normalized by the volume of individual neurite segments³⁸.

To calibrate the absolute value of [Mg²⁺]_i in boutons, subsequent to loading MgGrn into the cytoplasm, neurons were incubated in a Tyrode solution containing 10 μM A-23187 (a divalent ionophore; Invitrogen), 0.05–1.6 mM Mg²⁺, and 0 mM Ca²⁺ for 15 min to equilibrate intracellular and extracellular Mg²⁺ concentrations. Following confocal imaging of MgGrn, boutons were stained with FM4-64 elicited by the 600AP stimulation to estimate bouton volume. Normalizing MgGrn fluorescence in individual boutons by bouton volume, as mentioned above, the average normalized MgGrn fluorescence of boutons in the area of interest (AOI) was used to generate the calibration curve. This curve was fitted by the Hill equation, allowing us to calculate the absolute concentration of [Mg²⁺]_i.

Detection of vesicle turnover

To visualize vesicle turnover in single boutons, we employed styryl dyes including FM1-43 (10 μM), FM4-64 (20 μM), or FM5-95 (20 μM) (Supplementary Table 2), following the previously described protocols^38,85,111. In brief, the labeling procedure for vesicle turnover consisted of three steps: loading, washout, and unloading (refer to Supplementary Fig. 1a). Working solutions were pre-warmed and perfused into the chamber through a peristaltic pump. During loading, FM molecules were taken up by released vesicles that were elicited by different stimulation patterns such as 30AP@0.5 Hz, 6 × 5AP@100 Hz (or other bursting patterns as shown in Supplementary Fig. 1b), or 600AP@10 Hz. APs were evoked by a field stimulus (1 ms, 50 mA per pulse) generated by a stimulus isolator (A385; WPI) and delivered via parallel platinum electrodes placed at an 8 mm distance (RC-27NE2; Warner). After loading, nonspecific FM labeling was washed out using a solution containing low [Ca²⁺]_o (0.4 mM) and the quencher ADVASEP-7 (300 μM) (Supplementary Table 2). Importantly, the washout process did not affect the endocytosed FM in vesicles^38,85,111.

To exclude artifacts introduced by unhealthy boutons, an unloading procedure was performed to test whether the dyes could be exocytosed after delivering a 480AP@2 Hz stimulation. Images were captured (as described in the ‘Imaging systems’ section) after washout (F₁) and unloading (F₂), and the difference (F₂–F₁) was used to quantify the number of released vesicles in single boutons.

During the loading and unloading procedures, kynurenic acid (200 μM) or a combination of NBQX (10 μM) and AP5 (50 μM) (Supplementary Table 2) was applied to block synaptic transmission¹¹¹. The Pr or Pr_burst was measured using quantal analysis as previously described¹¹¹. Briefly, the fluorescence of a quantal release (F_Q) was measured by FM staining elicited by a single AP. The number of released vesicles per bouton (N_v) after 30 APs was calculated by dividing F_Q by its fluorescence, and subsequently, Pr was determined by N_v/30. To measure D, the number of FM⁺ puncta per unit area of distal dendritic branches (shaft diameter in mean ± SD was 0.62 ± 0.21 μm) was quantified. Dendrites were identified by post hoc labeling of microtubule-associated protein 2 (MAP2, a dendritic skeleton protein, see ‘Histology’), and their diameters were measured from corresponding differential interference contrast (DIC) images.

Calcium imaging and analysis

Synaptic Ca²⁺ imaging was conducted using a spinning disk confocal system (Yokogawa) equipped with a high-speed CCD camera (Andor). When imaging Ca²⁺ in boutons, kynurenic acid (200 μM) or a combination of NBQX (10 μM) and AP-5 (50 μM) was added to the working solution to exclude the involvement of NMDARs and prevent recurrent activity. For Ca²⁺ imaging in spines, NBQX (10 μM) was administered to exclude the participation of AMPARs. In some experiments, Ro25-6981 (1 μM) was applied to selectively block GluN2B*NMDARs.

The evoked change in fluorescence (ΔF/F₀) in single boutons or spines was quantified by averaging the responses from 30 sweeps (when stimulated by 30AP@0.5 Hz) or 6 sweeps (when stimulated by 6 × 5AP@100 Hz). To determine the total amount of 1AP-evoked Ca²⁺ influx in a single spine (referred to as w_Ca), the area under the ΔF/F₀ curve during the evoked Ca²⁺ event was calculated and averaged from 30 repeats. For quantifying ${w_{Ca}}_{burst}$ , the area under the ΔF/F₀ curve during a burst-evoked Ca²⁺ event was calculated and averaged from 6 repeats, and the value was further divided by 5 to normalize it to the number of APs in the burst.

To simultaneously image spine Ca²⁺ activity and presynaptic vesicle release, Ca²⁺ activity in spines was measured in the presence of FM5-95 (20 μM) and NBQX (10 μM). This allowed for recording the sweeps of evoked Ca²⁺ activity while visualizing AP-induced vesicle turnover (refer to ‘Detection of vesicle turnover’) in the same synapses. We compared the strength of vesicle release (Pr or Pr_burst) with and without NMDAR blockade using AP5 (50 μM) and found no significant difference between the two conditions, indicating that asynchronous release did not significantly affect our measurements of release probability.

Time-lapse images were aligned using the Image J (NIH) plugin ‘stabilizer’ and then analyzed using an automated pipeline CaImAn¹¹², with a signal-to-noise ratio (SNR) threshold set at > 1.5. The threshold of 1.5 × SNR was determined empirically based on a consensus between automated extraction of Ca²⁺ events and manual proofreading.

Visualization of GluN2B in spines

To visualize and quantify the presence of GluN2B in individual dendritic spines, two types of fluorescent proteins were transfected into cultured neurons: CaMKIIα-mKate2 (serving as a structural marker and internal control for expression level) and CaMKIIα-GFP-GluN2B (GFP-fused GluN2B subunits)⁶¹. To quantify the relative amount of transfected GluN2B in each spine ([GluN2B]_Sp), the fluorescence intensity of GFP (F_GFP) was divided by the fluorescence intensity of mKate2 (F_mKate2) within each individual spine. This normalization process considers the variations in spine volume and gene expression levels among different spines. The resulting ratio, F_GFP/F_mKate2, represents the relative abundance of exogenous GluN2B in each individual spine.

Plasmids and transfection

To transduce the plasmids encoding CaMKIIα-Synaptophysin-GCaMP6f, CaMKIIα-GCaMP6f, CaMKIIα-mKate2, and CaMKIIα-GFP-GluN2B into cultured neurons, the Ca²⁺ phosphate protocol was employed¹¹⁴ (for plasmids and reagents, see Supplementary Table 2). The process involved mixing the plasmids and CaCl₂ in Hank’s balanced solution to achieve a final DNA concentration of 20 ng μl^-1 immediately before transfection. The DNA–Ca²⁺-phosphate solution, with homogenous precipitates formed, was then applied to the cultured neurons on coverslips. The coverslips with the transfected neurons were incubated for 1 h under conditions of 5% CO₂, 37 °C, and saturated humidity. Subsequently, the precipitates were dissolved by transferring the coverslips to an incubator with 10% CO₂ and 37 °C for 15–20 min. Finally, the coverslips were returned to the original incubator with 5% CO₂, 37 °C, and saturated humidity to allow for gene expression. The transfected neurons, with a transfection rate ranging from 18% to 59%, were used for imaging purposes after maturation, which corresponds to > 1 week after the transfection. As a validation, it was observed that the transfection process itself did not have any effect on vesicle release probability (Supplementary Fig. 5b).

Histology

Cultured neurons

A strategy of retrograde immunofluorescence was employed for multiple rounds of labeling presynaptic proteins in a synaptic network (for a schematic, see Supplementary Fig. 6a), employing the method of ‘Single-synapse analysis using FM1-43 and immunofluorescence imaging array’ (SAFIA) as previously described³⁸. After imaging FM1-43 in the AOI with dimensions of 58.9 μm × 58.9 μm (see ‘Detection of vesicle turnover’), the culture coverslips were incubated in normal Tyrode solution with [Ca²⁺]_o at 1.2 mM for 20 min. Then, they were fixed in a solution of 1% paraformaldehyde (E.M.S.), 0.01% glutaraldehyde (Alfa Aesar), and 4% sucrose in 1 × PBS (pH 7.4) for 1 h at room temperature (RT). The fixatives were gently washed out several times using Tris buffer (pH 7.6), which consisted of Tris Base 25 mM, Tris-HCl 25 mM, and NaCl 150 mM (filtered through a 0.22 μm film before use).

Next, the coverslips were permeabilized and blocked in a freshly prepared blocking solution (in Tris buffer) containing 1% BSA, 0.1% saponin, and 300 μM ADVASEP-7 for 1.5 h at RT. This was followed by several rounds of immunostaining. In each round, two to three primary antibodies (1:200–1:500) are incubated for 2–4 h at RT, followed by incubation with fluorophore-conjugated secondary antibodies (1:200–1:500) for 2 h at RT (for antibodies, see Supplementary Table 2). Confocal fluorescent images were then captured in the AOI, with light-field DIC images used for recognizing landmarks. After each round of staining, the antibodies were eluted by a stripping buffer (0.2 M NaOH and 0.015% SDS in deionized water) for 20 min at RT, repeated twice. The coverslips were rinsed in Tris buffer for over 1 h at RT to wash out SDS. Confocal imaging validated that < 1% fluorescent signal of presynaptic proteins remained in individual boutons after elution as compared to before (Supplementary Fig. 6b). Extreme care was taken to avoid cell detachment during this process. The coverslips were then subjected to the next round of immunostaining using 2–3 primary antibodies, with one antibody used as an internal quality control and landmark for image registration in data analyses. Typically, a maximum of 4–5 rounds of immunostaining could be performed on a culture coverslip (Supplementary Fig. 6c).

Specifically, for immunostaining the extracellular epitope of GluA2*AMPARs, the neurons were incubated for 1 h at RT in the blocking solution with anti-GluA2 antibody (dilution, 3 μg ml^-1) but with no addition of any detergents to keep the membrane intact. This procedure was performed after measuring Pr in the same synapses using FM1-43 (see ‘Detection of vesicle turnover’).

For analyzing images using the SAFIA approach in cultured neurons, the acquired images were initially coarsely aligned using ‘Rigid Body Registration’¹¹⁵ and then further refined using ‘UnwarpJ’¹¹⁶ in Image J (NIH) to correct any physical distortions present. To normalize the fluorescence intensity of VGLUT1 and each individual CaSP (referred to as [CaSP_i]) within individual boutons, they were initially divided by their respective median values in the bouton population. The size of each bouton was estimated based on the normalized quantity of VGLUT1 fluorescence (referred to as [VGLUT1]), as there is a well-established correlation between [VGLUT1] and the total number of vesicles in individual boutons³⁸. To quantify the collective impact of all CaSPs on vesicle release within a bouton, the geometric mean of the quantity of all CaSPs (referred to as [CaSPs]) was calculated using the following formula

[CaSPs] = \frac{\prod_{i} [{CaSP}_{i}]}{[VGLUT 1]}

where CaSP_i represents the i^th CaSP, ∏ is the product operator.

Tissue slices

For immunostaining on ultrathin tissue slices of the hippocampus, procedures were taken as previously described³⁸. In detail, the rats were anesthetized and transcardially perfused with 1 × PBS and fixative solution (1% paraformaldehyde and 0.01% glutaraldehyde in 1 × PBS), subsequently. The CA1 stratum radiatum (s.r.) region of hippocampus was then sectioned at 100 μm thickness using a vibratome (VT1000S; Leica). These sections were further trimmed into < 1 mm² square blocks for either immunostaining or electron microscopy imaging (see ‘Electron microscopy-based 3D reconstruction’). The tissue blocks for immunostaining were treated with 1% tannic acid (Sigma) for 1 h, followed by treatment with 1% uranyl acetate in maleate acid buffer (pH 6.0) for 1 h. Subsequently, the blocks were dehydrated sequentially in 50%, 70%, 80%, 95%, 100%, and 100% ethanol containing 1% paraphenylenediamine (PPD, Sigma) for 15 min each. The tissue blocks were then infiltrated with a mixture of ethanol and LR White resin in various ratios, followed by pure resin, with each infiltration step lasting for 1 h. Finally, the blocks were placed in capsules filled with LR White resin and polymerized in a 55 °C oven for 48 h (for related reagents, see Supplementary Table 2). Ultrathin slices of 70 nm thickness were cut and mounted on coverslips for immunostaining, using primary antibodies for synaptic proteins at 1:300, incubated at 4 °C overnight and secondary antibodies at 1:500, incubated at RT for 2 h (for antibodies, see Supplementary Table 2).

Electron microscopy-based 3D reconstruction

Tissue blocks were dissected from the CA1 s.r. region of aged rats at 28 months of age, as described in the ‘Histology’ section. The dissected blocks were then post-fixed in a solution containing 1% osmium tetroxide and 1.5% potassium ferricyanide in Maleate buffer (pH 6.0) for 1 h. Subsequently, the blocks were stained with 3% uranyl acetate for 1 h. After staining, the blocks underwent a series of dehydration steps using sequential ethanol concentrations (50%, 70%, 80%, 95%, and 100%) for 15 min each. Following dehydration, the blocks were treated with 100% propylene oxide twice for 10 min each. These procedures were performed while keeping the blocks on ice. The next step involved the infiltration of the blocks with a mixture of 50% propylene oxide and 50% epoxy resin for 60 min at RT, followed by pure epoxy resin for 24 h at 4 °C. The blocks were then transferred to embedment molds filled with pure epoxy resin and placed in a 60 °C oven for 24 h to allow polymerization (for related reagents, see Supplementary Table 2).

Serial ultrathin slices with a thickness of 70 nm were cut using a diamond knife on a microtome (Leica) and mounted on silicon chips to enhance electro-conductivity. The slices were subsequently stained with 3% uranyl acetate and 0.4% (w/v) lead citrate in sequential steps. Images of the slices were captured using a scanning electron microscopy (Supra55, Zeiss) with specific imaging parameters (10 keV, 8000 × 8000 pixels, 2 nm pixel^-1, 15 μs pixel^-1). To correct any distortions, the serial electron microscopy images were registered using UnwarpJ in ImageJ¹¹⁶. The registered images were then utilized for the reconstruction of synapses. Individual synapses were randomly selected and reconstructed in 3D using the TrakEM2 plugin in Image J¹¹⁷.

Water maze

A circular metal tank of 150 cm in diameter and 50 cm in depth was filled with 22 °C water, 30 cm in water depth. In the training session, an acrylic platform (15 cm in diameter) was set in the center of a quadrant, immersed in the pool, with the upper surface 2 cm below the water. Four spatial cues distinct in shape and color were placed evenly around the tank. The training session was split into two 4 days, 5 trials per day with an 1 h inter-trial interval. The positions into the water were randomly selected. In each training trial, an individual rat was allowed for a maximum 90 s staying in the water. During this period, if the rat found the platform, it was allowed for standing on the platform for 30 s and then dried by towels and returned to the home cage prewarmed by a 37 °C heater; otherwise, it was guided to the platform, standing for 30 s. The latency (90 s at maximum) to reach the platform was recorded to generate the learning curve. After the training session, each rat was tested in the water maze for 90 s in the absence of platform 3 days after the last training trial, and the percentage of time spent in the quadrants was analyzed. The data were recorded and analyzed automatedly by a behavioral system (EthoVision XT, Noldus, Netherlands).

Information entropy

Information entropy of individual presynaptic boutons was calculated using the Shannon’s formula¹⁰², as follows.

H (\Pr) = - [{\Pr \cdot \log}_{2} (\Pr) + {(1 - \Pr) \cdot \log}_{2} (1 - \Pr)]

For each dendritic branch, the density of information entropy of presynaptic boutons was calculated by the total entropy of the synapses per unit area of dendrites.

Statistics

The normality of the data was tested using the Shapiro-Wilk test, and based on the results, either nonparametric or parametric statistical tests were chosen. For comparing two groups, paired or unpaired t-tests were used, depending on the nature of the data and the study design. When multiple comparisons were made, one-way or two-way ANOVA was performed, followed by post hoc Bonferroni’s test to determine specific group differences. The Kolmogorov–Smirnov test was employed to compare distributions between groups. All statistical tests were two-sided, meaning that both the possibility of a positive and a negative effect was considered. The significance level was set at P < 0.05. GraphPad Prism software was used for conducting all the statistical analyses.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Supplementary information

Supplementary Information^{(8.4MB, pdf)}

Peer Review File^{(7.6MB, pdf)}

Reporting Summary^{(2.5MB, pdf)}

Source data

Source Data^{(414.4KB, xlsx)}

Acknowledgements

We express our gratitude to Drs. T. Südhof (Stanford) and J. Feldman (UCLA) for their valuable input and critical review of the manuscript before submission. We would also like to acknowledge Drs. H. Han and X. Chen (CASIA) for their support with electron microscopy, Drs. L. Qi, C. Xu (USTC) for providing plasmids, Dr. F. Xu (SIAT) for support with the ultrafast imaging system, and Drs. P.-M. Lau (SIAT) and R. Zhao (Shenzhen Bay Laboratory) for their scientific inputs. This work was supported by the THU-CASIA Technical Cooperation Project (THU 20142001129) and Univ. SIAT Tenure-Track Startup (to H.Z.), National Natural Science Foundation of China (31630030) and Chinese Academy of Sciences (XDB32030200) (to G.-Q.B.), and THU Initiative Scientific Research Program (THU 20131080156) (to G.L.).

Author contributions

H.Z. and G.L. conceived the project and wrote the manuscript. H.Z., G.-Q.B. and G.L. designed the experiments and interpreted the data. H.Z. performed the experiments and data analyses. All authors edited and approved the final manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data are available in the main text or the supplementary materials. Source data are provided with this paper.

Code availability

The codes used in this study are open-source and accessible online. github.com/flatironinstitute/CaImAn.

Competing interests

G.L. is a cofounder of NeuroCentria, a company dedicated to developing drugs for brain diseases. H.Z. and G.-Q.B. declare no competing interests.

Footnotes

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Contributor Information

Hang Zhou, Email: zhouhang01@outlook.com.

Guosong Liu, Email: liu.guosong@gmail.com.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-47571-3.

References

1.Bliss TVP, Collingridge GL. A synaptic model of memory — long-term potentiation in the hippocampus. Nature. 1993;361:31–39. doi: 10.1038/361031a0. [DOI] [PubMed] [Google Scholar]
2.Martin SJ, Grimwood PD, Morris RGM. Synaptic plasticity and memory: an evaluation of the hypothesis. Annu. Rev. Neurosci. 2000;23:649–711. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]
3.Barbour B, Brunel N, Hakim V, Nadal JP. What can we learn from synaptic weight distributions? Trends Neurosci. 2007;30:622–629. doi: 10.1016/j.tins.2007.09.005. [DOI] [PubMed] [Google Scholar]
4.Neves G, Cooke SF, Bliss TV. Synaptic plasticity, memory and the hippocampus: a neural network approach to causality. Nat. Rev. Neurosci. 2008;9:65–75. doi: 10.1038/nrn2303. [DOI] [PubMed] [Google Scholar]
5.Mayford, M., Siegelbaum, S. A. & Kandel, E. R. Synapses and memory storage. Cold Spring Harb. Perspect. Biol.4, a005751, 1–18 (2012). [DOI] [PMC free article] [PubMed]
6.Caroni P, Donato F, Muller D. Structural plasticity upon learning: regulation and functions. Nat. Rev. Neurosci. 2012;13:478–490. doi: 10.1038/nrn3258. [DOI] [PubMed] [Google Scholar]
7.Malenka RC, Nicoll RA. Long-term potentiation-a decade of progress? Science. 1999;285:1870–1874. doi: 10.1126/science.285.5435.1870. [DOI] [PubMed] [Google Scholar]
8.Collingridge GL, Peineau S, Howland JG, Wang YT. Long-term depression in the CNS. Nat. Rev. Neurosci. 2010;11:459–473. doi: 10.1038/nrn2867. [DOI] [PubMed] [Google Scholar]
9.van Rossum MC, Bi GQ, Turrigiano GG. Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 2000;20:8812–8821. doi: 10.1523/JNEUROSCI.20-23-08812.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Bi G, Poo M. Synaptic modification by correlated activity: Hebb’s postulate revisited. Annu. Rev. Neurosci. 2001;24:139–166. doi: 10.1146/annurev.neuro.24.1.139. [DOI] [PubMed] [Google Scholar]
11.Teramae J-n, Fukai T. Computational implications of lognormally distributed synaptic weights. Proc. IEEE. 2014;102:500–512. doi: 10.1109/JPROC.2014.2306254. [DOI] [Google Scholar]
12.Lee KJ, et al. Motor skill training induces coordinated strengthening and weakening between neighboring synapses. J. Neurosci. 2013;33:9794–9799. doi: 10.1523/JNEUROSCI.0848-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Brunel N, Hakim V, Isope P, Nadal JP, Barbour B. Optimal information storage and the distribution of synaptic weights: perceptron versus purkinje cell. Neuron. 2004;43:745–757. doi: 10.1016/j.neuron.2004.08.023. [DOI] [PubMed] [Google Scholar]
14.Behabadi BF, Mel BW. Mechanisms underlying subunit independence in pyramidal neuron dendrites. Proc. Natl. Acad. Sci. USA. 2014;111:498–503. doi: 10.1073/pnas.1217645111. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Takahashi N, et al. Locally synchronized synaptic inputs. Science. 2012;335:353–356. doi: 10.1126/science.1210362. [DOI] [PubMed] [Google Scholar]
16.Branco T, Hausser M. Synaptic integration gradients in single cortical pyramidal cell dendrites. Neuron. 2011;69:885–892. doi: 10.1016/j.neuron.2011.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Branco T, Clark BA, Hausser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science. 2010;329:1671–1675. doi: 10.1126/science.1189664. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Gasparini S, Magee JC. State-dependent dendritic computation in hippocampal CA1 pyramidal neurons. J. Neurosci. 2006;26:2088–2100. doi: 10.1523/JNEUROSCI.4428-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Polsky A, Mel BW, Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nat. Neurosci. 2004;7:621–627. doi: 10.1038/nn1253. [DOI] [PubMed] [Google Scholar]
20.Liu G. Local structural balance and functional interaction of excitatory and inhibitory synapses in hippocampal dendrites. Nat. Neurosci. 2004;7:373–379. doi: 10.1038/nn1206. [DOI] [PubMed] [Google Scholar]
21.Spruston N. Pyramidal neurons: dendritic structure and synaptic integration. Nat. Rev. Neurosci. 2008;9:206–221. doi: 10.1038/nrn2286. [DOI] [PubMed] [Google Scholar]
22.Govindarajan A, Israely I, Huang SY, Tonegawa S. The dendritic branch is the preferred integrative unit for protein synthesis-dependent LTP. Neuron. 2011;69:132–146. doi: 10.1016/j.neuron.2010.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452:436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]
24.Harvey CD, Svoboda K. Locally dynamic synaptic learning rules in pyramidal neuron dendrites. Nature. 2007;450:1195–1200. doi: 10.1038/nature06416. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Major G, Larkum ME, Schiller J. Active properties of neocortical pyramidal neuron dendrites. Annu. Rev. Neurosci. 2013;36:1–24. doi: 10.1146/annurev-neuro-062111-150343. [DOI] [PubMed] [Google Scholar]
26.London M, Hausser M. Dendritic computation. Annu. Rev. Neurosci. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
27.Smith SL, Smith IT, Branco T, Hausser M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature. 2013;503:115–120. doi: 10.1038/nature12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Grillo FW, et al. A distance-dependent distribution of presynaptic boutons tunes frequency-dependent dendritic integration. Neuron. 2018;99:275–282.e273. doi: 10.1016/j.neuron.2018.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Yang G, et al. Sleep promotes branch-specific formation of dendritic spines after learning. Science. 2014;344:1173–1178. doi: 10.1126/science.1249098. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Lavzin M, Rapoport S, Polsky A, Garion L, Schiller J. Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature. 2012;490:397–401. doi: 10.1038/nature11451. [DOI] [PubMed] [Google Scholar]
31.Xu NL, et al. Nonlinear dendritic integration of sensory and motor input during an active sensing task. Nature. 2012;492:247–251. doi: 10.1038/nature11601. [DOI] [PubMed] [Google Scholar]
32.Cichon J, Gan WB. Branch-specific dendritic Ca2+ spikes cause persistent synaptic plasticity. Nature. 2015;520:180–185. doi: 10.1038/nature14251. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Dumitriu D, et al. Selective changes in thin spine density and morphology in monkey prefrontal cortex correlate with aging-related cognitive impairment. J. Neurosci. 2010;30:7507–7515. doi: 10.1523/JNEUROSCI.6410-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Peters A, Sethares C, Luebke JI. Synapses are lost during aging in the primate prefrontal cortex. Neuroscience. 2008;152:970–981. doi: 10.1016/j.neuroscience.2007.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Scheff SW, Price DA, Schmitt FA, Mufson EJ. Hippocampal synaptic loss in early Alzheimer’s disease and mild cognitive impairment. Neurobiol. Aging. 2006;27:1372–1384. doi: 10.1016/j.neurobiolaging.2005.09.012. [DOI] [PubMed] [Google Scholar]
36.Selkoe DJ. Alzheimer’s disease is a synaptic failure. Science. 2002;298:789–791. doi: 10.1126/science.1074069. [DOI] [PubMed] [Google Scholar]
37.Morrison JH, Baxter MG. The ageing cortical synapse: hallmarks and implications for cognitive decline. Nat. Rev. Neurosci. 2012;13:240–250. doi: 10.1038/nrn3200. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Zhou, H. & Liu, G. Regulation of density of functional presynaptic terminals by local energy supply. Mol. Brain17, 42, 1–21 (2015). [DOI] [PMC free article] [PubMed]
39.Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci. 2001;2:539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Lisman JE. Bursts as a unit of neural information: making unreliable synapses reliable. Trends Neurosci. 1997;20:38–43. doi: 10.1016/S0166-2236(96)10070-9. [DOI] [PubMed] [Google Scholar]
41.Buzsaki G, Horvath Z, Urioste R, Hetke J, Wise K. High-frequency network oscillation in the hippocampus. Science. 1992;256:1025–1027. doi: 10.1126/science.1589772. [DOI] [PubMed] [Google Scholar]
42.Jones MW, Wilson MA. Theta rhythms coordinate hippocampal-prefrontal interactions in a spatial memory task. PLoS Biol. 2005;3:e402. doi: 10.1371/journal.pbio.0030402. [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Colgin LL, et al. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
44.Singer W. Synchronization of cortical activity and its putative role in information processing and learning. Annu. Rev. Physiol. 1993;55:349–374. doi: 10.1146/annurev.ph.55.030193.002025. [DOI] [PubMed] [Google Scholar]
45.Izhikevich EM, Desai NS, Walcott EC, Hoppensteadt FC. Bursts as a unit of neural information: selective communication via resonance. Trend. Neurosci. 2003;26:161–167. doi: 10.1016/S0166-2236(03)00034-1. [DOI] [PubMed] [Google Scholar]
46.O’Keefe J. Place units in the hippocampus of the freely moving rat. Exp. Neurol. 1976;51:78–109. doi: 10.1016/0014-4886(76)90055-8. [DOI] [PubMed] [Google Scholar]
47.Harris KD, Hirase H, Leinekugel X, Henze DA, Buzsaki G. Temporal interaction between single spikes and complex spike bursts in hippocampal pyramidal cells. Neuron. 2001;32:141–149. doi: 10.1016/S0896-6273(01)00447-0. [DOI] [PubMed] [Google Scholar]
48.Ranck JB., Jr. Studies on single neurons in dorsal hippocampal formation and septum in unrestrained rats. I. Behavioral correlates and firing repertoires. Exp. Neurol. 1973;41:461–531. doi: 10.1016/0014-4886(73)90290-2. [DOI] [PubMed] [Google Scholar]
49.Buzsaki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/S0896-6273(02)00586-X. [DOI] [PubMed] [Google Scholar]
50.Larson J, Wong D, Lynch G. Patterned stimulation at the theta frequency is optimal for the induction of hippocampal long-term potentiation. Brain Res. 1986;368:347–350. doi: 10.1016/0006-8993(86)90579-2. [DOI] [PubMed] [Google Scholar]
51.Otto T, Eichenbaum H, Wiener SI, Wible CG. Learning-related patterns of CA1 spike trains parallel stimulation parameters optimal for inducing hippocampal long-term potentiation. Hippocampus. 1991;1:181–192. doi: 10.1002/hipo.450010206. [DOI] [PubMed] [Google Scholar]
52.Gainey MA, Hurvitz-Wolff JR, Lambo ME, Turrigiano GG. Synaptic scaling requires the GluR2 subunit of the AMPA receptor. J. Neurosci. 2009;29:6479–6489. doi: 10.1523/JNEUROSCI.3753-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Meng Y, Zhang Y, Jia Z. Synaptic transmission and plasticity in the absence of AMPA glutamate receptor GluR2 and GluR3. Neuron. 2003;39:163–176. doi: 10.1016/S0896-6273(03)00368-4. [DOI] [PubMed] [Google Scholar]
54.Duprat F, Daw M, Lim W, Collingridge G, Isaac J. GluR2 protein-protein interactions and the regulation of AMPA receptors during synaptic plasticity. Philos. T. Roy. Soc. B. 2003;358:715–720. doi: 10.1098/rstb.2002.1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Chen L, et al. Stargazin regulates synaptic targeting of AMPA receptors by two distinct mechanisms. Nature. 2000;408:936–943. doi: 10.1038/35050030. [DOI] [PubMed] [Google Scholar]
56.Kennedy MB. Signal-processing machines at the postsynaptic density. Science. 2000;290:750–754. doi: 10.1126/science.290.5492.750. [DOI] [PubMed] [Google Scholar]
57.Beique JC, et al. Synapse-specific regulation of AMPA receptor function by PSD-95. Proc. Natl. Acad. Sci. USA. 2006;103:19535–19540. doi: 10.1073/pnas.0608492103. [DOI] [PMC free article] [PubMed] [Google Scholar]
58.Chen XB, et al. PSD-95 family MAGUKs are essential for anchoring AMPA and NMDA receptor complexes at the postsynaptic density. Proc. Natl. Acad. Sci. USA. 2015;112:E6983–E6992. doi: 10.1073/pnas.1517045112. [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Sabatini BL, Oertner TG, Svoboda K. The life cycle of Ca2+ ions in dendritic spines. Neuron. 2002;33:439–452. doi: 10.1016/S0896-6273(02)00573-1. [DOI] [PubMed] [Google Scholar]
60.Schiller J, Major G, Koester HJ, Schiller Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature. 2000;404:285–289. doi: 10.1038/35005094. [DOI] [PubMed] [Google Scholar]
61.Luo JH, et al. Functional expression of distinct NMDA channel subunits tagged with green fluorescent protein in hippocampal neurons in culture. Neuropharmacology. 2002;42:306–318. doi: 10.1016/S0028-3908(01)00188-5. [DOI] [PubMed] [Google Scholar]
62.Collingridge GL, Isaac JT, Wang YT. Receptor trafficking and synaptic plasticity. Nat. Rev. Neurosci. 2004;5:952–962. doi: 10.1038/nrn1556. [DOI] [PubMed] [Google Scholar]
63.Liu L, et al. Role of NMDA receptor subtypes in governing the direction of hippocampal synaptic plasticity. Science. 2004;304:1021–1024. doi: 10.1126/science.1096615. [DOI] [PubMed] [Google Scholar]
64.Zhao MG, et al. Roles of NMDA NR2B subtype receptor in prefrontal long-term potentiation and contextual fear memory. Neuron. 2005;47:859–872. doi: 10.1016/j.neuron.2005.08.014. [DOI] [PubMed] [Google Scholar]
65.Shipton OA, Paulsen O. GluN2A and GluN2B subunit-containing NMDA receptors in hippocampal plasticity. Philos. Trans. R Soc. Lond. B Biol. Sci. 2014;369:20130163. doi: 10.1098/rstb.2013.0163. [DOI] [PMC free article] [PubMed] [Google Scholar]
66.Guther T, Vormann J, Forster R. Regulation of intracellular magnesium by Mg2+ efflux. Biochem. Biophys. Res. Commun. 1984;119:124–131. doi: 10.1016/0006-291X(84)91627-9. [DOI] [PubMed] [Google Scholar]
67.Neher E, Sakaba T. Multiple roles of calcium ions in the regulation of neurotransmitter release. Neuron. 2008;59:861–872. doi: 10.1016/j.neuron.2008.08.019. [DOI] [PubMed] [Google Scholar]
68.Chen TW, et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature. 2013;499:295–300. doi: 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
69.Dreosti E, Odermatt B, Dorostkar MM, Lagnado L. A genetically encoded reporter of synaptic activity in vivo. Nat. Methods. 2009;6:883–889. doi: 10.1038/nmeth.1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
70.Sudhof TC. The presynaptic active zone. Neuron. 2012;75:11–25. doi: 10.1016/j.neuron.2012.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
71.Sudhof TC. Neurotransmitter release: the last millisecond in the life of a synaptic vesicle. Neuron. 2013;80:675–690. doi: 10.1016/j.neuron.2013.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
72.Murthy VN, Sejnowski TJ, Stevens CF. Heterogeneous release properties of visualized individual hippocampal synapses. Neuron. 1997;18:599–612. doi: 10.1016/S0896-6273(00)80301-3. [DOI] [PubMed] [Google Scholar]
73.Murthy VN, Schikorski T, Stevens CF, Zhu Y. Inactivity produces increases in neurotransmitter release and synapse size. Neuron. 2001;32:673–682. doi: 10.1016/S0896-6273(01)00500-1. [DOI] [PubMed] [Google Scholar]
74.Awatramani GB, Price GD, Trussell LO. Modulation of transmitter release by presynaptic resting potential and background calcium levels. Neuron. 2005;48:109–121. doi: 10.1016/j.neuron.2005.08.038. [DOI] [PubMed] [Google Scholar]
75.Corlew R, Brasier DJ, Feldman DE, Philpot BD. Presynaptic NMDA receptors: newly appreciated roles in cortical synaptic function and plasticity. Neuroscientist. 2008;14:609–625. doi: 10.1177/1073858408322675. [DOI] [PMC free article] [PubMed] [Google Scholar]
76.Stellwagen D, Malenka RC. Synaptic scaling mediated by glial TNF-alpha. Nature. 2006;440:1054–1059. doi: 10.1038/nature04671. [DOI] [PubMed] [Google Scholar]
77.Futai K, et al. Retrograde modulation of presynaptic release probability through signaling mediated by PSD-95-neuroligin. Nat. Neurosci. 2007;10:186–195. doi: 10.1038/nn1837. [DOI] [PMC free article] [PubMed] [Google Scholar]
78.Holler S, Kostinger G, Martin KAC, Schuhknecht GFP, Stratford KJ. Structure and function of a neocortical synapse. Nature. 2021;591:111–116. doi: 10.1038/s41586-020-03134-2. [DOI] [PubMed] [Google Scholar]
79.Nusser Z, et al. Cell type and pathway dependence of synaptic AMPA receptor number and variability in the hippocampus. Neuron. 1998;21:545–559. doi: 10.1016/S0896-6273(00)80565-6. [DOI] [PubMed] [Google Scholar]
80.Kharazia VN, Weinberg RJ. Immunogold localization of AMPA and NMDA receptors in somatic sensory cortex of albino rat. J. Comp. Neurol. 1999;412:292–302. doi: 10.1002/(SICI)1096-9861(19990920)412:2<292::AID-CNE8>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
81.Schikorski T, Stevens CF. Quantitative ultrastructural analysis of hippocampal excitatory synapses. J. Neurosci. 1997;17:5858–5867. doi: 10.1523/JNEUROSCI.17-15-05858.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
82.Holderith, N. et al. Release probability of hippocampal glutamatergic terminals scales with the size of the active zone. Nat. Neurosci.10, 988–997 (2012). [DOI] [PMC free article] [PubMed]
83.Slutsky I, et al. Enhancement of learning and memory by elevating brain magnesium. Neuron. 2010;65:165–177. doi: 10.1016/j.neuron.2009.12.026. [DOI] [PubMed] [Google Scholar]
84.Davis GW, Muller M. Homeostatic control of presynaptic neurotransmitter release. Annu. Rev. Physiol. 2015;77:251–270. doi: 10.1146/annurev-physiol-021014-071740. [DOI] [PubMed] [Google Scholar]
85.Liu G, Tsien RW. Properties of synaptic transmission at single hippocampal synaptic boutons. Nature. 1995;375:404–408. doi: 10.1038/375404a0. [DOI] [PubMed] [Google Scholar]
86.Branco T, Staras K, Darcy KJ, Goda Y. Local dendritic activity sets release probability at hippocampal synapses. Neuron. 2008;59:475–485. doi: 10.1016/j.neuron.2008.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
87.Davis GW, Goodman CS. Synapse-specific control of synaptic efficacy at the terminals of a single neuron. Nature. 1998;392:82–86. doi: 10.1038/32176. [DOI] [PubMed] [Google Scholar]
88.Bloss EB, et al. Single excitatory axons form clustered synapses onto CA1 pyramidal cell dendrites. Nat. Neurosci. 2018;21:353–363. doi: 10.1038/s41593-018-0084-6. [DOI] [PubMed] [Google Scholar]
89.Scholl B, Wilson DE, Fitzpatrick D. Local order within global disorder: synaptic architecture of visual space. Neuron. 2017;96:1127–1138.e1124. doi: 10.1016/j.neuron.2017.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
90.Li W, Ma L, Yang G, Gan WB. REM sleep selectively prunes and maintains new synapses in development and learning. Nat. Neurosci. 2017;20:427–437. doi: 10.1038/nn.4479. [DOI] [PMC free article] [PubMed] [Google Scholar]
91.Cossell L, et al. Functional organization of excitatory synaptic strength in primary visual cortex. Nature. 2015;518:399–403. doi: 10.1038/nature14182. [DOI] [PMC free article] [PubMed] [Google Scholar]
92.Iacaruso MF, Gasler IT, Hofer SB. Synaptic organization of visual space in primary visual cortex. Nature. 2017;547:449–452. doi: 10.1038/nature23019. [DOI] [PMC free article] [PubMed] [Google Scholar]
93.Lee WC, et al. Anatomy and function of an excitatory network in the visual cortex. Nature. 2016;532:370–374. doi: 10.1038/nature17192. [DOI] [PMC free article] [PubMed] [Google Scholar]
94.Hayashi-Takagi A, et al. Labelling and optical erasure of synaptic memory traces in the motor cortex. Nature. 2015;525:333–338. doi: 10.1038/nature15257. [DOI] [PMC free article] [PubMed] [Google Scholar]
95.Hwang FJ, et al. Motor learning selectively strengthens cortical and striatal synapses of motor engram neurons. Neuron. 2022;110:2790–2801.e2795. doi: 10.1016/j.neuron.2022.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
96.Xu T, et al. Rapid formation and selective stabilization of synapses for enduring motor memories. Nature. 2009;462:915–919. doi: 10.1038/nature08389. [DOI] [PMC free article] [PubMed] [Google Scholar]
97.Choi J-H, et al. Interregional synaptic maps among engram cells underlie memory formation. Science. 2018;360:430–435. doi: 10.1126/science.aas9204. [DOI] [PubMed] [Google Scholar]
98.Chater TE, Goda Y. My neighbour hetero-deconstructing the mechanisms underlying heterosynaptic plasticity. Curr. Opin. Neurobiol. 2021;67:106–114. doi: 10.1016/j.conb.2020.10.007. [DOI] [PubMed] [Google Scholar]
99.Royer S, Pare D. Conservation of total synaptic weight through balanced synaptic depression and potentiation. Nature. 2003;422:518–522. doi: 10.1038/nature01530. [DOI] [PubMed] [Google Scholar]
100.Tong R, Chater TE, Emptage NJ, Goda Y. Heterosynaptic cross-talk of pre- and postsynaptic strengths along segments of dendrites. Cell Rep. 2021;34:108693. doi: 10.1016/j.celrep.2021.108693. [DOI] [PubMed] [Google Scholar]
101.El-Boustani S, et al. Locally coordinated synaptic plasticity of visual cortex neurons in vivo. Science. 2018;360:1349–1354. doi: 10.1126/science.aao0862. [DOI] [PMC free article] [PubMed] [Google Scholar]
102.Shannon CE. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27:623. doi: 10.1002/j.1538-7305.1948.tb00917.x. [DOI] [Google Scholar]
103.Mitra A, Mitra SS, Tsien RW. Heterogeneous reallocation of presynaptic efficacy in recurrent excitatory circuits adapting to inactivity. Nat. Neurosci. 2012;15:250–257. doi: 10.1038/nn.3004. [DOI] [PMC free article] [PubMed] [Google Scholar]
104.Gruget C, et al. Rearrangements under confinement lead to increased binding energy of synaptotagmin-1 with anionic membranes in Mg2+ and Ca2+ FEBS Lett. 2018;592:1497–1506. doi: 10.1002/1873-3468.13040. [DOI] [PubMed] [Google Scholar]
105.Grushin K, et al. Structural basis for the clamping and Ca2+ activation of SNARE-mediated fusion by synaptotagmin. Nat. Commun. 2019;10:2413. doi: 10.1038/s41467-019-10391-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
106.Delvendahl I, et al. Reduced endogenous Ca2+ buffering speeds active zone Ca2+ signaling. Proc. Natl. Acad. Sci. USA. 2015;112:E3075–E3084. doi: 10.1073/pnas.1508419112. [DOI] [PMC free article] [PubMed] [Google Scholar]
107.Liu G, Weinger JG, Lu ZL, Xue F, Sadeghpour S. Efficacy and safety of MMFS-01, a synapse density enhancer, for treating cognitive impairment in older adults: a randomized, double-blind, placebo-controlled trial. J. Alzheimer’s Dis. 2016;49:971–990. doi: 10.3233/JAD-150538. [DOI] [PMC free article] [PubMed] [Google Scholar]
108.Weinger JG, Liu G. [P4–001]: MMFS treatment ameliorates frontal cortex dysfunction in mild-moderate Alzheimer’s disease patients. Alzheimer’s Dement. 2017;13:P1253–P1253. doi: 10.1016/j.jalz.2017.06.1865. [DOI] [Google Scholar]
109.Wroolie TE, et al. Open label trial of magnesium L-theronate in patient with dementia. Innov. Aging. 2017;1:170–170. doi: 10.1093/geroni/igx004.661. [DOI] [Google Scholar]
110.Surman C, et al. L-threonic acid magnesium salt supplementation in ADHD: an open-label pilot study. J. Diet. Suppl. 2021;18:119–131. doi: 10.1080/19390211.2020.1731044. [DOI] [PubMed] [Google Scholar]
111.Slutsky I, Sadeghpour S, Li B, Liu G. Enhancement of synaptic plasticity through chronically reduced Ca2+ flux during uncorrelated activity. Neuron. 2004;44:835–849. doi: 10.1016/j.neuron.2004.11.013. [DOI] [PubMed] [Google Scholar]
112.Giovannucci, A. et al. CaImAn an open source tool for scalable calcium imaging data analysis. Elife8, e38173, 1–45 (2019). [DOI] [PMC free article] [PubMed]
113.Murthy VN, Stevens CF. Reversal of synaptic vesicle docking at central synapses. Nat. Neurosci. 1999;2:503–507. doi: 10.1038/9149. [DOI] [PubMed] [Google Scholar]
114.Jiang M, Chen G. High Ca2+-phosphate transfection efficiency in low-density neuronal cultures. Nat. Protoc. 2006;1:695–700. doi: 10.1038/nprot.2006.86. [DOI] [PubMed] [Google Scholar]
115.Thevenaz P, Ruttimann UE, Unser M. A pyramid approach to subpixel registration based on intensity. IEEE T. Image Process. 1998;7:27–41. doi: 10.1109/83.650848. [DOI] [PubMed] [Google Scholar]
116.Sorzano COS, Thevenaz P, Unser M. Elastic registration of biological images using vector-spline regularization. IEEE T. Bio. Med. Eng. 2005;52:652–663. doi: 10.1109/TBME.2005.844030. [DOI] [PubMed] [Google Scholar]
117.Cardona A, et al. TrakEM2 software for neural circuit reconstruction. Plos One. 2012;7:e38011. doi: 10.1371/journal.pone.0038011. [DOI] [PMC free article] [PubMed] [Google Scholar]
118.Ofer N, Berger DR, Kasthuri N, Lichtman JW, Yuste R. Ultrastructural analysis of dendritic spine necks reveals a continuum of spine morphologies. Dev. Neurobiol. 2021;81:746–757. doi: 10.1002/dneu.22829. [DOI] [PMC free article] [PubMed] [Google Scholar]
119.Arellano JI, Benavides-Piccione R, Defelipe J, Yuste R. Ultrastructure of dendritic spines: correlation between synaptic and spine morphologies. Front. Neurosci. 2007;1:131–143. doi: 10.3389/neuro.01.1.1.010.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information^{(8.4MB, pdf)}

Peer Review File^{(7.6MB, pdf)}

Reporting Summary^{(2.5MB, pdf)}

Source Data^{(414.4KB, xlsx)}

Data Availability Statement

All data are available in the main text or the supplementary materials. Source data are provided with this paper.

The codes used in this study are open-source and accessible online. github.com/flatironinstitute/CaImAn.

[CR1] 1.Bliss TVP, Collingridge GL. A synaptic model of memory — long-term potentiation in the hippocampus. Nature. 1993;361:31–39. doi: 10.1038/361031a0. [DOI] [PubMed] [Google Scholar]

[CR2] 2.Martin SJ, Grimwood PD, Morris RGM. Synaptic plasticity and memory: an evaluation of the hypothesis. Annu. Rev. Neurosci. 2000;23:649–711. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]

[CR3] 3.Barbour B, Brunel N, Hakim V, Nadal JP. What can we learn from synaptic weight distributions? Trends Neurosci. 2007;30:622–629. doi: 10.1016/j.tins.2007.09.005. [DOI] [PubMed] [Google Scholar]

[CR4] 4.Neves G, Cooke SF, Bliss TV. Synaptic plasticity, memory and the hippocampus: a neural network approach to causality. Nat. Rev. Neurosci. 2008;9:65–75. doi: 10.1038/nrn2303. [DOI] [PubMed] [Google Scholar]

[CR5] 5.Mayford, M., Siegelbaum, S. A. & Kandel, E. R. Synapses and memory storage. Cold Spring Harb. Perspect. Biol.4, a005751, 1–18 (2012). [DOI] [PMC free article] [PubMed]

[CR6] 6.Caroni P, Donato F, Muller D. Structural plasticity upon learning: regulation and functions. Nat. Rev. Neurosci. 2012;13:478–490. doi: 10.1038/nrn3258. [DOI] [PubMed] [Google Scholar]

[CR7] 7.Malenka RC, Nicoll RA. Long-term potentiation-a decade of progress? Science. 1999;285:1870–1874. doi: 10.1126/science.285.5435.1870. [DOI] [PubMed] [Google Scholar]

[CR8] 8.Collingridge GL, Peineau S, Howland JG, Wang YT. Long-term depression in the CNS. Nat. Rev. Neurosci. 2010;11:459–473. doi: 10.1038/nrn2867. [DOI] [PubMed] [Google Scholar]

[CR9] 9.van Rossum MC, Bi GQ, Turrigiano GG. Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 2000;20:8812–8821. doi: 10.1523/JNEUROSCI.20-23-08812.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR10] 10.Bi G, Poo M. Synaptic modification by correlated activity: Hebb’s postulate revisited. Annu. Rev. Neurosci. 2001;24:139–166. doi: 10.1146/annurev.neuro.24.1.139. [DOI] [PubMed] [Google Scholar]

[CR11] 11.Teramae J-n, Fukai T. Computational implications of lognormally distributed synaptic weights. Proc. IEEE. 2014;102:500–512. doi: 10.1109/JPROC.2014.2306254. [DOI] [Google Scholar]

[CR12] 12.Lee KJ, et al. Motor skill training induces coordinated strengthening and weakening between neighboring synapses. J. Neurosci. 2013;33:9794–9799. doi: 10.1523/JNEUROSCI.0848-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR13] 13.Brunel N, Hakim V, Isope P, Nadal JP, Barbour B. Optimal information storage and the distribution of synaptic weights: perceptron versus purkinje cell. Neuron. 2004;43:745–757. doi: 10.1016/j.neuron.2004.08.023. [DOI] [PubMed] [Google Scholar]

[CR14] 14.Behabadi BF, Mel BW. Mechanisms underlying subunit independence in pyramidal neuron dendrites. Proc. Natl. Acad. Sci. USA. 2014;111:498–503. doi: 10.1073/pnas.1217645111. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR15] 15.Takahashi N, et al. Locally synchronized synaptic inputs. Science. 2012;335:353–356. doi: 10.1126/science.1210362. [DOI] [PubMed] [Google Scholar]

[CR16] 16.Branco T, Hausser M. Synaptic integration gradients in single cortical pyramidal cell dendrites. Neuron. 2011;69:885–892. doi: 10.1016/j.neuron.2011.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR17] 17.Branco T, Clark BA, Hausser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science. 2010;329:1671–1675. doi: 10.1126/science.1189664. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR18] 18.Gasparini S, Magee JC. State-dependent dendritic computation in hippocampal CA1 pyramidal neurons. J. Neurosci. 2006;26:2088–2100. doi: 10.1523/JNEUROSCI.4428-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR19] 19.Polsky A, Mel BW, Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nat. Neurosci. 2004;7:621–627. doi: 10.1038/nn1253. [DOI] [PubMed] [Google Scholar]

[CR20] 20.Liu G. Local structural balance and functional interaction of excitatory and inhibitory synapses in hippocampal dendrites. Nat. Neurosci. 2004;7:373–379. doi: 10.1038/nn1206. [DOI] [PubMed] [Google Scholar]

[CR21] 21.Spruston N. Pyramidal neurons: dendritic structure and synaptic integration. Nat. Rev. Neurosci. 2008;9:206–221. doi: 10.1038/nrn2286. [DOI] [PubMed] [Google Scholar]

[CR22] 22.Govindarajan A, Israely I, Huang SY, Tonegawa S. The dendritic branch is the preferred integrative unit for protein synthesis-dependent LTP. Neuron. 2011;69:132–146. doi: 10.1016/j.neuron.2010.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR23] 23.Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452:436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]

[CR24] 24.Harvey CD, Svoboda K. Locally dynamic synaptic learning rules in pyramidal neuron dendrites. Nature. 2007;450:1195–1200. doi: 10.1038/nature06416. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR25] 25.Major G, Larkum ME, Schiller J. Active properties of neocortical pyramidal neuron dendrites. Annu. Rev. Neurosci. 2013;36:1–24. doi: 10.1146/annurev-neuro-062111-150343. [DOI] [PubMed] [Google Scholar]

[CR26] 26.London M, Hausser M. Dendritic computation. Annu. Rev. Neurosci. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]

[CR27] 27.Smith SL, Smith IT, Branco T, Hausser M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature. 2013;503:115–120. doi: 10.1038/nature12600. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR28] 28.Grillo FW, et al. A distance-dependent distribution of presynaptic boutons tunes frequency-dependent dendritic integration. Neuron. 2018;99:275–282.e273. doi: 10.1016/j.neuron.2018.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR29] 29.Yang G, et al. Sleep promotes branch-specific formation of dendritic spines after learning. Science. 2014;344:1173–1178. doi: 10.1126/science.1249098. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR30] 30.Lavzin M, Rapoport S, Polsky A, Garion L, Schiller J. Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature. 2012;490:397–401. doi: 10.1038/nature11451. [DOI] [PubMed] [Google Scholar]

[CR31] 31.Xu NL, et al. Nonlinear dendritic integration of sensory and motor input during an active sensing task. Nature. 2012;492:247–251. doi: 10.1038/nature11601. [DOI] [PubMed] [Google Scholar]

[CR32] 32.Cichon J, Gan WB. Branch-specific dendritic Ca2+ spikes cause persistent synaptic plasticity. Nature. 2015;520:180–185. doi: 10.1038/nature14251. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR33] 33.Dumitriu D, et al. Selective changes in thin spine density and morphology in monkey prefrontal cortex correlate with aging-related cognitive impairment. J. Neurosci. 2010;30:7507–7515. doi: 10.1523/JNEUROSCI.6410-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR34] 34.Peters A, Sethares C, Luebke JI. Synapses are lost during aging in the primate prefrontal cortex. Neuroscience. 2008;152:970–981. doi: 10.1016/j.neuroscience.2007.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR35] 35.Scheff SW, Price DA, Schmitt FA, Mufson EJ. Hippocampal synaptic loss in early Alzheimer’s disease and mild cognitive impairment. Neurobiol. Aging. 2006;27:1372–1384. doi: 10.1016/j.neurobiolaging.2005.09.012. [DOI] [PubMed] [Google Scholar]

[CR36] 36.Selkoe DJ. Alzheimer’s disease is a synaptic failure. Science. 2002;298:789–791. doi: 10.1126/science.1074069. [DOI] [PubMed] [Google Scholar]

[CR37] 37.Morrison JH, Baxter MG. The ageing cortical synapse: hallmarks and implications for cognitive decline. Nat. Rev. Neurosci. 2012;13:240–250. doi: 10.1038/nrn3200. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR38] 38.Zhou, H. & Liu, G. Regulation of density of functional presynaptic terminals by local energy supply. Mol. Brain17, 42, 1–21 (2015). [DOI] [PMC free article] [PubMed]

[CR39] 39.Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci. 2001;2:539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR40] 40.Lisman JE. Bursts as a unit of neural information: making unreliable synapses reliable. Trends Neurosci. 1997;20:38–43. doi: 10.1016/S0166-2236(96)10070-9. [DOI] [PubMed] [Google Scholar]

[CR41] 41.Buzsaki G, Horvath Z, Urioste R, Hetke J, Wise K. High-frequency network oscillation in the hippocampus. Science. 1992;256:1025–1027. doi: 10.1126/science.1589772. [DOI] [PubMed] [Google Scholar]

[CR42] 42.Jones MW, Wilson MA. Theta rhythms coordinate hippocampal-prefrontal interactions in a spatial memory task. PLoS Biol. 2005;3:e402. doi: 10.1371/journal.pbio.0030402. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR43] 43.Colgin LL, et al. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]

[CR44] 44.Singer W. Synchronization of cortical activity and its putative role in information processing and learning. Annu. Rev. Physiol. 1993;55:349–374. doi: 10.1146/annurev.ph.55.030193.002025. [DOI] [PubMed] [Google Scholar]

[CR45] 45.Izhikevich EM, Desai NS, Walcott EC, Hoppensteadt FC. Bursts as a unit of neural information: selective communication via resonance. Trend. Neurosci. 2003;26:161–167. doi: 10.1016/S0166-2236(03)00034-1. [DOI] [PubMed] [Google Scholar]

[CR46] 46.O’Keefe J. Place units in the hippocampus of the freely moving rat. Exp. Neurol. 1976;51:78–109. doi: 10.1016/0014-4886(76)90055-8. [DOI] [PubMed] [Google Scholar]

[CR47] 47.Harris KD, Hirase H, Leinekugel X, Henze DA, Buzsaki G. Temporal interaction between single spikes and complex spike bursts in hippocampal pyramidal cells. Neuron. 2001;32:141–149. doi: 10.1016/S0896-6273(01)00447-0. [DOI] [PubMed] [Google Scholar]

[CR48] 48.Ranck JB., Jr. Studies on single neurons in dorsal hippocampal formation and septum in unrestrained rats. I. Behavioral correlates and firing repertoires. Exp. Neurol. 1973;41:461–531. doi: 10.1016/0014-4886(73)90290-2. [DOI] [PubMed] [Google Scholar]

[CR49] 49.Buzsaki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/S0896-6273(02)00586-X. [DOI] [PubMed] [Google Scholar]

[CR50] 50.Larson J, Wong D, Lynch G. Patterned stimulation at the theta frequency is optimal for the induction of hippocampal long-term potentiation. Brain Res. 1986;368:347–350. doi: 10.1016/0006-8993(86)90579-2. [DOI] [PubMed] [Google Scholar]

[CR51] 51.Otto T, Eichenbaum H, Wiener SI, Wible CG. Learning-related patterns of CA1 spike trains parallel stimulation parameters optimal for inducing hippocampal long-term potentiation. Hippocampus. 1991;1:181–192. doi: 10.1002/hipo.450010206. [DOI] [PubMed] [Google Scholar]

[CR52] 52.Gainey MA, Hurvitz-Wolff JR, Lambo ME, Turrigiano GG. Synaptic scaling requires the GluR2 subunit of the AMPA receptor. J. Neurosci. 2009;29:6479–6489. doi: 10.1523/JNEUROSCI.3753-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR53] 53.Meng Y, Zhang Y, Jia Z. Synaptic transmission and plasticity in the absence of AMPA glutamate receptor GluR2 and GluR3. Neuron. 2003;39:163–176. doi: 10.1016/S0896-6273(03)00368-4. [DOI] [PubMed] [Google Scholar]

[CR54] 54.Duprat F, Daw M, Lim W, Collingridge G, Isaac J. GluR2 protein-protein interactions and the regulation of AMPA receptors during synaptic plasticity. Philos. T. Roy. Soc. B. 2003;358:715–720. doi: 10.1098/rstb.2002.1215. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR55] 55.Chen L, et al. Stargazin regulates synaptic targeting of AMPA receptors by two distinct mechanisms. Nature. 2000;408:936–943. doi: 10.1038/35050030. [DOI] [PubMed] [Google Scholar]

[CR56] 56.Kennedy MB. Signal-processing machines at the postsynaptic density. Science. 2000;290:750–754. doi: 10.1126/science.290.5492.750. [DOI] [PubMed] [Google Scholar]

[CR57] 57.Beique JC, et al. Synapse-specific regulation of AMPA receptor function by PSD-95. Proc. Natl. Acad. Sci. USA. 2006;103:19535–19540. doi: 10.1073/pnas.0608492103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR58] 58.Chen XB, et al. PSD-95 family MAGUKs are essential for anchoring AMPA and NMDA receptor complexes at the postsynaptic density. Proc. Natl. Acad. Sci. USA. 2015;112:E6983–E6992. doi: 10.1073/pnas.1517045112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR59] 59.Sabatini BL, Oertner TG, Svoboda K. The life cycle of Ca2+ ions in dendritic spines. Neuron. 2002;33:439–452. doi: 10.1016/S0896-6273(02)00573-1. [DOI] [PubMed] [Google Scholar]

[CR60] 60.Schiller J, Major G, Koester HJ, Schiller Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature. 2000;404:285–289. doi: 10.1038/35005094. [DOI] [PubMed] [Google Scholar]

[CR61] 61.Luo JH, et al. Functional expression of distinct NMDA channel subunits tagged with green fluorescent protein in hippocampal neurons in culture. Neuropharmacology. 2002;42:306–318. doi: 10.1016/S0028-3908(01)00188-5. [DOI] [PubMed] [Google Scholar]

[CR62] 62.Collingridge GL, Isaac JT, Wang YT. Receptor trafficking and synaptic plasticity. Nat. Rev. Neurosci. 2004;5:952–962. doi: 10.1038/nrn1556. [DOI] [PubMed] [Google Scholar]

[CR63] 63.Liu L, et al. Role of NMDA receptor subtypes in governing the direction of hippocampal synaptic plasticity. Science. 2004;304:1021–1024. doi: 10.1126/science.1096615. [DOI] [PubMed] [Google Scholar]

[CR64] 64.Zhao MG, et al. Roles of NMDA NR2B subtype receptor in prefrontal long-term potentiation and contextual fear memory. Neuron. 2005;47:859–872. doi: 10.1016/j.neuron.2005.08.014. [DOI] [PubMed] [Google Scholar]

[CR65] 65.Shipton OA, Paulsen O. GluN2A and GluN2B subunit-containing NMDA receptors in hippocampal plasticity. Philos. Trans. R Soc. Lond. B Biol. Sci. 2014;369:20130163. doi: 10.1098/rstb.2013.0163. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR66] 66.Guther T, Vormann J, Forster R. Regulation of intracellular magnesium by Mg2+ efflux. Biochem. Biophys. Res. Commun. 1984;119:124–131. doi: 10.1016/0006-291X(84)91627-9. [DOI] [PubMed] [Google Scholar]

[CR67] 67.Neher E, Sakaba T. Multiple roles of calcium ions in the regulation of neurotransmitter release. Neuron. 2008;59:861–872. doi: 10.1016/j.neuron.2008.08.019. [DOI] [PubMed] [Google Scholar]

[CR68] 68.Chen TW, et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature. 2013;499:295–300. doi: 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR69] 69.Dreosti E, Odermatt B, Dorostkar MM, Lagnado L. A genetically encoded reporter of synaptic activity in vivo. Nat. Methods. 2009;6:883–889. doi: 10.1038/nmeth.1399. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR70] 70.Sudhof TC. The presynaptic active zone. Neuron. 2012;75:11–25. doi: 10.1016/j.neuron.2012.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR71] 71.Sudhof TC. Neurotransmitter release: the last millisecond in the life of a synaptic vesicle. Neuron. 2013;80:675–690. doi: 10.1016/j.neuron.2013.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR72] 72.Murthy VN, Sejnowski TJ, Stevens CF. Heterogeneous release properties of visualized individual hippocampal synapses. Neuron. 1997;18:599–612. doi: 10.1016/S0896-6273(00)80301-3. [DOI] [PubMed] [Google Scholar]

[CR73] 73.Murthy VN, Schikorski T, Stevens CF, Zhu Y. Inactivity produces increases in neurotransmitter release and synapse size. Neuron. 2001;32:673–682. doi: 10.1016/S0896-6273(01)00500-1. [DOI] [PubMed] [Google Scholar]

[CR74] 74.Awatramani GB, Price GD, Trussell LO. Modulation of transmitter release by presynaptic resting potential and background calcium levels. Neuron. 2005;48:109–121. doi: 10.1016/j.neuron.2005.08.038. [DOI] [PubMed] [Google Scholar]

[CR75] 75.Corlew R, Brasier DJ, Feldman DE, Philpot BD. Presynaptic NMDA receptors: newly appreciated roles in cortical synaptic function and plasticity. Neuroscientist. 2008;14:609–625. doi: 10.1177/1073858408322675. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR76] 76.Stellwagen D, Malenka RC. Synaptic scaling mediated by glial TNF-alpha. Nature. 2006;440:1054–1059. doi: 10.1038/nature04671. [DOI] [PubMed] [Google Scholar]

[CR77] 77.Futai K, et al. Retrograde modulation of presynaptic release probability through signaling mediated by PSD-95-neuroligin. Nat. Neurosci. 2007;10:186–195. doi: 10.1038/nn1837. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR78] 78.Holler S, Kostinger G, Martin KAC, Schuhknecht GFP, Stratford KJ. Structure and function of a neocortical synapse. Nature. 2021;591:111–116. doi: 10.1038/s41586-020-03134-2. [DOI] [PubMed] [Google Scholar]

[CR79] 79.Nusser Z, et al. Cell type and pathway dependence of synaptic AMPA receptor number and variability in the hippocampus. Neuron. 1998;21:545–559. doi: 10.1016/S0896-6273(00)80565-6. [DOI] [PubMed] [Google Scholar]

[CR80] 80.Kharazia VN, Weinberg RJ. Immunogold localization of AMPA and NMDA receptors in somatic sensory cortex of albino rat. J. Comp. Neurol. 1999;412:292–302. doi: 10.1002/(SICI)1096-9861(19990920)412:2<292::AID-CNE8>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]

[CR81] 81.Schikorski T, Stevens CF. Quantitative ultrastructural analysis of hippocampal excitatory synapses. J. Neurosci. 1997;17:5858–5867. doi: 10.1523/JNEUROSCI.17-15-05858.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR82] 82.Holderith, N. et al. Release probability of hippocampal glutamatergic terminals scales with the size of the active zone. Nat. Neurosci.10, 988–997 (2012). [DOI] [PMC free article] [PubMed]

[CR83] 83.Slutsky I, et al. Enhancement of learning and memory by elevating brain magnesium. Neuron. 2010;65:165–177. doi: 10.1016/j.neuron.2009.12.026. [DOI] [PubMed] [Google Scholar]

[CR84] 84.Davis GW, Muller M. Homeostatic control of presynaptic neurotransmitter release. Annu. Rev. Physiol. 2015;77:251–270. doi: 10.1146/annurev-physiol-021014-071740. [DOI] [PubMed] [Google Scholar]

[CR85] 85.Liu G, Tsien RW. Properties of synaptic transmission at single hippocampal synaptic boutons. Nature. 1995;375:404–408. doi: 10.1038/375404a0. [DOI] [PubMed] [Google Scholar]

[CR86] 86.Branco T, Staras K, Darcy KJ, Goda Y. Local dendritic activity sets release probability at hippocampal synapses. Neuron. 2008;59:475–485. doi: 10.1016/j.neuron.2008.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR87] 87.Davis GW, Goodman CS. Synapse-specific control of synaptic efficacy at the terminals of a single neuron. Nature. 1998;392:82–86. doi: 10.1038/32176. [DOI] [PubMed] [Google Scholar]

[CR88] 88.Bloss EB, et al. Single excitatory axons form clustered synapses onto CA1 pyramidal cell dendrites. Nat. Neurosci. 2018;21:353–363. doi: 10.1038/s41593-018-0084-6. [DOI] [PubMed] [Google Scholar]

[CR89] 89.Scholl B, Wilson DE, Fitzpatrick D. Local order within global disorder: synaptic architecture of visual space. Neuron. 2017;96:1127–1138.e1124. doi: 10.1016/j.neuron.2017.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR90] 90.Li W, Ma L, Yang G, Gan WB. REM sleep selectively prunes and maintains new synapses in development and learning. Nat. Neurosci. 2017;20:427–437. doi: 10.1038/nn.4479. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR91] 91.Cossell L, et al. Functional organization of excitatory synaptic strength in primary visual cortex. Nature. 2015;518:399–403. doi: 10.1038/nature14182. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR92] 92.Iacaruso MF, Gasler IT, Hofer SB. Synaptic organization of visual space in primary visual cortex. Nature. 2017;547:449–452. doi: 10.1038/nature23019. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR93] 93.Lee WC, et al. Anatomy and function of an excitatory network in the visual cortex. Nature. 2016;532:370–374. doi: 10.1038/nature17192. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR94] 94.Hayashi-Takagi A, et al. Labelling and optical erasure of synaptic memory traces in the motor cortex. Nature. 2015;525:333–338. doi: 10.1038/nature15257. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR95] 95.Hwang FJ, et al. Motor learning selectively strengthens cortical and striatal synapses of motor engram neurons. Neuron. 2022;110:2790–2801.e2795. doi: 10.1016/j.neuron.2022.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR96] 96.Xu T, et al. Rapid formation and selective stabilization of synapses for enduring motor memories. Nature. 2009;462:915–919. doi: 10.1038/nature08389. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR97] 97.Choi J-H, et al. Interregional synaptic maps among engram cells underlie memory formation. Science. 2018;360:430–435. doi: 10.1126/science.aas9204. [DOI] [PubMed] [Google Scholar]

[CR98] 98.Chater TE, Goda Y. My neighbour hetero-deconstructing the mechanisms underlying heterosynaptic plasticity. Curr. Opin. Neurobiol. 2021;67:106–114. doi: 10.1016/j.conb.2020.10.007. [DOI] [PubMed] [Google Scholar]

[CR99] 99.Royer S, Pare D. Conservation of total synaptic weight through balanced synaptic depression and potentiation. Nature. 2003;422:518–522. doi: 10.1038/nature01530. [DOI] [PubMed] [Google Scholar]

[CR100] 100.Tong R, Chater TE, Emptage NJ, Goda Y. Heterosynaptic cross-talk of pre- and postsynaptic strengths along segments of dendrites. Cell Rep. 2021;34:108693. doi: 10.1016/j.celrep.2021.108693. [DOI] [PubMed] [Google Scholar]

[CR101] 101.El-Boustani S, et al. Locally coordinated synaptic plasticity of visual cortex neurons in vivo. Science. 2018;360:1349–1354. doi: 10.1126/science.aao0862. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR102] 102.Shannon CE. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27:623. doi: 10.1002/j.1538-7305.1948.tb00917.x. [DOI] [Google Scholar]

[CR103] 103.Mitra A, Mitra SS, Tsien RW. Heterogeneous reallocation of presynaptic efficacy in recurrent excitatory circuits adapting to inactivity. Nat. Neurosci. 2012;15:250–257. doi: 10.1038/nn.3004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR104] 104.Gruget C, et al. Rearrangements under confinement lead to increased binding energy of synaptotagmin-1 with anionic membranes in Mg2+ and Ca2+ FEBS Lett. 2018;592:1497–1506. doi: 10.1002/1873-3468.13040. [DOI] [PubMed] [Google Scholar]

[CR105] 105.Grushin K, et al. Structural basis for the clamping and Ca2+ activation of SNARE-mediated fusion by synaptotagmin. Nat. Commun. 2019;10:2413. doi: 10.1038/s41467-019-10391-x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR106] 106.Delvendahl I, et al. Reduced endogenous Ca2+ buffering speeds active zone Ca2+ signaling. Proc. Natl. Acad. Sci. USA. 2015;112:E3075–E3084. doi: 10.1073/pnas.1508419112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR107] 107.Liu G, Weinger JG, Lu ZL, Xue F, Sadeghpour S. Efficacy and safety of MMFS-01, a synapse density enhancer, for treating cognitive impairment in older adults: a randomized, double-blind, placebo-controlled trial. J. Alzheimer’s Dis. 2016;49:971–990. doi: 10.3233/JAD-150538. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR108] 108.Weinger JG, Liu G. [P4–001]: MMFS treatment ameliorates frontal cortex dysfunction in mild-moderate Alzheimer’s disease patients. Alzheimer’s Dement. 2017;13:P1253–P1253. doi: 10.1016/j.jalz.2017.06.1865. [DOI] [Google Scholar]

[CR109] 109.Wroolie TE, et al. Open label trial of magnesium L-theronate in patient with dementia. Innov. Aging. 2017;1:170–170. doi: 10.1093/geroni/igx004.661. [DOI] [Google Scholar]

[CR110] 110.Surman C, et al. L-threonic acid magnesium salt supplementation in ADHD: an open-label pilot study. J. Diet. Suppl. 2021;18:119–131. doi: 10.1080/19390211.2020.1731044. [DOI] [PubMed] [Google Scholar]

[CR111] 111.Slutsky I, Sadeghpour S, Li B, Liu G. Enhancement of synaptic plasticity through chronically reduced Ca2+ flux during uncorrelated activity. Neuron. 2004;44:835–849. doi: 10.1016/j.neuron.2004.11.013. [DOI] [PubMed] [Google Scholar]

[CR112] 112.Giovannucci, A. et al. CaImAn an open source tool for scalable calcium imaging data analysis. Elife8, e38173, 1–45 (2019). [DOI] [PMC free article] [PubMed]

[CR113] 113.Murthy VN, Stevens CF. Reversal of synaptic vesicle docking at central synapses. Nat. Neurosci. 1999;2:503–507. doi: 10.1038/9149. [DOI] [PubMed] [Google Scholar]

[CR114] 114.Jiang M, Chen G. High Ca2+-phosphate transfection efficiency in low-density neuronal cultures. Nat. Protoc. 2006;1:695–700. doi: 10.1038/nprot.2006.86. [DOI] [PubMed] [Google Scholar]

[CR115] 115.Thevenaz P, Ruttimann UE, Unser M. A pyramid approach to subpixel registration based on intensity. IEEE T. Image Process. 1998;7:27–41. doi: 10.1109/83.650848. [DOI] [PubMed] [Google Scholar]

[CR116] 116.Sorzano COS, Thevenaz P, Unser M. Elastic registration of biological images using vector-spline regularization. IEEE T. Bio. Med. Eng. 2005;52:652–663. doi: 10.1109/TBME.2005.844030. [DOI] [PubMed] [Google Scholar]

[CR117] 117.Cardona A, et al. TrakEM2 software for neural circuit reconstruction. Plos One. 2012;7:e38011. doi: 10.1371/journal.pone.0038011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR118] 118.Ofer N, Berger DR, Kasthuri N, Lichtman JW, Yuste R. Ultrastructural analysis of dendritic spine necks reveals a continuum of spine morphologies. Dev. Neurobiol. 2021;81:746–757. doi: 10.1002/dneu.22829. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CR119] 119.Arellano JI, Benavides-Piccione R, Defelipe J, Yuste R. Ultrastructure of dendritic spines: correlation between synaptic and spine morphologies. Front. Neurosci. 2007;1:131–143. doi: 10.3389/neuro.01.1.1.010.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Intracellular magnesium optimizes transmission efficiency and plasticity of hippocampal synapses by reconfiguring their connectivity

Hang Zhou

Guo-Qiang Bi

Guosong Liu

Abstract

Introduction

Results

Diversity of synaptic configuration across dendritic branches

Fig. 1. Influence of synaptic configuration on presynaptic release at dendrites.

Impact of synaptic configuration on presynaptic release at dendrites

Impact of synaptic configuration on postsynaptic AMPAR and PSD95 distributions

Fig. 2. Influence of synaptic configuration on excitatory synaptic transmission in dendrites.

Impact of synaptic configuration on transmission efficiency at dendrites

Impact of synaptic configuration on postsynaptic Ca2+ signals in dendrites

Fig. 3. Influence of synaptic configuration on postsynaptic Ca2+ signals in dendrites.

Impact of synaptic configuration on postsynaptic GluN2B distribution

Intracellular Mg2+ regulates synaptic configuration by inhibiting release probability

Fig. 4. Intracellular Mg2+ regulates synaptic configuration by inhibiting release probability.

Intracellular Mg2+ regulates configuration by increasing functional synapse density

Fig. 5. Intracellular Mg2+ regulates synaptic configuration by converting small boutons from silent to functional.

Multiple pathways converge on intracellular Mg2+ in regulating synaptic configuration

Fig. 6. Multiple pathways converge on intracellular Mg2+ levels in regulating synaptic configuration.

Elevating brain Mg2+ levels modifies hippocampal synaptic configuration

Fig. 7. Brain Mg2+ supplementation modifies synaptic configuration in the hippocampus.

Discussion

Organization principle of synapses along dendrites

Fig. 8. Summary of an intracellular Mg2+-mediated pathway regulating synaptic configuration.

Implications of synaptic configuration to information turnover

Intracellular Mg2+ crucially regulates synaptic configuration

Is intracellular Mg2+ a “memory molecule”?

Translational implications

Methods

Animals

Culture of hippocampal neurons

Pharmacological treatments

Imaging systems

Measurement of intracellular magnesium concentration

Detection of vesicle turnover

Calcium imaging and analysis

Visualization of GluN2B in spines

Plasmids and transfection

Histology

Cultured neurons

Tissue slices

Electron microscopy-based 3D reconstruction

Water maze

Information entropy

Statistics

Reporting summary

Supplementary information

Source data

Acknowledgements

Author contributions

Peer review

Peer review information

Data availability

Code availability

Competing interests

Footnotes

Contributor Information

Supplementary information

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Impact of synaptic configuration on postsynaptic Ca²⁺ signals in dendrites

Fig. 3. Influence of synaptic configuration on postsynaptic Ca²⁺ signals in dendrites.

Intracellular Mg²⁺ regulates synaptic configuration by inhibiting release probability

Fig. 4. Intracellular Mg²⁺ regulates synaptic configuration by inhibiting release probability.

Intracellular Mg²⁺ regulates configuration by increasing functional synapse density

Fig. 5. Intracellular Mg²⁺ regulates synaptic configuration by converting small boutons from silent to functional.

Multiple pathways converge on intracellular Mg²⁺ in regulating synaptic configuration

Fig. 6. Multiple pathways converge on intracellular Mg²⁺ levels in regulating synaptic configuration.

Elevating brain Mg²⁺ levels modifies hippocampal synaptic configuration

Fig. 7. Brain Mg²⁺ supplementation modifies synaptic configuration in the hippocampus.

Fig. 8. Summary of an intracellular Mg²⁺-mediated pathway regulating synaptic configuration.

Intracellular Mg²⁺ crucially regulates synaptic configuration

Is intracellular Mg²⁺ a “memory molecule”?