Abstract
There is a growing interest in inferring context specific gene regulatory networks from single-cell RNA sequencing (scRNA-seq) data. This involves identifying the regulatory relationships between transcription factors (TFs) and genes in individual cells, and then characterizing these relationships at the level of specific cell types or cell states. In this study, we introduce scGATE (single-cell gene regulatory gate) as a novel computational tool for inferring TF–gene interaction networks and reconstructing Boolean logic gates involving regulatory TFs using scRNA-seq data. In contrast to current Boolean models, scGATE eliminates the need for individual formulations and likelihood calculations for each Boolean rule (e.g. AND, OR, XOR). By employing a Bayesian framework, scGATE infers the Boolean rule after fitting the model to the data, resulting in significant reductions in time-complexities for logic-based studies. We have applied assay for transposase-accessible chromatin with sequencing (scATAC-seq) data and TF DNA binding motifs to filter out non-relevant TFs in gene regulations. By integrating single-cell clustering with these external cues, scGATE is able to infer context specific networks. The performance of scGATE is evaluated using synthetic and real single-cell multi-omics data from mouse tissues and human blood, demonstrating its superiority over existing tools for reconstructing TF-gene networks. Additionally, scGATE provides a flexible framework for understanding the complex combinatorial and cooperative relationships among TFs regulating target genes by inferring Boolean logic gates among them.
Keywords: scRNA-seq, scATAC-seq, transcription factor, Motif, Boolean logic gate, Bayesian inference
INTRODUCTION
TFs play a critical role in regulating gene expression and controlling cellular behavior. In recent years, there has been growing interest in reconstructing TF-gene networks using single-cell gene expression data. This involves inferring the regulatory relationships between TFs and genes in individual cells, which can provide insights into the complex regulatory networks that govern cellular behavior and function at the cell type level. To infer TF–gene interaction network, a variety of computational algorithms are proposed based on information theory [1], correlation analysis [2, 3] and machine learning [4, 5]. Logic-based models are a powerful tool for understanding the complex relationships among regulatory TFs to regulate their target gene. These models use Boolean logic, e.g. AND, OR and XOR operators, to describe the cooperative or competitive relationships among TFs, for details see [6]. The available tools for inferring Boolean logic have limited applications in single-cell gene expression data from quantitative real-time reverse-transcription PCR (qRT-PCR) [7, 8] or microarray [9] technologies, mostly due to the high computational complexity. The available logic-based tools have limited capacity to model regulatory networks with more than two TFs, e.g. Loregic [9], LogicTRN [10], and they require a priori-specified network structure for the Boolean logic inference in order to reduce the complexity of the problem to a feasible computational cost. Additionally, some of these tools require data binarization to infer the Boolean logic among TFs [11], which is a threshold-dependent process that may result in information loss. While recent studies such as CellOracle [12] have focused on inferring the directed graph of TF-gene (linear) interactions, logic-based models provide a flexible framework for understanding more complex relationships (i.e. second-order interactions) among TFs. By using Boolean logic to describe these relationships, researchers can gain insight into the precise mechanisms underlying gene expression and identify potential therapeutic targets for diseases. Here, we propose a tool (scGATE) for inferring the directed TF-gene network and, at the same time, to infer the Boolean logic gates among any number of TFs that regulate their targets. scGATE does not require scRNA-seq gene expression binarization and it models the continuous data by using a Hill activation function instead. This approach helps to avoid the potential information loss associated with binarization and enables more accurate modeling of regulatory relationships. In scGATE, the likelihood of the target gene is determined by fitting a mixture density of possible TF combinations to the target gene expression profile. A prior probability is considered for each combination among TFs in target regulation. Unlike other approaches, scGATE does not require a separate formulation and likelihood calculation for each Boolean logic (e.g. AND, OR, XOR) among candidate TFs in regulating their target. Instead, scGATE applies a Bayesian framework to update prior probabilities based on the data and infers the most probable Boolean rule a posteriori. While this approach can be generalized to other logic-based studies, it dramatically reduces the computational cost. In contrast to the other logic-based models that are limited to two TFs [8–10], scGATE can unravel the Boolean logic gate within a practical subset (<5) of TFs, where overfitting is not a concern.
We focus on the reconstruction of context specific gene regulatory networks (GRNs) [13] that consider regulatory relations in one or a few closely related cell types by using external hints such as TF binding site motifs and scATAC-seq data available from those cell populations. The context specific GRN inference is more reliable because (i) by focusing on specific cell types or cell states, we can increase the statistical power of the analysis, as it reduces the complexity and heterogeneity of the gene expression data being analyzed. (ii) Context-specific regulatory relationships can provide meaningful insights into regulatory relations and the molecular mechanisms that underlie a specific biological process of interest, e.g. cell differentiation, development or disease propagation.
By integrating external hints with scRNA-seq data, it is possible to infer context specific regulatory networks that reflect the unique regulatory relationships in specific cell types or tissues. This can provide a more accurate and biologically relevant representation of the regulatory networks that govern cellular behavior. For example, scATAC-seq data provide information about chromatin accessibility and TF binding site motifs provides additional information about the specific TFs that are binding to these accessible regions. By using this information to filter or prioritize potential regulatory relationships, it is possible to alleviate computational costs and also reduce the number of false positive and false negative edges in the inferred network. In absence of chromatin accessibility data, TF binding site motif data alone can also provide partial evidence for direct TF–gene interactions, and exclusion of non-relevant TFs in the model. One may also consider other sources of external information such as protein–protein interaction databases. We have evaluated the performance of scGATE using several synthetic and real tissue and cell-type–specific scRNA-seq datasets from mouse and human. Importantly, the case studies utilizing synthetic scRNA-seq data were conducted without any prior knowledge of the true underlying network structure. In analyses of real scRNA-seq data, chromatin accessibility data were utilized as the external hint to refine the list of candidate TFs. Benchmarking of scGATE against several other tools demonstrates that scGATE achieves superior performance.
METHOD
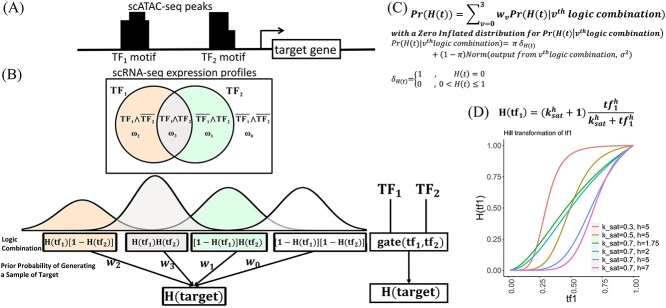
As Figure 1 shows, scATAC-seq and TF binding motif data can be used to generate a list of candidate TFs denoted by 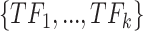 for each target gene, see Supplementary Figure S1 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for a detailed data processing pipeline in scGATE. The scGATE algorithm then uses scRNA-seq data to refine this list by removing any irrelevant TFs and to identify the logical relationships between the remaining TFs for the purpose of regulating the target gene. In scGATE, to account for read depth variations among cells in scRNA-seq studies, library size normalization is performed by dividing the raw unique molecular identifier count data of each cell by its total number of reads and then multiplying the result by a scaling factor, see Supplementary Figure S1 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for details. This transforms the raw read count scRNA-seq data into the (0,1) interval. To identify the optimal expression level of a TF that maximizes the activation of its target genes, both the TF and target gene expression profiles are further transformed using a Hill climbing function. For
for each target gene, see Supplementary Figure S1 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for a detailed data processing pipeline in scGATE. The scGATE algorithm then uses scRNA-seq data to refine this list by removing any irrelevant TFs and to identify the logical relationships between the remaining TFs for the purpose of regulating the target gene. In scGATE, to account for read depth variations among cells in scRNA-seq studies, library size normalization is performed by dividing the raw unique molecular identifier count data of each cell by its total number of reads and then multiplying the result by a scaling factor, see Supplementary Figure S1 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for details. This transforms the raw read count scRNA-seq data into the (0,1) interval. To identify the optimal expression level of a TF that maximizes the activation of its target genes, both the TF and target gene expression profiles are further transformed using a Hill climbing function. For  , the Hill function is expressed as
, the Hill function is expressed as
Figure 1.
Pipeline for scGATE (single-cell gene regulatory gate). (A) scATAC-seq data were utilized to identify accessible chromatin regions potentially targeted by TF binding. A motif analysis on these regions identified putative TF binding sites, generating a list of candidate TFs for regulating downstream target genes. (B) scRNA-seq data were used to refine the candidate TF list by removing non-functional TFs and infer the Boolean logic among regulatory TFs. For two TFs ( ), logical combinations are represented by distinct partitions in a Venn diagram, i.e.
), logical combinations are represented by distinct partitions in a Venn diagram, i.e. 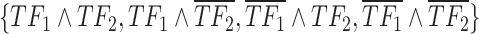 . Over-line, e.g.
. Over-line, e.g. 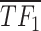 stands for the inhibitory effect of
stands for the inhibitory effect of  on target and ’
on target and ’ ’ shows the AND operator. The outputs from these partitions, i.e.
’ shows the AND operator. The outputs from these partitions, i.e. 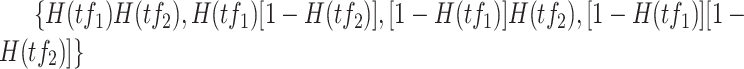 , defined the location parameters for normal densities, which generated observations for target gene expression with prior probabilities, i.e.
, defined the location parameters for normal densities, which generated observations for target gene expression with prior probabilities, i.e. 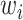 for
for  . The TF-gene network and logical relationships are then inferred a posteriori within a Bayesian framework. (C) We use a zero-inflated normal distribution to calculate the target gene probabilities under distinct normal densities. (D) A Hill climbing function (H) is applied to transform the gene expression profile.
. The TF-gene network and logical relationships are then inferred a posteriori within a Bayesian framework. (C) We use a zero-inflated normal distribution to calculate the target gene probabilities under distinct normal densities. (D) A Hill climbing function (H) is applied to transform the gene expression profile.
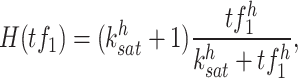 |
(1) |
where 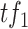 represents the expression level of
represents the expression level of  , and
, and 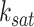 and
and  are parameters in the Hill function.
are parameters in the Hill function.  is a saturation constant that indicates the TF activity level at which the regulation nears maximal effect and
is a saturation constant that indicates the TF activity level at which the regulation nears maximal effect and  is hill coefficient that represents the cooperativity or sigmoidicity of the TF regulatory response. This transformation enables the model to learn complex and nonlinear relationships between input TFs and target gene expressions while also selectively accounting for the importance of the input TFs in regulating their target genes [14]. In scGATE, gene regulation is modeled as a Boolean logic gate, where the expression levels of TFs that regulate a target gene are treated as inputs to the gate, and the expression level of the target gene is treated as the output of the gate. The logic gate can be set up to model different types of interactions between the input TFs, such as cooperative (AND, OR) or competitive (XOR) regulation. For AND, scGATE combines the input signals from the TFs using a logical AND operator, such that the output is high only if all the input signals are high.
is hill coefficient that represents the cooperativity or sigmoidicity of the TF regulatory response. This transformation enables the model to learn complex and nonlinear relationships between input TFs and target gene expressions while also selectively accounting for the importance of the input TFs in regulating their target genes [14]. In scGATE, gene regulation is modeled as a Boolean logic gate, where the expression levels of TFs that regulate a target gene are treated as inputs to the gate, and the expression level of the target gene is treated as the output of the gate. The logic gate can be set up to model different types of interactions between the input TFs, such as cooperative (AND, OR) or competitive (XOR) regulation. For AND, scGATE combines the input signals from the TFs using a logical AND operator, such that the output is high only if all the input signals are high.
For XOR, scGATE combines the input signals from the TFs using a logical XOR operator, such that the output is high if only one of the input signals is high. With two candidate TFs ( ), there are four (
), there are four ( ) distinct ’logic combinations’ of the two TFs that can be made using logical operators, since each TF can activate or inhibit the target gene [15]. These logic combinations that are
) distinct ’logic combinations’ of the two TFs that can be made using logical operators, since each TF can activate or inhibit the target gene [15]. These logic combinations that are  are represented by distinct partitions in Venn diagram and generate
are represented by distinct partitions in Venn diagram and generate  outputs, respectively. Here, ’
outputs, respectively. Here, ’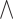 ’ represents the logical AND or the cooperative relationships between TFs, and the over-line, e.g.
’ represents the logical AND or the cooperative relationships between TFs, and the over-line, e.g.  , represents logical NOT or the inhibitory effect of the TF. These logic combinations are the possible ways to combine the input signals from the TFs to model gene regulation. In the scGATE, each scRNA-seq observation from the target gene could be generated from the
, represents logical NOT or the inhibitory effect of the TF. These logic combinations are the possible ways to combine the input signals from the TFs to model gene regulation. In the scGATE, each scRNA-seq observation from the target gene could be generated from the  th logic combination with a prior probability of
th logic combination with a prior probability of  , for
, for 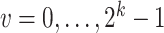 . Then, the likelihood of
. Then, the likelihood of 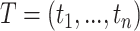 , as
, as 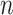 samples from the target gene, is as follows:
samples from the target gene, is as follows:
 |
(2) |
with  . Due to the typical bimodal gene expression patterns in scRNA-seq datasets (mainly corresponding to the population of cells in which a gene is expressed versus not expressed), we fit a zero-inflated distribution to calculate the probability of
. Due to the typical bimodal gene expression patterns in scRNA-seq datasets (mainly corresponding to the population of cells in which a gene is expressed versus not expressed), we fit a zero-inflated distribution to calculate the probability of  being generated from the
being generated from the  th logic combination. Lowly expressed genes may also constitute a ’dropout’ measurement, thus also considered in the zero-expression mode. Then, with a zero-inflated distribution, we can more accurately estimate the probabilities of different logic combinations generating the observed gene expression levels in scRNA-seq data. With fitting a zero-inflated distribution [16]
th logic combination. Lowly expressed genes may also constitute a ’dropout’ measurement, thus also considered in the zero-expression mode. Then, with a zero-inflated distribution, we can more accurately estimate the probabilities of different logic combinations generating the observed gene expression levels in scRNA-seq data. With fitting a zero-inflated distribution [16]
 |
(3) |
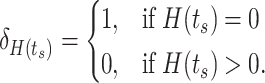 |
(4) |
For non-zero target values, equation (3) fits a normal density that is centered on the output from the  th logic combination. The width of the normal density that is determined by a scale parameter
th logic combination. The width of the normal density that is determined by a scale parameter  and the dropout percentage
and the dropout percentage  are estimated empirically based on data. Prior probabilities
are estimated empirically based on data. Prior probabilities  , for
, for 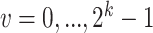 , are also estimated with Expectation-Maximization (EM) algorithm [17]. In scGATE, the likelihood significance is evaluated using the Bayes Factor (BF) [18]. The BF is calculated by dividing the maximized likelihood (
, are also estimated with Expectation-Maximization (EM) algorithm [17]. In scGATE, the likelihood significance is evaluated using the Bayes Factor (BF) [18]. The BF is calculated by dividing the maximized likelihood ( ) in equation (2) by the base likelihood (
) in equation (2) by the base likelihood ( ) obtained by setting the prior probabilities
) obtained by setting the prior probabilities  to
to  for
for  , and fixing the location parameters of
, and fixing the location parameters of  at
at 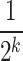 . After identifying a subset of candidate TFs with the most significant likelihood, as evaluated by the BF, the Boolean logic gate is identified. A logic gate is defined as a set of active (ON) logic combinations that have generated observations of a target gene. For this aim, scGATE calculates the posterior probability of each logic combination given observations of the target gene. Indeed, observation
. After identifying a subset of candidate TFs with the most significant likelihood, as evaluated by the BF, the Boolean logic gate is identified. A logic gate is defined as a set of active (ON) logic combinations that have generated observations of a target gene. For this aim, scGATE calculates the posterior probability of each logic combination given observations of the target gene. Indeed, observation 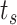 is generated from the logic combination
is generated from the logic combination 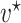 if
if
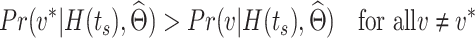 |
(5) |
with 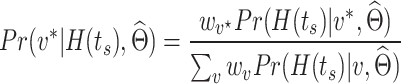 and
and 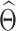 representing the estimated parameter vector
representing the estimated parameter vector 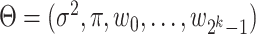 . Due to the low signal-to-noise ratio in scRNA-seq data [19, 20] and to control the False Discovery Rate, a logic combination (partition) is considered active (ON) if it has generated more than
. Due to the low signal-to-noise ratio in scRNA-seq data [19, 20] and to control the False Discovery Rate, a logic combination (partition) is considered active (ON) if it has generated more than  of the target gene observations.
of the target gene observations.
Figure 1 summarizes the inference of logic gates between 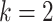 candidate TFs for descriptive purposes. While scGATE has the capability to infer Boolean logic gates among any number of candidate TFs involved in the target regulation, we recommend fitting logic gates among subsets with up to
candidate TFs for descriptive purposes. While scGATE has the capability to infer Boolean logic gates among any number of candidate TFs involved in the target regulation, we recommend fitting logic gates among subsets with up to  factors of the candidate TF lists. This approach helps prevent overfitting of the model and reduces the number of false positive predictions. In this manuscript, we utilize scGATE to evaluate logic gates among subsets with up to
factors of the candidate TF lists. This approach helps prevent overfitting of the model and reduces the number of false positive predictions. In this manuscript, we utilize scGATE to evaluate logic gates among subsets with up to  factors from the candidate TF list, see Supplementary file (see Supplementary Data available online at http://bib.oxfordjournals.org/) for results with
factors from the candidate TF list, see Supplementary file (see Supplementary Data available online at http://bib.oxfordjournals.org/) for results with 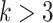 . For the inference of the directed TF-gene network, the predicted logic gates are sorted based on the BF confidence score. Subsequently, each candidate TF is scored using the BF value from the most significant logic gate that includes it.
. For the inference of the directed TF-gene network, the predicted logic gates are sorted based on the BF confidence score. Subsequently, each candidate TF is scored using the BF value from the most significant logic gate that includes it.
In our Bayesian inference framework, the prior probabilities, which are updated using data, serve to quantify the relative significance of distinct combinations of TFs in regulating their downstream targets. For example, in XOR logic gate 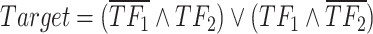 with weight intensities
with weight intensities 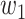 and
and 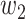 assigned to these combinations, we can assess the relative importance of
assigned to these combinations, we can assess the relative importance of  versus
versus  in the regulation of the target gene. While both combinations contribute to the regulation process, a larger value of
in the regulation of the target gene. While both combinations contribute to the regulation process, a larger value of  compared with
compared with  (i.e.
(i.e. 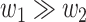 ) implies a more substantial contribution from
) implies a more substantial contribution from 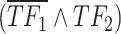 relative to
relative to  in the target regulation, and vice versa. Then, scGATE offers the potential for a better fit to datasets, particularly when distinct TF combinations such as
in the target regulation, and vice versa. Then, scGATE offers the potential for a better fit to datasets, particularly when distinct TF combinations such as  and
and  in the XOR logic gate have varying contributions to the regulation of downstream genes across different tissues or cell types. This variability could arise from imbalanced data or differences in the underlying biological processes present in different datasets. Moreover, in contrast to other Boolean-based models that require distinct formulations and likelihood calculations for each Boolean rule (e.g. AND, OR, XOR, NAND or NOR), scGATE utilizes a unified likelihood calculation for all possible Boolean rules among candidate TFs. In scGATE, the likelihood function is based on fitting a mixture density of possible TF combinations with corresponding prior probabilities, as in equation 2. By updating the prior probabilities based on data, scGATE infers the Boolean logic that is most consistent with the observed data within a Bayesian framework in equation 5. Specifically, for cases involving
in the XOR logic gate have varying contributions to the regulation of downstream genes across different tissues or cell types. This variability could arise from imbalanced data or differences in the underlying biological processes present in different datasets. Moreover, in contrast to other Boolean-based models that require distinct formulations and likelihood calculations for each Boolean rule (e.g. AND, OR, XOR, NAND or NOR), scGATE utilizes a unified likelihood calculation for all possible Boolean rules among candidate TFs. In scGATE, the likelihood function is based on fitting a mixture density of possible TF combinations with corresponding prior probabilities, as in equation 2. By updating the prior probabilities based on data, scGATE infers the Boolean logic that is most consistent with the observed data within a Bayesian framework in equation 5. Specifically, for cases involving  candidate TFs with
candidate TFs with 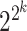 possible Boolean rules, the scGATE Bayesian framework reduces the number of required likelihood calculations from
possible Boolean rules, the scGATE Bayesian framework reduces the number of required likelihood calculations from 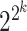 to 1. This reduction in calculations simplifies the computational burden and enables efficient inference of the underlying Boolean rules.
to 1. This reduction in calculations simplifies the computational burden and enables efficient inference of the underlying Boolean rules.
RESULTS
The performance of scGATE in reconstructing the context-specific TF-target networks and the associated Boolean logic gates is assessed using synthetic datasets from: (i) a network with 14 genes involving a series of toggle switches that produce 8 cell types. The BoolODE package [21] was utilized for simulating scRNA-seq data and demonstrating context specific network inference. (ii) Three networks with 15 TFs and 65 target genes, designed to mimic the evolutionarily related structures of three cell types in the differentiation process. The BoolODE and GeneNetWeaver (GNW) [22] packages were used for simulating data. In synthetic datasets from (i) and (ii), we perform the analyses without incorporating any prior knowledge or external hints regarding the network structure. The performance of scGATE is also assessed on three real datasets: (i) mouse haematopoiesis scRNA-seq dataset from Dahlin’s work [23] to study the blood cell differentiation toggle switch, where external hints on the network structure were obtained from Krumsiek’s work [24]; (ii) mouse scRNA-seq datasets from five tissues (Spleen, Lung, Liver, Kidney and Heart) obtained from the Tabula Muris project [25] (GSE109774), along with scATAC-seq datasets from the same tissues obtained from Cusanovich’s work [26] (GSE111586) serving as external hints; and (iii) human haematopoiesis scRNA-seq and scATAC-seq datasets from Buenrostro’s work [27] (GSE96772). See Supplementary Table S1 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the metadata, such as information about the sequencing platform, the origin tissue or cell type of the samples, and the number of cells sequenced for each dataset.
Synthetic toggle switch
We demonstrate an example use of scGATE to reconstruct context specific TF-gene network jointly with the underlying Boolean logic gates in toggle switches. A toggle switch is a type of genetic regulatory circuit that consists of two genes that mutually repress each other, forming a double-negative feedback loop. Figure 2A shows a toy GRN with 14 nodes that consists of a series of toggle switches with 8 different steady states. In each steady state, one of the eight extreme genes will be active, resulting in a distinct cell type and gene expression pattern. We considered ’AND’ relationships between any two genes that jointly regulate their target, e.g. 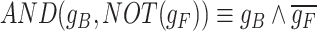 in regulating
in regulating  . We then utilized the BoolODE package [21] to generate synthetic gene expression profiles of 3000 single cells undergoing a differentiation process with a model type hill and 8 steps for the simulation time. These synthetic data are visualized with the
. We then utilized the BoolODE package [21] to generate synthetic gene expression profiles of 3000 single cells undergoing a differentiation process with a model type hill and 8 steps for the simulation time. These synthetic data are visualized with the  -distributed stochastic neighbour embedding (tSNE) graphs in Scanpy [28]. Cells are initially clustered using Louvain method [29]. In Figure 2B, the Louvain annotation identifies the stem cells in cluster 8 and differentiated cells in other clusters. DPT, an algorithm based on diffusion mapping, is utilized to calculate differentiation pseudotime [30] in Figure 2C. In the pseudotime-sorted cells, stem cells are shown in dark blue, while other cells along the differentiation trajectories are shown in light colors. Figure 2D depicts the expression patterns of genes
-distributed stochastic neighbour embedding (tSNE) graphs in Scanpy [28]. Cells are initially clustered using Louvain method [29]. In Figure 2B, the Louvain annotation identifies the stem cells in cluster 8 and differentiated cells in other clusters. DPT, an algorithm based on diffusion mapping, is utilized to calculate differentiation pseudotime [30] in Figure 2C. In the pseudotime-sorted cells, stem cells are shown in dark blue, while other cells along the differentiation trajectories are shown in light colors. Figure 2D depicts the expression patterns of genes  and
and  along the differentiation trajectory, with
along the differentiation trajectory, with  expressed on one side and
expressed on one side and  on the other side of the plot. To demonstrate how scGATE can be used to reconstruct context specific logic gates, we applied it for the joint inference of the network and underlying Boolean logic gates in two separate clusters (Clusters I and II) of cells along a differentiation trajectory, i.e. the network structure and gene–gene interactions were not specified a priori. As illustrated in Table 1, scGATE has identified the context specific regulatory gates for both clusters. For example, in cluster I, scGATE has identified the gate
on the other side of the plot. To demonstrate how scGATE can be used to reconstruct context specific logic gates, we applied it for the joint inference of the network and underlying Boolean logic gates in two separate clusters (Clusters I and II) of cells along a differentiation trajectory, i.e. the network structure and gene–gene interactions were not specified a priori. As illustrated in Table 1, scGATE has identified the context specific regulatory gates for both clusters. For example, in cluster I, scGATE has identified the gate 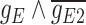 that regulates
that regulates  . In cluster II, scGATE has identified the gate
. In cluster II, scGATE has identified the gate 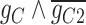 that regulates
that regulates 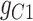 .
.
Figure 2.
scGATE reconstructs both the network and logical relationships among regulatory TFs or genes in a context specific manner. (A) A regulatory network with a series of toggle switches controlling the cell differentiation process, considering ’AND’ relationships between any two genes that jointly regulate downstream targets. (B) scGATE utilizes Louvain clustering to group cells along differentiation trajectories and then infers the directed network and underlying Boolean update rules per cell cluster. (C) Cells are sorted by dpt pseudotime, with stem cells shown in dark blue and differentiated cells in light colors. (D) Gene expression levels are visualized along the trajectories.
Table 1.
scGATE infers directed edge networks and logic gates among regulators in Clusters I and II of cells, unveiling context specific expression patterns in the synthetic toggle switch
| Cluster I | Cluster II | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Target gene |
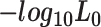
|

|

|
Logic gate | Target gene |

|

|
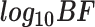
|
Logic gate |

|
173.9 | −268.57 | 442.47 |

|

|
167.69 | −266.17 | 433.87 |

|

|
51.85 | −234.65 | 286.50 |
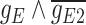
|
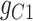
|
45.2 | −225.69 | 270.89 |
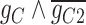
|
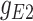
|
38.43 | −235.48 | 273.91 |

|
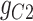
|
58.18 | −212.02 | 270.19 |
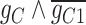
|
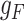
|
170.38 | −278.57 | 448.95 |

|

|
165.53 | −273.5 | 439.03 |

|

|
80.36 | −215.32 | 295.68 |
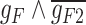
|
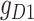
|
53.9 | −232.89 | 286.80 |

|

|
67.6 | −217.88 | 285.48 |
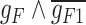
|

|
64.5 | −237.56 | 302.06 |
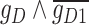
|
Note:  and
and 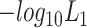 represent the negative of the logarithm (base 10) of the likelihood in scGATE, corresponding to the default parameters and the estimated parameters with data, respectively.
represent the negative of the logarithm (base 10) of the likelihood in scGATE, corresponding to the default parameters and the estimated parameters with data, respectively.  denotes the logarithm (base 10) of the Bayes Factor.
denotes the logarithm (base 10) of the Bayes Factor.
Blood cell differentiation toggle switch
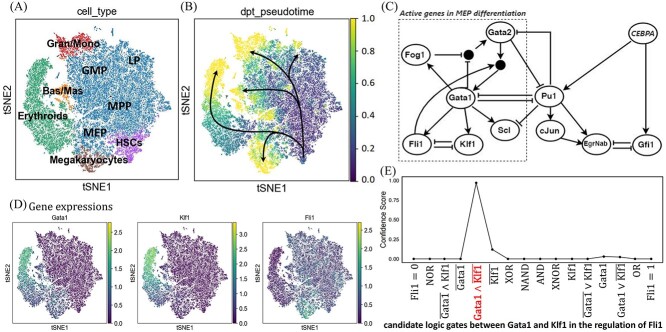
scGATE is assessed for its ability to reconstruct the cell-type–specific networks and logic gates using mouse haematopoiesis scRNA-seq dataset [23]. Figure 3A displays a tSNE plot for 44 802 hematopoietic cells from this dataset with annotated cell types such as HSCs (Hematopoietic Stem Cells), Meg (Megakaryocytes), Ery (Erythrocytes), Gran (Granulocytes), Mono (Monocytes), MPP (Multipotent Progenitor), GMP (Granulocyte-Monocyte Progenitor), LP (Lymphoid Progenitor), MEP (Megakaryocyte-Erythrocyte Progenitor), Bas (Basophil) and Mas (Mast). See Supplementary Figure S2 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the expression patterns of marker genes. Figure 3B illustrates the pseudotime-sorted cells along with the differentiation trajectories of HSCs into Meg, Ery, Gran and Mono. This differentiation process is previously modelled with a Boolean network of switch-like decisions [24], Figure 3C. The genes on the left side of this literature-derived network, namely Gata1, Gata2, Fog1, Scl, Fli1 and Klf1, play active roles in myeloid differentiation into Meg and Ery cells. Fli1 and Klf1 form a mutually inhibitory gene pair that are activated by Gata1 and determine the final cell fates, see Figure 3D for expression patterns. Klf1 is a transcription factor (TF) specific to erythrocytes, up-regulated in Ery cells and represses Fli1. In the megakaryocyte lineage, Fli1 acts as an antagonist counteracting the activity of Klf1. Boolean update rules for these genes are represented as  and
and  , respectively. Gata1 and Gata2 are early megakaryocyte-erythrocyte (MegE) factors with multiple Boolean update rules (OR relationships), denoted by black circles connecting edges in Figure 3C. Specifically, the Boolean update rule for Gata2 is
, respectively. Gata1 and Gata2 are early megakaryocyte-erythrocyte (MegE) factors with multiple Boolean update rules (OR relationships), denoted by black circles connecting edges in Figure 3C. Specifically, the Boolean update rule for Gata2 is  , indicating that Gata2 is synergistically inhibited by Gata1 and Fog1, as well as being inhibited by Pu1. The Boolean update rule
, indicating that Gata2 is synergistically inhibited by Gata1 and Fog1, as well as being inhibited by Pu1. The Boolean update rule  indicates that Gata1 is activated by both Gata2 and Fli1, in the absence of Pu1. Please refer to Supplementary Figure S2 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the expression patterns of all genes on tSNE plots. The Boolean logic gates controlling the differentiation process into Meg and Ery cells are also summarized in Supplementary Table S2 (see Supplementary Data available online at http://bib.oxfordjournals.org/).
indicates that Gata1 is activated by both Gata2 and Fli1, in the absence of Pu1. Please refer to Supplementary Figure S2 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the expression patterns of all genes on tSNE plots. The Boolean logic gates controlling the differentiation process into Meg and Ery cells are also summarized in Supplementary Table S2 (see Supplementary Data available online at http://bib.oxfordjournals.org/).
Figure 3.
Cell-type–specific logic gate inference in the mouse haematopoiesis scRNA-seq data [23]. (A) Cell-type annotated tSNE plot. (B) Pseudotime-sorted cells representing stem and differentiated cells are plotted along with distinct trajectories of HSCs differentiating into Meg/Ery and Gran/Mono cells. (C) Regulatory network with Boolean update rules controlling the cell differentiation process. Black circles connecting edges indicate the multiple possible update rules (OR relationships) between genes. (D) The expression profiles of Gata1, Klf1 and Fli1 are depicted. (E) The inference of the most probable logic gate between Gata1 and Klf1 in the regulation of Fli1, based on the scRNA-seq data from the MegE trajectory.
scGATE is applied for the network and gate inference for all genes involved in MegE differentiation using scRNA-seq data from MegE cells. As an example, Figure 3E displays the confidence scores associated with various candidate Boolean logic gates that involve Gata1 and Klf1 in the regulation of Fli1. Out of the 16 potential logic gates that investigate diverse cooperative and competitive relationships, scGATE has identified the logical rule  with the utmost confidence score. scGATE has also successfully predicted other interactions and logic gates, as indicated on the left side of Figure 3C, see Supplementary Table S2 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for further details.
with the utmost confidence score. scGATE has also successfully predicted other interactions and logic gates, as indicated on the left side of Figure 3C, see Supplementary Table S2 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for further details.
Cell-type specific network inference in synthetic scRNA-seq datasets
We benchmarked the performance of scGATE against other well-known algorithms for the network inference on the synthetic scRNA-seq datasets. For this purpose, we employed a probabilistic framework for network evolution to generate the network structure for 3 cell types consisting of 15 TFs and 65 target genes, resulting in networks with 214, 214 and 233 edges, Figure 4A. We have also considered Boolean logic gates among regulatory TFs when they are jointly controlling their target genes. We used BoolODE to synthesize scRNA-seq data with  ,
,  and
and 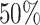 dropouts from cell-type-specific networks that included logic gates among TFs. We then applied scGATE to infer the cell-type-specific network using the synthesized datasets and compared the predicted network to the ground-truth network used in the data generation process. We benchmarked the performance of scGATE compared with well-known methods for network inference using AUROC (Area Under the Receiver Operating characteristic Curve), EPR (Early Precision Ratio), AUPRC (Area Under the Precision Recall Curve), Accuracy (ACC) and Kappa-coefficient metrics. AUROC is calculated with ROCR package [31] and it ranges between 0 and 1, where 1 represents perfect classifier performance. We also calculated the EPR to evaluate the precision among
dropouts from cell-type-specific networks that included logic gates among TFs. We then applied scGATE to infer the cell-type-specific network using the synthesized datasets and compared the predicted network to the ground-truth network used in the data generation process. We benchmarked the performance of scGATE compared with well-known methods for network inference using AUROC (Area Under the Receiver Operating characteristic Curve), EPR (Early Precision Ratio), AUPRC (Area Under the Precision Recall Curve), Accuracy (ACC) and Kappa-coefficient metrics. AUROC is calculated with ROCR package [31] and it ranges between 0 and 1, where 1 represents perfect classifier performance. We also calculated the EPR to evaluate the precision among  top-ranked predicted regulatory edges, where
top-ranked predicted regulatory edges, where 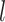 is the number of edges in the ground-truth network [21]. To calculate ACC and Kappa-coefficient metrics, we used a similar approach as in the EPR calculation to binarize the predictions, as the edge weights (confidence scores) in the predicted networks are on the continuous scale in the benchmarked algorithms. As shown in Figure 4B, scGATE outperforms other tools in terms of both AUROC and EPR metrics across all cell types and dropout levels. While other tools, e.g. GRNBOOST2, LEAP and CellOracle, reach a lower AUROC in cell type 3, scGATE consistently achieved an AUROC > 0.98 for all cell types. The superiority of scGATE is particularly evident in terms of the EPR metric, which suggests that scGATE was able to make more true positive predictions among its top-ranked predictions compared with other tools. See Supplementary Figure S3 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for comparisons in terms of the AUPRC, ACC and Kappa-coefficient metrics. In Figure 4C, we evaluated the performance of scGATE on the downsampled datasets with cell numbers reduced to 2000, 1000, 500 and 250. With 15 regulatory TFs, a minimum of 1000 cells, which is very common in many scRNA-seq datasets, guarantees an AUROC > 0.9 and an EPR > 0.6. See Supplementary Figure S4 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for evaluations in terms of the AUPRC, ACC and Kappa-coefficient metrics for the downsampled datasets. Subsequently, the prediction accuracy is assessed by examining the impact of varying numbers of TFs involved in the target gene regulation. Evaluations are repeated for 50 Bootstrap samples of regulatory TFs from the original candidate TF list. Figure 5A illustrates the AUROC and EPR values when 15, 10, 6 and 4 regulatory TFs are implicated in regulating the target genes. See middle panel in Supplementary Figure S5 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for results on other metrics. We also examined the effects of incorporating non-functional TFs, defined as TFs that do not modulate target gene expressions, on the performance of scGATE. As Figure 5B shows, the inclusion of non-functional TFs in the candidate list can decrease EPR considerably. See middle panel in Supplementary Figure S6 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for further details. Figure 5C displays the scGATE runtime per target gene for candidate TF lists of sizes 15, 10, 6 and 4. The results in this section were obtained by fitting Boolean logic gates that include up to
is the number of edges in the ground-truth network [21]. To calculate ACC and Kappa-coefficient metrics, we used a similar approach as in the EPR calculation to binarize the predictions, as the edge weights (confidence scores) in the predicted networks are on the continuous scale in the benchmarked algorithms. As shown in Figure 4B, scGATE outperforms other tools in terms of both AUROC and EPR metrics across all cell types and dropout levels. While other tools, e.g. GRNBOOST2, LEAP and CellOracle, reach a lower AUROC in cell type 3, scGATE consistently achieved an AUROC > 0.98 for all cell types. The superiority of scGATE is particularly evident in terms of the EPR metric, which suggests that scGATE was able to make more true positive predictions among its top-ranked predictions compared with other tools. See Supplementary Figure S3 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for comparisons in terms of the AUPRC, ACC and Kappa-coefficient metrics. In Figure 4C, we evaluated the performance of scGATE on the downsampled datasets with cell numbers reduced to 2000, 1000, 500 and 250. With 15 regulatory TFs, a minimum of 1000 cells, which is very common in many scRNA-seq datasets, guarantees an AUROC > 0.9 and an EPR > 0.6. See Supplementary Figure S4 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for evaluations in terms of the AUPRC, ACC and Kappa-coefficient metrics for the downsampled datasets. Subsequently, the prediction accuracy is assessed by examining the impact of varying numbers of TFs involved in the target gene regulation. Evaluations are repeated for 50 Bootstrap samples of regulatory TFs from the original candidate TF list. Figure 5A illustrates the AUROC and EPR values when 15, 10, 6 and 4 regulatory TFs are implicated in regulating the target genes. See middle panel in Supplementary Figure S5 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for results on other metrics. We also examined the effects of incorporating non-functional TFs, defined as TFs that do not modulate target gene expressions, on the performance of scGATE. As Figure 5B shows, the inclusion of non-functional TFs in the candidate list can decrease EPR considerably. See middle panel in Supplementary Figure S6 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for further details. Figure 5C displays the scGATE runtime per target gene for candidate TF lists of sizes 15, 10, 6 and 4. The results in this section were obtained by fitting Boolean logic gates that include up to 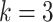 factors from the candidate TF lists. For scGATE results obtained by fitting logic gates among larger subsets of candidate TFs, such as
factors from the candidate TF lists. For scGATE results obtained by fitting logic gates among larger subsets of candidate TFs, such as 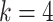 , refer to Supplementary Figure S5 (considering regulatory TFs in the network) and S6 (see Supplementary Data available online at http://bib.oxfordjournals.org/) (considering both regulatory and non-functional TFs in the network).
, refer to Supplementary Figure S5 (considering regulatory TFs in the network) and S6 (see Supplementary Data available online at http://bib.oxfordjournals.org/) (considering both regulatory and non-functional TFs in the network).
Figure 4.
Benchmarking scGATE predictions on synthetic scRNA-seq datasets. (A) Synthesizing cell-type-specific scRNA-seq data. I. Cell-type-specific GRNs are constructed with a probabilistic framework for the evolution of the network structure. II. The regulation of target genes by multiple TFs is modeled using Boolean logic, such as AND, OR and XOR. The BoolODE package is used to generate scRNA-seq datasets that match the GRN structures, with different levels of dropouts (dp) (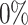 ,
,  and
and  ) included. (B) The performance of scGATE is then compared with other tools using AUROC and EPR measures. (C) scGATE is evaluated by reducing the number of cells in the datasets to 2000, 1000, 500 and 250, to assess its performance and robustness on scRNA-seq datasets of varying sizes, with
) included. (B) The performance of scGATE is then compared with other tools using AUROC and EPR measures. (C) scGATE is evaluated by reducing the number of cells in the datasets to 2000, 1000, 500 and 250, to assess its performance and robustness on scRNA-seq datasets of varying sizes, with 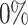 dropout in the data (similar results for other dropouts).
dropout in the data (similar results for other dropouts).
Figure 5.
scGATE is evaluated considering different numbers of regulatory and non-functional (decoy) TFs. Logic gates among up to  factors from the candidate TF list are fitted for the edge inference. (A) only regulatory TFs are included in the data, (B) with both regulatory and non-functional TFs in the data. (C) scGATE runtime per target gene for candidate TF list of different sizes.
factors from the candidate TF list are fitted for the edge inference. (A) only regulatory TFs are included in the data, (B) with both regulatory and non-functional TFs in the data. (C) scGATE runtime per target gene for candidate TF list of different sizes.
In our study, scGATE is also evaluated with datasets synthesized by GNW (GeneNetWeaver) [22], which does not specifically account for the Boolean rules among regulatory TFs in target regulations. We employed GNW to generate datasets comprising 3000 multi-factorial time series for each cell-type-specific network with 15 TFs and 65 targets that were used previously. Each time series consisted of 2000 time steps ( ) and 201 measured points. In order to incorporate noise into the simulated data, we followed the DREAM4 (Dialogue for Reverse Engineering Assessments and Methods) settings [32]. Subsequently, we randomly selected one time point from each time series and extracted the corresponding gene expressions for that time point. This selection process aimed to obtain a representative scRNA-seq dataset capturing the gene expression profiles at a specific moment in time for each individual cell. In summary, using the described process, we simulated scRNA-seq data consisting of 3000 individual cells for each of the 3 previously analyzed cell-type-specific networks, see Supplementary Figure S7 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for scGATE results. In the GNW simulated dataset in Supplementary Figure S7 (see Supplementary Data available online at http://bib.oxfordjournals.org/), where Boolean rules among regulatory TFs are not specifically accounted for in target regulations, scGATE outperforms other tools in terms of AUROC, EPR, ACC and Kappa-coefficient metrics. Additionally, it is among the top-performing tools in terms of AUPRC. However, as seen in Figure 4 for the BoolODE simulated dataset, in the same cell-type specific networks where Boolean rules among TFs are accounted for, scGATE exhibits significantly improved performance. This suggests that scGATE performs better in experimental conditions, biological contexts or data types where target genes are regulated by complex combinatorial Boolean rules among TFs. Indeed, modeling such complex scenarios in gene regulation is an advantage of scGATE over existing tools that solely rely on pairwise TF–gene interactions.
) and 201 measured points. In order to incorporate noise into the simulated data, we followed the DREAM4 (Dialogue for Reverse Engineering Assessments and Methods) settings [32]. Subsequently, we randomly selected one time point from each time series and extracted the corresponding gene expressions for that time point. This selection process aimed to obtain a representative scRNA-seq dataset capturing the gene expression profiles at a specific moment in time for each individual cell. In summary, using the described process, we simulated scRNA-seq data consisting of 3000 individual cells for each of the 3 previously analyzed cell-type-specific networks, see Supplementary Figure S7 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for scGATE results. In the GNW simulated dataset in Supplementary Figure S7 (see Supplementary Data available online at http://bib.oxfordjournals.org/), where Boolean rules among regulatory TFs are not specifically accounted for in target regulations, scGATE outperforms other tools in terms of AUROC, EPR, ACC and Kappa-coefficient metrics. Additionally, it is among the top-performing tools in terms of AUPRC. However, as seen in Figure 4 for the BoolODE simulated dataset, in the same cell-type specific networks where Boolean rules among TFs are accounted for, scGATE exhibits significantly improved performance. This suggests that scGATE performs better in experimental conditions, biological contexts or data types where target genes are regulated by complex combinatorial Boolean rules among TFs. Indeed, modeling such complex scenarios in gene regulation is an advantage of scGATE over existing tools that solely rely on pairwise TF–gene interactions.
Context specific network inference in mouse scRNA-seq datasets
To further assess the performance of scGATE, we utilized 10X Genomics scRNA-seq datasets from five different mouse tissues (Spleen, Lung, Liver, Kidney and Heart) obtained from the Tabula Muris project [25]. The scRNA-seq dataset from each tissue was subjected to the conventional processing pipeline in Seurat [33]. This involves applying quality control metrics to select and filter cells, specifically based on RNA count and the percentage of mitochondrial genes, to exclude low-quality cells. The data are then normalized and scaled, and highly variable features (genes) are identified. To narrow-down the candidate set of regulatory TFs for each target gene, we construct base GRNs for each tissue by identifying (i) accessible or open chromatin regions and (ii) TF binding site motifs within these regions. Here, accessible regulatory regions (enhancer or promoter of genes) are first identified with scATAC-seq data [34] from the same tissues where scRNA-seq data are available. This data profiles chromatin accessibility in around 100 000 single cells from 13 adult mouse tissues. We use Cicero [35] to predict cis-regulatory interactions that are co-accessible in scATAC-seq peaks and likely to be physically close to each other in the nucleus, such as interactions between enhancers and promoters. By running Cicero with default parameters, we identify pairs of peaks within a 500 kb distance that have a co-accessibility score  0.8. We retain peaks that are located within the Transcription Start Site (TSS) or that have an interaction with a cognate peak located in the TSS of a target gene. After identifying the scATAC-seq peaks that meet the criteria for co-accessibility and proximity to the TSS, the DNA sequences of these peaks are scanned for TF binding motifs. For TF motif analysis, we employed the gimmemotifs package in python (https://gimmemotifs.readthedocs.io/en/master/). This generates a list of tissue specific candidate regulatory TFs (base GRNs) for each target gene. The average number of candidate TFs per target gene varied within the range of 211–214 across different tissues. It should be noted that these base GRNs may contain connections that are not functional or are inactive, as the gene regulation can be affected by various factors beyond the accessibility of TF binding sites. Then, we applied the scGATE to further refine the base GRNs with tissue– or cell-type–specific scRNA-seq data.
0.8. We retain peaks that are located within the Transcription Start Site (TSS) or that have an interaction with a cognate peak located in the TSS of a target gene. After identifying the scATAC-seq peaks that meet the criteria for co-accessibility and proximity to the TSS, the DNA sequences of these peaks are scanned for TF binding motifs. For TF motif analysis, we employed the gimmemotifs package in python (https://gimmemotifs.readthedocs.io/en/master/). This generates a list of tissue specific candidate regulatory TFs (base GRNs) for each target gene. The average number of candidate TFs per target gene varied within the range of 211–214 across different tissues. It should be noted that these base GRNs may contain connections that are not functional or are inactive, as the gene regulation can be affected by various factors beyond the accessibility of TF binding sites. Then, we applied the scGATE to further refine the base GRNs with tissue– or cell-type–specific scRNA-seq data.
Similar to CellOracle [12], ground-truth GRNs for these tissues were generated from the mouse TF chromatin immunoprecipitation with sequencing (ChIP-seq) data available in ChIP-Atlas database (https://chip-atlas.org). To obtain tissue– or cell-type–specific ground-truth data for 80 TFs, a total of 1298 experimental datasets were utilized. The following steps were taken: (i) the mouse TF ChIP-seq data in bed file format were downloaded from the ChIP-Atlas database (https://chip-atlas.org). (ii) Data with fewer than 50 peaks and data obtained under non-physiological conditions, such as gene knockouts or adeno-associated virus treatment, were excluded. (iii) Peaks detected in multiple studies were selected. (iv) Data were grouped by TF, and TFs with less than 10 detected target genes were excluded. (v) The data were transformed into a binary network, where each network edge was assigned either 1 or 0 to indicate the presence or absence of ChIP-seq binding between genes. In the Spleen, Lung, Liver, Kidney and Heart, the ground-truth networks consist of 4, 4, 29, 11 and 12 TFs, respectively, regulating 1642, 329, 13 776, 10 405 and 2987 target genes. By default, scGATE is fitted with parameters 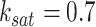 and
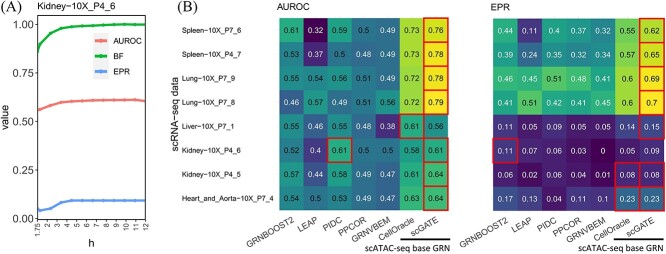
and  of the Hill climbing functions, for the scRNA-seq data from all tissues. However, it is possible to use the BF (Bayes Factor) as a guideline for parameter setting and choose the optimal parameters based on models with the highest BF rates. Figure 6A illustrates this process for a specific tissue from the kidney, where scGATE was fitted with various values of
of the Hill climbing functions, for the scRNA-seq data from all tissues. However, it is possible to use the BF (Bayes Factor) as a guideline for parameter setting and choose the optimal parameters based on models with the highest BF rates. Figure 6A illustrates this process for a specific tissue from the kidney, where scGATE was fitted with various values of  , ranging from 1.75 to 12, while keeping
, ranging from 1.75 to 12, while keeping 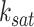 fixed at 0.7. As depicted in Figure 6A, the scGATE achieved the highest AUROC (in red) or EPR (in blue) when fitted with
fixed at 0.7. As depicted in Figure 6A, the scGATE achieved the highest AUROC (in red) or EPR (in blue) when fitted with  . This corresponds to the point where the model achieved the highest BF (as indicated by the green curve). As shown in Figure 6B, scGATE outperforms the other tools in 7 out of 8 scRNA-seq datasets based on AUROC and EPR measures. See Supplementary Figure S8 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for comparisons in terms of the AUPRC, ACC and Kappa-coefficient. Figure 7 shows the ROC and PR curves for TF-gene network inference in
. This corresponds to the point where the model achieved the highest BF (as indicated by the green curve). As shown in Figure 6B, scGATE outperforms the other tools in 7 out of 8 scRNA-seq datasets based on AUROC and EPR measures. See Supplementary Figure S8 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for comparisons in terms of the AUPRC, ACC and Kappa-coefficient. Figure 7 shows the ROC and PR curves for TF-gene network inference in  sample from mouse tissue. See Supplementary Figure S9 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the ROC and PR curves plotted for other samples. In Supplementary Table S3 (see Supplementary Data available online at http://bib.oxfordjournals.org/), the running time and memory usage of scGATE and other compared tools are reported for
sample from mouse tissue. See Supplementary Figure S9 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the ROC and PR curves plotted for other samples. In Supplementary Table S3 (see Supplementary Data available online at http://bib.oxfordjournals.org/), the running time and memory usage of scGATE and other compared tools are reported for  sample (similar result for other samples).
sample (similar result for other samples).
Figure 6.
Comparison of scGATE with other tools for TF-gene network inference in five mouse tissues. (A) Evaluation of scGATE predictions in a kidney dataset using different parameters in activation functions, measured by AUROC, EPR and BF values. (B) Comparative analysis of scGATE predictions with other tools. CellOracle and scGATE rely on the base GRNs derived from external hints to infer the network.
Figure 7.

ROC and PR curves are plotted for TF-gene network inference in the 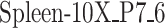 sample from mouse tissue.
sample from mouse tissue.
Context specific network inference in human haematopoiesis scRNA-seq dataset
scGATE was further assessed using 10X Genomics scRNA-seq datasets from human HSCs derived from CD34+ bone marrow [27]. Similar to the approach employed for the mouse tissues dataset, the HSCs dataset, consisting of 14 432 cells, underwent a processing pipeline in Seurat. This pipeline involved filtering out low-quality cells, performing data normalization and scaling to identify the highly variable features within the dataset. To refine the selection of potential regulatory TFs for each gene, we utilized a human haematopoiesis scATAC-seq dataset from the same study [27]. This scATAC-seq dataset enabled the identification of accessible cis-regulatory chromatin regions specific to haematopoiesis. Subsequently, these regulatory regions were scanned for TF binding site motifs, which allowed us to generate a comprehensive list of candidate regulatory TFs, serving as the base GRN, for each target gene. The average number of candidate TFs per target gene was 164. The performance of the predicted network was assessed by comparing it to the ground-truth network, which was derived from TF perturbation experiments (Cus KO) and ChIP-seq (Cus
KO) and ChIP-seq (Cus ChIP) assays conducted in the GM12878 lymphoblastoid cell line, as reported by Cusanovich’s work [36]. Additionally, the intersection of the perturbation and ChIP-seq studies (Cus
ChIP) assays conducted in the GM12878 lymphoblastoid cell line, as reported by Cusanovich’s work [36]. Additionally, the intersection of the perturbation and ChIP-seq studies (Cus KO
KO ChIP) was utilized to enhance the reliability of the ground-truth network. In Cus
ChIP) was utilized to enhance the reliability of the ground-truth network. In Cus KO, Cus
KO, Cus ChIP and Cus
ChIP and Cus KO
KO ChIP, the ground-truth networks consist of 50, 149 and 26 TFs, respectively, regulating 6108, 6179 and 2124 target genes. In Figure 8, scGATE is compared with the other tools on a subnetwork with 217 genes, including 25 TFs and 200 target genes, where 8 TFs could also play a role as target for other TFs. The genes in this sub-network were selected randomly from highly variable features as derived from Seurat analysis. See Supplementary Figure S10 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for more details. Figure 9 shows the ROC and PR curves for TF-gene network inference for human haematopoiesis dataset, with Cus
ChIP, the ground-truth networks consist of 50, 149 and 26 TFs, respectively, regulating 6108, 6179 and 2124 target genes. In Figure 8, scGATE is compared with the other tools on a subnetwork with 217 genes, including 25 TFs and 200 target genes, where 8 TFs could also play a role as target for other TFs. The genes in this sub-network were selected randomly from highly variable features as derived from Seurat analysis. See Supplementary Figure S10 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for more details. Figure 9 shows the ROC and PR curves for TF-gene network inference for human haematopoiesis dataset, with Cus KO
KO ChIP as the ground-truth network. See Supplementary Figure S11 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the ROC and PR curves plotted considering other ground-truth networks in evaluations. In Supplementary Table S3 (see Supplementary Data available online at http://bib.oxfordjournals.org/), the running time and memory usage of scGATE and other tools are reported for human haematopoiesis dataset. Compared with the mouse tissues, with an increased cell numbers in the human haematopoiesis dataset, scGATE requires more time and memory for the network inference than the other tools.
ChIP as the ground-truth network. See Supplementary Figure S11 (see Supplementary Data available online at http://bib.oxfordjournals.org/) for the ROC and PR curves plotted considering other ground-truth networks in evaluations. In Supplementary Table S3 (see Supplementary Data available online at http://bib.oxfordjournals.org/), the running time and memory usage of scGATE and other tools are reported for human haematopoiesis dataset. Compared with the mouse tissues, with an increased cell numbers in the human haematopoiesis dataset, scGATE requires more time and memory for the network inference than the other tools.
Figure 8.

Comparison of scGATE with other tools for TF-gene network inference in human haematopoiesis scRNA-seq dataset.
Figure 9.

ROC and PR curves are plotted for TF-gene network inference in human haematopoiesis scRNA-seq dataset. Cus KO
KO ChIP is utilized as the ground-truth network.
ChIP is utilized as the ground-truth network.
DISCUSSION
In this article, we propose scGATE as a reliable tool for inferring Boolean logic gates on TF-gene networks that represent the combinatorial interactions among regulatory TFs that control target gene expression. By modeling gene regulation as a logic gate, scGATE enables the identification of complex and nonlinear relationships between TFs and their target genes and provides a powerful framework for predicting the effects of perturbations, such as TF knockouts or overexpression, on gene expression and regulatory networks. Although case studies utilizing synthesized toggle switches and real scRNA-seq datasets validated the reliability of scGATE for reconstructing Boolean logic relationships in small-scale networks, our work highlights opportunities to further develop computational methodologies for inferring complex combinatorial gene regulation. Specifically, decoding high-order Boolean logic involving a greater number of transcriptional regulators (e.g. >5) governing a common target remains challenging, where overfitting is a major concern. Because of this computational limitation, scGATE shall currently be applied on a relatively small set of pre-selected TFs based on prior biological knowledge, or for refining combinatorial interactions at smaller parts of coarse-grained GRN constructions (e.g. models based on TF-gene coexpression or other linear relationships). While reconstructed networks depicting TF–gene or gene–gene interactions are informative, they do not convey details on the combinatorial relationships among regulating factors. This is because target genes are often modulated by complexes of TFs binding promoter and enhancer regions in a collaborative fashion. Thus, even directed TF-gene networks delineating activatory or inhibitory regulation fail to provide insights into the intricate collaborative interactions governing target gene expression. To more fully elucidate the mechanistic underpinnings of gene regulation, computational methods must move beyond modeling simple pairwise TF–gene relationships and work toward unraveling multipartite TF complexes that synergistically activate or repress transcriptional programs.
Our results on synthetic data suggest that reducing the number of regulatory TFs (lowering network complexities) leads to a significant increase in both AUROC and EPR, when using scGATE. This observation suggests that the reconstruction of context-specific networks with simplified structures enhances the reliability of the predictions. The presence of non-functional decoy TFs in the input TF repertoire can substantially deteriorate the accuracy of network reconstruction, in terms of EPR. Therefore, the integration of external hint data or prior biological knowledge is critical for filtering out irrelevant TFs. By refining the candidate TF pool, we enable an accurate inference of GRNs using a minimal set of bona fide regulatory TFs. We utilized scATAC-seq data to identify the accessible chromatin regions that are potential targets for TF binding. We then conducted a motif analysis on these regions to identify putative TF binding sites, which in turn allowed us to generate a list of candidate TFs for regulating downstream target genes. In scGATE, we then incorporated context-specific scRNA-seq data to further refine the regulatory interactions among those candidate TFs.
Among several other existing Boolean models, we also showed that scGATE provides a few advantages in terms of (i) computational complexity, (ii) consideration of continuous gene profiles without binarization, (iii) utilization of the Hill climbing function to tailor specific parameters to the dataset or context being studied, allowing for a more precise and customized representation of gene expression levels and activatory thresholds in the regulatory network under investigation, (iv) incorporation of prior network information derived from external hints and knowledge to improve the accuracy of network inference, and (v) the collective modeling of a reasonable number of regulatory TFs within a Boolean logic gate. The flexible maximum likelihood framework as we proposed has the potential of including higher order interactions and recognizing how multiple TFs can work together to control the target. Unlike correlation-based approaches that primarily focus on identifying statistical associations between variables, accounting for combinatorial control with Boolean rules can be more effective in capturing the non-linear causal relationships and interaction directionalities in a biological network.
We have demonstrated the ability of scGATE on predicting known combinatorial TFs regulatory relations on two simulated datasets and three real datasets. Our results justify the scope of reliability (as well as limitations) of scGATE’s predictions in application to new data with unknown regulatory interactions. We show that scGATE performs generally better when the search space is effectively reduced by usage of external hints such as mechanistically approved associations from ATAC-seq or ChIP-seq experiments. A comprehensive manual of data processing procedure and running the scGATE algorithm on new data is provided for users on the GitHub repository. scGATE is currently applicable to a rather small (<200) subset of genes with a refined list of candidate regulatory TFs based on external hints, prior information and speculative hypotheses, rather than attempting to infer the regulatory interactions from scratch in a large-scale dataset. Moreover, on large datasets with millions of cells, a cell downsampling strategy should be applied to reduce the scGATE’s runtime. To obtain statistically reliable inference, there should be a relationship between the numbers of genes and cells used in the analysis. To illustrate this, consider cell-type–specific networks in Figure 4 as example. These networks have an average number of 3.39 regulatory TFs (excluding non-functional TFs) acting per target gene. By considering 10 levels as a good approximation for the continuous expression profiles in the (0,1) interval, there are  states among regulatory TFs per target gene. In order to adequately sample this TFs’ state space, the cell numbers (
states among regulatory TFs per target gene. In order to adequately sample this TFs’ state space, the cell numbers (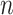 ) should be proportional to the TFs’ state numbers. Then,
) should be proportional to the TFs’ state numbers. Then, 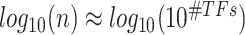 , which gives
, which gives  . This is evident in Figure 4, where we observe that the inference quality for this gene set saturates at around 3000 cells, with
. This is evident in Figure 4, where we observe that the inference quality for this gene set saturates at around 3000 cells, with 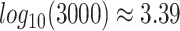 . As described before, 3.39 is the average number of regulatory TFs (input edges) per target gene in the synthesized cell-type–specific networks. Figure 5C also shows the scGATE’s runtime on 3000 cells considering all TFs (regulatory and decoy). As mentioned above, for an effective cell downsampling strategy on large datasets, the logarithm (base 10) of cell numbers should be at least equal to the average number of regulatory TFs (input edges) per target gene. The rough estimate of the input edge numbers per target gene can be obtained based on prior knowledge, speculations or association-based methods, e.g. Pearson correlation.
. As described before, 3.39 is the average number of regulatory TFs (input edges) per target gene in the synthesized cell-type–specific networks. Figure 5C also shows the scGATE’s runtime on 3000 cells considering all TFs (regulatory and decoy). As mentioned above, for an effective cell downsampling strategy on large datasets, the logarithm (base 10) of cell numbers should be at least equal to the average number of regulatory TFs (input edges) per target gene. The rough estimate of the input edge numbers per target gene can be obtained based on prior knowledge, speculations or association-based methods, e.g. Pearson correlation.
The ground-truth GRNs from ChIP-seq experiments that we used in the mouse tissues and human haematopoiesis, are consistent with our focus on identifying cooperative binding of TFs to the cis-regulatory regions of target genes, by incorporation of chromatin accessibility data as the external hint. However, several other types of interactions such as in large protein complexes will be missed both in our current model as well as the ground-truth. Then, besides scATAC-seq and TF binding motif data, incorporating protein–protein interaction networks as an additional source of external cues can enhance the effectiveness of the network inference algorithm. Another crucial avenue for future research involves the development of scGATE to effectively handle pseudotime-sorted single-cell data along differentiation trajectories. This approach would enable the modeling of temporal delays [37, 38] between dynamic alterations in epigenomic states, such as changes in chromatin accessibility and histone modifications within cis-regulatory elements such as enhancers, and the corresponding transcriptional profiles of target genes. Notably, during development, poised enhancers, which are known to exert crucial regulatory functions, exhibit changes in chromatin states and histone modifications prior to the activation of their target genes. By incorporating pseudotime-sorted single-cell data into the analysis, it would be possible to capture the temporal relationships and unravel the intricate interplay between epigenomic dynamics and gene expression during cellular differentiation. As computational approaches become increasingly vital for supporting experimental research in systems biology, these methodologies must continue to progress. Advancing the inference of intricate Boolean relationships among numerous factors with both high accuracy and computational efficiency represents an important future direction.
Even though, in this study, we focused on cooperative binding of TFs to the cis-regulatory regions of target genes, scGATE’s application can be extended to infer other types of regulatory interactions, by using knowledge from databases such as protein–protein affinity database STRING [39] or drug–target interaction DrugBank [40] for specific biological questions of interest. Specifically, employing scGATE for reconstructing higher order interactions, similar to those observed in large protein complexes involved in transcriptional regulation, would be an interesting research avenue. Moreover, scGATE enables researchers to unravel the effects of perturbations, such as gene knockout or overexpression experiments, on cellular states with greater precision. Unlike models that solely rely on first-order TF-gene interaction networks, scGATE employs Boolean logics to offer more reliable predictions regarding the state of target genes when their regulators are perturbed. This is crucial as it allows for a more comprehensive understanding of the intricate regulatory mechanisms governing gene expression in single-cell data [41]. scGATE can characterize the differential TF–gene interactions commonly observed between normal and diseased conditions. It provides insights into disease mechanisms and aids in identifying potential therapeutic targets for interventions.
Key Points
We introduce scGATE (single-cell gene regulatory gate) as a novel Boolean-based model for reconstructing context specific TF-gene networks using single-cell multi-omics data.
scGATE relies on the continuous scRNA-seq data, without binarization, to unveil complex combinatorial (higher order) interactions among regulatory TFs.
scGATE eliminates the need for individual formulations and likelihood calculations for each Boolean rule. Instead, it infers the Boolean rule within a Bayesian framework a posteriori, after fitting its specific model to the data.
scGATE outperforms other state-of-the-art tools in network inference.
ACKNOWLEDGEMENTS
The authors thank referees for their valuable comments and suggestions, which significantly improved this work.
CODE AND DATA AVAILABILITY
The mouse haematopoiesis scRNA-seq dataset is available from https://gottgens-lab.stemcells.cam.ac.uk/adultHSPC10X/. The processed file for the mouse haematopoiesis scRNA-seq dataset is also available at Zenodo https://doi.org/10.5281/zenodo.8353409. The base regulatory network associated with mouse haematopoiesis cell differentiation can be found in Krumsiek’s work [24]. Mouse tissues scRNA-seq dataset from Tabula Muris Consortium is downloaded from Gene Expression Omnibus (GEO) with accession ID GSE10974. This dataset is additionally available at https://github.com/czbiohub-sf/tabula-muris. Mouse tissues scATAC-seq dataset is downloaded from GEO with accession ID GSE11158. The ground-truth networks used in mouse tissues are derived by analyzing the TF ChIP-seq datasets in https://chip-atlas.org. Human haematopoiesis scRNA-seq dataset was downloaded from Supplementary file S2 from Buenrostro’s work [27] and human haematopoiesis scATAC-seq dataset is downloaded from GEO with accession ID GSE96772. The ground-truth networks (Cus KO and Cus
KO and Cus ChIP) used in the human haematopoiesis study are available in Cusanovich’s work [36]. The ground-truth networks for the mouse tissue and human haematopoiesis studies are additionally deposited at the GitHub page of this project at https://github.com/CompBioIPM/scGATE. All Jupyter and R notebooks for (synthesized and real scATAC-seq and scRNA-seq) dataset analyses are deposited at our GitHub page. The R package of scGATE, compiled in R version 4.1.3 and tested under both Windows and Linux environments, is available at our GitHub page. A detailed guideline with several example usages of scGATE is available in the Supplementary file (see Supplementary Data available online at http://bib.oxfordjournals.org/) and GitHub page https://github.com/CompBioIPM/scGATE. The base GRNs reconstructed with external hints in mouse tissue and human haematopoiesis datasets, together with other intermediate and processed files are available at Zenodo https://doi.org/10.5281/zenodo.8353409.
ChIP) used in the human haematopoiesis study are available in Cusanovich’s work [36]. The ground-truth networks for the mouse tissue and human haematopoiesis studies are additionally deposited at the GitHub page of this project at https://github.com/CompBioIPM/scGATE. All Jupyter and R notebooks for (synthesized and real scATAC-seq and scRNA-seq) dataset analyses are deposited at our GitHub page. The R package of scGATE, compiled in R version 4.1.3 and tested under both Windows and Linux environments, is available at our GitHub page. A detailed guideline with several example usages of scGATE is available in the Supplementary file (see Supplementary Data available online at http://bib.oxfordjournals.org/) and GitHub page https://github.com/CompBioIPM/scGATE. The base GRNs reconstructed with external hints in mouse tissue and human haematopoiesis datasets, together with other intermediate and processed files are available at Zenodo https://doi.org/10.5281/zenodo.8353409.
Supplementary Material
Author Biographies
Seyed Amir Malekpour is a senior postdoc research fellow at Institute for Research in Fundamental Sciences (IPM), with research interests in network reconstruction in biology leveraging logic-based models.
Laleh Haghverdi is leading the “Computational Methodologies and Omic Analytics” research group at the Berlin Institute for Medical Systems Biology, Max Delbrück Center (BIMSB-MDC) in the Helmholtz Association.
Mehdi Sadeghi is a professor and head of the Department of Medical Genetics at the National Institute of Genetic Engineering and Biotechnology. His research interests include bioinformatics and theoretical biology.
Contributor Information
Seyed Amir Malekpour, School of Biological Sciences, Institute for Research in Fundamental Sciences (IPM), 19395-5746, Tehran, Iran.
Laleh Haghverdi, Berlin Institute for Medical Systems Biology, Max Delbrück Center (BIMSB-MDC) in the Helmholtz Association, Berlin, Germany.
Mehdi Sadeghi, Department of Medical Genetics, National Institute of Genetic Engineering and Biotechnology, 1497716316, Tehran, Iran.
References
- 1. Chan TE, Stumpf MPH, Babtie AC. Gene regulatory network inference from single-cell data using multivariate information measures. Cell Systems 2017;5(3):251–267.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Specht AT, Li J. LEAP: constructing gene co-expression networks for single-cell RNA-sequencing data using pseudotime ordering. Bioinformatics 2016;33(5):764–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kim S. Ppcor: an r package for a fast calculation to semi-partial correlation coefficients. Commun Stat Appl Methods 2015;22(6):665–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Moerman T, Santos SA, González-Blas CB, et al. GRNBoost2 and Arboreto: efficient and scalable inference of gene regulatory networks. Bioinformatics 2018;35(12):2159–61. [DOI] [PubMed] [Google Scholar]
- 5. Sanchez-Castillo M, Blanco D, Tienda-Luna IM, et al. A Bayesian framework for the inference of gene regulatory networks from time and pseudo-time series data. Bioinformatics 2017;34(6):964–70. [DOI] [PubMed] [Google Scholar]
- 6. Malekpour SA, Shahdoust M, Aghdam R, et al. Wplogicnet: logic gate and structure inference in gene regulatory networks. Bioinformatics 2023;39(2):btad072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Moignard V, Woodhouse S, Haghverdi L, et al. Decoding the regulatory network of early blood development from single-cell gene expression measurements. Nat Biotechnol 2015;33(3):269–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Ocone A, Haghverdi L, Mueller NS, Theis FJ. Reconstructing gene regulatory dynamics from high-dimensional single-cell snapshot data. Bioinformatics 2015;31(12):i89–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Wang D, Yan K-K, Sisu C, et al. Loregic: a method to characterize the cooperative logic of regulatory factors. PLoS Comput Biol 2015;11(4):1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Yan B, Guan D, Wang C, et al. An integrative method to decode regulatory logics in gene transcription. Nat Commun 2017;8(1):1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Li L, Sun L, Chen G, et al. LogBTF: gene regulatory network inference using Boolean threshold network model from single-cell gene expression data. Bioinformatics 2023;39(5):btad256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Kamimoto K, Stringa B, Hoffmann CM, et al. Dissecting cell identity via network inference and in silico gene perturbation. Nature 2023;614:742–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Chen J, Cheong CW, Lan L, et al. DeepDRIM: a deep neural network to reconstruct cell-type-specific gene regulatory network using single-cell RNA-seq data. Brief Bioinform 2021; 22:08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Bashor CJ, Patel N, Choubey S, et al. Complex signal processing in synthetic gene circuits using cooperative regulatory assemblies. Science 2019;364(6440):593–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Malekpour SA, Alizad-Rahvar AR, Sadeghi M. Logicnet: probabilistic continuous logics in reconstructing gene regulatory networks. BMC Bioinform 2020;21(1):318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Cui T, Wang T. A comprehensive assessment of hurdle and zero-inflated models for single cell RNA-sequencing analysis. Brief Bioinform 2023;24:bbad272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Do C, Batzoglou S. What is the expectation maximization algorithm? Nat Biotechnol 2008;26(8):897–9. [DOI] [PubMed] [Google Scholar]
- 18. Vyshemirsky V, Girolami MA. Bayesian ranking of biochemical system models. Bioinformatics 2007;24(6):833–9. [DOI] [PubMed] [Google Scholar]
- 19. Chen G, Liu Z-P. Graph attention network for link prediction of gene regulations from single-cell RNA-sequencing data. Bioinformatics 2022;38(19):4522–9. [DOI] [PubMed] [Google Scholar]
- 20. Mao G, Pang Z, Zuo K, et al. Predicting gene regulatory links from single-cell RNA-seq data using graph neural networks. Brief Bioinform 2023;24:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Pratapa A, Jalihal AP, Law JN, et al. Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat Methods 2020;17(1):147–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Schaffter T, Marbach D, Floreano D. GeneNetWeaver: in silico benchmark generation and performance profiling of network inference methods. Bioinformatics 2011;27(16):2263–70. [DOI] [PubMed] [Google Scholar]
- 23. Dahlin JS, Hamey FK, Pijuan-Sala B, et al. A single-cell hematopoietic landscape resolves 8 lineage trajectories and defects in kit mutant mice. Blood 2018;131(21):e1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Krumsiek J, Marr C, Schroeder T, et al. Hierarchical differentiation of myeloid progenitors is encoded in the transcription factor network. PloS One 2011;6(8):1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. The Tabula Muris Consortium . Single-cell transcriptomics of 20 mouse organs creates a tabula muris. Nature 2018;562:367–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Cusanovich DA, Hill AJ, Aghamirzaie D, et al. A single-cell atlas of in vivo mammalian chromatin accessibility. Cell 2018;174(5):1309–1324.e18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Buenrostro JD, Ryan Corces M, Lareau CA, et al. Integrated single-cell analysis maps the continuous regulatory landscape of human hematopoietic differentiation. Cell 2018;173(6):1535–1548.e16PMID: 29706549; PMCID: PMC5989727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Alexander Wolf F, Angerer P, Theis FJ. Scanpy: large-scale single-cell gene expression data analysis. Genome Biol 2018;19(1):15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Blondel VD, Guillaume J-L, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks. J Stat Mech: Theory Exp 2008;2008(10):P10008. [Google Scholar]
- 30. Haghverdi L, Buettner F, Theis FJ. Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics 2015;31(18):2989–98. [DOI] [PubMed] [Google Scholar]
- 31. Sing T, Sander O, Beerenwinkel N, Lengauer T. ROCR: visualizing classifier performance in R. Bioinformatics 2005;21(20):3940–1. [DOI] [PubMed] [Google Scholar]
- 32. Greenfield A, Madar A, Ostrer H, Bonneau R. Dream4: combining genetic and dynamic information to identify biological networks and dynamical models. PLoS One 2010;5(10):1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Hao Y, Hao S, Andersen-Nissen E, et al. Integrated analysis of multimodal single-cell data. Cell 2021;184(13):3573–3587.e29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Cusanovich DA, Hill AJ, Aghamirzaie D, et al. A single-cell atlas of in vivo mammalian chromatin accessibility. Cell 2018;174(5):1309–1324.e18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Pliner HA, Packer JS, McFaline-Figueroa JL, et al. Cicero predicts cis-regulatory dna interactions from single-cell chromatin accessibility data. Mol Cell 2018;71(5):858–871.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Cusanovich DA, Pavlovic B, Pritchard JK, Gilad Y. The functional consequences of variation in transcription factor binding. PLoS Genet 2014;10(3):e1004226 PMID: 24603674; PMCID: PMC3945204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Zhang Y, Chang X, Liu X. Inference of gene regulatory networks using pseudo-time series data. Bioinformatics 2021;37(16):2423–31. [DOI] [PubMed] [Google Scholar]
- 38. Yu X, Chen J, Lyu A, et al. dynDeepDRIM: a dynamic deep learning model to infer direct regulatory interactions using time-course single-cell gene expression data. Brief Bioinform 2022;23:09. [DOI] [PubMed] [Google Scholar]
- 39. Szklarczyk D, Gable AL, Lyon D, et al. STRING v11: protein-protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res 2018;47(D1): D607–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Wishart DS, Feunang YD, Guo AC, et al. DrugBank 5.0: a major update to the DrugBank database for 2018. Nucleic Acids Res 2017;46(D1):D1074–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Nazaret A, Hong J, Azizi E, Blei D. Stable differentiable causal discovery. 2023; arXiv preprint arXiv:2311.10263.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The mouse haematopoiesis scRNA-seq dataset is available from https://gottgens-lab.stemcells.cam.ac.uk/adultHSPC10X/. The processed file for the mouse haematopoiesis scRNA-seq dataset is also available at Zenodo https://doi.org/10.5281/zenodo.8353409. The base regulatory network associated with mouse haematopoiesis cell differentiation can be found in Krumsiek’s work [24]. Mouse tissues scRNA-seq dataset from Tabula Muris Consortium is downloaded from Gene Expression Omnibus (GEO) with accession ID GSE10974. This dataset is additionally available at https://github.com/czbiohub-sf/tabula-muris. Mouse tissues scATAC-seq dataset is downloaded from GEO with accession ID GSE11158. The ground-truth networks used in mouse tissues are derived by analyzing the TF ChIP-seq datasets in https://chip-atlas.org. Human haematopoiesis scRNA-seq dataset was downloaded from Supplementary file S2 from Buenrostro’s work [27] and human haematopoiesis scATAC-seq dataset is downloaded from GEO with accession ID GSE96772. The ground-truth networks (Cus KO and Cus
KO and Cus ChIP) used in the human haematopoiesis study are available in Cusanovich’s work [36]. The ground-truth networks for the mouse tissue and human haematopoiesis studies are additionally deposited at the GitHub page of this project at https://github.com/CompBioIPM/scGATE. All Jupyter and R notebooks for (synthesized and real scATAC-seq and scRNA-seq) dataset analyses are deposited at our GitHub page. The R package of scGATE, compiled in R version 4.1.3 and tested under both Windows and Linux environments, is available at our GitHub page. A detailed guideline with several example usages of scGATE is available in the Supplementary file (see Supplementary Data available online at http://bib.oxfordjournals.org/) and GitHub page https://github.com/CompBioIPM/scGATE. The base GRNs reconstructed with external hints in mouse tissue and human haematopoiesis datasets, together with other intermediate and processed files are available at Zenodo https://doi.org/10.5281/zenodo.8353409.
ChIP) used in the human haematopoiesis study are available in Cusanovich’s work [36]. The ground-truth networks for the mouse tissue and human haematopoiesis studies are additionally deposited at the GitHub page of this project at https://github.com/CompBioIPM/scGATE. All Jupyter and R notebooks for (synthesized and real scATAC-seq and scRNA-seq) dataset analyses are deposited at our GitHub page. The R package of scGATE, compiled in R version 4.1.3 and tested under both Windows and Linux environments, is available at our GitHub page. A detailed guideline with several example usages of scGATE is available in the Supplementary file (see Supplementary Data available online at http://bib.oxfordjournals.org/) and GitHub page https://github.com/CompBioIPM/scGATE. The base GRNs reconstructed with external hints in mouse tissue and human haematopoiesis datasets, together with other intermediate and processed files are available at Zenodo https://doi.org/10.5281/zenodo.8353409.