A compartment and metapopulation model of Rocky Mountain spotted fever in southwestern United States and northern Mexico

Abstract

Rocky Mountain spotted fever (RMSF) is a fatal tick-borne zoonotic disease that has emerged as an epidemic in western North America since the turn of the 21st century. Along the US south-western border and across northern Mexico, the brown dog tick, Rhipicephalus sanguineus, is responsible for spreading the disease between dogs and humans. The widespread nature of the disease and the ongoing epidemics contrast with historically sporadic patterns of the disease. Because dogs are amplifying hosts for the Rickettsia rickettsii bacteria, transmission dynamics between dogs and ticks are critical for understanding the epidemic. In this paper, we developed a compartment metapopulation model and used it to explore the dynamics and drivers of RMSF in dogs and brown dog ticks in a theoretical region in western North America. We discovered that there is an extended lag—as much as two years—between introduction of the pathogen to a naïve population and epidemic-level transmission, suggesting that infected ticks could disseminate extensively before disease is detected. A single large city-size population of dogs was sufficient to maintain the disease over a decade and serve as a source for disease in surrounding smaller towns. This model is a novel tool that can be used to identify high risk areas and key intervention points for epidemic RMSF spread by brown dog ticks.

1. Introduction

Rocky Mountain spotted fever (RMSF) poses serious threat to public health and challenges paradigms surrounding the epidemiology of tick-borne diseases across North America. Caused by the bacterium Rickettsia rickettsii, small outbreaks of the disease associated with bites of brown dog ticks (Rhipicephalus sanguineus sensu lato) occurred during parts of the first half of the 20th century in rural villages in Mexico (Bustamante and Varela, 1943; Heyneman, 2001). From the 1950s onward, however, these epidemics diminished. In contrast, the disease continued sporadically in the United States, especially in the Midwest and eastern portions of the country, transmitted by the American dog tick (Dermacentor variabilis) (Biggs, 2016; Dalton et al., 1995; Treadwell et al., 2000; Álvarez-Hernández et al., 2017). In 2004, a cluster of RMSF cases was identified in eastern Arizona on American Indian tribal lands, and for the first time in the US, the disease was associated with brown dog ticks (Demma et al., 2005, 2006). Shortly thereafter, an epidemic of RMSF erupted in northern Sonora state in Mexico, followed by an epidemic in Mexicali in northern Baja California beginning in 2008 and then Tijuana about a decade later, continuing to extend farther south in Baja California (Zazueta et al., 2021; Álvarez-Hernández et al., 2017). Cases in Mexico now occur in urban centers, small towns, and rural areas in all states at the US-Mexican border and sporadically further south, with stunningly high case fatality rates, typically ranging from 10% to well over 30% and up to 47% in Sonora in 2022, compared with 5–7% in the US (Alvarez-Hernandez et al., 2015; Biggs, 2016; Secretaría de Salud Pública, Gobierno de Sonora, 2022). There is a disproportionate burden of disease and fatalities in children and people in marginalized neighborhoods (Alvarez-Hernandez et al., 2015; López-Castillo et al., 2018; Zavala-Castro et al., 2008). Outbreaks may occur in a city or neighborhood followed by an ongoing epidemic over multiple years, as has been the case in Mexicali, or the disease may disappear locally but reappear in another town, neighborhood, or region.

Explaining the drivers of the spread of RMSF and predicting human cases has proven challenging, and tools to guide early detection and intervention are needed. In silico models, where outbreaks can be simulated to predict disease emergence and assess the epidemiologic characteristics of disease, can be an invaluable tool to explain mechanisms of disease spread. Such models need to incorporate vector and host natural history and ecology. The RMSF epidemic in southwestern US and northern Mexico is dependent on the presence of dogs, both as hosts for the brown dog tick and amplifiers of disease (Piranda et al., 2011). In North America, the brown dog is two separate species, R. sanguineus sensu stricto (referred to as the temperate lineage) and a member of the R. sanguineus sensu lato group, or tropical lineage. In some regions, only a single lineage is found, while in others, lineages may be overlapping or even present simultaneously on the same dog (Brophy et al., 2022; Grant et al., 2023). They cannot be differentiated morphologically, are both associated with RMSF cases, and have very similar ecology (Brophy et al., 2022; Nava et al., 2015, 2018). Both lineages feed preferentially on dogs at all three host-feeding stages—larva, nymph, and adult—and a high density or consistently available dog population increases brown dog tick population density and shortens tick generation time (Dantas-Torres, 2010; Uspensky & Ioffe-Uspensky, 2002). Larvae and nymphs each feed once on a host, then molt to the next stage; the adult female feeds, mates with a male, and then lays a single, large clutch of eggs, before she dies (Dantas-Torres, 2008). All feeding stages are capable of transmitting R. rickettsii (Labruna et al., 2008; C. M. Ribeiro, Carvalho, et al., 2021). Most human cases in North America occur during summer months (Kjemtrup et al., 2022; Traeger et al., 2015; Zazueta et al., 2021; Álvarez-López et al., 2021) in part due to increased activity of brown and American dog ticks. For both lineages, increasing ambient temperature also decreases the duration of the preoviposition period for engorged brown dog tick females, incubation time for those eggs, and molt time for each life stage, while also causing ticks to approach hosts and feed more rapidly (Parola et al., 2008; Tian et al., 2022).

There are key host infection dynamics to model as well. Infected dogs may be rickettsemic for 3–10 days, during which time they may infect other attached ticks (Levin et al., 2014; Piranda et al., 2011). Although dogs may experience clinical signs or fatality with RMSF (Gasser et al., 2001; Keenan et al., 1977; Piranda et al., 2008), those that recover maintain IgG antibodies for at least a period of months and possibly longer (Levin et al., 2014; Piranda et al., 2008).

Outbreaks and persistent disease within an area depend on within-host and within-vector infection dynamics, host-vector interactions, density of dog population, demography of dogs (how fast the population turns over), and tick infestation levels (Pelosse et al., 2013; Rosà & Pugliese, 2007; Watts et al., 2009). Finally, disease dynamics overall depend on the interconnectedness of affected areas which can promote expansion and local re-emergence of the disease.

Identifying the key epidemiologic factors that have the greatest impact on RMSF transmission in dogs will help to prioritize further research and intervention, while characterizing metapopulation dynamics can inform improved surveillance. Transmission of R. rickettsii has been modeled in a number of ecological systems, but not for our target study region. For example, a model from Brazil showed that reduction of reservoir host (capybara) birth rate prevents disease establishment and spread (Polo et al., 2017). An early model found that American dog tick density was critical for RMSF transmission in the eastern United States, where the disease circulates between wildlife and ticks (Cooksey et al., 1990). Human cases in the US have been modeled as a function of environmental and socioeconomic conditions (Raghavan et al., 2016). None of these models, however, captures the ecology of the epidemic in northern Mexico and southwestern US, or addresses the spatial structure of pathogen spread. To address this gap, we developed a discrete time Markov Chain SIRS-SI compartment model—also known as an SIR model—to describe the transmission between domestic dogs and brown dog ticks. In an SIR model, dogs transition from susceptible (S) to infected (I) to recovered (R) and back to susceptible again (SIRS). The model was then adapted to a metapopulation framework to describe how RMSF moves between towns and cities within a region. A theoretical metapopulation, representing populations of dogs and ticks of multiple sizes consistent with those in towns and cities with brown dog tick-vectored RMSF, was used to explore dynamics of the disease in dogs and ticks. This foundational model provides an in silico framework that can be used to prioritize and test the effectiveness of dog and tick based interventions.

2. Methods

2.1. Pathogen dynamics: spread among dogs and ticks in a single patch

The model was built in R using R Studio, based on an earlier metapopulation compartment model (P. Foley et al., 2023; Plowright et al., 2011). In the model, dogs were infected with R. rickettsii after being bitten by infected ticks, and ticks were infected by feeding on infected dogs. Dog populations were assumed to remain constant due to equal per capita daily birth and death rates, and mortality caused by R. rickettsii infection was excluded from the model. Parameters for dog demographic characteristics, tick infestation rates, and pathogen transmission and acquisition were selected based, where possible, on published laboratory or field studies. When published data were unavailable, a range of biologically plausible values was tested via sensitivity analysis. The range of values used encompassed those relevant to both tropical and temperate lineages. The estimates and their sources are listed in Table 1.

Table 1.

Model parameters and symbology used in model. Estimate indicates value used in initial model trial; values in parentheses represent range of value used in sensitivity analysis.

Symbol	Description	Estimate	Range used in sensitivity analysis	Reference	Notes
${\beta }_{Larva}$	Probability larva will acquire pathogen from infected dog	0.11	0.05–0.30	Piranda et al. (2011)
${\beta }_{Nymph}$	Probability nymph will acquire pathogen from infected dog	0.35	0.1–0.7	Piranda et al. (2011)
${\beta }_{Adult}$	Probability adult will acquire pathogen from infected dog	0	0–0.25	Piranda et al. (2011)	Female ticks that are not infected until they are adults do not pass the infection on to offspring.
${\beta }_{Dog}$	Probability that a dog will become infected if fed on by infected tick	0.5	0.1–0.9	Binder et al. (2021)
$ToT$	Filial Transmission	0.37	0.05–0.75	Piranda et al. (2011)
$\gamma$	Recovery Rate	1/7	1/15-1/3	(Levin et al., 2014; Piranda et al., 2008, 2011)	Average duration of rickettsemia is 7 days
$\omega$	Loss of immunity	No loss of immunity	1/180-1/4000	Levin et al. (2014)
$\mu$	Daily per capita dog birth/death rate	0.001	0.0001–0.005	(Garcia et al., 2018; López-Pérez et al., 2020; Villatoro et al., 2016), others
$M_{Larva}$	Tick acquisition rate	25	7.25–100	(J. Foley et al., 2019; Tinoco-Gracia et al., 2009)	Maximum number of new ticks of each life stage feeding on a dog per day at highest point in season
$M_{Nymph}$		5	1.25–20
$M_{Adult}$		1	0.25–4
Time lag (Interstadial time)	Time (days) for ticks to move from one stage to the next	60	30–120	Louly et al. (2007)	Time it takes for tick to transition from one instar to next

Each tick life stage is divided into the proportion infected and the proportion susceptible and acquires the infection from infected dogs at a rate specific to the tick stage and subsequently maintains the infection through the molt to the next life stage (${\beta }_{L,N,A}$). A time lag ($TL$) was used to represent the time between ticks feeding on a dog (and potentially acquiring the infection) and feeding on a dog at a later time after molting; once a tick feeds, it drops out of the model for the duration of the time lag and re-enters the model as the next life stage. We initially set the $TL$ to 60 days, meaning that there would be two full tick life cycles occurring per year, and that the number of infected ticks feeding on dogs in the current time step was based on the infection rates from ticks of the previous instar that were feeding 60 days prior (t-60). A rolling average over three days of tick infection rates was used to account for real-life variability in molt time (for example ticks that molt and are host-seeking on day 200 of the model are likely to be a mix of ticks that fed 57 or 63 days prior, not all exactly 60 days prior). A subset of larvae emerging were already infected due to filial transmission (FT, the proportion of larvae emerging from eggs laid by an infected female).

We reported the maximum number of ticks expected to attach to a dog in a single day at the peak of tick season as the tick acquisition rate. Estimates for tick acquisition rate were derived from counts of adult ticks found on dogs in the literature, assuming that adult ticks feed for approximately 7 days (Levin et al., 2012), and that 20% of each life stage survives to re-infest and feed successfully during the next life stage (based on published ranges of values (Lorusso et al., 2010)). The tick acquisition rate was set to fluctuate throughout the year according to a coefficient created by a sinusoidal function that ranges between 0 and 1, with the highest number of ticks occurring midway through the year (North American summer), declining to 0 at December 31. To account for inter-annual variation, the beginning of each year for each model iteration was initialized using a coefficient that was selected randomly from a uniform distribution that determined whether tick numbers that year would be low, medium, or high.

The system of equations used for dogs in each compartment of the SIRS model is:

$$S\left(t+1\right)=S\left(t\right)+\mu \ast N-S\left(t\right)\ast \mu -NewI+\omega R\left(t\right)$$

$$I\left(t+1\right)=I\left(t\right)+NewI-\mu \ast I\left(t\right)-\gamma \ast I\left(t\right)$$

$$R\left(t+1\right)=R\left(t\right)+\gamma \ast I\left(t\right)-\mu \ast R\left(t\right)-\omega R\left(t\right)$$

The probability that a single dog is fed on and infected by at least one infected tick is described by the combined probability of being fed on by an infected tick of each stage. The number of ticks per stage varies according to time of year and whether it is a high, low or medium tick year, and is calculated as the product of the maximum tick acquisition rate for each tick stage, seasonal coefficient, and high/average/low tick year coefficient.

$$P_{\mathit{Inf}}=\left(1-{\left(1-I_{Larva}\left(t-TL\right)\right)}^{\#Larvae\left(t\right)}\ast {\left(1-I_{Nymph}\left(t-TL\right)\right)}^{\#Nymphs\left(t\right)}\ast {\left(1-I_{Adult}\left(t-TL\right)\right)}^{\#Adults\left(t\right)}\right)\ast \beta$$

The number of new expected cases in each time step is selected from the binomial distribution as a function of the total number of susceptible dogs (representing the total number of “trials”) and the probability of a single dog becoming infected.

$$NewI=Binomial\sim \left(S\left(t\right),P_{\mathit{Inf}}\right)$$

Because all ticks are either susceptible or infected, and ticks are accounted for as a proportion of total numbers, the susceptible population for each life stage is the proportion of infected ticks subtracted from one. The equations for infected ticks are:

$$I_{Larva}\left(t+1\right)=I_{Adult}\left(t\right)\ast \left(1-\frac{I_{Dog}\left(t\right)}{N_{Dog}}\right)\ast FT+I_{Adult}\left(t\right)\ast \left(\frac{I_{Dog}\left(t\right)}{N_{Dog}\left(t\right)}\right)\ast {\beta }_{Larva}$$

$$I_{Nymph}\left(t+1\right)=I_{Larva}\left(t\right)+S_{Larva}\left(t\right)\ast \left(\frac{I_{Dog}\left(t\right)}{N_{Dog}}\right)\ast {\beta }_{Nymph}$$

$$I_{Adult}\left(t+1\right)=I_{Nymph}\left(t\right)+S_{Nymph}\left(t\right)\ast \left(\frac{I_{Dog}\left(t\right)}{N_{Dog}}\right)\ast {\beta }_{Adult}$$

Pathogen dynamics within a single population of dogs and ticks were assessed by running the model across five canine population sizes, ranging from 500 to 500,000 dogs, representing the expected population sizes for small towns and cities. Infection was introduced to a completely naïve tick and dog population by introduction of a single infected dog at day 182 of the model (peak tick season designated for this model version). The model was run 1000 times per population size. Outcomes assessed were total number of infections in dogs, peak prevalence in dogs and infection rate in ticks, time between introduction and epidemic, proportion of introduction events that led to no outbreak (no secondary cases), a small outbreak (less than 20 secondary cases), or a large outbreak (>20 secondary cases), extinction of the pathogen (both prolonged absence of cases in dogs and tick infection rates reaching 0), number of outbreaks over the 10 year period, and relationship between tick infections and dog infections. In addition, the time until 1% of dogs (defined as epidemic-level) was assessed. The cutoff point between small and large outbreaks was determined post-hoc when it was determined that sustained outbreaks led to very large numbers of cases, while single outbreaks followed by pathogen extinction were associated with 20 or fewer cases.

2.2. Metapopulation dynamics

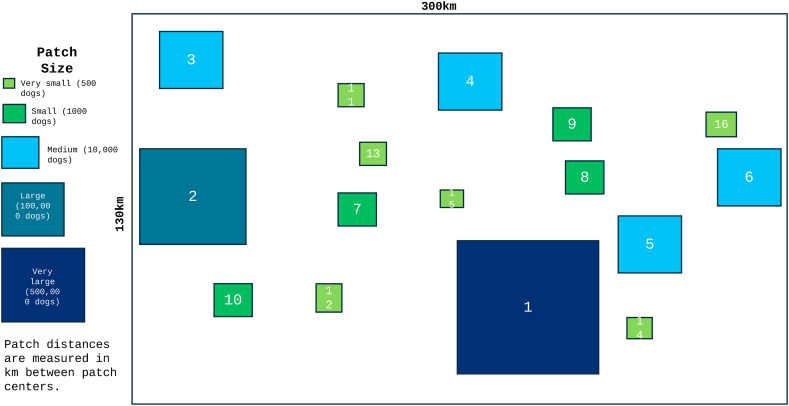
A geographically structured metapopulation was created to represent a diversity of patch sizes across a 39,000 km² region, for this exercise approximating impacted towns and cities in northern Baja California. Sixteen patches, ranging in population size from 500 dogs to 500,000 dogs, were placed within a 300 × 130 km grid (Fig. 1). Additional patches, patch locations, and patch characteristics can be adjusted and the metapopulation can be scaled up to any size; the geography used here is intended to represent the size of and range of distances between cities/towns found in northern Baja California. Distances between patch centroids were calculated within the model framework using R package geosphere based on latitude and longitude (Hijmans et al., 2022).

Fig. 1.

Schematic of the metapopulation structure, which spans a 300 km × 130 km area used in a compartment-metapopulation model of RMSF. Patch sizes range from 500 dogs (Very Small) to 500,000 dogs (Very Large). Patch size and distances between patches correspond to actual sizes and distances in an RMSF epidemic region in northern Mexico.

The number of infected dogs moving between each pair of patches, denoted as $I_{ij}$, was determined by: (1) the population size of the smaller patch and (2) a baseline estimate of 0.01% of dogs moving between patches with centers 1 km apart per day, decreasing inversely (at a rate of 1/distance in km) between patch centers. The actual number moving from each patch (${E(I}_{ij}\left)\right)$ was obtained by selecting a value from the Poisson distribution using $I_{ij}$ as the lambda value (${E(I}_{ij})\sim Pois\left(\left(I_{ij}\right)\right)\text{.}$ The population of the receiving patch was modified by increasing the number of infected dogs by the number being introduced and reducing the number of susceptible dogs by the same value, to prevent metapopulation interactions from changing dog population sizes. While the model allows for variability in birth/death rates and tick burden between patches, for this study we did not allow these values to vary among patches or model iterations.

The model was initially tested via the introduction of a single infected dog into Patch 2 (a large patch of 100,000 dogs) on the 182nd day of the first year of the model. Subsequently, the effect of introduction in patches of different size and connectivity was tested. The metapopulation model was run 1000 times for each trial. Measured outcomes included those used for single patch iterations, with addition of patch occupancy over the course of the model. A patch was defined as occupied if at least 5 cases occurred at any time point over the course of model duration. The model was then run for five additional sets of 1000 iterations, in which an infected dog was introduced to a different patch and patch occupancy and total number of cases assessed.

2.3. Large populations as a metapopulation

Although compartment models assume equal mixing within a population, this assumption is likely violated in large and very large towns and cities, where dog populations are, at least to some degree, separated by neighborhood. A single large patch was subdivided into 49 smaller patches comprising 10,200 dogs per neighborhood (equivalent to a single large patch of 500,000 dogs), and epidemic dynamics compared to the single large population.

2.4. Sensitivity analysis

To assess the impact of the size of dog population and dog movement on outbreak magnitude and metapopulation dynamics, these parameters were modified independently. For dog movement, we used 0.0001%, the baseline 0.001%, a reduced value of and 0.01%. For dog population, we compared results with half and double baseline dog population.

To assess model sensitivity to changes in the other input parameters, the model was run 1000 times using a random set of parameter values selected from the range of values from Table 1, using a uniform distribution for each range. For estimates that may be less than or greater than 1 (e.g., population multipliers), values were selected from the log of the value range, then exponentiated, to assure that the sampling space was of equal size on either side of 1. The impact of changing parameters on total number of cases, patch occupancy, and maximum infection rate in ticks was assessed via use of partial rank correlation coefficients (PRCC) using the epiR package in R (Carstensen et al., 2022). Resulting PRCC values closest to −1 or 1 indicating a parameter or model input with strong effects on the model output, while PRCC values closer to 0 indicate less sensitivity of the outputs to the given input parameter.

3. Results

3.1. Single patches

When running the model for patches of differing sizes, large outbreaks occurred in the majority of model iterations for all patch sizes between 91.5 and 93.9% of the model runs [Table 2]. Very small outbreaks (<20 cases) occurred in a 5.0–7.0% of model runs, and 0.9–1.5% of the model runs yielded no outbreak. Population size, therefore, had minimal impact on whether RMSF was able to spread in a patch (see Table 3).

Table 2.

Patch sizes and epidemiologic characteristics for single patches. Where median and mean values are calculated, only model iterations where cases occurred beyond the initial index case are included. Incident cases may exceed population size due to population turnover.

Patch Size	# of Dogs	Mean total number of incident cases ( ± SD)	Median Day of Peak Cases [Interquartile range]	Median First Day That Prevalence in Dogs >1%	% of iterations producing small outbreaks (1–20 cases)	% of iterations producing large outbreaks (>20 cases)	% Iterations with pathogen extinction in ticks by end of 10 years	Mean maximum prevalence in dogs (%) ( ± SD)
Very Small	500	1082 (567)	377 [321, 401]	231 [72, 299]	6.7	92.1	71.1	9.7 (2.4)
Small	1000	2527 (1179)	385 [365, 427]	294 [247, 322]	7.7	91.5	50.8	9.0 (2.2)
Medium	10,000	31578 (8659)	459 [402, 680]	367 [328, 426]	5.4	93.7	7.4	7.8 (2.2)
Large	100,000	305337 (87520)	679 [468, 752]	447 [387, 655]	5.9	92.8	7.3	7.1 (1.9)
Very Large	500,000	1506350 (395463)	744 [677, 819]	647 [447, 715]	5.0	93.9	6.1	7.2 (2.0)

Table 3.

Total number of cases, overall patch occupancy (percentage of patches occupied at any point over model run), and number of introductions leading to epidemic transmission).

Intro Patch Number	Patch Size	Total Cases ( ± SD)	Mean Patch Occupancy ( ± SD)	% of Introductions Leading to Epidemic in any patch
1	Very Large	1,728,299 (198,745)	16.6 (8.2)	91.6
2	Large	901,939 (592,137)	15.3 (8.0)	90.4
5	Medium	339,567 (528,603)	14.1 (8.4)	91.5
10	Small	32,866 (186,301)	7.5 (4.0)	90.4
12	Very Small	17,284 (148,445)	7.1 (3.2)	92.3

Regardless of patch size, all outbreaks followed a similar pattern after initial introduction. After introduction, no cases occur until the molt time (in this case 60 days) after which a maximum of 5 dogs/day is infected (or 10 in a small minority of outbreaks). Cases then quickly decline for at least several weeks in most iterations ahead of an epidemic if it occurred. However, the lag time until an epidemic occurred was markedly different between small and large patches. In Very Small and Small patches, epidemic-level prevalence is typically reached within the first year, with the epidemic peak occurring 377 days post-introduction for the very small patch [IQ range: 321–401] and 385 days for the small patch [IQ range: 365–427]) [Table 2]. In the Medium patch, prevalence exceeding 1% occurs at 367 days [IQ range: 328–426] and peaks three months after. In Large and Very Large patches, very low numbers of cases persist for much longer: for the Very Large patch, the median first day of epidemic-level transmission is 647 days post introduction (IQ range: 447–715) and the median epidemic peak occurs 2 years after introduction.

As expected, larger patches had larger numbers of total cases over the 10 years of the model duration. However, at the epidemic peak, maximum prevalence of dogs and infection rate in ticks was lower for larger patches. The maximum mean canine prevalence, calculated only using model iterations where outbreaks occurred, are shown in Table 2. The maximum mean adult tick infection rate ranged from 4.8% in very small patches to 4.1% in very large patches, following a similar pattern to that seen in dogs, where maximum prevalence was somewhat lower in Large than small patches, though maximum prevalence in dogs was markedly higher than maximum infection rate in ticks in all cases.

Extinction of R. rickettsii occurred much more frequently in smaller patches than larger patches over the 10 year model period. In the Very Small patch, the pathogen went extinct in 71.1% of iterations vs. 6.1% of iterations in the Very Large patch. Epidemic peaks—depending on the iteration—always occurred in spring, summer, or fall, and cases were always near zero around January 1, regardless of population size. In patches and iterations where epidemics occurred in multiple years—either annually or near annually—a small number of cases continued to occur through the winter months.

The median number of years in which peak prevalence in dogs reached 1% at least once was 6 for all patch sizes except for the Very Small patch which had a median number of years with outbreaks of 4. Both the Very Small and Small patches had much more variability across iterations in the number of years with epidemics (IQ range: 2–8 for the very small patch and 3–8 for the small patch) compared with larger patches (both the Large and Very Large patches had IQ ranges of 5–7).

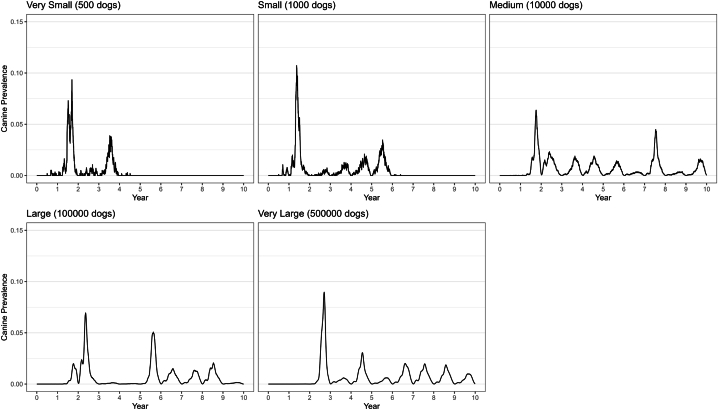
As shown in Fig. 2, in some cases—particularly for the Medium patch—infection in both ticks and dogs was maintained at very low levels for years before rising again and returning to seasonal oscillation.

Fig. 2.

Examples of typical results from a compartment-metapopulation model for each patch size (ranging from 500 to 500,000 dogs) showing RMSF prevalence in dogs over 10 years.

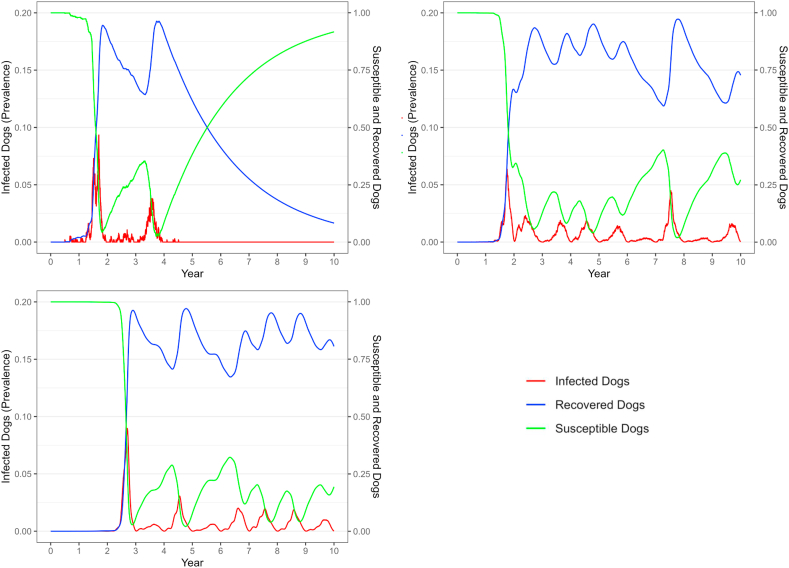
The development of population level immunity was highly dependent on patch size. In the Very Small and Small patches, nearly 100% of the population comprised recovered and immune dogs very early, then rapidly began to decline as cases declined, ultimately returning to nearly 0 by the end of 10 years due to lack of exposure and population turnover (Fig. 3). In the larger patches where cases continued to occur, the recovered population oscillated over a period of years between around 60% and 100%. When the susceptible population reached between 45 and 50%, a new surge of cases occurred in large populations.

Fig. 3.

RMSF susceptible, infected, and recovered dogs across time in three patch sizes from example iterations of a compartment-metapopulation model. Note that scale for Infected dogs is on the left axis and for Susceptible and Recovered on the right.

3.2. Relationship between prevalence in dogs and tick infection rate

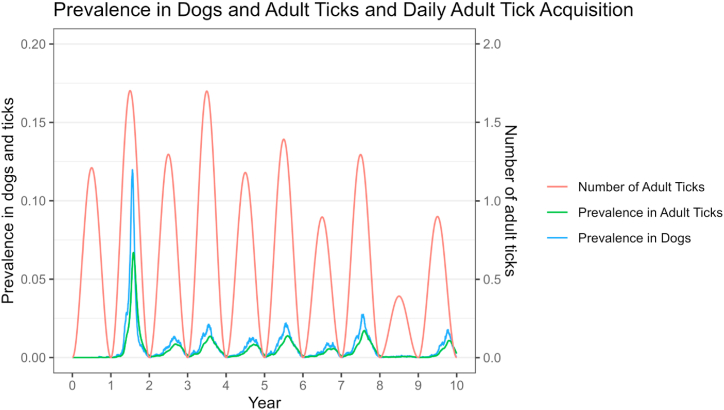
While varying in number depending on patch size, infection rate was always higher in adult vs. nymphal or larval ticks, due to adult ticks having more opportunities to have acquired the infection and incomplete transovarial transmission. Average adult infection infection rate was 1.7 times higher than nymphs, and nymphal infection rate was 1.3 times higher than larvae. There was a close relationship between number of ticks, infection infection rate in ticks, and prevalence in dogs, as shown in Fig. 5. However, in every year that there was an outbreak, tick numbers peaked before cases in dogs, and cases in dogs peaked 11–12 days before the peak in infection rate in ticks. There was more variability in the Small patches than Very Large (IQ range 6–16 days for Small and 10–14 days for Very Large). However, ticks that were becoming infected would not quest or feed again until the next life stage, increasing the time between the outbreak in dogs and detection of an increased infection rate in questing/hunting ticks.

Fig. 5.

Results from a compartment-metapopulation model showing number of adult ticks newly feeding on dogs per day and prevalence of R. rickettsii in adult ticks and dogs in a large patch (100,000 dogs).

3.3. Metapopulation results

When the metapopulation model was run introducing a single infected dog into large patch “#2”, 904 of 1000 iterations (90.4%) resulted in epidemics in at least one patch. The mean number of total cases across the entire metapopulation and full 10 years of the model, using only the 90.4% of iterations with epidemic transmission in at least one patch, was 901,939 ( ± 592,137).

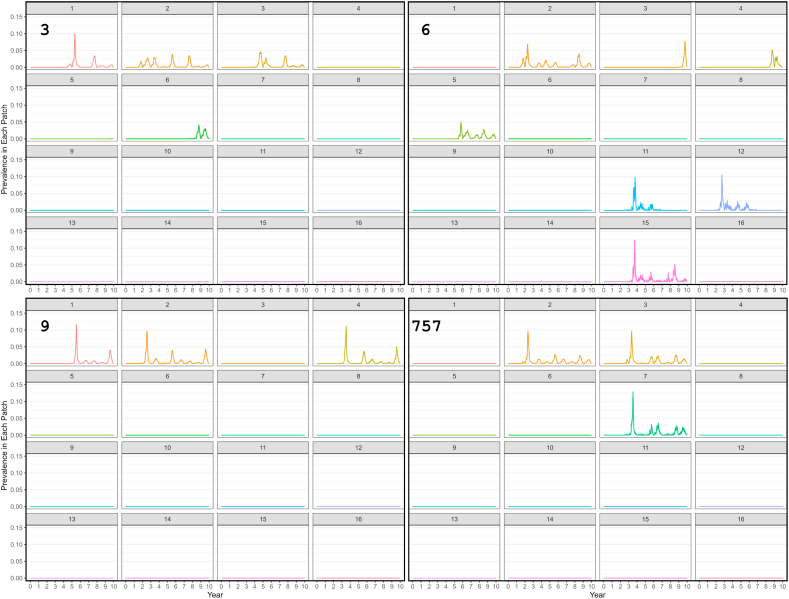
No iterations resulted in the presence of R. rickettsii in all patches (either simultaneously or at different times) over the course of the model; patch occupancy ranged from 6% of 16 patches where an outbreak occurred only in the introduction patch, to 50%. A representative summary of four outbreaks is shown in Fig. 4. All patches were occupied at least once in one or more model iteration, but smaller patches that were a greater distance from the introduction patch were occupied much less frequently: patches #12 and #14, for example (both very small patches), were the least frequently occupied, with occupancy only occurring in 1% of model iterations.

Fig. 4.

RMSF epidemic curves derived from a compartment-metapopulation model showing the variability in patch occupancy among four model iterations. Introduction of RMSF occurred in patch 2.

The average number of cases and patch occupancy over the course of ten years were sensitive to the particular patch into which the initial infection was introduced. When the pathogen established in a patch large enough to sustain it (i.e., a Large or Very Large patch), outbreaks occurred in other patches multiple years later throughout the 10 year model period. In some cases, this occurred primarily through sustained within-patch transmission, while in other cases, these recurring outbreaks were seen with extinct and then re-introduction in a particular patch, particularly in the smaller patches. In some cases, outbreaks in new patches continued to occur until almost the end of the model run of 10 years.

3.4. A single patch divided into a metapopulation

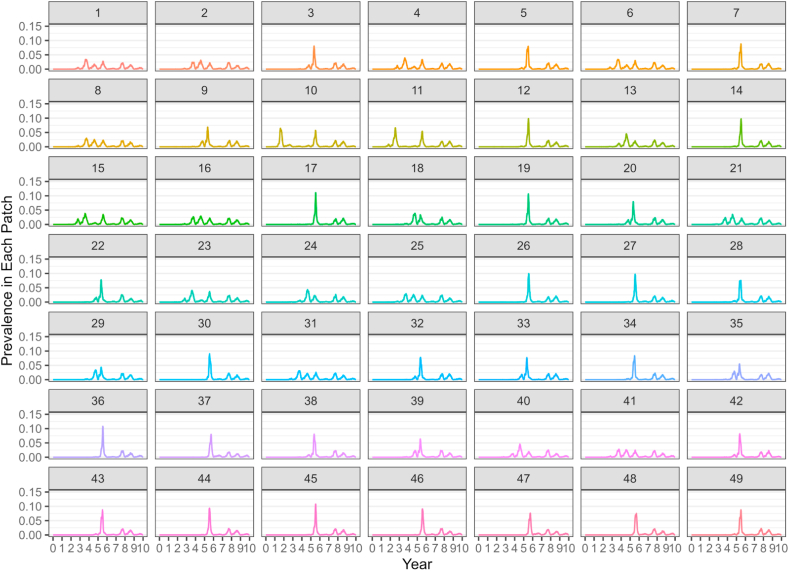
When a single large patch of 500,000 dogs was subdivided into 49 immediately patches of equal size, the mean number of total cases over the 10 year model period was 1,378,958 ( ± 133,811), which is lower than the 1,728,299 average cases in the single large patch. When the pathogen established in the introduction patch, it spread to all patches at least once for an overall patch occupancy of 100%. However, cases and epidemic peaks did not occur synchronously between all patches, with epidemic peaks occurring in year 2 for some patches and 3 or 4 for others. This delay may account for some of the reduction in cases. Additionally, in some iterations, complete extinction occurred in a subset of patches for short periods of time, then was maintained at very low levels prior to an epidemic peak occurring again late in the model run, as is shown in Fig. 6. In other iterations, synchronized, low amplitude annual outbreaks—with maximum annual prevalence less than 5%-- persisted through the end of the 10 year model run.

Fig. 6.

Results from a compartment-metapopulation model showing prevalence of RMSF in dogs in a very large population that has been subdivided into 49 patches of equal size (a 7 x 7 grid, 10,200 dogs per patch). The model was run for 10 years.

3.5. Sensitivity analysis: changing dog population and connectivity

Reducing the dog population across all patches by half resulted in a proportionate decrease in total cases: the mean number of cases in outbreaks was 490,469 ( ± 301,080) (median: 501,668, IQ range: 173,666–796,182), just over half of the number of cases in the baseline model run. Likewise, doubling the number of dogs resulted in an approximate doubling of the average total number of cases to 1,859,310 ( ± 1,198,514). Both decreasing and increasing the number of dogs increased the standard deviation, however. Mean patch occupancy remained essentially unchanged with both an increase and decrease in dog population: for the halved dog population, mean patch occupancy was 16.1% ( ± 8.0) and for the doubled population, it was 15.5% ( ± 8.0%).

Reducing the dog movement rate by 90% resulted in a marked decrease in total mean cases, to 409,525 ( ± 289,394), with a marked decrease in patch occupancy, to 7.2% ( ± 2.5%). Increasing the movement rate by 10 increased the mean number of cases to 1,776,448 ( ± 193,171), nearly double, and markedly increased the mean patch occupancy to 69.5% ( ± 13.4%).

3.6. Sensitivity analysis: PRCC

Results of the PRCC in the metapopulation indicated that total cases, maximum infection rate in ticks, and patch occupancy are all sensitive to both dog and tick related model parameters [Table 4]. The per capita birth rate and recovery rate (duration of infection) in dogs were both highly influential for the total number of cases and the maximum infection rate in ticks, with significant impacts on pathogen dynamics; patch occupancy was also sensitive to recovery rate, though not to the birth rate.

Table 4.

Partial rank correlation coefficient (PRCC) values for select model parameters and outputs.

	Outcome Measures
	Total Cases		Maximum Tick Infection Rate		Patch Occupancy over 10 years
Parameter	Estimate [95% CI]	p-value	Estimate [95% CI]	p-value	Estimate [95% CI]	p-value
Dog population size	0.33 [0.27, 0.39]	<0.01	−0.01 [-0.07, −0.05]	0.82	0.00 [-0.07, 0.06]	0.89
Dog movement	0.02 [-0.05, 0.08]	0.61	0.04 [-0.02, 0.10]	0.20	0.01 [-0.05, 0.07]	0.71
$\mu$ (Daily per capita birth/death rate)	0.48 [0.42, 0.53]	<0.01	0.10 [0.04, 0.16]	<0.01	0.24 [0.18, 0.30]	0.30
$\omega$ (Loss of Immunity)	−0.09 [-0.15, −0.02]	0.02	−0.02 [-0.08, 0.04]	0.51	−0.05 [-0.12, 0.01]	0.09
$M_{Adult}$	0.51 [0.45, 0.56]	0.01	0.57 [0.52, 0.62]	<0.01	0.46 [0.41, 0.52]	<0.01
$\gamma$ (recovery rate)	−0.38 [-0.44, −0.32]	<0.01	−0.76 [-0.80, −0.72]	<0.01	−0.44 [-0.49, −0.38]	<0.01
Ratio of adults to immature stages	0.1 [0.04, 0.17]	<0.01	0.54 [0.48, 0.59]	<0.01	0.37 [0.32, 0.43]	<0.01
${\beta }_{Larva}$	0.02 [-0.04, 0.08]	<0.53	0.18 [0.12, 0.24]	<0.01	0.04 [-0.03, 0.10]	0.27
${\beta }_{Nymph}$	0.27 [0.21, 0.23]	<0.01	0.68 [0.63, 0.72]	<0.01	0.26 [0.20, 0.32]	<0.01
${\beta }_{Adult}$	0.06 [0.00, 0.12]	0.07	0.33 [0.27, 0.39]	<0.01	0.03 [-0.03, 0.10]	0.13
$ToT$	0.47 [0.42, 0.43]	<0.01	0.90 [0.87, 0.92]	<0.01	0.43 [0.38, 0.49]	<0.01
Year 1: low, high, or medium tick year	0.10 [0.04, 0.17]	<0.01	0.10 [0.04, 0.16]	<0.01	0.12 [0.06, 0.18]	<0.01
Interstadial time (TL, or tick lag)	−0.07 [-0.13, −0.01]	0.02	−0.15 [-0.22, −0.09]	<0.01	−0.08 (−0.15, −0.02)	0.01

Allowing the number of adult ticks feeding on dogs to change resulted in significant changes in total number of cases occurring in all patches, patch occupancy, and maximum infection rate in ticks. Likewise, if it was year with higher numbers of ticks at the time of pathogen introduction to the metapopulation, all three values (cases, occupancy, and maximum infection rate in ticks) varied as well. Changing the ratio of immature ticks to adults also impacted the three outcomes significantly, as did changes in filial transmission and interstadial time, i.e. the time it takes for ticks to move from one life stage to the next. Shorter generation time which derived from shorter interstadial time increased pathogen transmission. Variation in the rates at which each tick stage acquires the pathogen from infected dogs ($\beta$ values) had less consistent impacts on the model. Total cases, maximum tick infection rate, and patch occupancy were all significantly sensitive to changes in ${\beta }_{Nymph}$, while total dog cases and patch occupancy were not sensitive to changes in ${\beta }_{Larva}$ and ${\beta }_{Adult}$ values.

Years with higher numbers of ticks at the time of introduction of a single infected dog in year 1 had increased numbers of infected dogs, infection rate in ticks, and patch occupancy. The frequency with which larval and nymphal ticks acquired R. rickettsii from dogs was also positively and significantly associated with those three model outcomes, though for adult ticks, only maximum infection rate in ticks was significant.

4. Discussion

With ongoing epidemics of RMSF in multiple areas near the US-Mexico border, managing dogs and brown dog ticks is essential for controlling the disease. Dogs amplify the pathogen when infected, serving as a source of infection for other feeding ticks, and ticks subsequently act as both vectors and reservoirs for the pathogen, maintaining it transovarially, passing it to future generations of ticks, and helping maintain endemic disease (Demma et al., 2006; Piranda et al., 2011). Epidemics in the southwestern United States and northern Mexico are driven by spillover from dogs and brown dog ticks (Parola et al., 2008; Zazueta et al., 2021), although the risk of human infection may also be mediated by factors such as weather/climatic conditions. Importantly, people's knowledge about risk and personal protection will also impact disease spread. Two information needs that could help address RMSF within a One Health context are to determine the most impactful and yet most feasible strategies to reduce RMSF, and to understand features of towns, cities, and neighborhoods that increase risk for RMSF. Modeling RMSF dynamics in canine and tick populations can inform how and when human cases may occur and could be a key tool in addressing the public health risks of rickettsial diseases.

To date, most of the epidemiological studies of RMSF in western North America have been either focused on human cases or been cross-sectional investigations into the prevalence and exposure to pathogen in dogs (Beristain-Ruiz et al., 2022; J. Foley et al., 2019; McQuiston et al., 2011). Informed by prior studies, we modeled RMSF using a combined compartment and metapopulation model, creating a framework that can be used across various geographic regions, with parameters and model inputs updated according to tick and dog information available in the area. We identified several key targets for interventions and further research, and demonstrated that disease may cycle continuously in a large population, serving as a source of repeated introductions and subsequent outbreaks in smaller populations.

When the SIR model simulated individual variably sized patches, pathogen extinction occurred much more frequently in smaller patches than larger patches. In the metapopulation, comprising a mix of larger and smaller patches consistent with dog populations in northern Baja California, patches of 100,000 and 500,000 dogs maintained RMSF consistently, whereas intermittent outbreaks occurred in smaller patches as extinction occurred and disease was then reintroduced. This is a pattern that has been observed when dynamics of other vector-borne diseases have been examined, where large subpopulations are responsible for maintaining pathogens (Adams & Kapan, 2009; Caraco et al., 2001). Compartment models typically assume that there is homogenous exposure within a population, which is unlikely to be the case for RMSF in large cities, where in reality, dogs closer to the point of introduction are likely to be exposed first. A large city would more accurately also be represented by a metapopulation, because dogs within a neighborhood share similar exposure risk that differs from adjacent neighborhoods. This problem of assuming homogenous mixing has been reported before for models even applied to a single patch (Zachreson et al., 2022). To explore this concern, we modeled a single very large population of dogs subdivided into 49 smaller patches. Resulting disease dynamics did not differ greatly from when the large population was modeled as a single unit, suggesting that the assumption of homogenous mixing within patches was not a major factor is the SIR model. The model also assumes that dogs within a patch all have equal tick exposure when in reality rates of infestation differ depending on use of tick preventives, breed, dog age (with younger dogs more likely to be infested than older dogs), and whether dogs live indoors or are free roaming (Dantas-Torres, 2010; Dantas-Torres & Otranto, 2011). With more data on these variables, the dog population could be stratified into different risk groups in the model, improving the precision of estimated pathogen dynamics.

As expected when comparing outcomes in differently sized patches, the total number of RMSF cases was significantly larger in larger than smaller patches, where there were more dogs present to be infected. However, the mean peak infection prevalence in dogs was 2.7% higher in very small patches than very large patches. This occurred because a single dog could infect a larger proportion of the total number of ticks in a small population than in a large population; therefore as soon as even the first infected dog is introduced, the infection rate in ticks—though still very low initially—is higher in the smaller patch, and a larger proportion of dogs are infected sooner. Early detection of RMSF circulating within the dog and tick population is critical for prevention of human cases and implementation of control efforts, and these results suggest that detection in a large population may be even more difficult in a large patch or population than small population. Potential targets for surveillance include collection and testing of ticks and use of dogs as sentinels. The results of this model, however, highlight several challenges with respect to surveillance. The lag observed between introduction of the pathogen and epidemic-level transmission (here defined as a prevalence greater than 1%) ranged from over a year in patches with smaller populations to over two years in very large populations. The time between epidemic-level transmission and the epidemic peak tended to be short—around 3 months or less, depending on patch size—leaving limited time between detection and opportunity for intervention. If there is reason to believe that RMSF may be present in an area, then tick numbers on dogs may serve as a proxy indicator of risk, as model results showed that tick numbers—both at the time of initial pathogen introduction and during outbreaks—were strong drivers of case numbers. In prior modeling research, tick (Ixodes ricinus) survival was the key predictor for time to establishment as well as increased prevalence of anaplasmosis and borreliosis (Ackleh & Veprauskas, 2022), sharing similar features with results obtained in this RMSF model and highlighting the importance of tick management.

Numerous studies have quantified adult R. sanguineus s.l. ticks infesting dogs, with many fewer larvae and nymphs found than adults (Dantas-Torres & Otranto, 2011; Lorusso et al., 2010; Tinoco-Gracia et al., 2009). Given the difficulty in detecting the much smaller larvae and nymphs, this is unsurprising, but it is a gap in knowledge that limits refinement of the model and understanding transmission. We assumed that there are five times more nymphs than adults feeding on a dog, and five times more larvae than nymphs. However, our results suggest that nymphs are responsible for a greater number of infections, and therefore, it becomes critical to detect and quantify nymphs and understand the seasonality of each life stage. We also assumed that numbers of ticks in each life stage fluctuate concordantly, but in reality seasonality may differ across life stages, and this seasonal pattern may be substantially different among geographic regions, with high synchrony and minimal fluctuation in tick populations in climates that are hospitable year round, and more asynchronous with greater annual variation in other regions (Gray et al., 2013; Tian et al., 2022). This seasonality appears to differ between lineages (Grant et al., 2023; Labruna et al., 2017) and is related to ecological conditions, but hasn't been well-described in the current epidemic regions. If further investigation indicates that there are significant differences in vectorial capacity and life history between tropical and temperate lineages, the model could be parameterized with separate sets of values for regions where the tropical lineage, temperate lineage, or a mix are present. In the model, reproductive and feeding characteristics for ticks can be updated according to observations in a particular location without needing to perform lineage testing, and given that weather and climatic variables affect both lineages, this is likely a more important knowledge deficit than lineage itself (Tian et al., 2022). A laboratory comparison of the vectorial competence of the two lineages remains a knowledge deficit that would improve both the model and disease interventions.

Ideally, model performance would be validated against field data. However, no published data (to this point) exists on RMSF cases in dogs over time at the population level. In contrast, serological data suggest that in areas of current and recent RMSF outbreaks in northern Mexico, exposure in dogs is extremely high—between 50 and 75%—which is consistent with model results (Backus et al., 2023; J. Foley et al., 2019). Given that exposure appears extremely high in dogs where outbreaks have occurred without widespread reports of canine fatalities, disease-specific mortality was excluded from the model. A prior model of disease in wolves indicated that disease (mange and distemper) may influence canine population structure and that population structure influences disease transmission (Brandell et al., 2021). Our model however does not examine the effects of RMSF on canine population structure, something that might be incorporated in future work.

The duration of time that dogs are infectious is another model parameter that is not well understood and could be important for disease dynamics. Unlike other rickettsial diseases, such as Mediterranean spotted fever caused by R. conorii, the RMSF infectious period is relatively short in dogs (estimated to be 7 days on average in the model). However, data on the infectious period comes from laboratory-infected dogs, who may receive higher infective doses than dogs that are naturally infected (Levin et al., 2014). Moreover, because model outcomes were strongly influenced by variation in the infectious period, data on infectious period variability are needed. Similarly, more data are needed on average and maximum duration of time that dogs remain immune after exposure. In all model runs performed here, it was assumed that return to susceptibility was negligible. The literature documents a 6–9 month minimum period of immunity in dogs (Levin et al., 2014; Piranda et al., 2011) and rickettsial antibodies in other species have been demonstrated to persist for years, which would likely be prolonged during repeated exposure when R. rickettsii exposure is widespread (Ramírez-Hernández et al., 2020). However, a population may become more susceptible (to any disease) either because previously infected and recovered dogs lose immunity or due to rapid population turnover (increased births of susceptible puppies and death of immune dogs). While the limits of canine duration of immunity are not clearly defined, sensitivity analysis confirmed that the model is more susceptible to the introduction of susceptible dogs via changes in birth rate than by return to immunity. This also highlights that reducing canine birth rates (e.g., via spay/neuter) is a key intervention point, and suggests that a more stable, long-lived population with a lower birth rate would likely decrease cases. Other control methods such as reducing dog overpopulation, and particularly reducing the number of free-roaming dogs), could contribute to risk reduction, as owned dogs that are permitted to roam have higher numbers of ticks than dogs that are not permitted to roam, and subsequently higher risk of RMSF exposure (J. Foley et al., 2024; Yaglom et al., 2018). Vaccines, if and when they become available, may also help reduce rates of circulating R. rickettsii by decreasing the size of the susceptible population (Ribeiro et al., 2021; Walker et al., 2022).

In the model, R. rickettsii was always introduced at the peak of tick season. However, if introduction were to occur at any other point during the year, secondary cases would likely occur less frequently due to there being fewer ticks available to feed on the infected dog. In addition, we did not consider possible movement between locations of infected ticks by an uninfected dog which theoretically could introduce the pathogen to a new location. With respect to the model, it is unlikely that this assumption significantly changes the outcome, given that infection rate in ticks reflects prevalence in dogs, and ticks move among patches in proportion to dog movement. When considering real-life interventions on movement of dogs, it is important to address that moving a healthy dog may still be risky if it is carrying infected ticks.

Compartment models have been utilized to model numerous human and veterinary diseases. The value of employing a metapopulation approach to account for spatial structure when modeling disease is increasingly recognized, especially when studying disease dynamics across a large area and at different spatial scales (Keeling et al., 2004). A good but slighter older paper provides a review of such approaches (Wang and Li 2014). A very recent paper compares host and pathogen dynamics in metapopulations of water voles exposed to vector-borne parasites with various life histories (Mackenzie et al., 2023). Coupled single and metapopulation disease models can become highly technical and may suffer in usefulness and tractability as a result (Watts et al., 2005). A previous model utilized a metapopulation and SIR framework to describe tick colonization in patches (Kada et al., 2017), and this present model was an extension of a model of mange transmission among canids in a metapopulation (P. Foley et al., 2023). Several researchers have highlighted the importance of allowing model parameters to vary among patches due to spatial heterogeneity in host and vector distribution (Gaff & Gross, 2007; Mackenzie et al., 2023), a technique that was employed in our model by allowing reproduction rates and tick burdens to vary among patches. Another feature that we considered to be crucial was stochasticity, because it is a feature of natural disease systems and becomes especially important in very early introductions. Stochasticity can be introduced into various parts of the tick, host, pathogen, and interaction terms in the model. A comparison of the same tick-borne disease model with and without stochasticity resulted in very important differences in outcome, with stochasticity making it clear that host (deer) movement and not tick introduction was particularly responsible for disease outbreaks (Maliyoni et al., 2017).

Continuing to refine model inputs as additional information is obtained will be critical to the model's utility as a tool to identify high risk populations and evaluate interventions. The data obtained here, as well as observation of the epidemic across northern Mexico, suggest that complete eradication will be unlikely, as the epidemic ebbs and recurs (Zazueta et al., 2021). Long term management, then, will require a combination of developing effective, multiple-modal interventions that are targeted to areas of highest risk. Development of a flexible, adaptable model is a key step in understanding the dynamics that drive RMSF epidemics, as well as directing surveillance and management resources effectively.

Funding

This project was funded by the Pacific Southwest Regional Center of Excellence for Vector-borne Diseases funded by the US Centers for Disease Control and Prevention (Cooperative Agreement 1U01CK000649).

Conflict of interest

Janet Foley, Laura Backus, and Patrick Foley report no conflicts of interest relating to this submitted work. The template link on the page https://www.keaipublishing.com/en/journals/infectious-disease-modelling/guide-for-authors/is non-functional and links to a “page not found”.

CRediT authorship contribution statement

Laura Backus: Writing – original draft, Formal analysis, Data curation, Conceptualization. Patrick Foley: Writing – original draft, Methodology, Formal analysis, Conceptualization. Janet Foley: Writing – review & editing, Writing – original draft, Supervision, Project administration, Funding acquisition, Conceptualization.

Handling Editor: Yijun Lou