Skip to main content
PMC home page
Health Research Alliance Author Manuscripts logoLink to Health Research Alliance Author Manuscripts
. Author manuscript; available in PMC: 2024 Apr 24.
Published in final edited form as: Ann Thorac Surg. 2020 Apr 3;110(5):1605–1614. doi: 10.1016/j.athoracsur.2020.02.064

Tricuspid annuloplasty rings: A quantitative comparison of size, non-planar shape, and stiffness

Mrudang Mathur 1, Marcin Malinowski 2,3, Tomasz A Timek 2, Manuel K Rausch 4,5,6
PMCID: PMC11040511  NIHMSID: NIHMS1984361  PMID: 32251659

Abstract

Background:

Functional tricuspid regurgitation due to annular and ventricular dilatation is increasingly recognized as a significant source of morbidity and mortality. To repair the annulus, surgeons implant one of many annuloplasty devices that differ in size, 3D shape, and stiffness. However, there have been no quantitative comparisons between various available devices.

Methods:

Three-dimensional scanning, μCT imaging, analytical methods, and mechanical tests were used to compare three Edwards Lifesciences and three Medtronic annuloplasty devices of all available sizes. We measured in-plane metrics of maximum diameter, perimeter, area, height as well as elevation and curvature profiles. Furthermore, we computed bending stiffness as well as the maximum and minimum axes of the bending stiffness.

Results:

Most annular prostheses differed little in their in-plane geometries but varied significantly in height. In-plane properties deviated significantly from measurements of healthy human tricuspid annuli. Height of the Edwards’ MC3 and Medtronic’s Contour 3D resembled healthy human tricuspid valve annuli, while the Edwards’ Physio and Classic, and Medtronic’s TriAd did not. Additionally, the elevation profiles of the MC3 and Contour 3D and curvature profiles between all devices were consistent and matched those of healthy human annuli. The tested devices also differed in their bending stiffness, both in terms of absolute values and their maximum and minimum axes.

Conclusions:

Contoured devices, such as Edwards’ MC3 and Medtronic’s Contour 3D, most accurately resembled the healthy human tricuspid annulus but differed significantly in bending stiffness. To what extent prosthesis properties and shape affect tricuspid valve function remains to be determined.

Graphical Abstract

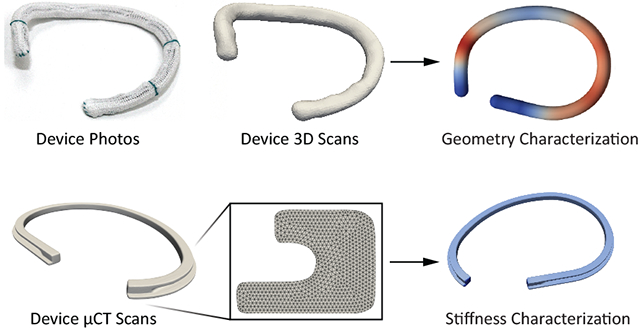
graphic file with name nihms-1984361-f0001.jpg

Introduction

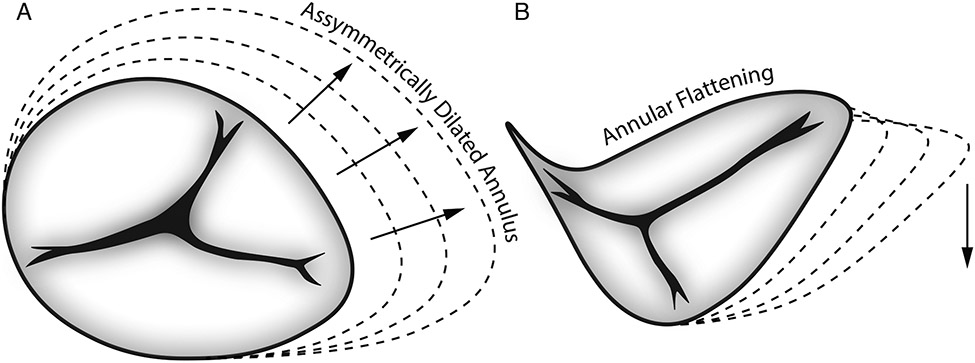
Functional tricuspid valve regurgitation (FTR) is a common co-morbidity of mitral valve disease with 30-50% of patients with severe mitral valve regurgitation also suffering from tricuspid valve insufficiency1. While FTR was mostly ignored in the past, today’s guidelines recommend treating tricuspid valve regurgitation concomitant to mitral valve surgery for mild-to-severe TR and for patients with annuli larger than 40 mm2. Currently, the majority of TR cases are treated surgically via prosthetic ring annuloplasty. Consequently, every year approximately 8000 patients in the US undergo implantation of annuloplasty devices designed to reshape and remodel the tricuspid annulus and reestablish proper valve coaptation and function3. In the great majority of surgical cases, TR is functional and believed to be due to valve-extrinsic causes rather than organic valve failure4. In functional TR, the tricuspid annulus is dilated and flattened5, Figure 1, thus annular devices are designed and selected to both downsize the annulus and to recreate its three-dimensional configuration6,7. To this end, numerous prostheses are commercially available but potentially differ in three key parameters: i) size, ii) 3D shape, iii) stiffness. Device shape may be denoted as “flat” or “remodeling/contoured” and stiffness described as “flexible”, “semi-rigid”, and “rigid”. While most manufacturers publish information about device size and 3D shape, these data are usually sparse and insufficient to describe the devices’ complex geometries and mechanical properties. As contemporary surgical outcomes of tricuspid annuloplasty are sub-optimal with recurrent significant TR in up to 18% of patients8,9, annuloplasty device selection, at least in part, may determine surgical success. To better inform device selection, the objective of this work was to accurately quantify and compare size, 3D shape, and stiffness of six commercially available annuloplasty devices.

Figure 1:

Figure 1:

Open in a new tab

Illustration of annular changes between the healthy and the diseased tricuspid valve.

Methods

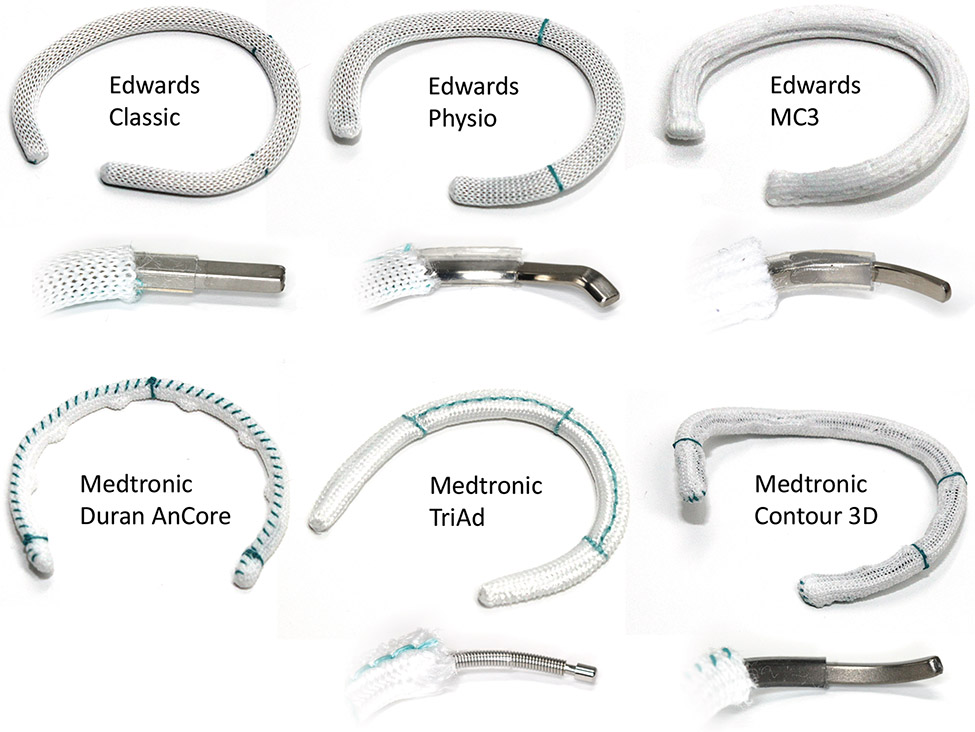
We tested Carpentier-Edwards Classic® Ring model 4500 (Classic), Carpentier-Edwards Physio® Tricuspid Ring model 6200 (Physio), Edwards MC3® Tricuspid Ring model 4900 (MC3) [Edwards Lifesciences, Irvine, CA, USA] and Medtronic Duran AnCore ® Band model 620B (Duran), TriAd Adams® Band model 900SFC (TriAd), and Contour 3D ® Ring model 690R (Contour) [Medtronic, Minneapolis, MN, USA] in all available sizes 26-36mm (Figure 2).

Figure 2:

Figure 2:

Open in a new tab

Photographs of six annuloplasty devices and their layered designs. Shown are sizes 30.

3D Scans and Geometric Modeling

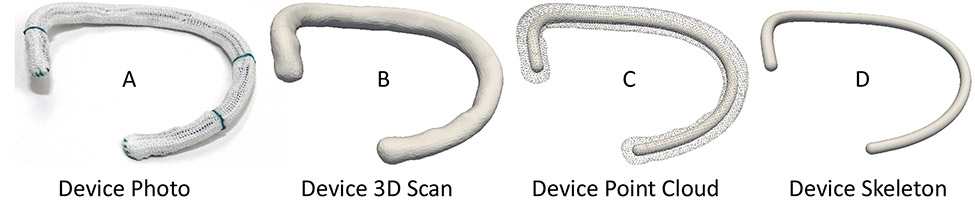
All annuloplasty devices (except for the Duran band) were carefully mounted on our 3D scanner (Ultra HD, NextEngine, Santa Monica, CA, USA). Next, 3D images were acquired and geometries were reconstructed, reduced to 3D point clouds, and point clouds skeletonized, see Figure 3. All simple geometric metrics (i.e., max diameter, perimeter, height, and area) and continuous metrics (i.e., elevation and curvature profiles) were based on those skeletonized centerlines.

Figure 3:

Figure 3:

Open in a new tab

Simple modeling pipeline from A) physical device to B) 3D scan to C) point cloud, and finally D) skeletonized center line. Shown as an example is the size 30 Medtronic Contour 3D device.

Specifically, we computed maximum diameter as the largest distance between any two points along the length of those centerlines, perimeter as the arc-length integral between the two ends of the centerline, height as the largest orthogonal distance between any two points along the centerline, and area as the area of the convex hull to the projection of the centerline onto its least-squares plane. Note, we are comparing these geometric measures in the results section against measures of the healthy and diseased annulus as published10,11. For the continuous elevation profiles, we computed the orthogonal distance between each point on the centerline and their least-squares plane. For the continuous curvature profiles, we computed the curvature using a standard formula based on the first and second derivatives of a best fit spline with respect to the arc-length parameter12,13.

Mechanical Testing

The stiffness of the Duran device and the flexible ends of the TriAd device were characterized using tensile testing. Two ends of the Duran and the TriAd devices’ flexible portions were clamped and displaced while measuring the required force. Subsequently, we converted the force-displacement data to engineering stress-strain data. Material stiffness was defined as the slope of the stress-strain curves.

μCT Scans

We also performed μCT scans (microXCT 400, Zeiss, Oberkochen, Germany) of one ring per ring design (size 30) to characterize their metal cores at a resolution of 18.8 μm (Figure 4).

Figure 4:

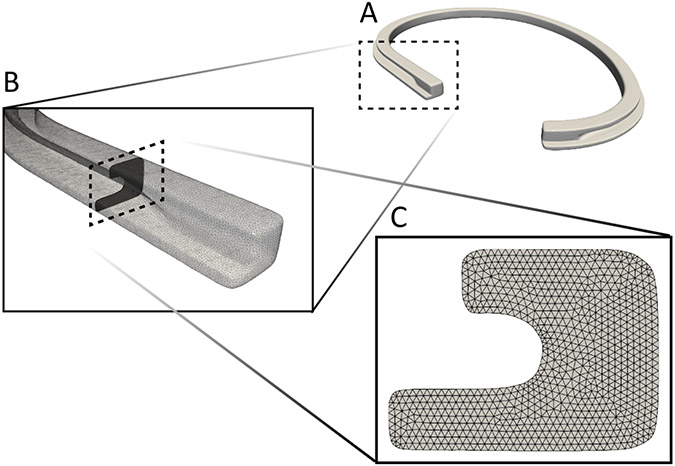
Figure 4:

Open in a new tab

Second moment of inertia computation based on A) μCT images, B) cross-sectional geometry extraction, and C) geometry triangulation. Shown is the Edwards Classic Ring of size 30.

Analytical Analysis

Based on μCT scans the cross-sectional geometries were extracted along the centerline. Next, we analytically computed the second moments of inertia and multiplied them by the Young’s moduli of the devices’ core material to obtain the devices’ bending stiffnesses. This value represents the material-dependent resistance of beams to bending with larger values indicating greater resistance to bending, which can vary with direction (anisotropy) and along its length (heterogeneity).

Results

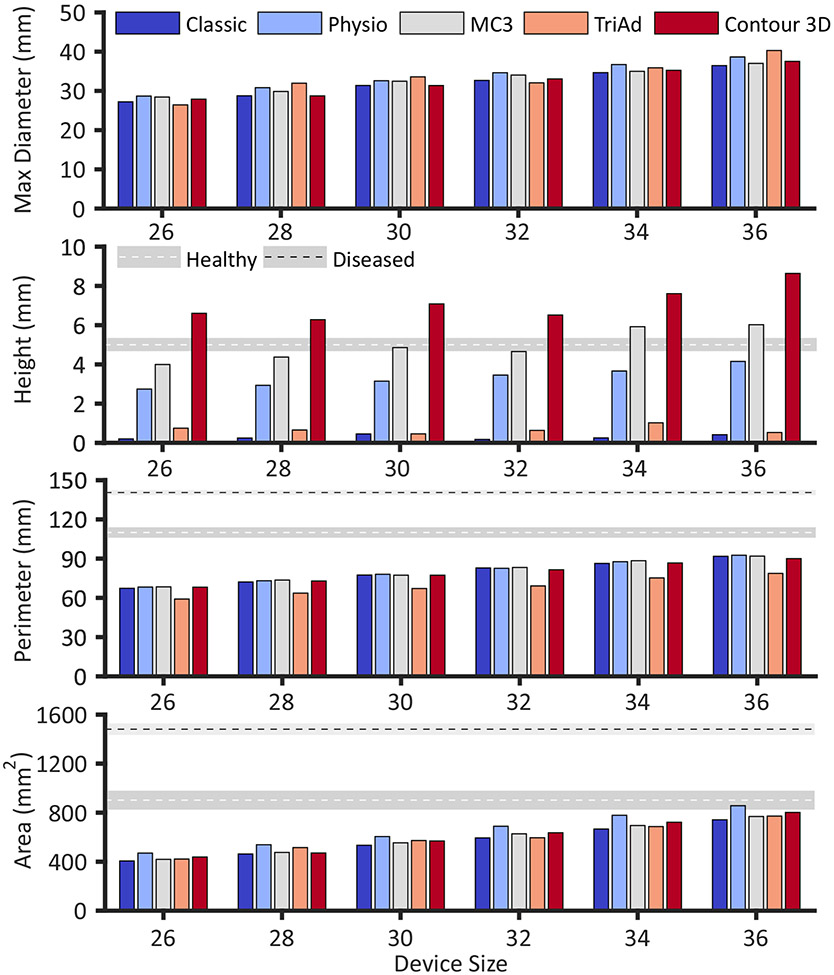
Geometric Measures

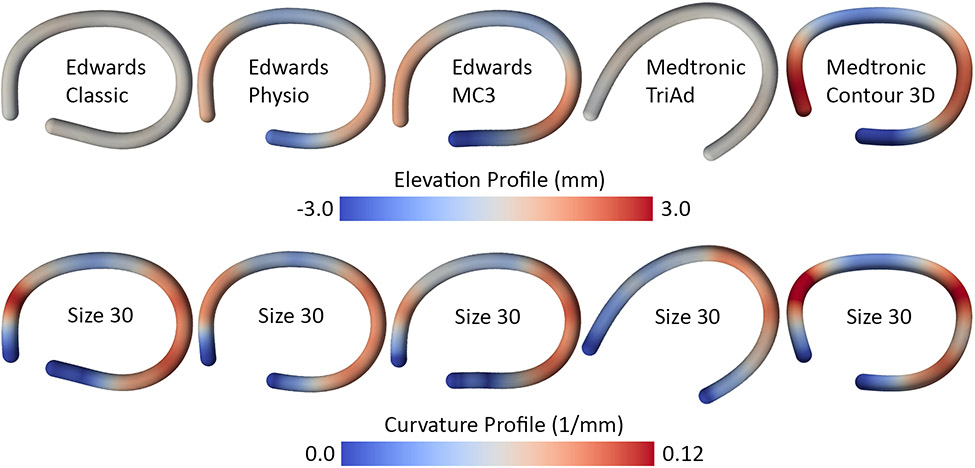
The shape of the six devices in terms of standard geometric measures are summarized in Figure 5 and Table 1, where they are compared to available values of the normal and diseased annulus. All metrics for all devices increased monotonically with device size, barring height. Maximum diameter, perimeter, and area varied little among the prostheses, while height varied significantly between devices. Specifically, the Classic and the TriAd rings had the smallest height of less than 1mm while the Physio (≈ 3-4mm height depending on size), MC3 (≈ 4-6mm), and the Contour (≈ 7-9mm) devices revealed progressively larger heights in their design.

Figure 5:

Figure 5:

Open in a new tab

Measures of device geometries. Dimensions for the healthy and diseased human tricuspid annulus (as available) are reported as mean ± 1 standard error according to Malinowski et al.10 and Ring et al.11 , respectively.

Table 1:

Summary of device geometry and stiffness measures. Dimensions for the healthy and diseased human tricuspid annulus are reported from Malinowski et al.10 and Ring et al.11 , respectively. Note, Ring et al. did not quantitatively report measures of standard deviation or error.

Max Diameter (mm)
Size
26		 Size 28 Size 30 Size 32 Size 34 Size 36
Classic 27.21 28.75 31.39 32.67 34.66 36.45
Physio 28.68 30.82 32.60 34.64 36.72 38.65
MC3 28.43 29.86 32.47 34.04 34.99 37.02
TriAd 26.43 31.96 33.58 32.06 35.89 40.30
Contour 3D 27.90 28.72 31.37 33.06 35.25 37.53
Height (mm)
Classic 0.20 0.25 0.46 0.17 0.25 0.42
Physio 2.74 2.93 3.15 3.46 3.66 4.15
MC3 4.00 4.37 4.86 4.66 5.92 6.02
TriAd 0.75 0.65 0.46 0.64 1.02 0.53
Contour 3D 6.61 6.28 7.08 6.51 7.61 8.64
Normal Annulus 10 5.0 ± 1.1 (mean ± 1 std)
Diseased Annulus 11 5.4 (mean)
Perimeter (mm)
Classic 67.34 72.19 77.49 82.90 86.36 91.81
Physio 68.29 73.10 78.07 82.65 87.69 92.63
MC3 68.44 73.63 77.36 83.28 88.46 91.95
TriAd 59.12 63.64 67.18 69.16 75.28 78.76
Contour 3D 68.22 72.93 77.37 81.52 86.71 90.05
Normal Annulus 10 110 ± 14 (mean ± 1 std)
Diseased Annulus 11 141 (mean)
Area (mm2)
Classic 406.11 462.91 534.18 594.30 666.73 742.22
Physio 470.21 538.43 605.13 689.43 778.73 856.73
MC3 419.44 475.68 554.00 627.63 695.27 768.93
TriAd 421.71 515.28 572.84 595.48 686.69 772.26
Contour 3D 438.40 470.98 569.09 636.21 722.15 802.15
Normal Annulus 10 902 ± 257 (mean ± 1 std)
Diseased Annulus 11 1482 (mean)
Bending Stiffness (Nm2)
Classic Physio MC3 TriAd Contour 3D
Maximum 26.65e-3 14.54e-3 18.60e-3 2.76e-3 22.86e-3
Minimum 46.69e-3 69.77e-3 32.73e-3 2.76e-3 25.37e-3
Open in a new tab

3D Contour and Curvature

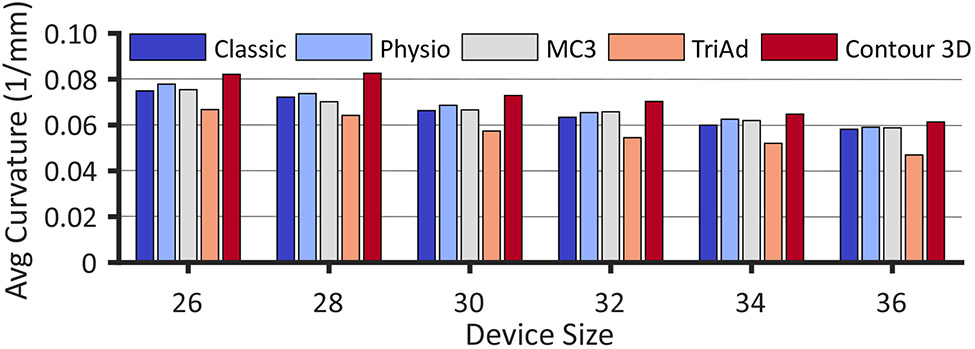
Furthermore, to sufficiently describe the 3D shape of these devices, we also analyzed their elevation and curvature profiles. Figure 6 representatively illustrates the profiles for all devices of size 30. The elevation profiles reflect the general pattern of height with the Classic and TriAd devices being essentially flat, the Physio of medium height, and the MC3 and Contour rings revealing the most significant out-of-plane deviations. Additionally, these profiles demonstrate the spatial variations of height. Both non-flat Edwards rings, the Physio and MC3, and the Medtronic Contour showed a remarkably similar elevation profile with peaks in the anterior-septal and posterior segments of the devices. Interestingly, the curvature profiles between all devices were almost identical as well with very localized peaks in curvature in the anterior segment and a widely distributed curvature in the posterior segment. The one outlier to this pattern was the TriAd device that showed only one distinct region of curvature in the posterior segment. To reduce curvature profiles to a single number in order to compare curvature between all devices and all sizes, we also computed the average curvature across the entire device length (Figure 7). We found that overall the average curvature decreased with device size and that the relative pattern between devices was consistent among all sizes. Interestingly, the Contour had the largest average curvature (i.e., was the most curved) due to its extreme height profile while the TriAd band had the lowest average curvature due to its simpler 3D shape with only one curvature peak along its length.

Figure 6:

Figure 6:

Open in a new tab

Elevation and curvature profiles of five devices representatively computed for devices of size 30.

Figure 7:

Figure 7:

Open in a new tab

Mean curvature values for each of the five devices and six sizes.

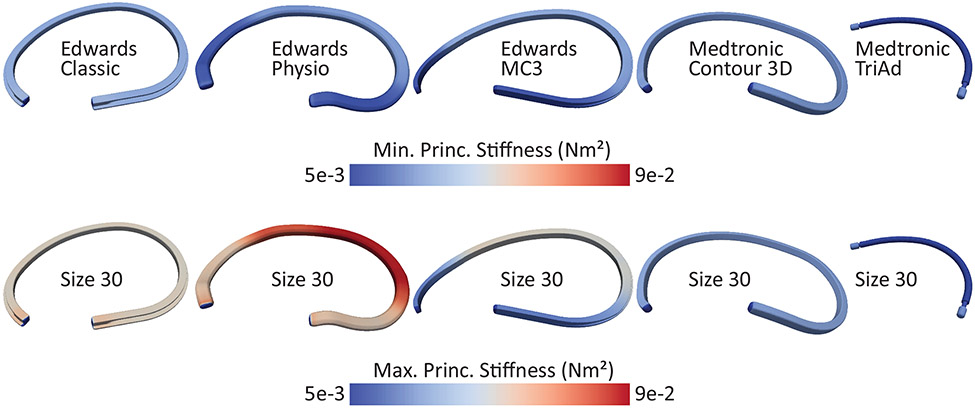
Bending and Axial Stiffness

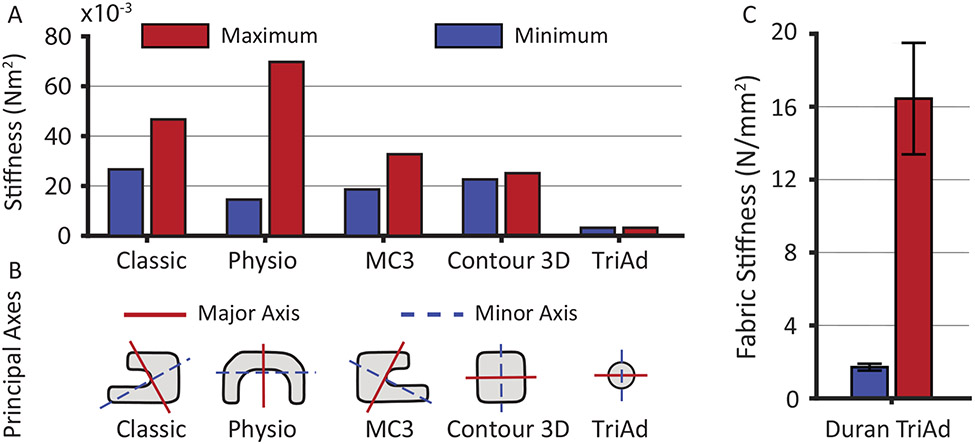
Figure 8 illustrates the maximum and minimum bending stiffness along the perimeter of each device of 30 mm size. Two patterns emerged: the Classic, the TriAd, and the Contour rings had homogeneous bending stiffness along their perimeters while the Physio and the MC3 did not. Specifically, the latter two prostheses had significantly reduced bending stiffness at both ends. Additionally, the contours also demonstrate that some devices had widely differing maximum and minimum bending stiffness (e.g. Physio) while others had only small differences (e.g. Contour). To compare the anisotropy (the ratio between maximum and minimum bending stiffness) in bending stiffness among devices, Figure 9A and Table 1 list the average (computed along the perimeter) maximum and minimum bending stiffness for all devices of size 30. These data illustrate vastly differing bending stiffness between devices as well as vastly differing degrees of anisotropy. Specifically, the Physio device had the largest maximum bending stiffness, while the Classic, MC3, and Contour had similar maximum bending stiffnesses. Interestingly, the Physio also had among the lowest minimum bending stiffness of all devices. Thus, the Physio was the most difficult to bend around its maximum principle axis, but the easiest to bend around its minimum principal axis. In other words, the Physio is selectively stiff. While the Classic and MC3 devices were also somewhat anisotropic, having both a stiffer direction and a softer direction, the Contour device was nearly isotropic, meaning that its stiffness only marginally depended around which axis it was bend. Figure 9B depicts the actual maximum principal and minimum principal axes. In the case of the Physio ring, it was easiest to bend the device in the out-of-annular-plan direction (i.e., up and down), while it was the hardest to bend in the in-plane direction. The nearly symmetrical shape of the Contour device renders the maximum and minimum principal axes meaningless in that the difference between the maximum and minimum bending stiffness is so small that the two axes are essentially interchangeable. Interestingly, the maximum and minimum principal axes of all other devices did not align with the annular plane. Thus, their maximum and minimum principal axes did not specifically support or prevent out-of-plane bending. Additionally, we computed the axial stiffness of the fabric of the Duran device and the flexible ends of the TriAd device. Importantly, while both are made of similar materials, the stiffness of the fabric varied significantly. The flexible ends of the TriAd device were significantly stiffer than the Duran device (1.59 ± 0.46 and 16.26 ± 7.00 N/mm2, p=0.0047 respectively via Welch t-test; Figure 9C).

Figure 8:

Figure 8:

Open in a new tab

Maximum and minimum principal bending stiffness based on μCT images of all devices of size 30.

Figure 9:

Figure 9:

Open in a new tab

A) Average (along the device perimeter) maximum and minimum principal bending stiffness based on μCT images of all devices of size 30. B) Maximum principal and minimum principal axes of the bending stiffness. The red line depicts the major axis around which it was the hardest to bend the device, while the blue line depicts the minor axis around which it was the easiest to bend the device. C) Comparison between the axial stiffness of the Duran device and the flexible ends of the TriAd device (data shown as mean ± 1 standard deviation, ** p<0.01).

Comment

The goal of surgical tricuspid annuloplasty is to remodel/reshape the diseased and deformed tricuspid annulus14. Specifically, in functional TR, the annulus is asymmetrically dilated and flattened15 (Figure 1), and the goal of tricuspid annuloplasty is to reduce annular size and re-establish normal three-dimensional shape. However, the annulus dynamically deforms during the cardiac cycle changing its area, shape, and height10. Assuming that the dynamic changes throughout the cardiac cycle are critical to the valve’s optimal function, preserving annular dynamics following tricuspid annuloplasty may be a secondary goal. Additionally, restriction of these dynamics may elicit reaction forces between the peri-annular tissue and the device that could put undue stress on sutures and cause ring dehiscence16. The challenge to the practicing surgeon lies not only in optimally performing the technical steps of tricuspid annuloplasty, but also to select the most optimal device to fulfill the above goals.

In the current study, we present the first direct comparison of size, geometry, and mechanical properties of six clinically used tricuspid annuloplasty devices that may provide some guidance in prosthesis selection. Our findings highlight that there was little difference in the in-plane geometric measurements between all devices. Observed values for area and perimeter were significantly below annular measurements from healthy subjects. Measurements of annular perimeter and area in healthy hearts during late systole reported by Ring et al were 1003mm2, and 118mm, respectively11, while those of Owais et al were 1090mm2 and 122mm17, and those by Malinowski et al were 902mm2 and 110mm10. Thus, even the largest ring size essentially downsizes the average non-dilated annulus by 100-200mm2 or approximately 20%.

In contrast to in-plane measurements, devices varied significantly in their 3D shape or height. The height of the contoured devices varied from 3-9 mm and was well aligned with the measurement of actual saddle height taken in patients. Ring et al reported a systolic height of 5.8mm11, while Malinowski et al reported a height of 5mm10. Maintaining anatomically correct height may be important to valve function. Salgo et al18 showed that the native saddle-shape of the mitral annulus minimized leaflet stress, thus identifying a teleological reason for the three-dimensional configuration of the mitral annulus. Spinner at al19 investigated whether the same may be true for the tricuspid annulus but did not find significant changes in anterior or posterior leaflet stretches in their in vitro preparation when changing the annulus from flat to saddle-shaped. Significant modifications to the valve when being explanted from the animal heart to a right-heart simulator may have contributed to this negative result. In vivo studies are needed to provide evidence for or against a teleological cause for the tricuspid valve three-dimensional annular configuration, either supporting or questioning the use of contoured annuloplasty devices.

The usefulness of comparing elevation and curvature profiles between devices lies in establishing quantitative means to identify devices which most likely re-establish normal annular shape. Our detailed geometric characterization of the investigated devices revealed little variation in elevation and curvature profiles as the contoured devices showed peaks and valleys in the same locations that also coincide with the reported shape of the non-dilated tricuspid annulus20. Similarly, the curvature profile of all devices was surprisingly similar as all (except for the TriAd) accurately reflecting the curvature of the human tricuspid annulus10. Additionally, absolute curvature values were well matched with the non-dilated human annulus. The TriAd was the one device defying this pattern. It showed only one area of peak curvature, which did not clearly coincide with regions of increased curvature in patients.

The current analysis of ring stiffness determined that some prostheses showed varying stiffness along their length. Specifically, the Physio and the MC3 were stiffer in the midsection of the device and softer at their ends. This design may permit the rings to conform to the natural dynamics of the annulus which shows significant curvature and length changes in those regions10,13. Additionally, devices showed varying degrees of anisotropy, e.g., the Physio bent easier out of the annular plane than within the annular plane. Again, these properties may better accommodate the natural dynamics of the annulus as the tricuspid annulus has been reported to fold out of plane during systole21. While the Classic and MC3 prostheses had some degree of anisotropy, it was not as prominent and the principal axes were not clearly aligned with the annular plane. Our in vivo ovine experiments22, however, have shown that the Duran, TriAd, and Contour rings despite their significantly different degrees of stiffness all essentially “froze” the natural dynamics of the tricuspid annulus. Similar findings have been reported with complete and partial mitral prostheses of varying flexibility23,24. Even the Duran ring, a "flexible" device, prevents the natural annular motion in sheep and human patients10,13, thereby calling in to question the added benefit of flexible and semi-rigid devices in preserving annular dynamics. However, in mitral prostheses, selective stiffness may reduce suture forces and thus reduce the risk of ring dehiscence25. Initial clinical reports of higher incidence of tricuspid ring dehiscence with rigid prostheses may partially corroborate these findings on the right side16. It is currently also unclear to what extent suture annuloplasty fits into the spectrum of device stiffness. Sutures may represent the lower limit of stiffness. Thus, clinical findings that rigid devices outperform suture annuloplasty could support rigid over flexible devices26,27. However, care must be taken in extrapolating these results as suture annuloplasty is a non-standardized technique which makes direct comparison with ring annuloplasty difficult. Finally, our data also highlight that not all “flexible” devices are equally stiff. The flexible ends of the TriAd device were almost ten times stiffer than the Duran device. Thus, care should be taken categorizing devices in overly broad terms.

The results of the current study may be used to facilitate annular prothesis choice during tricuspid annuloplasty. This process should be based on clinical presentation, detailed preoperative imaging, visual intraoperative inspection, and all mechanical and geometrical properties of the device. The majority of diseased tricuspid valves present with asymmetrically dilated and flattened annulus with or without concomitant regurgitation. We hypothesize that the former scenario requires a device that is not only able to restore the physiological shape (height) but also to maximize systolic leaflet coaptation while minimizing leaflet stresses. Here the stiff contoured device (MC3) may be preferred. While the Contour 3D device has similar properties as the MC3 device, its curvature and shape overcorrection may unnecessarily increase stress on the native annulus. In the latter case, ‘preventive’ annuloplasty may be adequately durable with the use of less stiff flat devices (Physio, TriAd) or even fully flexible protheses (AnCore). We question the usefulness of rigid flat rings (such as Classic) as they do not appear to offer any advantage over more tailored newer protheses. Unfortunately, no single ‘annular score’ exists for both the native annulus and the device that would allow for the perfect match in order to make this difficult operative decision automatic and to guarantee the long-term success.

Our long-term aim is to understand the effect of annuloplasty on tricuspid valve mechanics and to improve surgical outcomes by optimizing device design and choice. Toward this end, we have previously characterized tricuspid annular shape and dynamics in sheep and humans, in health10,13 and disease28, after tricuspid annuloplasty29, and as a function of downsizing30, and device type and size22. In the future, we will use the data from this work to perform virtual implantation of various annuloplasty device types and sizes in the same heart to compare their effect on the valve and the valvulo-ventricular complex31.

Limitations

First, we digitized and measured only one sample of each device type and size. It is possible, albeit unlikely, that manufacturing variations were not captured through our process. Note, we performed a verification and validation step to ensure that measurement-related errors were small. Specifically, for verification, we measured one of the devices five times and found maximum differences between scans being smaller than 1.1% for any of the measurements. Similarly, for validation, we 3D printed a circular ring of similar thickness as the annuloplasty devices with a sinusoidal out-of-plane deviation. After scanning those 3D printed rings, we compared the measured dimensions to the theoretical values and found errors smaller than 2%.

Conclusion

We comprehensively evaluated six tricuspid valve annuloplasty devices via 3D scanning, μCT imaging, analytical methods, and mechanical testing and found that all devices differed little in their in-plane geometries but varied significantly in their out-of-plane geometries. The elevation and curvature profiles of most prostheses resembled those of the healthy human tricuspid annulus. The investigated devices differed most significantly in their bending stiffness, both in overall resistance to bending and in the degree of bending stiffness anisotropy. The contoured devices (i.e., the Physio, MC3, and Contour) most accurately resembled the healthy human tricuspid annulus but differed significantly in bending stiffness (magnitude, heterogeneity, and anisotropy).

Acknowledgements

This work was supported by the AHA (#18CDA34120028).

Footnotes

Disclosures

Dr. Rausch has a speaking agreement with Edwards Lifesciences. None of the other authors have any potential conflicts of interest.

References

  • 1.Saitto G, Russo M, Nardi P. Tricuspid Valve Annuloplasty during Mitral Valve Surgery : A Risk or an Additional Benefit ? Ann Vasc Med Res. 2016;3(1):1–6. [Google Scholar]
  • 2.Nishimura RA, Otto CM, Bonow RO, et al. Valvular Heart Disease ∣ Management ∣ Guideline ∣ Executive Summary. J Am Coll Cardiol. 2014;63(22):2438–2488. [DOI] [PubMed] [Google Scholar]
  • 3.Stuge O, Liddicoat J. Emerging opportunities for cardiac surgeons within structural heart disease. J Thorac Cardiovasc Surg. 2006;132(6):1258–1261. [DOI] [PubMed] [Google Scholar]
  • 4.Benjamin EJ, Virani SS, Callaway CW, et al. Heart disease and stroke statistics - 2018 update: A report from the American Heart Association. Circulation. 2018;137(12):E67–E492. [DOI] [PubMed] [Google Scholar]
  • 5.Rogers JH, Bolling SF. The tricuspid valve: Current perspective and evolving management of tricuspid regurgitation. Circulation. 2009;119(20):2718–2725. [DOI] [PubMed] [Google Scholar]
  • 6.Ghoreishi M, Brown JM, Stauffer CE, et al. Undersized tricuspid annuloplasty rings optimally treat functional tricuspid regurgitation. Ann Thorac Surg. 2011;92(1):89–96. [DOI] [PubMed] [Google Scholar]
  • 7.Ratschiller T, Guenther T, Guenzinger R, et al. Early experiences with a new three-dimensional annuloplasty ring for the treatment of functional tricuspid regurgitation. Ann Thorac Surg. 2014;98(6):2039–2045. [DOI] [PubMed] [Google Scholar]
  • 8.Ito H, Mizumoto T, Sawada Y, Fujinaga K, Tempaku H, Shimpo H. Determinants of recurrent tricuspid regurgitation following tricuspid valve annuloplasty during mitral valve surgery. J Card Surg. 2017;32(4):237–244. [DOI] [PubMed] [Google Scholar]
  • 9.Maghami S, Ghoreishi M, Foster N, et al. Undersized Rigid Nonplanar Annuloplasty: The Key to Effective and Durable Repair of Functional Tricuspid Regurgitation. Ann Thorac Surg. 2016;102(3):735–742. [DOI] [PubMed] [Google Scholar]
  • 10.Malinowski M, Jazwiec T, Goehler M, et al. Sonomicrometry Derived Three-Dimensional Geometry of the Human Tricuspid Annulus. J Thorac Cardiovasc Surg. 2018. [DOI] [PubMed] [Google Scholar]
  • 11.Ring L, Rana BS, Kydd A, Boyd J, Parker K, Rusk RA. Dynamics of the tricuspid valve annulus in normal and dilated right hearts: a three-dimensional transoesophageal echocardiography study. Eur Heart J Cardiovasc Imaging. 2012;13(9):756–762. [DOI] [PubMed] [Google Scholar]
  • 12.Rausch MK, Bothe W, Kvitting JPE, et al. Characterization of mitral valve annular dynamics in the beating heart. Ann Biomed Eng. 2011;39(6):1690–1702. [DOI] [PubMed] [Google Scholar]
  • 13.Rausch MK, Malinowski M, Wilton P, Khaghani A, Timek TA. Engineering analysis of tricuspid annular dynamics in the beating ovine heart. Ann Biomed Eng. 2017;9(3):365–376. [DOI] [PubMed] [Google Scholar]
  • 14.Min SY, Song JMJKJMJK, Kim JH, et al. Geometric changes after tricuspid annuloplasty and predictors of residual tricuspid regurgitation: A real-time three-dimensional echocardiography study. Eur Heart J. 2010;31(23):2871–2880. [DOI] [PubMed] [Google Scholar]
  • 15.Ton-Nu TT, Levine RA, Handschumacher MD, et al. Geometric determinants of functional tricuspid regurgitation: Insights from 3-dimensional echocardiography. Circulation. 2006;114(2):143–149. [DOI] [PubMed] [Google Scholar]
  • 16.Pfannmüller B, Doenst T, Eberhardt K, Seeburger J, Borger MA, Mohr FW. Increased risk of dehiscence after tricuspid valve repair with rigid annuloplasty rings. J Thorac Cardiovasc Surg. 2012;143(5):1050–1055. [DOI] [PubMed] [Google Scholar]
  • 17.Owais K, Taylor CE, Jiang L, et al. Tricuspid annulus: A three-dimensional deconstruction and reconstruction. Ann Thorac Surg. 2014;98(5):1536–1542. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Salgo IS, Gorman JH, Gorman RC, et al. Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation. 2002;106(6):711–717. [DOI] [PubMed] [Google Scholar]
  • 19.Spinner EM, Buice D, Yap CH, Yoganathan AP. The effects of a three-dimensional, saddle-shaped annulus on anterior and posterior leaflet stretch and regurgitation of the tricuspid valve. Ann Biomed Eng. 2012;40(5):996–1005. [DOI] [PubMed] [Google Scholar]
  • 20.Fukuda S, Saracino G, Matsumura Y, et al. Three-dimensional geometry of the tricuspid annulus in healthy subjects and in patients with functional tricuspid regurgitation a real-time, 3-dimensional echocardiographic study. Circulation. 2006;114(Suppl. 1):I492–I498. [DOI] [PubMed] [Google Scholar]
  • 21.Kaplan SR, Bashein G, Sheehan FH, et al. Three-dimensional echocardiographic assessment of annular shape changes in the normal and regurgitant mitral valve. Am Heart J. 2000;139(3):378–387. [DOI] [PubMed] [Google Scholar]
  • 22.Malinowski M, Jazwiec T, Quay N, Goehler M, Rausch MK, Timek TA. The Impact of Tricuspid Annuloplasty Prostheses on Ovine Annular Geometry and Kinematics. J Thorac Cardiovasc Surg. September 2019. [DOI] [PubMed] [Google Scholar]
  • 23.Glasson JR, Green GR, Nistal JF, et al. Mitral annular size and shape in sheep with annuloplasty rings. J Thorac Cardiovasc Surg. 1999;117(2):302–309. [DOI] [PubMed] [Google Scholar]
  • 24.Dagum P, Timek T, Green GR, et al. Three-dimensional geometric comparison of partial and complete flexible mitral annuloplasty rings. J Thorac Cardiovasc Surg. 2001;122(4):665–673. [DOI] [PubMed] [Google Scholar]
  • 25.Pierce EL, Bloodworth CH, Imai A, et al. Mitral annuloplasty ring flexibility preferentially reduces posterior suture forces. J Biomech. 2018;75:58–66. [DOI] [PubMed] [Google Scholar]
  • 26.Parolari A, Barili F, Pilozzi A, Pacini D. Ring or Suture Annuloplasty for Tricuspid Regurgitation? A Meta-Analysis Review. Ann Thorac Surg. 2014;98:2255–2263. [DOI] [PubMed] [Google Scholar]
  • 27.Wang N, Phan S, Tian DH, Yan TD, Phan K. Flexible band versus rigid ring annuloplasty for tricuspid regurgitation: a systematic review and meta-analysis. Ann Cardiothorac Surg. 2017;6(3):194–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Rausch MK, Malinowski M, Meador WD, Wilton P, Khaghani A, Timek TA. The Effect of Acute Pulmonary Hypertension on Tricuspid Annular Height, Strain, and Curvature in Sheep. Cardiovasc Eng Technol. 2018;9(3):365–376. [DOI] [PubMed] [Google Scholar]
  • 29.Malinowski M, Schubert H, Wodarek J, et al. Tricuspid Annular Geometry and Strain after Suture Annuloplasty in Acute Ovine Right Heart Failure. Ann Thorac Surg. 2018;106(6):1804–1811. [DOI] [PubMed] [Google Scholar]
  • 30.Mathur M, Meador WD, Jazwiec T, Malinowski M, Timek TA, Rausch MK. The Effect of Downsizing on the Normal Tricuspid Annulus. Ann Biomed Eng. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Rausch MK, Zöllner AM, Genet M, Baillargeon B, Bothe W, Kuhl E. A virtual sizing tool for mitral valve annuloplasty. Int j numer method biomed eng. 2017;33(2). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Baillargeon B, Costa I, Leach JR, et al. Human Cardiac Function Simulator for the Optimal Design of a Novel Annuloplasty Ring with a Sub-valvular Element for Correction of Ischemic Mitral Regurgitation. Cardiovasc Eng Technol. 2015;6(2):105–116. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Annals of thoracic surgery are provided here courtesy of Health Research Alliance manuscript submission

RESOURCES