Skip to main content
NCBI home page
JACS Au logoLink to JACS Au
. 2024 Apr 2;4(4):1303–1309. doi: 10.1021/jacsau.4c00109

A Fresh Look at the Normal Mode Analysis of Proteins: Introducing Allosteric Co-Vibrational Modes

István Kolossváry 1,*
PMCID: PMC11040550  PMID: 38665643

Abstract

graphic file with name au4c00109_0004.jpg

We propose a new way of utilizing normal modes to study protein conformational transitions. Instead of considering individual modes independently, we show that a weighted mixture of low-frequency vibrational modes can reveal dynamic information about the conformational mechanism in more detail than any single mode can. The weights in the mixed mode, termed the allosteric covibrational mode, are determined using a simple model where the conformational transition is viewed as a perturbation of the coupled harmonic oscillator associated with either of the two conformations. We demonstrate our theory in a biologically relevant example of high pharmaceutical interest involving the V617F mutation of Janus 2 tyrosine kinase (JAK2).

Keywords: Normal mode analysis, Protein dynamics, Conformational transition, Co-vibrational modes

Introduction

Normal mode analysis (NMA) has been a staple in studying protein dynamics since the early days of computational chemistry,1−8 rooted in infrared (IR) spectroscopy.9−13 Arguably the most important aspect of NMA is that the lowest-frequency normal modes exhibiting the largest amplitudes are often relevant to biological function. It has been shown that so-called functional modes extracted from two different X-ray structures embodying two different functional conformations, such as apo vs holo, ligand bound or unbound, wild type vs mutant, etc., in many cases show significant similarities to the low-frequency vibrational modes.6,14 After superposition of two X-ray structures, the corresponding functional mode is represented by the displacement vector of the C-alpha (CA) atoms pointing from the reference conformation toward the other conformation. The similarity of the functional mode with respect to the normal modes of the reference structure is computed as the normalized projection of the functional mode vector onto the normal mode eigenvectors. When the functional mode has significant overlap with one of the normal modes, we can learn something about the dynamic aspects of the conformational transition resulting in a particular biological function. In this paper, we present a generalization of this idea. Instead of considering a single normal mode, we include all the low-frequency modes and ask the following question. How does a functional mode affect the overall vibration of the reference harmonic oscillator? We consider the functional mode to be a perturbation applied to the equilibrium state of the reference harmonic oscillator and wish to find out how the oscillator responds. We offer a very simple visual representation of this concept. The workhorse model for protein NMA is the elastic network model (ENM).15,16 ENM considers only CA atoms in the reference conformation and defines a multidimensional coupled harmonic oscillator by connecting nearby CA atoms with springs. The equilibrium state is typically defined by the geometry of an X-ray structure, and deviations from this reference geometry are considered perturbations of the native protein structure. To rephrase our question above, what happens if we pluck the ENM by displacing CA atoms along the functional mode vector and then let it go? The answer is remarkably simple and can be derived from the harmonic approximation of the equations of motion utilized in the theory of lattice dynamics: the (functional) perturbation will trigger a mixed-mode vibration of the reference harmonic oscillator, where the amplitudes of the individual normal modes can easily be calculated from the atomic displacements by projecting the vector of all atomic displacements onto the mode eigenvectors. We term these mixed modes allosteric covibrational (covib) modes in reference to the functional mode perturbation caused by a ligand molecule binding to an allosteric site in the protein. It should be noted that mixing normal modes or probing normal modes by plucking them is not new,17−23 but our approach provides a new perspective. In particular, mixed modes were employed in a similar manner as part of the definition of the so-called allosteric potential used to quantify allosteric effects upon ligand binding,21 but our covib modes are aimed at elucidating conformational mechanisms in terms of visualizing protein motions.

Results and Discussion

Theory

Standard NMA is based on eq 1 where the potential energy (E) is approximated by the harmonic term of the Taylor expansion of E around the reference conformation with its energy E0 arbitrarily set to zero. If E is computed with a general purpose force field, then the reference conformation should be energy minimized such that the gradient norm vanishes to within a desired numerical accuracy. If E is computed for an ENM, the reference conformation need not be minimized since by definition its gradient norm is equal to zero. 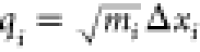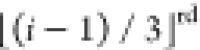N is the number of atoms and eq 1 is defined with mass-weighted coordinates Inline graphic where Δxi is the Cartesian coordinate displacement with respect to the reference conformation, and mi is the mass of the Inline graphic atom. The mixed second partial derivatives in eq 1 are commonly termed elements of the Hessian matrix Hij and are computed at the reference conformation.

graphic file with name au4c00109_m003.jpg 1

The normal modes of vibration are represented by the 3N eigenvectors vj of the Hessian matrix obeying the following expression H = V Λ VT. The eigenvectors are the columns of V and Λ is a diagonal matrix holding the eigenvalues λj. The eigenvector matrix V is orthogonal due to the fact that H is real and symmetric, which entails that VT = V–1, and the eigenvectors are normalized to unit length. A small displacement along an eigenvector (or its negative) ± Δvj represents concerted atomic movement associated with a single normal mode of vibration with frequency 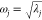Inline graphic. Only small amplitudes are physical, and wider amplitudes would require inclusion of higher terms in the Taylor expansion. Moreover, because eigenvectors are orthogonal, simultaneous small-amplitude displacements are possible without clashes in the protein structure. We show in this Letter that such mixed modes can be used to generalize the idea of pairing functional modes with only a single normal mode. Of course, in order to do this, we need a theory of how to determine the relative amplitudes of the mixed modes. NMA itself does not provide a definite answer, but Go̅ had shown theoretically that for a protein in thermal equilibrium, and for small fluctuations, the mass-weighted mean-square displacement of the atoms is equal to the weighted sum of the normal mode vectors where the weights are proportional to the inverse of the squared frequency of each mode.24 Go̅’s theorem provides the basis for using NMA and focusing only on the few lowest-frequency normal modes, as a first approximation to study protein dynamics. Our treatise, however, takes a different approach to mix normal modes based on the theory of lattice dynamics.

In terms of the harmonic approximation, solids and proteins are quite different. For solids the harmonic approximation is a highly accurate and powerful theory that allows for transposing Newton’s equations of motion to that of harmonic traveling waves expressed in normal mode coordinates. This is possible because atomic fluctuations in a solid under normal conditions are within the range of the harmonic approximation.25 In lattice dynamics, the normal mode eigenvectors are constant throughout the simulation and represent an absolute coordinate system, but the normal mode coordinates—projecting the vector of all atomic displacements onto the mode eigenvectors—fluctuate in time as the atoms move. This means that lattice vibrations that may look random can be decomposed into the sum of the normal modes of vibrations with different amplitudes and different phases.26

Proteins, however, undergo large conformational changes under physiological conditions and usually exhibit multiple free energy minima separated by thermal barriers on a complex free energy landscape. Nonetheless, even though a rigorous harmonic representation of protein dynamics overall is generally not possible, NMA remains an extraordinarily useful qualitative tool to study protein dynamics locally. Our principal motivation for introducing the concept of covibrational modes was that intuitively we should look at protein dynamics also in terms of superposition of low-frequency normal modes and not only a single mode. The question remains, of course, how can one determine the amplitudes such that they are biologically relevant?

The answer is remarkably simple. We learned from lattice dynamics that in any given configuration the normal mode coordinates themselves were, in fact, the amplitudes to be used to weight the normal modes.26 This leads to the following definition: considering two biologically linked conformations of a protein, we project the connecting functional mode vector onto each of the low-frequency normal mode vectors—all vectors mass-weighted, computed for the reference conformation—and define the allosteric covibrational mode to be the superposition of the low-frequency modes weighted by the projections, respectively. The covibrational mode vector sf with respect to a functional mode vector f can be calculated by eq 2.

graphic file with name au4c00109_m005.jpg 2

where f is the displacement vector between the two superposed conformations, typically including only the CA atoms, but, e.g., in our calculations, we used all atoms. f points from the chosen reference conformation toward the other, and the M low-frequency normal mode vectors vj are computed for the reference conformation. It is assumed that the eigenvectors are normalized. Note that while M ≪ N we found that it was more accurate to include significantly more eigenvectors in eq 2 than the handful of lowest-frequency modes that are typically considered in NMA. Especially in the presence of a bound ligand molecule, higher frequency modes can be biologically relevant and should be included in eq 2. Of course, the exact relationship would require M = 3N in which case sf would coincide with f itself, but that would be impractical and also unnecessary, as is demonstrated in the Application section. The covibrational mode sf represents a mixed vibrational mode that is the result of perturbing the reference harmonic oscillator by changing the conformation and then letting it go. Note that while the covibrational mode does not represent a whole transition path between two conformations, it does entail concerted atomic movement to initiate the transition and thus can reveal biologically relevant dynamic information obtained from two static structures, e.g., X-ray structures, and of course, the direction can be reversed by swapping the reference.

Application to an Allosteric Conundrum in JAK2

Janus kinase 2 (JAK2) plays a critical role in the signal transduction pathways of various cytokines and growth factors. The JAK2 V617F mutation is a specific gain-of-function mutation in the JAK2 gene and is associated with numerous hematological cancers and inflammatory conditions.27 Original research by McNally et al. discovered that Compound 2 in complex with the V617F domain (PDB code 6G3C) preferred the wild-type (WT) domain structure (PDB code 4fVQ) over the mutated oncogenic form (PDB code 4FVR).28 These X-ray structures suggest that certain ligands in the ATP site of pseudokinase domain JH2 can modulate the V617F mutant and restore the WT conformation. We recently conducted extensive molecular dynamics (MD) simulations on this system and found that our simulations agreed with the experimental observation that Compound 2 in complex with the V617F domain shifted the free energy landscape toward favoring the WT conformation.29

However, in our simulations, the putative conformational transition path was largely limited to the small conformational differences around the V617F mutation including loops enclosed in the orange surface and a displacement of the helix (WT purple, mutant green) as shown in Figure 1. Here we argue that a more natural transition model should include the entire protein, and our low-frequency covibrational modes accomplish just that. We computed the first 500 all-atom mode eigenvectors for the V617F conformation, and in Figure 2 we plotted the normalized projection (purple dots) of the functional mode vector V617F → WT onto the individual eigenvectors. Of course, the reverse direction would be equally valid, and very similar. The numerical value of the normalized projection is the cosine of the angle between the two vectors, and we can see that there is only one normal mode, the third lowest (red dot), which shows even a moderate overlap. Conversely, the covibrational modes (green curve) computed by including an increasing number of eigenvectors in eq 2 start showing significant overlap with even as few as M = 20.

Figure 1.

Figure 1

Open in a new tab

Conformational differences between the WT and V617F forms of JAK2 around the allosteric site. The main differences are the displacement of the helix in the middle (WT purple, mutant green) and different loop conformations enclosed in the orange surface.

Figure 2.

Figure 2

Open in a new tab

Overlap scores of JAK2 covib modes and normal modes with respect to the V617F → WT functional mode vector. The normalized projections of the functional mode onto the first 500 all-atom normal mode vectors are plotted as purple dots. The horizontal axis shows the mode serial numbers sorted by the eigenvalues. The vertical axis shows the overlap score in terms of the cosine (left) and angle (right) of the projection. The largest overlap belongs to mode #3 (red dot). The green curve shows the cumulative overlap score of the covib mode including and increasing number of modes M = 1–500 in eq 2.

In Figure 3, we show a visual comparison of the covib mode with M = 100, and normal mode 3. The covib mode is shown on the left (green), and mode 3 is shown on the right (red). The layered cartoon representation shows the spatial expansion of each mode with respect to the same arbitrarily chosen overall amplitude, and superposed on the WT conformation (purple). One can think of a full cycle of vibration as a pendulum swinging from one extreme to the other. In that respect, the green and red pendulums are identical; however, the atomic decomposition of the two vibrations show different atomic movements. There is a large degree of overall similarity, which is expected since mode 3 has the largest contribution to the covib mode, but there are significant differences. The biologically most relevant difference is that mode 3 leaves the α helix virtually intact, oriented at a small but noticeable angle with respect to the WT conformation (purple), whereas the covib mode includes a distinct seesaw motion of the helix resulting in a significant overlap with the WT helix. We included multiple animations in Video S3 and Video S4 in the Supporting Information offering a more vivid demonstration of eq 2 in action. For reference, we also highlighted in Figure 3 the V617F mutation in the allosteric site (orange) and McNally’s Compound 2 occupying the ATP binding site (blue). Our main result is that the covib mode describes the WT ↔ V617F conformational transition in significantly more detailed than any single normal mode.

Figure 3.

Figure 3

Open in a new tab

Visual comparison of the covib mode (M = 100), and normal mode 3. The covib mode is shown on the left (green), and mode 3 is shown on the right (red). The layered cartoon representation shows the spatial expansion of each mode superposed on the WT conformation (purple). Note the V617F mutation in the allosteric site (orange) and McNally’s Compound 2 occupying the ATP binding site (blue). See text for details, and Video S3 and Video S4 in the Supporting Information show 3D animations of this figure.

Conclusions

In conclusion, we introduced and propose using allosteric covibrational modes instead of single normal modes to characterize protein conformational transitions within the harmonic approximation. As intuitive normal modes themselves might be, the mode eigenvectors represent only the basis vectors of a coordinate system in which complex molecular vibrations can be approximated by a finite series expansion defined in eq 2. Furthermore, we found that the number of low-frequency normal modes included in eq 2 could be significantly more than the handful of modes typically used in NMA. Finally, we find it fascinating that covibrational modes can reveal a great deal of dynamic information related to biological function, solely based on two static (X-ray) structures.

Methods

Computational Details

Our code to compute covibrational modes was added to the low-mode conformational search module (LMOD)30−33 in the Amber24/AmberTools24 release of the Amber molecular dynamics program package.34−36 We ran our calculations on a Mac Studio Ultra workstation, using the ff14sb37 force filed, and a generalized Born implicit solvation model38 with infinite cutoffs. Data files and scripts with instructions to reproduce our JAK2 calculations are also publicly available in AmberTools24.

Eigenvector Calculations

The Hessian eigenvectors were calculated using the ARPACK software package39 designed for solving large scale eigenvector problems in the matrix-free fashion, i.e., H is never computed. All ARPACK requires is the repeated calculation of matrix-vector products of the form Hz where z is an arbitrary vector. To compute this, we use the following finite difference gradient formula.

graphic file with name au4c00109_m006.jpg 3

For each Hz product the gradient is computed at two different points, x representing the atomic position vector and (x + hz) is an infinitesimal step along z. We found 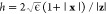Inline graphic (ϵ is the machine precision) a numerically stable and robust choice for the smallest possible step in eq 3.40 The bottleneck of computing the low-frequency Hessian eigenvectors this way is the computation of the gradient, but LMOD takes advantage of Amber’s parallel force computation engine to gain close to linear scaling across multiple CPU cores.

The ZIG-ZAG Algorithm

The mode eigenvectors represent linear displacement in Cartesian space. Note, however, that for atomic displacement the eigenvectors should be transformed back to non-mass-weighted coordinates. Linear displacement works only for very small amplitudes, especially in all-atom representation, because perturbation along a mode vector results in severe distortions in the hard degrees of freedom (mainly bond lengths and bond angles) and also leads to atomic clashes, even for small to moderate amplitudes. In order to visualize normal modes, we need curvilinear displacement instead of linear to achieve significant amplitudes. This is highly important when visualizing mixed modes because the non-mass-weighted mode eigenvectors are no longer strictly orthogonal and, therefore, atomic clashes can easily occur even at very small amplitudes. Our solution to this visualization problem is the zigzag algorithm in LMOD. The zigzag algorithm employs a series of alternating short LMOD moves along the mode eigenvector (zig) followed by a few steps of minimization (zag), which has been found in our hands very effective in relaxing excessive stretches and bends and also relieving clashes before affecting the soft degrees of freedom noticeably. The key is to stop minimization when the gradient norm falls below 1 kcal/mol/Å. In our experience 10–20 zigzag moves can readily be applied along any low-frequency normal mode or covibrational mode producing large-amplitude, curvilinear, and smooth moves for visualization. The videos in the Supporting Information were all produced with the zigzag algorithm.

Future Directions

Our future work includes: (1) a standalone ultrafast software for computing covibrational modes of elastic network models considering only CA atoms, (2) computing significantly more accurate vibrational modes using essential dynamics41,42 based on high-quality explicit-solvent MD simulations, and (3) combining covibrational modes from both directions to construct a physically meaningful conformational transition path.

Acknowledgments

I thank Scott Brozell for invaluable help with integrating LMOD into Amber, and Drew Rohskopf and Wayne Guida for stimulating discussions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.4c00109.

  • Video S1, the first 20 low-frequency normal modes of the WT structure (PDB code 4FVQ, ATP not shown); the side chains are included in the animation, but faded for clarity (All videos were animated employing the same zigzag settings (see Methods). Using the pendulum analogy from the main text, each mode is represented by two full swings of the pendulum. The motion starts at the center with the equilibrium structure and swings out to one extreme. Then, it swings back, passing the center, to the other extreme, and finishes up with another half swing back to the center. Each half swing contains 15 zigzag smoothed frames. The videos were generated with Pymol.43) (MP4)

  • Video S2, same as Video S1, but this is the mutated V617F structure (PDB code 4FVR); note that the two sets of vibrations are very similar, and that the pendulum amplitude was intentionally set to extra wide to make the point that even with zigzag smoothing, it is clear that low-frequency modes above the first half a dozen or so give rise to motions that look nonphysical if extended too far (MP4)

  • Video S3, covibrational mode (purple) computed with M = 100 (eq 2) starting from the V617F mutated structure (green); the WT structure (red) is also shown for reference; the animation distinctly shows the seesaw motion of the α helix transitioning from the green toward the red conformation, which is a much better visual clue than what we could provide as a still picture in the main text (Figure 3) (MP4)

  • Video S4, superposition of the covibrational mode (purple) onto the normal mode 3 (blue); there are two covib modes, one computed with M = 20 and the other with M = 100, but there is very little difference between them, both showing the key seesaw motion, which on the other hand, is entirely missing from mode 3 (MP4)

The author declares no competing financial interest.

Supplementary Material

au4c00109_si_001.mp4 (49.8MB, mp4)
au4c00109_si_002.mp4 (54.9MB, mp4)
au4c00109_si_003.mp4 (3MB, mp4)
au4c00109_si_004.mp4 (2MB, mp4)

References

  1. Bauer J. A.; Bauerová-Hlinková V. In Homology Molecular Modeling; Maia R. T., de Moraes Filho R. M., Campos M., M., Eds.; IntechOpen: Rijeka, 2020; Chapter 2. [Google Scholar]
  2. Bauer J. A.; Pavlović J.; Bauerová-Hlinková V. Normal Mode Analysis as a Routine Part of a Structural Investigation. Molecules 2019, 24, 3293–3312. 10.3390/molecules24183293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Wako H.; Endo S. Normal mode analysis as a method to derive protein dynamics information from the Protein Data Bank. Biophysical reviews 2017, 9, 877–893. 10.1007/s12551-017-0330-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bahar I.; Lezon T. R.; Bakan A.; Shrivastava I. H. Normal Mode Analysis of Biomolecular Structures: Functional Mechanisms of Membrane Proteins. Chem. Rev. 2010, 110, 1463–1497. 10.1021/cr900095e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Skjaerven L.; Hollup S. M.; Reuter N. Normal mode analysis for proteins. Journal of Molecular Structure: THEOCHEM 2009, 898, 42–48. 10.1016/j.theochem.2008.09.024. [DOI] [Google Scholar]
  6. Hayward S., de Groot B. L. In Molecular Modeling of Proteins; Kukol A., Ed.; Humana Press: Totowa, NJ, 2008; Chapter 5, pp 89–106. [Google Scholar]
  7. Ma J. Usefulness and Limitations of Normal Mode Analysis in Modeling Dynamics of Biomolecular Complexes. Structure 2005, 13, 373–380. 10.1016/j.str.2005.02.002. [DOI] [PubMed] [Google Scholar]
  8. Levitt M.; Sander C.; Stern P. S. The normal modes of a protein: Native bovine pancreatic trypsin inhibitor. Int. J. Quantum Chem. 1983, 24, 181–199. 10.1002/qua.560240721. [DOI] [Google Scholar]
  9. Ripanti F.; Luchetti N.; Nucara A.; Minicozzi V.; Venere A. D.; Filabozzi A.; Carbonaro M. Normal mode calculation and infrared spectroscopy of proteins in water solution: Relationship between amide I transition dipole strength and secondary structure. Int. J. Biol. Macromol. 2021, 185, 369–376. 10.1016/j.ijbiomac.2021.06.092. [DOI] [PubMed] [Google Scholar]
  10. Haris P. I. In Encyclopedia of Biophysics; Roberts G. C. K., Ed.; Springer: Berlin, 2013; pp 1095–1106. [Google Scholar]
  11. Barth A. Infrared spectroscopy of proteins. Biochimica et Biophysica Acta (BBA) - Bioenergetics 2007, 1767, 1073–1101. 10.1016/j.bbabio.2007.06.004. [DOI] [PubMed] [Google Scholar]
  12. Fabian H.; Mäntele W.. Infrared spectroscopy of proteins. Handbook of Vibrational Spectroscopy; Wiley, 2001; pp 1–27. 10.1002/0470027320.s8201 [DOI] [Google Scholar]
  13. Arrondo J. L. R.; Goñi F. M. Structure and dynamics of membrane proteins as studied by infrared spectroscopy. Progress in biophysics and molecular biology 1999, 72, 367–405. 10.1016/S0079-6107(99)00007-3. [DOI] [PubMed] [Google Scholar]
  14. Marques O.; Sanejouand Y.-H. Hinge-bending motion in citrate synthase arising from normal mode calculations. Proteins: Struct., Funct., Bioinf. 1995, 23, 557–560. 10.1002/prot.340230410. [DOI] [PubMed] [Google Scholar]
  15. Tirion M. M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
  16. López-Blanco J. R.; Chacón P. New generation of elastic network models. Curr. Opin. Struct. Biol. 2016, 37, 46–53. 10.1016/j.sbi.2015.11.013. [DOI] [PubMed] [Google Scholar]
  17. Madan L. K.; Welsh C. L.; Kornev A. P.; Taylor S. S. The “violin model”: Looking at community networks for dynamic allostery. J. Chem. Phys. 2023, 158, 081001. 10.1063/5.0138175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wagner J. R.; Lee C. T.; Durrant J. D.; Malmstrom R. D.; Feher V. A.; Amaro R. E. Emerging computational methods for the rational discovery of allosteric drugs. Chem. Rev. 2016, 116, 6370–6390. 10.1021/acs.chemrev.5b00631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gerek Z. N.; Ozkan S. B. Change in allosteric network affects binding affinities of PDZ domains: analysis through perturbation response scanning. PLoS computational biology 2011, 7, e1002154. 10.1371/journal.pcbi.1002154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Zheng W.; Brooks B. R.; Thirumalai D. Low-frequency normal modes that describe allosteric transitions in biological nanomachines are robust to sequence variations. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 7664–7669. 10.1073/pnas.0510426103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ming D.; Wall M. E. Quantifying allosteric effects in proteins. Proteins: Struct., Funct., Bioinf. 2005, 59, 697–707. 10.1002/prot.20440. [DOI] [PubMed] [Google Scholar]
  22. Erkip A.; Erman B. ynamics of large-scale fluctuations in native proteins. Analysis based on harmonic inter-residue potentials and random external noise. Polymer 2004, 45, 641–648. 10.1016/j.polymer.2003.10.094. [DOI] [Google Scholar]
  23. Amadei A.; Ceruso M. A.; Di Nola A. On the convergence of the conformational coordinates basis set obtained by the essential dynamics analysis of proteins’ molecular dynamics simulations. Proteins: Struct., Funct., Bioinf. 1999, 36, 419–424. . [DOI] [PubMed] [Google Scholar]
  24. G o̅ N. A theorem on amplitudes of thermal atomic fluctuations in large molecules assuming specific conformations calculated by normal mode analysis. Biophys. Chem. 1990, 35, 105–112. 10.1016/0301-4622(90)80065-F. [DOI] [PubMed] [Google Scholar]
  25. Dove M. Introduction to the theory of lattice dynamics. École thématique de la Société Française de la Neutronique 2011, 12, 123–159. 10.1051/sfn/201112007. [DOI] [Google Scholar]
  26. Rohskopf A.; Li R.; Luo T.; Henry A. A computational framework for modeling and simulating vibrational mode dynamics. Modell. Simul. Mater. Sci. Eng. 2022, 30, 045010. 10.1088/1361-651X/ac5ebb. [DOI] [Google Scholar]
  27. Jones A. V.; Kreil S.; Zoi K.; Waghorn K.; Curtis C.; Zhang L.; Score J.; Seear R.; Chase A. J.; Grand F. H.; et al. Widespread occurrence of the JAK2 V617F mutation in chronic myeloproliferative disorders. Blood 2005, 106, 2162–2168. 10.1182/blood-2005-03-1320. [DOI] [PubMed] [Google Scholar]
  28. McNally R.; Li Q.; Li K.; Dekker C.; Vangrevelinghe E.; Jones M.; Chène P.; Machauer R.; Radimerski T.; Eck M. J. Discovery and structural characterization of ATP-site ligands for the wild-type and V617F mutant JAK2 pseudokinase domain. ACS Chem. Biol. 2019, 14, 587–593. 10.1021/acschembio.8b00722. [DOI] [PubMed] [Google Scholar]
  29. Kolossváry I.; Sherman W. Comprehensive Approach to Simulating Large Scale Conformational Changes in Biological Systems Utilizing a Path Collective Variable and New Barrier Restraint. J. Phys. Chem. B 2023, 127, 5214–5229. 10.1021/acs.jpcb.3c02028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kolossváry I.; Guida W. C. Low mode search. An efficient, automated computational method for conformational analysis: Application to cyclic and acyclic alkanes and cyclic peptides. J. Am. Chem. Soc. 1996, 118, 5011–5019. 10.1021/ja952478m. [DOI] [Google Scholar]
  31. Keserü G. M.; Kolossváry I. Fully flexible low-mode docking: application to induced fit in HIV integrase. J. Am. Chem. Soc. 2001, 123, 12708–12709. 10.1021/ja0160086. [DOI] [PubMed] [Google Scholar]
  32. Kolossváry I.; Keserü G. M. Hessian-free low-mode conformational search for large-scale protein loop optimization: application to c-jun N-terminal kinase JNK3. J. Comput. Chem. 2001, 22, 21–30. . [DOI] [Google Scholar]
  33. Bereczki I.; Papp H.; Kuczmog A.; Madai M.; Nagy V.; Agocs A.; Batta G.; Milankovits M.; Ostorhazi E.; Mitrovic A. Natural Apocarotenoids and Their Synthetic Glycopeptide Conjugates Inhibit SARS-CoV-2 Replication. Pharmaceuticals 2021, 14, 1111. 10.3390/ph14111111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Salomon-Ferrer R.; Case D. A.; Walker R. C. An overview of the Amber biomolecular simulation package. Wiley Interdisciplinary Reviews: Computational Molecular Science 2013, 3, 198–210. 10.1002/wcms.1121. [DOI] [Google Scholar]
  35. Case D. A.; Cheatham T. E. III; Darden T.; Gohlke H.; Luo R.; Merz K. M. Jr.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber biomolecular simulation programs. Journal of computational chemistry 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. https://ambermd.org (accessed 03-25-2024).
  37. Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mongan J.; Simmerling C.; McCammon J. A.; Case D. A.; Onufriev A. Generalized Born model with a simple, robust molecular volume correction. J. Chem. Theory Comput. 2007, 3, 156–169. 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. https://github.com/opencollab/arpack-ng (accessed 03-25-2024).
  40. Derreumaux P.; Zhang G.; Schlick T.; Brooks B. A truncated Newton minimizer adapted for CHARMM and biomolecular applications. Journal of computational chemistry 1994, 15, 532–552. 10.1002/jcc.540150506. [DOI] [Google Scholar]
  41. Amadei A.; Linssen A. B.; Berendsen H. J. Essential dynamics of proteins. Proteins: Struct., Funct., Bioinf. 1993, 17, 412–425. 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
  42. David C. C.; Jacobs D. J. In Protein Dynamics: Methods and Protocols; Livesay D. R., Ed.; Humana Press: Totowa, NJ, 2014; pp 193–226. [Google Scholar]
  43. https://pymol.org/2/ (accessed 03-25-2024).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au4c00109_si_001.mp4 (49.8MB, mp4)
au4c00109_si_002.mp4 (54.9MB, mp4)
au4c00109_si_003.mp4 (3MB, mp4)
au4c00109_si_004.mp4 (2MB, mp4)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES