A variational reformulation of molecular properties in electronic-structure theory

Abstract

Conventional quantum-mechanical calculations of molecular properties, such as dipole moments and electronic excitation energies, give errors that depend linearly on the error in the wave function. An exception is the electronic energy, whose error depends quadratically on the error in wave function. We here describe how all properties may be calculated with a quadratic error, by setting up a variational Lagrangian for the property of interest. Because the construction of the Lagrangian is less expensive than the calculation of the wave function, this approach substantially improves the accuracy of quantum-chemical calculations without increasing cost. As illustrated for excitation energies, this approach enables the accurate calculation of molecular properties for larger systems, with a short time-to-solution and in a manner well suited for modern computer architectures.

Molecular properties like dipole moments and excitation energies are calculated more accurately with a simple mathematical trick.

INTRODUCTION

The use of accurate electronic-structure methods to describe the properties of molecules has become increasingly important in many scientific disciplines. These methods involve the construction of approximate wave functions for the electrons of the system at hand and the subsequent calculation of energies and other molecular properties such as dipole moments and excitation energies from the wave function (1–4). Determination of excitation energies and molecular properties constitutes a fundamental link between quantum chemistry and experimental spectroscopy, underlying a wide range of possible applications from photosynthesis to human vision, from single-molecule spectroscopy to bioimaging (5–10).

The time-consuming step in the calculation of molecular properties is typically the calculation of the wave function to the accuracy needed for the property of interest, while the calculation of the property from the wave function is less expensive. Over the years, many techniques have been developed to calculate wave functions to high accuracy and at sufficiently low cost. By contrast, less attention has focused on how, from a given approximate wave function, we may calculate the desired property to the highest accuracy possible.

We here show how the accuracy in the calculated properties can be improved markedly, at low cost and without modifying the underlying wave function. Specifically, assume that the approximate wave function Ψ contains an error δΨ = Ψ − Ψ^∗ relative to the exact wave function Ψ^∗. The corresponding error in a given molecular property M is then δM(Ψ) = M(Ψ) − M(Ψ^∗). In the standard way of calculating properties, this error is linear in the error of the wave function, $\mathrm{\delta }\mathit{M}(\mathrm{\Psi })=\mathcal{O}(\mathrm{\delta }\mathrm{\Psi })$ . We shall here show that there exists a variational Lagrangian reformulation ℳ of M such that ℳ(Ψ^∗) = M(Ψ^∗) but $\mathrm{\delta }\mathit{ℳ}(\mathrm{\Psi })=\mathcal{O}(\mathrm{\delta }{\mathrm{\Psi }}^2)$ .

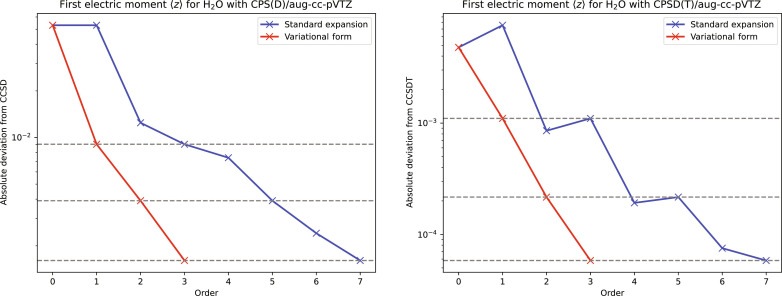
What can be gained by such a variational reformulation of a molecular property is illustrated by coupled-cluster (CC) calculations of the dipole moment of H₂O in Fig. 1. Beginning with the dipole moment calculated at a chosen truncation level of CC theory, we use cluster perturbation theory (CP) to generate a more and more accurate approximation to the dipole moment with increasing truncation level. At each order k > 0 in the perturbation expansion, we calculate the dipole moment both in a variational manner and in the traditional, nonvariational manner. As seen in Fig. 1, the variational formulation (red curve) provides a marked improvement on the corresponding nonvariational formulation (blue curve). The dipole moment calculated variationally to order k in the expansion is identical to the dipole moment calculated nonvariationally to order 2k + 1. Because the calculation of an electronic wave function to order 2k + 1 is enormously more complicated and expensive than the calculation of the wave function to order k and because the additional cost of a variational reformulation of the property is low compared with the construction of the wave function itself, the gains obtained by this approach are considerable. The variational reformulation may, in many cases, be the only way to achieve a given accuracy in the calculations.

Fig. 1. Convergence of the CP series of the dipole moment of H₂O calculated variationally (red) and nonvariationally (blue).

Errors (atomic units) plotted against the order of the perturbation expansion of the equilibrium dipole moment of H₂O, calculated variationally (red) and nonvariationally (blue). To the left, the coupled-cluster (CC) singles-and-doubles (CCSD) dipole moment is expanded about the CC singles (CCS) dipole moment; to the right, the CC singles-doubles-triples (CCSDT) dipole moment is expanded about the CCSD dipole moment. The wave functions that are used to calculate the red and blue curves are order by order the same; the only difference is how the dipole moment is calculated from these wave functions. All calculations are in the aug-cc-pVTZ basis, in the frozen-core approximation.

Variational Lagrangians have a long history in electronic-structure theory and are widely used for the calculation of the molecular electronic energy (11–14). Our purpose is to describe how the variational reformulation can be accomplished for all molecular properties, not just the energy, using the molecular dipole moment and electronic excitation energies as examples.

RESULTS

In the following, we first discuss in general terms the construction of a variational Lagrangian for molecular properties. Next, we review the computational framework within which we perform the variational calculations of molecular properties, namely, CC theory and CP theory. Last, we present the calculation of dipole moments and excitation energies using variational Lagrangians.

Construction of variational Lagrangians for molecular properties

Let us assume that we are interested in the molecular property M(λ) where λ is the collection of parameters that determine the many-electron wave function. Denoting the optimal (exact) wave-function parameters by λ^∗ and our current (approximate) wave-function parameters by λ₀, we have

$${\mathrm{\lambda }}_0={\mathrm{\lambda }}^{\ast }+\mathrm{\delta \lambda }$$ (1)

where δλ is the error in our description. Carrying out a Taylor expansion of M(λ) about λ^∗ and denoting its derivative with respect to λ at λ^∗ by M′ (λ^∗), we obtain

$$M({\mathrm{\lambda }}_0)=M({\mathrm{\lambda }}^{\ast })+M\prime ({\mathrm{\lambda }}^{\ast }) \mathrm{\delta \lambda }+\mathcal{O}({\mathrm{\delta \lambda }}^2)$$ (2)

The error in the property of interest is, therefore, proportional to the error in the wave function.

However, if M′ (λ^∗) vanishes, then the error in the property becomes quadratic in the error of the wave function. As is well-known, this situation arises for the ground-state energy E(λ) when the wave function is determined by satisfying the stationary condition E′ (λ^∗) = 0, giving

$$E({\mathrm{\lambda }}_0)=E({\mathrm{\lambda }}^{\ast })+\mathcal{O}({\mathrm{\delta }\mathrm{\lambda }}^2)$$ (3)

As we shall now see, quadratic error and improved accuracy can be obtained for any property, not just for the energy, by constructing a property Lagrangian.

Assume that the wave function is obtained by solving a set of (linear or nonlinear) equations, denoted symbolically by

$$e(\mathrm{\lambda })=0$$ (4)

and construct the property Lagrangian

$$\mathrm{ℳ}(\mathrm{\lambda },\overline{\mathrm{\lambda }})=M(\mathrm{\lambda })+\overline{\mathrm{\lambda }}e(\mathrm{\lambda })$$ (5)

where $\overline{\mathrm{\lambda }}$ contains the Lagrange multipliers, one for each constraint in Eq. 4. The stationary conditions on the Lagrangian are

$${\frac{\mathrm{\partial }\mathrm{ℳ}(\mathrm{\lambda },\overline{\mathrm{\lambda }})}{\mathrm{\partial }\overline{\mathrm{\lambda }}}|}_{\ast }=e({\mathrm{\lambda }}^{\ast })=0$$ (6)

$${\frac{\mathrm{\partial }\mathrm{ℳ}(\mathrm{\lambda },\overline{\mathrm{\lambda }})}{\mathrm{\partial }\mathrm{\lambda }}|}_{\ast }={\frac{\mathrm{\partial }M(\mathrm{\lambda })}{\mathrm{\partial }\mathrm{\lambda }}|}_{\ast }+\overline{\mathrm{\lambda }}{\frac{\mathrm{\partial }e(\mathrm{\lambda })}{\mathrm{\partial }\mathrm{\lambda }}|}_{\ast }=0$$ (7)

where the notation ∣_∗ indicates that the derivatives are calculated at the optimal values λ^∗ and ${\overline{\mathrm{\lambda }}}^{\ast }$ of λ and $\overline{\mathrm{\lambda }}$ , respectively. Because the stationary Lagrangian satisfies ℳ $({\mathrm{\lambda }}^{\ast },{\overline{\mathrm{\lambda }}}^{\ast })=M({\mathrm{\lambda }}^{\ast })$ , we may calculate properties from the variational Lagrangian ℳ rather than from the nonvariational M. The error in the Lagrangian is quadratic in the error of the wave function, as seen from the expansion

$$\mathrm{ℳ}({\mathrm{\lambda }}_0,{\overline{\mathrm{\lambda }}}_0)=M({\mathrm{\lambda }}^{\ast },{\overline{\mathrm{\lambda }}}^{\ast })+O({\mathrm{\delta }\mathrm{\lambda }}^2,\mathrm{\delta }{\overline{\mathrm{\lambda }}}^2,\mathrm{\delta }\mathrm{\lambda }\mathrm{\delta }\overline{\mathrm{\lambda }})$$ (8)

where Eqs. 6 and 7 make the first derivative vanish.

The construction of the property Lagrangian is typically relatively inexpensive—less expensive than the calculation of the wave function and much less expensive than the calculation of the wave function to higher accuracy, making the Lagrangian approach the most cost-effective way of calculating the property to a given accuracy. Note that the Lagrangian is constructed from the same ingredients as needed for the evaluation of properties in the traditional manner, namely, e(λ) and M(λ).

Let us now assume that we approach the optimal wave-function parameters λ^∗ perturbatively in the manner

$${\mathrm{\lambda }}^{\ast }={\mathrm{\lambda }}^{(0)}+{\mathrm{\lambda }}^{(1)}+{\mathrm{\lambda }}^{(2)}+\cdots$$ (9)

where the λ^(k) with k = 1,2, … provide smaller and smaller corrections to the zero-order description λ⁽⁰⁾. The corrections are calculated in succession, each new correction λ^(k) depending on all λ⁽ⁱ⁾ with i < k. The partial sum ${\mathrm{\lambda }}^k={\sum }_{i=0}^k {\mathrm{\lambda }}^{(i)}$ is then correct to order k relative to λ^∗, with an error ${\mathrm{\delta \lambda }}^k={\sum }_{i=k+1}^{\infty } {\mathrm{\lambda }}^{(i)}$ of order k + 1. The multiplier ${\overline{\mathrm{\lambda }}}^k$ associated with λ^k is likewise correct to order k relative to ${\overline{\mathrm{\lambda }}}^{\ast }$ , with an error $\mathrm{\delta }{\overline{\mathrm{\lambda }}}^k$ of order k + 1. From Eqs. 2 and 8, we find that M(λ^k) and $\mathrm{ℳ}({\mathrm{\lambda }}^k,{\overline{\mathrm{\lambda }}}^k)$ have errors relative to $M({\mathrm{\lambda }}^{\ast })=\mathrm{ℳ}({\mathrm{\lambda }}^{\ast },{\overline{\mathrm{\lambda }}}^{\ast })$ of orders k + 1 and 2k + 2, respectively. We hence arrive at the 2k + 1 rule (13), perfectly illustrated in Fig. 1: M(λ^k) and $\mathrm{ℳ}({\mathrm{\lambda }}^k,{\overline{\mathrm{\lambda }}}^k)$ calculated from the same parameters of order k are correct to orders k and 2k + 1, respectively.

In practice, the calculation of wave-function corrections is fairly straightforward up to second order in terms of floating-point operations, data flow, and data storage. Beyond second order, the increased interdependence on lower-order terms reduces the overall efficiency, making the calculation of third- and higher-order corrections expensive on modern computers and unsuitable for massively parallel implementations. It is therefore an important observation that the dipole moments calculated variationally from the first- and second-order wave functions in Fig. 1 are identical to those calculated nonvariationally from the third- and fifth-order wave functions, respectively.

CC hierarchy for correlated electronic wave functions

In all calculations presented here, we use CC theory, which was developed in nuclear physics in the 1950s (15) and adapted to quantum chemistry in the late 1960s (16, 17), where it has become the most accurate approach to molecular electronic-structure theory available today (1–4). In CC theory, the wave function ∣CC〉 is expressed in terms of an exponential operator working on the Hartree-Fock determinant ∣HF〉 in the manner

$$\mid \text{CC}(t)\rangle ={\mathrm{e}}^{T(t)}\mid \text{HF}\rangle$$ (10)

where the CC operator

$$T(t)={\displaystyle \sum _i} {\displaystyle \sum _{{\mathrm{\mu }}_i}} t_{{\mathrm{\mu }}_i}{\mathrm{\theta }}_{{\mathrm{\mu }}_i}$$ (11)

is a linear combination of excitation operators θ_μi multiplied by amplitudes t_μi. Applied to the Hartree-Fock state, each θ_μi generates an excited determinant ∣μ_i〉 = θ_μi∣HF〉 of excitation level i. The amplitudes t_μi are determined from the CC amplitude equations

$$\langle {\mathrm{\mu }}_i\mid H_t\mid \text{HF}\rangle =0$$ (12)

where $\langle {\mathrm{\mu }}_i\mid =\langle \text{HF}\mid {\mathrm{\theta }}_{{\mathrm{\mu }}_i}^{†}$ and where H_t = e^−T(t)He^T(t) is the similarity-transformed Hamiltonian.

From the amplitudes included in T(t), the ground-state CC energy can be calculated as

$$E(t)=\langle \text{HF}\mid H_t\mid \text{HF}\rangle$$ (13)

However, this energy expression is not variational in the amplitudes, which have been obtained by solving Eq. 12 rather than satisfying variational conditions on the energy.

Following the procedure outlined above, we now make the CC energy in Eq. 13 variational (i.e., stationary with respect to first-order variations in its variables) by adding to it the conditions on the amplitudes in Eq. 12 multiplied by Lagrange multipliers s, yielding (14)

$$\mathrm{ℰ}(t,s)=\langle \text{HF}+s\mid H_t\mid \text{HF}\rangle$$ (14)

where the bra state is given by

$$\langle \text{HF}+s\mid =\langle \text{HF}\mid +{\displaystyle \sum _i} {\displaystyle \sum _{{\mathrm{\mu }}_i}} s_{{\mathrm{\mu }}_i}\langle {\mathrm{\mu }}_i\mid$$ (15)

The multipliers s_μi are determined to make the energy stationary with respect to variations in the amplitudes by solving the equations

$$\langle \text{HF}+s\mid [H_t,{\mathrm{\theta }}_{{\mathrm{\mu }}_i}]\mid \text{HF}\rangle =0$$ (16)

An advantage of energy stationarity is that it makes the calculation of molecular properties such as molecular forces and force constants simpler (13, 14). This is a well-known result and not our main concern here. Rather, our purpose is to show that the Lagrangian approach is applicable to all molecular properties, not just the energy, and to illustrate the gains that this approach gives.

Different levels of CC theory differ in which excitation operators ${\mathrm{\theta }}_{{\mathrm{\mu }}_i}$ are included in the description. In CC singles (CCS) theory, only single excitations from occupied to unoccupied Hartree-Fock orbitals are included; in CC singles-and-doubles (CCSD) theory, all double excitations are added (18); next, in CC singles-doubles-triples (CCSDT) theory, we include also all triple excitations (19, 20), and so on. As more excitations are included, the description becomes more accurate, converging to the exact solution in the orbital basis chosen for the calculation.

Perturbation expansion of CC theory

Because high-order CC wave functions are expensive to calculate, a perturbational treatment may be preferable. In CP theory (21–24), we first construct a zero-order CC wave function in the usual manner, truncating the expansion at some excitation level p to obtain the zero-order wave function

$$\mid 0\rangle ={\mathrm{e}}^{T(t_0)}\mid \text{HF}\rangle$$ (17)

whose amplitudes are taken to satisfy the usual CC equations

$$\langle {\mathrm{\mu }}_i\mid H_{t_0}\mid \text{HF}\rangle =0,1\le i\le p$$ (18)

We next use the zero-order wave function as the starting point for a perturbative construction of a more elaborate CC wave function, truncated at a higher excitation level P > p

$$\mid \text{CC}(t_0+\mathrm{\delta }t)\rangle =e^{T(t_0+\mathrm{\delta }t)}\mid \text{HF}\rangle$$ (19)

using the fluctuation potential ϕ = H − f, where f is the Fock operator, as the perturbation operator. The perturbation series of the correction amplitudes δt = δt⁽¹⁾ + δt⁽²⁾ + ⋯ is obtained by solving the CC equations

$$\langle {\mathrm{\mu }}_i\mid H_{t_0+\mathrm{\delta }t}\mid \text{HF}\rangle =0,1\le i\le P$$ (20)

in orders of the zero-order similarity-transformed fluctuation potential ${\mathrm{\varphi }}_{t_0}$, keeping t₀ fixed. To ensure that relaxations within the zero-order excitation space are treated to zero order, ${\mathrm{\varphi }}_{t_0}$ is treated as a zero-order rather than first-order operator whenever it works entirely within this excitation space.

In the calculations presented here, we use the CPS(D) expansion (targeting the CCSD wave function from the CCS wave function) and the CPSD(T) expansion (targeting the CCSDT wave function from the CCSD wave function); see (21–24).

Construction and use of CP Lagrangian for dipole moments

Assuming that the CC ground-state energy has been cast in a variational form (Eq. 14), we can use the Hellmann-Feynman theorem (25, 26) and obtain the following expression for a given component X of the dipole moment

$$X(t,s)=\langle \text{HF}+s\mid X_t\mid \text{HF}\rangle$$ (21)

where X_t is the similarity-transformed dipole operator. However, this expression for the dipole moment is itself not variational since the arguments t and s do not satisfy stationary conditions on the dipole moment X(t, s) but rather conditions on the energy in Eqs. 12 and 16, respectively.

Multiplying the conditions in Eqs. 12 and 16 by undetermined multipliers $\overline{t}$ and $\overline{s}$ , respectively, and adding the resulting expressions to X(t, s), we arrive at the CP dipole Lagrangian

$$\mathcal{X}(t,s,\overline{t},\overline{s})=X(t,s)+ \langle \overline{t}\mid H_t\mid \text{HF}\rangle +\langle \text{HF}+s\mid [H_t,T(\overline{s})]\mid \text{HF}\rangle$$ (22)

where $\langle \overline{t}\mid ={\sum }_{{\mathrm{\mu }}_i} {\overline{t}}_{{\mathrm{\mu }}_i} \langle {\mathrm{\mu }}_i\mid$ and $T(\overline{s})={\sum }_{{\mathrm{\mu }}_i} {\overline{s}}_{{\mathrm{\mu }}_i}{\mathrm{\theta }}_{{\mathrm{\mu }}_i}$ . This Lagrangian is by construction stationary with respect to ${\overline{t}}_{{\mathrm{\mu }}_i}$ and ${\overline{s}}_{{\mathrm{\mu }}_i}$ , independent of their values, given that Eqs. 12 and 16 hold. To make it stationary also with respect to t and s, we solve the linear equations

$$\frac{\mathrm{\partial }\mathcal{X}}{\mathrm{\partial }{s}_{{\mathrm{\mu }}_i}}=\langle {\mathrm{\mu }}_i\mid X_t\mid \text{HF}\rangle +\langle {\mathrm{\mu }}_i\mid [H_t,T(\overline{s})]\mid \text{HF}\rangle =0$$ (23)

$$\begin{array}{c}\frac{\mathrm{\partial }\mathcal{X}}{\mathrm{\partial }{t}_{{\mathrm{\mu }}_i}}=\langle \text{HF}+s\mid [X_t,{\mathrm{\theta }}_{{\mathrm{\mu }}_i}]\mid \text{HF}\rangle +\rangle \overline{t}\mid [H_t,{\mathrm{\theta }}_{{\mathrm{\mu }}_i}]\mid \text{HF}\rangle +\\ \langle \text{HF}+s\mid \left\{[H_t,{\mathrm{\theta }}_{{\mathrm{\mu }}_i}],T\left(\overline{s}\right)\right\}\mid \text{HF}\rangle =0\end{array}$$ (24)

where the first equations determine $\overline{s}$ and the second equations $\overline{t}$ . The dipole moment in Eq. 22 is now stationary in all its variables t, s, $\overline{t}$ , and $\overline{s}$.

The usefulness of this variational reformulation is illustrated in Fig. 1, where we have plotted the errors in the CPS(D) expansion (left) and CPSD(T) expansion (right) of the dipole moment of H₂O. The expansion of $\mathcal{X}(t,s,\overline{t},\overline{s})$ (red curve) converges faster than the corresponding expansion of X(t, s) (blue curve), satisfying to each order the 2k + 1 rule.

Construction and use of CP Lagrangian for excitation energies

In CC theory, electronic excitation energies W_n are the eigenvalues of the non-Hermitian CC Jacobian J(t) with left and right eigenvectors L_n and R_n, respectively

$${\mathbf{L}}_n^{\mathrm{T}}\mathbf{J}(t)=W_n(t){\mathbf{L}}_n^{\mathrm{T}} \mathbf{J}(t){\mathbf{R}}_n=W_n(t){\mathbf{R}}_n$$ (25)

The elements of the Jacobian are given by

$$J_{{\mathrm{\mu }}_i,{\mathrm{\nu }}_j}(t)=\langle {\mathrm{\mu }}_i\mid [H_t,{\mathrm{\theta }}_{{\mathrm{\nu }}_j}]\mid \text{HF}\rangle$$ (26)

and depend on the CC amplitudes through the similarity-transformed Hamiltonian H_t.

In CP theory, the excitations energies may be obtained by solving the right Jacobian eigenvalue equation in Eq. 25 in orders k in the fluctuation potential. Introducing order expansions of all ingredients involved and assuming intermediate normalization ${[{\mathbf{L}}_n^{(0)}]}^{\mathrm{T}}{\mathbf{R}}_n^{(k)}={\mathrm{\delta }}_{0k}$ , we obtain

$$W_n^{(k)}={\displaystyle \sum _{q=1}^k} {[{\mathbf{L}}_n^{(0)}]}^{\mathrm{T}}{\mathbf{J}}^{(q)}{\mathbf{R}}_n^{(k-q)}$$ (27)

To determine $W_n^{(k)}$ , we must thus calculate ${\mathbf{R}}_n^{(q)}$ to order k − 1 and J^(q) to order k, which, by Eq. 26, requires the calculation of the amplitudes δt = t − t₀ to order k − 1. In the special case of the CPS(D) model, the second-order excitation energy $W_n^{(2)}$ is equivalent to the CIS(D) excitation energy introduced by Head-Gordon et al. (27).

Alternatively, we may determine the excitation energy corrections $W_n^{(k)}$ from a variational Lagrangian. From Eq. 25, we obtain the excitation energy function

$$W_n(t,{\mathbf{R}}_n,{\mathbf{L}}_n)=\frac{{\mathbf{L}}_n^{\mathrm{T}}\mathbf{J}\left(t\right){\mathbf{R}}_n}{{\mathbf{L}}_n^{\mathrm{T}}{\mathbf{R}}_n}$$ (28)

which is stationary in the left and right eigenvectors but not in the cluster amplitudes. Recalling that the cluster amplitudes satisfy the CC conditions in Eq. 12, we arrive at the following CP Lagrangian for the excitation energy

$${\mathcal{W}}_n(t,\overline{t},{\mathbf{R}}_n,{\mathbf{L}}_n)=W_n(t,{\mathbf{R}}_n,{\mathbf{L}}_n)+{\displaystyle \sum _i} {\displaystyle \sum _{{\mathrm{\mu }}_i}} {\overline{t}}_{{\mathrm{\mu }}_i}\langle {\mathrm{\mu }}_i\mid H_t\mid \text{HF}\rangle$$ (29)

which is stationary with respect to the multipliers ${\overline{t}}_{{\mathrm{\mu }}_i}$ by construction and made stationary with respect to the amplitudes t_μi by solving the linear equations

$${\displaystyle \sum _j} {\displaystyle \sum _{{\mathrm{\nu }}_j}} {\overline{t}}_{{\mathrm{\nu }}_j}{J}_{{\mathrm{\nu }}_j,{\mathrm{\mu }}_i}(t)=-\frac{\mathrm{\partial }{W}_n(t)}{\mathrm{\partial }{t}_{{\mathrm{\mu }}_i}}$$ (30)

The resulting Lagrangian is thus stationary in all its variables t, $\overline{t}$ , R_n, and L_n.

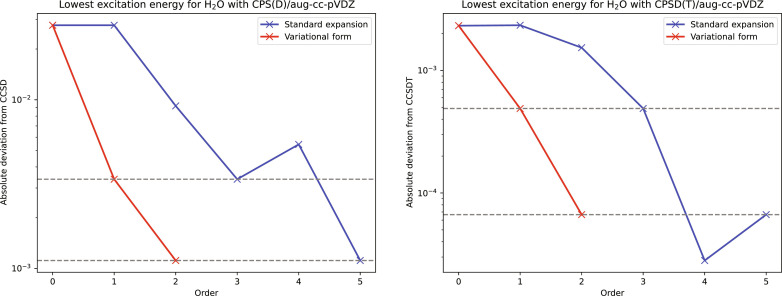
Using CP theory, we may determine order expansions of t, $\overline{t}$ , R_n, and L_n from the stationary conditions and insert these in ${\mathcal{W}}_n(t,\overline{t},{\mathbf{R}}_n,{\mathbf{L}}_n)$ . The kth-order excitation-energy correction $W_n^{(k)}$ in Eq. 27 can be determined from the kth-order expansion coefficient of the Lagrangian excitation energy ${\mathcal{W}}_n^{\left(k\right)}$ in Eq. 29 by applying the 2n + 1 rule for the primary variables R_n, L_n, and t and the 2n + 2 (13) rule for the multiplier $\overline{t}$ . For odd-order excitation energy corrections ${\mathcal{W}}_n^{(2k+1)}$, all variables R_n, L_n, t, and $\overline{t}$ are needed to order k; for even-order excitation-energy corrections ${\mathcal{W}}_n^{\left(2k\right)}$, the primary variables R_n, L_n, and t are needed to order k and the multiplier $\overline{t}$ to order k − 1. In Fig. 2, we have plotted the errors in the CPS(D) and CPSD(T) expansions of the lowest singlet excitation energy of H₂O, as obtained in the nonvariational formulation (blue curve) and variational formulation (red curve). In accordance with the 2k + 1 rule, the variational expansion of the wave function to first and second orders, respectively, gives the same result as the nonvariational expansion to the third and fifth orders, as also observed for the dipole moment in Fig. 1.

Fig. 2. Convergence of the CP series for the lowest singlet excitation energy of H₂O calculated variationally (red) and nonvariationally (blue).

The error in the lowest singlet excitation energy of H₂O (atomic units) plotted against the order of the CPS(D) expansion of the CCSD excitation energy (left) and the CPSD(T) expansion of the CCSDT excitation energy (right), calculated variationally (red) and nonvariationally (blue). All calculations have been performed in the aug-cc-pVDZ basis in the frozen-core approximation at the equilibrium geometry of H₂O.

We now examine in more detail the performance of the CPS(D) series for excitation energies, comparing with the full CCSD model for the QUEST#3 dataset (28), consisting of 131 singlet excitation energies for 26 organic molecules. We use the notation CPS(D)-qn to indicate that the excitation energies have been calculated variationally from the n-order CPS(D) wave function. All calculations were carried out in the aug-cc-pVTZ basis within the frozen-core approximation. The statistics in Table 1 are restricted to those (104) excitations for which the norm of the second-order singles correction of the excitation vector is less than 0.3.

Table 1. Performance of variational CPS(D) theory relative to full CCSD theory for singlet electronic excitation energies of organic molecules.

For each order 0 ≤ n ≤ 2 in the variational CPS(D)-qn expansion, statistical errors in calculated singlet excitation energies relative to full CCSD theory are listed; zero order corresponds to CCS theory. The statistics are over the 104 excitations in the QUEST#3 dataset (28) with norm of the second-order singles correction smaller than 0.3. All calculations have been carried out in the aug-cc-pVTZ basis, in the frozen-core approximation.

	CPS(D)-qn
	0	1	2
Mean absolute error (eV)	0.620	0.067	0.027
Maximum absolute error (eV)	2.533	0.729	0.183
Mean error (eV)	0.422	0.035	−0.017
SD (eV)	0.716	0.098	0.044
Mean relative error (%)	8.46	−0.60	0.28
Maximum relative error (%)	39.9	−9.96	2.90

For singles corrections larger than 0.3, the perturbation to the CCS excitation vector is so large that the resulting excitation energy correction cannot be trusted (23).

To the first and second orders, we obtain a mean error compared to CCSD excitation energies of 0.03 and −0.017 eV, respectively; the corresponding relative errors are 0.6 and 0.28%. These errors are much smaller than the typical errors of the CCSD model. If higher accuracy is needed, then the more advanced CPSD(T) model should be used instead.

We emphasize that the accuracy of the CPS(D)-qn models observed in Table 1 is achieved using solely first- and second-order wave-function and excitation-vector corrections. The first- and second-order variational excitation energies are in this formulation expressed in a form amenable to efficient implementations on modern computer architectures and suitable for large-scale parallelization; a detailed comparison of the computational cost of the CCSD and CPS(D)-qn methods will be presented elsewhere.

DISCUSSION

The calculation of dipole moments and excitation energies described here illustrates what can, in general, be accomplished for molecular properties using the variational Lagrangian formulation, whose construction follows the procedure outlined above. From the first- and second-order wave-function corrections, respectively, we obtain properties that are of the same accuracy as those calculated from third- and fifth-order wave functions using the traditional procedure. Our procedure is not restricted to CP theory but is applicable in all situations in quantum chemistry where molecular properties are calculated from hierarchies of electronic wave functions and in nuclear physics, when many-body theories including CC theory are used to solve the nuclear Schrödinger equation. The variational approach described here has been implemented in the LSDalton program (29) and will be available in a future release of the Dalton electronic-structure program.

Supplementary Materials

This PDF file includes:

Table S1

Dataset