Abstract
Signal multiplexing is necessary to reduce a large number of readout channels in positron emission tomography (PET) scanners to minimize cost and achieve lower power consumption. However, the conventional weighted average energy method cannot localize the multiplexed events and more sophisticated approaches are necessary for accurate demultiplexing. The purpose of this paper is to propose a non-parametric decision tree model for demultiplexing signals in prismatoid PET (Prism-PET) detector module that consisted of 16 × 16 lutetium yttrium oxyorthosilicate (LYSO) scintillation crystal array coupled to 8 × 8 silicon photomultiplier (SiPM) pixels with 64:16 multiplexed readout. A total of 64 regression trees were trained individually to demultiplex the encoded readouts for each SiPM pixel. The Center of Gravity (CoG) and Truncated Center of Gravity (TCoG) methods were utilized for crystal identification based on the demultiplexed pixels. The flood histogram, energy resolution, and depth-of-interaction (DOI) resolution were measured for comparison using with and without multiplexed readouts. In conclusion, our proposed decision tree model achieved accurate results for signal demultiplexing, and thus maintained the Prism-PET detector module’s high spatial and DOI resolution performance while using our unique light-sharing-based multiplexed readout.
Keywords: demultiplexing, decision tree model, Prism-PET
I. Introduction
POSITRON emission tomography (PET) is a nuclear medical imaging technique that involves the detection of pairs of 511 keV gamma-ray photons emitted by the annihilation process [1] [2]. PET detectors are designed to collect incoming high-energy photons by scintillation crystals and convert the optical signals into measurable electrical pulses using photodetectors [3] [4].
In principle, one-to-one coupling of scintillation crystals to photodetectors with individual readout channels can achieve the best PET detector performance with the highest signal-to-noise ratio (SNR), energy and timing resolution. However, it is costly and challenging to design and fabricate a large number of high-speed data acquisition (DAQ) channels, and therefore different signal multiplexing techniques have been proposed and implemented to reduce readout channels while minimizing performance degradations [5] [6].
The charge division multiplexing schemes that modulate the input signal from photosensors have been widely used to encode the interacted crystal position and photon energy information [7], which are commonly implemented in discretized positioning circuit [8]–[11] and row-column summing readout circuit [12]–[15].
Center of gravity (CoG) method [16], which is a generalization of Anger logic [17], extracts position information from the multiplexed readout. Moreover, the truncated center of gravity (TCoG) approach [18] has been proposed to reduce the noise based on the centroid algorithm to improve the accuracy of events’ position determination.
In our previous work, we designed a novel light-sharing PET detector module using prismatoid light guides and single-ended readout, called Prism-PET [19] [20], and developed a unique multiplexing scheme that took advantage of the deterministic and localized light-sharing pattern of Prism-PET [21]. However, directly using the weighted average energy method fails to localize events using multiplexed readout, and thus here we introduced a data-driven demultiplexing model based on decision tree algorithm. Finally, we characterized the energy resolution, depth of interaction (DOI) resolution, floodmap decoding error, and peak-to-valley ratio (PVR) of a Prism-PET detector module with and without multiplexed readouts and evaluated the accuracy of our proposed demultiplexing model.
II. Prism-PET and Imux Design
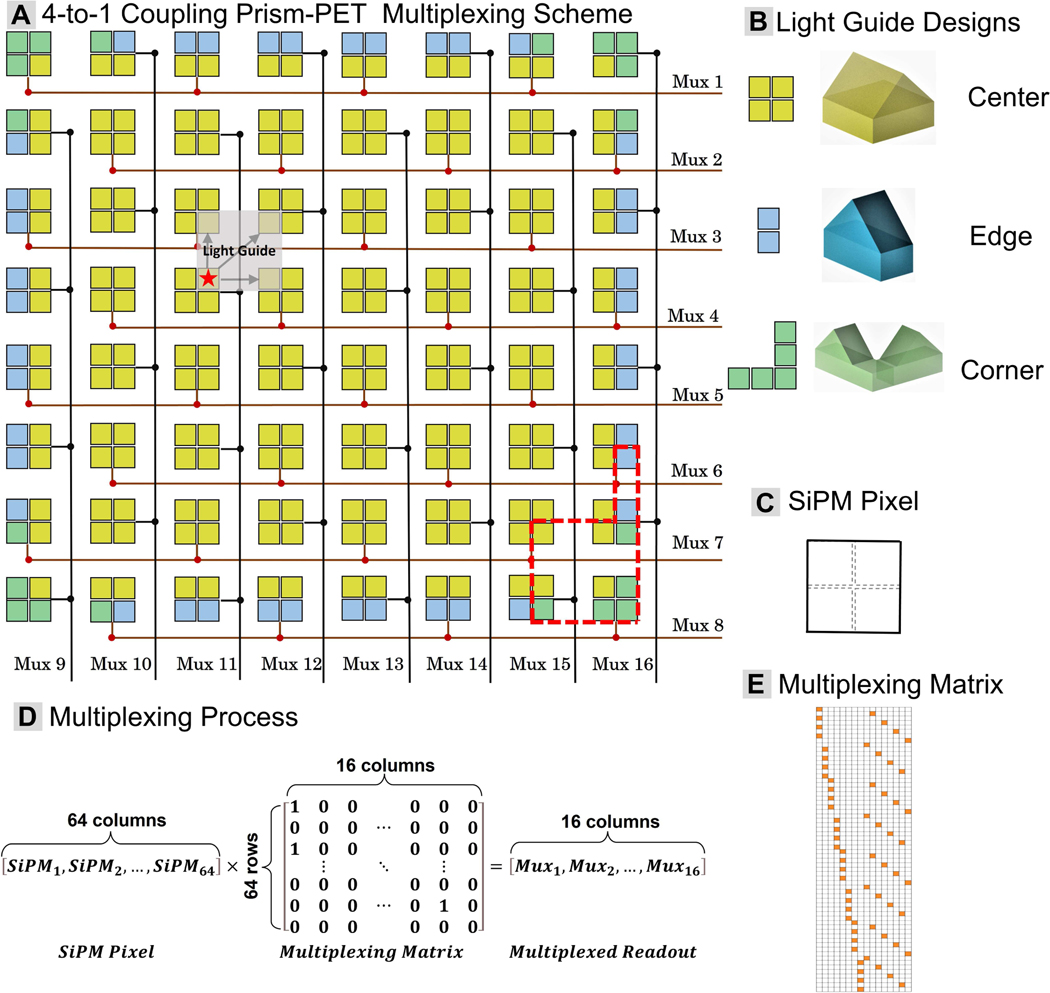
The 4-to-1 Prism-PET is an ultra-high resolution, single-ended readout depth-encoding detector module that consists of a 16 × 16 array of 1.5 × 1.5 × 20 mm3 lutetium yttrium oxyorthosilicate (LYSO) scintillation crystals couples to an 8 × 8 array of 3 × 3 mm2 silicon photomultiplier (SiPM) pixels on one side and a segmented prismatoid light guide array on the opposite side (Fig. 1A, 1B, and 1C). The individual prismatoid mirrors confine the incident light to only the nearest SiPM neighbors and three distinct shapes of light-guide mirrors are designed (center, edge, and corner) to enhance crystal identification even at the periphery of the detector. [19] [20].
Fig. 1.
(A) Diagrams of 4-to-1 coupling Prism-PET detector array with a segmented light guide array. The solid lines represent the connecting patterns of the iMux scheme design. The gray square shows the deterministic light-sharing pattern and the dashed line provides an example of distinct light guide designs for crystals located at different parts. (B) Individual light guide designs for center, edge and corner crystals. (C) Four crystals couple to a single SiPM pixel. (D) Multiplexing process. (E) Multiplexing matrix in an image description.
The proposed interleaved multiplexing (iMux) scheme only shorts the four anodes from every other SiPM pixel across rows and columns that are overlapped with distinct prismatoid light guides and connects them to the same readout channel [21]. This is to preserve the deterministic light-sharing pattern, enable accurate signal demultiplexing, and thus minimize any degradation in crystal identification. The iMux scheme achieves the same 4-to-1 multiplexing ratio as the conventional row-column summing circuit but with half the added capacitance and dark counts in each readout channel.
In this framework, the multiplexed readout is a linear combination of SiPM pixels, and the multiplexing scheme can be represented as a binary matrix where each element indicates whether the pixel is encoded or not (Fig. 1D and 1E).
III. Method
A. Data Acqusition
Prism-PET module was uniformly exposed to a 3 MBq Na-22 point source placed 15 cm away to acquire the standard flood data using TOFPET2 application-specific integrating circuits (ASIC) and a FEB/D v2 readout board from PETsys Electronics [22]. The experimental procedure was conducted under controlled conditions inside an Espec BTU-133 benchtop test chamber to maintain stable SiPM and ASIC temperatures. Furthermore, SiPM signal multiplexing was achieved by connecting the detector module to the iMux board, where 4 SiPM anodes are shorted together, and from the iMux board to the TOFPET2 ASIC.
B. Events Localization
The CoG method is a widely used technique that encodes the positional coordinates of interaction events as
| (1) |
| (2) |
| (3) |
| (4) |
where denotes the coordinates of the center of gravity of the light distribution on the flood histogram; and efer to the horizontal and vertical positions of the readout pixel in the SiPM array, respectively; and are the light signals detected by the readout ASIC; and represent the total number of column and row readout channels, respectively; and correspond to the sums of signals obtained from all readout channels for a single interaction event.
An alternative method for localizing the gamma events’ position is TCoG, which involves subtracting a predetermined fraction of the largest light signal from all readout channels [23]
| (5) |
| (6) |
| (7) |
where and are the truncated readout values in ith column and jth row, respectively, and is the experimentally determined coefficient.
C. Energy Resolution
The energy of each gamma-ray interaction event was determined through the sum of all readout signals, and the energy spectrums of individual crystals were estimated by analyzing the energy of localized events within each crystal using flood histograms. The energy window from 409 to 613 keV (±20%) was utilized to select 511 keV energy events and the energy resolution was measured as the full width at half maximum (FWHM) of the fitted energy spectrum with a Gaussian function divided by the 511 keV photopeak.
D. Peak-to-Valley Analysis
The peak-to-valley analysis entails the aggregation of values along the u− or v−axis to generate projection profiles of crystal signatures in flood histograms [24]. The profiles of the central row of the crystal spots were considered for peak-to-valley ratios calculation using the mean of the peak value divided by the two adjacent valleys.
E. Event Localization Accuracy
To quantitatively assess the accuracy of the decision tree-based demultiplexing model, we established a metric known as the event localization accuracy, which was defined as the percentage of gamma-ray events with synthetic multiplexed readout that were correctly positioned in the same crystal as with non-multiplexed readout.
F. Decision Tree Model Design
Demultiplexing signals from multiplexed readouts to SiPM pixels can be challenging due to the underdetermined nature of the system, which can result in an infinite number of potential solutions. To address this issue, we proposed a supervised learning-based demultiplexing model that utilizes the decision tree algorithm to effectively learn the Prism-PET deterministic light-sharing pattern, which enables it to accurately decode SiPM pixel signals from multiplexed readout values.
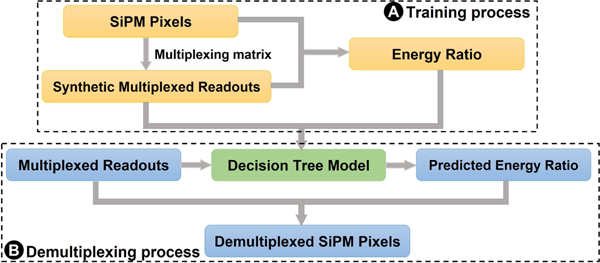
1). Building the training dataset:
We experimentally collected 1 million non-multiplexed gamma-ray interaction events (64 SiPM pixels) paired with synthetic multiplexed readouts (Fig. 1D) to build the training dataset (Fig. 2A). The SiPM signals were converted to the energy ratio
| (8) |
where is the ratio of SiPM signal to its corresponding multiplexed readout channel value, represents the light signal detected by the readout pixel in the SiPM array, is the encoded signal in kth multiplexed readout channel.
Fig. 2.
The framework of the demultiplexing model. (A) Data preprocessing for training the decision tree model. (B) The process of demultiplexing energy signals in SiPM pixels using the trained decision tree model.
The synthetic multiplexed data and the calculated energy ratios for each gamma-ray event were considered as the training inputs and ground truth labels for the model training, respectively.
2). Tree building:
The decision tree algorithm is characterized by a binary tree structure that is recursively partitioned using a binary splitting methodology to successively divide the predictor space. The procedure begins with a root node and iteratively generates branches that extend into internal nodes until further splitting is deemed incapable of producing a significant reduction in deviation, resulting in the generation of homogeneous subsets contained within the leaf nodes [25]. The best-split decision for each internal node is determined by searching for a splitting candidate that minimizes the sum of squared errors (SSE) of the subsets
| (9) |
where and represent the individual and average values of the samples belonging to groups and , respectively.
In order to enhance the generalization capability of the model and prevent overfitting, we imposed a threshold on the minimum number of samples in each leaf node and pruned the branches that result in only the marginal improvement to the model’s accuracy, thereby obtaining the optimal decision tree via the application of ten-fold cross-validation technique. Subsequently, we independently trained a total of 64 regression trees to predict the energy ratio in each individual SiPM pixel.
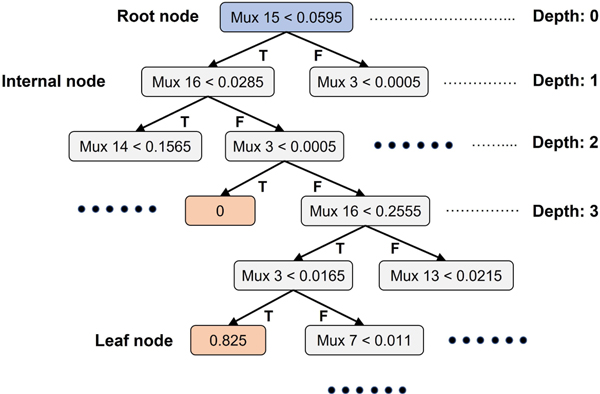
Fig. 3 depicts one of the 64 trained decision trees that have been implemented to estimate the energy ratio of one SiPM pixel. Within the tree diagram, the root node (denoted by a blue square) serves as the initial step in the estimation process, whereas the internal nodes (represented by grey squares) are utilized as splitting criteria for the tree. The leaf nodes (represented by orange squares) correspond to the final outcomes of the decision tree and signify the estimated energy ratio for the SiPM pixel.
Fig. 3.
One of the trained decision trees in the demultiplexing model. The root, internal, and leaf nodes have been annotated as blue, grey, and orange, respectively.
3). Demultiplexing SiPM pixels:
The multiplexed readout signals along with the predicted energy ratios derived from the model are employed in the process of demultiplexing energy signals in SiPM pixels (Fig. 2B)
| (10) |
where denotes the demultiplexed signal in the ith column and jth row of SiPM array, and is the predicted energy ratio from the trained decision tree model.
IV. Results
A. Flood Histograms and PVR Values
Representative floodmaps measured with and without multiplexed readouts are shown in Fig. 4A using CoG and TCoG coordinate calculation methods. Non-multiplexed readout for CoG and TCoG methods were found to exhibit clear separation of the 256 individual crystals, whereas flood histogram distortions and imperfect crystal identifications were expected using multiplexed readout. Thus, the decision tree-based demultiplexing model was developed to mitigate these distortions and successfully localize events that were captured with multiplexed readout.
Fig. 4.
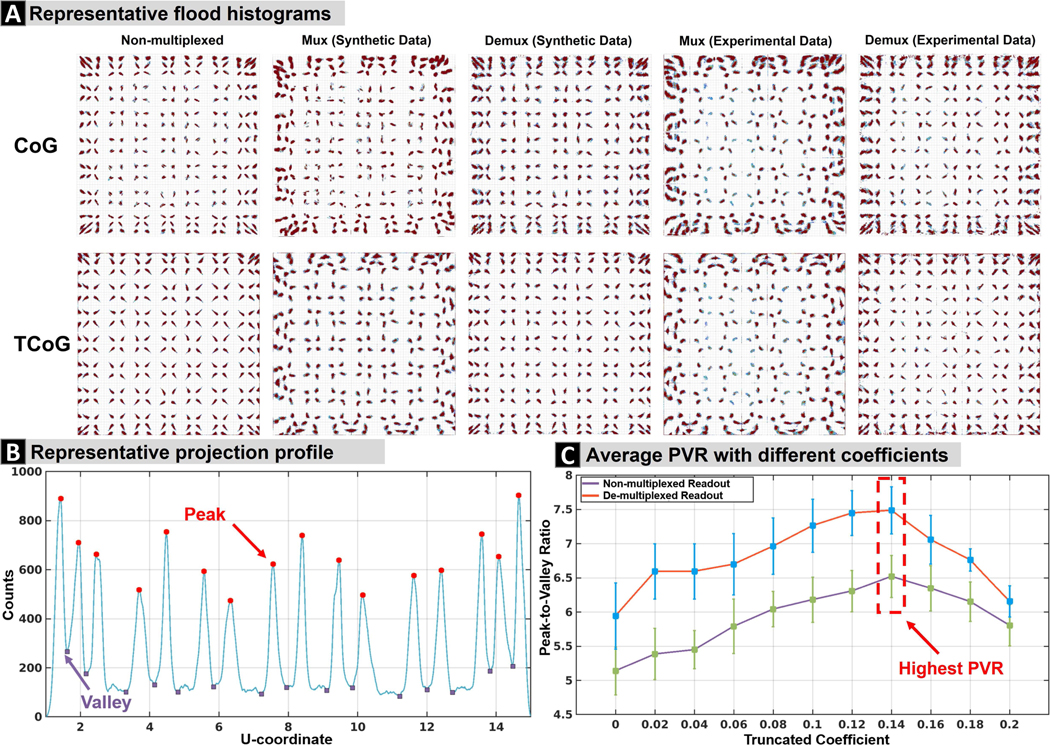
(A) Comparison of floodmaps generated using CoG and TCoG methods for non-multiplexed, synthetic/experimentally multiplexed, and demultiplexed readouts. The floodmaps were generated using a Na-22 source and plotted on the same scale. (B) A projection profile from a central row of crystals with ”peak” and ”valley” annotations is shown as an example. (C) The average PVR with standard deviation (error bar) in different truncated coefficients for non-multiplexed and demultiplexed synthetic encoded readouts.
Fig. 4B depicts a projection profile that is representative of the crystal signatures located on a single row of the floodmap. The peaks (red circle) and valleys (blue square) have been identified and subsequently applied in the computation of the peak-to-valley ratio that served as an indicator of the quality of crystal identification.
Fig. 4C demonstrates the average peak-to-valley ratio across the 10 rows (out of 16) in the middle part of a detector module with various truncated coefficients ranging from 0 to 0.2 with an increment of 0.02. Notably, the truncated coefficient value of 0.14 resulted in the highest achievable PVR for both non-multiplexed and demultiplexed signals.
B. Energy and DOI Performance
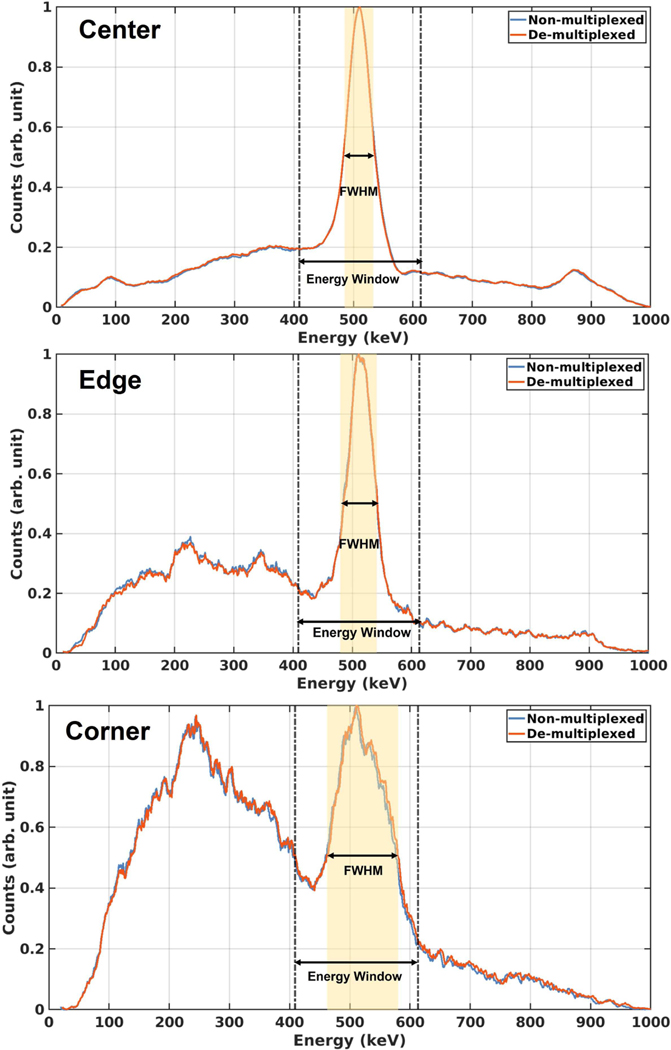
The energy spectra using non-multiplexed and demultiplexed signals from gamma events were found to almost perfectly overlap across the entire energy range (Fig. 5). Moreover, the study provides a quantitative evaluation of the energy and DOI resolutions (the measuring method proposed by [26]) of all crystals using both one-to-one (i.e., non-multiplexed) and 4-to-1 iMux readout. The measured average energy/DOI resolution of all crystals using non-multiplexed and iMux readouts were 8.6±1.1%/1.9±0.6 mm and 9.4±1.2%/1.7±0.6 mm FWHM, respectively (Table I).
Fig. 5.
Energy histograms for the center, edge, and corner crystals. Blue and red lines represent histograms for non-multiplexed and demultiplexed energy signals, respectively.
TABLE I.
Quantitative Evaluation of Energy and DOI Resolution Across All Crystals Utilizing Non-multiplexed and Imux Signals
| Energy Resolution | DOI Resolution | |||
|---|---|---|---|---|
|
|
||||
| w/o | w/ | w/o | w/ | |
|
|
||||
| Center | 8.3 ± 0.6% | 9.5 ± 0.9% | 1.9 ± 0.6 mm | 1.8 ± 0.5 mm |
| Edge | 9.5 ± 0.9% | 9.6 ± 0.9% | 1.8 ± 0.5 mm | 1.7 ± 0.4 mm |
| Corner | 9.9 ± 2.1% | 10.3 ± 2.2% | 2.1 ± 0.7 mm | 2.0 ± 0.8 mm |
C. Decision Tree Model
Table II presents a quantitative comparison between the fully grown decision tree and the optimized decision tree which have undergone a process of removing leaf nodes that do not affect the overall accuracy of the model. The results demonstrated that the fully grown decision tree exhibited a mean depth of 29 and required approximately 11.6 seconds for demultiplexing energy signals of one million gamma-ray events. Conversely, the optimized decision tree showed an average tree depth of 12 and required only 5.5 seconds for demultiplexing the same dataset. The test data obtained from two Prism-PET detector modules were utilized to evaluate the decision tree model’s ability to accurately localize gamma-ray events and to generalize to the new data. The results demonstrate a consistent performance with ∼95% accuracy using data collected from both detector modules.
TABLE II.
Quantitative Comparison between Fully Grown Tree and Optimized Tree
| Fully Grown Tree | Optimized Tree | |
|---|---|---|
|
| ||
| Average Depth of the Tree | 29 | 12 |
| Time Consumption (1M Events) | 11.6 s | 5.5 s |
| Accuracy on Detector A | 95.4% | 95.6% |
| Accuracy on Detector B | 95.5% | 95.6% |
V. Discussion
The floodmaps have demonstrated that the decision tree-based demultiplexing model in combination with the weighted average energy method is capable of localizing the gamma-ray interaction events using multiplexed readout. Given that TCoG and CoG are equivalent when the truncated coefficient is 0, the TCoG method with the optimized coefficient of 0.14 has shown a higher PVR than the basic CoG method and performed better in identifying crystals located on edges and corners, which is because CoG method is more sensitive to the asymmetry in light distribution and the noise from detector module that can lead to the distorted flood images.
Signal multiplexing techniques have been observed to have a negative impact on detector performance resulting in compromised energy and DOI resolutions when compared to using non-multiplexed readout [27]. However, it remains a widely used approach for reducing the cost of PET applications by reducing the number of DAQ readout channels. The insignificant difference of 0.8% in energy resolution and 0.2 mm in DOI resolution indicates the effectiveness of the proposed demultiplexing model in ensuring that detectors utilizing multiplexed readout can achieve comparable performance as using non-multiplexed readout.
In comparison to the fully grown trees, the optimized decision trees demonstrate a more compact model size and faster demultiplexing speed. Specifically, the average depth of the optimized trees is only 41% of that of the fully grown trees, and the time required for demultiplexing 1 million gamma events is 52% less. One must note that a typical PET scanner can generate gamma events on the order of 106 (e.g., hundreds of millions) which are detected and processed by the imaging system, thus the efficiency of the model is significant at each stage of data processing [28].
There is no significant difference observed in the event localization accuracy of the demultiplexing model utilizing fully grown and optimized decision trees. This can be contributed to the two types of decision trees demonstrating an ability to accurately demultiplex the highest energy ratio in the primary SiPM pixel. However, the fully grown trees may be overfitting on pixels with minimal energies, resulting in different predicted values compared to optimized trees. Nevertheless, the truncated center of gravity positioning method implements a fractional subtraction technique to reduce the impact of noise from non-primary pixels. As a result, both the fully grown and optimized decision trees exhibit consistent event localization accuracy when evaluated on test data.
The decision tree model is considered advantageous compared to other machine learning algorithms such as K-Nearest Neighbor (KNN) and deep neural networks (DNN) in terms of interpretability and visualization. Decision trees allow for a straightforward understanding of the rules and conditions that lead to specific predictions. Furthermore, compared to KNN, which requires the computation of distances between each data point and all other points in the training set, decision trees offer an efficient mechanism that only requires traversing the tree structure to make a prediction [25].
VI. Conclusion
A decision tree-based demultiplexing model has been developed to decode signals from multiplexed readout to SiPM pixels. The model was evaluated in combination with the TCoG algorithm, demonstrating highly accurate event localization and clear crystal identification using multiplexed readout. In addition, the model exhibited a generalization ability to new data from different Prism-PET detector modules. Furthermore, the proposed demultiplexing model preserved the high-resolution characterization of the Prism-PET detector module and produced competitive results using multiplexed readout.
Acknowledgment
The authors gratefully appreciate the helpful contribution of colleagues from PETsys Electronics for scientific discussion.
We gratefully acknowledge financial support from the National Institutes of Health (R01 EB030413)
Contributor Information
Yixin Li, Department of Electrical and Computer Engineering, College of Engineering and Applied Sciences, Stony Brook University, Stony Brook, NY 11794, US; Department of Radiology, Weill Cornell Medicine, Cornell University, NY 10021, US.
Xinjie Zeng, Department of Electrical and Computer Engineering, College of Engineering and Applied Sciences, Stony Brook University, Stony Brook, NY 11794, US; Department of Radiology, Weill Cornell Medicine, Cornell University, NY 10021, US.
Amir H. Goldan, Department of Radiology, Weill Cornell Medicine, Cornell University, NY 10021, US.
References
- [1].Moses William W. Trends in pet imaging. Nucl. Instrum. Methods Phys. Res. A: Accel. Spectrom. Detect. Assoc. Equip, 471(1–2):209–214, 2001. [Google Scholar]
- [2].Cherry Simon R and Dahlbom Magnus. Pet: physics, instrumentation, and scanners. In PET, pages 1–117. Springer, 2006. [Google Scholar]
- [3].Gonzalez-Montoro Andrea, Gonzalez Antonio J, Pourashraf Shirin, Miyaoka Robert S, Bruyndonckx Peter, Chinn Garry, Pierce Larry A, and Levin Craig S. Evolution of pet detectors and event positioning algorithms using monolithic scintillation crystals. IEEE trans. radiat. plasma med. sci, 5(3):282–305, 2021. [Google Scholar]
- [4].Gonzalez-Montoro Andrea, Ullah Muhammad Nasir, and Levin Craig S. Advances in detector instrumentation for pet. J. Nucl. Med, 63(8):1138–1144, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Du Junwei, Yang Yongfeng, Bai Xiaowei, Martin S Judenhofer Eric Berg, Di Kun, Buckley Steve, Jackson Carl, and Simon R Cherry. Characterization of large-area sipm array for pet applications. IEEE Trans. Nucl. Sci, 63(1):8–16, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Park Haewook, Yi Minseok, and Lee Jae Sung. Silicon photomultiplier signal readout and multiplexing techniques for positron emission tomography: a review. Biomed. Eng. Lett, pages 1–21, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Siegel Stefan, Robert W Silverman Yiping Shao, and Simon R Cherry. Simple charge division readouts for imaging scintillator arrays using a multi-channel pmt. IEEE Trans. Nucl. Sci, 43(3):1634–1641, 1996. [Google Scholar]
- [8].Downie Evan, Yang Xin, and Peng Hao. Investigation of analog charge multiplexing schemes for sipm based pet block detectors. Phys. Med. Biol, 58(11):3943, 2013. [DOI] [PubMed] [Google Scholar]
- [9].Stratos David, Maria Georgiou, Eleftherios Fysikopoulos, and George Loudos. Comparison of three resistor network division circuits for the readout of 4× 4 pixel sipm arrays. Nucl. Instrum. Methods Phys. Res. A, 702:121–125, 2013. [Google Scholar]
- [10].Park Haewook, Guen Bae Ko, and Jae Sung Lee. Hybrid charge division multiplexing method for silicon photomultiplier based pet detectors. Phys. Med. Biol, 62(11):4390, 2017. [DOI] [PubMed] [Google Scholar]
- [11].Kuang Zhonghua, Sang Ziru, Wang Xiaohui, Fu Xin, Ren Ning, Zhang Xianming, Zheng Yunfei, Yang Qian, Hu Zhanli, Du Junwei, et al. Development of depth encoding small animal pet detectors using dualended readout of pixelated scintillator arrays with si pm s. Med. Phys, 45(2):613–621, 2018. [DOI] [PubMed] [Google Scholar]
- [12].Shih YC, Sun FW, Macdonald LR, Otis BP, Miyaoka RS, Mc-Dougald W, and Lewellen TK. An 8× 8 row-column summing readout electronics for preclinical positron emission tomography scanners. In IEEE Nucl Sci Symp Conf Rec, pages 2376–2380. IEEE, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Yang Qian, Kuang Zhonghua, Sang Ziru, Yang Yongfeng, and Du Junwei. Performance comparison of two signal multiplexing readouts for sipm-based pet detector. Phys. Med. Biol, 64(23):23NT02, 2019. [DOI] [PubMed] [Google Scholar]
- [14].Du Junwei, Bai Xiaowei, and Simon R Cherry. A depth-encoding pet detector for high resolution pet using 1 mm sipms. Phys. Med. Biol, 65(16):165011, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Wang M, Wang Y, Zhang X, Song Z, Zhou X, Hu Y, Zhou Y, and Wu B. Development of a compact and cost-effective pet detector module for a small-animal pet system with fesa asic. J. Instrum, 17(09):P09045, 2022. [Google Scholar]
- [16].Poladyan Harutyun, Bubon Oleksandr, Teymurazyan Aram, Senchurov Sergii, and Reznik Alla. Gaussian position-weighted center of gravity algorithm for multiplexed readout. Phys. Med. Biol, 65(16):165003, 2020. [DOI] [PubMed] [Google Scholar]
- [17].Anger Hal O. Scintillation camera with multichannel collimators. 1964. [PubMed] [Google Scholar]
- [18].YJ Qi, Zhang MJ, Zhao CL, and Wojcik RF. Performance comparison of subtractive resistive readout with conventional resistive readout for a high-resolution compact gamma camera. In IEEE Nucl Sci Symp Conf Rec, volume 5, pages 3725–3728. IEEE, 2007. [Google Scholar]
- [19].Andy LaBella Xinjie Cao, Petersen Eric, Lubinsky Rick, Biegon Anat, Zhao Wei, and Goldan Amir H. High-resolution depth-encoding pet detector module with prismatoid light-guide array. J. Nucl. Med, 61(10):1528–1533, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Andy LaBella Wei Zhao, Lubinsky Rick, and Goldan Amir H. Prismatoid light guide array for enhanced gamma ray localization in pet: a monte carlo simulation study of scintillation photon transport. Phys. Med. Biol, 65(18):18LT01, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Andy LaBella Eric Petersen, Cao Xinjie, Zeng Xinjie, Zhao Wei, and Goldan Amir. 36-to-1 multiplexing with prism-pet for high resolution tof-doi pet, 2021. [Google Scholar]
- [22].Schug David, Nadig Vanessa, Weissler Bjoern, Gebhardt Pierre, and Schulz Volkmar. Initial measurements with the petsys tofpet2 asic evaluation kit and a characterization of the asic tdc. IEEE trans. radiat. plasma med. sci, 3(4):444–453, 2018. [Google Scholar]
- [23].Schug David, Wehner Jakob, Goldschmidt Benjamin, Lerche Christoph, Peter Michael Dueppenbecker Patrick Hallen, Weissler Bjoern, Gebhardt Pierre, Kiessling Fabian, and Schulz Volkmar. Data processing for a high resolution preclinical pet detector based on philips dpc digital sipms. IEEE Trans. Nucl. Sci, 62(3):669–678, 2015. [Google Scholar]
- [24].Aykac Mehmet, Grazioso Ronald, Bean Keith, and Schmand Matthias. New approach to obtain high resolution using conventional block designs in pet. IEEE Trans. Nucl. Sci, 53(1):18–24, 2006. [Google Scholar]
- [25].Breiman Leo. Classification and regression trees. Routledge, 2017. [Google Scholar]
- [26].Zeng Xinjie, Wang Zipai, Tan Wanbin, Petersen Eric, Cao Xinjie, Andy LaBella Anthony Boccia, Franceschi Dinko, Mony de Leon Gloria Chia-Yi Chiang, et al. A conformal tof–doi prism-pet prototype scanner for high-resolution quantitative neuroimaging. Medical Physics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Popov Vladimir, Majewski Stan, and Benjamin L Welch. A novel readout concept for multianode photomultiplier tubes with pad matrix anode layout. Nucl. Instrum. Methods Phys. Res. A, 567(1):319–322, 2006. [Google Scholar]
- [28].Andrew J Reader Stijn Ally, Bakatselos Filippos, Manavaki Roido, Walledge Richard J, Jeavons Alan P, Julyan Peter J, Zhao Sha, Hastings David L, and Zweit Jamal. One-pass list-mode em algorithm for high-resolution 3-d pet image reconstruction into large arrays. IEEE Trans Nucl Sci, 49(3):693–699, 2002. [Google Scholar]