Observation of magnetic amplification using dark spins

Significance

Magnetic-field quantum sensing is a promising path to achieve precision beyond the standard quantum limit and plays significant roles in diverse areas ranging from fundamental physics and material science to biomedical science. We observe magnetic amplification of long-lived nuclear spins present in noble gases and observe significant signal gain when the noble gas is placed in the dark. The observed amplification allows us to enhance magnetic fields by at least three orders of magnitude, thereby achieving a subfemtotesla level of measurement uncertainty in a single shot. Furthermore, we extend the amplification effect to a wide range of noble-gas isotopes and envision the possibility of achieving amplification surpassing 10⁴. Our findings will be an important stepping stone toward improved quantum sensing.

Abstract

Quantum amplification enables the enhancement of weak signals and is of great importance for precision measurements, such as biomedical science and tests of fundamental symmetries. Here, we observe a previously unexplored magnetic amplification using dark noble-gas nuclear spins in the absence of pump light. Such dark spins exhibit remarkable coherence lasting up to 6 min and the resilience against the perturbations caused by overlapping alkali-metal gas. We demonstrate that the observed phenomenon, referred to as “dark spin amplification,” significantly magnifies magnetic field signals by at least three orders of magnitude. As an immediate application, we showcase an ultrasensitive magnetometer capable of measuring subfemtotesla fields in a single 500-s measurement. Our approach is generic and can be applied to a wide range of noble-gas isotopes, and we discuss promising optimizations that could further improve the current signal amplification up to ${10}^4$ with ²¹Ne, ${10}^5$ with ¹²⁹Xe, and ${10}^6$ with ³He. This work unlocks opportunities in precision measurements, including searches for ultralight dark matter with sensitivity well beyond the supernova-observation constraints.

Quantum amplification provides powerful tools to enhance weak electromagnetic signals and finds application in various frontiers of science, ranging from low-noise masers (1–4), ultrasensitive magnetic resonance spectroscopy (5, 6), weak field and force measurements (7–11), and optical amplification (12) to searches for new physics beyond the standard model (13, 14). Both electron and nuclear spins have shown great potential for realizing signal amplification. This concept has been successfully implemented in various platforms, including systems such as atomic and molecular ensembles (1, 4), silicon- and nitrogen-vacancy spin-defect materials (2, 5), NMR (6), etc. Recent advances of spin amplification have led to significant progress in spin-based quantum technologies, for example, room-temperature solid-state masers (2, 4), spin magnetometers (15), Floquet masers (9), searches for exotic interactions between nucleons and dark-matter candidates (16, 17), tests of Lorentz, charge-parity, and charge-parity-time symmetries (18–21), and searches for spin-dependent couplings mediated by axions and other hypothetical particles (22, 23). The increasing demands in cutting-edge scientific endeavors highlight the current limitations encountered in practical implementations of quantum amplification. These limitations primarily arise from constraints associated with spin-polarization initialization, coherence time, and readout sensitivity. As a consequence, the performance of quantum amplifiers is hindered, particularly in terms of operation bandwidth, frequency, and gain. Overcoming these challenges is crucial to unlock the full potential of quantum amplification and enable its utilization in a broader range of applications.

In this Letter, we observe a previously unexplored amplification using dark spins that significantly enhance and measure magnetic fields with at least three orders of magnitude improvement. In the experiment, we use ¹²⁹Xe noble gas overlapping with ⁸⁷Rb atomic gas in the same vapor cell, where the embedded ⁸⁷Rb atoms are used to initialize and read out the ¹²⁹Xe nuclear spins, with Fermi-contact interaction during collisions between them (24–26). The key ingredient of our work is that we separate the signal amplification from noble-gas spin initialization and readout stages to suppress the detrimental effects of the latter on amplification. During signal amplification, the noble-gas spins placed in the dark exhibit remarkable coherence lasting up to 6 min, while remaining unaffected by perturbations caused by overlapping alkali-metal gas. The noble-gas spin coherence time is improved by one order of magnitude compared to previous works which apply continuous pump laser (27–31). The longer-lived nuclear-spin coherence, in turn, translates into enhanced spin amplification gain. Using this approach, we observe the magnetic-field amplification by “in-the-dark” ¹²⁹Xe gas spins by a factor of about 5,400. As a first application, we demonstrate that with this approach one can measure magnetic fields with subfemtotesla uncertainty in a single measurement for 500 s. Although demonstrated for the ¹²⁹Xe system, the observed amplification, referred to as “dark spin amplification,” is generic and can be applied to various other noble gases, including ³He and ²¹Ne. We further discuss potential optimizations that could improve the currently achievable signal amplification up to ${10}^4$ with ²¹Ne, ${10}^5$ with ¹²⁹Xe, and ${10}^6$ with ³He. We anticipate that the present amplification technique could stimulate many applications in applied and fundamental physics, for example, realizing attotesla-level magnetometry, searches for ultralight dark matter (32, 33), and investigating geophysical phenomena such as Schumann resonances (34, 35).

Results and Discussion

Fig. 1A shows the schematic of noble-gas spin amplification in the dark. The embedded ⁸⁷Rb atoms are optically polarized and probed, and simultaneously used for initializing ¹²⁹Xe spin polarization and readout by spin-exchange collisions between them (24–26). A bias magnetic field is applied along $z$ to tune the noble-gas Larmor frequency ${\nu }_0={\gamma }_n{B}_0/(2\pi )$ to match the oscillation frequency of the external transverse field ${\mathbf{B}}_{\text{ac}}$. Here, ${\gamma }_n\approx 2\pi \times$(0.01178 Hz/nT) is the gyromagnetic ratio of ¹²⁹Xe. The measurement process is divided into three stages: spin initialization, amplification and readout (Fig. 1B). In detail, ¹²⁹Xe nuclear spins are first polarized in collisions with optically polarized ⁸⁷Rb atoms. The number density of polarized ¹²⁹Xe nuclear spins is calibrated as about $6\times {10}^{17}{\text{cm}}^{-3}$. After the initialization of the ¹²⁹Xe spin polarization, the ⁸⁷Rb pump laser is turned off with a mechanical shutter, and the ¹²⁹Xe spins evolve under the influence of the external magnetic field during the interval of darkness (the amplification stage). The polarized ⁸⁷Rb atoms would generate an effective magnetic field on ¹²⁹Xe, leading to a shift in ¹²⁹Xe Larmor frequency. Due to the separation of the initialization and amplification, the ¹²⁹Xe frequency shift caused by the ⁸⁷Rb polarization is greatly suppressed. In our experiment, the coherence time $T_2$ of ¹²⁹Xe is measured to be about $T_2^{\mathrm{dark}}\approx 380$ s in the dark (SI Appendix, Noble-Gas Spin Coherence Time), which is about one order of magnitude longer than that in the presence of the pump light ($T_2^{\mathrm{light}}\approx 39$ s). The longer-lived nuclear-spin coherence, in turn, translates into enhanced spin amplification. In the readout stage, the pump light is applied once again. The effective amplified field generated by the ¹²⁹Xe amplifier is read out by ⁸⁷Rb magnetometer via the optical rotation of a linearly polarized probe beam (SI Appendix, Readout) (36, 37).

Fig. 1.

Schematic of noble-gas spin amplification in the dark. (A) A cubic vapor cell contains ¹²⁹Xe and ⁸⁷Rb atoms and buffer-gas N₂. A bias magnetic field is applied along $z$ to tune the ¹²⁹Xe Larmor frequency. (B) The measurement process can be divided into three stages: 1) Noble gas spin initialization. ¹²⁹Xe is polarized through spin-exchange collisions with optically polarized ⁸⁷Rb atoms (SI Appendix, Initialization) (44, 45); 2) Amplification of oscillating magnetic field. The pump light for ⁸⁷Rb is turned off. With the ¹²⁹Xe Larmor frequency tuned to match the frequency of the external field, ¹²⁹Xe spins are tilted away from $z$, and the induced nuclear magnetization generates an effective field on ⁸⁷Rb atoms with a large amplification factor; 3) Readout of the amplified field with pump light on. The embedded ⁸⁷Rb atoms act as a sensitive magnetometer to in situ read out the effective field.

We now consider the detailed amplification phenomenon where the noble-gas nuclear spins are placed in the dark. The amplification starts with turning off the pumping light at $t=0$. When the oscillation frequency $\nu$ of the external field ${\mathbf{B}}_{\text{ac}}$ is close to the Larmor frequency ${\nu }_0$, the in-the-dark noble-gas nuclear spins are tilted away from $z$ and result in a transverse magnetization that produces an effective field ${\mathbf{B}}_{\text{eff}}=\frac{8\pi {\kappa }_0}{3}{M}_0\mathbf{P}$ on the alkali-metal spins, due to the Fermi-contact interaction during collisions between ¹²⁹Xe and ⁸⁷Rb atoms (24–26, 38–41). Here, ${\kappa }_0\approx 540$ denotes the Fermi-contact enhancement factor between ¹²⁹Xe and ⁸⁷Rb (24), $M_0$ and $\mathbf{P}$ are magnetization with unity polarization and polarization vector of the noble gas, respectively. We find that the effective field can be much larger than the external field, as characterized with an amplification factor of $\Pi =|{\mathbf{B}}_{\text{eff}}|/|{\mathbf{B}}_{\text{ac}}|$. As derived in SI Appendix, Linear Response (42, 43), the in-the-dark amplification factor is time-dependent and can be well described by

$$\begin{array}{c}\hfill \Pi (t)=\lambda M_n{\gamma }_n\text{sinc}\left(\frac{\mathrm{\Delta }}{2}t\right)t{\text{e}}^{-\frac{t}{T_2}},\end{array}$$ [1]

where $\lambda =4\pi {\kappa }_0/3$, $M_n=M_0{P}_0$ is the magnetization of the noble gas with $P_0$ being the noble-gas initial polarization, $\mathrm{\Delta }=2\pi (\nu -{\nu }_0)$ denotes the frequency detuning, and $\text{sinc}(x)$ denotes $\text{sin}(x)/x$. Here, $t$ is referred to as “dark time” that represents the evolution time of nuclear spins in the dark. In the small-$t$ regime or near resonance occurs, i.e., $|\mathrm{\Delta }|·t\ll 1$, the amplification factor can be approximated as $\Pi \propto t{\text{e}}^{-t/T_2}$. Here, the external oscillating fields are assumed to be small. When increasing the oscillating-field amplitude, we find that the response of the dark spins to oscillating fields becomes nonlinear (SI Appendix, Nonlinear Response).

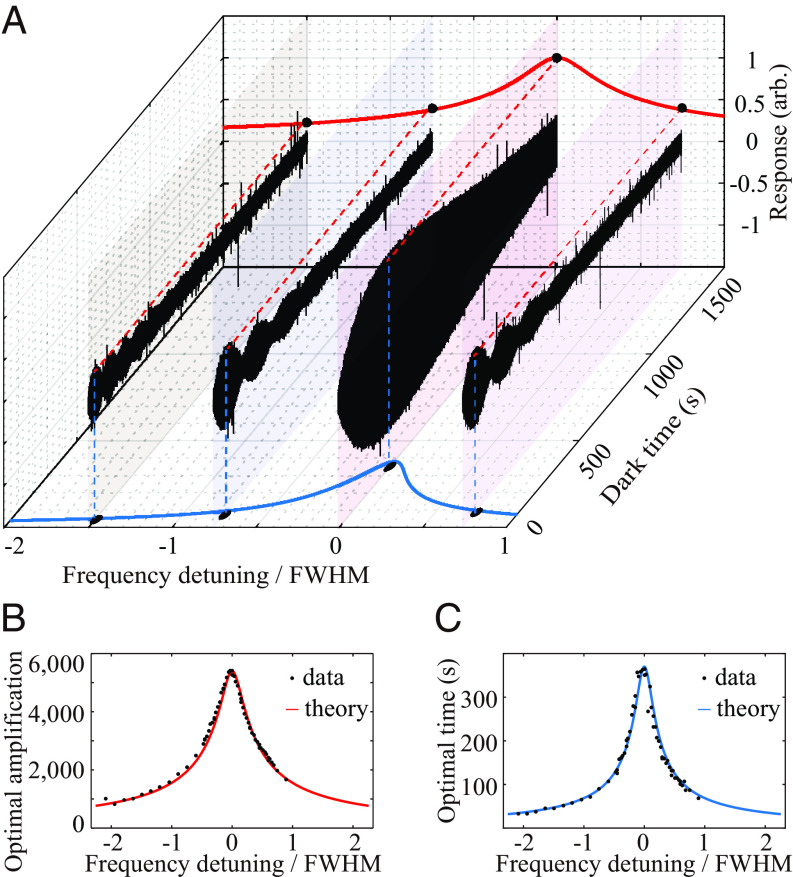
We illustrate the above theory by applying a series of about 10 pT oscillating test fields with different frequencies to ¹²⁹Xe-⁸⁷Rb cell and then recording the corresponding ¹²⁹Xe-response signals. In order to directly monitor the ¹²⁹Xe-response signal in the dark, we add a quarter-wave plate in the probe optical path before the vapor cell to make the probe light have a small ellipticity. The elliptically polarized probe light polarizes ⁸⁷Rb atoms and consequently the ⁸⁷Rb atoms could be sensitive to the measured effective field produced by ¹²⁹Xe spins. The probe light is far-detuned and its ellipticity is small, it has negligible impact on the dynamics of “dark spins” (SI Appendix, Noble-Gas Spin Dynamics in the Dark). The experimental results are shown in Fig. 2A, where the response curves contain oscillations. On resonance, the ¹²⁹Xe response first increases to a maximum value at a certain dark time and then decays. In the situation where the frequency detuning $\mathrm{\Delta }$ is comparable to or larger than the full width at half-maximum (FWHM $\approx 6.7$ mHz) of the ¹²⁹Xe frequency response, the amplification oscillates fast with dark time with gradually decaying amplitude. We find that the oscillation frequency of the amplification values is $\approx |\mathrm{\Delta }|/2$ and the maximum amplitude is inversely proportional to $\mathrm{\Delta }$. The observed response behavior of in-the-dark ¹²⁹Xe spins are in good agreement with our model described in Eq. 1.

Fig. 2.

Demonstration of noble-gas amplification in the dark. (A) Noble-gas spin response evolution under different frequency detunings. (B) Optimal amplification as a function of frequency detuning. The optimal amplification is defined as the maximum value of the amplification, as shown with the red dashed lines in A. The FWHM is measured to be $\approx 6.7$ mHz. (C) Optimal dark time as a function of frequency detuning.

Now we quantitatively investigate the optimal amplification and corresponding dark time. Experimental data are measured by varying the frequency of the test field (Fig. 2B) and, for each frequency, there is a maximum amplification called “optimal amplification” (red dashed lines in Fig. 2A), and its dark times (blue dashed lines in Fig. 2A) are shown in Fig. 2C. In order to directly compare our experimental results with theory, we also provide the theoretical values of optimal amplification and dark time with red lines through calculating $\partial \Pi /\partial t=0$ (SI Appendix, Linear Response), using parameters obtained from independent measurements. We find good agreement between experimental data and the theory. As discussed above, the optimal amplification on resonance should be $\lambda M_n{\gamma }_n{T}_2/\text{e}$ at $t=T_2$. In our experiment, a maximum amplification $\Pi \approx$5,400 is observed at $t\approx 364$s, which is close to the expected value $T_2^{\mathrm{dark}}\approx 380$ s. This shows that the external magnetic field can be significantly amplified by nearly four orders of magnitude, providing a sensitive approach to measuring magnetic and exotic fields.

Amplification factors are measured at various operation frequencies. Broadening the operation frequency of signal amplification by increasing bias fields is indispensable in various applications. However, a large magnetic field is also applied on the embedded ⁸⁷Rb magnetometer and deteriorates ¹²⁹Xe readout sensitivity. Because the amplification and readout stages are separated, the bias-field strength for matching the external field frequency in amplification is independent with that in readout stage. Thanks to such a separation, it is possible to perform high-frequency field amplification using a large bias field for tuning noble-gas resonance frequency, while retaining high sensitivity of the Rb magnetometer in the readout, during which the bias field is reduced. Fig. 3A shows the experimental sequence for the applied bias magnetic field and optical pumping. The bias field for amplification is chosen according to the measured-signal frequency, while the same small bias field of $\approx$857 nT is always used for the readout. Experimental amplification values with resonance frequencies ranging from 10 to 216 Hz are shown with the black points in Fig. 3B. We find that the amplification decreases with increasing resonance frequencies. This is due to the inhomogeneity of the applied bias field, which leads to the decrease of noble-gas coherence time. In order to characterize it, we built a model of ¹²⁹Xe spin relaxation caused by inhomogeneous field while undergoing restricted gas diffusion (SI Appendix, Noble-Gas Spin Coherence Time) (29, 46, 47) and measure ¹²⁹Xe spin relaxation rate in different bias field strength. Based on our analysis, the inhomogeneity of the bias field is estimated to be about $0.1\%$. The observed amplification values are numerically corrected by taking into account the effect of the bias-field inhomogeneity (SI Appendix, Noble-Gas Spin Coherence Time), as shown by the red points in Fig. 3B. The corrected values remain nearly constant ($\approx$5,000) over a broad range of resonance frequencies. This suggests the possibility for maintaining high signal amplification over a broad frequency range, when the bias-field gradient is eliminated, for example, using readily accessible gradient magnetic compensation technique as in conventional NMR experiments (48).

Fig. 3.

Demonstration of sensitive magnetometry using dark spin amplification. (A) Sequence for bias magnetic fields and optical pumping. (B) Amplification as a function of resonance frequencies. Black points represent the experimental data. The red points denote the data after numerically correcting the bias-field gradient and yield the average value of amplification of $\Pi \approx$5,000. (C) Magnetic field measurement uncertainty as a function of resonance frequency. Black points represent the experimental data with error bars from nine repeated experiments.

We would like to emphasize the main difference in amplification phenomenon between this work and other studies. First, our finding is significantly different from the Fermi-contact enhancement (21, 25, 26, 38–41, 49), which describes the phenomenon in which the noble-gas magnetization generates an effective magnetic field due to the internal spin-exchange collisions, and this process is unrelated to external magnetic-field response. In contrast, we demonstrate the spin amplification phenomenon where the external measured magnetic field induces noble-gas magnetization, producing an effective magnetic field that is much larger than the external magnetic field. It should be noted that the Fermi-contact enhancement ${\kappa }_0$ is only a part of the amplification factor $\Pi$, and is not enough to guarantee a significant amplification effect. Other parameters $\{{\gamma }_n,M_n,T_2\}$ are also important to realize large amplification factors. Second, previous works usually apply pump laser to continuously polarize the alkali-metal spins. We note that this operation would set severe limits on noble-gas amplification performance. In the presence of pump laser, the polarized ⁸⁷Rb atoms causes significant ¹²⁹Xe Larmor frequency shifts, which are inhomogeneous due to ⁸⁷Rb polarization gradient originating from the absorption of ⁸⁷Rb pump light Inhomogeneous shifts diminish the coherence of noble-gas spins, typically in the range of 2 to 50 s (27–31), thereby restricting the amplification capabilities. In contrast, we use dark spins in the absence of the pump light. In our experiment, the coherence time of ¹²⁹Xe is measured to be about $T^{\text{dark}}\approx 380$ s, which is improved by about one order of magnitude. Third, we compare the amplification of nuclear spins and electron spins. Despite the electron spin having a gyromagnetic ratio about three orders of magnitude greater than that of the nucleus, its estimated amplification gain is only around $G\approx 0.25$, significantly lower than that of nuclear spins (SI Appendix, Comparison of Amplification between Nuclear Spins and Electron Spins).

Combining our demonstrated amplification with magnetic-field sensing, we realize a magnetometer with subfemtotesla uncertainty in a single measurement for 500 s. A $\sim$10 pT magnetic field is applied as a test field, the resonant amplification takes the dark time equal to the noble-gas coherence time (here we set it as 360 s), and then 100 s data are recorded. The noise is obtained through the same process but without applying any test field. Based on the amplified signal and noise data, we obtain the minimum detectable magnetic field as the uncertainty. The obtained uncertainty in the frequencies from 10 to 216 Hz are below 1 fT. In particular, the measurement uncertainty is 0.1 $\pm$ 0.02 fT at 10 Hz, which is equivalent to the magnetic-field sensitivity of 3 fT/Hz^1/2. We find that the uncertainty degrades with increasing resonance frequencies due to the decrease in gain as discussed above. Our magnetometer can operate in a nonzero magnetic field, in contrast to spin-exchange-relaxation-free magnetometers that usually require the operation at near-zero fields below 100 nT (50).

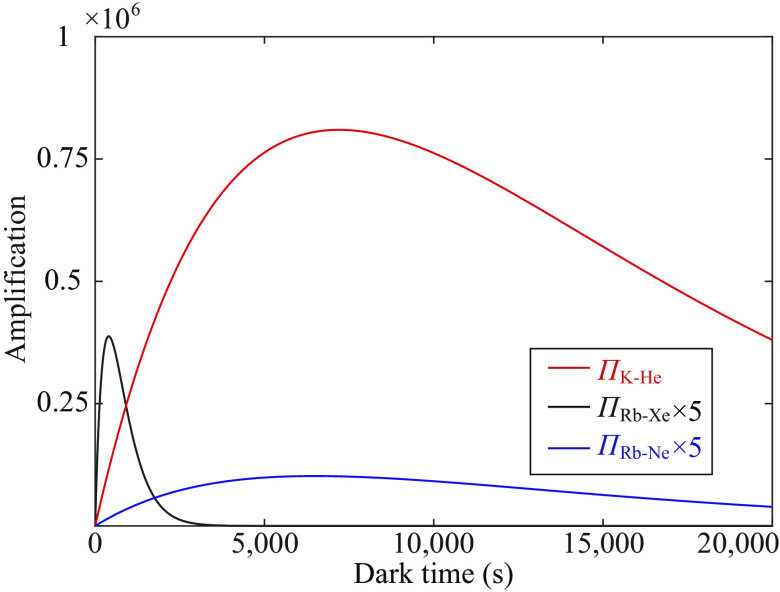
There is still room for improvement in noble-gas spin amplification. For example, we can increase the noble-gas nuclear magnetization $M_n$ by increasing the polarization and number density of the noble gas. In this case, the ¹²⁹Xe-⁸⁷Rb gain can reach a maximum on the order of ${10}^5$ (SI Appendix, Projected Amplification), as shown with the black line in Fig. 4. We suggest future amplification-in-the-dark experiments to carry out a systematic optimization, including the choice of the noble gas, for example, ³He or ²¹Ne. The most promising system appears to be ³He because ³He spins have much longer-lived coherence and larger gyromagnetic ratio compared to ¹²⁹Xe and ²¹Ne (25, 26). In addition, the ³He-K system has five orders of magnitude smaller spin-destruction cross-section than ¹²⁹Xe-Rb systems, and thus the embedded K magnetometer can realize femtotesla sensitivity (51). Using previously demonstrated experimental parameters (52), the proposed ³He-K amplification is shown with the red line in Fig. 4, which first increases to a maximum value and then decays. The maximum amplification for the ³He-K system is expected to reach close to ${10}^6$. These results are calculated based on the model described in Eq. 1 and are presented with more details in SI Appendix, Projected Amplification. The proposed enhancement of spin-exchange efficiency using laser excitation of the alkalis (53) may further increase ³He amplification. Moreover, we explore the standard quantum limit in spin amplification (54–56). The source of quantum noise that arises during the amplification process is the noble-gas spin-projection noise. Similarly, the alkali-metal spin-projection noise is introduced during the readout process. These quantum noises would set a standard quantum limit, which represents the minimum magnetic field that can be amplified through spin amplification. Our analysis estimates the total standard quantum limit for our amplification scheme to be approximately $90$ aT/Hz^1/2 (SI Appendix, Standard Quantum Limit for Spin Amplification). This indicates significant potential for enhancing the sensitivity of our system.

Fig. 4.

Proposal of dark spin amplification using various noble gas. The projected maximum amplification of ³He-K system (red line), ¹²⁹Xe-⁸⁷Rb system (black line), and ²¹Ne-⁸⁷Rb system (blue line) could reach $8\times {10}^5$, $7.8\times {10}^4$, $2\times {10}^4$ at time $T_2$, respectively. The dark time denotes the evolution time of noble gas in the dark.

Summary and Outlook

The present in-the-dark amplification technique can be used for a broad range of precision-measurement applications. For example, the technique can be used to search for hypothetical particles predicted by numerous theories beyond the standard model, such as axions and dark photons that are well-motivated dark matter candidates (57–60). These particles may couple with nuclear spins and behave as an oscillating quasi-magnetic field (14, 33, 61), the effect of which can be greatly enhanced with the noble-gas spin amplifier. With a one-day measurement, the search sensitivity of axion dark matter can reach $|g_{\text{aNN}}|⩽{10}^{-10}$ GeV⁻¹, which improves the most stringent supernova constraints (62, 63) by about two orders of magnitude. Here, $g_{\text{aNN}}$ is a constant characterizing axion-neutron coupling. Moreover, compared with the previous searches in the frequency range from 0.045 to 180 Hz corresponding to axion masses ranging from $1.9\times {10}^{-16}$ eV to $7.4\times {10}^{-13}$ eV (16, 64), our approach can allow one to extend the frequency range by one order of magnitude. Our approach can also be used to search for exotic spin-dependent interactions (65, 66). In particular, the searches for velocity-dependent exotic interactions (23, 67) would directly benefit from the extension to high-frequency signal amplification.

Our approach can also be used to investigate geophysical phenomena (34, 35), such as Schumann resonances, ionospheric Alfvén resonances, and acoustic gravity waves, which are relevant to the study of global climate. As an example, Schumann resonances are excited within the Earth-ionosphere waveguide primarily by lightning discharges and produce oscillating magnetic fields with subpicotesla-level amplitude at a frequency of around 8 Hz and its harmonics (68). The amplification technique offers the capability of measuring such Schumann fields with femtotesla-level sensitivity, which is better than that of previous methods such as fluxgate or search-coil magnetometers. In addition, our approach can be further extended to build a network of synchronized noble-gas amplifiers, because the apparatus used in our experiment is small-scale and low-cost. Such a network allows one to distinguish the correlated geophysical signal from spurious noise.

In conclusion, we demonstrate magnetic amplification using noble-gas nuclear spins in the dark, with an amplification factor of up to 5,400, and realize subfemtotesla measurement uncertainty in a single measurement. We also discuss prospects of dark spin amplification to other alkali and noble-gas pairs for even better performance, as well as various applications. The potential combination of dark amplification and Floquet engineering (for example, with the use of an oscillating magnetic field) could increase the detection frequency regimes by one order of magnitude (10). In order to increase readout sensitivity, we could use a train of alkali-spin $\pi$ pulses on ⁸⁷Rb for suppressing spin-exchange relaxation in a finite field (28). Instead of turning off pump light, the embedded alkali gradient effect could also be suppressed with hybrid optical pumping (31, 69) or by removing the alkalis from the gas mixture during the amplification stage. Rapid alkali-density control without thermal cycling can be accomplished using light-induced atomic desorption (LIAD) (70, 71).

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.