Abstract
The geometrical structures, relative stabilities, and electronic and magnetic properties of niobium carbon clusters, Nb7Cn (n = 1–7), are investigated in this study. Density functional theory (DFT) calculations, coupled with the Saunders Kick global search, are conducted to explore the structural properties of Nb7Cn (n = 1–7). The results regarding the average binding energy, second-order difference energy, dissociation energy, HOMO-LUMO gap, and chemical hardness highlight the robust stability of Nb7C3. Analysis of the density of states suggests that the molecular orbitals of Nb7Cn primarily consist of orbitals from the transition metal Nb, with minimal involvement of C atoms. Spin density and natural population analysis reveal that the total magnetic moment of Nb7Cn predominantly resides on the Nb atoms. The contribution of Nb atoms to the total magnetic moment stems mainly from the 4d orbital, followed by the 5p, 5s, and 6s orbitals.
Keywords: density functional theory, geometrical structure, stability, density of states, magnetic properties
1. Introduction
The research on nanoclusters represents a significant branch within the fields of nanoscience and nanotechnology, providing a potent pathway for crafting tailored nanomaterials characterized by unique physical and chemical attributes. Consequently, significant advancements have been achieved in this field over the past few decades [1,2,3,4,5,6,7]. Transition metal-carbide clusters possess unique electronic and magnetic properties that make them promising candidates for various applications, ranging from nanoelectronics to energy storage. By delving into the structures, stabilities, and electronic and magnetic properties of transition metal–carbon clusters, researchers can unravel the underlying principles governing the behavior of transition metal-carbide systems at the nanoscale. Moreover, the investigation of transition metal–carbon clusters offers insights into the intricate interplay between metal and carbon atoms within the cluster framework. The coordination environment of metal atoms with carbon atoms influences not only the structural stability but also the electronic and magnetic properties of the clusters. Understanding how these interactions manifest at the atomic level is crucial for designing nanomaterials with tailored functionalities. Niobium carbon clusters, NbnCm clusters, have been the subject of significant interest in recent years due to their potential applications in numerous areas including catalysis, optoelectronics, and materials science [8,9,10,11,12,13,14]. With niobium’s versatile oxidation states and carbide’s decisive role in determining cluster stability and reactivity, understanding the behavior of niobium carbide clusters is essential and could enable the design of advanced materials and catalysts with specific properties. Furthermore, the study of niobium carbon clusters can also contribute to the broader understanding of transition metal-carbide clusters.
Various experimental techniques, such as photoelectron spectroscopy [15,16,17,18], mass spectroscopy [19,20,21,22], X-ray diffraction spectroscopy [17,23], and infrared absorption spectroscopy [24], have been employed to explore the physical and chemical properties of niobium carbides and their ions. Wang and co-workers investigated a series of mono-niobium carbide clusters, NbCn− (n = 2–7), using anion photoelectron spectroscopy [16]. The linear NbCn− were observed to have high electron binding energies and exhibited an even–odd alternation, similar to that observed for pure linear carbon clusters in the same size range. NbC2− and NbC3− were shown to have C2v cyclic structures. The mass spectroscopic studies conducted by Duncan and co-workers [19] as well as Castleman and co-workers [20] have revealed that the smaller NbmCn+ clusters, especially for n = 2–4, are particularly stable. Jarrold and co-workers reported experimental studies of the structures of gas-phase NbCn+ (n = 28–50) clusters. The experiments, which use injected-ion drift-tube techniques, indicate that for fullerenes containing an even number of carbon atoms, the niobium metal is endohedral, but for fullerenes with an odd number of carbon atoms, the niobium metal is bound as part of the carbon cage [25]. Mafuné and co-workers determined ionization energies for a series of NbnCm (n = 3–10, m = 0–7) clusters [21].
Theoretical studies primarily focus on employing density functional theory (DFT) calculations to explore the geometric and electronic structures of pure niobium clusters and niobium carbon clusters. This provides crucial insights into their stability, reactivity, and electronic properties, which plays a pivotal role in customizing these clusters to meet specific application requirements. A theoretical investigation of structures, spectra, and energies of niobium clusters from Nb13 to Nb20 is performed by Pham and Minh [26]. The Nb15 system is observed to be stable and it can form a highly symmetric structure in all charged states with both open and closed electron shells. The geometric and electronic structures of niobium carbon clusters, ranging in size from [Nb2C2] to [Nb12C20], were discussed by Dance and Harris [27]. Vertical ionization energies and normalized binding energies are provided for all isomers. The species [Nb8C12] and [Nb14C13] have the same structures as the Ti analogs. Balasubramanian and co-workers determined the geometric and electronic structures of NbCn (n = 3–8), and equilibrium geometries, Gibbs free energies, and heat capacity functions as a function of temperatures were computed [28].
In this paper, we present the theoretical investigation of a series of niobium carbon clusters, Nb7Cn (n = 1–7). The geometric structures are predicted by employing the Saunders ‘Kick’ (SK) global search method combined with DFT calculation. To better understand how the Nb and C atoms affect the molecular orbitals, we plot the total density of states (TDOS) and the partial density of states (PDOS) of Nb7 and Cn. Meanwhile, the magnetic properties are discussed in detail.
2. Results and Discussion
2.1. Structure of Nb7Cn (n = 1–7)
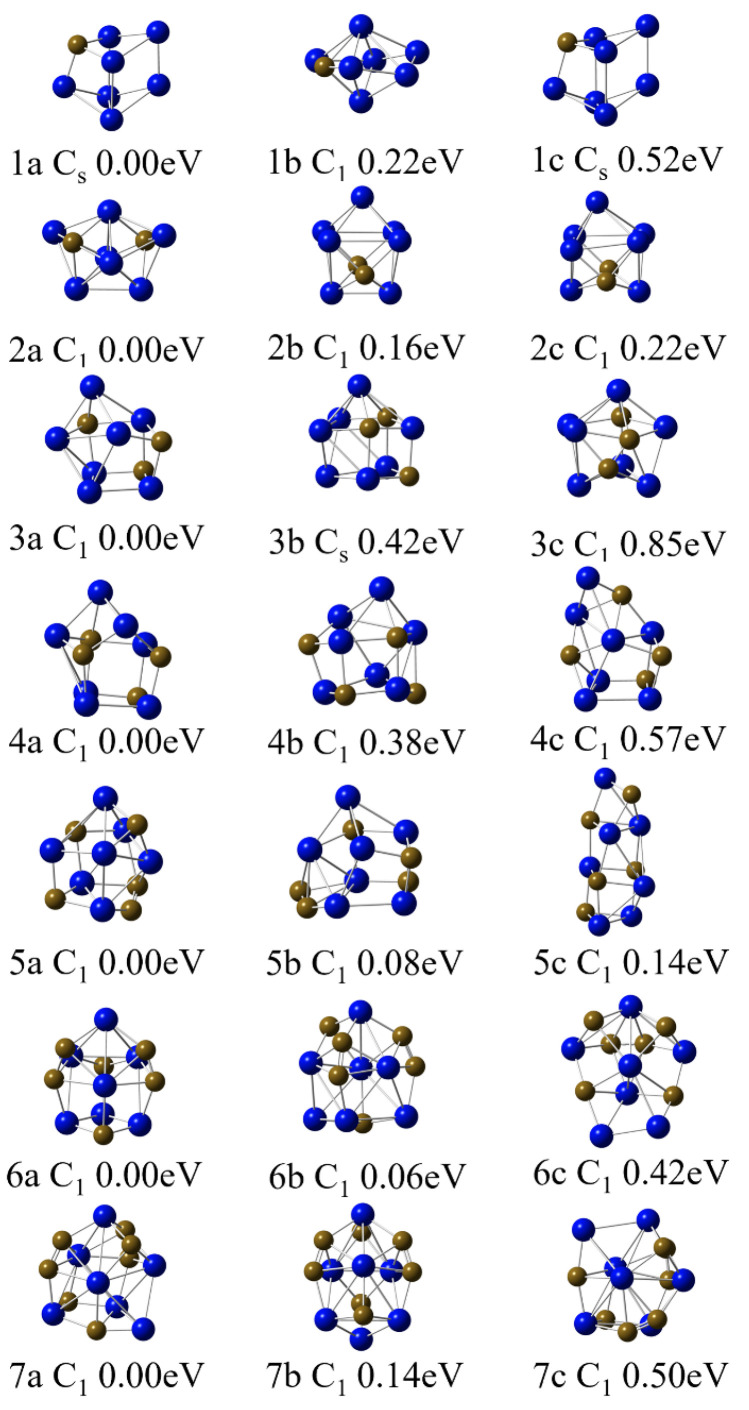
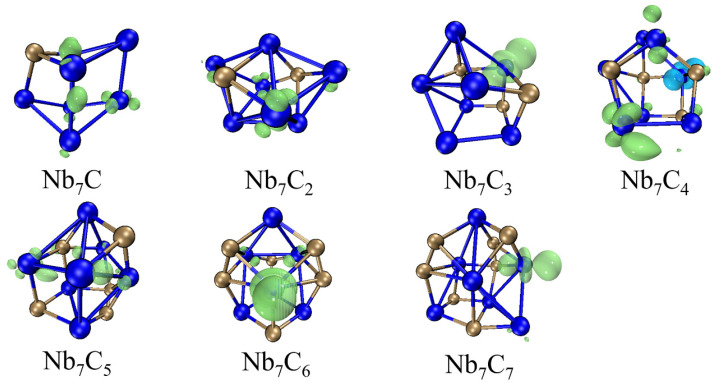
The lowest-energy structure and low-lying isomers of Nb7Cn (n = 1–7) at the B3LYP/Nb/SDD//C/6−311+G(2d) level are listed in Figure 1. The Cartesian coordinates of the lowest-energy structures of Nb7Cn (n = 1–7) are summarized in Table S1 of the Supplementary Materials. The two criteria for selecting the ground-state structure of clusters in this study are (1) the principle of lowest energy and (2) the agreement between theoretical predictions and experimental results of vertical ionization potential (VIP). The ground-state structures of the Nb7Cn series exhibit an outer body structure. It is predicted that as the number of C atoms increases, the structures of Nb7Cn clusters gradually tend towards hollow spherical structures. In addition, C atom aggregation areas will appear on the surface of the structure in the subsequent structural evolution process.
Figure 1.
Low-energy isomers of Nb7Cn (n = 1–7) clusters.
The lowest-energy structure 1a of the Nb7C cluster is a distorted tetragonal prism in which carbon atoms occupy one corner of the quadrangle. The point group symmetry is Cs and the spin state is a doublet state. Structure 1b exhibits a twisted hexagonal bipyramid-shaped structure higher in energy than the ground-state structure by 0.22 eV. The quartet-state structure 1c is higher in energy than doublet state 1a by 0.52 eV. The low-energy isomers of the Nb7C2 cluster all exhibit C1 symmetry. Among them, 2a adopts a twisted bipyramidal shape, while 2b and 2c are three-dimensional structures formed by splicing three twisted pyramids, with relative energies of 0.16 eV and 0.22 eV, respectively. Moving on to the Nb7C3 cluster, the three C atoms in 3a attach to the outer side of the C1 symmetric isomer, resulting in an irregular three-dimensional shape. Isomers 3b and 3c have relative energies 0.42 eV and 0.85 eV higher than that of 3a, respectively. The lowest-energy isomer 4a of Nb7C4 can be viewed as that obtained from the capping of a C atom to the lowest-energy structure of Nb7C3. Isomers 4b and 4c are less stable than 4a by 0.38 and 0.57 eV, respectively. The Nb7C5 system exhibits three isomers with 5a being the ground-state structure. Isomer 5b is only 0.08 eV higher than that of isomer 5a. Within the expected accuracy of the methods, isomers 5a and 5b can be regarded as nearly degenerate. In this case, we calculate the VIPs of both isomers 5a and 5b. The calculated VIPs of 5a and 5b are 4.86 and 5.14 eV, respectively. Compared with the results of isomers 5a and 5b, the calculated VIP value for structure 5a obviously agrees better with the experimental result of 4.7 ± 0.1 eV. These results indicate that isomer 5a is the most stable isomer in current DFT calculations of the Nb7C5 cluster. Isomer 5c is less stable than 5a by 0.14 eV. As for the neutral Nb7C6 cluster, the energy gap of isomers 6a and 6b is 0.06 eV. Given the small energy difference between structures 6a and 6b, we also performed VIPs calculations for both the isomers. The results found that the calculated VIP for isomer 6a (5.08 eV) is in better agreement with the experimental values (4.91 eV) than that for isomer 6b (5.16 eV). Therefore, isomer 6a should be the ground-state structure. In the doped Nb7C7 cluster, an equal number of Nb and C atoms does not result in a uniform distribution but instead leads to the aggregation of carbon atoms. This phenomenon results in shorter C-C bond lengths and greater bond energies, further enhancing the stability of the structure. Compared to the 7b isomer with a more uniform atomic distribution, the energy is 0.14 eV lower. The energy of 7c is 0.50eV higher than that of the ground-state structure.
Based on the lowest-energy structures, VIPs are calculated and compared with the experimental values, and the results are shown in Table 1. The vertical ionization potential is defined as VIP = E (cation at optimized neutral geometry) − E (optimized neutral geometry). From Table 1, we can see that the calculated VIPs are all in good agreement with the experimental results. The calculated VIP values of the lowest-energy structures 1a (5.16 eV), 2a (4.72 eV), 3a (4.78 eV), 4a (4.76 eV), 5a (4.86 eV), 6a (5.08 eV), and 7a (5.19 eV) agree well with the experimental values of 5.20 ± 0.08, 4.7 ± 0.1, 4.7 ± 0.08, 4.75 ± 0.07, 4.7 ± 0.1, 4.91 ± 0.07, and 5.1 ± 0.1 eV [21], respectively.
Table 1.
The vertical ionization potential (VIP), average binding energy (Eb), second-order difference energy (Δ2E), dissociation energy (DE), HOMO-LUMO gap (E-gap), and chemical hardness (η) for Nb7Cn (n = 1–7) clusters; all energies are in eV.
| Isomers | VIP | Eb | Δ2E | DE | E-Gap | η | |
|---|---|---|---|---|---|---|---|
| Calc. | Expt. [21] | ||||||
| Nb7C | 5.16 | 5.20 ± 0.08 | 4.01 | −0.39 | 7.21 | 1.36 | 3.80 |
| Nb7C2 | 4.72 | 4.7 ± 0.1 | 4.47 | −0.12 | 6.60 | 1.15 | 3.51 |
| Nb7C3 | 4.78 | 4.7 ± 0.08 | 4.79 | 1.27 | 7.72 | 1.24 | 3.57 |
| Nb7C4 | 4.76 | 4.75 ± 0.07 | 4.94 | −0.67 | 6.45 | 1.09 | 3.42 |
| Nb7C5 | 4.86 | 4.7 ± 0.1 | 5.13 | −0.60 | 7.12 | 1.11 | 3.48 |
| Nb7C6 | 5.08 | 4.91 ± 0.07 | 5.33 | −0.28 | 7.72 | 1.23 | 3.55 |
| Nb7C7 | 5.19 | 5.1 ± 0.1 | 5.52 | 8.00 | 1.25 | 3.64 | |
The infrared (IR) spectra of the lowest-energy structures of Nb7Cn (n = 1–7) clusters are computed based on DFT calculations. The calculated spectra are plotted in Figure S1 of the Supporting Information (ESI). Based on Figure S1, the IR spectra of Nb7Cn (n = 1–7) clusters cover the range of 0 to 2000 cm−1. We applied a frequency scaling factor of 0.9692 [29], determined at the B3LYP/6−311G(2d) level, to adjust the IR spectra during plotting. From Figure S1, it is evident that the IR spectra of Nb7Cn (n = 1–4) clusters span from 0 to 800 cm−1. However, for Nb7Cn (n = 5–7) clusters, a noticeable peak emerges within the range of 1200–1400 cm−1. In the case of Nb7C clusters, two distinct and strong spectral peaks are found around 600 and 700 cm−1, alongside some weaker peaks below 250 cm−1. For Nb7C2, the highest peak is centered at around 600 cm−1, and there are some minor peaks within the range of 100–400 cm−1. The highest-intensity peak of Nb7C3 is observed at around 670 cm−1, with several lower-intensity peaks falling between 100 and 350 cm−1. For Nb7C4, we mainly distinguish one broad band ranging from 450 to 750 cm−1, and the broadness of the peak suggests that it originates from multiple vibrational modes. The spectra of Nb7C5 and Nb7C6 clusters exhibit an intense peak at around 1300 cm−1, with some lower-intensity peaks below 800 cm−1. The spectrum for Nb7C7 contains two distinguishable peaks around 1250 and 1350 cm−1, as well as a wide band below 800 cm−1 with a maximum around 600 cm−1.
2.2. Stability
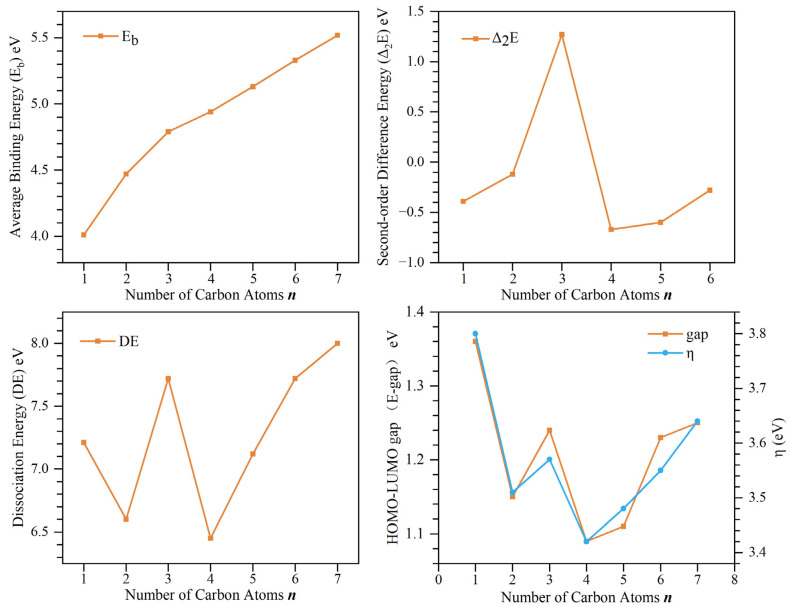
To explore the stability of the ground-state structure of Nb7Cn (n = 1–7) clusters, the average binding energy (Eb), second-order difference energy (Δ2E), dissociation energy (DE), HOMO-LUMO gap (E-gap), and chemical hardness (η) of the lowest-energy isomers are calculated in Table 1 and plotted in Figure 2. They are defined as follows:
| Eb(Nb7Cn) = [7E(Nb) + nE(C) − E(Nb7Cn)]/(7 + n) | (1) |
| Δ2E(Nb7Cn) = E(Nb7Cn+1) + E (Nb7Cn−1) − 2E(Nb7Cn) | (2) |
| DE(Nb7Cn) =E(Nb7Cn−1) + E(C) − E (Nb7Cn) | (3) |
| E-gap = ε(LUMO) − ε(HOMO) | (4) |
| η = VIP − VEA | (5) |
where E(Nb) represents the energy of a single Nb atom, E(C) represents the energy of a single C atom, and ε(HOMO) and ε(LUMO) represent the energy of the highest occupied orbit and the energy of the lowest empty orbit of the ground-state structure of Nb7Cn (n = 1–7) clusters, respectively.
Figure 2.
The average binding energy (Eb), second-order difference energy (Δ2E), dissociation energy (DE), HOMO-LUMO gap (E-gap), and chemical hardness (η) for Nb7Cn (n = 1–7) clusters.
As shown in Figure 2, the average binding energies of the ground-state structure of Nb7Cn (n = 1–7) clusters generally show an increasing trend, with an obvious slope change at n = 3, which indicates that isomer Nb7C3 has excellent thermal stability among Nb7Cn (n = 1–7) clusters. This corresponds to the high second-order differential energy and dissociation energy of the isomer Nb7C3. Chemical hardness and HOMO-LUMO gap represent the degree of response of the molecule to the outside world, especially the addition or removal of electrons under the action of external potential fields. The overall change trend of E-gap and η, which reflect the chemical stability of the ground-state structure of the Nb7Cn cluster, is the same. The E-gap and η values of isomer Nb7C1-a are highest among all ground-state isomers, indicating that its chemical stability is higher than those of other isomers. In addition, when the number of carbon atoms n > 4, as the number of incorporated carbon atoms increases, the energy indicators of the cluster increase monotonically. This is because Nb atoms can form Nb-C bonds by sharing electrons with C atoms. Moreover, owing to the lower energy levels of Nb’s d orbitals, they can donate electrons to the p orbitals of the C atoms, thereby reinforcing the Nb-C bonds. Additionally, the distance between Nb and C atoms is shorter compared to that between Nb atoms, indicating a stronger van der Waals interaction between Nb and C atoms, thereby enhancing the stability of the present clusters.
Among all ground-state isomers of Nb7Cn (n = 1–7) clusters, isomers Nb7C3 and Nb7C4 show obvious differences in stability. Isomer Nb7C3 shows a local maximum value among the ground-state isomers of all sizes of Nb7Cn (n = 1–7) clusters in the curves of Δ2E, DE, E-gap, and η shown in Figure 2. This observation suggests that Nb7C3 possesses higher thermodynamic and chemical stability, making it a potential candidate for a magic cluster. In contrast, minima appeared at n = 4, suggesting that isomer 4a has poor thermal and chemical stability and can be used as a potential detector material and chemical reaction indicator.
2.3. Density of States
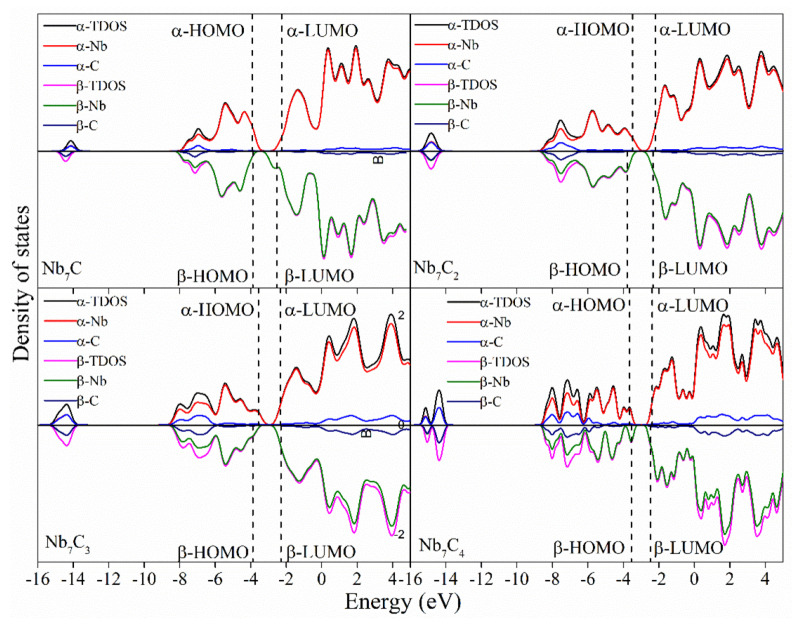
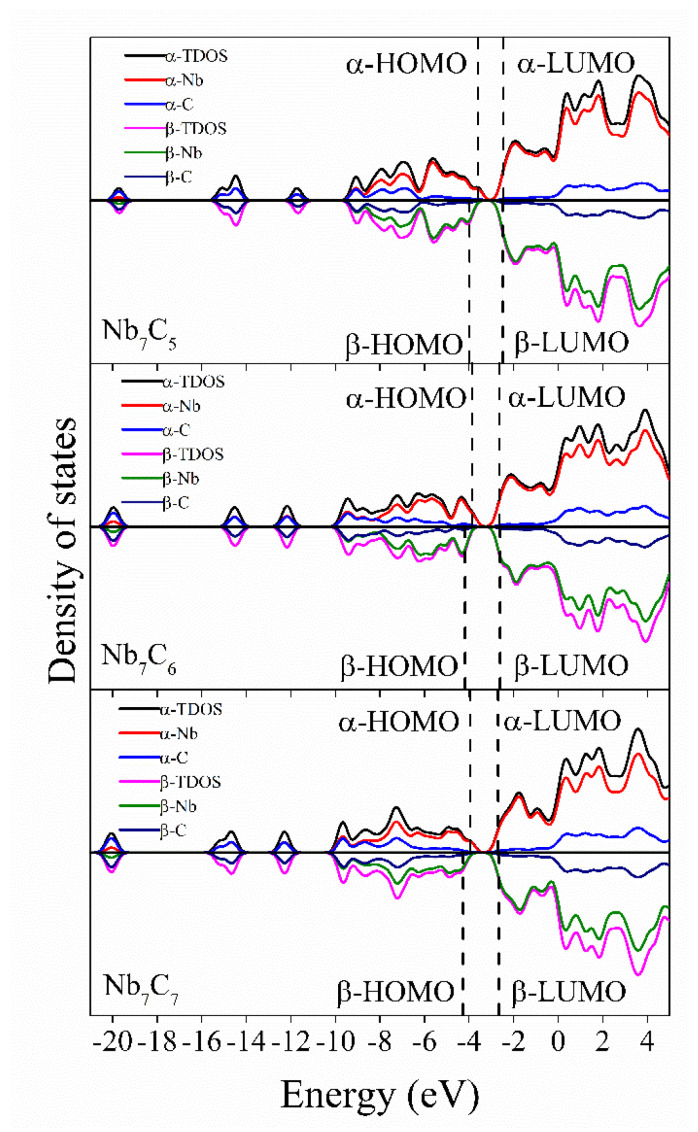
To further explore how Nb and C atoms affect the molecular orbital and HOMO-LUMO energy gap of the Nb7Cn (n = 1–7) clusters, the density of states diagram of the ground-state structures of the Nb7Cn (n = 1–7) clusters is shown in Figure 3 and Figure 4. Analysis of the total density of states (TDOS) plot for the lowest-energy structures of the Nb7Cn (n = 1–7) clusters reveal a negligible disparity in profile between the alpha-TDOS and beta-TDOS, thereby signifying a minimal degree of spin polarization. To offer a more nuanced evaluation of the contribution of Nb and C atoms to the total density of states, respectively, we plotted the partial density of states (PDOS) of Nb7 and Cn, respectively. Compared to the PDOS curves of Nb, the PDOS profiles of the C atoms generally exhibit lower magnitudes. At the HOMO and LUMO positions, the PDOS of the Nd fragment is very close to the TDOS. As the number of C atoms increases, a distinct aggregation phenomenon of carbon atoms is observed within the structure of the doped cluster. Upon comparing the density of states plots of Nb7Cn clusters (Figure 3 and Figure 4), it becomes evident that the contribution of carbon atoms to the frontier orbitals demonstrates a trend of localized enhancement to some degree. We provide the compositions of the frontier molecular orbitals (alpha-HOMO, alpha-LUMO, beta-HOMO, beta-LUMO) for Nb7Cn (n = 1–7) in Table 2.
Figure 3.
The total density of states (TDOS) and partial density of states (PDOS) of the Nb7Cn (n = 1−4) with a full−width at half−maximum (FWHM) of 0.5 eV.
Figure 4.
The total density of states (TDOS) and partial density of states (PDOS) of the Nb7Cn (n = 5−7) with a full−width at half−maximum (FWHM) of 0.5 eV.
Table 2.
The compositions of the frontier molecular orbitals for Nb7Cn (n = 1–7).
| Isomers | Atoms | α-HOMO | α-LUMO | β-HOMO | β-LUMO |
|---|---|---|---|---|---|
| Nb7C | Nb | 98.72% | 98.80% | 98.68% | 99.87% |
| C | 1.28% | 1.20% | 1.32% | 0.13% | |
| Nb7C2 | Nb | 99.45% | 97.73% | 98.88% | 99.47% |
| C | 0.55% | 2.27% | 1.12% | 0.53% | |
| Nb7C3 | Nb | 94.32% | 96.29% | 92.69% | 96.63% |
| C | 5.68% | 3.71% | 7.31% | 3.37% | |
| Nb7C4 | Nb | 91.37% | 95.49% | 96.44% | 92.42% |
| C | 8.63% | 4.51% | 3.56% | 7.58% | |
| Nb7C5 | Nb | 88.95% | 92.15% | 88.60% | 92.54% |
| C | 11.05% | 7.85% | 11.40% | 7.46% | |
| Nb7C6 | Nb | 93.80% | 94.57% | 84.35% | 94.29% |
| C | 6.20% | 5.43% | 15.65% | 5.71% | |
| Nb7C7 | Nb | 94.49% | 91.86% | 84.66% | 92.29% |
| C | 5.51% | 8.14% | 15.34% | 7.71% |
It can be seen in Table 2 that the percentage contribution of Nb in the front molecular orbitals is very high and far exceeds that of the C atom. For α-HOMO, Nb atoms contribute approximately from 88.95% to 99.45% to the Nb7Cn clusters. For α-LUMO, Nb atoms contribute approximately from 91.86% to 98.8%. For β-HOMO, Nb atoms contribute approximately from 84.35% to 98.88%. For β-LUMO, Nb atoms contribute approximately from 92.29% to 99.87%. This indicates that HOMO and LUMO are mainly composed of orbitals of the transition metal Nb, with a weak involvement of C atoms. Such an observation suggests the pivotal role played by Nb atoms in modulating the electronic structure within these isomers of Nb7Cn (n = 1–7) clusters.
2.4. Magnetic Properties
The magnetic moment is an important concept in physics, chemistry, and materials science, as it plays a significant role in understanding and controlling magnetic properties and phenomena. The spin density () refers to the distribution of unpaired electrons with different spin orientations within a molecule or material. It provides information about the electronic structure and magnetic properties of the system. We utilized Multiwfn in conjunction with the VMD program to visualize the spin-density isosurfaces of the lowest-energy structures of Nb7Cn (n = 1–7), as shown in Figure 5. The total magnetic moments of Nb7Cn (n = 1–7) as well as the local magnetic moments of Nb atoms and C atoms in Nb7Cn clusters are presented in Table 3.
Figure 5.
The spin density isosurfaces of lowest-energy structures of Nb7Cn (n = 1–7). The isosurface is set to ±0.01. The green and blue isosurfaces show that the spin density has positive and negative values, respectively.
Table 3.
Total magnetic moments of Nb7Cn clusters and local magnetic moments for the C atom and magnetic moments of 4d, 5s, 5p, 6s, and 6p orbitals for the Nb atoms; all units in μB.
| Isomers | Nb | C | Total | ||||
|---|---|---|---|---|---|---|---|
| 5s | 4d | 5p | 6s | 6p | |||
| Nb7C | 0.15 | 0.74 | 0.12 | 0.00 | −0.01 | −0.04 | 1 |
| Nb7C2 | 0.12 | 0.63 | 0.20 | 0.00 | 0.00 | −0.02 | 1 |
| Nb7C3 | 0.01 | 0.75 | 0.14 | 0.12 | 0.00 | −0.01 | 1 |
| Nb7C4 | 0.03 | 0.47 | 0.24 | 0.08 | 0.00 | 0.12 | 1 |
| Nb7C5 | 0.02 | 0.36 | 0.18 | 0.14 | 0.15 | 0.16 | 1 |
| Nb7C6 | 0.05 | 0.74 | 0.08 | 0.07 | 0.02 | 0.02 | 1 |
| Nb7C7 | 0.00 | 0.66 | 0.13 | 0.14 | 0.05 | 0.02 | 1 |
In Figure 5, the spin density diagram shows that the excess unpaired electrons are predominantly distributed around the Nb atoms. In Table 3, we can find that Nb7Cn clusters have total magnetic moments of 1 μB and the total magnetic moment is mainly located on the Nb atoms, whereas the magnetic moment located on the C atoms is almost negligible. To further understand the magnetic properties of Nb7Cn clusters, we performed a detailed analysis of the local magnetic moment of Nb atoms in Nb7Cn clusters by natural population analysis calculations. Table 3 shows that for the Nb7C and Nb7C2 clusters, the magnetic moment of Nb atoms is mainly from the 4d orbital, followed by the 5s and 5p orbitals with a small contribution to the magnetic moment of the Nb atom. For the other Nb7Cn (n = 1–7), the magnetic moment of Nb atoms still comes mainly from the 4d orbital, followed by 5p and 6s orbitals. For the Nb7C5 cluster, the contribution of 5p, 6s, and 6p orbitals to the magnetic moment of Nb atom is nearly equal. The contribution of C atoms to the total moment is minimal and mainly originates from the 2p orbitals.
3. Computational Methods
Global minimum searches for low-lying structures of Nb7Cn (n = 1–7) clusters were performed in three steps: Firstly, we employed the SK global search method [30,31,32] combined with DFT calculation to search and optimize the structure. In recent years, our research group has effectively predicted the ground-state structures and electronic properties of binary mixed clusters utilizing the SK-DFT method [33,34,35,36,37,38,39,40,41]. All the atoms are placed at the same point initially and then are “kicked” randomly with a sphere of some radius. The Kick method runs approximately 500 times at the B3LYP functional [42,43] using the 3–21 G [44] basis set until no new minima appear. Secondly, the isomers were ranked according to their total energy at the B3LYP/3-21G level. Thirdly, several pertinent lower-lying isomers were chosen for additional optimization employing the triply split basis set with polarization and diffuse functions. Specifically, the 6–311+G(2d) [45] basis set was employed for C. For the heavier atoms, previous studies [46,47,48,49] have confirmed the significance of relativistic effects in simulating the properties of systems involving heavy atoms. Therefore, using appropriate relativistic treatment methods is important when dealing with systems containing heavy atoms. The SDD pseudopotential basis set [50], which accounts for relativistic effects, was used for Nb. The interaction between valence electrons and the inert core is included in the pseudopotential. This allows us to reduce computational times and provide reliable calculations of geometry and electronic properties. Geometries are regarded as completing the optimization when the maximum force, the root-mean-square (RMS) force, the maximum displacement of atoms, and the RMS displacement of atoms have magnitudes less than 0.00045, 0.0003, 0.0018, and 0.0012 a.u., respectively. The self-consistent field convergence criterion was set as 10−8. Structural optimization with frequency analysis were considered at the same time. The image frequency would be eliminated until every structure optimized had no image frequency to confirm that the low-lying isomers were local minima. All calculations were performed with the GAUSSIAN09 program [51]. Density of states (DOS) and orbital composition analysis were performed by Multiwfn program [52] and visualized by Visual Molecular Dynamics (VMD 1.9.3) software [53].
4. Conclusions
We have investigated the structural, electronic, and magnetic properties of Nb7Cn (n = 1–7) clusters by employing density functional theory calculations. The relative stability analysis indicates that Nb7C3 is more stable than the other clusters, as it exhibits a higher second-order difference energy, dissociation energy, HOMO-LUMO gap, and chemical hardness. In contrast, Nb7C4 is less stable, as it shows lower values of these stability indicators. The composition of the frontier molecular orbitals reveals that the predominant contribution originates from Nb atoms, accounting for 84.35% to 99.87% of the molecular orbital. The total magnetic moment of Nb7Cn (n = 1–7) is mainly located on the Nb atoms, whereas the magnetic moment located on the C atoms is almost negligible. For the Nb atoms, the 4d orbit contributes most to the total magnetic moment, followed by the 5p, 5s, and 6s orbits.
Acknowledgments
The authors would like to express their gratitude to the School of Engineering, Huaqiao University, which is affiliated with Huaqiao University. This research was conducted at the School of Engineering, Huaqiao University.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules29081692/s1, Table S1: Cartesian coordinates for the lowest energy structure of Nb7Cn (n = 1−7) at the B3LYP/Nb/ SDD//C/6−311+G(2d) level. Figure S1: The IR spectra of the lowest energy structures of Nb7Cn (n = 1−7) clusters.
Author Contributions
Conceptualization, H.-F.L. and H.-Q.W.; methodology, H.-F.L. and H.-Q.W.; software, H.-Q.W.; validation, H.-F.L. and H.-Q.W.; formal analysis, H.-Q.W. and J.-M.Z.; investigation, H.-F.L.; resources, H.-Q.W.; data curation, H.-F.L.; writing—original draft preparation, H.-F.L., J.-M.Z., L.-X.Q. and H.Z.; writing—review and editing, H.-F.L., H.-Q.W., J.-M.Z., L.-X.Q., H.Z. and Y.-H.Z.; visualization, H.-F.L.; supervision, H.-Q.W.; project administration, H.-Q.W.; funding acquisition, H.-Q.W. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding Statement
The project was supported by the Natural Science Foundation of Fujian Province of China (Grant No. 2023J01141), the Natural Science Foundation of Xiamen (Grant No. 3502Z202373051), the Science and Technology Plan of Quanzhou (Grant Nos. 2018C077R and 2018C078R), and the New Century Excellent Talents in Fujian Province University (Grant No. 2014FJ-NCET-ZR07).
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Lu C., Gong W.G., Li Q., Chen C.F. Elucidating stress-strain relations of ZrB12 from first-principles studies. J. Phys. Chem. Lett. 2020;11:9165–9170. doi: 10.1021/acs.jpclett.0c02656. [DOI] [PubMed] [Google Scholar]
- 2.Zhao R., Chen R., Zhao H., Lin F., Han J.-G. Exploration on electronic properties of self-assembled Indium nitrogen nanosheets and nanowires by a density functional method. Molecules. 2023;28:7358. doi: 10.3390/molecules28217358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang T., Zhang M., Lu X.-Q., Yan Q.-Q., Zhao X.-N., Li S.-D. Sc@B28−, Ti@B28, V@B28+, and V@B292−: Spherically aromatic endohedral seashell-like metallo-borospherenes. Molecules. 2023;28:3892. doi: 10.3390/molecules28093892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Uchiyama T., Nakamura T., Hiyama M., Kudo T. Theoretical study of Si/C equally mixed dodecahedrane analogues. Molecules. 2023;28:2769. doi: 10.3390/molecules28062769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Khanna V., McGrady J.E. Mn2 dimers encapsulated in silicon cages: A complex challenge to MC-SCF theory. Molecules. 2022;27:7544. doi: 10.3390/molecules27217544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Duan X.F.F., Burggraf L.W., Huang L.Y. Searching for stable SinCn clusters: Combination of stochastic potential surface search and pseudopotential Plane-Wave Car-Parinello simulated annealing simulations. Molecules. 2013;18:8591–8606. doi: 10.3390/molecules18078591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen Y., Deng J.-J., Yao W.-W., Gurti J.I., Li W., Wang W.-J., Yao J.-X., Ding X.-L. Non-stoichiometric molybdenum sulfide clusters and their reactions with the hydrogen molecule. Phys. Chem. Chem. Phys. 2021;23:347–355. doi: 10.1039/D0CP04457A. [DOI] [PubMed] [Google Scholar]
- 8.Valeeva A.A., Gusev A.I. Effect of nonstoichiometry on elastic properties of niobium carbide NbCy. Int. J. Refract. Met. Hard Mater. 2021;95:105435. doi: 10.1016/j.ijrmhm.2020.105435. [DOI] [Google Scholar]
- 9.Jalalya M., Gotorb F.J., Sayagués M.J. Mechanochemical combustion synthesis of vanadium carbide (VC), niobium carbide (NbC) and tantalum carbide (TaC) nanoparticles. Int. J. Refract. Met. Hard Mater. 2019;79:177–184. doi: 10.1016/j.ijrmhm.2018.12.011. [DOI] [Google Scholar]
- 10.Laskoski M., Prestigiacomo J., Dyatkin B., Keller T.M., Mahzabeen W., Shepherd A.R., Daftary M.N., Clarke J.S., Neal A., Qadri S.B., et al. Synthesis and material properties of polymer-derived niobium carbide and niobium nitride nanocrystalline ceramics. Ceram. Int. 2021;47:1163–1168. doi: 10.1016/j.ceramint.2020.08.232. [DOI] [Google Scholar]
- 11.Yeh C.S., Byun Y.G., Afzaal S., Kan S.Z., Lee S., Freiser B.S., Hay P.J. Experimental and theoretical studies on Nb4C40/+: Reactivity and structure of the smallest cubic niobium-carbon cluster. J. Am. Chem. Soc. 1995;117:4042–4048. doi: 10.1021/ja00119a020. [DOI] [Google Scholar]
- 12.Byun Y.G., Lee S.A., Kan S.Z., Freiser B.S. Reactivities of metallocarbohedrenes: Nb8C12+ J. Phys. Chem. 1996;100:14281–14288. [Google Scholar]
- 13.Li S., Wu H., Wang L. Probing the electronic structure of metallocarbohedrenes: M8C12 (M = Ti, V, Cr, Zr, Nb) J. Am. Chem. Soc. 1997;119:7417–7422. doi: 10.1021/ja9710159. [DOI] [Google Scholar]
- 14.Yang D.S., Zgierski M.Z., Berces A., Hackett P.A., Roy P.N., Martinez A., Carrington T., Salahub D.R., Fournier R., Pang T., et al. Vibrational and geometric structures of Nb3C2 and Nb3C2+ from pulsed field ionization-zero electron kinetic energy photoelectron spectra and density functional calculations. J. Chem. Phys. 1996;105:10663–10671. doi: 10.1063/1.472873. [DOI] [Google Scholar]
- 15.Knappenberger K.L., Jr., Clayborne P.A., Reveles J.U., Sobhy M.A., Jones C.E., Gupta U.U., Khanna S.N., Iordanov I., Sofo J., Castleman A.W., Jr. Anion photoelectron spectroscopy and density functional investigation of diniobium-carbon clusters. ACS Nano. 2007;1:319–326. doi: 10.1021/nn700167c. [DOI] [PubMed] [Google Scholar]
- 16.Zhai H.J., Liu S.R., Wang L.S. Photoelectron spectroscopy of mono-niobium carbide clusters NbCn− (n = 2–7): Evidence for a cyclic to linear structural transition. J. Chem. Phys. 2001;115:5170–5178. doi: 10.1063/1.1395556. [DOI] [Google Scholar]
- 17.Chebanenko M.I., Danilovich D.P., Lobinsky A.A., Popkov V.I., Rempel A.A., Valeeva A.A. Novel high stable electrocatalyst based on non-stoichiometric nanocrystalline niobium carbide toward effective hydrogen evolution. Int. J. Hydrogen Energy. 2021;46:16907–16916. doi: 10.1016/j.ijhydene.2021.01.223. [DOI] [Google Scholar]
- 18.Il’in E.G., Parshakov A.S., Teterin Y.A., Maslakov K.I., Teterin A.Y. Surface morphology and composition of a NbC/C composite studied by scanning electron microscopy and X-ray photoelectron spectroscopy. Inorg. Mater. 2020;56:443–450. doi: 10.1134/S0020168520050052. [DOI] [Google Scholar]
- 19.Pilgrim J.S., Brock L.R., Duncan M.A. Photodissociation of niobium-carbon clusters and nanocrystals. J. Phys. Chem. 1995;99:544–550. doi: 10.1021/j100002a016. [DOI] [Google Scholar]
- 20.Wei S., Guo B.C., Deng H.T., Kerns K., Purnell J., Buzza S.A., Castleman A.W., Jr. Formation of met-cars and face-centered cubic structures: Thermodynamically or kinetically controlled? J. Am. Chem. Soc. 1994;116:4475–4476. doi: 10.1021/ja00089a046. [DOI] [Google Scholar]
- 21.Fukushima N., Miyajima K., Mafune F. Ionization energies of niobium carbide clusters NbnCm (n = 3–10, m = 0–7) J. Phys. Chem. A. 2009;113:2309–2315. doi: 10.1021/jp809915c. [DOI] [PubMed] [Google Scholar]
- 22.Dryza V., Addicoat M.A., Gascooke J.R., Buntine M.A., Metha G.F. Threshold photoionization and density functional theory studies of the niobium carbide clusters Nb3Cn (n = 1–4) and Nb4Cn (n = 1–6) J. Phys. Chem. A. 2008;112:5582–5592. doi: 10.1021/jp800691s. [DOI] [PubMed] [Google Scholar]
- 23.Gusev A.I. Anisotropy of microstructure and elastic properties of niobium carbide nanopowders. Solid State Sci. 2020;100:106092. doi: 10.1016/j.solidstatesciences.2019.106092. [DOI] [Google Scholar]
- 24.Heijnsbergen D.V., Fielicke A., Meijer G., Helden G.V. Structure determination of gas-phase niobium and tantalum carbide nanocrystals via infrared spectroscopy. Phys. Rev. Lett. 2002;89:013401. doi: 10.1103/PhysRevLett.89.013401. [DOI] [PubMed] [Google Scholar]
- 25.Clemmer D.E., Hunter J.M., Shelimov K.B., Jarrold M.F. Physical and chemical evidence for metallofullerenes with metal atoms as part of the cage. Lett. Nat. 1994;372:230–248. doi: 10.1038/372248a0. [DOI] [Google Scholar]
- 26.Pham V.N., Minh T.N. Structures, spectra, and energies of Niobium Clusters from Nb13 to Nb20. J. Phys. Chem. A. 2012;116:7405–7418. doi: 10.1021/jp302279j. [DOI] [PubMed] [Google Scholar]
- 27.Harris H., Dance I. The geometric and electronic structures of niobium carbon clusters. J. Phys. Chem. A. 2001;105:3340–3358. doi: 10.1021/jp0035535. [DOI] [Google Scholar]
- 28.Dai D., Roszak S., Balasubramanian K. Electronic structures of niobium carbides: NbCn (n = 3–8) J. Phys. Chem. A. 2000;104:9760–9769. doi: 10.1021/jp001412x. [DOI] [Google Scholar]
- 29.Jeffrey P.M., Damian M., Leo R. An evaluation of harmonic vibrational frequency scale factors. J. Phys. Chem. A. 2007;111:11683–11700. doi: 10.1021/jp073974n. [DOI] [PubMed] [Google Scholar]
- 30.Roy D., Corminboeuf C., Wannere C.S., King R.B., Schleyer P.V.R. Planar tetracoordinate carbon atoms centered in bare four-membered rings of late transition metals. Inorg. Chem. 2006;45:8902–8906. doi: 10.1021/ic060802g. [DOI] [PubMed] [Google Scholar]
- 31.Bera P.P., Sattelmeyer K.W., Saunders M., Schaefer H.F., Schleyer P.R. Mindless chemistry. J. Phys. Chem. A. 2006;110:4287–4290. doi: 10.1021/jp057107z. [DOI] [PubMed] [Google Scholar]
- 32.Saunders M. Stochastic search for isomers on a quantum mechanical surface. J. Comput. Chem. 2004;25:621–626. doi: 10.1002/jcc.10407. [DOI] [PubMed] [Google Scholar]
- 33.Xie B., Wang H.Q., Li H.F., Zhang J.M., Zeng J.K., Mei X.J., Zhang Y.H., Zheng H., Qin L.X. Making sense of the growth behavior of ultra-high magnetic Gd2-doped silicon clusters. Molecules. 2023;28:5071. doi: 10.3390/molecules28135071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang J.M., Wang H.Q., Li H.F., Mei X.J., Zeng J.K., Qin L.X., Zheng H., Zhang Y.H., Jiang K.L., Zhang B., et al. Aromatic and magnetic properties in a series of heavy rare earth-doped Ge6 cluster anions. J. Comput. Chem. 2024 doi: 10.1002/jcc.27317. in press . [DOI] [PubMed] [Google Scholar]
- 35.Li H.F., Wang H.Q. Stabilization of golden cages by encapsulation of a single transition metal atom. R. Soc. Open Sci. 2018;5:171019. doi: 10.1098/rsos.171019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fan Y.W., Wang H.Q., Li H.F. Structural and electronic properties of exohedrally doped neutral silicon clusters LnSin (n = 5, 10; Ln = Sm, Eu, Yb) Phys. Chem. Chem. Phys. 2020;22:20545–20552. doi: 10.1039/D0CP03754K. [DOI] [PubMed] [Google Scholar]
- 37.Fan Y.W., Kong X.Y., Zhao L.J., Wang H.Q., Li H.F., Zhan Q., Xie B., Xu H.G., Zheng W.J. A joint experimental and theoretical study on structural, electronic, and magnetic properties of MnGen− (n = 3–14) clusters. J. Chem. Phys. 2021;154:204302. doi: 10.1063/5.0053414. [DOI] [PubMed] [Google Scholar]
- 38.Xie B., Wang H.Q., Li H.F., Zeng J.K. Structural and electronic properties of Ln2Si6q: (Sm, Eu, Yb; q = 0, −1) clusters. Chem. Phys. 2023;566:111782. doi: 10.1016/j.chemphys.2022.111782. [DOI] [Google Scholar]
- 39.Fan Y.W., Wang H.Q., Li H.F. Probing the structural and electronic properties of anionic europium-doped silicon clusters by density functional theory and comparison of experimental photoelectron spectroscopy. Chem. Phys. 2020;538:110918. doi: 10.1016/j.chemphys.2020.110918. [DOI] [PubMed] [Google Scholar]
- 40.Wang H.Q., Li H.F. Structure identification of endohedral golden cage nanoclusters. RSC Adv. 2015;5:94685–94693. doi: 10.1039/C5RA19643D. [DOI] [Google Scholar]
- 41.Wang H.Q., Li H.F. Probing the structural and electronic properties of al-doped small niobium clusters. Chem. Phys. Lett. 2012;554:231–235. doi: 10.1016/j.cplett.2012.10.033. [DOI] [Google Scholar]
- 42.Becke A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
- 43.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- 44.Igel-Mann G., Stoll H., Preuss H. Pseudopotentials for main group elements (IIIa through VIIa) Mol. Phys. 1988;65:1321–1328. doi: 10.1080/00268978800101811. [DOI] [Google Scholar]
- 45.Mclean A.D., Chandler G.S. Contracted gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980;72:5639–5648. doi: 10.1063/1.438980. [DOI] [Google Scholar]
- 46.Ganesh M., Gamidi R.K., Sashi D., Anjan B. Origin of optoelectronic contradicions in 3,4-cycloalkyl[c]-chalcogenophenes: A computational study. Polymers. 2020;15:4240. doi: 10.3390/polym15214240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Shida N., Nishiyama H., Zheng F., Ye S., Seferos D.S., Tomita I., Inagi S. Redox chemistry of π-extended tellurophenes. Commun. Chem. 2019;2:124–132. doi: 10.1038/s42004-019-0228-y. [DOI] [Google Scholar]
- 48.Dishi O., Gidron O. Macrocyclic Oligofurans: A Computational Study. J. Org. Chem. 2018;83:3119–3125. doi: 10.1021/acs.joc.7b03030. [DOI] [PubMed] [Google Scholar]
- 49.Wu B., Melvina, Wu X., Lee Yeow E.K., Yoshikai N. Versatile telluracycle synthesis via the sequential electrophilic telluration of C(sp2)-Zn and C(sp2)-H bonds. Chem. Sci. 2017;8:4527–4532. doi: 10.1039/C7SC01162H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang R.Q., Chu T.S., Lee S.T. Computation of large systems with an economic basis set: Ab initio calculations of silicon oxide clusters. J. Chem. Phys. 2001;114:5531–5536. doi: 10.1063/1.1351883. [DOI] [Google Scholar]
- 51.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., et al. Gaussian 09, Revision C.01. Gaussian Inc.; Wallingford, CT, USA: 2010. [Google Scholar]
- 52.Lu T., Chen F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 53.Humphrey W., Dalke A., Schulten K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.