Facilitating clinically relevant skin tumor diagnostics with spectroscopy-driven machine learning

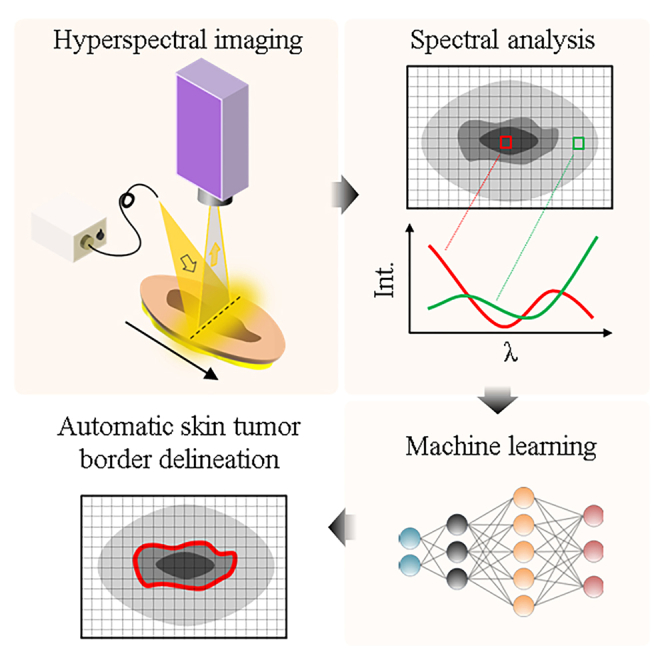
Summary

In the dawning era of artificial intelligence (AI), health care stands to undergo a significant transformation with the increasing digitalization of patient data. Digital imaging, in particular, will serve as an important platform for AI to aid decision making and diagnostics. A growing number of studies demonstrate the potential of automatic pre-surgical skin tumor delineation, which could have tremendous impact on clinical practice. However, current methods rely on having ground truth images in which tumor borders are already identified, which is not clinically possible. We report a novel approach where hyperspectral images provide spectra from small regions representing healthy tissue and tumor, which are used to generate prediction maps using artificial neural networks (ANNs), after which a segmentation algorithm automatically identifies the tumor borders. This circumvents the need for ground truth images, since an ANN model is trained with data from each individual patient, representing a more clinically relevant approach.

Graphical abstract

Highlights

• •Hyperspectral imaging enables noninvasive skin tumor characterization
• •Novel AI approach bypasses need for ground truth images in tumor delineation
• •Individual ANN models per patient enhance clinical relevance and objectivity
• •Promising for patient adaptability in future differential skin tumor diagnostics

Health sciences; Natural sciences; Computer science

Introduction

With over 1.5 million new cases in 2020, skin cancer is the third most common cancer worldwide.¹ Non-melanoma skin cancer (NMSC) is the most common group of cancers in western countries,² comprising basal cell carcinoma (BCC) and squamous cell carcinoma (SCC). Malignant melanoma is rarer than NMSC, but is also more aggressive and represents a growing disease burden in society.^3,4 Current clinical practice to diagnose and treat skin tumors is unfortunately rather time-consuming, involving excisional biopsy and histopathological analysis. With an increasing incidence worldwide,¹ there is a justified concern that a seemingly cumbersome diagnostic procedure may cause a bottleneck for the growing diagnostic demand.

There have been several reports over recent years implementing artificial intelligence (AI) and machine learning (ML) methods with dermatoscopy to facilitate more efficient diagnosis.^5,6 AI-based applications have emerged for mobile and handheld devices to assess malignancy of lesions and guide decision making in whether to perform a biopsy or apply other treatment measures.^7,8 However, while there is an obvious benefit of early classification of a suspected lesion, in order to improve survival rate, identifying skin tumor borders is also of high clinical importance relating to treatment and prognosis. Despite guidelines to lessen the risk of incomplete skin tumor removal,^9,10 upward of 22% of primary biopsies are discovered via histopathology to be non-radical,¹¹ which consequently requires re-surgery incurring additional health care costs and patient suffering, while unfortunately also reducing survivability.¹²

Driven by the clinical need for reducing the number of non-radical biopsy excisions, studies employing artificial neural networks (ANNs) to pre-surgically delineate skin tumors in order to assist surgeons are emerging.¹³ However, they suffer a few limitations considering their clinical applicability. Performance of AI models employing feature extraction depend heavily on image resolution.¹⁴ This may also be affected by patient motion during image acquisition. A recent report also demonstrates the relative ease at which a convolutional neural network (CNN) image classifier produces inconsistent predictions when simply rotating a dermoscopic tumor image.¹⁵ These examples underline the potential pitfalls of image classifiers that rely on spatial feature extraction.

Another major limitation for AI and ML implementations for skin tumor delineation is tied to how image classifiers fundamentally operate. Previous reports employing an image classifier to automatically identify skin tumor borders conventionally require training images where the tumor borders have been manually identified.^16,17 From a clinical perspective, this poses a challenge since the only reliable way to currently determine the border between healthy tissue and skin tumor is via histopathology. By chemically staining biopsy cross-sections, the spectral (color) contrast is enhanced such that healthy tissue and tumor can easily be differentiated, which otherwise would not be observable via direct visual inspection or using a dermatoscope.^18,19 While AI models certainly can automate the skin tumor delineation to a level of accuracy comparable to a clinician manually drawing them in dermoscopic images,^20,21,22 the real question is whether this is sufficient for clinical implementation since histopathology is still required. If an image does not contain the necessary spectral contrast in order to produce a clinically reliable diagnosis,²³ the data quality is automatically insufficient and alternative approaches should be considered.^24,25

In this work we present an alternative ML approach to pre-surgical skin tumor delineation that does not require manual identification of the tumor borders. Rather than analyzing spatial features in standard color images, our model instead builds on recognizing spectral patterns in hyperspectral images capturing information beyond the sensitivity of the naked eye.^26,27,28 We detail a model that trains on the spectra from image regions that belong to healthy tissue or skin tumor, which enables us to automatically determine and visualize the border between healthy tissue and tumor. A key aspect of our framework is that we train a single model instance for each tumor sample, i.e., the training data is contained within each individual patient, which has important clinical implications. Moreover, exploiting the ability to generate individualized ANN models for each sample, we demonstrate the adaptability of the approach to use the extended spectral contrast between healthy tissue and tumor for different patients and skin tumors types. This taps into the potential of using the presented approach for personalized medicine.

Results

Different spectra for healthy and tumor pixels

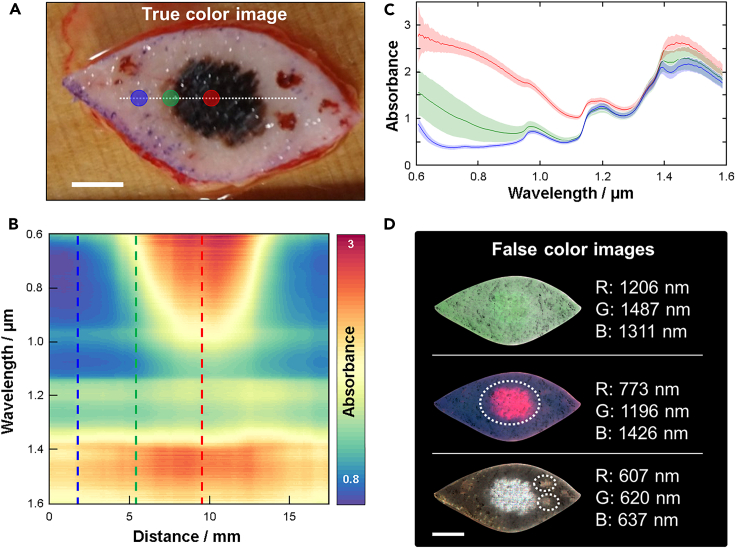
Figure 1 shows a representative example of the information that can be extracted from a hyperspectral image (see STAR Methods for instrument details). A regular color photo of a melanoma tumor sample is used as a reference (Figure 1A). Absorbance spectra are extracted from every pixel (averaged vertically over ±5 pixels) along the horizontal white dotted line spanning from and to healthy tissue across the tumor. Figure 1B shows all these spectra combined into a heatmap where it is evident there is spectral contrast comparing regions representing healthy tissue and tumor. This is most evident in the 600–1000 nm spectral range. However, some contrast can also be observed for longer wavelengths. Figure 1C shows three individual spectra extracted from the locations indicated in Figures 1A and 1B, where the spectral contrast becomes more evident. Figure 1D shows three examples of false color images that can be produced from the hyperspectral image dataset using a combination of monochromatic images from three unique spectral channels. From the 322 spectral channels available in the dataset, over 33 million unique false color images can in essence be created, which demonstrates the flexibility in image representation offered by our system. The three examples in Figure 1D highlight how the hyperspectral information can be used to display potentially clinically relevant information. The top image combines three spectral channels that represent the background information without any sign of the tumor. The middle image shows the tumor clearly, while the bottom image shows the tumor together with two additional spots presumed to be blood clots. While a trained clinician likely can differentiate between these different regions with the naked eye, the ability of HSI to completely separate and display these regions is not only important for conventional ML approaches based on spatial contrasts,²⁹ but also for the spectroscopy-guided ML methods discussed in this work.

Figure 1.

Hyperspectral features of a tumor sample

(A) Representative example of a color photo of a melanoma tumor.

(B) Spectra extracted from every point along the dashed line in (a) with 50 μm resolution plotted as a heatmap.

(C) Spectra extracted at three locations indicated in both (a) and (b) where blue likely represents healthy tissue, red represents the tumor and green some intermediate state in-between. Spectra are extracted from regions approximately represented by the solid circles in (a) where the data are plotted as the mean (solid traces) and standard deviation (shaded areas).

(D) False color images of the tumor generated by compiling a subset of three images from the hyperspectral imaging data to enhance different sample features. In the middle false color image, the suspected tumor is indicated with a white dashed line that can be differentiated from the blood clots identified in the bottom false color image. The scale bars represent 10 mm in all images.

Spectral analysis using MCR-ALS

Figure 1 provides insight into the abundance of spectral information that can yield a spatial contrast between tumor and healthy tissue. We employ multivariate curve resolution – alternating least squares (MCR-ALS)³⁰ analysis to systematically extract the most common spectral features from all tumors combined (see STAR Methods for further details). We refrain from starting with an analysis based on the tumor type since we do not have enough of each to minimize the expected effects of patient-to-patient variation. We also note that each spectral feature does not directly represent a particular tissue, but is rather a reflection of a particular composition of tissue. Further analysis can be implemented to inquire what each spectral component represents, but this falls out of the scope of current work.

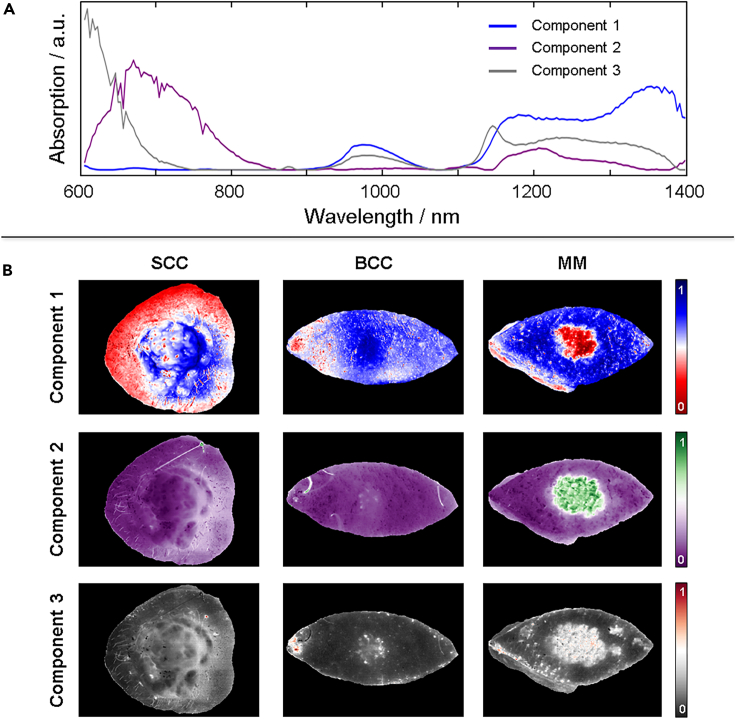
We assume that the difference in spectral features for all tumors compared with healthy tissue will be larger than the patient-to-patient variation of healthy tissue. Figure 2A shows the three most common spectral features from all tumors collectively. This suggests that all tumors can to some satisfying degree be described by a linear combination of these three spectral components. Figure 2B shows an example of three different tumor types (SCC, BCC and melanoma) that are shown in images that depict the contribution from each spectral component (see Figure S6 for all tumors). In all examples, some contrast can be observed between healthy tissue and the regions considered to represent tumor. However, the best contrast is observed for different spectral components depending on the tumor type, which unsurprisingly suggests that the different tumors have different spectral features. As mentioned, however, we cannot at this stage characterize these differences in detail. From inspection of the component maps (Figure S6) four skin tumor measurements could be identified which had insufficient signal-to-noise ratio (SNR) to reliably run the proceeding steps. These skin tumors were therefore excluded in the final comparison to histopathology, although the results from all analysis of each are found in the SI.

Figure 2.

MCR-ALS analysis

(A) Three most common spectral features (components) extracted from all tumor spectra using MCR-ALS.

(B) Three examples demonstrating how new images can be produced using each spectral component depicting the relative contribution of each spectral component represented in each pixel spectrum in different colors. The three examples show how different features become visible for different spectral components depending on the tumor type. See Figure S6 for all tumors and components.

Spectroscopically guided pixel prediction by machine learning

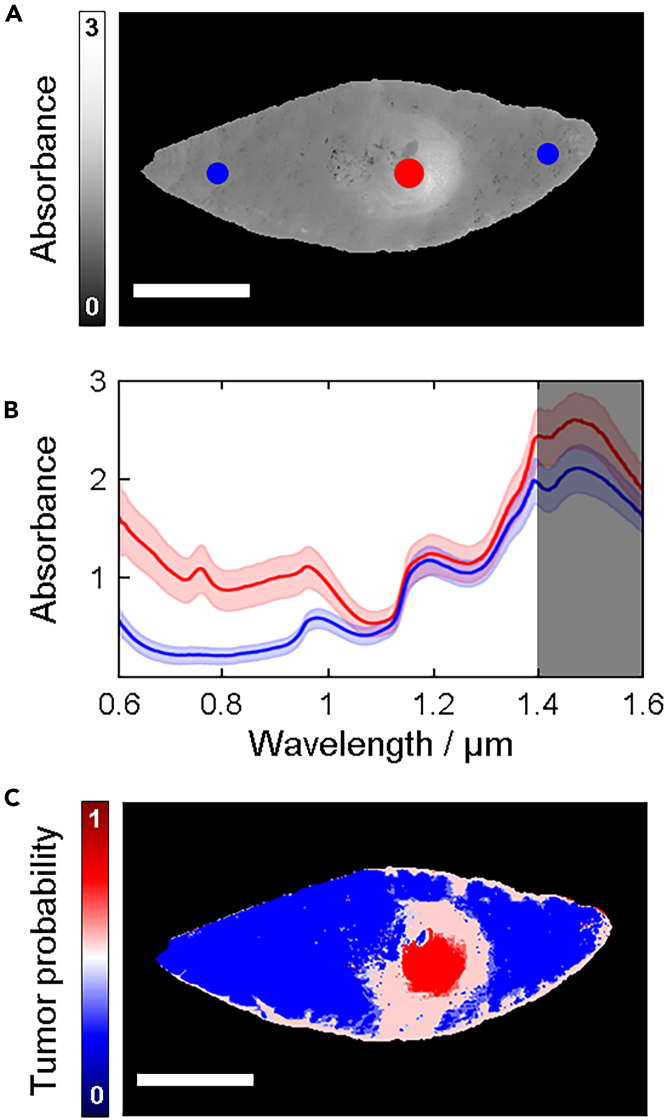
Under the assumption that there is a difference between spectra representing healthy tissue and tumor (Figure 1), an ANN-classifier should be able to learn to distinguish between the two. However, since it is not clearly known exactly where the tumor borders are located by visual inspection of the samples, standard deep learning methods for segmentation, e.g., the U-net,³¹ are not applicable. This type of network requires annotation for every individual pixel. Hence, we chose the approach to classify each pixel individually instead of treating the image as a whole unit. Even though the exact delineation is not known, we take advantage of the fact that one can easily identify the center of the tumor visually. We select pixels from the center area of the tumor and label them as tumor pixels with high certainty. In a similar manner, pixels from edge areas of the sample, where it is clear that the tumor is not located, and there is no influence from the incision, are selected and labeled with high certainty as healthy pixels (Figure 3A). These regions were confirmed via histopathology to have been correctly categorized. The selection of tumor and healthy pixels produced two distinct training spectra in most of our samples (Figure 3B). The average spectrum for the tumor pixels in general do not overlap with the average spectrum for the selection of healthy pixels, which suggests that classification is possible based on spectral features.³² We note that the SNR (signal to noise ratio) in the spectral range between 1400 and 1600 nm is significantly lower than the rest and was therefore excluded from the spectral analysis.

Figure 3.

Training regions and prediction maps

(A) Spectrally averaged image with regions representing healthy tissue (blue) and tumor (red) indicated in colored circles.

(B) Average spectra extracted from the regions indicated in (a). Due to the lower SNR in the spectral range between 1400 and 1600 nm (dark shaded region), this range was excluded in the MCR-ALS analysis.

(C) Prediction map of a malignant melanoma depicting tumor probability where red represents a 100% probability and blue represents 0% probability. The scale bars represent 10 mm. See Figure S2 and Table S2 for training regions for all the samples and Figures S6–S8 for the prediction map for each tumor and model type.

A key aspect of our method is that we only use data from one single patient to train one model instance. A model is trained on the selected training regions from one hyperspectral image. The trained model is, thereafter, used to categorize all the other pixels in the image. By treating each patient separately, no patient-to-patient biases are introduced. When we refer to a model being used on several samples, we mean that a separate, but identical, model instance is trained for each sample.

We devised three different Neural Network models as briefly described in STAR Methods below. A multilayer perceptron (MLP) and a 1-D CNN were trained on the raw spectral features and an additional MLP was trained on the MCR-ALS decomposition of the spectra. For each of the three models, every pixel of the tumor samples was classified individually. The convolution operation of the 1-D CNN was performed over the spectral range and is only is only taking 1 pixel as input at the time. Hence, the CNN works in a similar way as the MLP, but it takes neighboring spectral features into consideration. An MLP prediction map for the tumor was constructed from the model outputs (Figure 3C) where each pixel is assigned a value between 0 (100% predicted probability being healthy tissue) and 1 (100% predicted probability being tumor). From this, a colormap is generated showing blue (red) if a pixel has a higher probability of representing healthy tissue (tumor). White represents an equal probability being classified as either healthy tissue or tumor. We refer the reader to Figures S7–S9 for prediction maps of all tumors.

Viewing the prediction maps (Figures S7–S9) it is clear that they are not perfect representations of the tumors. In many cases, the prediction maps contain noise, which likely do not represent the tumor, but rather hair, marker pen used by the surgeon to identify the tumor, or a suture used to maintain the excised sample in place, which need to be removed.^33,34 Moreover, the incision appears to yield some degree of miss-classification, which is caused by the exposure of subcutaneous fat and blood yielding contrasting spectral features to that of healthy tissue. Miss-classification originating from incision artifacts will be reduced by imaging the tumors in situ in the future. In addition, segmentation will be an important step to reduce the influence of noise and artifacts, particularly those that are in a close proximity to the tumor, when determining its border to healthy tissue.

Segmentation

Since the spatial information contained in the data has hitherto not been utilized, we employ a segmentation algorithm to determine the tumor delineation. The individual pixels need to be put into context according to the pixels in their neighborhood. Furthermore, we must require from any segmentation algorithm which we may devise that it removes prediction noise and artifacts (e.g., blood stains and hair).

We chose an active contour algorithm since they are well suited to find borders of objects with irregular size.³⁵ The general approach of an active contour segmentation algorithm is that an active contour, which we refer to as a rope, tracks the contour of an object in an image. This is achieved by constructing an energy function which is minimized. The energy function has contributions both from internal properties of the rope such as stretching and curvature, and external properties derived from the image such as intensity. Furthermore, this type of algorithm offers the flexibility to choose the energy function to minimize, which makes it possible to adapt it to suit our specific problem.

A complication is that the prediction map is not directly suitable for an active contour algorithm. The quantity corresponding to intensity in a prediction map is the tumor probability, which does not provide enough context to a tumor pixel’s location within the tumor. Although the tumor probability may be lower near the edge of the tumor in some cases, that is not always so. Furthermore, noise and artifacts can also obtain high tumor probability. Thus, we first need to devise a more suitable intensity function from the prediction map, which should reflect a tumor pixel’s spatial location within the tumor. The sand-pile method (see STAR Methods) becomes ideal as it ensures that small regions of pixels misclassified as tumor (artifacts caused by e.g., blood, hair, marker pen or noise) will yield smaller sand-piles than large regions of pixels correctly classified as tumor. We refer the reader to STAR Methods for more details.

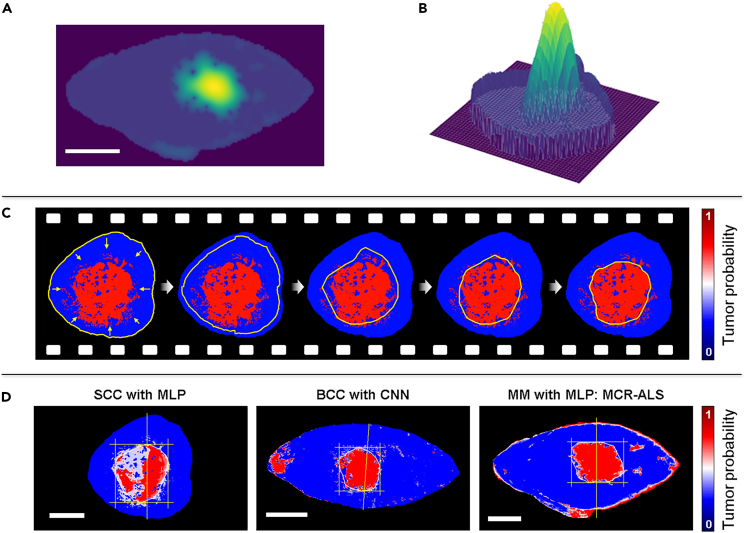
The resulting sand-pile landscape (Figures 4A and 4B) is used by the active contour algorithm. The rope is initialized along the edge of the sample (Figure 4C) and the energy is minimized as described in STAR Methods. The parameters of the rope have been balanced in such a way that the rope can pass over small sand-piles corresponding to artifacts, but not the tumor itself. They have also been balanced so that the rope does not track every small dent of the tumor outline to avoid unnecessary over-fitting. Video S1, from which a series of snapshots are shown in Figure 4C, demonstrates the active contour algorithm starting at the border of the sample and finally reaching an equilibrium position circumventing what it considers to be the tumor. Figure 4D show the final equilibrium position of the rope for three representative examples of different tumor types using different models together with the active contour algorithm to identify the tumor borders. We refer the reader to Table S5 for results on all tumors using the three different models.

Figure 4.

Automatic skin tumor delineation

Results after performing sand-piling of a melanoma skin tumor represented as (A) a 2D image and (B) a 3D contour plot, where in the latter the difference in height becomes evident.

(C) Snapshots of the active contour algorithm identifying the tumor borders by shrinking a rope from the sample borders toward the center where the tumor is.

(D) Results obtained of the tumor borders of three different skin tumor types using different algorithms to generate the prediction maps. The scale bars all represent 10 mm.

Comparison to histopathology

During histopathological analysis, we track the orientation of the cross-section cuts in relation to the sample, as well as the location at which the cross-section used to make the diagnosis is taken from. These are indicated with a vertical line as shown in Figure 4D. These are then the locations at which we extract the model predicted tumor widths in order to compare to histopathological findings. Figure 6 demonstrates the correlation between all tumor widths obtained with the three models: MLP (Figure 5A), CNN (Figure 5B) and MLP with MCR-ALS (Figure 5C). For each model, the Pearson correlation coefficient and relative mean squared error (MSE) were calculated. The relative MSE was used rather than the standard MSE since the tumors vary in size. The correlation coefficient for all three models is high, however, the tumor widths correlate differently depending on the model. This makes sense in light of the results demonstrated in Figure 3 where different prediction maps of different tumor types depict significant variations depending on which spectral component is used to contrast the spectral changes.

Figure 6.

Model performance on different spectral regions

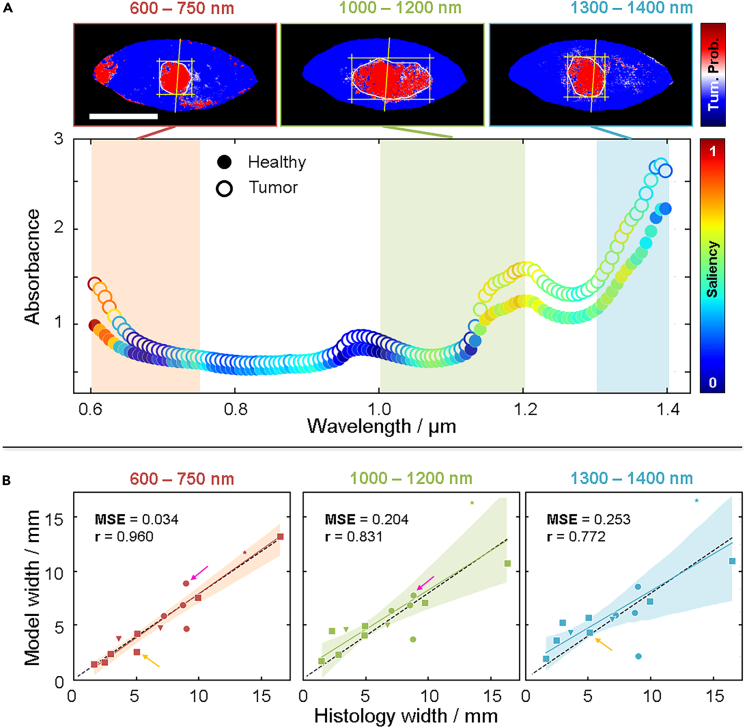
(A) Spectra taken from a BCC sample where the healthy tissue (solid markers) and tumor (hollow markers) are plotted with color-coding representing the saliency between 0 (blue) and 1 (red). Prediction maps are generated by reducing the spectral ranges used for the MCR-ALS generation of spectral components into three ranges: 600 nm–750 nm (red shaded area), 1000 nm–1200 nm (green shaded area), and 1300 nm–1400 nm (blue shaded area). See Figure S13 for the saliency for all tumors.

(B) Correlation plots for all tumors generated from prediction maps using the different spectral ranges where the spectral range between 600 nm–750 nm yields an overall improved correlation. The colored arrows indicate samples that actually improve in the model prediction width in the other two spectral ranges, although the overall correlation is worse. See Table S5 for numerical values of predicted and measured widths.

Figure 5.

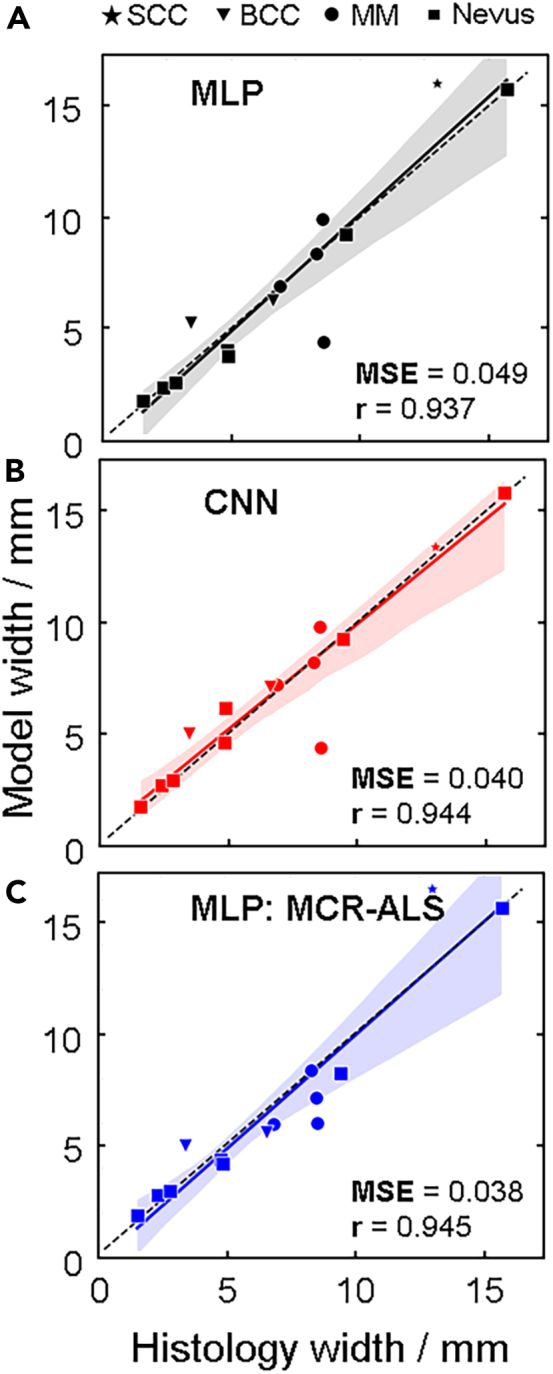
Model performance

Comparison between the histopathologically determined tumor widths and those obtained by (A) MLP, (B) CNN, and (C) MLP combined with MCR-ALS. In each panel, the Pearson correlation coefficient (r) is calculated and visualized with a solid and colored trace, where the black dashed trace indicates the ground truth. The relative mean squared error (MSE) is calculated for all correlation plots. See Table S5 for numerical values of predicted and measured widths.

Impact on model by using different spectral ranges

To assess the importance of different spectral ranges when classifying the pixels, we calculated the saliency (see STAR Methods), which is a measure of how the output changes when the different input features are subjected to perturbations. The larger change in output for an input perturbation, the more importance, and higher saliency, the input has. Figure 6A shows a representative example of a BCC tumor sample where the spectra of healthy tissue and tumor are plotted with each data point color coded according to the saliency. The saliency is, naturally, the same for each spectral channel for the healthy tissue and tumor pixels. Since this is a binary classification task, the same features that are important to classify a pixel as healthy are the same with the ones being important for classifying a pixel as tumor.

The spectral ranges that differ the most between tumor and healthy pixels generally seem to have the largest saliency. The saliency peaks in different spectral ranges depending on the tumor (see Figure S13 for all tumors), which is consistent with the results obtained in Figure 2. Considering this, we trained the three models again, but this time only using selected spectral ranges: 600 nm–750 nm, 1000 nm–1200 nm and 1300 nm–1400 nm. The three images in Figure 6A show how the resulting prediction maps obtaining the tumor borders for this BCC tumor change depending on the spectral range used by the MLP (see Figures S10–S12 for all tumors). Figure 6B shows how the correlation between the histology tumor width and model tumor widths change for all tumors depending on the spectral range used. While the 600 nm–750 nm spectral range yields an overall improved fit, demonstrated by a higher correlation coefficient and lower MSE, we note that this is again not the case for all tumors, which we show with the colored arrows that highlight some tumors that in fact improve when different spectral range are used. It is clear that the models pick up some different features depending on the spectral ranges and that the features are combined when using the full range. However, it is also apparent that each of the ranges contains enough information to naïvely find the tumors.

Until now we have demonstrated that both the type of model used to generate a prediction map, and the spectral range used as a foundation for the pixel classifier, will yield different results depending on the tumor type. As such, there are several parameters that can be tweaked in order to optimize the algorithm for a particular tumor. While all possible parameters for each tumor type are far too many to be explored at this stage, we demonstrate that tweaking some parameters in regard to both model type and spectral range can significantly change the overall correlation and MSE of all tumors (see Figure S4), which points to a variation of spectral features for different tumors being captured across the broad spectral range that is used.

Discussion

A tumor, by definition, constitutes a deviation in the molecular composition from healthy tissue. Our approach to skin tumor segmentation is therefore rooted in the fact that a change in the atomic or molecular composition translates into a change in the spectroscopic signature.³⁶ The limitation, however, is whether the spectroscopic change can be detected, which depends on both instrument capability and the molecular complexity of the examined tissue. While the molecular composition of healthy tissue is extremely complex and molecularly heterogeneous,³⁷ a tumor adds an unknown degree of molecular complexity. Additionally, since tissue properties are to an extent unique to each individual, it becomes challenging to develop one method accounting for all irregularities.³⁸ This work presents a solution focused on maximizing the amount of spectral information extracted, which in turn drives the analysis to identify spectral disparities between healthy tissue and tumor within the same individual.

Addressing a clinical need

A recent review addressing the challenges with employing ML for medical imaging highlights the lack of real clinical progress despite an increasing number of algorithms emerging aimed to facilitate more efficient diagnoses.³⁹ The need for labeled ground truth images in CNN-based skin tumor delineation, for example, is in reality unrealistic for clinical implementation, which is not only due to the need for histopathology, but also the potential systematic bias tied to the person doing the labeling.⁴⁰ This work is derived from the need to improve current diagnostic practice, which is why we develop an approach not relying on labeled images.

Circumventing dataset bias

A common hurdle for ML implementation is dataset bias, where the training data is not representative of the target population.⁴¹ The training data generated in our model certainly varies from patient to patient, however, this variation does not impede the performance. This is because the model does not identify spectral features that are similar between patients, but rather identifies how the spectrum representing tumor deviates from healthy tissue within the same patient. The training data and a trained model is therefore only applicable to the patient in which it is acquired, which may seem limiting. However, our fundamentally different approach automatically accounts for inter-individual variations,³⁸ which in fact increases its clinical applicability. Moreover, it may even find some utility in future tumor classification and differential diagnostics.⁴²

Spatial vs. spectral features for segmentation

In a recent review on different multispectral and hyperspectral spectroscopic approaches to various medical applications shows that most operate within the visible to near infra-red spectral range (400–1000 nm), with the number of spectral channels up to a 124.⁴³ Present work, to the best of our knowledge, employs the broadest spectral range (600–1400 nm) with the most spectral channels (235). Although the novelty of this work hinges on the fact that the spectral features, that are more closely tied to the molecular profile of the sample, drive the ML and segmentation algorithms, we stress that an abundance of spectral information provides additional opportunity in the spectral feature extraction. A recent report compared using spatial and spectral features for determining melanoma skin tumor borders,⁴⁴ although the spectral information was limited to only three channels in an RGB camera. Nonetheless, it was concluded that using the spectral information yielded the best results. With a broader and more resolved spectral range used in this work, more subtle spectral features can be identified, which should contribute to better differentiating between healthy tissue and tumor.

We also note that some considerations should be made in regard to the fact that a spectrum from a single pixel actually represents the interaction of light and tissue from a larger volume below. Understanding the extent to which this impacts the accuracy of the border estimation could require the use of Monte Carlo simulations, which extends beyond the scope of current work. However, we make the assumption that the expected error in tumor border identification due to this is still smaller than the obtained differences between the model and histopathology.

Adaptability of the ML algorithm

Besides the abundance of spectral information available for the analysis, the ML algorithm has several parameters that can be tweaked to optimize the accuracy of the tumor border determination. The large number of parameter settings yielding satisfying performance (Figure S4) indicates robustness of the algorithm. In our study, the tumor width correlation to histology changed for different tumors using the same set of parameters, and could be improved by changing the spectral range. This most likely reflects the expected changes in molecular profile between different tumors and patients, and shows that that the algorithm can be adapted to account for such changes. Some degree of consistency is certainly expected between skin tumors of the same type, however, we can at this stage not draw any conclusions in regard to this due to the limited dataset. We recognize that such conclusions would require not only a larger dataset representing multiple instances of every tumor type, but probably also adjustments for other patient-related variations such as age, skin type, smoking, and so on. An HSI system capable of generating an abundance of spectral information, coupled with a ML algorithm driven by spectral features has the potential to account for an increasing number of variables required for tumor border delineation.

Clinical impact

A careful and correct delineation of skin tumors prior to surgery would improve patient care by limiting the risk of non-radical excisions and subsequent re-operations, as well as sparing healthy tissue. In this study, hyperspectral imaging data from different skin tumor types was analyzed using ANNs to visualize the extent of the tumors with a clear unbiased distinction from healthy skin without data input about the final diagnosis. Since the presented skin tumor delineation does not require any input of the actual border or any spatial features, it has a more realistic potential for clinical implementation once some degree of reliability compared to histopathology can be determined through an extended clinical study. The only manual step of identifying the center of the tumor is a cheap and easy task so no clinical relevance is lost. Therefore, efforts to automate this step as well are postponed until more data are available. Within the framework of this study, a diagnosis of the tumor type based on spectral features was not possible due to the limited sample size, although previous studies suggest that classifying tumor type from regular dermoscopic images using ANNs is possible.⁴⁵ The capability of HSI to generate much larger amounts of spectral data than dermoscopy is promising for future tumor classification using the methods described in this study.

This study demonstrates the utility of extracting detailed spectral information from suspected skin tumors and surrounding healthy tissue using HSI and ML for determining skin tumor borders. Based on the notion that there must be a difference in the molecular composition between healthy tissue and tumor, we demonstrate how only a few spectra from sample regions representing healthy and skin tumor can be used to determine the skin tumor border. By tuning the parameters of the ML algorithm, as well as the spectral content that is used, we highlight the adaptability of our approach to skin tumors in different individuals, as well as types. The determination of the skin tumor border is driven by a comparison to healthy tissue in the same individual, and the fact that the results change depending on the spectral range that is used demonstrates that we not only detect inter-individual variability in the spectral content, but can adapt the analysis to account for it. Current work not only provides insight into the potential use for spectroscopy-guided ML to be employed in emerging skin tumor precision diagnostic, but may also have an impact on current skin tumor diagnostic practice with increased likelihood of radical excision while minimizing removal of healthy tissue.

Limitations of the study

A few limitations impact the results of the study. Primarily, we recognize the limited sample diversity and quantity. We do, however, emphasize that the study reports on a new approach for skin tumor delineation which can be directly applied to a larger sample set. Currently, the selection of the regions representing healthy tissue and tumor are manually selected. Prior to applying the analysis to a larger dataset, an algorithm that can automatically identify these regions would be useful. This could either be based on average spectral features or simply location in regard to the sample (i.e., borders vs. center). The adaptability of the proposed algorithm to account for inter-individual variations is a feature with promising clinical implications; however, we recognize that when developed on the basis of a relatively low and not so diverse sample set, its full potential is not revealed. While we are confident that a larger dataset strengthens the outcome of the study, we understand that it will likely present certain pitfalls that need to be addressed.

In regard to the data acquisition, a single instrument was used and the reproducibility of the results when the algorithms were applied to data generated by another similar instrument was not tested. We assume the accuracy of tumor size in comparison to histopathology would be affected in the event that either spatial and spectral resolution are reduced. A careful study would be of value to assess the extent these parameters, as well as the signal-to-noise ratio, would affect the outcome of the current study.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
MATLAB (version 2017b)	Mathworks	http://www.mathworks.com
Python (version 3.7)	Python Software Foundation	https://www.python.org/
Tensorflow (version 1.14)	Python Package	https://www.tensorflow.org/
Biological samples
Human tissue	This work	N/A

Resource availability

Lead contact

Further information and requests should be directed to the lead contact Aboma Merdasa (aboma.merdasa@med.lu.se).

Materials availability

This study did not generate new unique reagents.

Data and code availability

The hyperspectral imaging data used in this work, as well as code used to generate the results, can be made available upon request.

Experimental model and study participant details

Ethics

The study was approved by the Ethics Committee at Lund University, Sweden (2022-04900-02). The research adhered to the tenets of the Declaration of Helsinki as amended in 2013. Prior to surgery, all the patients participating in the study were given verbal and written information about the study and the voluntary nature of participation. All patients gave their informed written consent.

Subjects

21 patients were included in the study with a total of 22 skin tumors suspected of melanoma, basal cell carcinoma (BCC), or squamous cell carcinoma (SCC). One of the patients had 2 skin tumors. After histopathological diagnosis, three samples were excluded from analysis since diagnosis revealed either sun damaged skin or bluish colored skin with no measurable lesion sizes. One sample was removed due to the small size and difficulty in handling during ex vivo acquisition. On the Fitzpatrick scale, all samples ranged from skin type I (pale complexion) to type VI (dark complexion), with a vast majority being of skin type II. See Table S1 for details on the samples included for analysis in the study. Ages are reported as a range spanning 10 years (i.e., 60’s includes all ages between 60 and 69 years).

Examination and measurement procedure

All suspected tumors were excised under local anesthesia by experienced dermatologists, using standard local excision recommendations. They were then placed in isotonic saline for a short period of time before being imaged with HSI. After imaging, the tumors were placed in formaldehyde and sent for histopathological examination.

Method details

Hyperspectral imaging

A hyperspectral image can be generated in a few different ways. For a detailed description of the different HSI techniques see.²⁶ However, we describe here the essence of what separates the various techniques. HSI aims to acquire information in both the spectral and spatial domains, which is achieved over a period of time (temporal domain). This establishes a three-way trade-off in instrument design, where different methods maximize the information gained in one domain over another. Scanning the spectral domain in time ensures integrity in the spatial domain at the expense of integrity in the spectral domain. Scanning in the spatial domain, ensures spectral over spatial integrity. Snapshot HSI methods are emerging where a hyperspectral image is generated instantaneously, although this comes at the expense of sacrificing information in the both the spectral and spatial domains. One technique is not better than another, rather, the HSI approach should be suited for the type of sample that is imaged, and the measurement domain where data integrity is most critical.

As will be emphasized throughout this work, spectral information will be of primary importance, which is why we opt for a so-called ‘spatial scanning’ HSI technique. These techniques operate by imaging a single column (detection line) of the object onto a sensor array after having passed through some spectrally dispersive medium. At a cost of reducing the image to only one spatial dimension, complete spectral information is acquired for all points along the measured line. Thereafter, either the sample or the camera slightly moves to capture information from an adjacent line of the object (Figure S7A). The hyperspectral camera was custom-built in the HySpex model series (Norsk Elektro Optikk, Oslo, Norway). A halogen lamp with a peak temperature of 2900 K was used for excitation, which yielded a broad spectral emission profile with a peak wavelength at 1000 nm. A fiber-coupled light guide with a rod lens was used to generate an excitation line at the sample. The dimensions of the excitation line were significantly larger than the detection area in order to minimize intensity variations. The optical output power of the light source is 100 W, from which an estimated 1 W reaches the sample surface. This is accounting for a fiber NA of 0.57 and that the distance to the sample is 10 cm. With an excitation area of 10 cm², the effective flux is 0.1 W/cm², which is similar to solar flux. The sample surface therefore heats up slightly, but induces no damage.

The camera uses a combination of a Si and InGaAs detectors, which together with the excitation effectively enables VIS-NIR-SWIR spectral sensitivity in the range between 600 nm–1700 nm. The spectral bandwidth is divided into 322 spectral bands, yielding a spectral resolution of approximately 3.5 nm. A camera objective with an angular field-of-view of 16° and working distance of 75 mm was used resulting in an effective swath width of 32 mm. In combination with the sensor having 640 pixels, a spatial resolution of 50 μm is obtained. The exposure time of the camera ranges between 10 and 90 ms, which means that a sample 5 cm in length takes up to 90 s to measure.

Reference measurements, normalization and absorbance calculations

Push-broom HSI cameras require calibration of the scan speed in relation to the exposure time in order to avoid errors of either acquiring multiple spatially overlapping spectra (scan speed too slow in relation to exposure time) or spectra from regions that are separated by a distance larger than the effective pixel size (scan speed too fast in relation to exposure time). In order to optimize the scan speed for different exposure times, we imaged a round object and adjusted the scan speed to reproduce an image where the object appeared round, as opposed to an ellipse. This procedure was done for 10 different exposure times and tested for reproducibility in repeated measurements before setting the scan speed calibration.

Prior to imaging, an internal shutter is inserted in front of the camera and a signal is recorded at the specified exposure time which is thereafter subtracted from all recorded images. This accounts primarily for the readout noise generated by camera. To account for the ambient background light, a measurement is made without the excitation light source on (I_Bkg(λ)). A white reference signal is obtained by scanning across a Spectralon white reference (WS1, Ocean Optics) that is placed in the scanning path after the sample as demonstrated in Figure S7A. Thus, the white reference and the sample measurement are obtained in the same measurement. A white reference spectrum (I_Ref(λ)) is obtained in every pixel along the detection line to account for potential intensity variation perpendicular to the scan path. Thereafter, the spectrum (I(λ)) in every pixel in the image is normalized against the corresponding white reference spectrum obtained in the same horizontal line to ensure that the correct intensity from the light source is used. Thereafter, absorbance as a function of wavelength (A(λ)) can be calculated according to,

$$A\left(\lambda \right)=-{\mathit{log}}_{10}\left(I\left(\lambda \right)/I_{\text{Ref}}\left(\lambda \right)\right)$$ (Equation 1)

Pre-processing: Non-sample pixel removal & spectra extraction

Once the data has been normalized according to Equation 1 above, background pixels, i.e., pixels not part of the excised sample, needed to be removed. We based this analysis step on the notion that the most significant spectral variation in the entire image is between the sample and non-sample (background). We performed a principal component analysis (PCA) on all the pixel spectra. Using only the first two principal components, we clustered the pixels using HDBscan^46,47 with min_cluster_size = 500 and otherwise the standard parameters. Smaller clusters were merged until two clusters remained. Since the hyperspectral images were produced with the sample centered, the background cluster could automatically be identified as the one containing the corner pixels, and the remaining central cluster as the sample. Thereafter, all the background pixels were masked away (removed) and were not used in any of the subsequent analyses.

Multivariate curve resolution – Alternating least squares

To aid in visualization of the high-dimensional spectral data, MCR-ALS (multivariate curve resolution – alternating least squares) analysis³⁰ was applied to reduce dimensionality in an intuitive manner. All tumor hyperspectral images were merged into one composite hyperspectral image, then decomposed into a sum of eight spectra-like components, with their contributions to each pixel in the image being all non-negative. The number of components was chosen to capture most of the spectral variability without generating similar-looking or noise-dominated components. This spatial pattern was then defined by just eight numbers that may be visualized directly but also present an alternative to using the full spectra in subsequent analysis steps. In essence, this step generates a set of spectra that together capture the most common spectral features of all tumors combined. With this information, one can assess the extent to which each pixel spectrum for a particular tumor can be represented by each of these spectra, which assists in the visualization of potentially deviating tissue properties (i.e., tumor).

Computational framework

Machine learning is a type of artificial intelligence that uses training data to automatically improve computer algorithms, in order to make predictions. A model, for example an ANN or a support-vector machine (SVM), is used to train the system on a set of limited data, allowing the system to generalize to, and predict outcome of, unseen data.

We have devised a computational framework which predicts superficial shape and size of a skin tumor from a hyperspectral image. The structure of the data analysis framework, together with the data acquisition and pre-processing, is shown as a flowchart in Figure S7B. A single ANN model instance is only trained on the data from one single patient sample. With this strategy, no patient-to-patient biases are introduced. The ANN is trained on the spectra of individual pixels from a selection of pixels with known tumor/non-tumor state. We emphasize that no spatial features are needed or used to train the ML algorithm, rather, it is the spectral features that are used. The trained ANN is then used to predict whether the rest of the pixels in the same image belong to either tumor or non-tumor (presumed healthy tissue) regions. This generates a prediction map for the tumor which serves as input for a two-step segmentation algorithm (described below).

The total framework, consisting of a combination of an ANN and a segmentation algorithm, predicts the size and delineation of the tumor and does not rely on any prior knowledge of tumor borders. It only uses the information contained in one single HS image. Thus, patient variability, e.g., skin complexion, does not provide bias to the predictions. Neither is the framework restricted to certain types of tumors since only the spectral variation between the same patient’s healthy tissue and tumor is utilized. All details are found in the supporting information (SI), while we provide below only the necessary aspects needed for understanding the presented results.

Machine learning

Artificial neural networks

We developed three different machine learning models to classify individual pixels from individual images as either “healthy tissue” or “tumor” solely based on spectral information. As ANNs, we used a multilayer perceptron (MLP) trained on all spectral components between 600 nm and 1400 nm (235 channels), an MLP trained on the MCR-ALS decomposition (eight components; see STAR Methods) of the spectra, and a one-dimensional convolutional neural network (CNN) trained on all the spectral components between 600 nm and 1400 nm (see STAR Methods and Figure S5 for details on model parameters and training procedure). All models were developed using Python 3.7 and Tensorflow 1.14.

A separate model instance was trained for each tumor sample. We selected pixels from the center of the tumor and from regions of the sample likely representing healthy tissue and then used their spectra as training data for supervised training. To mitigate any artifacts resulting from the scanning direction of the camera, we chose two areas of healthy pixels, one from each side of the tumor along the scanning axis. The sizes of the two healthy areas were chosen so that they in total contain approximately as many pixels as the tumor area to ensure balanced training datasets (see Figure S2). An ensemble of classifiers was trained for each model and tumor sample using K-fold cross splitting with K = 5. The trained ensembles predict the probability of each pixel representing healthy tissue or tumor, where the average of the predicted value for each ensemble member is used as the ensemble prediction. A threshold of 0.5 was used to differentiate between pixels classified as healthy tissue and tumor (see STAR Methods – Detailed method descriptions for further information). This procedure was repeated, training a new model instance for each tumor sample.

Saliency

The saliency $S_k$ was used as a feature importance measure for each feature k. The saliency for a feature is defined as the change of the output value as response to a change in the input feature, averaged over all patterns,

$$S_k=\frac{1}{N}\sum _{n=1}^N\left|\frac{\partial y\left(x_n\right)}{\partial x_{nk}}\right|$$ (Equation 2)

where y is the output value given input pattern x_n and N is the number of patterns.

Segmentation

An active contour segmentation algorithm³⁵ was used to determine the tumor delineation. In the algorithm, an active contour, here referred to as a rope, tracks the outline of an object in an image by minimizing an energy function. The position of the rope can parametrically be described as $r\left(p\right)=\left(x\left(p\right),y\left(p\right)\right)$ with $r\left(0\right)=r\left(1\right)$ meaning that the rope is a closed loop. The general energy function of the rope consists of internal and external energy contributions as well as a constraint contribution.

$$E_{\text{rope}}=\underset{0}{\overset{1}{\int }}\left(E_{\text{internal}}\left(r\left(p\right)\right)+E_{\text{external}}\left(r\left(p\right)\right)+E_{\text{constraints}}\left(r\left(p\right)\right)\right)ds$$ (Equation 3)

Here, we use

$$E_{\text{internal}}=\beta \left(p\right){\left|r_{pp}\left(p\right)\right|}^2+\gamma \left(p\right){\left|\overline{r}\left(p\right)-r\left(p\right)\right|}^2$$ (Equation 4)

$$E_{\text{external}}=\omega \left(p\right)s\left(p\right)$$ (Equation 5)

and

$$E_{\text{constraints}}=0$$ (Equation 6)

where $\alpha \left(p\right),\beta \left(p\right)$ and $\omega \left(p\right)$ are hyper-parameters and s is the sand-pile function described below (see STAR Methods – Detailed method descriptions for computational details).

The sand-pile function $s\left(p\right)$ replaces the pixel intensity of standard active contour segmentation in the external energy. A sand-pile is constructed on the prediction maps to give each pixel classified as tumor a spatial context, i.e., if a pixel is located in the center or edge of the tumor. Conceptually, sand-piles are constructed by pouring sand on the pixels classified as tumorous. As the pixels classified as healthy tissue act as sinks, a sand-pile will emerge on the tumor. The height of the resulting sand-pile is greater in the center of the tumor. The rope in the active contour algorithm is then tightened around the sand-pile. We refer the reader to STAR Methods – Detailed method descriptions for supplementary mathematical and computational details.

Evaluation (statistical) methods

To evaluate the models, the histopathological measurements of the tumor widths were compared to the model predicted widths. The mean subtracted Pearson correlation was calculated, as well as the relative mean squared error (MSE), defined by

$$MSE=\frac{1}{N}\sum _{i=1}^N{\left(\frac{y_i}{x_i}-1\right)}^2$$ (Equation 7)

where $x_i$ is the histopathological width and $y_i$ is the model predicted width for sample $i$ and $N$ is the number of samples. We consider the model predictions with higher Pearson correlation coefficient and lower MSE to be the better ones.

Detailed method descriptions

Data description

The dataset consists of 18 samples. Table S2 lists the number of sample pixels (i.e., those pixels that were separated from the background pixels as described in STAR Methods above), and the number of pixels in the chosen training dots for tumor and healthy tissues respectively. Also the tumor widths measured by the pathologists are listed. The defined training dots are also displayed for all samples in Figure S2.

Training procedure

One model instance was trained for one tumor sample. The model was trained using data from the training regions defined in Figure S2. Once the model instance was fully trained, it was used to predict the class of every pixel in the same image, yielding a prediction map for that sample.

The hyperparameter search was conducted with a grid search where network architecture, learning rate and batch-size were changed, see the used values in Table S3. For the MLPs the hyperbolic tangent (tanh) was used as activation function, while rectified linear unit (ReLU) was used as activation function for the CNNs. All the models had one output node with the sigmoid function as output activation function. The binary cross-entropy was used as cost function and the models were optimized using Adam.⁴⁸ The MLPs were trained for 100 epochs and the CNNs for 20 epochs. It is important to note that the CNNs are 1-dimensional and the convolution operation is performed over the spectral range and is only taking 1 pixel as input at the time. The pixels in the training dots (Table S2; Figure 4A) were randomly divided into 5 equally sized parts. Each member of the ensemble used a different partition as validation set.

Validation procedure

Model selection could not be performed the conventional way by picking the model with the best performance on the validation performance since most models achieved perfect accuracy (1.0) and loss (0) on both training and validation data (Figure S3). This is due to the simplicity of the classification of the blue and red regions in Figures 2A and 2B, which corresponds to the training areas (blue and red dots) in Figures 4A and S2. However, the challenge of classifying tumor border pixels, which are outside these regions, remains. Model validation aiming to do model selection at this stage is not feasible since we do not have labels for the border pixels. The only measured data we can validate the models against is the histopathological tumor widths. Hence, we first need to predict the tumor widths with all the potential model settings before model selection can be performed.

For each model setting, the Pearson correlation coefficient and relative MSE (Metods) were calculated over all the tumor sample and were plotted against each other (Figure S4). Each dot represents a model setting in the scatterplot. A model setting is considered to perform better the higher the correlation and the lower the MSE are, corresponding to the top-left corner of the plot. The models showed results for are the top performing model setting of each model type: MLP, CNN and MLP: MCR-ALS. The details of the chosen models are shown in Figure S5.

Active contour segmentation

Computationally, the rope consists of a set of $n\left(t\right)$ points which are initially located along the sample border with one point per pixel. The position of the rope is iteratively updated where, at each time-step, each point is moved to the neighboring pixel which minimizes the energy function locally. The resolution of the rope is adaptive; the number of points comprising the rope changes. If the distance between two neighboring points of the rope gets more than 10 pixels apart, a new point is added between them. If two neighboring points get closer than 2 pixels apart, they are merged. During the first 30 steps, only the gravitational term contributes to the energy function to make sure that the rope does not get stuck on the sample border. The algorithm is terminated if the rope is identical after an update, or if a maximum number of updates has been made. The final position of the rope is considered as the tumor delineation. See Table S4 for the parameters used.

Sand-piles

This method can be formalized into a matrix problem as follows. All the pixels has a predicted probability for being tumorous $p_i$. Those with probability $t_i=\mathbb{P}\left(p_i\right)\ge 0.5$ are considered to be tumorous. These are collected into a vector

$$\mathit{t}=\left(t_1,t_2,\dots ,t_n\right)\text{,}$$ (Equation 8)

where $n$ is the number of pixels classified as tumorous. Only directly adjacent pixels are considered as neighbors, which can be summarized in a connectivity matrix

$$\mathbb{C}=\left(\begin{array}{cccc}1& w_{12}& \cdots & w_{1n}\\ w_{21}& 1& \cdots & w_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ w_{n1}& w_{n2}& \cdots & 1\end{array}\right)\text{,}$$ (Equation 9)

where

$$w_{ij}=\{\begin{array}{cc}1& \text{if}j\in \text{neigh}\left(i\right),\\ 0& \text{otherwise}.\end{array}$$ (Equation 10)

We want to construct a sand-pile

$$\mathit{s}=\left(s_1,s_2,\dots ,s_n\right)\text{,}$$ (Equation 11)

where each element represents the height of the sand-pile on the corresponding pixel. During each iteration in the sand-pile process, a fraction of sand $b$ is moved from each pixel onto its neighbors. This is formalized with the update matrix

$$\mathbb{U}=\mathbb{C}-4b\mathbb{I}=\left(\begin{array}{cccc}1-4b& w_{12}& \cdots & w_{1n}\\ w_{21}& 1-4b& \cdots & w_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ w_{n1}& w_{n2}& \cdots & 1-4b\end{array}\right)\text{,}$$ (Equation 12)

where $\mathbb{I}$ is the unit matrix. No matter if a tumorous pixel has four or less tumorous neighbors, $4b$ is removed, i.e., the healthy pixels act as sinks. During one iteration of the sand-pile process, a unit of sand proportional to $t_i$ is also placed on each pixel $i$. One iteration can be summarized as

$${\mathit{s}}^{\prime }=\mathbb{U}\mathit{s}+\mathit{t}\text{,}$$ (Equation 13)

where ${\mathit{s}}^{\prime }$ is the updated sand-pile. This can equivalently be expressed with an augmented update matrix and the sand-pile vector augmented with “1”:

$$\mathbb{M}=\left(\begin{array}{c}1\\ \mathit{t}\end{array}|\begin{array}{c}0\dots 0\\ \mathbb{U}\end{array}\right)=\left(\begin{array}{ccccc}1& 0& 0& \cdots & 0\\ t_1& 1-4b& w_{12}& \cdots & w_{1n}\\ t_2& w_{21}& 1-4b& \cdots & w_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ t_n& w_{n1}& w_{n2}& \cdots & 1-4b\end{array}\right)\text{,}$$ (Equation 14)

and

$$\mathit{v}=\left(\begin{array}{c}1\\ \mathit{s}\end{array}\right)\text{,}$$ (Equation 15)

i.e.,

$${\mathit{v}}^{\prime }=\mathbb{M}\mathit{v}\text{.}$$ (Equation 16)

The 1 in the augmented vector $\mathit{v}$ acts as a source together with the augmented column in $\mathbb{M}$. The zeroes in the top row are needed to not make the inflow of sand dependent on the amount of sand existing.

By repeatedly multiplying $\mathbb{M}$ with $\mathit{v}$ a large number $N$ times, a stable state will be reached. We initialize the process without a pre-existing sand-pile

$$\begin{array}{c}{\mathit{v}}^{\left(0\right)}={\left(1,0,\dots ,0\right)}^T{\mathit{v}}^{\left(1\right)}=\mathbb{M}{\mathit{v}}^{\left(0\right)}{\mathit{v}}^{\left(2\right)}=\mathbb{M}{\mathit{v}}^{\left(1\right)}=\mathbb{M}\left(\mathbb{M}{\mathit{v}}^{\left(0\right)}\right)={\mathbb{M}}^2{\mathit{v}}^{\left(0\right)}⋮{\mathit{v}}^{\left(N\right)}=\mathbb{M}{\mathit{v}}^{\left(N-1\right)}=\underset{N\text{times}}{\underbrace{\left(\mathbb{M}\mathbb{M}\right)}}{\mathit{v}}^{\left(0\right)}={\mathbb{M}}^N{\mathit{v}}^{\left(0\right)}\text{.}\end{array}$$ (Equation 17)

Now, the problem has been reduced to finding ${\mathbb{M}}^N$ for $N\to \infty$. A straight-forward strategy would be to diagonalize $\mathbb{M}$ with $\mathbb{M}=\left({\mathbb{P}\mathbb{D}\mathbb{P}}^{-1}\right)$ and find ${\mathbb{M}}^N$ by

$$\mathbb{M}={\left({\mathbb{P}\mathbb{D}\mathbb{P}}^{-1}\right)}^N=\stackrel{N\text{times}}{\overbrace{\left(\mathbb{P}\mathbb{D}\underset{\mathbb{I}}{\underbrace{{\mathbb{P}}^{-1}\left)\right(\mathbb{P}}}{\mathbb{D}\mathbb{P}}^{-1}\right)\dots \left({\mathbb{P}\mathbb{D}\mathbb{P}}^{-1}\right)}}\text{,}$$ (Equation 18)

but this is computationally heavy. A more practical way which requires just a few computations is to stepwise square $\mathbb{M}$, i.e.,

$$\begin{array}{c}{\mathbb{M}}^2=\mathbb{M}\mathbb{M}\\ {\mathbb{M}}^4={\mathbb{M}}^2{\mathbb{M}}^2\\ {\mathbb{M}}^8={\mathbb{M}}^4{\mathbb{M}}^4\\ ⋮\end{array}$$ (Equation 19)

It does not require many iterations to obtain a large enough $N$. We iterate 10 times, yielding $N=1024$.

Quantification and statistical analysis

All quantification and analyses were performed as described in the STAR Methods.

Published: April 1, 2024