髂动脉的流-固耦合模型及脉搏波传播特性分析

Abstract

本文研究髂动脉分叉几何特性对脉搏波传播特性的影响，应用多物理场分析软件，分别建立了基于髂动脉的直管分叉和曲管分叉流-固双向耦合有限元分析模型，对比分析了血管分叉角度对脉搏波传播特性的影响。研究发现，分叉几何特性对髂动脉脉搏波传播有明显影响，在一个心动周期内，这两种模型预测的压力脉搏波和速度脉搏波幅值在血管分叉前一致度较高；分叉后，曲管分叉模型预测的脉搏波幅值较低、压降小，更符合人体实际情况。另外，分叉点处伴随着血管壁的应力集中现象，速度脉搏波幅值出现瞬时增加，这与分叉部位容易出现动脉狭窄和硬化等现象相一致。本文的初步研究结果将为脉搏波形用于动脉疾病的诊断提供一定的参考。

0. 引言

在心脏周期性收缩和舒张过程中，血液压力、血流速度和血流量的脉动以及血管壁的变形在血管系统中的传播统称为脉搏波^[1]。脉搏波蕴含着丰富的人体生理和病理信息^[2]，临床上应用于评估高血压、冠心病等患者的心血管状况^[3-6]。人体动脉血管的几何结构多为带有弧形的分叉型，比如髂动脉具有明显的分叉特征，在分叉处极易血流受阻，发生病变，导致动脉粥样硬化、血栓形成等^[7-9]。髂动脉位于人体腹腔，发生病变时不易被发现，严重时会引起动脉破裂^[10]，导致大量出血，短时间内即可危及生命。因此，研究髂动脉的血流动力学及其脉搏波传播特性，对其病变的早期预防、诊断和治疗具有重要意义。

关于分叉血管血流动力学和脉搏波的研究，已有一些研究成果。譬如，Perktold等^[11-12]对颈动脉血流动力学进行了数值模拟，发现颈动脉的分叉角度对其内部血液流场有很大影响，以及分叉角减小是颈动脉发生病变的原因之一。王青等^[13]对出口流量分配比为6:4、7:3、8:2的分叉血管血液流场进行了三维数值模拟，重点分析了流量分配比和分叉几何特征对血管局部血液动力学的影响。Kotmakova等^[14]对髂动脉的血流也进行了数值分析，发现髂动脉的弹性对其血液流速以及血管内壁面应力有重要影响，动脉弹性下降会导致血管壁面应力增大。于风旭等^[15]根据实验用颈动脉分叉模型，建立了颈动脉分叉有限元分析模型，发现分叉动脉更易发生动脉粥样硬化疾病。Abbasi等^[16]通过影像技术研究了肺动脉分叉角对肺动脉栓塞疾病的影响，发现了肺动脉分叉角减小是诊断肺动脉栓塞的一个影像标准。彭红梅等^[17]分析了血流动力学特性的突变对双分叉动脉血管病变发展的影响，发现双分叉动脉主支管病变极易导致分支管分叉处粥样斑块病变。另外，张丽娜等^[18]将脉搏波信号用于动脉硬化患者的无创检测，提出了通过分析时域脉搏波信号辅助心血管疾病诊断的方法。然而，关于髂动脉分叉处分叉角对其血流动力学的影响和脉搏波传播特性的分析，尚未见报道。

因此，本文计及血液粘性和可压缩性，分别建立髂动脉的直管分叉和弯曲管分叉双向流-固耦合分析模型，通过对比研究血管分叉对血液流场和脉搏波传播速度的影响，探究髂动脉分叉角度与脉搏波传播特性及血管壁损伤的关系。本文初步研究结果或可为髂动脉无创检测的新方法提供理论指导，对髂动脉分叉前后病变的早期预防、诊断和治疗具有重要意义。

1. 髂动脉分叉血管的双向流-固耦合分析模型

1.1. 生物力学几何模型构建

对于人体髂动脉分叉段，在动脉无特殊病变的情况下，本文视血管壁为薄壁管，只考虑血管壁外膜参数，根据如文献[19-20]所述的人体髂动脉几何尺寸，选取髂动脉分叉血管几何模型参数，如表1所示，其中，D₀、h₀、L₁、L₂ 分别为血管内径、壁厚、分叉前轴线长度和分叉后轴线长度，并称D₀/h₀为径厚比，拟构建髂动脉分叉几何模型。

表 1. Parameters of vascular geometric model.

血管几何模型参数

参数	D0/mm	h0/mm	D0/h0	L1/mm	L2/mm
取值	8.6	0.6	14.33	200	200

为研究分叉角度对脉搏波传播的影响，暂不考虑髂动脉的特殊结构以及其分支，根据文献[21]对髂动脉的解剖分析，髂动脉单侧分叉角范围为20°～30°，由于分叉后动脉的弯曲对其内部的血流场有着重要影响，因此分别建立单侧分叉角α为：20°、25°、30°的直管分叉模型和曲管分叉模型，并进行对比，如图1所示。以直管中心为原点，模型关于yoz平面对称，红色、绿色区域分别表示血液和动脉壁。本研究选取直管分叉模型中的A₁、B₁、C₁，以及曲管分叉模型中的A₂、B₂、C₂作为监测点，分别位于髂动脉分叉前中点、分叉点、分叉管的中点。

图 1.

The diagram of bifurcated vessels geometric model

分叉血管几何模型示意图

1.2. 血流控制方程及动脉材料属性描述

本文设血液为绝热、可压缩的粘性牛顿流体，根据文献[22-24]，取血液的体积模量K_b=2.5 GPa，动力粘度为0.004 Pa⋅s^[25]，血液的体积压缩模量由血液密度ρ_b和压力p的函数关系描述，下标b指血液（blood），如式(1)所示：

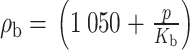1

根据文献[26]，血管壁用五参数超弹性本构关系，材料参数如表2所示，其中C₁₀、C₀₁、C₂₀、C₀₂、C₁₁分别为五参数超弹性本构关系中的各个参数，用于描述血管壁材料的刚度与非线性特性。

表 2. Five-parameter hyperelastic constructive material parameters for the vessel wall.

血管壁的五参数超弹性本构材料参数

参数	C10/kPa	C01/kPa	C20/kPa	C02/kPa	C11/kPa
数值	− 8 418	9 189	70 101	12 834	− 18 538

根据流体动力学理论，人体血液流动遵循质量守恒定律、动量守恒定律以及能量守恒定律。血液体积力矢量为F_b、流动速度矢量为v_b、流体压力为p。则，血液流动的质量、动量、能量等守恒方程如式(2)～(4)所示：

2

3

4

式中，t为血液流动时间，I为二阶单位张量，τ_b为血液粘性应力张量，E为系统能量，Q为单位质量由热辐射或内热源传给血液系统的热量，q为热通量。τ_b的表达式如式(5)所示：

5

式中，μ表示血液动力粘性系数。本文不考虑重力作用以及血液流动过程中的热量传递，且温度保持恒定，即F_b = 0，Q = 0，q = 0。因此，式(4)可进一步简化，如式(6)所示：

6

在内压p作用下，髂动脉血管壁薄壁模型的环向应力σ_θ和环向应变ε_θ分别如式(7)、式(8)所示：

7

8

式中，D为血管的外径，D₀为血管内径，h₀为壁厚。随着心动，髂动脉血管壁面压力发生变化，血管壁也发生变形；反之亦然。为此，血液与血管壁相接触面即为流-固耦合界面，在此双向流-固耦合有限元分析模型中，通过血液与血管壁的相互作用进行耦合分析。根据连续介质力学理论，在流-固耦合界面处，血液和血管壁应满足位移连续和应力连续边界条件，如式(9)所示：

9

式中，u_b、u_v分别表示血液和血管壁的位移矢量，σ_b、σ_v分别为血液和血管壁的应力矩阵，下标v表示血管壁（vessel）。

1.3. 实测脉搏波波形加载和边界条件

本研究在数值模拟中所加载的脉搏波波形数据采集于宁波市中医院，所采用的设备为脉诊仪（DS01-C，道生，中国）。招募的志愿者年龄在20～60周岁，受试者已签署知情同意书，所使用的脉搏波波形数据通过了宁波市中医院医学伦理委员会的批准采集并授权使用（编码:AF/SQ-01/03.1）。随机选取采集到的一位健康志愿者单周期脉搏波波形如图2所示，用于流-固双向耦合分析模型的加载，即入口为压力边界，出口也为压力边界，其值为40 mm Hg，计算时间步长为10⁻⁴ s。在双向流-固耦合分析模型中，本文设血液与血管壁内表面之间是无滑移层流流动，且血管壁的两端无轴向位移，外表面为自由壁面。血液和血管壁均采用四面体单元，经过网格无关性验证，选四面体单元为667 798个，网格节点为127 109个，误差为不超过2%。

图 2.

The pressure pulse wave of a healthy human

健康人体的压力脉搏波波形

在相同情况下，本文定义血液中两个相邻监测点的变化幅度∆_d，如式(10)所示：

10

式中，P_k（k = B₁、B₂、C₁、C₂）为监测点k的第一个波峰值，P_j（j = A₁、A₂、B₁、B₂）为监测点j的第一个波峰值，P_j0表示监测点j处，t = 0 s时的压力值。

1.4. 双向流-固耦合模型验证

为验证本文双向流-固耦合有限元模型，参照文献[27]中分叉血管单向耦合的有限元模型，建立几何模型，几何参数包括：分叉前直管的直径、长度分别为D₀ = 6 mm和L₁ = 10 mm，分叉管直径和长度分别为D₁ = 4.8 mm和L₂ = 7 mm，壁厚为h₀ = 0.4 mm。材料参数、边界条件与节1.2和1.3中一致。在入口边界处加载0.5 m/s的恒定速度波，网格类型为四面体，经网格无关性验证，可选总共网格数为19 563个，误差不超过2%。应用本文双向流-固耦合模型进行数值模拟计算，可得到血液流速、压力云图如图3所示。

图 3.

Cloud images of blood flow velocity and blood pressure

血液流速、压力云图

对比发现，本文双向流-固耦合模型计算的分叉血管中的血液流速、流线、压力的分布均与文献[27]中一致，其中血液最大流速均为0.6 m/s，且在血管分叉位置处，血液流速会出现突变。这种突变导致血流在分叉处形成一个低速度区域，同时分叉处会引发局部的涡流。在分叉处血液压力最大，这也说明了血管壁在分叉处出现应力集中现象。由此可见，本文血液-血管系统的双向流-固耦合有限元分析模型可用于分叉血管中的血流动力学分析，也可用来研究分叉血管中的脉搏波传播特性。

2. 髂动脉分叉几何特征对脉搏波传播的影响

根据前文构建的髂动脉双向流-固耦合有限元分析模型，本节探讨分叉角对髂动脉中脉搏波传播的影响，以压力脉搏波与轴向速度脉搏波分析为例。此三种分叉角度下，髂动脉压力脉搏波与轴向速度脉搏波传播情况分别如图4、图5所示。

图 4.

Pressure pulse wave curves

压力脉搏波曲线

图 5.

Velocity pulse wave curves

速度脉搏波曲线

由图4、图5可以看出，直管分叉模型和曲管分叉模型所预测的压力脉搏波和轴向速度脉搏波传播特点有明显差异，尤其是在分叉后的分支阶段。对于分叉角为20°的模型，直管分叉和曲管分叉模型所预测的压力脉搏波形，在分叉前直管段上，分别出现了3个波峰。大约过0.08 s后，相比分叉前的第一主波幅值，在分叉点处，监测点B₁、B₂的压力脉搏波的第一主波幅值分别降低约52.31%、38.83%。而在分叉段上，监测点C₁、C₂压力脉搏波的第一主波幅值分别降低约0.32%、47.89%；且曲管分叉模型下，分叉点处的主波波宽要比直管分叉模型下的小。对于直管分叉模型，在分叉前的直管段，分叉角度越大，第一主波压力峰值衰减越小；在分叉后，分叉角度越大，峰值衰减越大；如：在分叉前，分叉20°和30°的情形下，分别衰减52.31%、41.05%；在分叉后则分别衰减了0.31%、8.71%。而曲管分叉模型预测的结果反之。对曲管分叉模型，在分叉前的直管段，分叉角度越大，压力峰值衰减越大；对于分叉后的分支管，分叉角度越大，峰值衰减越小；如：在分叉前，分叉20°和30°的情形下，分别衰减38.83%、44.32%；在分叉后则分别衰减了47.89%、36.40%。

在分叉前，随着分叉角度的增加，轴向速度脉搏波幅值的变化不大，明显的变化是分叉前的轴向速度脉搏波形与分叉后的有较大不同，且分叉处速度脉搏波形振荡明显。分叉后轴向速度脉搏波的第一主波延迟约0.2 s，波形振荡少、平缓。对于第一主波峰，在分叉处，监测点B₁、B₂的峰值相对A₁、A₂的峰值增大；如：对分叉20°的情形，直管分叉模型与曲管分叉模型预测的结果，分别增大44.98%、54.79%。而在分叉管中，监测点C₁、C₂的峰值相对B₁、B₂的峰值降低；如：分叉角20°的情形下，直管分叉模型与曲管分叉模型预测的结果，分别降低24.31%、23.19%。

3. 结果与分析

3.1. 髂动脉压力脉搏波传播特性分析

根据压力脉搏波计算分析结果，监测点A₁～B₁、A₂～B₂、B₁～C₁、B₂～C₂的波速如表3所示。

表 3. Pulse wave velocity obtained from pressure pulse wave computing.

由压力脉搏波求得的压力脉搏波速

血管段	压力脉搏波波速/(m∙s−1)
	直管分叉20°	直管分叉25°	直管分叉30°	曲管分叉20°	曲管分叉25°	曲管分叉30°
分叉前直管	5.61	7.29	8.77	8.62	8.77	9.09
分叉管	47.62	19.61	15.15	2.99	3.14	3.21

由表3可知，直管分叉模型下，预测的血液在直管段传播时压力脉搏波波速要小于在分叉部分的压力脉搏波波速。且对不同的分叉角度，在分叉前，随着分叉角度增大，压力脉搏波波速随之增大，分叉30°情形的压力脉搏波波速较分叉20°情形的大约56.33%；在分叉后，随着分叉角增大，压力脉搏波波速随之减小。分叉30°情形的压力脉搏波波速较分叉20°情形的小约68.19%。曲管分叉模型下，预测的血液在直管段传播时压力脉搏波波速大于分叉后支管段上的压力脉搏波波速，并随着分叉角增大，压力脉搏波波速增大，在分叉前，分叉30°情形下的压力脉搏波波速较分叉20°情形的大约5.45%；在分叉后，分叉30°情形的压力脉搏波波速较20°情形的大约7.36%。

3.2. 髂动脉轴向速度脉搏波传播特性分析

根据速度脉搏波计算结果，可得出分叉血管中轴向速度脉搏波的传播速度，监测点A₁～B₁、A₂～B₂、B₁～C₁、B₂～C₂的速度脉搏波速如表4所示。

表 4. Velocity pulse wave velocity obtained from velocity pulse wave computing.

轴向速度脉搏波求得的速度脉搏波速

血管段	轴向速度脉搏波波速/(m∙s−1)
	直管分叉20°	直管分叉25°	直管分叉30°	曲管分叉20°	曲管分叉25°	曲管分叉30°
分叉前直管	12.99	13.16	13.26	4.20	4.46	4.76
分叉管	2.52	2.87	3.09	0.96	0.96	0.98

由表4可知，两种分析预测模型在分叉前的轴向速度脉搏波波速远大于分叉后的，髂动脉分叉20°时，直管分叉模型与曲管分叉模型分别预测的轴向速度脉搏波波速，分叉前比分叉后要大约80.60%、77.14%。这说明血管的分叉几何特性可明显降低速度脉搏波的传播速度。但不论是曲管分叉模型还是直管分叉预测模型，分叉20°情形时的轴向速度脉搏波波速最小。对于直管分叉预测模型，分叉前，分叉20°情形的比30°的小了约1.31%，而分叉后小了约18.45%；对于曲管分叉模型，在分叉前，分叉20°的情形的比30°的小了约11.76%，分叉后小了约2.04%。

3.3. 髂动脉中的应力场分析

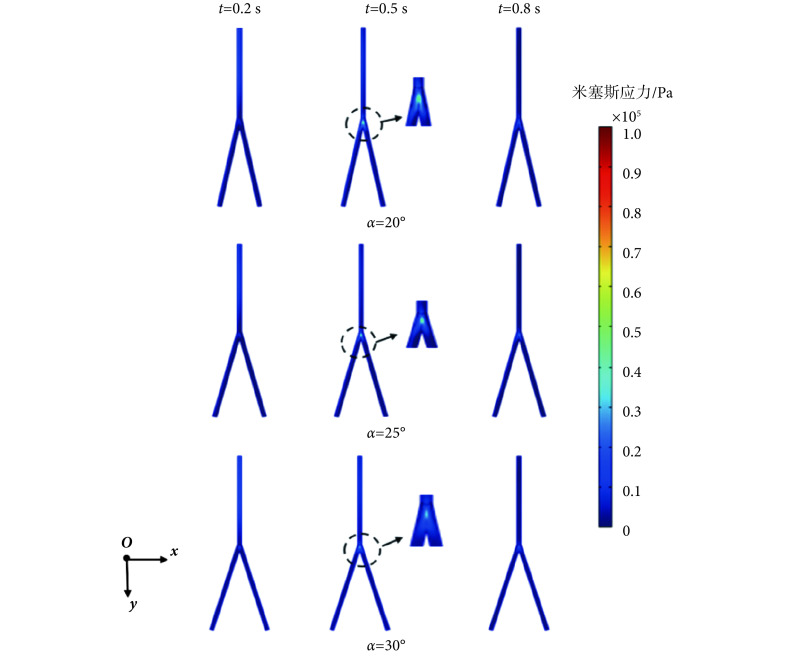
本节分析在一个心动周期内，髂动脉中的应力场分布情况，故选取分别代表一个心动周期的快速射血末期、收缩末期、舒张末期的0.2、0.5、0.8 s时刻点为例。在分叉血管分析预测模型下，血管壁上米塞斯应力云图分别如图6、图7所示。由图6、图7可知，在0.2 s时，髂动脉中的脉搏波传播仍在直管段部分，并没有传播到分叉点处和分叉管部分，此段上，并无应力集中现象，两种模型下预测的最大的米塞斯应力值几乎一致，数值较小。而当0.5 s时，脉搏波传播至分叉点和分叉血管部位，此时在血管分叉处应力集中现象明显。

图 6.

Von Mises stress distribution of straight bifurcated vessel model at different time

直管分叉模型下不同时刻米塞斯应力云图

图 7.

Von Mises stress distribution of curvilinear bifurcated vessel model at different time

曲管分叉模型下，不同时刻的米塞斯应力云图

直管和曲管分叉模型在0.2、0.5、0.8 s时的最大米塞斯应力如表5所示。在髂动脉分叉处，其内部的血流形态也发生了变化，髂动脉常因不能抵抗管腔内血流压力负荷而失衡，从而发生病变^[28-29]。由表5可知，对曲管分叉与直管分叉分析预测模型而言，在一个心动周期内，均是分叉20°情形的米塞斯应力最大，分叉25°情形的次之，分叉30°情形的最小。对分叉20°情形，直管分叉模型和曲管分叉模型下分别较分叉30°情形的大约60.6%、16.13%。这表明，分叉角较小情形的髂动脉更易发生病变；具有不同分叉角度的髂动脉的最大应力部位均在髂动脉的分叉处，与其它部位相比，髂动脉在分叉处更易发生病变。

表 5. Maximum of Von Mises stress of different bifurcated vessel model at 0.2、0.5、0.8 s.

不同分叉管模型在0.2、0.5、0.8 s的最大米塞斯应力

t/s	最大米塞斯应力/MPa
	直管分叉20°	直管分叉25°	直管分叉30°	曲管分叉20°	曲管分叉25°	曲管分叉30°
0.2	0.04	0.04	0.04	0.02	0.02	0.02
0.5	0.33	0.20	0.13	0.62	0.59	0.52
0.8	0.16	0.13	0.08	0.39	0.24	0.12

4. 结 论

本文建立了血液-血管系统的流-固双向耦合分析模型，经模拟分析发现，曲管分叉模型预测的压力脉搏波和速度脉搏波波形要更接近于实际。在髂动脉分叉前，分叉角度越大，曲管分叉模型下的压力脉搏波波幅衰减越大，而分叉后，波幅衰减越小。血管分叉后，轴向速度脉搏波随之衰减。另外，髂动脉的分叉几何特性对脉搏波传播有明显影响，且直管分叉模型和曲管分叉模型预测的脉搏波波形，在分叉前后有较大差别。对应一个心动周期内的心脏收缩区间，曲管分叉模型预测的压力脉搏波和轴向速度脉搏波幅值，在分叉前后，更接近于实际情况。在分叉后的曲管段，分叉角越大，压力脉搏波第一主波幅值越大，且随着心脏的收缩和舒张，第二主波波幅逐渐越小，传播速度也减小；轴向速度脉搏波幅值随着分叉角增大，幅值减小；曲管分叉模型预测的幅值衰减幅度低。此外，分叉点处伴随着血管壁的应力集中现象，这与髂动脉在分叉部位容易发生动脉狭窄和硬化等疾病的临床现象相一致。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献说明：孙雪航负责计算模型的后处理、论文写作及修改，李本森、卢意成负责论文的选题及有限元模型的搭建，缪馥星提供论文指导以及论文的审阅修订。

伦理声明：本文所使用的脉搏波波形数据得到宁波市中医院医学伦理委员会的批准采集并授权使用（编码：AF/SQ-01/03.1）。

Funding Statement

国家自然科学基金(11872218)；浙江省自然科学基金重点项目（LZ23A020001）