基于半监督神经网络的弹性模量分布重建

Abstract

在超声弹性成像中，准确重建组织弹性模量分布是一项重要挑战。现有的基于深度学习的全监督重建方法在训练中只使用了添加噪声的计算机仿真位移数据，不能完全模拟在体超声数据的复杂性和多样性。因此，本研究在训练中引入对在体超声射频信号追踪得到的位移数据（即真实位移数据），对模型进行半监督训练，旨在提高网络的预测准确度。实验结果显示，在仿体实验中，加入了真实位移数据的半监督模型的平均绝对误差和平均相对误差均在3%左右，而全监督模型的相应数据在5%左右。在处理真实位移数据时，半监督模型预测错误区域明显少于全监督模型。本文研究结果证实了所提方法的有效性和实用性，为在体超声数据在弹性模量分布重建的深度学习方法中的使用提供了新思路。

0. 引言

组织的弹性模量分布是临床诊断的重要依据^[1-5]。通常情况下，组织的弹性模量与一定程度的病理改变有关。重建弹性模量分布可以帮助临床医生确定相应组织或器官病理状态可能的发展，例如可以辅助识别乳腺肿瘤的特征和肝纤维化的分期^[6-7]。

弹性模量重建是弹性问题中的反问题。相较于给定一组弹性模量分布和边界条件，就可以通过有限元法求解出组织位移的正向问题^[1-4]，反问题的求解往往需要大量迭代计算和高质量的组织位移，成本更高^[5-7]。传统的弹性模量分布重建方法分为迭代求解法和直接求解法。迭代求解法，通常分为两步：首先，从形变前后的超声射频（radio frequency，RF）数据中追踪位移；然后，以得到的位移作为输入，通过求解反问题得到组织的弹性模量分布^[8-10]。该方法由于需要迭代计算，计算效率低，难以实现实时成像。并且，迭代求解法还需进行正则化参数的选择，参数的变动可能会极大地影响弹性重建结果，而不同数据的最佳参数并不相同，故在实际应用中很难确定出一组通用的最佳参数^[11]。直接求解法，是通过直接估计，将位移输入偏微分方程，也可直接求解该反问题^[12-14]。直接求解法降低了计算成本，但在实际应用中由于估计误差的影响，重建结果往往较差；且还需已知组织表面的弹性模量或位移/力边界条件，这在临床应用中往往难以实现^[15]。

针对上述问题，Chen等^[16]将弹性模量分布重建任务视为图像翻译任务，利用弹性本构关系和平衡方程作为深度神经网络的先验知识，通过最小化不平衡力图的优化任务，实现了从应变图像到弹性图像的无监督学习。他们提出的深度学习模型可以实现在没有测量的情况下预测弹性模量分布。然而，受超声换能器的限制，临床实际采集到的超声信号往往具有较高的轴向分辨率和较低的横向分辨率，导致无法提供高质量的横向位移图，进而无法提供该方法所需的高质量横向应变图，最终无法满足无监督方法对训练数据的需求。另外，由于预测的弹性模量分布没有直接标签，仅能通过平衡方程约束，导致无监督模型训练往往非常缓慢，根据弹性模量分布的复杂程度，耗时20～80 min不等^[16]，唯有通过有监督模型可以解决这一问题。Ni等^[17]和Zhang等^[18]分别以仿真应变图像和仿真位移图像为输入，配对的弹性模量分布图为标签，通过实验证明了深度神经网络仅利用轴向应变或轴向位移即可预测出较为准确的模量分布。在上述有监督模型的工作中，模型训练通常使用的是添加了噪声的配对仿真位移数据。然而，由于机械和电子噪声干扰、操作者采集手法无法保证统一、追踪算法以及在体环境的复杂性等原因，仿真位移数据难以完全重现在体超声的复杂性和多样性。即便是添加了各种噪声的大量仿真位移数据，依然无法完全替代追踪在体超声RF信号所得到的位移数据。值得借鉴的是，在超声成像的很多领域，如超声散斑运动追踪深度神经网络模型的相关研究工作中，已经证明了相比于只使用仿真位移数据，引入在体数据训练模型能取得更好的性能^[19-20]。基于上述原因，本文提出一种半监督的弹性模量分布重建深度神经网络，通过在训练过程中引入真实位移数据，可望进一步提升弹性模量分布重建模型对于真实位移数据的弹性模量分布重建的准确性，为临床医生准确诊断肿瘤或组织的病理发展提供可靠依据。

1. 方法

1.1. 半监督学习的最小二乘生成对抗网络

半监督学习是深度学习中训练深度神经网络模型的一种方法。在全监督学习中，模型只使用带标签的数据进行有监督的训练，而半监督学习则允许模型在一部分数据上进行有监督的训练，同时在另一部分数据上进行无监督的训练。在本研究中，半监督模型不仅会学习带有真实弹性模量分布的仿真位移数据，还会学习未知弹性模量分布的真实位移数据。半监督模型用最小二乘生成对抗网络（least squares generative adversarial network，LSGAN）^[21]来实现，网络结构如图1所示。LSGAN相比于常规生成对抗网络，在许多方面表现出更优秀的性能^[21-24]。LSGAN在图像翻译任务上，通过引入最小二乘损失函数，缓解了鉴别器训练中梯度消失的问题，从而使得训练更稳定，生成的图像纹理更清晰，模态更丰富^[21-22]。在医学图像重建任务上，半监督学习的LSGAN可以使用较少的标签达到较好的重建质量^[23-24]。如前所述，弹性模量分布重建任务可看作图像翻译任务，故本文采用LSGAN构建半监督神经网络。LSGAN由一个生成器和一个鉴别器组成。在学习过程中，鉴别器对于仿真位移数据的生成器生成结果进行鉴别的同时，还会将生成结果与其对应的真实弹性模量分布图作比较；而对于真实位移数据的生成器生成结果，仅有鉴别器鉴别真假，以此让生成器提前适应真实位移数据，提高模型泛化性。

图 1.

Schematic structure of the semi-supervised LSGAN model

半监督模型LSGAN的结构示意图

生成器是基于U型网络（U-Net）的深度神经网络，以单通道的轴向位移图为输入，通过多次卷积、下采样、上采样和跳跃链接后，输出弹性模量分布图。与原始工作相比，U-Net前四层卷积核被替换为了可变形卷积核，以更好地学习不规则的病变体形状^[25]；卷积层和输出层激活函数都采用带泄露修正线性单元（leaky rectified linear unit，LeakyReLU），其负数斜率为0.25，唯一不同的是输出层，负数斜率为0.1；其余与原始U-Net相同。生成器的目标是学习位移与弹性模量分布之间的高维映射，输出预测的弹性模量分布，希望欺骗鉴别器。对于真实位移数据，生成器仅需从鉴别结果中学习；而对于仿真位移数据，还需要额外学习生成结果与真实弹性模量分布图的差异。

鉴别器取自马尔可夫生成对抗网络^[26]，以单通道的模量图为输入，负责区分它是否是真实的弹性模量分布图像。鉴别器前四层均由卷积层、归一化层和激活函数LeakyReLU组成，每层的卷积核大小均为4 × 4，步长为2，输出通道数分别为64、128、256、512。第五层是输出层，是一个单独的卷积层。卷积核大小为4 × 4，步长和输出通道均为1。该鉴别器的鉴别结果和普通鉴别器仅输出一个二元评价值（真或假）不同，其结果最终被映射到N×N的矩阵中，矩阵中每一个值代表其对应的感受野在鉴别器中的评价。相较于普通的鉴别器，该鉴别器拥有更强的鉴别能力，能够缓解生成对抗网络的梯度消失问题，更好地指导生成器^[26]。

1.2. 损失函数

1.2.1. 生成器损失函数

生成器的损失函数由两部分组成。一部分是鉴别器对生成结果图和真实弹性模量分布图的鉴别误差，如式(1)和式(2)所示。另一部分来自于生成结果与真实弹性模量分布图的L₁损失，如式(3)所示：

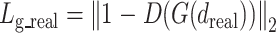1

2

3

其中，d_simu和d_real分别是输入生成器的仿真位移数据与真实在体位移数据；L_{g_real}代表鉴别器对真实位移数据的生成结果与实际弹性模量分布图的鉴别差异；L_{g_simu}代表鉴别器对仿真位移数据的生成结果与实际弹性模量分布图的鉴别差异； L₁ 代表生成结果与真实弹性模量分布图的L₁损失； G(∙)代表生成器对于任一输入的生成结果；D(∙)是鉴别器对于任一输入鉴别结果；y是d_simu的对应真实弹性模量分布图。生成器总的损失函数L_g，定义如式(4)所示：

4

其中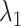， 和 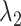是权重，在本文研究中固定为0.01。

1.2.2. 鉴别器损失函数

鉴别器的损失由两部分组成，一部分来自于鉴别器对真实位移数据生成结果的鉴别（以符号L_{d_real}表示），如式(5)所示；另一部分来自于鉴别器对仿真位移数据生成结果和真实弹性分布的鉴别（以符号L_{d_simu}表示），如式(6)所示；鉴别器总的损失函数L_d，定义如式(7)所示：

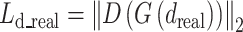5

6

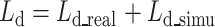7

2. 实验

本研究将半监督模型LSGAN和Zhang等^[18]提出的一种全监督模型进行比较，该全监督模型仅使用计算机仿真位移数据进行训练。全监督模型采用深度卷积生成对抗网络（deep convolution generative adversarial networks，DCGAN）作为网络架构^[27]，在训练中仅使用仿真位移数据，并且所有仿真位移数据均有真实的弹性模量分布图。为充分验证本文所提方法的有效性，本研究通过计算机数字体模实验、仿体体模实验和在体乳腺试验进行了定量和定性的比较。

在计算机数字体模实验中，本研究首先采用量化指标评估两种模型的重建结果与真实弹性模量分布图像之间的误差，以验证预测的准确度。然后，通过对数字体模仿真实验中的三组仿真位移数据，采用如2.1节中所述的方式对原始仿真位移添加1 000次噪声，统计所有的预测误差，以验证提出的方法面对噪声的鲁棒性。最后，通过将不同尺寸的仿真位移数据输入到本文所提出的方法中统计预测耗时，验证本文所提方法在弹性模量分布重建的计算效率。

在仿体实验中，本研究分别量化了两种模型预测结果与真实弹性模量分布图像之间的误差。而在体试验中，本研究将两种模型重建的弹性模量分布图像与现有临床诊断结果进行比较分析。

2.1. 训练数据

在本研究中，训练数据共包括162组真实位移数据和12 000组仿真位移数据，按照5∶1的比例划分训练集和测试集，最终训练集中包含135组真实位移数据和10 000组仿真位移数据。

真实位移数据由追踪在体超声RF信号得到的162组位移数据组成。这些超声RF数据来自27例经病理证实的乳腺病变受试者。数据采集均使用7.5 MHz的高频线性阵列换能器（Siemens Medical Solution Inc., 美国）获取，并得到了堪萨斯大学医学中心人类受试者委员会（机构审查委员会）的批准，且获得了患者的知情同意^[28-30]。每个患者的超声数据包含50～90 帧，从中随机选择6组相邻的帧，采用具有局部多项式拟合的贝叶斯区域增长运动跟踪算法（Bayesian region-growing motion tracking with local polynomial fitting，BRGMT-LPF）。该算法将贝叶斯推理与局部多项式拟合相结合，并纳入区域增长块匹配运动跟踪框架，使用最大后验概率密度函数来确定更加准确的位移向量。实验结果表明，相较于原始区域增长运动跟踪算法、贝叶斯推理区域增长和局部多项式拟合区域增长， BRGMT-LPF算法可以提供更加准确的运动跟踪结果^[28]，为后续神经网络输入高质量位移数据提供了基础和保障。

仿真位移数据由仿真软件MATLAB 2020a（The MathWorks Inc., 美国）偏微分方程工具箱生成。数字模体尺寸为40 mm × 40 mm × 1 mm，内部包裹一个椭圆包裹体。背景的杨氏模量固定为22 kPa。为了增加训练数据的多样性，本研究设计了半径、杨氏模量和位置均为随机值的椭圆包裹物。包裹物长轴范围为5～10 mm，长轴与短轴之比为0.2～1.0的随机数。包裹物的杨氏模量范围为36～100 kPa。长轴与X轴夹角范围为1°～180°。包裹物边缘与数值体模边缘之间的距离始终大于3 mm。泊松比设置为0.495，用以将组织视为一种几乎不可压缩的材料。数字体模在0.1%～5.0%的范围内进行随机轴向压缩，这样可以模拟超声弹性成像中的大多数变形情况。在给定模量分布条件下，基于平面应变模型，采用有限元法计算模体相应的位移分布。为进一步增加训练数据样本和样本的多样性，在输入深度神经网络之前，对通过偏微分方程工具产生的仿真位移数据d_smooth进行随机噪声添加。最终，训练输入的仿真位移数据d_simu定义如式(8)所示：

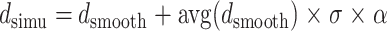8

其中，avg(∙)是均值函数，α是0.01～0.05的随机数，σ是均值为0、方差为1的标准正态分布噪声。需要说明的是，为适应网络的输入尺寸，本研究中的仿真位移数据、相对应的真实弹性模量分布图和真实位移数据均被调整为256 × 256像素，对深度神经网络进行半监督训练。

2.2. 计算机数字体模实验数据

本研究在计算机数字体模实验中使用了三组随机选择的仿真位移数据来验证所提出的方法。如前一节所述，用于评价的位移和弹性数据与用于训练的数据在生成方法上相同。以该位移数据作为输入，重建出相应的弹性模量分布。最后利用生成器重建的弹性模量分布与真实弹性模量分布之间的差异来量化重建误差。

2.3. 仿体体模数据

本研究使用一台配备L9-3线性阵列换能器的飞利浦iU22超声系统（Philips Medical Systems Inc., 美国）徒手扫描乳房弹性成像仿体（model 059, CIRS Inc., 美国）获取仿体实验射频数据。该仿体中分布有5个不同大小的球形包裹物，其硬度是背景的两倍。实验中，对仿体中直径分别为4.1 mm和6.5 mm的包裹物进行扫描并采集射频数据，得到的射频数据的采样频率为32 MHz，每个射频帧由320扫描线组成，轴向采样间距和横向采样间距分别为0.01 mm和0.12 mm。

2.4. 在体数据

在体试验数据来自一名已经临床诊断为浸润性导管癌（invasive ductal carcinoma，IDC）的乳腺癌患者。该数据使用配有7.5 MHz线性阵列传感器的扫描仪（Siemens Medical Solution Inc.，美国）获得。采集时，医生以徒手的方式压缩乳房，用以产生1.0%～1.5%的应变。射频数据采集频率为36 MHz。轴向采样间距和横向采样间距分别为0.021 mm和0.19 mm。数据采集同样得到了堪萨斯大学医学中心人类受试者委员会（机构审查委员会）的批准，并获得了患者的知情同意^[27-29]。本研究从连续采集的图像帧中随机选取两帧连续的图像帧来评估所提方法的性能。

2.5. 评价指标

本研究使用平均绝对误差（mean absolute error，MAE）和平均相对误差（mean relative error，MRE）作为评价指标，来衡量深度学习模型预测的弹性模量分布图像与计算机仿真得到的真实弹性模量分布图像之间的全局相似度，以定量评价所提方法在弹性模量分布重建上的误差，其定义如式(9)和式(10)所示：

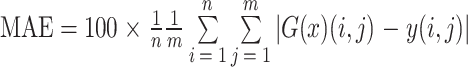9

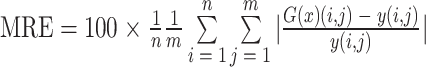10

其中，n和m分别是图像的高度和宽度。G(x)(i, j)和y(i, j)分别是预测的弹性模量分布图和真实弹性模量分布图在该处的弹性值。

2.6. 实现细节

本研究使用机器学习库PyTorch 1.7.0（Facebook Inc.，美国）实现了本文方法和对比方法的深度神经网络，并在配备图形处理器NVIDIA GeForce RTX 3090（NVIDIA，Inc.，美国）的工作站上进行训练。用于训练的优化器是自适应矩估计（adaptive moment estimation，Adam）。批大小、训练周期和学习率分别设置为16、400和5 × 10⁻⁵。

3. 结果

为了更直观地比较重建结果，本研究对模型预测的弹性模量分布结果进行了相对化处理。在实验结果图中，背景模量值始终为1，内部包裹物的模量值表现为背景模量的倍数，因此模量值不带单位。

3.1. 计算机数字体模实验结果

计算机数字体模的仿真实验结果如图2所示，其中纵列分别对应三组随机选取的仿真位移数据（仿真位移数据1、仿真位移数据2、仿真位移数据3），横排分别对应位移图、全监督模型结果、半监督模型LSGAN结果和真实弹性模量分布图。对于三组仿真位移数据，半监督模型LSGAN和全监督模型预测的椭球体的形状与真实的椭球体形状基本一致；同时从椭球体内部的模量数值来看，两种模型预测的弹性模量数值也与真实弹性模量分布图中椭球体的弹性模量值一致。

图 2.

Results of simulation experiments

仿真实验结果

仿真实验中半监督模型LSGAN和全监督模型预测的弹性模量值与真实弹性模量值之间的MAE和MRE如表1所示。对于三组仿真位移数据，半监督模型和全监督模型预测结果的MAE和MRE都在1.00%以内。两种模型预测得到的弹性模量分布图中的数值基本一致。这些结果证明了对于仿真位移数据，两种模型都能够准确预测弹性模量分布图。

表 1. MAE and MRE of model prediction value and real value in simulation experiments.

仿真实验中模型预测值与真实值的MAE和MRE

数据来源	算法	MAE	MRE
仿真位移数据1	全监督模型	0.13%	0.10%
	半监督模型LSGAN	0.38%	0.21%
仿真位移数据2	全监督模型	0.70%	0.66%
	半监督模型LSGAN	0.59%	0.52%
仿真位移数据3	全监督模型	0.65%	0.59%
	半监督模型LSGAN	0.67%	0.60%

如图3所示为本文提出的网络在面对添加噪声后仿真位移数据时的预测性能，噪声添加方式如2.1节所述。对于仿真位移数据而言，当位移噪声在1.0%～5.0%之间时，该网络对仿真位移数据的预测结果的MAE和MRE均低于1.5%。其中大部分情况MAE低于1.0%，而MRE在0.5%上下浮动。总体上看，在输入带有噪声数据的仿真位移数据时，本文所提出的网络模型依然可以预测得到具有较高质量的弹性模量分布图。

图 3.

Performance of elastic distribution reconstruction network with noisy displacement

弹性模量分布重建网络面对噪声位移时的性能表现

此外，网络预测一个输入所需时间如表2所示，基于U-Net的生成器对一个输入进行预测仅需要不到0.1 s，因此该网络对于弹性模量分布重建任务具有非常高的实时性。

表 2. Time required for elastic modulus distribution reconstruction by supervised model with different input size.

不同输入尺寸下监督模型重建弹性模量分布所需时间

输入尺寸	t/s
64	0.033 2 ± 0.004 7
128	0.047 3 ± 0.004 3
256	0.062 4 ± 0.005 1
512	0.093 7 ± 0.010 1

3.2. 仿体实验结果

如图4所示为两个模型对仿体实验数据预测的弹性模量分布重建结果，纵列展示了两组不同的仿体数据实验结果（仿体数据1、仿体数据2），横排分别为B模式图、位移图、轴向应变图、全监督模型结果、半监督模型LSGAN结果和真实弹性模量图。从视觉上看，两个模型预测结果的中间包裹物的形状与大小与其对应的真实弹性模量分布较为一致。另外，对于全监督模型预测得到的弹性模量分布图的背景区域出现了明显的错误模量值（箭头所指区域），而半监督模型LSGAN预测的弹性模量分布图与真实弹性模量分布较为一致。同时，从图4中可以看出，半监督模型LSGAN预测的弹性模量分布图中包裹物硬度约为背景的2倍，这与仿体中已知的包裹体与背景的弹性模量比是一致的。

图 4.

Results of phantom experiments

仿体实验结果

如表3所示为两个模型预测的弹性模量分布与真实弹性模量分布之间的MAE和MRE。对于这两组数据，半监督模型LSGAN预测结果均具有最低的 MAE 和 MRE。然而，值得注意的是，全监督模型也展现出了相当好的重建精度。从数据上看，两种方法预测结果的MAE和MRE均未超过6%。尤其需要指出的是，对于这两个仿体位移数据，半监督模型LSGAN预测结果的MAE分别仅为2.73%和3.79%，MRE分别仅为2.24%和3.25%。

表 3. MAE and MRE of model prediction value and real value in phantom experiments.

仿体实验中模型预测值与真实值的MAE和MRE

数据来源	算法	MAE	MRE
仿体位移数据1	全监督模型	5.88%	5.41%
	半监督模型LSGAN	2.73%	2.24%
仿体位移数据2	全监督模型	4.49%	4.04%
	半监督模型LSGAN	3.79%	3.25%

3.3. 在体试验结果

如图5所示为两个模型对在体数据进行弹性模量分布预测的结果，纵列分别展示了IDC病例在体乳房数据两帧图片试验数据（在体位移数据1，在体位移数据2），横排分别为B模式图、位移图、轴向应变图、全监督模型结果和半监督模型LSGAN结果。从两个网络模型预测的弹性模量分布图可以看出，病变体对应的弹性模量分布的位置、大小和形状与其在B模式图、轴向应变图像中的对应位置、大小、形状较吻合。从图5中还可以分析出病变体与背景的弹性模量比约为4：1。在文献[31]中，乳腺实质的杨氏模量为30～50 kPa，其中良性病变杨氏模量为（45.3 ± 41.1）kPa，恶性病变杨氏模量为（146.6 ± 40.05）kPa。基于以上知识，恶性病变与乳腺实质的比值大致在2.9～4.9之间。显然，两种模型预测的病变体的弹性模量分布图像均显示病变体是恶性的，符合临床诊断。需要指出的是，仅使用仿真位移数据训练得到的全监督模型的预测结果在背景中出现了较多的与临床实际不符的区域（箭头所指区域），而半监督模型LSGAN预测结果的背景区域能够有效排除噪声干扰，与该位置组织的真实弹性模量分布较为一致。

图 5.

Results of the in-vivo breast experiments.

在体乳腺试验结果

4. 讨论与总结

本文提出了一种半监督的弹性模量分布重建深度神经网络，将真实在体位移数据用于基于位移的弹性模量分布重建网络训练。实验结果表明，相较于只是用了仿真位移数据训练的全监督模型，引入了真实位移数据的半监督模型具有更好的弹性模量分布重建性能。

由于机械和电子噪声干扰、操作者采集手法无法保证统一、追踪算法以及在体环境的复杂性等原因，仿真位移数据难以完全重现在体超声的复杂性和多样性。即使通过添加噪声等数据增强手段，仿真位移数据仍然不能完全替代真实在体位移数据。相比只使用仿真数据训练的深度神经网络模型，引入在体数据训练的模型在超声成像的很多领域都取得更好的性能。特别是在超声散斑运动追踪深度神经网络模型中获得了成功的应用。基于此，本文在弹性模量分布重建的深度学习模型训练中引入真实位移数据，采用半监督学习的方法让模型学习真实位移数据和仿真位移数据的差异，以提高模型的泛化性，减少重建结果中与临床实际不符的区域。本文得到的模型进一步验证了在超声成像领域，使用在体数据可以进一步提升这些模型的性能。

本文所提出方法的泛化性是需要后续持续研究的一个问题，因为即使本文方法已经在训练中引入了真实在体位移数据和添加噪声的仿真位移数据一起训练，但受限于真实位移数据的数量，依然无法完全弥补仿真位移数据和真实位移数据存在的差异。另外，受限于真实数据的病变类型，本研究使用的所有训练数据均为病变的硬度高于背景硬度的数据。本文所得到的深度学习模型可能缺乏对较软的病变、空腔等的重建弹性模量分布能力。因此，引入更多的真实在体数据继续提升模型准确度将是下一步的研究方向。

还需要说明的是，本文的模型是将追踪真实在体超声数据得到的位移作为输入，因此散斑追踪算法的性能也会对本文所得到的模型结果有直接影响。鉴于前述基于光流的散斑追踪深度神经网络的成功，后续将基于光流的散斑追踪深度神经网络与本文所提方法构建为一个级联网络或者直接通过B模式图像进行模型训练以提升模型准确度也是一个重要的研究方向。

本文提出的基于半监督学习方法的弹性模量分布重建深度神经网络，可以为深度神经网络模型提供充足且具有更多复杂场景的训练数据，进一步提高弹性模量分布重建深度神经网络的鲁棒性和泛化能力。本文所提出的方法在弹性模量分布重建领域主要的优势在于：①能够更准确进行弹性模量分布重建任务，减少重建错误；②相对于传统方法不依赖于人工调参；③具有更快的重建速度，具有一定的临床实际应用价值。未来的研究将继续引入更多的没有标签的、具有不同病变类型的真实位移数据，使得到的模型具有更好的重建结果。

致谢

感谢威斯康星大学的Timothy Hall教授和密歇根理工大学的Jingfeng Jiang教授提供在体数据。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：彭博、罗建文负责设计整体研究方案；张潇负责算法研究与实现，以及实验、数据分析；张潇、彭博负责撰写论文；王锐、魏星月负责仿真位移数据算法的研究与实现。

伦理声明：本研究通过了堪萨斯大学医学中心人类受试者委员会机构伦理委员会的审批（批文编号：M1182）。

Funding Statement

国家自然科学基金（61871251）；四川省自然科学基金（2022NSFSC0833）；四川省南充市科技局（SXQHJH046, SXHZ019）

National Natural Science Foundation of China; Natural Science Foundation of Sichuan Province of China; Science and Technology Bureau of Nanchong, Sichuan Province