A Surface-Accelerated String Method for Locating Minimum Free Energy Paths

Abstract

We present a surface-accelerated string method (SASM) to efficiently optimize low-dimensional reaction pathways from the sampling performed with expensive quantum mechanical/molecular mechanical (QM/MM) Hamiltonians. The SASM accelerates the convergence of the path by using the aggregate sampling obtained from the current and previous string iterations, whereas approaches like the string method in collective variables (SMCV) or the modified string method in collective variables (MSMCV) update the path only from the sampling obtained from the current iteration. Furthermore, the SASM decouples the number of images used to perform sampling from the number of synthetic images used to represent the path. The path is optimized on the current best estimate of the free energy surface obtained from all available sampling, and the proposed set of new simulations are not restricted to be located along the optimized path. Instead, the umbrella potential placement is chosen to extend the range of the free energy surface and improve the quality of the free energy estimates near the path. In this manner, the SASM is shown to improve the exploration for a minimum free energy pathway in regions where the free energy surface is relatively flat. Furthermore, it improves the quality of the free energy profile when the string is discretized with too few images. We compare the SASM, SMCV, and MSMCV using 3 QM/MM applications: a ribozyme methyltransferase reaction using 2 reaction coordinates, the 2′-O-transphosphorylation reaction of Hammerhead ribozyme using 3 reaction coordinates, and a tautomeric reaction in B-DNA using 5 reaction coordinates. We show that SASM converges the paths using roughly 3 times less sampling than the SMCV and MSMCV methods. All three algorithms have been implemented in the FE-ToolKit package made freely available.

Graphical Abstract

1. Introduction

The ability to model chemical reactions in the condensed phase¹ using molecular simulations has far-reaching implications to the study of catalysis in biological systems.^2,3 Advances in fast, accurate quantum mechanical force fields^4,5 and machine learning models^6–11 have greatly extended the scope of applications that can be routinely addressed. Nonetheless, simulations of complex reaction pathways remain computationally intensive, and ongoing development of new methods to improve the robustness and computational cost are important.

Reaction mechanisms can be characterized by calculating a free energy surface in a set of relevant reaction coordinates, the determination of the minimum free energy profile (MFEP) through the surface, and identification of key stationary points along the MFEP. Many methods for calculating free energy surfaces have been developed. These approaches can be categorized as:¹² methods which analyze equilibrium statistics obtained from umbrella sampling,^13–16 methods which analyze nonequilibrium statistics^17–20 based on the work of Jarzynski,²¹ and methods that integrate auxiliary degrees of freedom, such as λ-dynamics^22–25 and metadynamics.^26,27 Similarly, there are two general approaches for locating a minimum free energy path.²⁸ The first approach is to sample the reaction over a wide range of reaction coordinate values to obtain a relatively complete picture of the free energy surface through which a path can be optimized. This approach can greatly benefit from enhanced sampling methods, such as replica exchange molecular dynamics²⁹ and integrated tempering sampling.³⁰ The second, and more cost-effective, approach is to use a chain-of-states method, such as nudged elastic band³¹ or the string method,^32,33 to direct the sampling toward the MFEP, thereby reducing the amount of effort spent simulating irrelevant, high-energy regions of the free energy surface.

Many variations of the string method^34–41 have been developed that are capable of being applied to large-scale problems, like protein folding.^36,37 These applications often describe the path using a large number of reaction coordinates,⁴² direct comparison of Cartesian coordinates,³² path collective variables,^28,43 the use of the hills method,^26,44 or machine learning techniques.⁴⁵ Although string method development was originally motivated by the desire to use many reaction coordinates,^34,35,38 many examples can be found of their use in quantum mechanical/molecular mechanical (QM/MM) applications involving only a few reaction coordinates.^46–52 String methods, such as the one presented in Ref. 38, are particularly appealing because it is performed with standard umbrella sampling with harmonic biasing potentials, which are widely supported across simulation packages. Because QM/MM sampling is very costly, the present work seeks to optimize the string method described in Ref. 38 specifically for cases involving QM/MM simulations with a few reaction coordinates. The new method reduces the number of string iterations required to reach convergence because it uses the current estimate of the unbiased free energy to accelerate the exploration of flat regions of the surface. In this respect, the new method draws inspiration from ideas behind the metadynamics approach;^26,27 however, the new method only requires sampling obtained using standard harmonic biasing potentials.

We describe a new surface-accelerated string method (SASM) and compare it to two similar algorithms: the string method in collective variables^34,35 (SMCV), and the modified string method in collective variables³⁸ (MSMCV). We have implemented all 3 of these methods in the ndfes software⁴⁹ freely distributed within the FE-ToolKit package.⁵³ The FE-ToolKit package has also been incorporated in the open source AmberTools simulation suite.⁵⁴ There are several key differences between the SASM and related string methods. First, the SASM is a hybrid of the two approaches for locating a MFEP (chain-of-states method versus calculation of a multidimensional free energy surface). Whereas the SMCV and MSMCV update the path from the sampling obtained in the most recent string iteration, the SASM optimizes the path on the current estimate of the multidimensional free energy surface calculated from the aggregate sampling of all string iterations. In this respect, the SASM is similar to some adaptive umbrella sampling strategies.⁵⁵ Second, the SASM decouples the number of images used to represent the path from the number of simulated images. The SMCV and MSMCV methods construct a new path by fitting a curve that interpolates a set of discrete control points obtained from a corresponding number of simulated images; therefore, if there was an insufficient number of images, the path may cut corners. By decoupling the representation of the path from the number of simulated images, the level of detail used to describe the path is not limited by the number of simulations. Third, unlike the SMCV and MSMCV the SASM does not require the images to be simulated along the current estimate of the path. We take advantage of this by introducing alternating stages of “exploration” and “refinement” steps. The exploration steps propose new simulations offset from the path in the direction that the path is moving, and the refinement steps place simulations along the path in a manner that improves the phase space overlap.

We compare the progress of the string optimizations using the SMCV, MSMCV and SASM with respect to the number of simulations per string, the sampling per simulation, and the spline representation of the path (either piecewise linear or Akima spline paths) in 3 applications. The first application uses 2 reaction coordinates to describe a ribozyme undergoing a methyl transfer reaction (MTR1)^56–58 (PDB ID 7V9E). The second application uses 3 reaction coordinates to model the 2′-O-transphosphorylation reaction of Hammerhead ribozyme (HHr)⁵⁹ (PDB ID 2OEU). The third application uses 5 reaction coordinates to optimize a tautomeric reaction pathway in B-DNA (PDB ID 113D).⁶⁰ Schematics of the 3 systems are shown in Figure 1. We demonstrate that the SASM converges the MFEP faster than the SMCV and MSMCV when we vary the amount of sampling. The SASM avoids artifacts that can occur in the path “reparametrization step” of the SMCV and MSMCV. Finally, we show that the SASM method will sample the path in an efficient manner that achieves good overlap between the biased simulations when the number of simulations is reduced.

Figure 1:

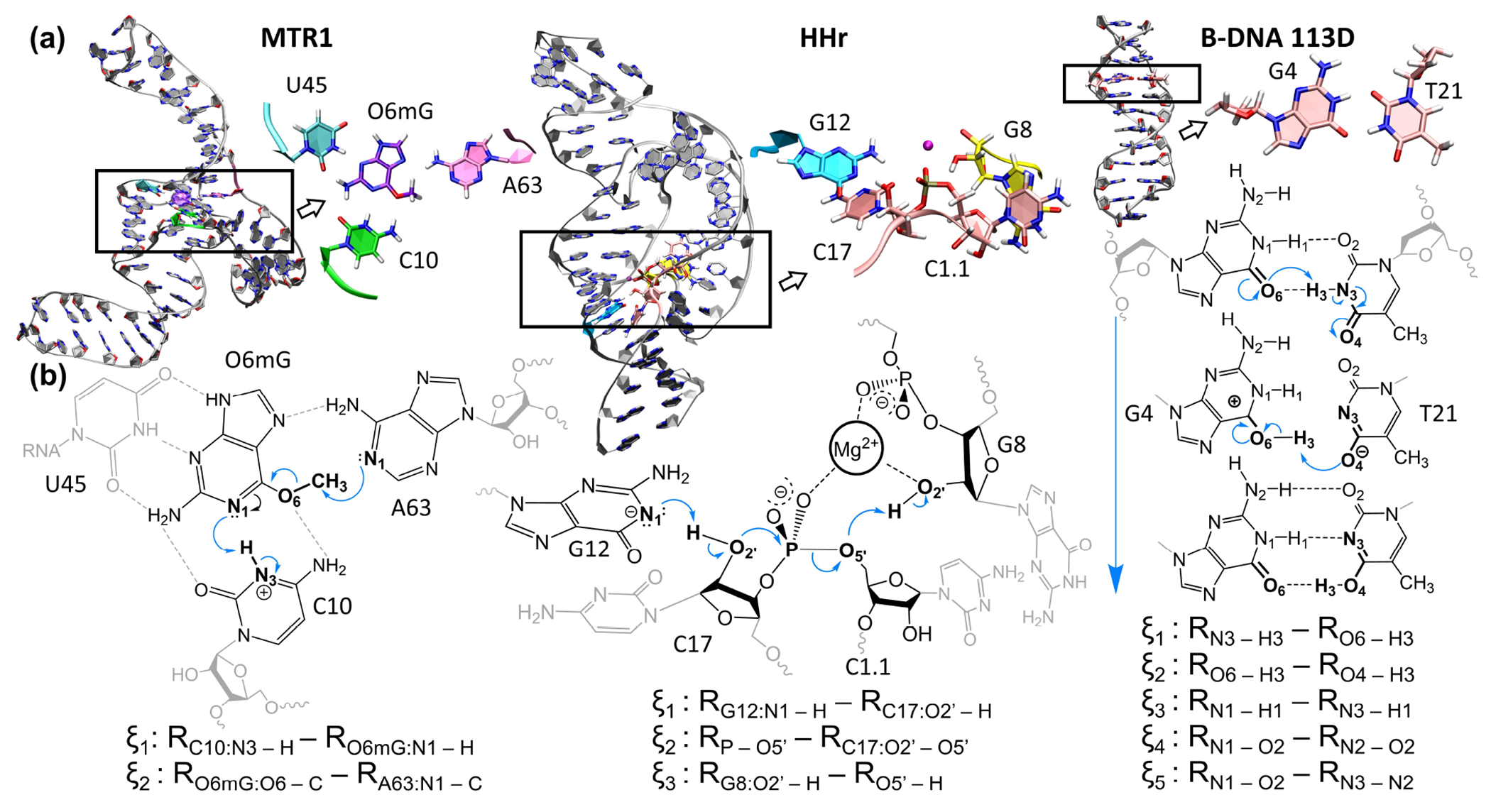
(a) The MTR1 ribozyme, HHr ribozyme, and a B-DNA with a GT wobble pair examined in this work. The rectangles highlight the active site region. (b) The reaction mechanisms and reaction coordinates. The B-DNA system is a tautomer reaction which transfers the T21 N3 proton to position O4 and reorganization of the G:T hydrogen bond network. The shown atomic configurations correspond to the reactant state. The black and gray atoms denote the QM region and nearby MM atoms, respectively.

2. Methods

2.1. String Method in Collective Variables

This section summarizes the SMCV method, which was originally described in Refs. 34 and 35. Let $\mathbf{x}$ and $\mathbf{q}\left(\mathbf{x}\right)$ be the 3N array of atomic positions and $N_{\mathrm{d}\mathrm{i}\mathrm{m}}$ reaction coordinate values, respectively. Umbrella sampling is performed at $N_{\text{img}}$ images along the path using a biased potential energy function, $U_n$.

$$U_n(\mathbf{x})=U(\mathbf{x})+W(\mathbf{q}(\mathbf{x});{\mathbf{k}}_n,{\mathbf{q}}_n)$$ (1)

Image $n$ is biased by a potential $W$ that is parametrized by $N_{\text{dim}}$ harmonic force constants ${\mathbf{k}}_n$ and equilibrium positions ${\mathbf{q}}_n$. In other words, $N_{\mathrm{d}\mathrm{i}\mathrm{m}}$ is the size of the reduced dimensional space of reaction coordinates.

$$W(\mathbf{q}(\mathbf{x});{\mathbf{k}}_n,{\mathbf{q}}_n)=\frac{1}{2}\sum _{d=1}^{N_{\mathrm{d}\mathrm{i}\mathrm{m}}}{k}_{nd}{(q_d(\mathbf{x})-q_{nd})}^2$$ (2)

The algorithm for calculating the SMCV consists of the following steps.

1. Sample each of the $N_{\text{img}}$ images along the path for some amount of time, $\text{Δ}t$. The images differ by their biasing potentials, which center the harmonic potentials at discrete points along the current estimate of the path, ${\mathbf{q}}_n$.

2. Analyze the sampling to update (evolve) the reaction coordinate values, ${\mathbf{q}}_{\mathrm{c},n}$. The “control points”, ${\mathbf{q}}_{\mathrm{c},n}$ are discrete estimates along the new path, but they do not necessarily uniformly discretize it. The calculation of the control points is sometimes called the “evolution step”.

3. Construct a parametric curve that interpolates the control points. The parametric curve is the new estimate of the path.

4. Uniformly discretize the parametric curve to obtain the biasing potential centers for the next iteration. The construction of a new curve and its discretization is sometimes called the “reparametrization step”.

The SMCV evolution step is given by eq. 3, where $q_{nd}^{\left(k\right)}$ is the value of the reaction coordinate $d$ of image $n$ at string iteration $k$, and $q_{\mathrm{c},nd}^{(k+1)}$ is a control point used to define the parametric curve in string iteration $k+1$, discussed in the next section. Each image is simulated for a length of time $\text{Δ}t$, and $⟨\cdot {⟩}_{{\mathbf{k}}_n,{\mathbf{q}}_n}$ denotes a time average obtained from image $n$.

$$q_{\mathrm{c},nd}^{(k+1)}=q_{nd}^{\left(k\right)}-\frac{\text{Δ}t}{\gamma }\sum _{d^{\prime }=1}^{N_{\mathrm{d}\mathrm{i}\mathrm{m}}}{M}_{d{d}^{\prime }}({\mathbf{k}}_n^{\left(k\right)},{\mathbf{q}}_n^{\left(k\right)})\nabla G_{n{d}^{\prime }}({\mathbf{k}}_n^{\left(k\right)},{\mathbf{q}}_n^{\left(k\right)})$$ (3)

$\nabla G_{nd}({\mathbf{k}}_n^{(k)},{\mathbf{q}}_n^{(k)})$ approximates the free energy gradient about the point ${\mathbf{q}}_n^{(k)}$ in dimension $d$.

$$\nabla G_{nd}({\mathbf{k}}_n,{\mathbf{q}}_n)=-{⟨\frac{\partial W(\mathbf{q}(\mathbf{x});{\mathbf{k}}_n,{\mathbf{q}}_n)}{\partial q_{nd}}⟩}_{{\mathbf{k}}_n,{\mathbf{q}}_n}$$ (4)

$\mathbf{M}$ is closely related to a product of mass weighted Wilson B-matrices;⁶¹ that is to say, ${\nabla }_{a}q$ is the gradient of the reaction coordinate value with respect to the atomic positions of atom $a$ and $m_a$ is an atomic mass.

$$M_{d{d}^{\prime }}({\mathbf{k}}_n,{\mathbf{q}}_n)={⟨\sum _{a=1}^N\frac{{\nabla }_a{q}_d(\mathbf{x})\cdot {\nabla }_a{q}_{d^{\prime }}(\mathbf{x})}{m_a}⟩}_{{\mathbf{k}}_n,{\mathbf{q}}_n}$$ (5)

$\gamma$ is a friction coefficient, a parameter of the method. The numerical stability of the SMCV critically depends on the ratio $\text{Δ}t{\gamma }^{-1}$. In Ref. 35, it was found that the method was stable when choosing $\gamma =1500{\mathrm{p}\mathrm{s}}^{-1}$ when $\text{Δ}t=20$ fs. In the present work, we adjust $\gamma$ to maintain this same ratio when $\text{Δ}t$ is varied. The construction of parametric curves and their uniform discretization are described in the next section.

2.2. Parametric Curves and the Reparametrization Step

We represent a continuous path as a parametric curve of reaction coordinates, $\mathbf{q}(p)$, where $p\in [0,1]$ is a progress variable such that $p=0$ and $p=1$ denote two ends of the path. In other words, the path at string iteration $k,{\mathbf{q}}^{\left(k\right)}\left(p\right)$ is an array of $N_{\text{dim}}$ one-dimensional splines that are chosen such that each spline interpolates the $N_{\text{img}}$ control points, $q_{\mathrm{c},nd}^{\left(k\right)}$ located at a common set of progress control values, $p_{\mathrm{c},n}^{\left(k\right)}$. Let ${\mathbf{p}}_{\mathrm{c}}^{\left(k\right)}=\{p_{\mathrm{c},1}^{\left(k\right)},\cdots ,p_{\mathrm{c},N_{\text{img}}}^{\left(k\right)}\}$ and ${\mathbf{q}}_{\mathrm{c},d}^{\left(k\right)}=\{q_{\mathrm{c},1,d}^{\left(k\right)},\cdots ,q_{\mathrm{c},N_{\text{img},d}}^{\left(k\right)}\}$ denote the $N_{\text{img}}\times 1$ arrays of progress control values and control points in dimension $d$, respectively. The spline representation of the path in dimension $d,q_d^{(k)}(p)$ is parametrized from these quantities.

$$q_d^{\left(k\right)}(p)\equiv q_d(p;{\mathbf{q}}_{\mathrm{c},d}^{\left(k\right)},{\mathbf{p}}_{\mathrm{c}}^{\left(k\right)})$$ (6)

In the context of the SMCV (or similar string methods), the control points are the new estimates of the reaction coordinates after the evolution step (eq. 3). In some cases, one may choose to reduce the numerical noise in the path by first applying a smoothing procedure, in which case the control points are the reaction coordinate values after smoothing. The results presented in this work use a smoothing algorithm implemented in the ndfes software when the parametric curve is modeled with Akima spline functions,⁶² but we do not apply smoothing to the control points when using piecewise linear paths. The details of the smoothing algorithm are described in the Supporting Information.

The parametric curve depends on the progress control values, which are interpreted as fractional arc lengths through the curve. If the path is a piecewise linear function connecting the control points, then the progress control values can be calculated from the Euclidean distance between adjacent points, as shown in eq. 7.

$$p_{\mathrm{c},n}^{\left(k\right)}\approx \left\{\begin{array}{ll}0,& \text{if}n=1\\ \frac{{\sum }_{m=2}^n\sqrt{{\sum }_{d=1}^{N_{\text{dim}}}{\left(q_{md}^{\left(k\right)}-q_{m-1,d}^{\left(k\right)}\right)}^2}}{{\sum }_{m=2}^{N_{\text{img}}}\sqrt{{\sum }_{d=1}^{N_{\text{dim}}}{\left(q_{md}^{\left(k\right)}-q_{m-1,d}^{\left(k\right)}\right)}^2}},& \text{otherwise}\end{array}\right.$$ (7)

Alternatively, if the parametric curve is a set of Akima spline functions⁶² (or any smooth interpolating function), then eq. 7 is only an approximation of the fractional arc lengths. Accurate values of the progress control values can be found by iteratively solving eq. 8.

$$p_{\mathrm{c},n}^{(k,i+1)}=\frac{{\int }_0^{p_{\mathrm{c},n}^{(k,i)}}\sqrt{{\sum }_{d=1}^{N_{\mathrm{d}\mathrm{i}\mathrm{m}}}{\left(\frac{\partial q_d(p;{\mathbf{q}}_{\mathrm{c},d}^{\left(k\right)},{\mathbf{p}}_{\mathrm{c}}^{(k,i)})}{\partial p}\right)}^{2}dp}}{{\int }_0^1\sqrt{{\sum }_{d=1}^{N_{\mathrm{d}\mathrm{i}\mathrm{m}}}{\left(\frac{\partial q_d(p;{\mathbf{q}}_{\mathrm{c},d}^{\left(k\right)},{\mathbf{p}}_{\mathrm{c}}^{(k,i)})}{\partial p}\right)}^{2}dp}}$$ (8)

Equation 8 describes the iterative solution of $p_{\mathrm{c},n}^{\left(k\right)}$ by introducing a second, auxiliary index $i,p_{\mathrm{c},n}^{(k,i)}$. The initial values, $p_{\mathrm{c},n}^{(k,0)}$ are the piecewise linear approximation shown in eq. 7, and we terminate the iterative solution when ${\sum }_{m=1}^{N_{\text{img}}}{\left(p_{\mathrm{c},m}^{(k,i+1)}-p_{\mathrm{c},m}^{(k,i)}\right)}^2<{10}^{-16}$. We drop the auxiliary index to denote the converged progress control values.

Given the the parametric spline representation of the path, the uniformly discretized images for string iteration $k+1$ is shown in eq. 9, where $p_n=(n-1)/(N_{\text{img}}-1)$.

$$q_{nd}^{(k+1)}=q_d(p_n;{\mathbf{q}}_{\mathrm{c},d}^{(k+1)},{\mathbf{p}}_{\mathrm{c}}^{(k+1)})$$ (9)

2.3. Modified String Method in Collective Variables

The modified string method in collective variables (MSMCV) was originally presented in Ref. 38; it differs from the SMCV only by replacing the evolution step (eq. 3) with eq. 10.

$$q_{\mathrm{c},nd}^{(k+1)}={⟨q_d(\mathbf{x})⟩}_{{\mathbf{k}}_n^{\left(k\right)},{\mathbf{q}}_n^{\left(k\right)}}$$ (10)

In other words, the control points for the new path are the mean observed positions of the reaction coordinates from the simulations performed along the current path. Upon finding the control points, a new parametric curve is fit. The curve is uniformly discretized to define the new positions of the biasing potentials.

2.4. Surface-Accelerated String Method

The surface-accelerated string method (SASM) constructs a $N_{\text{dim}}$ dimensional free energy surface from the available sampling and optimizes a path on that surface. A decision is then made to place a new set of simulations, which may or may not be along the optimized path. When the new simulations are placed along the path, we refer to it as a “refinement step”. Alternatively, we allow for “exploration steps” that offset the simulations from the path in the direction that the path is moving.

The algorithm for calculating the SASM consists of the following steps.

1. Sample each of the $N_{\text{img}}$ images for some amount of time.

2. Construct a $N_{\text{dim}}$ dimensional unbiased free energy surface by analyzing the aggregate sampling produced from all simulations and string iterations. This is the best estimate of the free energy surface from the available sampling. The $N_{\mathrm{d}\mathrm{i}\mathrm{m}}$ dimensional space is discretized into bins, and the free energy value and the number of observed samples in each bin are tabulated.

3. Create a smooth representation of the free energy surface, such that the free energy value and gradient can be readily computed at any point in the space of reaction coordinates.

4. Use the free energy surface to optimize a MFEP in the space of reaction coordinates. This optimization procedure does not involve the generation of additional sampling. Instead, the optimization is performed on a fixed free energy surface using a series of “synthetic string iterations”, described below.

5. If the current iteration is an even integer, then place the new simulations along the path. If the current iteration is an odd integer, then allow the new set of simulations to be displaced from the path by some amount in the direction that the path is moving.

The unbiased free energy can be calculated using established methods, such as the variational free energy profile method,^49,63,64 the multistate Bennett acceptance ratio (MBAR) method,⁶⁵ or the unbinned weighted histogram (UWHAM) method.^66,67 As discussed in Ref. 49, a smooth representation of the free energy surface can be made using one of many methods, including the use of Cardinal B-Splines,⁶⁸ radial basis functions,^69,70 or Gaussian process regression.⁷¹ In the present work, we calculate the free energy surface by solving the MBAR/UWHAM equations to reweight the biased sampling. The samples are histogrammed, and the free energy of each bin is tabulated. We use fourth-order Cardinal B-splines to represent the surface as a smooth function. A mathematical description of the B-spline interpolation is provided in the Supporting Information for completeness. The free energy values are formally defined only in those regions whose histogram bins are occupied by at least one sample. In practice, we exclude all bins containing fewer than 10 samples because their free energy values are often unreliable.

To optimize a path on a fixed free energy surface, we adapt the MSMCV by replacing eq. 10 with eq. 11, where $F\left(\mathbf{q}\right)$ is the value of the unbiased free energy at $\mathbf{q}$.

$$q_{\text{c},n}^{(k+1,s+1)}=\underset{q}{\text{arg min}}\left\{F(q)+W(q;{\overline{k}}^{(k)},q_n^{(k+1,s)})\right\}$$ (11)

$$q_n^{(k+1,s+1)}=q(p_n;q_{\text{c}}^{(k+1,s+1)},p_{\text{c}}^{(k+1,s+1)})$$ (12)

The $q_{\mathrm{c},nd}^{(k,s)}$ values are the control points of the synthetic images used to describe the path. Specifically, $n$ indexes the synthetic image, $d$ indexes the dimension, $k$ is the string iteration, and $s$ is the synthetic iteration. The number of synthetic images, $N_{\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{g}}$, does not need to be the same as the number of images used to perform explicit simulations, $N_{\text{img}}$. In the present work, we use $N_{\text{simg}}=100$ to describe the path. The biasing potential appearing in eq. 11 requires a set of force constants for each synthetic image. If the number of simulated images was the same as the number of synthetic images, then the simulation force constants could be reused to define the synthetic image biasing potentials. The number of synthetic images is often much larger than the number of simulated images; therefore, one needs to transform the $N_{\mathrm{i}\mathrm{m}\mathrm{g}}\times N_{\mathrm{d}\mathrm{i}\mathrm{m}}$ simulation force constants into a set of $N_{\text{simg}}\times N_{\text{dim}}$ force constants. Our choice is to use a common set of force constants for each synthetic image by averaging the simulated force constants; that is, ${\bar{k}}_d=N_{\mathrm{i}\mathrm{m}\mathrm{g}}^{-1}{\sum }_{n=1}^{N_{\mathrm{i}\mathrm{m}\mathrm{g}}} k_{nd}^{\left(k\right)}$. Equation 11 is analogous to the MSMCV, but instead of performing a biased simulation of $3N$ atomic coordinates to obtain the reaction coordinate distribution means, one performs a minimization directly on a biased $N_{\text{dim}}$ free energy surface. In other words, eq. 11 is a synthetic iteration that allows us to repeatedly propagate the string without producing additional sampling. The path is optimized with $N_{\text{siter}}$ iterations (or until convergence is sufficiently met), such that ${\mathbf{q}}_{\mathrm{o}\mathrm{p}\mathrm{t}}^{(k+1)}(p)\equiv \mathbf{q}(p;{\mathbf{q}}_{\mathrm{c}}^{(k+1,N_{\text{siter}})},{\mathbf{p}}_{\mathrm{c}}^{(k+1,N_{\text{siter}})})$ is the best estimate of the MFEP from the available sampling. The optimized synthetic control points also serve as the initial guess for the path in the next string iteration: ${\mathbf{q}}_{\mathrm{c},n}^{(k+1,0)}={\mathbf{q}}_{\mathrm{c},n}^{(k,N_{\text{siter}})}$.

By optimizing the MFEP on the current estimate of the free energy surface, the $N_{\text{img}}$ real images are no longer responsible for describing the path. Instead, their sole responsibility is to provide sampling to improve the the quality and range of the free energy surface. For this purpose, the SASM evolution step (eq. 13) includes two modifications relative to a simple uniform discretization.

$${\mathbf{q}}_n^{(k+1)}={\mathbf{q}}_{\mathrm{o}\mathrm{p}\mathrm{t}}^{(k+1)}(p_n+\text{Δ}{p}^{(k+1)})+\text{Δ}{\mathbf{q}}_n^{(k+1)}$$ (13)

The first modification is a shifting of the progress control points when discretizing the parametric curve,

$$p_n+\text{Δ}{p}^{(k+1)}=\left\{\begin{array}{ll}{p}_{n,0},& \text{if}N(p_{n,0})=0\\ p_{n,-1/3},& \text{else if}N(p_{n,-1/3})=0\\ p_{n,+1/3},& \text{else if}N(p_{n,+1/3})=0\\ p_{n,0},& \text{else if}\mathrm{m}\mathrm{o}\mathrm{d}(k,3)=0\\ p_{n,-1/3},& \text{else if}\mathrm{m}\mathrm{o}\mathrm{d}(k,3)=1\\ p_{n,+1/3},& \text{else if}\mathrm{m}\mathrm{o}\mathrm{d}(k,3)=2\end{array}\right.$$ (14)

where $p_{n,0}$ is a uniform discretization, and $p_{n,+1/3}$ and $p_{n,-1/3}$ shift the discretization by 1/3 of the distance to a neighboring image.

$$p_{n,x}=\mathrm{m}\mathrm{a}\mathrm{x}\left(0,\mathrm{m}\mathrm{i}\mathrm{n}\left(1,\frac{n-1+x}{N_{\mathrm{i}\mathrm{m}\mathrm{g}}-1}\right)\right)$$ (15)

$N\left(p\right)$ is the number of samples that have been observed at the point ${\mathbf{q}}_{\mathrm{o}\mathrm{p}\mathrm{t}}^{(k+1)}(p)$. In other words, the first 3 cases in eq. 14 check whether there are gaps in the sampling along the path. If there is a gap, then sampling at that position is prioritized. The last 3 cases in eq. 14 are a schedule that is followed when no gaps in the sampling are detected. The schedule alternates between these displacements during the course of the string optimization to help ensure that one obtains sufficient sampling along the path in the event that one underestimated an appropriate value of $N_{\mathrm{i}\mathrm{m}\mathrm{g}}$.

The second modification is the introduction of $\text{Δ}{\mathbf{q}}_n^{(k+1)}$ which displaces the image in the direction of the path’s movement.

$$\text{Δ}{\mathbf{q}}_n^{(k+1)}=\left\{\begin{array}{ll}0,& \text{if}\mathrm{m}\mathrm{o}\mathrm{d}(k,4)=0\\ [1-{\delta }_{0,N(p_n+\text{Δ}{p}^{(k+1)})}]h_1\frac{\text{Δ}{\mathbf{q}}_{\text{min},n}^{(k+1)}}{\mid \text{Δ}{\mathbf{q}}_{\text{min},n}^{(k+1)}\mid },& \text{if}\mathrm{m}\mathrm{o}\mathrm{d}(k,4)=1\\ 0,& \text{if}\mathrm{m}\mathrm{o}\mathrm{d}(k,4)=2\\ [1-{\delta }_{0,N(p_n+\text{Δ}{p}^{(k+1)})}]h_2\frac{\text{Δ}{\mathbf{q}}_{\text{min},n}^{(k+1)}}{\mid \text{Δ}{\mathbf{q}}_{\text{min},n}^{(k+1)}\mid },& \text{if}\mathrm{m}\mathrm{o}\mathrm{d}(k,4)=3\end{array}\right.$$ (16)

We refer to $\text{Δ}{\mathbf{q}}_n^{(k+1)}=0$ as a refinement step that places the simulations along the path, and the other cases are exploration steps intended to better describe the free energy surface in the vicinity of path in the direction of its movement. The exploration steps accelerate the evolution of the string through flat areas of the free energy surface. The leading Kronecker delta function causes the exploration step to be skipped if a gap in the sampling was previously detected in eq. 14. The exploration direction is determined from the difference between the optimized paths of the current and previous iterations.

$$\text{Δ}{\mathbf{q}}_{\mathrm{m}\mathrm{i}\mathrm{n},n}^{(k+1)}={\mathbf{q}}_{\mathrm{o}\mathrm{p}\mathrm{t}}^{(k+1)}(p_n+\text{Δ}{p}^{(k+1)})-{\mathbf{q}}_{\mathrm{o}\mathrm{p}\mathrm{t}}^{\left(k\right)}(p^{\ast })$$ (17)

The value of $p^{\ast }$ is the point on the previous path that is closest to the point $p_n+\text{Δ}{p}^{(k+1)}$ on the current path.

$$p^{\ast }=\underset{p}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}{\left|{\mathbf{q}}_{\mathrm{o}\mathrm{p}\mathrm{t}}^{(k+1)}(p_n+\text{Δ}{p}^{(k+1)})-{\mathbf{q}}_{\mathrm{o}\mathrm{p}\mathrm{t}}^{\left(k\right)}(p)\right|}^2$$ (18)

The $h_m$ values are the magnitude of the displacement, where $w_d$ is a width assigned to each dimension. In the present work, we use $w_d=0.15\text{Å}$ for all dimensions, which is also the width of the histogram bins used to construct the free energy surface.

$$h_m=\mathrm{m}\mathrm{i}\mathrm{n}\left(m{w}_1\frac{\mid \text{Δ}{\mathbf{q}}_{\mathrm{m}\mathrm{i}\mathrm{n},n}^{(k+1)}\mid }{\mid \text{Δ}{q}_{\mathrm{m}\mathrm{i}\mathrm{n},n,1}^{(k+1)}\mid },\cdots ,m{w}_{N_{\mathrm{d}\mathrm{i}\mathrm{m}}}\frac{\mid \text{Δ}{\mathbf{q}}_{\mathrm{m}\mathrm{i}\mathrm{n},n}^{(k+1)}\mid }{\mid \text{Δ}{q}_{\mathrm{m}\mathrm{i}\mathrm{n},n,N_{\mathrm{d}\mathrm{i}\mathrm{m}}}^{(k+1)}\mid }\right)$$ (19)

If one imagines the point at $p_n+\text{Δ}{p}^{(k+1)}$ as being located at the corner of a voxel, then eq. 19 can be interpreted as choosing the magnitude to be the maximum displacement that does not exceed the range of $m$ voxels.

The SASM method has several parameters that can be adjusted, including: the number of simulated images $N_{\text{img}}$, the number of synthetic images $N_{\text{simg}}$, the simulation length $\text{Δ}t$, the biasing potential force constants $\mathbf{k}$, the cyclic schedules shown in eqs. 14 and 16, and the voxel width $w_d$ appearing in eq. 19. Unlike the SMCV and MSMCV, the SASM requires an estimate of the unbiased free energy surface to propagate the string. The calculation of an unbiased free energy surface from solution of the MBAR/UWHAM equations requires overlap between the biased distributions,^65–67 so a suitably large value of $N_{\mathrm{i}\mathrm{m}\mathrm{g}}$ is necessary. An optimal choice of $N_{\mathrm{i}\mathrm{m}\mathrm{g}}$ depends on the length of the string, the gradient of the underlying free energy surface, and the values of $\mathbf{k}$ and $\text{Δ}t$. In practice, one can validate their choice of $N_{\mathrm{i}\mathrm{m}\mathrm{g}}$ by analyzing the sampling overlap produced from their initial guess pathway. In the event that the MFEP was significantly longer than the initial guess, $N_{\text{img}}$ may become too small during the course of the string method. We did not design the SASM to dynamically choose the value of $N_{\text{img}}$ based on the current string length because changes in $N_{\text{img}}$ may complicate resource allocation scheduling requests. Instead, the progress variable shifts (eq. 14) effectively increase $N_{\text{img}}$ over the course of several string iterations to minimize the consequences of having chosen an insufficiently small value. By using a cyclic schedule of length 3, eq. 14 acts to effectively increase $N_{\text{img}}$ by a factor of 3 over a series of string iterations. Alternatively, if the calculations were prepared with an excessive number of images, then the proposed shifts would be very small in relation to the length of the string, ${\mathbf{q}}_{\text{opt}}^{(k+1)}(p_n+\text{Δ}{p}^{(k+1)})\approx {\mathbf{q}}_{\text{opt}}^{(k+1)}(p_n)$, rendering the shifts unnecessary.

The displacement schedule (eq. 16) alternates between refinement and exploration iterations to avoid introducing a bias to the exploration direction (eq. 17). In other words, if the exploration direction was chosen by optimizing a path on a surface that introduced new sampling in areas offset from the current path, then the new path is more likely to move in the direction of the added sampling. Our recommended displacement schedule cycles every 4 iterations rather than 2 iterations. We have explored the use of 2 iteration schedules that alternate between refinement and exploration iterations with $h_1$ or $h_2$ (eq. 19) using $w_d=0.15\text{Å}$. In brief, the 2 iteration schedule involving $h_2$ was found to converge the MFEP faster than the 2 iteration schedule involving $h_1$, and it performed about as well as the 4 iteration schedule. We recommend the 4 iteration schedule because it is less likely to produce gaps in the sampling. Appropriate values of $h_m$ are coupled to the value of $w_d$. We use histogram bin widths of $0.15\text{Å}$ to construct the free energy surface because smaller bin widths are more likely to produce numerical noise in the free energy surface, which manifests as noise in the optimized path.⁴⁹ Furthermore, if the displacements become too large, then extended simulations may be necessary to equilibrate the system after making a significant change to the biasing potential. Once the SASM has converged, further iterations will fluctuate around the MFEP. These random fluctuations, when coupled with the displacement schedule, causes the sampling to envelope a tube of nearby histogram bins surrounding the MFEP.

2.5. Computational Details

All QM/MM simulations in this work were performed with the sander molecular dynamics software⁵⁴ using the default leapfrog integrator with a 1 fs integration time step. More efficient sampling with a longer integration time step may be obtained by using the recently developed “middle” thermostat scheme described in Refs. 72 and 73, which is already available in the Amber software. The SHAKE algorithm⁷⁴ was used to fix MM bonds involving hydrogen, whereas all QM bonds were left unconstrained. The covalent bonds at the QM/MM boundary were capped with the hydrogen link-atom approach.^75,76 Electrostatics were calculated with the particle mesh Ewald method^77–79 adapted for use within semiempirical QM/MM simulations^80,81 using tinfoil boundary conditions^82,83 a 1 ų reciprocal space grid, and 10 Å real space cutoffs. The Lennard-Jones interactions were similarly calculated to 10 Å and a long-range tail correction was included to account for the interactions beyond the cutoff.⁸⁴

The MTR1 ribozyme (PDB ID 7V9E⁵⁸) consists of 2, 207 atoms with a net 66– charge. The ribozyme was solvated with 18, 250 TIP4P/Ew waters, 113 sodium ions, and 47 chlorine ions in a truncated octahedron with real space lattice vectors of length 90.2 Å resulting in 75, 367 particles and an ion concentration of 140 mM. The ff99OL3 RNA force field⁸⁵ and Joung and Cheatham⁸⁶ monovalent ion parameters have been used. Details regarding the preparation and equilibration of this system have already been reported elsewhere.⁸⁷ In brief, the pressure and temperature were equilibrated for 50 ns with the MM force field potential to maintain 1 atm and 298 K in the isothermal-isobaric ensemble using the Berendsen barostat⁸⁸ and Langevin thermostat⁸⁹ with a collision frequency of 5 ps⁻¹. At this point, the MM force field was replaced with the DFTB3 QM/MM potential using the “3ob” parameter set.⁹⁰ The QM region consists of 48 atoms with net 1+ charge, as illustrated in Figure 1. A QM/MM simulation of the reactant state was equilibrated for 12.5 ps in the canonical ensemble at 298 K. The DFTB3 QM/MM umbrella production sampling was similarly performed at constant temperature with 200 kcal mol⁻¹ Å⁻² force constants on the two reaction coordinates describing the transfer of a proton, ${\xi }_1=R_{\mathrm{C}10:\mathrm{N}3\text{-}\mathrm{H}}-R_{\mathrm{O}6\mathrm{m}\mathrm{G}:\mathrm{N}1\text{-}\mathrm{H}}$, and methyl group, ${\xi }_2=R_{\text{O6mG:O6-C}}-R_{\text{A63:N1-C}}$ as visualized in Figure 1.

The HHr ribozyme (PDB ID 2OEU⁵⁹) consists of 2, 020 atoms with a net 62– charge. The ribozyme was solvated with 13, 319 TIP4P/Ew waters, 5 magnesium ions (replacing the crystal structure manganese ions), 86 sodium ions, and 34 chlorine ions in a truncated octahedron with real space lattice vectors of length 81.7 Å resulting in 55, 421 particles and an ion concentration of 140 mM. The ff99OL3 RNA force field,⁸⁵ Joung and Cheatham⁸⁶ monovalent ion, and Li-Merz⁹¹ 12-6-4 divalent ion parameters with Panteva^92,93 corrections, which ensure balanced interactions between metal ions and nucleic acids, have been used. Full details of the preparation and equilibration of this system has been reported elsewhere.⁹⁴ In brief, the pressure and temperature were equilibrated for 100 ns with the MM force field potential to maintain 1 atm and 298 K in the isothermal-isobaric ensemble. The MM force field was replaced with the AM1/d QM/MM potential.⁹⁵ The QM region consists of 85 atoms with net 1– charge. The QM region is illustrated in Figure 1; for clarity, the Mg²⁺ and the 4 waters directly coordinating the Mg²⁺ were including in the QM region. A QM/MM simulation of the reactant state was equilibrated for 50 ps in the canonical ensemble at 298 K. All AM1/d QM/MM umbrella production sampling was performed at constant temperature with 200 kcal mol⁻¹ Å⁻² force constants on the three reaction coordinates describing the proton transfer from the nucleophile to the general base, ${\xi }_1=R_{\mathrm{G}12:\mathrm{N}1\text{-}\mathrm{H}}-R_{\mathrm{C}17:\mathrm{O}2’\text{-}\mathrm{H}}$, and phosphoryl transfer, ${\xi }_2=R_{\mathrm{P}\text{-}\mathrm{O}5’}-R_{\mathrm{C}17:\mathrm{O}2’\text{-}\mathrm{O}5’}$. and the proton transfer from the general acid to the leaving group, ${\xi }_3=R_{\mathrm{G}8:\mathrm{O}2’\text{-}\mathrm{H}}-R_{\mathrm{O}5’\text{-}\mathrm{H}}$.

The B-DNA sequence (PDB ID 113D)⁶⁰ consists of 762 atoms with a net 22– charge. The ribozyme was solvated with 5, 151 TIP4P/Ew waters, 35 sodium ions, and 13 chlorine ions in a truncated octahedron with real space lattice vectors of length 59.3 Å resulting in 21, 414 particles and an ion concentration of 140 mM. The system was modeled with the OL5 DNA force field⁹⁶ and Joung and Cheatham⁸⁶ monovalent ion parameter set. The system was prepared by minimizing the solvent environment and hydrogen positions while restraining the DNA heavy atoms, followed by a gradual heating of the system from 0 to 298 K over the course of 300 ps in the NVT ensemble, and the system density was equilibrated at 1 atm for 8 ns in the NPT ensemble. The MM force field was replaced with the AM1/d QM/MM potential,⁹⁵ where the QM region (the G4 and T21 nucleobases depicted in Figure 1) consists of 31 atoms with net neutral charge. A QM/MM simulation of the reactant state was equilibrated for 50 ps in the canonical ensemble at 298 K. All AM1/d QM/MM umbrella production sampling was performed at constant temperature with 200 kcal mol⁻¹ Å⁻² force constants for each of the reaction coordinates listed in Figure 1.

To start any string method, one must first construct a series of structures to be used as the initial guess. For the MTR1 reaction, we consider two initial guesses: a concerted guess that uniformly discretizes a line connecting the approximate position of the reactant state ${\mathit{\xi }}_{\text{react.}}=(-1.4\text{Å},-2.5\text{Å})$ to the product state ${\xi }_{\text{prod.}}=(1.4\text{Å},2.5\text{Å})$, and a stepwise guess that uniformly discretizes a piecewise linear path connecting the reactant state, approximate intermediate state ${\mathit{\xi }}_{\text{inter.}}=(1.4\text{Å},-2.5\text{Å})$, and the product state. For the HHR reaction, the initial guess discretizes a linear transformation between the approximate reactant state ${\mathit{\xi }}_{\text{react.}}=(-1\text{Å},-2\text{Å},-1\text{Å})$ to the approximate product state ${\mathit{\xi }}_{\text{prod.}}=(1\text{Å},2\text{Å},1\text{Å})$. Similarly, the initial guess for the B-DNA tautomer reaction discretizes a linear transformation between the reactant ${\xi }_{\text{react.}}=(-0.86\text{Å},-0.60\text{Å}$, $-2.0\text{Å},-0.76\text{Å},-2.6\text{Å})$ and product states ${\mathit{\xi }}_{\text{react.}}=(0.67\text{Å},0.78\text{Å},-0.82\text{Å},0.84\text{Å},0.22\text{Å})$. The atomic coordinates were generated from a sequence of short (200 fs) simulations that restart each image from the final structure of the previous image. After this scan was completed, each image was independently equilibrated for an additional 4 ps. The final coordinates from these equilibrations became the starting structures to initiate the string method.

The SMCV, MSMCV, and SASM were performed multiple times while varying the number of images and length of production sampling. The MTR1 simulations performed for 4 ps/image and 500 fs/image saved 400 samples/image and 250 samples/image, respectively. The HHr simulations performed for 625 fs/image and 312 fs/image saved 125 samples/image and 156 samples/image, respectively. The B-DNA simulations were performed for 1 ps/image and 200 samples/image were saved. In all cases, we analyze only the last 75% of saved samples when solving the MBAR/UWHAM equations.

3. Results and Discussion

Here we compare the SMCV, MSMCV, and SASM string methods using three reactive chemical systems having varying number of reaction coordinates. 1. A 2D example of an artificially engineered methyltransferase ribozyme (MTR1)⁵⁶ that catalyzes the methylation of a target adenine. 2. A 3D example of a naturally occurring hammerhead ribozyme (HHr)⁵⁹ that catalyzes site-specific RNA self-cleavage. 3. A 5D example of tautomerization in dG·dT wobble pairs that lead to misincorporation during replication.⁹⁷

3.1. MTR1 catalytic mechanism

Evolutionary theories based on an RNA world^98,99 presumably would require RNA molecules to catalyze C-C and C-N bond formation essential for nucleic acid synthesis and early metabolic transformations. There are no known naturally occurring examples of RNA enzymes that have this ability. Recently, a methyltransferase ribozyme (MTR1) has been evolved in vitro⁵⁶ that binds O⁶-methylguanine and catalyzes the methylation of a target adenine (A63) at the N1 position^57,100 (Figure 1a). Computational enzymology studies performed by our group,⁸⁷ in collaboration with Huang, Lilley and co-workers,⁵⁸ revealed a surprising sophisticated mechanism that involves a protonated cytosine residue that acts as an acid in order to facilitate site-specific C-N bond formation, broadening the range of known RNA-catalyzed chemistry and further demonstrating versatility of RNA catalysis.¹⁰¹ In the computational study, we employed an early version of the string method and found it to be slowly convergent, making it extremely costly to perform ab initio QM/MM simulations. Hence, we use this as our first test system for developing improved string methods with accelerated convergence.

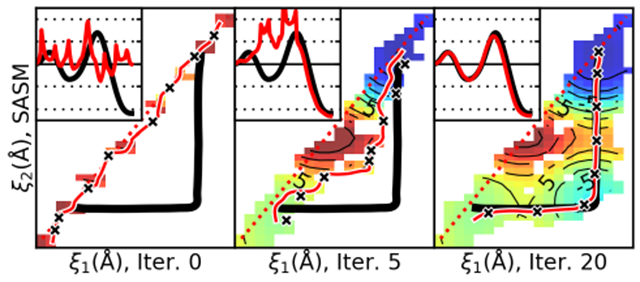
Figure 2 uses the MTR1 reaction to compare the progress of the SMCV, MSMCV, and SASM at string iterations 5, 15, 30, and 50. Each optimization was performed twice, starting from concerted and stepwise initial paths. Each string iteration samples 32 images for 4 ps/image (128 ps/iteration). The free energy surface is a best estimate made from the aggregate sampling of all iterations obtained from the 3 methods (38.4 ns of aggregate sampling). The black line is a reference MFEP, optimized on the aggregate free energy surface. The SMCV and MSMCV paths are Akima splines fit to the 32 evolved images, whereas the SASM paths are Akima splines fit to 100 synthetic images.

Figure 2:

Progress of the string methods at several iterations of the MTR1 reaction starting from concerted (red lines) and stepwise (green lines) initial guess paths. Parts a-d, e-h, and i-l illustrate the convergence of the SMCV, MSMCV, and SASM, respectively. Each string is composed of 32 images, and each image is sampled for 4 ps. The initial guesses are dashed lines. The colored areas are the best estimate of the free energy surface, calculated from the aggregate sampling produced by all string methods. The black line is the MFEP optimized on the best estimate of the surface. The insets are the reference free energy values along the paths (kcal/mol).

The three methods approach the MFEP at different rates. The SMCV and MSMCV make good progress during the first 15 iterations, but their progress stalls as they near the MFEP. This is due to the free energy surface becoming relatively flat near the MFEP. In contrast, the SASM gets closer to the MFEP at iteration 5 than the SMCV or MSMCV do at iteration 50. By placing the simulations around the path, the SASM is capable of exploring flat surfaces more efficiently.

To test whether the conclusions drawn from Figure 2 are sensitive to the simulation time scale (time/image), we re-performed the string methods using only 500 fs/image of sampling. The resulting comparison (Supporting Information Figure S1) is nearly indistinguishable from Figure 2.

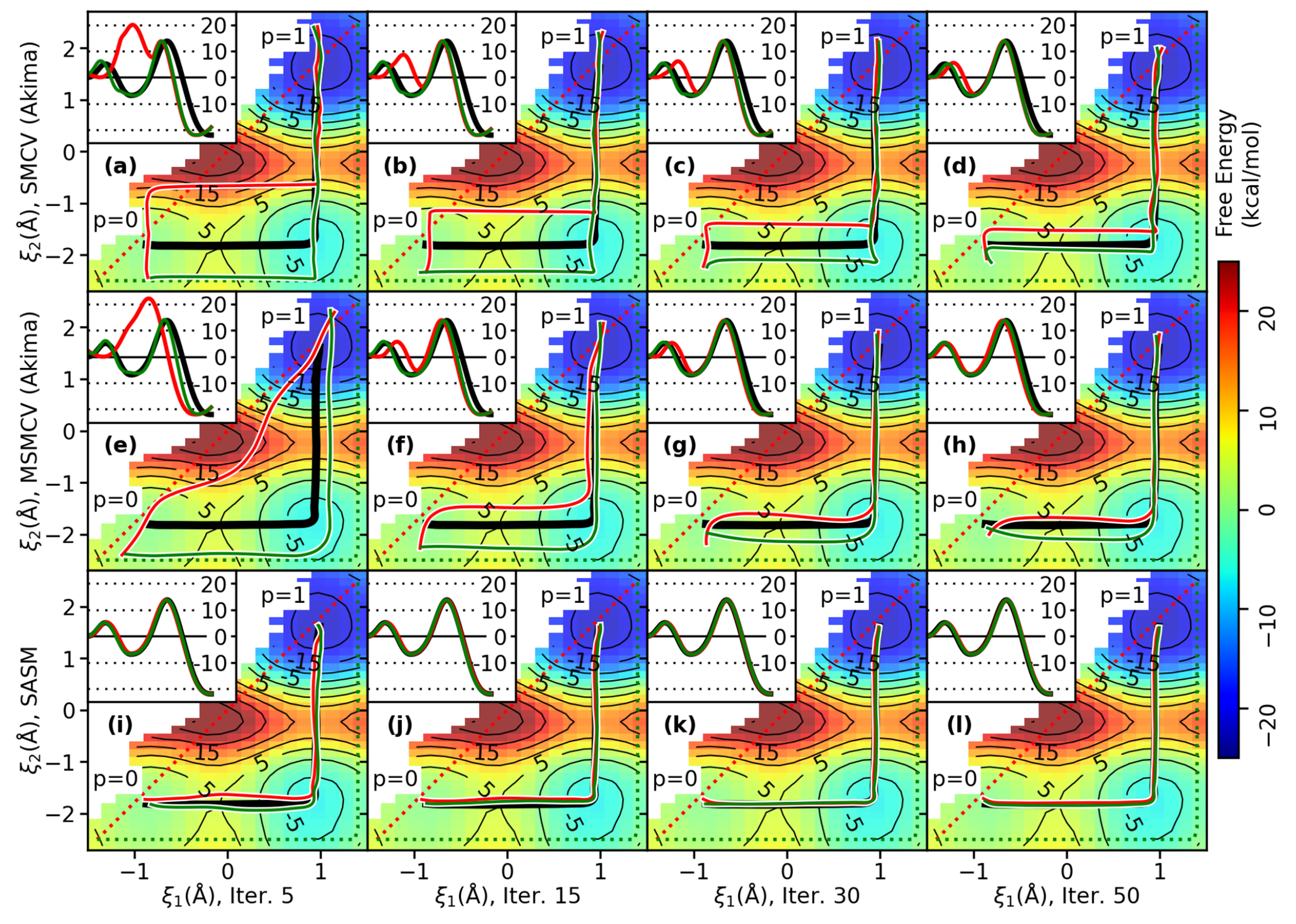
Figure 3 compares the string methods using fewer images and different spline representations of the path. The optimizations start from a concerted path, and each iteration samples 8 images for 4 ps/image. The colored areas are the current estimate of the free energy surface from the sampling produced by the current and previous iterations. The red line is the estimate of the path after the evolution step. The “x” marks are the proposed set of umbrella potential locations. The black line is the reference path shown in Figure 2. The insets display the free energy along the paths; the red line is the free energy of the current path from the available sampling, and the black line is the reference free energy along the reference path (made from 38.4 ns of aggregate sampling). The rows labeled “Akima” and “Linear” construct the parametric curve from Akima splines and piecewise linear functions, respectively. Whereas the SMCV and MSMCV paths are limited to 8 control points, the SASM path is constructed from Akima splines which interpolate 100 synthetic images optimized on the free energy surface.

Figure 3:

String iterations of MTR1 from a concerted (linear) initial guess (dashed red line). Each string is composed of 8 images, and each image is sampled for 4 ps. The solid red line is the current string, and the black “x” marks the next set of 8 simulations. The black line is a reference pathway, and the insets compare the current estimate of the free energy profile to the reference profile (kcal/mol). Parts a-d and e-h are the SMCV method using Akima and piecewise linear splines, respectively. Parts i-l and m-p similarly compare the MSMCV method. Parts q-t are the SASM method with 100 synthetic images.

Figure 3 illustrates that the SMCV and MSMCV methods are sensitive to the parametric form of the path when only a few (e.g., 8) images are simulated. Although the SMCV and MSMCV methods properly evolve the control points, both methods encounter artifacts within the reparametrization step when the path is modeled with Akima splines. The artifacts encountered by the SMCV are quite severe; reparametrization of the curve causes some images to be propagated in a direction away from the MFEP (Figure 3a–b), and the converged path differs significantly from the reference path (Figure 3d). The MSMCV similarly encounters artifacts between iterations 15 and 50, and it converges to an incorrect path (Figure 3l). The SMCV and MSMCV methods do approach the correct MFEP when using piecewise linear curves, however (see Figure 3h and p). The SASM does not exhibit artifacts using Akima splines because it is parametrized to 100 synthetic control points rather than 8 control points. By using more control points to define the path, the SASM also avoids corner cutting, which can be observed when using piecewise linear paths; for example, see the intermediate state in Figure 3p.

When only 8 images are simulated, the progress of the SASM is modestly better than SMCV (Linear) and MSMCV (Linear); however, the SASM does a much better job at producing samples to analyze the free energy surface. As can be seen in the insets of Figures 3a–p, the limited number of images causes the SMCV and MSMCV to produce sampling that does not well overlap, resulting in noisy free energy profiles. In contrast, the SASM evolution step shifts the progress values to improve the sampling between the set of uniformly discretized points, and the exploration steps provide sampling around the path. Consequently, the SASM free energy profile after 15 iterations reproduces the reference profile very well (Figure 3s). In fact, the SASM profile after 15 iterations is better than the SMCV and MSMCV profiles after 50 iterations. The SASM placement algorithm attempts to fill the gaps in the sampling, which is easiest to observe in Figure 3q. After sampling the initial guess, the optimized path remains similar to the initial guess because all areas of the surface which have not been sampled are assumed to have a high free energy. The first 3 cases in eq. 14 propose new simulations in the unoccupied regions along the path.

3.2. HHr Mechanism

The hammerhead ribozyme (HHr)^59,102–104 is a metal-dependent small endonucleolytic self-cleaving RNA that has been extensively studied experimentally^{105–107,107,108} and computationally,^109–115 and is an archetype model for RNA catalysis. The active site adopts an L-platform/L-scaffold architecture¹¹⁶ with an L-pocket guanine residue that forms a divalent metal ion binding site enabling electrostatic interactions⁹⁴ to facilitate the reaction. The 2′O-transphosphorylation mechanism can be described by three reaction coordinates, illustrated in Figure 1b.

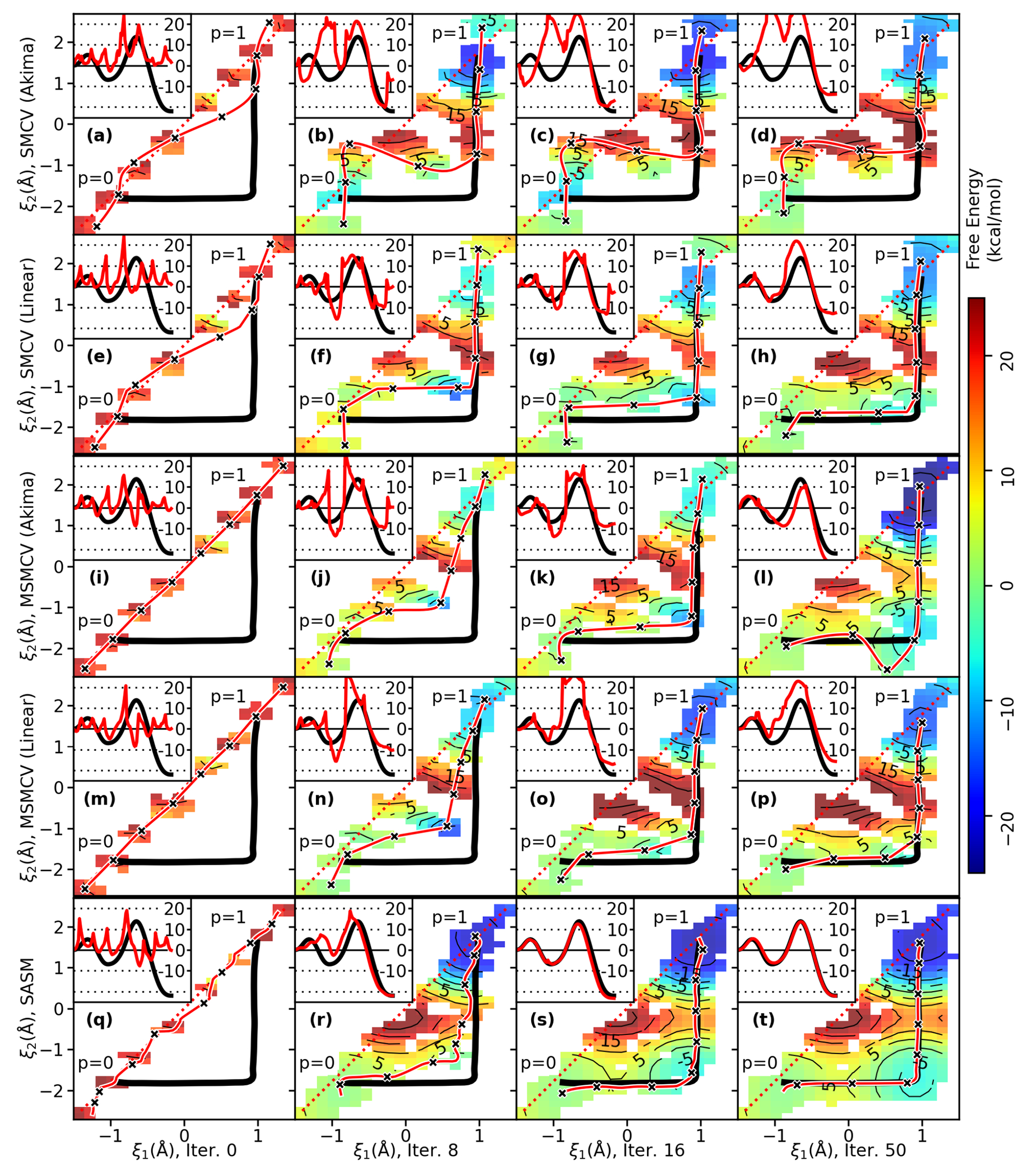
Figure 4 extends the comparisons to the 3 dimensional HHr transphosphorylation reaction profiles. The dashed line is the concerted initial guess, and the remaining lines are the paths at a series of string iterations. The reference path shown in each image is provided as a visual aid. The reference path is the SASM MFEP after 300 iterations using 32 images and 625 fs/image of sampling. In other words, it is the MFEP optimized on the 3 dimensional surface produced from the analysis of 6 ns of aggregate sampling. The string methods were performed multiple times by varying the number of images and the amount of sampling. Each column of Figure 4 successively halves the amount of sampling per string.

Figure 4:

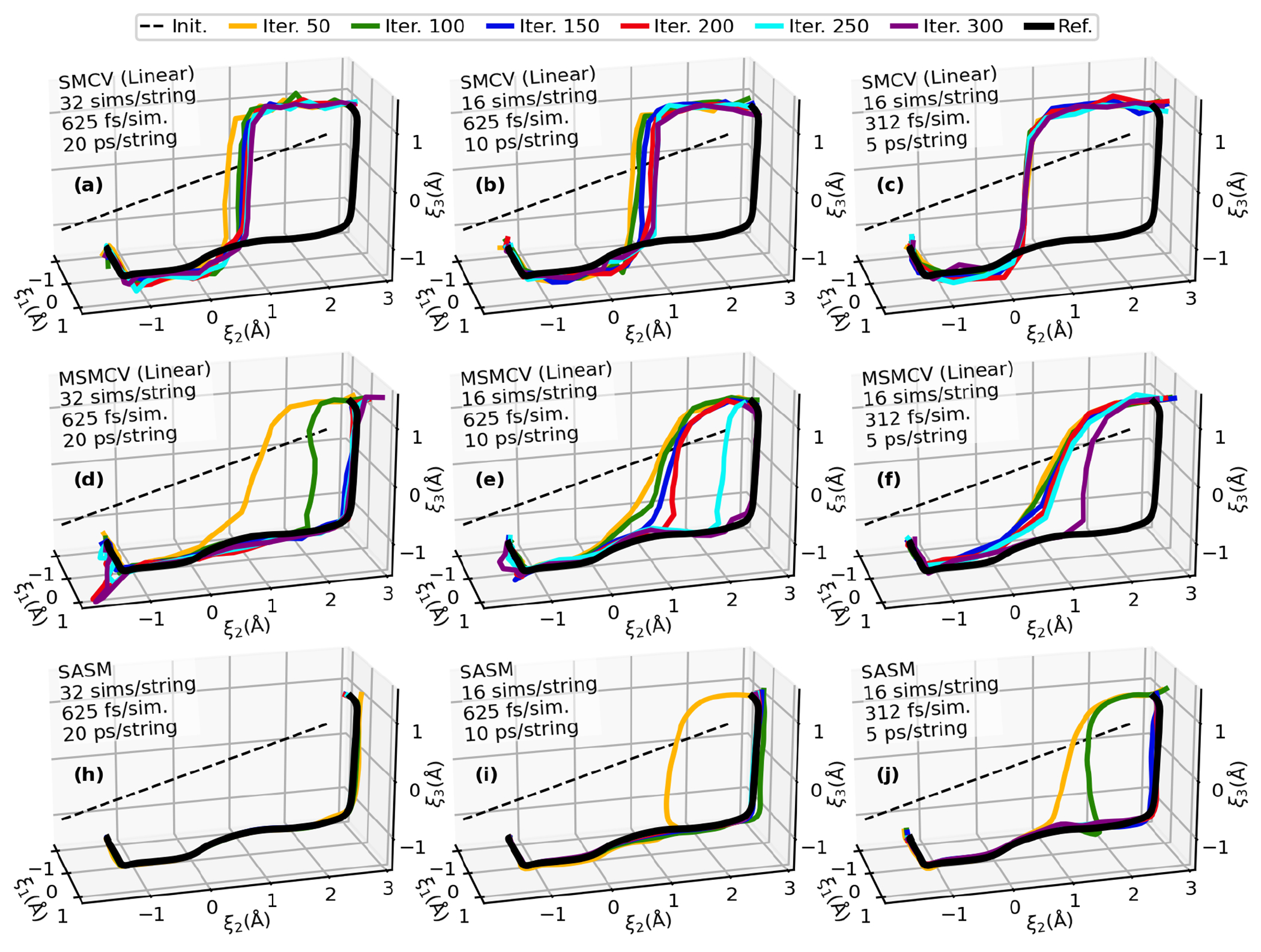
String iterations of HHr from a linear initial guess (dashed black line). Parts a-c, d-f, and h-j illustrate the convergence of the SMCV, MSMCV, and SASM, respectively, with several simulation protocols.

All of the string methods predict that the first stage of the reaction transfers a proton (the ${\xi }_1$ coordinate) from the O2′ to the N1 position of the G12 general base (Figure 1b). The more interesting part of the comparison is the behavior of the paths in the ${\xi }_2\text{-}{\xi }_3$ plane, where ${\xi }_2$ is the phosphoryl transfer coordinate, and ${\xi }_3$ measures the proton transfer between the O5′ and the G8 general acid. The SMCV fails to locate the MFEP after 300 iterations, although it is possible that it may find the MFEP if iterated further.

The MSMCV locates the MFEP, but it requires many iterations. The MSMCV requires 150 iterations to locate the MFEP when performed with 32 images and sampled for 625 fs/image (Figure 4d). This corresponds to 3 ns of aggregate sampling. When the number of images is reduced to 16 (Figure 4e), the amount of sampling per iteration is reduced, but the MSMCV now requires 300 iterations (3 ns of aggregate sampling) to locate the MFEP. Further reduction in the amount of sampling requires more than 300 MSMCV iterations (Figure 4f). Notice that the progress of the MSMCV in Figures 4e–f does not significantly change from iterations 50 to 150, which would likely cause one to incorrectly believe that the path has converged. In fact, previous application of the MSMCV to the HHr reaction incorrectly concluded that the mechanism was concerted because of this behavior,⁴⁹ whereas the extended iterations presented in Figure 4 suggest that the MFEP is stepwise. The fundamental reason why MSMCV progress stalls is because the free energy gradient in the directions perpendicular to the path are quite small (Figure 5). The qualitative similarity between the MSMCV path at iteration 50 to the paths produced by SMCV is suggestive that the SMCV fails for a similar reason.

Figure 5:

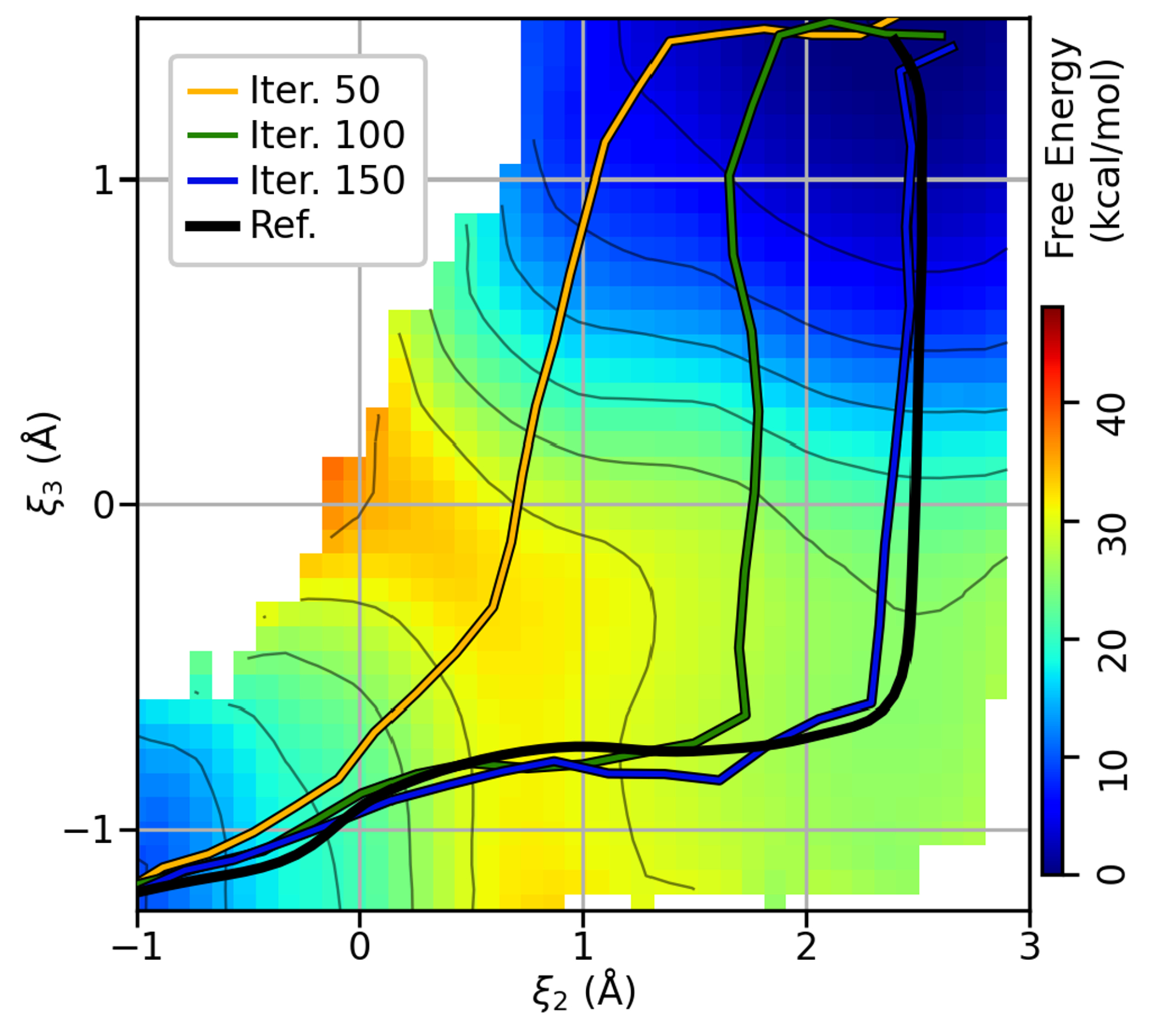
Two dimensional projection of the HHr free energy surface defined by the ${\xi }_1=0.95\mathrm{\AA }$ plane. The colored lines are the MSMCV paths at iterations 50, 100, and 150, and the black line is the SASM reference curve after 300 iterations, as shown in Figure 4d. The colored areas are the free energy values calculated from the aggregate sampling produced from 300 MSMCV and 300 SASM iterations (12 ns of sampling).

In this application, the SASM requires 3 times fewer iterations than MSMCV to reach convergence when using the same amount of sampling. Only 50 SASM iterations are required to converge the path using 32 images (Figure 4h) in comparison to 150 MSMCV iterations. When the number of images is reduced to 16 (Figure 4i), convergence is reached after 100 SASM iterations in comparison to 300 MSMCV iterations. The SASM requires fewer iterations because the synthetic string optimizations performed within the SASM can evolve the path to the fringes of the aggregate sampling, and the exploration steps increase the range of the free energy surface that can be used.

3.3. B-DNA G·T Wobble Tautomer Reaction

Rare tautomeric forms of nucleobases can cause Watson-Crick-like (WC-like) mispairs in DNA, and in turn lead to disease.¹¹⁷ In the WC model, nucleobase pairs are in their “keto” form,¹¹⁸ rather then “imino” or “enol” form. Recently, tautomerization has been reported for a G-T wobble pair ($G^{\text{enol}}T/U\leftrightarrow G{T}^{\text{enol}}/U^{\text{enol}}$) in B-DNA detected by NMR^97,119,120 and subsequently studied computationally.¹²¹ This tautomerization reaction can be described by 5 reaction coordinates (Figure 1b).

A pathway in 5D cannot be visualized in the same way as the 2D and 3D systems, hence Figure 6a illustrates the convergence of the MFEP for the B-DNA tautomer reaction by calculating the root mean square deviation (RMSD) between the current estimate of the path and the initial guess using the 5 reaction coordinates. The SASM RMSD values plateau at 50 iterations, whereas the MSMCV requires 150 iterations to reach a similar RMSD. Although both methods seek to locate the nearest MFEP, they use different representations of the path, so one would not expect the RMSD values to exactly agree. Specifically, the MSMCV path is a piecewise linear spline constructed from 32 images, whereas the SASM path is an Akima spline constructed from 100 synthetic images. After 150 iterations, the SASM and MSMCV paths fluctuate about the MFEP; however, the fluctuations in the SASM RMSD values are significantly dampened because the additional sampling introduced by each iteration represents a smaller percentage of the aggregate. Figure 6b shows the initial and final profiles of the ${\xi }_1=R_{\mathrm{N}3\text{-}\mathrm{H}3}-R_{\mathrm{O}6\text{-}\mathrm{H}3}$ and ${\xi }_2=R_{\mathrm{O}6\text{-}\mathrm{H}3}-R_{\mathrm{O}4\text{-}\mathrm{H}3}$ reaction coordinates. The other 3 reaction coordinates are excluded from the figure to improve legibility. The initial path directly transfers the proton from N3 to the O4 position. The optimized paths instead transfer the proton from the N3 to O6 while shifting the hydrogen bond pattern of the G:T basepair. This is followed by the transfer of the proton from O6 to the O4 position. The SASM and MSMCV produce very similar paths after 150 iterations. In summary, this application shows that the SASM can be extended to 5 dimensions and it can converge the path in fewer iterations than the MSMCV.

Figure 6:

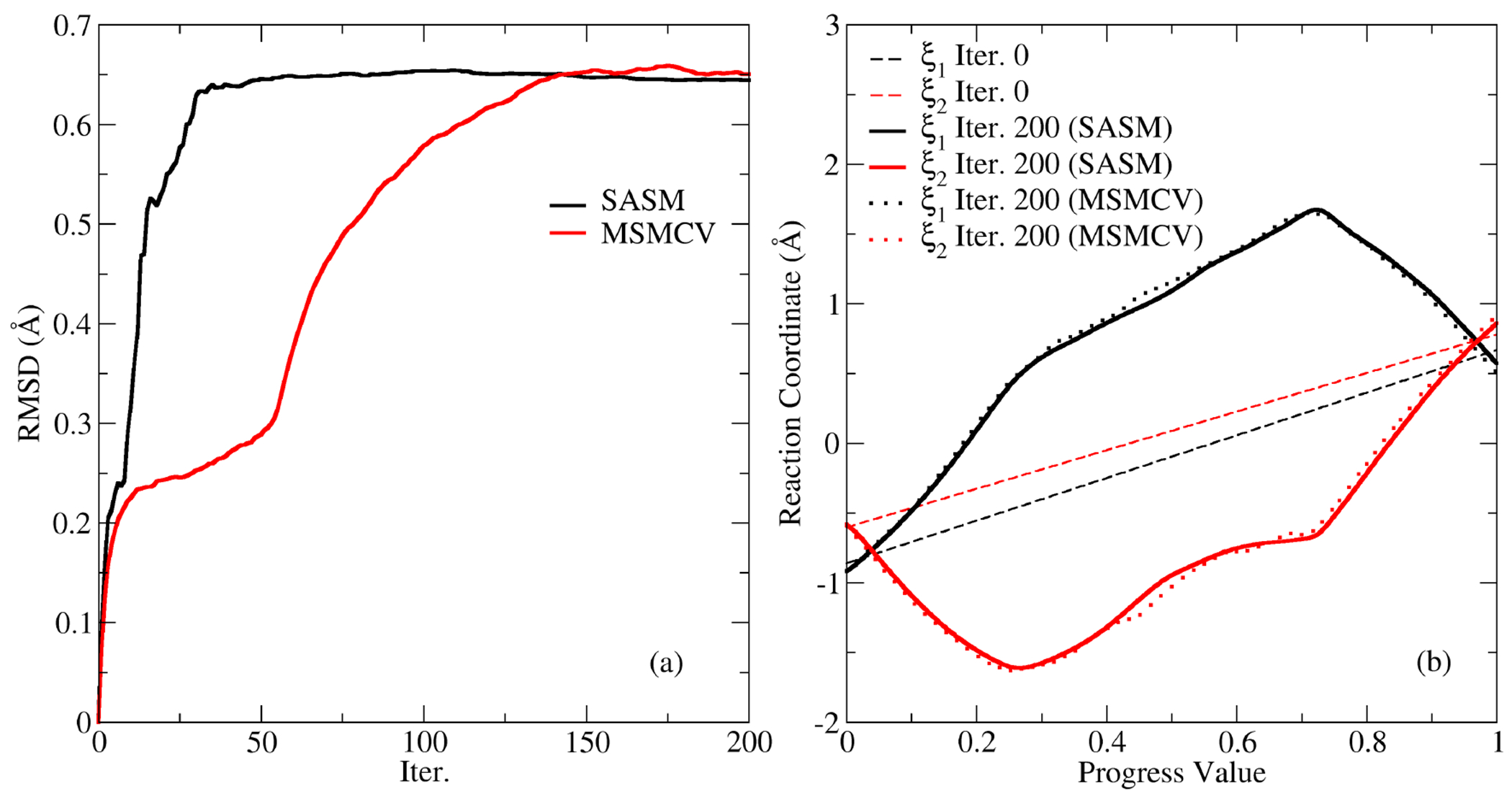
Convergence of the path describing the $\mathrm{w}\mathrm{G}\mathrm{T}\to {\mathrm{G}\mathrm{T}}^{\ast }$ tautomeric reaction in B-DNA. (a) The root mean square deviation of the 5 reaction coordinates relative to the concerted (linear) initial guess. (b) The ${\xi }_1$ and ${\xi }_2$ reaction coordinates along the initial and final pathways produced by the MSMCV and SASM. These two coordinates describe the proton transfer between N3-O6 and O6-O4, respectively.

3.4. Computational Cost

Table 1 compares the CPU resources needed to perform the string methods on the HHr system with 32 images and 625 fs/image of sampling and the B-DNA system with 32 images and 1 ps/image of sampling. The measurements were performed on a single core of an Intel Xeon E5-2630 v3 processor, and the software was compiled with GCC 9.2.1. The timings can be decomposed into two components: the resources used to perform the QM/MM simulations $T_{\text{sim}}$, and the resources used to perform the evolution step $T_{\text{evo}}$.

Table 1:

The number of CPU days required to perform MSMCV and SASM on the HHr and B-DNA systems for the specified number of iterations. Iteration 0 is the simulation and analysis of the initial path. Bold entries denote converged paths.

	HHr			B-DNA
Iter.	$T_{\text{MSMCV}}$	$T_{\text{SASM}}$	$\frac{T_{\text{SASM}}}{T_{\text{MSMCV}}}$	$T_{\text{MSMCV}}$	$T_{\text{SASM}}$	$\frac{T_{\text{SASM}}}{T_{\text{MSMCV}}}$
0	0.51	0.51	1.00	0.19	0.19	1.00
10	5.56	5.56	1.00	2.07	2.08	1.00
25	13.14	13.16	1.00	4.89	4.96	1.01
50	25.77	25.96	1.01	9.60	10.07	1.05
100	51.03	52.48	1.03	19.01	22.57	1.19
150	76.30	81.12	1.06	28.42	40.20	1.41

$$\begin{gathered} T(k)=\sum _{k^{\prime }=0}^k{T}_{\text{sim}}(k^{\prime })+T_{\text{evo}}(k^{\prime }) \\ =(k+1)T_{\text{sim}}+\sum _{k^{\prime }=0}^k{T}_{\text{evo}}(k^{\prime }) \end{gathered}$$ (20)

The MSMCV times only include the resources used to perform the QM/MM simulations; the string evolution step (eq. 10) requires a negligible amount of effort, $T_{\text{evo}}\left(k\right)\approx 0$. The cost of performing MSMCV for the HHr and B-DNA systems are given by eqs. 21 and 22, respectively.

$$T_{\text{MSMCV}}^{\text{HHr}}(k)=(k+1)(32\text{images})\left(\frac{0.625\text{ps}}{\text{image}}\right)\left(\frac{1\text{CPU day}}{39.6\text{ps}}\right)$$ (21)

$$T_{\text{MSMCV}}^{\text{B-DNA}}(k)=(k+1)(32\text{images})\left(\frac{1\text{ps}}{\text{image}}\right)\left(\frac{1\text{CPU day}}{170\text{ps}}\right)$$ (22)

The SASM timings also include the cost of the evolution step, which is further decomposed into the resources used to solve the MBAR/UWHAM equations, $T_{\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{R}}$, and the cost of performing an optimization on the resulting free energy surface, $T_{\text{opt}}$.

$$T_{\mathrm{S}\mathrm{A}\mathrm{S}\mathrm{M}}(k)=T_{\mathrm{M}\mathrm{S}\mathrm{M}\mathrm{C}\mathrm{V}}(k)+\sum _{k^{\prime }=0}^k{T}_{\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{R}}(k^{\prime })+T_{\mathrm{o}\mathrm{p}\mathrm{t}}(k^{\prime })$$ (23)

The solution of the MBAR/UWHAM equations formally scales $O(N_{\text{dim}}{N}_{\text{samples}}{N}_{\text{states}})$, where $N_{\text{samples}}$ is the number of samples to be reweighted and $N_{\text{states}}$ is the number of states. The dimensionality does not vary with string iteration, and $N_{\text{samples}}$ and $N_{\text{states}}$ are both proportional to the number of iterations, leading to $T_{\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{R}}(k)\approx A{(k+1)}^2$, where $A$ is coefficient fit to the observed times. This coefficient is $0.359\mathrm{s}$ and $0.876\mathrm{s}$ for the HHr and B-DNA systems, respectively. The quadratic dependence of $T_{\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{R}}\left(k\right)$ means that the aggregate cost for performing $k$ string iterations scales cubically. The cost of performing the optimization formally scales $O(o^{N_{\text{dim}}}{N}_{\text{siter}}{N}_{\text{simg}})$, where $o$ is the order of the Cardinal B-spline, $N_{\text{siter}}$ is the number of synthetic iterations, and $N_{\text{simg}}$ is the number of synthetic images used to describe the path. These quantities are independent of string iteration, so $T_{\text{opt}}\left(k\right)\approx B$, where $B$ is $0.7\mathrm{s}$ and $19.5\mathrm{s}$ for the HHr and B-DNA systems, respectively.

The timings listed in Table 1 suggest that the SASM increases the computational cost by 1%-5% relative to the MSMCV for the first 50 iterations. This small increase is reflected in the high computational cost of performing QM/MM sampling. Although the SASM is more expensive, it converges in fewer iterations. The SASM reduces the resources needed to converge the path by factors of 2.9 and 2.8 for the HHr and B-DNA systems, respectively. The SASM becomes increasingly expensive with respect to the number of iterations because the MBAR/UWHAM equations are solved using the aggregate sampling. To prevent the method from becoming too costly at high iterations, one could limit the analysis to the samples produced from the most recent 50 iterations, for example.

Figure 7 uses the first 50 SASM iterations of the B-DNA system to illustrate the cost of $T_{\text{MBAR}}$ and $T_{\text{opt}}$ as the number of reaction coordinates is varied. Although the sampling was performed with 5 reaction coordinates, we can measure $T_{\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{R}}$ and $T_{\mathrm{o}\mathrm{p}\mathrm{t}}$ by ignoring 1-or-more of the reaction coordinates during the analysis. As previously discussed, the solution of the MBAR/UWHAM equations has a linear dependence on $N_{\mathrm{d}\mathrm{i}\mathrm{m}}$, and B-spline evaluations of the free energy surface has an exponential dependence on $N_{\mathrm{d}\mathrm{i}\mathrm{m}}$. The dashed lines are linear and exponential fits to the observed times. Figure 7 demonstrates that the SASM quickly becomes impractical when using more than 6 reaction coordinates due to high cost of evaluating the free energy of a high-dimensional surface. Another aspect to consider is that each added dimension further subdivides the samples into different histogram bins. For a fixed amount of sampling, each subdivision reduces the average number of samples per occupied bin and thus increases the uncertainty of the free energy in that region. For these reasons, we do not view the SASM as a replacement for the MSMCV when a large number of reaction coordinates is needed. Instead, the SASM is a complimentary tool specifically tailored to accelerate the convergence of low-dimensional pathways frequently encountered in QM/MM applications. In these situations, the added expense of generating free energy surfaces and optimizing paths from the available sampling is worthwhile to reduce the number of QM/MM evaluations.

Figure 7:

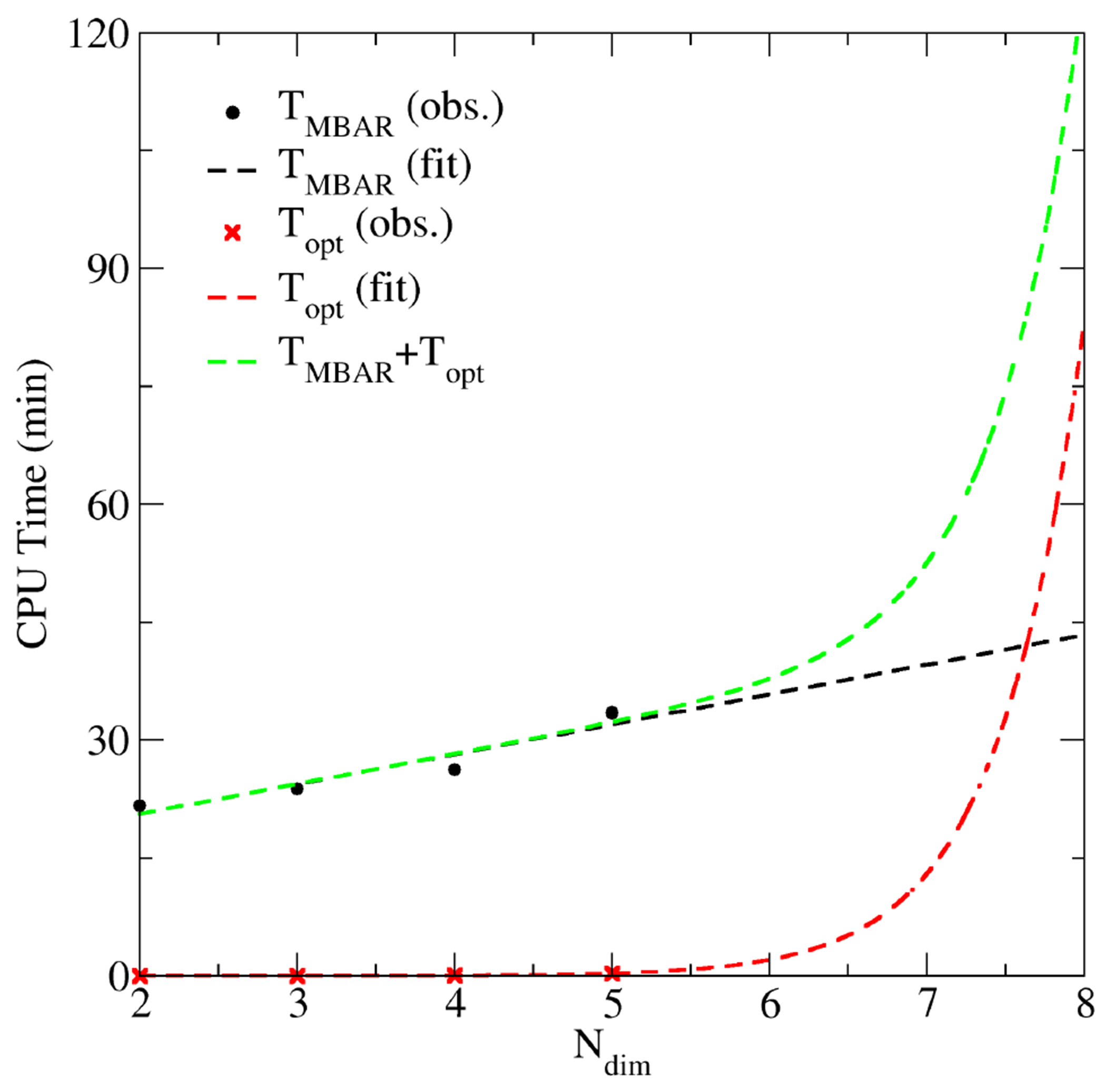
CPU time required to perform MBAR analysis $(T_{\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{R}})$ and path optimization $(T_{\mathrm{o}\mathrm{p}\mathrm{t}})$ on the resulting free energy surface. The observed times were measured using the B-DNA sampling at iteration 50. The black and red dashed lines are linear and exponential fits to $T_{\mathrm{M}\mathrm{B}\mathrm{A}\mathrm{R}}$ and $T_{\mathrm{o}\mathrm{p}\mathrm{t}}$, respectively.

The bond forming and breaking events of many biological mechanisms can be described with 6-or-fewer dimensions; however, this limitation may become problematic when the chemical events are coupled with conformational changes. As a specific example, a previous investigation of nucleobase tautomerization reactions used 13 interatomic distances to describe the change in hydrogen bond patterns.¹²¹ A compromise solution may be to explicitly model the bond forming and breaking coordinates with distances (or distance differences) and describe the conformational changes with path collective variables^28,43 or other strategies developed to reduce the dimensionality.^122–128 Alternatively, the SASM approach could greatly benefit from new methods that are exploring the use of deep neural networks to efficiently represent high-dimensional free energy surfaces.^129,130

The reader may question if there are ideas introduced in the SASM that can be directly used to improve the convergence of the SMCV and MSMCV methods when a high-dimensional free energy surface is too expensive to evaluate. Unfortunately, if the free energy surface is not available, then the synthetic optimizations (eq. 11) are clearly not possible. Furthermore, the SASM progress value shifting (eq. 14) and exploration (eq. 16) modifications rely on the fact that the simulated images are not responsible for describing the path, which is not the situation when using the SMCV or MSMCV methods. Nevertheless, the SASM approach is an enabling technology that allows one to explore new strategies that are not readily possible within the SMCV and MSMCV frameworks, as described below.

The reaction coordinates describing the chemical events are often assigned from chemical intuition, and one typically performs the string method several times starting from different initial guess pathways to compare a limited number of plausible mechanistic scenarios; for example, the associative versus dissociative mechanisms of phosphoryl transfer reactions. From a given initial guess, the SASM seeks to find the nearest MFEP. It is unlikely that that the SASM will discover an alternate pathway unless it was separated by a small barrier that could be leapfrogged by the exploration stage. We have investigated the idea of using the SASM to simultaneously propagate multiple strings, each starting from a different initial guess. Each image from every string is sampled, the sampling is aggregated to form a single free energy surface, and the MFEP of each string is obtained from independent synthetic optimizations on the unified surface. In other words, the SASM is performed for each string, but their progress is synchronized at each iteration to form a single, global view of the free energy surface. The present work did not elaborate on this strategy because we remain unconvinced that it offers a meaningful computational advantage in the few test cases we have performed, which involved pathways that did not significantly overlap with each other in areas other than the reactant and product states. In these situations, it is sufficient to independently converge each string and aggregate the sampling in a post-processing step. Furthermore, we note that the SASM formally provides the capability to sample with an inexpensive reference semiempirical Hamiltonian while propagating the string with a high-level target Hamiltonian by using the weighted thermodynamic perturbation method to construct the free energy surface.^71,131,132 We suspect, however, that a better strategy would be to converge the path with the reference potential, perform production sampling on the final path, and reweight the production sampling to estimate the target free energy surface only in the immediate vicinity of the MFEP.

4. Conclusions

We applied the SMCV, MSMCV and SASM methods to QM/MM sampling of the MTR1, HHr, and B-DNA G·T mispair systems. These applications served to compare the behavior and performance of the string methods using 2, 3, and 5 reaction coordinates. The SASM is a new method developed in this work that is robust and has performance advantages for systems up to approximately 6-dimensions $(N_{\mathrm{d}\mathrm{i}\mathrm{m}}\le 6)$. Rather than propagating the path from the sampling produced by the most recent set of images, the SASM uses the aggregate sampling from all string iterations. The sampling is used to construct the current best-estimate of a multidimensional free energy surface, and a MFEP is optimized on the surface. Consequently, the simulated images are no longer responsible for describing the parametric form of the path; their sole responsibility is to improve the quality and range of the sampling used to estimate the surface. The SASM exploits this freedom by alternating between “exploration” and “refinement” steps to rapidly traverse flat regions of the free energy surface.

Overall, the SMCV, MSMCV, and SASM methods are capable of converging to the correct MFEP if the right control parameters are found. In some cases, spline artifacts can be observed with the SMCV and MSMCV when only a few images (e.g., 8) are used. The SASM is found to be more robust, and it often requires approximately 1/3 of the string iterations to converge the MFEP. Analysis of computational timings indicate that the SASM increases the computational cost per string iteration by 5% or less relative to the MSMCV, but this is more than offset by requiring fewer iterations to reach convergence. The computational cost of representing a free energy surface with more than 6 reaction coordinates quickly becomes prohibitive; therefore, the SASM is not a blanket replacement for the MSMCV. Rather, it is a valuable tool that can be used to considerably accelerate convergence in QM/MM applications using a modest number of reaction coordinates.