Mathematical models of drug-resistant tuberculosis lack bacterial heterogeneity: A systematic review

Naomi M Fuller; Christopher F McQuaid; Martin J Harker; Chathika K Weerasuriya; Timothy D McHugh; Gwenan M Knight

doi:10.1371/journal.ppat.1011574

. 2024 Apr 10;20(4):e1011574. doi: 10.1371/journal.ppat.1011574

Mathematical models of drug-resistant tuberculosis lack bacterial heterogeneity: A systematic review

Naomi M Fuller ^1,^2,^3,^4,^*, Christopher F McQuaid ^1,^2,^3,⁴, Martin J Harker ^1,^2,^3,⁴, Chathika K Weerasuriya ^1,^2,^3,⁴, Timothy D McHugh ⁵, Gwenan M Knight ^1,^2,^3,⁴

Editor: Mark Robert Davies⁶

PMCID: PMC11060536 PMID: 38598556

Abstract

Drug-resistant tuberculosis (DR-TB) threatens progress in the control of TB. Mathematical models are increasingly being used to guide public health decisions on managing both antimicrobial resistance (AMR) and TB. It is important to consider bacterial heterogeneity in models as it can have consequences for predictions of resistance prevalence, which may affect decision-making. We conducted a systematic review of published mathematical models to determine the modelling landscape and to explore methods for including bacterial heterogeneity. Our first objective was to identify and analyse the general characteristics of mathematical models of DR-mycobacteria, including M. tuberculosis. The second objective was to analyse methods of including bacterial heterogeneity in these models. We had different definitions of heterogeneity depending on the model level. For between-host models of mycobacterium, heterogeneity was defined as any model where bacteria of the same resistance level were further differentiated. For bacterial population models, heterogeneity was defined as having multiple distinct resistant populations. The search was conducted following PRISMA guidelines in five databases, with studies included if they were mechanistic or simulation models of DR-mycobacteria. We identified 195 studies modelling DR-mycobacteria, with most being dynamic transmission models of non-treatment intervention impact in M. tuberculosis (n = 58). Studies were set in a limited number of specific countries, and 44% of models (n = 85) included only a single level of “multidrug-resistance (MDR)”. Only 23 models (8 between-host) included any bacterial heterogeneity. Most of these also captured multiple antibiotic-resistant classes (n = 17), but six models included heterogeneity in bacterial populations resistant to a single antibiotic. Heterogeneity was usually represented by different fitness values for bacteria resistant to the same antibiotic (61%, n = 14). A large and growing body of mathematical models of DR-mycobacterium is being used to explore intervention impact to support policy as well as theoretical explorations of resistance dynamics. However, the majority lack bacterial heterogeneity, suggesting that important evolutionary effects may be missed.

Author summary

The emergence of drug-resistant tuberculosis (DR-TB), where the causative bacterium Mycobacterium tuberculosis is resistant to key antibiotics such as rifampicin and isoniazid, poses a significant threat to TB control efforts. To gain a broader understanding of the challenges surrounding DR-TB, mathematical models are increasingly being employed to estimate the impact of interventions, effectiveness of treatment, and to predict the evolution of drug-resistance. However, pragmaticism surrounding model construction often means that important aspects, such as bacterial heterogeneity, are overlooked. We undertook a systematic review of the existing DR-mycobacterium modelling literature, with the specific aim of capturing methods for including bacterial heterogeneity. Our analysis revealed that most models of drug-resistance in mycobacteria primarily focus on intervention strategies and cost-effectiveness analyses, with minimal attention to bacterial heterogeneity. Where heterogeneity is included it mostly consisted of different fitness costs for resistance.

Introduction

Drug-resistant (DR-) strains of Mycobacterium tuberculosis (M. tuberculosis) are an urgent threat to the control of tuberculosis disease (TB) globally. For TB, the backbone antibiotics of standard therapy are rifampicin and isoniazid. In 2021, multidrug-resistant (combined rifampicin and isoniazid resistance) or rifampicin-resistant tuberculosis (MDR/RR-TB) caused an estimated 450,000 cases globally [1].

Routinely collected antimicrobial resistance (AMR) data use microbiological definitions of resistance, which are guided by threshold cut-offs for phenotypic resistance, resulting in discrete categorisations. For TB, these categorisations are further grouped with strains being classified as drug-susceptible (DS-), multidrug- or rifampicin-resistant- (MDR/RR-), pre-extensively-drug (pre-XDR) resistant (MDR plus resistance to a fluoroquinolone) or XDR- resistant (MDR plus resistance to a fluoroquinolone and a Group A drug) [1]. The MDR/RR grouping is based on the knowledge that isoniazid resistance is commonly acquired prior to rifampicin resistance and the wider prevalence of rifampicin-resistance testing through genotypic testing, making clinical management of RR- and MDR-TB similar [2,3]. These definitions are sufficient for patient care decision-making that does not need to account for the spectrum of phenotypic resistance levels (for example, those below the threshold for successful treatment) or any other bacterial characteristics (such as types of resistance-conferring mutations). However, bacterial populations are often highly diverse with a spectrum of characteristics. Hence, resistance categories will also have a high degree of bacterial heterogeneity, such as variation in transmission fitness between strains with the same phenotypic resistance, which affects the rate at which M. tuberculosis spreads between individuals.

Several important insights into the evolution of DR-TB, its emergence and spread, and the control of resistant bacteria more broadly have been generated by mathematical models. Some examples are the predominance of primary rather than acquired resistance, the effectiveness of TB surveillance for controlling DR-TB, and the potential impact of controlling HIV on reducing TB transmission [4–7]. Most mathematical models of AMR have typically adopted binary (e.g. resistant versus susceptible) categorisations. When bacterial heterogeneity is included in mathematical models, the predicted public health outcomes can be different from those when bacterial heterogeneity is ignored [8]. We may lose subtlety in model outputs when modelling antibiotic treatment as a selective pressure if the traits allowing for bacterial heterogeneity are not included. Models may miss key dynamics, such as competition between strains and antibiotic effectiveness against strains with varying resistance levels, and be at risk of incorrectly predicting the effectiveness of a treatment intervention. As Trauer et al. (2018) point out, strain diversity, virulence and fitness costs have implications for the trajectory of drug resistance in TB [9]. Decisions as to what to include in a model will depend on the questions being asked, the selective pressures modelled, and the time-frame studied. Assessing this balance in model design between detailed and generalised parameters to allow a pragmatic approach for public health interventions can often prove challenging. Hence, assessing the extent to which bacterial heterogeneity has been included in existing models that predict intervention impact for DR-TB control is highly important.

Previous systematic reviews have explored the landscape of mathematical models of AMR [7,10] and TB [11–14], with up to 43 DR-TB transmission and 52 within-host studies being found prior to 2016. To our knowledge, only one expert review from 2009 focused on mathematical models of DR-TB [4], emphasising the useful insights from modelling but also highlighting important knowledge gaps in the economics, biological impact of mutations and ability to control DR-TB. To date, there is little evidence on how bacterial heterogeneity is incorporated into DR-TB models and little evidence of the effect this would have on model outcomes.

Mycobacteria predominantly develop antibiotic resistance via mutation [15], resulting in different patterns of resistance dynamics to other bacterial genera. Mycobacterial species other than M. tuberculosis can often be used as experimental or theoretical models for M. tuberculosis and are also responsible for a clinical burden [16–18]. They are often used to understand the resistance dynamics of M. tuberculosis [19,20].

We aimed to support future modelling of interventions against DR-TB by systematically surveying the characteristics of mathematical models of mycobacteria, of which we expect the M. tuberculosis species to dominate due to its substantial clinical burden. Our secondary objective was categorising the amount and type of bacterial heterogeneity included in mathematical models of DR-mycobacteria. We envisaged two broad settings of papers to be included in this review, within-host and between-host transmission models. This was noted by Cohen et al. (2009), a previous review of the DR-TB modelling literature [4], where “between-host” models refer to models on the human population scale. Since 2009, there has been an increase in models of bacterial populations set in the laboratory. As the populations captured will be similar to within-host models, we combined laboratory models and within-host models and collectively called them “bacterial population” models.

The aims, dynamics and model structure of between-host models differ considerably from bacterial population models, namely by transmission of the pathogen and populations included, making them difficult to compare. Therefore, we defined heterogeneity differently for bacterial populations and between-host models to compare methods within these categories and gain a clearer picture of bacterial heterogeneity modelling. At the between-host level, we were interested in capturing those models that went beyond capturing resistance phenotypes but included any added dimension of bacterial variation, including what may affect survival, such as fitness effects. Models of bacterial populations that captured any resistance variation were included; distinct populations of resistant bacteria needed to be modelled, which differed in their parameter values (e.g. growth rate or mutation rate).

Methods

Our review consisted of two stages of selection and data analysis. In Stage 1 of the review, our aim was to identify and analyse the general characteristics of mathematical models pertaining to drug-resistant (DR-) mycobacteria, such as model type and aim. In Stage 2 of the review, our focus was to identify mathematical models of DR-mycobacteria that specifically incorporated the concept of bacterial heterogeneity, as elucidated by the definition in the inclusion and exclusion criteria section.

Search strategy

The systematic review was designed and conducted following the PRISMA reporting protocol to search and review mathematical modelling papers of DR-mycobacteria [21]. The search terms consisted of those relevant to [1] “mycobacteria”, [2] “mathematical modelling”, and [3] “antibiotic resistance” (S1 Text). The search was conducted in five databases (Medline, Embase, Global Health, Web of Science and Scopus) initially on January 22nd, 2021, and then repeated on April 1st, 2022. Duplicates were removed before screening.

Inclusion and exclusion criteria

The screening process of the papers adhered to predefined inclusion and exclusion criteria (Table 1). Initially, the titles and abstracts of the papers were screened to identify mathematical models specifically pertaining to DR-mycobacteria, followed by a full-text screening for inclusion in Stage 1. Finally, another round of full-text screening was carried out on the remaining papers to identify those appropriate for Stage 2 of the study.

Table 1. Inclusion and exclusion criteria used for title and abstract, stage 1 and stage 2 screening.

Inclusion Criteria		Exclusion Criteria
Stage 1	Stage 2	Exclusion Criteria
Mathematical model capturing at least one mycobacterial species	Mathematical model of resistance in mycobacteria with a heterogeneous bacterial component	Reviews, opinion pieces, editorials, letters, model comparison exercises, conference abstracts
Mathematical model with a population of antibiotic-resistant bacteria or individuals carrying resistant bacteria		Molecular modelling, drug development, genetic pathways, genetic evolution models, statistical analysis only
English language		Pharmacokinetics/Pharmacodynamics (PK/PD) model with no resistant bacterial population
		Models that use data but do not produce DR-mycobacteria results
		Animal (non-human) host

Open in a new tab

Mathematical models were defined as mechanistic models or simulation models reproducing a mathematically described scenario of DR-mycobacteria or of individuals carrying DR-mycobacteria. We excluded statistical analyses, such as regression models or risk analysis; molecular modelling (those focused on molecular structure of chemical compounds) or those only focused on drug development; models of drug-resistance that only used mycobacteria as an example or discussion point unless results for DR-mycobacteria were specifically included.

We split models into two groupings: “between-host” and “bacterial population” models, with the differences in their model scale, structure, and aims, resulting in a different bacterial heterogeneity definition. A “between-host” model was classed as a heterogenous model when strains infecting a human population resistant to the same drug varied in another characteristic such as fitness, rates of compensatory mutation evolution or associated treatment recovery rates. These characteristics were extracted during the full-text extraction stage. “Bacterial population” models included both within-host and models of bacterial populations capturing dynamics measured in laboratory or experimental conditions. A bacterial population model was classed as a heterogeneous model when there were distinct resistant strains captured which had different parameter values such as fitness, mutation rates and metabolic states. These parameter differences were extracted during the full-text extraction stage.

Selection and extraction: Stage 1

Title and abstract screening were performed for every paper by at least two authors (NMF, GMK, CFM, MJH and CKW) to determine if the paper likely included a mathematical model of DR-mycobacteria. High-level data extraction from these screened papers that continued to match the criteria for Stage 1 upon full-text screening provided a landscape analysis of DR-mycobacteria models. DR-mycobacteria models can address multiple aims with various methods, but they will have a common theme, such as parameter estimation or evaluation of the impact of interventions. We extracted information from the models to categorise and classify them into five categories, focusing on the main theme of the model. 1) model setting (such as geographic location), 2) model aims (7 categories of; non-treatment interventions that did not explore antibiotic usage (with and without cost-effectiveness), treatment interventions (with and without cost-effectiveness), parameter estimation, burden estimation or theoretical), 3) model type (7 categories of; bacterial dynamics, decision analytic, PK/PD, state transition (with and without a statistical component) or transmission (with or without an operational or state transition component), 4) mycobacterial species and 5) resistance classifications (such as MDR or XDR) (S2 Text). We extracted resistance classifications based on what the authors defined in their papers, as current resistance definitions are continuously updated. A resistance class is defined as a model stratification whereby strains (or the populations including them) are grouped across multiple antibiotic resistances (i.e. MDR could here be a single “resistance class” but represents resistance to multiple antibiotic agents). We only extracted which antibiotics were modelled in papers if their resistance was also considered. This extraction was performed by NMF and GMK, with discussions to resolve any conflicts.

Selection and extraction: Stage 2

For Stage 2, full-text screening of the Stage 1 papers was performed by three authors (NMF, GMK, CFM) to determine the models with bacterial heterogeneity, with subsequent discussions and consensus to resolve any discrepancies. NMF performed full-text extraction and data analysis of the extracted data from these papers (S2 Table). Stage 2 extracted data on the methods used to model heterogeneity, types of heterogeneity included, data sources and the effect of resistance inclusion (such as resistance effects on disease progression) (S3 Text).

Results

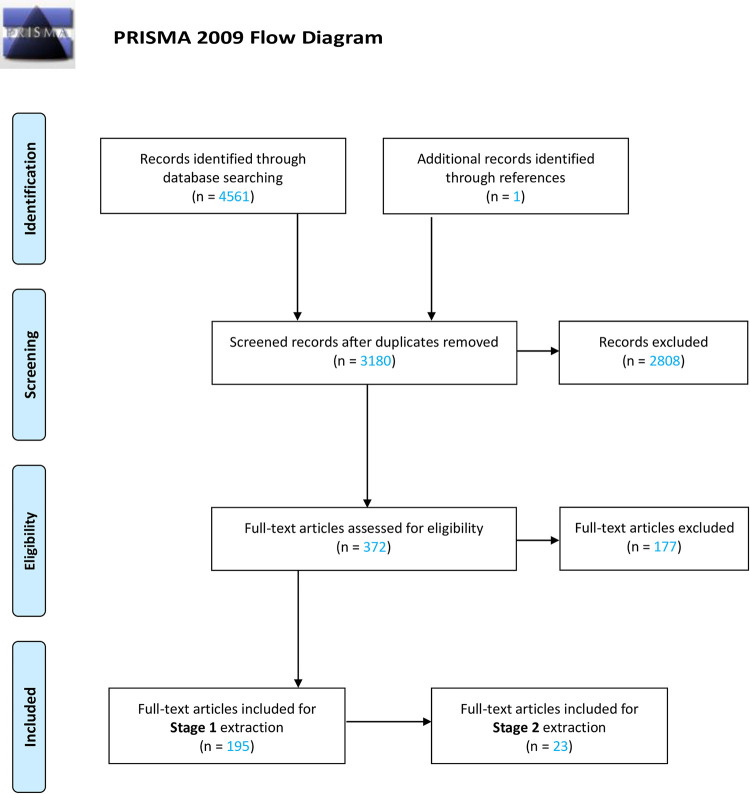
After the removal of duplicates, 3,180 papers were identified (Fig 1). Following a title and abstract screening, 372 papers remained for full-text screening. 195 papers were found to fulfil our Stage 1 criteria having a model of DR-mycobacteria strains (S1 Table). Of these papers, only 23 were found to meet the requirements of bacterial heterogeneity in mathematical models of DR-mycobacteria (S2 Table).

Stage 1 Results: DR-mycobacteria model landscape

Most models of mycobacteria were of M. tuberculosis (190 papers/97%) with HIV (59 papers) and diabetes mellitus (5 papers) often included. There was a rapid increase in the number of papers published on DR-mycobacterium from 2005 onwards (S1 Fig).

Settings captured

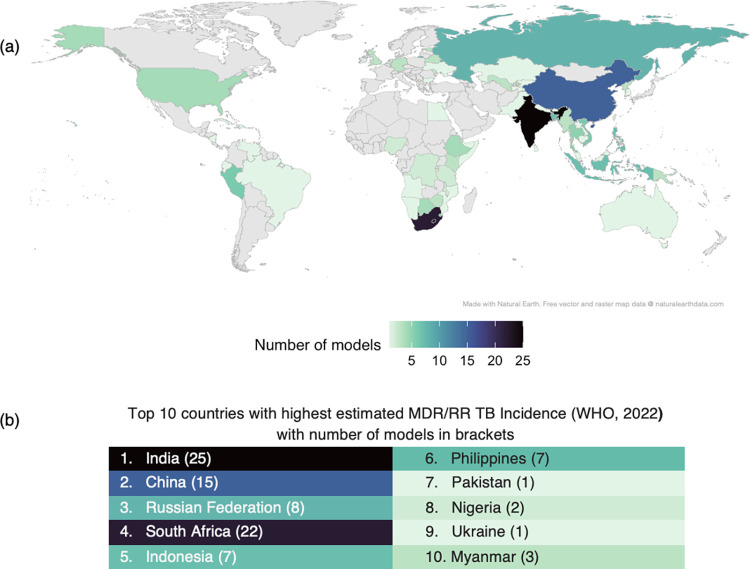
119 papers aimed to model a specific geographical location, typically at the national level (Fig 2A and S3 Table). This reflects the settings with the highest MDR-TB incidence but also highlights some countries that are not being focused on (Fig 2B). Of the 117 papers, 82 covered a single national analysis and 35 covered different countries. Other geographical locations included 7 models with a global focus, whilst 6 models covered regions with 4 models of Southeast Asia [22–24], and 1 of Eastern Europe [25] and 1 of the Asia-Pacific [26].

Model aims and types

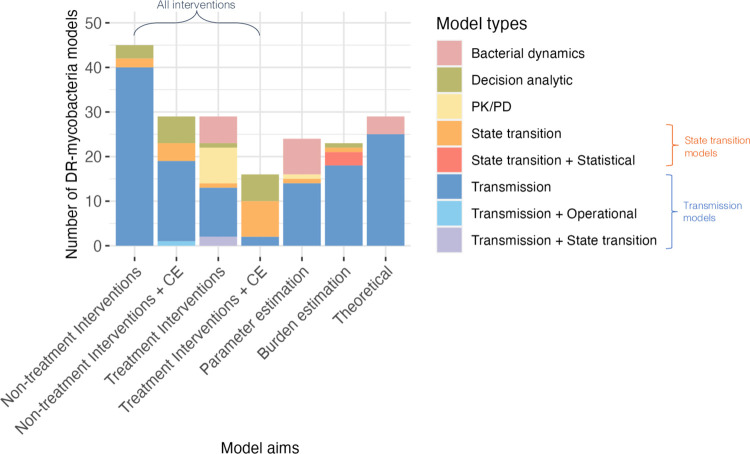
Of the seven distinct categories of study aim found (Fig 3), non-treatment interventions without cost-effectiveness considered (n = 45, 23%) was the most common. Transmission models (n = 129, 67%) were the most common model type used for all model aims, except for “treatment interventions with cost-effectiveness”, which mostly used state transition models (Fig 3). As would be expected, PK/PD models were used almost exclusively for “treatment interventions”, with one model being used for parameter estimation. Six models used a combination of methods: transmission and state transition [27,28], transmission and operational [29]and state transition and statistical [30–32]. “Bacterial dynamics” type models were used for “treatment interventions”, “theoretical” and “parameter estimation” aims only. “Decision analytic” type models were used for all aims other than “theoretical” and “parameter estimation”.

Resistance categories

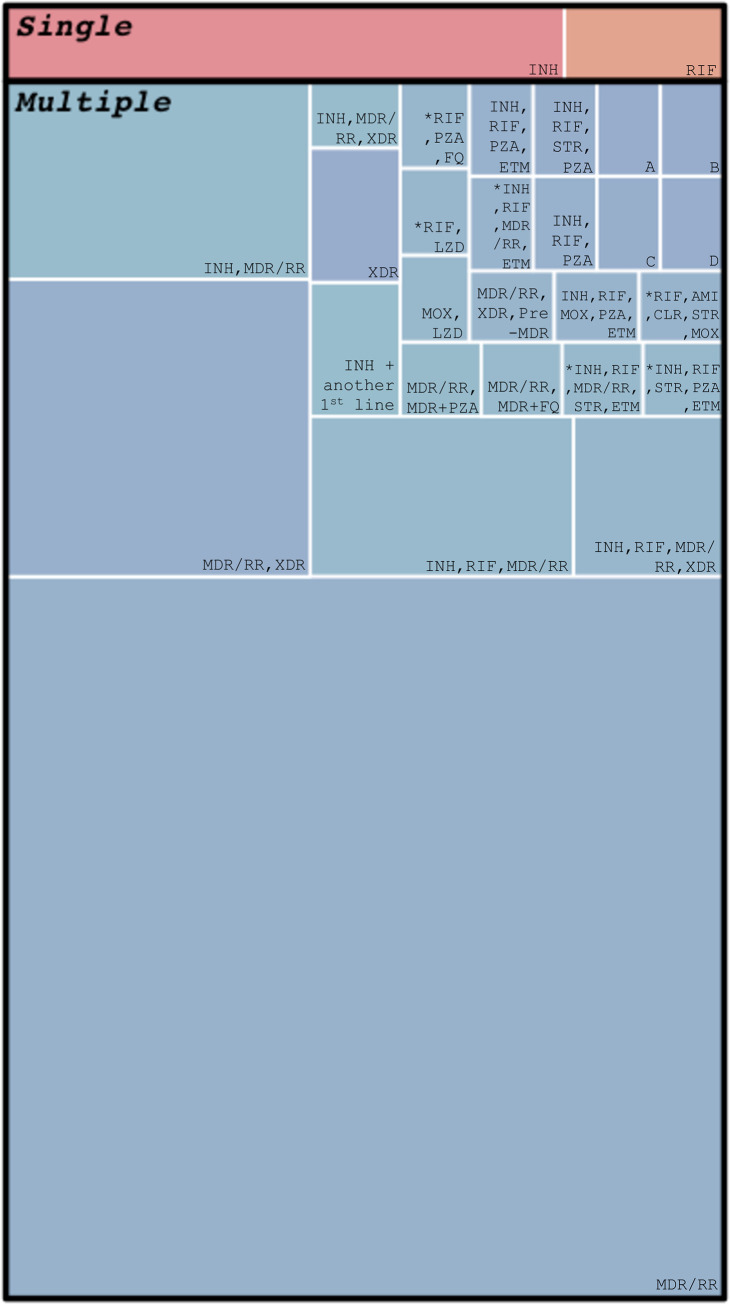
Most models of DR-mycobacteria capture resistance to fewer than three antibiotics. Six models considered all possible combinations of resistance to several antibiotics (‘*’, Fig 4). Of 16 models to capture four or more resistances at once, 11 of these models included antibiotic resistance as stepwise accumulation of resistance [22,30,33–41] and 5 models only included mono-resistance of resistance to multiple antibiotics [20,42–45].

Overall, for stage 1, most models included a resistance class of MDR/RR-TB (129 papers/67%, Fig 4) with 85 models that chose to model only a single resistance class of MDR/RR-TB alongside DS-TB (Fig 4). 40/195 models included isoniazid resistance (Fig 4) with 27/40 also including MDR/RR-TB. 21/195 models included rifampicin resistance separate from MDR with 15/21 including isoniazid and rifampicin resistance as mono-resistances that developed into MDR with 6/15 models including the development of XDR-TB. Of 18 models that modelled XDR, 16 included MDR/RR, while two did not [46,47]. Out of the first-line antibiotics used to treat TB, isoniazid (n = 40) and rifampicin (n = 27) resistance were modelled the most, followed by pyrazinamide (n = 8) and then ethambutol (n = 5) resistance. Pyrazinamide resistance was often found to be modelled alongside rifampicin and/or isoniazid resistance with only 3 models including resistance to all 4 first-line antibiotics, 2 with mono-resistances and 1 with a combination of all 4 resistances [33,37,42] (Fig 4).

41 theoretical models included resistance to a non-named antibiotic (S1 Table). One of these explored differences in drug action (bacteriostatic or bactericidal [48], and two explored antibiotic persistence [49,50] (S1 Fig). There were 38 theoretical modelling studies (S1 Fig) capturing “drug resistance”, with four of these models exploring firstly hypothetical and then antibiotic-specific resistance (S1 Table).

Stage 2 Results: Heterogeneous models

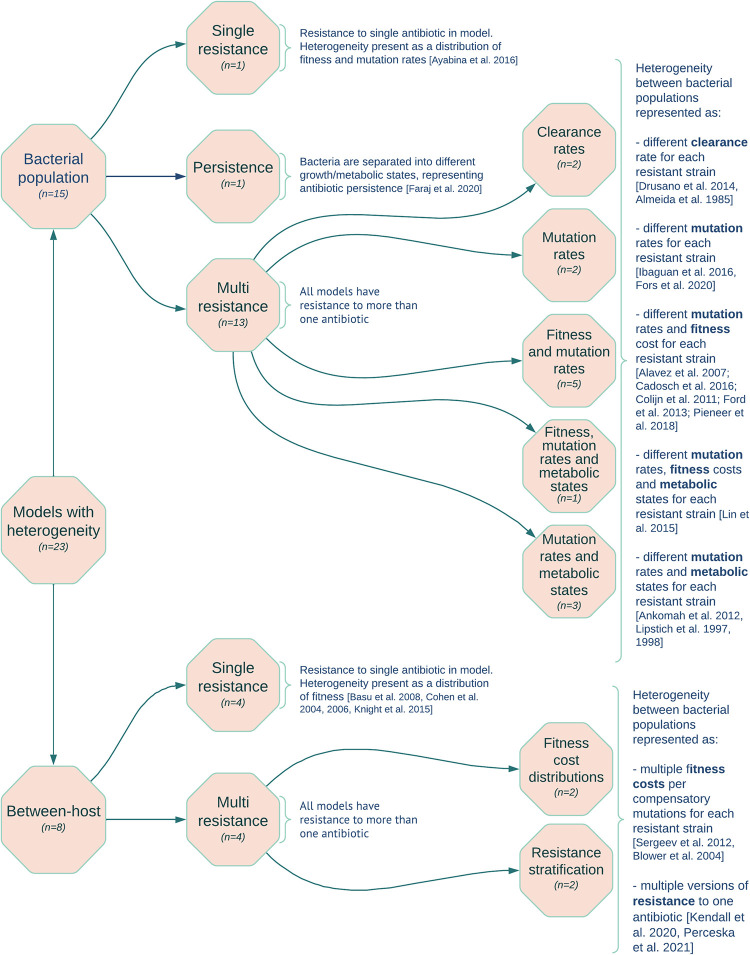
We found 23 models with bacterial heterogeneity—15 bacterial population and 8 between-host models (S2 Table) [8,20,33,34,37,43–45,48,49,51–63]. The distribution of model aims that these papers fall into were different from Stage 1 with 13 “parameter estimation”, 8 “treatment interventions”, 1 “theoretical”, and 1 “non-treatment intervention”. 12 of the 23 models modelled the immune system.

Bacterial population models

The fifteen bacterial population models mostly captured multiple resistance classes (n = 13) (Fig 5 and S2 Table). One other considered a single resistance class of isoniazid only in an M. tuberculosis population and explored deterministically the impact of antibiotic exposure on resistance dominance with or without heterogeneity in fitness and mutation distributions [52]. Including heterogeneity in fitness and mutation distributions was also the most common method for exploring variation in models with multiple resistance classes. This was true both for stochastic and deterministic model structures [33,43,51,57,59,62], though one deterministic model only explored differences in mutation rates [43]. Four models additionally explored the impact of variation in growth rates induced by different metabolic states [20,34,45,60], with one model including fitness variation too [45].

Different clearance rates were used in 2 models, a PK/PD model and a bacterial dynamics model to differentiate between two resistant bacterial strains with the aim of determining the most effective treatment combination [48,58].

One model did not include AMR as a direct resistance to an antibiotic, but instead as persistence [49]. This was modelled as non-replicating bacterial populations and antibiotics had little to no effect on these bacterial populations. The model implemented heterogeneity by including fast and slow-growing bacteria.

Between-host models

All eight between-host models were compartmental models. Six of these models explored the impact of including a distribution of fitness costs affecting transmission resulting from resistance-conferring mutations to prevalence of either a single [8,53,55,56] or multiple resistance classes [54,63]. Four of these six models were deterministic [53,55,56,63], with Knight et al. (2015) exploring a stochastic version in the supplementary materials [8]. Blower et al. (2004) explored a stochastic model that included heterogeneity by modelling strains of M. tuberculosis with different fitness rates but also cure, treatment, detection, and resistance mutation rates. The model aimed to estimate MDR-TB prevalence [54].

Two stochastic models were classified as heterogeneous as they included resistance compartments stratified with different resistant genotypes [44,61]. These papers had different aims: Kendall et al. [44] explored the impact of high and low levels of moxifloxacin resistance on treatment regimens and drug susceptibility testing. Pecerska et al. [61] estimated the fitness cost of MDR-TB with and without pyrazinamide resistance from a genetic data set.

Use of data derived from the literature

All Stage 2 papers used at least one parameter sourced from existing literature, so no models were entirely theoretical. Some models used a primary data set that was collected from experiments or a population study [20,49,52,58,59,61]. Data types used were experimental (83%), epidemiological (26%), clinical (4%), genetic (4%) and WHO data (30%). All bacterial population models used experimental data, with one paper also including clinical data [37]. Between-host models used a combination of experimental, epidemiological, and WHO data, with one using only genetic data.

Acquired or primary resistance and discrete resistance

All models with heterogeneity represented resistance as discrete categories, such as MDR/RR-TB, with no models including resistance as a spectrum. 6/8 between-host heterogenous models modelled resistance as both primary and acquired and two models had no primary resistance, with acquired resistance only [44,63].

Resistance effects in models

Resistance affected the ability of M. tuberculosis to transmit in 6/8 between-host heterogenous models, with resistant strains usually having a lower value for the transmission coefficient or fitness parameter than the susceptible strain.

Resistance affected disease progression in all models except Knight et al. (2015) [8]. For bacterial population models, this was defined as different growth rates. For between-host models, this was included as a separate disease progression parameter for resistant strains [54,55,63], different relapse rates for patients with resistant bacteria [44], different associated mortality rates for each resistant strain [61], variance in cross-immunity by resistant strain [53], or different natural history pathways for resistant strains [56].

13/23 models assumed resistance affected operational parameters. In nine, resistance reduced treatment efficacy [8,44,45,53–56,61,63], with one also including different diagnostic (GeneXpert rapid nucleic acid amplification test for M. tuberculosis) sensitivity parameters for each resistant strain [44]. Four bacterial population models had a different antibiotic kill rate [48,49,58,60], with one including different clinical conversion factors [49].

Discussion

Our review of the mathematical modelling landscape of drug resistance in mycobacteria has revealed a growing body of work mostly using transmission dynamic models to explore intervention impact. We found that a minority (33%) explore resistances other than MDR/RR-TB. Few models account for the known heterogeneity that exists in bacterial populations. Where heterogeneity was captured in both bacterial population and between-host models, it was mostly through a variation in the model-specific fitness parameter (with the definition of fitness varying broadly from being related to transmission, ability to cause disease or speed of bacterial growth).

Our Stage 1 landscape analysis found that several high MDR-TB burden countries (e.g. Pakistan, Nigeria, Ukraine, and Myanmar) are underrepresented in the English DR-TB literature. Increasing modelling of DR-TB in specific countries may aid understanding of epidemiology in the specific country and increase the global understanding of DR-TB, as well as improve estimates of intervention efficacy and hence design of context-specific interventions. This is highly relevant when considering that, as has been found for models of M. tuberculosis in general [11,64], most models aimed to estimate the impact of public health interventions. Transmission models were used more than any other type of model across all categories, except for the category of "treatment interventions + cost-effectiveness”, where state transition models were most used. This indicates that most modellers are interested in modelling M. tuberculosis at a between-human host population scale.

MDR-TB was the most common category of resistance modelled (67% of DR-mycobacterium models)—an expected result linked to the historical importance of this as a clinical treatment threshold and reflected in most data collection [1,3]. Mono-isoniazid resistance was more commonly modelled than explicit mono-rifampicin resistance, with 27 models capturing the pathway from isoniazid resistance developing into MDR-TB. XDR-TB was not considered without MDR-TB other than by two papers by Basu et al. (2008, 2009), who were interested in the burden and interventions specific to XDR-TB [46,47]. XDR-TB was often treated as a final state of resistance in modelling systems, with no further resistance being acquired. This reflects the historic clinical decision-making pathway (susceptible or MDR or XDR) and that XDR-TB is resistant to a large number of anti-TB antibiotics. However, there is a great variation in DR-TB and the pathways that may lead to each level of it. Understanding this variation in DR-TB will drive improvements in treatment success by identifying which antibiotics will be most effective and, therefore improve patient outcomes.

Rifampicin and isoniazid resistance were the most modelled mono-resistances, followed by pyrazinamide and ethambutol, reflecting first-line treatments and prophylaxis for TB and data availability. Testing for pyrazinamide and ethambutol resistance is typically reserved for reference settings, and there is widespread use of GeneXpert (Cepheid 6/10-colour instrument), which tests for rifampicin resistance. Only 21% of models (n = 41) captured resistances beyond these four drugs. This will need to be expanded as we move into a period with many more treatment options–constructing, parameterising, and exploring mathematical models of other antibiotic resistances is vitally needed to optimise future treatment and TB control interventions, as well as to explore evolutionary pathways. For example, we found only two papers which explicitly modelled resistance to bedaquiline [44,45], whilst two new treatment regimens containing bedaquiline were approved by the WHO in 2022 [65].

Models that capture non-specific DR-TB can be useful in the absence of data or to explore broad trends. We found 45 models in this category and found that these theoretical or non-specific systems were used to understand under what constraints DR-TB would dominate over DS-TB or explored the efficacy of a theoretical intervention.

When designing a model to answer a specific question such as the impact of a public health intervention, a balance needs to be struck between designing a detailed or generalised model to allow for a pragmatic approach. This pragmatism is likely the reason for our stage 2 results that revealed few models including bacterial heterogeneity. This is despite several models showing how heterogeneity in transmission fitness can affect DR-TB prevalence estimates [8,54–56]. Or how including multiple levels of resistance to one antibiotic can affect treatment outcomes [44,61]. Authors cannot capture all the subtlety of antibiotics as a selection pressure without including the related resistance dynamics and from this the population diversity it fosters. Mathematically, it can be difficult to include complexities in all aspects, for example, population mixing, and often there is little context-specific data on bacterial heterogeneity to inform models. However, if authors want to understand the risk of antibiotic resistance developing under a new treatment regimen it should follow that those resistances are then included in predictions. Some nuance may be beneficial in results that are only achievable with models that include bacterial heterogeneity, such as in Basu et al. (2008) where their conclusions suggested that a weaker immune response to a DR-TB infection with high fitness levels leads to higher DR-TB prevalence in HIV-positive and -negative populations [53].

Interestingly, we found that all models included resistance in a small number of discrete compartments, with no near-continuous distributions of resistance. Biologically speaking, resistance exists across a spectrum with strains having a range of minimum inhibitory concentrations, but for therapeutic and diagnostic uses they are classified with discrete values. Modelling resistance at multiple possible sub-levels would enable new research questions to be posed about pathways to evolution and competition due to multiple resistant levels. To our knowledge, such a question has not yet been asked regarding M. tuberculosis.

We found that transmission fitness levels, by contrast to resistance levels, were commonly allowed to vary across a distribution within resistant populations, likely reflecting the available historical data pointing to fitness differences between TB strains [66]. This contrasts with the lack of data linking resistant strain variation with treatment outcomes such as failure or recovery. Including such fitness effects is a relatively easy single-parameter effect within standard transmission dynamic or bacterial dynamics models and is commonly included in models of drug resistance outside of M. tuberculosis [7].

In this review, we identified 190 published papers which included drug-resistant strains of M. tuberculosis, a further 5 with a drug-resistant non-tuberculosis mycobacteria species, and 1 including both M. tuberculosis and M. marinum. Our update on the literature shows an increasing trend to model DR-TB.

The limitations of our review included that we conducted the search for English language articles when a substantial burden of DR-TB is found in non-English speaking settings such as Eastern Europe [1]. We did not capture which antibiotics were explored in the models as our focus was on the resistance captured nor time horizons for each model. Our stage 1 analysis only extracted high-level information as our main interest was the bacterial heterogeneity in stage 2. Future work could use this baseline set of literature to explore how resistance is modelled in the natural history of tuberculosis.

We encourage future modellers to consider if the bacterial component of their research question would benefit from the inclusion of bacterial heterogeneity. By not including it, models miss key features of bacterial populations, such as competition or treatment efficacy differences between strains and may, for example, under or overestimate the degree by which an intervention might increase resistance or prevalence of DR-TB.

We were unable to provide a comprehensive review of how resistance was included in Stage 1 models due to the lack of model information provided in many papers such as parameter tables, model diagrams or equations. Future mathematical models should aim for clear model reporting as suggested by the WHO [67] and Bennett et al. (2012) for transparency and to enable reproducible research [68].

In this review, we identified 195 drug-resistant mycobacteria mathematical models, with 190 DR-TB models and 23 models including bacterial heterogeneity. This has provided us with an understanding of how resistant mycobacterial species have been modelled, in terms of geographical settings, model aims and types, resistances modelled and further insights into the inclusion of bacterial heterogeneity. However, we found that bacterial heterogeneity was often ignored despite evidence of its importance at the population level. Balancing pragmaticism with biological reality when building mathematical models is vital within the fundamental evolutionary dynamics of AMR.

Supporting information

S1 Text. Search strings.

(DOCX)

ppat.1011574.s001.docx^{(17KB, docx)}

S2 Text. Details of extraction table for stage 1.

(DOCX)

ppat.1011574.s002.docx^{(20.4KB, docx)}

S3 Text. Details of extraction table for stage 2.

(DOCX)

ppat.1011574.s003.docx^{(20.1KB, docx)}

S1 Fig. Heatmap of all resistance categories in stage 1 models.

Heatmap of resistances included per DR-TB model (n = 195) indicates a lack of diversity in resistances modelled, with MDR/RR-TB featuring in over half of all 195 models. Each coloured line indicates a model (y axis) included in stage 1 (purple) or stage 2 (orange). The graph groups models into specific (captures resistance to a named antibiotic), non-specific (defined resistance that are not specific to an antibiotic) and hypothetical (captures antibiotic resistance not linked to a named drug). Antibiotic acronyms as follows: AMI = amikacin, BDQ = bedaquiline, CLR = clarithromycin, ETM = ethambutol, FQ = undefined fluroquinolone, LZD = linezolid, MOX = moxifloxacin, PA = pretomanid, PZA = pyrazinamide, STR = streptomycin, INH = isoniazid, RIF = rifampicin, MDR/RR = multidrug resistant/ rifampicin resistant, XDR = extensively drug-resistant, SLInject = second line injectable antibiotic (from WHO guidelines 2014), another 1st line = rifampicin, ethambutol, or pyrazinamide. Index links to paper number in S1 Table.

(DOCX)

ppat.1011574.s004.docx^{(225.9KB, docx)}

S2 Fig. Plot of number of publications over time.

(TIF)

ppat.1011574.s005.tif^{(163.7KB, tif)}

S1 Table. Extraction table results from stage 1.

(XLSX)

ppat.1011574.s006.xlsx^{(75.9KB, xlsx)}

S2 Table. Extraction table results from stage 2.

(XLSX)

ppat.1011574.s007.xlsx^{(79.9KB, xlsx)}

S3 Table. Geographic settings in models.

(DOCX)

ppat.1011574.s008.docx^{(20KB, docx)}

Acknowledgments

We would like to thank the support of library staff at the London School of Hygiene and Tropical Medicine. Thank you for the guidance and advice for this work from Quentin Leclerc and Alastair Clements.

Data Availability

All relevant data are within the manuscript and its Supporting Information files.

Funding Statement

This research and NMF was funded by the Biotechnology and Biological Sciences Research Council through the London Interdisciplinary Doctoral Training Programme (BBSRC LIDO, https://www.lido-dtp.ac.uk) at the London School of Hygiene and Tropical Medicine (LSHTM) in partnership with University College London (UCL), Grant code - BB/M009513/1. CFM was funded for other work by Bill and Melinda Gates Foundation (TB MAC OPP1135288, INV-059518, https://www.gatesfoundation.org) and Unitaid (20193–3-ASCENT, https://unitaid.org/calls/#en). CKW was supported by a grant from the Bill and Melinda Gates Foundation (INV-001754, https://www.gatesfoundation.org). GMK was supported by Medical Research Council UK, https://www.ukri.org/opportunity/career-development-award/ (MR/ W026643/1). The views expressed are those of the authors and not necessarily those of the BBSRC, LIDO, LSHTM or UCL. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1.World Health Organisation. Global tuberculosis report 2022 [Internet]. 2022 Oct. Available from: https://www.who.int/publications/i/item/9789240061729
2.World Health Organisation. WHO announces updated definitions of extensively drug-resistant tuberculosis [Internet]. 2021 [cited 2021 Jan 27]. Available from: https://www.who.int/news/item/27-01-2021-who-announces-updated-definitions-of-extensively-drug-resistant-tuberculosis
3.World Health Organisation. Definitions and reporting framework for tuberculosis–2013 revision: updated December 2014 and January 2020. 2013. Report No.: No. WHO/HTM/TB/2013.2.
4.Cohen T, Dye C, Colijn C, Williams B, Murray M. Mathematical models of the epidemiology and control of drug-resistant TB. Expert Review of Respiratory Medicine. 2009;3(1):67–79. doi: 10.1586/17476348.3.1.67 [DOI] [PubMed] [Google Scholar]
5.Cohen T, Sommers B, Murray M. The effect of drug resistance on the fitness of Mycobacterium tuberculosis. Lancet Infect Dis. 2003;3(1):13–21. doi: 10.1016/s1473-3099(03)00483-3 [DOI] [PubMed] [Google Scholar]
6.Borrell S, Gagneux S. Infectiousness, reproductive fitness and evolution of drug-resistant Mycobacterium tuberculosis. Int J Tuberc Lung Dis. 2009;13(12):1456–66. [PubMed] [Google Scholar]
7.Niewiadomska AM, Jayabalasingham B, Seidman JC, Willem L, Grenfell B, Spiro D, et al. Population-level mathematical modeling of antimicrobial resistance: a systematic review. BMC Med. 2019;17(1):81. doi: 10.1186/s12916-019-1314-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Knight GM, Colijn C, Shrestha S, Fofana M, Cobelens F, White RG, et al. The Distribution of Fitness Costs of Resistance-Conferring Mutations Is a Key Determinant for the Future Burden of Drug-Resistant Tuberculosis: A Model-Based Analysis. Clin Infect Dis. 2015;61Suppl 3(a4j, 9203213):S147–54. doi: 10.1093/cid/civ579 [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Trauer JM, Dodd PJ, Gomes MGM, Gomez GB, Houben RMGJ, McBryde ES, et al. The Importance of Heterogeneity to the Epidemiology of Tuberculosis. Clinical Infectious Diseases. 2019. Jun 18;69(1):159–66. doi: 10.1093/cid/ciy938 [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Spicknall IH, Foxman B, Marrs CF, Eisenberg JNS. A modeling framework for the evolution and spread of antibiotic resistance: Literature review and model categorization. American Journal of Epidemiology. 2013;178(4):508–20. doi: 10.1093/aje/kwt017 [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Melsew YA, Adekunle AI, Cheng AC, McBryde ES, Ragonnet R, Trauer JM. Heterogeneous infectiousness in mathematical models of tuberculosis: A systematic review. Epidemics. 2020;30:100374. doi: 10.1016/j.epidem.2019.100374 [DOI] [PubMed] [Google Scholar]
12.Castillo-Chavez C, Song BJ. Dynamical models of tuberculosis and their applications. Mathematical Biosciences and Engineering. 2004. Sep;1(2):361–404. doi: 10.3934/mbe.2004.1.361 [DOI] [PubMed] [Google Scholar]
13.Kirschner D, Pienaar E, Marino S, Linderman JJ. A review of computational and mathematical modeling contributions to our understanding of Mycobacterium tuberculosis within-host infection and treatment. Current Opinion in Systems Biology. 2017;3:170–85. doi: 10.1016/j.coisb.2017.05.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Ozcaglar C, Shabbeer A, Vandenberg SL, Yener B, Bennett KP. Epidemiological models of Mycobacterium tuberculosis complex infections. Math Biosci. 2012;236(2):77–96. doi: 10.1016/j.mbs.2012.02.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Eldholm V, Norheim G, von der Lippe B, Kinander W, Dahle UR, Caugant DA, et al. Evolution of extensively drug-resistant Mycobacterium tuberculosis from a susceptible ancestor in a single patient. Genome Biol. 2014;15(11):490. doi: 10.1186/s13059-014-0490-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Gopalaswamy R, Shanmugam S, Mondal R, Subbian S. Of tuberculosis and non-tuberculous mycobacterial infections–a comparative analysis of epidemiology, diagnosis and treatment. J Biomed Sci. 2020. Jun 17;27:74. doi: 10.1186/s12929-020-00667-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Maeda T, Kawada M, Sakata N, Kotani H, Furusawa C. Laboratory evolution of Mycobacterium on agar plates for analysis of resistance acquisition and drug sensitivity profiles. Sci Rep. 2021. Jul 23;11(1):15136. doi: 10.1038/s41598-021-94645-z [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Shiloh MU, DiGiuseppe Champion PA. To catch a killer. What can mycobacterial models teach us about Mycobacterium tuberculosis pathogenesis? Current Opinion in Microbiology. 2010. Feb;13(1):86–92. doi: 10.1016/j.mib.2009.11.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Gygli SM, Borrell S, Trauner A, Gagneux S. Antimicrobial resistance in Mycobacterium tuberculosis: mechanistic and evolutionary perspectives. FEMS Microbiology Reviews. 2017. May 1;41(3):354–73. doi: 10.1093/femsre/fux011 [DOI] [PubMed] [Google Scholar]
20.Ankomah P, Levin BR. Two-drug antimicrobial chemotherapy: a mathematical model and experiments with Mycobacterium marinum. PLoS Pathog. 2012;8(1):e1002487. doi: 10.1371/journal.ppat.1002487 [DOI] [PMC free article] [PubMed] [Google Scholar]
21.PRISMA-P Group, Moher D, Shamseer L, Clarke M, Ghersi D, Liberati A, et al. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015 statement. Syst Rev. 2015. Dec;4(1):1. doi: 10.1186/2046-4053-4-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Fofana MO, Shrestha S, Knight GM, Cohen T, White RG, Cobelens F, et al. A Multistrain Mathematical Model To Investigate the Role of Pyrazinamide in the Emergence of Extensively Drug-Resistant Tuberculosis. Antimicrob Agents Chemother. 2017;61(3). doi: 10.1128/AAC.00498-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Han WM, Mahikul W, Pouplin T, Lawpoolsri S, White LJ, Pan-Ngum W. Assessing the impacts of short-course multidrug-resistant tuberculosis treatment in the Southeast Asia Region using a mathematical modeling approach. PloS one. 2021;16(3):e0248846. doi: 10.1371/journal.pone.0248846 [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Kendall EA, Fojo AT, Dowdy DW. Expected effects of adopting a 9 month regimen for multidrug-resistant tuberculosis: a population modelling analysis. Lancet Respir Med. 2017;5(3):191–9. doi: 10.1016/S2213-2600(16)30423-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Winetsky DE, Negoescu DM, DeMarchis EH, Almukhamedova O, Dooronbekova A, Pulatov D, et al. Screening and rapid molecular diagnosis of tuberculosis in prisons in Russia and Eastern Europe: a cost-effectiveness analysis. PLoS Med. 2012;9(11):e1001348. doi: 10.1371/journal.pmed.1001348 [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Trauer JM, Denholm JT, McBryde ES. Construction of a mathematical model for tuberculosis transmission in highly endemic regions of the Asia-Pacific. J Theor Biol. 2014;358(k8n, 0376342):74–84. doi: 10.1016/j.jtbi.2014.05.023 [DOI] [PubMed] [Google Scholar]
27.Pereira RS, Bauch CT, Penna TJP, Espindola AL. A nested model for tuberculosis: Combining within-host and between-host processes in a single framework. INTERNATIONAL JOURNAL OF MODERN PHYSICS C. 2021. Dec;32(12). [Google Scholar]
28.Mehra M, Kambili C, Potluri R, Rhines A, Singh V, Thomas A. Modeling the impact of bedaquiline treatment strategies on the multidrug-resistant tuberculosis burden in India. Int J Tuberc Lung Dis. 2017;21(8):902–9. doi: 10.5588/ijtld.16.0717 [DOI] [PubMed] [Google Scholar]
29.Langley I, Lin HH, Egwaga S, Doulla B, Ku CC, Murray M, et al. Assessment of the patient, health system, and population effects of Xpert MTB/RIF and alternative diagnostics for tuberculosis in Tanzania: an integrated modelling approach. Lancet Glob Health. 2014;2(10):e581–91. doi: 10.1016/S2214-109X(14)70291-8 [DOI] [PubMed] [Google Scholar]
30.Dodd PJ, Sismanidis C, Seddon JA. Global burden of drug-resistant tuberculosis in children: a mathematical modelling study. Lancet Infect Dis. 2016;16(10):1193–201. doi: 10.1016/S1473-3099(16)30132-3 [DOI] [PubMed] [Google Scholar]
31.Houben RMGJ Dodd PJ. The Global Burden of Latent Tuberculosis Infection: A Re-estimation Using Mathematical Modelling. PLoS Med. 2016;13(10):e1002152. doi: 10.1371/journal.pmed.1002152 [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Knight GM, McQuaid CF, Dodd PJ, Houben RMGJ. Global burden of latent multidrug-resistant tuberculosis: trends and estimates based on mathematical modelling. Lancet Infect Dis. 2019;19(8):903–12. doi: 10.1016/S1473-3099(19)30307-X [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Cadosch D, Abel Zur Wiesch P, Kouyos R, Bonhoeffer S. The Role of Adherence and Retreatment in De Novo Emergence of MDR-TB. PLoS Comput Biol. 2016;12(3):e1004749. doi: 10.1371/journal.pcbi.1004749 [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Lipsitch M, Levin BR. Population dynamics of tuberculosis treatment: mathematical models of the roles of non-compliance and bacterial heterogeneity in the evolution of drug resistance. Int J Tuberc Lung Dis. 1998;2(3):187–99. [PubMed] [Google Scholar]
35.Oxlade O, Schwartzman K, Pai M, Heymann J, Benedetti A, Royce S, et al. Predicting outcomes and drug resistance with standardised treatment of active tuberculosis. Eur Respir J. 2010;36(4):870–7. doi: 10.1183/09031936.00151709 [DOI] [PubMed] [Google Scholar]
36.Chindelevitch L, Menzies NA, Pretorius C, Stover J, Salomon JA, Cohen T. Evaluating the potential impact of enhancing HIV treatment and tuberculosis control programmes on the burden of tuberculosis. Journal of the Royal Society Interface. 2015;12(106):20150146. doi: 10.1098/rsif.2015.0146 [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Fors J, Strydom N, Fox WS, Keizer RJ, Savic RM. Mathematical model and tool to explore shorter multi-drug therapy options for active pulmonary tuberculosis. PLoS Computational Biology. 2020;16(8):e1008107. doi: 10.1371/journal.pcbi.1008107 [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Menzies NA, Cohen T, Hill AN, Yaesoubi R, Galer K, Wolf E, et al. Prospects for tuberculosis elimination in the United States: Results of a transmission dynamic model. American Journal of Epidemiology. 2018;187(9):2011–20. doi: 10.1093/aje/kwy094 [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Menzies NA, Cohen T, Lin HH, Murray M, Salomon JA. Population health impact and cost-effectiveness of tuberculosis diagnosis with Xpert MTB/RIF: a dynamic simulation and economic evaluation. PLoS Med. 2012;9(11):e1001347. doi: 10.1371/journal.pmed.1001347 [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Schnippel K, Meyer-Rath G, Long L, Stevens WS, Sanne I, Rosen S. Diagnosing Xpert MTB/RIF negative TB: impact and cost of alternative algorithms for South Africa. SAMJ, S Afr med j. 2013;103(2):101–6. [DOI] [PubMed] [Google Scholar]
41.Sharma A, Hill A, Kurbatova E, van der Walt M, Kvasnovsky C, Tupasi TE, et al. Estimating the future burden of multidrug-resistant and extensively drug-resistant tuberculosis in India, the Philippines, Russia, and South Africa: a mathematical modelling study. Lancet Infect Dis. 2017;17(7):707–15. doi: 10.1016/S1473-3099(17)30247-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Gumbo T. New susceptibility breakpoints for first-line antituberculosis drugs based on antimicrobial pharmacokinetic/pharmacodynamic science and population pharmacokinetic variability. Antimicrob Agents Chemother. 2010;54(4):1484–91. doi: 10.1128/AAC.01474-09 [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Ibarguen-Mondragon E, Romero-Leiton JP, Esteva L, Burbano-Rosero EM. MATHEMATICAL MODELING OF BACTERIAL RESISTANCE TO ANTIBIOTICS BY MUTATIONS AND PLASMIDS. Journal of Biological Systems. 2016. Mar;24(1):129–46. [DOI] [PubMed] [Google Scholar]
44.Kendall EA, Malhotra S, Cook-Scalise S, Dowdy DW, Denkinger CM. Clinical impact of rapid drug susceptibility testing to accompany fluoroquinolone-containing universal tuberculosis regimens: A markov model. Clinical Infectious Diseases. 2020;71(11):2889–96. doi: 10.1093/cid/ciz1179 [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Lin YJ, Liao CM. Quantifying the impact of drug combination regimens on TB treatment efficacy and multidrug resistance probability. J Antimicrob Chemother. 2015;70(12):3273–82. doi: 10.1093/jac/dkv247 [DOI] [PubMed] [Google Scholar]
46.Basu S, Galvani AP. The transmission and control of XDR TB in South Africa: an operations research and mathematical modelling approach. Epidemiol Infect. 2008;136(12):1585–98. doi: 10.1017/S0950268808000964 [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Basu S, Friedland GH, Medlock J, Andrews JR, Shah NS, Gandhi NR, et al. Averting epidemics of extensively drug-resistant tuberculosis. Proc Natl Acad Sci U S A. 2009;106(18):7672–7. doi: 10.1073/pnas.0812472106 [DOI] [PMC free article] [PubMed] [Google Scholar]
48.Almeida JG, Chacko CJ. Computerized mathematical model of M. leprae population dynamics during multiple drug therapy. Indian J Lepr. 1985;57(4):780–9. [PubMed] [Google Scholar]
49.Faraj A, Clewe O, Svensson RJ, Mukamolova GV, Barer MR, Simonsson USH. Difference in persistent tuberculosis bacteria between in vitro and sputum from patients: implications for translational predictions. Sci rep. 2020;10(1):15537. doi: 10.1038/s41598-020-72472-y [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Magombedze G, Pasipanodya JG, Srivastava S, Deshpande D, Visser ME, Chigutsa E, et al. Transformation Morphisms and Time-to-Extinction Analysis That Map Therapy Duration From Preclinical Models to Patients With Tuberculosis: Translating From Apples to Oranges. Clinical Infectious Diseases. 2018. Dec;67:S349–58. doi: 10.1093/cid/ciy623 [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Alavez-Ramirez J, Castellanos JRA, Esteva L, Flores JA, Fuentes-Allen JL, Garcia-Ramos G, et al. Within-host population dynamics of antibiotic-resistant M. tuberculosis. Math Med Biol. 2007;24(1):35–56. doi: 10.1093/imammb/dql026 [DOI] [PubMed] [Google Scholar]
52.Ayabina D, Hendon-Dunn C, Bacon J, Colijn C. Diverse drug-resistant subpopulations of Mycobacterium tuberculosis are sustained in continuous culture. J R Soc Interface. 2016;13(124). doi: 10.1098/rsif.2016.0745 [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Basu S, Orenstein E, Galvani AP. The theoretical influence of immunity between strain groups on the progression of drug-resistant tuberculosis epidemics. J Infect Dis. 2008;198(10):1502–13. doi: 10.1086/592508 [DOI] [PubMed] [Google Scholar]
54.Blower SM, Chou T. Modeling the emergence of the ‘hot zones’: tuberculosis and the amplification dynamics of drug resistance. Nat Med. 2004;10(10):1111–6. doi: 10.1038/nm1102 [DOI] [PubMed] [Google Scholar]
55.Cohen T, Lipsitch M, Walensky RP, Murray M. Beneficial and perverse effects of isoniazid preventive therapy for latent tuberculosis infection in HIV-tuberculosis coinfected populations. Proc Natl Acad Sci U S A. 2006;103(18):7042–7. doi: 10.1073/pnas.0600349103 [DOI] [PMC free article] [PubMed] [Google Scholar]
56.Cohen T, Murray M. Modeling epidemics of multidrug-resistant M. tuberculosis of heterogeneous fitness. Nat Med. 2004;10(10):1117–21. doi: 10.1038/nm1110 [DOI] [PMC free article] [PubMed] [Google Scholar]
57.Colijn C, Cohen T, Ganesh A, Murray M. Spontaneous emergence of multiple drug resistance in tuberculosis before and during therapy. PLoS ONE. 2011;6(3):e18327. doi: 10.1371/journal.pone.0018327 [DOI] [PMC free article] [PubMed] [Google Scholar]
58.Drusano GL, Neely M, Van Guilder M, Schumitzky A, Brown D, Fikes S, et al. Analysis of combination drug therapy to develop regimens with shortened duration of treatment for tuberculosis. PLoS ONE. 2014;9(7):e101311. doi: 10.1371/journal.pone.0101311 [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Ford CB, Shah RR, Maeda MK, Gagneux S, Murray MB, Cohen T, et al. Mycobacterium tuberculosis mutation rate estimates from different lineages predict substantial differences in the emergence of drug-resistant tuberculosis. Nat Genet. 2013;45(7):784–90. doi: 10.1038/ng.2656 [DOI] [PMC free article] [PubMed] [Google Scholar]
60.Lipsitch M, Levin BR. The within-host population dynamics of antibacterial chemotherapy: conditions for the evolution of resistance. Ciba Found Symp. 1997;207(d7x, 0356636):112–30. doi: 10.1002/9780470515358.ch8 [DOI] [PubMed] [Google Scholar]
61.Pecerska J, Kuhnert D, Meehan CJ, Coscolla M, de Jong BC, Gagneux S, et al. Quantifying transmission fitness costs of multi-drug resistant tuberculosis. Epidemics. 2021;36:100471. doi: 10.1016/j.epidem.2021.100471 [DOI] [PubMed] [Google Scholar]
62.Pienaar E, Linderman JJ, Kirschner DE. Emergence and selection of isoniazid and rifampin resistance in tuberculosis granulomas. PLoS ONE. 2018;13(5):e0196322. doi: 10.1371/journal.pone.0196322 [DOI] [PMC free article] [PubMed] [Google Scholar]
63.Sergeev R, Colijn C, Murray M, Cohen T. Modeling the dynamic relationship between HIV and the risk of drug-resistant tuberculosis. Sci Transl Med. 2012;4(135):135ra67. doi: 10.1126/scitranslmed.3003815 [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Menzies NA, Wolf E, Connors D, Bellerose M, Sbarra AN, Cohen T, et al. Progression from latent infection to active disease in dynamic tuberculosis transmission models: a systematic review of the validity of modelling assumptions. The Lancet Infectious Diseases. 2018. Aug;18(8):e228–38. doi: 10.1016/S1473-3099(18)30134-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
65.World Health Organisation. WHO consolidated guidelines on tuberculosis. Module 4: treatment—drug-resistant tuberculosis treatment, 2022 update. 2022 Dec. [PubMed]
66.Gagneux S, Long CD, Small PM, Van T, Schoolnik GK, Bohannan BJM. The Competitive Cost of Antibiotic Resistance in Mycobacterium tuberculosis. Science. 2006. Jun 30;312(5782):1944–6. doi: 10.1126/science.1124410 [DOI] [PubMed] [Google Scholar]
67.World Health Organization. Guidance for country-level TB modelling [Internet]. Geneva: World Health Organization; 2018. [cited 2023 Jun 6]. 37 p. Available from: https://apps.who.int/iris/handle/10665/274279 [Google Scholar]
68.Bennett C, Manuel DG. Reporting guidelines for modelling studies. BMC Med Res Methodol. 2012. Dec;12(1):168. doi: 10.1186/1471-2288-12-168 [DOI] [PMC free article] [PubMed] [Google Scholar]

PLoS Pathog. doi: 10.1371/journal.ppat.1011574.r001

Decision Letter 0

Debra E Bessen, Mark Robert Davies

16 Oct 2023

Dear Dr Fuller,

Thank you very much for submitting your manuscript "Mathematical models of drug resistant tuberculosis show little consideration of bacterial heterogeneity: a systematic review" for consideration at PLOS Pathogens. As with all papers reviewed by the journal, your manuscript was reviewed by members of the editorial board and by several independent reviewers. It's evident that the the systematic review is timely, yet it's evident that a strong justification of 'how', 'why' and 'when' models should account for bacterial heterogeneity is required. In light of the reviews (below this email), we would like to invite the resubmission of a significantly-revised version that takes into account the reviewers' comments.

We cannot make any decision about publication until we have seen the revised manuscript and your response to the reviewers' comments. Your revised manuscript is also likely to be sent to reviewers for further evaluation.

When you are ready to resubmit, please upload the following:

[1] A letter containing a detailed list of your responses to the review comments and a description of the changes you have made in the manuscript. Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

[2] Two versions of the revised manuscript: one with either highlights or tracked changes denoting where the text has been changed; the other a clean version (uploaded as the manuscript file).

Important additional instructions are given below your reviewer comments.

Please prepare and submit your revised manuscript within 60 days. If you anticipate any delay, please let us know the expected resubmission date by replying to this email. Please note that revised manuscripts received after the 60-day due date may require evaluation and peer review similar to newly submitted manuscripts.

Thank you again for your submission. We hope that our editorial process has been constructive so far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Mark R. Davies, Ph.D

Academic Editor

PLOS Pathogens

Debra Bessen

Section Editor

PLOS Pathogens

Kasturi Haldar

Editor-in-Chief

PLOS Pathogens

orcid.org/0000-0001-5065-158X

Michael Malim

Editor-in-Chief

PLOS Pathogens

orcid.org/0000-0002-7699-2064

***********************

Reviewer's Responses to Questions

Part I - Summary

Please use this section to discuss strengths/weaknesses of study, novelty/significance, general execution and scholarship.

Reviewer #1: This paper provides a systematic overview of TB models which address questions related to drug resistance. The authors include a 2-stage review where they first identify within-host models and transmission models that consider questions related to drug resistance, then identify the subset of these models that allow for variation of resistant isolates (for the within-host models) or patients with resistant TB (for the transmission models).

The manuscript is useful in that provides a timely summary of the literature on modeling of DR-TB, with a specific question about how bacterial heterogeneity is handled (or omitted) from these models. A major challenge involved in this review is for the authors to provide clear description of the rationale for inclusion/exclusion of studies, the classification of these studies, and what is actually meant by “fitness” as this is a composite characteristic that may be modeled with a variety of mechanisms. I have some specific comments related to opportunities to improve these aspects of the paper below.

Further, I think the authors may want to soften the title and some of the language a bit. I agree with the authors that there may be important consequences for omitting consideration of such bacterial variation, but I do not think that every model-based analysis of drug resistant TB necessarily needs to include this type of variation to be useful. I suspect the authors agree with this, but the title sounds unnecessarily judgemental.

Reviewer #2: This manuscript aims to summarize the approaches used by published mathematical models of human mycobacterial infections (with a focus on tuberculosis) to evaluate whether and how they account for bacterial heterogeneity. This is an impressively comprehensive review of modeling studies, spanning the range from models of bacterial populations to decision-analytic models to evaluate the cost-effectiveness of tuberculosis treatment interventions. That alone makes this work highly valuable for tuberculosis researchers, and modelers in particular. There are a few key aspects of the work that could be improved to make it suitable for publication.

**********

Part II – Major Issues: Key Experiments Required for Acceptance

Please use this section to detail the key new experiments or modifications of existing experiments that should be absolutely required to validate study conclusions.

Generally, there should be no more than 3 such required experiments or major modifications for a "Major Revision" recommendation. If more than 3 experiments are necessary to validate the study conclusions, then you are encouraged to recommend "Reject".

Reviewer #1: Major comments:

1) Lines 131-135 and Lines 171-175 - I am not quite clear on the distinction being made between the types of heterogeneity considered for the i) within-host models vs. ii) transmission models. I assume the goal is to include models of each type when there is structure that allows the same pressure (ie drug treatment) to exhibit variable selection on mycobacteria of the same resistance phenotype (for within-host models) or individuals infected by mycobacteria with the same resistance phenotype (for transmission models)? In my view, being upfront about the ingredients needed to model selection of more fit DR variants provides a clear rationale for why some studies are included and others are not.

2) Relatedly, some of the wording is ambiguous in these sections and should be clarified, for example:

a. Line 133: “strains resistance (sic) to a single drug should also vary in another characteristic.” I assume this should be replaced by individuals infected with strains resistant to the same drug should also vary in another characteristic – that is, you are not interested in models that include INH and Rif monoresist TB of different transmission fitness, but rather models that include Rif resistant TB of variable transmission fitness.

b. Line 134: “multiple resistant strains were categorized and parameterized differently from eachother.” I assume this means that bacterial isolates of the same/similar resistance phenotype differed in way (e.g. growth rate)

3) For stage 1 review, I am wondering if the authors collected information about the time horizon modeled in each of the included studies (especially for the transmission models). Given the relatively slows dynamics of TB and DR-TB, I think readers would be interested in understanding the scope of the time horizons that have been modeled.

4) Figure 3: The categories of model types and aims for Figure 3 are confusing. Some of the type categories refer to the scale of the model (e.g. bacterial population) while some refer to the modeling approach (e.g. decision analytic), and some are subcategories of each other. The categories of model aims also seem a bit ad hoc and unclear and potentially overlapping (e.g. burden, data analysis vs theoretical, intervention). I find this difficult to make sense of and wonder if there is a more coherent way to categorize model types and usages for a reader such that the categories are mutually exclusive groups?

5) Figure 4: I understand the full matrix showing which papers included which resistance phenotypes is provided as a supplement and is probably too large to include in the main text as it is currently shown. But featuring these small subset of outliers with a large number of DR phenotypes in the main text (Figure 4 )doesn’t seem that helpful if the goal is to give the reader a fair sense for the scope of the literature. Wouldn’t it be possible to make a heatmap figure (or similar) that shows the frequency at which different DR phenotypes are included in all models in stage 1 (not just those with >3 pheotypes) even if you can’t show all of the details about the studies in the figure?

6) Line 406-7: “Where heterogeneity was captured, it was mostly through fitness variation”. I am unsure as what is really meant here as fitness is a composite characteristic. This is too vague a term and may differ for within host (eg differences in growth rates in absence of antibiotic pressure?) and transmission models (eg differences in transmission capacity?, differences in ability to cause disease after infection?).

7) I have questions about the completeness of the literature search (or maybe don’t quite understand the inclusion criteria), for example work from Abel zur Wiesch seems like it should have been included?

a. https://pubmed.ncbi.nlm.nih.gov/25972005/

8) I think there is a missed opportunity for the authors to use the Discussion to be more explicit about the consequences of not considering bacterial heterogeneity in these types of models – the decision (implicit or explicit) to omit this type of heterogeneity means that the models don’t allow for drug treatment to operate as a selective pressure. Whether this is a problem for models depends on the specific questions being asked, the specific selection pressure being exerted, and the time frame over which the effects are considered. The title of the paper suggests that this is almost always a problem, but I think worth considering being a bit less prescriptive. As the authors rightly argue elsewhere, all these models need to make simplifying decisions, so I would tend to be careful to suggest that models of DR TB always need to include such heterogeneity.

Reviewer #2: 1. What seems to be missing in the paper is a strong justification of why it matters to account for bacterial heterogeneity in models of tuberculosis. The authors mention that predicted outcomes may differ between models that do or do not account for heterogeneity but this is somewhat of a truism (we would expect that models with different structure and/or parameters would have different results). It would be helpful to provide more specifics in terms of the hypothesized differences (e.g., would we expect such models that do not include bacterial heterogeneity to underestimate or overestimate the development of resistance or effectiveness of treatments? Does the expected magnitude of these differences justify increasing model complexity?). If there is little evidence to date as to the value of incorporating bacterial heterogeneity in these models, than that can be stated as well, and can help to justify the need for this review.

2. Methods, line 132-135: can you please explain why bacterial heterogeneity was defined differently for bacterial vs. human population models?

**********

Part III – Minor Issues: Editorial and Data Presentation Modifications

Please use this section for editorial suggestions as well as relatively minor modifications of existing data that would enhance clarity.

Reviewer #1: Minor comments:

1) Line 92 – the MDR/RR designation also reflects that the scale up of Xpert, which reports Rif-R resistance but not INH-R, has meant that we often know Rif-R status but not INH-R.

2) Line 198 – for the second stage of literature review, how many reviewers also help to identify which of the papers met heterogeneity inclusion criteria?

3) Line 460 – “mathematically, it is difficult to include complexities in all aspects…” I don’t think it is the math that makes it challenging to include complexity.

Reviewer #2: 1. It would be helpful to state clearly which aspects of bacterial heterogeneity the authors analyze in this work (e.g., heterogeneity in fitness cost of specific mutations, persistence in anatomic compartments, response to specific drugs). Stating this clearly in the Introduction will help keep the reader focused on what the primary goals of the paper are.

2. Please consider moving some of the Results section to the appendix so that the Results focus on the main purpose of the paper, to evaluated the inclusion of bacterial heterogeneity. There is lots of other very valuable information (e.g., study settings, data sources, etc…) but presenting the results in a kind of laundry list raises the risk of readers getting lost. At the very least, I would recommend placing the results on bacterial heterogeneity first, followed by all of the other results.

3. In the Discussion the authors bring up the fact that most papers incorporate resistance as a discrete value, but use continuous distributions for fitness costs. One potential reason for that is that there are point estimates for response to treatment conditional on drug resistance available in the literature or from primary data, whereas such data are rare if at all available for fitness costs (thus forcing modelers to consider a broad range of potential values across a continuous distribution).

4. The wording used in the paper can sometimes be vague or confusing. For example, rather than referring to “different resistances”, I would suggest “types” or “patterns” of resistance. Similarly, in the Supplement, I would suggest rephrasing “actual” vs. “theoretical” resistance to “specific” vs. “hypothetical”.

5. Please consider rephrasing “data analysis” to “parameter estimation” when describing the aims of models.

6. Results, line 227: the authors state that the distribution of countries covered in the selected modeling papers does not reflect the settings with highest DR-TB incidence but this is not really true: The countries with the most modeling papers are all in the top 5 of DR-TB incidence.

7. In the legend to Figure 4, please specify that the papers listed are those considering resistance to 3 or more specific drugs (rather than just “multiple”). Also, please make sure to include the paper indices matching the Table S1 in the figure (as mentioned in the legend).

8. Please review the supplemental materials carefully for typographical and grammatical errors.

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Figure Files:

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org.

Data Requirements:

Please note that, as a condition of publication, PLOS' data policy requires that you make available all data used to draw the conclusions outlined in your manuscript. Data must be deposited in an appropriate repository, included within the body of the manuscript, or uploaded as supporting information. This includes all numerical values that were used to generate graphs, histograms etc.. For an example see here on PLOS Biology: http://www.plosbiology.org/article/info%3Adoi%2F10.1371%2Fjournal.pbio.1001908#s5.

Reproducibility:

To enhance the reproducibility of your results, we recommend that you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. Additionally, PLOS ONE offers an option to publish peer-reviewed clinical study protocols. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols

PLoS Pathog. 2024 Apr 10;20(4):e1011574. doi: 10.1371/journal.ppat.1011574.r002

Author response to Decision Letter 0

19 Dec 2023

Attachment

Submitted filename: Responses to Reviewer Questions.docx

ppat.1011574.s009.docx^{(27.2KB, docx)}

PLoS Pathog. doi: 10.1371/journal.ppat.1011574.r003

Decision Letter 1

Debra E Bessen, Mark Robert Davies

12 Feb 2024

Dear Dr Fuller,

Thank you very much for submitting your manuscript "Mathematical models of drug-resistant tuberculosis lack bacterial heterogeneity: a systematic review" for consideration at PLOS Pathogens. As with all papers reviewed by the journal, your manuscript was reviewed by members of the editorial board and by several independent reviewers. The reviewers appreciated the attention to an important topic. Based on the reviews, we are likely to accept this manuscript for publication, providing that you modify the manuscript according to the review recommendations.

The reviewers acknowledge substantial improvements to the manuscript. However, some minor comments have been raised that should be addressed.

Please prepare and submit your revised manuscript within 30 days. If you anticipate any delay, please let us know the expected resubmission date by replying to this email.

When you are ready to resubmit, please upload the following:

[1] A letter containing a detailed list of your responses to all review comments, and a description of the changes you have made in the manuscript.

Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out

[2] Two versions of the revised manuscript: one with either highlights or tracked changes denoting where the text has been changed; the other a clean version (uploaded as the manuscript file).

Important additional instructions are given below your reviewer comments.

Thank you again for your submission to our journal. We hope that our editorial process has been constructive so far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Mark R. Davies, Ph.D

Academic Editor

PLOS Pathogens

Debra Bessen

Section Editor

PLOS Pathogens

Michael Malim

Editor-in-Chief

PLOS Pathogens

orcid.org/0000-0002-7699-2064

***********************

Reviewer Comments (if any, and for reference):

Reviewer's Responses to Questions

Part I - Summary

Please use this section to discuss strengths/weaknesses of study, novelty/significance, general execution and scholarship.

Reviewer #1: (No Response)

Reviewer #2: The authors have appropriately addressed most of the comments from the first round of reviews. Again, this is an impressive and valuable review of approaches used to model durg resistance in mathematical models of tuberculosis. I only have minor editorial comments to improve the clarity for readers.

**********

Part II – Major Issues: Key Experiments Required for Acceptance

Please use this section to detail the key new experiments or modifications of existing experiments that should be absolutely required to validate study conclusions.

Reviewer #1: (No Response)

Reviewer #2: (No Response)

**********

Part III – Minor Issues: Editorial and Data Presentation Modifications

Please use this section for editorial suggestions as well as relatively minor modifications of existing data that would enhance clarity.

Reviewer #1: It does not seem consistent to list MDR/RR under the "multiple" drug resistant category as depicted in Figure 4, but then list models that only modeled MDR/RR as single resistance in Figure 5.

Perhaps I have misunderstood? But if not, this classification should be made consistent throughout the manuscript.

Reviewer #2: 1. I think that the manuscript would benefit from more clarity in the language used, especially when referring to drug resistance. Often the authors use terms such as "mutiple resistances". I would suggest selecting an alternative such as "classes of resistance", "categories of resistance" or "resistance phenotypes", and using it consistently throughout.

2. Similarly, the authors could consider distinghuishing the two broad classes of models that they considered as "bacterial population" vs. "human population".

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Figure Files:

Data Requirements:

Please note that, as a condition of publication, PLOS' data policy requires that you make available all data used to draw the conclusions outlined in your manuscript. Data must be deposited in an appropriate repository, included within the body of the manuscript, or uploaded as supporting information. This includes all numerical values that were used to generate graphs, histograms etc.. For an example see here: http://www.plosbiology.org/article/info%3Adoi%2F10.1371%2Fjournal.pbio.1001908#s5.

Reproducibility:

References:

Please review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript. If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

PLoS Pathog. 2024 Apr 10;20(4):e1011574. doi: 10.1371/journal.ppat.1011574.r004

Author response to Decision Letter 1

15 Mar 2024

Attachment

Submitted filename: Responses to Reviewer Questions 070324.docx

ppat.1011574.s010.docx^{(23.2KB, docx)}

PLoS Pathog. doi: 10.1371/journal.ppat.1011574.r005

Decision Letter 2

Debra E Bessen, Mark Robert Davies

25 Mar 2024

Dear Dr Fuller,

We are pleased to inform you that your manuscript 'Mathematical models of drug-resistant tuberculosis lack bacterial heterogeneity: a systematic review' has been provisionally accepted for publication in PLOS Pathogens.

Before your manuscript can be formally accepted you will need to complete some formatting changes, which you will receive in a follow up email. A member of our team will be in touch with a set of requests.

Please note that your manuscript will not be scheduled for publication until you have made the required changes, so a swift response is appreciated.

IMPORTANT: The editorial review process is now complete. PLOS will only permit corrections to spelling, formatting or significant scientific errors from this point onwards. Requests for major changes, or any which affect the scientific understanding of your work, will cause delays to the publication date of your manuscript.

Should you, your institution's press office or the journal office choose to press release your paper, you will automatically be opted out of early publication. We ask that you notify us now if you or your institution is planning to press release the article. All press must be co-ordinated with PLOS.

Thank you again for supporting Open Access publishing; we are looking forward to publishing your work in PLOS Pathogens.

Best regards,

Mark R. Davies, Ph.D

Academic Editor

PLOS Pathogens

Debra Bessen

Section Editor

PLOS Pathogens

Michael Malim

Editor-in-Chief

PLOS Pathogens

orcid.org/0000-0002-7699-2064

***********************************************************

Minor comments from reviewers have been adequately addressed.

Reviewer Comments (if any, and for reference):

PLoS Pathog. doi: 10.1371/journal.ppat.1011574.r006

Acceptance letter

Debra E Bessen, Mark Robert Davies

3 Apr 2024

Dear Ms Fuller,

We are delighted to inform you that your manuscript, "Mathematical models of drug-resistant tuberculosis lack bacterial heterogeneity: a systematic review," has been formally accepted for publication in PLOS Pathogens.

We have now passed your article onto the PLOS Production Department who will complete the rest of the pre-publication process. All authors will receive a confirmation email upon publication.

The corresponding author will soon be receiving a typeset proof for review, to ensure errors have not been introduced during production. Please review the PDF proof of your manuscript carefully, as this is the last chance to correct any scientific or type-setting errors. Please note that major changes, or those which affect the scientific understanding of the work, will likely cause delays to the publication date of your manuscript. Note: Proofs for Front Matter articles (Pearls, Reviews, Opinions, etc...) are generated on a different schedule and may not be made available as quickly.

Soon after your final files are uploaded, the early version of your manuscript, if you opted to have an early version of your article, will be published online. The date of the early version will be your article's publication date. The final article will be published to the same URL, and all versions of the paper will be accessible to readers.

Thank you again for supporting open-access publishing; we are looking forward to publishing your work in PLOS Pathogens.

Best regards,

Michael Malim

Editor-in-Chief

PLOS Pathogens

orcid.org/0000-0002-7699-2064

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Text. Search strings.

(DOCX)

ppat.1011574.s001.docx^{(17KB, docx)}

S2 Text. Details of extraction table for stage 1.

(DOCX)

ppat.1011574.s002.docx^{(20.4KB, docx)}

S3 Text. Details of extraction table for stage 2.

(DOCX)

ppat.1011574.s003.docx^{(20.1KB, docx)}

S1 Fig. Heatmap of all resistance categories in stage 1 models.

(DOCX)

ppat.1011574.s004.docx^{(225.9KB, docx)}

S2 Fig. Plot of number of publications over time.

(TIF)

ppat.1011574.s005.tif^{(163.7KB, tif)}

S1 Table. Extraction table results from stage 1.

(XLSX)

ppat.1011574.s006.xlsx^{(75.9KB, xlsx)}

S2 Table. Extraction table results from stage 2.

(XLSX)

ppat.1011574.s007.xlsx^{(79.9KB, xlsx)}

S3 Table. Geographic settings in models.

(DOCX)

ppat.1011574.s008.docx^{(20KB, docx)}

Attachment

Submitted filename: Responses to Reviewer Questions.docx

ppat.1011574.s009.docx^{(27.2KB, docx)}

Attachment

Submitted filename: Responses to Reviewer Questions 070324.docx

ppat.1011574.s010.docx^{(23.2KB, docx)}

Data Availability Statement

All relevant data are within the manuscript and its Supporting Information files.

[ppat.1011574.ref001] 1.World Health Organisation. Global tuberculosis report 2022 [Internet]. 2022 Oct. Available from: https://www.who.int/publications/i/item/9789240061729

[ppat.1011574.ref002] 2.World Health Organisation. WHO announces updated definitions of extensively drug-resistant tuberculosis [Internet]. 2021 [cited 2021 Jan 27]. Available from: https://www.who.int/news/item/27-01-2021-who-announces-updated-definitions-of-extensively-drug-resistant-tuberculosis

[ppat.1011574.ref003] 3.World Health Organisation. Definitions and reporting framework for tuberculosis–2013 revision: updated December 2014 and January 2020. 2013. Report No.: No. WHO/HTM/TB/2013.2.

[ppat.1011574.ref004] 4.Cohen T, Dye C, Colijn C, Williams B, Murray M. Mathematical models of the epidemiology and control of drug-resistant TB. Expert Review of Respiratory Medicine. 2009;3(1):67–79. doi: 10.1586/17476348.3.1.67 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref005] 5.Cohen T, Sommers B, Murray M. The effect of drug resistance on the fitness of Mycobacterium tuberculosis. Lancet Infect Dis. 2003;3(1):13–21. doi: 10.1016/s1473-3099(03)00483-3 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref006] 6.Borrell S, Gagneux S. Infectiousness, reproductive fitness and evolution of drug-resistant Mycobacterium tuberculosis. Int J Tuberc Lung Dis. 2009;13(12):1456–66. [PubMed] [Google Scholar]

[ppat.1011574.ref007] 7.Niewiadomska AM, Jayabalasingham B, Seidman JC, Willem L, Grenfell B, Spiro D, et al. Population-level mathematical modeling of antimicrobial resistance: a systematic review. BMC Med. 2019;17(1):81. doi: 10.1186/s12916-019-1314-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref008] 8.Knight GM, Colijn C, Shrestha S, Fofana M, Cobelens F, White RG, et al. The Distribution of Fitness Costs of Resistance-Conferring Mutations Is a Key Determinant for the Future Burden of Drug-Resistant Tuberculosis: A Model-Based Analysis. Clin Infect Dis. 2015;61Suppl 3(a4j, 9203213):S147–54. doi: 10.1093/cid/civ579 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref009] 9.Trauer JM, Dodd PJ, Gomes MGM, Gomez GB, Houben RMGJ, McBryde ES, et al. The Importance of Heterogeneity to the Epidemiology of Tuberculosis. Clinical Infectious Diseases. 2019. Jun 18;69(1):159–66. doi: 10.1093/cid/ciy938 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref010] 10.Spicknall IH, Foxman B, Marrs CF, Eisenberg JNS. A modeling framework for the evolution and spread of antibiotic resistance: Literature review and model categorization. American Journal of Epidemiology. 2013;178(4):508–20. doi: 10.1093/aje/kwt017 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref011] 11.Melsew YA, Adekunle AI, Cheng AC, McBryde ES, Ragonnet R, Trauer JM. Heterogeneous infectiousness in mathematical models of tuberculosis: A systematic review. Epidemics. 2020;30:100374. doi: 10.1016/j.epidem.2019.100374 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref012] 12.Castillo-Chavez C, Song BJ. Dynamical models of tuberculosis and their applications. Mathematical Biosciences and Engineering. 2004. Sep;1(2):361–404. doi: 10.3934/mbe.2004.1.361 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref013] 13.Kirschner D, Pienaar E, Marino S, Linderman JJ. A review of computational and mathematical modeling contributions to our understanding of Mycobacterium tuberculosis within-host infection and treatment. Current Opinion in Systems Biology. 2017;3:170–85. doi: 10.1016/j.coisb.2017.05.014 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref014] 14.Ozcaglar C, Shabbeer A, Vandenberg SL, Yener B, Bennett KP. Epidemiological models of Mycobacterium tuberculosis complex infections. Math Biosci. 2012;236(2):77–96. doi: 10.1016/j.mbs.2012.02.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref015] 15.Eldholm V, Norheim G, von der Lippe B, Kinander W, Dahle UR, Caugant DA, et al. Evolution of extensively drug-resistant Mycobacterium tuberculosis from a susceptible ancestor in a single patient. Genome Biol. 2014;15(11):490. doi: 10.1186/s13059-014-0490-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref016] 16.Gopalaswamy R, Shanmugam S, Mondal R, Subbian S. Of tuberculosis and non-tuberculous mycobacterial infections–a comparative analysis of epidemiology, diagnosis and treatment. J Biomed Sci. 2020. Jun 17;27:74. doi: 10.1186/s12929-020-00667-6 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref017] 17.Maeda T, Kawada M, Sakata N, Kotani H, Furusawa C. Laboratory evolution of Mycobacterium on agar plates for analysis of resistance acquisition and drug sensitivity profiles. Sci Rep. 2021. Jul 23;11(1):15136. doi: 10.1038/s41598-021-94645-z [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref018] 18.Shiloh MU, DiGiuseppe Champion PA. To catch a killer. What can mycobacterial models teach us about Mycobacterium tuberculosis pathogenesis? Current Opinion in Microbiology. 2010. Feb;13(1):86–92. doi: 10.1016/j.mib.2009.11.006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref019] 19.Gygli SM, Borrell S, Trauner A, Gagneux S. Antimicrobial resistance in Mycobacterium tuberculosis: mechanistic and evolutionary perspectives. FEMS Microbiology Reviews. 2017. May 1;41(3):354–73. doi: 10.1093/femsre/fux011 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref020] 20.Ankomah P, Levin BR. Two-drug antimicrobial chemotherapy: a mathematical model and experiments with Mycobacterium marinum. PLoS Pathog. 2012;8(1):e1002487. doi: 10.1371/journal.ppat.1002487 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref021] 21.PRISMA-P Group, Moher D, Shamseer L, Clarke M, Ghersi D, Liberati A, et al. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015 statement. Syst Rev. 2015. Dec;4(1):1. doi: 10.1186/2046-4053-4-1 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref022] 22.Fofana MO, Shrestha S, Knight GM, Cohen T, White RG, Cobelens F, et al. A Multistrain Mathematical Model To Investigate the Role of Pyrazinamide in the Emergence of Extensively Drug-Resistant Tuberculosis. Antimicrob Agents Chemother. 2017;61(3). doi: 10.1128/AAC.00498-16 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref023] 23.Han WM, Mahikul W, Pouplin T, Lawpoolsri S, White LJ, Pan-Ngum W. Assessing the impacts of short-course multidrug-resistant tuberculosis treatment in the Southeast Asia Region using a mathematical modeling approach. PloS one. 2021;16(3):e0248846. doi: 10.1371/journal.pone.0248846 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref024] 24.Kendall EA, Fojo AT, Dowdy DW. Expected effects of adopting a 9 month regimen for multidrug-resistant tuberculosis: a population modelling analysis. Lancet Respir Med. 2017;5(3):191–9. doi: 10.1016/S2213-2600(16)30423-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref025] 25.Winetsky DE, Negoescu DM, DeMarchis EH, Almukhamedova O, Dooronbekova A, Pulatov D, et al. Screening and rapid molecular diagnosis of tuberculosis in prisons in Russia and Eastern Europe: a cost-effectiveness analysis. PLoS Med. 2012;9(11):e1001348. doi: 10.1371/journal.pmed.1001348 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref026] 26.Trauer JM, Denholm JT, McBryde ES. Construction of a mathematical model for tuberculosis transmission in highly endemic regions of the Asia-Pacific. J Theor Biol. 2014;358(k8n, 0376342):74–84. doi: 10.1016/j.jtbi.2014.05.023 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref027] 27.Pereira RS, Bauch CT, Penna TJP, Espindola AL. A nested model for tuberculosis: Combining within-host and between-host processes in a single framework. INTERNATIONAL JOURNAL OF MODERN PHYSICS C. 2021. Dec;32(12). [Google Scholar]

[ppat.1011574.ref028] 28.Mehra M, Kambili C, Potluri R, Rhines A, Singh V, Thomas A. Modeling the impact of bedaquiline treatment strategies on the multidrug-resistant tuberculosis burden in India. Int J Tuberc Lung Dis. 2017;21(8):902–9. doi: 10.5588/ijtld.16.0717 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref029] 29.Langley I, Lin HH, Egwaga S, Doulla B, Ku CC, Murray M, et al. Assessment of the patient, health system, and population effects of Xpert MTB/RIF and alternative diagnostics for tuberculosis in Tanzania: an integrated modelling approach. Lancet Glob Health. 2014;2(10):e581–91. doi: 10.1016/S2214-109X(14)70291-8 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref030] 30.Dodd PJ, Sismanidis C, Seddon JA. Global burden of drug-resistant tuberculosis in children: a mathematical modelling study. Lancet Infect Dis. 2016;16(10):1193–201. doi: 10.1016/S1473-3099(16)30132-3 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref031] 31.Houben RMGJ Dodd PJ. The Global Burden of Latent Tuberculosis Infection: A Re-estimation Using Mathematical Modelling. PLoS Med. 2016;13(10):e1002152. doi: 10.1371/journal.pmed.1002152 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref032] 32.Knight GM, McQuaid CF, Dodd PJ, Houben RMGJ. Global burden of latent multidrug-resistant tuberculosis: trends and estimates based on mathematical modelling. Lancet Infect Dis. 2019;19(8):903–12. doi: 10.1016/S1473-3099(19)30307-X [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref033] 33.Cadosch D, Abel Zur Wiesch P, Kouyos R, Bonhoeffer S. The Role of Adherence and Retreatment in De Novo Emergence of MDR-TB. PLoS Comput Biol. 2016;12(3):e1004749. doi: 10.1371/journal.pcbi.1004749 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref034] 34.Lipsitch M, Levin BR. Population dynamics of tuberculosis treatment: mathematical models of the roles of non-compliance and bacterial heterogeneity in the evolution of drug resistance. Int J Tuberc Lung Dis. 1998;2(3):187–99. [PubMed] [Google Scholar]

[ppat.1011574.ref035] 35.Oxlade O, Schwartzman K, Pai M, Heymann J, Benedetti A, Royce S, et al. Predicting outcomes and drug resistance with standardised treatment of active tuberculosis. Eur Respir J. 2010;36(4):870–7. doi: 10.1183/09031936.00151709 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref036] 36.Chindelevitch L, Menzies NA, Pretorius C, Stover J, Salomon JA, Cohen T. Evaluating the potential impact of enhancing HIV treatment and tuberculosis control programmes on the burden of tuberculosis. Journal of the Royal Society Interface. 2015;12(106):20150146. doi: 10.1098/rsif.2015.0146 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref037] 37.Fors J, Strydom N, Fox WS, Keizer RJ, Savic RM. Mathematical model and tool to explore shorter multi-drug therapy options for active pulmonary tuberculosis. PLoS Computational Biology. 2020;16(8):e1008107. doi: 10.1371/journal.pcbi.1008107 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref038] 38.Menzies NA, Cohen T, Hill AN, Yaesoubi R, Galer K, Wolf E, et al. Prospects for tuberculosis elimination in the United States: Results of a transmission dynamic model. American Journal of Epidemiology. 2018;187(9):2011–20. doi: 10.1093/aje/kwy094 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref039] 39.Menzies NA, Cohen T, Lin HH, Murray M, Salomon JA. Population health impact and cost-effectiveness of tuberculosis diagnosis with Xpert MTB/RIF: a dynamic simulation and economic evaluation. PLoS Med. 2012;9(11):e1001347. doi: 10.1371/journal.pmed.1001347 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref040] 40.Schnippel K, Meyer-Rath G, Long L, Stevens WS, Sanne I, Rosen S. Diagnosing Xpert MTB/RIF negative TB: impact and cost of alternative algorithms for South Africa. SAMJ, S Afr med j. 2013;103(2):101–6. [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref041] 41.Sharma A, Hill A, Kurbatova E, van der Walt M, Kvasnovsky C, Tupasi TE, et al. Estimating the future burden of multidrug-resistant and extensively drug-resistant tuberculosis in India, the Philippines, Russia, and South Africa: a mathematical modelling study. Lancet Infect Dis. 2017;17(7):707–15. doi: 10.1016/S1473-3099(17)30247-5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref042] 42.Gumbo T. New susceptibility breakpoints for first-line antituberculosis drugs based on antimicrobial pharmacokinetic/pharmacodynamic science and population pharmacokinetic variability. Antimicrob Agents Chemother. 2010;54(4):1484–91. doi: 10.1128/AAC.01474-09 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref043] 43.Ibarguen-Mondragon E, Romero-Leiton JP, Esteva L, Burbano-Rosero EM. MATHEMATICAL MODELING OF BACTERIAL RESISTANCE TO ANTIBIOTICS BY MUTATIONS AND PLASMIDS. Journal of Biological Systems. 2016. Mar;24(1):129–46. [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref044] 44.Kendall EA, Malhotra S, Cook-Scalise S, Dowdy DW, Denkinger CM. Clinical impact of rapid drug susceptibility testing to accompany fluoroquinolone-containing universal tuberculosis regimens: A markov model. Clinical Infectious Diseases. 2020;71(11):2889–96. doi: 10.1093/cid/ciz1179 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref045] 45.Lin YJ, Liao CM. Quantifying the impact of drug combination regimens on TB treatment efficacy and multidrug resistance probability. J Antimicrob Chemother. 2015;70(12):3273–82. doi: 10.1093/jac/dkv247 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref046] 46.Basu S, Galvani AP. The transmission and control of XDR TB in South Africa: an operations research and mathematical modelling approach. Epidemiol Infect. 2008;136(12):1585–98. doi: 10.1017/S0950268808000964 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref047] 47.Basu S, Friedland GH, Medlock J, Andrews JR, Shah NS, Gandhi NR, et al. Averting epidemics of extensively drug-resistant tuberculosis. Proc Natl Acad Sci U S A. 2009;106(18):7672–7. doi: 10.1073/pnas.0812472106 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref048] 48.Almeida JG, Chacko CJ. Computerized mathematical model of M. leprae population dynamics during multiple drug therapy. Indian J Lepr. 1985;57(4):780–9. [PubMed] [Google Scholar]

[ppat.1011574.ref049] 49.Faraj A, Clewe O, Svensson RJ, Mukamolova GV, Barer MR, Simonsson USH. Difference in persistent tuberculosis bacteria between in vitro and sputum from patients: implications for translational predictions. Sci rep. 2020;10(1):15537. doi: 10.1038/s41598-020-72472-y [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref050] 50.Magombedze G, Pasipanodya JG, Srivastava S, Deshpande D, Visser ME, Chigutsa E, et al. Transformation Morphisms and Time-to-Extinction Analysis That Map Therapy Duration From Preclinical Models to Patients With Tuberculosis: Translating From Apples to Oranges. Clinical Infectious Diseases. 2018. Dec;67:S349–58. doi: 10.1093/cid/ciy623 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref051] 51.Alavez-Ramirez J, Castellanos JRA, Esteva L, Flores JA, Fuentes-Allen JL, Garcia-Ramos G, et al. Within-host population dynamics of antibiotic-resistant M. tuberculosis. Math Med Biol. 2007;24(1):35–56. doi: 10.1093/imammb/dql026 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref052] 52.Ayabina D, Hendon-Dunn C, Bacon J, Colijn C. Diverse drug-resistant subpopulations of Mycobacterium tuberculosis are sustained in continuous culture. J R Soc Interface. 2016;13(124). doi: 10.1098/rsif.2016.0745 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref053] 53.Basu S, Orenstein E, Galvani AP. The theoretical influence of immunity between strain groups on the progression of drug-resistant tuberculosis epidemics. J Infect Dis. 2008;198(10):1502–13. doi: 10.1086/592508 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref054] 54.Blower SM, Chou T. Modeling the emergence of the ‘hot zones’: tuberculosis and the amplification dynamics of drug resistance. Nat Med. 2004;10(10):1111–6. doi: 10.1038/nm1102 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref055] 55.Cohen T, Lipsitch M, Walensky RP, Murray M. Beneficial and perverse effects of isoniazid preventive therapy for latent tuberculosis infection in HIV-tuberculosis coinfected populations. Proc Natl Acad Sci U S A. 2006;103(18):7042–7. doi: 10.1073/pnas.0600349103 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref056] 56.Cohen T, Murray M. Modeling epidemics of multidrug-resistant M. tuberculosis of heterogeneous fitness. Nat Med. 2004;10(10):1117–21. doi: 10.1038/nm1110 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref057] 57.Colijn C, Cohen T, Ganesh A, Murray M. Spontaneous emergence of multiple drug resistance in tuberculosis before and during therapy. PLoS ONE. 2011;6(3):e18327. doi: 10.1371/journal.pone.0018327 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref058] 58.Drusano GL, Neely M, Van Guilder M, Schumitzky A, Brown D, Fikes S, et al. Analysis of combination drug therapy to develop regimens with shortened duration of treatment for tuberculosis. PLoS ONE. 2014;9(7):e101311. doi: 10.1371/journal.pone.0101311 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref059] 59.Ford CB, Shah RR, Maeda MK, Gagneux S, Murray MB, Cohen T, et al. Mycobacterium tuberculosis mutation rate estimates from different lineages predict substantial differences in the emergence of drug-resistant tuberculosis. Nat Genet. 2013;45(7):784–90. doi: 10.1038/ng.2656 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref060] 60.Lipsitch M, Levin BR. The within-host population dynamics of antibacterial chemotherapy: conditions for the evolution of resistance. Ciba Found Symp. 1997;207(d7x, 0356636):112–30. doi: 10.1002/9780470515358.ch8 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref061] 61.Pecerska J, Kuhnert D, Meehan CJ, Coscolla M, de Jong BC, Gagneux S, et al. Quantifying transmission fitness costs of multi-drug resistant tuberculosis. Epidemics. 2021;36:100471. doi: 10.1016/j.epidem.2021.100471 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref062] 62.Pienaar E, Linderman JJ, Kirschner DE. Emergence and selection of isoniazid and rifampin resistance in tuberculosis granulomas. PLoS ONE. 2018;13(5):e0196322. doi: 10.1371/journal.pone.0196322 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref063] 63.Sergeev R, Colijn C, Murray M, Cohen T. Modeling the dynamic relationship between HIV and the risk of drug-resistant tuberculosis. Sci Transl Med. 2012;4(135):135ra67. doi: 10.1126/scitranslmed.3003815 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref064] 64.Menzies NA, Wolf E, Connors D, Bellerose M, Sbarra AN, Cohen T, et al. Progression from latent infection to active disease in dynamic tuberculosis transmission models: a systematic review of the validity of modelling assumptions. The Lancet Infectious Diseases. 2018. Aug;18(8):e228–38. doi: 10.1016/S1473-3099(18)30134-8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ppat.1011574.ref065] 65.World Health Organisation. WHO consolidated guidelines on tuberculosis. Module 4: treatment—drug-resistant tuberculosis treatment, 2022 update. 2022 Dec. [PubMed]

[ppat.1011574.ref066] 66.Gagneux S, Long CD, Small PM, Van T, Schoolnik GK, Bohannan BJM. The Competitive Cost of Antibiotic Resistance in Mycobacterium tuberculosis. Science. 2006. Jun 30;312(5782):1944–6. doi: 10.1126/science.1124410 [DOI] [PubMed] [Google Scholar]

[ppat.1011574.ref067] 67.World Health Organization. Guidance for country-level TB modelling [Internet]. Geneva: World Health Organization; 2018. [cited 2023 Jun 6]. 37 p. Available from: https://apps.who.int/iris/handle/10665/274279 [Google Scholar]

[ppat.1011574.ref068] 68.Bennett C, Manuel DG. Reporting guidelines for modelling studies. BMC Med Res Methodol. 2012. Dec;12(1):168. doi: 10.1186/1471-2288-12-168 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Mathematical models of drug-resistant tuberculosis lack bacterial heterogeneity: A systematic review

Naomi M Fuller

Christopher F McQuaid

Martin J Harker

Chathika K Weerasuriya

Timothy D McHugh

Gwenan M Knight

Roles

Abstract

Author summary

Introduction

Methods

Search strategy

Inclusion and exclusion criteria

Table 1. Inclusion and exclusion criteria used for title and abstract, stage 1 and stage 2 screening.

Selection and extraction: Stage 1

Selection and extraction: Stage 2

Results

Fig 1. PRISMA flow diagram outlining the systematic selection of studies to include in the analysis.

Stage 1 Results: DR-mycobacteria model landscape

Settings captured

Fig 2. Uneven geographical distribution of mathematical models of DR-mycobacteria (a) and correspondence with MDR/RR-TB incidence (b).

Model aims and types

Fig 3. Model aims broken down by model types (colours) highlights transmission models are the most used for DR-mycobacteria modelling.

Resistance categories

Fig 4. Treemap of specific resistance classes included in models in stage 1 shows that the majority of models included MDR/RR and few included more than two resistance classes.

Stage 2 Results: Heterogeneous models

Bacterial population models

Fig 5. Classifications of models including heterogeneity in their bacterial population (Stage 2) were split into bacterial population and between-host models and then stratified by whether they considered single or multiple resistance classes.

Between-host models

Use of data derived from the literature

Acquired or primary resistance and discrete resistance

Resistance effects in models

Discussion

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Debra E Bessen

Mark Robert Davies

Roles

Author response to Decision Letter 0

Decision Letter 1

Debra E Bessen

Mark Robert Davies

Roles

Author response to Decision Letter 1

Decision Letter 2

Debra E Bessen

Mark Robert Davies

Roles

Acceptance letter

Debra E Bessen

Mark Robert Davies

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases