Abstract
Automatic modulation classification (AMC) is a challenging topic in the development of cognitive radio, which can sense and learn surrounding electromagnetic environments and help to make corresponding decisions. In this paper, we propose to complete the real-time AMC through constructing a lightweight neural network MobileViT driven by the clustered constellation images. Firstly, the clustered constellation images are transformed from I/Q sequences to help extract robust and discriminative features. Then the lightweight neural network called MobileViT is developed for the real-time constellation image classification. Experimental results on the public dataset RadioML 2016.10a with edge computing platform demonstrate the superiority and efficiency of MobileViT. Furthermore, the extensive ablation tests prove the robustness of the proposed method to the learning rate and batch size. To the best of our knowledge, this is the first attempt to deploy the deep learning model to complete the real-time classification of modulation schemes of received signals at the edge.
Keywords: Cognitive radio, Constellation image classification, Modulation recognition, Lightweight neural network, Real-time reasoning
Introduction
Nowadays, wireless communication system plays a crucial role in people’s work and life. As one of the key technologies to achieve efficient, reliable and secure communication, cognitive radio (CR) with the automatic modulation classification (AMC) algorithm as the core has become a hot research topic. AMC aims to identify modulation schemes for signals from unknown heterogeneous devices. It plays a critical role between signal detection and demodulation, laying the foundation for spectrum monitoring and management in the current fifth-generation (5G), beyond 5G (B5G), and upcoming 6G communication environments (Gui et al. 2020). In the current era where available spectrum resources are becoming increasingly constrained, AMC is the best solution to improve the spectrum efficiency. It can also be applied in various civil and military applications, such as adaptive modulation (Zhang et al. 2022) and coding (Zheng et al. 2022), spectrum sensing (Zheng et al. 2021), Internet-of-Things (IoT) (Zhao et al. 2020), threat analysis (You et al. 2022), and electronic warfare (Akyön et al. 2018). In the communication environments with adaptive modulation and coding, AMC is able to reduce the signaling overhead of the receiver. During the spectrum sensing process, AMC is helpful to determine the legality of frequency bands. In addition, the recognition of modulation schemes of enemy’s signals is the prerequisite of implementing radio interference and deception in electronic warfare.
At present, the typical AMC methods are mainly divided into two categories: (1) likelihood estimation based statistical modelling (LEbSM) methods and (2) feature extraction based pattern classification (FEbPC) methods. For example, common LEbSM methods include average likelihood ratio test (ALRT) (Chung 2013) and hybrid LRT (Zheng and Y. Lv”, 2018). LEbSM methods regard the AMC as a multi hypothesis test problem and obtains the optimal solution in Bayesian sense, but it inevitably exists a series of problems, such as the lack of closed form solutions, high computational complexity, and probability mismatch. Besides, the likelihood function usually becomes complex for high-order modulation schemes and thus it is difficult to deploy in actual applications. Compared with LEbSM methods, FEbPC methods are more prominent in practical implementations. The key of developing FEbPC methods is concentrated on the extraction of robust features (e.g., high-order cumulants (Wang, et al. 2021), cyclic spectrum (Yan et al. 2017), amplitude moments (Shimbo and Oka 2010)) and the design of machine learning models (e.g., support vector machine (SVM) (Zheng et al. 2020a), random forests (RF) (Liu et al. 2020), autoencoder (Zheng et al. 2018)). Although FEbPC methods are not optimal in Bayesian sense, their lower computational complexity and simplicity of deployment make them attractive. However, the estimation results of communication parameters of received signals have a serious impact on FEbPC methods. Specifically, some ideal conditions including accurate carrier recovery, perfect timing synchronization, high signal-to-noise ratio (SNR), and transmission channels with additive Gaussian white noise are difficult to satisfy simultaneously, which lead to a significant degradation of model generalization performance.
In recent years, deep learning has achieved remarkable success in the field of pattern classification, and it has been gradually developed for AMC. Deep learning integrates feature extraction and classification by building an end-to-end neural network model, avoiding complex feature design and feature engineering process. Due to the driving force of massive data and the nonlinear fitting capability of large-scale structures, the deep learning model shows a good generalization ability across various environments and scenes. A large number of advanced deep learning models are specially designed or transferred to AMC, such as IBCNN (Kim et al. 2021) and ConvLSTMAE (Shi et al. 2022). Although the existing deep learning models are well established, most of the existing work cannot avoid high computational complexity and the degraded accuracy at low SNR.
Meanwhile, the optimal representation forms of received signals as inputs to deep learning models is still being discussed and studied. Since it is demanding for over-parameterized deep learning models to learn regularized knowledge such as Fourier transform (FT) (Zheng et al. 2020b), the discriminative information hidden in the frequency domain of in-phase/quadrature (I/Q) modulated temporal signals is hard to be used effectively. Deep learning models fed with FT-based spectrum images, on the other hand, face the difficulty in considering both time and frequency resolution at the same time. Moreover, a lot of deep learning models driven by the constellation images have also been developed for AMC, such as ACTC-BMCNet (Xu et al. 2022) and Shuffle Unit (Luan et al. 2021). Compared to temporal I/Q signals, the constellation images can better reflect the phase information and relative relationships of symbols. The temporal information reflected by I/Q matrix is usually meaningless for the classification of modulation schemes. The clustered constellation image further supplements the density information of symbols to characterize the modulation information more comprehensively. However, signal transmission process usually undergoes the severe fading, and signal distortion makes naive constellation image based AMC challenging.
In practice, existing spectrum monitoring techniques can obtain a large amount of radio signal and real-time spectrum data using micro sensors deployed in various environments. However, current state-of-the-art deep learning models driven by such data are difficult to achieve sufficient AMC accuracy with computational efficiency that allows for implementation on the low-cost edge computing platform.
In this paper, we propose to complete the real-time AMC through constructing a lightweight neural network MobileViT driven by the clustered constellation images. Compared with I/Q temporal-series and naive constellation images, clustered constellation images can help extract better robustness features. The deep learning model composed of MobileViT block and MobileNetV2 block is then developed to process the clustered constellation images in real time to complete feature extraction and modulation classification. The separable depth convolution and ReLU6 activation functions in MobileViT are critical to improve the inference efficiency. The stacking of multi-layer two-dimensional convolutions and nonlinear transformations is suitable for extracting key modulation features from clustered constellation images. Besides, the feature fusion based on local representation extracted by convolutional layers and global representation extracted by Transformers can further enhance the robustness of features to noise and solve AMC tasks under various SNRs. Compared with a series of deep learning models on public dataset RadioML 2016.10a (O’Shea et al. 2018) with edge computing platform Jetson Nano, experimental results demonstrate the superiority and real-time performance of MobileViT.
The remainder of this paper is organized as follows. In Section "Related work", we summarize the related work of AMC. In Section “Clustered constellation image representation”, we present the construction of clustered constellation images. The proposed lightweight network MobileViT is introduced in Section “Lightweight network mobileviT”. Then simulation results and analysis are reported in Section “Experimental results and analysis”. Limitations and future directions are discussed in Section "Discussion". Finally, our work is concluded in Section “Conclusion”.
Related work
In this section, we introduce the related work of deep learning for AMC from two aspects: (1) approaches driven by temporal representations and (2) approaches driven by high-dimensional images. According to statistical analysis (Peng et al. 2021), more and more studies are turning to deep learning methods driven by images that introduce expert prior knowledge.
Approaches driven by temporal representations
Wang et al. (2019) proposed a CNN model trained on I/Q samples to distinguish modulation schemes that are relatively easy to recognize. Dong et al. (Dong, et al. 2022) designed a spatio-temporal hybrid deep neural network named MCMBNN for real-time AMC driven by multi-channel inputs. The proposed model is consisted of parameter estimation block, spatial information extraction block, and temporal feature extraction and Softmax blocks, which can improve the classification accuracy while reducing model complexity. In (Zhang et al. 2019), eight kinds of temporal features were extracted for fine-tuning the CNN to improve its AMC classification performance, and achieved an accuracy of 92.5% at − 4 dB SNR, but the edge deployment and reasoning speed in practical applications were ignored. Zhang et al. (Zhang et al. 2020) developed a dual stream structure integrating CNN and LSTM for AMC, which effectively explores the feature interactions and spatio-temporal properties of original complex temporal signals. Compared with existing CNN structures, Hermawan et al. (Hermawan et al. 2020) have adjusted the number of layers and introduced new types of layers to meet the estimated latency standard in B5G communications. Ke et al. (Ke and Vikalo 2021) experimented with a learning framework based on the compact neural network models for automatically extracting stable and robust features from noisy radio signals and for inferring modulation schemes.
For real-time inference, many model pruning algorithms and lightweight network structures have been developed. Wang et al. (Wang et al. 2020a) proposed to introduce scaling factors for each neuron in the CNN and enhance the sparsity of scaling factors through compressive sensing, thus improving the inference speed of the model. Then Wang et al. proposed an AMC method based on distributed learning and reasoning strategies (Wang et al. 2020b), which rely on the cooperation of multiple edge devices and model averaging (MA) algorithm. Fu et al. (Fu et al. 2021) adopted separable convolutions rather than standard convolutions (SCs) and removed most of the fully connected layers to reduce the structural complexity of the model. Ma et al. (Ma et al. 2020) constructed a lightweight hybrid network consisting of convolutional and recurrent layers, and guided its learning by means of the knowledge distillation. Experimental results show that it improves the reasoning speed by six times, but only brings a slight loss of accuracy. In (Roy et al. 2021), a lightweight hybrid model composing of CNN, long short-term memory (LSTM), and gated recurrent unit (GRU) layers, is deployed to perform AMC on mobile and edge devices, but its recognition accuracy at low SNR is unsatisfactory.
The above related work focused on the development and application of temporal signals or features based deep learning models, but still faces the problem of poor generalization across various communication scenarios and difficulties in meeting practical needs in terms of inference speed.
Approaches driven by high-dimensional images
In (Kim et al. 2021), a hybrid deep learning model based on signal and image is designed for AMC in CR, where the size of optimal filters is concerned. In view of low accuracy of deep learning models under the conditions of low SNR, high computing cost, and excessive label dependency, Shi et al. (Shi et al. 2022) developed a spatial feature extractor with convolutional auto-encoder (AE) and LSTM-AE in parallel as the backbone. Xu et al. (Xu et al. 2022) first utilized the blind zero-forcing (ZF) equalization algorithm to reconstruct damaged signals and enhance signal representation, and then drove the training of CNN with compact accumulated constellation images. Further, a modified constellation image (Luan et al. 2021) based on the score function satisfying Cauchy distribution is proposed as a robust feature to impulse noise. Lin et al. (Lin et al. 2021) introduced a framework for converting complex signals into statistically significant contour star images, which can transfer deep statistical information from the original wireless signal waveforms when expressed in image data format. Peng et al. (Peng et al. 2018) developed several methods to represent modulated signals in data formats with grid like topologies for CNN.
Due to the rich expert knowledge and implicit information hidden in the signal, increasingly signal representations based on high-dimensional images are designed for AMC. In (Kumar et al. 2020), a constellation density matrix (CDM) based AMC algorithm is proposed to classify modulation schemes of different orders. In (Yan et al. 2018), the unified mesh model fed by constellation images is constructed for classifying QAM. In (Lee et al. 2019), various features are transformed in a two-dimensional image and fed into the CNN. In (Jajoo et al. 2019), a AMC method based on the constellation structure is proposed to identify PSK and QAM of different orders, in the slow and flat fading channel. In (Sun and Ball 2022), a graphic representation of features (GRF) is proposed, which represents the statistical features as a spider image for machine learning.
Extensive experimental results suggest that waveforms in the physical layer may not be applicable to the popular deep learning models transferred from image processing. Therefore, it is critical to bridge the gap between signal representations (e.g., waveforms, constellation images, spectrograms) and deep learning-compatible data formats. Moreover, the suitable deep learning structures specifically for the AMC task need to be explored.
Clustered constellation image representation
In this section, we first introduce the communication system model and then present the construction process of clustered constellation images.
Communication system model
In the current wireless communication systems, transmitted signals are usually stored in the format of I/Q, which is a pair of in-phase and quadrature baseband components, which are able to improve the spectral efficiency but cannot eliminate noises. Considering a single input and single output (SISO) wireless communication system with the additive white Gaussian noise (AWGN) channel as shown in Fig. 1, the received radio signal r can be expressed as
| 1 |
where h represents the channel coefficient following Rayleigh distribution at the range of (0, 1], and N is the number of signal symbols. f0 and φ0 denote the carrier frequency offset (CFO) and carrier phase offset (CPO), respectively. No timing error is considered since synchronization can be easily accomplished for SISO system. sc(n) is the n-th symbol generated by m-th modulation scheme in which c = 1, 2, …, ξ and ξ is the total number of candidate modulation schemes. All the symbols are extracted with equal probability from candidate modulation schemes. w[n] is the AWGN of zero mean and σ2 variance. In this case, the SNR for symbols from unit power constellations is computed as
| 2 |
Fig. 1.
SISO wireless communication system
In the absence of priori information such as modulation order, symbol rate, and channel types in the non-collaborative communications, modulation features extracted directly from I/Q signals are vulnerable and not discriminative, especially in low SNR conditions.
Clustered constellation image
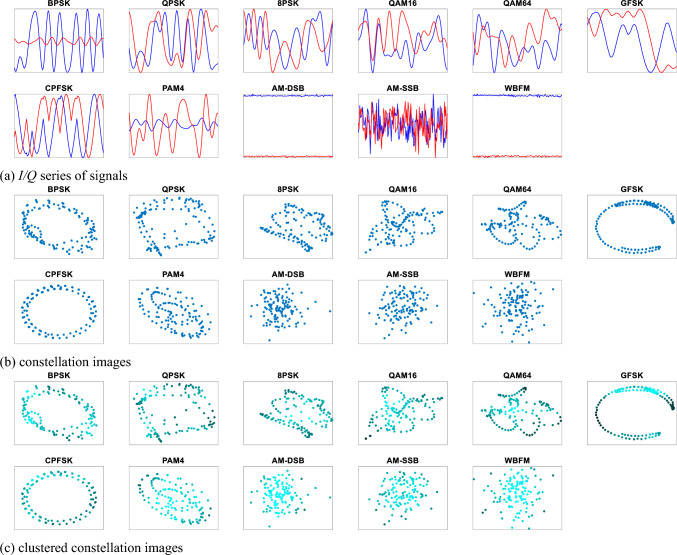
In fact, the constellation image X of each I/Q signal can be regarded as a group of points in a complex plane, in which the horizontal real axis and vertical imaginary axis representing the I and Q components of the signal r, respectively. The angle of each point represents the phase shift between the carrier and the reference phase, and the distance from the origin represents the amplitude of the signal. Influenced by channel noises and other types of impairments, part of the received sample points may be shifted from nominal positions. In addition, the constellation images may be considered incomplete due to sampling rate, symbol rate, and other factors.
To better express the modulation information of received signals, color information reflecting the density is introduced into the original constellation image, as given by
| 3 |
where e denotes the Hadamard product. is defined as the constellation density matrix, which reflects the density within a certain range u of constellation points and can be calculated according to Algorithm 1.
| Algorithm 1 Construction of constellation density matrix |
|---|
| input: the constellation image X, radius u |
| 1: for each point X(i, q) in the constellation image do |
| 2: from X(i − u, q − u) to X(i + u, q + u) do |
| 2: count the number of points p within radius u; |
| 3: end |
| 4: end |
| 5: compute the average value pave; |
| 6: for each point X(i, q) in the constellation image do |
| 7: if 2p > pave |
| 8: update the element Ψ ← p + 1; |
| 9: else |
| 10: update the element Ψ ← 1; |
| 11: end |
| 12: end |
| 13: min–max normalization: ; |
| output: the constellation density matrix Ψ |
The min–max normalization approach is applied to ensure that the scale of the constellation density matrix is compressed within [0, 1], while not changing the overall distribution of all samples. In the constellation density matrix, the constellation points within the distance u are counted to construct their cluster if the number of points is greater than half of the average (i.e., p > 0.5pave), otherwise we think that these are some noise points that have drifted from the original position, where half of the average 0.5pave is an empirical setting based on the overall characteristics of the samples. In an extreme case of u = 0, the clustered constellation image can be degenerated to the original state. On the other hand, the two-level loop can be completed by one iteration after the first clustered constellation image has been generated.
Before being used as input to the deep learning model, all values in the clustered constellation image are mapped to the RGB three-channel space. The first channel stores constellation points and indicates the positions. The density values of normal constellation points is stored in the corresponding position of the second channel, represented by the number of points within the radius u. The last channel stores the density value of noise points, i.e., 1. By distinguishing between normal constellation points and noise points, and providing density information, the feature expression ability of the original constellation map can be improved. Colors and shapes in the clustered constellation image characterize the fine-grained features of the radio signal, as it considers the positional relationships and overlap factors of the sampled points. Therefore, the order of modulations is unnecessarily estimated in advance, and the density of received symbols in the constellation diagram can help determine the number of clusters. Furthermore, the inference efficiency of deep learning model is independent of the number of sampling points of the signal, so it has more advantages in the face of long period sequences.
For the clustered constellation image transformed from a baseband radio signal, our goal is to maximize the probability of accurately recognizing its modulation scheme by adjusting deep learning model parameters, as given by
| 4 |
where Fθ (·) represents the deep learning classifier and θ is learnable parameters. Yi denotes the one-hot modulation label of i-th signal, in which is 1 and other elements are 0.
Lightweight network mobileviT
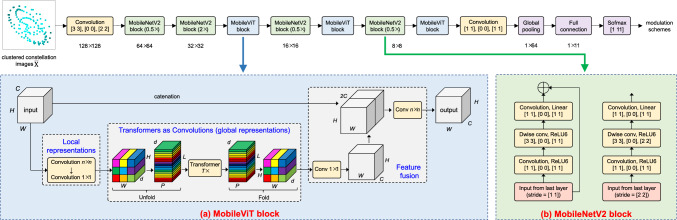
In this section, a lightweight network based on the MobileViT (Mehta and Rastegari 2022) is designed to accomplish the AMC of received signals, as shown in Fig. 2.
Fig. 2.
Specific structure of the lightweight network MobileViT
Model structure
The proposed lightweight network MobileViT driven by the clustered constellation images is composed of the following parts: convolutional layers, MobileNetV2 blocks, MobileViT blocks, global pooling layer, fully connected layer, and softmax layer for outputting modulation classification results.
The first convolutional and the last convolutional layers are added to help extract the low-level features and encode the high-level features from the clustered constellation images and feature maps, respectively. In each convolutional layer, the size, padding, and stride of convolution kernels are presented in detail, e.g., ([3 3], [0 0], [2 2]). Batch normalization (BN) (Ioffe and Szegedy 2015) is followed to accelerate the convergence of model objective function and is defined as
| 5 |
where
| 6 |
| 7 |
In the above equations, x represents the output of last layer. γ and β are learnable scaling scales and offsets respectively. M is the batch size of mini-batch set. ε is a small constant to avoid numerical explosions. To realize nonlinear transformation of outputs, ReLU6 (Sandler et al. 2018) is used as the activation function because of its robustness when used with low-precision computation, which can be calculated by
| 8 |
The curves of various activation functions are shown in Fig. 3. It can be seen that ReLU6 has the same properties as ReLU, but with good numerical resolution with limited storage of Float16 bits on the mobile side.
Fig. 3.
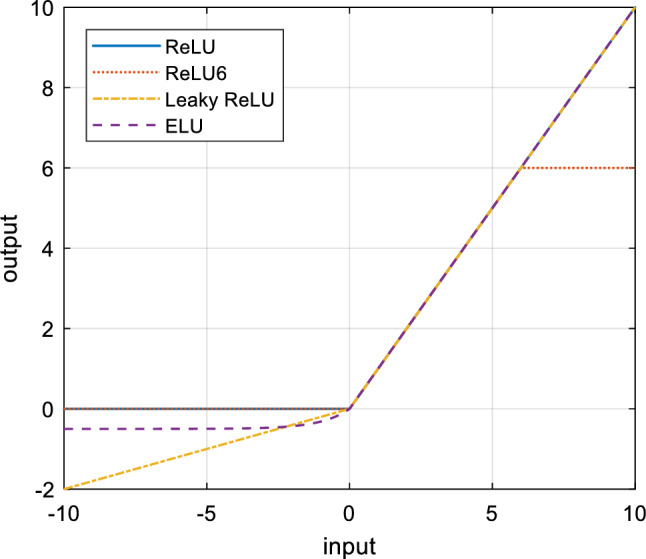
Illustration of various activation functions
After the first convolutional layer, the MobileNetV2 block is adopted to further encode features. In MobileNetV2 blocks, depthwise separable convolution (DSC) is designed to replace traditional convolution to speed up the reasoning of the model. DSC is consisted of a separate filtering layer and a separate combining layer, where one filter is applied to a single input channel. This kind of decomposition operation can greatly help to reduce the structural complexity of deep learning models. Specifically, the depthwise convolution with one filter per input channel (i.e., input depth) can be written as
| 9 |
where Ki+p-1, j+q-1, l represents the l-th convolution kernel of size DK × DK × M at the i-th channel. xi, j, l and yi, j, l are input and output feature maps with size DI × DI × I and DO × DO × O respectively. As the dimensions of feature maps are not changed, we can obtain DI = Do. Then the computational cost of DSC can be computed as DK × DK × M × DI × DI, which is extremely efficient relative to standard convolution. Next, an additional layer for computing the linear combination of depthwise convolution output via 1 × 1 convolution (i.e. pointwise convolution) is introduced to output the final feature maps. The total computation costs of DSC can be computed as CCDSC = DK × DK × M × DI × DI + M × C × DI × DI, in which C represents the number of channels. By reorganizing the standard convolution into a two-stage process of filtering and combining, the computation reduction can be expressed according to
| 10 |
In MobileNetV2 blocks, the DSC adopting 3 × 3 convolution kernels can save 9 times of calculation time compared with the standard convolution. Moreover, it is worth noting that the middle layer of MobileNetV2 block uses the linear bottleneck and inverted residual connection, which reduces the number of parameters while maintaining the knowledge expression ability of the model, making it suitable for real-time constellation image analysis.
The MobileViT block aims to model the local and global information in an input tensor with fewer parameters. For a given input tensor , a DSC layer with kernels of size n × n is applied to produce high-dimensional feature maps as local representations. To enable the MobileViT block to learn global representations with spatial inductive bias, we unfold xL into L non-overlapping flattened image patches , in which P = wh, L = WH/wh is the number of patches, w and h are width and height of each patch respectively. For each patch , the inter-patch relationships are encoded by applying transformers, as given by
| 11 |
Unlike vision transformer that loses the spatial order of pixels, MobileViT block neither loses the patch order nor the spatial order of pixels within each patch Thus, we can fold xG to obtain xF, which is projected to low-dimensional space through the point-wise convolution and combined with the original input x via concatenation. Then another convolutional layer with n × n kernels is used to fuse these concatenated features as output.
The hierarchical attention mechanism developed in the MobileViT block allows the model to capture the multi-scale feature information without requiring high computational and storage requirements. The attention mechanism is sensitive to different SNRs in each mini-batch set, so it is suitable for the AMC task.
By stacking above blocks, the label corresponding to the maximum posteriori probability output by the softmax layer is used as the AMC result.
Learning process
All learnable parameters of MobileViT are updated using error back propagation based stochastic gradient descent (SGD) method Adam (Jais et al. 2019). The overall training and testing process are shown in Fig. 4.
Fig. 4.

Training and testing process of MobileViT
For trainable parameters θ at t-th training iteration, they can be updated according to
| 12 |
where αt denotes the learning rate at the t-th training iteration. and denote modified first and second moment estimates respectively, and can be calculated by
| 13 |
| 14 |
where
| 15 |
| 16 |
In the above equations, and represent the exponential decay rates of moment estimates, respectively. ▽t denotes the batch gradient determining the descent direction at t-th training iteration and can be calculated by
| 17 |
where refers to the loss function like cross entropy, which is defined as
| 18 |
Finally, we can obtain the convergent neural network Fθ* by continuously iterating through the above steps, i.e., from Eq. (12) to Eq. (18).
Experimental results and analysis
In this section, we present experimental setup and classification performance of the proposed method (i.e., MobileViT driven by clustered constellation images) and a series of comparison approaches.
Experimental setup
During experimental process, the public dataset RadioML 2016.10a dataset (O’Shea et al. 2018) is used to evaluate the AMC performance (i.e., accuracy and efficiency) of MobileViT. This dataset is consisted of 220000 I/Q signals with 11 modulation schemes, including 8 digitals (BPSK, QPSK, 8PSK, QAM16, QAM64, GFSK, CPFSK, PAM4) and 3 analogs (AM-DSB, AMSSB, WBFM). These signals with 1 MHz bandwidth in SNR range of − 20 dB ~ 18 dB are evenly distributed among 11 categories. The training, validation, and test set are randomly divided according to the ratio of 6:2:2. In Fig. 5, we visualized typical signal examples for each modulation at 18 dB SNR and corresponding constellation images. Although it seems that there are part of similarities and differences between modulation schemes, even human experts cannot easily distinguish them visually due to pulse shaping, distortion, and other complex channel effects.
Fig. 5.
Experimental signal examples with + 18 dB SNR and corresponding constellation images
Although the optimal hyper-parameters can be obtained through grid search, the hyper-parameters in deep learning are usually set empirically considering its expensive training costs. All the hyper-parameters before the network training, such as maximum training epochs, range, learning rate, batch size, exponential decay rate β1 and β2, small constant, weight decay, and dropout rate, are set to 30, 0.2, 0.01, 64, 0.9, 0.999, 10−8, 0.0001, and 0.2, respectively. The learning rate is gradually reduced by 0.95 with training iterations in an exponential way. Since all the modulation schemes are independent of the order of symbols, all the constellation diagrams are flipped for data augmentation. Finally, we stop the training process to prevent MobileViT from overfitting when the validation loss starts to increase for more than 5 consecutive epochs.
The training of MobileViT is performed using PyTorch framework based on Python. All models are trained five times from scratch and the average value is taken as the result. In the testing phase, models are deployed in the computing edge device NVIDIA Jetson Nano to test whether it can meet the requirements of AMC accuracy and efficiency. The structure of developer kit Jetson Nano is shown in Fig. 6. It is 70 × 45 mm in size and consists of a ARM Cortex A57 CPU with 4 cores, a Maxwell GPU with 128 cores, 4 GB RAM and 16 GB ROM, which is able to achieve the computing power of 0.5TFLOPs driven by 15W power. The GPU with compute unified device architecture (CUDA) acceleration is used for inference.
Fig. 6.

Edge computing platform Jetson Nano
AMC performance
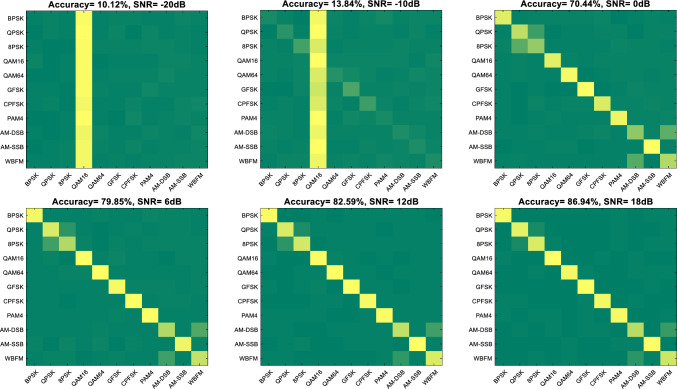
The training process of MobileViT, i.e., the optimization process of the objective function, is shown in Fig. 7. It can be seen that the model converges well at the minimum position of the training loss, while the generalization error (i.e., the gap between training loss and validation loss) is acceptable. The AMC accuracy and loss of training, validation, and test sets is reported in Table 1. The overall AMC accuracy of MobileViT on the test set reaches 54.60% due to the extreme difficulty in identifying the modulation scheme of signals with low SNR, e.g., AMC accuracy of 10.12% at − 20 dB. According to the results of the confusion matrix shown in Fig. 8, signals at low SNRs tend to be distinguished to a particular class due to heavy interference from noise. Signals at high SNRs (SNRs > 0 dB) can be almost completely classified, except for AM-SSB and WBFM, QPSK and 8PSK, which are not distinguishable due to silence time in the speech signal.
Fig. 7.
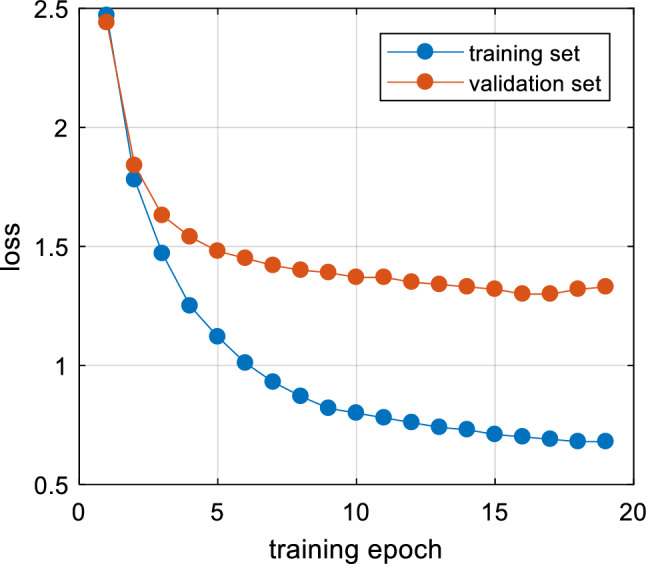
Loss optimization curve of MobileViT
Table I.
AMC performance of training,validation, and test set
| Metrics | Training set | Validation set | Testing set |
|---|---|---|---|
| Loss | 0.6774 | 1.3326 | 1.3408 |
| Accuracy (%) | 72.18 | 55.43 | 54.60 |
Fig. 8.
Confusion matrices of MobileViT at -20, -10, 0, 6, 12, and 18 dB SNRs
Then we compared AMC performance of a series of deep learning models tested on Jetson Nano, including ConvLSTM AE (Shi et al. 2022), LightAMC (Wang et al. 2020a), and MobileNet (Sandler et al. 2018), as shown in Fig. 9. According to results, the specifically designed MobileViT for AMC achieves state-of-the-art classification accuracy with a good reasoning efficiency (12 ms of average inference time per clustered constellation image), especially under high SNR conditions. The latency of converting I/Q signals into cluster constellation images is less than 1 ms, which can be ignored compared to the inference time of the model. This means that MobileViT is able to meet real-time requirements of practical intelligent wireless communication tasks. On the other hand, the average AMC accuracy of MobileViT is about 1% higher than previous state-of-the-art results. When the SNR exceeds 10 dB, the AMC accuracy of MobileViT can reach up to about 90%. In terms of inference speed, the LSTM-based model (Shi et al. 2022) considering temporal information is difficult to meet the actual needs. By contrast, the spatial representation based on clustered constellation contains temporal information, which improves the AMC efficiency while meeting the requirements of signal analysis.
Fig. 9.
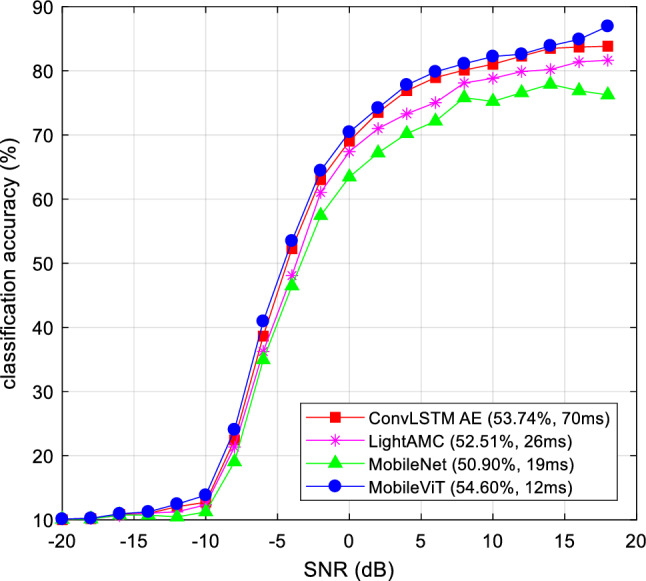
Comparison of a series of deep learning models
Ablation studies
In this part, we tested the AMC performance of the model driven by various signal representations including I/Q temporal series, naive constellation images, and clustered constellation images, and the results are shown in Fig. 10. It can be seen that the classification accuracy of the deep learning model driven by original constellation images and I/Q temporal series is close. Clustered constellation images show a significant performance improvement, increasing the average classification accuracy by about 3.4%. This also demonstrates the advantages of clustered constellation images in describing structure of symbols under various modulation schemes. From the perspective of inference efficiency, the temporal signal has fewer elements, but usually requires a more complex structured model such as LSTM to achieve an acceptable classification accuracy. Although image representations contain more elements, they are easier to drive the lightweight neural network model to complete the mining of key features and the analysis of modulation schemes.
Fig. 10.

Impact of signal representations on AMC accuracy of MobileViT
Robustness analysis
In practical applications, transmitted signals are subject to interference from various environmental factors, such as the geographical location of base stations, weather, cable, etc. The attenuated signals pose a greater challenge for deep learning models to identify their modulation schemes. Typically, deep learning models need to be re-trained or fine-tuned for specific data. Inevitably, a series of hyper-parameters are introduced in this process. Therefore, the robustness of deep learning models is one of the key considerations in its practical application. In Fig. 11, 12, we report AMC accuracies of MobileViT trained by different hyper-parameters setting. Based on the results, it can be deduced that the model is robust to the learning rate and batch size. The classification accuracy of MobileViT fluctuates with the learning rate by no more than 1%. Even with a small learning rate 0.001, the model was able to converge to a suitable position. At a large learning rate 0.02, the classification accuracy of the model decreases slightly, which may be caused by the large step size that makes the model unable to converge to a stable local minimum. Different from that the learning rate determines the descending step size of each iteration, the batch size affects the convergence direction of the model. Since the optimization space under the constraints of model structure and data space tends to construct a flat minimum region, the model optimization results are almost independent of the batch size. The classification accuracy varied less than 2% under various batch sizes, which indicates the robustness of MobileViT to different learning rate and batch size settings.
Fig. 12.
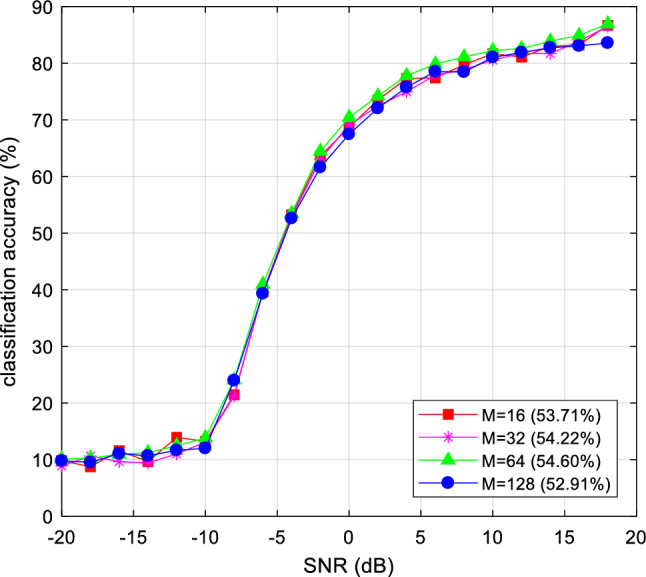
Impact of batch size on AMC accuracy of MobileViT
Fig. 11.

Impact of the initial learning rate on AMC accuracy of MobileViT
Discussion
Although MobileViT has achieved superior AMC accuracy on the public dataset RadioML 2016.10A, the interference faced by practical wireless communication environments is much more complex, posing a serious challenge to the generalization capability of deep learning models. The noise, CFO, CPO, and timing error caused by multipath attenuation and different types of channels all affect the quality of received radio signals. It is generally believed that introducing prior knowledge is helpful for model learning features, such as accurate SNR estimation. In addition, generalization techniques from the perspective of machine learning, such as data augmentation, can help improve the adaptability of the model to the environment. The suitable signal representation form is also worth further exploration, such as multi-modal data fusion, considering that the clustered constellation image is hard to mine hidden frequency domain information.
On the other hand, there are usually a large number of various modulation schemes simultaneously in actual wireless communication scenarios, which puts higher demands on the feature extraction and classification capability of the model. More candidate modulation schemes typically require more complex structures to learn discriminative features, which is detrimental to the model’s inference speed. Therefore, how to balance model complexity and classification accuracy is a key research direction. In addition to directly designing lightweight models, the application of iterative weight pruning technique is more advantageous for reducing model size while maintain its AMC accuracy, although it requires more training costs.
Conclusion
In this paper, we propose to complete the real-time AMC task through constructing a lightweight neural network MobileViT driven by clustered constellation images. Firstly, the clustered constellation images are transformed from I/Q sequences to help extract robust and discriminative features. A lightweight deep neural network MobileViT is then developed for real-time constellation image classification. Experimental results on the public dataset RadioML 2016.10a through the edge computing platform demonstrate the superiority and real-time performance of the proposed method. To the best of our knowledge, this is the first time to deploy the deep learning model to complete the real-time modulation classification of received signals at the edge device.
In the future, we plan to develop regularization techniques to further improve the generalization ability of MobileViT and help it better cope with more complex realistic communication conditions, such as unknown scale, translation, dilation, and impulsive noise. Furthermore, the pruning techniques based on weight importance or some other metrics are considered for further compression of the model.
Acknowledgements
This research was supported by Shandong Provincial Natural Science Foundation, grant number ZR2023QF125.
Data availability
Data will be made available on reasonable request.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Akyön FC, Alp Y, Gök G, Arikan O (2018) Deep learning in electronic warfare systems: automatic intra-pulse modulation recognition. Paper presented at IEEE 26th signal processing and communications applications conference (SIU), Izmir, Turkey, pp. 1–4
- Chung WH. Sequential likelihood ratio test under incomplete signal model for spectrum sensing. IEEE Trans Wirel Commun. 2013;12(2):494–503. doi: 10.1109/TWC.2012.12.100663. [DOI] [Google Scholar]
- Dong B, et al. A lightweight decentralized learning-based automatic modulation classification method for resource-constrained edge devices. IEEE Internet Things J early access. 2022;9(24):24708–24720. doi: 10.1109/JIOT.2022.3194508. [DOI] [Google Scholar]
- Fu X, et al. Lightweight automatic modulation classification based on decentralized learning. IEEE Trans Cogni Commun Netw. 2021;8(1):57–70. doi: 10.1109/TCCN.2021.3089178. [DOI] [Google Scholar]
- Gui G, Liu M, Tang F, Kato N, Adachi F. 6G: Opening new horizons for integration of comfort, security, and intelligence. IEEE Wirel Commun. 2020;27(5):126–132. doi: 10.1109/MWC.001.1900516. [DOI] [Google Scholar]
- Hermawan AP, Ginanjar RR, Kim DS, Lee J. CNN-based automatic modulation classification for beyond 5G communications. IEEE Commun Lett. 2020;24(5):1038–1041. doi: 10.1109/LCOMM.2020.2970922. [DOI] [Google Scholar]
- Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Int conf mach learn PMLR. 2015;37:448–456. [Google Scholar]
- Jais I, Ismail A, Nisa S. Adam optimization algorithm for wide and deep neural network. Knowl Eng Data Sci. 2019;2(1):41–46. doi: 10.17977/um018v2i12019p41-46. [DOI] [Google Scholar]
- Jajoo G, Kumar Y, Yadav S. Blind signal PSK/QAM recognition using clustering analysis of constellation signature in flat fading channel. IEEE Commun Lett. 2019;23(10):1853–1856. doi: 10.1109/LCOMM.2019.2929127. [DOI] [Google Scholar]
- Ke Z, Vikalo H. Real-time radio technology and modulation classification via an LSTM auto-encoder. IEEE Trans Wirel Commun. 2021;21(1):370–382. doi: 10.1109/TWC.2021.3095855. [DOI] [Google Scholar]
- Kim S, Moon C, Kim J, Kim D. A hybrid deep learning model for automatic modulation classification. IEEE Wirel Commun Lett. 2021;11(2):313–317. doi: 10.1109/LWC.2021.3126821. [DOI] [Google Scholar]
- Kumar Y, Sheoran M, Jajoo G, Yadav S. Automatic modulation classification based on constellation density using deep learning. IEEE Commun Lett. 2020;24(6):1275–1278. doi: 10.1109/LCOMM.2020.2980840. [DOI] [Google Scholar]
- Lee J, Kim K, Shin Y (2019) Feature image-based automatic modulation classification method using CNN algorithm. In: IEEE international conference on artificial intelligence in information and communication (ICAIIC), Okinawa, Japan, pp 1–4
- Lin Y, Tu Y, Dou Z, Chen L, Mao S. Contour stella image and deep learning for signal recognition in the physical layer. IEEE Trans Cognit Commun Netw. 2021;7(1):34–46. doi: 10.1109/TCCN.2020.3024610. [DOI] [Google Scholar]
- Liu Y, Yang M, Li J, Zheng Q, Wang D. Dynamic hand gesture recognition using 2D convolutional neural network. Eng Lett. 2020;28(1):243–254. [Google Scholar]
- Luan S, Gao Y, Zhou J, Zhang Z. Automatic modulation classification based on Cauchy-score constellation and lightweight network under impulsive noise. IEEE Wirel Commun Lett. 2021;10(11):2509–2513. doi: 10.1109/LWC.2021.3105978. [DOI] [Google Scholar]
- Ma H, et al. Cross model deep learning scheme for automatic modulation classification. IEEE Access. 2020;8:78923–78931. doi: 10.1109/ACCESS.2020.2988727. [DOI] [Google Scholar]
- Mehta S, Rastegari M (2022) Mobilevit: light-weight, general-purpose, and mobile-friendly vision transformer. In:international conference on learning representations (ICLR), pp 1–26
- O’Shea TJ, Roy T, Clancy TC. Over-the-air deep learning based radio signal classification. IEEE J Sel Top Signal Process. 2018;12(1):168–179. doi: 10.1109/JSTSP.2018.2797022. [DOI] [Google Scholar]
- Peng S, et al. Modulation classification based on signal constellation diagrams and deep learning. IEEE Trans Neural Netw Learn Syst. 2018;30(3):718–727. doi: 10.1109/TNNLS.2018.2850703. [DOI] [PubMed] [Google Scholar]
- Peng S, Sun S, Yao Y. A survey of modulation classification using deep learning: Signal representation and data preprocessing. IEEE Trans Neural Netw Learn Syst. 2021;33(12):7020–7038. doi: 10.1109/TNNLS.2021.3085433. [DOI] [PubMed] [Google Scholar]
- Roy C, et al. An ensemble deep learning model for automatic modulation classification in 5G and beyond IoT networks. Comput Intell Neurosci. 2021;2021(5047355):1–8. doi: 10.1155/2021/5047355. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Sandler M, Howard A, Zhu M, Chen L (2018) Mobilenetv2: inverted residuals and linear bottlenecks. In: IEEE conference on computer vision and pattern recognition (CVPR), Salt Lake City, USA, pp 4510–4520
- Shi Y, Hua X, Lei J, Zisen Q. ConvLSTMAE: a spatiotemporal parallel autoencoders for automatic modulation classification. IEEE Commun Lett. 2022;26(8):1804–1808. doi: 10.1109/LCOMM.2022.3179003. [DOI] [Google Scholar]
- Shimbo D, Oka I (2010) A modulation classification using amplitude moments in OFDM systems. In: International Symposium on Information Theory & Its Applications, Taichung, Taiwan, pp 288-293
- Sun Y, Ball EA. Automatic modulation classification using techniques from image classification. IET Commun. 2022;16(11):1303–1314. doi: 10.1049/cmu2.12335. [DOI] [Google Scholar]
- Wang Y, Liu M, Yang J, Gui G. Data-driven deep learning for automatic modulation recognition in cognitive radios. IEEE Trans Veh Technol. 2019;68(4):4074–4077. doi: 10.1109/TVT.2019.2900460. [DOI] [Google Scholar]
- Wang Y, Yang J, Liu M, Gui G. LightAMC: lightweight automatic modulation classification via deep learning and compressive sensing. IEEE Trans Veh Technol. 2020;69(3):3491–3495. doi: 10.1109/TVT.2020.2971001. [DOI] [Google Scholar]
- Wang Y, et al. Distributed learning for automatic modulation classification in edge devices. IEEE Wirel Commun Lett. 2020;9(12):2177–2181. doi: 10.1109/LWC.2020.3016822. [DOI] [Google Scholar]
- Wang D, et al. Multiple high-order cumulants-based spectrum sensing in full-duplex-enabled cognitive IoT networks. IEEE Internet Things J. 2021;8(11):9330–9343. doi: 10.1109/JIOT.2021.3055782. [DOI] [Google Scholar]
- Xu Y, Xu G, Ma C. A novel blind high-order modulation classifier using accumulated constellation temporal convolution for OSTBC-OFDM systems. IEEE Trans Circuits Syst II Express Briefs. 2022;10(11):2509–2513. [Google Scholar]
- Yan X, Feng G, Wu H-C, Xiang W, Wang Q. Innovative robust modulation classification using graph-based cyclic-spectrum analysis. IEEE Commun Lett. 2017;21(1):16–19. doi: 10.1109/LCOMM.2016.2618868. [DOI] [Google Scholar]
- Yan X, Zhang G, Wu H. A novel automatic modulation classifier using graph-based constellation analysis for M-ary QAM. IEEE Commun Lett. 2018;23(2):298–301. doi: 10.1109/LCOMM.2018.2889084. [DOI] [Google Scholar]
- You L, et al. (2022) GPU-accelerated faster mean shift with euclidean distance metrics. In: IEEE 46th annual computers, software, and applications conference (COMPSAC),Los Alamitos, USA, pp 211-216
- Zhang Z, Wang C, Gan C, Sun S, Wang M. Automatic modulation classification using convolutional neural network with features fusion of SPWVD and BJD. IEEE Trans Signal Inf Process over Netw. 2019;5(3):469–478. doi: 10.1109/TSIPN.2019.2900201. [DOI] [Google Scholar]
- Zhang Z, Luo H, Wang C, Gan C, Xiong Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Trans Veh Technol. 2020;69(11):13521–13531. doi: 10.1109/TVT.2020.3030018. [DOI] [Google Scholar]
- Zhang X, et al. NAS-AMR: neural architecture search-based automatic modulation recognition for integrated sensing and communication systems. IEEE Trans Cognit Commun Netw. 2022;8(3):1374–1386. doi: 10.1109/TCCN.2022.3169740. [DOI] [Google Scholar]
- Zhao M, Chang CH, Xie W, Xie Z, Hu J. “Cloud shape classification system based on multi-channel CNN and improved fdm. IEEE Access. 2020;8:44111–44124. doi: 10.1109/ACCESS.2020.2978090. [DOI] [Google Scholar]
- Zheng J, Lv Y. Likelihood-based automatic modulation classification in OFDM with index modulation”. IEEE Trans Veh Technol. 2018;67(9):8192–8204. doi: 10.1109/TVT.2018.2839735. [DOI] [Google Scholar]
- Zheng Q, Yang M, Yang J, Zhang Q, Zhang X. Improvement of generalization ability of deep CNN via implicit regularization in two- stage training process. IEEE Access. 2018;6:15844–15869. doi: 10.1109/ACCESS.2018.2810849. [DOI] [Google Scholar]
- Zheng Q, Tian X, Yang M, Su H. CLMIP: cross-layer manifold invariance based pruning method of deep convolutional neural network for real-time road type recognition. Multidimens Syst Signal Process. 2020;32(1):239–262. doi: 10.1007/s11045-020-00736-x. [DOI] [Google Scholar]
- Zheng Q, et al. PAC-bayesian framework based drop-path method for 2D discriminative convolutional network pruning. Multidimens Syst Signal Process. 2020;31(3):793–827. doi: 10.1007/s11045-019-00686-z. [DOI] [Google Scholar]
- Zheng Q, Zhao P, Zhang D, Wang H. MR-DCAE: manifold regularization-based deep convolutional autoencoder for unauthorized broadcasting identification. Int J Intell Syst. 2021;36(12):7204–7238. doi: 10.1002/int.22586. [DOI] [Google Scholar]
- Zheng Q, Zhao P, Wang H, Elhanashi A, Saponara S. Fine- grained modulation classification using multi-scale radio transformer with dual-channel representation. IEEE Commun Lett. 2022;26(6):1298–1302. doi: 10.1109/LCOMM.2022.3145647. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on reasonable request.