Abstract
Multidimensional correlation spectroscopy is emerging as a novel MRI modality that is well suited for microstructure and microdynamic imaging studies, especially of biological specimens. Conventional MRI methods only provide voxel-averaged and mostly macroscopically averaged information; these methods cannot disentangle intra-voxel heterogeneity on the basis of both water mobility and local chemical interactions. By correlating multiple MR contrast mechanisms and processing the data in an integrated manner, correlation spectroscopy is able to resolve the distribution of water populations according to their chemical and physical interactions with the environment. The use of a non-parametric, phenomenological representation of the multidimensional MR signal makes no assumptions about tissue structure, thereby allowing the study of microscopic structure and composition of complex heterogeneous biological systems. However, until recently, vast data requirements have confined these types of measurement to non-localized NMR applications and prevented them from being widely and successfully used in conjunction with imaging. Recent groundbreaking advancements have allowed this powerful NMR methodology to be migrated to MRI, initiating its emergence as a promising imaging approach. This review is not intended to cover the entire field of multidimensional MR; instead, it focuses on pioneering imaging applications and the challenges involved. In addition, the background and motivation that have led to multidimensional correlation MR development are discussed, along with the basic underlying mathematical concepts. The goal of the present work is to provide the reader with a fundamental understanding of the techniques developed and their potential benefits, and to provide guidance to help refine future applications of this technology.
Keywords: diffusometry, inversion, Laplace, MRI, multidimensional, multiexponential, relaxometry
1 |. INTRODUCTION
In vivo MRI histology or microstructure imaging are names given to the enterprise of obtaining information about tissue composition and distinct components within tissues, which are generally not revealed using conventional MRI methods. There is interest by neuroanatomists, neuropathologists and neuroscientists in obtaining such information, eg axon diameter distributions, glial and neural cell densities and extracellular matrix fractions.
There are two philosophical approaches that have been employed to “drill down into the voxel” to obtain these compositional, structural or architectural features. One entails using parametric models of tissue organization or structure, in which one prescribes the number and types of cell and structures within a tissue voxel a priori and then collects MRI data in order to estimate the parameters of this model. Another approach is to develop phenomenological or empirical frameworks in which no a priori assumptions are made about what type and how many components are present in a voxel or their relationship, and then go about estimating different distributions or spectra of quantitative MR parameters that might reveal them. The first approach has an Aristotelian character, in which the modeler imposes some assumed foreknowledge about the complex tissue composition, structure, architecture and organization a priori, based upon precedent or, in some cases, pure supposition. The second approach, a more skeptical one, makes no such a priori assumptions but generally requires a plethora of data, more than the former methods require.
Until recently, the second empirical approach described above has been out of reach via conventional preclinical and clinical MRI because of the extremely long scan times required to obtain enough useful data, and conceptual and mathematical challenges inherent in reconstructing such data, owing to the often ill posed character of the inverse problems underlying these methods. To reiterate, scalar MRIs, which provide voxel-averaged data, usually obtained on the order of a cubic millimeter, conceal details of the various physical and chemical microenvironments within the voxel, and the local heterogeneity and anisotropy of different properties at multiple length and timescales.
Generally in biological and clinical applications of MRI, one measures features of water, as it is so abundant (of the order of 55 M) and produces a strong MR signal owing to the large gyromagnetic ratio of water protons. Water pools exist in different microenvironments (such as intra- and extracellular spaces) within the voxel, and may have distinct diffusivities or relaxivities. While relaxivities are affected by the local composition and chemical environment, diffusion-weighted (DW) MR has the potential to probe molecular mobility over different length and time scales, and hence inform on tissue microstructure.1–7 There is no a priori basis for assuming that only one or a small number of diffusivities or relaxivities can characterize a microscopically heterogeneous and/or anisotropic tissue block, owing to the fact that there may be multiply exchanging water pools, and active transport processes, differences in macromolecular composition and concentration etc. These are expected to produce non-mono-exponential , and DW signal attenuations.8–15 Thus, moving from conventional MRI, which provides voxel-averaged scalar images, to spectral based MRI methods, which provide empirical distributions, has great merit, making it possible to obtain effectively higher spatial resolution while detecting salient features of different microenvironments within each voxel.
While we do not want to give short shrift to analytical modeling approaches, the empirical or phenomenological framework for modeling a spatially resolved MR signal and extracting useful features related to exchange, relaxation, diffusion and possibly other features is the subject of this review article.
2 |. NON-PARAMETRIC INVERSION OF MULTIDIMENSIONAL DATA
The challenge of obtaining spectra from MR data is that the MR signal represents a “convolution” of the spectrum with a kernel that embodies the way each MR perturbation weights each component of the particular spectrum. The goal of spectral analysis of MRI data is to invert this expression and find the spectrum hidden in the signal. In the case of finding diffusion or relaxation spectra, where the kernels are assumed to have an exponential form, the inversion resembles an inverse Laplace transformation (ILT) of the MR signal. Because of the limited spectral bandwidth and the non-negativity constraints that are always enforced when solving these problems, an analytical ILT cannot be performed. Nevertheless, this method is often termed “Laplace NMR” or “Laplace MRI”. Using this pipeline, one can, in principle, obtain a model-free description of the spectral components and their relative signal fraction (SF) as a way to quantify intra-voxel variability.
Laplace MR received a significant boost in 1982 with the development of a theoretical framework and algorithm for solving constrained, regularized inverse problems by Steven Provencher, and the dissemination of his software subroutine called CONTIN.16 Subsequently, Kroeker and Henkelman were the first NMR physicists to use CONTIN on NMR relaxation data to obtain “continuous” and distributions. The first published examples were obtained from mouse limbs, as shown in Figure 1.17 The motivation of their pioneering work was to explore the expected heterogeneity of these biological samples. Following this groundbreaking research, there were many subsequent examples of 1D NMR measurements of relaxivity and diffusivity distributions to study different types of biological component18–23: most notably, observations of two or three distinct components of the water distribution in nerve tissue, which all pointed to the existence of distinct water microenvironments. These have been assigned as arising from myelin water,24 extracellular water and intracellular water (short to long ).9–11,24–28
FIGURE 1.
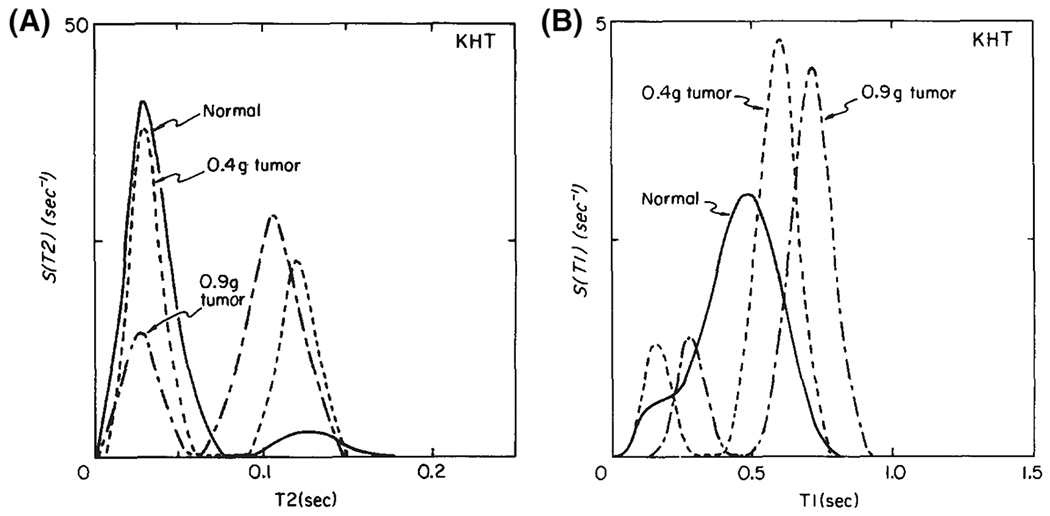
First NMR application of a regularized inversion algorithm16 to estimate and distributions from in vivo legs of C3H mice in normal conditions and after injection of tumor cells (KHT). In all cases, multiple components were detected. The average values of both and increased with tumor size. The peaks shift to the right as the tumor grows; the peaks redistribute to the right. Adapted from the work of Kroeker and Henkelman17
This 1D framework is extendable to two and even higher dimensions through the acquisition of MR signals that are weighted by more than one MR parameter, such as diffusion, etc. This idea was first proposed in 1991,29 and subsequently such 2D data without spatial localization (ie NMR) have been used by the porous media community to quantify pore size distribution, porosity and permeability, primarily of non-biological porous media (Figure 2).13,31–41 Two dimensional correlation NMR studies, correlating mainly and ,42–45 but also diffusion in different directions,46,47 were performed on biological specimens as well, in particular neural tissue. These studies have suggested the multicomponent character of biological tissue as well, with some examples shown in Figure 3. Recently, higher dimensional correlation NMR, mainly focused on pore shape and orientation, were developed and applied on phantoms and in simulations.48,49
FIGURE 2.
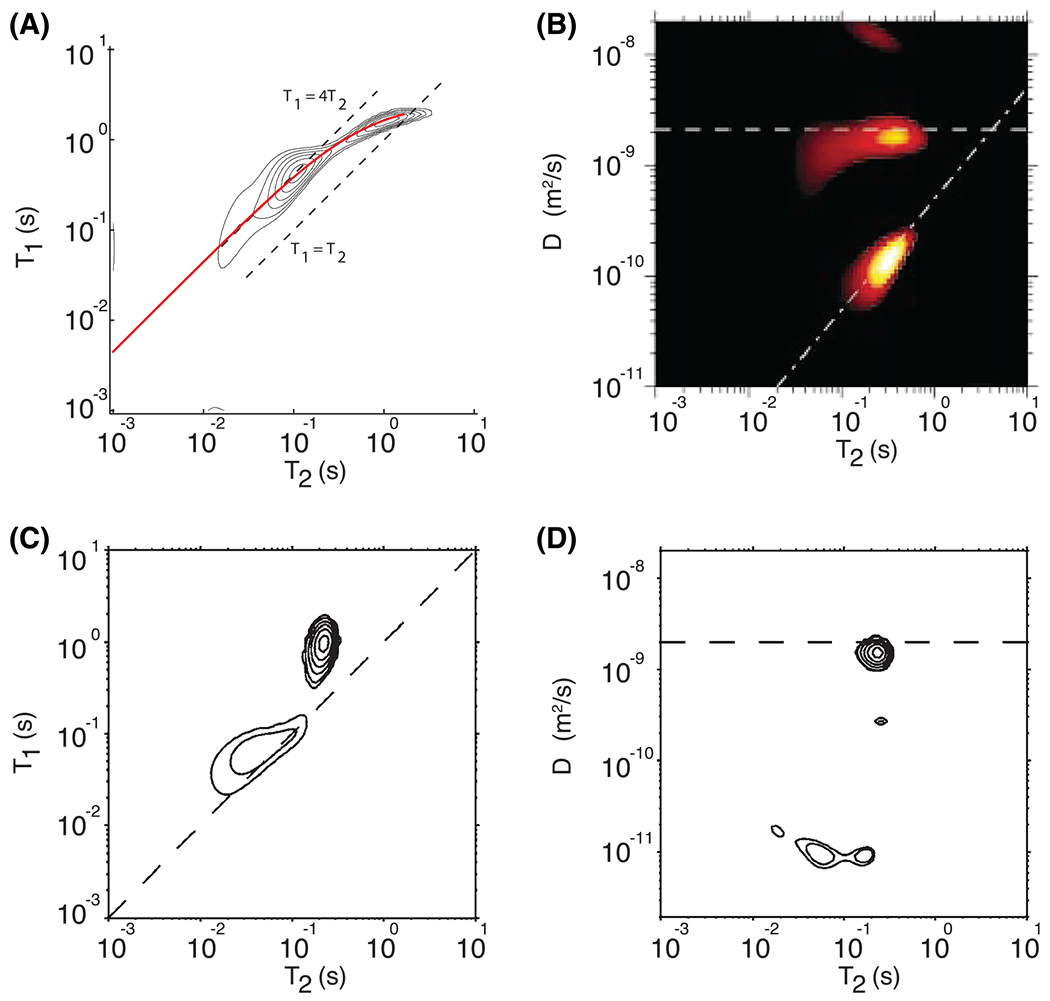
Two dimensional correlation NMR studies on non-biological samples. A, the correlation spectrum for oolitic limestone. The solid thick red line is the theoretical behavior of the sum of the surface and bulk contributions to and . Adapted from the work of Song et al.30 B, the correlation spectrum for Berea sandstone saturated with a mixture of water and oil. The contributions of the water and oil phases are clearly separated in the two dimensions. Adapted from the work of Hurlimann et al.31 C, D, comparison of (C) and (D) distributions measured on heavy cream. The dashed lines in the distribution functions indicate , whereas in the distribution functions they indicate the diffusion coefficient of water. Adapted from the work of Hürlimann et al32
FIGURE 3.
Two dimensional correlation studies on biological samples. A, the correlation spectrum for trigeminal nerve data averaged from seven rats. The three components are clear and their relative fractions and mean and values are shown, along with the standard deviation of these measurements across the seven rats. Adapted from the work of Does and Gore.43 B, the correlation spectrum for trigeminal nerve data averaged from seven frogs. The three components deemed to be nerve water, representing 88% of the total signal, are shown in black; the remaining spurious components are shown in gray. Adapted from the work of Travis and Does.45 C, the correlation spectrum for chromated rat WM. By washing the samples with chromium, a WM-specific enhancer, the long component in the distribution was split into two. Adapted from the work of Dortch et al.44 D, the diffusion–diffusion correlation spectrum averaged across the entire mouse brain. Correlations were measured between displacements along two arbitrary orthogonal directions. Adapted from the work of Zong et al47
MR contrasts, based on water diffusivity in particular, can probe different time and length scales in addition to exchange between and among different microenvironments, so a multidimensional MR framework could have great potential for studying biological tissue. However, characterizing the heterogeneity of tissues such as white matter (WM) and gray matter (GM) at macroscopic, microscopic and mesoscopic length scales has been challenging. Combining multidimensional NMR-based spectral methods with spatial localization via MRI is required in order to be able to assess the heterogeneous properties of such tissue. For more than two decades, this challenge has seemed insurmountable, owing to the vast amount of data required and other computational challenges. In the next section, we cover promising new ways in which investigators have addressed the migration of multidimensional correlation methods from NMR to MRI.
3 |. THEORY
For 1D MR encoding, we can express the relationship between the measured MR signal, , and the distribution of the MR relaxation or diffusion parameter, , according to a distribution governed by the MR parameter , using the 1D Fredholm integral equation, which has the general form
| (1) |
where is the MR experimental variable, and is the kernel, which weights and relates the MR parameter and variable to the MR signal. Generally, for diffusion, and -type relaxation processes, the kernels will have the exponential forms: and , respectively. Here the encoding variables are the inversion time, , the echo time, , and the diffusion weighting, , respectively, where is the gyromagnetic ratio, is the diffusion pulse duration with amplitude , and is the diffusion time.
To numerically perform the inversion, Equation (1) is discretized as the following discrete sum17:
| (2) |
where is the experimental noise, which is often assumed to be Gaussian. Because has an exponential form, Equation (2) would have represented a ILT relationship if it were not for two spectral constraints that are always imposed: (1) the discrete distribution, , is composed of non-negative components; and (2) is defined on a finite range. To estimate the 1D distribution of a given MR parameter, , the corresponding experimental parameter should be sampled times. In this case, Equation 2 can be written in matrix form as
| (3) |
where and . To find , the estimate of , the following basic optimization problem can be formulated and solved:
| (4) |
where is the norm. Solving Equation (4) is ill posed in the sense that small changes in the data can cause arbitrarily large changes in the solution; this is reflected in the matrix of the discrete model being ill conditioned, with this problem increasing as the dimension increases. It is therefore necessary to perform some regularization to filter out the influence of the noise, which we will touch on after introducing the multidimensional generalization.
Expanding Equation (1) to include on MR experimental variables, or dimensions, would result in
| (5) |
Equation (5). can be discretized to matrix notation by ordering the spectral and kernel elements in a consistent manner and writing the continuous distribution as , with , the multidimensional signal as , with , and the kernel matrix as . Equation (5) can be written as Equation (3) then solving Equation (4) we can estimate .
Practically, the main limitation of multidimensional inversion is the number of free parameters and experimental variables. Typically, the density distribution is sampled over a uniform grid, such that , leading to polynomial growth in the number of free parameters as the number of dimensions increases. The large data burden hampered the use of multidimensional NMR, and certainly prevented it from being used in conjunction with MRI. We will discuss below several strategies and methods employed to reduce the demand for such data.
Now that we have formulated the inversion problem and its clear ill posed nature, we will briefly discuss strategies to overcome this obstacle. First, compressing the data using a truncated singular value decomposition (TSVD), which is in fact a regularization step that enforces a smooth solution (ie non-oscillatory ),50,51 is commonly used prior inversion. In addition, a standard approach to solving ill posed problems is to regularize them.12,16,17,22,25
Regularization methods apply the principle of parsimony by penalizing oscillatory solutions. If the objective function in Equation (4) can be thought of as a fidelity term, regularization adds a second term to the objective function that penalizes specific solutions, and is tuned by the regularization parameter, α,
| (6) |
Most regularization methods employ the norm, ie Tikhonov regularization52 with , and is the identity matrix12,16,17,22,25; however, there are cases where the norm is preferable.53–55 The regularization term forces neighboring points in to be close to each other, while rejecting solutions with large numbers of peaks, thus enforcing the principle of parsimony, which is suitable when the underlying distribution is expected to be smooth. Tikhonov regularization is especially appealing to use because the quadratic nature of the second term in Equation (6) guarantees the existence of a unique solution.56
The choice of a good regularization parameter should yield a fair balance between the perturbation error and the regularization error. A variety of optimal selection strategies have been developed and proposed; among them are the Butler-Reeds-Dawson (BRD) algorithm56 and its practical application, the S-curve,30 the L-curve method57,58 and generalized cross-validation (GCV).59
Recently, it was suggested to repurpose a Monte Carlo (MC) approach60 as an inversion technique, to avoid the use of regularization and perform a non-negative least squares (NNLS) estimation (Equation (6) without the right-hand term). Because of the adverse instability of such an estimation, inversion is achieved using a MC approach by repeating the NNLS estimation with multiple data subsets (if these are available), obtaining an ensemble of solutions and adopting the average.61
4 |. PRECLINICAL AND CLINICAL TRANSLATION OF MULTIDIMENSIONAL MRI: PITFALLS AND CHALLENGES
4.1 |. Data acquisition
The challenges of translating multidimensional NMR methods to MRI for biological, preclinical or clinical applications are manifold. Clinical MRI scans are typically no more than 20 min and in vivo small animal studies generally cannot take more than about 1.5 h. We can perform a “back of the envelope” calculation to estimate the scan time required for a typical whole-brain relaxation experiment performed on a 3 T clinical scanner with a 32-channel RF receive coil, a single-shot spin-echo EPI readout, 2 mm isotropic voxel resolution and a repetition time of 10 s with a single average. Then, the number of data points required for a 2D correlation experiment ranges from 102442 to 225 000 62 which translates to a scan time from about 3 h to 625 h! Increasing the repetition time increases the acquisition time proportionately. Clearly, without massive efficiencies in data acquisition and spectral estimation, 2D spectroscopic imaging using conventional imaging approaches is not biologically feasible. One widely used method to accelerate multidimensional NMR for spectrum measurements entails using a CPMG acquisition as a way to expedite measurements at different echo times, .63 However, this approach requires a train of 180° RF pulses, which precludes its use in high field scanners owing to their high specific absorption rate, resulting in RF energy deposition above FDA safety limits.64 In addition, the CPMG readout can be used for acquisitions, but is not applicable when or encoding is desired.
The ZEBRA pulse sequence represents a recent advancement of data acquisition efficiency.65 ZEBRA is a sequence that efficiently samples the acquisition parameter spaces required for and diffusion by slice-level interleaved diffusion encoding and multiple spin and gradient echoes, thereby reducing the amount of time required to acquire multidimensional data.
4.2 |. Strategies for dimensionality reduction and spectrum visualization
While multidimensional NMR produces one- to three-dimensional (and even higher) spectral data, combining this with MRI necessitates three additional spatial dimensions. This further increases the data dimensionality; the need to summarize spectral data begs more compact representations.
The most common means of dimensionality reduction is to summarize the spectra by reporting the relative SFs for each spectral peak in each voxel and then displaying these as an image. This concept was proposed in the early 1990s by Labadie et al66 and Mackay et al[9] and has been used widely ever since. This data compression method entails summing (ie numerically integrating) over peaks whose boundaries are well defined. It is usually assumed that the MR SF is proportional to the volume fraction of water protons, conferring a physical meaning to the value of the spectral SF. The relationship between the observed SF and the actual water volume fraction depends on many factors, including MR pulse sequence and magnetization transfer (MT) efficiency.67,68 Thus, one should report these as SFs.
There are other challenges with measuring and mapping SFs. In many cases, spectral peaks may merge or overlap with one another, making it difficult to compute an SF robustly.69,70 Moreover, an automated method to identify spectral components and determine their boundaries is required when there are many voxels and many peaks in each spectrum. Parameterizing the empirically measured spectra using a suitable mixture model, for example a mixture of lognormal distributions, can help address this issue.70 This can provide a more compact representation of the spectra once the features and shapes of the various peaks are known, and can help resolve overlapping spectral peaks. In the first implementation of this approach, the number of peaks in the spatially resolved 1D diffusivity distribution was assumed to be two in ex vivo fixed spinal cord, resulting in robust intensity images of SFs of slow and fast diffusion components. This approach can also be generalized to higher dimensions when appropriate. Certainly, assuming a bimodal distribution when the spectrum may contain more or fewer than two peaks can be problematic, and should be addressed in future applications.
4.3 |. Strategies for accelerating and stabilizing the inversion
We should reiterate that reducing the time required to perform a multidimensional scan is of paramount importance to be able to translate these methods. Achieving this requires a two-pronged approach: improving both hardware and pulse sequences, and acquisition and post-processing strategies. Technological innovations including parallel imaging, multichannel coils and novel pulse sequence designs are facilitating the migration of these approaches preclinically and clinically; however, the greatest gains appear to be made using novel acquisition and post-processing strategies, which aim to reduce the amount of required data to reconstruct 2D and higher dimensional spectra with high fidelity.
The need to further reduce the amount of data required for multidimensional MR experiments emerged when its integration with MR imaging was first contemplated. In 2014, the use of compressed sensing (CS) was proposed to reduce the data needed to reconstruct 2D spectra by randomly sampling the space of the relevant experimental variables.71 The idea was to use a significantly down-sampled version of the original data matrix, G, and then use a matrix completion method72 to recover the spectrum using only a fraction of the required measurements. The CS approach was used to image a spinal cord sample in which a maximal acceleration factor of 3.5 was achieved, reducing the number of acquisitions from 1800 to 450.73 Although this reduction represented a significant improvement, a factor of 3.5 could not achieve the promised land of clinical MRI applications.
An alternative strategy to stabilize and reduce the amount of required data to reconstruct multidimensional spectra in imaging applications was first proposed in a 2D diffusion–diffusion correlation study, in which applying additional spectral constraints was suggested.74 This approach was later refined and tested using combined relaxation-diffusion data and became known as the marginal distributions constrained optimization (MADCO) framework.54 MADCO is a general mathematical approach that was first demonstrated experimentally on a MRI phantom. It outperformed the conventional inversion method so dramatically that even when only 2% to 4% of the full dataset was used spectra could be reconstructed faithfully with an acceleration factor of 25 to 50, depending on the spectral complexity, as shown in Figure 4.54,75 An intuitive explanation of MADCO with respect to CS can be illustrated by considering the Milton Bradley board game Battleship. In Battleship, two players place toy ships somewhere on a discrete rectangular grid representing a body of water, with the goal of finding all the opponent’s ships first. A reasonable search strategy, resembling CS, is for each player to choose random points within the grid from a uniform distribution. Suppose we modify the rules of the game so that in the first two moves each player obtains additional (1D) projections of the mass distribution of the opponents’ ships along the columns and rows of the grid. The optimal search strategy then changes considerably. The information from each row and each column would provide powerful new constraints to allow each player to find most of the opponent’s ships, usually within a few guesses. CS provides a reasonable strategy when no a priori information is given about the features of the spectrum. However, when we can acquire projections or marginal distributions of the multidimensional spectrum, we have much more information to apply in the form of linear constraints with which to force the convergence of the final spectral estimate.
FIGURE 4.
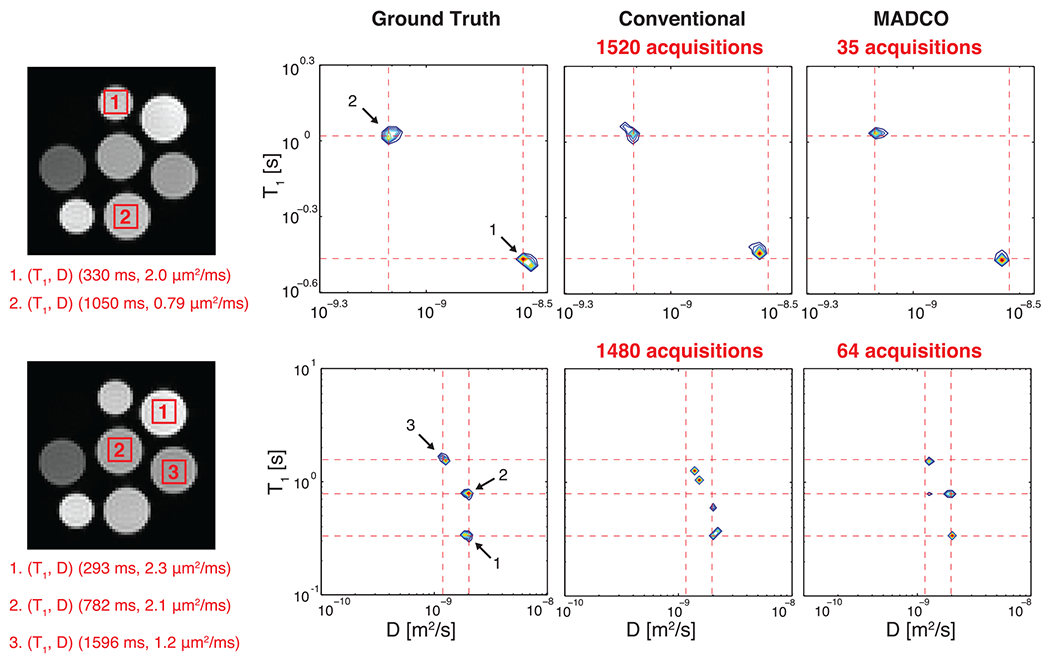
Experimental validation of the MADCO framework. ROIs drawn on DW-IR images of the MRI phantom resulted in two75 (top) and three54 (bottom) distinct peaks. The averaged data were then used to reconstruct the spectra by using full (conventional) and partial (MADCO) datasets. Note the higher accuracy of the MADCO-reconstructed three-peak spectrum, with only 4% of the data used, compared with results from the conventional approach. Adapted from the work of Benjamini and Basser54,75
A third approach for improving the robustness of the spectral inversion method is to use spatial regularization, which was first suggested in a 1D MRI study76 and subsequent applications,14,77 and later extended to study 2D relaxation-diffusion correlations.78 By assuming spatial contiguity, this approach employs spatial constraints within the imaging domain rather than employing physical constraints in the spectral domain to help minimize the cost function. The rationale for this former approach is the relative immunity to noise of the Fourier transform as a means to overcome the inherent ill posed nature of the multiexponential inversion. Spatial constraints (in the image domain) act as a spatial low pass filter by effectively averaging over neighboring voxels. Nonetheless, this method should be implemented with great care, particularly when applied on a heterogeneous specimen, in which intervoxel variability may contain valuable information that can be smoothed or averaged over. In particular, applying a spatial low pass filter to imaging pathological tissue may smooth over salient aberrant signals arising from pathological voxels. In an attempt to address both the issues of dimensionality reduction and inversion stability, an expectation–maximization based method, termed InSpect, was recently suggested.79 Instead of estimating non-parametric spectra, with this approach a predefined number of canonical spectra are assumed to exist, which are then assigned to individual voxels. Although this approach is governed by a subjective choice of the number of clusters (ie the canonical spectra), and also may be susceptible to low spectral sensitivity, it is computationally more stable and results in low dimensional information that is easier to visualize.
4.4 |. Sparse data sampling and its effects on accuracy and robustness
It is clear that the biggest obstacle to wide scale application of multidimensional correlation MRI is data requirements. Traditionally, such experiments were designed with uniform and dense sampling of the relevant MR parameter space (eg for ). Before multidimensional correlation MR had started to be used in conjunction with imaging, there was no particular need to reduce the acquired data. A systematic study of the effects of the sparsity of the data collection had therefore never been conducted.
In an attempt to start this important discussion, we performed a numerical simulation study that tested the effect of sparse sampling on the most commonly used inversion techniques, the and regularizations, the MC NNLS and MADCO. A ground truth distribution with three components that resembles the expected spectral signature from a complex brain volume was used, as illustrated in Figure 5. This 200 × 200 distribution was used to create synthetic 2D data, to which noise with a Gaussian distribution, zero mean and a standard deviation scaled to provide was added.
FIGURE 5.
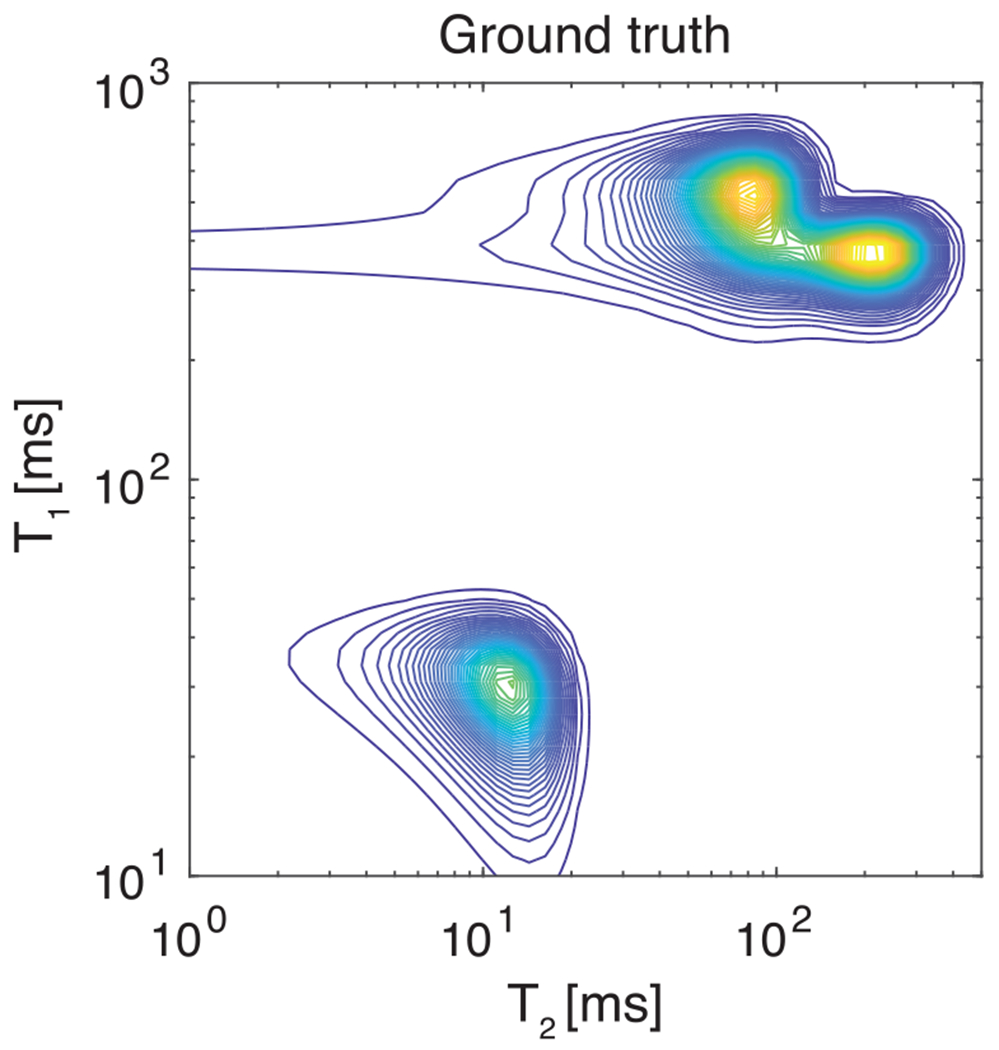
The ground truth multicomponent probability distribution that is used to generate the simulated data matrix with added Gaussian distributed noise of zero mean to provide
The full dataset was comprised of logarithmically sampled and over the ranges of 15 ms to 4000 ms and 5 ms to 200 ms, respectively. All reconstructed spectra had elements. We tested the above-mentioned optimization frameworks using the full dataset (100%), and three sparse subsamples of it: (1) 50% and (2) 25% of the data randomly sampled with replacement from the complete dataset, and (3) a hierarchical sampling, and in 1D and highly sparse encoding of 20 data points in the 2D parameter space (total of , about 5.5% of the full dataset).
For and regularizations, a TSVD procedure was carried out prior to the inversion,51 and the regularization parameter was chosen according to the GCV method59 and an adjusted criterion,55 respectively. MC NNLS was performed with 1000 bootstrap samples each containing two-thirds61 of the dataset (eg, with the full dataset, 1350 datapoints) randomly sampled with replacement. With MADCO, the marginal distributions and were first obtained from 1D data, and then used as additional spectral constraints with an regularization inversion.54
Performance of the inversion strategies at different sampling sparsity was assessed by computing the Jensen difference (JD)80 between each estimated distribution and the ground truth. The reconstructed spectra under the different conditions are shown in Figure 6. With a full dataset (left column), the regularization inversion (Figure 6A) produced the most accurate spectrum. Despite a relatively high JD value, the regularization provided moderate accuracy in the locations of the estimated components, albeit very sparsely distributed, as expected (Figure 6B). The NNLS MC inversion with the full dataset (Figure 6C) resulted in a spectrum that exhibited similar characteristics to the one obtained using regularization, with the exception of spectral noise manifested at the low end of the reconstructed distribution. The apparent high sensitivity of the MC NNLS to noise in the data, even when using the full dataset, can be explained by considering that repeated non-regularized estimations of different noisy datasets would all result in a similar manifestation in the spectral domain, in this case short-lived and components. Averaging the bootstrap spectra would not eliminate these noise components. Finally, MADCO with regularization optimization using the full dataset resulted in a relatively accurate distribution, yielding a slight increase in the JD compared with regularization only (Figure 6D).
FIGURE 6.

Application of several inversion strategies as a function of data acquisition sparsity. A, TSVD procedure followed by regularization. The regularization parameter was chosen according to the GCV method. B, TSVD procedure followed by regularization. The regularization parameter was chosen according to the GCV method, using an adjusted criterion.51 C, MC NNLS with 1000 bootstrap samples each containing two-thirds of the dataset, randomly sampled with replacement. D, MADCO reconstruction using the marginal distributions and , with regularization and GCV method. Different columns show different dataset subsamplings, 100%, 50%, 25% and 5.5% (left to right)
With the exception of MADCO and the regularization with 50% data, all of the investigated inversion approaches displayed a considerable decline in the accuracy and robustness as the sparsity of the acquired data increased (Figure 6, columns left to right). With 5.5% of the data, the only distribution that preserved its accuracy and robustness is the one estimated using the MADCO framework. In fact, the subsampling of the data did little to affect the robustness and accuracy of the MADCO-derived spectra, with JD ranging from 0.22 to 0.16 with a standard deviation of 0.02.
5 |. NOVEL APPLICATIONS OF MULTIDIMENSIONAL CORRELATION MRI
First and foremost, one should ask “What are the benefits of integrating relaxation and diffusion acquisitions and their processing frameworks over existing approaches? What information, otherwise invisible to scalar MRI methods and 1D approaches, can only be gleaned using multidimensional MRI methods?” Below, we have included a few important examples that epitomize the value added by such an approach.
5.1 |. Spinal cord
To date, two studies using different spectral inversion approaches have produced multidimensional correlation MRI data on ex vivo spinal cord. Spinal cord was chosen because of its relative neuroanatomical simplicity compared with the brain, the known segregation of GM and WM regions and the presence of coherent axon fiber orientation, while possessing cells and cell types found in the central nervous system (CNS).
5.2 |. Spatially regularized spectral reconstructions
The use of spatial regularization was extended from 1D inversion MRI applications14,76,77 to 2D diffusion-relaxation by investigating correlations from three control and three injured ex vivo mouse spinal cords.78 The applied encoding scheme consisted of a total of 28 data points covering the ranges of 40 to 160 ms and 0 to 5000 s/mm2 for and , respectively, with an in-plane resolution of 78 × 78 μm2 and slice thickness of 1 mm.
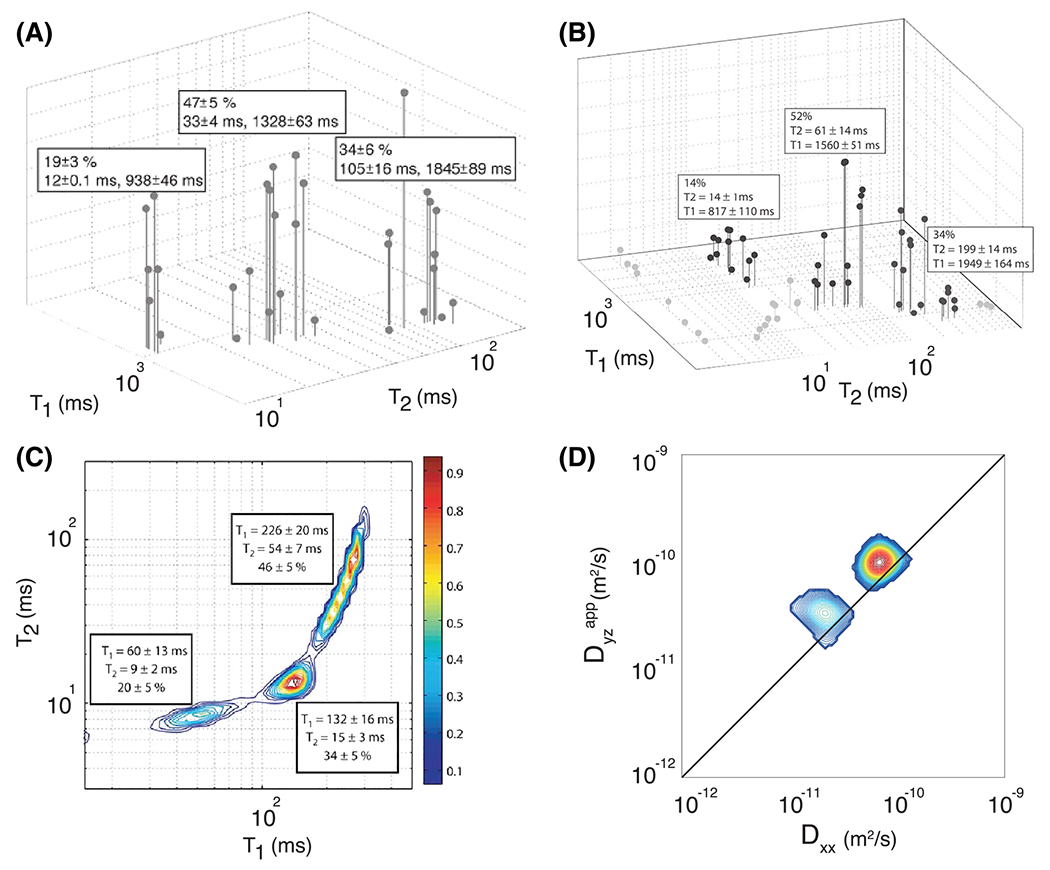
Spinal cord injury was caused by direct impact, which normally results in significantly reduced normal-appearing WM volume and decreased motor function compared with that of controls.81 Ranges of the diffusivity and values of the spectral components were determined, followed by numerical integration that resulted in their respective SF images. Averaged spectra from the entire control and injured samples, their spectral regions of integration and the resulting SF images are shown in Figure 7 The control distribution contains two well separated spectral peaks, with a single value and two distinct diffusivities, slow and fast (Components 1 and 2 in Figure 7). A third peak is also indicated (Component 3); however, it is not clear what makes this spectral region unique from either Component 1 or 2. The control SF images in the bottom panel of Figure 7 indicate that Components 1 and 3 correspond to WM and component 2 to GM. An additional component, with fast diffusivity and shorter , is evident in the injured samples (Component 4). Integration over this component resulted in SF images with intensities mostly evident in the injured sample, indicating sensitivity and specificity to the spinal cord injury.
FIGURE 7.
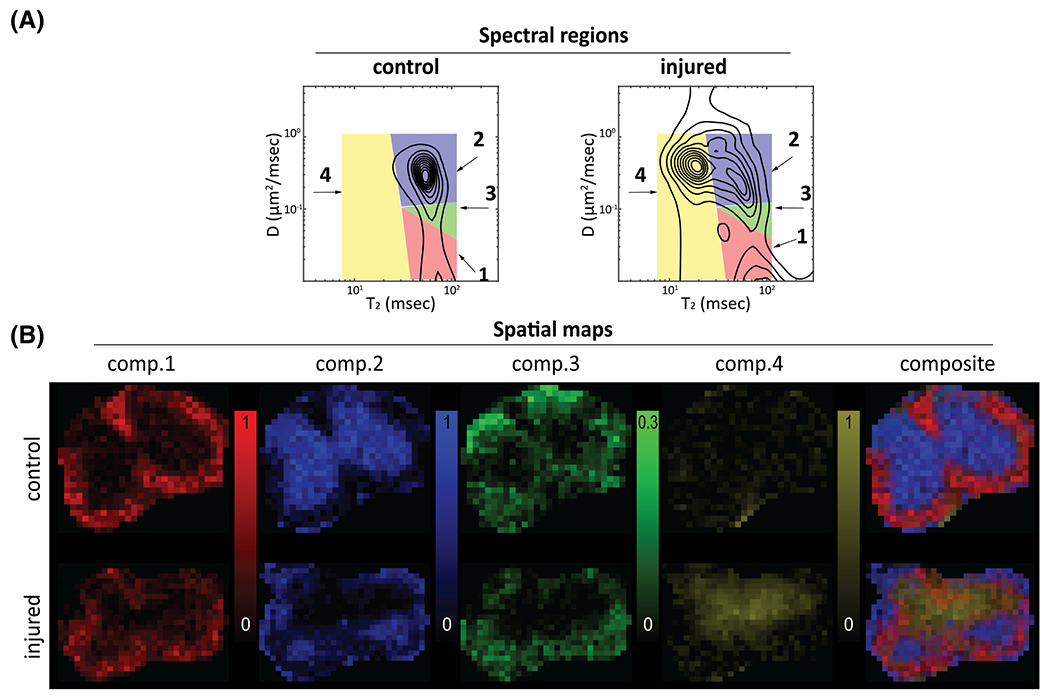
Spatial maps of the SFs from the control and injured spinal cords. A, spatially averaged distributions with the spectral regions that are integrated to generate the spatial maps (red, comp. 1; blue, comp. 2; green, comp. 3; yellow, comp. 4). B, the spatial maps corresponding to the spectral regions. Adapted from the work of Kim et al.78 (comp. = component)
In this study, both normal WM and GM contained a single peak in space, contradicting findings in many previous studies that have reported both and diffusivity to be multiexponential.11,12,15,22,43,70,82,83 The lack of spectral sensitivity in this study may be explained by the small range of diffusion and encodings combined with an overall relatively small number of data points, and thus spectral resolution. An additional confound may have been the spatial averaging that was performed by applying spatial regularization, which may have smoothed over important spectral features. These results highlight the importance of using both the appropriate acquisition and analysis methodologies to adequately reconstruct the spectrum. Nevertheless, the joint distribution of was shown to be able to distinguish between normal and injured tissue on the basis of spectral signatures. Furthermore, the reproducibility and robustness of this approach was demonstrated by the consistency of the spectra across the control and injured specimens.
5.3 |. Spectrally constrained approach
The first study that applied the MADCO framework was aimed at investigating the correlation between , and , and their spatial distribution in CNS tissue.15 Three encoding schemes were applied on a ferret spinal cord sample, , and , with a total of 88 data points covering the ranges of 20 to 3000 ms, 10.7 to 150 ms and 0 to 25068 s/mm2 for , and , respectively, with an in-plane resolution of 100 × 100 μm2 and slice thickness of 2.5 mm.
Having estimated the multidimensional spectra in each spinal cord voxel, dimensionality reduction was performed by identifying spectral peaks, integrating over them and obtaining their respective SFs. To make these steps possible, WM and GM ROIs were first selected, resulting in the spectra shown in the top panel of Figure 8. For convenience, the MR dimensions were partitioned into length ranges for and and mobility ranges for diffusion. In WM, four distinct components were identified (labeled A, B, D and F in Figure 8): slow , long ; slow , intermediate ; intermediate , long , and intermediate , short . In GM, three distinct spectral components were identified: intermediate , long ; fast , long , and fast , short , labeled C, E and G, respectively. These WM and GM spectral components can be compared with previous 1D and 2D NMR studies on similar specimens; specific similarities include the presence of low and high water mobility,12,22,70 the partitioning into intracellular and extracellular water based on ,43,83 and the existence of a myelin-associated MT component at short 14,84 and short 9,85
FIGURE 8.

spectral information from a spinal cord specimen, gathered by using MADCO. The top panel shows WM and GM unique spectral peaks (A-G). Additionally, a WM-GM mixture is shown, with well separated spectral components according to short, intermediate and long relaxation values and slow, intermediate and fast diffusivities. All the identified WM and GM peaks had a unique multispectral signature, thus allowing their unequivocal identification in the more challenging, and more realistic, case of mixed GM and WM. The bottom panel shows the spatial SF maps corresponding to the above spectral regions, separated according to water mobility and tissue type specificity. (inter. = intermediate.) adapted from the work of Benjamini and Basser15
It was also demonstrated that most of the spectral components are distinct and can still be identified once the GM and WM spectral MR data are averaged together (Figure 8, middle panel). Although such mixtures of “pure” WM and GM do not entirely mimic partial volume voxels found in the brain, they provide a reasonable approximation. Seven spectral components could be identified in such a case, leading to rich intra-voxel information and a powerful demonstration of the potential and added value of multidimensional correlation MRI.
The SF images in the bottom panel of Figure 8 show the spatial arrangement of intensities of spectral components. These can largely be divided according to lower and higher water mobilities, and GM and WM specificity. Based upon previous 1D diffusion and imaging,22,83 it was argued that the lower and higher water mobilities should be associated with intra- and extracellular water, respectively. It was proposed that the short -short component, which is modulated by MT, was myelin associated. It was then shown that intracellular and myelin SF images correlated strongly with histopathological measurements of various immunohistochemical stains.
The richness of the intra-voxel multidimensional spectra and the information that it provides can only be gleaned using a higher-dimensional MR acquisition and processing framework. These works make a clear case for the benefits of using integrated relaxation and diffusion contrasts when investigating biological tissue properties.
5.4 |. Placenta
Another excellent example of the use of multidimensional correlation MRI was provided by Slator et al, who investigated spectra of in vivo human placenta86 using ZEBRA.65 The motivation for this study was to combine the two most widely used MR contrasts for characterizing the placenta, , which is related to oxygenation levels, and diffusion, which probes tissue membranes and cellularity. Images were acquired in vivo with 3 mm3 voxels, diffusion encoding in the range of 0 to 1600 s/mm2 in multiple directions with a total of 66 b-vectors and five echo times in the range of 78 to 222 ms. This type of encoding typically requires 330 separate acquisitions, but only 66 are needed for the ZEBRA sequence with five gradient echoes, with each full scan taking approximately 8.5 min. Seventeen pregnant women, grouped by clinical status (healthy control, chronic hypertensive, pre-eclampsia and fetal growth restriction) were scanned using this approach.
A representative whole-organ spectrum from a control subject is shown in the top panel of Figure 9. Three distinct ADC peaks with similar values were observed consistently across almost all the control cases. These three diffusion components in the placenta are also consistent with findings from previous studies.87 The components were identified solely on the basis of their diffusivity values—slow, intermediate and fast—and are shown in Figure 9 as Peaks 1 through 3, respectively. As in previous studies, dimensionality reduction via numerical integration was performed, and SF images of the three spectral components were obtained and are also shown here. The slow diffusion component shown in these images is associated with areas within the placenta, while the intermediate and fast diffusivities are more prominent in the uterine wall. It was speculated, based on previous findings,87 that Peak 1 is stationary water within the tissue, Peak 3 originates from perfusing fetal blood and Peak 2 arises from water in the chorion transitioning between the maternal and fetal circulatory systems.
FIGURE 9.
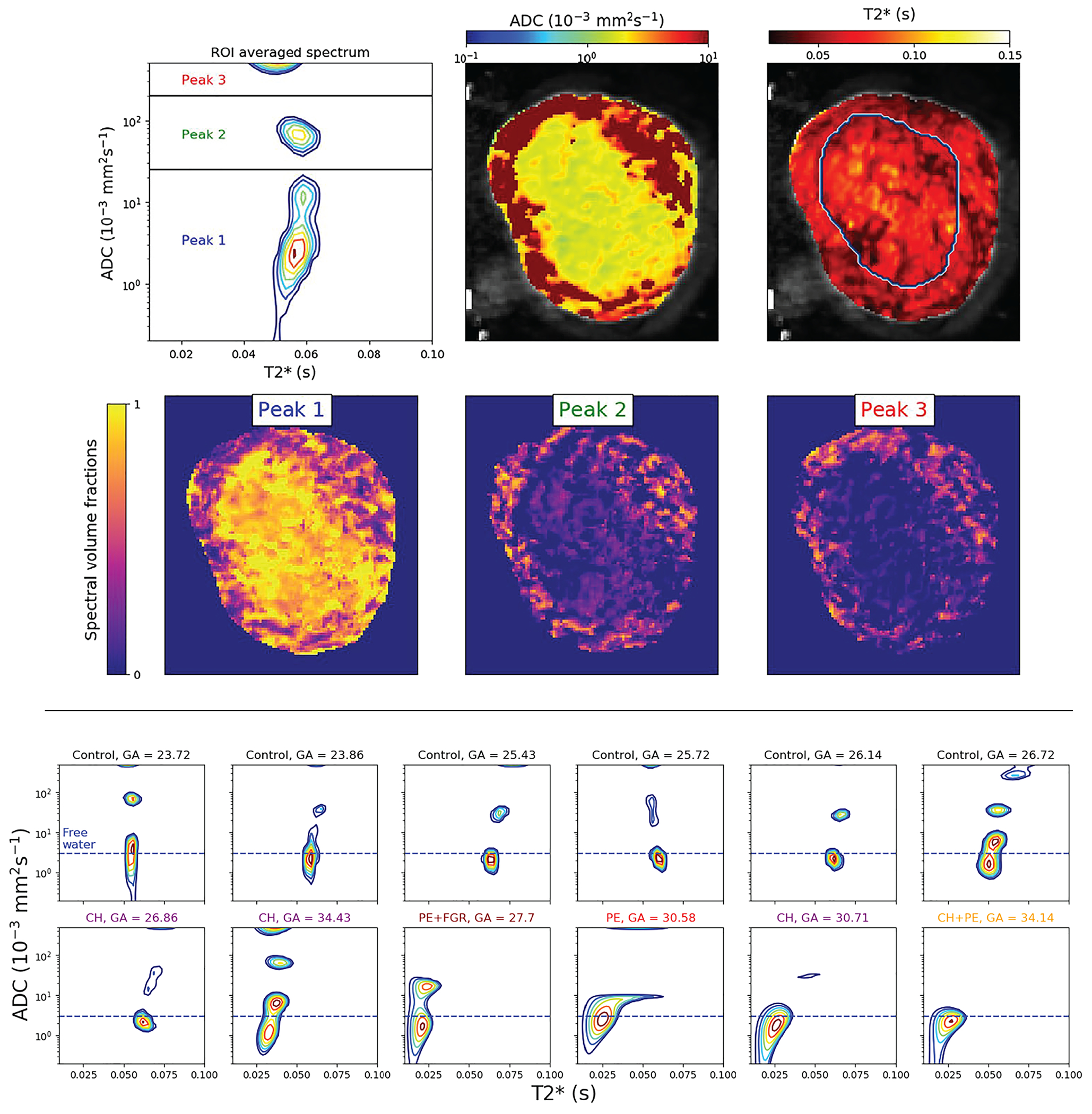
spectra show anatomical specificity. Top panel: spectrum derived from spatially averaged signal from the entire placenta and uterine wall, with the three spectral regions that are integrated to generate the spatial SF maps below. Bottom panel: spectra derived from the spatially averaged signal of control and abnormal cases. Horizontal, dashed blue lines represent the approximate diffusivity of water in free media at 37°C. (GA, gestational age; CH, chronic hypertensive; PE, pre-eclampsia; FGR, fetal growth restriction). Adapted from the work of Slator et al86
The bottom panel of Figure 9 shows representative ROI signal-averaged spectra of control and abnormal participants. Two prominent trends can discriminate between the two groups: (1) a shift toward shorter values that mirrors previously reported in placentas with pre-eclampsia and intrauterine fetal growth restriction88,89 and (2) a shift toward slower diffusivities (with instances of the disappearance of either Peak 2 or 3), hypothesized to occur because of increased water hindrance due to inflammation. This study concluded that the value of the slowest diffusion component was the most predictive of complications found in pregnancy. Although this information could have been obtained by using a 1D diffusion-filtered measurement, the study provided a proof of concept for the applicability of multidimensional correlation MRI in a clinical environment. Compared with the rich water-mobility spectrum, the poor spectral resolution (ie the detection of a single component), may have been due to insufficient encoding, which entailed using only five echo times.
6 |. OUTLOOK AND PERSPECTIVE
Dozens of multidimensional inversion NMR/MRI studies spanning more than 30 years have resulted in reliable, reproducible and unique micro-structural and chemical information, which is otherwise invisible using other methods. The multidimensional inversion frameworks reviewed here are phenomenological methods that make no or few explicit assumptions about tissue structure or composition. Through the use of innovative spectral reconstruction approaches, robust strategies and procedures have been developed to make multidimensional correlation MR feasible for biological and clinical imaging applications for the first time.
Although no published papers to date have directly compared multidimensional correlation MRI with 1D scalar approaches , our work on the spinal cord conclusively showed that multiple microenvironments exist in the tissue.15 Moreover, some components could not have been resolved by investigating separately the , and dimensions.
With this new imaging modality, enhanced spectral resolution can often compensate for sometimes limited MRI spatial resolution, still yielding unprecedented information about intra-voxel components, separated on the basis of their physical and chemical microenvironments. However, the exact nature and definition of these microenvironments is very important if one would like to provide biological interpretation. Specifically, the microenvironments that lead to distinct MR spectral components are not necessarily the classical, biological microenvironments one would refer to, such as intracellular and extracellular spaces. In other words, a more plausible interpretation of, eg, a low diffusivity component is low water mobility, which points to proximity to barriers or membranes, and not necessarily intracellular or extracellular water. This apparent discrepancy is not surprising and is not limited to multidimensional correlation MR but applies to all MR applications; the traditional biologically derived microenvironments (or compartments) do not align with the MR measurables because of the differences in length and temporal scales. Despite the caveat of the partial incompatibility of MR and biological microenvironments, being able to measure the former and infer the latter, as was shown by histological correlations15 and clinical diagnosis,86 is in essence the promise of multidimensional correlation MRI.
ACKNOWLEDGEMENTS
This work was supported by funds provided by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) (Grant No. ZIAHD000266), and the Center for Neuroregenerative Medicine (CNRM) under the auspices of the Henry Jackson Foundation (Grant No. 306135-2.01-60855).
REFERENCES
- 1.Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66(1):259–267. 10.1016/S0006-3495(94)80775-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Frank LR. Characterization of anisotropy in high angular resolution diffusion-weighted MRI. Magn Reson Med. 2002;47(6):1083–1099. 10.1002/mrm.10156 [DOI] [PubMed] [Google Scholar]
- 3.Shepherd TM, Ozarslan E, King MA, Mareci TH, Blackband SJ. Structural insights from high-resolution diffusion tensor imaging and tractography of the isolated rat hippocampus. Neuroimage. 2006;32(4):1499–1509. 10.1016/j.neuroimage.2006.04.210 [DOI] [PubMed] [Google Scholar]
- 4.Alexander DC, Hubbard PL, Hall MG, et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage. 2010;52(4):1374–1389. 10.1016/j.neuroimage.2010.05.043 [DOI] [PubMed] [Google Scholar]
- 5.Szczepankiewicz F, Lasič S, van Westen D, et al. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors. Neuroimage. 2015;104:241–252. 10.1016/j.neuroimage.2014.09.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Benjamini D, Komlosh ME, Holtzclaw LA, Nevo U, Basser PJ. White matter microstructure from nonparametric axon diameter distribution mapping. Neuroimage. 2016;135:333–344. 10.1016/j.neuroimage.2016.04.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Magin RL. Models of diffusion signal decay in magnetic resonance imaging: capturing complexity. Concepts Magn Reson a. 2016;45A(4):e21401. 10.1002/cmr.a.21401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Le Bihan D, Moonen CT, van Zijl PC, Pekar J, DesPres D. Measuring random microscopic motion of water in tissues with MR imaging: a cat brain study. J Comput Assist Tomogr. 1991;15(1):19–25. http://www.ncbi.nlm.nih.gov/pubmed/1987198 [DOI] [PubMed] [Google Scholar]
- 9.MacKay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med. 1994;31(6):673–677. 10.1002/mrm.1910310614 [DOI] [PubMed] [Google Scholar]
- 10.Harrison R, Bronskill MJ, Henkelman RM. Magnetization transfer and T2 relaxation components in tissue. Magn Reson Med. 1995;33(4):490–496. 10.1002/mrm.1910330406 [DOI] [PubMed] [Google Scholar]
- 11.Beaulieu C, Fenrich FR, Allen PS. Multicomponent water proton transverse relaxation and T2-discriminated water diffusion in myelinated and non-myelinated nerve. Magn Reson Imaging. 1998;16(10):1201–1210. [DOI] [PubMed] [Google Scholar]
- 12.Pfeuffer J, Provencher SW, Gruetter R. Water diffusion in rat brain in vivo as detected at very large b values is multicompartmental. Magn Reson Mater Phys Biol Med. 1999;8(2):98–108. 10.1007/BF02590526 [DOI] [PubMed] [Google Scholar]
- 13.Celik H, Bouhrara M, Reiter DA, Fishbein KW, Spencer RG. Stabilization of the inverse Laplace transform of multiexponential decay through introduction of a second dimension. J Magn Reson. 2013;236:134–139. 10.1016/j.jmr.2013.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Labadie C, Lee J-H, Rooney WD, et al. Myelin water mapping by spatially regularized longitudinal relaxographic imaging at high magnetic fields. Magn Reson Med. 2014;71(1):375–387. 10.1002/mrm.24670 [DOI] [PubMed] [Google Scholar]
- 15.Benjamini D, Basser PJ. Magnetic resonance microdynamic imaging reveals distinct tissue microenvironments. Neuroimage. 2017;163:183–196. 10.1016/j.neuroimage.2017.09.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Provencher SW. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comput Phys Commun. 1982;27(3):213–227. 10.1016/0010-4655(82)90173-4 [DOI] [Google Scholar]
- 17.Kroeker RM, Henkelman RM. Analysis of biological NMR relaxation data with continuous distributions of relaxation times. J Magn Reson. 1986;69(2):218–235. 10.1016/0022-2364(86)90074-0 [DOI] [Google Scholar]
- 18.Whittall KP, Mackay AL, Graeb DA, Nugent RA, Li DKB, Paty DW. In vivo measurement of distributions and water contents in normal human brain. Magn Reson Med. 1997;37(1):34–43. 10.1002/mrm.1910370107 [DOI] [PubMed] [Google Scholar]
- 19.Vavasour IM, Whittall KP, Mackay AL, Li DKB, Vorobeychik G, Paty DW. A comparison between magnetization transfer ratios and myelin water percentages in normals and multiple sclerosis patients. Magn Reson Med. 1998;40(5):763–768. 10.1002/mrm.1910400518 [DOI] [PubMed] [Google Scholar]
- 20.Moore GRW, Leung E, MacKay AL, et al. A pathology-MRI study of the short-T2 component in formalin-fixed multiple sclerosis brain. Neurology. 2000;55(10):1506–1510. 10.1212/WNL.55.10.1506 [DOI] [PubMed] [Google Scholar]
- 21.Flynn SW, Lang DJ, Mackay AL, et al. Abnormalities of myelination in schizophrenia detected in vivo with MRI, and post-mortem with analysis of oli-godendrocyte proteins. Mol Psychiatry. 2003;8(9):811–820. 10.1038/sj.mp.4001337 [DOI] [PubMed] [Google Scholar]
- 22.Ronen I, Moeller S, Ugurbil K, Kim D-S. Analysis of the distribution of diffusion coefficients in cat brain at 9.4 T using the inverse Laplace transformation. Magn Reson Imaging. 2006;24(1):61–68. 10.1016/j.mri.2005.10.023 [DOI] [PubMed] [Google Scholar]
- 23.Reiter DA, Lin P-C, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magn Reson Med. 2009;61(4):803–809. 10.1002/mrm.21926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vasilescu V, Katona E, Simplâceanu V, Demco D. Water compartments in the myelinated nerve. III Pulsed NMR Res Experientia. 1978;34(11):1443–1444. 10.1007/BF01932339 [DOI] [PubMed] [Google Scholar]
- 25.Menon RS, Allen PS. Application of continuous relaxation time distributions to the fitting of data from model systems and excised tissue. Magn Reson Med. 1991;20(2):214–227. 10.1002/mrm.1910200205 [DOI] [PubMed] [Google Scholar]
- 26.Menon RS, Rusinko MS, Allen PS. Proton relaxation studies of water compartmentalization in a model neurological system. Magn Reson Med. 1992;28(2):264–274. 10.1002/mrm.1910280208 [DOI] [PubMed] [Google Scholar]
- 27.Stewart WA, Mackay AL, Whittall KP, Moore GRW, Paty DW. Spin-spin relaxation in experimental allergic encephalomyelitis. Analysis of CPMG data using a non-linear least squares method and linear inverse theory. Magn Reson Med. 1993;29(6):767–775. 10.1002/mrm.1910290608 [DOI] [PubMed] [Google Scholar]
- 28.Webb S, Munro CA, Midha R, Stanisz GJ. Is multicomponent a good measure of myelin content in peripheral nerve? Magn Reson Med. 2003;49(4):638–645. 10.1002/mrm.10411 [DOI] [PubMed] [Google Scholar]
- 29.English AE, Whittall KP, Joy MLG, Henkelman RM. Quantitative two-dimensional time correlation relaxometry. Magn Reson Med. 1991;22(2):425–434. 10.1002/mrm.1910220250 [DOI] [PubMed] [Google Scholar]
- 30.Song Y-Q, Venkataramanan L, Hürlimann MD, Flaum M, Frulla P, Straley C. correlation spectra obtained using a fast two-dimensional Laplace inversion. J Magn Reson. 2002;154(2):261–268. 10.1006/jmre.2001.2474 [DOI] [PubMed] [Google Scholar]
- 31.Hürlimann MD, Venkataramanan L, Flaum C. The diffusion-spin relaxation time distribution function as an experimental probe to characterize fluid mixtures in porous media. J Chem Phys. 2002;117(22):10223. 10.1063/1.1518959 [DOI] [Google Scholar]
- 32.Hürlimann MD, Burcaw L, Song Y-Q. Quantitative characterization of food products by two-dimensional and distribution functions in a static gradient. J Colloid Interface Sci. 2006;297(1):303–311. 10.1016/j.jcis.2005.10.047 [DOI] [PubMed] [Google Scholar]
- 33.Callaghan P. Translational Dynamics and Magnetic Resonance: Principles of Pulsed Gradient Spin Echo NMR. Oxford University Press; 2011. [Google Scholar]
- 34.Benjamini D, Komlosh ME, Basser PJ. Imaging local diffusive dynamics using diffusion exchange spectroscopy MRI. Phys Rev Lett. 2017;118(15):158003. 10.1103/physrevlett.118.158003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bai R, Benjamini D, Cheng J, Basser PJ. Fast, accurate 2D-MR relaxation exchange spectroscopy (REXSY): beyond compressed sensing. J Chem Phys. 2016;145(15):154202. 10.1063/1.4964144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Haber-Pohlmeier S, Stapf S, van Dusschoten D, Pohlmeier A. Relaxation in a natural soil: comparison of relaxometric imaging, T1-T2 correlation and fast-field cycling NMR. Open Magn Reson J. 2010;3(1):57–62. 10.2174/1874769801003010057 [DOI] [Google Scholar]
- 37.McDonald PJ, Korb J-P, Mitchell J, Monteilhet L. Surface relaxation and chemical exchange in hydrating cement pastes: a two-dimensional NMR relaxation study. Phys Rev E. 2005;72(1):011409. 10.1103/physreve.72.011409 [DOI] [PubMed] [Google Scholar]
- 38.Casieri C, Terenzi C, De Luca F. Two-dimensional longitudinal and transverse relaxation time correlation as a low-resolution nuclear magnetic resonance characterization of ancient ceramics. J Appl Phys. 2009;105(3):034901. 10.1063/1.3072685 [DOI] [Google Scholar]
- 39.Weber D, Mitchell J, McGregor J, Gladden LF. Comparing strengths of surface interactions for reactants and solvents in porous catalysts using two-dimensional NMR relaxation correlations. J Phys Chem C. 2009;113(16):6610–6615. 10.1021/jp811246j [DOI] [Google Scholar]
- 40.Seland JG, Washburn KE, Anthonsen HW, Krane J. Correlations between diffusion, internal magnetic field gradients, and transverse relaxation in porous systems containing oil and water. Phys Rev E. 2004;70(5):051305. 10.1103/PhysRevE.70.051305 [DOI] [PubMed] [Google Scholar]
- 41.Silva MD, Helmer KG, Lee J-H, Han SS, Springer CS, Sotak CH. Deconvolution of compartmental water diffusion coefficients in yeast-cell suspensions using combined and diffusion measurements. J Magn Reson. 2002;156(1):52–63. 10.1006/jmre.2002.2527 [DOI] [PubMed] [Google Scholar]
- 42.Does MD, Beaulieu C, Allen PS, Snyder RE. Multi-component relaxation and magnetisation transfer in peripheral nerve. Magn Reson Imaging. 1998;16(9):1033–1041. 10.1016/S0730-725X(98)00139-8 [DOI] [PubMed] [Google Scholar]
- 43.Does MD, Gore JC. Compartmental study of and in rat brain and trigeminal nerve in vivo. Magn Reson Med. 2002;47(2):274–283. 10.1002/mrm.10060 [DOI] [PubMed] [Google Scholar]
- 44.Dortch RD, Apker GA, Valentine WM, Lai B, Does MD. Compartment-specific enhancement of white matter and nerve ex vivo using chromium. Magn Reson Med. 2010;64(3):688–697. 10.1002/mrm.22460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Travis AR, Does MD. Selective excitation of myelin water using inversion-recovery-based preparations. Magn Reson Med. 2005;54(3):743–747. 10.1002/mrm.20606 [DOI] [PubMed] [Google Scholar]
- 46.Callaghan PT, Furó I. Diffusion-diffusion correlation and exchange as a signature for local order and dynamics. J Chem Phys. 2004;120(8):4032. 10.1063/1.1642604 [DOI] [PubMed] [Google Scholar]
- 47.Zong F, Ancelet LR, Hermans IF, Galvosas P. Determining mean fractional anisotropy using DDCOSY: preliminary results in biological tissues. Magn Reson Chem. 2017;55(5):498–507. 10.1002/mrc.4492 [DOI] [PubMed] [Google Scholar]
- 48.de Almeida Martins JP, Topgaard D. Two-dimensional correlation of isotropic and directional diffusion using NMR. Phys Rev Lett. 2016;116(8):087601. 10.1103/physrevlett.116.087601 [DOI] [PubMed] [Google Scholar]
- 49.Topgaard D. Multidimensional diffusion MRI. J Magn Reson. 2017;275:98–113. 10.1016/j.jmr.2016.12.007 [DOI] [PubMed] [Google Scholar]
- 50.Hansen PC. The truncated SVD as a method for regularization. BIT Numer Math. 1987;27(4):534–553. 10.1007/bf01937276 [DOI] [Google Scholar]
- 51.Venkataramanan L, Song Y-Q, Hurlimann MD. Solving Fredholm integrals of the first kind with tensor product structure in 2 and 2.5 dimensions. IEEE Trans Signal Process. 2002;50(5):1017–1026. 10.1109/78.995059 [DOI] [Google Scholar]
- 52.Tikhonov A, Arsenin V. Solutions of Ill-Posed Problems. New York, NY: Winston; 1977. [Google Scholar]
- 53.Urbańczyk M, Bernin D, Koźmiński W, Kazimierczuk K. Iterative thresholding algorithm for multiexponential decay applied to PGSE NMR data. Anal Chem. 2013;85(3):1828–1833. 10.1021/ac3032004 [DOI] [PubMed] [Google Scholar]
- 54.Benjamini D, Basser PJ. Use of marginal distributions constrained optimization (MADCO) for accelerated 2D MRI relaxometry and diffusometry. J Magn Reson. 2016;271:40–45. 10.1016/j.jmr.2016.08.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Reci A, Sederman AJ, Gladden LF. Obtaining sparse distributions in 2D inverse problems. J Magn Reson. 2017;281:188–198. 10.1016/j.jmr.2017.05.010 [DOI] [PubMed] [Google Scholar]
- 56.Butler JP, Reeds JA, Dawson SV. Estimating solutions of first kind integral equations with nonnegative constraints and optimal smoothing. SIAM J Numer Anal. 1981;18(3):381–397. 10.1137/0718025 [DOI] [Google Scholar]
- 57.Miller K. Least squares methods for ill-posed problems with a prescribed bound. SIAM J Math Anal. 1970;1(1):52–75. 10.1137/0501006 [DOI] [Google Scholar]
- 58.Lawson CL, Hanson RJ. Solving Least Squares Problems. Englewood Cliffs, NJ: Prentice-Hall; 1974. 10.2307/2005340. [DOI] [Google Scholar]
- 59.Golub GH, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter. Dent Tech. 1979;21(2):215. 10.2307/1268518 [DOI] [Google Scholar]
- 60.Prange M, Song Y-Q. Quantifying uncertainty in NMR T2 spectra using Monte Carlo inversion. J Magn Reson. 2009;196:54–60. [DOI] [PubMed] [Google Scholar]
- 61.de Almeida Martins JP, Topgaard D. Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model-free investigations of heterogeneous anisotropic porous materials. Sci Rep. 2018;8(1):2488. 10.1038/s41598-018-19826-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Seland JG, Bruvold M, Brurok H, Jynge P, Krane J. Analyzing equilibrium water exchange between myocardial tissue compartments using dynamical two-dimensional correlation experiments combined with manganese-enhanced relaxography. Magn Reson Med. 2007;58(4):674–686. 10.1002/mrm.21323 [DOI] [PubMed] [Google Scholar]
- 63.Meiboom S, Gill D. Modified spin-echo method for measuring nuclear relaxation times. Rev Sci Instrum. 1958;29(8):688–691. 10.1063/1.1716296 [DOI] [Google Scholar]
- 64.Shellock FG. Radiofrequency energy-induced heating during MR procedures: a review. J Magn Reson Imaging. 2000;12(1):30–36. [DOI] [PubMed] [Google Scholar]
- 65.Hutter J, Slator PJ, Christiaens D, et al. Integrated and efficient diffusion-relaxometry using ZEBRA. Sci Rep. 2018;8(1):15138. 10.1038/s41598-018-33463-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Labadie C, Lee JH, Vetek G, Springer CS. Relaxographic imaging. J Magn Reson B. 1994;105(2):99–112. 10.1006/jmrb.1994.1109 [DOI] [PubMed] [Google Scholar]
- 67.Edzes HT, Samulski ET. The measurement of cross-relaxation effects in the proton NMR spin-lattice relaxation of water in biological systems: hydrated collagen and muscle. J Magn Reson. 1978;31(2):207–229. 10.1016/0022-2364(78)90185-3 [DOI] [Google Scholar]
- 68.Gochberg DF, Gore JC. Quantitative imaging of magnetization transfer using an inversion recovery sequence. Magn Reson Med. 2003;49(3):501–505. 10.1002/mrm.10386 [DOI] [PubMed] [Google Scholar]
- 69.Levesque IR, Chia CLL, Pike GB. Reproducibility of in vivo magnetic resonance imaging-based measurement of myelin water. J Magn Reson Imaging. 2010;32(1):60–68. 10.1002/jmri.22170 [DOI] [PubMed] [Google Scholar]
- 70.Benjamini D, Basser PJ. Water mobility spectral imaging of the spinal cord: parametrization of model-free Laplace MRI. Magn Reson Imaging. 2019;56:187–193. 10.1016/j.mri.2018.12.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Cloninger A, Czaja W, Bai R, Basser PJ. Solving 2D Fredholm integral from incomplete measurements using compressive sensing. SIAM J Imaging Sci. 2014;7(3):1775–1798. 10.1137/130932168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Candès EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math. 2009;9(6):717–772. 10.1007/s10208-009-9045-5 [DOI] [Google Scholar]
- 73.Bai R, Cloninger A, Czaja W, Basser PJ. Efficient 2D MRI relaxometry using compressed sensing. J Magn Reson. 2015;255:88–99. 10.1016/j.jmr.2015.04.002 [DOI] [PubMed] [Google Scholar]
- 74.Benjamini D, Basser PJ. Joint radius-length distribution as a measure of anisotropic pore eccentricity: an experimental and analytical framework. J Chem Phys. 2014;141(21):214202. 10.1063/1.4901134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Benjamini D, Basser PJ. Towards clinically feasible relaxation-diffusion correlation MRI using MADCO. Microporous Mesoporous Mater. 2018;269:93–96. 10.1016/j.micromeso.2017.02.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Jones CK, Whittall KP, MacKay AL. Robust myelin water quantification: averaging vs. spatial filtering. Magn Reson Med. 2003;50(1):206–209. 10.1002/mrm.10492 [DOI] [PubMed] [Google Scholar]
- 77.Hwang D, Du YP. Improved myelin water quantification using spatially regularized non-negative least squares algorithm. J Magn Reson Imaging. 2009;30(1):203–208. 10.1002/jmri.21783 [DOI] [PubMed] [Google Scholar]
- 78.Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP. Diffusion-relaxation correlation spectroscopic imaging: a multidimensional approach for probing microstructure. Magn Reson Med. 2017;78(6):2236–2249. 10.1002/mrm.26629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Slator PJ, Hutter J, Marinescu RV., et al. InSpect: INtegrated SPECTral component estimation and mapping for multi-contrast micro-structural MRI. In: Chung A, Gee J, Yushkevich P, Bao S, eds. Information Processing in Medical Imaging. IPMI 2019. Lecture Notes in Computer Science. Cham: Springer;2019:755–766. 10.1007/978-3-030-20351-1_59. [DOI] [Google Scholar]
- 80.Endres DM, Schindelin JE. A new metric for probability distributions. IEEE Trans Inf Theory. 2003;49(7):1858–1860. 10.1109/TIT.2003.813506 [DOI] [Google Scholar]
- 81.Kim JH, Tu T-W, Bayly PV, Song S-K. Impact speed does not determine severity of spinal cord injury in mice with fixed impact displacement. J Neurotrauma. 2009;26(8):1395–1404. 10.1089/neu.2008.0728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Whittall KP, MacKay AL. Quantitative interpretation of NMR relaxation data. J Magn Reson. 1989;84(1):134–152. 10.1016/0022-2364(89)90011-5 [DOI] [Google Scholar]
- 83.Peled S, Cory DG, Raymond SA, Kirschner DA, Jolesz FA. Water diffusion, T2, and compartmentation in frog sciatic nerve. Magn Reson Med. 1999;42(5):911–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.van Gelderen P, Jiang X, Duyn JH. Effects of magnetization transfer on contrast in human brain white matter. Neuroimage. 2016;128:85–95. 10.1016/j.neuroimage.2015.12.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Dula AN, Gochberg DF, Valentine HL, Valentine WM, Does MD. Multiexponential , magnetization transfer, and quantitative histology in white matter tracts of rat spinal cord. Magn Reson Med. 2010;63(4):902–909. 10.1002/mrm.22267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Slator PJ, Hutter J, Palombo M, et al. Combined diffusion-relaxometry MRI to identify dysfunction in the human placenta. Magn Reson Med. 2019;82(1):95–106. 10.1002/mrm.27733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Solomon E, Avni R, Hadas R, et al. Major mouse placental compartments revealed by diffusion-weighted MRI, contrast-enhanced MRI, and fluorescence imaging. Proc Natl Acad Sci U S A. 2014;111(28):10353–10358. 10.1073/pnas.1401695111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Sinding M, Peters DA, Frøkjaer JB, et al. Placental magnetic resonance imaging T2* measurements in normal pregnancies and in those complicated by fetal growth restriction. Ultrasound Obstet Gynecol. 2016;47(6):748–754. 10.1002/uog.14917 [DOI] [PubMed] [Google Scholar]
- 89.Sinding M, Peters DA, Poulsen SS, et al. Placental baseline conditions modulate the hyperoxic BOLD-MRI response. Placenta. 2018;61:17–23. 10.1016/j.placenta.2017.11.002 [DOI] [PubMed] [Google Scholar]


