Abstract

Hydraulic fracturing technology has been widely used in the tight reservoir reconstruction. Unfortunately, with the deepening of mining depth and the increase of geo-stress, the propagation mechanism of medium-pressure fractures in the reservoir is significantly different from that of conventional shallow reservoirs. Based on the combined finite discrete element method, this paper conducts numerical simulation research on deep tight sandstone reservoirs in the west. The discrete fracture network modeling method is used to establish a tight sandstone reservoir model with natural bedding, and the influence of geo-stress difference and natural fracture strength on hydraulic fracture propagation law in a high geo-stress environment is discussed in detail. The results show that the difference between geo-stress and the strength of natural fractures has a significant effect on the shape and expansion of hydraulic fractures under the high geo-stress conditions. The greater the difference in ground stress, the more obvious the tendency of the main fractures of the reservoir, and the shorter the branch fractures. With the increase of natural fracture strength, the changes in propagation pressure, fracture length, area, and width, which can be fitted with a linear function with a goodness of fit as high as 0.99. In addition, the morphological results of hydraulic fractures in the simulation are not only affected by the constitutive parameters of the model but also may be affected by the randomness of the natural fracture network, thus, showing a certain degree of dispersion. Therefore, it is extremely necessary to build a reservoir fracturing model in a specific area based on more detailed geological monitoring data to guide actual construction. The above achievements have certain reference significance for the field operation of deep tight sandstone reservoirs.
1. Introduction
Hydraulic fracturing technology, as an effective permeability enhancement technology for tight reservoirs, has been widely used to enhance the permeability of tight reservoirs, improve the oil and gas production of reservoirs, and achieve efficient and commercial development of tight oil and gas.1−5 Unfortunately, with the increase in mining depth, field monitoring has found that the lithology of deep tight sandstone reservoirs in western China is more complex, and there may be complex natural fractures in local areas.6−8 At the same time, the ground stress of deep reservoirs is greater, so the law of hydraulic fracture initiation and development in shallow reservoirs is no longer applicable, which brings great inconvenience to the efficient exploitation of deep tight sandstone reservoirs in the west.9−11 Therefore, it is extremely necessary to explore the effects of stress difference and natural fracture strength on hydraulic fracture propagation under high geo-stress conditions.
Limited by equipment size, funds, and other factors, numerical simulation technology is the main research means of reservoir-scale fracture propagation law.12−16 Predecessors have done a lot of research on the law of hydraulic fracture propagation and developed a series of numerical simulation methods including the finite element method, discrete element method, discrete element method based on the continuous medium, finite element discrete element method, boundary element, etc.1,15,17−23 These methods have their advantages and disadvantages. For example, the finite element method is relatively mature, and can accurately simulate the fracture propagation law in a single fracture and homogeneous reservoir. The particle flow dispersion element method assumes that the rock is composed of microparticles, which can more accurately depict the microparticle structure of reservoir rocks, but is not convenient for numerical simulation of reservoir scale.,7,24 By combining the characteristics of the finite element method and the discrete element method, the finite element discrete element method (FDEM) is developed. This method assumes that the reservoir rock is composed of smaller rock blocks and adjacent fracturing interfaces. It can not only describe the characteristics of natural fractures and mechanical heterogeneity of the reservoir in a more detailed way but is also more reasonable to use blocks to assume at different scales. Therefore, hydraulic fracturing simulations based on the finite element discrete element method have received more and more attention. For example, some scholars15,16,22,25−27 systematically studied the effects of different control mechanisms and different heterogeneous structures on the hydraulic fracture propagation of reservoir rocks by using the finite element discrete element method. However, the geo-stress environment commonly used in the existing simulation research is low geo-stress, so the existing laws may no longer apply to the prediction of hydraulic fracture propagation laws in deep tight sandstone reservoirs. At the same time, there may be distant natural fractures in deep tight sandstone reservoirs in western China, and their impact has not been revealed in existing simulation studies. Therefore, it is extremely necessary to carry out numerical simulation research on the hydraulic fracture propagation law of reservoirs with remote natural fractures by combining the finite element and discrete element method.
In this paper, based on discrete fracture network modeling, the geometric model of a fractured reservoir with a tendency bedding network is established. Subsequently, combined with the FDEM simulation method, a fracturing simulation model is constructed. Appropriate parameters are set according to the tight sandstone reservoir environment and construction conditions in the west. Then, the influence of geo-stress difference and natural fracture strength on the development of the geometric shape of the compression fractures in deep tight sandstone reservoirs under the influence of a high geo-stress environment is discussed.
2. Numerical Model
To explore the influence of the deep geo-stress environment and the natural fracture strength in the reservoir on the fracturing propagation process of the deep fractured sandstone reservoir. We introduce the interface element constitutive model and the numerical solution method used to simulate fracture propagation. Then, the construction method of the geometric model for simulating a fractured reservoir is described, and the finite discrete element model used in this study is constructed accordingly. Finally, according to the field investigation and experimental test results, the simulation parameters used in this simulation are determined.
2.1. Cohesive Element
The reservoir scale usually spans tens of meters. Therefore, if the particle flow dispersion element and other methods are used for numerical simulation, the particle size in the model may reach the decimeter level due to the limitation of simulation calculation efficiency, which is significantly different from reality. Therefore, it is more appropriate to assume that the reservoir is composed of discrete rock blocks and fracturing interfaces. Therefore, this article intends to carry out numerical research based on the FDEM simulation method. Based on the FDEM method, it is assumed that the reservoir is composed of rock block elements and zero thickness fracturing interface elements. Before the compression fracture extends, the fracture interface simulating the compression fracture obeys the linear elastic constitutive relation28,29
| 1 |
where σcoh is the stress matrix of the interface element, σcoh_n and σcoh_s represent the normal and tangential stresses of the interface element under two-dimensional conditions, respectively. Kcoh and εcoh are the stiffness matrix and strain matrix of interface element, respectively. It is worth noting that although the true thickness of the interface element for simulating fracturing is zero before fracturing, it is a constitutive thickness. The calculation of element stress and strain usually requires parameters, such as the shape and area of the element, while the cohesive element does not have a thickness. Therefore, it is necessary to define the constitutive thickness to achieve the calculation of tensile stress and strain. is required for the calculation of element stress and deformation in the simulation, which is set as T0. In this case, εcoh_n and εcoh_s in the above equation can be calculated by the following formula:
| 2 |
where dn is the normal displacement of representative interface element and ds is the tangential displacement of representative interface element.
When the hydraulic fractures extend forward, the interface element simulating the compression fracture will be damaged. The damage failure criterion of interface element is
| 3 |
where σn and 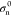 are the normal stress of the interface
element and the critical value when it breaks, σs and
are the normal stress of the interface
element and the critical value when it breaks, σs and 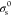 are the tangential stress of the interface
element and the critical value when it breaks. ⟨.⟩ indicates
that the compression failure of the interface element is ignored,
λ is the decision constant, and it is usually set between 1
and 1.05. After the interface element is damaged and destroyed, the
weakening of the element stiffness matrix is obtained by quantifying
the damage parameters so as to further simulate the subsequent damage
development. At this time, the elastic modulus of the interface element
after damage can be calculated through the damage variable (SDEG) d(30)
are the tangential stress of the interface
element and the critical value when it breaks. ⟨.⟩ indicates
that the compression failure of the interface element is ignored,
λ is the decision constant, and it is usually set between 1
and 1.05. After the interface element is damaged and destroyed, the
weakening of the element stiffness matrix is obtained by quantifying
the damage parameters so as to further simulate the subsequent damage
development. At this time, the elastic modulus of the interface element
after damage can be calculated through the damage variable (SDEG) d(30)
| 4 |
where 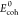 represents the elastic modulus of the interface
element before damage occurs, Ecoh represents
the elastic modulus of interface element after damage. The damage
variable d is controlled by displacement change,
so it can be calculated by the following formula:31
represents the elastic modulus of the interface
element before damage occurs, Ecoh represents
the elastic modulus of interface element after damage. The damage
variable d is controlled by displacement change,
so it can be calculated by the following formula:31
| 5 |
where 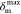 is the maximum displacement of interface
element during loading,
is the maximum displacement of interface
element during loading, 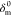 represents the displacement when the interface
element is damaged, and
represents the displacement when the interface
element is damaged, and 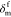 is the displacement when the interface
element is completely destroyed. The changes in the displacement of
the interface elements above correspond to the opening and propagation
of hydraulic fractures, respectively. The stress change of the fluid
pressure is mainly provided by fluid injection. At this time, the
fluid flow in the interface element simulating fracturing is given
by the following formula:15,32
is the displacement when the interface
element is completely destroyed. The changes in the displacement of
the interface elements above correspond to the opening and propagation
of hydraulic fractures, respectively. The stress change of the fluid
pressure is mainly provided by fluid injection. At this time, the
fluid flow in the interface element simulating fracturing is given
by the following formula:15,32
| 6 |
where w represents the actual thickness of the interface element, which is obtained through its displacement calculation. In the early stage of fracturing, the thickness of all the cohesive elements is zero. As the fracturing progresses, the cohesive elements undergo deformation and failure, resulting in a certain degree of opening. Therefore, the fluid flows through open interface elements. μ represents the viscosity of the fluid in the interface element. p represents the fluid pressure in interface element.
2.2. Method Validation
To determine the feasibility of the simulation method, the Khristinaovic–Geertsma–deKlerk (KGD) model was first used for comparative verification testing of theoretical solutions and simulation results. In the theoretical solution of the KGD model,33,34 the fracture length at time t is
| 7 |
where t [s] is the injection time; L(t) [m] denotes the hydraulic fracture length at time, t; Q [m2/s] is the applied constant injection rate; u [cp] is the Newtonian fluid viscosity; and E′ [GPa] represents the equivalent modulus of elasticity, which can be calculated by:
| 8 |
where v is the Poisson’s ratio.
The hydraulic fracture aperture near the injection point, w0(t), at time t is calculated as:
| 9 |
The simulation model settings used to compare theoretical solutions need to follow the assumptions of the theoretical solutions, so most of them are relatively uniform.15,16,29 Therefore, this section directly references the theoretical solutions of existing research to compare and verify the simulation model settings. Meanwhile, it is worth mentioning that the simulation results are highly susceptible to the influence of the simulation parameters. Therefore, this section directly selects the simulation parameters used in existing research26 for comparative testing of simulation methods, and the corresponding parameters are shown in Table 1.
Table 1. Main Parameters for KGD and Simulation Models.
| parameters | KGD model | simulation model |
|---|---|---|
| E (GPa) | 20 | 20 |
| v (dimensionless) | 0.22 | 0.22 |
| μ (cp) | 1 | 1 |
| Q (m2/s) | 1 × 10–4 | 1 × 10–4 |
| t (s) | 6 | 6 |
| cl (m/Pa·s) | - | 10–12 |
| σn0, σs0 (MPa) | - | 2, 6 |
| δmf (mm) | - | 0.001 |
Figure 1 shows the difference between the theoretical solution and the results of a more ideal simulation model. Obviously, the theoretical solution results are consistent with the simulation results. As time increases, both the total length of reservoir fractures and the aperture of injection point fractures show an increasing trend. Meanwhile, in the early stage of injection, the fracture aperture at the injection point rapidly increases, and then the rate of increase slows down. There are only slight differences between the simulation results and the theoretical results, which may be caused by factors such as the model mesh. Therefore, the simulation method selected in this article for the fracturing simulation is reliable.
Figure 1.
Comparison between the theoretical and numerical results in terms of (a) fracture length versus injection time and (b) fracture aperture versus injection time.
2.3. Simulation Model Setup
According to previous experimental research and outcrop observations, tight sandstone reservoirs in the west have a certain bedding tendency. Therefore, the influence of natural bedding on fracture propagation should be considered in the modeling. The natural fracture network with typical bedding characteristics generally consists of one or more groups of natural fractures with similar lengths and inclines. Therefore, based on the PYTHON language, the relevant natural fracture network modeling method and code are developed in ABAQUS. The main steps of building the geometric model of the fractured sandstone reservoir in this study are setting the attribute parameters of the random natural fracture network, mainly including the number of fracture groups, the density of fractures, the probability distribution density function that the fracture location, occurrence, and fracture length meet, and the corresponding parameters. The Monte Carlo method is used to generate a set of line segments that meet the preset distribution function. Each line segment represents a natural fracture, and then two end points of the line segment are recorded. The end points of the line segments in each fracture group are classified into a set. Using PYTHON language, preprocessing modeling is carried out in ABAQUS. First, a two-dimensional part is created, and then line segments are generated in the part area according to the presaved fracture end point data. Then, the generated line segments are used to partition the parts, and a set of fractures of the same occurrence is established in a set. Finally, the geometric model of the reservoir with bedding tendency fractures can be formed.
After on-site monitoring of tight sandstone, it was found that there is a certain distance between natural fractures and fracturing wells in the target block’s tight sandstone. Meanwhile, the density of natural fractures is relatively low, presenting a certain orthogonal distribution feature. Therefore, we explored the fracture propagation law of reservoirs with natural fractures in the peripheral area and without natural fractures in the central area. Then, based on the conventional cohesive element modeling process1,19,28 the specific conditions are as follows: (1) model size is 1000 × 100 m, the injection point is at the center of the model; (2) two groups of natural fractures are generated. The included angle between the first group of natural fractures and the x-axis is 30°, and the included angle between the second group of natural fractures and the x-axis is 150°. The length of the natural fractures is 0.9–1.2. The interval is 4–5 m. At the same time, delete the middle 40 m. The natural fractures within the 40 m area are used to simulate the situation that there are no natural fractures near the injection point. There are 335 natural fractures in the whole model. (3) The xdirection is the minimum horizontal principal stress direction, and the y-direction is the vertical principal stress direction. (4) After grid division, there are 34 896 rock block elements and 69 592 interface elements. (5) The outer boundary of the model is a fixed displacement and impermeable boundary condition. (6) The upper and lower boundaries constrain the y-direction displacement, and the left and right boundaries constrain the x-direction displacement. (7) Two injection points and initial fracture elements are set in the center. Then, the fracturing model formed according to the above model conditions is shown in Figure 2.
Figure 2.
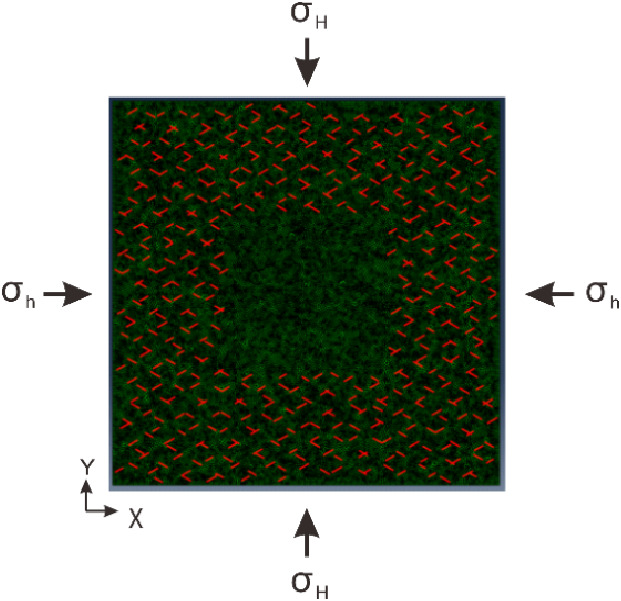
Schematic of the hydraulic fracturing model (1000 × 100 m).
To analyze the influence of different parameters on the hydraulic fracture growth behavior, it is necessary to carry out a sensitivity analysis on each parameter. Therefore, it is necessary to select a group of parameters as the benchmark example first and then change the corresponding parameters for subsequent sensitivity analysis. In the early experimental testing, it was found that Young’s modulus in the target area is between 18 and 23 GPa, the Poisson’s ratio is between 0.19 and 0.25, and the reservoir rock density is about 2600 kg/m3, with a porosity of about 0.1. Under high confining pressure conditions, there is a certain variation in the tensile strength of rocks, and the tensile strength under confining pressure conditions in this study is about 10 MPa. Meanwhile, the main injection flow rate during construction is 6 m3/min, and the fluid viscosity is about 5 mPa00b7s. In addition, we refer to the stratigraphic environment and previous construction parameters of tight sandstone reservoirs in the west. In the benchmark calculation example, the injection displacement is 6 m3/min, the injection duration is 100 s, and the difference between the overburden pressure and the minimum horizontal principal stress is 52 MPa. In addition, according to the effective stress principle proposed by Terzaghi,35 the total stress on any plane in saturated rock and soil can be divided into two parts: effective stress and pore water pressure, and the relationship between them always satisfies: σ = σ′ + u. When modeling is based on ABAQUS, the influence of pore pressure can be directly reduced using a super hydrostatic pressure system. Therefore, the simulation uses a super hydrostatic pressure system,1,28 and the stress conditions at the boundary are based on the effective stress. Based on the above results, the basic parameters used in the benchmark example are shown in Table 2.
Table 2. Main Parameters Used in the Simulation Models.
| input parameters | value |
|---|---|
| Young’s modulus (GPa) | 20 |
| Poisson’s ratio (dimensionless) | 0.22 |
| density (kg/m3) | 2600 |
| tensile strength of rock matrix (MPa) | 10 |
| permeability coefficient (m/s) | 1e-7 |
| porosity (dimensionless) | 0.1 |
| tensile strength of natural fractures (MPa) | 2 |
| critical damage displacement (m) | 0.001 |
| injection rate (m3/min) | 6 |
| fracturing fluid viscosity (mPa·s) | 5 |
3. Results and Discussions
Compared with conventional shallow reservoirs, deep reservoirs are characterized by high geo-stress at first. Under these conditions, there may be a significant difference between the reservoir fracturing mechanism and the conventional reservoir fracturing mechanism. To study the influence of geo-stress difference and natural fracture strength on pressure fracture propagation under a high geo-stress environment, the following results are obtained by adjusting the geo-stress parameters and natural fracture strength parameters based on the benchmark model, and then the pressure fracture propagation law is analyzed.
3.1. Influence of Geo-Stress Difference
By keeping the minimum horizontal principal stress (120 MPa) unchanged and increasing the maximum horizontal principal stress (120–152 MPa), we set the horizontal stress differences of 0, 6, 12, 24, and 32 MPa, and analyze the influence of different horizontal stress differences on the fracture propagation path and the complexity of the final hydraulic fracture. According to the aperture distribution of pressure fractures and the interaction diagram of natural fractures, dynamic changes in pressure fractures under different stress conditions can be observed. Based on this, the propagation process of pressure fractures and their interaction with natural fractures when the stress difference increases are analyzed.
Figure 3 shows the morphological results of artificial fractures at different times and their intersection with natural fractures when the horizontal stress difference is 0 MPa. As shown in Figure 3a, the fracturing fluid first flows from the fluid reservoir at the fluid injection point (central perforation position) and then generates a curved artificial fracture near the fracture initiation point. With the continuous injection of fluid, the bending and compression fractures appear as a local bifurcation. At a certain time, the compression fractures bifurcate and expand at the two ends of the bending fractures formed by the previous calculation result, forming two fractures (Figure 3b). It is worth noting that the natural fracture area in this model is in the periphery of the model area, while the location of the observed artificial bifurcated fracture appears near the junction of the area without natural fracture and the area with natural fracture. The results show that the bifurcation phenomenon of pressure fractures may be more common when the artificial fractures extend close to or in the natural fracture area. It can be seen from Figure 3c that only the three branch fractures formed in Figure 4b continue to extend. This phenomenon shows that the branch fractures formed in the fracturing process are affected by natural fractures, and there are two situations: sustainable expansion and unsustainable expansion. When the fluid is further injected, the branch fractures gradually connect with the natural fracture area and the intersection of artificial fractures and natural fractures occurs (Figure 3c), thus forming a fracturing network developed by artificial fracturing. The above phenomena show that under the condition of zero geo-stress difference, it is conducive to the formation of bending and branching multistage fracturing.
Figure 3.
Morphological results of artificial fractures at different times when the horizontal stress difference is 0 MPa and their intersection with natural fractures.
Figure 4.
Morphological results of artificial fractures at different times when the horizontal stress difference is 8 MPa and their intersection with natural fractures.
When the horizontal geo-stress difference increases to 6 MPa, it can be seen from Figures 3a and 4a that the hydraulic fracture tendency formed at the initial stage of fracturing is relatively close, and only the bending shape is different. With the continuous injection of fluid, the bifurcation position of the medium-pressure fracture in Figure 4b seems to be closer to the natural fracture area than that in Figure 3b. This phenomenon shows that under the combined effect of natural fractures and ground stress difference, there are certain differences in the initial stage of fracture propagation. With the increase of geo-stress difference, the bifurcated position of pressure fractures may be closer to the natural fracture area. Compared with Figure 4b,c, the branch fractures in the lower wing of Figure 4b gradually closed, and new branch fractures appeared in the lower wing of the subsequent expansion. Meanwhile, the branch fractures on the left side of the upper wing did not extend further. In addition, it can be seen from Figure 4d that when the artificial fracture extends to the natural fracture, it is not always able to communicate with the natural fracture due to the influence of the natural fracture location, dip angle, length, and strength. Therefore, it is extremely necessary to comprehensively consider the influence of natural fracture combination distribution factors in the study. To sum up, when the stress difference rises from 0 to 6 MPa, the branching phenomenon of pressure fractures occurs later, the lateral propagation range of pressure fractures is narrower, and the communication with natural fractures tends to decrease.
When the horizontal geo-stress increases to 16 MPa, it can be seen from the comparison of Figure 5 above that the hydraulic fracture tendency formed at the initial stage of fracturing is relatively close; only the bending shape is different. The bifurcations of the pressure fractures are obviously reduced; for example, two bifurcated fractures and four main bifurcated fractures appear in Figures 3 and 44. However, in Figure 5, there are only three branch main fractures. Meanwhile, Figure 5 shows that with the continuous injection of fluid, the fracturing fracture seems to be more inclined to expand along the dominant main fracture area, while some branch fractures do not appear to continue to expand. To sum up, with the increase of the geo-stress, the main fracture of the compression fracture expands more significantly, while the secondary fracture may not extend until it reaches a certain extent. This phenomenon significantly reduces the communication range of artificial fractures.
Figure 5.
Morphological results of artificial fractures at different times when the horizontal stress difference is 16 MPa and their intersection with natural fractures.
Continue to increase the horizontal geo-stress difference, as shown in Figure 6, the hydraulic geo-stress difference is increased to 24 MPa, and the main hydraulic fracture has approximately expanded along the direction of the maximum horizontal principal stress. At the initial stage of the expansion, the main fracture formed some small fractures (Figure 6b), and the fractures are gradually closed at the later stage of the expansion. The main hydraulic fractures intersect with several natural fractures in the process of expansion and fully or partially activate the natural fractures. Compared with the low-stress difference, the phenomenon that the main hydraulic fractures deflect and extend a certain distance along the natural fractures increases. In addition, although some short secondary fractures were formed around the hydraulic fractures in the early stage, branch fractures with a certain aperture could not be observed before the main hydraulic fractures extended to the boundary, and the branch fractures were closed. When the local stress difference further increases to 32 MPa, there is no visible bifurcation phenomenon in the fracturing fractures despite the communication between artificial fractures and natural fractures during the whole fracturing period. This phenomenon shows that when the local stress difference increases to a certain extent, the influence of the stress difference on fracture propagation will not be significant.
Figure 6.
Morphological results of artificial fractures at different times when the horizontal stress difference is 24 MPa and their intersection with natural fractures.
Figure 7 shows the difference in the artificial fracture morphological results at the final moment under different horizontal stress differences. The difference in the pressure fracture morphological results is not significant when the geo-stress difference is 24 and 32 MPa. Therefore, Figure 7 does not compare the situation when the ground stress difference is 24 MPa. It can be clearly seen from this figure that with the continuous increase of the geo-stress difference, the lateral propagation range of the pressure fracture decreases significantly. Therefore, when the local stress difference increases to 32 MPa, the pressure fracture is basically a curved, nonbifurcated main fracture. The above phenomena show that the geo-stress difference has a significant impact on the formation of pressure fractures. With the increase of the geo-stress difference, the lateral propagation range of pressure fractures is significantly reduced, thus showing a parallel phenomenon with the direction of the maximum horizontal geo-stress. Under the condition of a low-level ground stress difference, the branch joint has a certain scale. Under the condition of a high-level ground stress difference, the length of the branch joint formed is extremely short. The formation of a complex fracture network is indeed hindered by high-stress differences. Even in the stratum where fractures are developed, it is still difficult to form network fractures under the condition of a high-stress difference.
Figure 7.
Differences of artificial fracture morphological results at the final time under different horizontal stress differences.
The final value difference results of the conventional parameter change curve under different stress differences are extracted, as shown in Figure 8. It can be seen from this figure that, compared with the maximum value of the conventional parameter change curve, most of the final value difference results of the conventional parameter change curve show a significant negative correlation trend. The quantized curve equation fitted according to this equation is as follows:
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
Figure 8.
Differences of final value of conventional parameter change curve under different stress differences.
where P represents fluid pressure, L denotes fracture length, Wmax represents maximum fracture width, Wini is fracture aperture at injection point, S represents fracture area, and Rt is the tensile failure ratio.
3.2. Influence of Natural Fracture Strength
To further study the influence of fracturing fluid viscosity on fracturing fracture propagation, a fracturing simulation model was built with five parameters of natural fracture, namely, 2, 4, 6, 8, and 10 (MPa). Note that the other parameter conditions are consistent with those of the initial model. The obtained results of the artificial fracture morphology at different times under the influence of different natural fracture strengths and their intersection with natural fractures are shown in the figure below.
It can be seen from the above figure that there is a certain difference between the morphological results of pressure fractures when the natural fracture strength is 2 MPa and the morphological results of natural fractures when the tensile strength is 4, 6, 8, and 10 MPa. However, if only from the above morphological display results, the differences described above are not significant. This may be due to the dispersion of natural fractures in the model, and the distribution of natural fractures is far from the injection point. Therefore, in the process of fracturing, although fracturing has been communicated with natural fractures, it is not significantly affected by natural fractures. The phenomenon of passing through the middle area of the natural fractures occurs. Therefore, the maximum value of the conventional parameter quantization result is extracted, as shown in Figure 9.
Figure 9.
Results of artificial fracture morphology at different times under the influence of different natural fracture strengths and their intersection with natural fractures.
It can be seen from Figure 10 that with the increase of natural fracture strength, the difference in the final values of conventional parameters in the fracturing results is relatively significant. There is a positive correlation trend. Based on the above results, the fitting curve equation with a significant influence trend is extracted as follows:
| 16 |
| 17 |
| 18 |
| 19 |
Figure 10.
Difference of the final value of the conventional parameter change curve under different injection rates.
From the above formula, the maximum values of the maximum fracture width, injection point fracture width, compression fracture area, and tensile failure ratio have a significant positive correlation trend (goodness of fit is greater than 0.56). This phenomenon also confirms the previous conjecture: even if the natural fractures are relatively discrete, widely distributed, and far from the injection point, the artificial fractures penetrate the natural fracture area. In numerical value, the strength of natural fractures has a certain influence on the propagation of fracturing fractures. Among them, for the final fracturing results, the influence of natural fracture strength on the maximum fracture width, injection point fracture width, total fracture area, and tensile failure ratio of the fracturing fractures is also very significant. The corresponding quantitative results can be calculated using the above formula.
4. Conclusions
Based on numerical simulation technology, this paper aims to explore the fracture propagation law of tight sandstone reservoirs with natural fractures at the far end under the influence of differential geo-stress and natural fracture strength under the high geo-stress environment. Based on discrete fracture network modeling, the geometric model of a fractured reservoir with a natural bedding network is established, and combined with the FDEM simulation method, the fracturing simulation model is established, and appropriate parameters are set according to the environment and construction conditions of a tight sandstone reservoir in the west. The influence of the ground stress difference and the strength of natural fractures on the geometric shape of reservoir fractures are discussed. The main conclusions are as follows:
(1) The comparison results show that the geo-stress difference has a significant impact on the formation of pressure fractures. With the increase of the geo-stress difference, the lateral propagation range of pressure fractures is significantly reduced, thus showing a parallel phenomenon with the maximum horizontal geo-stress direction.
(2) Under the condition of low-level ground stress difference, the branch joint has a certain scale. Under the condition of high-level ground stress difference, the length of the branch joint formed is extremely short. Meanwhile, the formation of a complex fracture network is indeed hindered by high-stress differences. Even in the stratum where fractures are developed, it is still difficult to form network fractures under the high-stress difference conditions.
(3) In the quantitative rule, under the influence of ground stress and its difference, the quantitative parameters of conventional fracturing and field variables show a certain rule, which can be fitted by a linear function. The strength of natural fractures also has a significant impact on fracture propagation. Unfortunately, when the spatial and length distributions of natural fractures in the model are relatively discrete, it is subjective to use general qualitative analysis and it is difficult to accurately reveal their changing laws. Therefore, a quantitative analysis was carried out. The results show that under the influence of natural fracture strength, the variation law of some conventional quantitative parameters of fracturing shows a significant correlation, and some parameters can be fitted by a linear function with a goodness of fit of up to 0.99.
Acknowledgments
We wish to thank Dr. Mingyang Wu, State Key Laboratory of Geomechanics and Geotechnical Engineering, Wuhan Institute of Rock and Soil Mechanics, Chinese Academy of Science, for his help of this paper.
Data Availability Statement
The data underlying this study are not publicly available due to the confidentiality regulations for on-site data. The data are available from the corresponding author upon reasonable request.
The authors declare no competing financial interest.
References
- Cheng S.; et al. Numerical study of hydraulic fracturing near a wellbore using dual boundary element method. Int. J. Solids Struct. 2022, 239–240, 111479. 10.1016/j.ijsolstr.2022.111479. [DOI] [Google Scholar]
- Li Y.; et al. Optimization method of oriented perforation parameters improving uneven fractures initiation for horizontal well fracturing. Fuel 2023, 349, 128754. 10.1016/j.fuel.2023.128754. [DOI] [Google Scholar]
- Li Y.; et al. Thermo-hydro-mechanical coupling simulation for fracture propagation in CO2 fracturing based on phase-field model. Energy 2023, 284, 128629. 10.1016/j.energy.2023.128629. [DOI] [Google Scholar]
- Song R.; Liu J.; Cui M. A new method to reconstruct structured mesh model from micro-computed tomography images of porous media and its application. Int. J. Heat Mass Transfer 2017, 109, 705–715. 10.1016/j.ijheatmasstransfer.2017.02.053. [DOI] [Google Scholar]
- Song R.; et al. A Comprehensive Experimental Study on Mechanical Behavior, Microstructure and Transport Properties of 3D-printed Rock Analogs. Rock Mechanics And Rock Engineering 2020, 53, 5745–5765. 10.1007/s00603-020-02239-4. [DOI] [Google Scholar]
- Xie J.; et al. A 3-D hydraulic fracture propagation model applied for shale gas reservoirs with multiple bedding planes. Eng. Fract. Mech. 2020, 228, 106872. 10.1016/j.engfracmech.2020.106872. [DOI] [Google Scholar]
- Wu M.; et al. Comparative study on hydraulic fracturing using different discrete fracture network modeling: Insight from homogeneous to heterogeneity reservoirs. Eng. Fract. Mech. 2023, 284, 109274. 10.1016/j.engfracmech.2023.109274. [DOI] [Google Scholar]
- Liu Q.; et al. Complex wettability behavior triggering mechanism on imbibition: A model construction and comparative study based on analysis at multiple scales. Energy 2023, 275, 127434. 10.1016/j.energy.2023.127434. [DOI] [Google Scholar]
- Guo C.; et al. Experimental study and numerical simulation of hydraulic fracturing tight sandstone reservoirs. Fuel 2015, 159, 334–344. 10.1016/j.fuel.2015.06.057. [DOI] [Google Scholar]
- Song R.; et al. Study on the multiphase heat and mass transfer mechanism in the dissociation of methane hydrate in reconstructed real-shape porous sediments. Energy 2022, 254, 124421. 10.1016/j.energy.2022.124421. [DOI] [Google Scholar]
- Song R.; et al. 3D Printing of natural sandstone at pore scale and comparative analysis on micro-structure and single/two-phase flow properties. Energy 2022, 261, 125226. 10.1016/j.energy.2022.125322. [DOI] [Google Scholar]
- Jia L.; et al. Experimental study on propagation of hydraulic fracture in volcanic rocks using industrial CT technology. Pet. Explor. Dev. 2013, 40, 405–408. 10.1016/S1876-3804(13)60051-8. [DOI] [Google Scholar]
- Bohloli B.; de Pater C. J. Experimental study on hydraulic fracturing of soft rocks: Influence of fluid rheology and confining stress. J. Petrol. Sci. Eng. 2006, 53, 1–12. 10.1016/j.petrol.2006.01.009. [DOI] [Google Scholar]
- Liu C.; Zhang D.; Zhao H.; Li M.; Song Z.; et al. Experimental study on hydraulic fracturing properties of elliptical boreholes. Bull. Eng. Geol. Environ. 2022, 81, 18. 10.1007/s10064-021-02531-9. [DOI] [Google Scholar]
- Huang L.; et al. Exploring the influence of rock inherent heterogeneity and grain size on hydraulic fracturing using discrete element modeling. Int. J. Solids Struct. 2019, 176–177, 207–220. 10.1016/j.ijsolstr.2019.06.018. [DOI] [Google Scholar]
- Wu M.; et al. Influence of rock heterogeneity on hydraulic fracturing: A parametric study using the combined finite-discrete element method. Int. J. Solids Struct. 2022, 234–235, 111293. 10.1016/j.ijsolstr.2021.111293. [DOI] [Google Scholar]
- Liu Y.; et al. Numerical simulation of hydraulic fracturing-assisted depressurization development in hydrate bearing layers based on discrete fracture models. Energy 2023, 263, 126146. 10.1016/j.energy.2022.126146. [DOI] [Google Scholar]
- Pezzulli E.; et al. Finite element simulations of hydraulic fracturing: A comparison of algorithms for extracting the propagation velocity of the fracture. Eng. Fract. Mech. 2022, 274, 108783. 10.1016/j.engfracmech.2022.108783. [DOI] [Google Scholar]
- Wu M.; et al. The pixel crack reconstruction method: From fracture image to crack geological model for fracture evolution simulation. Constr. Build. Mater. 2021, 273, 121733. 10.1016/j.conbuildmat.2020.121733. [DOI] [Google Scholar]
- Zhang F.; et al. Discrete-Element-Method/Computational-Fluid-Dynamics Coupling Simulation of Proppant Embedment and Fracture Conductivity After Hydraulic Fracturing. Spe. J. 2017, 22, 632–644. 10.2118/185172-PA. [DOI] [Google Scholar]
- LI Y.; et al. A hydraulic fracture height mathematical model considering the influence of plastic region at fracture tip. Pet. Explor. Dev. 2020, 47, 184–195. 10.1016/S1876-3804(20)60017-9. [DOI] [Google Scholar]
- Huang L.; et al. Hydraulic fracture height growth in layered rocks: Perspective from DEM simulation of different propagation regimes. Int. J. Solids Struct. 2022, 238, 111395. 10.1016/j.ijsolstr.2021.111395. [DOI] [Google Scholar]
- Huang L.; Tan J.; Fu H.; Liu J.; Chen X.; Liao X.; Wang X.; Wang C.; et al. The non-plane initiation and propagation mechanism of multiple hydraulic fractures in tight reservoirs considering stress shadow effects. Eng. Fract. Mech. 2023, 292, 109570. 10.1016/j.engfracmech.2023.109570. [DOI] [Google Scholar]
- Munjiza A. A.The combined finite-discrete element method; John Wiley & Sons, 2004. [Google Scholar]
- Huang L.; et al. 3D lattice modeling of hydraulic fracture initiation and near-wellbore propagation for different perforation models. J. Pet. Sci. Eng. 2020, 191, 107169. 10.1016/j.petrol.2020.107169. [DOI] [Google Scholar]
- Wu M.; et al. Exploring the influence of heterogeneity on hydraulic fracturing based on the combined finite–discrete method. Eng. Fract. Mech. 2021, 252, 107835. 10.1016/j.engfracmech.2021.107835. [DOI] [Google Scholar]
- Zheng Y.; et al. Exploring the effect of engineering parameters on the penetration of hydraulic fractures through bedding planes in different propagation regimes. Computers and Geotechnics 2022, 146, 104736. 10.1016/j.compgeo.2022.104736. [DOI] [Google Scholar]
- Guo J.; et al. Numerical simulation of interaction of hydraulic fracture and natural fracture based on the cohesive zone finite element method. J. Nat. Gas Sci. Eng. 2015, 25, 180–188. 10.1016/j.jngse.2015.05.008. [DOI] [Google Scholar]
- Wu M. Y.; Zhang D. M.; Wang W. S.; Li M. H.; Liu S. M.; Lu J.; Gao H. Numerical simulation of hydraulic fracturing based on two-dimensional surface fracture morphology reconstruction and combined finite-discrete element method. J. Nat. Gas Sci. Eng. 2020, 82, 103479. 10.1016/j.jngse.2020.103479. [DOI] [Google Scholar]
- Dahi Taleghani A.; Gonzalez M.; Shojaei A. Overview of numerical models for interactions between hydraulic fractures and natural fractures: Challenges and limitations. Computers and Geotechnics 2016, 71, 361–368. 10.1016/j.compgeo.2015.09.009. [DOI] [Google Scholar]
- Dahi Taleghani A.; et al. Numerical simulation of hydraulic fracture propagation in naturally fractured formations using the cohesive zone model. J. Pet. Sci. Eng. 2018, 165, 42–57. 10.1016/j.petrol.2018.01.063. [DOI] [Google Scholar]
- Dontsov E. V. An approximate solution for a plane strain hydraulic fracture that accounts for fracture toughness, fluid viscosity, and leak-off. Int. J. Fract. 2017, 205, 221–237. 10.1007/s10704-017-0192-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yew C. H.; Weng X.. Chapter 1 - Fracturing of a wellbore and 2D fracture models. In Mechanics of Hydraulic Fracturing, 2nd ed.; Yew C.H.; Weng X.; Gulf Professional Publishing: Boston, 2015; pp. 1–22. [Google Scholar]
- Valko P.; Economides M.. Hydraulic Fracture Mechanics; Wiley, 1995. [Google Scholar]
- Terzaghi K.Stress Conditions for Failure in Soils. In Theoretical Soil Mechanics; John Wiley and Sons, 1943; pp. 7–25. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data underlying this study are not publicly available due to the confidentiality regulations for on-site data. The data are available from the corresponding author upon reasonable request.











