Intrinsic tensile ductility in strain hardening multiprincipal element metallic glass

Significance

The intrinsic ductility we have found offers fascinating insights from a purely scientific perspective. Unlike previous works, the strain hardening observed in our MPEMG (multiprincipal element metallic glass) originates from shear-induced elemental segregation and subsequent ordering. This unique mechanism allows us to surpass the 1% limit of tensile ductility encountered in previous rejuvenation methods. In traditional MGs, shear-induced dilation typically results in disordering, leading to strain softening and brittle fracture. However, our research demonstrates that shear-induced dilation can also be achieved via ordering in MPEMGs. This phenomenon facilitates strain hardening and tensile ductility, offering a promising pathway for designing strong and ductile MGs and other densely packed glasses, like high entropy ceramic glasses.

Abstract

Traditional metallic glasses (MGs), based on one or two principal elements, are notoriously known for their lack of tensile ductility at room temperature. Here, we developed a multiprincipal element MG (MPEMG), which exhibits a gigapascal yield strength, significant strain hardening that almost doubles its yield strength, and 2% uniform tensile ductility at room temperature. These remarkable properties stem from the heterogeneous amorphous structure of our MPEMG, which is composed of atoms with significant size mismatch but similar atomic fractions. In sharp contrast to traditional MGs, shear banding in our glass triggers local elemental segregation and subsequent ordering, which transforms shear softening to hardening, hence resulting in shear-band self-halting and extensive plastic flows. Our findings reveal a promising pathway to design stronger, more ductile glasses that can be applied in a wide range of technological fields.

MGs (metallic glasses) are a kind of important material whose applications span across different industries, from consumer products, automotive manufacturing (1), micro-electro-mechanical systems (2) to aerospace engineering (3), due to their desirable properties. For instance, Lai et al. (4) have successfully developed a series of Co-based MGs with remarkable properties, such as ultrahigh strength (~5 GPa) and distinct plastic deformation (0.8 to 5.1%) under compression. In addition to their high strength, MGs exhibit superior anticorrosion properties and can be utilized for the fabrication of superhydrophobic surfaces. These characteristics make MGs highly promising for applications in blood-contact devices within the field of biomedical engineering (5, 6). However, despite their technological significance (7–9), traditional MGs, which are based on one or two principal elements, are typically known for their lack of tensile ductility due to their inability to strain harden (10, 11). Shear banding has been extensively studied as the primary mechanism for accommodating plasticity in MGs. Brechtl et al. (12) conducted a systematic study on the effects of thermal annealing and strain rate on serrated flows induced by shear bands. Their findings revealed that both thermal annealing and high strain rate contribute to a more complex serrated flow behavior in MGs. This behavior can be attributed to the annihilation of soften-zone “defects” in the case of annealing, or the promotion of “defect” interactions at high strain rates. To address the limitation, numerous methods have been developed to alleviate tensile ductility (13, 14), such as thermomechanical treatments for deep glass rejuvenation (15). Although these methods have shown potential for improving tensile ductility at room temperature, reported results of intrinsic tensile ductility tend to be limited (<1%) with a low strain hardening capability and reduction in strength. Unlike conventional MGs, which are based on one and rarely two principal elements, MPEMGs comprise a number of principal elements. According to the confusion principle, viable crystallization could be interrupted because of the competition of multiple crystallization processes in a multiprincipal element alloy, hence leading to a stable metallic liquid and, ultimately, vitrification when supercooled. Meanwhile, utilizing the mixture rule, MPEMGs combine properties of each component, which provides an additional direction to solve the embrittlement of MGs. For example, Zhao et al. (16) designed MPEMGs with low modulus, resulting in T_g close to room temperature by mixing metals with low elastic modulus. The large ratio of ambient temperature to T_g successfully avoids shear bands under low strain rates, which results in high compression ductility at room temperature.

However, none of above studies solve the shear thinning of MGs, the essence of brittle failure. Here, we present a MPEMG with unique multifunctional properties, including high strength, remarkable strain hardening ability, and most importantly, 2% uniform tensile ductility at room temperature, which is about twofold of the previous records (~1%) obtained from the deeply rejuvenated MGs (17).

Results

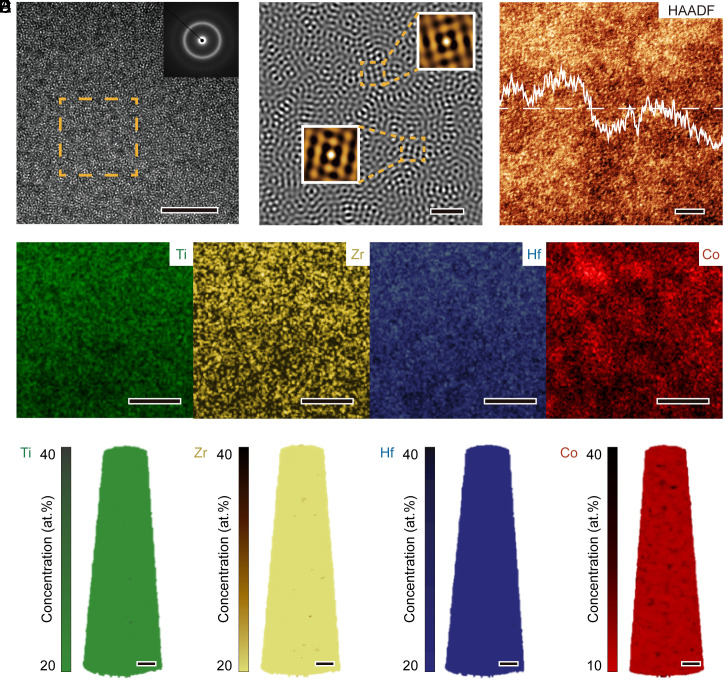
We prepared the quaternary alloy ribbon with the nominal composition of Ti₂₅Zr₂₅Hf₂₅Co₂₅ (in atomic percentage) via vacuum melt spinning (Materials and Methods). The atomic structure of the alloy was analyzed using X-ray diffraction (XRD) (SI Appendix, Fig. S1A) and transmission electron microscopy (TEM) (Fig. 1 A, Inset), which collectively confirmed the overall structural amorphousness. We utilized elemental energy-dispersive X-ray spectroscopy (EDS) to analyze the elemental distribution of our alloy, which exhibited microscale homogeneities with an overall composition of Ti_25.7Zr_24.9Hf_24.6Co_24.8 (SI Appendix, Fig. S1 B and C), closely aligning with the nominal composition of our alloy. Notably, unlike conventional MGs (18, 19), our alloy lacks a unique base element, which classifies it as MPEMG according to literature (20, 21). Moreover, our MPEMG comprises elements with significant size mismatch, consisting of three comparable large-sized elements (namely, Ti, Zr, and Hf) and one small-sized element (Co). Although the alloy is overall amorphous, a detailed examination of the atomic structure reveals crystal-like short-range ordering (Fig. 1 B, Inset). To mitigate any artifacts resulting from fast fourier transformation (FFT) filtering, we utilized FFT filters with varying widths to investigate the local atomic structure of our MPEMG (SI Appendix, Fig. S2). Remarkably, consistent results regarding the local atomic ordering were obtained, further reinforcing the reliability of our findings. Additionally, our alloy’s elemental distribution was analyzed using aberration-corrected high-angle annular dark field scanning TEM (HAADF-STEM), revealing a nanoscale nonuniform distribution as seen in Fig. 1C. In comparison to typical Zr-based MGs, as depicted in SI Appendix, Fig. S3, our MPEMG exhibits notable heterogeneities in both atomic structures and chemical distributions. Specifically, Co exhibits significant clustering at the nanoscale, whereas the other three elements have uniform distributions (Fig. 1D). To conduct a more thorough investigation, we employed three-dimensional atom probe tomography (APT) to examine the distribution of elements. The results demonstrate that while Ti, Zr, and Hf are distributed in a nearly random pattern, with a Pearson coefficient of less than 0.07 if fitted by the binomial distribution (see Fig. 1E and SI Appendix, Fig. S1D), Co shows noticeable clustering at the nanoscale, corresponding to a Pearson coefficient of 0.3 after data fitting.

Fig. 1.

Structure characterization of as-spun Ti₂₅Zr₂₅Hf₂₅Co₂₅ MPEMG. (A) The HRTEM and SAED pattern (Inset) of as-spun Ti₂₅Zr₂₅Hf₂₅Co₂₅. (B) The FFT-filtered image of the area selected from A (indicated by the dashed box). The Insets show the spatial autocorrelation of locally ordered structures marked by the dashed box. (C) The STEM-HAADF image of the as-spun Ti₂₅Zr₂₅Hf₂₅Co₂₅ ribbon. Note that the contrast represents Z contrast. The intensity of the Z contrast averaged over the whole image (dashed line) versus averaged over the pixels along each column (solid line). (D) The elemental mapping obtained by STEM-EDS. (E) The APT reconstruction map showing the nanoscale variations of the elemental concentration in the sample. [Scale bars, 5 nm (A, D, and E), 1 nm (B), and 2 nm (C).]

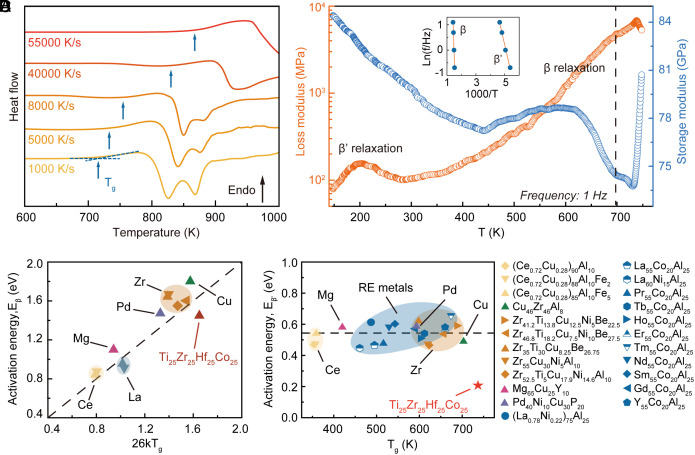
Differential scanning calorimetry (DSC) was performed on the Ti₂₅Zr₂₅Hf₂₅Co₂₅ MPEMG using various heating rates, as described in the Materials and Methods section. The DSC curves in Fig. 2A showed the glass transition signal only when the heating rate was 1,000 K/s or higher. In contrast, the corresponding DSC curves in SI Appendix, Fig. S4A revealed only the crystallization peaks when the heating rate was below 1,000 K/s. By fitting the detected glass transition temperatures (T_g) to the Vogel-Fulcher-Tamman relation (SI Appendix, Fig. S4B), T_g values were extracted for heating rates below 1,000 K/s (SI Appendix, Fig. S4A). For example, at a heating rate of 10 K/min, T_g was fitted to be 667 K, slightly higher than the corresponding crystallization temperature of 657 K. This suggests that crystallization may interrupt the glass transition for slow heating. Additionally, we calculated the fragility index (m) of our MPEMG from DSC data, which was found to be 153, much higher than conventional MGs (SI Appendix, Fig. S4C). As reported in ref. 22, a higher m value indicates that the supercooled liquid is more heterogeneous, which implies that the heterogeneous amorphous structure observed in Fig. 1 C–E may originate from the corresponding supercooled liquid (22).

Fig. 2.

Dynamic mechanical and thermal analyses of as-spun Ti₂₅Zr₂₅Hf₂₅Co₂₅ ribbon. (A) The flash DSC heat flow curves of the as-spun samples obtained when the heating rate varies between 1,000 K/s and 55,000 K/s. (B) The temperature dependence of storage modulus, E’ and loss modulus, E” at the driven frequency of 1 Hz. The Inset shows the Arrhenius plots of frequency versus 1/T (T = peak temperature) for the β relaxation and β’ relaxation. (C) The activation energy of β relaxation versus 26kT_g of Ti₂₅Zr₂₅Hf₂₅Co₂₅ ribbon compared with other MGs (23). (D) The plots of the activation energy, E_β’ versus glass transition temperature T_g for a variety of MGs (23).

We conducted a comprehensive isochronal dynamic mechanical analysis (DMA) on the Ti₂₅Zr₂₅Hf₂₅Co₂₅ MPEMG, revealing pronounced peaks on the loss modulus (E") curves between 140 K and 280 K, as shown in Fig. 2B and SI Appendix, Fig. S5A. This relaxation process, known as the fast relaxation process, has been observed in various MGs (23), and it is attributed to the presence of quenched-in “liquid-like” atoms (24). However, the intensity of the fast relaxation process in our MPEMG was unusually high (>130 MPa), which was much higher than those reported in the literature (23) (SI Appendix, Fig. S5B). At a temperature of ~670 K and a frequency of 1 Hz, we detected a β relaxation that appeared as a shoulder to the main α relaxation (SI Appendix, Fig. S5C). The activation energies of both relaxation processes were calculated following the literature (23, 25), with the β relaxation having an activation energy of 1.45 ± 0.1eV (SI Appendix, Fig. S5C), which was similar to that of conventional MGs (Fig. 2C) and around ~26 kT_g. The fast relaxation process, on the other hand, had an activation energy of 0.21 eV, less than half of that (~0.5 eV) reported for conventional MGs (23) (Fig. 2D). As the temperature increased, the α relaxation process emerged in our MPEMG, leading to a significant drop in the storage modulus (E'). However, when the temperature reached 700 K, the α relaxation process was interrupted, and the storage modulus (E') increased, indicating that ordering or even crystallization occurred in the middle of the glass transition. This observation was consistent with our DSC data.

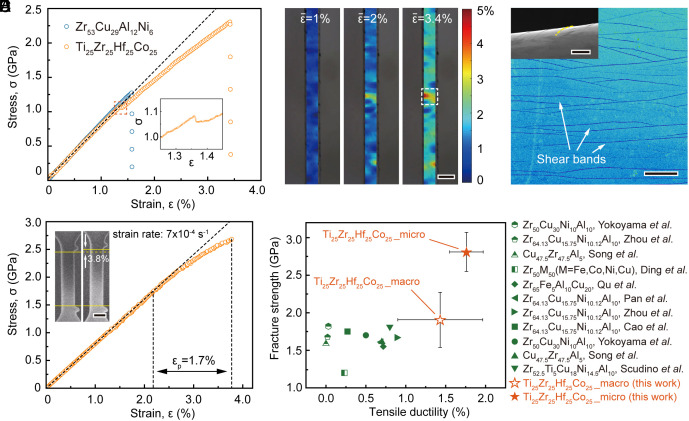
In this study, uniaxial tensile tests were conducted to investigate the mechanical properties of Ti₂₅Zr₂₅Hf₂₅Co₂₅ MPEMG. The as-spun ribbon was stretched at a constant strain rate of 10⁻⁴ s⁻¹, and the strain was measured using digital image correlation (DIC) analyses, as described in the Materials and Methods section. The resulting tensile stress–strain curve of the MPEMG demonstrated yielding at a stress of ~1.1 GPa, which corresponded to a sudden stress drop (Inset of Fig. 3A) but was followed by pronounced strain hardening and then fractured at the strength of ~2.3 GPa with a total plastic strain of 2.0% (Movie S1). This behavior is in sharp contrast with conventional MGs (26).

Fig. 3.

Multiscale mechanical characterization of as-spun Ti₂₅Zr₂₅Hf₂₅Co₂₅. (A) The stress–strain curves of Ti₂₅Zr₂₅Hf₂₅Co₂₅ and Zr₅₃Cu₂₉Al₁₂Ni₆ obtained via conventional tensile tests at the nominal strain rate of 1e-4 s⁻¹. The Inset shows the details of shear offset marked with rectangle. (B) The strain mappings in Ti₂₅Zr₂₅Hf₂₅Co₂₅ obtained by DIC at different overall or macroscopic strains. (C) The plan view of shear bands on the surface of the elongated Ti₂₅Zr₂₅Hf₂₅Co₂₅ obtained by SEM. The Inset shows the side view of the self-arresting shear bands. The dashed line indicates the position of one of the shear bands. (D) The typical stress–strain curve of Ti₂₅Zr₂₅Hf₂₅Co₂₅ obtained from in situ SEM micro tensile testing. The Insets show the photos of the Ti₂₅Zr₂₅Hf₂₅Co₂₅ microtensile sample before and after an elongation of 3.8%. (E) The plot of fracture strength versus tensile ductility of Ti₂₅Zr₂₅Hf₂₅Co₂₅ compared to other MGs obtained under uniaxial tensile loading (see SI Appendix, Table S1 for details). [Scale bars, 400 μm (B), 40 μm (C), 5 μm (the Inset of C), and 300 nm (the Inset of D).]

In extensive previous studies (27–29), similar tensile tests were conducted on various as-spun MG ribbons. However, these tests consistently resulted in brittle fractures without any observed plastic deformation. Our experimental results on conventional Zr-based MG ribbons align with these findings, as they also exhibited no plasticity and abrupt fracture upon yielding (Movie S2). During the single roller melt spinning, there exists a cooling rate gradient along the thickness of the ribbon, estimated to be on the order of 10⁶ K/s (30). This gradient can lead to variations in properties such as hardness and modulus. The length scale associated with this cooling rate gradient can be estimated as ~√D/η, where D represents the thermal diffusivity and η denotes the cooling rate (31, 32). In the case of crystalline metals, D ranges from 10⁻⁴ to 10⁻⁵ m²/s, yielding a length scale estimation of 10 μm. This estimation is consistent with experimental measurements conducted on crystalline ribbons (33, 34). However, for MGs, D is approximately 10⁻⁶ m²/s or even smaller (35), resulting in a length scale on the order of 1 μm or below. Considering that this length scale is significantly smaller than the ribbon’s thickness, we expect any potential gradient effect, if present, would likely be confined to the surface of the ribbon. To evaluate the possible influence of the cooling rate, we performed nanoindentation on the cross-section of our Ti₂₅Zr₂₅Hf₂₅Co₂₅ MG ribbon. As shown in SI Appendix, Fig. S6, there is no clear indication of hardness drop along the thickness direction. Additionally, we measured the nanoscale stiffness of the ribbon surface in contact with and away from the copper roller using amplitude-modulation atomic force microscopy (AM-AFM). As depicted in SI Appendix, Fig. S7, the local stiffness of both surfaces exhibits a similar distribution with comparable average values. These results collectively suggest that any cooling rate effect in our Ti₂₅Zr₂₅Hf₂₅Co₂₅ MG ribbon is negligible.

As reported by Li et al. (36), geometric imperfections, such as miscut and nonorthogonal geometry, have the potential to enhance the compressive plasticity of MGs through plasticity induced by local tilting and bending. Therefore, the observed increase in compressive plasticity can be attributed to a geometric effect rather than intrinsic material properties. Additionally, it is important to highlight that this geometric effect in compression does not result in strain hardening and typically leads to premature fracture under tension (37). This behavior stands in stark contrast to our MPEMG, which exhibits significant strain hardening under tension, regardless of any geometric imperfections. Although the use of structural heterogeneities has been proposed as a practical approach to enhance ductility and strain hardening in MGs under compression (38), it remains uncertain whether a similar strategy can be employed to improve tensile ductility in MGs with a physical mechanism, as demonstrated in our present study.

Our MPEMG also exhibited nonuniform strain distribution with strain concentrations near individual shear bands after yielding (Fig. 3B), and substantial shear bands were observed at the plastically deformed MPEMG surface (Fig. 3C). However, in contrast to conventional MGs (10), these shear bands observed in the MPEMG did not transverse through the alloy but instead halted after propagating approximately several hundred nanometers into the surface (the Inset of Fig. 3C). Plan views of the fractured MPEMG and Zr-based MG revealed shear bands near the fracture surface of the MPEMG but none near that of the Zr-based MG, indicating brittle fracture in the latter case (SI Appendix, Fig. S8 A and B). In addition, indentation tests on both alloys (Materials and Methods) revealed indentation pile-up in the Zr-based MG, which can be attributed to strain softening (39), but indentation sink-in in the MPEMG, suggesting plasticity strain hardening (40) (SI Appendix, Fig. S8 C and D). Meanwhile, SI Appendix, Fig. S9 compares the fracture surfaces observed on the cross-section of our MG with those of a conventional Zr-based MG. Both surfaces show typical vein patterns, a characteristic feature of fracture in amorphous alloys, indicating that the final fracture of our MG still occurs within an amorphous structure. However, the much finer and more complex vein patterns suggest that the final fracture in Ti₂₅Zr₂₅Hf₂₅Co₂₅ is preceded by a complex interaction of cracking and our amorphous structure.

Furthermore, we conducted in situ scanning electron microscopy (SEM) microtensile tests on our MPEMG, following the methodology described in reference (Materials and Methods) (41). The microtensile tests revealed that the MPEMG yielded at a stress of ~1.7 GPa, which was higher than the yield stress (~1.1 GPa) measured in the macroscale tests, possibly due to a sample size effect (42, 43). Consistent with the macroscale results, the microtensile tests showed that yielding in our MPEMG was followed by pronounced strain hardening before fracture at a plastic strain of 1.8% (SI Appendix, Fig. S10 A–E). To ensure data reproducibility, we performed multiple macro- and microscale tensile tests. As shown in Fig. 3E, our MPEMG outperformed conventional MGs that have been reported to exhibit detectable plasticity under uniaxial tension (SI Appendix, Table S1). Evidently, our MPEMG showed higher fracture strength with superior plasticity compared to other MGs.

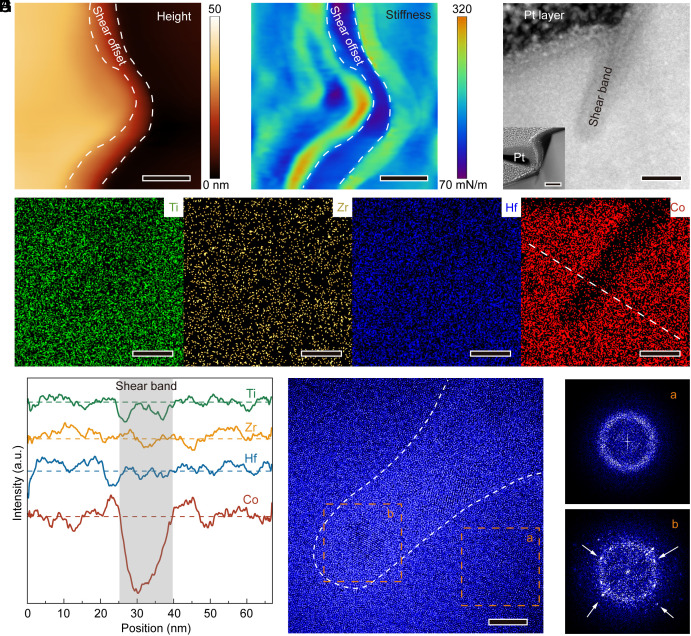
We performed comprehensive nanomechanical and structural analyses of the self-halting shear bands. As shown in Fig. 4 A and B, dual mode AFM (44) (Materials and Methods) was used to obtain height and stiffness images around a shear offset (i.e., a shear protrusion created by a shear band). In stark contrast to shear-band-induced softening reported for conventional MGs (10, 39), the local stiffness along the shear offset was significantly higher than that in other regions, indicating shear-induced hardening. According to the cross-sectional STEM-HADDF images (Fig. 4 C, Inset), Co was almost depleted in the shear banding region, while Hf, Ti, and Zr remained randomly distributed across the shear band (Fig. 4 D and E). Moreover, HRTEM inspection revealed significant local ordering and nano crystallization within the shear band (Fig. 4 F, Inset), while the atomic structure remained amorphous in other regions (Fig. 4 G and H). Co segregation was also observed in nanocrystals formed in our MPEMG subjected to isothermal annealing (Materials and Methods), as shown in SI Appendix, Fig. S11 A and B. Interestingly, different from the chemical distribution observed in the shear-induced nanocrystals, Ti segregation and Zr enrichment were observed in the annealing induced nanocrystals (SI Appendix, Fig. S11 C and D). Based on the local diffraction patterns, we could identify both FCC and HCP nanocrystals in the MPEMG after thermal annealing, while only HCP nanocrystals were found within shear bands (SI Appendix, Fig. S12 A–G). It is noteworthy that the lattice parameters of the shear-induced HCP nanocrystals (a = 0.34 ± 0.002 nm, c = 0.58 ± 0.016 nm) were about 13% larger than that of the annealing-induced HCP nanocrystals (a = 0.30 ± 0.003 nm, c = 0.54 ± 0.051 nm), as demonstrated in SI Appendix, Fig. S12 C and E.

Fig. 4.

The nanomechanical and electron microscopy imaging of the self-halting nano-sized shear bands in Ti₂₅Zr₂₅Hf₂₅Co₂₅. The height (A) and local stiffness (B) image of the surface of the deformed MG that contains the shear offset produced by a self-arresting shear band. (C) The cross-sectional HAADF image of the self-arresting shear band with an apparent thickness of ~17 nm in Ti₂₅Zr₂₅Hf₂₅Co₂₅ after tension. The Inset shows the entire shear offset of ~270 nm long. (D) The elemental mappings around the shear band obtained by STEM-EDS. (E) The elemental intensity profiles along the line that crosses the shear band in D. (F) The HRTEM image of the shear band with its outline indicated by the white dash line. (G and H) show the FFT of the local region (a) at the tip of the shear band and away from it (b), which are both marked by the dashed rectangles in F. The white arrows indicate bright points in the FFT image, which correspond to nanocrystals within the shear band. [Scale bar, 50 nm (A and B), 20 nm (C), 100 nm (the Inset of C), 15 nm (D), and 5 nm (F).]

To explore the atomic origins of shear-induced ordering in our MPEMG, we conducted comprehensive first-principles calculations and developed a neural network interatomic potential (NNAP) using deep learning techniques (45) (refer to Materials and Methods section and SI Appendix, Methods). This approach enabled us to perform large-scale molecular dynamics (MD) simulations. For our study, we constructed a series of atomic models with the general composition of (TiZrHf)_1-xCo_x with 0.06 < x < 0.4, to replicate the experimentally observed heterogeneous distribution of Co (Fig. 1E). One such model, as depicted in Fig. 5A, demonstrates a heterogeneous distribution of Co, ranging from 6 to 14%, and a uniform distribution of Ti, Zr, and Hf (see Materials and Methods for more details). By utilizing these atomic models, we initially investigated the activation energies associated with stress relaxation processes in the Ti–Zr–Hf–Co system, employing the activation-relaxation technique (46). Our simulations revealed that this alloy exhibited an average activation energy of approximately 0.2 eV for the fast relaxation process and around 1.5 eV for the secondary relaxation process (SI Appendix, Fig. S13 A and B, Properties). These values, obtained with Co concentrations ranging from 6% to 40%, align well with our DMA results (Fig. 2 B–D).

Fig. 5.

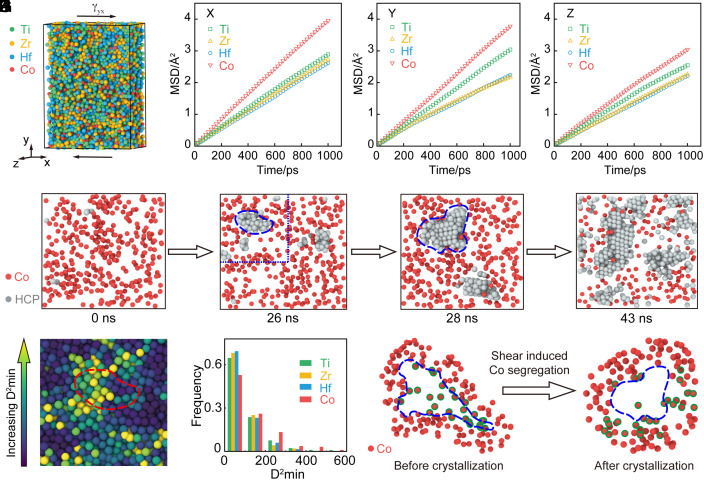
Understanding shear-induced elemental segregation and ordering in (TiZrHf)_1-xCo_x (0.06 < x < 0.4) with atomistic simulations. (A) Illustration of the MD model prepared for simple shear. (B–D) The mean squared displacement (MSD) of the constituent elements in the x, y, and z directions during shear. (green square = Ti, yellow triangle = Zr, blue circle = Hf, and red triangle = Co). (E–H) The shear-induced nucleation and growth of HCP nanocrystals (red spheres = Co, and gray spheres = HCP atoms. (I) The distribution of D² min value that corresponds to the region enclosed by the blue dash box in F. The red dashed line depicts the nucleation region in F. (J) The frequency plot of the D² min value for the constituent elements, normalized by the total number of each element. (K) Shear-induced segregation of Co out of the ordering region. The spheres with a green border represent the Co atoms diffusing out of the ordering region (blue dashed line).

We subsequently examined the plastic flow behavior of our model glass with Co concentrations ranging from 6 to 14%, corresponding to the Co lean regions identified in our MPEMG (Fig. 1E). Fig. 5 B–D illustrates the time-dependent average mean squared displacement of the constituent elements in three dimensions, derived from the MPEMG subject to the shear strain γ_yx. Interestingly, the Co element exhibited rapid diffusion in all three directions, followed by Ti, Zr, and Hf. Specifically, along the shearing direction, the movement of Co atoms was significantly faster than the other three elements. This resulted in pronounced shear-induced local ordering, a stark contrast to traditional MGs typically characterized by shear-induced disordering (47). In-depth structural analyses revealed that these local ordering regions were nanocrystals displaying HCP symmetry (Fig. 5 E–H) and were rich in Ti, Hf, and Zr (SI Appendix, Fig. S13C), which is reminiscent of our STEM observations (Fig. 4). Interestingly, the average atomic volume of the Voronoi cell increased from 20.2 ų to 21.6 ų after shear-induced crystallization, corresponding to a volume expansion of about 7%. Moreover, this local ordering correlates with large nonaffine displacements (Fig. 5I), with the most substantial contributions coming from Co atoms (Fig. 5J). According to our MD simulations, crystallization was preceded by the segregation of Co atoms away from the regions of nonaffine displacement (Fig. 5K and Movie S3). Furthermore, by following the method in ref. 48, we calculated the enthalpy of mixing between Co and TiZrHf in the Co_x(TiZrHf)_1-x system at 300 K, employing the Isothermal–isobaric (NPT) ensemble (SI Appendix, Properties). As depicted in SI Appendix, Fig. S21, the enthalpy of mixing between Co and TiZrHf at 300 K increases with the decreasing concentration of Co. Furthermore, we observed an increase in the degree of structural ordering within the simulation cell as the Co concentration decreases. This finding suggests a propensity for Co segregation in regions with low Co content, which may also serve as sites for crystal nucleation. Conversely, when the Co concentration exceeded 14%, we did not observe shear-induced crystallization in our model glass within the same simulation time. These results are significant, suggesting that shear-induced ordering can be attributed to the Co lean regions in our MPEMG.

Discussion

Generally, the plastic flow of amorphous materials is often accompanied by shear-induced dilation (49), a process indicative of shear-induced disordering in traditional MGs (10). However, under extreme conditions, such as nanoindentation-induced plasticity (50) or following a sudden, brittle-like fracture that causes a local temperature surge on the fracture plane (51), shear-induced local crystallization, typically linked to densification, has also been observed. According to the free volume theory (52), yielding in MGs occurs when the shear-induced excess free volume surpasses a critical threshold (53). Ref. 54 suggests that the excess free volume under compression is less than 10% of that under tension. From a thermodynamic perspective (55), this substantial excess free volume under tension can result in the formation of voids due to free volume condensation. Consequently, this will cause a sudden fracture upon yielding or lead to tensile brittleness.

Strain-induced ordering has long been recognized as an effective method to prevent void formation and impart tensile ductility to amorphous materials [e.g., spider silk (56), rubber (57)]. Stretching amorphous materials with a complex molecular structure can cause molecular reorientation, rotation, and/or even tangling, which can induce crystallization under tension. This is a critical toughening mechanism to develop strain-hardening amorphous materials with inherent ductility. While the presence of nanocrystals in shear bands has been observed in MGs under compression, such as Zr-based MGs (58–60), however, their occurrence during uniaxial tension accompanied by strain hardening has not been reported yet. One plausible explanation is that the accumulation of free volume is significantly higher under tension compared to compression, thereby creating favorable conditions for nucleation and growth of voids (61). Conventional MGs, which lack complex molecular structures, typically crystallize into a few lattice structures that cause local densification, a process geometrically incompatible with shear flows involving volume dilation. Interestingly, our MPEMG, due to its multiple principal elements, can crystallize into various intermediate lattices with a wide range of lattice volumes. SI Appendix, Fig. S13D displays the lattice volumes of crystals calculated using density functional theory (DFT) (Materials and Methods), which are all possible Ti–Zr–Hf–Co subsystems. Meanwhile, compared to the equiatomic composition, the unit cell volume of the crystals first increased with decreasing Co and then decreased as the atomic fraction of Ti reduced. These results are in line with our experimental observations (SI Appendix, Figs. S11 and S12), suggesting that shear-induced dilation in MPEMGs can be achieved via shear-induced ordering, therefore leading to strain hardening and tensile ductility.

In addition to the intrinsic tensile ductility resulting from shear-induced ordering, it is important to note that tensile ductility can be imparted to MGs through extrinsic methods. These include creating surface compressive stresses through short peening (13) or introducing geometric defects, such as holes (14) and pre-existing shear bands (62), which redirect and stabilize shear banding with enhanced local stress triaxiality. However, these postprocessing techniques often lead to a reduction of yield strength and negligible strain hardening in MGs, which differs fundamentally from the approach taken in our current study. Nonetheless, we anticipate that these postprocessing methods could be applied to our MPEMG to further enhance its tensile ductility. Moreover, using the cold joining method (63), we can fabricate bulk samples from MPEMG ribbons. Therefore, our current work, coupled with these previous results, offers a promising pathway for designing strong and ductile glasses that can be used in a broad range of technological fields.

In summary, we have successfully developed an MPEMG, specifically Ti₂₅Zr₂₅Hf₂₅Co₂₅, that exhibits remarkable multifunctional properties, including high yield strength, significant strain hardening, and room-temperature tensile ductility of up to 2%. These exceptional attributes can be attributed to the presence of highly mobile atoms that facilitate rapid atomic rearrangement and crystallization under shear banding. Consequently, shear softening is effectively transformed into shear hardening during shear banding. Notably, the dilated crystallization process, which aligns with shear-induced volume dilation, plays a pivotal role in preventing shear-induced void formation. This process further enhances the material’s flow stress and ductility. By overcoming the long-standing issue of room-temperature tensile brittleness in MGs, our strain-hardening MPEMG opens up transformative possibilities for a wide range of applications. These findings offer a promising pathway for the design and development of stronger and more ductile MGs, as well as other densely packed glassy materials.

Materials and Methods

Vacuum Melt Spinning.

The alloy ingots with the alloy composition of Ti₂₅Zr₂₅Hf₂₅Co₂₅ (at. %) were prepared by mixing molten pure metals in an Ar atmosphere at the pressure of 8 × 10⁻⁴ Pa. The purities of the raw materials for each element were at least 99.9 wt.%. The ingots were remelted at least five times to ensure chemical homogeneity. Ribbons were fabricated afterward using a single copper roller melt spinner at the rotating speed of 80 r/s and the working pressure of 8 × 10⁻⁴ Pa.

XRD.

The amorphous structure of our alloy was identified using XRD (Rigaku Smartlab) with a Cu target and an X-ray wavelength of 1.54059 Å. X-ray scanning was performed from 20° to 100° at a speed of 10° per minute.

STEM.

The HADDF-STEM observations were conducted on a JEM-ARM300F TEM equipped with double spherical aberration correctors. The TEM samples for STEM observation were prepared by a FEI SEM/focused-ion beam (SEM/FIB) system. At first, a 2-μm-thick Pt protection layer was deposited on the region of interest. Subsequently, a rectangular 12 μm × 1.5 μm × 8 μm lamina was carved and lifted out from the sample and mounted on a Mo grid. Both sides of the lamina were thinned alternatively at the tilt angle of ±1.2° at 30 kV until the lamina thickness was reduced to <100 nm. The lamina was then polished in two steps (i.e., with an ion beam of 48 pA at 5 kV and then with an ion beam of 27 pA at 2 kV).

SEM.

The microstructure characterization was carried out using a SEM (Quanta FEG 450) operating at 20 kV voltage. EDS was employed to study the chemical composition of our alloy, providing the actual composition of 25.7Ti-24.9Zr-24.6Hf-24.8Co (at. %).

3D APT.

To create the needle-shaped specimens required for APT, annular milling was performed in an FEI Scios-FIB/SEM. APT characterizations were then conducted using a local electrode atom probe (CAMEACA LEAP 5000 XR) at 70 K, in a voltage mode, with a pulse repetition rate of 200 kHz, a pulse fraction of 20%, and an evaporation detection rate of 0.2% atom per pulse. The AP Suite 6.1 workstation was utilized for 3D reconstructions and subsequent data analyses. The measured chemical composition of Ti_24.6Zr_26.1Hf_23.7Co_25.6 closely matched the nominal composition of our alloy and the EDS results.

DMA.

The experiments were carried out by applying a sinusoidal stress at the frequency of 0.5 Hz, 1 Hz, 2 Hz, and 3 Hz during continuous heating at the constant heating rate of 2 K/min. The samples had the dimension of 10 × 0.4 × 0.02 mm³. The complex modulus (G = G’ +iG”) was deduced from the cyclic stress–strain measurements, where G’ represented the storage modulus while G” the loss modulus. The loss factor $tan\delta =G^{″}/G^{\prime }$ was calculated based on the measured G’ and G”.

Flash DSC.

The ultrafast DSC experiments were performed on Ti₂₅Zr₂₅Hf₂₅Co₂₅ with the Flash DSC instrument (Flash DSC 2+, METTLER) over the temperature range from −70 °C to 1,000 °C with the heating rate ranging from 1,000 K/s to 55,000 K/s.

Regular Tensile Test.

The regular tensile tests were conducted on the mechanical tester (SEMtester 1000, MTI instruments) at the nominal strain rate of 10⁻⁴ s⁻¹. The tensile experiments were recorded using an optical microscope for strain analyses based on image correlation. Before tensile experiments, the tensile samples were decorated with a uniform speckle pattern to facilitate subsequent strain measurements.

DIC.

To perform image correlation and strain measurements, we utilized the open-source 2D DIC algorithm, Ncorr, based on MATLAB. Images were extracted from the recorded videos of our tensile experiments at a rate of one frame per second for strain analyses. We used experimental time as the intermediate variable to correlate the stress and strain measurements.

In Situ SEM Microtensile Test.

Quantitative tensile tests were performed with the Hysitron™ PI 85 PicoIndenter installed in the SEM (FEI Quanta™ 450FEG), which was operated at 15 kV. The in situ tensile tests were carried out at the nominal strain rate of 10⁻³ s⁻¹ to 10⁻⁴ s⁻¹.

Nanoindentation and AFM.

The hardness along thickness direction is measured by Nanoindentation (TI950, Bruker) using Berkovich tip. The tip area function is corrected on quartz. The loading time is 15 s with a maximum load of 8 mN. The tests were repeated 3 times on different samples to ensure data reliability.

The surface topography and stiffness of the sample were measured using an AFM (MFP-3D Infinity, Oxford Instruments) in the AM-frequency modulation mode. The calibrated spring constant for the silicon AFM tip was approximately 1.8 N/m, and the set point was set at 0.4 to ensure that the stiffness contrast was derived from a repulsive force between the tip and the sample or the viscoelasticity in the sample.

Isothermal Annealing.

Isothermal annealing experiments were performed with a tube furnace (OTF-1200X). Ti₂₅Zr₂₅Hf₂₅Co₂₅ ribbons were annealed at 793 K for 30 min in an Ar atmosphere.

DFT Calculations.

The Vienna ab initio simulation package (64) was used for all DFT calculations. The all-electron projector augmented wave (65) method was employed to describe the electron–nuclear interaction, while the Perdew–Burke–Ernzerhof (PBE) (66) exchange-correlation functional was used to account for electron–electron correlation energies under the generalized gradient approximation. A plane wave cutoff energy of 350 eV was utilized to expand the wave functions. Reciprocal space integrations of periodic structures were performed using a uniform K-point mesh with a spacing of 0.3 Å⁻¹, and a single Γ point was used otherwise. The DFT energy convergence criterion was set as 1 × 10⁻⁵ eV. All DFT calculations in this article use this set of parameters.

Artificial Neural Network Derived NNAP.

We used Spherical Chebyshev (SC) basis as the structural descriptor and selected the polynomial cut-off function. The parameters of the SC basis used for all elements: n_max = 4, l_max = 8, and cutoff r_c =7 Å. For each species, a four-hidden-layer NN architecture of 90 ×16 × 16 × 16 × 16 × 1 was employed, resulting in a total of 9,156 degrees of freedom. The activation function was set to the sigmoid linear unit (SiLU) function: SiLU (x) = x/(1 + e^−x). The L-BFGS-B (67) optimizer, implemented in our in-house NNAP code (68), was used for training, with a ℓ₂ -regularization factor of λ = 0.005 to reduce overfitting. The divergence of the rmse of testing set was 9.07 meV/atom. The precision testing and dataset component distribution of the NNAP were presented in SI Appendix, Methods.

MD Simulations.

NNP-MD simulations were performed by the large-scale atomic/molecular massively parallel simulator (LAMMPS) (69) package with the in-house LAMMPS-NNAP interface. The MD time step was set to 2 fs. Our prepared 40,912-atom glass sample possessed a gradient Co concentration, ranging from 6 to 14% and with an average of 10%. The sample was cooled down from 2,400 K to 300 K at a rate of 10¹³ K/s. Once the sample reached 300 K, the system was allowed to relax for 2 ns using the NPT ensemble, in which the temperature and pressure were controlled by the Nosé–Hoover and Parrinello–Rahman methods, respectively. Subsequently, we employed a shear rate of 10⁸s⁻¹ to shear the sample. The sample was fixed at the upper and lower ends in the y direction to simulate a rigid interface (set force and velocity zero). Throughout the shear flow simulation, we used the Lees–Edwards boundary conditions (70).

Supplementary Material

Appendix 01 (PDF)

Movie S1.

The regular tensile test of Ti₂₅Zr₂₅Hf₂₅Co₂₅ ribbon.

Movie S2.

The regular tensile test of Zr₅₃Cu₂₉Al₁₂Ni₆ ribbon.

Movie S3.

Diffusion of Co during shearing.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.