Disentangling sex-dependent effects of APOE on diverse trajectories of cognitive decline in Alzheimer’s disease

Abstract

Current diagnostic systems for Alzheimer’s disease (AD) rely upon clinical signs and symptoms, despite the fact that the multiplicity of clinical symptoms renders various neuropsychological assessments inadequate to reflect the underlying pathophysiological mechanisms. Since putative neuroimaging biomarkers play a crucial role in understanding the etiology of AD, we sought to stratify the diverse relationships between AD biomarkers and cognitive decline in the aging population and uncover risk factors contributing to the diversities in AD. To do so, we capitalized on a large amount of neuroimaging data from the ADNI study to examine the inflection points along the dynamic relationship between cognitive decline trajectories and whole-brain neuroimaging biomarkers, using a state-of-the-art statistical model of change point detection. Our findings indicated that the temporal relationship between AD biomarkers and cognitive decline may differ depending on the synergistic effect of genetic risk and biological sex. Specifically, tauopathy-PET biomarkers exhibit a more dynamic and age-dependent association with Mini-Mental State Examination scores (p < 0.05), with inflection points at 72, 78, and 83 years old, compared with amyloid-PET and neurodegeneration (cortical thickness from MRI) biomarkers. In the landscape of health disparities in AD, our analysis indicated that biological sex moderates the rate of cognitive decline associated with APOE4 genotype. Meanwhile, we found that higher education levels may moderate the effect of APOE4, acting as a marker of cognitive reserve.

1. Introduction

Alzheimer’s disease (AD) is defined by its underlying pathologic processes that can be measured in vivo by imaging biomarkers (Jack et al., 2018, 2013). The most commonly used imaging biomarkers in the research and clinic areas include amyloid β (Aβ) deposition, pathologic tau, and neurodegeneration (such as cortical thickness), which constitute the backbone of A-T-[N] research framework of AD (Jack et al., 2018). Since AD is clinically heterogeneous in both presentation and progression, converging evidence shows that the one-model-fits-all scenario has limited power to capture the complex relationship between imaging biomarkers and the clinical phenotypes that often demonstrate variable topographic distributions, progression rates, and perhaps underlying mechanisms (Anchisi et al., 2005; Dong et al., 2017b; Lam et al., 2013; Tatsuoka et al., 2013).

It is a common practice to disentangle the heterogeneous population into a set of sub-groups using the clustering technique (Chen et al., 2023; Mu et al., 2023, 2022; Wolk et al., 2009; Young et al., 2018), which stratifies the population based on subject-to-subject biomarker similarities. However, little attention has been paid to characterizing the temporal behavior where the contribution of AD biomarkers to cognitive decline might exhibit diverse trajectories in the long-time course of disease progression. We used the simulated data to demonstrate the importance of stratifying disease progression trajectories and its advantage over existing data clustering methods. As shown in Fig. 1 (bottom-left), a single linear regression model is limited to capturing the complex relationship between imaging phenotypes and the clinical outcome, where the red, purple, and black axes denote the imaging data, outcome score, and age, respectively. To disentangle the massive data heterogeneity, it is common to first cluster subjects into a set of sub-groups based on the imaging (or omics) phenotypes and then apply the statistical inference to each group separately. As shown in Fig. 1 (top-left), the statistical power of the current two-step approach is still not strong enough even applying the non-linear statistical model to the stratified groups. Indeed, the problem is rooted in the gap between population stratification and statistical inference, where the subject-to-subject similarity (drives data clustering) does not necessarily align with the brain-to-phenotype relationship. Since the clinical outcome information is not used in the clustering step, the sub-optimal stratification result is responsible for the underpower issue of statistical analysis. In this regard, it is of high demand to investigate the temporal behaviors of the brain-to-phenotype relationship. As shown in the bottom-right of Fig. 1, the two-stage stratification has significantly improved linear regression performance by jointly detecting the transition of the relationship and applying statistical inference.

Fig. 1.

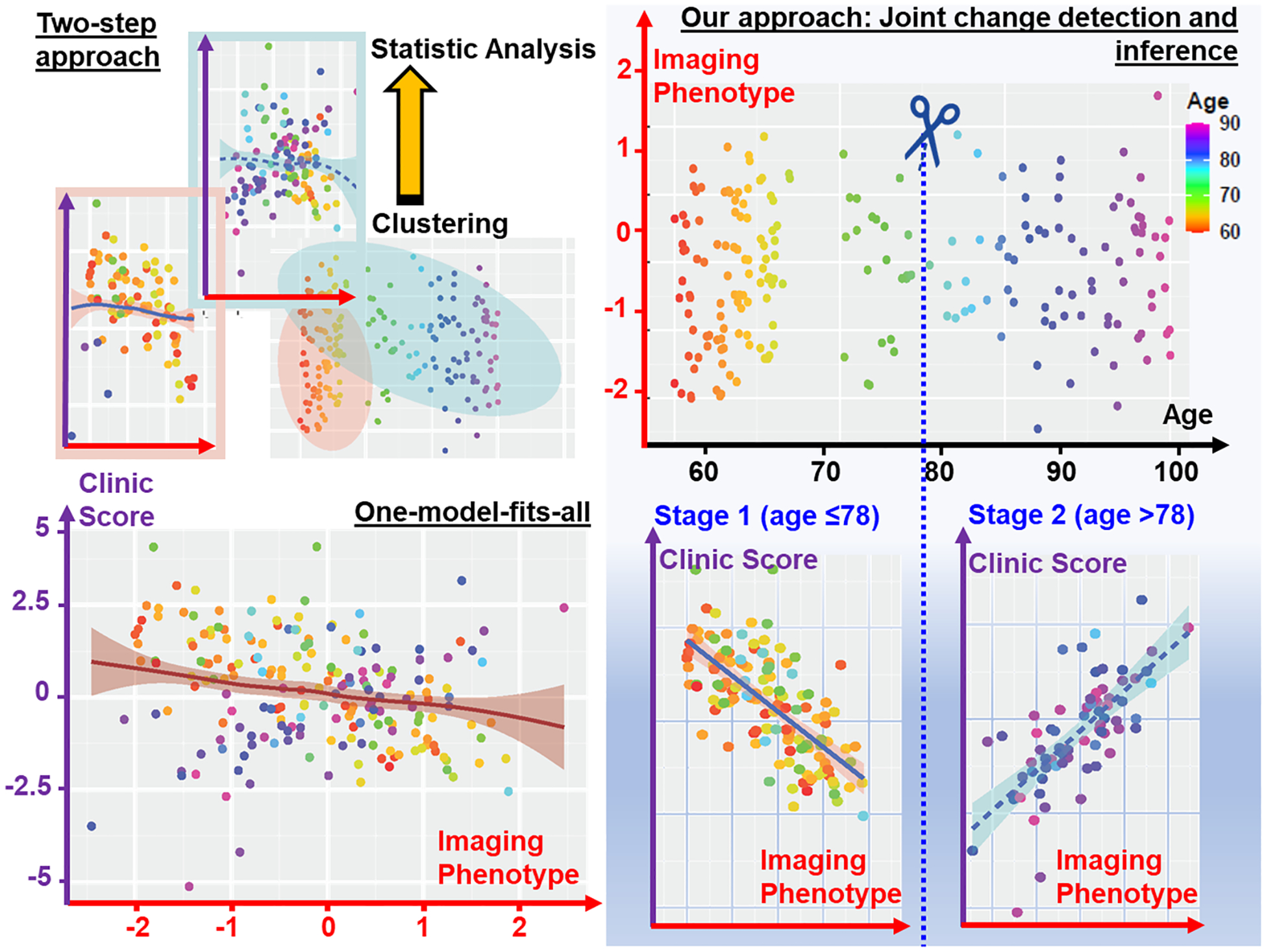
Current two-step approach (top-left) vs our joint change detection and statistical inference (bottom-right). The distribution of simulated data was shown in top-right, where applying a global regression model on the whole data (bottom-left) does not have the statistical power to model the relationship between imaging phenotype and clinical outcomes. Since current two-step approaches applied clustering and statistical analysis separately, the clustering result might be sub-optimal for statistical inference. Our method disentangled the heterogeneity of temporal behavior (i.e., the relationship between imaging phenotype and clinical outcome) and thus yielded significantly higher statistical power in understanding the factors behind the clinical outcomes.

In light of this, we sought to uncover the multi-stage mechanism of the A-T-[N] framework by capturing the critical fluctuation (change point) of the biomarker-to-outcome relationship as the cognitive status progressively declines. The concept of our change point detection (CPD) model is shown in Fig. 2, which is designed to detect possible changing points in the relationship between imaging biomarkers (between A, T, [N] biomarkers) and MMSE (mini-mental state examination) score (Arevalo-Rodriguez et al., 2015), where biological sex, APOE4 status, and education level are included as additional covariates in the model. Thus, under the hood of change point detection, our statistical inference model was essentially a spatial-temporal clustering approach on high-dimension neuroimaging biomarkers with a statistical guarantee on the effect size and significance of data-driven findings.

Fig. 2.

Our statistical model identified change points, sorted by age, by examining the latent piecewise linear relationship between regional AD biomarkers and clinical outcomes. Using the results from temporal stratification, we were able to explore how biological sex and education level dynamically contribute to modifying the impact of APOE4 on cognitive decline across multiple stages of AD progression.

We would like to highlight that the identified change points are not predetermined but are detected using a data-driven process, implemented within our hypothesis testing framework for change point detection. Our CPD model was specifically crafted to pinpoint critical change points in the progression of AD. These change points were characterized by shifts in the relationship between clinical scores and brain imaging along the age of candidates, which in turn signal different stages of AD (Ma et al., 2022). In particular, for each AD biomarker, we first tested whether the change point exists and whether multiple change points exist. Next, we projected the detected change point to the chronic age axis, which allows us to stratify the diverse progression of AD into a set of distinct stages. On top of identified change points in the progression of AD, we put the spotlight on the multi-factorial mechanism of AD risk disparities (such as biological sex and APOE4 status) that contributes to diverse incidence and prevalence of AD. At each identified change point, we investigated the relationship between AD biomarkers and clinical assessment before and after the change point, stratified by males and females, by APOE carriers and non-carriers, and by high-education and low-education, respectively. The secondary analysis was to repeat the main analysis with respect to memory-specific and executive-function-specific composite scores separately.

The output of our analysis provided a novel insight into the diversities and disparities in AD, where the stratified progression stages allow us to disentangle the heterogeneities in AD. Since presymptomatic or early symptomatic interventions may ultimately constitute the best long-term therapeutic strategy, the disentangled temporal behavior of cognitive decline offers a new window to manage the priority of risk factors more effectively in AD treatment.

Relevant works.

Since AD is a multi-factorial disease (Iqbal and Grundke-Iqbal, 2010), the extant literature supports that there are multiple factors (such as demographic data, genetic risks, and lifestyles) contributing to the heterogeneous trajectories of cognitive decline. In this regard, various clustering approaches have been employed to identify latent sub-groups based on the distribution of neuroimaging data (Dong et al., 2016; Hwang et al., 2016; Jack et al., 2016; Noh et al., 2014). For example, K-median clustering analysis on [¹⁸F]AV-1451 tau-PET data was used to determine how AD subjects vary in the relative involvement of the entorhinal cortex and neocortex (Whitwell et al., 2018), where three subtypes were reported likely corresponding to the postmortem subtypes. Semi-supervised machine learning methods (Dong et al., 2017a) have been applied to Alzheimer’s Disease Neuroimaging Initiative (ADNI) data to elucidate the heterogeneity of neuroanatomical differences between subjects with mild cognitive impairment (MCI), AD, and cognitively normal (CN) individuals, with the focus on establishing neuroanatomical and neuropathological (e.g. amyloid and tau deposition) dimensions in AD and its prodromal stages. Despite the fact that the disease progression in AD often involves dynamic interaction between genetic determinants and environmental exposures (Dunn et al., 2019; Eid et al., 2019; Elbaz et al., 2007), current clustering-based methods have not taken varying progression rates among AD patients into consideration.

Recently, event-based statistical modeling has come to the stage to characterize the progression of AD, which models the transition from normal to abnormal using a set of predefined events (Firth et al., 2020). Such an event-based strategy has been extended to model a more flexible piecewise linear function as well as multiple trajectories for quantifying the progression heterogeneity in AD (Vogel et al., 2021; Young et al., 2018). Despite a plethora of ways to model the trajectory, current methods often rely on some assumptions about the form of the trajectory function. More critically, longitudinal data with event changes (such as conversion from CN to MCI) are required to infer the parameters in the event-based models. Thus, a limited number of longitudinal data might undermine the potential of event-based approaches in clinical applications. In contrast, our CPD method was designed to characterize the temporal trajectory of neurodegeneration, at a population level, using cross-sectional neuroimages.

Our CPD method effectively modeled the relationship between AD biomarkers and clinical scores using a linear regression model. In low-dimensional settings where the number of covariates is fewer than the number of observations, change point, and segmentation inference are well-established (Chan et al., 2014; Jin et al., 2013; Maidstone et al., 2017). However, the challenge arises in AD analysis, where data exhibit a high-dimensional structure where the number of biomarkers is larger than the number of observations. In such scenarios, traditional low-dimensional methods were computationally infeasible. Despite recent advancements in high-dimensional change point detection, as explored by (Lee et al., 2016; Zhang et al., 2015), our work presented distinct benefits and differences. Firstly, while existing methods mainly concentrate on estimating the positions of change points, our approach focused on change point inference. This was achieved by employing bootstrap techniques to maintain the Type I error rate at any given significance level. Therefore, the detected change points have fewer false positives compared to others without statistical inference. Secondly, our CPD method, enhanced with binary segmentation techniques, was adept at detecting and identifying multiple change points in the regression function. Specifically, once we detected the first significant change point, the algorithm then iteratively examined each half of the data before and after that change point. In each iteration, it looked for evidence of other significant changes in the relationship between clinical scores and AD biomarkers. If a potential change point was detected in a segment, that segment was further divided into two, and the process was repeated for multiple change point detection. This aspect was particularly crucial for modeling the multi-stage neurodegeneration characteristic of AD, setting our method apart in its application and efficacy in AD research.

2. Participants

The data used in our study were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (www.ida.loni.usc. edu). ADNI enrolls participants between the ages of 55 and 90 who are recruited at 57 sites in the United States and Canada. After obtaining informed consent, participants undergo a series of initial tests that are repeated at intervals over subsequent years, including clinical evaluation, neuropsychological tests, genetic testing, lumbar puncture, and MRI and PET scans. There were four phases of the ADNI study (ADNI1, ADNI-GO, ADNI2, and ADNI3). Some participants were carried forward from previous phases for continued monitoring, while new participants were added with each phase to further investigate the progression of Alzheimer’s disease.

The ADNI data used in this work consisted of neuroimaging biomarkers, CSF biomarkers, genetics data, demographic data, clinical outcomes, and socioeconomic status. Table 1 summarized the data statistics. Specifically, we collapsed the APOE genotype into two sub-groups: (1) subjects carrying any ε4 alleles (homozygous ε4/ε4 and heterozygous ε4/−) and (2) subjects with no ε4 risk alleles (−/−). Hence, the APOE genotype served as a binary variable in our study (carrier and non-carrier). We adopted the CSF p-tau/Aβ₄₂ ratio (Campbell et al., 2021) as the CSF hallmark in the following analysis, where higher CSF tau/Aβ₄₂ indicated a higher risk of developing AD.

Table 1.

Demographic characteristics of participants in amyloid, tau, and FDG change point detection.

		Amyloid (N=1071)	Tau (N=245)	FDG (N=1360)
Age	Mean (SD)	75.2 (7.64)	78.3 (6.99)	74.5 (7.41)
	Median [Min, Max]	75.4 [55.2, 96.6]	78.4 [61.4, 94.5]	74.7 [55.2, 95.8]
Biological Sex	Male	578 (54.0 %)	138 (56.3 %)	752 (55.3 %)
	Female	493 (46.0 %)	107 (43.7 %)	608 (44.7 %)
Memory Composite Score	Mean (SD)	0.331 (1.018)	0.522 (0.888)	0.274 (0.962)
	Median [Min, Max]	0.423 [−2.86, 3.14]	0.580 [−2.39, 2.72]	0.331 [−2.86, 3.20]
EF Composite Score	Mean (SD)	0.258 (1.127)	0.566 (1.057)	0.187 (1.098)
	Median [Min, Max]	0.309 [−3.31, 2.99]	0.565 [−2.72, 2.99]	0.238 [−3.06, 2.99]
Education (Years)	Mean (SD)	16.222 (2.671)	16.523 (2.651)	16.026 (2.764)
	Median [Min, Max]	16 [6, 20]	16 [6, 20]	16 [6, 20]
APOE4 Status	Non-Carrier	600 (56.0 %)	152 (62.0 %)	740 (54.4 %)
	Carrier	471 (44.0 %)	93 (38.0 %)	620 (45.6 %)
AD Stage	CN-SMC	376 (35.1 %)	126 (51.4 %)	439 (32.3 %)
	EMCI	298 (27.8 %)	68 (27.8 %)	301 (22.1 %)
	LMCI-AD	397 (37.1 %)	51 (20.8 %)	620 (45.6 %)

Regarding neuroimaging data, we followed the Destrieux atlas (Destrieux et al., 2010) and used our in-house analytic pipeline based on FreeSurfer (Fischl, 2012). Major image processing steps included (1) noise reduction and bias correction on T1-weighted MRI, (2) skull striping, (3) tissue segmentation, (4) cortical surface reconstruction, (5) spatial image alignment which warps the atlas as well as the corresponding label information to the underlying subject space. The output was a whole-brain parcellation that includes 148 cortical regions and 12 sub-cortical structures. After that, we registered PET image to the T1-weighted MR image. Based on the Destrieux parcellation, we calculated regional Standard Uptake Value Ratio (SUVR) from amyloid, tau, and FDG-PET scans and obtained the whole-brain A, T, [N] imaging biomarkers, respectively, which were normalized by using the whole cerebellum as the reference region.

In addition to MMSE score, ADNI provided various neuropsychological batteries. Specifically, we put the spotlight on the effect of AD-related pathology on memory decline (MEM) and executive function (EF) decline, respectively, by following the calculation methods in (Crane et al., 2012; Gibbons et al., 2012). Specifically, MEM score was a weighted average of Rey Auditory Verbal Learning Text (RAVLT, 2 versions), AD assessment Schedule – Cognition (ADAS-Cog, 3 versions), MMSE, and Logical Memory data (Crane et al., 2012). EF score was a weighted average of EF indicators from two secondary domains (Category Fluency items and Clock Drawing items), which included (1) counts in a pre-specified time span (Category Fluency, WAIS-R Digit Symbol), (2) times to completion (Trails), (3) number of items completed correctly (Digit Span Backwards), and (4) dichotomous correct/incorrect (clock drawing) (Gibbons et al., 2012).

3. Methods

Ethics statement.

We have obtained the necessary permission and approval to access and use ADNI data. Data are publicly and freely available from the http://adni.loni.usc.edu/data-samples/access-data/ Institutional Data Access / Ethics Committee (contact via http://adni.loni.usc.edu/data-samples/access-data/) upon sending a request that includes the proposed analysis and the named lead investigator. More details can be found about the ADNI project and data acquisition and sharing policies and protocol as follows: Data sharing policy and data access process: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_DSP_Policy.pdf; ADNI steering committee and list of acknowledgement for publications using ADNI repository: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf; ADNI protocol and ethics statement: http://adni.loni.usc.edu/wp-content/themes/freshnews-dev-v2/documents/clinical/ADNI-2_Protocol.pdf.

Principle of change point detection.

The primary goal of our CPD methodology was to identify the latent transition points, indicating shifts in the multi-stage progression of relationships between biomarkers and clinical outcomes. By stratifying subjects temporally (e.g., by age), our CPD method sought to statistically test the significance of these temporal transitions in relation to the aforementioned relationships. Specifically, let ${\left(Y_i,X_i\right)}_{i=1}^N$ be N chronically ordered independent realizations of (Y, X) by another variable Z, such as age. We employed a linear regression model $Y_i=X_i^T\beta +{\epsilon }_i$ to fit the relationships between p-dimensional biomarker data X_i and clinical outcome Y_i. Here, β represented the p-dimensional unknown vector of coefficients, and ε_i was the error term. Our objective was to test whether the regression coefficients β that describe the regression plane of Y ~ X has a change point among the observations. Let β⁽¹⁾ and β⁽²⁾ be two p-dimensional vectors of coefficients. We considered the following linear regression model with a potential change point:

$$\begin{array}{ll}{Y}_i=X_i^T{\beta }^{\left(1\right)}+{\epsilon }_i,\hfill & \text{if} Z_i\le a*;\hfill \end{array}$$

$$\begin{array}{ll}{Y}_i=X_i^T{\beta }^{\left(2\right)}+{\epsilon }_i,\hfill & \text{if} Z_i>a*.\hfill \end{array}$$

Here, a* represented the position of the change point on the range of Z. If Z was specified as the ages of subjects, then for those subjects that were younger than a*, the relationship between Y ~ X was characterized by β⁽¹⁾, while for subjects that elder than a*, the relationship was captured by β⁽²⁾. In this case, a* served as the critical change point that we aim to detect, marking a significant transition in the biomarker-to-outcome relationship. This change was crucial to detect in the context of AD progression.

Our CPD model aimed to identify and estimate this specific time point where there was a significant shift between the regression models before and after that moment. We considered the following hypothesis testing framework:

$$H_0:{\beta }^{(1)}={\beta }^{(2)}\text{\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}a,\text{\hspace{0.17em}v.s.}$$

$$H_1:{\beta }^{(1)}\ne {\beta }^{(2)}\text{\hspace{0.17em}for\hspace{0.17em}specific\hspace{0.17em}}a*.$$

In other words, under H₀, the regression coefficients were homogeneous across all observations, while under H₁, there was a change point at an unknown time point a*, resulting a sudden shift in regression coefficients after a*. By conducting statistical inference based on the above hypothesis testing framework, our CPD model can provide a p-value using bootstrap to describe the significant level of the detected change point (van de Geer et al., 2014). A significant p-value leaded to the rejection of null hypothesis, thereby supporting the existence of a change point. Then, our second goal was to estimate the change point location when we concluded the existence of the change point. By adopting the hypothesis testing framework, one of the advantages of our approach was the reduced risk of detecting false positives in change points, making the methodology more robust and reliable for applications in clinical research.

Integrated solution of change point detection.

The methodology of our CPD model was structured into four main steps, enabling the identification of significant transition points in the progression of relationships:

Step 1: High Dimensional Regression Analysis.

We started by discretizing the time domain into n segments. For each potential cut point, de-biased lasso estimators were computed to model the relationship before and after the cut point. This step was crucial in setting the groundwork for identifying possible transition points in the data.

Step 2: Change point detection.

We employed an argmax-based change point estimator (Liu et al., In press). This involved synthesizing information from various potential change point locations. The underlying rationale was that the largest discrepancy in model coefficients should manifest at the actual transition point, indicating a significant shift in the data.

Step 3: Bootstrap.

Bootstrap techniques were then utilized to assess the significance of the statistics obtained from the previous step. This analysis yielded a p-value, which was critical for the hypothesis testing process. It helped in determining the statistical significance of the identified change points.

Step 4: Multiple change point detection.

Finally, our model incorporated a refitting step combined with a binary segmentation technique, an approach conducive for detecting multiple change points (Fryzlewicz, 2014). This recursive process involved iteratively examining each data segment pre and post the initial change point. If subsequent significant change points were detected within a segment, the segment was further split, and the process was reiterated. This iterative approach was particularly adept at unraveling the multifaceted stages of AD progression.

If the p-values for each binary split were significant, the CPD algorithm outputs the precise locations of the change points along with regression estimations for each identified time period. This comprehensive detection mechanism offers a nuanced understanding of the multiple stages in AD progression (Liu et al., 2021, 2022; Liu et al., 2020), which is pivotal for informed clinical decision-making and targeted therapeutic interventions (Liu et al., 2021, 2022; Liu et al., 2020).

4. Results

In this section, we delved into the results of our AD analysis. We started with simulation studies that served as a precursor to real data application. In Section 4.1, we designed the simulation settings to replicate the complexities of AD analysis, served as a critical preliminary test for our CPD method. The primary objective here was to evaluate the robustness and sensitivity of the method. These simulations yielded promising outcomes, showcasing the method’s effectiveness in accurately identifying and locating change points, which demonstrated a testament to its potential in analyzing AD degeneration.

With this strong simulation-based foundation, we transited to real data analysis in the subsequent sections. Here, we applied our CPD method to key AD biomarkers: A, T, and [N]. In Section 4.2, we spotlighted a significant revelation: the Tau biomarker was more sensitive than A and [N] in monitoring cognitive decline. This critical finding, marked by the detection of multiple significant change points in Tau linked to AD degeneration, naturally shifted our analytical focus toward Tau in the following analysis.

Progressing to Sections 4.3 and 4.4, we focused on interpreting the changes detected by the Tau biomarker at each identified change point in AD progression. This exploration was enriched by considering important biomarkers, such as biological sex and APOE4 status. These factors were crucial, as they offered insights into the biomarkers’ differential impacts across diverse individual’s profiles. Further broadening our analysis in Section 4.5, we incorporated socioeconomic factors, such as education level, into our study. This inclusion acknowledged the potential influence of social determinants on the progression of AD, adding depth to our understanding of AD progression.

Finally, in Section 4.6, we confronted the multifaceted nature of cognitive decline in AD. By dissecting the global MMSE score into Memory (MEM) and Executive Functioning (EF) composite scores, we strived to disentangle the complex, time-dependent interactions between AT[N] biomarkers and these specific cognitive domains. The analysis on splitting the MMSE score not only provided insights on the varied clinical presentations of AD but also enhanced our comprehension of its progression.

4.1. Sensitivity and robust analysis

To test the stability and robustness of our CPD method, we conducted the following comprehensive simulation studies. These studies were designed to encapsulate three distinct cases: (1) No change point case; (2) Single change point detection; (3) Multiple change point detection. For the design matrix X, we generated i.i.d X_i that followed multivariate normal distribution N(0, Σ) where $\sum ={\left(\sigma \right)}_{i,j=1}^p$ and σ_i,j = 0.5^|i–j|. The error terms ε_i’s were i.i.d. generated from standard normal distributions. To mimic the real data, we chose age as the sorting variable Z, represented in years, and generated it from a truncated normal distribution N(75, 10) within the interval [50, 100]. In the regression model, the first five covariates were assigned with non-zero coefficients, while the coefficients of the remaining p – 5 covariates were set to zero. These non-zero coefficients were independently and identically drawn from a uniform distribution U(0, 2).

In the no change point case, we maintained a uniform regression function across all observations, characterized by a single set of regression coefficients β⁽¹⁾. For the single change point case, the true regression function was designed to change for subjects older than 75 years old. We added a signal jump $\delta =\sqrt{\frac{log\left(p\right)}{n}}$ to the 5 non-zero covariates of β⁽¹⁾ to generate β⁽²⁾. For the multiple change point case, we considered three change points at ages 70, 75, and 80 years old. The above three change points divided the data into four segments, each with distinct regression coefficientsβ⁽¹⁾, β⁽²⁾, β⁽³⁾, and β⁽⁴⁾. At each change point, a signal jump $\delta =\sqrt{\frac{log\left(p\right)}{n}}$ was introduced to the non-zero covariates, ensuring a systematic shift in the dataset’s underlying structure. This underlying structure of regression model tended to mimic the multi-stage degeneration of AD.

For tuning parameter selection of de-biased lasso in Step 1 of our CPD method, we applied 5-fold cross-validation using mean square error as the evaluation metric. To assess the method’s robustness and sensitivity, we varied the sample size from 500 to 1000 and increased the dimension of covariates from 100 to 200. The number of bootstrap replications for statistical inference was set at B = 100, with a significance level of 0.05. All numerical results in above three cases were based on 50 replications. Our hypothesis testing aimed to demonstrate that (1) no significant change point should be detected in the first case, (2) a single significant change point close to the age of 75 should be detected in the second case, and (3) three significant change points around 70, 75, and 80 years should be detected in the third case.

As shown in Table 2, for the no change point case, nearly all combinations of sample size and covariate dimensions yielded non-significant p-values, indicating a low risk of false positives for change point detection. In the single change point case, significant p-values (0.00) were consistently returned, with the estimated change point closely approximating 75 years and exhibiting small standard errors, affirming our method’s accuracy even when we reduced sample sizes to 500 and increased dimensions to 200. Fig. 3 showcased the density plots for the detected change points across multiple scenarios. Notably, the plots featured three distinct peaks, each corresponding to the true change points identified at ages 70, 75, and 80. This clear delineation of peaks at the specific ages reinforced the accuracy of our CPD method in pinpointing the precise moments of transition in the regression function. Even under conditions of smaller sample sizes and higher dimensions, our method successfully identified these change points with a probability. This consistent detection of key transition ages in the plots underscored the robustness and reliability of our CPD approach, particularly in its capability to detect multiple stages in AD progression.

Table 2.

Simulation results for no change point case and single change point case.

	Sample Size N and Dimension of Covariates p	% of Detecting Significant Change Point in 50 Replications	Average p-values for the First Detected Change Point in 50 Replications	Estimated Change Point Location: Mean with Standard Error
No Change Point Case	N = 500, p = 100	6 %	0.42	N/A
	N = 500, p = 200	8 %	0.53	N/A
	N = 1000, p = 100	0 %	0.57	N/A
	N = 1000, p = 200	2 %	0.58	N/A
Single Change Point Case	N = 500, p = 100	100 %	0.00	74.96 (0.32)
	N = 500, p = 200	100 %	0.00	74.88 (0.31)
	N = 1000, p = 100	100 %	0.00	74.94 (0.19)
	N = 1000, p = 200	100 %	0.00	74.98 (0.18)

Fig. 3.

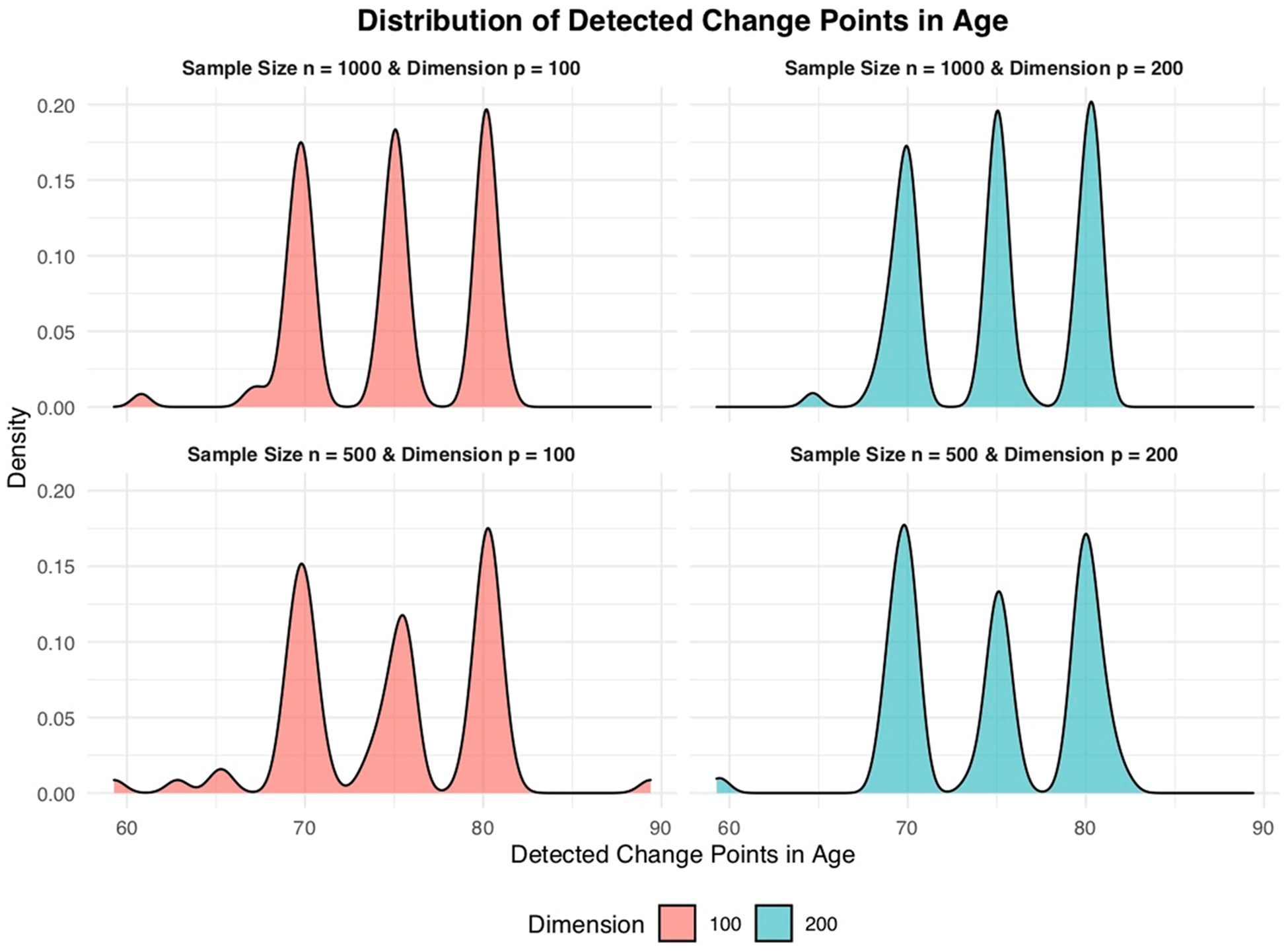
Density plots of detected change points for multiple change point case.

4.2. Tau biomarker is more sensitive to monitoring cognitive decline than a and [N] biomarkers

Building on the foundation of the simulation analysis, we transitioned to real data analysis, applying our CPD method to distinct biomarkers: Amyloid (A), Tau (T), and Neurodegeneration [N]. The change point detection results for A~MMSE, T~MMSE, and [N]~MMSE were summarized in Table 3. The relationship between T and MMSE appeared to have three critical transition points at the ages of 72, 78, and 83. When compared to A-Biomarker, which showed no significant change point in the 55–97 age range, the temporal relationship between T and MMSE was more heterogeneous, displaying multiple progression stages. As shown in Fig. 4(a), the strongest change point in the T~MMSE relationship occurred at 78 years old, with the largest difference in slope between the two linear models. At a significant level of p < 0.001, a one-unit increase in tauopathy burden resulted in a 1.13 decrease in MMSE score before the age of 78 (left panel in Fig. 4(b1)). However, after age 78, the decline became much more rapid, with a one-unit increase in tauopathy burden leading to a 2.44 decrease in MMSE score (right panel in Fig. 4(b1)). To substantiate the significant temporal shift in the T-biomarkers relationship after age 78, we further executed a z-test specifically aimed at comparing the regression coefficients of the whole brain Tau SUVR. The resulting p-value, calculated to be 0.03, aligned coherently with the significant differences highlighted by our CPD model. Additionally, the second and third significant change points occurred at the ages of 72 and 83, respectively. The fitted linear relationships between the T-biomarker and MMSE score were displayed in Fig. 4(b2) for three age ranges: before 72, between 72 and 83, and after 83, where T-biomarkers were closely correlated with MMSE score (p < 0.001). In contrast, the p-value of 0.38 obtained from the z-test on the whole brain A-biomarker indicates that, the decline of slopes due to A-biomarker did not manifest a significant difference before (β = − 1.25) and after (β = − 0.74) the identified change point (age 77), albeit the A-biomarkers showed a strong correlation to MMSE score (p < 0.001) both before and after change point (Fig. 5(a)).

Table 3.

Estimated change points and p-values (sorted by age) using AD biomarkers. The change point detection results with p-value<0.1 are highlighted.

	1st Change Point (p-value)	2nd Change Point (p-value)	3rd Change Point (p-value)
A-Biomarker	Age 77 (0.40)
T-Biomarker	Age 78 (0.001)	Age 72 (0.01)	Age 83 (0.025)
[N]-Biomarker	Age 72 (0.03)

Fig. 4.

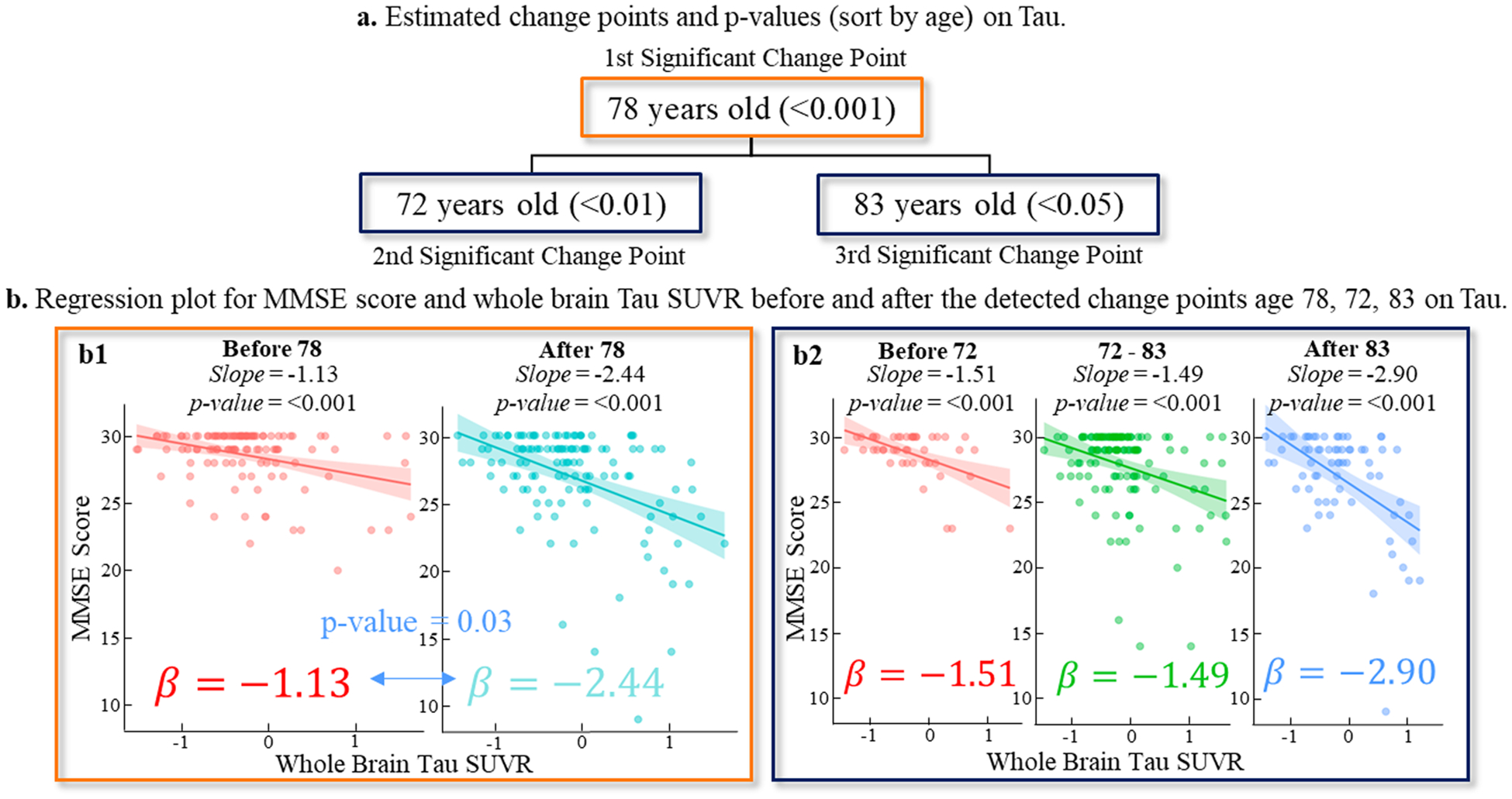
The change point detection results on T-biomarker. (a) There were three significant change points occurring at the ages of 72, 78, and 83, where the temporal patterns of T~MMSE relationship manifested significant difference before and after changing point. (b) The fitted line of T~MMSE relationships before and after change points.

Fig. 5.

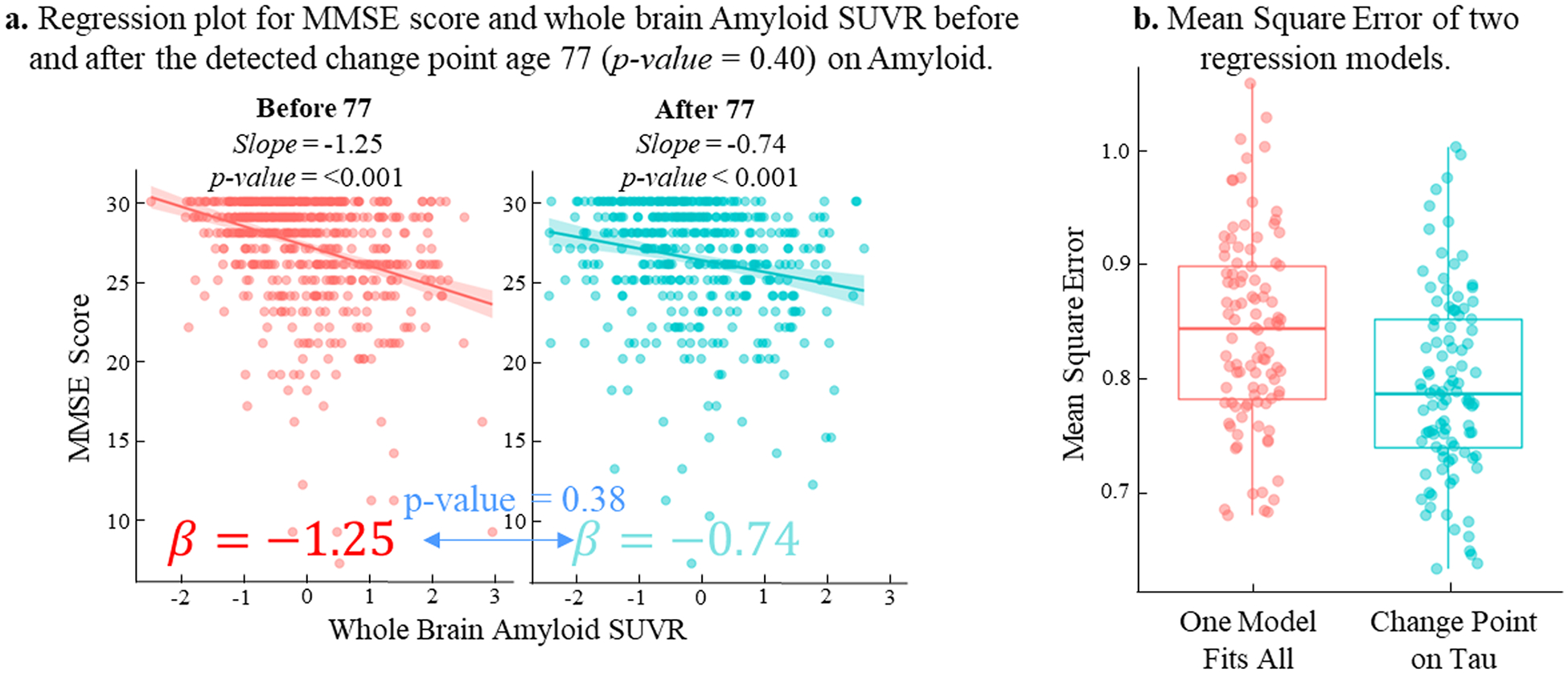
The change point detection results on A biomarker. (a) We have not found significant change point in A~MMSE relationship as the linear model before the age of 77 (in red) does not show significant difference with comparison to that after the age of 77 (in green). (b) Reduced fitting error of T~MMSE relationship by piecewise line fitting (in green) for each progression stage, compared to global linear model (in red).

In Fig. 5(b), we demonstrated the fitting error using a global linear regression model (in red) and a piecewise linear regression model (in green) that leveraged the identified change points. It was evident that using piecewise line fitting has reduced the T~MMSE fitting error by 6.3 % in terms of the residual between observed MMSE and linearly-fitted MMSE scores, suggesting the importance of stratifying the temporal heterogeneity of T~MMSE in disease progression.

Remarks.

Since AD biomarkers consisted of regional SUVRs from 160 brain regions, we used the whole-brain average as a global measurement to quantify their collective impact on MMSE score (as shown in Figs. 4(b) and 5(a)). To identify the brain regions that have the most significant impact on the occurrence of changing points, we utilized a fused LASSO model (Tibshirani, 1996) to select a collection of brain regions that made the largest contribution to the changing points underlying the T~MMSE relationship. The fusion penalty helped to penalize the spurious difference of the regression coefficients for each covariate across the estimated stages (Arnold and Tibshirani, 2016). From left to right, we displayed the selected brain regions that are associated with critical transition ages 72, 78, and 83 in Fig. 6(a), where the node size was proportional to the impact level. The summary of these brain regions was listed in Fig. 6(b).

Fig. 6.

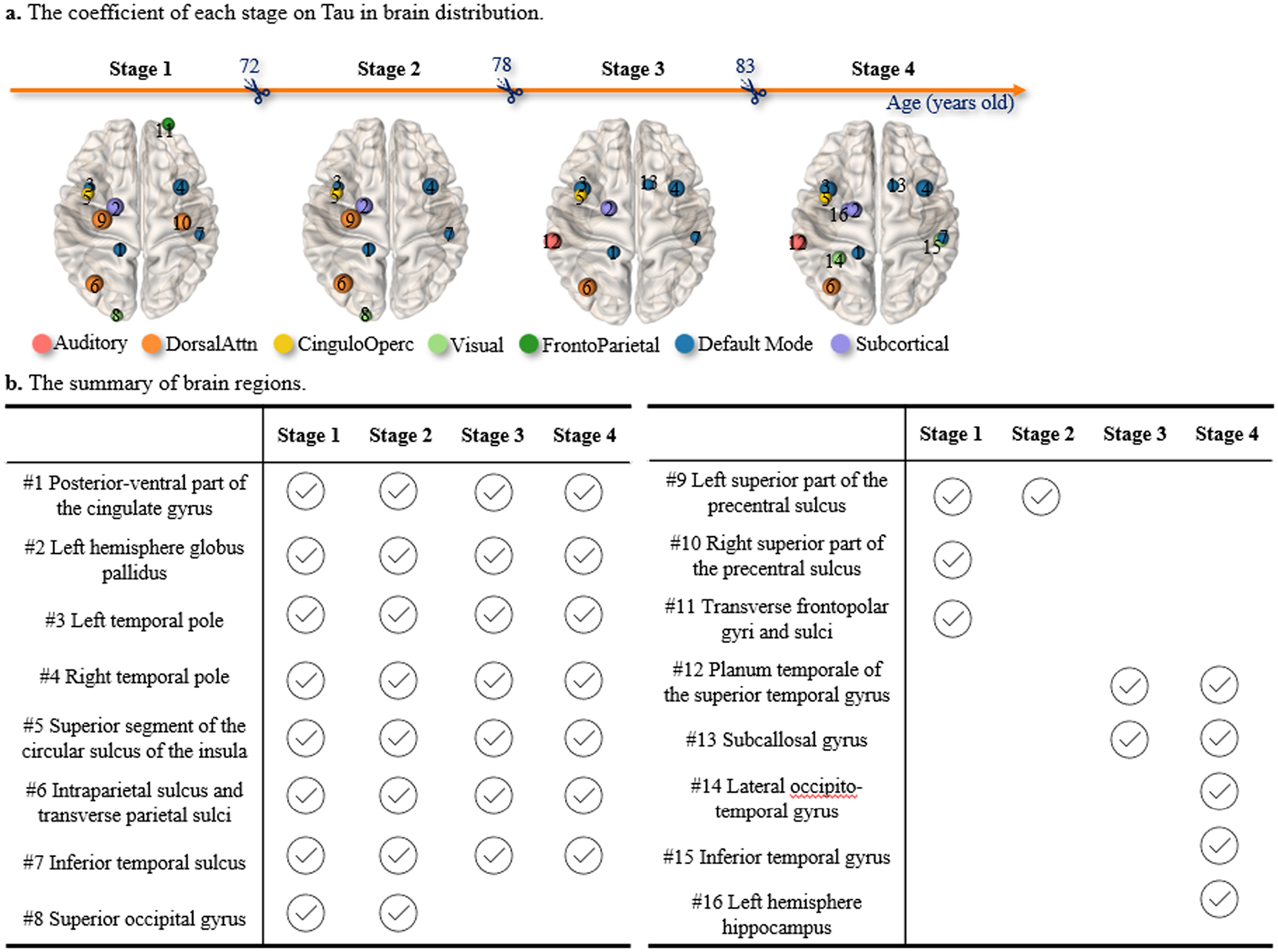
The change point detection results on T biomarker. (a) The brain regions on which T-biomarkers have top-ranked contributions to the transitions. (b) The summary of brain regions that have the most significant impact on the occurrence of changing points.

4.3. Main effect of biological sex and APOE4 status in T~MMSE relationship

To deepen our understanding of AD progression, we focused on interpreting the relationships between AD biomarkers and clinical assessments at each identified change point in Tau. We started by considering variations across important biomarkers: biological sex and APOE4 status. In piecewise linear regression model of T~MMSE relationship, we found that the effect size of both biological sex and APOE4 status are significant (p < 0.05). In this context, we sought to examine the stratified T~MMSE relationship for sex and APOE4 status separately. Due to the clinical significance of the age of 72 and 78 as the top two critical transition points in the T~MMSE relationship for early prevention of AD, we further applied the linear regression model before and after the change point for males and females (Fig. 7), and APOE4 carriers and non-carriers (Fig. 8), respectively.

Fig. 7.

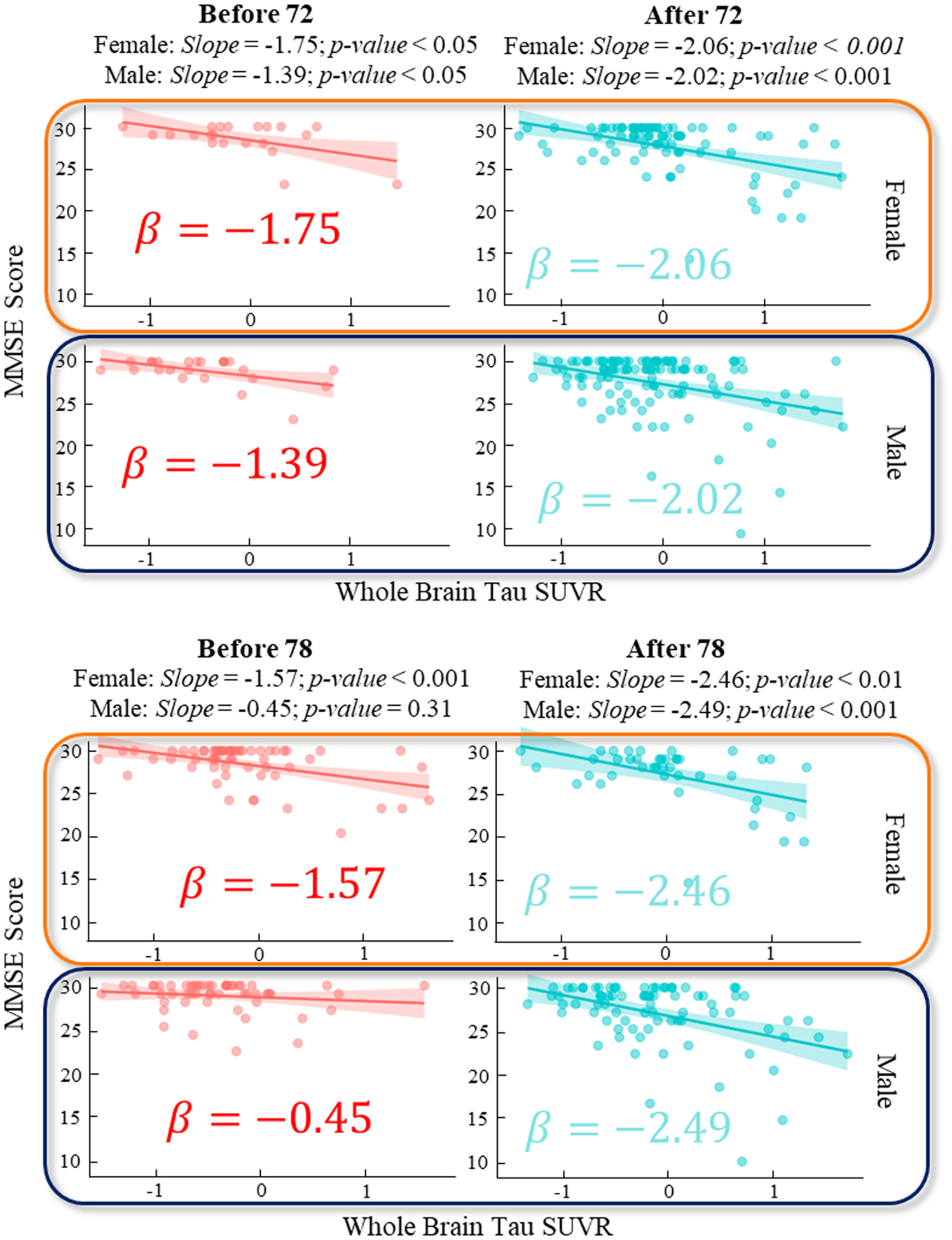
Regression plot for MMSE score and whole brain Tau SUVR before and after the detected change points age 72 (top) and 78 (bottom) on Tau and stratified by sex.

Fig. 8.

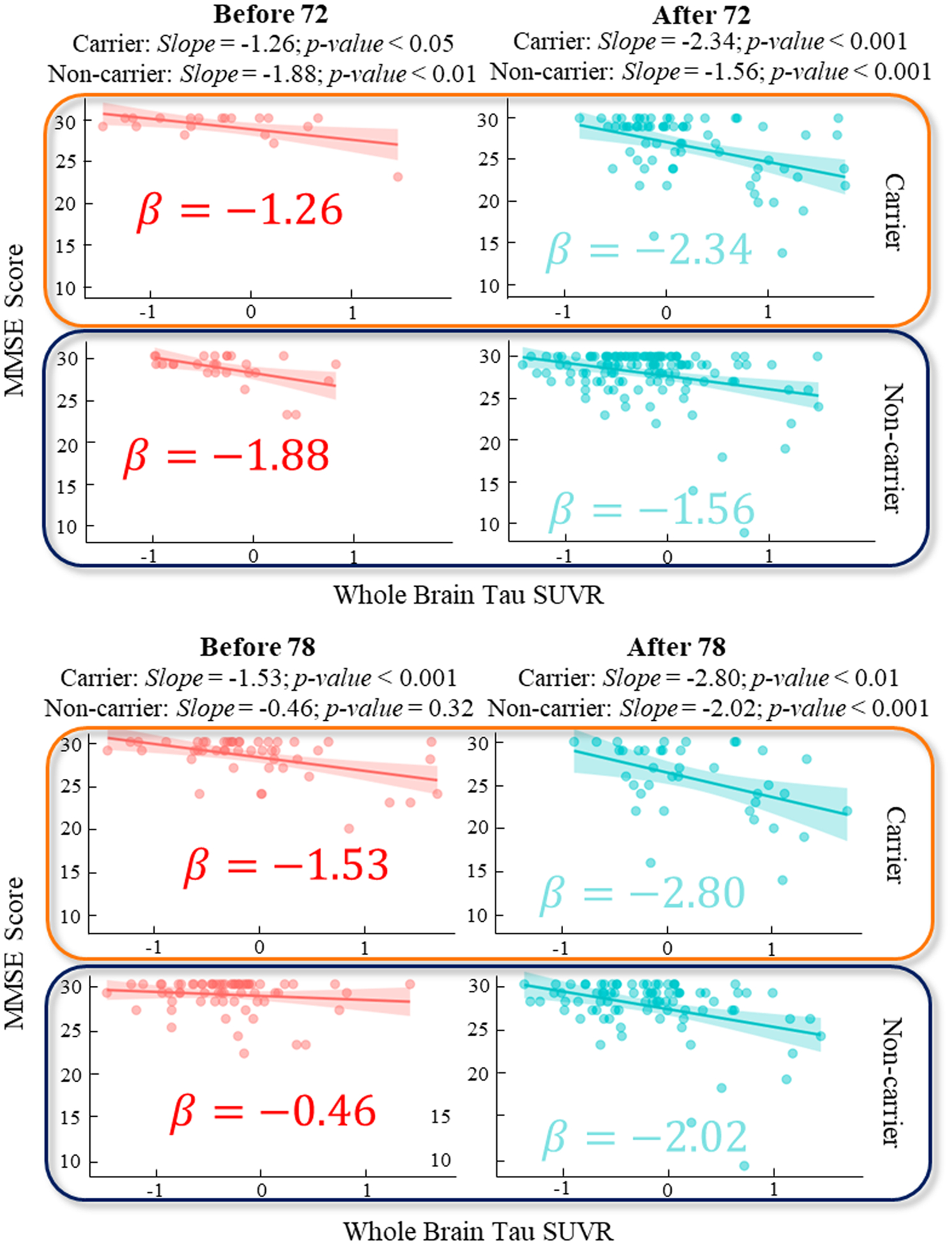
Regression plot for MMSE score and whole brain Tau SUVR before and after the detected change points age 72 (top) and 78 (bottom) on Tau and stratified by APOE4 carrier and non-carrier.

Our analysis revealed notable gender-specific differences in the progression of cognitive decline associated with whole brain Tau SUVR prior to the identified change point at age 78. Stratifying the data by gender, we observed a marked disparity in the regression coefficients before the age of 78: a z-test yielded a p-value of 0.019, indicating a significant difference between genders. Specifically, for females, a one-unit increase in whole-brain tau burden corresponded to a 1.57 unit decrease in the MMSE score before age 78, in stark contrast to a 0.45 unit decrease observed in males. This suggested a more rapid cognitive decline in females compared to males in the pre-78 age group. Interestingly, after age 78, this decline in cognitive function becomes more uniform across genders, as indicated by a p-value of 0.27. This convergence in decline rates after the age of 78 implied a diminishing gender disparity in the progression rate at later stages.

Additionally, our stratification analysis based on APOE4 status revealed a universally steeper decline slope in APOE4 carriers as compared to non-carriers, with a significant p-value of 0.039 observed before the age of 78. This finding suggests that APOE4 was a significant risk factor for AD progression, with carriers being at a higher risk than non-carriers for more rapid cognitive decline.

4.4. Sex-dependent APOE effect on cognitive decline

Along with current findings in AD (Altmann et al., 2014; Andrew and Tierney, 2018; Barnes et al., 2005; Davis et al., 2021), our results in Figs. 7 and 8 indicated that, in the early stages of Alzheimer’s Disease, there appeared to be a more rapid cognitive decline in women compared to men, and APOE4 carriers seemed to experience a more pronounced decline than non-carriers. In this regard, we sought to investigate how the mechanistic role of AD biomarkers changes in mediating the effect of APOE4 on the cognitive decline before and after the change point. We followed the classic mediation analysis to estimate the direct effect β_D (DE) and mediation effect β_M (ME) for the mechanistic pathways of APOE4→MMSE and APOE4→AD biomarker→MMSE, respectively.

Mediation analysis for T-biomarker prior to and after the age of 78 (1st change point)

Firstly, we examined the direct pathway of APOE4 affecting MMSE score and the indirect pathway that was mediated by whole-brain T-biomarker (average of tau SUVRs across 160 brain regions). At a significant level of 0.01, APOE4 significantly contributed to the decrease of MMSE score via the increase of whole-brain tau aggregates (shown in Fig. 9(a)). Prior to the change point (age of 78), the estimated β_D and β_M were −0.01 and −0.18, respectively, with the indirect pathway accounting for 94.6 % proportion of the effect on the decrease of MMSE score. However, after the change point, both direct and indirect pathways equally affected cognition, with the proportion between DE (β_D = − 0.26) and ME (β_M = − 0.27) balanced at 50.8 %. It was apparent that (1) the risk associated with APOE4 became more pronounced as age advances, and (2) there was a noteworthy transition from a ME-dominant pattern of APOE4 effect on the cognitive decline to the neurodegeneration pattern where the direct and indirect pathways were more evenly balanced.

Fig. 9.

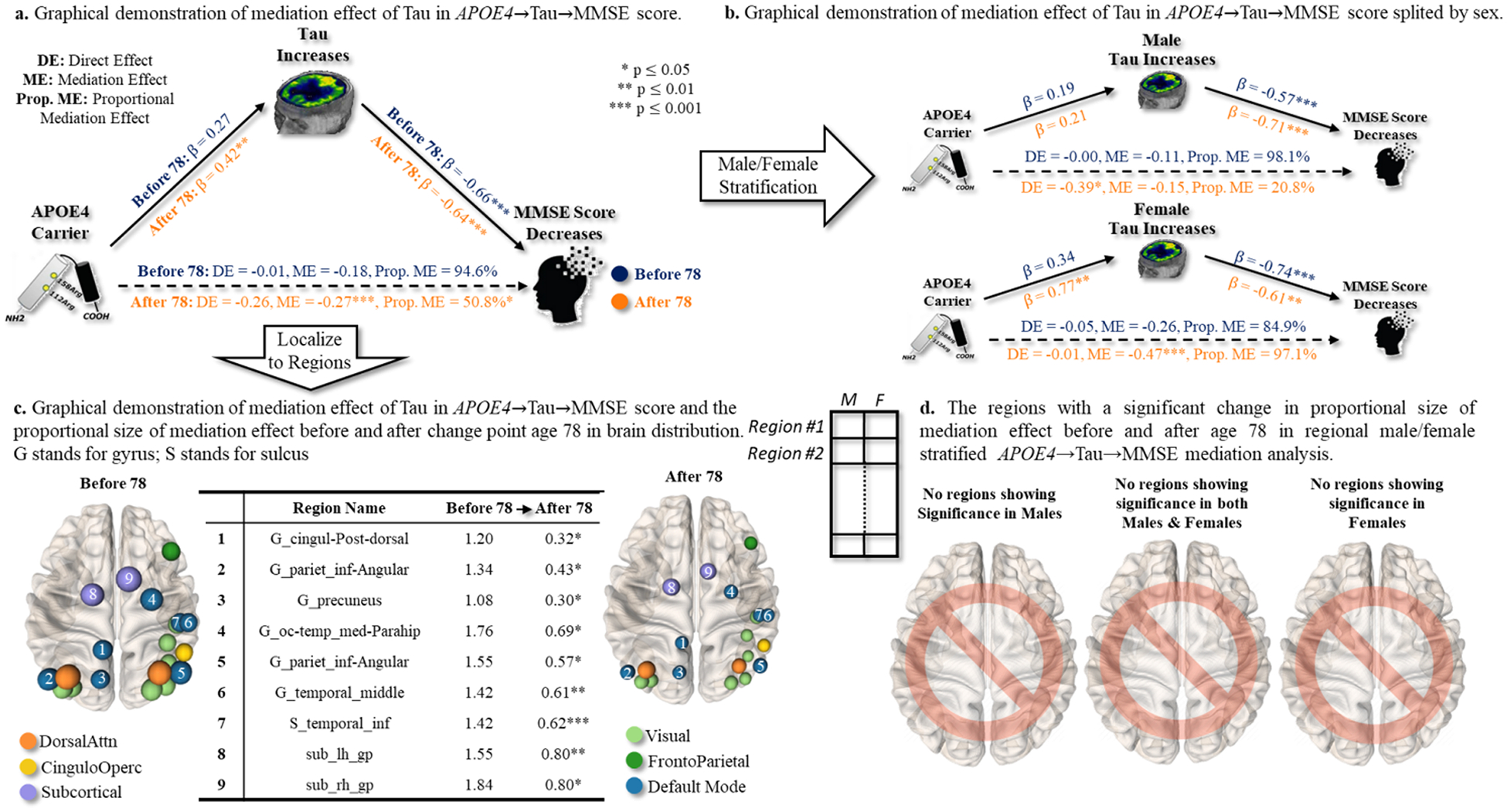
Sex-dependent effect of APOE4 on cognitive decline, possibly mediated by T-biomarker in the APOE4→Tau→MMSE pathway. (a) We first examined the direct effect (APOE4→MMSE) and the corresponding indirect effect mediated by whole-brain T biomarkers before and after particular change point. (b) Then, we stratified the same mediation analysis to males and females separately. (c) Furthermore, we conducted the same mediation analysis (males and females together) at each brain region. We displayed the mediation effect before and after change point (right), where the node size indicated the proportion of mediation effect size. (d) Finally, we investigated whether the regional APOE4→Tau→MMSE pathways manifest significant changes in the proportion of mediation effect (by T-biomarker) before and after age 78 in the male/female stratified mediation analysis.

Secondly, we sought to investigate the driving factor behind such pattern shifts before and after the change point. We hypothesized that the change in the ME/(ME+DE) proportion from 94.6 % to 50.8 % was sexually dimorphic. To do so, we stratified the same medication analysis to males and females, as shown in Fig. 9(b). Specifically, our findings indicated that the cognitive decline in female APOE4 carriers was consistently influenced by the accumulation of tau aggregates in the whole brain, as evidenced by the ME/(ME+DE) proportions of 84.9 % before the age of 78 and 97.1 % after the age of 78. On the contrary, the ME/(ME+DE) proportion in males decreased from 98.1 % to 20.8 %, showing that (1) the impact of APOE4 risk factor on cognitive decline is primarily mediated by the whole-brain tau aggregates in both males and females prior to the change point, (2) male APOE4 carriers experienced a significant shift from the indirect pathway (β_M = − 0.15) to the direct pathway (β_D = − 0.39) after the change point. This piece of evidence suggested that APOE4 may have a sex-specific effect on the cognitive decline that changes over time.

Thirdly, we localized the mediation analysis by replacing the whole-brain tau aggregation level with regional SUVR. Among 160 brain regions, 4.4 % of regions exhibited more than a 100 % decrease in ME/(ME+DE) ratio after the change point, and 53.1 % of regions exhibited more than a 50 % decrease in ME/(ME+DE) ratio after the change point. The table in the middle of Fig. 9(c) presented the mediation effect β_M in nine top-ranked brain regions, sorted in a decreasing order based on the amount of mediation effect β_M before and after age 78. This result indicated that the temporal changes in the way how APOE4 affected cognitive decline might be region selective. In Fig. 9(c), we displayed the top nine brain regions where the mediated effect of APOE4 on cognitive decline (via regional tau SUVR) significantly decreased after the change point (indicated by region size). Furthermore, we colored these selected brain regions with respect to the topological location in large-scale functional brain networks (color notation shown at the bottom of Fig. 9(c)). It was apparent that the brain regions experiencing significant ME/(ME+DE) proportion transition of APOE4 effect were located in sub-cortical areas (purple) and default-mode network (dark blue), which indicated the region-selective pattern in terms of the topological location underlying functional networks.

Fourthly, we sought to identify brain regions that manifest sex differences in terms of changes in medication effect before and after the change point, by combining the male/female stratification analysis on top of the regional mediation analysis of APOE4→Tau→MMSE pathways. At the significance level of p < 0.05, we have not detected any brain region exhibiting a significant change in the proportion of mediation effects before and after age 78 in the stratification analysis between males and females.

Mediation analysis for [N]-biomarker prior to and after the age of 72 (1st change point)

Since age 72 is the only significant change point detected in [N] ~MMSE relationship, we investigated the mechanistic role of [N] biomarker in regulating the effect of APOE4 on cognitive decline. The major findings of mediation analysis in the APOE4→FDG→MMSE pathway were summarized below.

• We found that only 38.2 % of APOE4 effect on the decrease of MMSE has been mediated by the decrease of whole-brain metabolism level (approximated by the average of regional FDG-SURVs) before the change point (shown in Fig. 10(a)), at a significant level p < 0.01. After the age of 72, the ME portion was further reduced to 15.4 %, indicating that the APOE4 risk factor exerted a direct effect on cognitive decline underlying the APOE4→[N]→MMSE pathway.

• We found that both men (from 42.9 % before age 72 to 15.8 % after age 72) and women (from 35.3 % before age 72 to 15.9 % after age 72) contributed to the decline of ME/(ME+DE) proportion prior to and after the change point, as shown in Fig. 10(b).

• We conducted the same mediation analysis for each brain region. Our findings indicated that 7.5 % of regions exhibit more than a 100 % decrease in ME/(ME+DE) ratio after the change point, and 60 % of regions exhibit more than a 50 % decrease in ME/(ME+DE) ratio after the change point. In this context, it was possible that the role of [N] biomarkers in the APOE4→[N]→MMSE pathway undergoes temporal changes that were specific to certain regions at the change point. The top eleven brain regions with the largest decrease in ME/(ME+DE) ratio before and after the change point were displayed in Fig. 10(c), where the before vs. after mediation effects β_M as well as the significance levels were listed in the middle of Fig. 10(c). In general, most of the top-ranked brain regions were located in the default mode network.

• On top of the regional mediation analysis in Fig. 10(c), we further stratified the statistical tests into males and females separately. In the middle of Fig. 10(d), we first displayed the brain regions where the proportion of medication effects manifested significant change before and after age 72 in both males and females, at a significance level of p < 0.01. It is evident that most of the brain regions in the default mode network manifested the change of mediation role by the reduced metabolism level. This temporal pattern was observed in both males and females. Second, male-specific and female-specific brain regions that exhibited the same temporal changing patterns were displayed in Fig. 10(d) left and right, respectively.

Fig. 10.

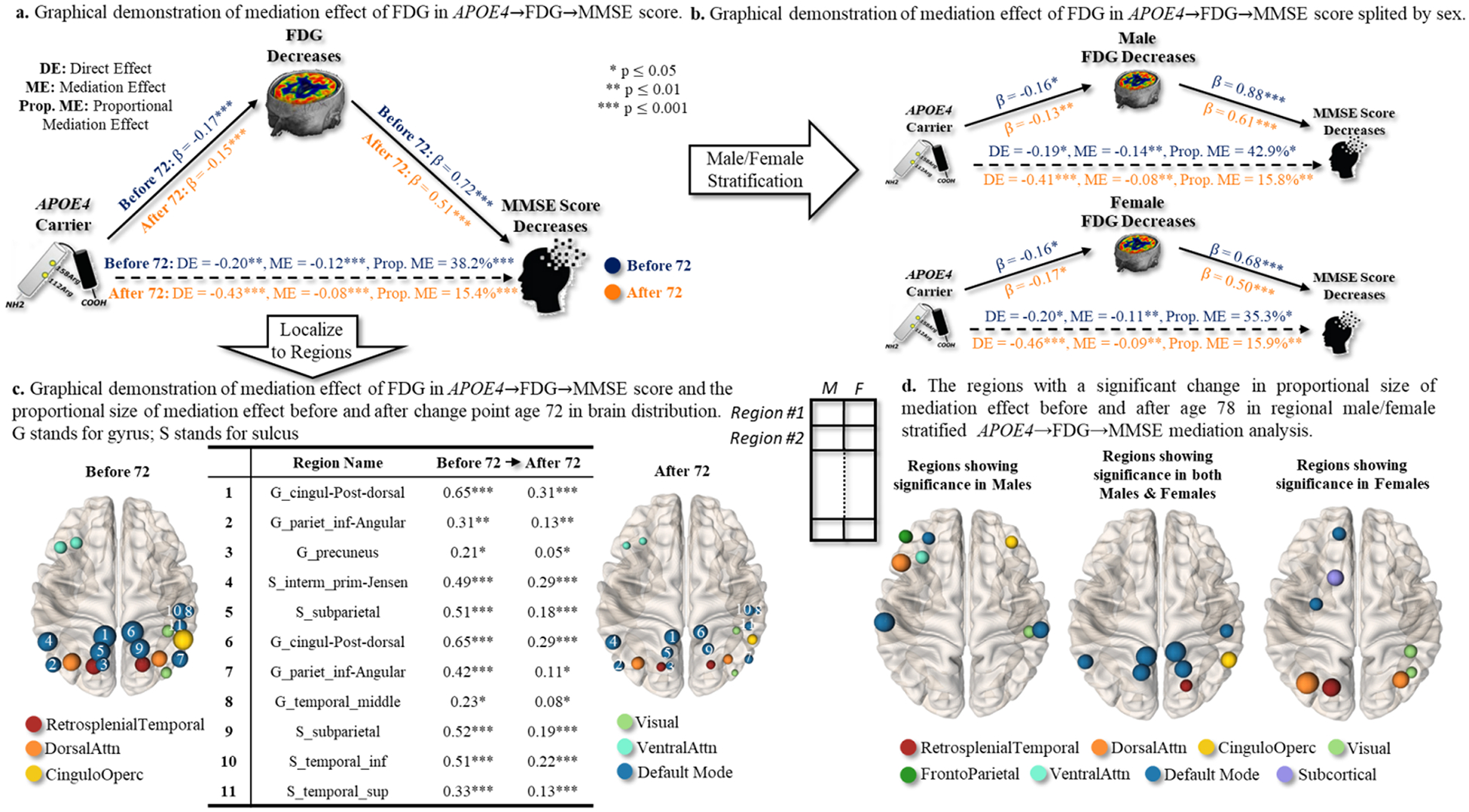
Sex-dependent effect of APOE4 on cognitive decline, possibly mediated by [N]-biomarker in the APOE4→FDG→MMSE pathway. (a) We first examined the direct effect (APOE4→MMSE) and the corresponding indirect effect mediated by whole-brain [N] biomarkers before and after particular change point. (b) Then, we stratified the same mediation analysis to males and females separately. (c) Furthermore, we conducted the same mediation analysis (males and females together) at each brain region. We displayed the mediation effect before and after change point (right), where the node size indicates the proportion of mediation effect size. (d) Finally, we investigated whether the regional APOE4→FDG→MMSE pathways manifest significant changes in the proportion of mediation effect (by [N]-biomarker) before and after age 72 in the male/female stratified mediation analysis.

4.5. Role of socioeconomic status in modifying multi-stage progression of AD biomarkers

Multiple lines of findings have reported that socioeconomic status significantly modifies the progression of AD. In our change point detection model, we found that education level also manifested a significant association in the multi-stage T~MMSE and [N]~MMSE relationships. Hence, we stratified the statistical analysis underlying the T~MMSE relationship for the low education group (less than 16 school years) and high education group (more than 16 school years) at the age of 78 (most critical change point).

Impact of education level on T~MMSE relationship prior to and after the age of 78

Firstly, we found that both low and high-education groups exhibited a moderate-to-rapid decline pattern before and after the change point, as shown in Fig. 11(a). Using the significant level p < 0.05, the decline in the low-education group (−1.65 before age 78 and −2.88 after age 78) was more severe than that in the high-education group (−0.99 before age 78 and −2.03 after the change point).

Fig. 11.

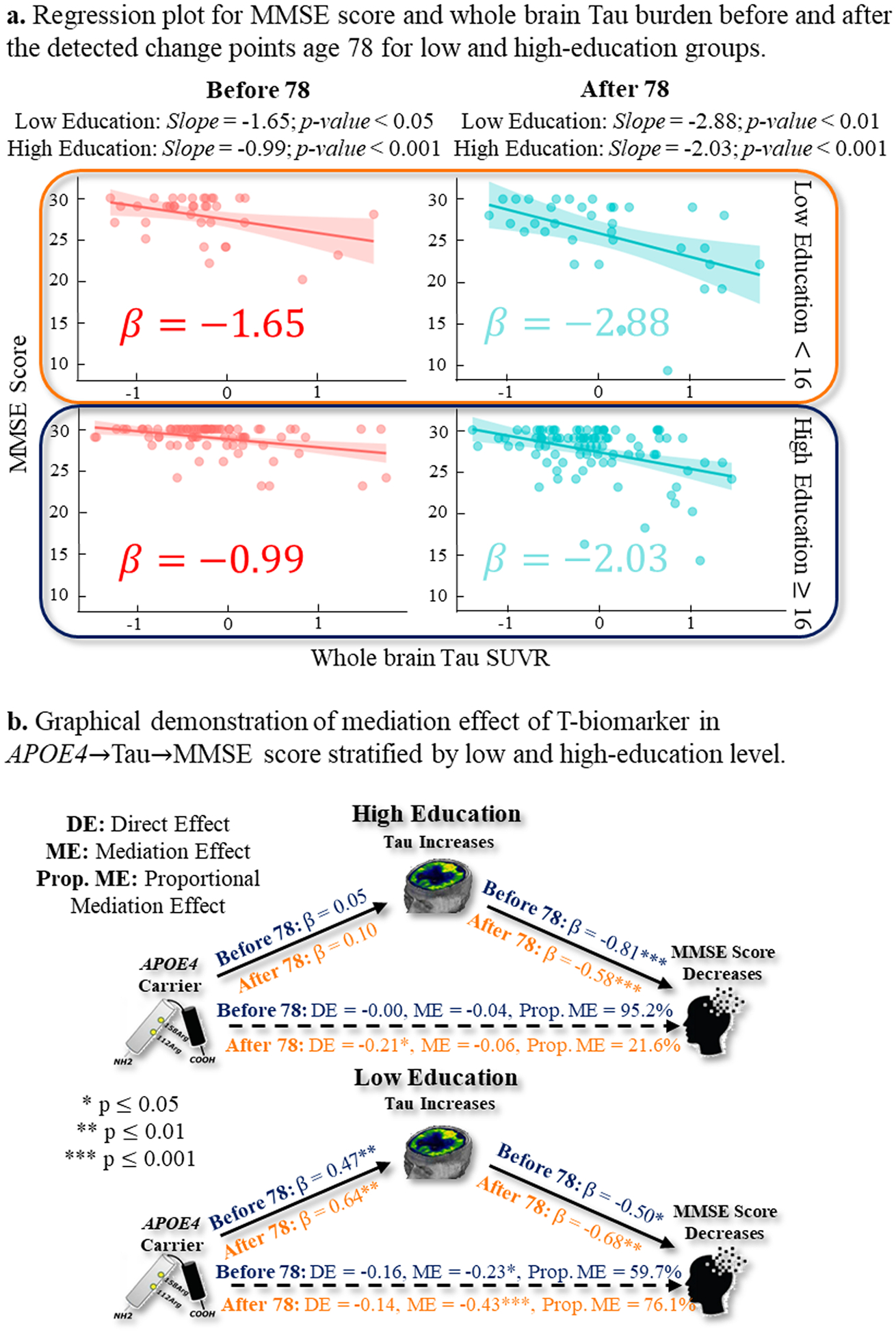
(a) The T~MMSE relationship before (in red) and after (in green) the change point of age 78 for low-education (top) and high-education (bottom) groups. (b) The mediation analysis result of APOE→T→MMSE pathway before and after the change point for low-education (top) and high-education (bottom) groups.

Secondly, we examined the direct and indirect effects along the APOE4→T→MMSE pathway. For the high-education group (Fig. 11(b) top), the proportion of the mediation effect of APOE4 on MMSE decreased from 95.2 % to 21.6 % after age 78. On the contrary, the low-education group showed the opposite pattern, where the proportion of mediation effect of APOE4, ME/(ME+DE), on MMSE increased from 59.7 % to 76.1 % after age 78. This observation implied that education level could be a modifying factor in the pathophysiological mechanism underlying the impact of APOE4 risk factor on cognitive decline. Since education level has been found to be a strong predictor of cognitive reserve (Stern, 2012), we provided an in-depth discussion in Section 5.

Impact of education level on [N]~MMSE relationship prior to and after the age of 72

Similarly, we investigated the role of education level in [N]~MMSE relationship before and after age 72 (the only change point). At a significance level p < 0.001, the reduced metabolism level (measured by whole-brain concentration level from FDG-PET scan) showed increased effect size (1.44 prior to age 72 and 1.61 after age 72) in the low education group (Fig. 12(a) top). However, the high education group manifested an opposite changing pattern where the effect size of a unit decrease of metabolism level was associated with a 1.49 unit decrease of MMSE score before age 72 while reduced to a 1.28 unit decrease of MMSE score after the change point (Fig. 12(a) bottom).

Fig. 12.

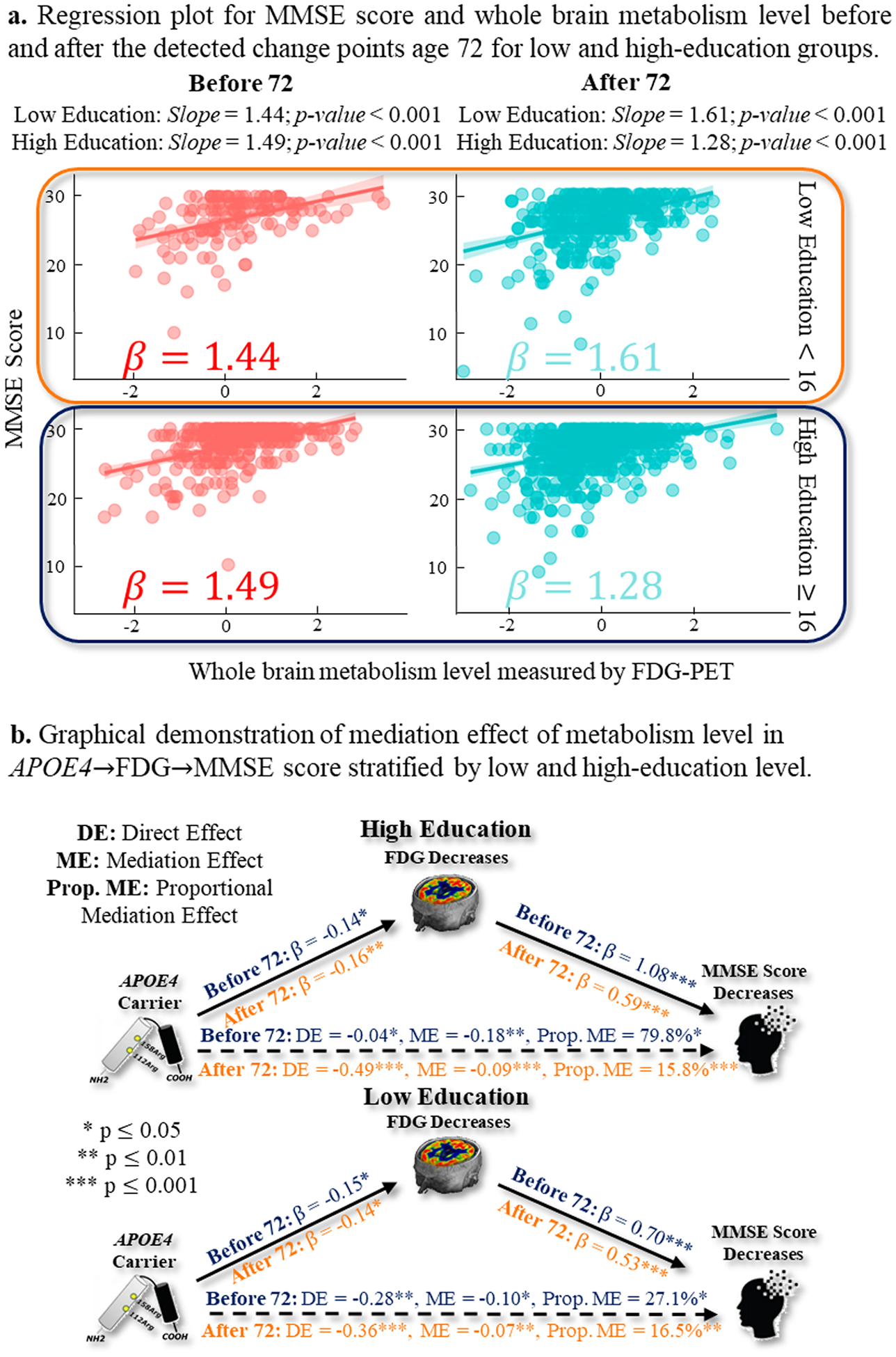
(a) The [N]~MMSE relationship before (in red) and after (in green) the change point of age 72 for low-education (top) and high-education (bottom) groups. (b) The mediation analysis result of APOE→[N]→MMSE pathway before and after the change point for low-education (top) and high-education (bottom) groups.

At a significance level of p < 0.05, the mediation analysis results in Fig. 12(b) top suggested that high education group exhibited a more profound indirect pathway prior to the age 72 (i.e., the majority of APOE4 effect on cognitive decline was mediated by the reduced whole-brain metabolism level), where the proportion of medication effect can reach 79.8 %. After the change point, however, there was a pronounced change in the high education group that the effect of APOE4 on cognitive decline shifted to the direct pathway, as indicated by the drop of the proportion of medication effect to 15.8 %. Regarding the medication analysis of APOE4→[N]→MMSE pathway in low-education group (Fig. 12(b) bottom), our finding suggested that APOE4 effect on cognitive decline was primarily driven by the direct pathway. Furthermore, we observed a moderate change in the proportion of the mediation effect, with a decrease from 27.1 % before the age of 72 to 16.5 % after the age of 72.

4.6. Multi-stage association between cognitive composite score and AD hallmarks

Cognitive function is complex and multidimensional, which is partially responsible for the heterogeneous clinical manifestations reported in the progression of AD. In this regard, we sought to break the global MMSE score into MEM and EF composite scores and disentangle the temporal heterogeneity underlying the relationships of AT[N] biomarker~MEM (in Table 4) and AT[N] biomarker~EF (in Fig. 13), respectively.

Table 4.

Identified change points (sorted in age) and the associated p-value in the AT[N]~MEM relationship.

	1st Change Point (p-value)	2nd Change Point (p-value)
A-Biomarker	74 (0.47)
T-Biomarker	80 (0.07)	86 (0.10)
[N]-Biomarker	74 (0.93)

Fig. 13.

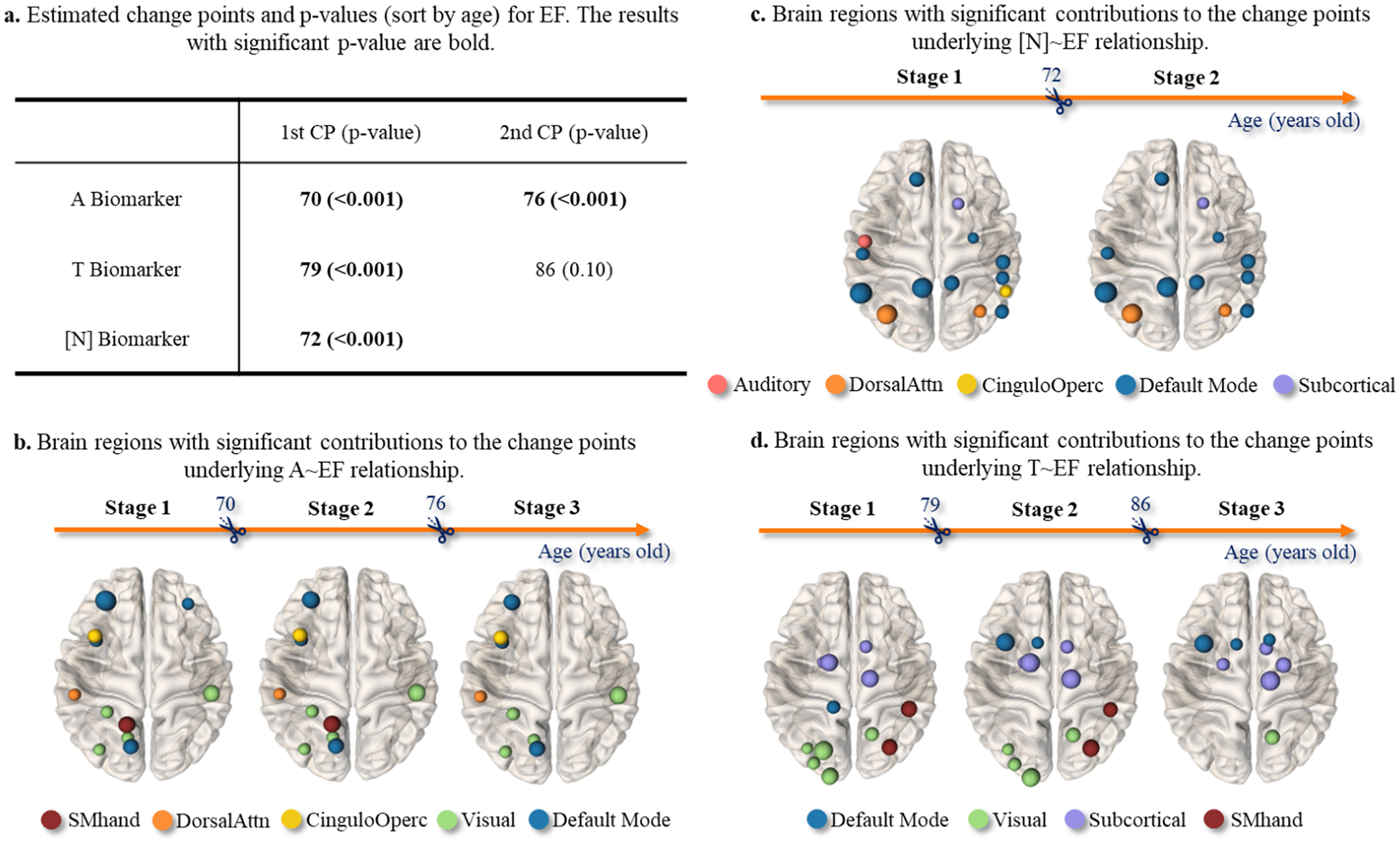
Identified change points (sorted in age) and the associated p-value in the AT[N]~EF relationship are shown in (a). The brain regions showing significant contribution to the change points underlying A~EF, T~EF, and [N]~EF relationship were displayed in (b), (c), and (d), respectively. The node size and color indicated the effect size and topological location in the large-scale functional networks.

Firstly, we have detected one change point underlying A~MEM relationship at the age of 74, one change point underlying [N]~MEM relationship at the age of 74, and two change points underlying T~MEM relationship at the ages of 80 and 86. However, none of the change points in the A~MEM, T~MEM, and [N]~MEM relationship passed the statistical significance test at the significance level of p < 0.05 (shown in Table 4). This finding suggested that the linear effect of AT[N] biomarkers on memory performance does not show significant change over time.

Secondly, we found that AT[N] biomarkers exhibit a multi-stage impact on the decline in EF performance (shown in Fig. 13(a)). Using a significant level of p < 0.001, we identified two change points underlying A~EF relationship: the first occurred at the age of 70, followed by a second change point at the age of 76. T~EF relationship showed two change points occurring at the age of 79 and 86, respectively. However, the second change point (86-year-old) was not significant. There was only one statistically significant change point in the [N]~EF relationship occurring at the age of 72. These findings suggested that the effect of AT[N] biomarkers on EF performance is much more dynamic than AT[N]~MEM relationship. From Fig. 13(b–d), we displayed the brain regions on which the regional A, T, and [N] burdens have a significant impact on the decline of EF performance (The node size is proportional to the effect size). Furthermore, we localized these brain regions in the context of large-scale functional brain networks. We found that (1) most brain regions underlying A~EF relationship were located in the left hemisphere, (2) the accumulation of tau aggregates in the default mode network was associated with the multi-stage T~EF relationship, (3) the decreased metabolism levels in the sub-cortical area and visual cortex underlined the temporal change of [N]~EF relationship.

4.7. Multi-stage relationship between imaging biomarkers and the CSF biomarkers

Note that our CPD method was not limited to sorting the individuals by chronological age. Instead, it offered the flexibility to sort based on various continuous variables related to AD. This versatility allowed us to adapt our approach to different aspects of AD research, enriching the comprehension of AD’s intricacies. As an illustration of its utility, we applied our CPD method to the CSF biomarkers, and identified change points across the spectrum of CSF biomarker values. In Fig. 14, we demonstrated the application of disentangling the latent multiple stages in the evolving [N]~MMSE relationship as the accumulation of CSF biomarkers. Since it is common to use the CSF tau/Aβ42 ratio in clinical practice, we adopted the CSF tau/Aβ42 ratio as the sorting variable, where a larger CSF tau/Aβ42 indicated a higher risk of developing AD. Therefore, each subject has a collection of 160 regional [N] biomarkers from the FDG-PET scan, MMSE score, and the CSF tau/Aβ42 biomarker. As shown at the top of Fig. 14, the first (most critical) change point in the [N]~MMSE relationship occurred at the early stage of CSF biomarker accumulation (tau/Aβ42 = 0.37), followed by the second and third change points occurring at tau/Aβ42 =0.61 (middle stage of AD progression) and tau/Aβ42 = 0.89 (late stage of AD progression). In Fig. 14 bottom, we displayed the brain regions on which the reduced metabolism level has a strong contribution to the change of the linear relationship between [N] biomarker and MMSE score.

Fig. 14.

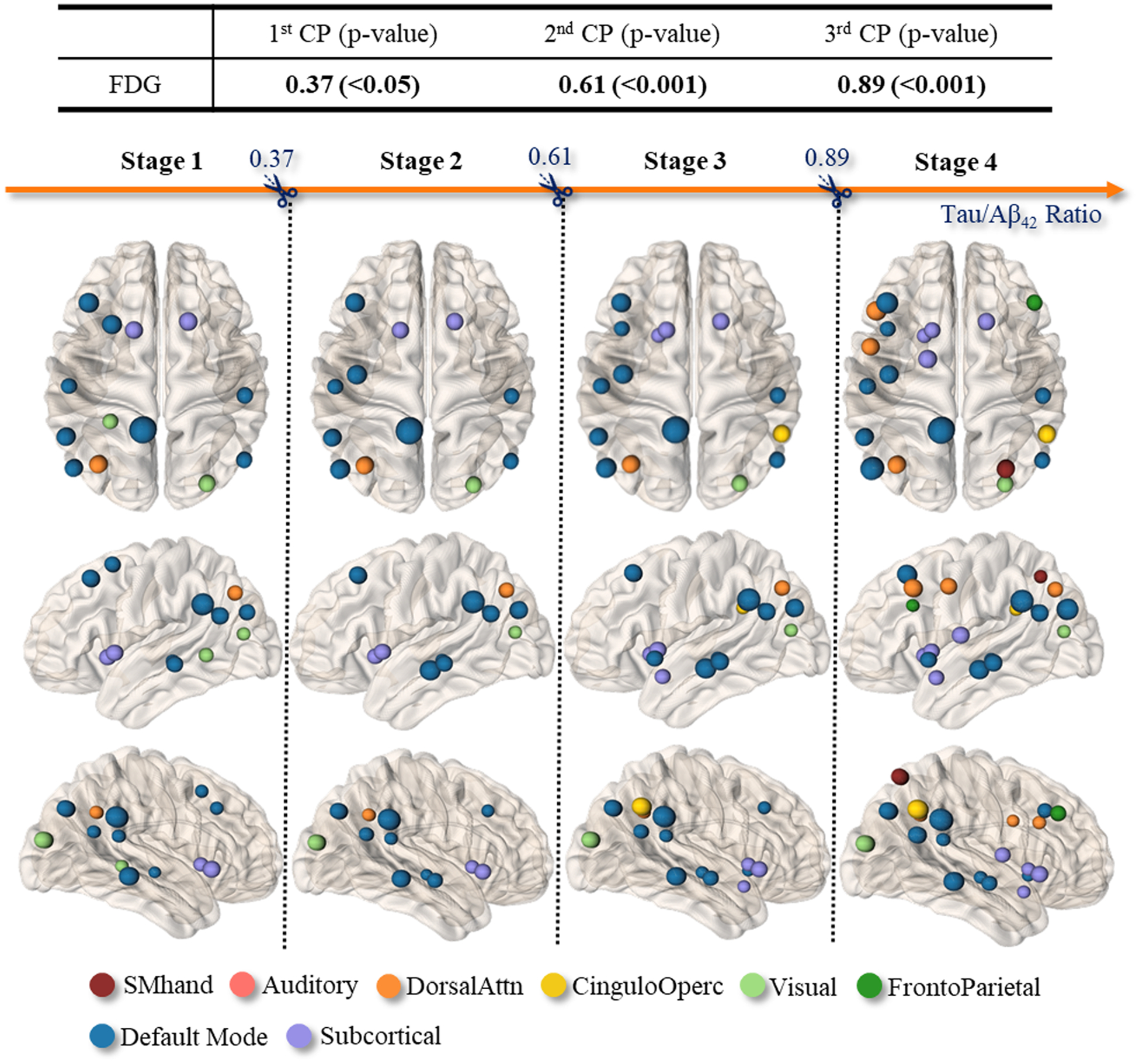
Top: Three change points have been detected (sort by CSF tau/Aβ₄₂ biomarker) in [N]~MMSE relationship. Bottom: The brain regions with strong contributions to the changes of [N]~MMSE relationships prior to and after each change point.

5. Discussion

Clinic impact of our work.

AD is the most common form of dementia that affects older people of varying ethnicities, sexual and gender identities, and lifestyles (Organization, 2012). The heterogeneity in the presentation and progression of clinical symptoms posed great challenges to fully elucidating the complex interaction between disparities and diversities in AD. In this regard, an in-depth understanding of health disparities will set the stage for the development of precision medicine in AD by encompassing personalized strategies for prevention, detection, drug development, and disease-modifying therapy. Specifically, the identified change points in AD progression would be beneficial for (1) a comprehensive underpinning of the interaction between health disparities and cognitive change over time that might provide practice guidelines for analyzing and understanding diversities in drug development and disease-modifying therapeutics for AD, (2) a new neurobiological mechanism that links biological indicators with environmental exposures which provides an in-depth understanding of health disparities in AD, and (3) a more effective health care system that is accessible and equal for all Americans, regardless of gender, race, ethnicity, geography, and socioeconomic status.

In this work, we investigated the synergistic effect of APOE4 and biological sex on the diversities of cognitive decline in AD, with the focus on (i) common and distinct dynamic patterns of disease progression across amyloid (A), tau (T), and neurodegeneration (N) biomarkers (Figs. 4–6), (ii) sex-dependent effect of APOE4 status on the long period of neurodegeneration (Figs. 7–10), and (iii) the protective factors behind the health disparities at the different stages of AD (Figs. 11 and 12).

Education, a marker of cognitive reserve, is protective against cognitive decline.

Education has long been recognized as an important indicator of greater cognitive reserve, which is the brain’s ability to compensate for age-related brain changes and greater neuropathological burden (Stern, 2006, 2012). In our study, the impact of APOE4 on cognitive decline was found to be moderated by level of premorbid education (Fig. 11(b) top), where the total effect size (DE+ME) of APOE4 are −0.04 before age 78 and −0.27 after age 78, compared to low education group (Fig. 11(b) bottom), where the total effects of APOE4 are −0.39 before age 78 and −0.57 after age 78. This suggested that education may provide a cognitive ‘buffer’ that helps to delay the onset of AD. These findings underscored the importance of lifelong learning and the value of education in promoting healthy aging and maintaining cognitive function in old age.

Refinement for multiple comparisons and data double use.

To enhance the robustness and accuracy of our discoveries related to the identification of CPs in AD progression, we further integrated a strategic methodological refinement. By adopting a data splitting strategy within our analytical framework, we split our dataset into two pivotal segments. The initial segment was used to identify CPs related to cognitive decline and neuroimaging biomarkers through our CPD method. Concurrently, the subsequent segment was earmarked for the independent verification and nuanced interpretation of these CPs. This methodical division was designed to mitigate the inherent risks associated with multiple comparisons and circumvent potential biases by segregating the dataset used for CP identification from that employed in their validation. Such a methodological enhancement solidified our confidence in the identified CPs as definitive indicators of crucial transitions within the AD progression spectrum.

Our refined analysis confirms several key observations: (1) Tauopathy-PET biomarkers persist in demonstrating a pronounced and age-sensitive correlation with cognitive decline, validated through statistical significance (p < 0.05), with the most significant change point notably positioned around the age of 78. This confirmation underscored tauopathy’s unique contribution to AD progression in contrast to amyloid-PET and FDG-PET biomarkers. (2) Verification within the independent data segment underscored significant gender-specific disparities in cognitive decline associated with whole-brain Tau SUVR preceding the identified age 78 change point. This phase of the analysis highlighted a steeper cognitive decline in females relative to males within the pre-age 78 demographic, signifying a pronounced vulnerability in females during this period. (3) Our analysis, when stratified by APOE4 carrier status, disclosed a universally more acute decline in cognitive functions among APOE4 carriers versus non-carriers before the age of 78, achieving statistical significance (p < 0.05). This pivotal insight accentuated APOE4′s substantial influence as a significant risk factor for AD, underscoring the heightened susceptibility of carriers to expedited cognitive deterioration.

Limitation of current work and future direction.

There were several methodology and application-wise limitations in our current approach. In the following, we discussed each limitation and possible solutions.

1. Cross-sectional vs. longitudinal. Our current CPD method was designed for modeling the population-wise change of neuro-degeneration trajectory from cross-sectional data. Specifically, we simultaneously stratified the subjects in the temporal domain (by age) and tested whether the temporal transitions show statistical significance in terms of the biomarker~outcome relationship. Since subject-specific changes were oftentimes more relevant to disease progression, future work should take subject-specific longitudinal change into account by integrating the mixed-effect model into our CPD method.

2. Normal aging v.s. highly selective disease data. The data analysis in this work used ADNI data only, which is a clinical research study in AD. However, the presence and incidence of AD might not be accurately reflect the general aging population in the clinic routine. To address this issue, our future work includes extending the data analysis to multi-site studies by exploring other public datasets such as Biocard (Sacktor et al., 2017) and UK Biobank (Fawns-Ritchie and Deary, 2020).

3. Multi-factorial mechanisms of health disparities in AD. Since AD is a multi-factorial disease (Iqbal and Grundke-Iqbal, 2010), the extant literature supported the hypothesis that there were multiple factors contributing to the presence of diverse disease progression in the aging population. However, little attention (including our work) has been given to understanding their relationship and how their interaction affected the trajectory of cognitive decline. For example, APOE4 risk tends to vary by race. Although it is important to examine whether race plays a role, the majority body of recruited subjects in ADNI are genetically related to European ancestry. In this regard, our work was unable to detect race differences. Advanced multivariate statistical models were in high demand to elucidate the synergistic effect of phenotypic variables on the progression of AD.

4. Cognitive reserve in AD prevention. A major challenge in the care and management of AD is the paradoxical relationship between the burden of AD pathology and its clinical outcome (Stern, 2002; van Loenhoud et al., 2019). Recent evidence shows cognitive reserve, the brain’s capability to preserve cognition despite underlying AD pathology, is a key determinant that moderates clinical progression (Medaglia et al., 2017; Reed et al., 2010; Stern, 2002, 2006, 2012, 2017; van Loenhoud et al., 2019, 2017). Following this notion, we investigated the role of education level in change points, and we found that greater education might buffer against cognitive decline. While education level is thought to be an important marker of cognitive reserve, other markers, including premorbid verbal IQ, occupational complexity, and others have also been suggested as providing important proximal markers of this complex construct (Stern et al., 2020). Future studies may therefore, benefit from the incorporation of additional measures of cognitive reserve to comprehensively assess this protective factor.

5. Extend from AT[N] to ATX[N] framework. The AT[N] framework (Jack et al., 2018) is the most popular AD research framework that characterizes individuals using amyloid-β pathway (A), tau-mediated pathophysiology (T), and neurodegeneration biomarker (N). Our current work followed the AT[N] framework. Recently, the biomarker matrix has been expanding to an ATX[N] system (Hampel et al., 2021), where X represents novel candidate biomarkers such as neuroimmune dysregulation, synaptic dysfunction, and blood-brain barrier alterations. Upon the availability of new biomarker data in the public database, it is worthwhile to investigate the temporal behaviors of X biomarkers in the aging population.

6. Conclusions

Our findings provided critical refinements that delineate previously undifferentiated heterogeneity within AD progression using a powerful multi-variate statistical model of change point detection. Our investigation focused on the multi-stage progression between AD biomarkers and clinical phenotypes. Our findings extent prior work demonstrating differential associations between AD biomarkers and clinical decline by showing that the T-biomarker exhibits more change points than the A and [N] biomarkers as cognition declines during AD progression. We also observed that genetic risk (i.e. APOE4), biological sex, and cognitive reserve exert important influences on the transition from AD biomarker elevations to clinical phenotypes. Our results highlighted the critical importance of delineating individual differences influencing the impact of AD biomarkers on clinical phenotype.

It is important to recognize that understanding differential risks and rate of AD progression is a critical challenge in the development of precision medicine for the disease. Personalized strategies for prevention, detection, drug development, and disease-modifying therapy can only be effective if they take into account the complex interactions between health disparities and cognitive change over time. Our data-driven approach can help achieve this goal in several ways. Firstly, it can provide a comprehensive understanding of the impact of health disparities on cognitive change over time, which can be used to develop practice guidelines for analyzing and understanding diversities in drug development and disease-modifying therapeutics for AD. Secondly, our approach can reveal new neurobiological mechanisms that link biological indicators with environmental exposures, providing a more in-depth understanding of health disparities in AD. Thirdly, our findings can inform the development of a more effective healthcare system that is accessible and equitable for all Americans, regardless of gender, race, ethnicity, geography, or socioeconomic status.

Data availability

Data will be made available on request.