Feature Selection for Unsupervised Machine Learning

Abstract

Compared to supervised machine learning (ML), the development of feature selection for unsupervised ML is far behind. To address this issue, the current research proposes a stepwise feature selection approach for clustering methods with a specification to the Gaussian mixture model (GMM) and the $k$-means. Rather than the existing GMM and $k$-means which are carried out based on all the features, the proposed method selects a subset of features to implement the two methods, respectively. The research finds that a better result can be obtained if the existing GMM and $k$-means methods are modified by nice initializations. Experiments based on Monte Carlo simulations show that the proposed method is more computationally efficient and the result is more accurate than the existing GMM and $k$-means methods based on all the features. The experiment based on a real-world dataset confirms this finding.

I. Introduction

Feature selection, also known as variable selection, is a popular machine learning (ML) approach for high-dimensional data. The goal is to select a few features (i.e., explanatory variables) from many candidates, such that the result can be better interpreted and understood. Feature selection is particularly important in the case when the number of features (i.e., $p$) is larger than the number of observations (i.e., $n$), known as the large $p$ and small $n$ problem. Currently, feature selection is mostly applied to supervised ML problems, where it assumes that there is a response variable to be interpreted by the explanatory variables. Although unsupervised ML problems are also important in practice, the corresponding feature selection method has not been well-understood. This motivates the goal of the current research.

Rather than supervised ML, unsupervised ML assumes that there is no response in the data. A well-known problem is clustering. Basically, clustering treats all variables as features. It assumes that there is no response in the data. The goal is to partition the data into many clusters (i.e., subsets), such that observations within clusters are the most homogeneous and observations between clusters are the most heterogeneous. Many clustering methods have been proposed. Examples include the $k$-means [1], the $k$-medians [2], the $k$-modes [3], the generalized $k$-means [4], and the Gaussian mixture model (GMM) [5]. Among those, the $k$-means and the GMM are considered the most straightforward and popular. In the literature, clustering is carried out based on all the features. An obvious drawback is that the resulting model may be too complicated if the number of features is large. To address this issue, an convenient way is to apply a feature selection method to select a subset of features. Here we propose a stepwise feature selection approach for clustering methods with specifications to the GMM and the $k$-means, which has obvious advantages over previous methods.

Although our idea can be implemented in any clustering method, we focus our presentation on the $k$-means and the GMM. We assume that data with $n$ observations and $p$ features can be generally expressed as $𝒟=\left\{{\mathit{x}}_1,\dots ,{\mathit{x}}_n\right\}$ with ${\mathit{x}}_i={(x_{i1},\dots ,x_{ip})}^{\mathrm{\top }}\in {ℝ}^p$ representing the $i$th observation for $i\in ℛ=\{1,\dots ,n\}$, where $ℛ$ represents the set of observations (i.e., records). The goal of clustering is to partition $ℛ$ into many clusters (e.g., $k$ clusters) denoted as $𝒞=\left\{C_1,\dots ,C_k\right\}$, which satisfies $C_r\cap C_s=\mathrm{\varnothing }$ for any $r\ne s$ and ${\bigcup }_{r=1}^k{C}_r=ℛ$. To carry out the clustering method, it is necessary to provide the distance between $C_r$ and $C_s$. The distance is often defined by dissimilarity between points with the form of $d({\mathit{x}}_i,{\mathit{x}}_j)$ where $d(\cdot ,\cdot )$ is a certain distance function between points. To carry out feature selection, we treat $d({\mathit{x}}_{iA},{\mathit{x}}_{jA})$ as the distance between the $i$th and $j$th observations, where ${\mathit{x}}_{iA}$ and ${\mathit{x}}_{jA}$ are sub-vectors of ${\mathit{x}}_i$ and ${\mathit{x}}_j$ with their subscripts belonging to some $A\subseteq ℱ=\{1,\dots ,p\}$, respectively. If the partition provided by clustering with feature selection is close to that without, then the number of features is reduced from $p$ to $\left|A\right|$; otherwise, another option of $A\subseteq ℱ$ is investigated. If $p$ is large but $\left|A\right|$ is small, then the result of clustering with feature selection is much easier to understand and better to interpret than that without.

In our experiments, we evaluate our method via Monte Carlo simulations and real-world data. In our simulation study, we find that the number of features can be significantly reduced in both the $k$-means and GMM by our method. For real-world data, we apply our methods to single-cell spatial transcriptomics (SCST) multi-modal dataset [6]. The dataset has $n=\mathrm{79,876}$ observations and $p=981$ variables. Because $p$ is large, we use our method to select important features for clustering. We find that our method works well when 30 features are adopted. We successfully reduce the number of features from 981 to 30.

The contributions of this article are:

• We point out that feature selection is needed in unsupervised ML. This problem has not been well understood yet.

• We define the feature selection problem for a general clustering method with specifications to the $k$-means and GMM.

• We implement our feature selection method to a real data example with many variables. We successfully reduce the number of features to a low level, indicating that our method works well. We find that this cannot be achieved by previous methods.

The remainder of the paper is structured as follows. In Section II, we review the relevant background. In Section III, we propose our method. In Section IV, we evaluate our method by experiments, including both Monte Carlo simulation and real-world application. In Section V, we conclude the article.

II. Background

In the literature, feature selection is usually carried out by the PML approach for a supervised ML problem. An example is the high-dimensional linear model with a large number of features. The purpose is to set the estimates of the regression coefficients for all of the unimportant features to be zero. To achieve this goal, feature selection uses a Lagrangian form objective function with penalty functions added [7].

Two typical clustering methods in unsupervised ML are the GMM and the $k$-means. The GMM assumes that the data are collected from a mixture model with $k$ components with the distribution of the $r$th component given by the PDF of $𝒩({\mathit{\mu }}_k,{\mathbf{\Sigma }}_k)$ denoted as $\phi ({\mathit{x}}_i;{\mathit{\mu }}_r,{\mathbf{\Sigma }}_r),r=1,\dots ,k$. Let ${\mathit{z}}_i={\left(z_{i1},\dots ,z_{ik}\right)}^{\mathrm{\top }}$ be the ground truth of the $i$th observation with $z_{ir}\in \{0,1\}$ and ${\sum }_{r=1}^k{z}_{ir}=1$. Then, ${\mathit{z}}_i$ is the cluster assignment of ${\mathit{x}}_i$, meaning that $z_{ir}=1$ iff ${\mathit{x}}_i$ belongs to the $r$ cluster. The mixture model can be expressed by a complete data version and an incomplete data version. The complete data version assumes that both ${\mathit{x}}_i$ and ${\mathit{z}}_i$ are available, leading to the complete data set as ${𝒟}_c=\left\{\left({\mathit{x}}_i;{\mathit{z}}_i\right):i=1,\dots ,n\right\}$ with the underlying distribution as

$${\mathit{x}}_i\mid {\mathit{z}}_i{\sim }^{iid}\sum _{r=1}^k{z}_{ir}{\phi }_r\left({\mathit{x}}_i;{\mathit{\mu }}_r,{\mathbf{\Sigma }}_r\right).$$ (1)

The incomplete data version treats ${\mathit{z}}_i$ as unobserved latent variables, leading to the observed data set as $𝒟=\left\{{\mathit{x}}_1,\dots ,{\mathit{x}}_n\right\}$. Assume that ${\mathit{z}}_i$ are iid from a Dirichlet distribution with probability vector $\pi ={\left({\pi }_1,\dots ,{\pi }_k\right)}^{\mathrm{\top }}$. By integrating ${\mathit{z}}_i$ out from (1), the distribution of $𝒟$ is obtained as

$${\mathit{x}}_i{\sim }^{iid}\sum _{r=1}^k {\pi }_r{\phi }_r\left({\mathit{x}}_i;{\mathit{\mu }}_r,{\mathbf{\Sigma }}_r\right).$$ (2)

A usable clustering method can only be developed under (2), implying that (1) can only be used for theoretical evaluations.

If ${\mathbf{\Sigma }}_r={\sigma }^2\mathbf{I}$ for $r=1,\dots ,k$, then (2) is the $k$-means (i.e., spherical) model. If ${\mathbf{\Sigma }}_r$ for all $r=1,\dots ,k$ are distinct, then (2) is the quadratic discriminant analysis (QDA) model. The linear discriminant analysis (LDA) model is derived if we assume that all ${\mathbf{\Sigma }}_r$ are identical. To be consistent with the $k$-means problem, it is usually assumed that ${\mathit{\mu }}_r$ are all distinct, leading to the GMM with distinct mean vectors.

The GMM clustering is carried out by an EM algorithm. At the current iteration (i.e., the $t$th iteration), the EM-algorithm updates current iterated values ${\pi }_r^{\left(t\right)},{\mathit{\mu }}_r^{\left(t\right)}$, and ${\mathbf{\Sigma }}_r^{\left(t\right)}$ of ${\pi }_r,{\mathit{\mu }}_r$, and ${\mathbf{\Sigma }}_r$ based on the previous ${\pi }_r^{(t-1)},{\mathit{\mu }}_r^{(t-1)}$, and ${\mathbf{\Sigma }}_r^{(t-1)}$. In the end, the EM algorithm estimates the partition by

$${\hat{C}}_r=\{i:{\hat{z}}_{ir}=\underset{j\in \{1,\dots ,k\}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}{\hat{z}}_{ij}\},r=1,\dots ,k,$$ (3)

where ${\stackrel{\mathit{ˆ}}{\mathit{z}}}_i={\left({\hat{z}}_{i1},\dots ,{\hat{z}}_{ik}\right)}^{\mathrm{\top }}$ is the $i$th final imputed ${\mathit{z}}_i$.

The $k$-means directly computes the current iterative value ${\mathit{z}}_i^{\left(t\right)}$ of ${\mathit{z}}_i$ given the previous centroids ${\mathit{\mu }}_1^{(t-1)},\dots ,{\mathit{\mu }}_k^{(t-1)}$. It then update the current centroids and obtains ${\mathit{\mu }}_1^{\left(t\right)},\dots ,{\mathit{\mu }}_k^{\left(t\right)}$. In the end, it estimates the partition by ${\hat{C}}_r=\left\{i:{\hat{z}}_{ir}=1\right\}$ and the parameters by ${\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_r=(1/|{\hat{C}}_r|){\sum }_{i\in {\hat{C}}_r}{\mathit{x}}_i,r=1,\dots ,k$, where ${\hat{z}}_i={\left({\hat{z}}_{i1},\dots ,{\hat{z}}_{ik}\right)}^{\mathrm{\top }}$ is the final imputed vector of the ground truth. Neither the EM algorithm nor the $k$-means method uses the ground truth $z_i$ in the derivation of ${\hat{C}}_r$. Instead, they use the imputed ${\hat{z}}_i$. Therefore, they are usable.

Although a few variable selection methods for clustering have been proposed, computational prohibition has been identified in the case when the number of variables is moderate due to exponential growth of the computational burden with the number of variables [8]. This issue has been overcome by several methods, such as the sparse $k$-means [9], and the model-based variable selection [10]–[13]. These methods can be implemented by the sparcl, clustvarsel, VarSelLCM packages of R. However, a recent study points out that most of those have not been evaluated by a comprehensive experimental study and there is a lack of theoretical evaluations about how variable selection affects the performance of clustering [14]. This concern is addressed by our work.

III. Methodology

Feature selection for unsupervised learning is fundamentally different from that for supervised ML. The goal is to select a subset of features such that the result of clustering based on the subset can be as accurate as or even more accurate than that based on the entire set. In particular, let $A=\left\{j_1,\dots ,j_a\right\}\subseteq ℱ$ be a candidate subset of features, where $a=\left|A\right|$ is the cardinality of $A$. As both $a$ and $A$ are unknown, there may be as large as $2^p$ subsets to be considered if the brute force approach is adopted. This is impossible if $p$ is only moderate (e.g., $p=20$). Thus, we discard the brute force method and propose a stepwise approach to determine the best $A$. We find that the complexity of our method is $o(p^{2}n)$, indicating that it can be easily implemented even if $p$ is extremely large. We introduce our method below.

We present our method for the case when $A$ is given first and then move our interest to the case when $A$ is selected by the stepwise approach. For a given $A$, we have two ways to implement a clustering method. In the first, we only use the features contained by $A$. We treat ${\mathit{x}}_{iA}={(x_{i{j}_1},\dots ,x_{i{j}_a})}^{\mathrm{\top }}$ as the feature vector of the $i$th observation. We obtain a partition of $ℛ$ denoted as ${𝒞}_A=\left\{C_{1A},\dots ,C_{kA}\right\}$. In the second, we use all of the features. We treat ${\mathit{x}}_i$ as the feature vector of the $i$th observation. We obtain a partition of $ℛ$ denoted as $𝒞=\left\{C_1,\dots ,C_k\right\}$. Because the first only uses $a$ features but the second uses all of the $p$ features, we expect that ${𝒞}_A$ and $𝒞$ are different. We need to study the difference between ${𝒞}_A$ and $𝒞$.

We use the likelihood approach to measure the difference between ${𝒞}_A$ and $𝒞$. We specify the approach to the GMM and the $k$-means methods, respectively. Because ${\mathit{z}}_i$ has been imputed, we can use (1) to compute the imputed complete data loglikelihood under $𝒞$ as

$$\ell (𝒞)=\sum _{r=1}^k\sum _{i\in C_r}\mathrm{l}\mathrm{o}\mathrm{g}[\phi ({\mathit{x}}_i;{\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_r,{\stackrel{\mathbf{ˆ}}{\mathbf{\Sigma }}}_r)],$$ (4)

where ${\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_r={\sum }_{i\in C_r}{\mathit{x}}_i/\left|C_r\right|$ and ${\stackrel{\mathbf{ˆ}}{\mathbf{\Sigma }}}_r={\sum }_{i\in C_r}({\mathit{x}}_i-{\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_r){({\mathit{x}}_i-{\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_r)}^{\mathrm{\top }}/(\left|C_r\right|-1)$ are the estimates of ${\mathit{\mu }}_r$ and ${\mathbf{\Sigma }}_r$, respectively. Similarly, we can compute the imputed complete data loglikelihood based on ${𝒞}_A$ by $\ell \left({𝒞}_A\right)$ after ${\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_r$ and ${\stackrel{\mathbf{ˆ}}{\mathbf{\Sigma }}}_r$ are replaced with ${\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_{rA}={\sum }_{i\in C_{rA}}{\mathit{x}}_i/\left|C_{rA}\right|$ and ${\stackrel{\mathbf{ˆ}}{\mathbf{\Sigma }}}_{rA}={\sum }_{i\in C_{rA}}({\mathit{x}}_i-{\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_{rA}){({\mathit{x}}_i-{\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_{rA})}^{\mathrm{\top }}/(\left|C_{rA}\right|-1)$ under ${𝒞}_A$ in (4), respectively. We use

$$d\left(𝒞,{𝒞}_A\right)=\ell \left(𝒞\right)-\ell \left({𝒞}_A\right)$$ (5)

to measure the difference between $𝒞$ and ${𝒞}_A$ in the GMM method. In the $k$-means method, we use ${\mathbf{\Sigma }}_r={\sigma }^2\mathbf{I}$ for all $r=1,\dots ,k$ to compute the modified imputed complete data loglikelihood $\tilde{\ell }\left(𝒞\right)$ under $𝒞$. Similarly, we compute the modified imputed complete data $\mathrm{l}\mathrm{o}\mathrm{g}$ likelihood $\tilde{\ell }\left({𝒞}_A\right)$ under ${𝒞}_A$. We use

$$\tilde{d}\left(𝒞,{𝒞}_A\right)=\tilde{\ell }\left(𝒞\right)-\tilde{\ell }\left({𝒞}_A\right)$$ (6)

to measure the difference between $𝒞$ and ${𝒞}_A$ in the $k$-means method. We treat the difference given by (5) in the GMM method or (6) in the $k$-means method as the loss of $A$. It is denoted as $\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\left(A\right)$.

As (5) and (6) can only be applied based on a given $A$, we devise our method for the selection of the best $A$. In particular, we compute $\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\left(A\right)$ under a number of $A\subseteq ℱ$ with the best $A$ determined by the minimum loss value. To reduce the number of candidate subsets, we propose a stepwise approach to search for the best $A$. It reduces the number of candidate subsets from $2^p$ to $p^2$, implying that our method can be implemented even if $p$ is large.

The stepwise approach starts with the empty set and adds one of the most important features to $A$ once a time at each step of the iteration. The process continues until no more important features are identified. In the first step, we search for the most important feature in the entire $ℱ$. To achieve this, we compute $\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\left(A\right)$ with $A=\left\{j\right\}$ for all $j\in ℱ$. The most important $j$ is determined by

$$j_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\left(1\right)}=\underset{j\in ℱ}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}loss(\{j\}).$$ (7)

The first step provides $A=\{j_{\text{min}}^{\left(1\right)}\}$ with $a=1$. In the $t$th step for any $t>1$, let $A^{(t-1)}=\left\{j_1,j_2,\dots ,j_{t-1}\right\}$ be the set of important features selected by the previous $t-1$ steps. In the $t$th step, we search the most important feature in $ℱ$ but not in $A^{(t-1)}$. To achieve this, we compute $loss\left(A\right)$ with $A=A^{(t-1)}\cup \left\{j\right\}$ for all $j\in ℱ\setminus A^{(t-1)}$. The most important $j$ is determined by

$$j_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\left(t\right)}=\underset{j\in ℱ\setminus A^{(t-1)}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}loss(A^{(t+1)}\cup \{j\}).$$ (8)

The $t$th step updates the set of important features by $A^{\left(t\right)}=A^{(t-1)}\cup \{j_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\left(t\right)}\}$ with $a=t$. We keep doing this until we cannot find any important features. To determine this, we can use the well-known BIC approach. In this research, we find that the BIC approach is not necessary to be used. This is fundamentally different from variable selection for a supervised learning problem, where BIC or a modification of BIC is considered as necessary. Then, we propose Algorithm 1.

Algorithm 1.

Feature selection for the GMM or the $k$-means

Input: Data set $𝒟=\left\{{\mathit{x}}_1,\dots ,{\mathit{x}}_n\right\}$ and the number of clusters $k$

Output: labels $1,\dots ,k$ for each ${\mathit{x}}_i\in 𝒟$ with the best $A\subseteq ℱ$

Initialization

1: Determine the first $j_{\min }^{(1)}$ by (7) with $loss(A)=d\left(𝒞,{𝒞}_A\right)$ given by (5) if the GMM method is adopted or $loss(A)=\tilde{d}\left(𝒞,{𝒞}_A\right)$ given by (6) if the $k$-means method is adopted

Begin Iteration

2: Let $A^{(t-1)}=\{j_{\min }^{(1)},j_{\min }^{(2)},\dots ,j_{\min }^{(t-1)}\}$ be the previous set of important features and determine the current $j_{\min }^{(t)}$ by (8) and update $A^{(t)}=A^{(t-1)}\cup \{j_{\min }^{(t)}\}$

3: Stop if $t=p$ or no important feature is found; otherwise continue

End Iteration

4: Output

An important issue is to specify $k$ (i.e., the number of clusters) in Algorithm 1. This can be easily solved. There are two scenarios. If $k$ is given, then we can simply use the value of $k$; otherwise, $k$ should be determined by the GMM or the $k$-means with an unknown $k$. The determination of the number of clusters is considered a challenging problem in the implementation of a clustering method. This issue has been previously investigated in the literature. The idea is to implement a given clustering method to a set of candidates of $k$ with the best $k$ to be selected by a predefined criterion. A few criteria have been proposed in the literature. Examples include the minimum message length (MML) criterion [15], the minimum description length (MDL) criterion [16], the Bayesian information criterion (BIC) [4], the silhouette score [17], and the Gap Statistics [18]. We evaluate this issue and find that the determination of $k$ is not a concern. The reason is that we can use the same $k$ determined by the case when all features are used. We assume that $k$ does not vary with $A$ in Algorithm 1. Therefore, $k$ can be assumed to be known in variable selection for a clustering method.

IV. Experiments

We investigate the properties of our method via Monte Carlo simulation and a real-world data example. In both, we use the adjusted rand index (ARI) for the evaluation of the performance. ARI is one of the well-known measures for the accuracy of a clustering method. It is defined as the number of true positives and negatives divided by the total number of pairs. A true positive is a pair of observations claimed in the same cluster by a clustering method and also claimed by the truth. A true negative is a pair of observations claimed in the different clusters by a clustering method and also claimed by the truth. The ARI value is between −1 and 1, with a low value indicating that the result provided by a clustering method does not agree with the truth and 1 indicating that the result is identical to the truth. As the computation of ARI needs the ground truth, it is only used after feature selection is obtained. We determine the best $A\subseteq ℛ$ by $loss\left(A\right)$, which does not need the ground truth. Therefore, ARI is only used for the performance of feature selection.

A. Simulation

We consider two cases in our simulation. In the first case, we simulate data from ${ℝ}^{30}$ with $k=10$ clusters. We represent the feature set as $ℱ=\{1,\dots ,30\}$ and the cluster centers as ${\mathit{\mu }}_r={({\mu }_{r1},\dots ,{\mu }_{r30})}^{\mathrm{\top }}$ for $r=1,\dots ,10$. We assume that the first 3 features are extremely important, the next 3 are weakly important, and the remaining 24 are unimportant. We use a three-step procedure to generate the clusters. In the first step, we generate centres by ${\mu }_{r1},{\mu }_{r2},{\mu }_{r3}{\sim }^{\text{iid}}𝒩(0,1)$, ${\mu }_{r4},{\mu }_{r5},{\mu }_{r6}{\sim }^{iid}𝒩(0,{\varphi }^2)$, and ${\mu }_{r7}=\cdots ={\mu }_{r30}=0$. In the second step, we generated the cluster sizes $n_r{\sim }^{iid}𝒫\left(25\right)$. In the third step, we generate the observations within the clusters. For each cluster, we independently generate $n_r$ observations from $𝒩({\mathit{\mu }}_r,{0.1}^2\mathbf{I})$. Thus, the total number of observations within the $r$th cluster is $n_r$. The total number of observations in the entire data set is $n={\sum }_{r=1}^k{n}_r$. The distance between the clusters is primarily controlled by the first three features with the adjustment by the second three features based on $\varphi$ with $\varphi =0.0,0.1,0.2,0.3$, respectively.

We investigate four clustering methods. All of them assumes that ${\mathbf{\Sigma }}_r={\sigma }^2\mathbf{I}$ for all $r=1,\dots ,10$. The GMM partitions the data by $loss\left(A\right)$ given by (5) in Algorithm 1. The iterations of the basic $k$-means and the $k$-means++ methods are the same. They partition the data with $loss\left(A\right)$ given by (6) in Algorithm 1. The difference is that the basic $k$-means randomly chooses its initialization, but the $k$-means++ uses a probability distribution to determine its initialization. As the performance of both the $k$-means and the $k$-means++ is bad, we also consider another version of the $k$-means method proposed by [19]. As it improves the initialization of the $k$-means by the max-min principal, we denote this method as $k$-meansMM.

We simulate 100 datasets for each selected $\varphi$ value. For each generated data set, we use Algorithm 1 to select features. After the best $A$ is determined, we compare their performance by examining their ARI values. We calculate the average ARI values based on the 100 replications (Table I). We find that the $k$-meansMM method is the best and the GMM is the worst. To understand this issue, we study the ARI curves obtained from each of the simulated datasets (e.g., Figure 1). We find that the curves of the GMM, the basic $k$-means, and the $k$-means++ are unstable, leading to their low ARI values. In the $k$-meansMM, it is enough to use the three most important features, implying that 90% of the features can be ignored. Overall, the $K$-meansMM performs the best. It is significantly better than the GMM, the basic $k$-means, and the $k$-means++ in feature selection, implying that initialization is a critical issue in the clustering methods.

TABLE I:

Simulated ARI values obtained from 100 replications for the comparison of feature selection with respect to the $k$-meansMM ($k\text{MM}$), the GMM, the basic $k$-means $\left(k\right)$, and the $k$-means++ ($k\text{++}$) methods.

		Number of Features $\left(a\right)$
Method	$\varphi$	1	2	3	4	5
$k\text{MM}$	0.0	0.599	0.928	0.963	0.962	0.963
	0.1	0.595	0.925	0.960	0.958	0.958
	0.2	0.606	0.933	0.987	0.988	0.989
	0.3	0.593	0.938	0.992	0.996	0.996
GMM	0.0	0.357	0.500	0.491	0.483	0.486
	0.1	0.410	0.558	0.543	0.549	0.546
	0.2	0.445	0.607	0.620	0.596	0.602
	0.3	0.442	0.622	0.621	0.608	0.615
$k$	0.0	0.591	0.764	0.798	0.798	0.801
	0.1	0.577	0.762	0.803	0.813	0.801
	0.2	0.594	0.787	0.812	0.804	0.805
	0.3	0.582	0.779	0.821	0.828	0.827
$k\text{++}$	0.0	0.588	0.761	0.790	0.788	0.783
	0.1	0.580	0.756	0.792	0.800	0.792
	0.2	0.586	0.756	0.786	0.791	0.793
	0.3	0.578	0.783	0.818	0.814	0.818

Fig. 1:

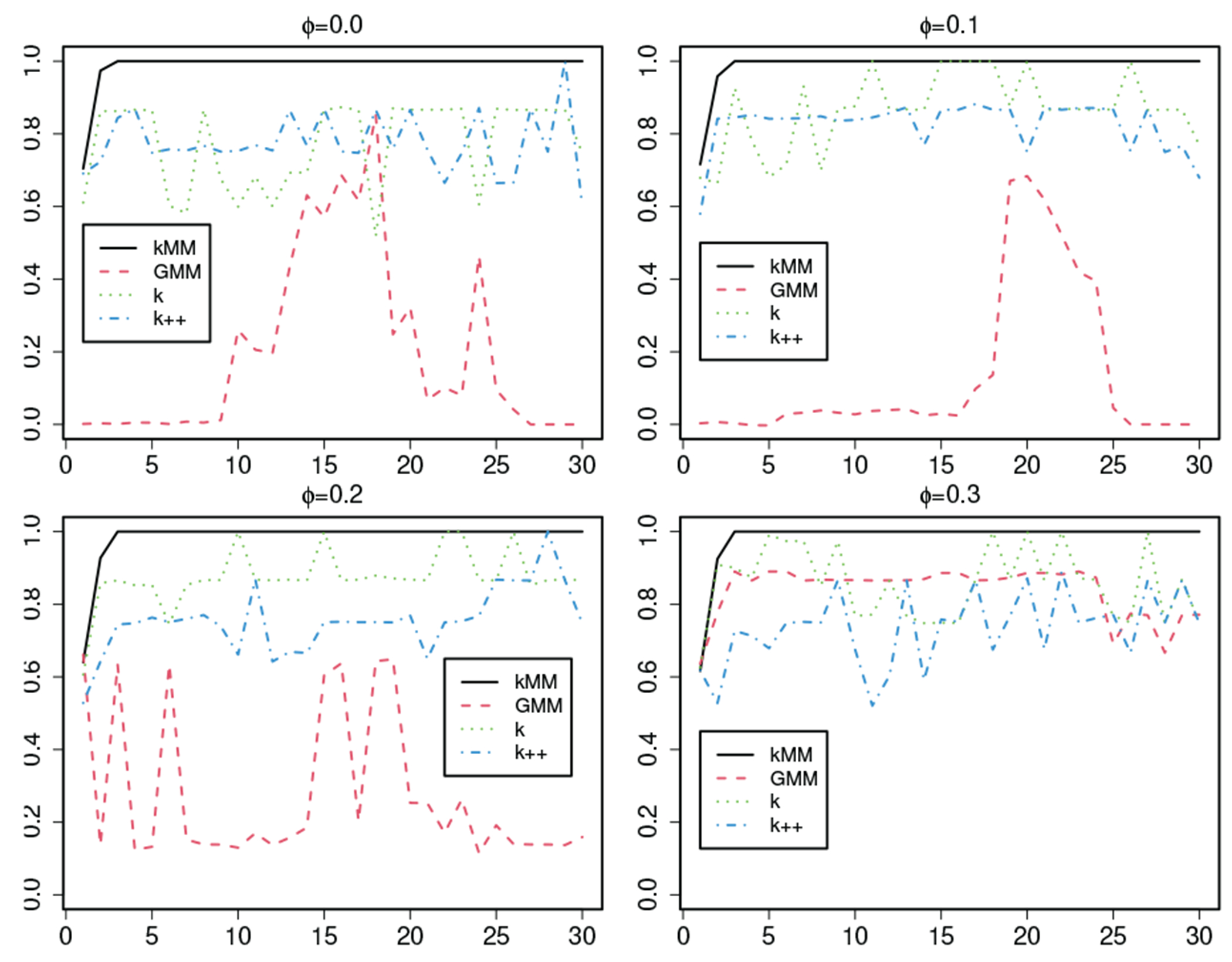
ARI curves obtained from a simulated dataset with feature sets selected by Algorithm 1 with respect to the $k$-meansMM ( $k\text{MM}$), the GMM, the basic $k$-means $\left(k\right)$, and the $k$-means++ ($k\text{++}$) methods, where the horizontal axis represents the number of clusters and the vertical axis represents the ARI values.

In the second case, we simulated data from ${ℝ}^{1000}$ with $k=2$ clusters (i.e., $p=1000$). We choose cluster centers as ${\mathit{\mu }}_r={({\mu }_{r1},\cdots ,{\mu }_{rp})}^{\mathrm{\top }}$ with ${\mu }_{11}={\mu }_{12}=0.16$, ${\mu }_{21}={\mu }_{22}=-0.16$, and ${\mu }_{rj}=0$ if $j\ge 3,r=1,2$. For each cluster, we independently generated $n_r=10$ observations from $𝒩({\mathit{\mu }}_r,{0.1}^2\mathbf{I})$. We then implement the basic $k$-means, the $k$-means++, the $k$-meansMM, and the GMM to the first $q$ features. We calculate the average ARI values based on 1000 replications (Figure 2). We find that the ARI values decrease with $q$. Note that only the first 2 features are useful. The simulation indicates that the performance of clustering becomes bad if non-informative features are used. If non-informative variables are removed by a variable selection method, then the accuracy of clustering becomes better for all of the methods that we have studied. Therefore, we conclude that variable selection can improve the performance of clustering.

Fig. 2:

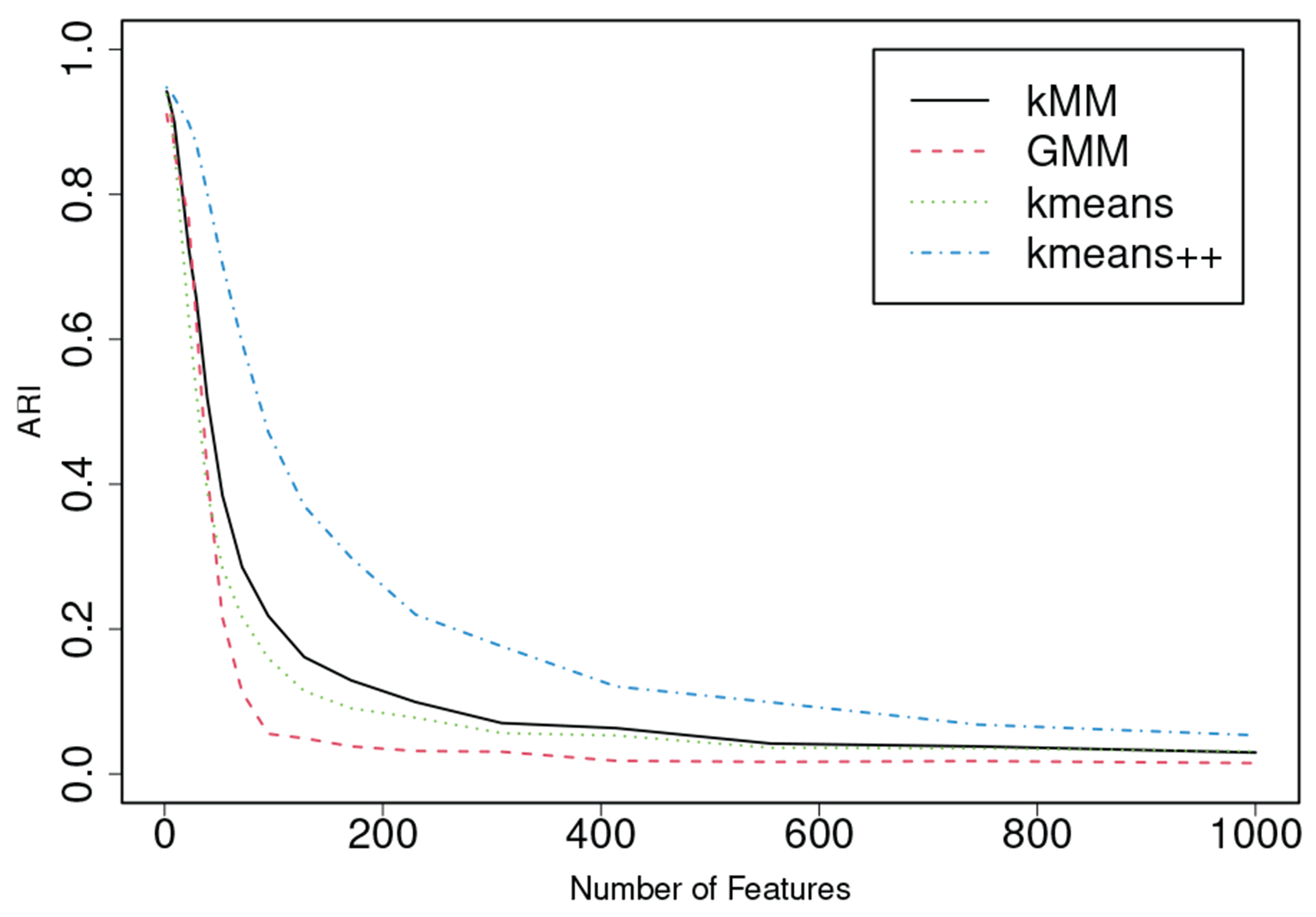
ARI curves obtained from simulation with 1000 replications when $k=2$ and ${\mathit{x}}_i\sim 𝒩({\mathit{\mu }}_r,{0.1}^2\mathbf{I})$ independently, where ${\mathit{\mu }}_2=-{\mathit{\mu }}_1,{\mu }_{11}={\mu }_{12}=0.16,{\mu }_{1j}=0$ for all $j\ge 3$.

B. Application

We apply our method to the single-cell spatial transcriptomics (SCST) multi-modal data set [6]. The SCST data set collects the gene expression based on the SCST images for lung cancer from the NanoString CosMx^™ SMI platform (Figure 3). The date set mainly contains six kinds of cells, including 37281 tumor, 13368 fibroblast, 11664 lymphocyte, 7560 Mcell, 5731 neutrophil, and 4272 endothelial cells. Regarding the NanoString Lung-9-1 dataset, the composite images of the DAPI, PanCK, CD45, and CD3 channels from 20 fields of views (FOVs), the cell center coordinates (from the cell metadata file), the single-cell gene expression file of 960 genes are used. For each cell, four images of 120-by-120 pixels with the cell at the center are cropped from the images. The spatial adjacent graph is constructed based on the cell-to-cell distance (Euclidian distance) $\le 80$ pixels. NanoString’s annotations of cell types are obtained from their provided Giotto object. A feature extractor was applied to project the gene expression into the high-dimensional latent space, which provided 21 additional variables [20].

Fig. 3:

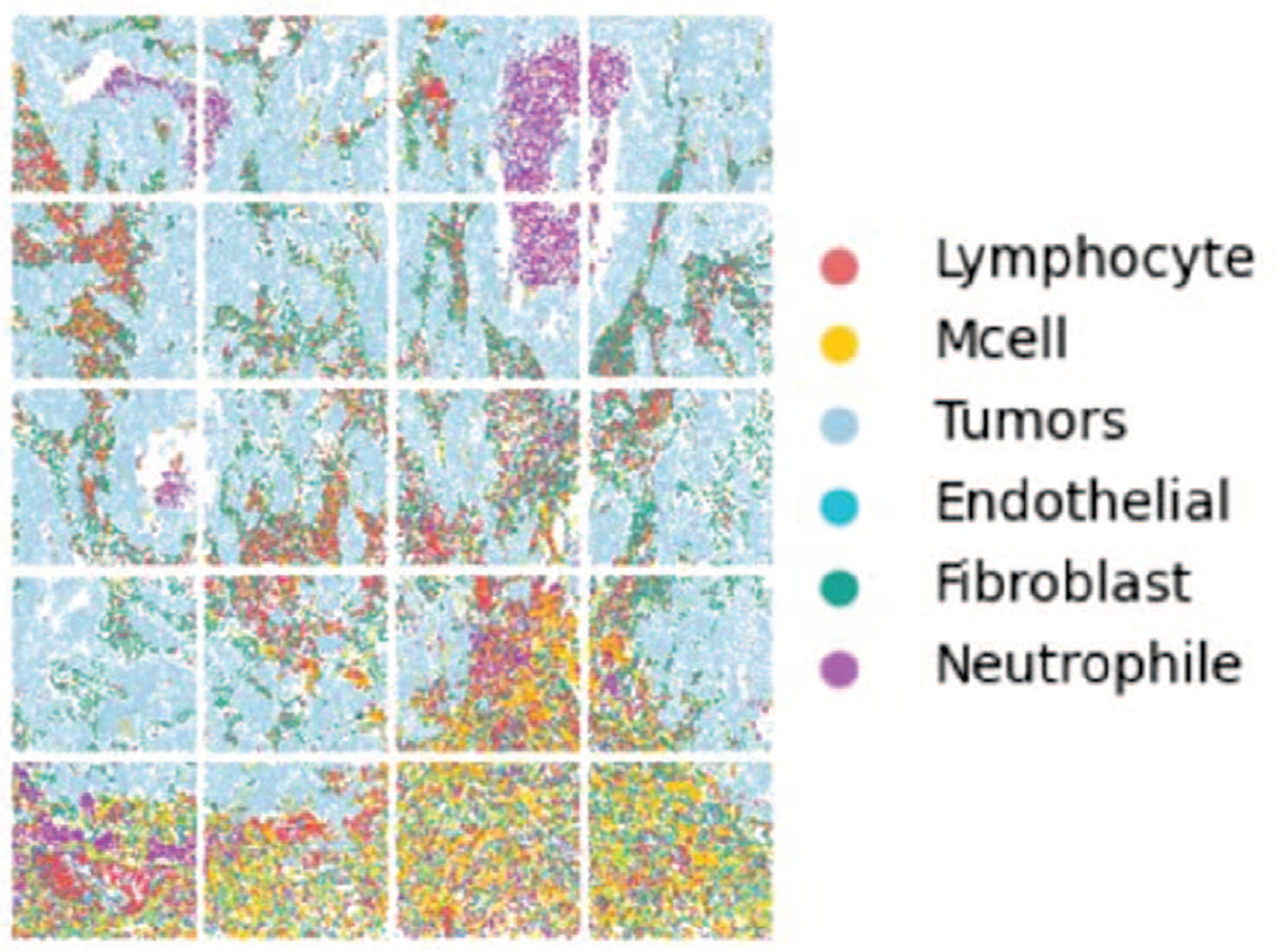
The SCST Images for Lung Cancer from the NanoString CosMx^™ SMI platform

We apply Algorithm 1 with $k=6$ to three clustering methods. The first is the GMM-LDA, which assumes that ${\mathbf{\Sigma }}_r$ are all identical. The second is the GMM-Sphere, which assumes ${\mathbf{\Sigma }}_r={\sigma }^2\mathbf{I}$ for all $r=1,2,3,4,5,6$. The third is the $k$-means method. We consider two initialization frameworks. The first uses a random initialization. The second searches for a nice initialization by investigating hundreds of initializations with the best one reported by that with the minimum loss value. We carry out feature selection to the three clustering methods with two initialization frameworks, implying that we have six methods. For each of those, we use $loss\left(A\right)$ to select the best $A$ with a number of candidates of $a=\left|A\right|$. After $A$ is derived, we evaluate their performance by examining their ARI values (Table II). We find that the best $a$ is about 27. To confirm this, we study the curves of $1-R^2=SSE/SST$, where $SSE$ is the sum of squares of errors and $SST$ is the sum of squares of the total. The best options should have the lowest $1-R^2$ values. In the end, we conclude that the GMM-LDA with a nice initialization is the best method for the implementation of our method.

TABLE II:

ARI of feature selection for the GMM-LDA, the GMM-Sphere, and the $k$-means clustering methods with random and nice initialization respectively for the SCST multimodal data

	Number of Features $\left(a\right)$
Method	26	27	28	29	30
LDA Nice	0.450	0.659	0.536	0.537	0.537
LDA Random	0.378	0.457	0.430	0.500	0.462
Sphere Nice	0.392	0.395	0.534	0.545	0.545
Sphere Random	0.340	0.273	0.349	0.391	0.391
$k$-means Nice	0.387	0.499	0.518	0.535	0.534
$k$-means Random	0.376	0.390	0.310	0.389	0.286

We check the GMM-LDA, the GMM-Sphere, and the $k$-means when all the 981 features are used. Our result shows that the ARI values of the GMM-LDA and the GMM-Spheres with a random initialization are 0.554 and 0.280, respectively. The ARI value of the $k$-means with a random initialization is 0.375. If the nice initialization approach is considered, then the ARI values of the GMM-Sphere and the $k$-means are 0.368 and 0.463, respectively. We are not able to derive that for the GMM-LDA, because each computation takes more than 5 fours, implying the derivation needs over a thousand hours.

In the end, we compare our method with a few previous methods. These include the sparse clustering (by sparcl package of R) [9], the model-based clustering (by clustvarsel package of R) [10], and another model-based clustering (by VarSelLCM package of R) [11]. Our experiment shows that the sparcl was out-of-memory with an error message saying that it could not allocate a vector of size 47.5GB, the clustvarsel did not provide anything within two days, and the VarSelLCM selected all 980 features by 1.72 days with ARI 0.216. As the computational time was less than 15 minutes, we conclude that our method is more computationally efficient and more accurate than our competitors.

V. Conclusion and Future Work

We treat our method as the first variable selection method for unsupervised machine learning problems because this problem has never been studied previously. We expect that our idea can be applied to arbitrary clustering methods, although we focus on the GMM and $k$-means. To carry out variable selection, it is important to investigate the initialization issue in existing clustering methods. We have proposed an approach to the $k$-means and GMM methods. For other clustering methods beyond the $k$-means and the GMM, this should also be investigated. This is left to future research.

Fig. 4:

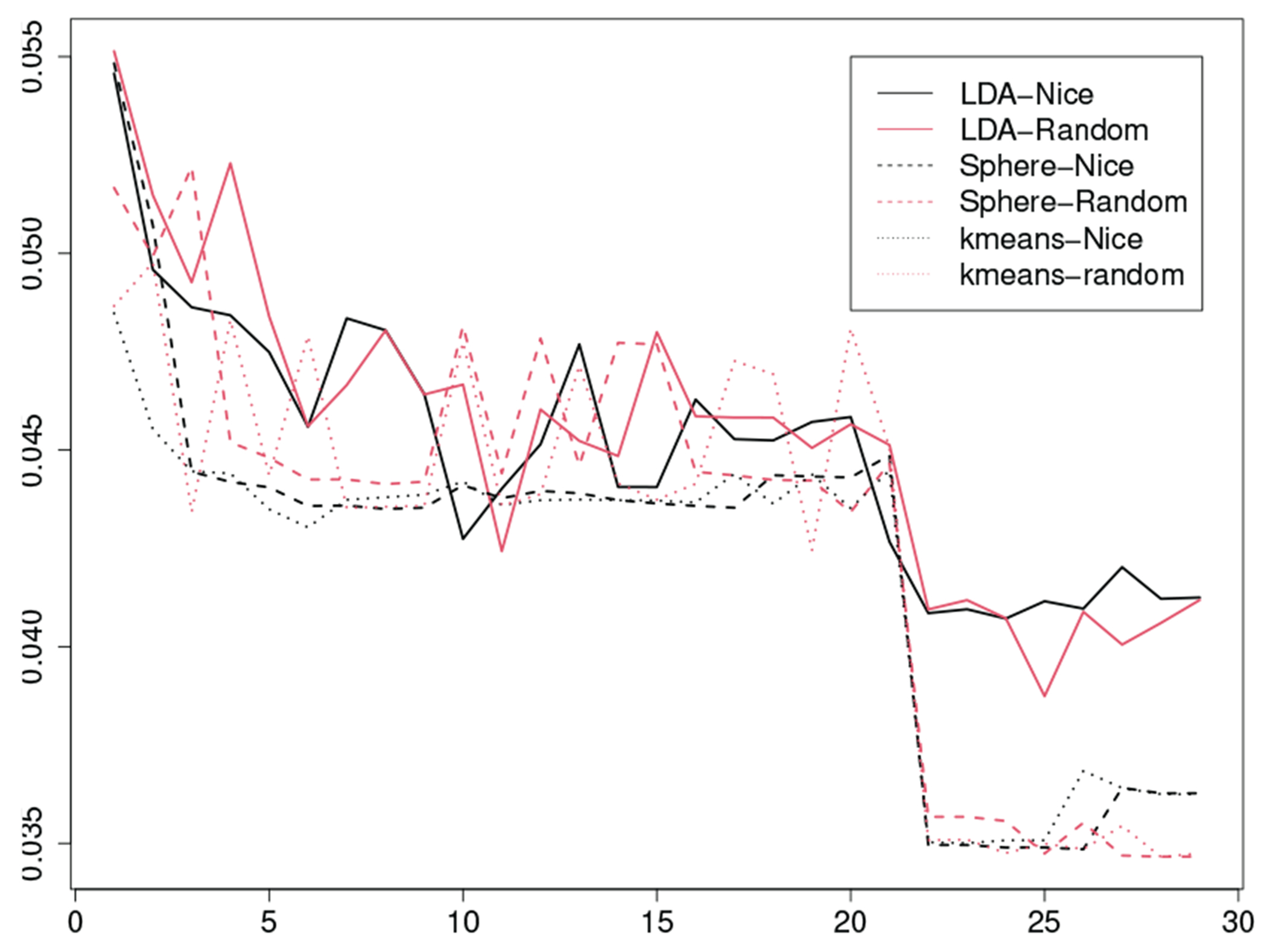
The $1-R^2$ curves for the GMM-LDA, the GMM-Sphere, and the $k$-means with a nice initialization and a random initialization, respectively, where the horizontal axis represents the number of features and the vertical axis represents the values of $1-R^2=SSE/SST$.