Abstract
目的
构建一种处理混合相依删失数据的非参数比例风险(PH)模型, 探讨心脏移植手术风险与风险因子直接的关系并预测心脏移植手术风险。
方法
基于混合相依区间删失数据的复杂性, 考虑失效时间过程与观测时间过程的相依关系, 假设风险因子与心脏移植手术风险存在非线性函数关系, 建立具有非参数结构的比例风险模型, 并给出两步Sieve估计极大似然算法。根据观测过程模型建立估计方程, 获得脆弱变量的估计; 再分别利用I-样条和B-样条去近似基准风险函数和非参数结构函数, 获得Sieve空间中的工作似然函数, 对于模型参数求偏导获得得分方程; 最后通过求解方程获得参数的极大似然估计, 绘制风险因子影响心脏移植手术风险的函数曲线。
结果
模拟研究揭示了各种设置下所提方法获得的估计量是相合的且渐近有效的, 同时获得很好的参数拟合曲线。心脏移植手术数据分析结果显示, 心脏供体的年龄对患者手术风险影响呈现正向线性关系, 患者(受体)发病年龄影响先增大后平稳, 最后有缓慢增大, 供体与受体的年龄差对患者手术风险影响呈现正向线性关系。
结论
本研究建立了一个可分析复杂相依删数据的非参数PH模型, 该模型应用于分析预测心脏移植手术风险, 通过模型可探索出心脏移植手术风险与风险因子之间的函数关系。
Keywords: 心脏移植手术, 相依区间删失, 非参数比例风险模型, 两步估计方法, Sieve极大似然估计
Abstract
Objective
To construct a nonparametric proportional hazards (PH) model for mixed informative interval-censored failure time data for predicting the risks in heart transplantation surgeries.
Methods
Based on the complexity of mixed informative interval-censored failure time data, we considered the interdependent relationship between failure time process and observation time process, constructed a nonparametric proportional hazards (PH) model to describe the nonlinear relationship between the risk factors and heart transplant surgery risks and proposed a two-step sieve estimation maximum likelihood algorithm. An estimation equation was established to estimate frailty variables using the observation process model. Ⅰ-spline and B-spline were used to approximate the unknown baseline hazard function and nonparametric function, respectively, to obtain the working likelihood function in the sieve space. The partial derivative of the model parameters was used to obtain the scoring equation. The maximum likelihood estimation of the parameters was obtained by solving the scoring equation, and a function curve of the impact of risk factors on the risk of heart transplantation surgery was drawn.
Results
Simulation experiment suggested that the estimated values obtained by the proposed method were consistent and asymptotically effective under various settings with good fitting effects. Analysis of heart transplant surgery data showed that the donor's age had a positive linear relationship with the surgical risk. The impact of the recipient's age at disease onset increased at first and then stabilized, but increased against at an older age. The donor-recipient age difference had a positive linear relationship with the surgical risk of heart transplantation.
Conclusion
The nonparametric PH model established in this study can be used for predicting the risks in heart transplantation surgery and exploring the functional relationship between the surgery risks and the risk factors.
Keywords: heart transplantation surgery, informative interval-censored, nonparametric proportional hazards model, two step estimation method, sieve likelihood estimation
在生物医学数据分析中,不完全数据是由于实验条件等客观因素的局限性而产生,其数据类型包括缺失数据和删失数据等。区间删失是生存分析中一种常见且复杂的数据类型,该数据中感兴趣事件的时间只能在某一时间区间内,但不知道准确时间。更一般化的区间删失数据是K型区间删失数据,对每一个个体兴趣存在一系列的观测时间或者随机K个观测时间点,兴趣事件发生的时间落在K个观测时间形成的最小区间内[1-3],因此Case K型区间包括Ⅰ型区间删失数据[4, 5]和Ⅱ型区间删失删失数据[6, 7]。特别地,当K=1时,表示为Ⅰ型区间删失数据或者现状数据,表示个体只被观测1次,仅知道在观测时间处兴趣事件是否发生,即个体所处状态。当K=2时为Ⅱ型区间删失数据,表明个体被观测2次,兴趣事件发生在第1次观测,或者发生在两次观测之间,或者发生在第2次观测之后。
在医学疾病数据分析中,常常通过构建参数模型来分析删失数据。参数模型的使用前提假设是生存时间服从特定的概率分布,但在实际应用中该条件并不一定满足。参数模型在选择分布假设时需要良好的先验知识和对数据的充分理解,若假设分布不适合实际数据,参数模型可能产生偏差或无效。在现实生活中大多数据都具有非线性结构[8, 9],并且在实际应用中将非线性问题转换成线性问题的假设是错误的。现在已有的文献都是解决线性数据的,非线性数据的应用没有得到解决[10, 11]。因此,需要利用非参数模型对非线性删失数据的进行研究。
非参数模型可以不对生存分布的形状进行任何假设,从而提供了更灵活和广泛适用的分析框架。相比于传统的参数化模型,非参数模型的分布假设灵活性,其不需要事先假设生存分布的具体形状,使得它们可以适应更广泛的生存数据模式和分布特征。非参数模型倾向于更加数据驱动,能够基于实际观察到的数据模式推断风险函数,而不受事先设定的参数假设的限制。传统的参数化模型在处理偏斜分布的生存数据时可能会遇到困难,而非参数模型则不受此限制,能够更好地适应不同形态的生存数据[12]。非参数模型在生存分析中能够更好地分析和理解生存数据的特征和关联性。
在生存分析研究中,感兴趣的往往是各个风险因子与失效时间风险函数之间的关系,因此考虑加性风险模型[13, 14]和比例风险模型[15, 16]的假设,建立风险因子与兴趣事件发生时间的风险模型。Wang等[2]、Zhao等[17]和Wang等[18]将可加性风险模型应用到疾病的临床数据中,研究者们还考虑了比例风险模型的情况[3, 19]。以上研究是在线性结构下考虑的,而现实生活中的许多实际问题是具有非线性结构的,现有方法无法解决具有非线性结构的实际问题。因此,本文考虑了非参数比例风险脆弱模型来解决协变量与失效时间之间的关系。在非参数比例结构的模型中,估计非参数函数以及其他参数十分困难,为解决该问题,考虑Sieve空间近似方法[2, 20, 21],从而实现非参数结构及其他函数的估计。
1. 统计模型和方法
1.1. Case K区间删失数据
对于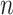 个受试者组成的失效时间的研究,设
个受试者组成的失效时间的研究,设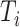 表示第
表示第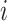 个受试者对感兴趣事件的失效时间,
个受试者对感兴趣事件的失效时间,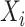 表示第
表示第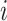 个受试者的
个受试者的 维协变量,其中
维协变量,其中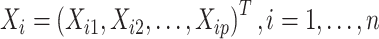 。在实际问题中,失效时间
。在实际问题中,失效时间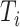 经常不能被精确观测到,仅能观测到一系列的观测时间点
经常不能被精确观测到,仅能观测到一系列的观测时间点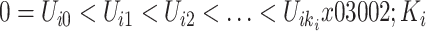 表示第
表示第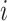 个受试者的观测次数。关于第
个受试者的观测次数。关于第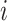 个受试者,定义示性函数
个受试者,定义示性函数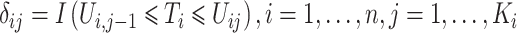 以及观测过程为
以及观测过程为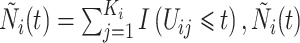 表示第
表示第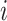 个受试者截止到时间
个受试者截止到时间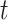 的观测次数之和,
的观测次数之和,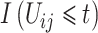 为观测时间点小于
为观测时间点小于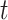 的示性函数。设
的示性函数。设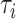 表示的是第
表示的是第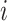 个受试者的观测的终止时间,且与失效时间
个受试者的观测的终止时间,且与失效时间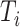 独立。设
独立。设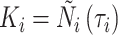 ,其中
,其中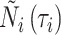 表示第
表示第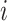 个受试者到时间
个受试者到时间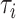 为止的观测总次数。Case
为止的观测总次数。Case 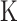 区间删失数据的结构为
区间删失数据的结构为
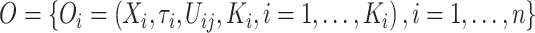 |
当个体的观测次数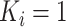 时,删数据表示为Case Ⅰ型区间删失数据,当个体的观测次数
时,删数据表示为Case Ⅰ型区间删失数据,当个体的观测次数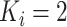 时,删数据表示为Case Ⅱ型区间删失数据。在Case K区间删失数据中,观测过程与失效时间经常存在相依关系,从而产生相依或信息区间删失数据。
时,删数据表示为Case Ⅱ型区间删失数据。在Case K区间删失数据中,观测过程与失效时间经常存在相依关系,从而产生相依或信息区间删失数据。
1.2. 非参数比例风险模型
非参数比例风险模型作为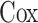 比例风险模型的扩展,涉及到风险回归的协变量效应的可加性非线性组合, 模型形式更加灵活。为描述失效时间过程与观测过程之间的关系,假设存在一个共享的潜变量
比例风险模型的扩展,涉及到风险回归的协变量效应的可加性非线性组合, 模型形式更加灵活。为描述失效时间过程与观测过程之间的关系,假设存在一个共享的潜变量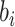 ,在给定协变量
,在给定协变量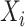 和潜变量
和潜变量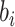 时,失效时间
时,失效时间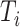 满足非参数比例风险模型
满足非参数比例风险模型
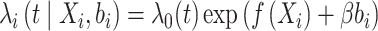 |
1 |
其中,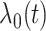 是一个完全未知的基准风险函数,β是一个未知的回归参数。对于协变量Xi,根据Sleepe等[22]的想法,非参数函数
是一个完全未知的基准风险函数,β是一个未知的回归参数。对于协变量Xi,根据Sleepe等[22]的想法,非参数函数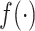 为
为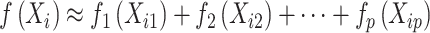 ,其中
,其中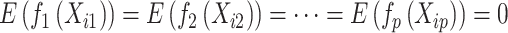 。
。
为描述观测过程,假设观测过程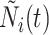 的模型为
的模型为
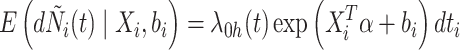 |
2 |
其中,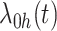 是一个未知的连续基准比率函数,α是一个回归参数的向量。
是一个未知的连续基准比率函数,α是一个回归参数的向量。
给定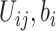 和
和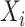 所得的条件似然函数为
所得的条件似然函数为
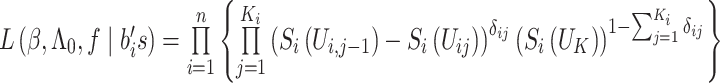 |
其中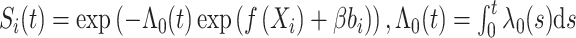 。在计算过程中需要考虑到潜变量bi分布,计算会变得复杂。为了避免这些问题,接下来采用两步估计法。
。在计算过程中需要考虑到潜变量bi分布,计算会变得复杂。为了避免这些问题,接下来采用两步估计法。
1.3. 两步估计法
假设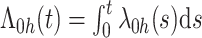 ,并且
,并且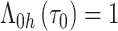 ,其中
,其中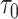 表示最长的随访时间。首先,估计模型(2)。具体地,定义
表示最长的随访时间。首先,估计模型(2)。具体地,定义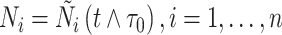 ,
,
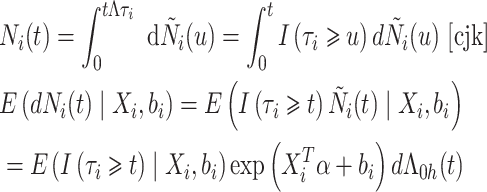 |
在模型(2)的假设下,给定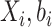 ,则
,则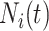 的条件期望表示为
的条件期望表示为
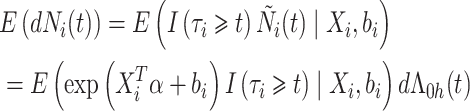 |
在上述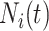 条件期望下,参考Zhao等[17]可得
条件期望下,参考Zhao等[17]可得
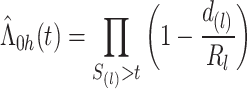 |
3 |
其中,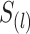 是有序的观测时间
是有序的观测时间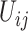 的不同值,
的不同值,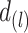 是观测时间
是观测时间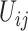 等于
等于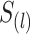 的次数,
的次数,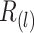 是观测时间和观测终止时间满足
是观测时间和观测终止时间满足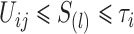 的观测事件总数。为了估计回归参数
的观测事件总数。为了估计回归参数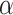 ,注意到
,注意到
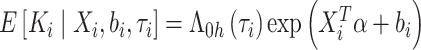 |
因此推导出
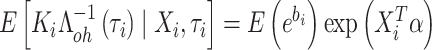 |
从而,可获得估计方程为
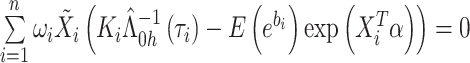 |
其中,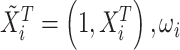 是依赖于
是依赖于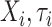 和
和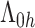 的权重。设
的权重。设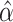 表示参数
表示参数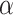 的估计量,
的估计量,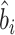 表示参数
表示参数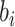 的估计量,
的估计量,
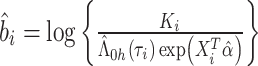 |
进而,给定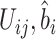 和
和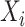 所得的条件似然函数为
所得的条件似然函数为
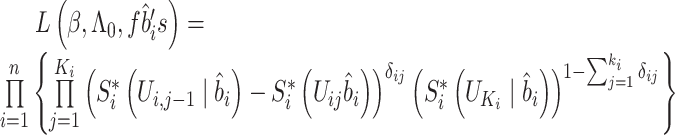 |
其中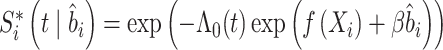 。
。
1.4. Sieve极大似然估计
由于似然函数中的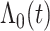 和
和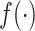 都是一个无限维的未知函数,其估计过程相对比较困难。因此,基于多项式样条近似非参数函数
都是一个无限维的未知函数,其估计过程相对比较困难。因此,基于多项式样条近似非参数函数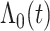 和
和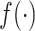 的近似函数
的近似函数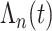 和
和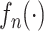 [23, 24]。具体地,假设
[23, 24]。具体地,假设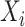 取
取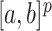 中的值,其中
中的值,其中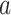 和
和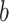 是有限数。设
是有限数。设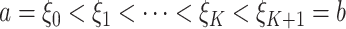 是将
是将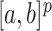 划分为
划分为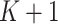 个子区间的一组节点,示性函数
个子区间的一组节点,示性函数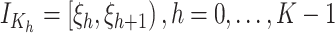 ,和
,和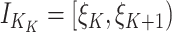 ,其中
,其中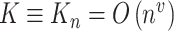 表示与样本容量相关的正整数,满足
表示与样本容量相关的正整数,满足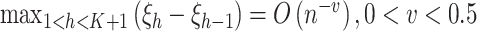 。由Stone等[25]研究可知,在
。由Stone等[25]研究可知,在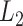 范数中,非参数估计在
范数中,非参数估计在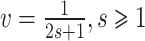 时可以实现的最优收玫速度
时可以实现的最优收玫速度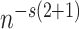 ,这表明
,这表明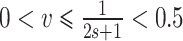 。
。
在这些条件下,假设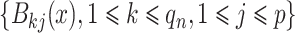 表示B样条基函数,基函数的个数
表示B样条基函数,基函数的个数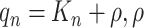 表示样条的阶数,
表示样条的阶数,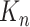 表示样条的节点数,非参数函数
表示样条的节点数,非参数函数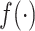 的近似函数
的近似函数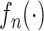 可以写成
可以写成
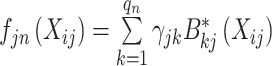 |
且
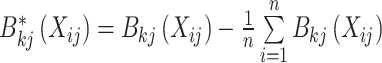 |
因此,
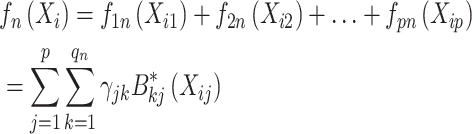 |
其中,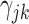 表示样条函数的系数。
表示样条函数的系数。
利用类似的近似方式,通过I样条函数近似累积基准风险函数。假设观测时间在区间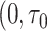 ] 上是紧集,对这个区间进行划分,使得
] 上是紧集,对这个区间进行划分,使得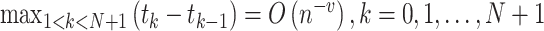 ,其中
,其中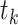 是节点,
是节点,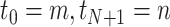 和
和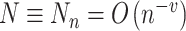 。累积基准风险函数的近似函数
。累积基准风险函数的近似函数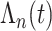 可以写成
可以写成
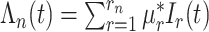 |
其中,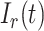 表示I样条基函数,
表示I样条基函数,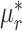 表示样条系数,根据Schumaker等[26]的定理5.9,通过对系数的约束来保证
表示样条系数,根据Schumaker等[26]的定理5.9,通过对系数的约束来保证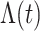 的非负性和单调性,因此样条系数满足
的非负性和单调性,因此样条系数满足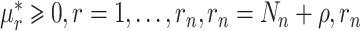 表示基函数的个数,
表示基函数的个数,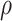 表示I样条基函数的阶数,
表示I样条基函数的阶数,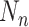 表示I样条的节点个数。为了将单调约束问题转化为没有约束的问题,对I样条系数重新参数化,则假设
表示I样条的节点个数。为了将单调约束问题转化为没有约束的问题,对I样条系数重新参数化,则假设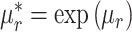 ,因此
,因此
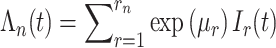 |
4 |
在样条近似下,可以得到工作似然函数
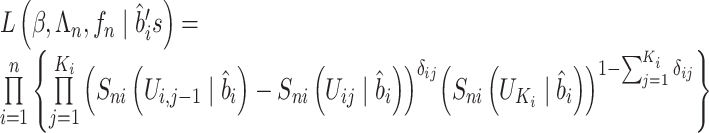 |
其中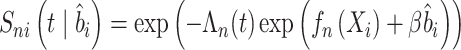 。
。
为了优化该似然函数,得到它的估计量作为极大似然估。得到的对数似然为
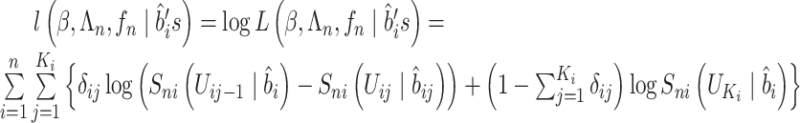 |
定义非参数函数的系数向量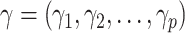 ,其中
,其中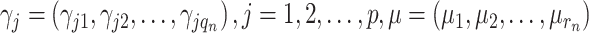 。为了获得模型的参数估计,基于一阶偏导数可获得如下得分方程
。为了获得模型的参数估计,基于一阶偏导数可获得如下得分方程
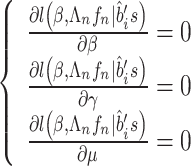 |
假设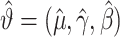 表示模的极大似然估计,可得
表示模的极大似然估计,可得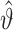 为上述方程(5)式的解。为获得参数估计
为上述方程(5)式的解。为获得参数估计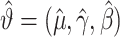 的方差,借用Efron等[27]提出的Bootstrap重抽样方法进行计算。具体地,假设正整数B表示预先给定的常数。对于每个
的方差,借用Efron等[27]提出的Bootstrap重抽样方法进行计算。具体地,假设正整数B表示预先给定的常数。对于每个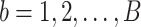 ,从观测数据
,从观测数据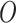 中抽取1个大小
中抽取1个大小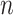 为的随机样本
为的随机样本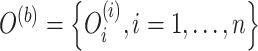 ,令
,令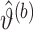 表示基于重抽样数据集
表示基于重抽样数据集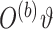 的估计量。
的估计量。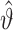 的协方差矩阵的估计量由(6)式计算得出
的协方差矩阵的估计量由(6)式计算得出
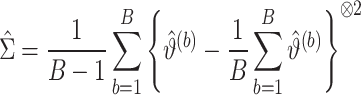 |
其中,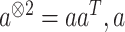 表示一个向量。
表示一个向量。
2. 数值模拟
为验证Case K区间删失数据下提出方法的优良性质,本节进行了大量的数值模拟。假设协变量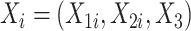 ,且协变量
,且协变量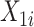 服从均匀分布
服从均匀分布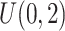 ,且协变量
,且协变量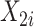 服从均匀分布
服从均匀分布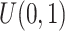 以及协变量
以及协变量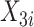 服从均匀分布
服从均匀分布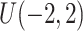 。考虑两种脆弱变量
。考虑两种脆弱变量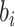 ,第1种假设
,第1种假设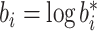 ,且
,且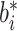 服从形状参数为2,逆尺度参数为
服从形状参数为2,逆尺度参数为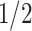 的伽马分布,即
的伽马分布,即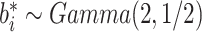 。第2种假设是
。第2种假设是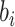 服从均值为0,方差为4的正态分布,即
服从均值为0,方差为4的正态分布,即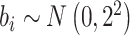 。为了生成失效时间,考虑两种基准风险函数, 第一种是假设基准风险函数是二次函数
。为了生成失效时间,考虑两种基准风险函数, 第一种是假设基准风险函数是二次函数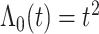 和复杂
和复杂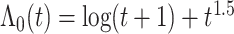 。假设
。假设
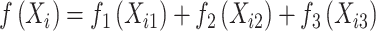 |
且
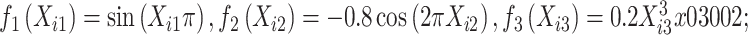 |
因此基于模型(1)生成了真实失效时间Ti's。
为生成观测时间,首先在区间[2, 3]上生成服从均匀分布的τi's,其次设置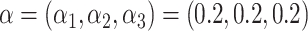 。假设均值为
。假设均值为
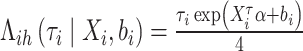 |
的非齐次泊松分布,并生成观测次数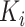 。最后在区间
。最后在区间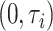 上生成
上生成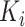 个随机数据排序获得观测时间
个随机数据排序获得观测时间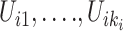 。比较失效时间与观测时间的关系获得示性函数
。比较失效时间与观测时间的关系获得示性函数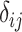 。
。
表 1汇总了样本容量n = 200,400,脆弱变量的系数β = 0,-0.2,0.2,重复次数为1000次的模拟结果。结果包括估计值减去真实值得到的平均偏差(Bias)、理论标准差(SEE)和重复1000次获得的经验标准差(SSE)以及经验覆盖概率(CP)。从表中结果可知估计量的平均偏差较小,且接近于0,估计值基本接近真实值,理论标准差(SEE)和经验标准差近似相等,覆盖概率的估计值在0.95左右波动,因此估计结果是相合。随样本量的增大,估计量的Bias和SEE均减小,因此,提出的方法获得估计量是相合的且渐近有效的。在改变脆弱变量的分布假设时,提出方法的估计结果表现一致,因此该表脆弱变量假设时,所获得的结果是稳健的。此外,根据表中结果发现,变化累积基准风险函数假设为二次函数时,脆弱变量的系数估计结果表现良好,改变基准风险函数形式时,参数估计仍然是稳健的。
表 1.
基于基于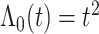 和
和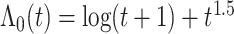 的
的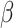 估计的模拟结果
估计的模拟结果
Simulation results on estimation of 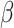 based on
based on 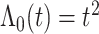 and
and 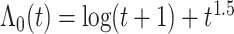
| β | Bias | SSE | SEE | CP | Bias | SSE | SEE | CP |
| n = 200 | n = 400 | |||||||
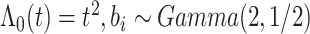
| ||||||||
| β=0.2 | 0.0458 | 0.2098 | 0.1884 | 0.956 | -0.0355 | 0.1294 | 0.1174 | 0.952 |
| β = 0 | -0.0053 | 0.2129 | 0.1976 | 0.966 | -0.0042 | 0.1277 | 0.1293 | 0.935 |
| β = -0.2 | 0.0437 | 0.2111 | 0.1925 | 0.943 | 0.0369 | 0.1261 | 0.1282 | 0.934 |
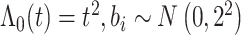
| ||||||||
| β=0.2 | 0.0530 | 0.2049 | 0.1616 | 0.964 | 0.0417 | 0.1207 | 0.1164 | 0.926 |
| β = 0 | -0.0003 | 0.2024 | 0.1688 | 0.981 | 0.0014 | 0.1201 | 0.1122 | 0.949 |
| β = -0.2 | -0.0474 | 0.2161 | 0.1952 | 0.936 | -0.0236 | 0.1214 | 0.1145 | 0.943 |
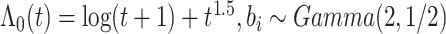
| ||||||||
| β=0.2 | -0.0411 | 0.2213 | 0.1916 | 0.959 | -0.0357 | 0.1310 | 0.1278 | 0.920 |
| β = 0 | -0.0062 | 0.2163 | 0.1925 | 0.966 | -0.0137 | 0.1257 | 0.1316 | 0.952 |
| β = -0.2 | 0.0486 | 0.2090 | 0.1961 | 0.970 | 0.02652 | 0.1254 | 0.1173 | 0.953 |
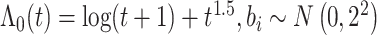
| ||||||||
| β=0.2 | 0.0361 | 0.2147 | 0.1788 | 0.990 | 0.0461 | 0.1216 | 0.1127 | 0.963 |
| β = 0 | -0.0052 | 0.2060 | 0.1849 | 0.980 | 0.0013 | 0.1185 | 0.1177 | 0.946 |
| β = -0.2 | -0.0469 | 0.2070 | 0.1888 | 0.96 | -0.0213 | 0.1204 | 0.1192 | 0.950 |
图 1~4汇总了上述设置下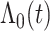 的函数曲线估计以及协变量
的函数曲线估计以及协变量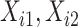 和
和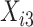 对应的非参数函数
对应的非参数函数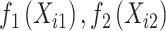 和
和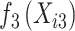 的曲线估计。图中实线表示真实值的曲线,虚线表示估计曲线。从图中可以看到估计曲线与真实曲线是比较接近的,偏离程度相对较小,并且拟合程度随着样本的增大而增高,所以从图 1~4中可以得出估计量是相对无偏的。比较图 1、图 2可知,随着n的增大,真实值和估计值的曲线之间的距离减小,函数估计更接近于真实函数;比较图 2、图 3可知函数的曲线估计在不同脆弱变量假设下是相合且稳健的;比较图 2、图 4可以看出在不同基准风险函数的假设对于曲线的拟合效果无太大的影响,这表明函数估计不依赖于基准风险函数假设。这些结果表 1表现一致。
的曲线估计。图中实线表示真实值的曲线,虚线表示估计曲线。从图中可以看到估计曲线与真实曲线是比较接近的,偏离程度相对较小,并且拟合程度随着样本的增大而增高,所以从图 1~4中可以得出估计量是相对无偏的。比较图 1、图 2可知,随着n的增大,真实值和估计值的曲线之间的距离减小,函数估计更接近于真实函数;比较图 2、图 3可知函数的曲线估计在不同脆弱变量假设下是相合且稳健的;比较图 2、图 4可以看出在不同基准风险函数的假设对于曲线的拟合效果无太大的影响,这表明函数估计不依赖于基准风险函数假设。这些结果表 1表现一致。
图 1.
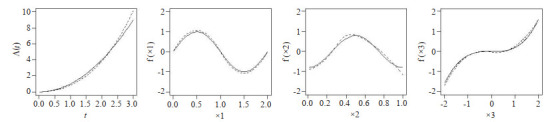
在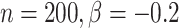 下基于
下基于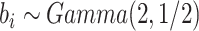 和
和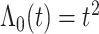 的模拟结果
的模拟结果
Simulation results based on 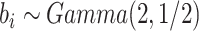 and
and 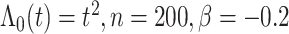 .
.
图 4.
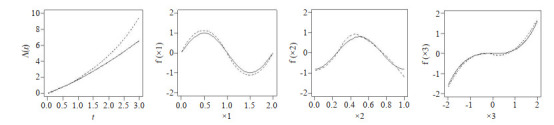
在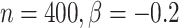 下基于
下基于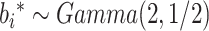 和
和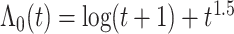 的模拟结果
的模拟结果
Simulation results based on 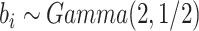 and
and 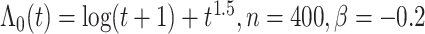 .
.
图 2.
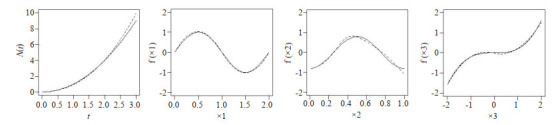
在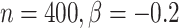 下基于
下基于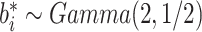 和
和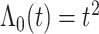 的模拟结果
的模拟结果
Simulation results are based on 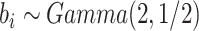 and
and 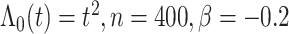 .
.
图 3.
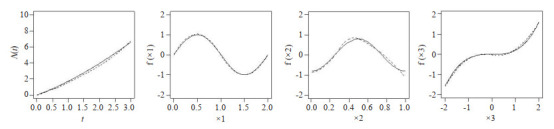
在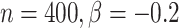 下基于
下基于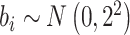 和
和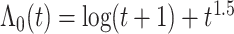 的模拟结果
的模拟结果
Simulation results based on 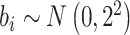 and
and 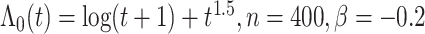 .
.
为验证协变之间存在相关关系时,提出方法的稳健性,在样本n = 400时,设置第1种脆弱变量假设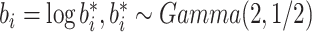 。同时考虑从均值向量为0向量且协方差矩阵为
。同时考虑从均值向量为0向量且协方差矩阵为
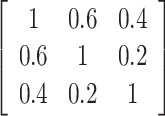 |
的多元正态分布中生成协变量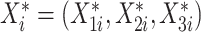 ,通过归一化的方式,分别将协变量
,通过归一化的方式,分别将协变量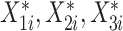 限制在区间
限制在区间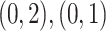 和
和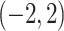 上,从而获得协变量
上,从而获得协变量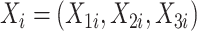 ,其他设置与表 1设置一致。模拟结果如表 2、图 5。根据表 2结果可得,协变量之间存在相关系时,脆弱变量的系数估计仍然是稳健的。此外,从图 5中真实值和估计值的曲线之间的距离减小,函数估计更接近于真实函数。协变量存在相关关系时,协变量函数的估计是相合且稳健的。
,其他设置与表 1设置一致。模拟结果如表 2、图 5。根据表 2结果可得,协变量之间存在相关系时,脆弱变量的系数估计仍然是稳健的。此外,从图 5中真实值和估计值的曲线之间的距离减小,函数估计更接近于真实函数。协变量存在相关关系时,协变量函数的估计是相合且稳健的。
表 2.
协变量正态设置下β估计的模拟结果
Simulation results on estimation of β under the normal setting of covariates
| β | Bias | SSE | SEE | CP | Bias | SSE | SEE | CP |
| Λ0(t)= t2 | Λ0(t)= log(t + 1)+ t1.5 | |||||||
| β=0.2 | -0.0452 | 0.1384 | 0.1249 | 0.944 | -0.0246 | 0.1407 | 0.1396 | 0.941 |
| β = 0 | 0.0002 | 0.1307 | 0.12786 | 0.945 | 0.0131 | 0.1337 | 0.1322 | 0.976 |
| β = -0.2 | -0.0451 | 0.1301 | 0.1291 | 0.961 | 0.0484 | 0.1267 | 0.1220 | 0.922 |
图 5.
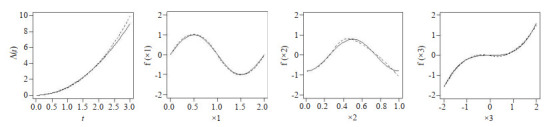
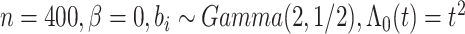 ,正态协变量时的模拟结果
,正态协变量时的模拟结果
Simulation results under the normal setting of covariates, 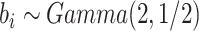 and
and 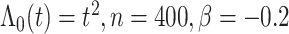 .
.
3. 实例分析
本文所提出的相关方法应用于Sharples等[28]的研究中心脏病患者进行心脏移植的手术风险的相关数据,并从R包中获得了原始数据。CAV(同种异体心脏移植血管病变)是心脏移植术后死亡的常见原因,由于不能准确地观察到CAV发生的确切时间,感兴趣事件的失效时间只能落在K次观测时间点中的某一段时间,因此数据类型符合于Case K区间删失数据。该数据共纳入583例患者为研究对象,探究不同心脏捐献者年龄、心脏移植受者的年龄以及心脏移植受者与心脏捐献者的年龄差能否对心脏移植手术的造成显著影响。
设第i例心脏捐献者年龄为Xi1,受体心脏所移植对应的的年龄设为Xi2,以及第i个例受体的年龄与其所移植心脏的捐献者年龄之差的绝对值为Xi3,即Xi3 = |Xi1 - Xi2|。为方便计算协变量进行归一化处理,同时计算了协变量Xi3与Xi1,Xi3与Xi2,Xi1与Xi2的相关系数分别为0.2171,-0.6258,0.4286表现为中等相关关系。相关系数与模拟研究中的设置是近似相等的,对于提出方法的估计并不产生影响。因此引入心脏捐献者年龄Xi1、心脏移植受体的年龄Xi2以及心脏病捐献者和心脏移植受体相差Xi3建立模型(1),并利用提出的估计方法获得模型的参数估计(图 6)。
图 6.
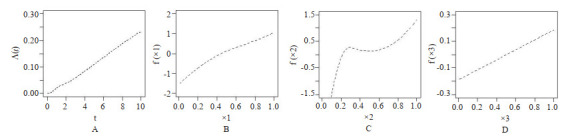
风险函数及协变量函数的估计曲线
Estimation curve of risk function and covariate functions.
图 6A表示基准累积风险函数Λ0(t) 的估计,图 6B~D分别表示协变量Xi1, Xi2和Xi3的函数的估计。可得出以下结论:f1(Xi1) 随着Xi1的增大呈现单调递增的趋势(图 6B),即随着心脏捐献者年龄的增加,CAV首次发生的风险也随之增加;f2(Xi2) 随着Xi2的增大由单调递增至趋于平稳再到单调递增(图 6C),即受体的年龄在成年之前随着年龄的增加,风险函数呈现梯度增加。随着受体成年之后,即随着受体年龄的增长,CAV首次发生的风险相对趋于稳定,但当受体迈入老年时期后,随着年龄的增长,手术失败的风险也随之增大;f3(Xi3)
是严格单调递增的(图 6D),即受体与捐献者年龄之差越大,CAV发生的风险也就越大,反之,手术的风险也就越小。因此,进行心脏移植的供体与受体的匹配时尽力缩短二者年龄差值,以此来提高手术的成功率。最后,本文获得脆弱变量系数的估计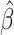 =1.4742,对应的理论标准差的估计为0.2651,为检验假设β=0所获得的P值几乎为零,因此观测过程与失效时间过程显著正相关。即检查次数多的患者身体状况更差一些。
=1.4742,对应的理论标准差的估计为0.2651,为检验假设β=0所获得的P值几乎为零,因此观测过程与失效时间过程显著正相关。即检查次数多的患者身体状况更差一些。
4. 讨论
在心脏移植手术数据中,主要关心的是术后患者生存函数以及风险函数与个风险因子之间的关系,同时预测手术后患者生存概率,常见的方式建立手术后生存时间的比例风险模型[17, 28],探索各个风险因子对生存函数与风险函数的线性影响。Zhao等[17]研究发现不考虑其他风险因素的条件下,缺血性心脏病心脏移植手术的风险显著高于扩张型心肌病变心脏移植手术的风险。Wang等[29]考虑了手术移植后复发情况,得到了相同的结论;Wang等[30]研究假设数据集中含有不敏感个体,因此在不考虑其他风险因子建立了含有治愈子组的加法风险模型,获得了与部分研究[17, 29, 30]一致的结论。但在Sharples等[28]提供的数据资料中,在经典的Cox模型假设下,患者病发年龄以及心脏供体年龄均会对患者手术后的生存概率产生显著影响,同时发现患者病发年龄与心脏供体年龄过高均会增加手术后恢复风险,但是这种建模忽略了非线性影响情况,从而在实际问题的解释中需要局限在一定范围内。因此本文提出了非参数Cox比例风险模型并利用两步估计法、样条方法、bootstrap方法以及Sieve极大似然估计法给出了模型的参数估计,获得了很好的预测与解释效果。
与运用传统Cox模型分析相比,本文考虑供体年龄与患者年龄以及年龄差距,并建立了心脏供体年龄、心脏受体年龄以及心脏供受体年龄差距的非线性结构Cox模型。经研究发现,心脏供体年龄对生存函数与风险函数的呈现线性趋势,且年龄越大风险越大,该结论与Sharples等[28]研究结论一致;心脏受体年龄呈现出非线性函数曲线形式,且受体的年龄在成年之前随着年龄的增加,风险函数呈现阶段性增加趋势。受体成年之后,即随着受体年龄的增长,对风险函数的影响相对趋于稳定,但当受体进入老年时期,随着年龄的增长,风险也随之增大。这与Sharples等[28]的结论有了显著性区别。本文发现心脏供体年龄以及心脏受体年龄差距对风险函数的影响呈现线性关系,年龄差距越大风险越大。因此本文提出的方法在实际问题的解释中更具有优势,有更高的实用性与可靠性。
本研究的局限性:本文提出的模型尽管削弱了线性假设,但是实际计算中增加了计算的复杂性,会引起一定的计算误差,因此考虑新的计算可以提高计算效率,提高计算精度。其次,本文考虑的风险因子数目有限,在实际问题中会存在更多的风险因子或者非线性因子,从而导致高维或者超高维,因此提出具有非线性结构的变量选择方法是具有重要意义。最后,尽管Cox模型形式有着非常广泛的应用,但在实际问题中,检验数据是否满足模型假设也是重要问题。因此本文的后续工作为在临床实践中,通过模型检验分析确认模型假设的合理性与可靠性。
综上所述,本文在混合信息区间Case K删失数据下建立的的非参数结构Cox比例风险模型不会对潜在变量的分布加以任何假设,并且更灵活,增强了可解释性,提出的计算方法简单容易实现。可为临床医学中的预后评估、术后治疗决策提供重要参考,进而推动临床医学精准医疗诊治,对不同状态的患者降低风险,提高患者的生存概率。
Biography
王淑影,博士,副教授,博士生导师,E-mail: wangshuying0601@163.com
Funding Statement
吉林省自然科学基金优秀青年项目(20230101371JC)
Contributor Information
王 淑影 (Shuying WANG), Email: wangshuying0601@163.com.
赵 波 (Bo ZHAO), Email: jgtjx0313@163.com.
References
- 1.Wang PJ, Zhao H, Sun JG. Regression analysis of case K intervalcensored failure time data in the presence of informative censoring. Biometrics. 2016;72(4):1103–12. doi: 10.1111/biom.12527. [DOI] [PubMed] [Google Scholar]
- 2.Wang SY, Wang CJ, Wang PJ, et al. Estimation of the additive hazards model with case K interval-censored failure time data in the presence of informative censoring. Comput Stat Data Anal. 2020;144:106891. doi: 10.1016/j.csda.2019.106891. [DOI] [Google Scholar]
- 3.Du MY, Zhao H, Sun JG. A unified approach to variable selection for Cox's proportional hazards model with interval-censored failure time data. Stat Methods Med Res. 2021;30(8):1833–49. doi: 10.1177/09622802211009259. [DOI] [PubMed] [Google Scholar]
- 4.Hu T, Zhou QN, Sun JG. Regression analysis of bivariate current status data under the proportional hazards model. Can J Statistics. 2017;45(4):410–24. doi: 10.1002/cjs.11344. [DOI] [Google Scholar]
- 5.Ma L, Hu T, Sun JG. Sieve maximum likelihood regression analysis of dependent current status data. Biometrika. 2015;102(3):731–8. doi: 10.1093/biomet/asv020. [DOI] [Google Scholar]
- 6.Sun JG. The statistical analysis of interval-censored failure time data. New York: Springer; 2006. [Google Scholar]
- 7.Wang LM, McMahan CS, Hudgens MG, et al. A flexible, computationally efficient method for fitting the proportional hazards model to interval-censored data. Biometrics. 2016;72(1):222–31. doi: 10.1111/biom.12389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen SN, Khan S. Semiparametric estimation of a partially linear censored regression model. Econ Theory. 2001;17(3):567–90. doi: 10.1017/S0266466601173032. [DOI] [Google Scholar]
- 9.Zou YB, Zhang JJ, Qin GY. Semiparametric accelerated failure time partial linear model and its application to breast cancer. Comput Stat DataAnal. 2011;55(3):1479–87. doi: 10.1016/j.csda.2010.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lian H, Chen X, Yang JY. Identification of partially linear structure in additive models with an application to gene expression prediction from sequences. Biometrics. 2012;68(2):437–45. doi: 10.1111/j.1541-0420.2011.01672.x. [DOI] [PubMed] [Google Scholar]
- 11.Cheng G, Shang ZF. Joint asymptotics for semi-nonparametric regression models with partially linear structure. Ann Statist. 2015;43(3):1351–80. [Google Scholar]
- 12.Tian T, Sun JG. Variable selection for nonparametric additive Cox model with interval-censored data. Biometrical J. 2023;65(1):310–7. doi: 10.1002/bimj.202100310. [DOI] [PubMed] [Google Scholar]
- 13.Cox DR. Regression models and life-tables. J R Stat Soc Ser B Methodol. 1972;34(2):187–202. doi: 10.1111/j.2517-6161.1972.tb00899.x. [DOI] [Google Scholar]
- 14.Huang J. Efficient estimation for the proportional hazards model with interval censoring. Ann Statist. 1996;24(2):540–68. [Google Scholar]
- 15.Lin DY, Oakes D, Ying ZL. Additive hazards regression with current status data. Biometrika. 1998;85(2):289–98. doi: 10.1093/biomet/85.2.289. [DOI] [Google Scholar]
- 16.Martinussen T, Scheike TH. Efficient estimation in additive hazards regression with current status data. Biometrika. 2002;89(3):649–58. doi: 10.1093/biomet/89.3.649. [DOI] [Google Scholar]
- 17.Zhao B, Wang SY, Wang CJ, et al. New methods for the additive hazards model with the informatively interval-censored failure time data. Biom J. 2021;63(7):1507–25. doi: 10.1002/bimj.202000288. [DOI] [PubMed] [Google Scholar]
- 18.Wang SY, Wang CJ, Wang PJ, et al. Semiparametric analysis of the additive hazards model with informatively interval-censored failure time data. Comput Stat DataAnal. 2018;125:1–9. doi: 10.1016/j.csda.2018.03.011. [DOI] [Google Scholar]
- 19.Wang PJ, Zhao H, Du MY, et al. Inference on semiparametric transformation model with general interval-censored failure time data. J Nonparam Stat. 2018;30(3):758–73. doi: 10.1080/10485252.2018.1478091. [DOI] [Google Scholar]
- 20.Zhao H, Wu QW, Li G, et al. Simultaneous estimation and variable selection for interval-censored data with broken adaptive ridge regression. JAm StatAssoc. 2020;115(529):204–16. doi: 10.1080/01621459.2018.1537922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen XR, Hu T, Sun JG. Sieve maximum likelihood estimation for the proportional hazards model under informative censoring. Comput Stat DataAnal. 2017;112(C):224–34. [Google Scholar]
- 22.Sleeper LA, Harrington DP. Regression splines in the cox model with application to covariate effects in liver disease. J Am Stat Assoc. 1990;85(412):941–9. doi: 10.1080/01621459.1990.10474965. [DOI] [Google Scholar]
- 23.Lu XW, Song PXK. Efficient estimation of the partly linear additive hazards model with current status data. Scandinavian J Statistics. 2015;42(1):306–28. doi: 10.1111/sjos.12108. [DOI] [Google Scholar]
- 24.Xu D, Zhao SS, Hu T, et al. Regression analysis of informatively interval-censored failure time data with semiparametric linear transformation model. J Nonparam Stat. 2019;31(3):663–79. doi: 10.1080/10485252.2019.1626383. [DOI] [Google Scholar]
- 25.Stone CJ. Additive regression and other nonparametric models. Ann Statist. 1985;13(2):689–705. [Google Scholar]
- 26.Schumaker L. Spline Functions: Basic Theory. Cambridge, UK: Cambridge University Press; 2007. [Google Scholar]
- 27.Efron B. Bootstrap methods: another look at the jackknife. Ann Statist. 1979;7(1):1–26. [Google Scholar]
- 28.Sharples LD, Jackson CH, Parameshwar J, et al. Diagnostic accuracy of coronary angiography and risk factors for post-heart-transplant cardiac allograft vasculopathy. Transplantation. 2003;76(4):679–82. doi: 10.1097/01.TP.0000071200.37399.1D. [DOI] [PubMed] [Google Scholar]
- 29.Wang SY, Wang CJ, Song XY, et al. Joint analysis of informatively interval-censored failure time and panel count data. Stat Methods Med Res. 2022;31(11):2054–68. doi: 10.1177/09622802221111559. [DOI] [PubMed] [Google Scholar]
- 30.Wang SY, Wang CJ, Sun JG. An additive hazards cure model with informative interval censoring. Lifetime Data Anal. 2021;27(2):244–68. doi: 10.1007/s10985-021-09515-7. [DOI] [PubMed] [Google Scholar]


