Abstract
Objectives
To develop a mapping model between skin surface motion and internal tumour motion and deformation using end-of-exhalation (EOE) and end-of-inhalation (EOI) 3D CT images for tracking lung tumours during respiration.
Methods
Before treatment, skin and tumour surfaces were segmented and reconstructed from the EOE and the EOI 3D CT images. A non-rigid registration algorithm was used to register the EOE skin and tumour surfaces to the EOI, resulting in a displacement vector field that was then used to construct a mapping model. During treatment, the EOE skin surface was registered to the real-time, yielding a real-time skin surface displacement vector field. Using the mapping model generated, the input of a real-time skin surface can be used to calculate the real-time tumour surface. The proposed method was validated with and without simulated noise on 4D CT images from 15 patients at Léon Bérard Cancer Center and the 4D-lung dataset.
Results
The average centre position error, dice similarity coefficient (DSC), 95%-Hausdorff distance and mean distance to agreement of the tumour surfaces were 1.29 mm, 0.924, 2.76 mm, and 1.13 mm without simulated noise, respectively. With simulated noise, these values were 1.33 mm, 0.920, 2.79 mm, and 1.15 mm, respectively.
Conclusions
A patient-specific model was proposed and validated that was constructed using only EOE and EOI 3D CT images and real-time skin surface images to predict internal tumour motion and deformation during respiratory motion.
Advances in knowledge
The proposed method achieves comparable accuracy to state-of-the-art methods with fewer pre-treatment planning CT images, which holds potential for application in precise image-guided radiation therapy.
Keywords: tumour tracking, SGRT, surface reconstruction
Introduction
Lung tumour stands as the predominant contributor to mortality among tumour-related afflictions on a global scale.1–3 Radiotherapy is an important means of controlling lung tumour. However, its accuracy in delivering the dose can be compromised by respiration-induced motion and deformation of structures. Due to the high fractional radiation doses and the close proximity of critical anatomy to the lesions undergoing radiosurgical ablation, this inaccuracy can lead to poor tumour control4 and serious complications such as radiation pneumonitis and radiation-induced cardiovascular disease.5,6 Motion-induced dose errors can be substantially problematic for advanced radiotherapy techniques, eg, stereotactic body radiotherapy (SBRT), proton/heavy ion radiotherapy.7 Extending the internal target volume to compensate respiratory tumour motion can cause an increased risk of complications in normal tissues, and also limit the ability to escalate the target dose for improved tumour control.8
Advanced techniques have been implemented to reconstruct planning 4DCT images, eg, 4D Cone-Beam CT (CBCT), 4D magnetic resonance imaging with the improvement of computer performance. However, even though 4D images are acquired before treatment, there may still be discrepancies compared to real-time imaging.
To reduce target volume while maintaining tumour control, various real-time navigation systems have been developed for radiotherapy. The first approach considers utilising respiratory gating to obtain external surrogate signals driving from the patient’s chest and abdominal surface, such as the Varian Real-time Position Management (RPM). However, this method oversimplifies respiratory motion by only considering the anterior-posterior (AP) direction, thus limiting its accuracy.9 The second method uses a kV source-detector pair that is positioned orthogonally to the LINAC gantry, enabling real-time X-ray fluoroscopy. This method can result in additional imaging dose10 and is limited by the lack of sufficient information in a 2D image, making it ineffective at monitoring target motion when the imaging beam is parallel to the motion. Another approach involves implanting markers in the target area for real-time tracking, which is an invasive operation requiring additional imaging doses, unless specialized detectors like the Varian Calypso system and radiofrequency beacons are utilized.
Compared to the internal motion and deformation, external information acquisition can be achieved noninvasively and without dose. For example, real-time optical surface 3D imaging systems can provide 3D surface data that offers more information than traditional 1D gating systems. However, surface data alone cannot directly display internal motion and deformation, which are necessary for tumour tracking. A correlation between the displacement vector fields (DVFs) of internal structures and surface data has been demonstrated in previous studies.11
Respiratory motion models utilizing surface data can be categorized into two types. The first type is a global model that utilizes 4D CT scans of the general population to extract internal and external surrogate signals,12,13 but falls short in accuracy for individual patients. The second type is a patient-specific model that uses 4D CT data from individual patients to predict internal motion.11,14 While the latter yields superior outcomes, it comes at the cost of higher radiation exposure, as 4D CT scans typically deliver 4-12.8 times more radiation than conventional 3D CT scans, and carry a higher relative risk of cancer.15,16
In this work, a patient-specific respiratory motion model that relies solely on 3D CT images of the end-of-exhalation (EOE) and the end-of-inhalation (EOI) phases was developed in order to achieve a balance between prediction accuracy and radiation dose. By utilizing motion information of the external skin surface, the model can estimate the displacement vector field (DVF) of tumours. By applying the tumour DVF to the tumour surface reconstructed from planning 3D CT images, the system can provide real-time generation of tumour position and surface information. In addition, validation experiments were conducted on tumour location and tumour surface based on 4D CT images of 15 patients, and the results were compared with other methods in the field. This model could potentially be used as a non-ionizing image guided radiation therapy, providing a real-time tumour surface estimation based off real-time skin surface. Compared to traditional methods, this solution enables a 4D visualization of tumour position and surface without requiring additional radiation dose during treatment and planning CT image acquisition.
Methods
Method of segmentation and reconstruction for skin and tumour
Using only the 3D CT images for EOE and EOI phases, the next step involves registering these to the real-time 3D skin surface scans and creating a real time visualization of the estimated tumour surface. To achieve this, it is required to reconstruct 3D surface images of the patient’s skin and tumour, respectively from the 3D CTs of the two phases.
Firstly, the skin surface was segmented from the CT, as shown in Figure 1. Initially, each slice of the 3D CT image is binarized. Then, an opening operation is performed to remove the back plate. The largest sub-block is extracted and holes are filled, and the processed 3D CT is used as input for the Marching Cubes (MC) algorithm. An isovalue of 0.5 is set for 3D reconstruction, resulting in a 3D skin surface image. The posterior part of the 3D skin surface image is then removed and simplified to 10 000 faces to improve efficiency during subsequent registration steps and meet real-time tumour tracking requirements.
Figure 1.
Flow chart of 3D reconstruction of skin surface.
Secondly, to obtain a 3D image of the tumour surface, it is necessary to obtain the tumour mask in advance, which is usually annotated by a radiation oncologist. In this work, the tumour was segmented using deep learning model for small cell lung cancer outlined in Primakov et al,17 however, it is necessary to check whether the segmentation is correct and make adjustments if necessary. Then, all layers of the binary mask image are used as input for the MC algorithm, with an isovalue of 0.5, resulting in a 3D reconstruction of the tumour surface image. The entire process is shown in Figure 2, where the lungs are displayed to better illustrate the location of the reconstructed tumour surface.
Figure 2.
Flow chart of 3D reconstruction of tumour surface.
In addition, a graphical user interface (GUI) for the 3D reconstruction function has been developed, enabling efficient reconstruction of skin and tumour surfaces from a large amount of 4D CT data. The GUI was developed using PyQt 5.15.1,18 which is a set of development tools that provide platform-independent abstractions for GUIs. This allows the GUI to run on both Windows and Linux platforms with Python 3.8.0 installed. In addition, the Insight Segmentation and Registration Toolkit (ITK)19 is used for the implementation of certain functionalities. The GUI is shown in Figure 3.
Figure 3.
Graphical user interface (GUI) for 3D reconstruction function.
Method of motion model parameterization
Ideally, at the EOI time, the amplitude of the skin and tumour should be maximum, while the amplitude at time satisfies a functional relationship with ,20 as shown in Figure 4.
Figure 4.

Graph of the function showing the ideal variation of the amplitude with respect to time .
The functional expression can be represented as:
| (1) |
where represents the EOE time of a respiratory cycle, represents the EOI time of a respiratory cycle.
Assuming that the movement of each point of the skin and tumour is linear, specific to any point , the displacement and time exhibit a trigonometric relationship that corresponds to the amplitude. In this scenario, as the displacement ratio (ie, the ratio of displacement magnitude to the full process) of each point in the local region tends to be the same, therefore, the displacement vector field of all points in the region at time can be estimated based on the displacement ratio of an arbitrary point in the region:
| (2) |
where represents the DVF of the local region from the EOE time to the EOI time, and represent the displacement vector of point from the EOE time to the EOI time and from the EOE time to time , respectively. For larger regions, the motion features of each point may vary, and points that are closer together should have more similar motion features. The displacement ratio of unknown points can be calculated using the known displacement ratios of nearby points through an weighted average method, where the weights are determined by the inverse distances between points.
Method of real-time tumour estimation
The 3D images of the skin and tumour surface were reconstructed from the 3D CT images obtained at EOE and EOI time before treatment, and were registered to obtain DVFs. Specifically, the skin and tumour surface at EOE time were registered to those at EOI time, respectively. Furthermore, when the 3D image of the patient’s skin surface was obtained through real-time optical imaging equipment capable of capturing 3D point clouds (such as Kinect21) at time during the treatment, the skin surface at EOE time was registered to the skin surface obtained at time to obtain DVF.
Let the point set of the 3D skin surface image at EOE time be represented by , and the point set of the 3D tumour surface image at EOE time be represented by . The DVF of from EOE time to EOI time is denoted as , the DVF of from EOE time to time is denoted as , and the DVF of from EOE time to EOI time is denoted as Then the displacement ratio of the skin surface motion field at time is denoted as , where:
| (3) |
In “Method of motion model parameterization” section, we have derived that for a relatively large region, the displacement ratio of an unknown point can be calculated using a weighted average with inverse distance weighting based on the displacement ratios of known points. Therefore, for the entire surface area of the skin and tumour, , which represents the displacement ratio of , can be estimated through:
| (4) |
| (5) |
For the following two reasons, filtering was applied to and involved in the calculation of in Equation (4) to achieve a more precise estimation: (1) The displacement of the skin surface during respiratory motion may contain points with displacements far smaller than the noise included in the registration results, resulting in a calculated displacement ratio that deviates far from the true value, which requires removing these points. (2) In “Method of motion model parameterization” section, it is assumed that the motion of each point of is linear, hence necessitating the removal of points that cause large angle between vectors and .
Let the index set be denoted as
| (6) |
where is the displacement filtering threshold, and is the vector angle filtering threshold. In this study, is set to 0.05 mm, and is set to . Then the filtered skin surface point set and displacement ratio field is:
| (7) |
| (8) |
The displacement ratio of at time after filtering is:
| (9) |
According to , , which represents the DVF from the EOE time to the EOI time, can be calculated through:
| (10) |
Then , which represents the point set of the tumour surface at time , can be estimated through:
| (11) |
The entire process can be referred to in Figure 5, where the process within the dashed box on the left is conducted before treatment, while the process within the dashed box on the right is conducted during treatment. In the DVF image, different coloured lines represent the displacement of points. In the motion ratio field image, the ratio of displacement from the EOE time to real-time, compared to the displacement from the EOE time to the EOI time, is represented by the darker portion of each line. It should be noted that our model uses a patient-specific approach, where each patient’s 3D-CT image corresponds to a different model.
Figure 5.
Flow chart of real-time tumour estimation based on skin surface image.
To achieve reliable and efficient registration of 3D images of skin and tumour surface, the Non-Rigid Registration Using Accelerated Majorization-Minimization (AMM_NRR) algorithm22 proposed by Yao et al and its open-source C++ code were utilized in this paper. In summary, the algorithm is a robust non-rigid registration approach based on a globally smooth robust norm for alignment and regularization, which can effectively handle outliers and partial overlaps. The main feature of the algorithm is the use of Welsch’s function as a robust measure for both the alignment and regularization terms. This helps to reduce errors in corresponding points caused by the nearest-neighbour principle and large local motion, which can negatively impact registration performance. In addition, each iteration of the algorithm is simplified as a convex quadratic problem with a closed-form solution, and Anderson acceleration is applied to speed up the solver’s convergence.
After simplifying the reconstructed skin surface from a 3D CT image of size 512512142 to 10 000 faces, the average registration time using a computer with an Intel(R) Core(TM) i5-7400 CPU @ 3.00 GHz processor and 16 GB of RAM is 1.30 s. The registration time determines the single tumour surface estimate time after obtaining real-time surface of the patient’s skin during radiotherapy.
Patient data test
The performance of our method was tested on 4D CT images from 15 patients. Three patients’ 4D CT images were obtained from publicly available datasets provided by the Léon Bérard Cancer Centre.23 These images were obtained using a Philips 16-Slice Brilliance CT Big Bore Oncology system with a 2 mm slice thickness. To capture breathing correlated data, the accompanying Pneumo Chest bellows from Lafayette Instruments were utilized. The tumour masks were segmented using a deep learning model17 proposed by Primakov et al for non-small cell lung cancer segmentation, and were validated manually. The remaining 12 patients’ 4D CT images were obtained from The Cancer Imaging Archive (TCIA) 4D-Lung dataset,24 which included RTSTRUCT files containing target contours specifically segmented by a radiation oncologist. The tumour masks were extracted from these RTSTRUCT files using software developed by Thomas et al.25 For patients with multiple 4D CT images, only the planning 4D CT were used in this study. These 4D CT images were obtained using a 16-slice helical CT scanner (Brilliance Big Bore, Philips Medical Systems, Andover, MA) with a 3 mm slice thickness. These publicly available data have all undergone ethical review and approval by the Institutional Review Board.
The accuracy of our model in estimating the position and surface of tumours was evaluated using the 4D CT images from the 15 patients. For each patient, 3D images of the skin and tumour surface were reconstructed for each phase and reordered based on the average height of skin surface points in the supine position, resulting in ten phases labelled P1 to P10, where P1 represented the EOE phase and P10 represented the EOI phase. The 3D images of the skin and tumour surface at EOE and EOI phases were used to construct the model, while the 3D images of the skin surface at other phases were considered to be obtained in real-time during radiation therapy, and the 3D images of the tumour surface at other phases were used to test whether the model could predict the deformation of unseen data. To test the robustness of the proposed method to potential noise in the optical signal, simulated Gaussian noise with a standard deviation of 0.5 mm was added to the skin surface height outside the EOE phase, with an amplitude consistent with the accuracy of the previously reported optical surface monitoring system.26 The tumour estimation was then performed using the prediction method outlined in “Method of real-time tumour estimation” section.
The tumour position error (TPE) refers to the Euclidean distance between the reconstructed tumour centre point and the estimated tumour centre point, and is used to evaluate the accuracy of the model in estimating the position of the tumour.
The accuracy of tumour surfaces in the 4D-Lung dataset was assessed using the dice similarity coefficient (DSC), 95%-Hausdorff distance (95%-HD) and mean distance to agreement (mean-DTA). DSC is calculated according to the definition provided by Balik et al24:
| (12) |
where A and B represent two tumour surfaces being compared, |A∩B| represents the volume of their intersection, and |A|+|B| represents the sum of their volumes. 95%-HD and mean-DTA respectively represent the 95th percentile value and the average value of the minimum distance from points on a surface to any point on another surface.27 metrics indicates the surface deformation of the tumour from the EOE phase to phase due to respiratory motion. In contrast, metrics indicates the extent to which the surface variation can be restored by using the model proposed in this paper to predict the deformation between the EOE phase and phase .
Furthermore, the Shapiro-Wilk test indicated that the various metrics of each patient’s 8 cases (phases) conformed to a normal distribution in statistical terms (P > 0.05), whereas the metrics of all 120 (15 × 8) cases did not conform to a normal distribution (P < 0.001). Consequently, for each patient’s case metrics, the mean ± standard deviation were reported, while for all cases’ metrics, the mean, standard deviation, median, upper quartile, and lower quartile were reported. In addition, non-parametric Wilcoxon signed-rank test was conducted on all cases’ indicators to determine statistical significance, and the resulting P-values were reported.
Results
Accuracy of tumour centre point
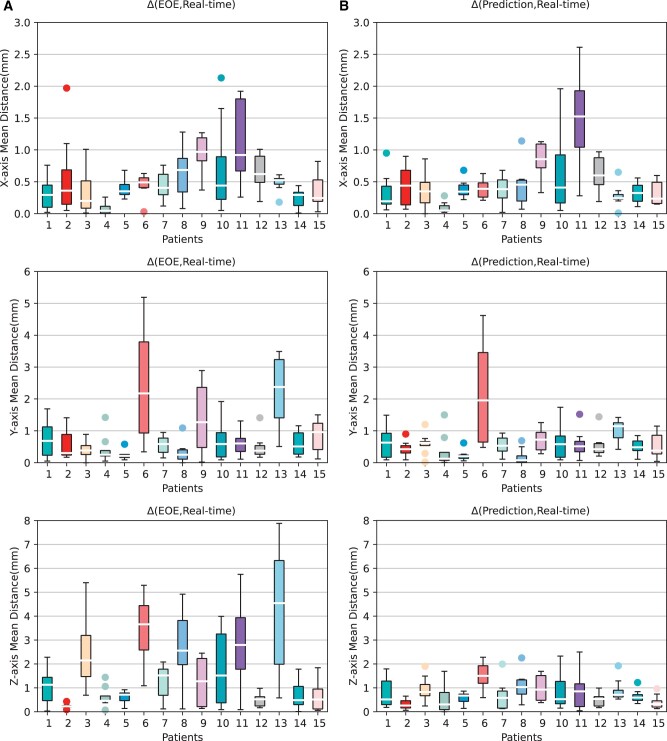
Figure 6 displays the mean displacement distribution (mm) of tumour centre positions between EOE phase and phases from P2 to P9 (A), and between the model-generated and original tumour centre positions at phases from P2 to P9 (B), respectively, on the 4D CT images of 15 patients. Figure 7 displays the components of these displacements in X, Y, and Z axes.
Figure 6.
Boxplot of the mean tumour centre point distance for each patient at phases P2-P9 comparing end-of-exhalation (EOE) and each phase (A) as well as model-generated and ground-truth each phase (B).
Figure 7.
Boxplot of the mean tumour centre point distance in X-axis (left/right, the first row), Y-axis (anterior/posterior, the second row) and Z-axis (superior/inferior, the third row) direction for each patient at phases P2-P9 comparing end-of-exhalation (EOE) and each phase (A) as well as model-generated and ground-truth each phase (B).
For the tumour centre coordinates, the displacement between EOE and different phases varied greatly. Although respiration can cause tumour centre point displacements of up to 9 mm, the upper quartile decreased to below 5 mm and the average error of the model-generated tumour centre positions is only about 1 mm after applying the DVF generated by the proposed model. Furthermore, it can be observed that the results exhibited larger variance for patients 6, 10, and 11. This could be attributed to the complex nature of their tumour shapes, combined with the typically lower resolution of CT images along the Z-axis. Figure 8 depicts the tumour consecutive slices and 3D surface images of patient 6 with a higher variance and patient 13 with a lower variance. Patient 6 exhibits a more intricate tumour shape than patient 13, which is further influenced by the low resolution of CT images along the Z-axis. Consequently, there are significant variations in tumour shape between discrete slices, indicating the loss of crucial fine-grained continuous information within discrete slices. This limitation impedes the accurate delineation of the actual tumour shape through segmentation and reconstruction. Moreover, due to low resolution along the Z-axis in the acquired CT images, the accurate representation of the size and displacement of the tumour may exhibit higher uncertainty in the z direction.
Figure 8.

Comparative illustration of tumour shapes between patient 6 and patient 13. Rows 1 and 3 display ten consecutive slices of the tumour mask for patient 6 and patient 13, respectively. Rows 2 and 4 display reconstructed 3D surface images of the tumours at ten phases for patient 6 and patient 13, respectively.
In Figure 9, the TPEs of eight phases from P2 to P9 of 15 patients are listed. As inhalation progresses, the errors are slightly increased, primarily due to the increased tumour displacement. In addition, a reduction in TPE at P9 compared to P8 was observed, which may be attributed to the more accurate tumour information obtained from the model constructed using the EOE and EOI phases that are closer in time to these phases. Furthermore, the end phases (P7-P9) have a larger error compared to the earlier phases (P2-P4). This could be attributed to the increased inhalation during the later phases, resulting in a slower rate of skin expansion and reduced differences in the 3D surface images of the skin across different phases and consequently leading to larger registration errors.
Figure 9.
The tumour centre position error in 10 patients and 8 different phases. Pi, i = 2…9, is the serial number of the respiratory phase reordered according to according to the average height of the skin surface on the anterior half of the torso in the supine position of the patient, P1 is the end-of-exhalation (EOE) phase while P10 is the end-of-inhalation (EOI) phase.
Table 1 lists the mean TPEs and their X-axis (left/right), Y-axis (anterior/posterior), and Z-axis (superior/inferior) components of each patient from the EOE to each phase from P2 to P9 using our model, as well as the validation results obtained by introducing noise simulation during surface motion. Table 2 provides a comparison of these metrics in three different scenarios: the initial state (EOE versus each phase), model generation (EOE after Model Distortion versus each phase), and model generation with noise. The P-values were reported to determine statistical significance. The results indicate that the average translational positioning error (TPE) obtained using our model in the presence of noise was 1.33 mm, which is comparable to the TPE value of 1.29 mm obtained without noise (P = 0.215). Moreover, it significantly outperformed the initial TPE of 2.73 mm (P < 0.001). However, the differences in the X-axis component of TPE between the initial state and model generation were not statistically significant (P = 0.048). This could be attributed to the loss of continuous information with rapid changes between slices in the X and Y axes due to the relatively low resolution of the Z-axis (see Figure 8). Consequently, this led to the accumulation of errors in later stages. Furthermore, the impact of errors was more pronounced due to the relatively small displacement component in the X-axis (0.53 mm). The high errors observed in the X or Y axes for patients 6, 10, and 11 with complex tumour morphology, as depicted in Figure 7, also support this observation. Conversely, the relatively low error in the Z-axis can be clearly observed in Figure 7. This is attributed to the higher imaging resolution of the X and Y axes, resulting in smaller errors, and the relatively larger displacement component in the Z-axis (1.63 mm), which has a lesser impact.
Table 1.
Mean ± standard deviation of tumour centre position error (TPE) and its components on the X (left/right), Y (anterior/posterior), and Z (superior/inferior) axes using our model on each phase, and validation results with simulated noise (Validation).
| Patient No. | TPE (mm) | Validation (mm) | X-axis (mm) | Y-axis (mm) | Z-axis (mm) |
|---|---|---|---|---|---|
| 1 | 1.22 ± 0.57 | 1.35 ± 0.61 | 0.33 ± 0.28 | 0.67 ± 0.51 | 0.77 ± 0.57 |
| 2 | 0.77 ± 0.29 | 0.84 ± 0.29 | 0.45 ± 0.30 | 0.43 ± 0.24 | 0.32 ± 0.21 |
| 3 | 1.26 ± 0.47 | 1.50 ± 0.49 | 0.38 ± 0.28 | 0.60 ± 0.32 | 0.95 ± 0.49 |
| 4 | 0.74 ± 0.70 | 0.79 ± 0.69 | 0.10 ± 0.08 | 0.36 ± 0.49 | 0.55 ± 0.59 |
| 5 | 0.78 ± 0.22 | 0.78 ± 0.22 | 0.39 ± 0.14 | 0.23 ± 0.16 | 0.60 ± 0.23 |
| 6 | 2.86 ± 1.41 | 2.76 ± 1.51 | 0.39 ± 0.14 | 2.22 ± 1.60 | 1.50 ± 0.54 |
| 7 | 1.05 ± 0.50 | 1.02 ± 0.56 | 0.39 ± 0.20 | 0.54 ± 0.27 | 0.67 ± 0.58 |
| 8 | 1.26 ± 0.52 | 1.19 ± 0.57 | 0.44 ± 0.31 | 0.19 ± 0.24 | 1.08 ± 0.56 |
| 9 | 1.55 ± 0.52 | 1.53 ± 0.52 | 0.85 ± 0.26 | 0.71 ± 0.34 | 0.99 ± 0.54 |
| 10 | 1.46 ± 0.93 | 1.53 ± 0.75 | 0.67 ± 0.66 | 0.67 ± 0.57 | 0.88 ± 0.74 |
| 11 | 2.20 ± 1.15 | 2.15 ± 0.93 | 1.47 ± 0.82 | 0.59 ± 0.41 | 0.94 ± 0.81 |
| 12 | 1.08 ± 0.24 | 1.08 ± 0.24 | 0.63 ± 0.26 | 0.54 ± 0.37 | 0.51 ± 0.27 |
| 13 | 1.44 ± 0.42 | 1.54 ± 0.29 | 0.28 ± 0.17 | 1.02 ± 0.33 | 0.89 ± 0.45 |
| 14 | 0.92 ± 0.29 | 0.96 ± 0.32 | 0.33 ± 0.16 | 0.50 ± 0.24 | 0.65 ± 0.26 |
| 15 | 0.80 ± 0.36 | 0.94 ± 0.22 | 0.32 ± 0.18 | 0.52 ± 0.37 | 0.40 ± 0.28 |
Table 2.
Mean, standard deviation, median, Q1 (lower quartile), Q3 (upper quartile), and P-value (Wilcoxon signed-rank test) for initial tumour position error (ITPE), TPE using our model (MTPE), validation results with simulated noise (Val.), initial X-axis (left/right), Y-axis (anterior/posterior) and Z-axis (superior/inferior) distance (IX-axis, IY-axis, and IZ-axis), X-axis, Y-axis and Z-axis distance using our model (MX-axis, MY-axis, and MZ-axis) across 120 (158) cases.
| Mean | SD | Median | Q1 | Q3 | P-value | |
|---|---|---|---|---|---|---|
| ITPEs (mm) | 2.13 | 1.84 | 1.50 | 0.80 | 2.73 | 0.001 |
| MTPEs (mm) | 1.29 | 0.84 | 1.08 | 0.72 | 1.56 | |
| Vals. (mm) | 1.33 | 0.83 | 1.13 | 0.81 | 1.67 | 0.215 |
| IX-axis (mm) | 0.53 | 0.52 | 0.44 | 0.19 | 0.70 | 0.048 |
| MX-axis (mm) | 0.49 | 0.46 | 0.37 | 0.20 | 0.62 | |
| IY-axis (mm) | 0.84 | 0.96 | 0.50 | 0.24 | 1.07 | 0.001 |
| MY-axis (mm) | 0.65 | 0.71 | 0.51 | 0.20 | 0.80 | |
| IZ-axis (mm) | 1.63 | 1.68 | 0.98 | 0.39 | 2.25 | 0.001 |
| MZ-axis (mm) | 0.78 | 0.59 | 0.64 | 0.33 | 1.04 |
Accuracy of tumour surface
As an example, Figure 10 displays the 3D surface images of the lung (grey) and tumour (red) for phase 10 (reordered as the phase P9) of patient 13. The tumour surface of the EOE phase (A, green) and the model-generated phase P9 (B, green) are also overlaid for visual comparison. The average DSC, 95%-HD, and mean-DTA calculated between the model-generated phase P9 and the reference tumour surface in Figure 10B are 0.942, 8.94 mm, and 4.77 mm, respectively, which are better than the values of 0.451, 1.48 mm, and 0.78 mm in Figure 10A. The detailed metric results for all phases are presented in Table 3. In this table, “time phase” refers to the original phase information, where 00-60 represents exhalation and 60-90 represents inhalation. The “reordered phase” refers to the phase that has been reordered based on the height of the skin surface.
Figure 10.
(A) Tumour surface on phase P9 (transparent, ground-truth) and end-of -exhalation (EOE) phase (opaque); (B) Tumour surface on phase P9 (transparent, ground-truth) and model-generated tumour surface on phase P9 (opaque).
Table 3.
Metrics before applying the model in patient 13: initial dice similarity coefficient (IDSC), Initial 95%-Hausdorff distance (IHD), initial distance to agreement (IDTA), and metrics after applying the model with noise: model dice similarity coefficient (MDSC) Val., model Hausdorff distance (MHD) Val., model distance to agreement (MDTA) Val.
| Time Phase | Reordered Phase | IDSC | MDSC Val. | IHD (mm) | MHD Val. (mm) | IDTA (mm) | MDTA Val. (mm) |
|---|---|---|---|---|---|---|---|
| 00 | P10 (EOI) | / | / | / | / | / | / |
| 10 | P9 | 0.451 | 0.942 | 8.94 | 1.48 | 4.77 | 0.78 |
| 20 | P8 | 0.429 | 0.922 | 8.35 | 1.97 | 4.74 | 0.99 |
| 30 | P6 | 0.655 | 0.856 | 5.75 | 2.97 | 2.55 | 1.61 |
| 40 | P4 | 0.85 | 0.835 | 3.65 | 4.22 | 1.26 | 1.84 |
| 50 | P3 | 0.959 | 0.845 | 1.73 | 2.75 | 0.63 | 1.49 |
| 60 | P1 (EOE) | / | / | / | / | / | / |
| 70 | P2 | 0.846 | 0.892 | 2.81 | 2.02 | 1.38 | 0.99 |
| 80 | P5 | 0.681 | 0.811 | 5.38 | 2.86 | 2.72 | 1.56 |
| 90 | P7 | 0.524 | 0.924 | 7.69 | 1.50 | 4.05 | 0.88 |
| Mean | 0.674 | 0.878 | 5.54 | 2.47 | 2.76 | 1.27 | |
Table 4 lists the average DSC, 95%-HD and mean-DTA between the EOE tumour surfaces and the estimated tumour surfaces of phases from P2 to P9, the average DSC between actual and estimated tumour surfaces of phases from P2 to P9, and the validation results obtained by introducing simulated noise for the 15 patients, respectively. The average DSC obtained in the presence of noise were 0.920, which are comparable to the value of 0.924 obtained without noise. Table 5 provides a comparison of these metrics in three different scenarios: the initial state, model generation, and model generation with noise. The P-values were reported to determine statistical significance. Statistically significant differences (P < 0.001) were observed in all metrics between the initial state and model generation groups, whereas no significant differences (P > 0.05) were found between the model generation and model generation with noise groups.
Table 4.
Mean ± standard deviation of dice similarity coefficient (DSC), 95%-Hausdorff distance (HD) and mean distance to agreement (DTA) metrics between ground-truth versus model-generated tumour surfaces on each phase, and validation results with simulated noise (Val.) for 15 patients, respectively.
| No. | DSC | DSC Val. | HD (mm) | HD Val. (mm) | DTA (mm) | DTA Val. (mm) |
|---|---|---|---|---|---|---|
| 1 | 0.943 ± 0.008 | 0.940 ± 0.006 | 2.57 ± 0.28 | 2.59 ± 0.26 | 1.11 ± 0.13 | 1.10 ± 0.13 |
| 2 | 0.972 ± 0.013 | 0.970 ± 0.011 | 2.15 ± 0.48 | 2.22 ± 0.47 | 0.90 ± 0.29 | 0.93 ± 0.28 |
| 3 | 0.915 ± 0.015 | 0.908 ± 0.015 | 3.39 ± 0.54 | 3.24 ± 0.49 | 1.52 ± 0.16 | 1.45 ± 0.15 |
| 4 | 0.965 ± 0.033 | 0.956 ± 0.024 | 2.33 ± 0.64 | 2.37 ± 0.61 | 0.83 ± 0.27 | 0.84 ± 0.26 |
| 5 | 0.986 ± 0.005 | 0.986 ± 0.005 | 1.87 ± 0.46 | 1.87 ± 0.46 | 0.33 ± 0.08 | 0.33 ± 0.08 |
| 6 | 0.828 ± 0.138 | 0.824 ± 0.020 | 6.06 ± 1.12 | 6.36 ± 1.09 | 2.22 ± 0.28 | 2.25 ± 0.21 |
| 7 | 0.920 ± 0.015 | 0.916 ± 0.015 | 3.28 ± 0.22 | 3.32 ± 0.21 | 1.41 ± 0.10 | 1.42 ± 0.06 |
| 8 | 0.891 ± 0.022 | 0.881 ± 0.042 | 2.75 ± 0.28 | 2.79 ± 0.31 | 1.30 ± 0.08 | 1.39 ± 0.21 |
| 9 | 0.910 ± 0.114 | 0.910 ± 0.014 | 2.53 ± 0.21 | 2.53 ± 0.21 | 1.05 ± 0.07 | 1.04 ± 0.07 |
| 10 | 0.896 ± 0.016 | 0.895 ± 0.013 | 3.07 ± 0.93 | 3.05 ± 0.93 | 1.34 ± 0.15 | 1.36 ± 0.16 |
| 11 | 0.871 ± 0.028 | 0.869 ± 0.021 | 3.03 ± 0.37 | 3.01 ± 0.25 | 1.38 ± 0.13 | 1.41 ± 0.07 |
| 12 | 0.981 ± 0.071 | 0.985 ± 0.004 | 2.15 ± 0.34 | 2.15 ± 0.34 | 0.50 ± 0.07 | 0.50 ± 0.07 |
| 13 | 0.893 ± 0.031 | 0.878 ± 0.045 | 2.32 ± 0.86 | 2.47 ± 0.86 | 1.19 ± 0.39 | 1.27 ± 0.37 |
| 14 | 0.941 ± 0.009 | 0.937 ± 0.013 | 2.50 ± 0.11 | 2.42 ± 0.15 | 1.21 ± 0.11 | 1.17 ± 0.07 |
| 15 | 0.949 ± 0.014 | 0.948 ± 0.022 | 1.46 ± 0.34 | 1.48 ± 0.27 | 0.67 ± 0.10 | 0.71 ± 0.07 |
Table 5.
Mean, standard deviation, median, Q1 (lower quartile), Q3 (upper quartile), and P-value (Wilcoxon signed-rank test) for dice similarity coefficient (IDSC), DSC using our model (MDSC), validation results with simulated noise (DSC Val.), initial 95%-Hausdorff distance (IHD), 95%-HD using our model (MHD), validation results with simulated noise (HD Val.), initial mean distance to agreement (IDTA), DTA using our model (MDTA), and validation results with simulated noise (DTA Val.) across 120 (158) cases.
| Mean | SD | Median | Q1 | Q3 | P-value | |
|---|---|---|---|---|---|---|
| IDSCs | 0.883 | 0.088 | 0.896 | 0.844 | 0.961 | 0.001 |
| MDSCs | 0.924 | 0.043 | 0.927 | 0.900 | 0.967 | |
| DSC Val. | 0.920 | 0.046 | 0.922 | 0.897 | 0.960 | 0.051 |
| IHDs (mm) | 3.54 | 1.88 | 2.95 | 2.35 | 4.15 | 0.001 |
| MHDs (mm) | 2.76 | 1.16 | 2.51 | 2.08 | 3.17 | |
| HD Val. (mm) | 2.79 | 1.20 | 2.59 | 2.09 | 3.06 | 0.089 |
| IDTAs (mm) | 1.53 | 0.91 | 1.36 | 0.91 | 1.93 | 0.001 |
| MDTAs (mm) | 1.13 | 0.48 | 1.17 | 0.75 | 1.40 | |
| DTA Val. (mm) | 1.15 | 0.48 | 1.18 | 0.80 | 1.41 | 0.224 |
Comparison results with other methods
Table 6 compares our method with the Global method (Ehrhardt13) and the patient-specific methods (Ladjal,28 LS-SVM,29 Wang30) in terms of target position error and the number of planning 3DCT images required. Our approach achieves better results while requiring fewer 3DCT phases.
Table 6.
Comparison of methods in target position error and required number of planning 3D CT phases (CT phases count).
In addition, compared to the state-of-the-art deep learning-based method proposed by Huang et al,31 which achieved a similar improvement to ours in average 3D tumour DSC (from 0.883 to 0.920 for our method versus from 0.804 to 0.835 for their method), our method needed lower radiation exposures (2 CT scans versus 10) for patients. Our average baseline DSC was higher than that of their method because their method calculated the average DSC between two extreme phases.
Discussion
Respiratory motion can cause tumour motion and deformation and further seriously affect the radiotherapy accuracy of tumour. A patient-specific respiratory motion model was proposed in this study, which mapped external skin surface to internal tumour motion, so as to compensate for respiratory motion. The model relies only on the EOE and EOI phases of 3D CT images, and obtains both prediction accuracy and lower radiotherapy dose without using expensive hardware, ie, conventional LINACs. Compared to previous studies of linear 4D CT models, this model achieves desired images with lower radiotherapy doses but comparable accuracy.
In this study, the 3D images of the skin and tumour surfaces were reconstructed from the planning CT images before constructing the model. For the skin surface, only the front half is retained and simplified to 10 000 faces, with random noise added to improve registration efficiency and match with optical imaging devices. The registration-based respiratory motion mapping model typically uses algorithms such as pTV-reg to perform non-rigid registration on the voxels of the original 3D CT slices,30–32 while present study uses the AMM-NRR algorithm to register the skin and tumour surfaces reconstructed from the 3D CT data. There are four reasons for this choice. First, non-rigid registration algorithms for targets of 3D point clouds obtained by structured light or depth cameras generally require a mesh containing edges as a source. Second, although the pTV-reg algorithm has the advantage of avoiding excessive smoothness in the DVF across organ boundaries, it may still be insufficiently precise because the b-spline-based registration is usually too smooth to accurately propagate the tumour contour.31 In such cases, by reconstructing the tumour surface mesh in advance and registering it non-rigidly, we can more accurately propagate the tumour contour. Third, non-rigid registration of the entire 3D CT slice is time-consuming. In the time-optimized algorithm proposed by Wang et al,30 the registration time is as long as 12 min, while our method achieves an average registration time of only 1.30 s. Finally, using the reconstructed mesh, the registration and tumour tracking processes can be easily visualized.
As expected, the error gradually increased slightly with inhalation (Figure 9), indicating that the motion amplitude was one of the factors affecting the error. Despite the noise causing a slight deterioration in the results, the robustness of the proposed method has been validated, as shown in Tables 2 and 5.
The results indicate that DVF provides more accurate compensation for the motion along the Z-axis compared to the X and Y axes. This is attributed to the larger displacement along the Z-axis, which facilitates better distinction of Z-axis motion. In addition, the high thickness of CT imaging leads to errors in the reconstruction and registration of the X and Y axes.
The poorer matches between the predicted tumour surface and the actual surface in some patients may be attributed to the complexity of the tumour contour and the increased thickness of the CT slices (see Figure 8). Therefore, the model may be better suited for non-late-stage tumour patients with relatively regular tumour morphology. For patients with highly complex tumour shapes, an alternative approach would be to predict the radiation treatment planning target volume (PTV) that encompasses a larger extent than the tumour but has a more regular shape.
In this study, we used the front half of the patient’s torso surface as the region of interest (ROI) instead of smaller, specified ROI on the skin proposed by Huang et al.31 There are two reasons. Firstly, our proposed method considered the influence of the position information of ROI points on the displacement of the tumour surface, and smaller ROI regions contain less position information. Secondly, to find accurate correspondences between CT images and images obtained by optical imaging is more difficult for smaller ROI regions. So, we directly used the entire front half of the patient’s torso surface as the ROI without the need for correspondence searching.
Theoretically, the registration accuracy represents the upper limit of the accuracy of the proposed weighted interpolation method. Quantitative evaluation results show that the AMM_NRR we used is superior to the previous state-of-the-art methods in terms of registration accuracy and computational speed.22 The robustness of the AMM_NRR algorithm has been validated in real optical scanning data with partial overlap, which registration accuracy is the highest in registration accuracy compared to other algorithms.22
The real-time DVF of the tumour was estimated using a linear weighted interpolation method in our model. However, nonlinear weighted interpolation is feasible because the affine transform field consisting of displacement vectors and rotation matrices for each point is provided by the AMM_NRR algorithm used in registration. Boldea et al reported that a straight-line trajectory closely approximates the motion between EOE and EOI phases for most lung points.33 Therefore, it is believed that limited benefits can only be provided by performing nonlinear interpolation while reducing efficiency, and nonlinear interpolation was not used. For the skin surface, our method is compatible with non-linear motion, even though we assumed in “Method of motion model parameterization” section that the motion was linear. When calculating the displacement ratio, we filtered out displacement vectors whose direction angle differences between the EOE-to-real-time DVF and EOE-to-EOI DVF were more than 15 degrees, and selected points with nearly linear displacement to calculate the displacement ratio. Therefore, our proposed method does not directly increase estimate error due to non-linear motion of the points.
Despite the significantly lower dosage administered during CT scans compared to therapeutic radiation doses in lung tumour treatment, minimizing the dose of planning CT imaging remains consequential.16 This is due to the potential for an accumulation of radiation dose in normal tissues from 4DCT scans, which may result in a 15.98-fold increase in relative cancer risk compared to 3DCT.16 In addition, the methodologies used in this study can be readily applied to percutaneous lung nodule biopsy procedures which do not require radiation therapy.
Despite achieving favourable results, this work still has certain limitations. The proposed method takes into account the changes of the tumour’s DVF in both time and space dimensions, but it may be related to more dimensions of information, eg, tissue anatomy, morphology. In addition, the model maps the absolute position information of the skin to the absolute position information of the tumour, which leads to an inability to differentiate between the two different respiratory patterns of inhalation and exhalation. In the next step, we will optimize the method by using a deep learning-based model to learn more dimensions of information.
The present research is constrained by the distinctions between simulation and clinical implementation, as it serves as an initial exploratory investigation. The effectiveness of the proposed method might be affected by the performance of optical imaging equipment, eg, image acquisition time lag, imaging errors. Moreover, CT imaging with a higher slice thickness may lead to larger estimation errors along the X and Y axes, particularly when dealing with complex tumour morphology. Before clinical implementation, more prospective studies based on real patient data are necessary.
Conclusions
The study proposes and validates a patient-specific model constructed solely from 3D CT images of EOE and EOI phases, to predict internal tumour motion and deformation during respiration. The method might potentially apply in precise radiotherapy based on real-time 4D surface image and planning CT images.
Contributor Information
Ziwen Wei, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China; Science Island Branch of the Graduate School, University of Science and Technology of China, Hefei 230026, Anhui, P.R. China.
Xiang Huang, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China.
Aiming Sun, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China.
Leilei Peng, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China.
Zhixia Lou, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China.
Zongtao Hu, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China.
Hongzhi Wang, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China.
Ligang Xing, Department of Radiation Oncology, School of Medicine, Shandong University, Shandong Cancer Hospital and Institute, Shandong First Medical University and Shandong Academy of Medical Sciences, Jinan 250117, Shandong, P.R. China.
Jinming Yu, Department of Radiation Oncology, School of Medicine, Shandong University, Shandong Cancer Hospital and Institute, Shandong First Medical University and Shandong Academy of Medical Sciences, Jinan 250117, Shandong, P.R. China.
Junchao Qian, Anhui Province Key Laboratory of Medical Physics and Technology, Institute of Health and Medical Technology, Hefei Institutes of Physical Science, Hefei Cancer Hospital, Chinese Academy of Sciences, Hefei 230031, P.R. China; Science Island Branch of the Graduate School, University of Science and Technology of China, Hefei 230026, Anhui, P.R. China; Department of Radiation Oncology, School of Medicine, Shandong University, Shandong Cancer Hospital and Institute, Shandong First Medical University and Shandong Academy of Medical Sciences, Jinan 250117, Shandong, P.R. China.
Funding
This work was supported by the National Natural Science Foundation of China (grant numbers U1932158, 81871085, and 82271519), Natural Science Foundation of Shandong Province (grant number ZR2019LZL018), Anhui Province Funds for Distinguished Young Scientists (grant number 2208085J10), Collaborative Innovation Program of Hefei Science Center, CAS (grant number 2019HSC-CIP003), China Postdoctoral Science Foundation (grant number 2019M652403), and Project of Postdoctoral Innovation of Shandong Province (grant number 202002048).
Conflicts of interest
The authors declare no conflicts of interest regarding the publication of this article.
References
- 1. Siegel R, Ma J, Zou Z, Jemal A.. Cancer statistics. CA Cancer J Clin. 2014;64(1):9-29. [DOI] [PubMed] [Google Scholar]
- 2. Howlader N, Forjaz G, Mooradian MJ, et al. The effect of advances in lung-cancer treatment on population mortality. N Engl J Med. 2020;383(7):640-649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Mahadevan A, , EmamiB, , Grimm J,. et al. Potential clinical significance of overall targeting accuracy and motion management in the treatment of tumors that move with respiration: lessons learnt from a quarter century of stereotactic body radiotherapy from dose response models. Front Oncol. 2020;10:591430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Li H, Park P, Liu W, et al. Patient-specific quantification of respiratory motion-induced dose uncertainty for step-and-shoot IMRT of lung cancer. Med Phys. 2013;40(12):121712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Akushevich I, Kravchenko J, Yashkin AP, et al. Partitioning of time trends in prevalence and mortality of lung cancer. Stat Med. 2019;38(17):3184-3203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Arroyo-Hernández M, Maldonado F, Lozano-Ruiz F, et al. Radiation-induced lung injury: current evidence. BMC Pulm Med. 2021;21(1):9-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Molitoris JK, Diwanji T, Snider IJW, et al. Advances in the use of motion management and image guidance in radiation therapy treatment for lung cancer. J Thorac Dis. 2018;10(Suppl 21):S2437-S2450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Langen KM, Jones DTL.. Organ motion and its management. Int J Radiat Oncol Biol Phys. 2001;50(1):265-278. [DOI] [PubMed] [Google Scholar]
- 9. Gierga DP, Brewer J, Sharp GC, et al. The correlation between internal and external markers for abdominal tumours: implications for respiratory gating. Int J Radiat Oncol Biol Phys. 2005;61(5):1551-1558. [DOI] [PubMed] [Google Scholar]
- 10. Nakamura M, Ishihara Y, Matsuo Y, et al. Quantification of the kV X-ray imaging dose during real-time tumour tracking and from three-and four-dimensional cone-beam computed tomography in lung cancer patients using a Monte Carlo simulation. J Radiat Res. 2018;59(2):173-181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Fayad H, Pan T, Pradier O, et al. Patient specific respiratory motion modeling using a 3D patient's external surface. Med Phys. 2012;39(6):3386-3395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Klinder T, Lorenz C, Ostermann J. Prediction framework for statistical respiratory motion modeling. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010: 13th International Conference, Beijing, China, September 20-24, 2010, Proceedings, Part III. Springer Berlin Heidelberg; 2010:327-334. [DOI] [PubMed]
- 13. Ehrhardt J, Werner R, Schmidt-Richberg A, et al. Statistical modeling of 4D respiratory lung motion using diffeomorphic image registration. IEEE Trans Med Imag. 2010;30(2):251-265. [DOI] [PubMed] [Google Scholar]
- 14. Wu G, Wang Q, Lian J, et al. Estimating the 4D respiratory lung motion by spatiotemporal registration and super-resolution image reconstruction. Med Phys. 2013;40(3):031710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Mori S, Ko S, Ishii T, et al. Effective doses in four-dimensional computed tomography for lung radiotherapy planning. Med Dosim. 2009;34(1):87-90. [DOI] [PubMed] [Google Scholar]
- 16. Yang C, Liu R, Ming X, Liu N, Guan Y, Feng Y.. Thoracic organ doses and cancer risk from low pitch helical 4-dimensional computed tomography scans. Biomed Res Int. 2018;2018:8927290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Primakov SP, Ibrahim A, van Timmeren JE, et al. Automated detection and segmentation of non-small cell lung cancer computed tomography images. Nat Commun. 2022;13(1):3423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. RiverBank Computing. What is PyQt? 2023. Accessed August, 2023. https://pypi.org/project/PyQt5/
- 19. Ibáñez L, Schroeder W, Ng L, Cates J.; InsightSoftwareConsortium. The ITK Software Guide. 2003. Accessed August, 2023. http://www.itk.org
- 20. Tanabe Y, Kiritani M, Deguchi T, Hira N, Tomimoto S.. Patient-specific respiratory motion management using lung tumors vs fiducial markers for real-time tumor-tracking stereotactic body radiotherapy. Phys Imaging Radiat Oncol. 2023;25:100405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Silverstein E, Snyder M.. Implementation of facial recognition with Microsoft Kinect v2 sensor for patient verification. Med Phys. 2017;44(6):2391-2399. [DOI] [PubMed] [Google Scholar]
- 22. Yao Y, Deng B, Xu W, et al. Fast and robust non-rigid registration using accelerated majorization-minimization. IEEE Trans Pattern Anal Mach Intell. 2023;45(8):9681-9698. [DOI] [PubMed] [Google Scholar]
- 23. David S. Validation Data for Deformable Image Registration. 2019. Accessed August, 2023. https://www.creatis.insa-lyon.fr/rio/dir_validation_data
- 24. Balik S, Weiss E, Jan N, et al. Evaluation of 4-dimensional computed tomography to 4-dimensional cone-beam computed tomography deformable image registration for lung cancer adaptive radiation therapy. Int J Radiat Oncol Biol Phys. 2013;86(2):372-379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Thomas P, Thomas A, Skylar G, Mathis ER. Sikerdebaard/dcmrtstruct2nii: dcmrtstruct2nii v5. 2023. Accessed August, 2023. 10.5281/zenodo.4037864 [DOI]
- 26. Nguyen D, Farah Jad, Barbet N, Khodri M.. Commissioning and performance testing of the first prototype of AlignRT InBore™ a Halcyon™ and Ethos™-dedicated surface guided radiation therapy platform. Phys Med. 2020;80:159-166. [DOI] [PubMed] [Google Scholar]
- 27. Beasley WJ, McWilliam A, Aitkenhead A, et al. The suitability of common metrics for assessing parotid and larynx autosegmentation accuracy. J Appl Clin Med Phys. 2016;17(2):41-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Ladjal H, Beuve M, Giraud P, et al. Towards non-invasive lung tumour tracking based on patient specific model of respiratory system. IEEE Trans Biomed Eng. 2021;68(9):2730-2740. [DOI] [PubMed] [Google Scholar]
- 29. He T, Xue Z, Lu K, et al. A minimally invasive multimodality image-guided (MIMIG) system for peripheral lung cancer intervention and diagnosis. Comput Med Imaging Graph. 2012;36(5):345-355. [DOI] [PubMed] [Google Scholar]
- 30. Wang T, He T, Zhang Z, et al. A personalized image-guided intervention system for peripheral lung cancer on patient-specific respiratory motion model. Int J Comput Assist Radiol Surg. 2022;17(10):1751-1764. [DOI] [PubMed] [Google Scholar]
- 31. Huang Y, Dong Z, Wu H, et al. Deep learning‐based synthetization of real‐time in‐treatment 4D images using surface motion and pretreatment images: A proof‐of‐concept study. Med Phys. 2022;49(11):7016-7024. [DOI] [PubMed] [Google Scholar]
- 32. Wang T, Xia G, Li H, et al. Patient specific respiratory motion model using two static CT images. In: Proceedings of the 2nd International Symposium on Artificial Intelligence for Medicine Sciences (ISAIMS 2021), Beijing, China, October 29-31, 2021. Association for Computing Machinery, 2021:488-492.
- 33. Boldea V, Sharp GC, Jiang SB, et al. 4D‐CT lung motion estimation with deformable registration: quantification of motion nonlinearity and hysteresis. Med Phys. 2008;35(3):1008-1018. [DOI] [PubMed] [Google Scholar]