Implementing l-DNA analogs as mirrors of PCR reactant hybridization state: theoretical and practical guidelines for PCR cycle control

Abstract

In previous reports, we described a PCR cycle control approach in which the hybridization state of optically labeled l-DNA enantiomers of the d-DNA primers and targets determined when the thermal cycle was switched from cooling to heating and heating to cooling. A consequence of this approach is that it also “adapts” the cycling conditions to compensate for factors that affect the hybridization kinetics of primers and targets. It assumes, however, that the hybridization state of the labeled l-DNA analogs accurately reflects the hybridization state of the d-DNA primers and targets. In this report, the Van't Hoff equation is applied to determine the l-DNA concentration and ratio of l-DNA strands required by this assumption. Simultaneous fluorescence and temperature measurements were taken during l-DNA controlled cycling, and the optical and thermal switch points compared as a function of both total l-DNA concentration and ratio of strands. Based on the Van't Hoff relationship and these experimental results, l-DNA best mirrors the hybridization of PCR primers and targets when total l-DNA concentration is set equal to the initial concentration of the d-DNA primer of interest. In terms of strand ratios, l-DNA hybridization behavior most closely matches the behavior of their d-DNA counterparts throughout the reaction when one of the l-DNA strands is far in excess of the other. The l-DNA control algorithm was then applied to the practical case of the SARS-CoV-2 N2 reaction, which has been shown to fail or have a delayed Cq when PCR was performed without nucleic acid extraction. PCR Cq values for simulated “unextracted” PCR samples in a nasopharyngeal background and in an NaCl concentration similar to that of viral transport media were determined using either the l-DNA control algorithm (N = 6) or preset cycling conditions (N = 3) and compared to water background controls run in parallel. For preset cycling conditions, the presence of nasopharyngeal background or a high salt background concentration significantly increased Cq, but the l-DNA control algorithm had no significant delay. This suggests that a carefully designed l-DNA-based control algorithm “adapts” the cycling conditions to compensate for hybridization errors of the PCR d-DNA reactants that produce false negatives.

Hybridization kinetics of DNA are explored and applied to improve accuracy of annealing in sensitive PCR reactions through l-DNA hybridization-based cycling control.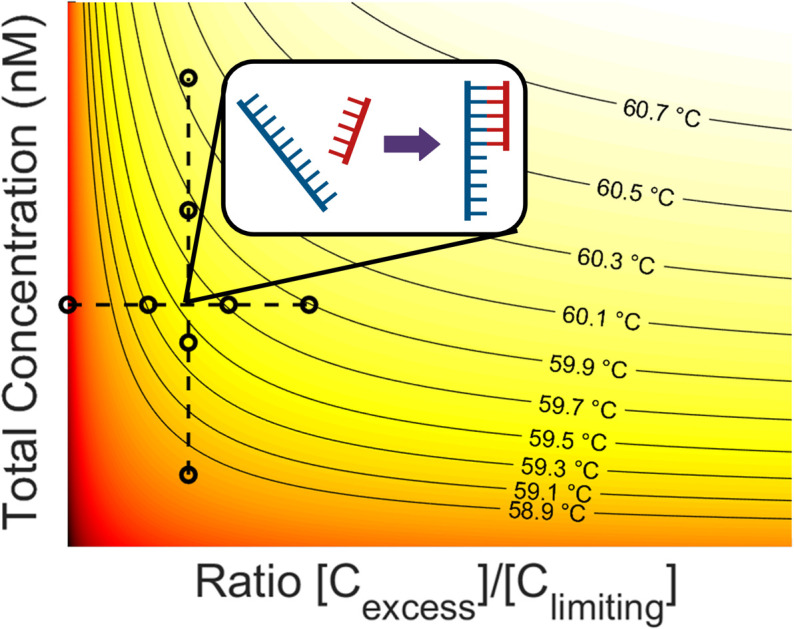

Introduction

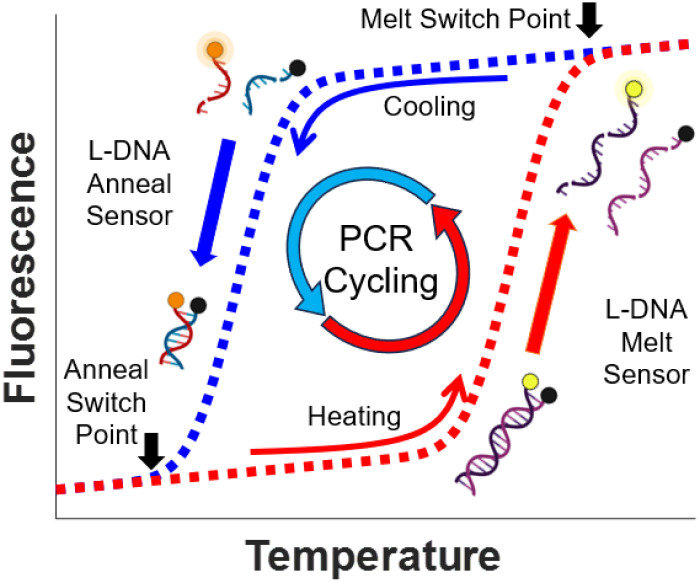
We have previously proposed a method to use the hybridization of l-DNA analogs of d-DNA PCR targets and primers to control the heating and cooling of PCR reactions.^1–3 These l-DNA strands are enantiomers of their d-DNA counterparts, and do not exist in nature. They do not interact with PCR enzymes, but have the same annealing and melting characteristics as sequence-matched d-DNA counterparts.^4,5 In this approach, thermal cycle switch points are identified optically using fluorophore and quencher labels on complementary l-DNA analogs of the PCR reaction d-DNA primer and target strand.³ The change in fluorescence signal of the l-DNA strand interactions is assumed to mirror the annealing and melting behavior of d-DNA PCR primers and targets and cycle switch points are determined from the changing l-DNA fluorescence (Fig. 1, adapted from previous work).¹ The l-DNA hybridization switch points replace the preset times and temperatures of standard PCR instrumentation. Since these switch points are based directly upon the observed annealing and melting behavior of the l-DNA analogs, any non-stereospecific background interferents that alter hybridization behavior—whether stabilizing duplex formation, as in the case of salts,⁶ or destabilizing duplex formation, as in alcohols⁷—are accounted for by a corresponding shift in l-DNA behavior. Thus, this approach allows the l-DNA controlled PCR instrument to “adapt” its annealing and melting points to certain interferents. Traditional PCR has preset timings and temperatures that do not respond to reaction contents. Thermal calibration of the instrument and calculation of annealing and melt temperatures are also unnecessary, as the heating and cooling are controlled via continuous measurements of the l-DNA hybridization state via the two l-DNA sensors. Switching from cooling to heating is critical for effective annealing, and the predictive power of the l-DNA analogs is most important in determining the switch point from the cooling phase to the heating phase. Shifting the annealing temperature a few degrees can cause nonspecific binding or diminish PCR efficiency, while the high temperature required to achieve the separation of the amplicon strands merely needs to be high enough to ensure all double stranded DNA is separated.^8,9 Therefore, in this study we use a previously developed long, high melt temperature sequence for selection of melting switch points and focus our evaluation primarily on the primer-target annealing interactions.

Fig. 1. Basic principle of l-DNA controlled PCR. During the heat cycle, melting of DNA target sequences is monitored by the fluorescence of the longer l-DNA melt sensor. When the increase in fluorescence slows, the system selects a melt switch point and shifts to cooling. During the cooling cycle, annealing of primers to targets is monitored using the fluorescence of the l-DNA anneal sensor. When the decrease in fluorescence slows, the system selects an annealing switch point and shifts back to heating.

Other than creating l-DNA strands with exact sequence homology to their d-DNA counterparts, no clear guiding theory and practice has been proposed to ensure that the l-DNA analogs closely mimic the d-DNA molecular events during the annealing and melting phases of a PCR reaction. In standard PCR reactions, primers complementary to the expected target are added in extremely high concentrations relative to the target concentration (i.e., on the scale of 6–12 orders of magnitude greater, depending on initial target concentration). Primers anneal to any target strands present, and during the extension phase these primers are incorporated into new copies of the amplicon sequence. Until the plateau phase is reached, this results in an increase in the number of amplicons and a decrease in the number of primers with each PCR cycle. Several explanations exist for the plateau phase, including exhaustion of PCR reagents (primers, dNTPs, and polymerase),^10,11 and inhibition of polymerase activity by an abundance of double-stranded amplicon.^12,13 Regardless of the explanation for the plateau phase, the ratio of the d-DNA components changes exponentially in the pre-plateau cycles of the reaction. An obvious concern, therefore, is how accurately the fixed concentration of the l-DNA analogs represents the changing PCR primer and amplicon concentrations.

For both d-DNA and l-DNA, the theoretical relationship between the fraction of DNA in a hybridized state (f) at a given temperature T_f and total concentration of complementary strands ([C]) is described by Van't Hoff kinetic theory¹⁴

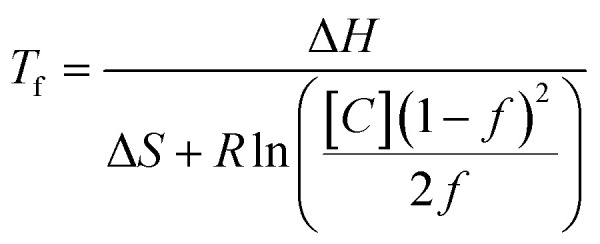1

where ΔH and ΔS are enthalpy and entropy respectively, and R the universal gas constant. ΔH and ΔS are dependent on sequence length and base composition, but constant between l and d-DNA. Eqn (1) assumes that the concentrations of the complementary annealing strands are equal. You, et al.¹⁵ showed that the Van't Hoff relationship for an anneal fraction of 0.5 can also be rewritten to include the case of unequal concentration of complementary annealing strands as

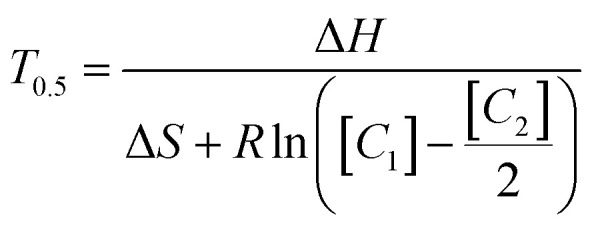2

where C₁ and C₂ are the concentrations of each single strand of complementary DNA in the pair, with C₁ being the strand in excess. These equations are combined to show the dependence of T_f on strand ratio (see ESI for derivation†), becoming

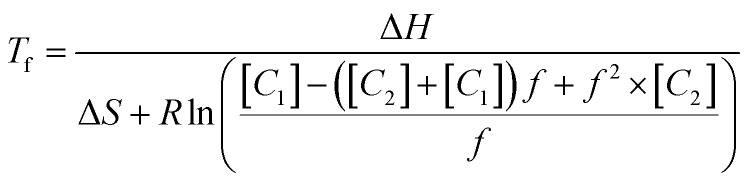3

In this expression, if C₁ is set to be equal to C₂, eqn (3) simplifies to eqn (1). If f is set to 0.5, eqn (3) simplifies to eqn (2).

The Van't Hoff equation suggests that both total concentration and strand ratios affect the annealing behavior of both l-DNA and d-DNA. For the l-DNA analogs, C₁ and C₂ remain constant over all cycles of a PCR reaction, while for d-DNA strands the concentrations and primer-target strand ratio change with each PCR cycle. Since these changing concentrations affect the value of T_f, eqn (3) surprisingly suggests that despite the preset times and temperatures traditionally used in PCR, the temperature for a fixed fraction of primers to anneal is not constant.

In addition to eliminating the need to preset the reaction temperature, this l-DNA control approach also promises to “adapt” cycling conditions to compensate for variation in reaction conditions.¹ For example, performing PCR directly using a sample without nucleic extraction has proven useful in screening applications, particularly in resource limited conditions such as point of care settings.¹⁶ But because sample preparation is not incorporated into these direct PCR workflows, false negatives can occur. One particular cause of these false negatives is that unextracted reaction interferents, e.g. salts and proteins, may be present and affect strand interactions in PCR. An example of this is the CDC 2019-Novel Coronavirus (2019-nCoV) Real-Time RT-PCR Diagnostic Panel, which has been shown to produce false negatives when performed with unextracted nasopharyngeal samples without annealing temperature adjustment.¹⁷ In this case, a small variation in annealing temperature (on the scale of 2 °C) resulted in a Cq delay of 5 or greater.¹⁸ As these variations in primer-target hybridization behavior should also be reflected in changes in the hybridization behavior of their l-DNA analogs, the l-DNA control algorithm can account for them—provided other factors, such as total concentration and strand ratio, are accounted for.

In this report, experimental data guided by the Van't Hoff equation are used to predict the d-DNA hybridization kinetics in a PCR reaction. The l-DNA total concentration and the l-DNA strand ratio are then determined experimentally so that their hybridization state at a particular temperature matches the d-DNA reactants as closely as possible. These theoretical optimizations are combined with practical considerations, such as minimum detectable fluorescence signal and reagent cost, to show that l-DNA additives provide an accurate mirror for d-DNA reactants across almost all cycles, but especially the early cycles where C₁ (primers) is far in excess of C₂ (amplicons). These optimizations are then applied to SARS-CoV-2, demonstrating the “adaptive” nature of the L-DNA cycle control approach and reducing the false negatives in unextracted nasopharyngeal testing.

Methods

Modeling of theoretical amplicon and primer numbers in PCR

A qualitative analysis of PCR copy numbers after each cycle of the reaction was developed to better understand how the annealing characteristics of PCR components change over the course of a PCR reaction. A simple recursive model was created using primer exhaustion as a cause for the plateau phase,¹⁰ and calculated using MATLAB. This simple model (see ESI for derivation and plot†) bears a qualitative resemblance to more complex models from literature,¹¹ but precision of the model was unimportant for an approximate analysis as long as the overall character of the PCR curve was preserved. Annealing temperature was defined as the temperature where greater than 90% of primers were annealed to targets and calculated using eqn (3) with primer and target concentrations from the model. The thermodynamic constants ΔH and ΔS were derived from the annealing temperature data found in the “Effect of l-DNA strand ratio on annealing switch point” experiments below.¹⁹ Initial primer concentration and amplicon copy numbers were set to 500 nM and 10⁶, respectively.

Oligonucleotides, primers probes and synthetic RNA

Labeled l-DNA oligonucleotides and primers were synthesized by Biomers (Ulm, Germany). Labeled d-DNA oligonucleotides, unlabeled primers, and probes were synthesized by Integrated DNA Technologies (Coralville, IA). SARS-CoV-2 N1 and N2 synthetic RNA amplicons were synthesized by Biosynthesis (Lewisville, TX). Full sequences are shown in Table 1. The N2 forward primer sequence was used to synthesize the l-DNA annealing control sequences, with the anneal sensor fluorescent strand matching the base composition and length of the N2 forward primer to ensure similar thermodynamic behavior. The anneal sensor quencher strand has additional base pairs to offset the quencher from the fluorophore and diminish the effects of fluorophore-quencher interactions on the melt temperature of the sequence.²⁰ Since the precision of melting is less important,²¹ a long sequence with a high melting temperature was used to ensure complete melting of targets and was not examined further in this report. The molecular beacon used for reverse transcription was established in previous research and was not explored here.²

Oligonucleotide sequences used in experiments^a.

Description/name		Sequence (5′-3′)
Control l-DNA	Anneal sensor fluorescent strand	TEX—TTACAAACATTGGCCGCAAA
	Anneal sensor quencher strand	TTTGCGGCCAATGTTTGTAATCAGT—BHQ2
	Melt sensor fluorescent strand	HEX—ACAAGAAAGGGATCTTCACTCGCGACCGCAAACCGA AGTCGGCGGCTTTTCTGCTGCAAAAACGCTGGACTGGCATG
	Melt sensor quencher strand	CATGCCAGTCCAGCGTTTTTGCAGCAGAAAAGCCGCCGACTTCGGTTTGCGGTCGCGAGTGAAGATCCCTTTCTTGT—BHQ2
	RT beacon2	FAM—GCGAGAAAAAAAAAAAAAAACTCGC—BHQ1
Labeled d-DNA	N2 fluorescent forward primer	HEX—TTACAAACATTGGCCGCAAA
	N2 quencher reverse complement	TTTGCGGCCAATGTTTGTAATCAGT—BHQ2
SARS CoV2 PCR assay	N1 forward primer	GACCCCAAAATCAGCGAAAT
	N1 reverse primer	TCTGGTTACTGCCAGTTGAATCTG
	N1 probe	FAM—ACCCCGCATTACGTTTGGTGGACC—BHQ1
	N1 synthetic RNA target	rGrArCrCrCrCrArArArArUrCrArGrCrGrArArArUrGrCrArCrCrCrCrGrCrArUrUrArCrGrUrUrUrGrGrUrGrGrArCrCrCrUrCrArGrArUrUrCrArArCrUrGrGrCrArGrUrArArCrCrArGrA
	N2 forward primer	TTACAAACATTGGCCGCAAA
	N2 reverse primer	GCGCGACATTCCGAAGAA
	N2 probe	Cy5—ACAATTTGCCCCCAGCGCTTCAG—BHQ2
	N2 synthetic RNA target	rUrUrArCrArArArCrArUrUrGrGrCrCrGrCrArArArUrUrGrCrArCrArArUrUrUrGrCrCrCrCrCrArGrCrGrCrUrUrCrArGrCrGrUrUrCrUrUrCrGrGrArArUrGrUrCrGrCrGrC

^aHEX = hexachloro-fluorescein, FAM = fluorescein, TEX = texas red, Cy5 = cyanine 5, BHQ 1 and BHQ 2 = black hole quenchers 1 and 2.

Comparison of thermal and fluorescence anneal switch points

The l-DNA PCR control algorithm uses fluorescence to monitor the hybridization state of end-labeled, double-stranded l-DNA and switch between the heating and cooling phases of the PCR cycle. In some experiments, switch temperatures were directly measured during each cycle by placing a thermocouple within the sample vial using a 3D-printed holder. Simultaneous temperature and fluorescence measurements were taken for 20 cycles. The clocks on both the thermocouple DAQ and the l-DNA controlled instrument were synchronized, and the switch times for the control algorithm retrieved from the instrument's log file. Temperature values were interpolated from the timestamps provided from the fluorescence data to compensate for differences in sampling frequency between the two measurements, and the switch point temperatures were found using the switch times recorded from the fluorescence data. Except for the first total concentration sample group, the last 10 annealing temperature measurements in each sample run were averaged, and the overall sample group averages were compared. In the case of the first total concentration sample group, the instrument was run for 10 cycles and the last 5 cycles were averaged. The final cycles in each group were selected to reduce the effects environmental conditions have on the first few cycles. All ratio switch point samples contained 1X TaqPath master mix (TaqPath™ 1-Step RT-qPCR, Applied Biosystems Catalog #A15299), while total l-DNA concentration experiments were performed in 1X Luna master mix (Luna Universal One-Step RT-qPCR, New England Biolabs Catalog #E3005L).

Effect of total l-DNA concentration on annealing switch point

Based on the Van't Hoff equation, the total concentration of double-stranded DNA, for either l or d, is expected to affect the kinetic behavior of the annealing process.²² Therefore, since the primary aim of the l-DNA analogs is to accurately reflect the d-DNA primer annealing process, total concentration of the l-DNA analogs must be considered. The effects of total concentration of double-stranded DNA on l-DNA controlled PCR annealing temperature were tested using the internal thermocouple and synchronized fluorescence measurement scheme described above to determine the effect of l-DNA concentration on anneal switch point. In order to capture a large range of primer concentrations both lower and higher than the typical 500 nM of each primer, total l-DNA concentrations of 219, 438, 656, and 875 nM at a fixed strand ratio of l-DNA N2 fluorescent forward primer to N2 quencher reverse complement of 1 : 2.5 were investigated (N = 3 for each group).

Effect of l-DNA strand ratio on annealing switch point

Similarly to total concentration, Van't Hoff theory also predicts that the ratio between the complementary l-DNA single strands added to the reaction will affect the annealing characteristics of l-DNA. Strand ratio experiments were carried out in the l-DNA controlled PCR instrument with four different ratios of the N2 fluorescent forward primer and N2 quencher reverse complement. Synchronized temperature and fluorescence measurements were taken using the same scheme as the total concentration experiments. In this case, the total concentration of control DNA was held constant at 500 nM while the ratio of forward to reverse complement was shifted from equal concentrations (e.g. 1 to 1 ratio) until the quencher labeled strand was far in excess of the fluorescently labeled strand. While the PCR primers and targets are typically at far higher ratios, eqn (2) indicates that the greatest change in the annealing temperature will occur closest to a balanced ratio of strands, (e.g. C₁ = C₂) so the ratio of C₁/C₂ was increased linearly from 1. The groups tested were [C₁]/[C₂] equivalent to 1, 2, 3, and 4, or 250 nM/250 nM, 333 nM/166 nM, 375 nM/125 nM, and 400 nM/100 nM respectively, in terms of actual concentrations (N = 4 for each group).

l-DNA switch point control in salt sensitive SARS-CoV-2 reactions

The N2 SARS-CoV-2 PCR reaction was used to demonstrate that l-DNA control “adapts” to background interferents and “rescues” sensitive reactions, with annealing strand l-DNA concentration and ratio selected based on the guidance of the earlier experiments. PCR reactions were prepared according to CDC SARS-CoV-2 EUA protocol (TaqPath™ 1-Step RT-qPCR, Applied Biosystems Catalog #A15299). Briefly, each reaction contained 1X TaqPath master mix, d-DNA primers at a final concentration of 500 nm, l-DNA fluorescent forward primers and molecular beacon at a final concentration of 125 nM (1.506 × 10¹² copies), and L-DNA reverse complement quencher at 312 nM (3.76 × 10¹² copies). These matched the closest tested concentration group (438 nM) to our total primer concentration of 500 nM, and were at the 1 : 2.5 ratio identified as a good balance of fluorescence signal and ratio matching in the ratio switch point experiments. De-identified SARS-CoV-2 negative specimens (nasopharyngeal matrix in viral transport media) were obtained from Vanderbilt University Medical Center under Institutional Review Board IRB #201708 and #201804. To simulate patient samples the 2 × 10⁵ copies of synthetic N1 and N2 RNA were spiked into either water, 35 mM NaCl, or heat-inactivated nasopharyngeal matrix. Then the samples were run immediately to prevent any RNase activity from degrading the RNA. RotorGene-Q Instrument: According to the CDC SARS-CoV-2 EUA cycling conditions were hold at 55 °C for 15 minutes (reverse transcription), hold at 95 °C for 2 minutes then 45 cycles of 95 °C for 3 seconds and 55 °C for 30 seconds. These were also repeated in triplicate with an annealing temperature of 61 °C instead of the CDC prescribed 55 °C. Adaptive PCR Instrument: All samples were covered with a layer of PCR grade mineral oil to prevent evaporation during heating, which is not necessary in the RotorGene instrument due to its spinning action. These were placed in the “adaptive” PCR instrument.¹ One experiment consisted of a comparison of six 35 mM NaCl samples and six 0 mM NaCl samples, while the other compared six nasopharyngeal samples and six “extracted” samples. Reverse transcription temperature control was set using the molecular beacon included in the reaction mixture as established in prior work.² For control of PCR cycling, the HEX and Texas Red fluorescence channels were used for l-DNA monitoring. Since the adaptive instrument does not use set temperatures, the annealing holds were set by the control algorithm at the desired reaction activity, using the raw fluorescence value as a proxy for primer annealing to target. Final data comparisons were made by comparing the cycle threshold values of the PCR curves, which were calculated using LinRegPCR.²³ Cycle threshold values were compared using an unpaired Student's t-test.

Results

Modeling of theoretical amplicon and primer numbers in PCR

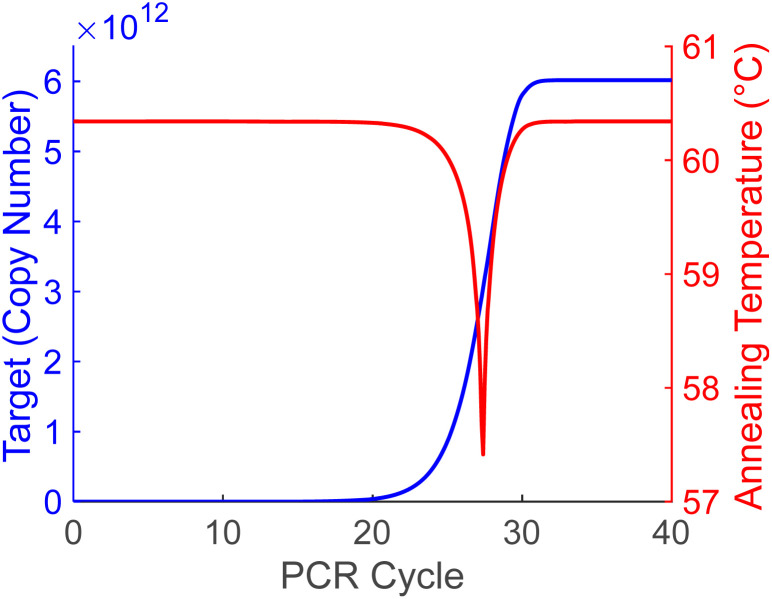
The amplicon copy number calculated using the simple recursive model bears a qualitative resemblance to standard PCR curves, with baseline, exponential, linear and plateau phases, and a Cq around 23 (Fig. 2, blue). The Van't Hoff calculated annealing temperature is also plotted using the simple PCR model of copy numbers and eqn (3), defining the annealing temperature as when more than 90% of the primers are hybridized to targets (Fig. 2, red). This model shows a constant annealing temperature of 60.3 °C across the first 20 cycles, until the PCR reaction exponential phase, where the annealing temperature dips sharply for a few cycles before returning to the constant temperature during the plateau phase. The lowest annealing temperature reached in the center of the exponential phase is 57.4 °C. In early cycles where the annealing temperature is constant, primers are in great excess of amplicons, while in later cycles where the annealing temperature is constant, the amplicons are in great excess of the primers as the primers are assumed to be exhausted in the plateau phase. The lower annealing temperatures during the exponential phase are caused by the ratio of d-DNA primers to amplicons approaching 1 : 1, returning to the higher temperature as the ratio once again becomes extreme.

Fig. 2. Theoretical PCR copy number plotted as a function of cycle (blue) with annealing temperature calculated using eqn (3) (red). Annealing temperature remains at 60.3 °C at the extremes, but drops to 57.4 °C around cycle 27.

Comparison of thermal and fluorescence anneal switch points

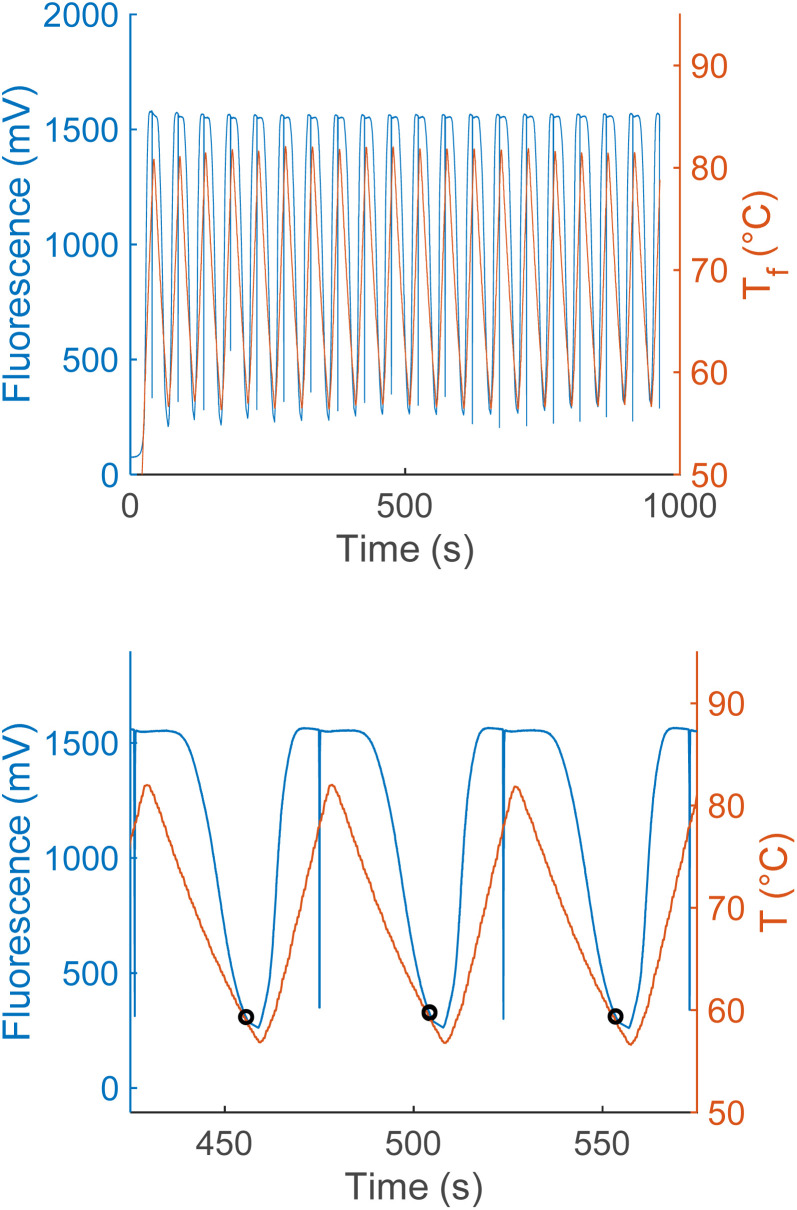
Anneal switch points in a representative plot of thermal and fluorescence data display remarkable consistency across consecutive cycles (Fig. 3, upper panel), with a maximum standard deviation within a sample of 0.36 °C and most lying below 0.2 °C. Three representative heating and cooling cycles of a PCR reaction show the methodology used to acquire anneal switch point data for the concentration and ratio experiments (Fig. 3, lower panel). The shapes and timing of the two plots in the lower panel remain constant, with both showing a sharp rise, peak, and drop off with time. The temperature rises and falls linearly with sharp peaks, in a sawtooth form. On the other hand, the fluorescence rises to a plateau value and remains constant for about 20 seconds due to complete melting of the l-DNA analogs. This plateau reflects an equilibrium state where all fluorescently labeled strands are separated from quencher strands and fluorescence cannot increase further, regardless of temperature. Note: the vertical blue lines in the fluorescence data are a data collection artifact created by the instrument changing channels from the HEX fluorophore used to determine the melting switch point to the Texas Red fluorophore used to determine the annealing switch point.

Fig. 3. Twenty cycles of synchronized fluorescence and temperature measurements taken from an PCR reaction (upper panel), plotting raw fluorescence (blue), and temperature (red). Zoomed in view of three cycles of simultaneous PCR fluorescence and temperature measurements from the same PCR reaction (lower panel). Black circles show the fluorescence and temperature when the reaction cycle switched from cooling to heating.

Effect of total l-DNA concentration and strand ratio on annealing switch point

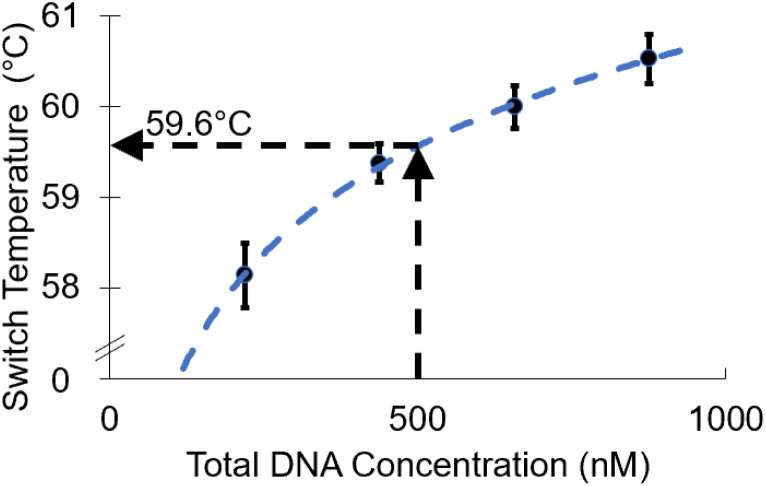
As the total concentration of l-DNA analogs included in a reaction is increased, the annealing switch point temperature also increases. Fig. 4 shows the average switch temperatures determined for each of the four l-DNA concentrations at a constant strand ratio of ([C₁]/[C₂]) = 2.5, ranging between 58.1 and 60.5 °C. As hypothesized from theory, the overall dependence of switch temperature on total DNA concentration is logarithmic (y = 1.7091 ln(x) + 48.942), with an R² value of 0.99.

Fig. 4. As total l-DNA concentration increases, the anneal cycle switch temperature increases (mean ± s.d., N = 3). A logarithmic fit shows the overall trend in the data (dotted blue line). When the l-DNA concentration is set equal to the d-DNA primer concentration, the predicted switch temperature is 59.6 °C.

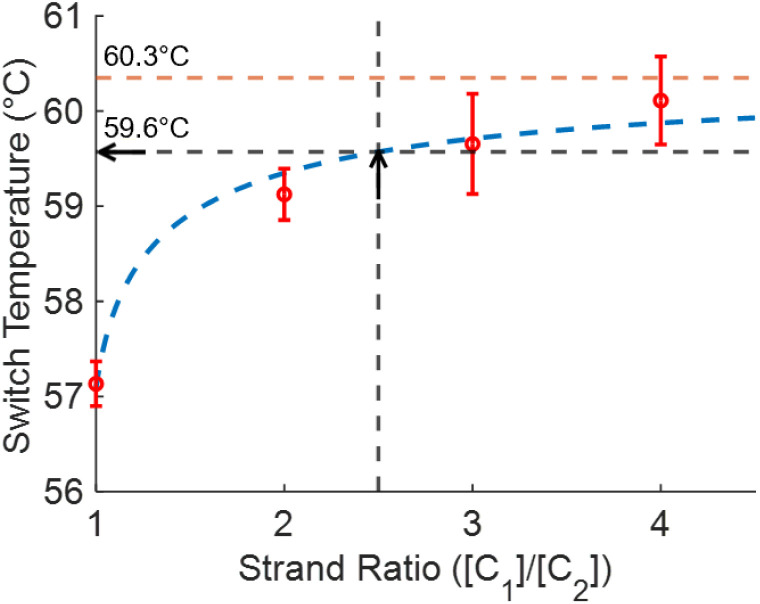
Similarly, as the ratio of quencher to fluorophore strands increases, the anneal switch temperature also increases (Fig. 5). The last ten cycles average anneal switch temperatures are shown as a function of the ratio of the two strands ([C₁]/[C₂]) at a fixed total concentration for each ratio ([C₁] + [C₂] = 500 nM). Results are consistent with literature, where melt temperatures increase with the ratio of the excess strand to the limiting strand.¹⁵Eqn (3) is plotted as a function of ratio with ΔH and ΔS values fitted from these trials to show the overall trend in the data (blue). The orange line indicates the theoretical annealing switch temperature if the ratio approaches infinity for a constant 500 nM concentration of l-DNA. The ratio of l-DNA analogs used in the rest of this report ([C₁]/[C₂] = 2.5) is indicated with a black arrow. The black arrows in both Fig. 4 and 5 correspond to an equivalent DNA total concentration and ratio of 500 nM, and [C₁]/[C₂] = 2.5, respectively.

Fig. 5. Measured anneal switch temperature as a function of ratio of l-DNA quencher strand to fluorophore strand (red circles, mean ± s.d., N = 4). Eqn (3) with ΔH and ΔS calculated from the experimental data shows the overall trend of the data (dashed blue line). The 2.5 ratio used for the total concentration experiments also results in a switch temperature of 59.6 °C (black dashed line and arrow). The limit of the switch temperature as ([C₁]/[C₂]) approaches infinity for a fixed total concentration of 500 nM is 60.3 °C (dashed orange line).

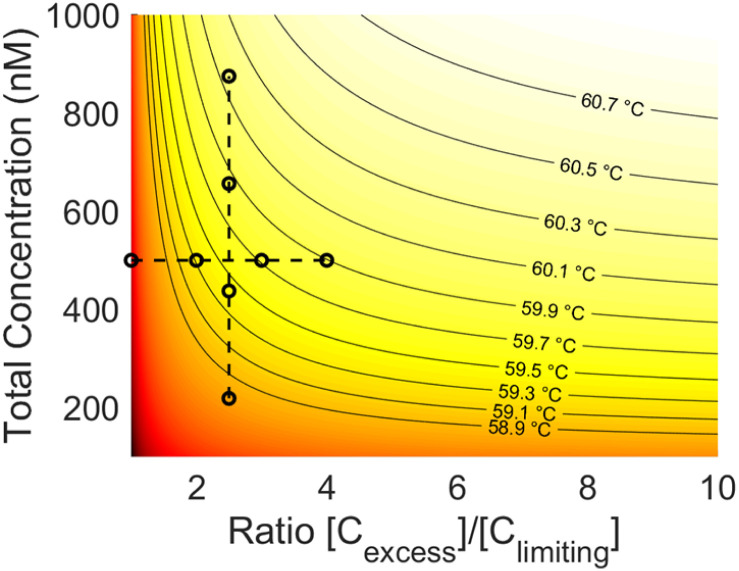
The data collected in these experiments were combined and used to calculate empirical ΔH and ΔS values for the primer model strand (see ESI for methodology†). Using these constants and eqn (3), a heat map of theoretical annealing temperature as a function of both total concentration and ratio of strands was created (Fig. 6). Theoretical annealing temperature is constant in arcs that come down from high concentrations and extend to high ratios, with steeper temperature gradients seen at lower concentrations and ratios, as shown by the faster color changes and closer grouping of the black isolines. All 8 sample groups from the ratio and concentration experiments are plotted on the heatmap to show the part of the graph within the scope of experimental data. The 59.6 °C temperature indicated with the arrows in Fig. 4 and 5 is shown at the intersection of the dashed lines that connect the experimental data.

Fig. 6. Heat map of theoretical annealing temperature as a function of both total concentration and strand ratio. Darker shades of red represent lower temperatures. Isolines are graphed at constant temperature intervals (solid lines). The data used to derive the heatmap is also plotted (black circles). Constant ratio experiments are connected vertically and constant concentration experiments horizontally (dashed lines).

l-DNA switch point control in salt sensitive SARS-CoV-2 reactions

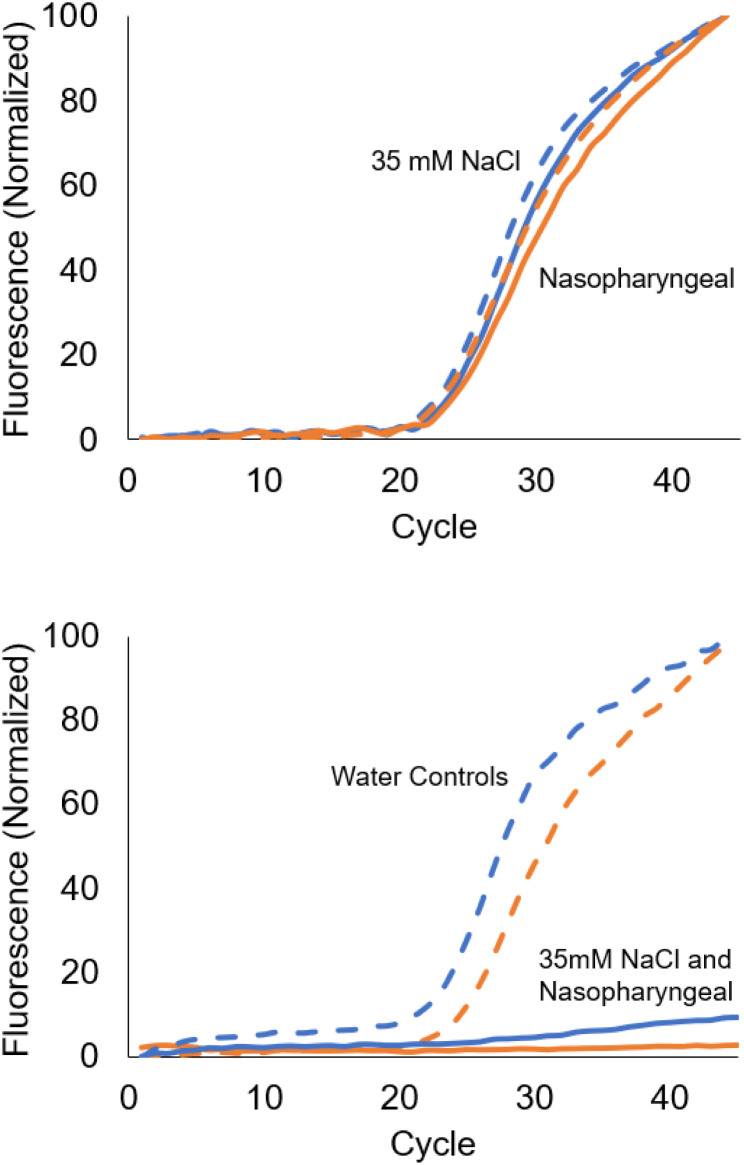
The “adaptive” instrument trials demonstrated success regardless of the background sample conditions (Fig. 7, top panel solid lines). With no external calibration or procedure changes from water samples to those with the salt or nasopharyngeal matrix background, all samples produced the expected positive results for the N2 sequence. Moreover, there were no statistically significant Cq differences when comparing samples in these backgrounds to those prepared in water (also shown in Fig. 7, top panel, corresponding dashed lines).

Fig. 7. Top panel: “Adaptive” PCR results for N2 reactions conducted in nasopharyngeal and 35 mM NaCl backgrounds with paired water controls (N = 6, duplicates). Nasopharyngeal trials (solid orange) display no change from control (dashed orange). 35 mM NaCl trials (solid blue) similarly show no difference from water background control (dashed blue). Bottom panel: identical samples conducted instead in traditional PCR, according to the CDC SARS-CoV-2 EUA (N = 3, duplicates). In contrast with the adaptive PCR results, all conducted in the nasopharyngeal (solid orange) and NaCl (solid blue) backgrounds failed, displaying false negative results. In comparison, the paired controls (dashed lines) all displayed similar performance to l-DNA controlled PCR.

However, for traditional PCR methods the previously observed failure¹⁸ of the N2 reaction in RT-PCR (without sample preparation) was consistent with previous research.^17,18 The N2 reaction completely failed in nasopharyngeal matrix with a 55 °C annealing temperature and had a Cq delay > 20 in 35 mM NaCl at 55 °C, reinforcing that the SARS-CoV-2 N2 reaction is sensitive to background contaminant interference (Fig. 7, bottom panel). In all cases, identical unextracted samples returned a false negative result when performed according to the CDC SARS-CoV-2 EUA. The N1 positive control showed consistent Cq values in all samples for both the l-DNA control algorithm and traditional PCR methods, with small Cq delays in some groups but no complete failures (see ESI† for adaptive PCR N1 and a comparison of traditional PCR N2 data for a 61 °C annealing temperature).

Discussion

Theory and experiments suggest that the three l-DNA variables (sequence, total concentration, strand ratio) can be used to ensure that the hybridization characteristics of the l-DNA analogs closely match the hybridization kinetics of the primers and targets during a PCR reaction. Our prior work has shown that matching the l-DNA sequences with the d-DNA primers ensures similar behavior,¹ and this report establishes that the Van't Hoff theory can be used to theoretically determine the total l-DNA concentration and ratio of strands to best mirror the d-DNA hybridization behavior. The “adaptive” PCR system was then applied to a practical example of salt and nasopharyngeal interference in the case of the SARS-CoV-2 N2 reaction, and complete rescue of the sensitive reaction occurred in both nasopharyngeal and NaCl backgrounds.

Total DNA concentration experiments confirmed that total concentration of l-DNA should be selected carefully to best mimic the annealing behavior of d-DNA primers. The annealing temperature of primers and targets increases logarithmically with total concentration of complementary strands, meaning a mismatch in l-DNA and d-DNA total concentration would cause a similar mismatch in the annealing kinetics of the strands (Fig. 4). From a practical standpoint, while the concentration of the d-DNA primer is known, it is impossible to know how many copies of the d-DNA target sequence are in a real-world sample. However, it is safe to assume that the primer concentrations are in great excess of the target, so the total l-DNA concentration can be set equal to the total concentration of the d-DNA primer as a good approximation of total d-DNA complementary strand concentration. As an example, in our N1 and N2 experiments, there were 6.02 × 10¹² primer copies per sample, versus only 2 × 10⁵ target copies (Fig. 7). Moreover, since each primer consumed by the PCR process is extended to become one target strand, the total d-DNA complementary strand concentration does not change from cycle to cycle, so this approximation is equally valid throughout the reaction.

In addition to matching the total l-DNA concentration to the d-DNA primer concentration, the ratio of l-DNA strands should be set as high as is practical to ensure a good approximation of the exponential decrease of ratio between primers and targets in PCR (Fig. 5). Our data suggests that a ratio of 1 : 2.5 (F : Q) works well (Fig. 7, for example), but because d-DNA primer to amplicon strand ratios change with each PCR cycle, a more detailed examination was performed to identify the cycles of a PCR reaction in which l-DNA hybridization state best mirrors the state of the d-DNA primer-target annealing. Because total concentration of l-DNA is matched to that of l-DNA, a large increase in strand ratio of quencher to fluorophore reduces the concentration of the fluorescently labeled strand to undetectable levels, which limits experimental testing. However, it is possible to use the kinetic constants derived from the experiment and eqn (3) to get a qualitative picture of the effects of strand ratio on annealing temperature over the entire cycle (Fig. 2). Although preset temperatures and times for control of PCR conditions assume that the annealing temperature does not change with cycle, the Van't Hoff theory predicts that the ideal annealing temperature changes across the cycles of a PCR reaction. At the two extremes (C_primer/C_amplicon approaches infinity and C_amplicon/C_primer approaches infinity), the primer annealing temperature is 60.3 °C (Fig. 5). In practice, the ratio of l-DNA components cannot approach infinity and practical considerations like fluorescence strength still need to be met.

While the annealing temperature between the extremes is difficult to predict, the amplicon and primer copy number estimates from a simple PCR model were used in the Van't Hoff equation to estimate the annealing temperature for each cycle and compared to the constant value of the l-DNA analogs. Models leading up to the Cq value are plentiful, but those that include the plateau phase are less common and use various explanations of the plateau phase in late PCR. Two of the primary explanations are primer exhaustion, and polymerase inhibition from overabundance of double-stranded amplicon. The simple model used here assumes that primer exhaustion is the cause of the PCR plateau phase because it has the most extreme ratio change of the commonly proposed plateau phase models. However, the choice of model is not critical as long as it demonstrates the phases of the PCR reaction, and a simplistic one with the largest possible ratio change was chosen for demonstration purposes. Eqn (3) was used with a PCR model based on this theory to calculate primer-amplicon annealing temperature as a function of PCR cycle (Fig. 2, red line, and Fig. 8, numbers). As seen from the theoretical data, the primer annealing temperature stays constant for most of the reaction, only differing for a few cycles in the midst of the exponential phase where it falls to 57.4 °C. This could have interesting implications for traditional PCR, as current methodologies typically do not vary the annealing temperature between cycles. While a potentially higher efficiency could be gained in the exponential phase of the reaction by accounting for this phenomenon, it is unlikely to produce large differences in outcomes as it occurs after Cq values are determined. Moreover, without knowing the cycle range of the exponential phase ahead of time, preset temperatures for each cycle would be difficult to set.

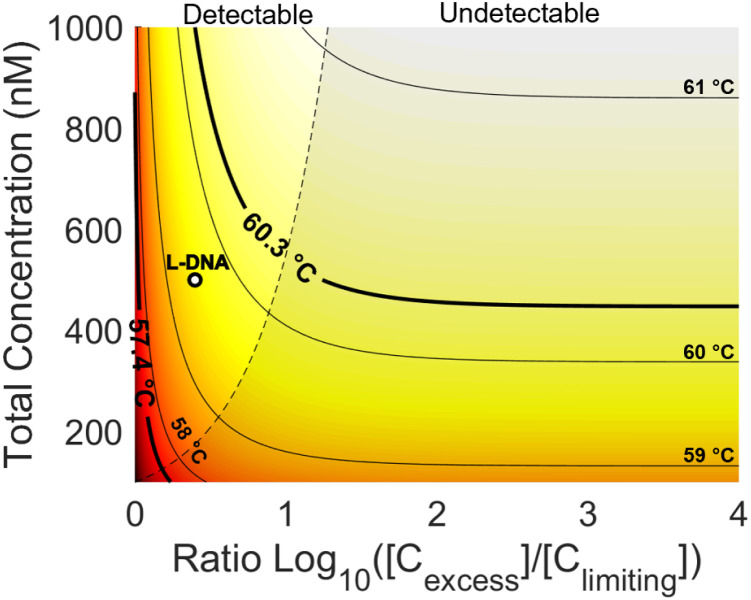
Fig. 8. Heatmap of theoretical PCR annealing temperature as a function of total concentration and strand ratio. Isolines show constant temperatures at integer degrees (light black lines). Theoretical minimum and maximum annealing temperatures during PCR are also shown (heavy black lines) with the current l-DNA implementation (white dot). The tinted region (right) shows the total concentrations and strand ratios where the fluorophore concentration is undetectable.

In terms of the l-DNA controlled approach, the practical experimental strand ratio of 2.5 times the amount of quencher as fluorophore produces a 0.7 °C underestimate in the l-DNA annealing temperature when compared to the d-DNA annealing temperature for most of the reaction (Fig. 5). Although it is unclear if this is an important difference, it could be reduced by either increasing the l-DNA concentration or increasing the quencher to fluorophore ratio. Compensating for the deviation during the exponential phase would be more difficult. However, because it occurs briefly and late in PCR cycles, after a Cq can be determined, correcting for it may not be necessary. In any event, traditional PCR cycle control based on fixed times and temperatures does not compensate for this deviation either. Thus, the ideal constant annealing temperature to aim for is the extreme case, given the sensitivity of the reaction in the pre-exponential phase.

There are some practical limitations of these potential l-DNA modifications. Increasing the total concentration will require more l-DNA per reaction, increasing reagent cost. Increasing the ratio of quencher to fluorophore while keeping total concentration constant, on the other hand, will diminish the fluorescence signal necessary for the control algorithm to function. The quickest method of calculating an l-DNA anneal sensor concentration is to match the total concentration of primers, then use the highest possible strand ratio while maintaining good fluorescence signal. This method is how the l-DNA implementation used in this report was calculated, which has the 0.7 °C underestimate mentioned above. If a more precise estimate is desired, ΔH and ΔS can be obtained either experimentally or calculated and a heatmap like Fig. 8 can be created to find the ideal concentration and ratio to match the d-DNA primers and amplicons. As seen in the figure and predicted by theory, the annealing temperature for a given total concentration approaches a limit as the ratio of strands approaches infinity. Therefore, a more precise estimate for early PCR cycles can be calculated from this chart by going straight across from the total primer concentration to the right, then following along the isoline back to a detectable fluorescence that emulates the extreme ratios present for most of the PCR reaction. The bold isoline at 60.3 °C in Fig. 8 shows where this would be done for the experiments in this report, following it back from the right and out of the tinted, undetectable region on the right of the figure.

In terms of a practical demonstration, applying these findings to the SARS-CoV-2 N2 reaction by using them to inform the selected l-DNA annealing sensor concentration and strand ratio showed an insignificant amount of performance loss in even unextracted samples (Fig. 7, top panel), while the traditional PCR entirely failed using published CDC procedure (Fig. 7, bottom panel). The hybridization-controlled PCR produced positive results for all positive samples with no adjustment or calibration necessary, “adapting” the length of its cooling cycle—and thus the annealing temperature—to the change in sample background. Some small delays from the water controls were seen in both N1 and N2, none of which were statistically significant, and inconsequential in comparison to the 20 or more cycle delay in the N2 samples performed in a standard fixed cycle PCR instrument. This delay can likely be attributed to the CDC's prescribed annealing temperature of 55 °C already being below the optimal annealing temperature for the N2 reaction in an extracted sample, which IDT's web tools indicates should be around 57.6 °C (T_m – 5 °C). The CDC's choice of annealing temperature was likely chosen by the multiplexed nature of the original assay, and that it worked well with the sample preparation procedures in their EUA. It did not work well when performed in unextracted nasopharyngeal samples. However, since these salts affect l-DNA and d-DNA hybridization equally, controlling the heating and cooling cycles using the l-DNA fluorescence shifts to optimize primer-target annealing.

While this approach overcomes limitations in standard PCR, the adaptive instrument does have its own practical challenges. One primary limitation of the adaptive instrument is that it can only be tuned for one set of primers in a multiplexed reaction. In this case, for example, the adaptive instrument based thermal cycling on N2 l-DNA and was not tuned to N1. The N2 reaction was chosen as it was found to be the more sensitive to annealing temperature in prior work.¹⁸ Choosing the most sensitive reaction allows that sequence to control the critical annealing phase, and is recommended as a simple way of deciding which sequence the l-DNA analogs should mirror. It is important to note that the l-DNA controlled approach does not correct for all background interferents. Direct polymerase inhibition by background molecules such as hemoglobin will not be accounted for by a hybridization control mechanism.²⁴ Similarly, substances that affect fluorescent dye reporting²⁵ and stereospecific molecules such as proteins that bind to d-DNA²⁶ will not affect the biologically inert, end-labeled l-DNA and thus will not be compensated for. This approach primarily compensates for kinetic interference by common background components like salts and alcohols, as well as instrumentation inconsistencies. Finally, use of the l-DNA control method requires using two of the limited number of fluorescent channels available on the instrument for cycling control, making them unavailable for PCR. While we have previously reported using a single channel² to monitor annealing and melting, the two-channel approach reported here was used for greater precision and cycling reliability for these experiments. Improvements to the instrument and control algorithm design (to be discussed in a manuscript in preparation) should reclaim these channels and allow greater multiplexing in these reactions.

Conclusion

An examination of the PCR process within the context of Van't Hoff theory revealed that the ideal annealing temperature of primers to targets is relatively constant at the extremes, but has a sharp, temporary decrease in the exponential phase, after a Cq has been determined. Therefore, with the exception of this transient decrease, l-DNA analogs for the control of PCR accurately mirror the hybridization of d-DNA PCR primers and targets when the l-DNA concentration matches d-DNA primer concentration and the ratio of the l-DNA strands is set as high as practically possible.

Conflicts of interest

There are no conflicts to declare.