Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2024 May 10;45(7):e26699. doi: 10.1002/hbm.26699

A cautionary tale on the effects of different covariance structures in linear mixed effects modeling of fMRI data

Harm Jan van der Horn 1, Erik B Erhardt 2, Andrew B Dodd 1, Upasana Nathaniel 1, Tracey V Wick 1, Jessica R McQuaid 1, Sephira G Ryman 1, Andrei A Vakhtin 1, Timothy B Meier 3,4,5, Andrew R Mayer 1,6,7,8,✉
PMCID: PMC11082918  PMID: 38726907

Abstract

With the steadily increasing abundance of longitudinal neuroimaging studies with large sample sizes and multiple repeated measures, questions arise regarding the appropriate modeling of variance and covariance. The current study examined the influence of standard classes of variance–covariance structures in linear mixed effects (LME) modeling of fMRI data from patients with pediatric mild traumatic brain injury (pmTBI; N = 181) and healthy controls (N = 162). During two visits, participants performed a cognitive control fMRI paradigm that compared congruent and incongruent stimuli. The hemodynamic response function was parsed into peak and late peak phases. Data were analyzed with a 4‐way (GROUP×VISIT×CONGRUENCY×PHASE) LME using AFNI's 3dLME and compound symmetry (CS), autoregressive process of order 1 (AR1), and unstructured (UN) variance–covariance matrices. Voxel‐wise results dramatically varied both within the cognitive control network (UN>CS for CONGRUENCY effect) and broader brain regions (CS>UN for GROUP:VISIT) depending on the variance–covariance matrix that was selected. Additional testing indicated that both model fit and estimated standard error were superior for the UN matrix, likely as a result of the modeling of individual terms. In summary, current findings suggest that the interpretation of results from complex designs is highly dependent on the selection of the variance–covariance structure using LME modeling.

Keywords: cognitive neuroscience, covariance, fMRI, linear mixed models

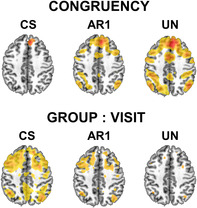
Differences in whole‐brain activation (at p < .001) between linear mixed effects models using compound symmetry (CS), autoregressive order 1 (AR1), and unstructured (UN) covariance matrices.

graphic file with name HBM-45-e26699-g003.jpg

1. INTRODUCTION

As the field of neuroimaging progresses, there is increasing recognition of the need for prospective studies with large sample sizes (N) to address questions about longitudinal changes in brain functioning, which may vary across groups, time, and experimental contexts (Madhyastha et al., 2018; Mayer et al., 2022; Thompson et al., 2020). Several reviews have discussed the benefits and issues associated with the analyses of large N neuroimaging datasets (Smith et al., 2015; Smith & Nichols, 2018; Thompson et al., 2014), and much consideration has been given to the impact of covariance (autocorrelation) in single‐subject functional magnetic resonance imaging (fMRI) timeseries data (Monti, 2011). In contrast, the statistical quandaries associated with modeling both variance and covariance in complex imaging designs with multiple repeated measures (hereafter referred to as Level II analyses) remain a relatively understudied topic (Chen et al., 2013; Madhyastha et al., 2018).

Specifically, it is known that most neuropsychiatric disease states will exhibit increased variance relative to typical control groups (Yang et al., 2014), and it is increasingly recognized that there are differences in variance and covariance based on biological sex and other host factors (Dennis et al., 2021; Ewing‐Cobbs et al., 2016). For cross‐sectional analyses or analyses with only fixed effects, this does not impose any problems when selecting an appropriate variance–covariance matrix (also commonly referred to as covariance matrix as well as correlation matrix in various statistical notations) (Chen et al., 2013). However, for studies that incorporate multiple repeated measures, specifying the most appropriate variance–covariance structure of the data becomes pivotal. The variance–covariance structure of imaging data may vary due to time‐dependent changes in the variable of interest as a result of disease‐specific neurodegeneration, recovery from injury or secondary to typical aging (Madhyastha et al., 2018; Weiner et al., 2010). Similarly, different variance–covariance structures may be superimposed on repeat assessment or practice effects due to secondary disease processes, such as the inability to learn as a result of dementia (Jahn, 2013).

These factors require a more nuanced consideration of the variance–covariance matrix utilized to model neuroimaging data (Smith & Nichols, 2018; Thompson et al., 2014). There are currently few imaging programs that allow users to select different variance–covariance matrices for Level II analyses across common neuroimaging software platforms (FSL, AFNI and SPM), that permit choices to account for missing data (missing at random versus missing completely at random), that model random in addition to fixed effects, and that specify cross‐nested effects (Chen et al., 2013; Madhyastha et al., 2018). The current study therefore examined the effects of variance–covariance matrix selection on fMRI data using both AFNI's 3dLME program and the “Linear and Nonlinear Mixed Effects Models (nlme) package” in R (Chen et al., 2013; Pinheiro & Bates, 2023; R Core Team, 2023). These experiments were conducted using data from a recently published, large N (343 participants) task‐based fMRI study on pediatric mild traumatic brain injury (pmTBI) (van der Horn et al., 2023).

2. METHODS

The current study used an identical sample, identical preprocessing methods, and identical Level I deconvolution analyses as a previous publication (van der Horn et al., 2023). Briefly, 181 patients with pmTBI (ages 8–18 years; N = 136 returning for follow‐up) and 162 healthy controls (HC; N = 147 returning) were studied at two time points (subacute (SA): ~1 week, and early chronic (EC): ~4 months post‐injury; VISIT = 1st repeated measures factor) with similar intervals for HC. The distribution of sex (χ 2 = 0.2, p = .66) and age (t = −1.06, p = .29) was similar for the two groups. During a multimodal fMRI‐paradigm, participants attended to either auditory or visual stimuli (modeled separately) while ignoring congruent or incongruent stimuli in the opposite modality (CONGRUENCY = 2nd repeated measures factor). Only data from the auditory condition were examined in the current investigation. The hemodynamic response function (HRF) for attending to auditory probes was further decomposed into peak and late peak phases (PHASE = 3rd repeated factor). Level II analyses were conducted with a full hierarchical 4‐way [GROUP (pmTBI vs. HC) × VISIT (SA vs. EC) × CONGRUENCY (Congruent vs. Incongruent) × PHASE (Peak vs. Late Peak)] linear mixed effects model, with inclusion of mean framewise displacement (FD) as a (fixed) nuisance covariate, and estimation of subject‐specific intercept random effects. Models were fit using AFNI's 3dLME package, which uses the nlme package in R with type III sums of squares (i.e., marginal effects) tests to obtain F‐statistics for the individual model terms. Mathematic details on modeling in 3dLME can be found in the original publication by Chen and colleagues (Chen et al., 2013).

The following repeated measures data order was used for all analyses as in our previous publication (van der Horn et al., 2023): Visit, Phase, then Congruency (hereafter referred to as Order 1).1 Analyses were run on a GPU server and the number of jobs in 3dLME was set at 20. Results were family‐wise error corrected at a two‐sided statistical threshold of α = 0.001, and a cluster volume ≥711 μL, which was computed using Monte Carlo simulation (10,000 iterations) and spherical autocorrelation estimates (Cox et al., 2017).

The nlme package fits linear and nonlinear mixed effects models when dealing with hierarchical or nested data structures, where experimental factors or overlapping conditions group data points. The computational methods of the nlme package follow the general framework of Lindstrom and Bates (Lindstrom & Bates, 1988). The model formulation is described in (Laird & Ware, 1982). The variance–covariance parametrizations are described in (Pinheiro & Bates, 1996). The different correlation structures available for the correlation argument are described in other publications (Box et al., 1994; Littell et al., 1996; Venables & Ripley, 2002). The use of variance functions for linear and nonlinear mixed effects models has also been previously presented in detail (Marie Davidian, 1995). Standard classes of variance–covariance matrices can be specified in the nlme package (Figure 1), such as compound symmetry (CS) corresponding to a constant correlation, autoregressive process of order 1 (AR1), and unstructured (UN) correlation. The estimated structure for each variance–covariance matrix can be found in Figure 2a. Note that nlme computes a correlation and not a variance–covariance matrix. However, for readability, the term variance–covariance matrix is used throughout the manuscript.

FIGURE 1.

FIGURE 1

Open in a new tab

Matrix structure for compound symmetry (CS), first order autoregressive (AR1) and unstructured (UN) as used in the current study. Note that correlation instead of variance–covariance matrices are depicted, that is, ones instead of variances on the diagonal and correlations instead of covariances on the off‐diagonal. The number of parameters correspond to the number of estimated covariances (i.e., off diagonal correlations).

FIGURE 2.

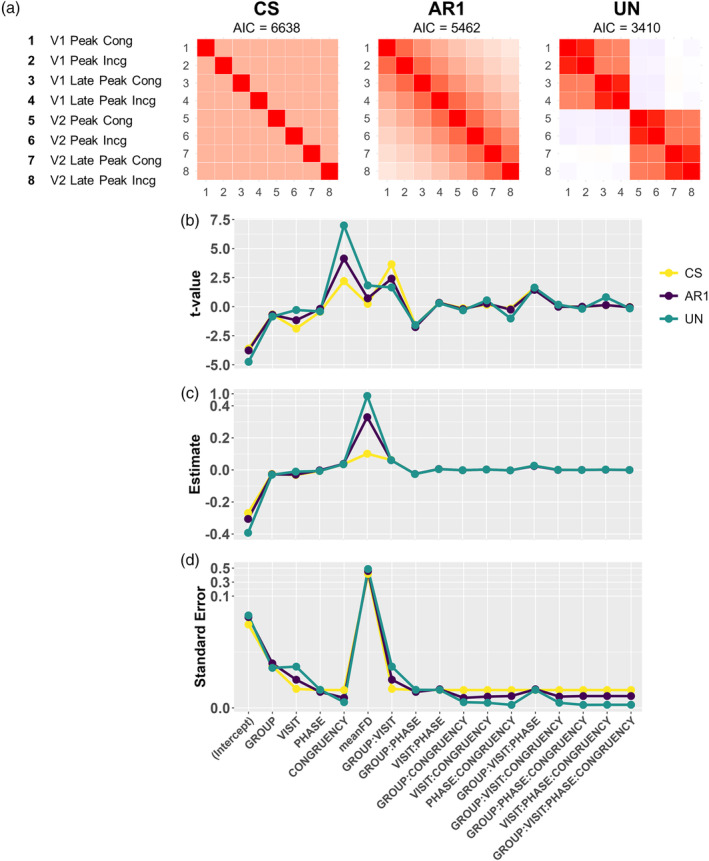
FIGURE 2

Open in a new tab

Summary statistics and model parameters for the three variance–covariance structures for a single voxel located in the right precuneus. Panel a shows the variance–covariance structures and Akaike Information Criterion (AIC). The t‐statistics, estimates (unstandardized beta coefficients) and standard errors are plotted in Figure 2b–d, exhibiting the inverse relationship between the t‐values and standard errors. Note the piecewise linear y‐axis scales in Panels c and d.

The precompiled AFNI 3dLME program only implemented the CS (default) and AR1 variance–covariance structures. The current study therefore modified the 3dLME source code to specify UN. The modified code can be found on GitHub (https://github.com/jling‐NM/Different‐Covariance‐Structures‐in‐Linear‐Mixed‐Effects‐Modeling‐of‐fMRI‐Data), and Supporting Information contains detailed instructions for running the code. In addition, the developers of AFNI have indicated that a new version of 3dLME (named 3dLME2) will be forthcoming that will also support the implementation of an unstructured covariance matrix. For AR1 and UN, variance–covariance structures can be manually specified as follows:

AR1:

Correlation=corAR10.3form=~1Subject

Note that the correlation needs to be manually specified for AR1, and the default in 3dLME is 0.3.

UN:

Correlation=corSymmform=~1Subject

In case of a UN variance–covariance matrix, the total formula in the nlme package would be:

lme(y~GROUP*VISIT*CONGRUENCY*PHASE+meanFD, random=~1Subject,correlation=corSymmform=~1Subject)

AR1 was included in the current manuscript for investigatory purposes only. Specifically, AR1 is not an appropriate variance–covariance matrix for the current dataset, given that there are multiple repeated measures rather than a single repeated measure with more than 2 levels and a decreasing correlation structure.

In addition to whole‐brain voxel‐wise analyses, the effects of variance–covariance matrix selection were examined using a representative voxel within the right precuneus/cingulate cortex (Talairach coordinates x = 7, y = −44, z = 34). A full 4‐way interaction model was fit for each variance–covariance structure using a specified order (VISIT, PHASE, then CONGRUENCY). For each main effect and interaction, the t‐value, parameter estimate and standard error were plotted. The Akaike Information Criterion (AIC) is reported for all single voxel results as a metric of overall model fit.

Brain overlays were made using AFNI (Cox, 1996). Binary masks for specific model terms were made using AFNI's 3dcalc; voxel F‐value dumps were performed using AFNI's 3dmaskdump (Cox, 1996). Plots were made using the R ggplot2 package (R Core Team, 2023; Wickham, 2016).

All study procedures were conducted according to the declaration of Helsinki. All participants provided written informed consent (i.e., parents and children aged 18 years) or assent (children less than 18 years) in accordance with the University of New Mexico School of Medicine guidelines.

3. RESULTS

3.1. Whole‐brain voxel‐wise results

Runtimes for the models using CS, AR1 and UN were 3, 17, and 386 h, respectively. Figure 3 shows the output of whole‐brain voxel‐wise analyses that were run in 3dLME using CS, AR1, and UN variance–covariance structures. Large differences in activation were observed for the CONGRUENCY and GROUP:VISIT terms for the CS and UN matrices, with AR1 showing intermediate effects. F‐values for all activated voxels were also visualized using boxplots. For the CS matrix, F‐values were relatively lower for the CONGRUENCY effect and higher for GROUP:VISIT effect, while the opposite pattern was observed for the UN matrix. From a cognitive neuroscience perspective, robust activation of the salience and executive control networks, collectively also denoted as the cognitive control network, was expected for the Incongruent vs. Congruent contrast, which was observed for the UN but not CS variance–covariance matrix. These results demonstrate that inferences about the longitudinal effects of neuropsychiatric conditions on brain activation during processing of multimodal information are highly dependent on the selected variance–covariance matrix.

FIGURE 3.

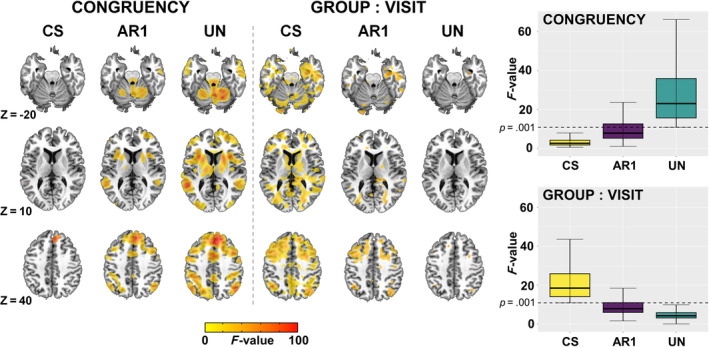
FIGURE 3

Open in a new tab

3dLME output showing differences in whole brain activation between CS, AR1 and UN for the CONGRUENCY and GROUP:VISIT terms (thresholded at p = .001). Additionally, boxplots for F‐values are shown at the right for both terms. For the CONGRUENCY term, F‐values were plotted based on a mask from the UN model whereas for the GROUP:VISIT interaction it was done based on the CS model.

No main effects were found for Group in any of the covariance structures. For full results with regard to the effects of pmTBI, we refer the reader to our previously published work on the same sample (van der Horn et al., 2023).

3.2. Single voxel results

Figure 2 displays variance–covariance matrices, t‐values, model coefficients and standard error of the mean for the three covariance structures within a single voxel located in the right precuneus. Panel a indicates that the AIC was over 3000 units less for the UN (AIC = 3410) compared to the CS (AIC = 6638) variance–covariance matrix, suggesting that the additional complexity for estimating individual variance/covariance parameters in the UN matrix justified the reduction in degrees‐of‐freedom. The magnitudes of the t‐statistics, coefficient estimates and standard errors are plotted in Figure 2b–d, demonstrating large differences in effects for both repeated measures and interaction terms based on the variance–covariance matrix selected (i.e., comparing main effect of CONGRUENCY versus GROUP:VISIT interaction terms) similar to results obtained in whole‐brain analyses. For the VISIT and GROUP:VISIT terms, the standard errors are higher for UN, while for the CONGRUENCY and the other interaction terms the standard errors are equal or lower for UN compared to the other covariance structures. Standard error terms are inversely related to the t statistics (t = estimated coefficient/estimated standard error of the coefficient), and are therefore likely driving some of the differences across variance/covariance structures given that the standard error represents the denominator in formula for t‐ and F‐values. The differences in results across the various variance–covariance structures are likely to be caused by the fact that both CS and AR1 impose constraints on covariance estimation, while UN does not. Furthermore, mean FD has the highest t‐values and parameter estimates for UN relative to other variance–covariance structures, which indicates more accurate modeling of noise sources such as head motion.

Figure 4 illustrates the importance of interpreting the contrasts rather than the parameter estimates when (insignificant) higher‐order interactions are retained in the model for the purpose of model uniformity over many voxels. A contrast is a linear combination of parameters whose coefficients add up to zero, allowing comparison of different conditions. In the current model all terms are binary, with the exception of mean FD (which is continuous). Baseline levels of these binary predictors are included in the model intercept. Thus, the main effect of GROUP is the difference between the patient group versus the baseline control group (contrast = pmTBI − HC). While significance (t‐statistics and p‐value) are equal for the estimate and contrast, the contrast “averages out” the portions of the effect potentially explained by higher‐order interaction estimates (i.e., the marginal means with type III sum of squares). The contrasts are often larger in magnitude and more variable than the estimates. Similarly, two‐way interactions estimate the “difference of differences.” For example, for the GROUP:VISIT interaction term, the contrast is the difference between patient group vs. control group at Visit 2 compared to that same difference at Visit 1, contrast = [pmTBI(V2) − HC(V2)] − [pmTBI(V1) − HC(V1)].

FIGURE 4.

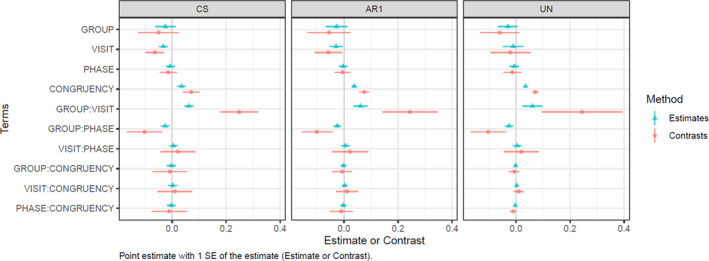
FIGURE 4

Open in a new tab

A plot of parameter estimates vs. contrasts in compound symmetry (CS), autoregressive order 1 (AR1) and unstructured (UN) variance–covariance matrices. The parameter estimates are the unstandardized beta coefficients (centers) ± 1 standard error (bar). The contrasts represent the difference in the marginal means between various factors and interactions (centers), ± one standard error (bar).

From the contrast plots in Figure 4, it can be observed that the standard error for the CONGRUENCY term is higher for CS than for UN, while the opposite is true for the GROUP:VISIT term. Furthermore, the standard errors are also much lower for the 2‐way interactions that include the CONGRUENCY term in the UN versus CS matrices.

Figures S1 and S2 (in Supporting Information) present differences both between and within the various variance–covariance matrices depending on the selected ordering of repeated measures terms. While this effect appears to be unique to the nlme R package relative to other tested statistical packages (i.e., SPSS version 20 and MATLAB version R2019b) due to the ability for the user to specify factor ordering, it can have a significant impact on findings. While this was expected for the AR1 variance–covariance matrix, the large differences observed in Figures S1 and S2 for UN were unexpected. In particular, for Order 1, the negative off‐diagonal blocks match the Pearson correlation, but Orders 2 and 3 do not have negative estimates where Pearson does. Thus, the ordering of repeated measures in the nlme package are another large point of consideration, and measures should be ordered by the variable with the highest number of repeat factors (i.e., there are four repeated factors nested within visit, see Figure 2a) to match results from other statistical packages.

4. DISCUSSION

Based on our findings, we propose that UN variance–covariance matrices should be considered when analyzing large‐N task‐fMRI datasets and complex models with multiple within‐subjects repeated measures. Applying a CS variance–covariance structure resulted in a poor fit of the marginal covariance terms. The standard error estimates from the UN matrix were also smaller for multiple interaction terms and for the main effect of Congruency. In combination these factors would dramatically alter the subsequent inferences on the (longitudinal) effects of pmTBI on brain activation when selecting a CS (i.e., large influences of pmTBI on neurovascular recovery from injury) relative to a UN matrix (i.e., minimal influences of pmTBI on neurovascular recovery from injury). The selection of the UN matrix also resulted in increased activity in the cognitive control network during the processing of incongruent stimuli, a finding that is supported by an extensive body of cognitive neuroscience research on cognitive control (Cole & Schneider, 2007; Menon & D'Esposito, 2022). This finding therefore provides additional face and convergent validity for the selection of the UN matrix in the current study.

To our knowledge, 3dLME is the only voxel‐wise analysis software that allows for the specification of multiple classes of variance–covariance structures (Chen et al., 2013). Importantly, manual adjustment of the source code was required to apply a UN variance–covariance matrix (see Supporting Information). A new 3dLME2 program is also being developed by the AFNI team to provide additional variance–covariance structures to the imaging community (personal communication; Dr. Gang Chen). There remains a contentious discussion in the literature about the use of fully specified models (such as our model using UN, although without random slopes) versus more parsimonious models (Barr et al., 2013; Matuschek et al., 2017). Applying an UN variance–covariance structure results in the unconstrained estimation of each element in the variance–covariance matrix separately, and thus is likely to result in the best fit (i.e., lowest AIC). Briefly, the use of fully specified models is thought to be more appropriate for large datasets, and protects against Type I errors, while parsimonious models (such as CS) may be more suitable for smaller datasets (and thus lower degrees of freedom) as it preserves power, and prevents over‐fitting. Another disadvantage is that more complex models with UN variance–covariance matrix may not always fully converge. As with any modeling choice, users must make educated decisions about the potential benefits (i.e., in this case more accurate results) and costs (e.g., computational time, convergence) of each approach. In the current linear mixed effects software for neuroimaging data, the statistical model and variance–covariance structure are manually specified and then fit at each individual voxel. However, it is reasonable to assume that one variance–covariance structure might not be suitable for every voxel or region in the brain. Software is available that allows for model selection by showing whole‐brain AIC differences between models (Madhyastha et al., 2018). Similarly, we consider it an important future goal to develop software that determines the optimal variance–covariance structure at each voxel, for example based on the AIC. Theoretically, one would expect UN to result in the best model fit in most cases. However, a minimal improvement of model fit may come at the expense of power (due to loss of degrees‐of‐freedom). Also, a full factorial model might not be desirable for every voxel, when one is only interested in lower order interactions (e.g., two way) and/or main effects. While it is considered best practice to reduce the model complexity and only interpret the highest‐order effects, computational considerations may make the interpretation of lower‐order effects attractive when higher‐order effects remain in the model, as was done in the current study.

The largest limitation for the current study is the amount of time required to execute the UN matrix. Specifically, the UN model required 23 (vs. AR1) to 129 (vs. CS) times more time to complete a single analysis relative to the simpler models. Importantly, the current manuscript has already demonstrated the benefits of using the UN variance–covariance matrix based on both traditional statistical metrics (i.e., information criterion) as well as cognitive neuroscience inferences (i.e., activation of the cognitive control network), and computational time can be further improved through the utilization of parallel computing strategies and additional computing power. Future software packages may offer a more flexible modeling strategy that permits modeling on the individual voxel level. For example, AFNI recently released the 3dLMEr package which entails additional constraints on the variance–covariance structure but has significant advantages in computation time.

In summary, current results suggest that care should be exercised when selecting the variance–covariance matrix in the modeling of complex task‐fMRI data as it may have a significant impact on the results and the conclusions made based on the data. Until more sophisticated software becomes available, researchers may consider running model tests on data obtained from multiple voxels to determine the appropriate variance–covariance structure before fitting a single model to whole‐brain data.

FUNDING INFORMATION

This research was supported by grants from the National Institutes of Health [https://www.nih.gov; grant numbers NIH 01 R01 NS098494‐01A1, R01 NS098494‐03S1A1, and P30 GM122734] to Andrew R. Mayer. The NIH had no role in study review, data collection and analysis, decision to publish, or preparation of the manuscript.

CONFLICT OF INTEREST STATEMENT

The authors report no competing interests.

Supporting information

Data S1. Supporting Information.

HBM-45-e26699-s001.docx (2.1MB, docx)

ACKNOWLEDGMENTS

The authors would like to thank Gang Chen for his valuable contributions via email correspondence and during digital meetings.

van der Horn H. J., Erhardt, E. B. , Dodd, A. B. , Nathaniel, U. , Wick, T. V. , McQuaid, J. R. , Ryman, S. G. , Vakhtin, A. A. , Meier, T. B. , & Mayer, A. R. (2024). A cautionary tale on the effects of different covariance structures in linear mixed effects modeling of fMRI data. Human Brain Mapping, 45(7), e26699. 10.1002/hbm.26699

Footnotes

1

The order of variables can have a large influence on the results in the R nlme package due to manual specification of the input data. In contrast, ordering is performed automatically in other statistical programs such as SPSS or MATLAB and therefore does not result in ordering effects.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available in FITBIR at https://fitbir.nih.gov/, reference number FITBIR‐STUDY0000339.

REFERENCES

  1. Barr, D. J. , Levy, R. , Scheepers, C. , & Tily, H. J. (2013). Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of Memory and Language, 68(3), 255–278. 10.1016/j.jml.2012.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Box, G. E. P. J. , Gwilym, M. , & Reinsel, G. C. (1994). Time series analysis: Forecasting & control (3rd ed.). Prentice Hall. [Google Scholar]
  3. Chen, G. , Saad, Z. S. , Britton, J. C. , Pine, D. S. , & Cox, R. W. (2013). Linear mixed‐effects modeling approach to FMRI group analysis. Neuroimage, 73, 176–190. 10.1016/j.neuroimage.2013.01.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cole, M. W. , & Schneider, W. (2007). The cognitive control network: Integrated cortical regions with dissociable functions. Neuroimage, 37(1), 343–360. 10.1016/j.neuroimage.2007.03.071 [DOI] [PubMed] [Google Scholar]
  5. Cox, R. , Chen, G. , Glen, D. R. , Reynolds, R. C. , & Taylor, P. A. (2017). FMRI clustering in AFNI: False positive rates redux. Brain Connectivity, 7(3), 152–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cox, R. W. (1996). AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical Research, 29, 162–173. [DOI] [PubMed] [Google Scholar]
  7. Dennis, E. L. , Caeyenberghs, K. , Hoskinson, K. R. , Merkley, T. L. , Suskauer, S. J. , Asarnow, R. F. , Babikian, T. , Bartnik‐Olson, B. , Bickart, K. , Bigler, E. D. , Ewing‐Cobbs, L. , Figaji, A. , Giza, C. C. , Goodrich‐Hunsaker, N. J. , Hodges, C. B. , Hovenden Aa, E. S. , Irimia, A. , Konigs, M. , Levin, H. S. , … Wilde, E. A. (2021). White matter disruption in pediatric traumatic brain injury: Results from ENIGMA pediatric moderate to severe traumatic brain injury. Neurology, 97(3), e298–e309. 10.1212/WNL.0000000000012222 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ewing‐Cobbs, L. , Johnson, C. P. , Juranek, J. , DeMaster, D. , Prasad, M. , Duque, G. , Kramer, L. , Cox, C. S. , & Swank, P. R. (2016). Longitudinal diffusion tensor imaging after pediatric traumatic brain injury: Impact of age at injury and time since injury on pathway integrity. Human Brain Mapping, 37(11), 3929–3945. 10.1002/hbm.23286 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Jahn, H. (2013). Memory loss in Alzheimer's disease. Dialogues in Clinical Neuroscience, 15(4), 445–454. 10.31887/DCNS.2013.15.4/hjahn [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Laird, N. M. , & Ware, J. H. (1982). Random‐effects models for longitudinal data. Biometrics, 38(4), 963–974. 10.2307/2529876 [DOI] [PubMed] [Google Scholar]
  11. Lindstrom, M. J. , & Bates, D. M. (1988). Newton‐Raphson and EM algorithms for linear mixed‐effects models for repeated‐measures data. Journal of the American Statistical Association, 83(404), 1014–1022. 10.2307/2290128 [DOI] [Google Scholar]
  12. Littell, R. C. , Milliken, G. A. , Stroup, W. W. , & Wolfinger, R. D. (1996). SAS systems for mixed models. SAS Institute.
  13. Madhyastha, T. , Peverill, M. , Koh, N. , McCabe, C. , Flournoy, J. , Mills, K. , King, K. , Pfeifer, J. , & McLaughlin, K. A. (2018). Current methods and limitations for longitudinal fMRI analysis across development. Developmental Cognitive Neuroscience, 33, 118–128. 10.1016/j.dcn.2017.11.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Marie Davidian, D. M. G. (1995). Nonlinear mixed effects models for repeated measurement data (1st ed.). Chapman and Hall. [Google Scholar]
  15. Matuschek, H. , Kliegl, R. , Vasishth, S. , Baayen, H. , & Bates, D. (2017). Balancing type I error and power in linear mixed models. Journal of Memory and Language, 94, 305–315. 10.1016/j.jml.2017.01.001 [DOI] [Google Scholar]
  16. Mayer, A. R. , Ling, J. M. , Dodd, A. B. , Stephenson, D. D. , Pabbathi Reddy, S. , Robertson‐Benta, C. R. , Erhardt, E. B. , Harms, R. L. , Meier, T. B. , Vakhtin, A. A. , Campbell, R. A. , Sapien, R. E. , & Phillips, J. P. (2022). Multicompartmental models and diffusion abnormalities in paediatric mild traumatic brain injury. Brain, 145(11), 4124–4137. 10.1093/brain/awac221 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Menon, V. , & D'Esposito, M. (2022). The role of PFC networks in cognitive control and executive function. Neuropsychopharmacology, 47(1), 90–103. 10.1038/s41386-021-01152-w [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Monti, M. M. (2011). Statistical analysis of fMRI time‐series: A critical review of the GLM approach. Frontiers in Human Neuroscience, 5, 28. 10.3389/fnhum.2011.00028 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Pinheiro, J. C. , & Bates, D. M. (1996). Unconstrained parametrizations for variance‐covariance matrices. Statistics and Computing, 6(3), 289–296. 10.1007/BF00140873 [DOI] [Google Scholar]
  20. Pinheiro, J. C. , & Bates, D. M. (2023). nlme: Linear and Nonlinear Mixed Effects Models. R package version 3.1‐163. https://CRAN.R-project.org/package=nlme
  21. R Core Team . (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
  22. Smith, S. M. , & Nichols, T. E. (2018). Statistical challenges in “Big Data” human neuroimaging. Neuron, 97(2), 263–268. 10.1016/j.neuron.2017.12.018 [DOI] [PubMed] [Google Scholar]
  23. Smith, S. M. , Nichols, T. E. , Vidaurre, D. , Winkler, A. M. , Behrens, T. E. , Glasser, M. F. , Ugurbil, K. , Barch, D. M. , van Essen, D. C. , & Miller, K. L. (2015). A positive‐negative mode of population covariation links brain connectivity, demographics and behavior. Nature Neuroscience, 18(11), 1565–1567. 10.1038/nn.4125 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Thompson, P. M. , Jahanshad, N. , Ching, C. R. K. , Salminen, L. E. , Thomopoulos, S. I. , Bright, J. , Baune, B. T. , Bertolin, S. , Bralten, J. , Bruin, W. B. , Bulow, R. , Chen, J. , Chye, Y. , Dannlowski, U. , de Kovel, C. G. F. , Donohoe, G. , Eyler, L. T. , Faraone, S. V. , Favre, P. , … ENIGMA Consortium . (2020). ENIGMA and global neuroscience: A decade of large‐scale studies of the brain in health and disease across more than 40 countries. Translational Psychiatry, 10(1), 100. 10.1038/s41398-020-0705-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Thompson, P. M. , Stein, J. L. , Medland, S. E. , Hibar, D. P. , Vasquez, A. A. , Renteria, M. E. , Toro, R. , Jahanshad, N. , Schumann, G. , Franke, B. , Wright, M. J. , Martin, N. G. , Agartz, I. , Alda, M. , Alhusaini, S. , Almasy, L. , Almeida, J. , Alpert, K. , Andreasen, N. C. , … Saguenay Youth Study (SYS) Group . (2014). The ENIGMA consortium: Large‐scale collaborative analyses of neuroimaging and genetic data. Brain Imaging and Behavior, 8(2), 153–182. 10.1007/s11682-013-9269-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. van der Horn, H. J. , Dodd, A. B. , Wick, T. V. , Robertson‐Benta, C. R. , McQuaid, J. R. , Hittson, A. K. , Ling, J. M. , Zotev, V. , Ryman, S. G. , Erhardt, E. B. , Phillips, J. P. , Campbell, R. A. , Sapien, R. E. , & Mayer, A. R. (2023). Neural correlates of cognitive control deficits in pediatric mild traumatic brain injury. Human Brain Mapping, 44, 6173–6184. 10.1002/hbm.26504 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Venables, B. , & Ripley, B. D. (2002). Modern applied statistics with S (4th ed.). Springer‐Verlag. 10.1007/978-0-387-21706-2 [DOI] [Google Scholar]
  28. Weiner, M. W. , Aisen, P. S. , Jack, C. R., Jr. , Jagust, W. J. , Trojanowski, J. Q. , Shaw, L. , Saykin, A. J. , Morris, J. C. , Cairns, N. , Beckett, L. A. , Toga, A. , Green, R. , Walter, S. , Soares, H. , Snyder, P. , Siemers, E. , Potter, W. , Cole, P. E. , Schmidt, M. , & Alzheimer's Disease Neuroimaging Initiative . (2010). The Alzheimer's disease neuroimaging initiative: Progress report and future plans. Alzheimers Dement, 6(3), 202–211.e207. 10.1016/j.jalz.2010.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. Springer‐Verlag. https://ggplot2.tidyverse.org [Google Scholar]
  30. Yang, G. J. , Murray, J. D. , Repovs, G. , Cole, M. W. , Savic, A. , Glasser, M. F. , Pittenger, C. , Krystal, J. H. , Wang, X. J. , Pearlson, G. D. , Glahn, D. C. , & Anticevic, A. (2014). Altered global brain signal in schizophrenia. Proceedings of the National Academy of Sciences of the United States of America, 111(20), 7438–7443. 10.1073/pnas.1405289111 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Data S1. Supporting Information.

HBM-45-e26699-s001.docx (2.1MB, docx)

Data Availability Statement

The data that support the findings of this study are openly available in FITBIR at https://fitbir.nih.gov/, reference number FITBIR‐STUDY0000339.

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES