Meta-evaluation for 3D Face Reconstruction Via Synthetic Data

Abstract

The standard benchmark metric for 3D face reconstruction is the geometric error between reconstructed meshes and the ground truth. Nearly all recent reconstruction methods are validated on real ground truth scans, in which case one needs to establish point correspondence prior to error computation, which is typically done with the Chamfer (i.e., nearest neighbor) criterion. However, a simple yet fundamental question have not been asked: Is the Chamfer error an appropriate and fair benchmark metric for 3D face reconstruction? More generally, how can we determine which error estimator is a better benchmark metric? We present a meta-evaluation framework that uses synthetic data to evaluate the quality of a geometric error estimator as a benchmark metric for face reconstruction. Further, we use this framework to experimentally compare four geometric error estimators. Results show that the standard approach not only severely underestimates the error, but also does so inconsistently across reconstruction methods, to the point of even altering the ranking of the compared methods. Moreover, although non-rigid ICP leads to a metric with smaller estimation bias, it could still not correctly rank all compared reconstruction methods, and is significantly more time consuming than Chamfer. In sum, we show several issues present in the current benchmarking and propose a procedure using synthetic data to address these issues.

1. Introduction

“Good evaluation requires that evaluation efforts themselves be evaluated.”

—Daniel Stufflebeam, “Meta-evaluation”, 1974

Reconstructing the 3D shape of objects from 2D data is a long-standing and fundamental problem in computer vision [19, 27, 10]. As in any problem, defining proper benchmark metrics to accurately evaluate a reconstruction method is a paramount concern. However, measuring the similarity between a reconstructed 3D mesh and the corresponding ground truth is not trivial, as these two meshes typically differ in topology (e.g., the number and density of the points), and one must establish point correspondence between the 3D objects before the evaluation of their similarity.

The Chamfer (i.e., nearest neighbor) criterion is the standard approach for establishing point correspondence between a reconstructed mesh and its ground truth (Section 2), and it is the de facto benchmarking metric for face reconstruction methods. However, the geometric error computed through the Chamfer criterion must be treated as a mere estimation of the true error, since the true point correspondences are unknown when one uses real data. This raises critical questions, which proved surprisingly elusive: how can one determine which geometric error metric is more appropriate for benchmarking a face reconstruction method? Does the default (i.e., Chamfer) metric allow for a fair comparison, or is it likely to under or overestimate error at different rates for different reconstruction methods? In sum, no study to our knowledge evaluated the evaluation metric itself, yet this becomes increasingly more urgent as the performance gap between reconstruction methods closes. That is, we must be able to measure small differences accurately if we are to assess the state of the art correctly.

In this paper, using synthetic data, we study the ability of geometric estimators to be used as benchmark metrics for face reconstruction. First, we highlight the pressing need for such a meta-evaluation by showing that the performance ranking of reconstruction methods can change significantly depending on how point correspondence is established (Section 4.1), even if one uses the same reference points for rigid pre-alignment. Next, we define a meta-evaluation framework that is based on using synthetic data to compare the true vs. estimated geometric error. We outline evaluation criteria in this context and define meta-metrics to quantify the degree to which these criteria are satisfied. Finally, we conduct experiments and comprehensively evaluate four existing geometric error estimators.

Our results uncover important limitations of current metrics and highlight a number of future directions. First, we show that the Chamfer estimator significantly underestimates the true error, therefore is limited in its ability to measure the metrical (i.e., absolute) error of a reconstruction method, which is a recently addressed problem [50]. Second, Chamfer is limited in its ability to discern small relative error differences between reconstruction methods, as it may squash the performance differences or even alter the true performance ranking of the compared methods. Third, we show that, while the more time-consuming nonrigid ICP (NICP) approach can significantly reduce the estimation bias, it provides little, if any, improvement in terms of estimation variance. Fourth, NICP leads to better but not perfect ranking of compared methods. As such, the estimation of geometric error in a fair and computationally efficient manner emerges as an open problem, and one that is critical for accurately assessing the state of the art.

The contributions of this paper are as follows. First, to our knowledge, we present the first meta-evaluation framework to measure the accuracy of a geometric error estimator and asses its suitability to serve as a metric for face reconstruction. Second, we conduct comprehensive experiments on four geometric estimators in terms of the criteria put forth by our framework, namely estimation bias and variance, and dependence on reconstruction method (Section 4.3). Third, we expose how the compared metrics behave on real data with different characteristics, and which metrics behave more consistently across datasets. The code is made publicly available.¹

2. Related Work

The standard benchmark metric to measure the geometric error in 3D face reconstruction is the Chamfer Distance (CD), which is computed by summing the squared distances between nearest neighbor correspondences of two point clouds. The major problem with this metric is that the point correspondences should be semantically consistent, i.e., nosetips or eyes corners should be matched, which cannot be guaranteed by a nearest neighbor criterion. The standard practice is to compute CD after applying ICP or a keypoint-based rigid alignment [4, 12, 18, 31, 35, 38, 40, 41, 44, 45, 48, 50, 13], which is assumed sufficient to provide meaningful semantic correspondences. However, the suitability of this metric for comparing different reconstruction methods is questionable due to some severe limitations that have been observed in the literature. In [1], a phenomenon defined as “Chamfer blindness” was observed; it states that in case of overly high density of points, CD can lose discriminative ability as one of its two summands becomes significantly smaller than the other given the presence of a few sparsely placed points in the non populated locations. Under a different perspective, Nguyen et al. [28] demonstrated that, given that CD only cares about the nearest neighbour of a point rather than their local distribution, as long as the supports of the compared meshes are close, then the corresponding CD will be small and less informative, while their corresponding distributions might be different. Both works thus point to the conclusion that CD might underestimate the true error. To account for this issue, several attempts have been made to go beyond the nearest-neighbor criterion, as for example with the point-to-plane [49], or normal-ray scheme [23] variants. Despite being more accurate in some circumstances, such as in case of high curvature [23], none of the above really address the problem of semantic correspondence, which is crucial for a meaningful error estimation. Other distances were investigated to measure the geometric similarity of shapes irrespective of mesh parameterization or rotations to eliminate the need for establishing dense point correspondence, such as the varifold metric [21, 32]. However, a kernel needs to be defined to induce the metric on the shapes, which might have varying properties. Also, their robustness to real data has not been yet convincingly explored. A workaround is to extend the rigid alignment step to a non-rigid one to improve point correspondence. The most popular technique in this field is the NICP [2], which is often used to densely align raw scans to a known template in order to build a 3D morphable model (3DMM) [5]. Being itself based on a nearest-neighbor objective though, it was recently shown falling short in providing accurate correspondence even for semantically crucial points (i.e., facial landmarks) [14]. Several alternatives for non-rigid surface registration have been proposed [46, 42, 14], yet they are either based on learning, or rely on specific 3DMMs. This can limit their use as a benchmark metric, as being based on specific learned models limits fair comparability. Also, techniques including several hyper-parameters or measures that are learned via neural networks [42] may behave unpredictably and inconsistently.

In order to overcome the above, Chai et al. [7] recently proposed an alternative benchmark, named REALY. They collected a large set of high quality 3D faces in a constrained setting, which are then all processed to be in consistent topology. To improve the point correspondence estimation between their scans and reconstructed faces, they also provided region annotations to compute per-region alignment and error. This serves also to mitigate the bias in different reconstruction methods, which tend to be more accurate on specific face areas. Whereas REALY represents a significant step toward a fairer benchmark, the evaluation scheme still relies on NICP for alignment, which is extremely time consuming and cannot guarantee accurate correspondence as discussed above. Furthermore, its applicability is limited to the released dataset only. Finally, while Chai et al. [7] argue that the problem with the nearest-neighbor based error is sensitivity to reference points (for rigid alignment), we show that this criterion is problematic even rigid alignment is performed with a fixed set of points.

The literature discussed above evidences the raising awareness about the issues of the current benchmark, yet a systematic study on its limitations and the extent to which it can compromise a correct and fair comparison across reconstruction methods is missing. In this paper, we try to fill this gap by providing robust evidence that estimating the geometric reconstruction accuracy is an open problem, and that the current benchmark is not reliable to this aim. In response, we propose a meta-evaluation framework to evaluate geometric error estimators via synthetic data. The usefulness of synthetic data in the 3D face domain is not an innovative finding, and many previous works successfully employed synthetic 3D faces to, for example, improve the robustness of recognition [24, 25], reconstruction [34], tracking [26] or even generative methods [29]. However, to our knowledge, no study investigated to what extent synthetic data can serve for benchmarking purposes, or used it to systematically evaluate the ability of a benchmark metric to fairly compare reconstruction methods.

3. Background and Notation

The problem addressed in this paper is measurement of the geometric error between a reconstructed 3D face mesh and the corresponding ground truth. Suppose that the reconstructed mesh $R$ contains $N$ points represented as an $N\times 3$ matrix $R={\left(r_1^T,r_2^T,\dots ,r_N^T\right)}^T$, and that the ground truth $G$ contains $M$ points as $G={\left(g_1^T,g_2^T,\dots ,g_M^T\right)}^T$. The meshes $R$ and $G$ are assumed to be rigidly aligned to each other.

Typically, the points in $R$ arise from a specific mesh topology (e.g., the topology of a 3DMM). Therefore, the index $i$ of a point $r_i$ determines the location of the point relative to other points in $R$, and one knows in advance the indices of the points that correspond to each facial feature (e.g., eyes, nose). However, this is not the case for the ground truth mesh $G$, when it is obtained with a 3D scanner. In this case, the indices of the points $g_i$ provide no information about the facial feature or region to which the point belongs and, in general, $M\ne N$. Therefore, one needs to establish the point correspondence between $R$ and $G$ before measuring the error. This requires, for each point $r_i$, to find the index $c_i$ of the corresponding point $g_{c_i}$ on $G$.

3.1. The Chamfer approach

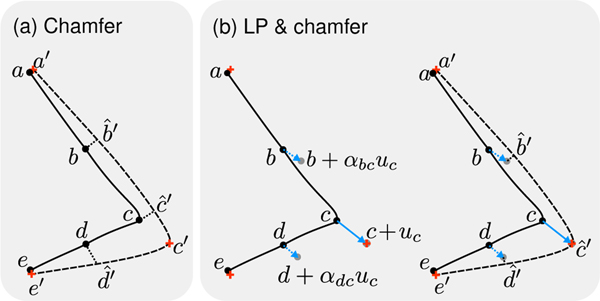
The standard solution to establish point correspondence for a point $r_i$ is using the Chamfer approach; that is:

$$c_i=\text{arg}\underset{j}{\text{min}}{\Vert r_i-g\Vert }_j,$$ (1)

where $\Vert \cdot \Vert$ is the Euclidean distance. However, the Chamfer approach underestimates the geometric error and tends to establish semantically incorrect point correspondences as illustrated in Figure 1a with an example, where the nose tip as well as other points are mismatched. The underestimation problem can also be shown formally. To this end, let us assume that for any point $r_i$ there is a distinct corresponding point $g_i^{\prime }$ on $G$. Then, since Chamfer correspondence is the nearest neighbor of $r_i$ on $G$, we have by definition:

$$\underset{j}{\text{min}}{\Vert r_i-g\Vert }_j=\Vert r_i-g_{c_i}\Vert \le \Vert r_i-g_i^{\prime }\Vert .$$ (2)

As shown in Figure 2, error underestimation by Chamfer may not be benign. In the experiments, we show that this is not an exception, and the Chamfer approach significantly underestimates the real error.

Figure 1.

Establishing point correspondence between the ground truth (dashed curve) and the reconstructed mesh (solid curve) with (a) the Chamfer and (b) the LP & Chamfer approach. We focus on the part of the meshes and ground truth landmarks (red crosses $a^{\prime }$, $c^{\prime }$ and $e^{\prime }$) on the nose. The estimated nose tip with the Chamfer method, ${\widehat{c}}^{\prime }$, is far from the true nose tip $c^{\prime }$. Also, the point $b$ is approximately in the middle of the nose root $a$ and tip $c$, but its counterpart ${\widehat{b}}^{\prime }$ estimated with the Chamfer method is closer to $a^{\prime }$ than $c^{\prime }$ (a similar observation holds for $d$ and ${\widehat{d}}^{\prime }$). LP non-rigidly aligns the meshes by “pulling” the nose tip $c$ towards $c^{\prime }$ with a force of $u_c$ and dragging all the points on the mesh. Thus, LP & Chamfer finds better correspondences ${\widehat{b}}^{\prime }$ and ${\widehat{d}}^{\prime }$ as well as ${\widehat{c}}^{\prime }$.

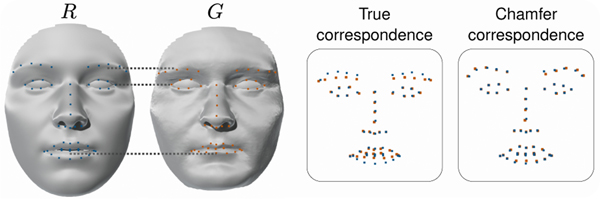
Figure 2.

Underestimation of geometric error by Chamfer-based point correspondence on a real example. The reconstructed mesh $R$ fails to correctly capture facial features like brows. While true correspondence shown for landmarks highlights this inconsistency, Chamfer correspondence misleadingly suggests that the landmarks are captured very well, leading to underestimated error.

3.2. Non-rigid ICP

NICP is an iterative approach that non-rigidly aligns the reconstructed mesh $R$ to the ground truth $G$, until a conver-gence criterion is met. A by-product of this process is the set of estimated point correspondences between $R$ and $G$, which can be used for measuring geometric error between the (unwarped) $R$ and $G$. The computational cost of NICP is significantly higher than that of Chamfer, as the former typically takes minutes on a CPU, whereas the latter takes a few seconds. Despite the added computational complexity, there is no guarantee that NICP will lead to better point correspondences than Chamfer, since the objective function to minimize is based on the latter [14]. To our knowledge, no study directly evaluated whether the NICP-based point correspondences are accurate enough to enable a fair comparison of reconstruction methods. Our evaluation framework (Section 4) and experiments address this open issue.

3.3. Landmark-based pre-alignment

If some landmark points are annotated on the ground truth mesh $G$, one can use them to apply a (nonrigid) landmark-based pre-alignment (LP) to the reconstructed mesh in a way that the corresponding landmarks match (Figure 3). This procedure can improve point correspondence not only for the landmarks themselves, but also for the points close to them (Figure 1b). Such strategies have been used for establishing point correspondence while constructing 3DMMs [5, 15, 8, 43] or when training 3DMM fitting methods [36]. In our study, we investigate the potential benefits of applying such a pre-alignment strategy. The LP approach that we use is outlined in Appendix A.

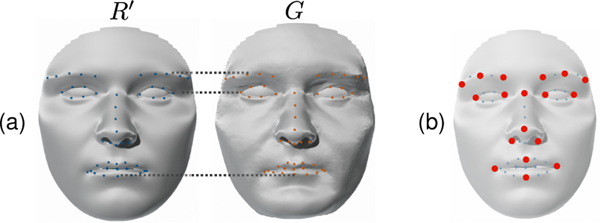
Figure 3.

(a) Feature-level registration of the mesh $R$ in Figure 2 to the $G$ in the same figure. The registered mesh $R^{\prime }$ eliminates the misalignment of the brows and the lower lip observed in Figure 2. (b) The 18 landmarks that we use for feature-level registration.

4. The Meta-evaluation Framework

4.1. Why Do We Need Meta-evaluation?

Table 1 compares four face reconstruction methods in terms of (estimated) geometric error on the widely used BU4DFE data [47]. Error is estimated with two different approaches in a controlled manner, as we implemented all reconstruction methods from scratch and used the same exact reconstructed meshes while computing error—the only difference between the errors reported in the two columns is the manner in which point correspondence is established.

Table 1.

Performance of four methods according to two different error estimators. Estimator 1 is the Chamfer error and Estimator 2 is LP+NICP (Section 5.1). Bold, italic and underlined text indicate first, second and third best method according to an estimator.

	Estimated Error (mm)
	Estimator 1	Estimator 2
INORig [4]	1.72	3.06
Deep3DFace [9]	1.74	3.05
3DI [39]	1.81	2.80
3DDFAv2 [18]	2.04	3.50
Mean error	1.83	3.10
Standard dev.	0.13	0.25

The results in Table 1 show a concerning outcome: The ranking of the methods depends significantly on the estimator that is used to measure error. Moreover, the range of the reported errors shows a significant difference; the mean error of compared methods is 1.83 according to one estimator, and 3.10 according to the other. Finally, the performance differences between the methods is also squashed; standard deviation of the errors estimated by the Estimator 2 is almost the double of that of Estimator 1.

In sum, it is difficult to know which reconstruction method is the best without knowing which error estimator is more reliable. Further, estimating the absolute error is also problematic: at least one estimator under or overestimates error, and we do not know which one it is. The meta-evaluation framework presented in this paper aims to fill this critical gap by presenting tools and procedures that allow us to know which estimator is more likely to predict the correct ranking or produce less estimation bias.

4.2. Comparison on Synthetic Data

The goal of our framework is to evaluate the quality of a geometric error estimator, which is essentially done by comparing the geometric error estimated by a specific method (e.g., Chamfer) with the true error. However, computing the true geometric error requires the knowledge of exact point correspondence, therefore one has to use a synthetic dataset in these comparisons, as the real data collected from 3D scanners do not adhere to a pre-determined mesh topology (Section 3), and manual annotation over a dense set of points is not an option. More precisely, we synthesize data that is consistent with the mesh topology of the reconstruction method(s).

4.3. Evaluation criteria

There can be a number of criteria to evaluate an error estimator, and depending on the context and application, some criteria be more prioritized. In this paper, we focus on three evaluation criteria. The first one is estimation bias, which evaluates if an estimator systematically underestimates or overestimates the true error. An unbiased estimator is critical when determining whether a face reconstruction method is appropriate for an application where one, say, needs to measure the distance between facial features during online eyeglass shopping. The second criterion is estimation variance. A low variance is necessary when estimating error for a specific subject, or the average error of a reconstruction method on a dataset with a relatively small number of participants. The third criterion for estimated error is dependence to reconstruction method, which is particularly critical when one compares several 3D reconstruction methods—performance comparison cannot be fair if error is over or underestimated at different rates for different methods.

4.4. Meta-metrics

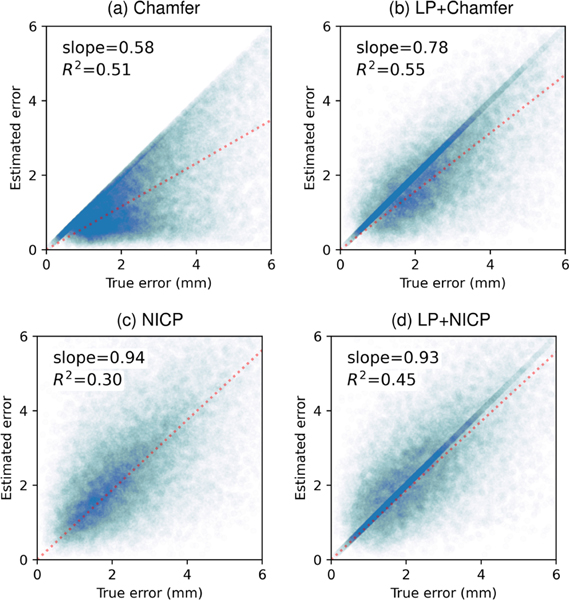
To quantify error estimation bias and variance, we fit a linear model² to the true vs. estimated error values, and report the slope of the linear model and the $R^2$ score, as in Figure 4. The slope of the fitted line, $m$, determines if the estimation is biased; $m=1$ means that the estimation is unbiased, $m<1$ means that error is underestimated, whereas $m>1$ means that it is overestimated. The $R^2$ score is (inversely) related to the variance of the estimator, as it quantifies the proximity of the estimated errors to the fitted line. It takes values in the range of [0,1]—the higher the better.

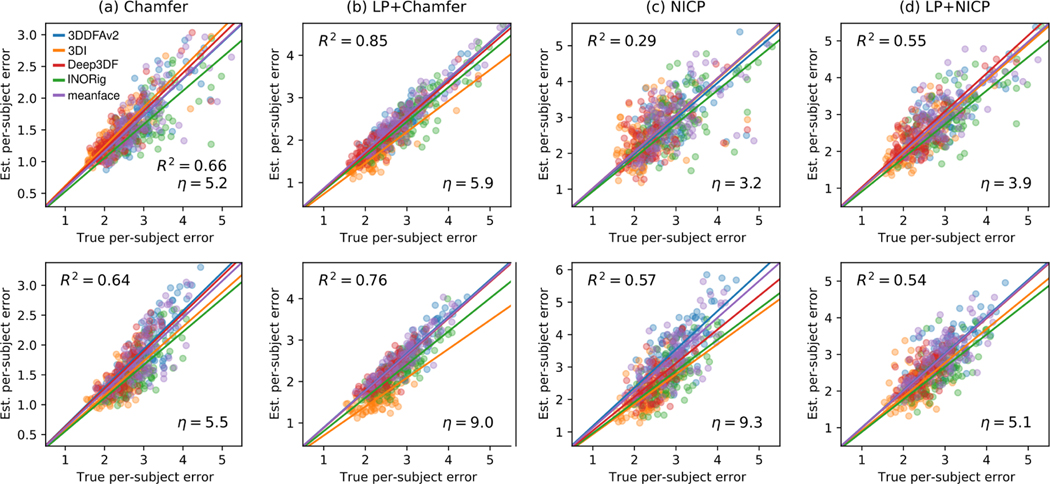
Figure 4.

True vs. estimated point-wise error of 50k randomly selected points from reconstructed meshes on the BFM-synth dataset, shown for the 4 metrics in (a–d). A line (dotted) is fit to each plot and its slope and $R^2$ score (Section 4.4) are reported.

To quantify the degree to which an error estimator is likely to lead to an unfair performance comparison (i.e., dependence to reconstruction method; see Section 4.3), we follow a similar approach based on line fitting, but we fit separate lines for the errors of different reconstruction methods, and compare whether the slopes of the lines are consistent. Suppose that we are comparing $K$ reconstruction methods on a dataset of $N$ subjects, and that the estimated geometric error for the $i$th subject with the $k$th method is ${\widehat{\epsilon }}_i^k$, whereas the true error is ${\epsilon }_i^k$. To compute the rate of under- or over-estimation of the error for the $k$th method, we fit a linear model to the pairs $\left({\epsilon }_1^k,{\widehat{\epsilon }}_1^k\right),\left({\epsilon }_2^k,{\widehat{\epsilon }}_2^k\right),\dots ,\left({\epsilon }_N^k,{\widehat{\epsilon }}_N^k\right)$ and use the slope of this model, $m_k$. Then, the rate of inconsistency (ROI) of the geometric error estimator, $\eta$, is computed as the coefficient of variation as:

$$\eta ={\sigma }_m/\overline{m},$$ (3)

where $\overline{m}$ and ${\sigma }_m$ are, respectively, the average and standard deviation of the values $m_1,m_2,\dots ,m_K$. The lower the $\eta$ the better, as this indicates that any bias in the estimation of the geometric error is consistent across reconstruction methods. On the contrary, a large ROI may lead to an incorrect ranking of the compared methods.

5. Experiments

We experimentally show the use of our meta-evaluation framework by comparing four error estimators in terms of: (i) prediction of point-wise errors on reconstructed meshes (Section 5.2); (ii) prediction of average per-subject errors and consistency across reconstruction methods (Section 5.3); and (iii) predicted ranking of reconstruction methods (Section 5.4).

5.1. Experimental setup

Compared geometric error estimators.

We compared four geometric error estimators: (i) Chamfer error; (ii) LP+Chamfer, which is the error computed from correspondences obtained via the Chamfer criterion after LP (Section 3.3); (iii) NICP, which is the error computed after establishing point correspondence via NICP [2]; (iv) LP+NICP, which is the error computed through point correspondences based on NICP established after LP. Chamfer-based errors are computed unidirectionally.

Datasets.

We conducted experiments on two synthesized datasets, as well as two real datasets (Florence [3] and BU4DFE [47]). The first synthesized dataset, referred to as BFM-synth, includes meshes and texture data of 100 subjects, obtained by randomly generating shape and texture coefficients using the Basel Face Model (BFM) [30]. We rendered 50 images per subject from various poses, and performed 3D reconstruction experiments using 1, 10, or 50 frames per subject. We included a second variant, the BFM-synth-biased dataset, to ensure that reconstructions similar to BFM mean face do not get unfair advantage. This variant is generated in a similar way to BFM-synth, except that the shape coefficients are not zero-mean—they are subject to a bias that we enforced by randomly forcing some of the generated shape coefficients to be positive. The second dataset, FLAME-synth was generated similarly from the FLAME model [22]. With Florence and BU4DFE datasets, we used texture and shape data to similarly render 50 images per subject. All meshes and rendered images are neutral with no added illumination variation or occlusion.

Pre-alignment.

Prior to estimating 3D reconstruction error, we rigidly aligned the ground truth to the reconstructed mesh by using 5 keypoints (mouth corners, outer eye corners, nose tip). The 18 landmarks (Figure 3b) needed for the LP were computed automatically with the same strategy used by Booth et al. [5], which is based on rendering multiple 2D images per mesh, then detecting 2D landmarks [6], and finally re-mapping the landmarks to 3D.

Compared reconstruction methods.

We implemented a total of six reconstruction methods: 3DDFAv2 [18], 3DI [39], DECA [11], Deep3DFace [9], INORig [4] and RingNet [37]. Four methods (3DDFAv2, 3DI, Deep3DFace, INORig) are based on the BFM mesh topology, and we use them to directly compare the known error on the synthesized BFM data with estimated errors. Similarly, the methods based on FLAME mesh topology are used to compare true vs. estimated error on the FLAME-synth dataset. Main experiments are based on BFM-based methods, and FLAME-based methods are provided in Appendix B. For BFM-based methods, we reported results for the 23,470 mesh points that are common to the meshes produced by all BFM-based methods. For natively multi-frame methods (3DI and INORig), we performed reconstruction using $F=10$ and $F=50$ frames per subject. Single-frame methods that produce frontal and neutral meshes were extended to multi-frame by naive-averaging [17] of $F=10,50$ frames per subject. Unless stated otherwise, results are reported for $F=50$ frames.

5.2. Point-wise error prediction

We investigated how well the true geometric error of an arbitrary point on a reconstructed mesh can be predicted by the estimated error. Figure 4 compares the four benchmark metrics by plotting true vs. estimated error for points of reconstructed meshes obtained by the four BFM-based methods on the BFM-synth dataset.

Figure 4a confirms that Chamfer is only a lower bound of the true error (Section 3.1), and the slope of $m=0.58$ (Section 4.4) suggests that the error is significantly underestimated for a large number of points. In comparison, LP+Chamfer has significantly less bias, as the slope of $m=0.78$ is closer to 1, indicating that LP is a promising strategy. Appendix B shows that LP+Chamfer provides a similar improvement over Chamfer on the FLAME topology and data. The NICP-based approaches in Figure 4c,d have even less bias than LP+Chamfer, with slopes significantly closer to 1. However, NICP without LP has the lowest $R^2$ score $(R=0.30)$, indicating that a very large estimation variance is expected. The usage of LP along with NICP leads to a better estimation variance $(R=0.45)$.

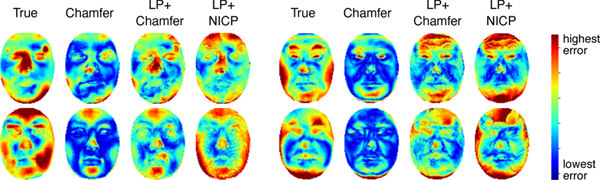
In sum, although the usage of NICP reduces bias significantly, none of the compared error estimators produces a notably high $R^2$ score, indicating that the error of an arbitrary point on a reconstructed mesh is likely to be estimated unreliably. Nevertheless, NICP-based approaches or LP+Chamfer have significantly less bias than Chamfer, since the latter largely underestimates true error, as seen also in the heatmap representation in Figure 5.

Figure 5.

Point-wise error for four BFM-synth meshes visualized via heatmaps. Colors indicate amount of error for each mesh consistently across error metrics.

5.3. Per-subject error prediction

We also compared geometric error estimators in their ability to predict the average per-vertex error of a mesh, which is the building block of statistics that are used to compare reconstruction methods. Figure 6 plots the true vs. estimated per-subject error for all compared benchmark metrics on the BFM-synth and BFM-synth-biased datasets, along with the $R^2$ scores; the plotted lines depict the slopes $m_k$ for each reconstruction method (Section 4.4). The wider these lines are spread (i.e., the higher the $\eta$) for an estimator, the more likely that this estimator will be unfair to some reconstruction method(s). The $R^2$ score of LP+Chamfer is higher than that of Chamfer, indicating that the usage of LP improves average per-subject estimation error. However, the $\eta$ value of LP+Chamfer is also higher, as the this estimator favors the 3DI method, which likely stems from the high accuracy of 3DI on landmarks (Table 2). That is, the landmark-based alignment, LP, causes relatively little warping for the 3DI method, therefore the Chamfer bias remains stronger. Overall, the lowest $\eta$ is obtained by LP+NICP, therefore this estimator will likely lead to fairer comparison of reconstruction methods. The $R^2$ of LP+NICP is relatively low, which means that the error for a specific subject’s mesh may not be estimated accurately, although the average over per-subject estimations over a dataset may be estimated more accurately given that the dataset has sufficiently many subjects.

Figure 6.

True vs. estimated per-subject error (in mm), shown separately for the four compared benchmark metrics; top row: results for the BFM-synth dataset: bottom row results for the BFM-synth-biased dataset. The colors of the points indicate the reconstruction method that is used, and the line (with the same color) indicates the slope of the linear model fit to the true vs. estimated errors of the same method.

Table 2.

Mean landmarks error (in mm) comparison.

3DI	3DDFAv2	Deep3DFace	INORig	meanface
1.30	2.36	1.96	2.38	2.45

An interesting outcome is that the INORig method’s error seems to be systematically underestimated; it has either the lowest or second lowest slope on any plot in Figure 6. The fact that error can be systematically more underestimated for a specific method is a critical issue for benchmarking, therefore we conducted further analyses to understand the reason behind it, which lead to a surprising outcome: The reconstruction method that is used has a very strong effect on a reconstructed mesh $R$, to the point that the meshes of two different subjects obtained by the same reconstruction method are in general more similar than the meshes of the same subject obtained by different methods (Appendix C). As such, it is not implausible that error can be under or overestimated more for a specific reconstruction method compared to others.

5.4. Predicting ranking of reconstruction methods

A fundamental use of a benchmark metric is to compare reconstruction methods. Table 3 shows the true and predicted error of nine variants of reconstruction methods on the (zero-mean) BFM-synth dataset, as well as the error obtained by simply using the mean face (of the BFM)—a practice suggested in the literature [10]. The methods are ranked based on their true error, and the highlighted cells depict the cases where the estimated errors lead to an incorrect ranking or artificially equate methods. Table 3 shows that Chamfer leads to incorrect ranking for several methods. Even if the ranking is correct, performance differences may be squashed; e.g., the true error difference between Deep3DFace₁ and 3DDFAv2₁ is 0.30mm, but according to Chamfer it is 0.10mm. Overall, the NICP-based methods are the most successful in terms of recovering the correct ranking, but none of the estimators correctly rank all reconstruction methods. In particular, the INORig method seems to be consistently getting an unfair advantage.

Table 3.

True and estimated average error (in mm) of reconstruction methods on BFM-synth data. Highlighted cells indicate cases where ranking according to estimated error is inconsistent with true ranking. The subscript of reconstruction methods is the number of frames used per reconstruction. Bold, italic, and underlined text indicate the best, second and third methods, respectively.

		Estimated error
Rec. method	True	Cham.	LP+Cham.	NICP	LP+NICP
3DI50	2.33	1.47	1.75	2.51	2.30
Deep3DFace50	2.41	1.45	2.04	2.52	2.49
Deep3DFace10	2.42	1.45	2.06	2.60	2.51
3DI10	2.47	1.54	1.87	2.66	2.44
Deep3DFace1	2.55	1.54	2.20	2.78	2.69
3DDFAv250	2.85	164	2.45	2.86	2.85
3DDFAv21	2.86	1.64	2.45	2.83	2.85
Mean face1	3.03	1.75	2.62	3.14	3.04
INORig50	3.10	1.64	2.52	2.98	2.88
INORig10	3.12	1.66	2.53	3.02	2.90

We next evaluate how the compared geometric error estimators behave on real datasets, namely Florence and BU4DFE. Table 4 reports the (estimated) errors and ranking of the reconstruction methods on synthesized and real data. To reduce the unfair advantage that the mean face “reconstruction” can have on the synthesized data, we used the BFM-synth-biased data in these experiments, as the mean face is the optimal constant face shape on the BFM-synth data but not on BFM-synth-biased.

Table 4.

True and estimated average error (Chamfer or LP+NICP) on synthesized (BFM-synth-biased) and real data. Subscript F is number of frames per reconstruction. Bold, italic, and underlined text indicate the best, second and third methods, respectively.

	Synthesized data			Florence data		BU4DFE data
Rec. Method	True	Ch.	LP+ NICP	Ch.	LP+ NICP	Ch.	LP+ NICP
3DI50	2.30	1.33	2.15	1.64	2.58	1.81	2.80
3DI10	2.42	1.39	2.24	1.64	2.62	1.85	2.89
Deep3DF50	2.49	1.57	2.50	1.83	3.13	1.74	3.05
Deep3DF10	2.50	1.57	2.51	1.83	3.15	1.73	3.06
Deep3DF1	2.69	1.70	2.71	1.93	3.38	1.86	3.28
INORig50	2.89	1.60	2.57	1.77	3.19	1.72	3.06
INORig10	2.89	1.60	2.57	1.78	3.20	1.74	3.09
3DDFA50	2.94	1.81	2.97	1.95	3.39	2.04	3.50
3DDFA10	3.00	1.92	3.04	1.96	3.41	2.08	3.57
Mean face	3.04	1.95	3.07	2.07	3.56	2.19	3.77

A critical result in Table 4 is that the Chamfer-based ranking on real data has little consistency with the Chamferbased ranking on synthesized data. The Chamfer-based ranking on the BU4DFE dataset is particularly inconsistent with all other rankings. This is unexpected, as we followed identical 2D image rendering procedures and used only on neutral scans/images. The Chamfer error’s lack of consistency between real datasets (Florence and BU4DFE) may be due to the difference in the effective resolution of the meshes in the two respective datasets (Figure 7).

Figure 7.

3D meshes from the Florence and BU4DFE datasets. The effective resolutions of the two datasets seem to be different; the Florence mesh provides sharper and more detailed 3D data.

The ranking of reconstruction methods in Table 4 based on the LP+NICP metric is more consistent between the three datasets, namely the BU4DFE, Florence and BFM-synth-biased. Since we do not have access to the true error on the real datasets, we cannot reach any conclusive inference about which error estimator works better on the real data. However, it is reasonable to assume that the LP+NICP metric predicts the ranking better, as one would expect methods to be ranked similarly when all the experimental conditions (i.e., image generation procedures and facial expression on meshes) are identical across datasets. Moreover, we can readily see that LP+NICP makes fewer ranking errors than the Chamfer on synthesized datasets (Table 3,4). As such, one may conjecture that the LP+NICP error predicts the ranking of compared methods better on real data.

6. Limitations

We evaluated methods that perform reconstruction by using a 3D face template (i.e., mesh topology); however, there exist approaches that do not necessarily use one [20, 16, 33]. In these cases, using synthetic data is not helpful, since the topology of the reconstruction is not known and might differ from sample to sample. We also remark that the sensitivity of a geometric error estimator to the (effective) resolution of ground truth meshes should be made a criterion for meta-evaluation, as Section 5.4 suggests that resolution may significantly alter the output of some error estimators. Thus, our meta-evaluation framework may be extended to quantify how an error estimator responds to resampling or smoothing of the ground truth meshes. Finally, while we used simple (3DMM-generated) synthetic data in this initial study, one can use synthetic 2D/3D data that is more realistic and challenging; nevertheless, the meta-evaluation procedure can be used as it is.

7. Conclusion

We presented a meta-evaluation framework to assess error estimators for benchmarking 3D face reconstruction. Specifically, we introduced a procedure to measure the bias and variance in estimated error, and the dependence of the estimator to the reconstruction method. Further, we used the framework to evaluate four approaches to geometric error estimation. Critically, results exposed limitations of the standard benchmark approach, namely the Chamfer distance, by showing that the latter largely underestimates true errors, and can also squash relative performance differences between reconstruction methods or even alter true ranking. While the usage of non-rigid ICP (NICP) with landmark-based (non-rigid) pre-alignment led to more consistent ranking and less bias, it still did not correctly rank all reconstruction methods. Moreover, the computational intensity of NICP may prove prohibitive for some applications. In sum, our study exposed the limitations in benchmarking reconstruction methods, and provided a set of tools to measure the needed progress.