Tissue flows are tuned by actomyosin-dependent mechanics in developing embryos

Abstract

Rapid epithelial tissue flows are essential to building and shaping developing embryos. However, the mechanical properties of embryonic epithelial tissues and the factors that control these properties are not well understood. Actomyosin generates contractile tensions and contributes to the mechanical properties of cells and cytoskeletal networks in vitro, but it remains unclear how the levels and patterns of actomyosin activity contribute to embryonic epithelial tissue mechanics in vivo. To dissect the roles of cell-generated tensions in the mechanics of flowing epithelial tissues, we use optogenetic tools to manipulate actomyosin contractility with spatiotemporal precision in the Drosophila germband epithelium, which rapidly flows during body axis elongation. We find that manipulating actomyosin-dependent tensions by either optogenetic activation or deactivation of actomyosin alters the solid-fluid mechanical properties of the germband epithelium, leading to changes in cell rearrangements and tissue-level flows. Optogenetically activating actomyosin leads to increases in the overall level but decreases in the anisotropy of tension in the tissue, whereas optogenetically deactivating actomyosin leads to decreases in both the level and anisotropy of tension compared to in wild-type embryos. We find that optogenetically activating actomyosin results in more solid-like (less fluid-like) tissue properties, which is associated with reduced cell rearrangements and tissue flow compared to in wild-type embryos. Optogenetically deactivating actomyosin also results in more solid-like properties than in wild-type embryos but less solid-like properties compared to optogenetically activating actomyosin. Together, these findings indicate that increasing the overall tension level is associated with more solid-like properties in tissues that are relatively isotropic, whereas high tension anisotropy fluidizes the tissue. Our results reveal that epithelial tissue flows in developing embryos involve the coordinated actomyosin-dependent regulation of the mechanical properties of tissues and the tensions driving them to flow in order to achieve rapid tissue remodeling.

INTRODUCTION

Within developing embryos, epithelial tissue sheets can dramatically deform to lay out and shape the body plan of the animal. Many epithelial tissue movements are rapid and involve significant remodeling of the tissue through local cell rearrangements that alter the relative positions of cells within the tissue, similar to the deformation and flow of fluid materials [1–3]. Based on this similarity, tissue flow via cell rearrangements is often referred to as tissue fluidity. In physical models of epithelia, if the energy barriers to rearrangement are small or the driving forces are large, cell rearrangements occur and the tissue can flow in a fluid-like manner [4–10]. Thus, to understand the origins of tissue-scale flows, we must understand both the mechanical forces that drive flow and the mechanical properties that determine how the tissue resists flowing in response to those forces. Recent studies suggest that the mechanical behavior of tissues in developing embryos are regulated in space and time to allow (or prevent) tissue remodeling and flow [11–15], but the mechanisms underlying these changes in mechanics are not known.

Contractile networks of F-actin and non-muscle myosin II, jointly referred to as actomyosin, are a primary force-generating machinery in epithelial cells. Specific patterns of actomyosin localization and activity are regulated by the Rho/Rho-kinase signaling pathway and are correlated with tissue-level flow patterns during development [3,16–18]. In addition, the mechanical behavior of the actomyosin cytoskeleton has been implicated in the mechanical properties of cells and tissues, with increased actomyosin-generated tension often associated with stiffer cells and more solid-like tissues [5,19–21], which would be predicted to increase resistance to flow. Given these potential dual—and possibly opposing—roles for actomyosin in regulating both tissue-scale driving forces and tissue mechanical properties, it is not well understood how patterns of actomyosin contractility tune tissue mechanical properties and overall tissue flow.

Body axis elongation in the Drosophila embryo is a powerful model system for studying the physical and biological mechanisms that contribute to epithelial tissue flows [22–26]. Recent work from our group and others has demonstrated that the onset of rapid cell rearrangements in the germband epithelium is predicted by a solid-to-fluid transition in anisotropic vertex models of epithelial tissues [13], suggesting that the mechanical properties of the germband might be regulated to promote this rapid change in tissue shape.

Dissecting the roles of actomyosin-generated tension in the flowing germband requires precise perturbation of actomyosin contractility patterns, so as not to influence neighboring regions of the embryo. Recent studies have demonstrated that emerging light-gated optogenetics approaches can be used for precise spatial and temporal manipulation of actomyosin in the Drosophila embryo and other systems [27–31]. These tools provide unprecedented access to manipulate actomyosin contractility with high precision for quantitative studies of tissue mechanics.

Here, we dissect the roles of actomyosin in germband tissue flows during Drosophila body axis elongation, using recently developed optogenetic tools for targeted and precise manipulation of actomyosin. We use quantitative image analysis and laser ablation to analyze how perturbing actomyosin affects cell rearrangements, tissue mechanical properties, and mechanical tensions in the tissue. Our findings indicate that actomyosin influences solid-fluid tissue mechanical properties, in addition to expected roles in generating driving forces, and reveal how distinct aspects of actomyosin tensions promote cell rearrangement and tissue flow.

RESULTS

Optogenetic manipulation of actomyosin disrupts cell rearrangements and tissue flow during convergent extension

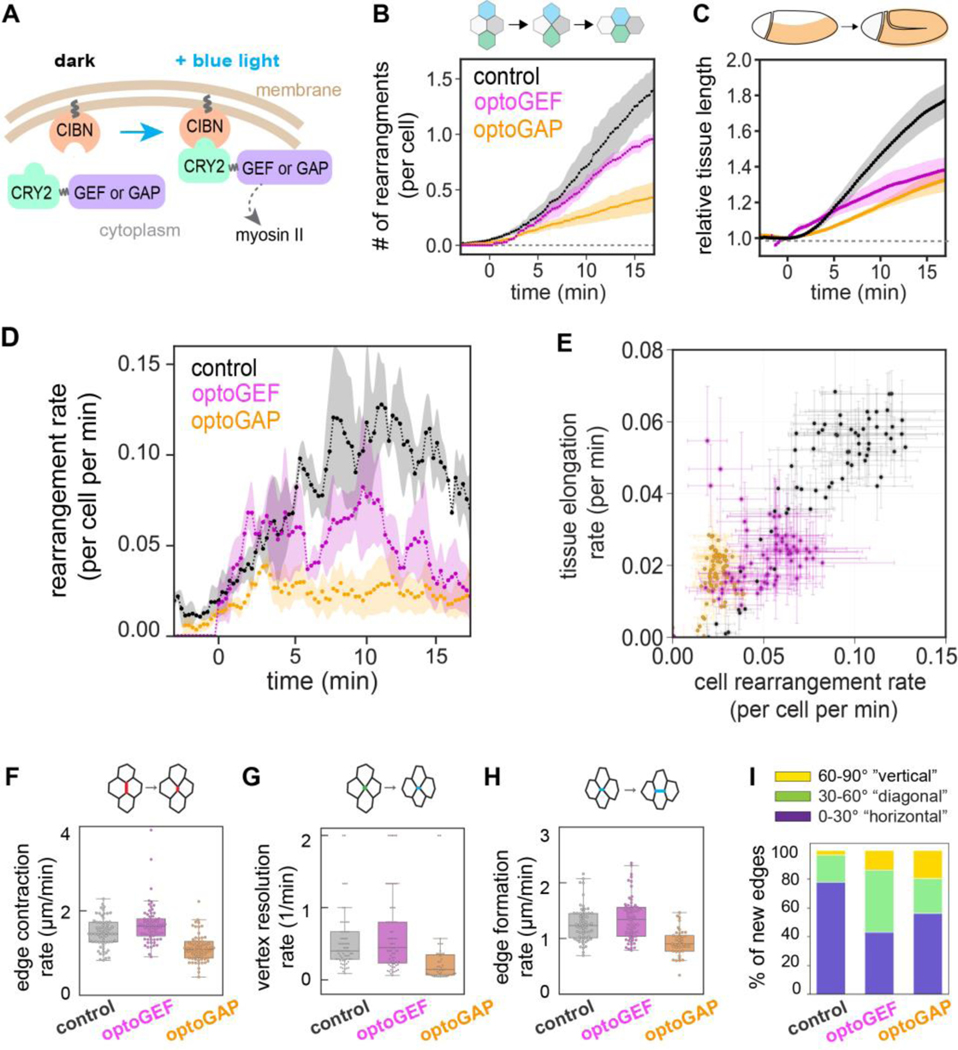
To test how actomyosin contractility influences tissue fluidity, we employed two previously described optogenetic tools, optoGEF and optoGAP (Fig. 1A) [31], to activate or deactivate actomyosin contractility, respectively, in the Drosophila germband and analyzed the effects on cell rearrangements and tissue flow. We generated embryos expressing the optoGEF or optoGAP tool using the Gal4/UAS system and illuminated the apical surface of the ventrolateral region of the germband epithelium with blue light (488 nm) beginning at the onset of body axis elongation, which we define as $t=0$, and captured time-lapse confocal movies of tissue flow.

Figure 1.

Optogenetic manipulation of actomyosin tunes cell rearrangement rates and tissue flow during Drosophila body axis elongation. (A) Schematic of optogenetic tools. CIBN is targeted to the cell membrane. The light-sensitive PHR domain of CRY2 is fused to upstream myosin II regulators of the Rho/Rho-kinase pathway, RhoGEF2 (GEF) or RhoGAP71E (GAP). Under blue light illumination, CRY2 dimerizes with CIBN, and the regulators accumulate at the cell membrane. (B) Number of cell rearrangements initiated in control, optoGEF, and optoGAP embryos, including both T1 processes and higher-order rosette rearrangement events. (C) Elongation of the germband tissue during convergent extension quantified by PIV analysis of time-lapse confocal movies of embryos. The length of the tissue was normalized to the value at $t=0$. (D) Instantaneous rate of rearrangements per cell per minute. (E) Correlation between the instantaneous rates of tissue elongation and cell rearrangement. Each data point represents the mean between embryos at an individual time point. The mean ± SEM between embryos is shown, n=3–5 embryos per genotype. (F) AP cell edge contraction rate, (G) vertex resolution rate, and (H) new edge formation rate during cell rearrangements in the germband tissue of photoactivated embryos. Each data point represents a cell rearrangement initiated by contraction of an AP edge. n=10–25 edges/embryo from 3–5 embryos (n=48–69 edges per genotype). (I) The orientation of newly formed cell edges during cell rearrangements. While most of the new edges in control embryos correspond to edges oriented parallel to the anterior-posterior axis of the embryo (orientation 0–30°), optoGEF embryos showed an increase in edges with diagonal orientation (30–60°), n=3–5 embryos per genotype, 10–25 junctions/embryo. See details in the Materials and Methods section.

We analyzed the effects of optogenetic perturbation on the number of cell rearrangements in the tissue as a metric for tissue fluidity. We observe a reduction in the number of rearrangements per cell in both photoactivated optoGEF embryos (0.93 ± 0.05,$P=0.04$) and photoactivated optoGAP embryos (0.40 ± 0.12,$P=0.03$) compared to control embryos expressing only CIBN-pmGFP (1.25 ± 0.19 cell rearrangements per cell) during the first 15 min of axis elongation (Fig. 1B). Rearrangement numbers in control embryos were similar to in wild-type embryos [32–36]. Consistent with reduced cell rearrangements, photoactivated optoGEF and optoGAP embryos displayed a decrease in average vertex coordination number in the germband compared to control embryos (Fig. S1A of Supplemental Material [37]). Analysis of the macroscopic tissue flow shows a reduction in germband elongation in photoactivated optoGEF (1.37 ± 0.09-fold, $P=0.06$) and optoGAP (1.29 ± 0.05-fold, $P=0.02$) compared to control embryos (1.71 ± 0.09-fold), consistent with the notion that cell rearrangements mediate tissue flow during convergent extension (Fig. 1C).

To take a closer look at the relationship between cell rearrangements and tissue flow, we analyzed the instantaneous rates of cell rearrangement and tissue elongation. In control embryos, the rates of cell rearrangements and relative tissue elongation increase during the first ~10 min of axis elongation, followed by a decrease during the rest of the process (Fig. 1D and Fig. S1B in Supplemental Material [37]). In optoGEF and optoGAP embryos, the rates of relative tissue elongation and cell rearrangement were both decreased (Fig. 1D and Fig. S1B–D in Supplemental Material [37]). At $t=10\min$, the rate of tissue elongation was reduced to 0.02 ± 0.01 min⁻¹ in optoGEF ($P=0.09$) and 0.02 ± 0.06 min⁻¹ in optoGAP ($P=0.03$) compared to 0.05 ± 0.01 min⁻¹ in control embryos (Fig. S1B–D in Supplemental Material [37]). Similarly, the rate of cell rearrangements was 0.08 ± 0.03 cell⁻¹ min⁻¹ in optoGEF ($P=0.45$) and 0.04 ± 0.02 cell⁻¹ min⁻¹ in optoGAP embryos ($P=0.09$), compared to 0.12 ± 0.04 cell⁻¹ min⁻¹ in control embryos (Fig. 1D). The instantaneous rates of tissue elongation and cell rearrangements are correlated in all embryo groups (Fig. 1E, correlation coefficient for control=0.93, optoGEF=0.58, optoGAP=0.71), consistent with a central role for tissue fluidity in promoting tissue elongation.

Notably, the rate of cell rearrangement was the least predictive of tissue elongation rate for the optoGEF perturbation. Further analysis of the distinct cell edge contraction, vertex resolution, and edge growth steps during cell rearrangement revealed that perturbation with optoGEF resulted in only mild defects in the speed of rearrangements (Fig. 1F–H) but that the rearrangements that did initiate were poorly oriented (Fig. 1I and Fig. S1E–H in Supplemental Material [37]). This may help explain the reduction in tissue-level elongation (Fig. 1C). In contrast, perturbation with optoGAP resulted in slower and poorly oriented cell rearrangements compared to controls (Fig. 1F–I and Fig. S1E–H in Supplemental Material [37]), consistent with a role for actomyosin contractility both in edge contraction and in vertex resolution [24,34,36,38–42].

Taken together, these results demonstrate that optogenetic perturbation of actomyosin activity disrupts oriented cell rearrangements, decreasing the ability of the tissue to remodel and flow like a fluid during convergent extension.

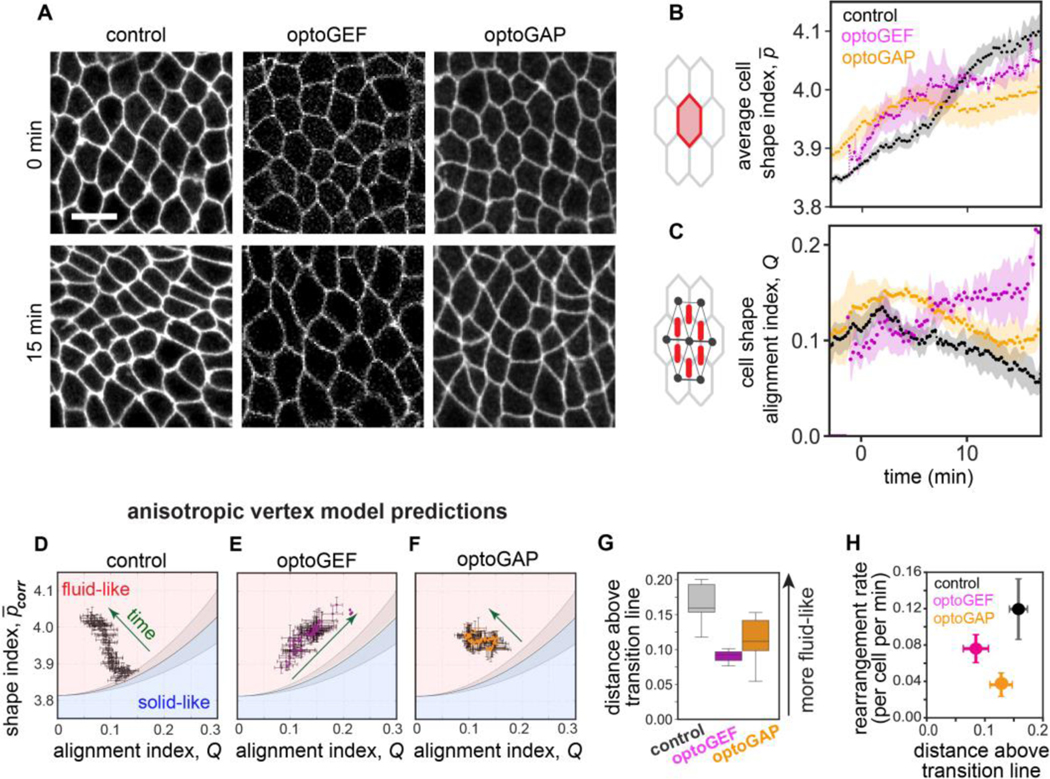
Actomyosin influences cell packings and tissue mechanical properties

Actomyosin contractility has been proposed to influence the mechanical properties of epithelial tissues, with increased actomyosin-generated tension predicted to increase the resistance of the tissue to flow [5]. We wondered if effects of actomyosin on tissue mechanical properties could explain the observed reductions in cell rearrangement rates when actomyosin is perturbed. Because direct mechanical measurements to probe the mechanical response of the germband remain a significant experimental challenge, we gained insight from predictions of anisotropic vertex models of epithelial tissues.

Recent work from our group and others has demonstrated that the fluid-solid behavior of epithelia can be predicted from cell packings in the tissue [13,14,43,44]. For anisotropic tissues like the germband, the average cell shape index $\stackrel{-}{p}$, cell shape alignment index $Q$, and average vertex coordination number $z$ are sufficient to classify a given packing as either solid-like or fluid-like, where the predicted solid-fluid transition line is given by:

$$\stackrel{-}{p}=3.818+(z-3)/B+4b{Q}^2,$$

or alternatively, ${\overline{p}}_{corr}=3.818+4b{Q}^2$ [13], where $B=3.85$ [45], $b=0.6\pm 0.2$[46], and ${\stackrel{-}{p}}_{corr}=\stackrel{-}{p}-(z-3)/B$. This link between cell shapes and tissue mechanics can be understood from vertex models of epithelia in which cell packings reflect the energy barriers to cell rearrangement.

To gain insight into how actomyosin influences tissue mechanical properties, we quantified how $\stackrel{-}{p}$ (cell perimeter divided by the square root of cell area, averaged across the cells in the tissue) and $Q$ (average cell elongation across the tissue, similar to a nematic order parameter but modulated by the extent of cell elongation) [13], varied over time in photoactivated embryos (Fig. 2A–C). In control embryos, $\stackrel{-}{p}$ increased over time and $Q$ peaked around $t=2\min$ (Fig. 2A–C), similar to in wild-type embryos [13]. Comparing these results to the predictions of the anisotropic vertex model [13], suggests that the germband tissue in control embryos starts out near the predicted solid-fluid transition line and over time moves deeper into the predicted fluid-like region (Fig. 2D), consistent with the tissue becoming more fluid-like to minimize resistance to flow during axis elongation.

Figure 2.

Cell packings and tissue mechanics in optogenetically manipulated germband tissue. (A) Stills from confocal movies showing cell packings during axis elongation. Anterior, left. Ventral, down. Bar, 10 μm. See also Movies S1–3 in Supplemental Material [37]. (B) The average cell shape index $\stackrel{-}{p}$ during convergent extension in photoactivated control, optoGEF, and optoGAP embryos. The mean ± SEM between embryos is shown, n=3–5 embryos per genotype. (C) The cell shape alignment index $Q$ during convergent extension in photoactivated control, optoGEF, and optoGAP embryos. The mean ± SEM between embryos is shown, n=3–5 embryos per genotype. (D-F) Relationship between the corrected averaged cell shape index and cell shape alignment in the germband for control (D), optoGEF (E), and optoGAP (F) embryos. The corrected cell shape index and cell shape alignment can be used to predict tissue mechanical behavior using an anisotropic vertex model [13]. Each data point represents the mean between embryos at an individual time point, n=3–5 embryos per genotype. Solid line represents the predicted solid-fluid transition line, shaded area represents the range of predicted values for the transition from prior vertex model simulations (see Materials and Methods section). (G) Distance to the predicted solid-fluid transition line, evaluated during the rapid phase of tissue elongation ($t=15\min$). (H) Relationship between cell rearrangement rate and predicted solid-fluid properties.

Cell packings in the germband of photoactivated optoGEF and optoGAP embryos were altered in distinct ways, leading to differences in predicted tissue mechanical properties. In photoactivated optoGAP embryos, the average cell shape index $\stackrel{-}{p}$ was lower than in controls after the first 10 min of the process, and the alignment index $Q$ showed similar trends as controls but with somewhat elevated values throughout the process (Fig. 2A–C). Comparing these results to the vertex model predictions suggests that in optoGAP embryos, the germband starts out near the predicted solid-fluid transition line, similar to controls, but does not move as deeply into the predicted fluid-like region (Fig. 2D,F), possibly consistent with less fluid-like behavior and more resistance to flow.

In photoactivated optoGEF embryos, although $\stackrel{-}{p}$ displays similar trends as in the optoGAP case, $Q$ shows qualitatively different behavior, remaining high throughout the process and not relaxing back down to low levels as observed in controls (Fig. 2A–C). These results suggest that the germband in optoGEF embryos again starts out near the predicted solid-fluid transition line in the vertex model but takes a path through the $p-Q$ parameter space over time that follows along the transition line instead of relaxing deeper into the fluid-like region (Fig. 2D,E), consistent with significantly less fluid-like behavior and more resistance to flow.

To compare the predicted tissue mechanical properties in the control, optoGEF, and optoGAP groups, we measured the distance to the predicted solid-fluid transition line in the $p-Q$ parameter space. During the rapid phase of tissue elongation, the distance above the transition line was reduced in optoGAP ($P=0.05$) and significantly reduced in optoGEF ($P=0.005$) compared to in control embryos (Fig. 2G). Taken together, these findings suggest that tissue mechanical properties, which capture how a tissue resists flowing under an applied force, are altered by activation (optoGEF) or deactivation (optoGAP) of actomyosin in the germband. In both cases, the germband is predicted to be less fluid-like than in control embryos, which is consistent with the observed reduction in cell rearrangements and tissue flow (Fig. 1D and 2H).

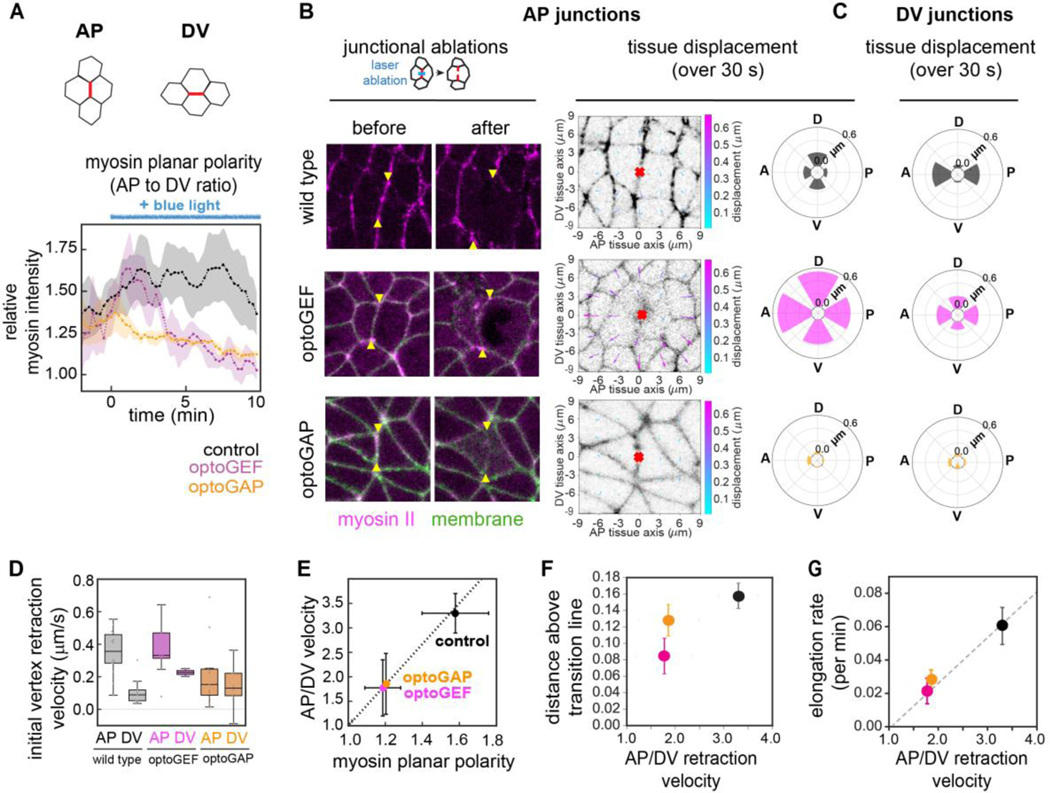
Anisotropic tension patterns generated by actomyosin contractility promote tissue fluidity

We wondered if differences in the patterns of mechanical tensions might help account for the changes in mechanical properties in optoGEF and optoGAP embryos. During germband extension, planar polarized patterns of myosin II localization and activity are thought to provide anisotropic tension patterns at cell contacts that produce driving forces for cell rearrangements and tissue flow [23,24,32,34,38–40,47–49]. To test how patterns of myosin-generated tensions are influenced by the optogenetic perturbations, we examined myosin II junctional localization as well as junctional tensions in photoactivated optoGEF and optoGAP embryos.

First, we analyzed the dynamics of myosin II localization after optogenetic manipulation by time-lapse confocal imaging using an mCherry-tagged myosin regulatory light chain. Following photoactivation of optoGEF, myosin localization at AP and DV cell junctions initially increased, following the same trends as in control embryos, before beginning to decrease 3–5 min after the start of blue light exposure (Fig. S2A–C in Supplemental Material [37]), producing a strong decrease in myosin planar polarity (Fig. 3A). In contrast, photoactivation of optoGAP resulted in an immediate but gradual decrease in junctional myosin (Fig. 3A and Fig. S2A–C in Supplemental Material [37]). The majority of the reduction in cortical myosin occurred over a timescale of ~5 min and was associated with an almost immediate decrease in myosin planar polarity compared to in control embryos (Fig. 3A).

Figure 3.

Patterns of actomyosin-generated tension at cell junctions in optogenetically manipulated germband tissue are linked with tissue fluidity. (A) Ratio of mean myosin intensities at AP compared to at DV junctions before and during tool activation beginning at $t=0$ (duration of blue light exposure indicated by blue line). Ratios for each embryo at each time point were calculated, and the mean ± SEM between embryo is shown. n=3–4 embryos, >10 cells/embryo. See also Movie S4 in Supplemental Material [37]. (B) (left panel) Ablations at AP cell junctions in optogenetically manipulated germband tissue. Cells before (left) and 1 min after (right) ablation. Myosin II (magenta), CIBN-pmGFP (green). Arrowheads indicate the vertices connected to the junction in which the cut was made. Anterior, left. Ventral, down. Image size, 20 × 20 μm. (right panel) Maps of displacements in the surrounding tissue in the 30 s following AP ablations. The tissue in a 174 μm² region surrounding the ablation point (red mark) was analyzed by PIV analysis following ablation. Radial plots show the mean total displacement after AP ablation, averaged over the regions in 60° angular bins, along the anterior, posterior, dorsal, or ventral tissue axes, n = 3–11 ablations per condition. (C) Radial plots showing the mean total displacement following DV ablations. (D) Initial vertex retraction velocities after ablation. Mean ± SEM between junctions is shown, n=10–15 AP, 3–10 DV junctions per condition. (E) Mechanical anisotropy was reduced in optoGEF and optoGAP embryos and correlates with myosin planar polarity at 5 min after optogenetic activation. Mechanical anisotropy was calculated as the ratio of mean AP to mean DV peak retraction velocities, n = 3–15 edges per condition. (F) Relationship between predicted fluid-solid tissue properties and tension anisotropy. As a readout of anisotropy, the ratio of AP to DV peak retraction velocities after ablation of junctional myosin was used. (G) Relationship between tissue elongation rate and tension anisotropy. Dashed lines, guide to the eye. Photoactivated control embryos (black), optoGEF (magenta), and optoGAP (orange).

Next, we tested if the altered myosin localization patterns in photoactivated optoGEF and optoGAP embryos resulted in changes to the anisotropic mechanical tension in the tissue. We used a laser to ablate individual junctional domains at the contacts between neighboring cells (Fig. 3B, C and Fig. S2D in Supplemental Material [37]) [7,39,40,50,51]. Retraction of the tissue away from the ablation site reflects the mechanical tension in the tissue prior to ablation, with the initial retraction velocity being proportional to tension and inversely related to viscous drag. The decreased myosin planar polarity in optoGEF and optoGAP embryos would be predicted to result in reduced anisotropy in tension along AP compared to DV cell junctions. In wild-type control embryos, the mean initial retraction velocities were 0.36 ± 0.04 μm/s at AP junctions and 0.11 ± 0.03 μm/s at DV junctions (Fig. 3D and Fig. S2E,F in Supplemental Material [37]), producing a significant mechanical anisotropy in the tissue (comparison between AP and DV velocities, $P=9\times {10}^{-6}$, $t$-test) (Fig. 3E), consistent with previous studies in the germband of wild-type embryos [34,39,40]. In contrast, the mechanical anisotropies in photoactivated optoGEF and optoGAP embryos were reduced (Fig. 3D,E), such that the differences between velocities at AP junctions and at DV junctions were less significant ($P=0.04$, $P=0.16$ respectively, $t$-test).

To better understand how tissue mechanical behavior is linked to myosin-dependent tensions, we plotted the relationship between the ablation results, solid-fluid tissue properties, and tissue flow. As a readout of mechanical properties, we used the distance above the predicted solid-fluid transition line in the vertex model, where larger distances are associated with less resistance to flow. We find a strong relationship between tension anisotropy and predicted tissue properties (Fig. 3F) and tissue flow (Fig. 3G, Fig. S3A–D in Supplemental Material [37]), indicating that tissues with the highest tension anisotropy are most fluid-like, consistent with a central role for tension anisotropy in tissue fluidity.

These results demonstrate that optogenetic activation or deactivation of Rho signaling nearly abolishes myosin planar polarity and disrupts the anisotropic contractile tensions at cell junctions. Taken together, these findings reveal that disrupted tension anisotropy is associated with more solid-like tissue behavior, suggesting that tension anisotropy can fluidize the tissue.

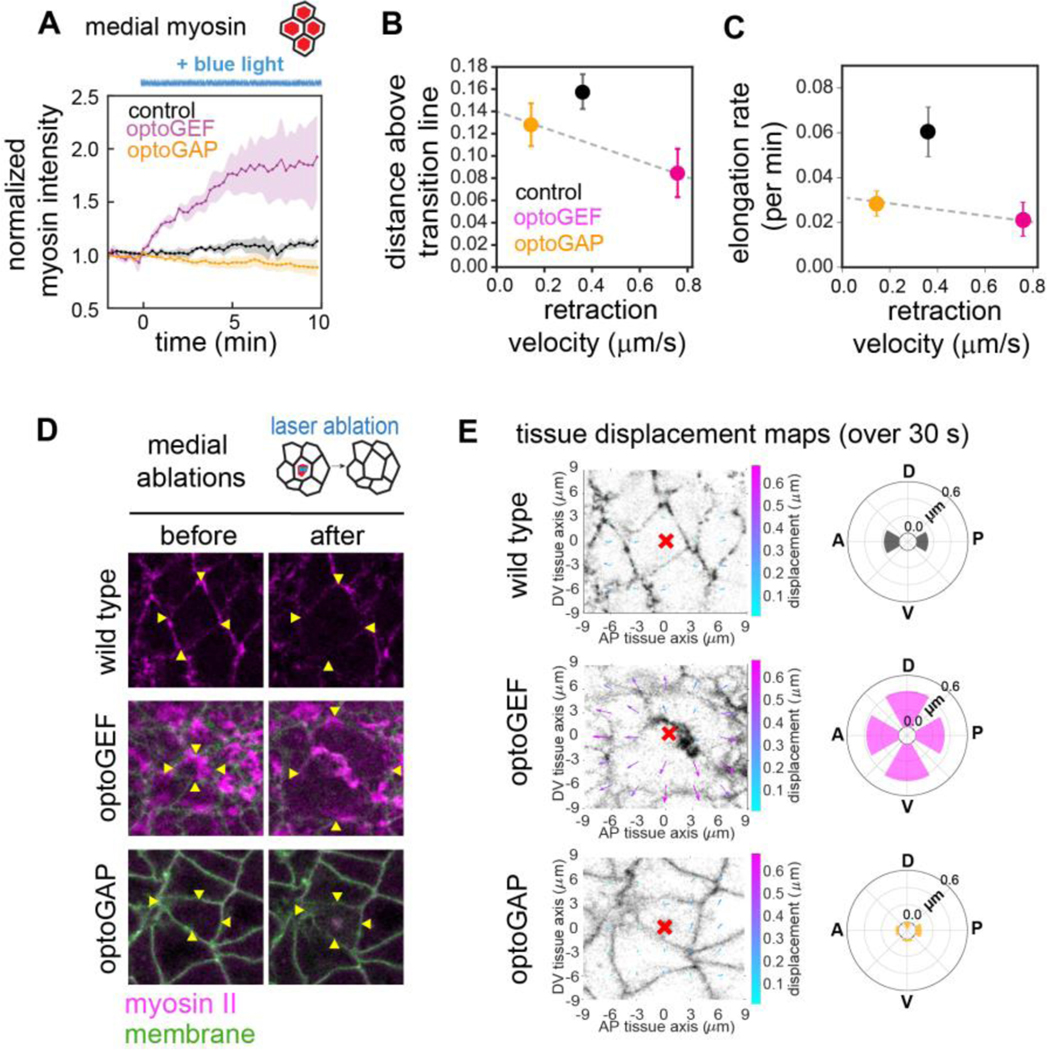
Overall tension levels generated by actomyosin correlate with more solid-like behavior in isotropic tissues

We wondered what additional features of myosin-dependent tensions might contribute to the distinct defects in photoactivated optoGEF and optoGAP embryos. One notable feature of myosin II localization in the optoGEF embryos is the enhanced accumulation of myosin at the medial-apical domain of cells (Fig. S2A in Supplemental Material [37]). In optoGEF embryos, we observed that following blue light exposure starting at $t=0$, myosin rapidly accumulated at the medial-apical cortex, with a 22 ± 4% increase in medial myosin within 1 min and a 66 ± 14% increase over 5 min, compared to 3 ± 2% in 1 min and 9% ± 2% in 5 min in control embryos (Fig. 4A). This increase led to the formation of a radial pattern of myosin reminiscent of those found in tissues exhibiting apical constriction. In contrast, photoactivation of optoGAP resulted in an immediate but gradual decrease in medial myosin (Fig. 4A).

Figure 4.

Levels of actomyosin-generated tension at the medial-apical domain in optogenetically manipulated germband tissue are linked with tissue fluidity. (A) Mean myosin intensity in the medial-apical domain of cells over time before and during tool activation beginning at $t=0$. n=3–4 embryos, >10 cells/embryo. (B) Relationship between tissue mechanical properties and overall level of tissue tension in photoactivated embryos. As a readout of overall tension levels, the average magnitude of tissue retraction velocity after medial ablation was used. (C) Relationship between tissue elongation rate and overall level of tissue tension. Dashed lines, guides to the eye. (D) Ablations in the medial-apical domain of cells in optogenetically manipulated germband tissue. Cells before (left) and 1 min after (right) ablation. Myosin II (magenta), CIBN-pmGFP (green). Arrowheads indicate the vertices connected to the cell in which the cut was made. Anterior, left. Ventral, down. Image size, 20 μm. (E) Maps of displacements in the surrounding tissue in the 30 s following ablations. The tissue in a 174 μm² region surrounding the ablation point (red mark) was analyzed by PIV analysis following ablation. Radial plots show the mean total displacement, averaged over the regions in 60° angular bins, along the anterior, posterior, dorsal, or ventral tissue axes, n = 3–11 ablations per condition.

To test how the enhanced medial-apical myosin in optoGEF embryos influences mechanical tension levels in the tissue, we used a laser to ablate myosin in the medial-apical domains of individual cells (Fig. 4D,E). In optoGEF embryos after 5 min of photoactivation, ablation in the medial-apical domain in a single cell led to dramatic retraction of the surrounding tissue along both the AP and DV axes (Fig. 4D,E), which was significantly enhanced compared to medial ablations in wild-type embryos ($P=0.018$) and optoGAP embryos ($P=0.009$), in which there was less medial myosin present (Fig. 4A). In addition, tissue retraction in optoGEF embryos was more isotropic than in controls. In contrast, medial ablations in photoactivated optoGAP embryos resulted in retractions more similar in magnitude to control embryos ($P=0.39$) (Fig. 4E). These results indicate that the myosin accumulating at the apical cortex of germband cells in optoGEF embryos is actively contributing to mechanical tensions in the tissue and that these tensions appear more isotropic than in control embryos.

By restricting our attention to embryos with strongly reduced tension anisotropy (optoGEF and optoGAP), we see that the tissues with the highest overall tensions are predicted to have increased resistance to flow (Fig. 4B) and exhibit reduced elongation (Fig. 4C, Fig. S3E–H in Supplemental Material [37]) This is consistent with how tension contributes to tissue properties in isotropic vertex models, where increased tension is associated with increased resistance to flow [5].

In summary, our results are consistent with the idea that overall actomyosin-dependent tension levels contribute to more solid-like tissue behavior in the case of relatively isotropic tissue, while strong tension anisotropy patterns are essential for harnessing cell rearrangement for tissue-level flow in wild-type embryos.

DISCUSSION

Here we report multiple roles for actomyosin-dependent tension in the mechanics underlying epithelial tissue flows in the germband of developing Drosophila embryos. We find that either activation (optoGEF) or deactivation (optoGAP) of actomyosin in the germband alters cell shapes and packings. The cell packings in the perturbed tissues suggest less fluid-like (more solid-like) tissue mechanical properties in both cases compared to wild-type embryos, consistent with the reduced cell rearrangements and tissue flow observed in these perturbations. These results demonstrate a role for actomyosin in controlling the solid-fluid mechanical properties of the germband. In this study, tissue mechanical properties were inferred from vertex models of epithelial tissues. This approach has been used because theoretical models of epithelia have been used extensively to link cell shapes to tissue mechanics [5–8,13,39,43–45,52–56], and although techniques to measure tissue mechanical properties have been developed [3,11,57–62], direct characterization of epithelia in the developing Drosophila embryo remains a significant challenge.

That either activation or deactivation of actomyosin reduces tissue fluidity can be explained by our finding of two, sometimes opposing, roles for actomyosin in controlling mechanical tension patterns in the tissue. First, when myosin planar polarity is abolished by optogenetic perturbations that produce isotropic germband tissue, we find that high actomyosin-dependent tension levels are associated with cellular packings expected to be more solid-like, consistent with the isotropic vertex model predictions. Second, in highly anisotropic tissue like the wild-type germband, we find that the tension anisotropy arising from planar polarized junctional myosin is associated with increased fluid-like behavior, consistent with the idea that these anisotropic tensions can fluidize the tissue. In prior studies in other tissue types and experimental systems, actomyosin has been reported to have opposing effects on embryonic tissue mechanical properties. In Xenopus explants, actomyosin has been shown to promote stiffening of the tissue [21], whereas during zebrafish posterior body axis elongation, inhibition of myosin II activity is associated with rigidification during zebrafish posterior body axis elongation [11], possibly reflecting distinct roles for and patterns of actomyosin activity in different tissues.

Our findings reveal that planar polarized patterns of junctional myosin are required for rapid cell rearrangements and tissue-level elongation, whereas isotropic patterns of medial-apical myosin are sufficient to promote rearrangements but do not orient rearrangements to produce tissue-level flows in this context. Cell rearrangements within a tissue can lead to macroscopic tissue-level shape changes if rearrangements are spatially and temporally coordinated across the tissue, or alternatively, no tissue-level shape changes if rearrangements occur in a more randomly oriented fashion [2]. We found that optogenetically increasing (optoGEF) or decreasing (optoGAP) actomyosin activity in the germband led to similar decreases in tissue-level flow, even though more rearrangements were initiated in the optoGEF compared to optoGAP embryos. Our studies reveal that the perturbations in optoGEF embryos led to cell rearrangements that were more likely to resolve in the wrong direction, consistent with prior findings that tension distributions affect the orientation of vertex resolution and new edge formation [42,63]. By comparison, in the Drosophila pupal notum, a tissue that exhibits cell rearrangements but no macroscopic tissue-level deformation, myosin II is not planar polarized and cell rearrangements may be transient or occur in random orientations [63]. Taken together, these findings highlight the key role of myosin activity in spatially organizing cell rearrangements to harness tissue fluidity for rapid tissue shape change.

Our results support the notion that pulsatile medial-apical contractility might provide active tension fluctuations that can promote cell rearrangements and fluidize tissues. Although we observed similar disruptions to myosin planar polarity and tension anisotropy in both the optoGEF and optoGAP perturbations compared to controls, these two cases are distinguished by the different rates of cell rearrangements, with roughly 2-fold more rearrangements per cell per minute in optoGEF compared to optoGAP embryos. This is despite the fact that the germband in the optoGEF embryos is predicted to be less fluid-like and have higher energy barriers to rearrangement within the existing anisotropic vertex model framework, which might be expected to result in fewer cell rearrangements. A notable feature of these perturbations that correlates with the observed rearrangement rates is the enhanced medial-apical myosin in optoGEF and decreased medial-apical myosin in optoGAP embryos. By studying retraction of the tissue in response to laser ablation of the medial myosin domain, we demonstrated that this enhanced medial-apical myosin pool produces enhanced tension. The presence of cell rearrangements in optoGEF embryos suggests that pulsatile contractile forces originating from the medial-apical domain of cells might suffice to promote cell rearrangements in the absence of planar polarized driving forces, though such rearrangements are more likely to resolve in the wrong direction. This is consistent with a prior study from our group in which we showed that the enhanced medial-apical myosin pool in photoactivated optoGEF cells displays dynamic pulsing behavior that is correlated with apical cell area fluctuations [31]. In wild-type embryos, previous studies have demonstrated roles for pulsatile myosin activity during cell edge contraction [48] and for medial myosin pulsation in the adjacent cells during new edge formation [41,42] to promote oriented cell rearrangement.

The existing anisotropic vertex model framework [13] we used for predicting solid-fluid mechanical behavior from cell packings (c.f. Fig 2D–G) does not fully capture the observed tissue behaviors in the optoGEF and optoGAP perturbations. One possible explanation is that this model does not currently incorporate active fluctuations. Theoretical studies have begun to explore how active fluctuations and motility influence the solid-fluid mechanical behavior of model tissues in the case of isotropic tissue [6,64–66]. In the isotropic context, fluctuations can help cells overcome finite collective energy barriers associated with cell rearrangement, with enhanced tension fluctuations promoting cell rearrangement in a tissue that would otherwise be solid-like, effectively shifting the predicted solid-fluid transition line. However, it remains unclear how active fluctuation effects might play out in the more complex context of anisotropic tissues like the germband. In one 3D vertex model simulation study that incorporated anisotropy and fluctuations but did not directly explore tissue mechanical properties, it was found that anisotropic tensions and active fluctuations play complementary but not completely overlapping roles in promoting directional cell rearrangements and tissue-level flow [67]. Future theoretical studies will be needed to address this question, and the quantitative results presented here will be essential to building and testing these models.

Even though optogenetic perturbations significantly altered actomyosin patterns in the germband, influencing cell packings and producing tissues predicted to have increased energy barriers to cell rearrangement and less fluid-like properties, these perturbations were not sufficient to produce cell packings during germband extension characteristic of solid-like tissues. This raises the question of what additional molecular and mechanical factors are involved in controlling the solid-fluid properties of tissues. The contributions of cellular adhesive machineries and their interplay with the actomyosin cytoskeleton will need to be investigated. Ultimately, to understand how emergent tissue mechanics and flows are regulated in space and time across the developing embryo to generate functional three-dimensional embryonic structure, we will need to identify the master upstream regulators that tune and coordinate force generation and tissue mechanical properties to achieve both the local cell structure and global tissue shape required for proper function. The approaches and findings we report here will be useful in this endeavor.

MATERIALS AND METHODS

Fly lines and genetics.

Embryos were maintained at 23°C and experiments were performed at room temperature (~ 21°C). The fly stock w[*]; P[w+, UASp>CIBN-caax] was generated in this study by PCR amplification of the CIBN-caax fragment from plasmid pPW_CIBNcaax (gift from Stefano De Renzis). The fragment was cloned into the pENTR/D-Topo vector (Life Technologies) and recombined into UASp-attB destination vector (gift from F. Wirtz-Peitz) using the Gateway cloning system (Life Technologies) for subsequent expression using the Gal4/UAS system [68]. The plasmid was inserted into the attP40 site on chromosome II to generate transgenic flies (Bestgene).

The fly stocks w*;; w+, UASp>mCherry-CRY2PHR-RhoGEF2 and w*;; w+, UASp>mCherry-CRY2PHR-RhoGAP71E were crossed with w*; P[w+, UASp>CIBN-pmGFP]/CyO; Sb/TM3,Ser (gift of Stefano De Renzis, EMBL, Heidelberg, Germany) [29]. The stocks w*;; w+, UASp> CRY2PHR-RhoGEF2 and w*;; w+, UASp> CRY2PHR-RhoGAP71E were crossed with w*; P[w+, UASp>CIBN-pmGFP]/CyO; Sb/TM3,Ser (gift of Stefano De Renzis, EMBL, Heidelberg, Germany) or w*; w+, UASp>CIBN-caax;. The constructs were expressed using the maternal α-tubulin matα-tub15 or matα-tub67 Gal4-VP16 drivers (mat67, mat15, gift of D. St Johnston).

To visualize myosin II, mat15 and sqh>sqh-mCherry (BDSC 59024, donated by Beth Stronach and Elane Fishilevich) were recombined on chromosome III. To protect the embryos from light, crosses were maintained in the dark, and fly sorting was performed in the dark on a stereoscope equipped with Red 25 Kodak Wratten Filter.

Embryos were the progeny of females of the following genotypes:

UASp>CIBN-pmGFP/mat67 (II); sqh>sqh-mCherry/+ (III)

UASp>CIBN-pmGFP/+ (II); UASp>mCherry-CRY2PHR-RhoGEF2/mat15 (III)

UASp>CIBN-pmGFP/+ (II); UASp>CRY2PHR-RhoGEF2/sqh>sqh-mCherry, mat15 (III)

UASp>CIBN-pmGFP/mat67 (II); UASp>mCherry-CRY2PHR-RhoGAP71E/mat15 (III)

UASp>CIBN-pmGFP/mat67 (II); UASp>CRY2PHR-RhoGAP71E/sqh>sqh-mCherry, mat15 (III)

Fly stocks used in this study:

w*; w+, UASp>CIBN-pmGFP/CyO; Sb/TM3,Ser (Stefano De Renzis, EMBL, Heidelberg, Germany)

w*; w+, UASp> CIBN-caax; (this study)

w*;; w+, UASp>mCherry-CRY2PHR-RhoGEF2/TM3,Sb

w*;; w+, UASp>CRY2PHR-RhoGEF2/TM3,Sb

w*;; w+, UASp>mCherry-CRY2PHR-RhoGAP71E/TM3,Sb

w*;; w+, UASp>CRY2PHR-RhoGAP71E/TM3,Sb

w*;; sqh>sqh-mCherry

w*; w+, UASp>CIBN-pmGFP, mat67; sqh>sqh-mCherry

w*;; mat15

w*; mat67; mat15

w*;; sqh>sqh-mCherry, mat15

w*; mat67; sqh>sqh-mCherry, mat15

Embryo preparation.

Embryos were prepared and collected in a dark room illuminated with red light. Embryos in early stage 6 were dechorionated with 50% bleach for 2 min, washed with water, and mounted using a mixture 50:50 of halocarbon oil 27:700 on a custom-made imaging chamber between an oxygen-permeable membrane (YSI Incorporated) and a glass coverslip.

Imaging.

Embryos were positioned ventrolaterally for observation of the germband. Photoactivation and imaging was performed with a Zeiss LSM 880 confocal microscope with Airyscan detector and equipped with an Argon laser for 488 nm excitation and a diode laser for 561 nm excitation (Carl Zeiss, Germany). Imaging was performed with C-Apo 40X/1.2 NA water-immersion or Plan-Apo 63X/1.40 NA Oil-immersion objectives (Carl Zeiss, Germany). The bright field illumination light was filtered through a Red 25 Kodak Wratten Filter to prevent unwanted photoactivation. Image acquisition was performed with ZEN black software (Carl Zeiss, Germany) using the standard LSM mode unless otherwise noted. For myosin II and Rok imaging, the Airyscan FAST module was utilized. Images were acquired as 10 μm z-stacks with a 1 μm z-step (40X objective, LSM mode) or a 0.7 μm z-step (63X objective, Airyscan FAST), beginning at the apical side of the tissue. Z-stacks were acquired every 15 s. Photoactivation was achieved by scanning with blue laser light ($\lambda =488\text{nm}$) over the same ventrolateral region of the germband that was being imaged, at every imaging z-plane and time-step.

Image analysis.

Confocal time-lapse movies of the cell outlines visualized using CIBN-pmGFP, were projected using the ImageJ distribution Fiji software [69,70] and used to calculate tissue elongation during body axis elongation using the particle image velocimetry (PIV) software PIVlab version 1.41 [71] in MATLAB as previously described [34,71]. To quantify vertex coordination number and number of rearrangements per cell, movies with fluorescently-tagged cell membranes were segmented using the SEGGA tissue segmentation and analysis software [35]. The instantaneous rate of rearrangements was calculated as a moving average of the cell rearrangement rate over 1.5 min windows.

Signal intensity quantification.

For myosin II analysis, still frames shown and confocal movies analyzed correspond to the maximum intensity projections of 5 μm at the apical side of the tissue, starting apically. Images were processed and analyzed using the ImageJ distribution Fiji software [69,70]. The mean junctional myosin intensity at each cell edge was quantified manually using 6 pixel-wide lines (excluding vertex regions) in a 40 μm square region, and the intensity and orientation of each edge was obtained. Medial apical myosin intensity was quantified manually as the mean intensity in a polygon manually drawn just inside the cell membrane outline. At least 10 cells and 40 junctions were analyzed per embryo. Planar polarity was obtained as the ratio of the mean intensity of AP (“vertical”) edges to the mean intensity of DV (“horizontal”) edges for each embryo.

Cell rearrangement analysis.

To quantify the number of rearrangements per cell (Fig. 1), movies with fluorescently-tagged cell membranes were segmented using the SEGGA tissue segmentation and analysis software [35]. To analyze the speed and orientation of rearrangements (Fig. 1 and Fig. S1 in Supplemental Material [37]), cell rearrangements were manually analyzed for 10–25 vertical cell edges per embryo (n=48–69 edges in total from 3–5 embryos per genotype). AP edges were selected at the beginning of axis elongation, and their fate was tracked over 30 min. Edge contraction rate was calculated from changes in edge length during the 2 min before vertex formation. New edge growth rate and orientation were calculated over the 2 min following vertex resolution. Vertex lifetime corresponds to the time between when the edge contracts to a vertex and when the new edge is > 1 μm long. Vertices that did not resolve corresponded to AP edges that contracted to a vertex but did not resolve to form a new edge within the tracking time-window (vertices that formed >20min after the start of the analysis window were not included in the analysis). Vertices that resolved in the wrong direction correspond to AP edges that contracted to a vertex and then resolved to reform an AP cell edge instead of forming a new contact between dorsal and ventral cell neighbors.

Laser ablation.

Samples for ablation studies were prepared in a dark room illuminated with red light. Embryos were dechorionated and mounted in a 50:50 mixture of halocarbon oils 27 and 700 within a custom-made imaging chamber. Ablations were performed using a Chameleon Ultra2 laser set to 710 nm on a Zeiss LSM 880 confocal microscope equipped with a Plan-Apo 63X/1.4 NA oil DIC M27 immersion objective. Embryos expressing optogenetic tools were photoactivated with blue light from an Argon laser ($\lambda =488\text{nm}$) at every z-plane (10 μm z-stacks with 1 μm steps) every 15 s per stack during the 5 min prior to ablations. The following laser settings were used for ablation: 60% laser power, 1 iteration, scan speed of 0.0143 ms per pixel, 1.3 μm line. After ablation, single z-plane images were acquired every 1 s for at least 30 s. For vertex retraction measurements following ablation of junctions, the distance between the vertices connected to the ablated edge were manually measured over time. To generate tissue displacement maps, displacements were quantified by particle image velocimetry (PIV) analysis (Matlab PIVlab version 1.41) [71] using a 5 by 5 grid (3.3 μm between grid points) in a 174 μm² region surrounding the ablation point over the course of 30 s following ablation. For radial plots, mean displacements were calculated in 60° angular bins along the anterior, posterior, dorsal, or ventral tissue axes, taking the ablation point as the origin.

Cell shape index and cell shape alignment analysis.

Cell outlines were segmented using the SEGGA tissue segmentation and analysis software [35]. For each segmented cell within a specified region of interest, the perimeter ($P$) and area ($A$) was measured and the ratio $P/\sqrt{A}$ was calculated. The average shape index $\stackrel{-}{p}$ is the average value of $P/\sqrt{A}$ for all cells. To account for effects of cell packing disorder, the corrected shape index ${\stackrel{-}{p}}_{corr}$ was calculated by subtracting the term ($z-3)/B$ from $\stackrel{-}{p}$, where $z$ is the vertex coordination number (average number of cells meeting at a single vertex) and $B$ is 3.85 [45], as previously described [13]. To calculate the cell shape alignment $Q$, the tissue was triangulated as previously described [13,46,72]. For each triangle, an alignment tensor is calculated, and $Q$ is the magnitude of the area-weighted average of the alignment tensors as described in [13,46,72]. As previously described, the predicted solid-fluid transition line is given by $\stackrel{-}{p}=3.818+(z-3)/B+4b{Q}^2,$ or alternatively, ${\overline{p}}_{corr}=3.818+4b{Q}^2$[13], where $b=0.6\pm 0.2$ based on previously reported vertex model simulation results [46].

Statistical analysis.

Data are presented as mean values +/− the standard error of the mean (SEM). The nonparametric Kruskal-Wallis test with post-hoc Dunn test was used to determine P-values unless otherwise noted.