Abstract
Graph convolutional deep learning has emerged as a promising method to explore the functional organization of the human brain in neuroscience research. This paper presents a novel framework that utilizes the gated graph transformer (GGT) model to predict individuals’ cognitive ability based on functional connectivity (FC) derived from fMRI. Our framework incorporates prior spatial knowledge and uses a random-walk diffusion strategy that captures the intricate structural and functional relationships between different brain regions. Specifically, our approach employs learnable structural and positional encodings (LSPE) in conjunction with a gating mechanism to efficiently disentangle the learning of positional encoding (PE) and graph embeddings. Additionally, we utilize the attention mechanism to derive multi-view node feature embeddings and dynamically distribute propagation weights between each node and its neighbors, which facilitates the identification of significant biomarkers from functional brain networks and thus enhances the interpretability of the findings. To evaluate our proposed model in cognitive ability prediction, we conduct experiments on two large-scale brain imaging datasets: the Philadelphia Neurodevelopmental Cohort (PNC) and the Human Connectome Project (HCP). The results show that our approach not only outperforms existing methods in prediction accuracy but also provides superior explainability, which can be used to identify important FCs underlying cognitive behaviors.
Keywords: Graph deep learning, transformer, fMRI, functional connectivity, human cognition
I. Introduction
Functional magnetic resonance imaging (fMRI) is a non-invasive technique that measures brain activity by detecting changes in the blood-oxygenation-level-dependent (BOLD) signal in brain tissue. It provides valuable insights into the functional organization of the brain. This makes it a useful tool for studying neurological and psychiatric disorders, including autism, Alzheimer’s disease, and schizophrenia [1], [2]. Previous research has demonstrated the potential of functional connectivity (FC) as brain fingerprints for predicting cognitive and behavioral traits [3]–[5] while also reveal brain mechanisms underlying cognitive and behavioral processes [6]–[8]. There is an increasing interest in modeling and extracting connectivity patterns from brain imaging to leverage their potential for advancing neuroscience research.
On the other hand, Graph Neural Networks (GNNs) [2], [9]–[11] have demonstrated great potential for examining brain FC. This is evidenced by the successful application of GNNs to extracting meaningful information from intricate connectivity patterns in neuroimaging studies. GNNs have been used in forecasting cognitive abilities, detecting brain disorders, and deciphering brain signals [12]–[15]. For instance, Qu et al. [16] analyzed FC networks from multi-paradigm fMRIs to predict phenotypes and identify the corresponding biomarkers. Zhao et al. [17] utilized a dynamic graph convolutional network to incorporate topological information from FC graphs into quantifying brain dysfunctions associated with attention deficit hyperactivity disorder (ADHD). Nonetheless, a significant obstacle in using GNNs for neuroimaging is identifying the graph structure representing the connections between brain regions. This challenge is particularly daunting in the case of neuroimaging. Recent studies have suggested utilizing transformer GNNs [18]–[20] as an effective way to address this challenge. Transformer GNNs can analyze a densely connected graph with the use of edge features as additional inputs and no explicit graph structural information is needed. However, the transformer GNNs also have limitations. These models take a simplistic approach by only fusing edge features at the hidden layer, hence leading to difficulty in the interpretation of the model. In addition, transformer GNNs may not perform as well as traditional GNNs when the connectivity between brain regions is weak [21], which is a typical scenario in brain network analysis.
To address the aforementioned limitations of the transformer GNNs, we present a novel framework that utilizes the gated graph transformer (GGT), which is further applied to predict individual cognitive ability based on FCs. Our framework leverages a sophisticated random-walk diffusion strategy to capture the associations between brain regions and incorporates prior spatial knowledge about brain networks. The learnable structural and positional encodings (LSPE) [21] and a gating mechanism are employed to decouple and fuse the learning of node positional encodings (PE) and graph structure, respectively. This allows us to treat initial graph connections as adjustable constraints during optimization. Additionally, the self-attention mechanism, by learning multi-view node feature embeddings and dynamically distributing propagation weights between nodes and their neighbors, can capture more complex relationships between brain regions. By selectively updating node representations based on the neighbors’ representations through the gating mechanism, the network can focus on relevant information while disregarding irrelevant or noisy information, which can improve both computational efficiency and prediction accuracy. Furthermore, we generate an attention heatmap to visualize the strength of the relationship between nodes, thereby bolstering the model’s interpretability, which in turn helps identify significant brain regions associated with cognitive ability. To demonstrate the practical use for the prediction of cognitive behaviors with our proposed method, we perform experiments on two widely used datasets: the Philadelphia Neurodevelopmental Cohort (PNC) [22] and the Human Connectome Project (HCP) [23]. In the analysis, the Computerized Neurocognitive Battery (CNB) scores are used as the prediction labels obtained through computerized tests to measure cognitive ability. Our GGT outperforms several baseline models, including GNN variants and conventional machine learning models. We also conduct an ablation study to measure the contribution of each component of the GGT model to the performance of predicting individual cognitive ability.
Our contributions can be encapsulated as follows:
Simultaneous Integration of Frequency and Structural Information: The incorporation of LSPE in our model enables an advanced integration of frequency-specific information with graph topologies, consequently refining the depiction of functional connectivities and their structural intricacies.
Effective Information Filtering: By ingeniously leveraging the gating mechanism in conjunction with the graph transformer, our model adeptly sifts through vast pools of information, giving precedence to and prioritizing the most pertinent features.
Enhanced Model Interpretability: Our incorporation of an attention heatmap has significantly advanced the model’s interpretability, providing a clearer insight into the essential brain region correlations with cognitive functions.
Empirical Evaluations: Our empirical evaluation on the PNC and the HCP datasets demonstrates a balance between computational efficiency and predictive accuracy, validating the GGT framework’s improved performance over conventional benchmarks.
This paper is systematically organized as follows: Section II sets the stage by providing the foundational background. Our GGT model and the analytical framework are presented in Section III. In Section IV, we empirically assess the GGT model using real datasets including the comparison with other models, the study of sensitivity of important parameters, and the identification of brain functional networks (BFN). The limitations of our model with an outlook on future research are discussed in Section V with conclusion in Section VI.
II. Related Work
A. Message passing graph neural network
Message passing graph neural networks (MPGNNs) are the collections of GNNs using message-passing algorithms to propagate and construct features from a graph structure [25]. Each node in MPGNN will recursively update the self features based on the received messages from its neighbors. There are two types of message-passing algorithms: gated message passing and non-gated message passing. Gated message-passing algorithms use a gate to control the flow of messages between nodes. The gate allows the algorithm to determine which nodes should receive a message and which nodes should not. Non-gated message-passing algorithms do not use a gate but instead rely on the graph structure to propagate messages. In both cases, the messages are propagated through the graph to capture local and global patterns. MPGNNs have been applied to various tasks, such as link prediction [26], node classification, graph generation [27], and embedding representation of graphs in a low-dimensional space [28].
Given the features on node at the layer of the MPGNNs, the message passing model can be generalized as follows.
| (1) |
where , Aggregate, Update are the feature representation functions (i.e., Principal component analysis, linear embedding, neural networks, .etc), aggregation function, and updating function, respectively; and denotes the set of all the neighbor nodes of the node.
B. Transformer GNN
Numerous studies [29], [30] have harnessed the potential of inherent structural data within networks, underscoring its importance in yielding better graph representations. An example is the transformer GNNs. They adopt a sophisticated self-attention mechanism to meticulously capture complex node interactions and incorporate prior knowledge about graph structure, especially for the purposes of PE. However, while they demonstrate many promising applications, current research has also shown their limitations [19], [20]. Specifically, they often have difficulties in dynamic updating of edge features and PE during the phase of information propagation.
In light of these observations, we introduce the GGT model to incorporate prior graph structure information, providing enhanced representational depth for both edge features and PE. A unique feature of the GGT model is the deliberate decoupling of structural and positional information. Specifically, it can dynamically adjust edge features and PE during information exchange, fostering a continuous and refined information flow throughout the graph, and thus mitigating the limitations with conventional transformer GNNs.
III. Methodology
A. Gated graph transformer
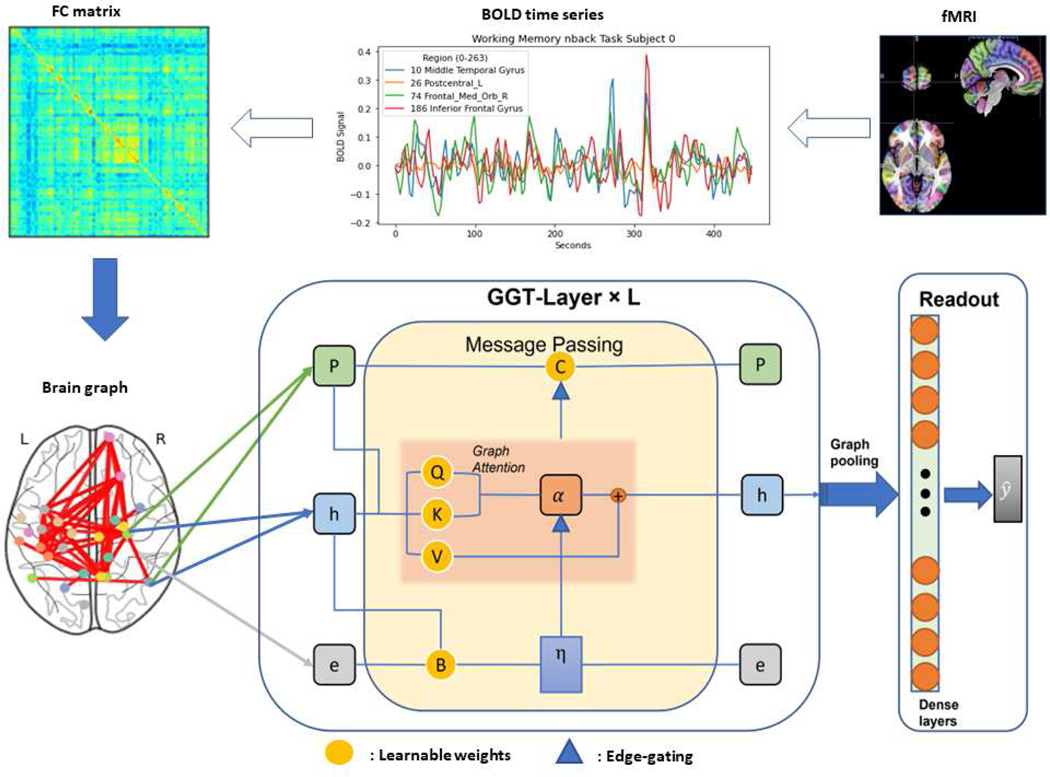
We propose an end-to-end GGT model, as shown in Fig.1, combining the learnable PE [21] with brain network structure to boost the predictive power. Let be a graph with the adjacency matrix and degree matrix , in which nodes and edges represent the brain regions of interest (ROIs) and the associated connections between ROIs, and is the number of nodes. We assume to be the edge features, to be the node features, and to be the node PE at the layer of GGT, where is the number of edges on the graph, and , , and are feature, edge, and PE dimensions, respectively. We begin by learning 3 weights to transform the node features into multiple views. Subsequently, the graph attention mechanism is employed to compute the relevance between paired ROIs. This is accomplished by estimating the similarity scores between multi-view features and assigning varying weights to different neighbors of each node based on their importance, thereby allowing the model to focus on crucial neighbors. Consider a scenario with three learnable embedding weights: , , , where and represent the input and output feature dimensions, respectively. Graph attention is then defined as follows.
Fig. 1:
The proposed pipeline: the fMRI signal is first preprocessed and the brain is parcellated into ROIs, between which functional connectivity is represented as an FC matrix [24]. In the brain network or graph, the node features use FC vectors and the edge features contain both the distance measured in Montreal Neurological Institute (MNI) space and Pearson correlation between brain regions. The combination of , , and PE is used as the input to the stacked GGT layers followed by a readout network for the prediction of the cognitive behaviors.
| (2) |
where and are the non-linear activation functions, e.g., sigmoid and hyperbolic tangent, respectively. The attention score is calculated by taking the dot product of the query and key to quantify their similarity, thereby determining the level of attention that should be directed towards a particular neighbor of each node. The GGT, analogizing to the gated control system to fuse the edge features and PE, can then be formulated in Eq.3.
| (3) |
where , are learnable parameters, and are the normalized and unnormalized edge gating, as defined in Eq.4, that act within these local exchanges, controlling the amount of information transmitted across edges of the graph. The edge gating can be viewed as a form of edge-varying graph filter, where each edge is independently parameterized using both the node and edge features.
| (4) |
where , , are the parameters to fuse the node and edge features for edge gating. Specifically, the edge gating mechanism, represented by and , operates directly on edges and modulates the importance of the message being propagated across the graph. Although edge gating is parameterized using both node and edge features, its primary function is to regulate the communication between nodes along each edge. After acquiring the embeddings for , , and , normalization techniques such as layer and batch normalization are applied to enhance the stability of the learning process. These normalization methods help the model to handle internal covariate shift effectively, resulting in enhanced training performance and more stable convergence.
B. Positional Encoding with MNI Coordinates
The initial PE of the node, denoted as , is obtained through a random walk diffusion process [31], [32] (Eq.5) that combines FC graph frequency information and MNI coordinates, which is a coordinate system used for indexing voxels within a brain volume, applicable to individual MRI volumes and anatomical atlases.
| (5) |
where encodes the probabilities of transitioning from a node to any other node in steps based on the weights of the FC-derived edges connecting them; MX, MY, MZ represent the MNI coordinates, which are oriented along the axes (right, anterior, posterior); and is the dimension of the PE. Importantly, the diffusion process integrates both neighborhood proximity and extended connectivity patterns, thus capturing the graph’s spectral attributes. Building upon the anatomical principle that ”structure determines function,” nodes proximate in MNI coordinates likely exhibit enhanced functional connectivities. While MNI coordinates don’t directly quantify functional connectivity strength, they provide a consistent spatial information for ROIs. Utilizing MNI coordinates, the model adeptly fuses both spatial and frequency domains alongside the convergence of structural and functional insights, thereby augmenting the FC analysis. The label prediction is accomplished by using the readout with one dense layer, taking the mean graph pooling as the input.
C. Objective Function with Constraints
The objective function consists of three terms. In addition to the mean square error (MSE) term, which measures the prediction error, we use a manifold regularization term to smooth the learned PE based on their similarity (Eq. 6). We also include a constraint term in the last graph transformer (GGT) layer to ensure the learned PE is centered and has unit norm. This term encourages similar nodes in the graph to have similar PE vectors, thus promoting smoothness in the embedding space. Specifically,
| (6) |
where with being the learned PE vector of the node, and is the graph Laplacian. During training, each PE vector is normalized to have a unit norm, and the graph-specific mean is subtracted to center the PE vectors for each graph. These differentiable steps combined with the backpropagation procedure ensure the compliance with the constraints during the optimization.
The loss function, denoted by Eq.7, can be approximated as a composite of three key components: the MSE, the manifold regularization with an associated parameter , and a constraint accompanied by a parameter that penalizes deviations from the orthonormality of the PE matrix. This formulation mitigates overfitting by precluding the model from relying on redundant or correlated features throughout the learning process, and by excluding values in the matrix from causing instability or convergence issues. Consequently, this configuration leads to a more robust, precise, and well-generalized model.
| (7) |
where and are the prediction and label, and are the tuning parameter to balance between the prediction accuracy and the smoothness and orthonormality of the learned PE vectors, leading effective graph representation. Notably, the manifold regularization and constraint term are highly dependent on the size of the matrix. As a result, it is important to scale the parameters by the matrix dimensions (i.e., the number of nodes and PE dimension), as shown in Table.I.
TABLE I:
The default hyperparameters.
| Hyperparamter | Value |
|---|---|
| GGT Network Architecture (channels) | [256, 256, 128] |
| Number Neighbor nodes | 30 |
| Initial Learning rate | 1e-3 |
| Maximum Epochs | 100 |
| Optimizer | ADAM |
| Batch size (b) | 4 |
| PE dimension | 32 |
| weight decay | 1e-6 |
IV. Experiment
A. Datasets
1). PNC data:
Our experiments were performed on the Philadelphia Neurodevelopmental Cohort, which included brain fMRI data collected from a total of 975 subjects (463 males and 512 females). We used three distinct fMRI paradigms: resting-state fMRI (rest), emotion task fMRI (emoid), and working memory fMRI (nback). All BOLD scans were acquired using a single-shot, interleaved multislice, gradient-echo, echo-planar imaging sequence on a 3T Siemens TIM Trio whole-body scanner. The voxel resolution was set to 3×3×3 mm with 46 slices, and imaging parameters were optimized to achieve whole-brain coverage with a TR of 3000 ms, TE of 32 ms, and flip angle of 90 degrees. During the rest fMRI scan, subjects were instructed to remain stationary with their eyes open for 6.2 minutes (124 TR). During the emoid fMRI scan, subjects viewed faces displaying different emotions and labeled the emotion type for 10.5 minutes (210 TR). During the nback fMRI scan, subjects performed the nback memory tasks for 11.6 minutes (231 TR) to evaluate their lexical processing and working memory abilities [22]. The computerized neurocognitive battery (CNB) was used to assess individual academic achievement, nonverbal reasoning, and verbal reasoning abilities using the Wide Range Achievement Test (WRAT), Penn Matrix Reasoning Test (PMAT), and Penn Verbal Reasoning Test (PVRT), respectively.
The WRAT [33] is a measure of an individual’s ability in reading, spelling, comprehending, and solving mathematical problems. It is commonly used as a metric for assessing general human intelligence [34].
The PVRT is designed to measure complex cognitive ability that is mediated by language. The task comprises a series of analogy problems modeled after the Educational Testing Service factor-referenced test kit [35].
The PMAT assesses nonverbal reasoning ability by utilizing matrix reasoning problems similar to those used in the Raven’s Progressive Matrices Test [36].
We performed motion correction, spatial normalization, and smoothing with a 3mm Gaussian kernel using SPM12 [37]. Multiple regressions were applied to remove the effects of confounders, including head motion, age, and gender. To further reduce the influence of age on behavioral evaluations, participants under 16 years of age were removed from the study. Consequently, the correlation coefficients for WRAT, PVRT, and PMAT shifted to 0.008, 0.038, and −0.059, respectively, from their previous values of −0.0755, 0.4439, and 0.2843. Our predictive analysis ultimately included 353 subjects (149 males and 204 females) between the ages of 16 and 22 years. Lastly, we identified 264 ROIs utilizing the Power atlas [38] with a sphere radius of 5mm. This radius was a strategic choice to ensure high-resolution capture of functional brain hierarchies and to reduce inter-regional signal overlap, aligning with the protocols of established graph-theoretic methods for accurate representation of the brain’s macroscopic functional structures.
2). HCP data:
The publicly available S1200 Data Release of the Human Connectome Project (HCP) was utilized for this research. The fMRI data was obtained using a whole-brain multiband gradient-echo (GE) echoplanar (EPI) sequence with parameters: TR/TE = 720/33.1 ms, flip angle = 90 degrees, FOV = 208 × 180 mm, matrix = 104 × 90 (RO × PE), multiband factor = 8, echo spacing = 0.58 ms, slice thickness = 2 mm. The resulting normal voxel size was 2.0 × 2.0 × 2.0 mm. The resting-state (R1 and R2) runs were obtained in separate sessions on two different days but only the R1 was used for this study. Tasks included emotion processing, working memory, resting-state, gambling, language, motor, relational processing, and social cognition. In contrast to the PNC dataset, which comprised a trio of metrics, i.e., WRAT, PMAT, and PVRT, the HCP dataset solely included the PMAT assessment.
Our selection protocol was stringent to ensure data quality and completeness. We initially screened 1200 healthy adults from the HCP S1200 Data Release [39], identifying 889 participants with complete datasets across the core 3T MRI paradigms (structural, resting-state, task-related, and diffusion MRI). To align with the PNC, we selected participants with inclusive data on resting-state, working memory, and emotion task fMRI. Additional fMRI task data was integrated when available. The final selected cohort consisted of 862 participants, aged 22–35, split between 409 males and 453 females. The left-to-right encoding runs were applied to avoid potential effects of different phase encoding directions on the findings. More information on the S1200 Data Release of the HCP can be found in the reference manual [39]. The fMRI dataset underwent a standard preprocessing, which included gradient distortion correction, head motion correction, image distortion correction, spatial normalization to standard MNI and intensity normalization [40]. Additionally, preprocessing procedures were utilized to reduce biophysical and other noise sources in the processed fMRI data. These procedures included the removal of linear components related to the 12 motion parameters (original motion parameters and their first-order deviations), linear trend removal, and band-pass filtering (0.01–0.1 Hz). Subsequent to registration, the fMRI data were parcellated into 268 discrete ROIs via the Shen atlas [41]. This process, leveraging groupwise clustering within MNI space, ensured a synthesis of collective and individual anatomical signatures and enabled the refinement of ROI extraction without necessitating spatial constraints.
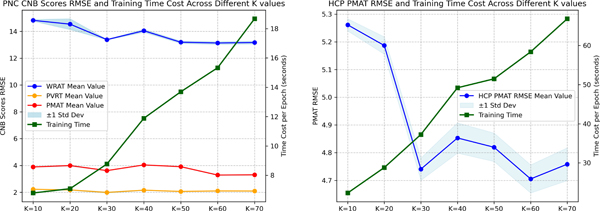
Using a variety of datasets with different preprocessing techniques, such as diverse filtering settings and brain parcellation atlases, allowed us to better assess the robustness of our model by introducing distinct factors. We then utilized the FC obtained from Pearson’s correlation of fMRI data as the initial node features in our model and incorporated edge features by merging a sparse FC matrix (keeping only the top neighbors for each node) with the related MNI distance matrix. The selection of affected the complexity of the graph and the associated computational costs, and its optimization was grounded on the prediction accuracy of resting-state fMRI, as shown in Fig. 2. Consequently, our analysis suggested that = 30 achieves an optimal balance between computational cost and predictive accuracy for both the PNC and HCP datasets. We utilized a multivariate regression approach to predict multiple CNB scores simultaneously in the PNC dataset. To account for the relative importance of each CNB score, we assigned weights of 0.1, 0.55, and 0.35 for WRAT, PVRT, and PMAT scores, respectively, which were optimized based on the range of each score measurement. This approach enabled us to more accurately approximate overall human cognitive function than using a single score metric and allowed for a more comprehensive and nuanced understanding of the underlying cognitive processes, given the diverse range of abilities measured by the CNB scores.
Fig. 2:
Left: the RMSE for PNC CNB scores juxtaposed with epoch-wise time cost against varying values; Right: the RMSE for HCP PMAT scores juxtaposed with epoch-wise time cost against varying values. The experiments were conducted on a system provisioned with an Intel Core i7–12700K processor and NVIDIA RTX 3090 24GB.
B. Experiment set-up
In this study, the data was randomly split into three sets: training, validation, and testing, with a ratio of 70%, 10%, and 20%, respectively. The model was trained on the training set, and its hyperparameters were tuned using the validation set. The performance of the model was evaluated on the test set by calculating the root mean square error (RMSE) between the predicted and observed CNB scores. To reduce the risk of sampling bias, bootstrap analysis was employed to measure and compare the performance of the model. The analysis was repeated 10 times, with each repetition involving random data splitting, model training, and testing. The default hyperparameters were shown in Table.I. Our model scheduled the learning rate using the plateau strategy, which reduced the initial learning rate based on the RMSE of the validation set when the metric plateaus exceeded the patience number.
The results obtained from our proposed model were compared with those of other approaches, and the p-values of pairwise t-tests were reported to demonstrate the statistically significant improvement achieved by our approach. Specifically, we compared GGT with several other methods, including
Linear Regression (LR): a straightforward statistical technique used as a baseline method for CNB score regression. We apply an L2 regularization term and the vectorized upper triangular FC matrix as the input to reduce the number of parameters.
Multi-layer Perceptron (MLP): a neural network that consists of stacked dense layers for FC embeddings. Similar to LR, we use the upper triangular FC matrix as the input, and incorporate dropout and L2 regularization terms to reduce overfitting.
Graph Convolutional Networks (GCN) [42]: a GNN applies graph convolutional filters to combine information from neighboring nodes. In particular, we use the GCN model introduced in [9], which simplifies the graph kernel using Chebyshev polynomials.
Graph Attention Network (GAT) [43]: a GNN uses graph attention to compute hidden representations of nodes by attending to their neighbors through self-attention.
Graph Transformer (GT) [18]: a generalized graph transformer model that incorporates Laplacian eigenvectors as node PE, and utilizes graph attention mechanism on the neighborhood connectivity.
Spectral Attention Network (SAN) [19]: a transformer-based architecture that utilizes learnable PE to capture the Laplace spectrum of a given graph.
GatedGCN-LSPE (GGCN) [20]: an anisotropic GNN that utilizes residual connections, edge gating, and the same LSPE term as GGT in its message-passing mechanism.
For a fair comparison of the predictive performance between our proposed model and other methods, we maintained consistency in the number of GNN/MLP layers, the readout layer, and the parameters of the optional LSPE across all experiments. This allowed us to isolate the effect of the graph attention mechanism and evaluate its impact on the model’s overall performance. We fine-tuned each method’s parameters meticulously, including but not limited to feature channels/neurons per layer, learning rate, and L2 regularization, to ascertain maximal predictive accuracy. The results displayed in Table II and Table III underscore the exceptional predictive performance of our proposed GGT model when compared to alternative methods. The experimental results presented in Table II and Table III indicate that the GGT model attains a notably lower root mean square error (RMSE) in comparison to other models for most fMRI paradigms across both datasets. Although the GGT model may not always claim the top rank (e.g., in the PMAT prediction using nback fMRI on PNC, GT attains the lowest MSE, but the p-value from t-tests is approximately 0.5187, indicating the difference is not statistically significant), its unwavering performance ensures that it frequently ranks among the top two or even higher, further accentuating its robustness. These findings imply that the graph attention mechanism in our proposed model is adaptive at capturing the intricate relationships between brain connectivity patterns and cognitive abilities, resulting in improved prediction accuracy.
TABLE II:
The prediction results of PNC data with different models(mean ± standard deviation).
| Model | Paradigm | WRAT RMSE | p-value | PVRT RMSE | p-value | PMAT RMSE | p-value |
|---|---|---|---|---|---|---|---|
|
| |||||||
| LR | emoid | *14.3332 ± 0.0773 | <1e-5 | 2.3863 ± 0.0809 | <1e-5 | 4.1283 ± 0.1779 | <1e-5 |
| nback | 13.7302 ± 0.5156 | 0.0017 | 2.4570 ± 0.2442 | 1.176e-5 | 4.0618 ± 0.6491 | 0.0161 | |
| rest | 16.7479 ± 0.1272 | <1e-5 | 2.2918 ± 0.0815 | <1e-5 | 4.0996 ± 0.0685 | <1e-5 | |
|
| |||||||
| MLP | emoid | 14.8311 ± 0.0889 | <1e-5 | 2.2003 ± 0.0184 | <1e-5 | 3.8380 ± 0.0229 | <1e-5 |
| nback | 14.7806 ± 1.8392 | 0.0132 | 2.7818 ± 0.6738 | 0.0020 | 3.9569 ± 0.2941 | 0.0001 | |
| rest | 16.7823 ± 0.1171 | <1e-5 | 2.1083 ± 0.0099 | <1e-5 | 3.8560 ± 0.0312 | <1e-5 | |
|
| |||||||
| GCN | emoid | 15.9073 ± 0.0007 | <1e-5 | 2.3066 ± 0.0057 | <1e-5 | 3.8213 ± 0.0023 | <1e-5 |
| nback | 14.2264 ± 0.1086 | <1e-5 | 2.3031 ± 0.0283 | <1e-5 | 3.7225 ± 0.0430 | <1e-5 | |
| rest | *16.6089 ± 0.1950 | <1e-5 | * 2.0941 ± 0.0109 | <1e-5 | 3.8881 ± 0.0108 | <1e-5 | |
|
| |||||||
| GAT | emoid | 16.0062 ± 0.0516 | <1e-5 | 2.4162 ± 0.0164 | <1e-5 | 3.8800 ± 0.0277 | <1e-5 |
| nback | 14.4641 ± 0.0001 | <1e-5 | 2.1784 ± 0.0054 | <1e-5 | 3.5969 ± 0.0304 | <1e-5 | |
| rest | 17.0622 ± 0.2401 | <1e-5 | 2.1457 ± 0.0241 | <1e-5 | 3.9033 ± 0.0316 | <1e-5 | |
|
| |||||||
| GT | emoid | 15.9038 ± 0.0265 | <1e-5 | 2.3992 ± 0.0056 | <1e-5 | *3.7724 ± 0.0334 | <1e-5 |
| nback | 15.0393 ± 0.1169 | <1e-5 | 2.1514 ± 0.0037 | <1e-5 | 3.4735 ± 0.0614 | 0.5187 | |
| rest | 16.9933 ± 0.1175 | <1e-5 | 2.2137 ± 0.0112 | <1e-5 | 3.8591 ± 0.0131 | <1e-5 | |
|
| |||||||
| SAN | emoid | 15.8577 ± 0.0283 | <1e-5 | 2.4263 ± 0.0018 | <1e-5 | 3.8102 ± 0.0021 | <1e-5 |
| nback | 16.1831 ± 0.0668 | <1e-5 | 2.2192 ± 0.0062 | <1e-5 | 3.5888 ± 0.0093 | <1e-5 | |
| rest | 16.7446 ± 0.1126 | <1e-5 | 2.2371 ± 0.0202 | <1e-5 | *3.8379 ± 0.0197 | <1e-5 | |
|
| |||||||
| GGCN | emoid | 15.8852 ± 0.2412 | <1e-5 | *2.1968 ± 0.0231 | <1e-5 | 3.7969 ± 0.0128 | <1e-5 |
| nback | *13.6968 ± 0.0189 | <1e-5 | 2.2591 ± 0.0028 | <1e-5 | 3.5776 ± 0.0296 | <1e-5 | |
| rest | 18.1212 ± 0.1180 | <1e-5 | 2.2428 ± 0.0246 | <1e-5 | 3.9843 ± 0.0130 | <1e-5 | |
|
| |||||||
| GGT | emoid | 13.8288 ± 0.0295 | - | 1.8209 ± 0.0029 | - | 3.3989 ± 0.0077 | - |
| nback | 13.0951 ± 0.0462 | - | 1.9700 ± 0.0097 | - | *3.4873 ± 0.0136 | - | |
| rest | 13.3879 ± 0.0190 | - | 1.9924 ± 0.0043 | - | 3.6198 ± 0.0055 | - | |
p-values are obtained using t-tests to compare the performance of our model with that of other competing models across repeated experiments. Bold values indicate the best results, while those marked with
represent the second-best results.
TABLE III:
The prediction results of HCP data with different models (mean ± standard deviation).
| Model | Paradigm | PMAT RMSE | p-value | Paradigm | PMAT RMSE | p-value |
|---|---|---|---|---|---|---|
|
| ||||||
| LR | rest | 5.0405 ± 0.1228 | <1e-5 | emoid | 5.0786 ± 0.0885 | <1e-5 |
| language | 4.9347 ± 0.0736 | 0.0010 | moto | 4.9889 ± 0.1904 | <1e-5 | |
| wm | *4.8480± 0.0302 | <1e-5 | social | 5.0267 ± 0.1050 | <1e-5 | |
| relational | 5.3336 ± 0.1563 | 1.108e-5 | gambling | 4.9104 ± 0.1109 | <1e-5 | |
|
| ||||||
| MLP | rest | 5.1230 ± 0.0220 | <1e-5 | emoid | 5.0206 ± 0.0067 | <1e-5 |
| language | *4.8807± 0.0046 | 0.0036 | moto | 4.8488 ± 0.0038 | <1e-5 | |
| wm | 4.9068 ± 0.0289 | <1e-5 | social | 4.9811 ± 0.0139 | <1e-5 | |
| relational | 5.1883 ± 0.0173 | <1e-5 | gambling | 4.9050 ± 0.0642 | <1e-5 | |
|
| ||||||
| GCN | rest | 5.1515 ± 0.0457 | <1e-5 | emoid | 5.3406 ± 0.1581 | <1e-5 |
| language | 4.9495 ± 0.0287 | 0.0003 | moto | 5.0865 ± 0.0642 | <1e-5 | |
| wm | 5.0854 ± 0.0506 | <1e-5 | social | *4.8116± 3.6e-5 | <1e-5 | |
| relational | 5.3586 ± 0.1553 | <1e-5 | gambling | 5.0296 ± 0.0593 | <1e-5 | |
|
| ||||||
| GAT | rest | 5.2024 ± 0.0584 | <1e-5 | emoid | 5.0874 ± 0.0041 | <1e-5 |
| language | 5.1928 ± 0.0431 | <1e-5 | moto | *4.7785± 0.0291 | <1e-5 | |
| wm | 5.1237 ± 0.0571 | <1e-5 | social | 4.9302 ± 0.0003 | <1e-5 | |
| relational | 5.4881 ± 0.0987 | <1e-5 | gambling | 4.8727 ± 0.0190 | <1e-5 | |
|
| ||||||
| GT | rest | 4.9170 ± 0.0104 | <1e-5 | emoid | 4.9337 ± 0.0091 | <1e-5 |
| language | 4.9206 ± 0.0083 | 0.0008 | moto | 4.9175 ± 0.0096 | <1e-5 | |
| wm | 4.8937 ± 1.2e-5 | <1e-5 | social | 4.8826 ± 0.0086 | <1e-5 | |
| relational | 5.2106 ± 0.0144 | <1e-5 | gambling | *4.8608± 0.0071 | <1e-5 | |
|
| ||||||
| SAN | rest | *4.8952± 0.0053 | <1e-5 | emoid | *4.9233±0.0047 | <1e-5 |
| language | 4.9186 ± 0.0078 | 0.0008 | moto | 4.9407 ±0.0074 | <1e-5 | |
| wm | 4.8989 ± 0.0039 | <1e-5 | social | 4.8957 ± 0.0078 | <1e-5 | |
| relational | *5.1327± 0.0021 | 0.0001 | gambling | 4.8989 ± 0.0035 | <1e-5 | |
|
| ||||||
| GGCN | rest | 5.5097 ± 0.1026 | <1e-5 | emoid | 5.7735 ± 0.0474 | <1e-5 |
| language | 5.6053 ± 0.2631 | <1e-5 | moto | 5.8380 ± 0.4989 | <1e-5 | |
| wm | 5.7114 ± 0.2643 | <1e-5 | social | 6.2893 ± 0.7541 | <1e-5 | |
| relational | 5.5010 ± 0.0565 | <1e-5 | gambling | 5.9816 ± 0.4169 | <1e-5 | |
|
| ||||||
| GGT | rest | 4.7406 ± 0.0403 | - | emoid | 4.6006 ± 0.0440 | - |
| language | 4.6856 ± 0.1748 | - | moto | 4.5487 ± 0.0888 | - | |
| wm | 4.6568 ± 0.0377 | - | social | 4.4884 ± 0.0386 | - | |
| relational | 4.9416 ± 0.1178 | - | gambling | 4.4327 ± 0.0238 | - | |
p-values are obtained using t-tests to compare the performance of our model with that of other competing models across repeated experiments. Bold values indicate the best results, while those marked with
represent the second-best results.
C. Ablation study
In the ablation study, we evaluated the impact of several factors on the GGT model’s performance, emphasizing the importance of positional representations with or without atlas information. We confined our analysis to resting-state fMRI data to facilitate a more coherent comparison process. To assess the effectiveness of various model configurations, we studied the following scenarios: GGT exclusively employing random walk PE, GGT incorporating solely atlas-based information PE, and GGT without any valid initial PE, achieved by setting the tensor to an all-ones tensor. As demonstrated by Table.IV, both MNI and RW PEs substantially impacted CNB score prediction, emphasizing their crucial roles within the GGT model. Remarkably, the use of MNI alone performed well as using only RW PE. This finding highlighted the potential and utility of MNI as a PE for transformer models in brain network analysis.
TABLE IV:
Ablation Analysis of PNC and HCP Data in Resting-State fMRI.
| PE | Scores | Dataset | RMSE | p-value | ∆RMSE |
|---|---|---|---|---|---|
|
| |||||
| MNI | WRAT | PNC | 13.9318 ± 0.0332 | <1e-5 | 3.88 % |
| PVRT | PNC | 2.0255 ± 0.0044 | <1e-5 | 1.41 % | |
| PMAT | PNC | 3.8151 ± 0.0078 | <1e-5 | 5.17 % | |
| PMAT | HCP | 5.1304 ± 0.0363 | <1e-5 | 8.22 % | |
|
| |||||
| RW | WRAT | PNC | 14.1127 ± 0.0315 | <1e-5 | 5.23 % |
| PVRT | PNC | 2.0661 ± 0.0073 | <1e-5 | 3.44 % | |
| PMAT | PNC | 3.8252 ± 0.0077 | <1e-5 | 5.45 % | |
| PMAT | HCP | 5.1194 ± 0.0312 | <1e-5 | 7.99 % | |
|
| |||||
| × | WRAT | PNC | 14.7059 ± 0.1188 | <1e-5 | 9.65 % |
| PVRT | PNC | 2.1133 ± 0.0133 | <1e-5 | 5.80 % | |
| PMAT | PNC | 3.8574 ± 0.0102 | <1e-5 | 6.34 % | |
| PMAT | HCP | 5.2282 ± 0.0388 | <1e-5 | 10.29% | |
The p-values are obtained using t-test to compare the performance of the original settings and alternative model configurations throughout multiple experiments. The symbol × indicates that no valid PE is utilized, while the ∆Performance column displays the percentage decrease in the predicted MSE.
D. Attention heatmap and model interpretation
To gain insights into the relationship between cognitive abilities and BFNs [44], we used the attention heatmap to interpret our model. In the PNC dataset, we utilized the Power atlas to identify the following BFNs: Sensory/somatomotor network, Auditory network, Cingulo-opercular task control Network, Default mode network, Visual network, Frontoparietal Task Control, Salience network, Subcortical network, Ventral attention Network, Dorsal attention network, and Cerebellar. For the HCP dataset, we employed the Shen atlas to define the following BFNs: Medial Frontal network, Frontoparietal network, Default Mode network, Subcortical-cerebellum network, Motor network, and Visual network (Visual I, Visual II, Visual Association). Our analysis of the attention heatmap allowed us to identify the BFNs that were most strongly associated with cognitive abilities, providing valuable insights into the functional organization of the human brain. To ensure that our model produces an interpretable heatmap for the FC derived from the Pearson correlation values, we made several adjustments. Specifically, for neighbor nodes and , we set , made identical to , and ignored the normalization denominator in the attention calculation, as shown in Eq.8.
| (8) |
To calculate the attention heatmap for each fMRI paradigm, we utilized the hyperbolic tangent activation function and generated the heatmap by taking the mean of attention scores for all subjects and scaling with min-max. We then visualized the heatmaps using a hot color map and nearest interpolation, as shown in Fig.5 and Fig.6 for the PNC and HCP datasets, respectively.
Fig. 5:
The attention heatmaps displayed correspond to the multivariate regression analysis of WRAT, PVRT, and PMAT for the (a) rest: resting-state, (b) emoid: emotion task, and (c) nback: working-memory task fMRI paradigms, respectively, conducted on the PNC dataset.
Fig. 6:

The attention heatmaps displayed correspond to the regression analysis of PMAT for the (a) emotion processing , (b) working memory, (c) resting-state, (d) gambling , (e) language, (f) motor, (g) relational processing, and (h) social cognition fMRI paradigms, respectively, conducted on the HCP dataset.
V. Discussion
A. Brain functional network identification via GGT
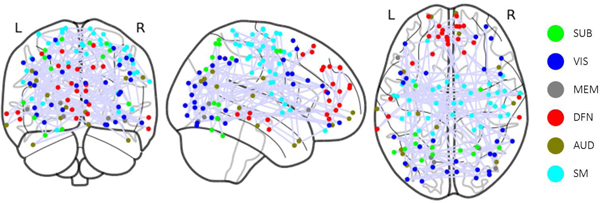
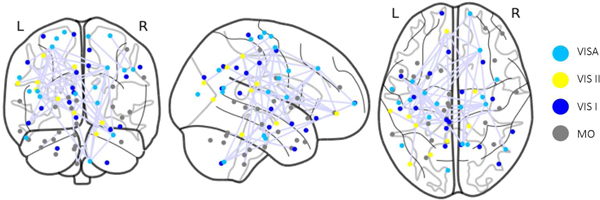
The heatmap generated from GGT enables the examination of associations of specific BFNs with cognitive functions. This analysis not only confirms existing research findings on the relationship between BFNs and human cognitive function but also provides new insights. The study of the PNC dataset using the Power atlas reveals that numerous BFNs are distinctly visible on the heatmap, even without imposing the group sparsity constraint, as shown in Fig.3. Some BFNs, such as sensory/somatormotor, memory retrieval, auditory, visual, and subcortical networks, display more pronounced connectivity patterns. High attention scores in the heatmap are also evident in some ROIs within the default mode, salience, cerebellar, ventral, cingulo-opercular task control, and dorsal attention networks. Previous research has shown that the Sensory/somatormotor network plays a vital role in various cognitive functions, including verbal creativity, memory retrieval, imaginative processes, and feedback-based control of vocal pitch [45]–[47]. The cingulo-opercular task control network is crucial for cognitive control and maintains cognitive functions accessible for current processing, acting as a downstream node in the functional network [48], [49]. Memory, a central component of human cognitive function, is essential for numerous tasks [50]. In this experiment, WRAT scores are employed to gauge human cognitive ability, reflecting a subject’s academic aptitude. However, this measurement may result in an underestimation of the memory retrieval network’s significance. According to [51], auditory discrimination tasks can detect attention and cognitive control networks, but there is scarce evidence of a direct link between the auditory network and human cognitive ability. During specific learning processes, communication between visual cortex regions occurs in the early stages when subjects are still familiarizing themselves with visual cues and not yet achieving high task completion rates [52]. The identification of the visual network may also be attributed to the data collection context [22], [53], as subjects were instructed to concentrate on a crosshair during fMRI data collection, potentially engaging visual networks. Although the cerebellum is traditionally associated with movement control, recent studies [54], [55] suggest its involvement with cognitive functions such as language, attention, and responses to fear or stress. The DMN, the largest functional network in the brain with numerous connections to other brain regions, has been closely linked to ongoing cognition in both goal-directed and goal-irrelevant tasks, as shown in prior research [45], [56]–[58]. The Shen atlas is then utilized to parcellate brain from the HCP dataset to define BFNs. The resulting clusters differ from those obtained from the PNC dataset. Notably, the motor, Visual I, Visual II, and Visual Association networks, as shown in Fig.4, exhibit higher attention scores compared to other BFNs identified in [59]. Additionally, our analysis reveals two distinct but highly correlated connectivity patterns within the motor network, suggesting the potential for further refining and identifying new BFNs based on the graph attention mechanism, a promising avenue for future research.
Fig. 3:
ROIs Visualization for the BFNs with high attention scores in the PNC; SUB: Subcortical, VIS: Visual, MEM: Memory Retrieval, DFN: Default Mode, AUD: Auditory, SM: Sensory/somatomotor.
Fig. 4:
ROIs Visualization for the BFNs with high attention scores in the HCP; VISA: Visual Association, VIS II: Visual II, VIS I: Visual I, MO: Motor.
The heatmaps generated from various fMRI paradigms using our GGT model demonstrate great consistency, affirming the reliability of our approach in BFN identification. Moreover, our findings suggest that attention scores are a reliable metric for assessing the importance of BFNs in the human brain. Therefore, it is crucial to consider different datasets and parcellation schemes when studying BFNs as these factors significantly impact the identification and characterization of these networks, as evident from the observed differences in attention scores in our study. Further research is necessary to elucidate the underlying mechanisms and functional significance of these BFNs and their relationships with cognitive processes.
B. Limitations and future work
Despite the success in predicting cognitive ability demonstrated by our work, several limitations exist, which warrant further investigation. First, our analysis assumes static FC, overlooking the dynamics of brain network [60]. Future studies should examine time-varying fMRI series and dynamic FC. Second, although our study exhibits consistency in heatmaps generated from different fMRI tasks or paradigms, their fusion [16], [61] may yield more meaningful results. In addition, the combination with other modalities such as MEG can combine both spatial and temporal information, leading to better prediction of cognitive behaviors.
While the attention mechanism presents a promising way for interpreting the results from GNN, incorporating additional metrics such as the gradient in conjunction with visualizing the gate parameters, may yield a more holistic comprehension of the model’s layered dynamics. Additionally, examining classification tasks across different conditions and disorders can provide insights into the subtleties of the gating mechanism in distinguishing between group differences.
VI. Conclusion
In conclusion, we introduce an innovative framework that leverages the GGT to predict individual cognitive abilities based on FCs derived from fMRI. Several methods such as random-walk diffusion strategy, LSPE, and gating mechanism are integrated into a novel pipeline, leading to both improved accuracy and interpretability. By incorporating spatial information, our model uncovers complex relationships between brain regions. Furthermore, the self-attention mechanism strengthens the interpretability of the model, enabling us to identify important FCs. The experimental results on two large brain studies (e.g., PNC and HCP) demonstrate that the framework can deliver valuable insights into the relationships between FC and cognition. In comparison with several conventional learning methods (e.g., MLP, LR) and GNN models (e.g., GCN, GAT, GT), our proposed framework offers a promising approach with superior prediction accuracy and interpretability, which can find widespread applications in brain research.
Acknowledgments
This work was partially supported by NIH Grants R01 GM109068, R01 MH121101, R01 MH104680, R01 MH107354, P20 GM103472, P20 GM144641, R01 REB020407, R01 EB006841, and 2U54MD007595, NSF Grant #1539067, NSFC Grant No. 62202442, and Anhui Provincial Natural Science Foundation Grant No. 2208085QF188.
Contributor Information
Gang Qu, Department of Biomedical Engineering, Tulane University, New Orleans, LA, USA..
Anton Orlichenko, Department of Biomedical Engineering, Tulane University, New Orleans, LA, USA..
Junqi Wang, Department of Radiology, Cincinnati Children’s Hospital Medical Center, Cincinnati, OH, USA..
Gemeng Zhang, Department of Biomedical Engineering, Tulane University, New Orleans, LA, USA..
Li Xiao, School of Information Science and Technology, University of Science and Technology of China and Institute of Artificial Intelligence, Hefei Comprehensive National Science Center, Hefei, China. Kun Zhang is with the Department of Computer Science, Xavier University of Louisiana, New Orleans, LA, USA..
Kun Zhang, Department of Computer Science, Xavier, University of Louisiana, New Orleans, LA, USA..
Tony W. Wilson, Institute for Human Neuroscience, Boys Town National Research Hospital, Boys Town, NE, USA. Julia M. Stephen is with Mind Research Network, Albuquerque, NM, USA.
Julia M. Stephen, Mind Research Network, Albuquerque, NM, USA.
Vince D Calhoun, Tri-Institutional Center for Translational Research in Neuroimaging and Data Science (TReNDS), (Georgia State University, Georgia Institute of Technology, Emory University), Atlanta, GA, USA..
Yu-Ping Wang, Department of Biomedical Engineering, Tulane University, New Orleans, LA, USA..
References
- [1].Hu W et al. , “Adaptive sparse multiple canonical correlation analysis with application to imaging (epi)genomics study of schizophrenia,” IEEE Transactions on Biomedical Engineering, vol. 65, no. 2, pp. 390–399, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Yan W et al. , “Deep learning in neuroimaging: Promises and challenges,” IEEE Signal Processing Magazine, vol. 39, no. 2, pp. 87–98, 2022. [Google Scholar]
- [3].Wang J et al. , “Functional network estimation using multigraph learning with application to brain maturation study,” Human brain mapping, vol. 42, no. 9, pp. 2880–2892, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Du Y et al. , “Classification and prediction of brain disorders using functional connectivity: promising but challenging,” Frontiers in neuroscience, vol. 12, p. 525, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Guo X et al. , “Shared and distinct resting functional connectivity in children and adults with attention-deficit/hyperactivity disorder,” Translational psychiatry, vol. 10, no. 1, p. 65, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Hu W et al. , “Interpretable multimodal fusion networks reveal mechanisms of brain cognition,” IEEE transactions on medical imaging, vol. 40, no. 5, pp. 1474–1483, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Qu G et al. , “A graph deep learning model for the classification of groups with different IQ using resting state fmri,” in Medical Imaging 2020: Biomedical Applications in Molecular, Structural, and Functional Imaging, vol. 11317, International Society for Optics and Photonics. SPIE, 2020, pp. 52–57. [Google Scholar]
- [8].Orlichenko A et al. , “Latent similarity identifies important functional connections for phenotype prediction,” IEEE Transactions on Biomedical Engineering, vol. 70, no. 6, pp. 1979–1989, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Kipf TN and Welling M, “Semi-supervised classification with graph convolutional networks,” international conference on learning representations, 2017. [Google Scholar]
- [10].Lei D et al. , “Graph convolutional networks reveal network-level functional dysconnectivity in schizophrenia,” Schizophrenia Bulletin, vol. 48, no. 4, pp. 881–892, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Parisot S et al. , “Disease prediction using graph convolutional networks: Application to autism spectrum disorder and alzheimer’s disease,” Medical Image Analysis, vol. 48, pp. 117–130, 2018. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1361841518303554 [DOI] [PubMed] [Google Scholar]
- [12].Li X et al. , “Braingnn: Interpretable brain graph neural network for fmri analysis,” Medical Image Analysis, vol. 74, p. 102233, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Tang H et al. , “Contrastive brain network learning via hierarchical signed graph pooling model,” IEEE Transactions on Neural Networks and Learning Systems, pp. 1–13, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Orlichenko A et al. , “Phenotype guided interpretable graph convolutional network analysis of fmri data reveals changing brain connectivity during adolescence,” in Medical Imaging 2022: Biomedical Applications in Molecular, Structural, and Functional Imaging, vol. 12036. SPIE, 2022, pp. 294–303. [Google Scholar]
- [15].Wang J et al. , “Dynamic weighted hypergraph convolutional network for brain functional connectome analysis,” Medical Image Analysis, p. 102828, 2023. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S1361841523000889 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Qu G et al. , “Ensemble manifold regularized multi-modal graph convolutional network for cognitive ability prediction,” IEEE Transactions on Biomedical Engineering, pp. 1–1, 2021. [DOI] [PubMed] [Google Scholar]
- [17].Zhao K et al. , “A dynamic graph convolutional neural network framework reveals new insights into connectome dysfunctions in adhd,” NeuroImage, vol. 246, p. 118774, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Dwivedi VP and Bresson X, “A generalization of transformer networks to graphs,” AAAI Workshop on Deep Learning on Graphs: Methods and Applications, 2021. [Google Scholar]
- [19].Kreuzer D et al. , “Rethinking graph transformers with spectral attention,” Advances in Neural Information Processing Systems, vol. 34, pp. 21618–21629, 2021. [Google Scholar]
- [20].Ying C et al. , “Do transformers really perform badly for graph representation?” Advances in Neural Information Processing Systems, vol. 34, pp. 28877–28888, 2021. [Google Scholar]
- [21].Dwivedi VP et al. , “Graph neural networks with learnable structural and positional representations,” in International Conference on Learning Representations, 2022. [Online]. Available: https://openreview.net/forum?id=wTTjnvGphYj [Google Scholar]
- [22].Satterthwaite TD et al. , “Neuroimaging of the philadelphia neurodevelopmental cohort,” Neuroimage, vol. 86, pp. 544–553, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Van Essen DC et al. , “The human connectome project: a data acquisition perspective,” Neuroimage, vol. 62, no. 4, pp. 2222–2231, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Orlichenko A et al. , “Identifiability in functional connectivity may unintentionally inflate prediction results,” ArXiv, pp. arXiv–2308, 2023. [Online]. Available: 10.48550/arXiv.2308.01451 [DOI] [Google Scholar]
- [25].Gilmer J et al. , “Neural message passing for quantum chemistry,” in International conference on machine learning. PMLR, 2017, pp. 1263–1272. [Google Scholar]
- [26].Zhang M and Chen Y, “Link prediction based on graph neural networks,” Advances in neural information processing systems, vol. 31, 2018. [Google Scholar]
- [27].Simonovsky M and Komodakis N, “Graphvae: Towards generation of small graphs using variational autoencoders,” in Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, October 4–7, 2018, Proceedings, Part I 27. Springer, 2018, pp. 412–422. [Google Scholar]
- [28].Zhang C et al. , “Heterogeneous graph neural network,” in Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, 2019, pp. 793–803. [Google Scholar]
- [29].Yan J et al. , “Modeling spatio-temporal patterns of holistic functional brain networks via multi-head guided attention graph neural networks (multi-head gagnns),” Medical Image Analysis, vol. 80, p. 102518, 2022. [DOI] [PubMed] [Google Scholar]
- [30].Tang H et al. , “Signed graph representation learning for functional-to-structural brain network mapping,” Medical image analysis, vol. 83, p. 102674, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Fouss F et al. , “Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation,” IEEE Transactions on Knowledge and Data Engineering, vol. 19, no. 3, pp. 355–369, 2007. [Google Scholar]
- [32].Masuda N et al. , “Random walks and diffusion on networks,” Physics reports, vol. 716, pp. 1–58, 2017. [Google Scholar]
- [33].Test RA, “Wide range achievement test 4 (wrat4),” Journal of Occupational Psychology, Employment and Disability, vol. 11, no. 1, p. 49, 2009. [Google Scholar]
- [34].Kareken DA et al. , “Reading on the wide range achievement test-revised and parental education as predictors of iq: comparison with the barona formula,” Archives of Clinical Neuropsychology, vol. 10, no. 2, pp. 147–157, 1995. [PubMed] [Google Scholar]
- [35].Nettles MT et al. , “Performance and passing rate differences of african american and white prospective teachers on praxistm examinations: a joint project of the national education association (nea) and educational testing service (ets),” ETS Research Report Series, vol. 2011, no. 1, pp. i–82, 2011. [Google Scholar]
- [36].Raven J, “The raven’s progressive matrices: change and stability over culture and time,” Cognitive psychology, vol. 41, no. 1, pp. 1–48, 2000. [DOI] [PubMed] [Google Scholar]
- [37].Ashburner J, Barnes G, Chen C-C, Daunizeau J, Flandin G, Friston K, Kiebel S, Kilner J, Litvak V, Moran R et al. , “Spm12 manual,” Wellcome Trust Centre for Neuroimaging, London, UK, vol. 2464, no. 4, 2014. [Google Scholar]
- [38].Power JD et al. , “Functional network organization of the human brain,” Neuron, vol. 72, no. 4, pp. 665–678, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].WU-Minn H, “1200 subjects data release reference manual,” URL https://www.humanconnectome.org, 2017. [Google Scholar]
- [40].Glasser MF et al. , “The minimal preprocessing pipelines for the human connectome project,” Neuroimage, vol. 80, pp. 105–124, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Shen X et al. , “Groupwise whole-brain parcellation from resting-state fmri data for network node identification,” Neuroimage, vol. 82, pp. 403–415, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Qu G et al. , “Brain functional connectivity analysis via graphical deep learning,” IEEE Transactions on Biomedical Engineering, vol. 69, no. 5, pp. 1696–1706, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Veličković P et al. , “Graph attention networks,” in International Conference on Learning Representations, 2018. [Online]. Available: https://openreview.net/forum?id=rJXMpikCZ [Google Scholar]
- [44].Xu J et al. , “Large-scale functional network overlap is a general property of brain functional organization: Reconciling inconsistent fmri findings from general-linear-model-based analyses,” Neuroscience & Biobehavioral Reviews, vol. 71, pp. 83–100, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Chenji S et al. , “Investigating default mode and sensorimotor network connectivity in amyotrophic lateral sclerosis,” PLoS One, vol. 11, no. 6, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Paracampo R et al. , “Sensorimotor network crucial for inferring amusement from smiles,” Cerebral cortex, vol. 27, no. 11, pp. 5116–5129, 2017. [DOI] [PubMed] [Google Scholar]
- [47].Chang EF et al. , “Human cortical sensorimotor network underlying feedback control of vocal pitch,” Proceedings of the National Academy of Sciences, vol. 110, no. 7, pp. 2653–2658, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Sadaghiani S and D’Esposito M, “Functional characterization of the cingulo-opercular network in the maintenance of tonic alertness,” Cerebral Cortex, vol. 25, no. 9, pp. 2763–2773, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Wallis G et al. , “Frontoparietal and cingulo-opercular networks play dissociable roles in control of working memory,” Journal of Cognitive Neuroscience, vol. 27, no. 10, pp. 2019–2034, 2015. [DOI] [PubMed] [Google Scholar]
- [50].Unsworth N et al. , “Working memory and fluid intelligence: Capacity, attention control, and secondary memory retrieval,” Cognitive psychology, vol. 71, pp. 1–26, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Westerhausen R et al. , “Identification of attention and cognitive control networks in a parametric auditory fmri study,” Neuropsychologia, vol. 48, no. 7, pp. 2075–2081, 2010. [DOI] [PubMed] [Google Scholar]
- [52].Bogdanov P et al. , “Learning about learning: Mining human brain subnetwork biomarkers from fmri data,” PloS one, vol. 12, no. 10, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Satterthwaite TD et al. , “The philadelphia neurodevelopmental cohort: A publicly available resource for the study of normal and abnormal brain development in youth,” Neuroimage, vol. 124, pp. 1115–1119, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Wolf U et al. , “Evaluating the affective component of the cerebellar cognitive affective syndrome,” The Journal of neuropsychiatry and clinical neurosciences, vol. 21, no. 3, pp. 245–253, 2009. [DOI] [PubMed] [Google Scholar]
- [55].Stoodley CJ, “The cerebellum and cognition: evidence from functional imaging studies,” The Cerebellum, vol. 11, no. 2, pp. 352–365, 2012. [DOI] [PubMed] [Google Scholar]
- [56].Anticevic A et al. , “The role of default network deactivation in cognition and disease,” Trends in cognitive sciences, vol. 16, no. 12, pp. 584–592, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].BUCKNER R et al. , “The brain’s default network: Anatomy, function, and relevance to disease,” Annals of the New York Academy of Sciences, vol. 1124, no. 1, pp. 1–38, 2008. [DOI] [PubMed] [Google Scholar]
- [58].Sormaz M et al. , “Default mode network can support the level of detail in experience during active task states,” Proceedings of the National Academy of Sciences, vol. 115, no. 37, pp. 9318–9323, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Finn ES et al. , “Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity,” Nature neuroscience, vol. 18, no. 11, pp. 1664–1671, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Cai B et al. , “Capturing dynamic connectivity from resting state fmri using time-varying graphical lasso,” IEEE Transactions on Biomedical Engineering, vol. 66, no. 7, pp. 1852–1862, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Hu W et al. , “Deep collaborative learning with application to the study of multimodal brain development,” IEEE Transactions on Biomedical Engineering, vol. 66, no. 12, pp. 3346–3359, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]