Abstract
Quantitative photoacoustic tomography (qPAT) holds great potential in estimating chromophore concentrations, whereas the involved optical inverse problem, aiming to recover absorption coefficient distributions from photoacoustic images, remains challenging. To address this problem, we propose an extractor-attention-predictor network architecture (EAPNet), which employs a contracting–expanding structure to capture contextual information alongside a multilayer perceptron to enhance nonlinear modeling capability. A spatial attention module is introduced to facilitate the utilization of important information. We also use a balanced loss function to prevent network parameter updates from being biased towards specific regions. Our method obtains satisfactory quantitative metrics in simulated and real-world validations. Moreover, it demonstrates superior robustness to target properties and yields reliable results for targets with small size, deep location, or relatively low absorption intensity, indicating its broader applicability. The EAPNet, compared to the conventional UNet, exhibits improved efficiency, which significantly enhances performance while maintaining similar network size and computational complexity.
Keywords: Quantitative photoacoustic tomography, Optical inverse problem, Deep learning, Image reconstruction, Absorption coefficient estimation
1. Introduction
Photoacoustic tomography (PAT) is a rapidly advancing imaging modality with rich optical contrast and high acoustic resolution, even at depths reaching several centimeters [1], [2], [3]. The photoacoustic (PA) effect states that biological media irradiated by pulsed laser light can absorb photon energy and subsequently generate local acoustic pressure increases through thermoelastic expansion [4]. This effect is universally observed in both endogenous chromophores, such as oxygenated and deoxygenated hemoglobin, and exogenous contrast agents like nanoparticles [5], [6], [7]. From the PA signals detected by ultrasonic transducers placed around the object’s surface, PA images can be reconstructed by solving a well-established acoustic inverse problem [8], [9], [10]. Quantitative photoacoustic tomography (qPAT) aims to estimate chromophore concentrations from multispectral PA images, and the key challenge is to solve the optical inverse problem referring to recovering absorption coefficients from raw PA images [11], [12]. Specifically, is proportional to the product of and the local fluence , while only the former is directly related to the concentration of chromophores in spectroscopic analysis [13], [14], [15].
In an earlier study, Cox et al. introduced a fixed-point iteration algorithm to recover the distribution by iteratively solving a system of equations [16]. On this basis, Zhang et al. [17] recently developed a pixel-wise reconstruction method based on a two-step iterative algorithm (TSIA), yielding noteworthy results in both simulated and experimental data. A more rigorous strategy is to employ an optimization framework, in which desired optical properties are iteratively updated, typically absorption and scattering coefficients, until the difference between the result obtained from forward modeling and measured data is minimized [18], [19], [20], [21]. Although with high theoretical accuracy, methods within this category are computationally intensive and time-consuming, rendering real-time measurements nearly unfeasible. Some researchers attempted to directly measure fluence distributions through other techniques, such as diffuse optical tomography [22] and acousto-optic theory [23], while these methods require additional devices in a standard PA imaging system.
In the last decade, deep neural networks, especially convolutional neural networks (CNN), have made significant strides, emerging as promising tools in biomedical imaging [24], [25], [26], [27], [28], [29], [30], [31], [32], [33]. In the context of qPAT, models adopt an end-to-end supervised learning manner and automatically learn the abstract feature representations from input data [34], [35]. Cai et al. [29] initially extended a residual UNet to this field and gained promising results. Luke et al. [30] introduced an O-Net architecture consisting of two parallel UNets networks dedicated to the tasks of blood oxygen saturation () estimation and vascular segmentation, respectively. Bench et al. [31] extended the O-Net framework to accommodate the 3-dimensional(3-D) nature of the PA process by using 3-D neural units. Li et al. [32] proposed a dual-path network comprising two UNets to estimate the absorption coefficient and fluence, respectively. Real images of fluence, absorption coefficient, and initial pressure were all used for supervised training, resulting in a joint loss function that more effectively guides parameter optimization. Zou et al. [33] integrated the anatomical features extracted from the ultrasound image by a pre-trained ResNet-18 in a standard UNet to enhance the network performance on estimating .
However, these models are founded on a UNet architecture [36]. The vanilla UNet comprises a contracting–expanding structure and a linear projection layer. Although UNet has shown impressive performance in previous studies, its nonlinear modeling capacity exclusively depends on the contracting–expanding structure. This may potentially hinder its efficiency in addressing highly nonlinear regression tasks. While increasing the width and depth of the contracting–expanding structure can compensate for this drawback, it also leads to a proliferation in network complexity. Additionally, convolutional attention mechanisms [37], [38], [39] have been widely proven to improve model performance in various imaging modalities (e.g. PAT [26], [27] and computed tomography [28]). However, there is a lack of related research in the qPAT domain.
On the other hand, inspired by the pixel imbalance issue in dense object detection [40], [41], we find that the mean squared error (MSE) loss [29], [33], a plain per-pixel loss function commonly used in previous qPAT research, may result in the network delivering adequate performance only in specific imaging regions. Specifically, regions of high absorption or large sizes contribute the majority of the MSE loss value, exerting a dominant influence on the adjustment of network parameters. Consequently, predicted values associated with other regions are not adequately optimized during training. This optimization imbalance can cause severe spatial variations in accuracy across the output images, rendering corresponding networks unsuitable for applications involving targets of low absorption or small size. Furthermore, training with a biased focus on specific regions can result in an incomplete learning of input data, hindering the network from capturing fundamental features, and consequently deteriorating both its performance and generalization capability.
To address the above limitations, we propose a deep learning-based method utilizing an extractor-attention-predictor network architecture (EAPNet) and a balanced loss function (Bloss) for the optical inverse problem. Within the EAPNet, a contracting–expanding structure functions as an extractor for learning contextual representations containing global dependency information. Meanwhile, a pixel-wise multilayer perceptron (MLP) serves as a predictor, establishing the mapping relationship between latent features and the desired output, which can efficiently reinforce the network’s nonlinear modeling capacity on a per-pixel basis. Within the E-P structure, a spatial attention module is employed to improve the capturing and utilization of important information in input images. Moreover, the Bloss function normalizes the impact of absorption intensity and size of each region on the loss value by utilizing a joint weighting factor to enhance the consistency of accuracy across the entire predicted image. Simulated and real-world validations demonstrate that our method achieves the best image-wise quantitative scores in almost all experimental scenarios and broader applicability to targets with diverse properties. Additionally, it significantly outperforms other competing methods in qualitative assessment, providing clean edges and superior agreement with ground truth images. The EAPNet proves to be more suitable and efficient compared to UNet, enhancing the accuracy of predicted images while maintaining similar network parameters and computational complexity.
2. Method
2.1. Physical fundamentals
PA images represent initial acoustic pressure distributions generated inside media. The pressure , at a given point , can be formulated as:
| (1) |
where , , and are the local absorption coefficient, scattering coefficient, anisotropy, and fluence, respectively. denotes the Grüneisen coefficient, which is typically assumed to be a constant of 1. Then, is directly equal to the product of and . The fluence map can be described by a light propagation model such as the well-established radiative transfer equation [4], [42] or its approximate forms (e.g., the -Eddington model [43] and diffusion equation [44]). For simplicity, and are typically treated as homogeneous constants since their spatial variations, compared to , within biological tissues are relatively small [17]. Then, Eq. (1) can be expressed in a simplified form:
| (2) |
where represents the mapping function from to , describing the forward process of the PA effect. Mathematically, the optical inverse problem in qPAT aims to find an inverse operator that satisfies .
The operator is featured with high nonlinearity, due to depends on in an intricate manner [12], [45]. Moreover, has a global dependency on the image, stemming from the term (Eq. (2)). It suggests that , in turn, has a global dependency on the image. The coupling of high nonlinearity and global dependency presents a challenge in solving .
2.2. EAPNet architecture
The proposed extractor-attention-predictor network (EAPNet) is shown in Fig. 1 and can be formulated as:
| (3) |
| (4) |
where , , and denote the operators of extraction, attention module and prediction, respectively. The extractor adopts a contracting–expanding structure, in which the contracting path learns multiscale spatial dependencies by gradually expanding the receptive field through downsampling feature maps. After aggregating the information received from skip connections, the expanding path outputs a feature map containing contextual representation vectors of all pixels. The feature map is then proceeded by a convolutional block spatial attention module (sAM) [37], [38], [46], to generate an attention-augmented feature map . Finally, a multilayer perceptron (MLP) is utilized to establish the mapping function between the and on a per-pixel basis, which is mathematically a vector-to-pixel regression task.
Fig. 1.
Overview of the proposed EAPNet architecture, which can be divided into three successive phases: extractor, spatial attention module, and predictor. The output feature map in the first row is fed into the second row as the input. and denote the height and width of feature maps. The numbers annotated alongside the network indicate their corresponding number of channels. The MLP consists of two hidden layers, each having 16 channels. It maps to as a vector-to-pixel regression task.
Within the sAM, two maps ( and ) that aggregate channel information [37] are first extracted by conducting the max-pooling and average-pooling operations on along the channel dimension. Then, the spatial attention map is derived by sequentially using a 5 5 convolution layer and a softmax activation function to the concatenated and , which is expressed as:
| (5) |
where is a hyper-parameter. We empirically designate as 0.5 in this study, which appears to be an optimal value as presented in the section “Parameters selection” of the supplementary materials. The attention-augmented feature map is eventually derived by dot-multiplying the raw with the attention map . Compared with the seminal work in Ref. [37], there are several modifications in our attention module. Firstly, we do not employ channel attention due to the absence of discernible improvements in the associated experiment. Moreover, since our sAM operates on the feature map from the extractor, which already integrates contextual information, the convolutional layer in our sAM utilizes a reduced kernel size of 5 5. Particularly, we employ a softmax function to activate our sAM because it computes spatial attention weights by considering the entire image, unlike the commonly used sigmoid function [28], [37], [38], which computes attention weights independently on a per-pixel basis. Specifically, the Softmax produces the output of each pixel based on its relative intensity in the input data. Since the attention map sums to a constant value of 1, we argue that utilizing the softmax can introduce a competitive attention mechanism. This mechanism benefits spatial information interaction, enhancing the network’s capacity to distinguish and leverage informative pixels.
2.3. Loss function
To address the unbalanced optimization issue during training, as discussed in Section 1, we adopt a balanced loss function (Bloss), which, mathematically, is a form of weighted MSE loss and is expressed as:
| (6) |
where and denote the number of pixels and the tissue index, respectively. is a factor corresponding to the th tissue. Within the Bloss, the absolute error is divided by the to normalize the absorption intensity. Additionally, the set by the reciprocal of tissue-wise volume fractions is employed to balance the contributions of tissues with varying pixel occupancies.
2.4. Network training
All models shared the same training scheme and were implemented using PyTorch on an NVIDIA GTX 3090Ti graphics card. The ADAM optimizer was employed with an initial learning rate of 10−4. All models were trained for 100 epochs with a batch size of 32. The source code is available at https://github.com/WZQ7/EAPNet.
3. Experiment
3.1. Simulation data generation
We generated four simulation datasets, as outlined in Table 1, to consider multiple application scenarios. Fluence distributions are simulated using MCXLAB [47]. Each simulation process lasts for one nanosecond to sufficiently capture contributions from scattered photons, and a total of photons are emitted. Photons leaving the domain are terminated. The simulation domain of the vasculature (Va) and sparse target (ST) datasets is 128 × 64 pixels with a single line source placed along the surface. The random shape (RS) and acoustic reconstruction (AR) datasets are simulated within a 256 × 256 pixels field, and line sources are placed along all four sides to ensure wide-field illumination. For all datasets, the pixel length is 0.1 mm, and the Grüneisen parameter is assumed constant at 1, leading to being equal to the product of and . Each dataset comprises 4000 annotated image pairs, divided into training, validation, and testing sets in an 8:1:1 ratio. Networks are trained and evaluated on their respective datasets. The validation set is utilized for selecting hyperparameters. Before being fed into a network, all input images were normalized to their maximum values.
Table 1.
A brief summary of all simulation datasets.
| Datasets | Major characteristics |
|---|---|
| RS | Graded absorption ranges; a deep located and small tissue. |
| Va | Complex vessel structures. |
| ST | Sparsely distributed targets. |
| AR | Low image quality; acoustic noise and artifacts. |
(i) Random shape dataset. The dataset consists of circular phantoms with a physical radius of 25.6 mm. Each phantom comprises four random shapes mimicking biological tissues and a small circle. Typical geometries are illustrated in Fig. 2. Tissue positions are determined based on prescribed locations with random perturbations, to enrich the data distribution. Different absorption ranges are assigned to these tissues, as detailed in Table S3 of the supplementary materials. Throughout the entire phantom, a reduced scattering coefficient of 1 and an anisotropy parameter of 0.9 are consistently utilized.
Fig. 2.
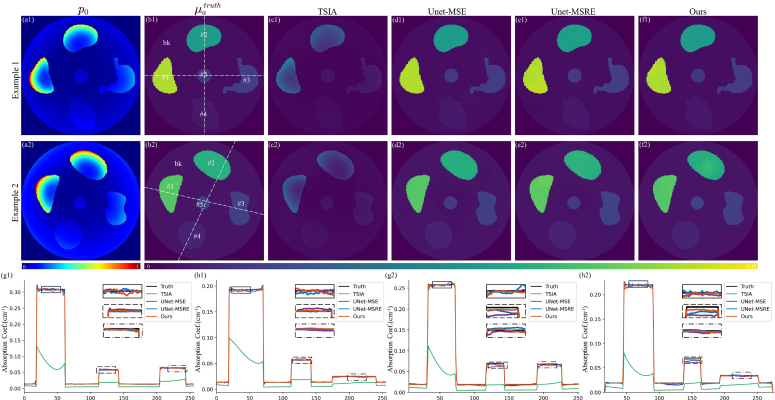
Example images of the RS dataset. Tag numbers indicate the example index. (a) Raw PA images. (b) Ground truth, . (c–f) obtained from different methods. (g) Profiles along the horizontal white dotted line in (b). (h) Profiles along the vertical white dotted line in (b). In (g) and (h), the contained insets show the enlarged parts within the black boxes that are labeled by corresponding line styles. “bk” is the abbreviation of “background”. Quantitative metrics of example images are detailed in Table S4.
(ii) Vasculature dataset. The purpose of this dataset is to assess our method’s performance in retrieving intricate structures and subtle textures. Each phantom is constructed based on a two-layer skin model measuring 128 × 64 pixels. The top three rows of pixels represent the epidermis layer, while the remainder constitutes the dermis layer. The vessels utilized are sourced from the publicly available FIVES dataset comprising 800 fundus photographs [48]. Each raw image is downsampled and then evenly divided into nine patches of 128 × 64 pixels, with a 25% overlap between adjacent patches for data augmentation. After a manual review to remove those with insufficient or unclear vessels, each remained patch is implanted in an individual dermis layer. All patches are used only once, ensuring a distinct vascular structure for each phantom. Optical properties are determined using empirical equations and parameters from Refs. [31], [49] to enhance data realism. Additionally, pixel-wise variations in absorption are introduced to augment textural richness.
(iii) Sparse target dataset. This dataset aims to assess the effectiveness of our method in reconstructing sparsely distributed and small-size targets, in which the phantoms employ the identical two-layer skin model and optical parameter assignment approach as those in the Va dataset. The sparsely distributed vascular structures are extracted from a publicly available lung image dataset.1 As shown in Fig. 4(b), the imaging field is largely occupied by the skin tissue.
Fig. 4.
Example images of the ST dataset. Tag numbers indicate the example index. (a) Raw PA images. (b) Ground truth, . (c–f) obtained from different methods. The ROI of each example is delineated by a white dotted box in (b) and magnified for better visualization. These ROIs are also used for calculating CgCNR. Quantitative metrics of example images are detailed in Table S4.
(iv) Acoustic reconstruction dataset. The PA images in the three mentioned datasets represent ideal initial pressure distributions. However, real images are susceptible to corruption from factors such as system noise and imperfect detection conditions during the acquisition process. To account for these influences, we created the AR dataset by simulating the acoustic measurement process on the RS dataset using the MATLAB toolbox k-Wave [50]. The images are reconstructed from the simulated time-domain PA signals using a time reversal algorithm [9]. Implementation details are available in the supplementary materials.
3.2. Phantom experiment
To verify the feasibility of our method in real-world scenarios, we applied it to phantom images acquired by a commercial photoacoustic tomography system mentioned in Section 3.4. The geometries of real phantoms are close to that of the RS dataset. Each phantom, with a radius of 9.6 mm, contains five inclusions, as shown in Fig. 6. Based on the recipe in Ref. [51], we first mixed 1% agar powder solution (A-1296, Sigma) with 20% Intralipid to produce a base solution. The solutions constituting different tissues were prepared by adding corresponding concentrations of India ink into the base solution. We provide more details on preparing phantoms in supplementary materials.
Fig. 6.
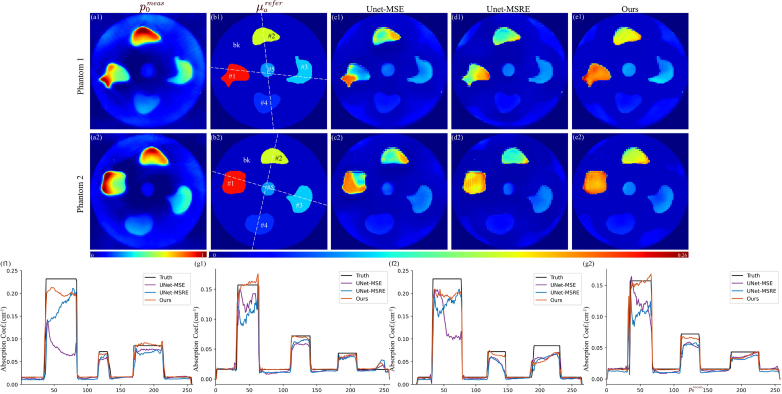
Results of the phantom experiment. Tag numbers indicate the example index. (a) Experimentally acquired PA images. (b) Reference value of determined experimentally. (c–e) images obtained from different methods. (f) Profiles along the horizontal white dotted line in (b). (g) Profiles along the vertical white dotted line in (b). “bk” is the abbreviation of “background”.
In the acquisition process, we initially averaged the raw time-domain signals from ten repetitive measurements to improve the signal-to-noise ratio (SNR). Subsequently, a high-accuracy model-based iterative reconstruction algorithm [8], [52] processed the averaged signals and generated raw images. Finally, these images were normalized to their maximum values to remove scalar factors associated with system parameters.
All networks used in this phantom experiment were trained on the AR dataset. For quantitative assessment of network performance, we annotated several phantom images with determined by the following experimental procedure. First, each used material was poured into a mold consisting of two glass slides and a U-shaped spacer to prepare a corresponding slab-shaped test sample. Subsequently, a spectrophotometer (LAMBDA 950, PerkinElmer) equipped with an integrating sphere was used to measure the total transmittance and reflectance of these samples. Optical properties were then derived via the inverse adding-doubling algorithm [53], assuming a constant anisotropy of 0.9.
3.3. In vivo experiment
We conducted a preliminary validation in an in vivo scenario. A healthy nude female mouse weighing approximately 15 grams was imaged after anesthesia. Cross-sectional PA images were acquired at the abdominal region, mainly treating kidneys as the regions of interest. The acquisition adhered to the procedure outlined in Section 3.2. Animal procedures adhered to the Guidelines for Care and Use of Laboratory Animals of Shanghai Jiao Tong University, and experiments received approval from its Animal Ethics Committee. Since constructing a specialized training dataset for in vivo data is non-trivial and usually regarded as an independent research task, the networks for this initial experiment are trained using synthetic data. We explain this dataset in the supplementary materials.
3.4. PAT imaging system
All experimental data was acquired by a commercial small-animal multispectral optoacoustic tomography system (MSOT inVision256, iThera Medical). The light source consists of a pulsed Nd:YAG laser (9 ns pulse width and 10 Hz repetition rate) and an optical parametric oscillator, enabling a multi-wavelength irradiation ranging from 680 to 1200 nm. Incident light is delivered to sample surfaces via a ten-arm fiber bundle to achieve 360-degree illumination in the imaging plane. PA waves are recorded by a ring-shaped transducer array consisting of 256 cylindrical-focused elements characterized by a central frequency of 5 MHz and a bandwidth of 60%. These transducer elements are arranged in a 270-degree arc with a radius of 40.5 mm.
3.5. Comparative methods
For comparison, we employed the two-step iterative algorithm (TSIA) [17] as a conventional method and UNet (Fig.S1) as the network benchmark. UNet was trained with mean squared error (UNet-MSE) and mean squared relative error loss (UNet-MSRE) to explore the impact of different loss functions. We provide details on the implementation of comparative methods in supplementary materials. Notably, the comparison experiments focus on the superiority of EAPNet as a fundamental architecture, and only UNet was employed here because, in the context of qPAT, most models are built upon UNet. Strategies, including employing multiple UNets [30], [32] and using modified convolution units (such as the residual block [29] and 3-D block [31]), could be readily applied to EAPNet and achieve corresponding enhancements from an improved performance baseline, while these are beyond the scope of our investigation.
Table 2.
Quantitative evaluation (MEAN ± SD) for 400 test images from the RS dataset. SD denotes the standard deviation of a single metric across the test set. As explained in Section 3.6, the tissue-wise metrics (i.e., and ) refer to the result within a specific tissue region. The tSD refers to the standard deviation across the mean values of tissue-wise metrics of a given method. The tMRE and tPSNR are used as image-wise metrics. The regions corresponding to the labels “bk” and “#1”–“#5” can be found in Fig. 2.
| Algorithms | Tissue-wise metrics |
tSD | tMRE (top) tPSNR (bottom) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| bk | #1 | #2 | #3 | #4 | #5 | ||||
| Unet-MSE | 0.058 ± 0.013 | 0.007 ± 0.003 | 0.009 ± 0.003 | 0.031 ± 0.009 | 0.054 ± 0.026 | 0.064 ± 0.036 | 0.023 | 0.037 ± 0.009 | |
| Unet-MSRE | 0.034 ± 0.007 | 0.022 ± 0.006 | 0.023 ± 0.009 | 0.026 ± 0.012 | 0.033 ± 0.015 | 0.052 ± 0.029 | 0.010 | 0.032 ± 0.007 | |
| Ours | 0.014 ± 0.006 | 0.016 ± 0.005 | 0.016 ± 0.005 | 0.017 ± 0.006 | 0.018 ± 0.007 | 0.021 ± 0.012 | 0.002 | 0.017 ± 0.005 | |
| PSNR (dB) | Unet-MSE | 22.437 ± 1.731 | 40.498 ± 2.513 | 38.268 ± 2.419 | 28.673 ± 2.106 | 24.571 ± 3.148 | 24.338 ± 4.507 | 7.057 | 29.797 ± 1.428 |
| Unet-MSRE | 27.284 ± 1.654 | 31.009 ± 1.995 | 31.230 ± 2.344 | 30.097 ± 2.587 | 28.567 ± 2.917 | 25.749 ± 4.064 | 2.010 | 28.989 ± 1.318 | |
| Ours | 35.517 ± 2.528 | 34.005 ± 2.273 | 33.891 ± 2.137 | 33.702 ± 2.255 | 33.241 ± 2.595 | 33.611 ± 3.999 | 0.722 | 33.994 ± 1.703 | |
3.6. Evaluation metrics
Evaluation metrics in previous studies may inadequately reflect the overall accuracy of predicted images in some cases. Per-pixel metrics, such as mean absolute error and mean relative error (MRE) [32], [54], are inclined to reflect the error levels within those large tissues. The peak signal-to-noise ratio (PSNR), directly computed from the maximum , may result in a biased value when there is a significant disparity in between different tissues [55]. To address these limitations, two metrics adopted in this study, and , are computed on a per-tissue basis. Specifically, tissue-wise metrics ( or ) are computed initially, where represents the tissue index. Evaluation metrics for the predicted image ( or ) are subsequently derived by averaging these tissue-wise metrics. is formulated as:
| (7) |
| (8) |
where and denote the domain of the th tissue and the number of pixels within it, respectively. is the number of tissue types. can be formulated as:
| (9) |
| (10) |
| (11) |
where indicates the maximum possible value within .
Moreover, the standard deviation across tissue-wise metrics (the mean values of or on the test set are adopted here) is employed to assess the consistency of prediction accuracy among various tissues for each method, and we denote it as tSD.
In addition, we introduce a constrained generalized contrast-to-noise ratio (gCNR) [55], [56], [57], denoted as CgCNR, to evaluate the efficacy of our method in recovering intricate or fine structures. CgCNR is exclusively applied to the ST and Va datasets since the RS and AR datasets only consist of simple structures.
Previous studies have proven that gCNR is directly associated with the separability of the target from the background, offering a better metric of distinction (or sharpness) compared to contrast and contrast-to-noise ratio [57]. However, gCNR fails to consider the agreement between the target distribution and the ground truth, and only a high distinction does not match the goal of qPAT. CgCNR is a modification of the standard gCNR and can be expressed as follows:
| (12) |
where denotes the pixel value. and represent the probability density functions of the target and background, specifically referring to the vascular and dermal areas in this context. From Eq. (12), CgCNR shares an identical optimization problem with gCNR but poses a lower limit for as an additional constraint. Under this constraint, the CgCNR only evaluates the separability of target pixels sufficiently close to the ground truth. Target pixels whose predicted values below are directly treated as false negatives because they lack practical significance for quantification applications. In our study, was set to 75% of the mean value of in vascular regions. Implementation details are available in the supplementary materials.
4. Result
4.1. Simulation data analysis
Upon a preliminary observation of Fig. 2, Fig. 3, Fig. 4, Fig. 5, we can easily find that there is a depth-dependent decline in the intensities of images due to fluence attenuation. In addition, the TSIA produces acceptable results only in certain cases [Figs. 3(c1,c2) and 4(c1,c2)] because the -Eddington model used performs poorly in regions near light sources or with high absorption. Therefore, TSIA demonstrates inadequate robustness against variations in illumination conditions and the optical properties of the imaging medium. Due to the significantly lower accuracy of TSIA compared to DL-based methods across all datasets, we focus our comparison on DL-based methods in the following parts.
Fig. 3.
Example images of the Va dataset. Tag numbers indicate the example index. (a) Raw PA images. (b) Ground truth, . (c–f) obtained from different methods. The ROI of each example is delineated by a white dotted box in (b) and magnified for better visualization. These ROIs are also used for calculating CgCNR. (g) Profiles along the horizontal red dotted line in (b). (h) Profiles along the vertical red dotted line in (b). Quantitative metrics of example images are detailed in Table S4.
Fig. 5.
Example images of the AR dataset. Tag numbers indicate the example index. (a) Reconstructed PA images as inputs, . (b) Initial pressure distributions (perfect PA images). (c) Ground truth, . (d–f) images obtained from different methods. (g) Profiles along the horizontal white dotted line in (c). (h) Profiles along the vertical white dotted line in (c). In (g) and (h), the contained insets show the enlarged parts within the black boxes that are labeled by corresponding line styles. “bk” is the abbreviation of “background”. Quantitative metrics of example images are detailed in Table S4.
(i) Random shape dataset. As shown in Table 2, our method outperforms other algorithms significantly in terms of both and comparisons. Moreover, tissue-wise evaluation reveals a distinct variation in the accuracy of both UNet-MSE and UNet-MSRE across different tissues. UNet-MSE’s performance deteriorates as tissue absorption decreases, leading to relatively large errors in regions with low absorption (e.g., the background and tissues #3–#5), while UNet-MSRE exhibits relatively subpar performance in the small-sized tissue #5. The non-uniform accuracy causes unreliable results in practical applications, as the target tissues are not always of high absorption or large size. Our method is insensitive towards tissue properties and enables greater uniformity in accuracy across tissues, as evidenced by the minimal tSD. This also implies that our method has broader applicability.
There is no marked visual distinction among the images of different methods (Fig. 2). The profiles and their magnified regions display subtle differences, indicating that results predicted by our method provide closer concordance with the ground truth.
(ii) Vasculature dataset. Due to the highly unbalanced contributions of different tissues to the loss value, the performance of both UNet-MSE and UNet-MSRE varies significantly across them, as shown in Table 3. While excelling in the epidermal and dermal regions, respectively, the two methods underperform in vascular regions of significant medical interest. Our method provides distinct superiority in vascular regions and also better overall accuracy, achieving the lowest , the second-highest , and the minimal .
Table 3.
Quantitative evaluation (MEAN ± SD) for 400 test images from the Va dataset. A detailed explanation of all used metrics can be found in Table 2.
| Algorithms | Tissue metrics |
tSD | tMRE (top) tPSNR (bottom) | |||
|---|---|---|---|---|---|---|
| Epidermis | Dermis | Vessel | ||||
| Unet-MSE | 0.023 ± 0.028 | 0.349 ± 0.150 | 0.186 ± 0.055 | 0.133 | 0.186 ± 0.058 | |
| Unet-MSRE | 0.024 ± 0.023 | 0.065 ± 0.010 | 0.254 ± 0.155 | 0.100 | 0.114 ± 0.051 | |
| Ours | 0.062 ± 0.030 | 0.070 ± 0.013 | 0.081 ± 0.030 | 0.008 | 0.071 ± 0.020 | |
| PSNR (dB) | Unet-MSE | 36.142 ± 8.917 | 4.160 ± 3.522 | 13.832 ± 2.271 | 13.392 | 18.045 ± 2.812 |
| Unet-MSRE | 31.777 ± 4.944 | 22.051 ± 1.373 | 11.462 ± 4.168 | 8.296 | 21.763 ± 1.540 | |
| Ours | 22.700 ± 3.525 | 20.468 ± 2.929 | 20.168 ± 3.169 | 1.130 | 21.112 ± 2.738 | |
Fig. 3 showcases three skin models with progressively enhanced epidermal absorption, representing Caucasian, Asian, and African skin types. The enlarged images display regions of interest (ROIs) highlighted by white dotted boxes in Fig. 3(b). UNet-MSE performs poorly in preserving delicate features and structures. It outputs vessels with blurred edges and may produce non-existent vessels, as indicated by the red arrow in Fig. 3(d3). In cases of relatively strong epidermal absorption, UNet-MSRE fails to adequately compensate for the effects of fluence attenuation, notably underestimating of deep vessels, thereby rendering them unobservable in the images. Our method reconstructs vascular structures with exceptional fidelity and well-defined edges, demonstrated by the highest score in Table S5 of the supplementary materials. The line profiles illustrate that the predicted of our method exhibits a greater degree of alignment with the ground truth. Meanwhile, UNet-MSE and UNet-MSRE are sensitive to the epidermal absorption intensity, resulting in a decrease in image quality with its escalation. In contrast, our method shows sufficient robustness to this variation.
(iii) Sparse target dataset. As illustrated in Table 4, the sparse distribution of blood vessels significantly impacts the performance of UNet-MSRE, resulting in considerable estimation biases in vascular regions. This is because MSRE only corrects for the unbalanced impact of absorption intensity on loss values. In contrast, our method utilizes the weight factor to effectively address the training imbalance resulting from the difference in pixel occupancy among tissues, making it robust to sparse targets, as evidenced by significantly better performance in vascular regions and the lowest .
Table 4.
Quantitative evaluation (MEAN ± SD) for 400 test images from the ST dataset. A detailed explanation of all used metrics can be found in Table 2.
| Algorithms | Tissue-wise metrics |
tSD | tMRE (top) tPSNR (bottom) | |||
|---|---|---|---|---|---|---|
| Epidermis | Dermis | Vessel | ||||
| Unet-MSE | 0.010 ± 0.019 | 0.171 ± 0.050 | 0.173 ± 0.058 | 0.076 | 0.118 ± 0.032 | |
| Unet-MSRE | 0.017 ± 0.014 | 0.045 ± 0.011 | 0.645 ± 0.187 | 0.290 | 0.236 ± 0.060 | |
| Ours | 0.049 ± 0.030 | 0.055 ± 0.016 | 0.076 ± 0.030 | 0.012 | 0.060 ± 0.020 | |
| PSNR (dB) | Unet-MSE | 43.686 ± 9.127 | 13.136 ± 3.048 | 15.888 ± 3.032 | 13.799 | 24.237 ± 2.378 |
| Unet-MSRE | 34.397 ± 4.380 | 25.700 ± 2.257 | 5.587 ± 2.565 | 12.066 | 21.895 ± 1.391 | |
| Ours | 24.204 ± 3.025 | 24.123 ± 2.551 | 22.444 ± 3.533 | 0.811 | 23.590 ± 2.568 | |
Representative images of three skin types (Caucasian, Asian, and African) are displayed in Fig. 4. Similar to the findings in Fig. 3, UNet-MSE overly smooths vessel boundaries, sacrificing structural details. The images produced by UNet-MSRE fail to adequately distinguish deep vessels. Our method recovers vessels of superior sharpness, which is also demonstrated by the highest in Table S6 of the supplementary materials.
(iv) Acoustic reconstruction dataset. From Fig. 5, it is evident that the images are distorted compared to the ideal images due to noise and artifacts. Metrics for 400 test images are listed in Table 5. As expected, utilizing non-ideal input data results in reduced performance across all methods compared to the results presented in Table 2. The tMRE and tPSNR demonstrate that the overall performance of our method ranks at the top. Meanwhile, our method surpasses other methods in , suggesting our method effectively provides consistent accuracy for different tissues. The profile images further confirm the accuracy advantage of our method, particularly in tissue #5 and the background.
Table 5.
Quantitative evaluation (MEAN ± SD) for 400 test images from the AR dataset. A detailed explanation of all used metrics can be found in Table 2. The regions corresponding to the labels “bk” and “#1”–“#5” can be found in Fig. 5.
| Algorithms | Tissue-wise metrics |
tSD | tMRE (top) tPSNR (bottom) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| bk | #1 | #2 | #3 | #4 | #5 | ||||
| Unet-MSE | 0.148 ± 0.064 | 0.040 ± 0.022 | 0.043 ± 0.025 | 0.092 ± 0.051 | 0.108 ± 0.059 | 0.101 ± 0.047 | 0.038 | 0.088 ± 0.022 | |
| Unet-MSRE | 0.085 ± 0.025 | 0.075 ± 0.025 | 0.071 ± 0.024 | 0.100 ± 0.044 | 0.110 ± 0.054 | 0.139 ± 0.050 | 0.023 | 0.097 ± 0.019 | |
| Ours | 0.035 ± 0.018 | 0.068 ± 0.031 | 0.066 ± 0.030 | 0.082 ± 0.042 | 0.072 ± 0.040 | 0.073 ± 0.042 | 0.015 | 0.066 ± 0.018 | |
| PSNR (dB) | Unet-MSE | 12.214 ± 2.704 | 26.052 ± 3.277 | 25.764 ± 3.420 | 20.187 ± 3.597 | 18.748 ± 2.844 | 18.150 ± 2.844 | 4.749 | 20.186 ± 1.555 |
| Unet-MSRE | 19.345 ± 2.242 | 16.678 ± 1.481 | 17.533 ± 1.501 | 17.816 ± 2.267 | 18.143 ± 2.952 | 13.991 ± 1.654 | 1.660 | 17.251 ± 1.137 | |
| Ours | 23.868 ± 2.445 | 19.518 ± 2.297 | 20.045 ± 2.241 | 20.243 ± 3.037 | 21.864 ± 3.402 | 21.133 ± 3.438 | 1.449 | 21.112 ± 1.592 | |
4.2. Phantom data analysis
Fig. 6 shows the phantom experiment results. The acquired images contain severe artifacts and have weak visibility in the deep area. There is a noticeable degradation across all evaluation indicators compared to the simulation results since the networks were only trained on the AR dataset. Although possessing similar internal geometries and optical properties, the AR dataset still fails to sufficiently represent the phantom data, leading to networks lacking an understanding of the features specific to the experimental domain. Here are several specific manifestations. In our imaging system, the ring-like transducer array provides only 270-degree angular coverage around the object, leaving the top 90 degrees uncovered to accommodate the mouse holder. The limited view results in signal loss and significant reconstruction errors in neighboring regions, notably for tissue #2 and the upper regions of tissues #1 and #3. Moreover, significant errors can be observed at phantom boundaries due to mismatches in illumination conditions. Despite these challenges, it seems that all methods can output reasonable images, suggesting that networks trained on synthetic datasets, to some extent, can be applicable to real data with sufficient similarity.
Quantitative indicators of the phantom results are shown in Table 6. Our method obtains the best scores for the tMRE and tPSNR. For the images, our method effectively corrects out the spatial varying fluence, and tissues obtain enhanced signal homogeneity. This advantage is further shown by the profile images. Particularly for the background area with low fluence, both UNet-MSE and UNet-MSRE are inclined to underestimate , whereas our method consistently aligns closely with the reference value.
Table 6.
Quantitative evaluation of the phantom results in Fig. 6 (MEAN ± SD). A detailed explanation of all used metrics can be found in Table 2. The regions corresponding to the labels “bk” and “#1”–“#5” can be found in Fig. 6.
| Algorithms | Tissue-wise metrics |
tMRE (top) tPSNR (bottom) | ||||||
|---|---|---|---|---|---|---|---|---|
| bk | #1 | #2 | #3 | #4 | #5 | |||
| UNet-MSE | 0.253 ± 0.029 | 0.407 ± 0.121 | 0.222 ± 0.023 | 0.243 ± 0.075 | 0.137 ± 0.006 | 0.315 ± 0.090 | 0.263 ± 0.008 | |
| UNet-MSRE | 0.270 ± 0.014 | 0.319 ± 0.088 | 0.277 ± 0.026 | 0.284 ± 0.062 | 0.218 ± 0.015 | 0.330 ± 0.118 | 0.283 ± 0.015 | |
| Ours | 0.194 ± 0.073 | 0.165 ± 0.004 | 0.097 ± 0.001 | 0.240 ± 0.082 | 0.137 ± 0.002 | 0.110 ± 0.043 | 0.157 ± 0.009 | |
| PSNR (dB) | UNet-MSE | 4.285 ±0.640 | 6.673 ± 2.174 | 11.333 ± 0.530 | 11.309 ± 1.751 | 15.883 ± 0.322 | 9.231 ± 2.216 | 9.786 ± 0.334 |
| UNet-MSRE | 6.030 ± 1.307 | 8.833 ± 2.316 | 10.021 ± 0.556 | 9.828 ± 1.306 | 12.420 ± 0.598 | 8.286 ± 2.169 | 9.236 ± 0.032 | |
| Ours | 3.649 ± 1.309 | 13.274 ± 0.745 | 15.476 ± 0.321 | 10.958 ± 1.769 | 15.682 ± 0.011 | 14.544 ± 1.044 | 12.264 ± 0.071 | |
Notably, while experimentally obtained of each tissue offers a reasonable reference, uncertainties introduced by human and equipment factors are unavoidable.
4.3. In vivo data analysis
Fig. 7 shows the results of the cross-sectional abdominal images at a wavelength of 760 nm. In the acquired images, the signal is stronger on the body surface, and the visibility diminishes in the central region. Our method efficiently corrects internal fluence attenuation, restoring the arterial signal to a relatively normal magnitude. In the profiles, signals of identical organs exhibit a depth-dependent decrease, whereas they become more homogeneous in predicted images obtained from our method, as indicated by the corresponding black dotted lines and red arrows [Fig. 7(c–f)]. To enable a convenient comparison between two measurements of the same slice, we horizontally flipped example 1 ( image) to generate example 2, which, for the network, is equivalent to distinct imaging data [58], [59]. The predicted values for corresponding locations from the two images show satisfactory agreement, further confirming the network’s effectiveness.
Fig. 7.
Results of the in vivo experiment. Pictures with the same label number correspond to the results of one example. (a) Experimentally acquired PA images. (b) The predicted images obtained from our method. (c, e) Profiles of along the two white dotted lines in (a). (d, f) Profiles of the predicted images along the two white dotted lines in (a). Description of markers: A: artery; IVC: inferior vena cava; K: kidney; Sp: spine; Brc: boundary region of the renal cortex.
It is important to mention that, as our network was not trained on specialized in vivo data, its effectiveness shown in this validation is relatively limited, and only qualitative analysis was conducted. The lack of labeled in vivo data undoubtedly hinders our network from reaching its full performance potential. We elaborate on these challenges associated with in vivo applications in Section 5.
4.4. Ablation study
An ablation study was conducted on the RS and Va datasets, examining the network architecture, loss function, and attention module:
(1) Network ablation: UNet-Bloss;
(2) Loss ablation: EAPNet with the MSE loss function (EAPNet-MSE) and EAPNet with the MSRE loss function (EAPNet-MSRE).
(3) Attention module ablation: removing the proposed sAM from EAPNet (EPNet-Bloss), and replacing our activation function with the sigmoid function in the sAM [EAPNet-Bloss (sigmoid)].
The results for the RS and Va datasets are listed in Table 7 and Table S7, respectively, which consistently demonstrate our method obtains the best evaluation metrics. This ablation study confirms that each proposed module in our method is valuable and contributes to better performance.
Table 7.
Results of the ablation study on the RS dataset (MEAN ± SD). A detailed explanation of all used metrics can be found in Table 2.
| Algorithms | |||
|---|---|---|---|
| Full method | Ours | 0.017 ± 0.005 | 33.994 ± 1.703 |
| Network ablation | UNet-Bloss | 0.030 ± 0.006 | 29.567 ± 1.270 |
| Loss ablation | EAPNet-MSE | 0.035 ± 0.009 | 30.552 ± 1.543 |
| EAPNet-MSRE | 0.019 ± 0.005 | 33.174 ± 1.554 | |
| sAM ablation | EPNet-Bloss | 0.029 ± 0.007 | 30.217 ± 1.479 |
| EAPNet-Bloss (sigmoid) | 0.028 ± 0.006 | 30.275 ± 1.392 | |
4.5. Network design analysis
Table S8 of the supplementary materials presents information regarding the number of parameters, floating point operations (FLOPs), and computational time for each network. Compared to the UNet, EAPNet shares a comparable network size and computational complexity, yet consistently obtains superior performance conditioning on the identical loss function, as shown by the ablation experiments.
To further demonstrate the superiority of our network architecture, we trained two more complex UNets with the Bloss on the RS dataset, one wider and one deeper. Compared to the base UNet, the channel dimension of each convolution layer in the wider UNet is doubled, and the deeper UNet includes an extra contracting block and an extra expanding block The comparison results are listed in Table S8. While widening or deepening the contracting–expanding structure of UNet benefits in improved performance, it also results in a significant increase in the model size by 300% and 303%, respectively. Our EAPNet achieves the best performance with only a negligible increase in parameters and computational load, demonstrating its better suitability for addressing the optical inverse problem.
4.6. Attention module analysis
As presented Table 7 and Table S7, the network’s performance degrades whether removing the entire sAM or just the softmax function, thereby fully confirming the effectiveness of the proposed sAM.
To better understand the benefits of our sAM, we visualized the attention maps of two samples from the RS dataset in Fig. 8, which indicate attention weights assigned to every pixel. It turns out that the sAM activated by the commonly used sigmoid function generates attention maps lacking discernible features and displaying a nearly uniform distribution Fig. 8(b). In contrast, our sAM, benefiting from the attention competition mechanism, yields attention maps possessing increased distinction Fig. 8(e). Moreover, we investigated the influence of loss functions on our sAM. MSE guides the sAM to assign more attention weights to inclusions with high absorption and their vicinities. When implemented with MSRE, our sAM produces larger attention weights in background areas. In contrast, the proposed Bloss assists our sAM in gaining broader and more uniform attention on inclusions, including deep-located tissue #5, despite its considerably weaker signal in the input images.
Fig. 8.
Attention map analysis of two examples in the RS dataset. Tag numbers indicate the example index. (a) Ground truth, . (b–e) Attention maps obtained from different methods, from left to right: proposed sAM with Bloss but using the sigmoid function as the activation function, proposed sAM with MSE, proposed sAM with MSRE, proposed sAM with Bloss (ours).
5. Discussion
We have conducted simulation validations, including multiple potential application scenarios. Besides achieving improved image-wise quantitative metrics, the proposed method delivers multifaceted advantages. Firstly, our method demonstrates impressive robustness to the intrinsic properties of targets (e.g., size, location, and relative absorption intensity), achieving superior consistency in tissue-wise accuracy. This suggests that our method has broader applicability and higher reliability in practical scenarios. Consistent accuracy in the spatial domain also enhances edge sharpness and target distinction, which is crucial for precise segmentation of regions of interest (ROIs) from the predicted image, thereby aiding further tasks like spectral unmixing. Further, the mean values within ROIs can be utilized as a statistically more reliable estimate if ROIs can be assumed optically homogeneous. The proposed Bloss plays a crucial role in the mentioned accuracy consistency. It effectively balances the contribution of each tissue to the loss function, enabling unbiased optimization of the entire image domain during training.
On the other hand, the EAPNet is a high-efficiency architecture for qPAT, which effectively enhances the performance baseline while maintaining a comparable level of network complexity to the conventional UNet (Table S8). The advance arises from two key components: the proposed E-P structure and sAM. In the E-P framework, spatial information capture and aggregation occur exclusively during the extraction phase, wherein the extractor learns global dependencies and generates contextual representation vectors for each pixel. Based on the extraction phase, the predictor can operate on a per-pixel basis and enhance nonlinear modeling capability in a parameter-efficient and computation-friendly manner. Consequently, the extractor and predictor primarily focus on global dependency and high nonlinearity, respectively, which suggests that the network, to some degree, deals with the two intractable features of the optical inverse problem in a stepwise manner, consequently reducing overall complexity. In addition, our sAM employs a novel attention competition mechanism, which aids the extractor in discerning valuable information from input images and its effective utilization in the predictor. Further, guided by the Bloss, our sAM can effectively attend to subtle yet crucial pixels in images (Fig. 8).
The phantom and in vivo experiments demonstrate the promising feasibility of our method in real-world scenarios. However, further in vivo research remains challenging. First, PA images are input data for models, while they often severely distort in practice, due to the non-ideal imaging system, as depicted in Fig. 7(a). Consequently, networks are forced to deal with PA image restoration, which is out of its intended task, resulting in degraded performance. Besides, low-quality regions, where noise overwhelms the signal, can contaminate the contextual representation vectors captured by the extractor and induce large prediction errors. To obtain accurate results, the quality of PA images should be carefully considered. Image restoration techniques may be applied beforehand if needed. Additionally, due to the lack of reliable in vivo measuring techniques for absorption coefficients, all experimental data of this study was processed by networks trained on simulated data. The simulated data is generated based on approximate models of physical processes, detector characteristics, and noise, and inevitably suffers a domain gap to real data. Consequently, networks cannot learn real-world information adequately. Recently, there has been rapid progress in generative networks and unsupervised learning, which may provide new opportunities for tackling this challenge [34], [45].
Another potential limitation is related to using the softmax as the activation function. In our sAM, the constant total attention is distributed to all pixels, including ones outside the imaging medium. These meaningless pixels may get a considerable portion of the attention weight when they contain significant noise levels. To mitigate it, a straightforward approach is to filter out signals originating from outside the imaging medium before inputting them into the network, as depicted in Fig. 7(a).
6. Conclusion
In this study, we propose a deep learning-based method for recovering the absorption coefficient distribution from PA images. The EAPNet proves to be a more suitable and efficient architecture than UNet, as it boosts the accuracy of predicted images with nearly identical network parameters and computational complexity. In addition, the Bloss effectively mitigates the difference in prediction accuracy between diverse tissues and consequently improves the applicability and reliability of our method in practice. Simulation and phantom experiment results demonstrate the improved performance of our method concerning both quantitative metrics and image quality. Our method also shows a promising result in a preliminary in vivo experiment. Our future work focuses on constructing high-quality experimental datasets to enable more complex real-world validations and thus facilitate the clinical translation process.
CRediT authorship contribution statement
Zeqi Wang: Writing – original draft, Software, Methodology, Conceptualization. Wei Tao: Writing – review & editing, Supervision, Resources, Project administration, Funding acquisition. Hui Zhao: Writing – review & editing, Validation, Supervision, Resources, Project administration, Investigation, Funding acquisition, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research was funded by National Natural Science Foundation of China , grant number 61873168.
Code availability
The code is provided in https://github.com/WZQ7/EAPNet, and the data involved in the main text is also provided.
Biographies

Zeqi Wang received the B.E. degree in measurement and control technology and instruments from Sichuan University, Chengdu, China, in 2016.
He is currently working towards the Ph.D. degree in instrumentation science and technology with the School of Electronic Information and Electric Engineering, Shanghai Jiao Tong University, Shanghai, China.

Wei Tao received the B.S., M.S. and Ph.D. degrees in Instrument science and technology from Harbin Institute of Technology, Harbin, China, in 1997,1999 and 2003, respectively. She became a Professor of Shanghai Jiao Tong University in 2018. She is the author of three books, more than 100 articles and more than 40 inventions. Her research interests include opto-electronic measurement technology and application, methods and algorithms in vision measurement process, and laser sensors and measurement instruments.

Hui Zhao received the Ph.D. degree in the department of instrument engineering from Harbin Institute of Technology, Harbin, China, in 1996. Since 2000, he has been a Professor with the Department of Instrument Science and Engineering, Shanghai Jiao Tong University. His research interests include novel sensors and vision measurement method. He is the author of three books, more than 150 articles, and more than 50 inventions. He serves as the Vice Chair of Precision Mechanism Federation of China Instrument and Control Society, and the Vice Chair of Mechanical Quantity Measurement Instrument Federation of China Instrument and Control Society. He is a reviewer of IEEE Transaction on Instrument & Measurement, Sensors, Measurement, IEEE Sensors Journal, Optik, and several other journals.
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.pacs.2024.100609.
Public Lung Image Database, http://www.via.cornell.edu/lungdb.html.
Contributor Information
Zeqi Wang, Email: wangzeqi7@sjtu.edu.cn.
Wei Tao, Email: taowei@sjtu.edu.cn.
Hui Zhao, Email: huizhao@sjtu.edu.cn.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
.
Data availability
Data will be made available on request.
References
- 1.Wang L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photon. 2009;3(9):503–509. doi: 10.1038/nphoton.2009.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang L.V., Hu S. Photoacoustic tomography: In vivo imaging from organelles to organs. Science. 2012;335(6075):1458–1462. doi: 10.1126/science.1216210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Xu M., Wang L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006;77(4) doi: 10.1063/1.2195024. [DOI] [Google Scholar]
- 4.Wang L.V., Wu H.-i. John Wiley & Sons; 2012. Biomedical Optics: Principles and Imaging. [Google Scholar]
- 5.Le T.D., Kwon S.-Y., Lee C. Segmentation and quantitative analysis of photoacoustic imaging: A review. Photonics. 2022;9(3):176. doi: 10.3390/photonics9030176. [DOI] [Google Scholar]
- 6.Li M., Tang Y., Yao J. Photoacoustic tomography of blood oxygenation: A mini review. Photoacoustics. 2018;10:65–73. doi: 10.1016/j.pacs.2018.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Taruttis A., Ntziachristos V. Advances in real-time multispectral optoacoustic imaging and its applications. Nat. Photon. 2015;9(4):219–227. doi: 10.1038/nphoton.2015.29. [DOI] [Google Scholar]
- 8.Rosenthal A., Razansky D., Ntziachristos V. Fast semi-analytical model-based acoustic inversion for quantitative optoacoustic tomography. IEEE Trans. Med. Imaging. 2010;29(6):1275–1285. doi: 10.1109/TMI.2010.2044584. [DOI] [PubMed] [Google Scholar]
- 9.Treeby B.E., Zhang E.Z., Cox B.T. Photoacoustic tomography in absorbing acoustic media using time reversal. Inverse Problems. 2010;26(11) doi: 10.1088/0266-5611/26/11/115003. [DOI] [Google Scholar]
- 10.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E. 2005;71(1) doi: 10.1103/PhysRevE.71.016706. [DOI] [PubMed] [Google Scholar]
- 11.Laufer J., Delpy D., Elwell C., Beard P. Quantitative spatially resolved measurement of tissue chromophore concentrations using photoacoustic spectroscopy: Application to the measurement of blood oxygenation and haemoglobin concentration. Phys. Med. Biol. 2007;52(1):141–168. doi: 10.1088/0031-9155/52/1/010. [DOI] [PubMed] [Google Scholar]
- 12.Cox B.T., Laufer J.G., Beard P.C., Arridge S.R. Quantitative spectroscopic photoacoustic imaging: A review. J. Biomed. Opt. 2012;17(6) doi: 10.1117/1.JBO.17.6.061202. [DOI] [PubMed] [Google Scholar]
- 13.An L., Cox B.T. Estimating relative chromophore concentrations from multiwavelength photoacoustic images using independent component analysis. J. Biomed. Opt. 2018;23(07):1. doi: 10.1117/1.JBO.23.7.076007. [DOI] [PubMed] [Google Scholar]
- 14.Gröhl J., Kirchner T., Adler T.J., Hacker L., Holzwarth N., Hernández-Aguilera A., Herrera M.A., Santos E., Bohndiek S.E., Maier-Hein L. Learned spectral decoloring enables photoacoustic oximetry. Sci. Rep. 2021;11(1):6565. doi: 10.1038/s41598-021-83405-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hochuli R., An L., Beard P.C., Cox B.T. Estimating blood oxygenation from photoacoustic images: Can a simple linear spectroscopic inversion ever work? J. Biomed. Opt. 2019;24(12):1. doi: 10.1117/1.JBO.24.12.121914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cox B.T., Arridge S.R., Köstli K.P., Beard P.C. Two-dimensional quantitative photoacoustic image reconstruction of absorption distributions in scattering media by use of a simple iterative method. Appl. Opt. 2006;45(8):1866. doi: 10.1364/AO.45.001866. [DOI] [PubMed] [Google Scholar]
- 17.Zhang S., Liu J., Liang Z., Ge J., Feng Y., Chen W., Qi L. Pixel-wise reconstruction of tissue absorption coefficients in photoacoustic tomography using a non-segmentation iterative method. Photoacoustics. 2022;28 doi: 10.1016/j.pacs.2022.100390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.B.T. Cox, S.R. Arridge, P.C. Beard, Gradient-Based Quantitative Photoacoustic Image Reconstruction for Molecular Imaging, in: A.A. Oraevsky, L.V. Wang (Eds.), Biomedical Optics (BiOS) 2007, San Jose, CA, 2007, p. 64371T, 10.1117/12.700031. [DOI]
- 19.Hochuli R., Powell S., Arridge S., Cox B. Quantitative photoacoustic tomography using forward and adjoint Monte Carlo models of radiance. J. Biomed. Opt. 2016;21(12) doi: 10.1117/1.JBO.21.12.126004. [DOI] [PubMed] [Google Scholar]
- 20.Leino A.A., Lunttila T., Mozumder M., Pulkkinen A., Tarvainen T. Perturbation Monte Carlo method for quantitative photoacoustic tomography. IEEE Trans. Med. Imaging. 2020;39(10):2985–2995. doi: 10.1109/TMI.2020.2983129. [DOI] [PubMed] [Google Scholar]
- 21.Pulkkinen A., Cox B.T., Arridge S.R., Kaipio J.P., Tarvainen T. A Bayesian approach to spectral quantitative photoacoustic tomography. Inverse Problems. 2014;30(6) doi: 10.1088/0266-5611/30/6/065012. [DOI] [Google Scholar]
- 22.Mahmoodkalayeh S., Zarei M., Ansari M.A., Kratkiewicz K., Ranjbaran M., Manwar R., Avanaki K. Improving vascular imaging with co-planar mutually guided photoacoustic and diffuse optical tomography: A simulation study. Biomed. Opt. Express. 2020;11(8):4333. doi: 10.1364/BOE.385017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hussain A., Petersen W., Staley J., Hondebrink E., Steenbergen W. Quantitative blood oxygen saturation imaging using combined photoacoustics and acousto-optics. Opt. Lett. 2016;41(8):1720. doi: 10.1364/OL.41.001720. [DOI] [PubMed] [Google Scholar]
- 24.Guan S., Khan A.A., Sikdar S., Chitnis P.V. Fully dense UNet for 2-D sparse photoacoustic tomography artifact removal. IEEE J. Biomed. Health Inf. 2020;24(2):568–576. doi: 10.1109/JBHI.2019.2912935. [DOI] [PubMed] [Google Scholar]
- 25.Lan H., Jiang D., Yang C., Gao F., Gao F. Y-Net: Hybrid deep learning image reconstruction for photoacoustic tomography in vivo. Photoacoustics. 2020;20 doi: 10.1016/j.pacs.2020.100197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Guo M., Lan H., Yang C., Liu J., Gao F. AS-Net: fast photoacoustic reconstruction with multi-feature fusion from sparse data. IEEE Trans. Comput. Imaging. 2022;8:215–223. [Google Scholar]
- 27.Chen P., Liu C., Feng T., Li Y., Ta D. Improved photoacoustic imaging of numerical bone model based on attention block U-net deep learning network. Appl. Sci. 2020;10(22):8089. [Google Scholar]
- 28.Chao L., Zhang P., Wang Y., Wang Z., Xu W., Li Q. Dual-domain attention-guided convolutional neural network for low-dose cone-beam computed tomography reconstruction. Knowl.-Based Syst. 2022;251 doi: 10.1016/j.knosys.2022.109295. [DOI] [Google Scholar]
- 29.Cai C., Deng K., Ma C., Luo J. End-to-end deep neural network for optical inversion in quantitative photoacoustic imaging. Opt. Lett. 2018;43(12):2752. doi: 10.1364/OL.43.002752. [DOI] [PubMed] [Google Scholar]
- 30.Luke G.P., Hoffer-Hawlik K., Van Namen A.C., Shang R. 2019. O-Net: a convolutional neural network for quantitative photoacoustic image segmentation and oximetry. arXiv preprint arXiv:1911.01935. [Google Scholar]
- 31.Bench C., Hauptmann A., Cox B. Toward accurate quantitative photoacoustic imaging: Learning vascular blood oxygen saturation in three dimensions. J. Biomed. Opt. 2020;25(08) doi: 10.1117/1.JBO.25.8.085003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li J., Wang C., Chen T., Lu T., Li S., Sun B., Gao F., Ntziachristos V. Deep learning-based quantitative optoacoustic tomography of deep tissues in the absence of labeled experimental data. Optica. 2022;9(1):32–41. [Google Scholar]
- 33.Zou Y., Amidi E., Luo H., Zhu Q. Ultrasound-enhanced Unet model for quantitative photoacoustic tomography of Ovarian Lesions. Photoacoustics. 2022;28 doi: 10.1016/j.pacs.2022.100420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gröhl J., Schellenberg M., Dreher K., Maier-Hein L. Deep learning for biomedical photoacoustic imaging: A review. Photoacoustics. 2021;22 doi: 10.1016/j.pacs.2021.100241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hsu K.-T., Guan S., Chitnis P.V. Comparing deep learning frameworks for photoacoustic tomography image reconstruction. Photoacoustics. 2021;23 doi: 10.1016/j.pacs.2021.100271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ronneberger O., Fischer P., Brox T. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Navab N., Hornegger J., Wells W.M., Frangi A.F., editors. Vol. 9351. Springer International Publishing; Cham: 2015. U-Net: Convolutional networks for biomedical image segmentation; pp. 234–241. [DOI] [Google Scholar]
- 37.Woo S., Park J., Lee J.-Y., Kweon I.S. In: Computer Vision – ECCV 2018. Ferrari V., Hebert M., Sminchisescu C., Weiss Y., editors. Vol. 11211. Springer International Publishing; Cham: 2018. CBAM: Convolutional block attention module; pp. 3–19. [DOI] [Google Scholar]
- 38.Oktay O., Schlemper J., Folgoc L.L., Lee M., Heinrich M., Misawa K., Mori K., McDonagh S., Hammerla N.Y., Kainz B., Glocker B., Rueckert D. 2018. Attention U-Net: Learning where to look for the Pancreas. arXiv:1804.03999. [Google Scholar]
- 39.J. Hu, L. Shen, G. Sun, Squeeze-and-excitation networks, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 7132–7141.
- 40.T.-Y. Lin, P. Goyal, R. Girshick, K. He, P. Dollár, Focal loss for dense object detection, in: Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 2980–2988.
- 41.Jadon S. A survey of loss functions for semantic segmentation. 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology; CIBCB; IEEE; 2020. pp. 1–7. [Google Scholar]
- 42.Tarvainen T., Vauhkonen M., Kolehmainen V., Kaipio J.P. Finite element model for the coupled radiative transfer equation and diffusion approximation. Internat. J. Numer. Methods Engrg. 2006;65(3):383–405. doi: 10.1002/nme.1451. [DOI] [Google Scholar]
- 43.Brochu F.M., Brunker J., Joseph J., Tomaszewski M.R., Morscher S., Bohndiek S.E. Towards quantitative evaluation of tissue absorption coefficients using light fluence correction in optoacoustic tomography. IEEE Trans. Med. Imaging. 2017;36(1):322–331. doi: 10.1109/TMI.2016.2607199. [DOI] [PubMed] [Google Scholar]
- 44.Piao D., Patel S. Simple empirical Master–Slave Dual-Source configuration within the diffusion approximation enhances modeling of spatially resolved diffuse reflectance at short-path and with low scattering from a semi-infinite homogeneous medium. Appl. Opt. 2017;56(5):1447. doi: 10.1364/AO.56.001447. [DOI] [PubMed] [Google Scholar]
- 45.Wang Z., Tao W., Zhao H. The optical inverse problem in quantitative photoacoustic tomography: A review. Photonics. 2023;10(5):487. doi: 10.3390/photonics10050487. [DOI] [Google Scholar]
- 46.Abraham N., Khan N.M. 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) IEEE; 2019. A novel focal tversky loss function with improved attention u-net for lesion segmentation; pp. 683–687. [Google Scholar]
- 47.Fang Q., Boas D.A. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt. Express. 2009;17(22):20178. doi: 10.1364/OE.17.020178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jin K., Huang X., Zhou J., Li Y., Yan Y., Sun Y., Zhang Q., Wang Y., Ye J. FIVES: A fundus image dataset for artificial intelligence based vessel segmentation. Sci. Data. 2022;9(1):475. doi: 10.1038/s41597-022-01564-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lyu T., Yang C., Zhang J., Guo S., Gao F., Gao F. 2022. Photoacoustic digital skin: Generation and simulation of human skin vascular for quantitative image analysis. arXiv:2011.04652. [Google Scholar]
- 50.Treeby B.E., Cox B.T. K-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010;15(2) doi: 10.1117/1.3360308. [DOI] [PubMed] [Google Scholar]
- 51.Cubeddu R., Pifferi A., Taroni P., Torricelli A., Valentini G. A solid tissue phantom for photon migration studies. Phys. Med. Biol. 1997;42(10):1971–1979. doi: 10.1088/0031-9155/42/10/011. [DOI] [PubMed] [Google Scholar]
- 52.Buehler A., Rosenthal A., Jetzfellner T., Dima A., Razansky D., Ntziachristos V. Model-based optoacoustic inversions with incomplete projection data. Med. Phys. 2011;38(3):1694–1704. doi: 10.1118/1.3556916. [DOI] [PubMed] [Google Scholar]
- 53.Prahl S.A. Everything I Think You Should Know About Inverse Adding-Doubling. Oregon Medical Laser Center, St. Vincent Hospital; 2011. pp. 1–74. [Google Scholar]
- 54.Zheng S., Yingsa H., Meichen S., Qi M. Quantitative photoacoustic tomography with light fluence compensation based on radiance Monte Carlo model. Phys. Med. Biol. 2023;68(6) doi: 10.1088/1361-6560/acbe90. [DOI] [PubMed] [Google Scholar]
- 55.Madasamy A., Gujrati V., Ntziachristos V., Prakash J. Deep learning methods hold promise for light fluence compensation in three-dimensional optoacoustic imaging. J. Biomed. Opt. 2022;27(10) doi: 10.1117/1.JBO.27.10.106004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rodriguez-Molares A., Rindal O.M.H., D’hooge J., Måsøy S.-E., Austeng A., Bell M.A.L., Torp H. The generalized contrast-to-noise ratio: A formal definition for lesion detectability. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2019;67(4):745–759. doi: 10.1109/TUFFC.2019.2956855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kempski K.M., Graham M.T., Gubbi M.R., Palmer T., Bell M.A.L. Application of the generalized contrast-to-noise ratio to assess photoacoustic image quality. Biomedical Optics Express. 2020;11(7):3684–3698. doi: 10.1364/BOE.391026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chen D., Tachella J., Davies M.E. Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021. Equivariant imaging: Learning beyond the range space; pp. 4379–4388. [Google Scholar]
- 59.Lan H., Huang L., Nie L., Luo J. 2023. Cross-domain unsupervised reconstruction with equivariance for photoacoustic computed tomography. arXiv preprint arXiv:2301.06681. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
.
Data Availability Statement
Data will be made available on request.