Abstract
Brain-wide association studies (BWASs) have attempted to relate cognitive abilities with brain phenotypes, but have been challenged by issues such as predictability, test-retest reliability, and cross-cohort generalisability. To tackle these challenges, we proposed a machine-learning “stacking” approach that draws information from whole-brain magnetic resonance imaging (MRI) across different modalities, from task-fMRI contrasts and functional connectivity during tasks and rest to structural measures, into one prediction model. We benchmarked the benefits of stacking, using the Human Connectome Projects: Young Adults (n=873, 22–35 years old) and Human Connectome Projects-Aging (n=504, 35–100 years old) and the Dunedin Multidisciplinary Health and Development Study (Dunedin Study, n=754, 45 years old). For predictability, stacked models led to out-of-sample r~.5-.6 when predicting cognitive abilities at the time of scanning, primarily driven by task-fMRI contrasts. Notably, using the Dunedin Study, we were able to predict participants’ cognitive abilities at ages 7, 9, and 11 using their multimodal MRI at age 45, with an out-of-sample r of 0.52. For test-retest reliability, stacked models reached an excellent level of reliability (ICC>.75), even when we stacked only task-fMRI contrasts together. For generalisability, a stacked model with non-task MRI built from one dataset significantly predicted cognitive abilities in other datasets. Altogether, stacking is a viable approach to undertake the three challenges of BWAS for cognitive abilities.
Classification: Major Category: Biological Sciences, Minor Category: Psychological and Cognitive Sciences, Brain-Wide Association Studies, Cognitive Abilities, Stacking, Task fMRI, Reliability, Generalisability
Introduction
Individual differences in cognitive abilities are stable across the lifespan(1) and have relatively high heritability(2). They are key indicators of educational achievements(3), career successes(4), well-being(5), socioeconomic stability(6) and health outcomes(7). Recent studies have also demonstrated a widespread relationship between impairments in cognitive abilities and various psychopathological disorders(8, 9). Accordingly, relating individual differences in cognitive abilities to neuroimaging data has been a primary goal for cognitive neuroscientists, from both basic and applied science perspectives(10). This approach allows neuroscientists to scientifically quantify the presence of information related to cognitive abilities from each neuroimaging type or modality. It also paves the way for identifying neural indicators of cognitive abilities, which could be useful for understanding the etiology of neuro- and psychopathology(11). Indeed, a leading transdiagnostic framework for psychiatry, the Research Domain Criteria (RDoC), treats cognitive abilities as one of the main functional domains for psychopathology across diagnoses. Having a robust neural indicator of cognitive abilities, in addition to behavioral and genetic indicators, is central to the RDoC framework(12).
The availability of large-scale neuroimaging databases(13) and the accessibility of predictive modelling methodologies(11, 14) have provided encouraging avenues to pursue a neural indicator of cognitive abilities. Accordingly, several researchers have built prediction models to predict cognitive abilities from brain magnetic resonance imaging (MRI) signals and evaluated the models’ performance on separate, unseen data in the so-called Brain-Wide Association Studies (BWAS)(11, 15). BWAS can be conducted using either univariate (also known as mass-univariate) or multivariate (also known as machine learning) methods to draw MRI information. White univariate methods draw data from one region/voxel at a time, multivariate methods draw MRI information across regions/voxels (11, 16, 17). These multivariate methods, from particular MRI modalities, appear to boost predictability for cognitive abilities (11, 16–18). For examples, Marek and colleagues(16) conducted BWAS on several large datasets can concluded, “More robust BWAS effects were detected for functional MRI (versus structural), cognitive tests (versus mental health questionnaires) and multivariate methods (versus univariate).”
Akin to Genome-Wide Association Studies (GWAS) in genetics(19) that can integrate information across SNPs across the genome to create a predicted, propensity score for a phenotype of interest (e.g., cognitive abilities), known as polygenic scores, BWAS can also be used to create a similar predicted score for each individual based on his/her neuroimaging data. For instance, Marek and colleagues(16) used trained multivariate methods to predict cognitive abilities from brain MRI data using part of the data (known as training set) and applied the trained model to the unseen participants (known as test set). Participants in the test set then had a predicted score of their cognitive abilities, based on their brain MRI data. Yet, BWAS for cognitive abilities has faced several challenges, including but not limited to predictability, test-retest reliability and generalisability, as detailed below(16, 20, 21). These challenges have led to headlines, such as “Cognitive Neuroscience at the Crossroads”(22) and “Scanning the Brain to Predict Behavior, a Daunting ‘Task’ for MRI”(23). To address these issues, we(24, 25) have recently proposed a potential solution, “stacking”(26), which allows us to combine different modalities of MRI into one prediction model. In this study, we aim to formally benchmark the benefits of stacking in improving predictability, test-retest reliability and generalisability, using three large-scale neuroimaging databases(27–29).
First, predictability, or out-of-sample prediction, pertains to the ability of prediction models to predict a target variable, e.g., cognitive abilities, based on features, e.g., functional MRI (fMRI) data, of unseen participants, not part of the model-building processes(30). More specifically, we refer to an application of a validation within one dataset. Here researchers usually take a relatively large dataset, split it into training and test sets, then build a model from the training set and apply the model to the test set. In addition to doing one split, researchers could also apply a cross-validation strategy by splitting a dataset into different non-overlapping training-test folds and looping through folds to calculate the average performance across the test sets(31, 32). Several earlier studies(33–35) did not apply any validation when predicting cognitive abilities from MRI, possibly causing inflated predictability(16). With proper data splitting, a recent meta-analysis(15) estimated the predictability of multivariate methods on brain MRI of different modalities with a validation for cognitive abilities to be a Pearson’s correlation r of 0.42 on average.
While this level of predictability is encouraging, there is still room for improvement. Given that different MRI modalities may convey different information about the brain, drawing information across different MRI modalities could allow us to improve predictability further. Stacking enables researchers to draw information across MRI modalities, which seems to improve predictability over relying on any single MRI modality (24–26, 36, 37). In this framework (see Figure 1), researchers first build ‘non-stacked’ prediction models separately for each MRI set of features (e.g., cortical thickness or cortical area), and computed predicted values from each of these non-stacked’ models. They then treat these predicted values as features for ‘stacked’ prediction models, allowing them to draw information across different MRI sets of features. Still, most studies use one single type of MRI to build prediction models. The popular choices include resting-state fMRI functional connectivity (Rest FC, or correlations in blood-oxygen-level-dependent (BOLD) time series across areas during rest)(38–40), task fMRI functional connectivity (Task FC, or correlations in BOLD time series across brain regions during each task)(41–48) and structural MRI (including measures such as thickness, area and volume in cortical/subcortical areas)(49). While it is less common to use task-fMRI contrasts (Task Contrasts, or fMRI BOLD activity relevant to events in each task) to predict cognitive abilities, studies have started to show the superior predictability of contrasts from certain tasks, compared to other MRI modalities(24, 25, 39, 50). Nonetheless, previous attempts at stacking often ignored task contrasts (36, 37), and as a result, while improving over non-stacked models, they have not led to satisfactory predictive performance. We(24, 25) have started to show a boost in predictability when applying stacking to combine task contrasts with other MRI modalities. Here, to ensure the robustness of this approach, we examined the benefits of stacking task contrasts, along with other MRI modalities, on multiple large-scale datasets.
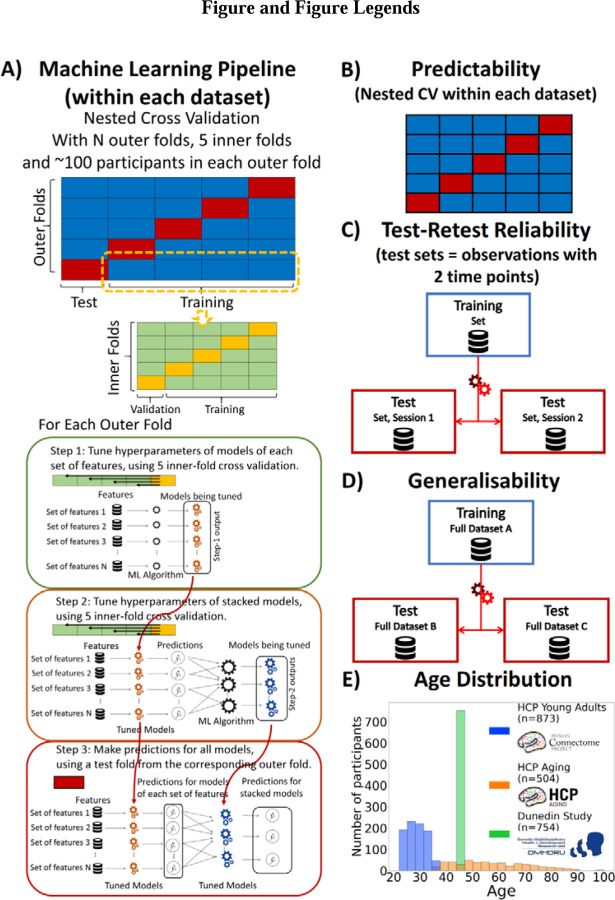
Figure 1. Overview of Study Methodology.
We used three datasets: Human Connectome Project Young Adults (HCP Young Adults), Human Connectome Project Aging (HCP Aging) and Dunedin Multidisciplinary Health and Development Study (Dunedin Study). A) Machine Learning Pipeline. Here, we depict the process we used for building prediction models for testing predictability within each dataset. Briefly, we used nested cross-validation (CV) by splitting the data into outer folds with around 100 participants in each. In each outer-fold CV loop, we then treated one of the outer folds as an outer-fold test set and treated the rest as an outer-fold training set. We then divided each outer-fold training set into five inner folds and applied inner-fold CV to build prediction models in three steps. In the first step (known as a non-stacking layer), one of the inner folds was treated as an inner-fold validation set, and the rest was treated as an inner-fold training set in each inner-fold CV. We used grid search to tune prediction models for each set of features. In the second step (known as a stacking layer), we treated different combinations of the predicted values from separate sets of features as features to predict the cognitive abilities in separate “stacked” models. In the third step, we applied the already tuned models from the first and second steps to the outer-fold test set. B) Predictability. Here, we examined the predictive performance across outer-fold test sets within each dataset. C) Test-Retest Reliability. Here, we used HCP Young Adults and Dunedin Study and treated participants who were scanned twice across MRI sessions as the test set and the rest as the training set. We then examined the intraclass correlation (ICC) of the predicted values in the test set between the first and second MRI sessions. D) Generalisability. Here, we examined the predictive performance of the models built from a different dataset. We treated one of the three datasets as a training set and the other two as two separate test sets. E) Age Distribution. Here, we show the age of participants at the time of scanning in each dataset.
Second, test-retest reliability pertains to the rank stability of measurements across different time points, assuming the absence of significant changes between assessments (e.g., treatment exposure, injury and/or disease progression)(51, 52). For instance, if some people score higher than their peers at time one, they should also score higher than their peers at time two. To use prediction models as an indicator for individual differences in cognitive abilities, the predicted values should be reliable across time. A recent study challenged the test-retest reliability of task contrasts(20). Here the researchers examined test-retest reliability of Task Contrasts in certain areas, known to be strongly elicited in each task, across two-time points and found a poor level of test-retest reliability across different tasks and two datasets: the Human Connectome Project Young Adult (HCP Young Adults)(29), and the Dunedin Multidisciplinary Health and Development Study (Dunedin Study)(28). This poor level of test-retest reliability from Task Contrasts is concerning, especially when compared to the higher levels of test-retest reliability found from structural MRI, Rest FC and Task FC(20, 53, 54). In fact, structural MRI provided reliability that was almost at the ceiling(20). Yet these studies simply took task contrasts from certain areas; they did not create prediction models or use multivariate methods and stacking to draw information across the whole brain and across different tasks/MRI modalities. It is possible that Task Contrasts could be more reliable once the models consider information across the whole brain, across different tasks and across different MRI modalities. Following this conjecture, we(25) recently showed that multivariate methods and stacking substantively boosted reliability, reaching a much higher level of reliability in HCP Young Adults(29). To ensure the robustness of our findings, we need to test the benefits of this stacking approach in another, independent dataset: the Dunedin Study(28), for example.
Third, generalisability, or more specifically cross-cohort generalisability, pertains to the ability of prediction models built from one dataset to predict the cognitive abilities of participants of another dataset(21). Different datasets, for instance, use different MRI scanners, recruit participants from different cultures and age groups, or implement different cognitive-ability measurements. Thus, while predictability within one dataset provides the performance of prediction models within specific, harmonised contexts of one dataset, generalisability across datasets allows us to gauge the performance of prediction models in broader contexts. This means that generalisability situates closer to how deployable the prediction models are in indicating cognitive abilities in the real world(21). Yet, only a few studies have investigated the generalisability of MRI prediction models for cognitive abilities, and most have focused on functional connectivity during rest and/or tasks(55–57). The generalisability of stacked models is currently unknown.
Our overarching goal is to benchmark the impact of stacking on predictability, test-retest reliability and generalisability of MRI prediction models for cognitive abilities. To achieve this, we used three large-scale neuroimaging databases, including HCP Young Adults(29), Human Connectome Project Aging (HCP-Aging)(27) and Dunedin Study(28). The databases vary in various aspects, such as participants’ age (see Figure 1) and cultures, physical scanners, scanning parameters and cognitive-ability assessments. Note that, unlike our previous implementation of stacking(25), we also included Task FC in addition to Task Contrasts to capture wider information during task scanning. Specifically, here we built stacked models from eight different combinations of functional and structural MRI sets of features: “Task Contrast” including Task Contrasts from all of the tasks, “Task FC” including Task FC from all of the tasks, “Non Task” including Rest FC and structural MRI, “Task Contrast & FC” including task contrasts and task FC from all of the tasks, “All” including all sets of features, “All excluding Task Contrast” including every set of features except Task Contrasts, “All, excluding Task FC” including every set of features except Task FC, “Resting and Task FC” including FC during rest and tasks.
For predictability (see Figure 1), we applied nested cross-validation (CV) within each dataset to evaluate the predictability of stacked models from multimodal MRI. To build the stacked models, we applied 16 combinations of multivariate predictive-modelling algorithms (including Elastic Net(58), Support Vector Regression(59), Random Forest(60) and XGBoost(61)). Moreover, the nature of the Dunedin Study’s longitudinal measurements(28) allowed a unique opportunity for us to predict cognitive abilities from MRI data at the time of scanning (at the age of 45 years old), but also at much earlier times (at the age of 7, 9 and 11 years old), as well as to predict the residual scores that reflect relative changes in cognitive abilities during 36 years, compared to participants’ peers(62). For test-retest reliability (see Figure 1), we examined the rank stability of stacked models from participants who were scanned twice in HCP Young Adults and Dunedin Study. Lastly, for generalisability (see Figure 1), we built stacked models from one dataset and evaluated their performance on the other two. Due to the different tasks used in different datasets, we unfortunately could only examine the generalisability of the “Stacked: Non Task” model, which combined all MRI modalities that did not involve tasks.
Results
1. Predictability
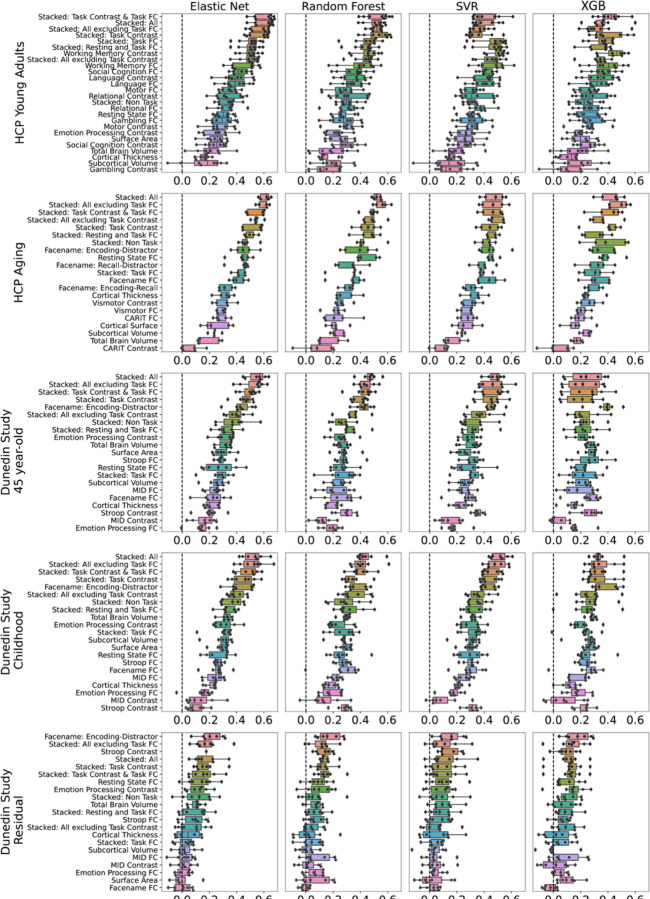
We showed performance indices of stacked and non-stacked models for each predictive-modelling algorithm and dataset in Figure 2–3 and Figures S1-8 and their bootstrapped 95% CI in Figure 4 and Figures S9-16. Overall, when predicting cognitive abilities at the time of scanning, the prediction models from multimodal MRI across different predictive-modelling algorithms varied in their performance, reflected by Pearson’s correlation (r) between predicted and observed values, ranging from around 0 to .6, across the three datasets. Notably, combining different sets of MRI features into stacked models constantly led to higher predictive performance. “Stacked: All”, which included all sets of MRI features, gave rise to top-performing models across algorithms and the three datasets. Additionally, using Elastic Net across both non-stacking and stacking layers regularly resulted in prediction models that were either equally good or better than other prediction models based on other algorithms (see the bootstrapped differences in Figure S17-26). For instance, using Elastic Net across both layers for “Stacked: All” led to r at mean(M)=.60 (95%CI[.56, .64]), M=.61 (95%CI[.56, .66]) and M=.55 (95%CI[.49, .60]) for HCP Young Adults, HCP Aging and Dunedin Study, respectively.
Figure 2. Dense scatter plot illustrating observed and predicted cognitive abilities (Z scores) using Stacked-All models with Elastic Net across two layers.
Stacked All include all sets of MRI features. Panels A-E show predicted versus observed cognitive abilities across different datasets. Panel F present observed cognitive abilities at ages 7, 9, and 11 compared to age 45 from the Dunedin Study. Panel G displays predicted cognitive abilities at ages 7, 9, and 11 compared to age 45 from the Dunedin Study. ICC=Interclass Correlation.
Figure 3. Predictability (Pearson’s correlation, r) of stacked and non-stacked models for each predictive-modelling algorithm and dataset.
Higher is better. Each dot represents predictive performance at each outer-fold test set. For the coefficient of determination (R2) and mean absolute error (MAE), see Figures S1-S2, respectively. Note that, for the stacked models, we only showed those with the same predictive algorithm across both layers here. For stacked models with different predictive algorithms between layers, please see Figures S3-S8. For Dunedin Study, childhood scores reflect cognitive abilities, averaged across 7, 9 and 11 years old, and negative residual scores reflect a stronger decline in cognitive abilities, as expected from childhood cognitive abilities, compared to participants’ peers. SVR = Support Vector Regression; XGB = XGBoost; FC = Functional Connectivity.
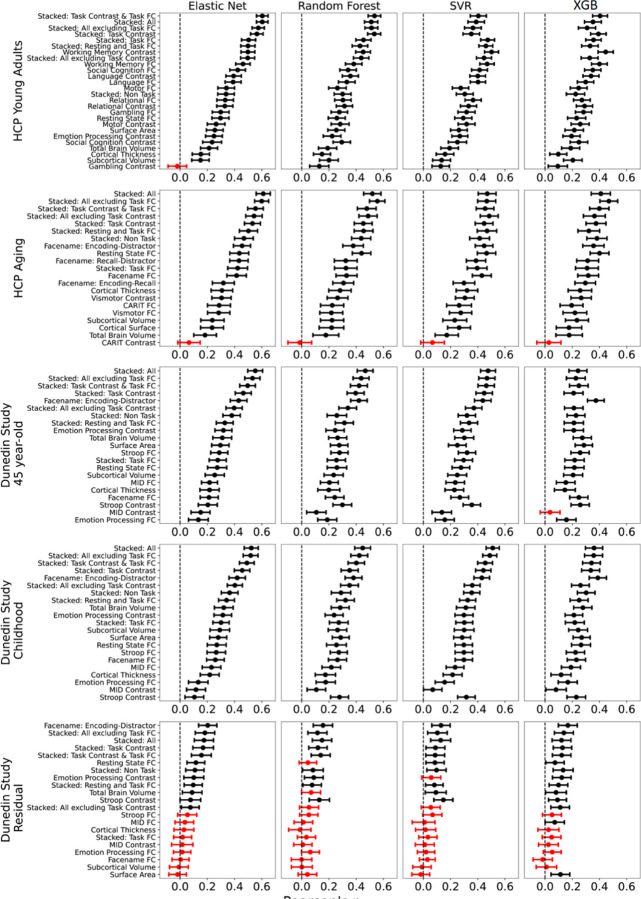
Figure 4. Bootstrapped predictability (Pearson’s correlation, r) of stacked and non-stacked models for each predictive-modelling algorithm and dataset.
Higher is better. Each dot and bar represent the median and 95% confidence intervals (CI) of bootstrapped distributions, respectively. If 95% CI was higher than zero (indicated by the black colour), then predictability from a particular prediction model was better than chance. For the coefficient of determination (R2) and mean absolute error (MAE), see Figures S9-S10, respectively. Note that, for the stacked models here, we only showed those with the same predictive algorithm across both layers. For stacked models with different predictive algorithms between layers, please see Figures S11-S16. For Dunedin Study, childhood scores reflect cognitive abilities, averaged across 7, 9 and 11 years old, and negative residual scores reflect a stronger decline in cognitive abilities, as expected from childhood cognitive abilities, compared to participants’ peers. SVR = Support Vector Regression; XGB = XGBoost; FC = Functional Connectivity.
Among the non-stacked models that predicted cognitive abilities at the time of scanning, we found varied predictive performance associated with different sets of MRI features. On the one hand, Task Contrasts from certain tasks led to top-performing models across the three datasets: the working memory task in HCP Young Adults and the facename task in HCP Aging and Dunedin Study. With Elastic Net, these three task contrasts led to r at M=.5 (95%CI[.45, .59]) for HCP Young Adults, M=.46 (95%CI[.39, .51]) for HCP Aging, M=.43 (95%CI[.37, .49]) for Dunedin Study. On the other hand, Task Contrasts from some other tasks led to poor-performing models, such as the gambling task in HCP Young Adults (r could not be calculated due to the models resulting in the same predicted values on certain folds), the Conditioned Approach Response Inhibition Task (CARIT) task in HCP Aging, r at M =.07 (95%CI[−.02, .15]), and the monetary incentive delay (MID) task in Dunedin Study, r at M=.16 (95%CI[.08, .22]).
For Dunedin Study, the prediction models that predicted cognitive abilities at the time of scanning (i.e., when participants were 45 years old) performed similarly to those that predicted cognitive abilities, collected much earlier than the scanning time (i.e., when they were 7, 9 and 11 years old). For instance, the “Stacked: All” models using Elastic Net across both non-stacking and stacking layers predicted cognitive abilities at 45 years old and at 7, 9 and 11 years old with r at M=.55 (95%CI [.49, .60]) and M=.52 (95%CI [.47, .57]), respectively. And Task Contrasts from the facename task led to top-performing models across two time points: with r at M=.43 (95%CI[.36, .48]) at 7, 9 and 11 years old, compared to M=.43 (95%CI[.37, .49]) at 45 years old.
In contrast, the performance of models predicting the residual scores for cognitive abilities from multimodal MRI was much poorer. Note that the negative residual scores reflect a stronger decline in cognitive abilities, as expected from childhood cognitive abilities, compared to participants’ peers. The highest-performing model predicting the residual scores across algorithms was the model with the encoding vs distractor contrast from the facename task, followed by various stacked models. With Elastic Net, the best model that predicted the residual scores led to r at M=.21 (95%CI[.14, .27]). And with Elastic Net across both layers for “Stacked: All” led to r at M=.17 (95%CI[.10, .24]). While these r levels were statistically better than chance according to bootstrapping (see Figure 3), it was much lower than those from prediction models that predicted cognitive abilities at the time of scanning or much younger age.
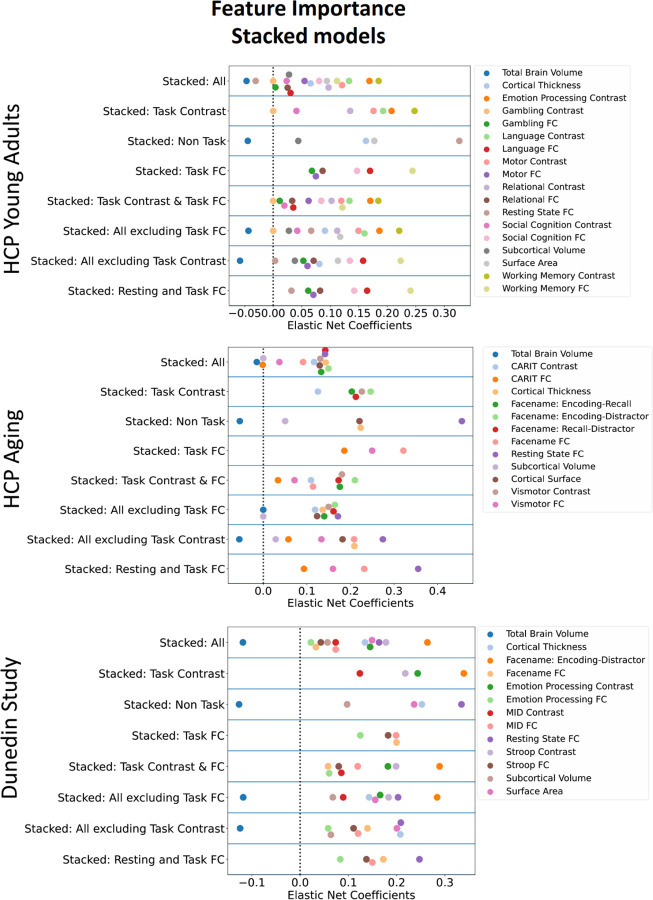
To understand the contribution of each MRI feature, we examined feature importance of each model based on Elastic Net coefficients. Given that Elastic Net features are linear and additive, the linear combination of Elastic Net coefficients reflects how the algorithm makes prediction. For non-stacked models, S27-S28 shows the feature importance of for each MRI modality, study and target variable. Figure 5 and Table S1-10 show the feature importance of the top-performing, non-stacked models for each study and target variable. For stacked models, Figure 6 shows the feature importance of stacked models for each dataset when predicting cognitive abilities at the time of scanning. The top-performing Task Contrasts contributed stronger in the stacked models across the three datasets.
Figure 5. Feature importance of the top-performing non-stacked models with with Elastic Net, as indicated by Elastic Net coefficients.
We grouped brain ROIs from the Glasser atlas (67) into 13 networks based on the Cole-Anticevic brain networks (66). In each figure, the networks are ranked by the mean Elastic Net coefficients, with the rankings shown to the right of each figure. The network partition illustration is sourced from the Actflow Toolbox https://colelab.github.io/ActflowToolbox/. We provid actual values of the feature importance in Table S1-10.
Figure 6. Feature importance of stacked models with Elastic Net, indicated by Elastic Net Coefficients, for each dataset, when predicting cognitive abilities at the time of scanning.
A higher magnitude of a coefficient indicates a stronger contribution to the prediction. FC = Functional Connectivity
Note that we provided tables of the numerical values of the predictability indices on our github page: https://github.com/HAM-lab-Otago-University/Predictability-Reliability-Generalizability/tree/main/4_Supplementary.
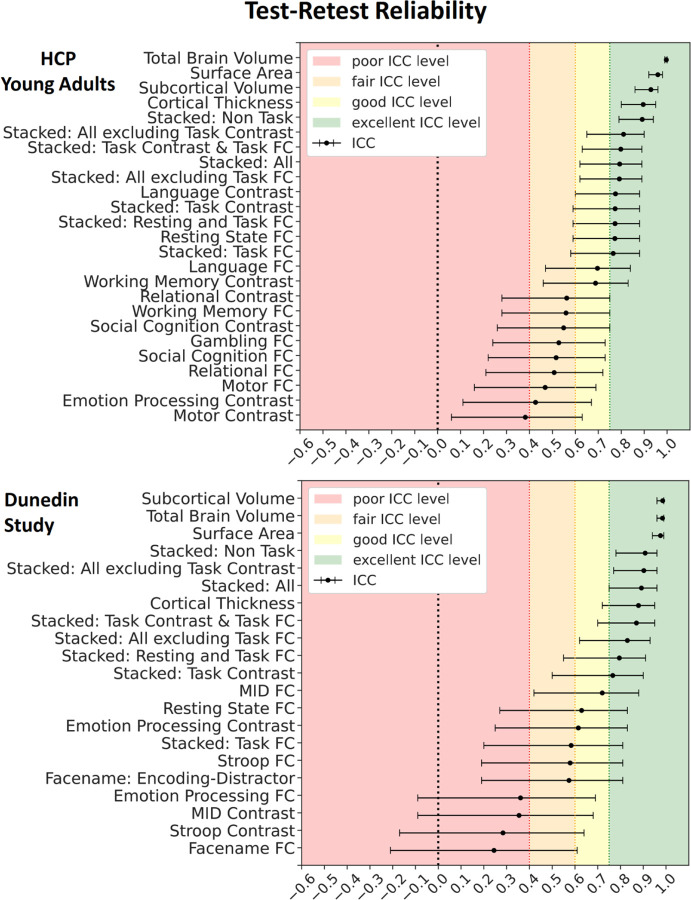
2. Test-Retest Reliability
Figure 7 shows the test-retest reliability. Here we tested the rank stability of predicted values from prediction models across two sessions, as indicated by interclass correlation (ICC). Given the availability of the test-retest participants, we examined the test-retest reliability of the stacked and non-stacked models from HCP Young Adults and Dunedin Study. We provided predicted values across two scanning sessions for each participant in Figures 8–9 and ICC for each MRI feature before prediction modelling in Figures S30-S33. Overall, for both datasets, prediction models with structural MRI, including total brain and subcortical volume, surface area and cortical thickness, led to the highest level of test-retest reliability.
Figure 7. Test-retest reliability of the predicted values of the stacked and non-stacked models, indicated by Interclass Correlation (ICC) for HCP Young Adults and Dunedin Study.
Each dot represents ICC, while each bar represents a 95% Confidence Interval.
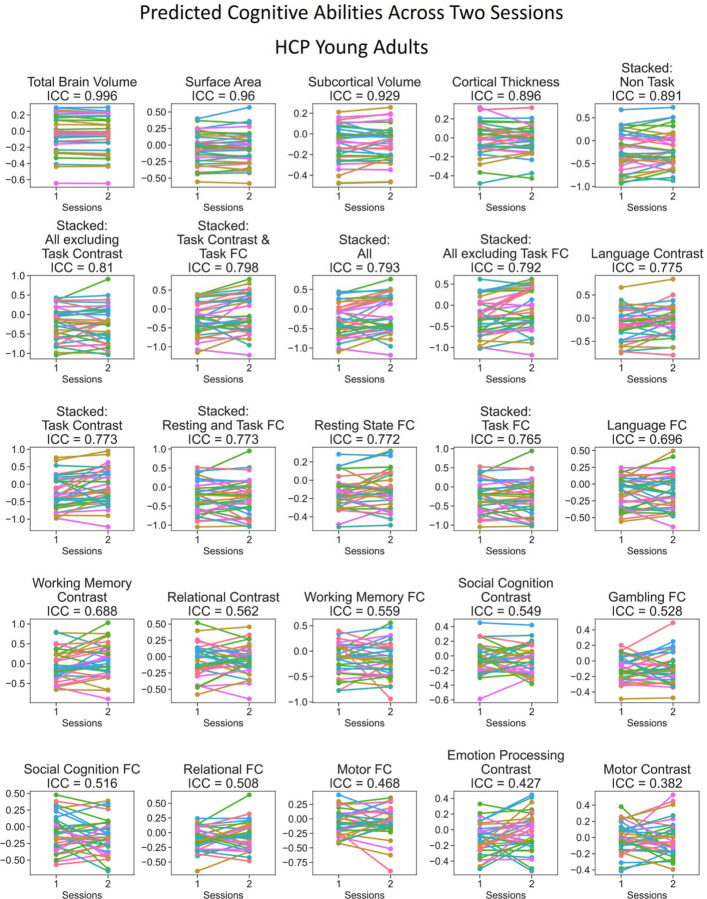
Figure 8. Predicted values of stacked and non-stacked models across two scanning sessions, ranked by interclass correlation (ICC) for HCP Young Adults.
Each line represents each participant. Lines would be completely parallel with each other in the case of perfect test-retest reliability.
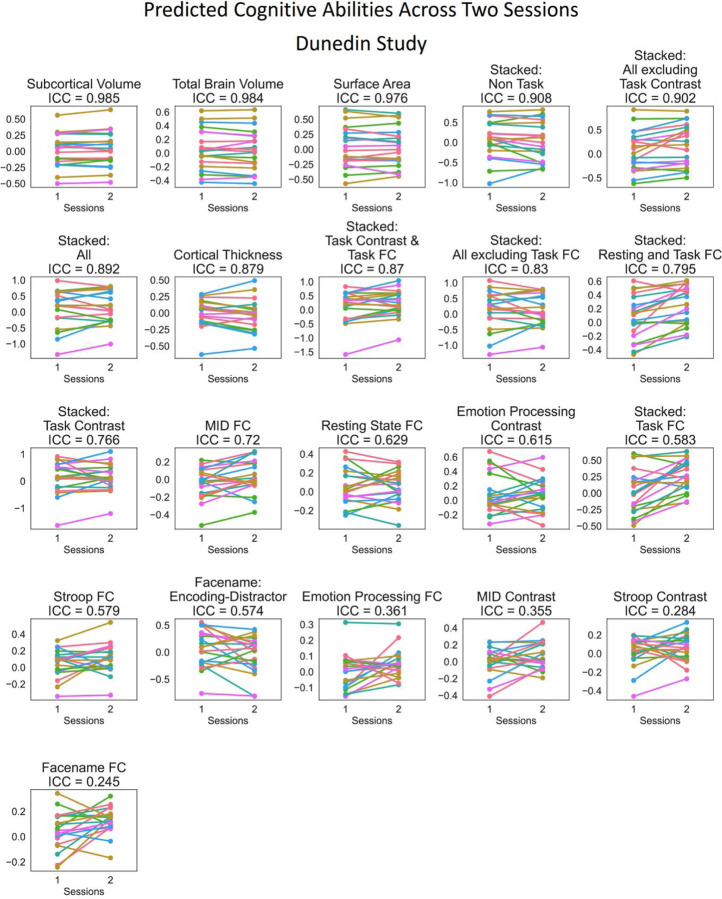
Figure 9. Predicted values of stacked and non-stacked models across two scanning sessions, ranked by interclass correlation (ICC) for Dunedin Study.
Each line represents each participant. Lines would be completely parallel with each other in the case of perfect test-retest reliability.
Similar to predictability, combining different sets of MRI features into stacked models mostly gave rise to high test-retest reliability. “Stacked: All”, which included all sets of MRI features, resulted in an excellent ICC at .79 and .89 for HCP Young Adults and Dunedin Study, respectively. Moreover, we also found the boosting effect of stacking even when only fMRI during tasks was included in the models. For instance, “Stacked: Task Contrast and Task FC”, which included the contrasts and functional connectivity (FC) from all of the fMRI tasks within each dataset, led to an excellent ICC at .8 and .87 for HCP Young Adults and Dunedin Study, respectively. Similarly, “Stacked: Task Contrast”, which included the contrasts, but not functional connectivity (FC), from all of the fMRI tasks within each dataset, still led to an excellent ICC at .77 and .77 for HCP Young Adults and Dunedin Study, respectively.
Among the non-stacked models that predicted cognitive abilities from fMRI (including Task Contrasts, Task FC and Rest FC), some models showed a good-to-excellent level of ICC. These include a contrast from the language task (ICC=.77) and FC during rest (ICC=.77) in HCP Young Adults and FC during the monetary incentive delay (MID) task (ICC=.72) and rest (ICC=.63) in Dunedin Study. Yet, some models from fMRI provided a poor level of ICC, including a contrast during the motor task (ICC=.38) in HCP Young Adults and FC, a contrast during the MID (ICC=.35) and Stroop (ICC=.28) tasks and FC (ICC=.24) during the emotion processing and facename tasks in Dunedin Study.
3. Generalisability
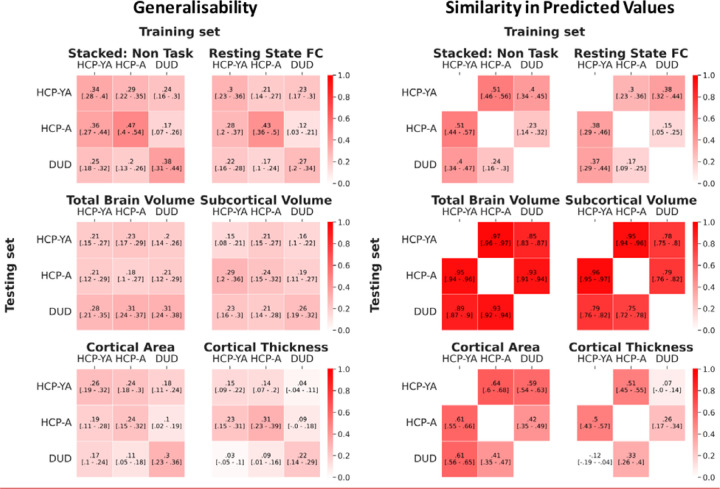
Figure 10 shows the generalisability among the three datasets. Here we tested the performance of the prediction models trained from one dataset in predicting the cognitive abilities of participants from another separate dataset, as indicated by Pearson’s correlation (r) between predicted and observed cognitive abilities. Given the different fMRI tasks used in different datasets, we only examined the generalisability of the prediction models using non-task sets of features (including rest FC, cortical thickness, cortical surface area, subcortical volume, total brain volume and their combination, or “Stacked: Non Task”). Note that even the fMRI tasks with the same name, “the facename task” and “face or emotion processing” tasks were implemented differently across different datasets (see Methods).
Figure 10. Generalisability and similarity in predicted values among the three datasets, as indicated by Pearson’s correlation, r.
Note that due to the different tasks used in different datasets, we only examined the generalisability of prediction models built from non-task sets of features (including rest FC, cortical thickness, cortical surface area, subcortical volume, total brain volume and their combination, or “Stacked: Non Task”). For generalisability, the off-diagonal values reflect the level of generalisability from one dataset to another, while the diagonal values reflect the predictability of the models built from the same dataset via nested cross-validation (CV). For the similarity in predicted values, the off-diagonal values reflect the level of similarity in predicted values between two datasets. Higher values are better. The values in square blankets reflect a bootstrapped 95% Confidence Interval (CI). If 95% CI did not include zero, then generalisability/similarity in predictive values was better than chance. HCP-YA = HCP Young Adults; HCP-A = HCP Aging; DUD = Dunedin Study.
The “Stacked: Non Task” model showed generalisability at M=.25 (SD=.06). This level of cross-dataset generalisability was significantly better than chance (see the 95%CI in Figure 10) and was similar to, albeit numerically smaller than, the within-dataset predictability of the models built from nested cross-validation (CV) (M=.4, SD=.05). There were some differences in generalisability among pairs of studies. Generalisability was numerically higher between HCP Young Adults and HCP Aging (M=.33, SD=.04), as compared to between Dunedin Study and the other two datasets (M=.22, SD=.03).
Similarly, the non-stacked models with non-task sets of features showed generalisability at M=.18 (SD=.05). Apart from cortical thickness, the generalisability of every other non-task set of features was significantly better than chance (see the 95% CI in Figure 10). Additionally, this level of cross-dataset generalisability from the non-task sets of features was similar to the within-dataset predictability of the models built from nested CV (M=.25, SD=.05).
We also examined the similarity in predicted values among the three datasets. Here we tested the Pearson’s correlation (r) in predicted values between the prediction models built from the same dataset and those built from another dataset (Figure 10). The “Stacked: Non Task” model showed similarity in predicted values at M=.38 (SD= .12). This level of similarity was significantly better than chance (see the 95%CI in Figure 10). As for the non-stacked models with non-task sets of features, we found the similarity in predicted values on average at M=.57 (SD=.11) and all of them were significantly better than chance (see the 95%CI in Figure 10). Yet, some non-task sets of features appeared to be stronger in similarity than others. For instance, the similarity in predicted values for the total brain volume (M=.92, SD=.04) and subcortical volume (M=.84, SD=.09) were numerically higher than those for rest FC (M= .29, SD= .10), cortical area (M= .55, SD= .09) and cortical thickness (M= .26, SD= .22).
Discussion
Here, we examined stacking as a potential solution for improving BWAS for cognitive abilities in three key aspects: predictability, test-retest reliability and generalisability(16, 20, 21). Most BWASs use one single modality of MRI to build prediction models, but here, we drew information across different MRI modalities via stacking(26). Stacked models demonstrated improvement in all three aspects and performed better than any individual modality in isolation. For predictability, stacked models led to high predictability, relative to what has been reported in the literature, across the three datasets when predicting cognitive abilities at the time of scanning. Notably, using the Dunedin Study, we were able to predict participants’ cognitive abilities at ages 7, 9, and 11 using their multimodal MRI at age 45, relatively well (r=.52). We found this predictive performance was driven by task contrasts, followed by task connectivity, across the three datasets. For test-retest reliability, stacked models reached an excellent level of reliability across HCP Young Adults and Dunedin Study, even when we only included fMRI during tasks in the models. For generalisability, combining non-task MRI features into a stacked model led to models that were applicable to other datasets, giving a level of performance that is better than chance. Altogether, the results optimistically support stacking as a viable approach to address the three challenges of BWAS for cognitive abilities.
Stacking Improved Predictability
Combining MRI across different sets of features via stacking consistently and substantially improved predictability within each dataset. Indeed, we found this improved predictability across three large-scale datasets that varied in age, culture, scanner manufacturer, scanning parameters and cognitive-ability assessments(27–29). This is consistent with our previous findings(24, 25). For cognitive abilities at the time of scanning, stacked models with all MRI sets of features led to r up to around .6, higher than those of non-stacked models in the current study, as well as those reported in a recent meta-analysis (r=.42 with CI95%=[0.35,0.50])(15). Moreover, our stacked models that included Task Contrasts along with other modalities showed a much higher predictive performance (e.g., r=.604, R2=. 352 based on “Stacked: All” with Elastic Net across both layers done on the HCP Young Adults), compared to the stacked models that did not include Task fMRI in the current study as well as to the models in a previous study that also modelled the data from HCP Young Adults (R2 = .078)(37). This confirms a) that different MRI sets of features provide independent but complementary information about individual differences in cognitive abilities and b) that Task Contrasts, which are often ignored, could significantly help improve the predictive performance.
The superior predictability of Task Contrasts from certain tasks, especially when predicting cognitive abilities at the time of scanning, was also consistent with previous work(24, 25, 39, 50). The working-memory task in HCP Young Adults and the facename task in HCP Aging and Dunedin Study created non-stacked models with the highest predictability for each dataset. The more popular MRI modalities, Task FC and Rest FC(15), did not perform as strongly as the Task Contrasts from working-memory and facename tasks. And structural MRI seemed to provide much poorer predictability across datasets, consistent with earlier work(49). It is important to note that not all Task Contrasts produced prediction models with high predictability. In fact, the worst prediction models across the three studies were also Task Contrasts (e.g., the gambling, CARIT and MID tasks in HCP Young Adults, HCP Aging and Dunedin Study, respectively). This suggests the selectivity of the fMRI BOLD activity relevant to events for different tasks--some tasks were related to individual differences in cognitive abilities and some tasks were not. The best tasks here were related to either working memory or episodic memory, which might reflect what was being measured with the cognitive-ability assessments(17, 63), i.e., through NIH Toolbox(64) or Wechsler Adult Intelligence Scale (WAIS)(65). Accordingly, to further improve the predictability of BWAS for cognitive abilities via task contrasts, future research will need to determine which tasks are more relevant to cognitive abilities.
We also examined the predictability of stacked models in light of the Dunedin Study’s longitudinal measurements for cognitive abilities(28). Stacked models with all MRI sets of features were able to predict cognitive abilities, collected 36 years before the scanning time, at a similarly high level of performance to those at the time of scanning (r=.55 vs. r=.52, respectively). Yet, when predicting the residual scores, the stacked models with all MRI sets of features gave much lower predictability, albeit still significant, at r=.17. These residual scores reflect changes in cognitive abilities from childhood to middle age, compared to participants’ peers. This pattern of results may suggest that brain information revealed by multimodal MRI, obtained in the middle age (i.e., 45 years old), is more related to the stable trait of cognitive abilities, but less to the changes over 35 years. Perhaps this is because individual differences in cognitive abilities were stable over the lifespan(1), making it easier for multimodal MRI to capture their inter-variability over intra-individual variability. Using the Dunedin Study, we indeed found a high rank stability of this trait: that childhood cognitive abilities were related to middle-aged cognitive abilities at ICC=.78, and that the multimodal MRI predicted values of cognitive abilities based on either time points led to very similar scores at r=.94 (see Figure 2F and 2G). Accordingly, if the aim of BWAS is to capture the stable trait of cognitive abilities, the current approach of stacking multimodal MRI data from one time point seems appropriate.
To explain how each model made predictions, we treated Elastic Net coefficients as indicators of feature importance. Examining the feature importance in the stacked models revealed that the top-performing modality, specifically the best Task Contrasts, was the strongest contributor. This pattern was consistent across datasets. This suggests that the top-performing Task Contrasts, such as the working-memory task in HCP Young Adults and the facename task in HCP Aging and the Dunedin Study, provided strong and unique contributions to the overall prediction of the stacked models. Examining the feature importance of these top-performing Task Contrasts illustrates the contribution from each brain area. We grouped brain areas into 13 different networks based on the Cole-Anticevic definition (66). Contributions from different brain networks varied depending on the specific Task Contrasts, datasets, and cognitive target variables. Nonetheless, some patterns emerged. For instance, Task Contrasts from brain areas within the default mode network were mostly associated with negative predicted scores. Conversely, Task Contrasts from brain regions within the dorsal attention network were associated with positive predicted scores, including cognitive abilities at the time of scanning, cognitive abilities 35 years prior, and the residual scores. Accordingly, we demonstrated the contribution from certain networks within the context of the specific tasks in predicting cognitive abilities.
Stacking Improved Test-Retest Reliability
Creating prediction models from separate MRI sets of features and combining them via stacking also improved reliability for Dunedin Study(28), especially for Task Contrasts, similar to our previous findings(25) with HCP Young Adults(29). This approach, in effect, addresses the poor reliability of Task Contrasts, found earlier in the same two datasets(20). That is, previous work(20) focused on the reliability of Task Contrasts at specific brain areas from certain tasks and found low test-retest reliability (also demonstrated here in Figure S30-31). Here instead of focusing on specific areas, we used multivariate methods and stacking to draw information across the whole brain and tasks and found a boost in reliability. Indeed, stacked models that combined only Task Contrasts and that combined Task Contrasts and FC together both gave the ICC at excellent levels (i.e., ICC≥.75) across the two datasets.
While the prediction models from structural MRI sets of features, e.g., surface area, total brain volume, subcortical volume, led to the highest level of test-retest reliability, these models provided poorer predictability for cognitive abilities. This high level of test-retest reliability from structural MRI is not surprising since we should not expect drastic changes in brain anatomy in a short period of time, assuming no major brain incidents (e.g., concussion or stroke) (20). In contrast, the stacked models from Task Contrasts and FC also provided an excellent level of test-retest reliability (albeit not as high as structural MRI models), but they gave much higher predictability. Accordingly, future BWAS for cognitive abilities that would like to optimise both reliability and predictability might prefer stacking Task Contrasts and FC, or better yet stacking all the MRI data available, rather than relying on structural MRI.
Stacking of Non-Task MRI Sets of Features Led to Better-Than-Chance Generalisability
Unlike predictability and reliability, we could only focus on the Non-Task MRI sets of features (including rest FC, cortical thickness, cortical surface area, subcortical volume and total brain volume) for cross-cohort generalisability, given the differences in fMRI tasks used in each dataset. We found that the “Stacked: Non Task” models, built from one dataset, predicted the cognitive abilities of the participants in the other two datasets better than chance. Still, if we treated the within-dataset predictability as the ceiling of cross-dataset generalisability, the cross-dataset generalisability of the “Stacked: Non Task” Models (r=.25) was numerically lower than, the ceiling (r=.4).
One caveat is that the generalisability of the “Stacked: Non Task” models between HCP Young Adults and HCP Aging (r=.33) is numerically higher than those between Dunedin Study and the two HCP datasets (r=.22). Consistent with this is the numerically higher similarity in predicted values between HCP Young Adults and HCP Aging (r=.51) compared to between Dunedin Study and the two HCP datasets (r=.32). This may reflect a higher homogeneity between the two HCP datasets. While the two HCP datasets differed in the age of participants and certain scanning parameters (e.g., TR length), HCP Aging(27) was modelled after the earlier success of HCP Young Adults(29). The two HCP datasets, for instance, used the NIH Toolbox(64) to access cognitive abilities, while Dunedin Study(28) used WAIS(65). Nonetheless, testing generalisability on Dunedin study that was conducted independently from the Human Connectome Projects may provide a more realistic picture of how deployable the “Stacked: Non Task” models to indicate cognitive abilities in the real world.
As for the non-stacked models, cross-cohort generalisability was mostly significant, except for cortical thickness. This is in line with previous studies focusing on cross-dataset generalisability of Rest FC(55–57). The generalisability of structural MRI sets of features was more varied. Some structural MRI sets gave generalisability close to predictability and provided high similarity in predicted values: total brain volume (generalisability=.24, predictability=.23 and similarity=.92) and subcortical brain volume (generalisability=.21, predictability=.22 and similarity=.84). But other structural MRI sets did not: cortical areas (generalisability=.16, predictability =.27 and similarity=.55) and cortical thickness (generalisability=.10, predictability=.23 and similarity r=.26). It is hard to pinpoint whether this is due to the differences in scanning parameters between datasets or, instead, due to the nature of the sets of features. Future research with a larger number of datasets is needed to pinpoint the characteristics of the datasets and/or features that could lead to better generalisability.
Limitations and Future Directions
The current study has several limitations. First, it would have been desirable to examine the generalisability of stacked models involving Task Contrasts and Task FC in all cohorts. Stacked models involving Task Contrasts and FC scored high in both predictability (especially when compared to “Stacked: Non Task” models) and reliability. The inability to test their generalisability means that we cannot know for sure how deployable these highly predictable models are. Thus, for the time being, we advise researchers who would like to apply the stacked models with task fMRI on new data to follow the procedures of the original datasets as much as possible. This could be task design and scanning parameters among others.
Second, we mainly relied on the fMRI tasks and pre-processing pipelines chosen by the original investigators of each dataset. However, the fMRI tasks they chose might not be optimised for predictability, reliability and generalisability for cognitive abilities. As suggested elsewhere(52), perhaps fMRI tasks need to be designed from the ground up, using tools such as item response theory, to ensure that they capture individual differences well. Fortunately, some of the fMRI tasks (e.g., the working-memory and language tasks) provided relatively high predictability and reliability for cognitive abilities. Based on our results, in a situation where optimisation of the tasks is unknown, stacking Task Contrasts and Task FC across all of the available fMRI tasks should provide the best performance possible, given the choice of the tasks used. Similarly, each dataset’s pre-processing approach might not be optimised for BWAS with cognitive abilities as a target. For instance, for Rest FC in HCP Young Adults, we treated a choice of the two denoising strategies as another hyperparameter to select from the training sets: the investigators’ recommended method, ICA-FIX (67) and an alternative method, aCompCor(68). We found that aCompCor(68) performed better in the training sets across different prediction algorithms (see Figure S29), despite not being used in the original pre-processing pipeline(29, 69, 70). While using the recommended pre-processing pipeline for each dataset allowed for easier reproducibility, we still need to test if predictability, reliability and generalisability could be further improved with more refined pipelines, optimised for predicting cognitive abilities.
Third, while predictability, reliability and generalisability are important for multimodal MRI to be applied as a neural indicator for cognitive abilities(21), other aspects still need to be accomplished for cognitive neuroscientists to truly understand the relationship between cognitive abilities and multimodal MRI measures. For instance, to reveal how the prediction models draw information from each MRI set of features, we need prediction models with good explainability(17, 71). Yet, the current prediction models are optimised for predictability, but not explainability. To improve explainability, researchers, for instance, may need to tune the models such that each fold provides a similar pattern of feature importance or apply a transformation, such as Haufe’s transformation, to improve the feature-importance stability (72). However, optimising explainability is beyond the scope of this study.
Conclusions
Cognitive neuroscientists have long dreamt of the ability to associate individual differences in cognitive abilities with brain variations(10). Yet, BWASs need to be improved in their predictability, test-retest reliability and generalisability before they can produce a robust neural indicator for cognitive abilities(16, 20, 21, 73, 74). Based on our benchmark, combining different modalities of MRI into one prediction model via stacking seems to be a viable approach to realise this dream of cognitive neuroscientists.
Materials and Methods
1. Datasets
In this study, we used three datasets with 2,131 participants in total (see Figure 1 for their age distribution):
1.1. Human Connectome Project Young Adults (HCP Young Adults):
HCP Young Adults S1200 Release included multiple MRI modalities and cognitive measurements from 1,206 healthy participants (22–35 years old)(29, 75). We excluded participants with the “A” (anatomical anomalies) or “B” (segmentation and surface) flag, with any known major issues(76) or with any incomplete MRI or cognitive measurements(25). These exclusions left 873 participants (473 females, M=28.7 (SD=3.7) years old) in our analysis.
1.2. Human Connectome Project Aging (HCP Aging):
HCP Aging 2.0, released on 24th February 2021, consisted of ‘typical-aging’ participants, from 36 to 100 years old, without identified pathological causes of cognitive decline (e.g., stroke and clinical dementia)(27). This release provided data from 725 participants. After applying the same exclusion criteria as HCP Young Adults, 504 participants (293 females, M=57.83 (SD=14.25) years old) remained in our analysis.
1.3. The Dunedin Multidisciplinary Health and Development Study (Dunedin Study):
Dunedin Study is a longitudinal study of the health and behaviours of 1,037 individuals, born between April 1972 and March 1973 in Dunedin, a small city in the South Island of New Zealand(28). Dunedin Study has conducted many assessments on the participants since birth. The study collected MRI data of multiple modalities from 875 participants when they were 45 years old. After excluding incomplete MRI or cognitive measurements, 754 participants (373 females) remained in our analysis.
1.4. Test-Retest Subsets:
HCP Young Adults and Dunedin Study had a subset of participants who completed the entire MRI procedure twice. In HCP Young Adults, 45 participants were scanned M=139 (SD=67.3) days apart, and the exclusion criteria left 34 participants. In Dunedin Study, 20 participants were scanned M=79 (SD=10.4) days apart.
2. Features: Multimodal MRI
We used the following MRI modalities: task-fMRI contrasts, task-fMRI functional connectivity, resting state fMRI connectivity and structural MRI.
2.1. Task-fMRI contrasts (Task Contrasts)
Task Contrasts reflect fMRI BOLD activity relevant to events in each task. We used Task Contrasts, pre-processed by each of the three studies.
HCP Young Adults:
HCP Young Adults provided complete details of scanning parameters and pre-processing pipeline elsewhere(29, 69, 70). Briefly, they implemented 720-ms TR, B0 distortion correction, motion correction, gradient unwrap, boundary-based co-registration to T1-weighted image, non-linear registration to MNI152 space, grand-mean intensity normalization, high-pass filtering with a cut-off at sigma = 200s, surface generation and the multimodal alignment protocol (MSMAll)(67). The study included seven fMRI tasks, each with two runs with different phase encodings: left-to-right (LR) and right-to-left (RL). HCP Young Adults applied a general-linear model (GLM) to combine the two runs and computed GLM contrasts in a Connectivity Informatics Technology Initiative (CIFTI) format, containing both cortical surface and subcortical volume. We parcellated these contrasts into 379 regions of interest (ROIs), consisting of 360 cortical-surface ROIs from the Glasser atlas(67) and 19 subcortical ROIs from the Freesurfer’s Automatic subcortical SEGmentation (ASEG) atlas (77). We then extracted the average value for each ROI.
In each of the seven tasks, we chose only one GLM contrast between the main experimental vs. control conditions. The study provided full task descriptions for these conditions in the release documentation(69, 78). We used the following contrasts: face vs. shape for the face, or emotion-processing, task(79), reward vs. punishment for the gambling task(80–83), story vs. math for the language task(84), averaged movement vs. cue for the motor task(85–88), relational vs. match for the relational task(89), theory of mind vs. random for the social cognition task(90–93) and 2-back vs. 0-back for the working memory task(94). Accordingly, we obtained seven sets of 379 (i.e., ROIs) task-contrast features for HCP Young Adults.
HCP Aging:
HCP Aging used similar scanning parameters and a pre-processing pipeline to HCP Young Adults(27, 70, 95). There were a few differences: task fMRI was collected using TR at 800 ms (as opposed to 720 ms) and using the posterior-to-anterior (PA) phase (as opposed to LR and RL), and the investigators applied linear detrend (as opposed to high-pass filtered cut-off at sigma = 200s ) and ICA-FIX(67).
HCP Aging did not provide task contrasts, but rather pre-processed time series in the CIFTI format for each task. To extract task contracts from the time series, we applied the “fake” NIFTI approach(96) using FMRI Expert Analysis Tool (FEAT) from FMRIB Software Library (FSL)(97). Here we first transformed the CIFTI file into a 32767×3 NIFTI array, then conducted GLM and converted the output contrasts back into the CIFTI format. For the GLM, we modified the fsf-template file, given by the HCP Aging (https://github.com/Washington-University/HCPpipelines/tree/master/Examples/fsf_templates/HCP-Aging). Specifically, we regressed the time series on the convolved task events using a double-gamma canonical hemodynamic response function (HRF). We used a default high pass cut-off in FSL at sigma = 200s. Similar to HCP Young Adults, we parcellated the contrasts into 379 ROIs using the Glasser(67) and ASEG(77) atlases for cortical and subcortical regions, respectively.
HCP Aging included three fMRI tasks(27). Similar to HCP Young Adults, we chose GLM contrasts between the main experimental vs. control conditions. We used the following contrasts for each task: encoding vs. distractor, recall vs. distractor and encoding vs. recall for the facename task(98–100), NoGo vs. Go for the Conditioned Approach Response Inhibition Task (CARIT) go-nogo task (101), and stimulus vs. baseline for the visual motor (VisMotor) task(27). Note the facename task taps into episodic memory. There were three blocks: “Encoding” when participants needed to memorise the names of faces, “Distractor” when participants were distracted by an irrelevant task and “Recall” when participants needed to recall the names of the previously shown faces. Because each block reflects different processes of episodic memory, we chose all possible pairs of contrasts for this task. Accordingly, we obtained five sets of 379 task-contrast features for HCP Aging.
Dunedin Study:
Dunedin Study provided complete details of the scanning parameters and pre-processing pipeline elsewhere(20, 53). Briefly, the Dunedin Study investigators implemented 2000-ms TR, B0 distortions correction(102), despike(103), slice-timing and motion correction(103), boundary-based co-registration to T1-weighted image(104) and non-linear registration to MNI space(105, 106). The study applied a general-linear model (GLM) using the AFNI 3dREMLfit(103)and applied the HCP Minimal Preprocessing Pipeline (MPP) (https://github.com/Washington-University/HCPpipelines/releases) to project the contrast images into Cifti format. Similar to the HCP Young Adults and HCP Aging, the study parcellated the contrasts into 379 ROIs using the Glasser(67) and ASEG(77) atlases using the Ciftify toolbox (https://github.com/edickie/ciftify).
Dunedin Study included four fMRI tasks(20). The study provided us with the following contrasts: encoding vs. distractor for the facename task(100), face vs. shape for the face, or emotion processing, task(79), gain vs. neutral anticipation for the monetary incentive delay (MID) task(107) (see https://www.haririlab.com/methods/dbis_vs.html) and incongruent vs. congruent for the Stroop task (see https://www.haririlab.com/methods/dbis_control.html). Note the facename task in Dunedin Study was different from that in HCP Aging. During “Distractor”, participants in the Dunedin study had to perform an odd/even-number identification task (https://www.haririlab.com/methods/dbis_hippocampus.html) whereas participants in the HCP Aging had to perform a Go/NoGo task(27, 100). The face, or emotion processing, task in Dunedin Study was also different from that in HCP Young Adults. The Dunedin Study version included four different facial expressions: fearful, angry, surprised or neutral (see https://www.haririlab.com/methods/dbis_amygdala.html) and lasted 6:40 minutes, whereas the HCP Young Adults version had only two facial expressions: angry and fearful and lasted only 2:16 minutes. Altogether, we obtained four sets of 379 task-contrast features for Dunedin Study.
2.2. Task-fMRI functional connectivity (Task FC)
Task FC reflects functional connectivity during each task. Studies have considered task FC as an important source of individual differences(53, 108, 109). As opposed to creating contrasts from fMRI time series during each task as in Task Contrasts, here we computed functional connectivity, controlling for HRF-convolved events from each task.
HCP Young Adults:
Because HCP Young Adults did not provide denoised fMRI time series for each task, we denoised the time series ourselves. We first converted raw task fMRI data into Brain Imaging Data Structure (BIDS)(110) using the hcp2bids function from MICA (https://github.com/MICA-MNI/micapipe-supplementary/blob/main/functions/hcp2bids). To pre-process the BIDS data, we applied fMRIPrep(111, 112) without slice-timing correction. We then used XCP-D(113) to further process the data. Specifically, we used the aCompCor(68) flag and created customised regressors for task events, leaving the following regressors of no interest in our GLM: HRF-convolved task events, 12 motion estimates (i.e., x, y, z rotation and translation and their derivatives), five white-matter and five cerebrospinal fluid aCompCor components, a linear trend, a cosine (1/128Hz) and an intercept. We, then, concatenated LR and RL runs and parcellated the time series into 379 ROIs using the Glasser(67) and ASEG(77) atlases. Subsequently, we computed r-to-z transformed Pearson’s correlations across all possible pairs, resulting in 71,631 non-overlapping FC indices for each task. To reduce the dimensionality of task FC, we applied principal component analysis (PCA) of 75 components (37, 39, 114). To avoid data leakage, we conducted PCA on each training set and applied its definition to the corresponding test set. Note we calculated task FC for all of the tasks in HCP Young Adults except the emotion processing task due to its short duration (2:16 mins). Accordingly, we obtained six sets of 75 task FC features for HCP Young Adults.
HCP Aging:
Unlike HCP Young Adults, the fMRI time series for each task in HCP Aging was denoised by ICA-FIX(67). Accordingly, we did not implement fMRIprep(111, 112) and XCP-D(113) to clean the HCP Aging time series further. Instead, we only regressed out the HRF-convolved task events from the time series and applied a high-pass filter at 0.008 Hz following previous work(53) using nilearn(115). For each of the three tasks, we applied the same parcellation, Pearson’s correlation, r-to-z transformation and PCA as we did for HCP Young Adults. Accordingly, we obtained three sets of 75 task FC features for HCP Aging.
Dunedin Study:
The study provided denoised time series and details on their denoising strategies elsewhere(53). Briefly, they applied the following regressors of no interest in their GLM: 12 motion estimates with derivatives, five CompCor components from white-matter and from cerebrospinal fluid(68), the mean global signal, and task-evoked coactivations via AFNI TENT(103). The study also implemented bandpass filtering between 0.008 and 0.1 Hz and censored motion artefacts with thresholds of 0.35-mm framewise displacement and 1.55 standardised DVARS. For each of the four tasks, we used the same parcellation, Pearson’s correlation, r-to-z transformation and PCA as we did for HCP Young Adults and HCP Aging. Accordingly, we obtained four sets of 75 task FC features for Dunedin Study.
2.3. Resting-state fMRI functional connectivity (Rest FC)
Rest FC reflects functional connectivity during rest. Both HCP Young Adults and HCP Aging included four runs of rest FC, each at 14:33 min and 6:42 min long, respectively. Dunedin Study included only one run of rest FC with 8:16 min long.
HCP Young Adults:
We applied two denoising strategies on the fMRI time series during rest. The first strategy was ICA-FIX(67) which was done by the study. Specifically, we high-pass-filtered the provided ICA-FIX-denoised time series at 0.008Hz using nilearn(115) and concatenated them across four runs. The second strategy was aCompCor(68). We applied the same pre-processing steps on rest FC as we did on task FC for HCP Young Adults (see above), except that here we did not use HRF-convolved task events as regressors of no interest since there were no events. We chose to apply this aCompCor strategy in addition to ICA-FIX, so that rest FC and task FC for HCP Young Adults were consistent with each other.
HCP Aging:
The study applied ICA-FIX(67) to denoise fMRI time series during both rest and tasks, meaning that the denoising strategies done by the study for rest FC and task FC were already consistent with each other. Accordingly, we only used ICA-FIX(67) here. Like HCP Young Adults, we further applied high-pass filtered at 0.008Hz on the provided ICA-FIX-denoised time series and concatenated them across four runs.
Dunedin Study:
The Dunedin Study investigators applied the same denoising strategies to Rest FC as they did to Task FC(53) (see above), leaving bandpass-filtered time series.
For each of the three datasets, we took the denoised, filtered time series and applied the same parcellation, Pearson’s correlation, r-to-z transformation and PCA as we did for Task FC. Accordingly, we obtained one set of 75 rest FC features for each of the datasets.
2.4. Structural MRI
Structural MRI reflects individual differences in brain anatomy. The three studies applied Freesurfer(77) to quantify these individual differences. Here we focused on four sets of features: cortical thickness, cortical surface area, subcortical volume and total brain volume. For cortical thickness and cortical surface area, we parcellated the cortical regions into 148 ROIs using the Destrieux atlas(116), leaving two sets of 148 features. For subcortical volume, we parcellated the subcortical regions into 19 ROIs using the ASEG atlas(77), leaving one set of 19 features. For total brain volume, we included five summary statistics from Freesurfer(77): total cortical grey matter volume (FS_TotCort_GM_Vol), total cortical white matter volume (FS_Tot_WM_Vol), total subcortical grey matter volume (FS_SubCort_GM_Vol), estimated intra-cranial volume (FS_IntraCranial_Vol) and ratio of brain segmentation volume to estimated total intracranial volume (FS_BrainSegVol_eTIV_Ratio). This left another set of five features.
3. Target: Cognitive abilities
Cognitive abilities were measured outside of the MRI. HCP Young Adults and HCP Aging measured cognitive abilities using the NIH Toolbox (64). Here we used a summary score (CogTotalComp_Unadj) that covered behavioural performance from several tasks, including picture sequence memory, Flanker, list sorting, dimensional change card sort, pattern comparison, reading tests and picture vocabulary.
Dunedin Study measured cognitive abilities in several visits. We computed three scores and used them as separate targets. The first score is cognitive abilities, collected as part of the MRI visit at 45 years old via the Wechsler Adult Intelligence Scale (WAIS) IV scale(65). The second score is cognitive abilities, averaged across 7, 9 and 11 years old, collected using the Wechsler Intelligence Scale for Children - Revised (WISC-R)(117). The third score is the residual scores for the cognitive abilities(62), calculated as follows. We, first, used linear regression to predict cognitive abilities at 45 years old from cognitive abilities at 7, 9, and 11 years old. We, then, subtracted the predicted values of this linear regression from the actual cognitive abilities at 45 years old, creating the residual cognitive abilities. Negative scores of these residual cognitive abilities reflect a stronger decline in cognitive abilities, as expected from childhood cognitive abilities, compared to participants’ peers. Note see Prediction models below for our approach to prevent data leakage when calculating this residual score.
4. Prediction models
Similar to our previous work(25), we employed nested cross-validation (CV) to predict cognitive abilities from multimodal MRI data (see Figure 1). Initially, we divided the data from each study into outer folds. The number of outer folds was determined to ensure at least 100 participants per fold. Consequently, we had eight outer folds for HCP Young Adults, five for HCP Aging, and seven for the Dunedin Study. For HCP Young Adults, which included participants from the same families, we created the eight outer folds based on approximately 50 family groups, ensuring that members of the same family were in the same outer fold.
We then iterated through the outer folds, treating one fold as the test set and the remaining folds as the training set. This approach resulted in around 100 participants in each outer-fold test set for all three studies, with approximately 700, 400, and 600 participants in the outer-fold training sets for HCP Young Adults, HCP Aging, and the Dunedin Study, respectively. Next, we split each outer-fold training set into five inner folds. We iterated through these inner folds to tune the hyperparameters of the prediction models, selecting the final models based on the coefficient of determination (R²), a default option in sklearn. To prevent data leakage between the outer-fold training and test sets when calculating residual scores for cognitive abilities in the Dunedin Study, we created linear regression models to predict cognitive abilities at age 45 from abilities at ages 7, 9, and 11 using the outer-fold training set, and applied these models to the corresponding outer-fold test set.
Apart from using each of the sets of multimodal MRI features in separate prediction models, known as “non-stacked” models, we also combined different sets together via stacking, known as “stacked” models (see Figure 1). Here, we first computed predicted values from different sets of features from each outer-fold training set. We then treated these predicted values as features to predict cognitive abilities, creating the stacked models. We tuned these stacked models using the same inner-fold CV as the non-stacked models. Accordingly, the training of stacked and non-stacked models did not involve outer-fold test sets, preventing data leakage. We created eight stacked models: “Task Contrast” including Task Contrasts from all of the tasks, “Task FC” including Task FC from all of the tasks, “Non Task” including Rest FC and structural MRI, “Task Contrast & FC” including task contrasts and task FC from all of the tasks, “All” including all sets of features, “All excluding Task Contrast” including every set of features except Task Contrasts, “All, excluding Task FC” including every set of features except Task FC, “Resting and Task FC” including FC during rest and tasks. Note that we used two strategies, ICA-FIX(67) and aCompCor(68), to denoise Rest FC for HCP Young Adults. We ultimately picked aCompCor(68) to be included in the stacked models since it led to a better predictive performance in the outer-fold training sets (see Figure S29).
We applied corrections to reduce the influences of potential confounds. First, for all three studies, we controlled for biological sex by residualising biological sex from all MRI features and cognitive abilities. For HCP Young Adults and HCP Aging, we also controlled for age, in addition to biological sex, from all MRI features and cognitive abilities. We did not control for age in Dunedin Study because all of the participants were scanned at around 45 years old. Additionally, we residualised motion (average of relative displacement, Movement_RelativeRMS_mean) from task contrasts for HCP Young Adults and Dunedin Study. We did not residualise motion from task contrasts for HCP Aging as well as task FC and rest FC for all studies since either ICA-FIX(67) or aCompCor(68) was already applied to each participant. We also standardised all MRI features. To avoid data leakage, we first applied all residualisation and standardisation on each outer-fold training set. We then applied the parameters of these residualisation and standardisation to the corresponding outer-fold test set.
As in our previous article(25), we implemented four multivariate, predictive-modelling algorithms via Scikit-learn (118): Elastic Net(58), Support Vector Regression (SVR)(59, 119), Random Forest(60) and XGBoost(61). For stacked models, we needed to apply the algorithm to two layers: 1) non-stacked layer (Step 1, Figure 1), or on each set of features and 2) stacked layer (Step 2, Figure 1), or on the predicted values from each set. Accordingly, we implemented 16 (i.e., four-by-four across two layers) combinations of algorithms for the stacked models.
Elastic Net(58) is a general form of penalized regression. Elastic Net has two hyperparameters: 1) ‘α’, determining the degree of penalty to the sum of the feature’s slopes and 2) ‘l1 ratio’, determining the degree to which the sum of either the squared (known as ‘Ridge’; l1 ratio=0) or absolute (known as ‘Lasso’; l1 ratio=1) slopes is penalised. We performed a logarithmic scale grid search on the 70 possible α values, ranging from 10−1 to 102, and a linear scale grid search on the 25 possible l1 ratio values, ranging from 0 to 1.
Support Vector Regression (SVR) (59, 119) is a kernel-based algorithm. Unlike Elastic Net, SVR with the Radial Basis Function (RBF) allows for non-linearity between each feature and the target and interaction among features. We tuned the following hyperparameters: 1) ‘ε’, determining the margin of tolerance where no penalty is given to errors, 2) ‘γ’, determining the kernel coefficient, 3) ‘C’ or ‘complexity,’ determining penalty for high complexity. We performed a linear scale grid search on the 10 possible ε values, ranging from 0.02 to 0.22. We also performed a grid search on 20 possible γ values, using the following set: 10−8, 10−7, 10−6, 10−5, 10−4, 10−3, 3*10−8, 3*10−7, 3*10−6, 3*10−5, 3*10−4, 3*10−3, 6*10−8, 6*10−7, 6*10−6, 6*10−5, 6*10−4, 6*10−3 as well as one over the multiplication of the number of features and variance of features (known as ‘scale’ in sklearn) and one over the number of features (known as ‘auto’ in sklearn). Finally, we also performed a grid search on eight possible C values using the following set: 1, 6, 9, 10, 12, 15, 20 and 50.
Random Forest(60) is a tree-based algorithm. The algorithm bootstraps observations and incorporates a random subset of features at each split of tree building. The algorithm made predictions based on an aggregation of predicted values across bootstrapped trees. Like SVR with RBF, Random Forest allows for a non-linear relationship between each feature and the target and for interactions amongst features. Here we used 5000 trees (‘n_estimators’) and tuned two hyperparameters: 1) ‘max_depth’, determining the maximum depth of each tree and 2) ‘max_feature’, determining the number of features that are randomly sampled at each split. We performed a grid search for 10 possible max_depth values, using the integers ranging from 1 to 10. We also performed a grid search for three possible max_feature values: the number of features itself, the square root of the number of features and log-based 2 of the number of features.
XGBoost(61) is another tree-based algorithm, which also allows for non-linearity and interaction. It generates sequential trees where a current tree adapts from the gradients of previous trees. We used ‘gbtree’ as a booster and tuned four hyperparameters: 1) ‘max_depth’, determining the maximum depth of each tree, 2) ‘γ’, determining a minimum loss reduction required to make a further partition on a leaf node of the tree, 3) ‘subsample’, determining the ratio of the training instance, 4) ‘learning_rate’, determining the speed of tree adaptation. We performed a linear scale grid search on nine possible max_depth values using integers, ranging from 1 to 9. We also performed a logarithmic scale grid search on the six possible γ values, ranging from 10−5 to 0.7. Next, we performed a grid search on three possible subsample values: 0.6, 0.8 and 1. Lastly, performed a logarithmic scale grid search on the five learning_rate values, ranging from 10−5 to 10−0.1. For other hyperparameters, we used their default values (see https://xgboost.readthedocs.io/).
5. Predictability
To evaluate the predictability of prediction models, we computed the predicted values of the models at each outer-fold test set and compared them with the observed cognitive abilities. We calculated three performance indices for predictability: Pearson’s correlation (r), the coefficient of determination (R2) and mean absolute error (MAE). Note for R2, we applied the sum of squares definition (i.e., R2 = 1 – (sum of squares residuals/total sum of squares)) and not the square of r, following a previous recommendation(31).
To quantify the uncertainty around these performance indices, we calculated bootstrapped 95% confidence intervals (CI)(120). Here, we combined predicted and observed cognitive abilities across outer-fold test sets, sampled these values with replacement 5,000 times and computed the three performance indices each time, giving us a bootstrapped distribution for each index. If the 95% CI of the r or R2 bootstrapped distribution were higher than zero, then the predictability from a particular prediction model was better than chance.
To compare predictability among prediction models, we also used the bootstrapping approach(120). Similar to the above, we sampled, with replacement for 5,000 times, the observed cognitive abilities along with their predicted values from different prediction models across outer-fold test sets. In each sample, we computed each performance index of each prediction model and subtracted this index from that of the prediction model with the highest predictability of each dataset. If the 95% CI of this distribution of the subtractions were higher than zero, then we concluded that the prediction model we tested had significantly poorer performance than the prediction model with the highest predictability. We applied this approach separately for non-stacked and stacked models, allowing us to evaluate the best non-stacked and stacked models for each dataset.
To understand how the prediction models drew information across multimodal MRI features, we plotted Elastic-Net coefficients. We chose Elastic-Net coefficients because 1) Elastic Net led to high predictability, as high as or higher than other algorithms (see Results), and 2) the Elastic Net coefficients are readily interpretable. Elastic Net creates a predicted value from a weighted sum of features, and therefore a stronger magnitude of an Elastic Net coefficient means a higher contribution to the prediction.
Our use of nested CV led to separate Elastic-Net models, one for each outer fold, making it hard to visualise Elastic-Net coefficients across all participants in each dataset. To address this, we retrained Elastic Net using the whole data (i.e., without splitting the data into outer folds) in each dataset and applied five CVs to tune the model. We then plotted the Elastic-Net coefficients on brain images using brainspace(121) and nilearn(115). Note we modelled Task FC and Rest FC after reducing their dimension via PCA. To extract the feature importance at each ROI-pair index, we multiplied the absolute PCA scores with Elastic Net coefficients and then summed the multiplied values across the 75 components, resulting in 71,631 ROI-pair indices.
6. Test-Retest Reliability
Given the high predictability of Elastic Net (see Figures S17-26), we evaluated the test-retest reliability of the prediction models based on Elastic Net. To evaluate test-retest reliability, we used HCP Young Adults and Dunedin Study test-retest subjects (i.e., participants who were scanned twice) as the test set and the rest of the participants in each dataset as a training set. Within the training set, we used the same five CVs to tune the Elastic Net models, as described above. We then examined the test-retest reliability of the predicted values between the first and second MRI sessions, as quantified by intraclass correlation (ICC) 3,1(122) via pingouin (https://pingouin-stats.org/):
where is mean square for participants, is mean square for error, and is the number of time points. We used the following criteria to interpret ICC(123). ICC < 0.4 as poor, ICC ≥ 0.4 and < 0.6 as fair, ICC ≥ 0.6 and < 0.75 as good and ICC ≥ 0.75 as excellent reliability.
7. Generalisability
Similar to test-retest reliability, we evaluated the generalisability of the prediction models based on Elastic Net given the high predictability of Elastic Net based on bootstrapped comparisons (see Figures S17-26). For features, because the three datasets used mostly different fMRI tasks, we focused on the generalisability of non-task sets of features (including rest FC, cortical thickness, cortical surface area, subcortical volume and total brain volume) and their stacked model, “Stacked: Non Task”. For the target, we standardised cognitive abilities using a Z-score within each dataset, so that the target for each dataset was at the same standardised scale before model fitting. This is because Dunedin Study used WAIS-IV for measuring cognitive abilities, while HCP-YA and HCP-A used NIH toolbox(64). Note, for Dunedin Study, we only focused on cognitive abilities collected during the MRI visit at age 45 (as opposed to during earlier visits) as the target, given that the other two studies only provided cognitive abilities during the MRI visit.
To evaluate generalisability across datasets, we treated one of the three datasets as a training set and the other two as two separate test sets. We computed the predicted values of the models at each test dataset and compared them with the observed cognitive abilities using Pearson’s correlation (r). To examine if the generalisability was statistically significant, we bootstrapped r 5000 times. If the 95% bootstrapped CI were higher than zero, the r was statistically significantly better than chance. We also compared generalisability across datasets to predictability within each dataset using nested CVs. For predictability within each dataset, we combined predicted values across outer test sets and compared them with the observed cognitive abilities. We considered the predictability within each dataset as the ceiling of how high generalisability across datasets could be.
To further understand the extent to which the prediction models built from one dataset are different from those built from another, we also examined the similarity between predictive values. Here, using Pearson’s correlation (r), we compared the correlation in predictive values from the prediction models built from the same dataset and those built from another dataset. Similar to generalisability, to test if the similarity between predictive values was statistically significant, we bootstrapped r 5000 times. If the 95% bootstrapped CI were higher than zero, the r was statistically significantly better than chance.
Supplementary Material
Significance statement.
For decades, psychologists and neuroscientists have attempted to predict cognitive abilities from brain magnetic resonance imaging (MRI) data but have had limited success, casting doubt on the predictive ability of brain MRI. Here we proposed a machine learning method, called stacking, which allows us to draw information across different types of brain MRI. Using three large databases (n=2,131, 22–100 years old), we found stacking to make the prediction of cognitive abilities 1) closer to actual cognitive scores when applied to a new individual, not part of the modelling process, 2) reliable over times and 3) applicable to the data collected from different age groups and MRI scanners. Indeed, stacking, especially with fMRI task contrasts, allowed us to use MRI of people aged 45 to predict their childhood cognitive abilities reasonably well. Accordingly, stacking may help MRI realise its potential to predict cognitive abilities.
Acknowledgements
We thank the Dunedin Study members, their families and friends for their long-term involvement. Thank Dunedin Unit Director, Professor Reremoana (Moana) Theodore, Unit research staff, Professor Terrie E. Moffitt, Professor Avshalom Caspi, previous Study Director, Emeritus Distinguished Professor, the late Richie Poulton, for his leadership during the Study’s research transition from young adulthood to aging (2000–2023) and Study founder, Dr Phil A. Silva. Professor Terrie E. Moffitt was especially helpful in providing comments on earlier drafts. The Dunedin Multidisciplinary Health and Development Research Unit is supported by the New Zealand Health Research Council and New Zealand Ministry of Business, Innovation and Employment. Funding support was also received from The New Zealand Health Research Council Programme Grant (16–604), US-National Institute on Aging grants AG049789–06, and R01AG032282–11 and UK Medical Research Council grants MR/X021149/1. Additional data were provided by the Human Connectome Project – Young Adults and the Human Connectome Project in Aging. The Human Connectome Project – Young Adults, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) was funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell center for Systems Neuroscience at Washington University. The Human Connectome Project in Aging was supported by the National Institute on Aging of the National Institutes of Health under Award Number U01AG052564 and by funds provided by the McDonnell Center for Systems Neuroscience at Washington University in St. Louis. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The author(s) wish to acknowledge the use of New Zealand eScience Infrastructure (NeSI) high performance computing facilities, consulting support and/or training services as part of this research. New Zealand’s national facilities are provided by NeSI and funded jointly by NeSI’s collaborator institutions and through the Ministry of Business, Innovation & Employment’s Research Infrastructure programme. URL https://www.nesi.org.nz. A.T., T.M. and N.P. were supported by Health Research Council Funding (grant number 21/618), by the University of Otago and by Neurological Foundation of New Zealand (grant number 2350 PRG).
Footnotes
Data sharing plans
All codes are available at https://github.com/HAM-lab-Otago-University/Predictability-Reliability-Generalizability.
Instructions for data access can be found here:
HCP Young Adults https://www.humanconnectome.org/study/hcp-young-adult, HCP Aging https://www.humanconnectome.org/study/hcp-lifespan-aging and Dunedin Study https://dunedinstudy.otago.ac.nz/.
While we did not preregister our data-analysis plan for HCP Young Adults and HCP Aging, we preregistered our plan to test predictability and test-retest reliability for the Dunedin study prior to having access to the dataset at https://dunedinstudy.otago.ac.nz/files/1639954373_Pat%20Multimodal%20brain%20concept%20paper_NP%20TEMsigned.docx.pdf.
References
- 1.Deary I. J., Pattie A., Starr J. M., The Stability of Intelligence From Age 11 to Age 90 Years: The Lothian Birth Cohort of 1921. Psychol Sci 24, 2361–2368 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Tucker-Drob E. M., Briley D. A., Continuity of genetic and environmental influences on cognition across the life span: A meta-analysis of longitudinal twin and adoption studies. Psychological Bulletin 140, 949–979 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Deary I. J., Strand S., Smith P., Fernandes C., Intelligence and educational achievement. Intelligence 35, 13–21 (2007). [Google Scholar]
- 4.Schmidt F. L., Hunter J., General Mental Ability in the World of Work: Occupational Attainment and Job Performance. Journal of Personality and Social Psychology 86, 162–173 (2004). [DOI] [PubMed] [Google Scholar]
- 5.Llewellyn D. J., Lang I. A., Langa K. M., Huppert F. A., Cognitive function and psychological well-being: findings from a population-based cohort. Age and Ageing 37, 685–689 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Strenze T., Intelligence and socioeconomic success: A meta-analytic review of longitudinal research. Intelligence 35, 401–426 (2007). [Google Scholar]
- 7.Calvin C. M., et al. , Childhood intelligence in relation to major causes of death in 68 year follow-up: prospective population study. BMJ j2708 (2017). 10.1136/bmj.j2708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.East-Richard C., Mercier A. R., Nadeau D., Cellard C., Transdiagnostic neurocognitive deficits in psychiatry: A review of meta-analyses. Canadian Psychology / Psychologie canadienne 61, 190–214 (2020). [Google Scholar]
- 9.Abramovitch A., Short T., Schweiger A., The C Factor: Cognitive dysfunction as a transdiagnostic dimension in psychopathology. Clinical Psychology Review 86, 102007 (2021). [DOI] [PubMed] [Google Scholar]
- 10.Deary I. J., Penke L., Johnson W., The neuroscience of human intelligence differences. Nat Rev Neurosci 11, 201–211 (2010). [DOI] [PubMed] [Google Scholar]
- 11.Sui J., Jiang R., Bustillo J., Calhoun V., Neuroimaging-based Individualized Prediction of Cognition and Behavior for Mental Disorders and Health: Methods and Promises. Biological Psychiatry 88, 818–828 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Morris S. E., Cuthbert B. N., Research Domain Criteria: cognitive systems, neural circuits, and dimensions of behavior. Dialogues in Clinical Neuroscience 14, 29–37 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Horien C., et al. , A hitchhiker’s guide to working with large, open-source neuroimaging datasets. Nat Hum Behav 5, 185–193 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Woo C.-W., Chang L. J., Lindquist M. A., Wager T. D., Building better biomarkers: brain models in translational neuroimaging. Nat Neurosci 20, 365–377 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vieira B. H., et al. , On the prediction of human intelligence from neuroimaging: A systematic review of methods and reporting. Intelligence 93, 101654 (2022). [Google Scholar]
- 16.Marek S., et al. , Reproducible brain-wide association studies require thousands of individuals. Nature 603, 654–660 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pat N., Wang Y., Bartonicek A., Candia J., Stringaris A., Explainable machine learning approach to predict and explain the relationship between task-based fMRI and individual differences in cognition. Cerebral Cortex 33, 2682–2703 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Spisak T., Bingel U., Wager T. D., Multivariate BWAS can be replicable with moderate sample sizes. Nature 615, E4–E7 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Choi S. W., Mak T. S.-H., O’Reilly P. F., Tutorial: a guide to performing polygenic risk score analyses. Nature Protocols 15, 2759–2772 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Elliott M. L., et al. , What Is the Test-Retest Reliability of Common Task-Functional MRI Measures? New Empirical Evidence and a Meta-Analysis. Psychol Sci 31, 792–806 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wu J., Li J., Eickhoff S. B., Scheinost D., Genon S., The challenges and prospects of brain-based prediction of behaviour. Nat Hum Behav 7, 1255–1264 (2023). [DOI] [PubMed] [Google Scholar]
- 22.Nature, Cognitive neuroscience at the crossroads. Nature 608, 647–647 (2022). [DOI] [PubMed] [Google Scholar]
- 23.APS, Scanning the Brain to Predict Behavior, a Daunting ‘Task’ for MRI. Association for Psychological Science - APS (2020). Available at: https://www.psychologicalscience.org/news/releases/scanning-the-brain-fmri.html [Accessed 27 September 2020]. [Google Scholar]
- 24.Pat N., et al. , Longitudinally stable, brain based predictive models mediate the relationships between childhood cognition and socio demographic, psychological and genetic factors. Human Brain Mapping 43, 5520–5542 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tetereva A., Li J., Deng J. D., Stringaris A., Pat N., Capturing brain cognition relationship: Integrating task based fMRI across tasks markedly boosts prediction and test retest reliability. NeuroImage 263, 119588 (2022). [DOI] [PubMed] [Google Scholar]
- 26.Engemann D. A., et al. , Combining magnetoencephalography with magnetic resonance imaging enhances learning of surrogate-biomarkers. eLife 9, e54055 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bookheimer S. Y., et al. , The Lifespan Human Connectome Project in Aging: An overview. NeuroImage 185, 335–348 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Poulton R., Moffitt T. E., Silva P. A., The Dunedin Multidisciplinary Health and Development Study: overview of the first 40 years, with an eye to the future. Soc Psychiatry Psychiatr Epidemiol 50, 679–693 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Van Essen D. C., et al. , The WU-Minn Human Connectome Project: An overview. NeuroImage 80, 62–79 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yarkoni T., Westfall J., Choosing Prediction Over Explanation in Psychology: Lessons From Machine Learning. Perspect Psychol Sci 12, 1100–1122 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Poldrack R. A., Huckins G., Varoquaux G., Establishment of Best Practices for Evidence for Prediction: A Review. JAMA Psychiatry 77, 534–540 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Varoquaux G., et al. , Assessing and tuning brain decoders: Cross-validation, caveats, and guidelines. NeuroImage 145, 166–179 (2017). [DOI] [PubMed] [Google Scholar]
- 33.Genç E., et al. , Diffusion markers of dendritic density and arborization in gray matter predict differences in intelligence. Nat Commun 9, 1905 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Narr K. L., et al. , Relationships between IQ and Regional Cortical Gray Matter Thickness in Healthy Adults. Cerebral Cortex 17, 2163–2171 (2007). [DOI] [PubMed] [Google Scholar]
- 35.Ohtani T., et al. , Medial Frontal White and Gray Matter Contributions to General Intelligence. PLOS ONE 9, e112691 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Krämer C., et al. , Prediction of cognitive performance differences in older age from multimodal neuroimaging data. GeroScience 46, 283–308 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rasero J., Sentis A. I., Yeh F.-C., Verstynen T., Integrating across neuroimaging modalities boosts prediction accuracy of cognitive ability. PLOS Computational Biology 17, e1008347 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dubois J., Galdi P., Paul L. K., Adolphs R., A distributed brain network predicts general intelligence from resting-state human neuroimaging data. Philosophical Transactions of the Royal Society B: Biological Sciences 373, 20170284 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sripada C., Angstadt M., Rutherford S., Taxali A., Shedden K., Toward a “treadmill test” for cognition: Improved prediction of general cognitive ability from the task activated brain. Human Brain Mapping 41, 3186–3197 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sripada C., et al. , Brain-wide functional connectivity patterns support general cognitive ability and mediate effects of socioeconomic status in youth. Transl Psychiatry 11, 1–8 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gao S., Greene A. S., Constable R. T., Scheinost D., Combining multiple connectomes improves predictive modeling of phenotypic measures. NeuroImage 201, 116038 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jiang R., et al. , Task-induced brain connectivity promotes the detection of individual differences in brain-behavior relationships. NeuroImage 207, 116370 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Xiao L., Stephen J. M., Wilson T. W., Calhoun V. D., Wang Y.-P., Alternating Diffusion Map Based Fusion of Multimodal Brain Connectivity Networks for IQ Prediction. IEEE Trans. Biomed. Eng. 66, 2140–2151 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Xiao L., Stephen J. M., Wilson T. W., Calhoun V. D., Wang Y.-P., A Manifold Regularized Multi-Task Learning Model for IQ Prediction From Two fMRI Paradigms. IEEE Trans. Biomed. Eng. 67, 796–806 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Keller A. S., et al. , Personalized functional brain network topography is associated with individual differences in youth cognition. Nat Commun 14, 8411 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhao W., et al. , Task fMRI paradigms may capture more behaviorally relevant information than resting-state functional connectivity. NeuroImage 270, 119946 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen J., et al. , Shared and unique brain network features predict cognitive, personality, and mental health scores in the ABCD study. Nat Commun 13, 2217 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Greene A. S., Gao S., Scheinost D., Constable R. T., Task-induced brain state manipulation improves prediction of individual traits. Nat Commun 9, 2807 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mihalik A., et al. , ABCD Neurocognitive Prediction Challenge 2019: Predicting Individual Fluid Intelligence Scores from Structural MRI Using Probabilistic Segmentation and Kernel Ridge Regression in Adolescent Brain Cognitive Development Neurocognitive Prediction, Lecture Notes in Computer Science., Pohl K. M., Thompson W. K., Adeli E., Linguraru M. G., Eds. (Springer International Publishing, 2019), pp. 133–142. [Google Scholar]
- 50.Makowski C., et al. , Leveraging the adolescent brain cognitive development study to improve behavioral prediction from neuroimaging in smaller replication samples. Cerebral Cortex 34, bhae223 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Noble S., Scheinost D., Constable R. T., A guide to the measurement and interpretation of fMRI test-retest reliability. Current Opinion in Behavioral Sciences 40, 27–32 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Elliott M. L., Knodt A. R., Hariri A. R., Striving toward translation: strategies for reliable fMRI measurement. Trends in Cognitive Sciences 25, 776–787 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Elliott M. L., et al. , General functional connectivity: Shared features of resting-state and task fMRI drive reliable and heritable individual differences in functional brain networks. NeuroImage 189, 516–532 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Knodt A. R., et al. , Test–retest reliability and predictive utility of a macroscale principal functional connectivity gradient. Human Brain Mapping 44, 6399–6417 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Avery E. W., et al. , Distributed patterns of functional connectivity predict working memory performance in novel healthy and memory-impaired individuals. Journal of cognitive neuroscience 32, 241–255 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jiang R., et al. , Gender Differences in Connectome-based Predictions of Individualized Intelligence Quotient and Sub-domain Scores. Cerebral Cortex 30, 888–900 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wu J., et al. , Cross-cohort replicability and generalizability of connectivity-based psychometric prediction patterns. NeuroImage 262, 119569 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zou H., Hastie T., Regularization and Variable Selection Via the Elastic Net. Journal of the Royal Statistical Society Series B: Statistical Methodology 67, 301–320 (2005). [Google Scholar]
- 59.Cortes C., Vapnik V., Support-vector networks. Mach Learn 20, 273–297 (1995). [Google Scholar]
- 60.Breiman L., Random Forests. Machine Learning 45, 5–32 (2001). [Google Scholar]
- 61.Chen T., Guestrin C., XGBoost: A Scalable Tree Boosting System in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ‘16., (Association for Computing Machinery, 2016), pp. 785–794. [Google Scholar]
- 62.Barrett-Young A., et al. , Associations Between Retinal Nerve Fiber Layer and Ganglion Cell Layer in Middle Age and Cognition From Childhood to Adulthood. JAMA Ophthalmology 140, 262–268 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Salthouse T. A., Localizing age-related individual differences in a hierarchical structure. Intelligence 32, 541–561 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Weintraub S., et al. , The Cognition Battery of the NIH Toolbox for Assessment of Neurological and Behavioral Function: Validation in an Adult Sample. Journal of the International Neuropsychological Society 20, 567–578 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Weschler D., Wechsler Adult Intelligence Scale—Fourth Edition. Stat. Solut 1–3 (2008). [Google Scholar]
- 66.Ji J. L., et al. , Mapping the human brain’s cortical-subcortical functional network organization. NeuroImage 185, 35–57 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Glasser M. F., et al. , The Human Connectome Project’s neuroimaging approach. Nat Neurosci 19, 1175–1187 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Behzadi Y., Restom K., Liau J., Liu T. T., A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. NeuroImage 37, 90–101 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Barch D. M., et al. , Function in the human connectome: Task-fMRI and individual differences in behavior. NeuroImage 80, 169–189 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Glasser M. F., et al. , The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 80, 105–124 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Tejavibulya L., et al. , Predicting the future of neuroimaging predictive models in mental health. Mol Psychiatry 27, 3129–3137 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Chen J., et al. , Relationship between prediction accuracy and feature importance reliability: An empirical and theoretical study. NeuroImage 274, 120115 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Rosenberg M. D., Finn E. S., How to establish robust brain–behavior relationships without thousands of individuals. Nat Neurosci 25, 835–837 (2022). [DOI] [PubMed] [Google Scholar]
- 74.Makowski C., Nichols T. E., Dale A. M., Quality over quantity: powering neuroimaging samples in psychiatry. Neuropsychopharmacol. 1–9 (2024). 10.1038/s41386-024-01893-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.WU-Minn Consortium Human Connectome Project, 1200 Subjects Data Release—Connectome. (2018). [Google Scholar]
- 76.Elam J., HCP Data Release Updates: Known Issues and Planned fixes—Connectome Data Public— HCP Wiki (2021). [Google Scholar]
- 77.Fischl B., et al. , Whole Brain Segmentation: Automated Labeling of Neuroanatomical Structures in the Human Brain. Neuron 33, 341–355 (2002). [DOI] [PubMed] [Google Scholar]
- 78.WU-Minn HCP, 1200 subjects data release reference manual. https://www.humanconnectome.org/storage/app/media/documentation/s1200/HCP_S1200_Release_Reference_Manual.pdf (2017).
- 79.Hariri A. R., Tessitore A., Mattay V. S., Fera F., Weinberger D. R., The Amygdala Response to Emotional Stimuli: A Comparison of Faces and Scenes. NeuroImage 17, 317–323 (2002). [DOI] [PubMed] [Google Scholar]
- 80.Delgado M. R., Nystrom L. E., Fissell C., Noll D. C., Fiez J. A., Tracking the Hemodynamic Responses to Reward and Punishment in the Striatum. Journal of Neurophysiology 84, 3072–3077 (2000). [DOI] [PubMed] [Google Scholar]
- 81.Forbes E. E., et al. , Altered Striatal Activation Predicting Real-World Positive Affect in Adolescent Major Depressive Disorder. AJP 166, 64–73 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.May J. C., et al. , Event-related functional magnetic resonance imaging of reward-related brain circuitry in children and adolescents. Biological Psychiatry 55, 359–366 (2004). [DOI] [PubMed] [Google Scholar]
- 83.Tricomi E. M., Delgado M. R., Fiez J. A., Modulation of Caudate Activity by Action Contingency. Neuron 41, 281–292 (2004). [DOI] [PubMed] [Google Scholar]
- 84.Binder J. R., et al. , Mapping anterior temporal lobe language areas with fMRI: A multicenter normative study. NeuroImage 54, 1465–1475 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Bizzi A., et al. , Presurgical Functional MR Imaging of Language and Motor Functions: Validation with Intraoperative Electrocortical Mapping. Radiology 248, 579–589 (2008). [DOI] [PubMed] [Google Scholar]
- 86.Buckner R. L., Krienen F. M., Castellanos A., Diaz J. C., Yeo B. T. T., The organization of the human cerebellum estimated by intrinsic functional connectivity. Journal of Neurophysiology 106, 2322–2345 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Morioka T., et al. , Comparison of magnetoencephalography, functional MRI, and motor evoked potentials in the localization of the sensory-motor cortex. Neurological Research 17, 361–367 (1995). [PubMed] [Google Scholar]
- 88.Yeo B. T. T., et al. , The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology 106, 1125–1165 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Smith R., Keramatian K., Christoff K., Localizing the rostrolateral prefrontal cortex at the individual level. NeuroImage 36, 1387–1396 (2007). [DOI] [PubMed] [Google Scholar]
- 90.Castelli F., Happé F., Frith U., Frith C., Movement and Mind: A Functional Imaging Study of Perception and Interpretation of Complex Intentional Movement Patterns. NeuroImage 12, 314–325 (2000). [DOI] [PubMed] [Google Scholar]
- 91.Castelli F., Frith C., Happé F., Frith U., Autism, Asperger syndrome and brain mechanisms for the attribution of mental states to animated shapes. Brain 125, 1839–1849 (2002). [DOI] [PubMed] [Google Scholar]
- 92.Wheatley T., Milleville S. C., Martin A., Understanding Animate Agents: Distinct Roles for the Social Network and Mirror System. Psychol Sci 18, 469–474 (2007). [DOI] [PubMed] [Google Scholar]
- 93.White S. J., Coniston D., Rogers R., Frith U., Developing the Frith-Happé animations: A quick and objective test of Theory of Mind for adults with autism. Autism Research 4, 149–154 (2011). [DOI] [PubMed] [Google Scholar]
- 94.Drobyshevsky A., Baumann S. B., Schneider W., A rapid fMRI task battery for mapping of visual, motor, cognitive, and emotional function. NeuroImage 31, 732–744 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Harms M. P., et al. , Extending the Human Connectome Project across ages: Imaging protocols for the Lifespan Development and Aging projects. NeuroImage 183, 972–984 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Burgess G., Winkler A., Practical 11: Task fMRI Analyses & PALM; HCP Course 2019. (2019). [Google Scholar]
- 97.Woolrich M. W., Ripley B. D., Brady M., Smith S. M., Temporal Autocorrelation in Univariate Linear Modeling of FMRI Data. NeuroImage 14, 1370–1386 (2001). [DOI] [PubMed] [Google Scholar]
- 98.McCarty D. L., Investigation of a visual imagery mnemonic device for acquiring face–name associations. Journal of Experimental Psychology: Human Learning and Memory 6, 145–155 (1980). [PubMed] [Google Scholar]
- 99.Sperling R. A., et al. , Encoding novel face-name associations: A functional MRI study. Human Brain Mapping 14, 129–139 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Zeineh M. M., Engel S. A., Thompson P. M., Bookheimer S. Y., Dynamics of the Hippocampus During Encoding and Retrieval of Face-Name Pairs. Science 299, 577–580 (2003). [DOI] [PubMed] [Google Scholar]
- 101.Winter W., Sheridan M., Previous reward decreases errors of commission on later ‘No-Go’ trials in children 4 to 12 years of age: evidence for a context monitoring account. Developmental Science 17, 797–807 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Jezzard P., Balaban R. S., Correction for geometric distortion in echo planar images from B0 field variations. Magnetic Resonance in Medicine 34, 65–73 (1995). [DOI] [PubMed] [Google Scholar]
- 103.Cox R. W., AFNI: Software for Analysis and Visualization of Functional Magnetic Resonance Neuroimages. Computers and Biomedical Research 29, 162–173 (1996). [DOI] [PubMed] [Google Scholar]
- 104.Greve D., Fischl B., A Boundary-Based Cost Function for Within-Subject, Cross-Modal Registration. NeuroImage 47, S100 (2009). [Google Scholar]
- 105.Avants B. B., Epstein C. L., Grossman M., Gee J. C., Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis 12, 26–41 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Klein A., et al. , Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage 46, 786–802 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Knutson B., Adams C. M., Fong G. W., Hommer D., Anticipation of Increasing Monetary Reward Selectively Recruits Nucleus Accumbens. J. Neurosci. 21, RC159–RC159 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Fair D. A., et al. , A method for using blocked and event-related fMRI data to study “resting state” functional connectivity. NeuroImage 35, 396–405 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Gratton C., et al. , Functional Brain Networks Are Dominated by Stable Group and Individual Factors, Not Cognitive or Daily Variation. Neuron 98, 439–452.e5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Gorgolewski K. J., et al. , The brain imaging data structure, a format for organizing and describing outputs of neuroimaging experiments. Sci Data 3, 160044 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Esteban O., et al. , fMRIPrep: a robust preprocessing pipeline for functional MRI. Nature methods 16, 111–116 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Esteban O., et al. , Analysis of task-based functional MRI data preprocessed with fMRIPrep. Nature protocols 15, 2186–2202 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Adebimpe A., et al. , XCP-D : A Robust Postprocessing Pipeline of fMRI data. (2023). 10.5281/zenodo.7641626. Deposited 14 February 2023. [DOI]
- 114.Sripada C., et al. , Basic Units of Inter-Individual Variation in Resting State Connectomes. Sci Rep 9, 1900 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Abraham A., et al. , Machine learning for neuroimaging with scikit-learn. Frontiers in Neuroinformatics 8 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Destrieux C., Fischl B., Dale A., Halgren E., Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. NeuroImage 53, 1–15 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Wechsler D., Wechsler intelligence scale for children-revised (Psychological Corporation, 1974). [Google Scholar]
- 118.Pedregosa F., et al. , Scikit-learn: Machine learning in Python. the Journal of machine Learning research 12, 2825–2830 (2011). [Google Scholar]
- 119.Drucker H., Burges C. J., Kaufman L., Smola A., Vapnik V., Support vector regression machines. Advances in neural information processing systems 9 (1996). [Google Scholar]
- 120.Efron B., Tibshirani R. J., An introduction to the bootstrap (CRC press, 1994). [Google Scholar]
- 121.Vos De Wael R., et al. , BrainSpace: a toolbox for the analysis of macroscale gradients in neuroimaging and connectomics datasets. Commun Biol 3, 103 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Shrout P. E., Fleiss J. L., Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin 86, 420–428 (1979). [DOI] [PubMed] [Google Scholar]
- 123.Cicchetti D. V., Sparrow S. A., Developing criteria for establishing interrater reliability of specific items: applications to assessment of adaptive behavior. Am J Ment Defic 86, 127–137 (1981). [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.