Viscous dynamics associated with hypoexcitation and structural disintegration in neurodegeneration via generative whole‐brain modeling

Abstract

INTRODUCTION

Alzheimer's disease (AD) and behavioral variant frontotemporal dementia (bvFTD) lack mechanistic biophysical modeling in diverse, underrepresented populations. Electroencephalography (EEG) is a high temporal resolution, cost‐effective technique for studying dementia globally, but lacks mechanistic models and produces non‐replicable results.

METHODS

We developed a generative whole‐brain model that combines EEG source‐level metaconnectivity, anatomical priors, and a perturbational approach. This model was applied to Global South participants (AD, bvFTD, and healthy controls).

RESULTS

Metaconnectivity outperformed pairwise connectivity and revealed more viscous dynamics in patients, with altered metaconnectivity patterns associated with multimodal disease presentation. The biophysical model showed that connectome disintegration and hypoexcitability triggered altered metaconnectivity dynamics and identified critical regions for brain stimulation. We replicated the main results in a second subset of participants for validation with unharmonized, heterogeneous recording settings.

DISCUSSION

The results provide a novel agenda for developing mechanistic model‐inspired characterization and therapies in clinical, translational, and computational neuroscience settings.

1. BACKGROUND

The global challenge of dementia is exacerbated by limited brain‐phenotype associations and dynamic mechanisms in diverse populations. ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ By 2050, a 4‐fold increase in dementia is expected in the Global South, where 71% of dementia cases will come from underserved regions and developing countries. ² , ⁹ , ¹⁰ The lack of robust mechanistic explanations of whole‐brain dynamics ¹¹ and adequate biomarkers make these underserved popualtions even more vulnerable. ¹² Non‐generalizable brain–phenotype associations require mechanistically oriented models for population heterogeneity. ¹ , ¹³ Tailored brain–phenotype biomarkers and robust computational approaches are critically needed to face global dementia challenges.

Alzheimer's disease (AD) and behavioral variant frontotemporal dementia (bvFTD) ¹⁴ , ¹⁵ are two common subtypes of dementia associated with cognitive decline, reduced life expectancy, family burden, and an overload of health‐care systems. ¹⁶ Mainstream dementia frameworks rely on pathological biomarkers such as amyloid beta (Aβ) and tau proteins, quantified through positron emission tomography (PET)—especially in AD. ¹⁷ However, these biomarkers present caveats for global settings. PET is not widely available (i.e., the percentage of PET access for patients in Latin America is < 1% ⁹ , ¹² ) or cost effective, ¹⁸ and does not provide a conclusive diagnosis ¹⁹ or discriminate very well against FTD variants. ²⁰ Fluid biomarkers, such as plasma, show promise, ²¹ but are not yet widely accessible. Plasma biomarkers lack systematic validation in diverse and non‐stereotypical populations. ⁹ Additionally, their influence on whole‐brain dynamics and brain–phenotype mechanisms across heterogeneous settings is unknown. These limitations call for additional strategies for developing biomarkers in non‐stereotypical samples.

Scalable and cost‐effective biomarkers for dementia in global contexts can be provided by high temporal resolution methods such as electroencephalography (EEG). ²² High‐density EEG can potentially identify the changes ascribed to neurodegenerative diseases across diverse settings due to its low cost, non‐invasiveness, portability, and wide availability in clinical research. ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ Despite progress, spectral and connectivity analyses often yield unclear results due to small sample sizes and variable metrics, ²⁸ requiring large samples for reproducible results. ¹⁸ Generative brain activity models ¹¹ may allow more robust results with moderate sample sizes, ²⁹ , ³⁰ , ³¹ provide causal mechanisms (biophysical‐inspired) ³² , ³³ , ³⁴ , ³⁵ , and brain stimulation potential targets by in silico perturbations. ¹³ , ³⁶ , ³⁷ By generating EEG‐like signals based on the biophysical properties of local and mesoscale circuits these models can provide mechanistic interpretations and test more focused hypotheses. ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ , ⁴²

EEG dementia research has traditionally focused on pairwise functional connectivity and spectral analysis. ¹⁴ , ²⁴ , ⁴³ , ⁴⁴ Beyond this traditional approach, the assessment of high‐order interactions allows the characterization of emergent properties of brain networks ⁴⁵ reflecting more biologically plausible approaches to complex brain dynamics in healthy aging, ⁴⁶ , ⁴⁷ cognition, ⁴⁸ and dementia. ⁴⁹ Metaconnectivity tackles third and fourth functional interactions between brain regions ⁵⁰ , ⁵¹ and has been used to characterize aging processes, with a shift toward more viscous (uncoordinated) brain dynamics in older adult subjects. ⁵¹ , ⁵² Although little tested in dementia research, ⁵³ combining high‐order metaconnectivity with whole‐brain mechanistic models and perturbational approaches ¹¹ enables us to explore and predict whole‐brain dynamics in neurodegeneration.

We developed a novel approach using generative whole‐brain semi‐empirical modeling with source space metaconnectivity, anatomical priors, and a perturbational approach, to investigate brain dynamics of dementia in a sample of underrepresented patients from the Global South. We explored how metaconnectivity patterns changed across EEG frequency bands in dementia, and if metaconnectivity was associated with multimodal disease severity. Then, we tested two possible mechanisms ascribed to neurodegeneration to reproduce the altered metaconnectivity in dementia: structural connectivity disintegration ⁵⁴ , ⁵⁵ , ⁵⁶ and alterations in the excitatory/inhibitory (E/I) balance. ⁵⁷ , ⁵⁸ , ⁵⁹ , ⁶⁰ Third, we used in silico perturbations through the model to induce transitions between the pathological and healthy states (and vice versa) and to identify possible therapeutic targets for brain stimulation. Finally, we replicated our core results in a second subset of participants, validating our results in an unharmonized and more heterogeneous setting. Through the simultaneous testing of these hypotheses, this novel computational framework has the potential to identify novel markers of metaconnectivity dynamics in dementia subtypes, associated with specific mechanisms of hypoexcitation and structural disintegration. This framework can also help identify the transitions between healthy and pathological brain states.

2. METHODS

2.1. Participants

2.1.1. Full sample

The full sample comprised 332 participants recruited from clinical centers in Argentina (CNC, Universidad de San Andrés), Chile (GERO/CMYN, Universidad de Chile), Colombia (Pontificia Universidad Javeriana), and Turkey, as part of the Multi‐Partner Consortium to Expand Dementia Research in Latin America (ReD‐Lat), ⁶¹ , ⁶² BrainLat, ⁸ , ⁶³ and EuroLad. ⁶⁴ Data from Turkey were collected from the cohort of Brain Dynamics Multidisciplinary Research Center, Dokuz Eylül University, Izmir. Among the participants, 141 patients met the National Institute of Neurological and Communicative Disorders and Stroke–Alzheimer's Disease and Related Disorders Association criteria for typical AD, ⁶⁵ , ⁶⁶ while 44 patients met the revised criteria for probable bvFTD. ⁶⁷ All patients were in the early/mild stages of the disease. A total of 147 with preserved cognition conformed to the healthy controls group (CN). None of the participants had a history of substance abuse, psychiatric disorders, or other neurological illnesses. Demographic data for the whole sample are reported in Table 1. The study was approved by the institutional ethics committee of each center. All participants provided written informed consent following the Declaration of Helsinki.

TABLE 1.

Demographics (full sample and subsamples).

Full sample	CN (N = 147)	AD (N = 141)	bvFTD (N = 44)
				${\chi }^2$ test
Sex (M/F)	53/94	66/75	35/9	AD vs. CN	bvFTD vs. CN
				${\chi }^2$ = 7.07, P = 0.008	${\chi }^2$ = 17.01, P < 0.0001
				Student t test
Age (years)	67 ± 8.3	74 ± 6.2	69.5 ± 8.0	AD vs. CN	bvFTD vs. CN
				t = 7.56, P < 0.0001	t = 1.87, P = 0.0630
				Student t test
Education (years)	13.2 ± 4.5	10.2 ± 4.9	13.1 ± 5.3	AD vs. CN	bvFTD vs. CN
				t = −5.66, P < 0.001	t = −0.73, P = 0.4688

Sample 1	CN (N = 45)	AD (N = 31)	bvFTD (N = 18)
				${\chi }^2$ test
Sex (M/F)	17/29	14/17	13/5	AD vs. CN	bvFTD vs. CN
				${\chi }^2$ = 0, P = 1	${\chi }^2$ = 10.74, P = 0.001
				Student t test
Age (years)	71 ± 7.2	76 ± 7.5	68 ± 9.9	AD vs. CN	bvFTD vs. CN
				t = 2.70, P = 0.008	t = −1.25, P = 0.22
				Student t test
Education (years)	14.7 ± 4	9.9 ± 4.9	15.4 ± 4.8	AD vs. CN	bvFTD vs. CN
				t = −4.63, P < 0.001	t = 0.57, P = 0.57

Sample 2	CN (N = 101)	AD (N = 110)	bvFTD (N = 26)
				${\chi }^2$ test
Sex (M/F)	36/65	53/58	26/10	AD vs. CN	bvFTD vs. CN
				${\chi }^2$ = 7.09, P = 0.008	${\chi }^2$ = 7.09, P < 0.0048
				Student t test
Age (years)	65.6 ± 8.2	73.3 ± 5.7	70.4 ± 6.3	AD vs. CN	bvFTD vs. CN
				t = 8.09, P < 0.0001	t = 2.98, P = 0.0034
				Student t test
Education (years)	12.6 ± 4.5	10.3 ± 4.9	11.7 ± 5.0	AD vs. CN	bvFTD vs. CN
				t = −3.74, P = 0.0002	t = −1.34, P = 0.1826

Notes: Values constituted by proportion (sex) and mean ± standard deviation (age and education). Categorical variables were analyzed with Pearson chi‐squared (${\chi }^2$) test. Continuous variables were analyzed through Student t tests.

Abbreviations: AD, Alzheimer's disease; bvFTD, behavioral variant of frontotemporal dementia; CN, healthy controls.

RESEARCH IN CONTEXT

1. Systematic review: Electroencephalography (EEG) constitutes a cost‐effective method for characterizing dementia globally. However, the lack of mechanisms and non‐replicable results in the field hinder dementia research. This problem is of special concern in non‐stereotypical, underrepresented, and heterogenous populations, like patients in the Global South. We proposed novel metaconnectivity biomarkers, which tackled high‐order interactions, with a mechanistic hypothesis tested in computational models.

2. Interpretation: We discovered robust biomarkers for characterizing dementia using metaconnectivity, and altered metaconnectivity patterns predicted the disease's progression. Through computational modeling, we found that the structural disintegration of the human connectome and a shift to hyperexcitation in brain dynamics triggered the altered metaconnectivity patterns observed in patients. We also proposed critical brain regions that can be used as therapeutic targets for brain stimulation. Our results are robust to more heterogeneous EEG settings and populations, as confirmed in a validation of the core results with additional datasets.

3. Future directions: Our results proposed novel biomarkers that can be used for dementia screening and provide open‐source semi‐empirical modeling tools for the neuroscience community. Our work will inspire new experiments and settings for testing therapeutical targets in dementia. Future work will validate our results using large sample sizes and comparing stereotypical and non‐stereotypical patients to test the generalization and specificity of our findings.

2.1.2. Initial subsample (harmonized dataset)

A first subsample of participants was used to identify the metaconnectivity alterations in patients, fit the whole‐brain model to empirical data, and test connectome and stimulation perturbations. This subsample comprised 95 subjects from Argentina and Chile from the ReD‐Lat consortium. ⁶¹ , ⁶² Of these, 31 AD patients presented memory deficits and showed middle‐temporal/hippocampal and posterior atrophy among other regions commonly affected by this condition (Section 1 in Table S1, Figure S1A in supporting information). Another 18 bvFTD patients presented changes in personality and social behavior according to caregivers and showed fronto‐temporo‐insular atrophy (Table S2, Figure S1B in supporting information). The remaining 46 CN participants had preserved cognition and served as healthy controls. All participants underwent a comprehensive battery of neurological, neuropsychiatric, and neuropsychological assessments following harmonized procedures. ⁶⁷ , ⁶⁸ , ⁶⁹ , ⁷⁰ , ⁷¹ , ⁷² A multidisciplinary team established clinical diagnoses following a formal criterion and ReD‐Lat standardized diagnostic procedures ⁶¹ , ⁶² to prevent potential biases in diagnostic evaluation. Cognitive functioning was assessed with the Montreal Cognitive Assessment (MoCA) (Section 2 in supporting information). Demographic and cognitive data for the whole sample are reported in Table 1 and Table S3 in supporting information. Additionally, we included a subsample matched by age, education, and sex for further analysis (Table 2), which was selected using the PsmPy package for Python ⁷³ (pypi.org/project/psmpy/).

TABLE 2.

Demographics of the matched subsample.

	AD vs. CN		bvFTD vs. CN
Matched sample	CN (N = 22)	AD (N = 31)	CN (N = 18)	bvFTD (N = 18)
					${\chi }^2$ test
Sex (M/F)	11/11	14/17	12/6	13/5	AD vs. CN	bvFTD vs. CN
					${\chi }^2$ = 0.29, P = 0.59	${\chi }^2$ = 0.25, P = 0.62
					Student t test
Age (years)	73.5 ± 3.2	75.7 ± 7.5	69.7 ± 7.6	68.2 ± 9.9	AD vs. CN	bvFTD vs. CN
					t = −1.27, P = 0.21	t = 0.50, P = 0.62
					Student t test
Education (years)	11.9 ± 4.0	9.8 ± 4.0	16.2 ± 3.9	15.4 ± 4.8	AD vs. CN	bvFTD vs. CN
					t = 1.60, P = 0.12	t = 0.52, P = 0.61

Notes: Values constituted by proportion (sex) and mean ± standard deviation (age and education). Categorical variables were analyzed with Pearson chi‐squared (${\chi }^2$) test. Continuous variables were analyzed through Student t tests.

Abbreviations: AD, Alzheimer's disease; bvFTD, behavioral variant of frontotemporal dementia; CN, healthy controls.

2.1.3. Second subsample (non‐harmonized dataset)

A second subsample was used to validate the metaconnectivity features and mechanisms previously characterized using the initial subsample. The dataset comprised 237 subjects from Chile, Colombia, and Turkey from ReD‐Lat ⁶¹ , ⁶² and EuroLad consortiums. ⁶⁴ The subsample included 110 AD patients, 26 bvFTD patients, and 101 healthy controls. Demographic data and cognitive assessment for this subsample are presented in Table 1 and supporting information.

2.2. Magnetic resonance imaging acquisition and analysis

Magnetic resonance imaging (MRI) was used to estimate the brain atrophy in patients from the first subsample, recorded at various centers (see details in supporting information). Images were preprocessed using the DARTEL Toolbox for SPM12 (https://www.fil.ion.ucl.ac.uk/spm/software/spm12/) ⁷⁴ running in MATLAB. The preprocessing pipeline included segmentation into gray matter, white matter, and cerebrospinal fluid. Those images were used to estimate the total intracranial volume. Then, a template based on gray and white matter segmentations was created for the complete data set (default parameters) to improve between‐subject alignment. This template was used to affine transformation into Montreal Neurological Institute space to all individual gray matter images. Finally, images were modulated by Jacobian determinants and smoothed with a full‐width half‐maximum kernel of 10 mm. The gray matter maps were used to characterize the atrophy patterns of patients, compared to healthy controls, and to find associations between atrophy and metaconnectivity (see Section 1 in supporting information).

2.3. Diffusion‐weighted imaging acquisition and preprocessing

Structural connectivity was used as priors of our whole‐brain model, for simulating the EEG‐like dynamics specific to AD, bvFTD, and CN. Structural connectivity matrices were obtained by applying diffusion tensor imaging (DTI) to diffusion‐weighted imaging (DWI) recordings. Data preprocessing was then performed using FSL BEDPOSTX (Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques toolbox) ⁷⁵ (see Section 4 in supporting information). After preprocessing, a matrix with 90 × 90 components was obtained per subject, representing the connectivity between automated anatomical labeling (AAL) region pairs. Finally, the structural connectivity matrices for each group were obtained by taking the average of the matrices of the CN, AD, and bvFTD participants separately.

2.4. EEG acquisition and preprocessing

2.4.1. Initial subsample

Participants sat in a comfortable chair inside an electromagnetically shielded EEG room and were instructed to remain still, awake, and with their eyes closed. Following previous works of our team, ⁶¹ , ⁶² we analyzed 10‐minute resting‐state EEG (rsEEG) using a Biosemi ActiveTwo 128‐channel acquisition system. For recording eye blinks and eye movements, electrodes were also placed in periocular zones. Reference electrodes were placed on linked mastoids, and signals were sampled at a rate of 1024 Hz.

2.4.2. Second subsample

Participants across all sites were instructed to sit comfortably in an electromagnetically shielded EEG chamber, remaining still, awake, and with their eyes closed. Although data acquisition instructions were consistent across all sites, each location used its protocols. The Chilean site used a Biosemi ActiveTwo 128‐channel acquisition system, sampling signals at 1024 Hz. The Bogotá site operated an ANT Neuro 128‐channel acquisition system, with signal sampling at 512 Hz. In Medellín, an ANT Neuro 64‐channel acquisition system was used, sampling signals at 1000 Hz. Finally, the Turkish site used a BrainAmp 32‐channel DC system, sampling signals at 512 Hz. All reference points were standardized and set to the average during preprocessing. Signals were resampled at 512 Hz during preprocessing and subjected to a high‐pass filter of 40 Hz and a low‐pass filter of 0.5 Hz.

2.4.3. EEG preprocessing

The rsEEG was preprocessed offline using standard procedures described elsewhere. ⁷⁶ The analog filters were adjusted to a range of 0.03 and 100 Hz. Recordings were band‐pass filtered at 0.5 to 40 Hz and re‐referenced to the average of all channels. Malfunctioning channels were identified and replaced using statistically weighted spherical interpolation (based on neighbor sensors). ⁷⁷ Independent component analysis ⁷⁸ and a visual inspection protocol ⁷⁹ , ⁸⁰ , ⁸¹ , ⁸² were used to correct blink artifacts and eye movements.

2.5. Source space functional connectivity and metaconnectivity estimation

Brain sources of the rsEEG were estimated using the standardized low‐resolution brain electromagnetic tomography analysis (sLORETA). ⁸³ The sLORETA estimates the standardized current densities for a grid of 6242 predefined virtual sensors (voxel size 5 × 5 × 5 mm) located in the cortical gray matter and hippocampus of a reference brain (MNI 305, Brain Imaging Centre, Montreal Neurologic Institute). Voxels were grouped in N = 82 brain areas defined by the AAL parcellation ⁸⁴ (Figure 1A and Table S4 in supporting information). The time series for each brain compartment was obtained by vector averaging across voxels the current densities calculated at each time point, resulting in a time x regions matrix. 

FIGURE 1.

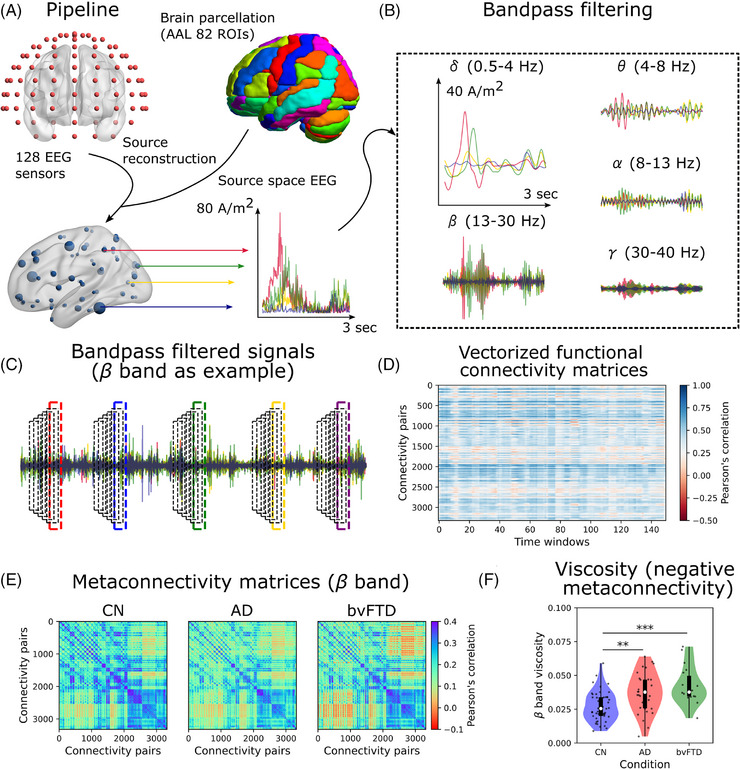
Pipeline for metaconnectivity dynamics estimation. A, Source reconstruction (sLORETA) was used to extract the regional time series (82 ROIs, brain regions, of the AAL parcellation). B, Signals were bandpass filtered in the common EEG frequency bands to compute functional connectivity and metaconnectivity. C, Time‐resolved functional connectivity was characterized using the sliding windows method, in which functional connectivity was estimated using fixed (8 seconds) and overlapped (80%) time windows. The procedure was performed for all frequency bands. The results of the $\beta$ band are presented as an example. D, Dynamic functional connectivity matrix was built using the vectorized upper triangular of functional connectivity matrices. E, By correlating the connectivity pairs’ time series across time windows, the metaconnectivity matrices can be estimated. These matrices capture high‐order correlations (between three and four pairs of brain regions). In the example, the matrices in the $\beta$ band of EEG are shown for CN, AD, and bvFTD patients. F, Dynamics viscosity is defined as the absolute sum of the negative values within the metaconnectivity matrices. $\beta$ band viscosity was higher in AD and bvFTD with respect to CN. *|D| > 0.5, **|D| > 0.8, ***|D| > 1.2. Data points in violin plots correspond to subjects. Box plots were built using the first and third quartiles, the median, and the maximum and minimum values of distributions. AAL, automated anatomical labeling; AD, Alzheimer's disease; bvFTD, behavioral variant frontotemporal dementia; CN, healthy control; EEG, electroencephalography; ROI, region of interest; sLORETA, standardized low‐resolution brain electromagnetic tomography analysis.

The rsEEG time series were band‐pass filtered in the common EEG bands: $\delta$ (0.5–4 Hz), $\theta$ (4–8 Hz), $\alpha$ (8–13 Hz), $\beta$ (13–30 Hz), and $\gamma$ (30–40 Hz; Figure 1B). Functional connectivity matrices were built using the pairwise Pearson correlation between the filtered time series in both empirical and simulated data (simulation described below). Metaconnectivity matrices were built using the sliding windows method, as described in Arbabyazd et al. ⁵¹ (Figure 1C). Windows of 8 seconds length with 80% overlap were used to compute the time‐resolved functional connectivity (the rationale behind windows’ length is provided in Figure S2 in supporting information). Then, functional connectivity matrices were vectorized, taken from their upper triangular, and concatenated into the dynamic functional connectivity matrix (Figure 1D) of dimension Q x Q (Q connectivity pairs, w time windows). Time series within the dynamic functional connectivity matrix were correlated (using Pearson r) against each other, and the outcome corresponded to the metaconnectivity matrix of dimension Q x Q (Figure 1E). These matrices capture high‐order interactions. ⁵¹ Finally, we computed the absolute value of the average sum of the negative values of the metaconnectivity matrices, called dynamics viscosity (Figure 1F). A higher viscosity is a dynamical signature of a less integrated brain activity. ⁵¹

2.6. Dimensionality reduction

We used linear discriminant analysis (LDA) ⁸⁵ to reduce the set of selected metaconnectivity features (see subsection 2.8) to single components. For empirical data, the LDA was used independently for discriminating AD or bvFTD from CN using the best features obtained through machine learning. For simulated data, the same features based on metaconnectivity were used for LDA and validated on empirical data. This time, we combined the three groups (CN, AD, and bvFTD) and fitted LDA to empirical data. Then, we projected the simulated data using the fitted LDA model to represent it in a two‐dimensional space (two LDA components). The centroids of the groups in the reduced space by LDA correspond (in the model) to different “brain states” (CN‐, AD‐, and bvFTD‐like states).

2.7. Whole‐brain modeling and perturbations

2.7.1. Neural mass model description

We used a modified ⁸⁶ , ⁸⁷ Jansen and Rit neural mass model ⁸⁸ to model whole‐brain source networks (Figure 2). Each brain area was composed of two subpopulations of neural masses (Figure 2A), each tuned to oscillate in the $\alpha$ and $\gamma$ frequency bands (around 10 and 45 Hz, respectively; Figure 2A). The contribution of each subpopulation in generating the postsynaptic potential (PSP) of pyramidal neurons was weighted by the parameter $r^{\alpha }$, as defined in Otero et al. ⁸⁷ The model's parameters are summarized in Table S5 in supporting information. Macroscopically, each brain area i was connected to another area j using a structural connectivity matrix M (DTI; Figure 3B). We used the average connectome across subjects, leading to group‐specific CN, AD, and bvFTD structural connectivity matrices. The strength of the coupling was scaled by a global coupling parameter K. Considering that long‐range projections are mainly excitatory, ⁸⁹ , ⁹⁰ connections between brain areas involved only pyramidal neurons. Each region received background input, whose values were randomly sampled from a normal distribution with a mean $⟨p(t)⟩=220$ Hz and a standard deviation ${\sigma }_p=31$ (similar values used in Otero et al. ⁸⁷ ). The complete system of equations for the $\alpha$ subpopulation consisted of

$$\begin{array}{cc}\hfill \frac{d{x}_{0,i}^{\alpha }\left(t\right)}{dt}& =y_{0,i}^{\alpha }\left(t\right)\hfill \\ \hfill \frac{d{y}_{0,i}^{\alpha }\left(t\right)}{dt}& =A^{\alpha }{a}^{\alpha }S\left(x_{1,i}\left(t\right)-x_{2,i}\left(t\right)\right)-2a^{\alpha }{y}_{0,i}^{\alpha }\left(t\right)-a^{{\alpha }^2}{x}_{0,i}^{\alpha }\left(t\right)\hfill \\ \hfill \frac{d{x}_{1,i}^{\alpha }\left(t\right)}{dt}& =y_{1,i}^{\alpha }\left(t\right)\hfill \\ \hfill \frac{d{y}_{1,i}^{\alpha }\left(t\right)}{dt}& =A^{\alpha }{a}^{\alpha }\left(p_i\left(t\right)+C_{2}S\left(C_1{x}_{0,i}\left(t\right)\right)\right)\hfill \\ & +KC\sum _{j=1,j\ne i}^N{M}_{ij}S\left(x_{1,j}\left(t\right)-x_{2,j}\left(t\right)\right)-2a^{\alpha }{y}_{1,i}^{\alpha }\left(t\right)-a^{{\alpha }^2}{x}_{1,i}^{\alpha }\left(t\right)\hfill \\ \hfill \frac{d{x}_{2,i}^{\alpha }\left(t\right)}{dt}& =y_{2,i}^{\alpha }\left(t\right)\hfill \\ \hfill \frac{d{y}_{2,i}^{\alpha }\left(t\right)}{dt}& =B^{\alpha }{b}^{\alpha }\left(C_{4}S\left(C_3{x}_{0,i}\left(t\right)\right)\right)-2b^{\alpha }{y}_{2,i}^{\alpha }\left(t\right)-b^{{\alpha }^2}{x}_{2,i}^{\alpha }\left(t\right)\hfill \\ \hfill S\left(v\right)& =\frac{{\zeta }_{max}}{1+\exp \left(-r\left(v-v_{th}\right)\right)}\hfill \end{array}$$

where $A^{\alpha }$ ($B^{\alpha }$) and $a^{\alpha }$ ($b^{\alpha }$) corresponded to the excitatory (inhibitory) postsynaptic potentials’ maximal amplitude and inverse characteristic time constant, respectively. The first pair of equations represents the excitatory feedback loop, the second represents the outputs from pyramidal neurons, and the third represents the inhibitory feedback loop. Populations of neurons were connected through constants $C_1$, $C_2$, $C_3$, and $C_4$; all of them scaled with a common local connectivity constant $C$. The postsynaptic potentials, $v$, were transformed into firing rates through a sigmoid function $S(v)$, with a maximal output, slope, and threshold given by ${\zeta }_{max}$, $r$, and $v_{th}$. The equations for the subpopulations are identical, except for the $\gamma$ superscript. Further details of the model can be found in supporting information (Section 5). The model's final output corresponded to EEG‐like signals in the source space (Figure 3C,D).

FIGURE 2.

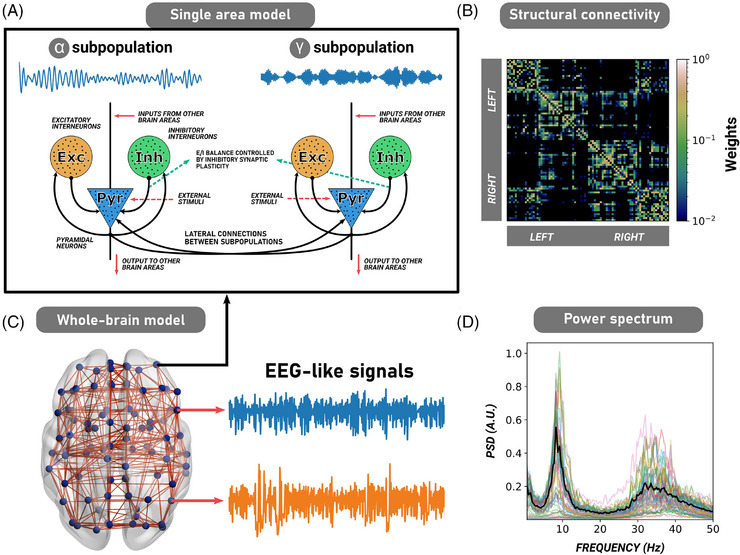
Description of the whole‐brain computational model. A, The original Jansen and Rit neural mass model for one single cortical column (brain region) involving three populations of neurons: pyramidal neurons (blue), excitatory (orange), and inhibitory (green) interneurons. In the model, long‐range projections from and toward other cortical regions involved only pyramidal neurons. B, In our modified version of the model, we coupled two subpopulations of cortical columns (one oscillating in $\alpha$, and the other in $\gamma$). The combined subpopulations formed a single cortical column. Our model also incorporates inhibitory synaptic plasticity. C, Brain areas were connected through a human empirical structural connectivity matrix (in this figure, the CN structural connectivity matrix averaged across subjects), parcellated in 82 brain regions using the AAL parcellation. This matrix is weighted and undirected (symmetric). D, Whole‐brain neural mass model simulating EEG‐like signals at the source level. The model's EEG power spectrum fitted to the CN (through functional connectivity matrices) shows two different peaks at the $\alpha$ and $\gamma$ frequency bands. AAL, automated anatomical labeling; CN, healthy control; EEG, electroencephalography.

FIGURE 3.

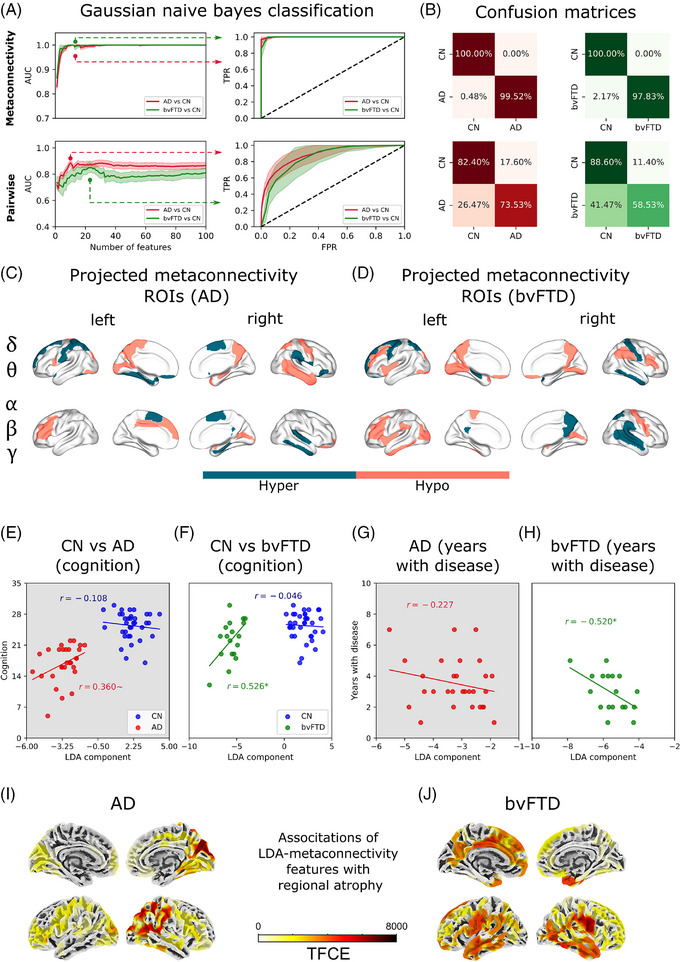
Spatiotemporal characterization and validation of viscosity (metaconnectivity) in AD and bvFTD. A, The area under the curve of the ROC curve was used to evaluate the performance of the classifier. Higher values (near 1) allow a good classification of healthy controls from patients. The first and second columns correspond to the features based on functional connectivity and metaconnectivity, respectively. At the left, features ranked using MRMR were added one by one, and model performance was assessed using the AUC. The minimal set of features guaranteeing the highest AUC values consisted of the optimal number of features for classification. At the right, the ROC curves for a fixed number of features (the best ones highlighted by the dotted lines). B, Confusion matrices using metaconnectivity (first row) and functional connectivity (second row). C, D, Brain regions characterized using metaconnectivity, projected on the brain's surface for AD and bvFTD. Colors indicate if the regions are involved in hypo or hyper patterns of metaconnectivity (based just on the sign of the Cohen D effect sizes). E, A trend of LDA component to be positively correlated with cognition (MoCA scores) was found, but not with (G) years with disease. G, LDA component was positively correlated with cognition, and (H) negatively correlated with years with disease. I, J, Model's scores validation through surface‐based morphometry. LDA values were associated with cortical thickness using a linear regression for every clinical group individually joined with healthy controls. To correct for multiple comparisons, a TFCE correction was used. *P < 0.05, ^∼ P $\approx$ 0.1. AD, Alzheimer's disease; AUC, area under the curve; bvFTD, behavioral variant frontotemporal dementia; CN, healthy control; EEG, electroencephalography; LDA, linear discriminant analysis; MoCA, Montreal Cognitive Assessment; MRMR, minimal redundancy maximum relevance; ROC, receiver operating characteristic; ROI, region of interest; TFCE, threshold‐free cluster enhancement.

2.7.2. Synaptic plasticity

Following Abeysuriya et al. ⁹¹ we incorporated within our model inhibitory synaptic plasticity as an additional differential equation:

$$\frac{\tau C_4\left(t\right)}{dt}={\zeta }_{inh}\left(t\right)\left({\zeta }_{pyr}\left(t\right)-\rho \right){\left(\frac{C_4\left(t\right)}{C}-\frac{C_{4,min}}{C}\right)}^{\beta }$$

The plasticity updates the feedback inhibition to control the firing rate of pyramidal neurons, preventing the full saturation of their sigmoid function. In the equation, $\tau$ represents the inverse of the learning rate; ${\zeta }_{inh}(t)$ and ${\zeta }_{pyr}(t)$ the firing rates of the inhibitory interneurons and pyramidal neurons at time t, respectively; $\rho$ the target firing rate; and $\beta$ a bounding exponent that controls the convergence to $C_{4,min}=0$ (for avoiding non‐plausible negative connectivity values). We used $\beta =1$ (soft‐bound), but other choices are possible. ⁹² The two critical parameters for plasticity are the learning rate $\tau$ and the target firing rate $\rho$. We chose values of $\tau =2$ s and $\rho =2.5$ Hz. ⁹¹ , ⁹³

2.7.3. Model fitting, data augmentation, and model's observables

We ran simulations with the same time length as the empirical data (610 seconds discarding the first 10 seconds) using different random seeds for model fitting (100 seeds), data augmentation (300 seeds), and model perturbation (50 seeds). The details of the simulations are presented in the supporting information (Section 6). From the simulated data, we extracted the same features based on metaconnectivity of the empirical data, including functional connectivity and metaconnectivity matrices in each frequency band. The features extracted from simulated data were reduced to two LDA components using the LDA fitted to empirical data (see subsection 2.6). The fitting procedure consisted of minimizing the distance between the simulated data and the empirical centroids of CN, AD, and bvFTD groups, to reproduce the empirical metaconnectivity features. In addition, we also explored the more traditional fitting to the functional connectivity matrices using the structural similarity index (SSIM). ⁹⁴ , ⁹⁵ The SSIM is a method for measuring the similarity between two images. In the context of functional connectivity, it constitutes a trade‐off between Pearson correlation and Euclidean distance, that is, for SSIM both the pattern of connectivity and the mean functional connectivity matter. The SSIM has been widely used in the field of whole‐brain modeling. ³³ , ⁹⁵

2.7.4. Connectome perturbation

To test the hypothesis that alterations in structural connectivity may lead to functional disturbances in AD and bvFTD, ⁵⁴ , ⁵⁵ , ⁵⁶ we performed in silico perturbations of the healthy connectome (CN). Our analysis was based on the participation coefficient, $P{C}^w$, and modularity, $Q^w$, measures of integration and segregation, respectively. ⁹⁶ We obtained the modular structure of the connectomes using a combination of the Louvain algorithm and consensus clustering. We then classified nodes according to their nodal participation coefficient, $P{C}_i^w$. ⁹⁶ Next, we produced iteratively altered connectomes decreasing the connectivity between nodes with the highest $P{C}_i^w$, while preserving the nodal strength and the original modular organization of the connectome. This perturbation changed the topological properties of structural connectivity toward segregation. Simulations were performed for $K=0.25$ (CN) using the perturbed connectomes. The complete procedure is described in supporting information.

2.7.5. In silico perturbation

To investigate the transitions from the pathological to the healthy state and vice versa, we implemented two different perturbation protocols to pairs of homotopic nodes ³⁷ , ⁹⁷ by changing the magnitude of the background input $p$ by an amount $+\mathrm{\Delta }p$ (excitatory protocol) or $-\mathrm{\Delta }p$ (inhibitory protocol). For each pair of homotopic nodes, we swept $\mathrm{\Delta }p$ from 0 to 600 Hz in steps of 30 Hz.

2.7.6. Modeling E/I balance disturbances

We also simulated a possible effect of E/I imbalance triggered by neurodegeneration ⁵⁷ , ⁵⁸ , ⁵⁹ by directly decreasing or increasing the target firing rate $\rho$ of synaptic plasticity. The rationale behind this was similar to that of the perturbation protocols: increasing (decreasing) $\rho$ moves the model toward hyperexcitation (hypoexcitation). Starting from the model fitted to the CN condition, we searched the best global coupling, $K$, and target firing rate, $\rho$, parameters to adjust the model to AD and bvFTD groups. We repeated the inverse procedure from AD or bvFTD to CN, starting from the model fitted to the pathological conditions.

2.8. Data analysis

2.8.1. Empirical data

We used independent sample Student t tests to compare pairwise differences between CN versus AD or bvFTD, and Cohen D effect size was reported. Pearson correlation was used to assess the relationship between empirical features (LDA and viscosity scores), MoCA scores, and years of disease. We validated our empirical features using surface‐based morphometry through a regression between LDA and cortical thickness with the Cat12 toolbox (https://neuro‐jena.github.io/cat/) in MATLAB 2018A. Cortical thickness was regressed out with LDA to validate the metrics of the model using surface‐based morphometry (see Section 3 in supporting information for further details). All P values were corrected for multiple comparisons (CN vs. AD or bvFTD) across frequency bands and for all correlations using the Benjamini–Hochberg method, ⁹⁸ for decreasing the probability of making type I errors (false positives).

2.8.2. Simulated data

For simulated data, we computed Cohen D to report the results in terms of effect size, ⁹⁹ as P values can be artificially inflated by sample size computing additional model realizations. ⁹⁹ We also used the Euclidean distance between centroids in the reduced latent space (through LDA ⁸⁵ ) to assess the proximity between different brain states (e.g., AD vs. CN, or between a trajectory and a target centroid). To investigate the relationship between viscosity and the degree of integration ($P{C}^w)$ of the perturbed connectomes, we calculated the Spearman correlation between the average viscosity and $P{C}^w.$

2.8.3. Validation of the features based on metaconnectivity

We compared pairwise and high‐order features based on functional connectivity and metaconnectivity to discriminate patients from CN. Features consisted of functional connectivity and metaconnectivity links (connectivity values within matrices). Features were pre‐selected by ranking them according to the absolute value of the Cohen D effect size (AD or bvFTD vs. CN) in each frequency band. The best and least redundant 100 features were selected using the minimal redundancy maximum relevance (MRMR) feature selection algorithm in Python (https://github.com/smazzanti/mrmr). For classification, we used a Gaussian Naive Bayes classifier to discriminate between AD or bvFTD and CN (GaussianNB function from Python sklearn library). The Naive Bayes classifiers are highly efficient, quickly trained, and make accurate predictions even with large datasets. They have only one hyperparameter, a smoothing parameter, that is usually used when working with categorical variables to avoid zero probabilities. Because that is not our case, we set the smoothing parameter to 0. Then we split the dataset into training and test sets (80% vs. 20%, respectively) using a 5‐fold cross‐validation. Features were added one by one from the MRMR ranking. In each step, we evaluated the performance of the model through (1) confusion matrices, (2) model accuracy, (3) the area under the curve (AUC) of the receiver operating characteristic curve (false positives vs. true positives rates), (4) F1 score, (5) sensitivity, and (6) specificity. To avoid artificial inflation of P values due to sample size, we computed Cohen D to report the results in terms of effect size. The performance of the model was assessed 300 times using different random seeds, and we computed the averaged performance across folds in each iteration.

2.9. Data and code availability

The scripts for all simulations and data analysis are available at the following GitHub repository: https://github.com/carlosmig/EEG‐Dementias.git. The Brain Connectivity Toolbox for Python (https://github.com/fiuneuro/brainconn) ⁹⁶ was used for graph analysis, and BrainNet Viewer toolbox ¹⁰⁰ was used for visualization of brain plots. Data are available upon request from the corresponding authors, and a formal data‐sharing agreement must be established.

3. RESULTS

3.1. Dementia is better characterized by higher viscous dynamics than by functional connectivity

We investigated the characterization of dementia by using metaconnectivity ⁵¹ to capture high‐order interactions in each frequency band. Unlike functional connectivity, metaconnectivity matrices captured third‐ and fourth‐order correlations among different brain areas. At the global level, $\beta$‐band metaconnectivity matrices had more negative entries, indicating less coordinated brain dynamics (Figure 1E,F). We observed higher viscosity, that is, the absolute value of the averaged sum of negative metaconnectivity values, ⁵¹ , ⁵² in both AD and bvFTD in β compared to the CN (P = 0.00374, t = 3.45, D = 0.80 for AD vs. CN; P = 0.00021, t = 4.65, D = 1.29 for bvFTD vs. CN). In bvFTD, an increment in viscosity was observed in $\alpha$ (P = 0.00633, t = 3.21, D = 0.89) and $\gamma$ (P = 0.02158, t = 2.69, D = 0.75) bands, as well in the across bands average (P = 0.00061, t = 4.15, D = 1.15; Figure S3 in supporting information). Therefore, uncoordinated viscous brain dynamics characterized AD and bvFTD, particularly in higher frequency bands, and the effect was stronger in bvFTD compared to AD compared to CN. The increment in viscosity reflects a change in the global brain dynamics of patients beyond the alterations at the level of individual metaconnectivity interactions. However, individual metaconnectivity values can be used to discriminate between patients and controls, as addressed below.

The validation of viscosity/metaconnectivity involved a comparison with classical connectivity metrics using the best features. The top metaconnectivity values considering all frequency bands with the highest Cohen D absolute values were ranked using an MRMR algorithm, and the resulting ordered vector was used as input for a Gaussian Naïve Bayes classifier (Figure 3A). The AUC values reached a maximum (0.999 AD or bvFTD vs. CN) using the first 12 features for AD versus CN, and for bvFTD versus CN. In contrast, using pairwise connectivity values resulted in lower AUC values (of 0.855 for AD versus CN, and 0.850 for bvFTD versus CN) than the viscosity metrics. Table S6 in supporting information contains brain regions belonging to the top 12 best metaconnectivity features, and Table S7 in supporting information all statistical analyses. The confusion matrices are shown in Figure 3B. To verify whether the selected features were the best discriminators, we re‐classified subjects using random partitions of features (up to 12 features) 10,000 times, generating surrogate distributions for AUC and accuracy. Both AUC and accuracy were higher when using the original features for AD (P = 0.0047 for AUC, and P = 0.0008 for accuracy) and bvFTD (P = 0.0468 for accuracy, and P = 0.0570 for AUC), compared to randomly selected features (Figure S4 in supporting information). These results were replicated with a harmonized and matched sample (Figure S5 in supporting information). Tables S7 and S8 in supporting information summarize all metrics.

Brain regions associated with viscous dynamics are reported in Figure 3C,D. To facilitate visualization, we grouped the regions in “slow‐like” ($\delta +\theta$) and “fast‐like” oscillations ($\alpha +\beta +\gamma$). The colors in Figure 3C,D indicate whether the brain region contributes to an increase or decrease of the metaconnectivity values, based on the sign of Cohen D effect sizes while discarding the magnitude. Across AD and bvFTD, we found regions involved in both increased and decreased metaconnectivity. Further, the faster the frequency bands, the decreased metaconnectivity was more pronounced, especially in bvFTD. In AD, decreased metaconnectivity in faster frequencies was observed in the calcarine fissure and the amygdala, while increased metaconnectivity in the slower bands was seen in frontal areas (superior/inferior frontal gyrus, olfactory cortex, Rolandic operculum). In bvFTD, faster oscillations involved decreased metaconnectivity in frontal areas (middle and inferior frontal gyrus), insula, and amygdala. In contrast, increased metaconnectivity in the slower bands was found in the precentral area, hippocampus, superior parietal gyrus, and inferior parietal gyrus. Thus, the most affected brain regions in AD and bvFTD were pattern specific in terms of oscillations, connectivity, and anatomy.

Finally, we used metaconnectivity to provide discrimination between patients in the harmonized dataset. In this new scenario, metaconnectivity showed the great capability of differentiating bvFTD from AD, reaching AUC values close to 0.99 (Figure S6 and Table S9 in supporting information). We observed decreased metaconnectivity in the bands for several brain regions, including the left superior frontal gyrus (dorsolateral and orbital parts), the right parahippocampal gyrus, the right superior temporal gyrus, among others (Table S10 in supporting information). Consequently, metaconnectivity not only provides an accurate classification between patients and healthy controls but also is sensitive to discrimination between different dementia subtypes (bvFTD vs. AD).

3.2. Metaconnectivity predicts multimodal disease presentation

We investigated the relationship between metaconnectivity and cognitive scores (MoCA scores), years with the disease, and regional atrophy in patients with AD and bvFTD. Using LDA, we independently built a composited variable for the AD‐ and bvFTD‐specific features. LDA separated AD patients from CN (Figure 3E), and a trend was observed for the LDA component to be positively correlated with cognitive impairment in AD (P = 0.1074, r = 0.360), but not with years with disease (P = 0.2358, r = −0.227, Figure 3G). In bvFTD, LDA also distinguished patients from CN (Figure 3F) and correlated positively with cognitive impairment (P = 0.0493, r = 0.526) and negatively with years with disease (P = 0.0493, r = −0.520; Figure 3H).

Furthermore, we found an association between atrophy (measured in terms of cortical thickness) and metaconnectivity (LDA components) using a linear regression model with threshold‐free cluster enhancement correction (TFCE), as shown in supporting information 3. In AD, an anatomic‐specific temporo‐posterior metaconnectivity–atrophy association was observed, while in bvFTD, a fronto‐temporal metaconnectivity–atrophy association was observed (Figure 3I,J). Thus, metaconnectivity was associated with cognitive impairment (in both conditions, but at a trend level in AD), age of disease (bvFTD), and specific brain atrophy patterns (AD, bvFTD).

3.3. Hypoexcitation and structural disintegration explain metaconnectivity dynamics in neurodegeneration

We used a modified version of the Jansen and Rit neural mass model ⁸⁸ to study the metaconnectivity dynamics in neurodegeneration, by simulating potential disruptions in structural connectivity and E/I balance. To ensure the accuracy of our simulations, we first characterized the model with synaptic plasticity through parameter explorations, which resulted in a good fit for empirical data. Specifically, we used functional connectivity fitting in healthy subjects and demonstrated the efficacy of our approach in Figures S7, S8, and S9 in supporting information.

We fitted the model to CN, AD, and bvFTD groups, using the empirical structural connectivity matrices specific to each group. The global coupling parameter, K, and the target firing rate of pyramidal neurons, $\rho$, were swept while the proportion of the $\alpha$ generator neurons within a single brain region was fixed in $r^{\alpha }=0.5$, based on our previous explorations. We extracted the same features from simulated data based on metaconnectivity as those characterized in empirical data and projected them onto the two‐dimensional LDA space, using the LDA trained with the empirical features. The optimization function was the distance between the simulated data and the CN, AD, and bvFTD centroids in the LDA space. Figure 4 shows the fitting results, where lower distance values indicate a better fit of the model to empirical data. We used the notation $\mathrm{\Delta }\rho$ to represent the deviation from the default target firing rate value (2.5 Hz); positive values of $\mathrm{\Delta }\rho$ move the model toward hyperexcitation, and negative ones toward hypoexcitation. Our results suggest that lower $K$ values (compared to AD and bvFTD) and near‐zero values of $\mathrm{\Delta }\rho$ best reproduce the empirical features in CN (Figure 4A, with a blue dot indicating the pairs of parameters associated with the lowest distance, equivalent of highest goodness of fit). However, the best fit of the model to patients’ empirical data was obtained by increasing $K$ and decreasing $\mathrm{\Delta }\rho$ (Figure 4B,C, with red and green dots for AD and bvFTD best parameters). This suggests that, to simulate the specific empirical LDA–metaconnectivity, the brain dynamics must be shifted toward hypoexcitation. Furthermore, lower values of $\mathrm{\Delta }\rho$ should be used for fitting the model to bvFTD data compared to AD. For visualization purposes, we compared the projected empirical data (Figure 4D) to the simulated data (Figure 4E) and found a good correspondence indicating that the fitted model captured the empirical features. Finally, we measured the distance between each point in the simulated LDA space and the CN centroid to test the capability of the model in characterizing patients and healthy controls (Figure 4F). Our results show that our model produces a good discrimination between AD versus CN (Cohen D = 4.89) and bvFTD versus CN (Cohen D = 7.70). Overall, to reproduce empirical metaconnectivity patterns in AD and bvFTD, the brain dynamics must be shifted toward hypoexcitation, especially in bvFTD, and pushed to greater global coupling values indicating higher connectivity strength, compared to healthy subjects.

FIGURE 4.

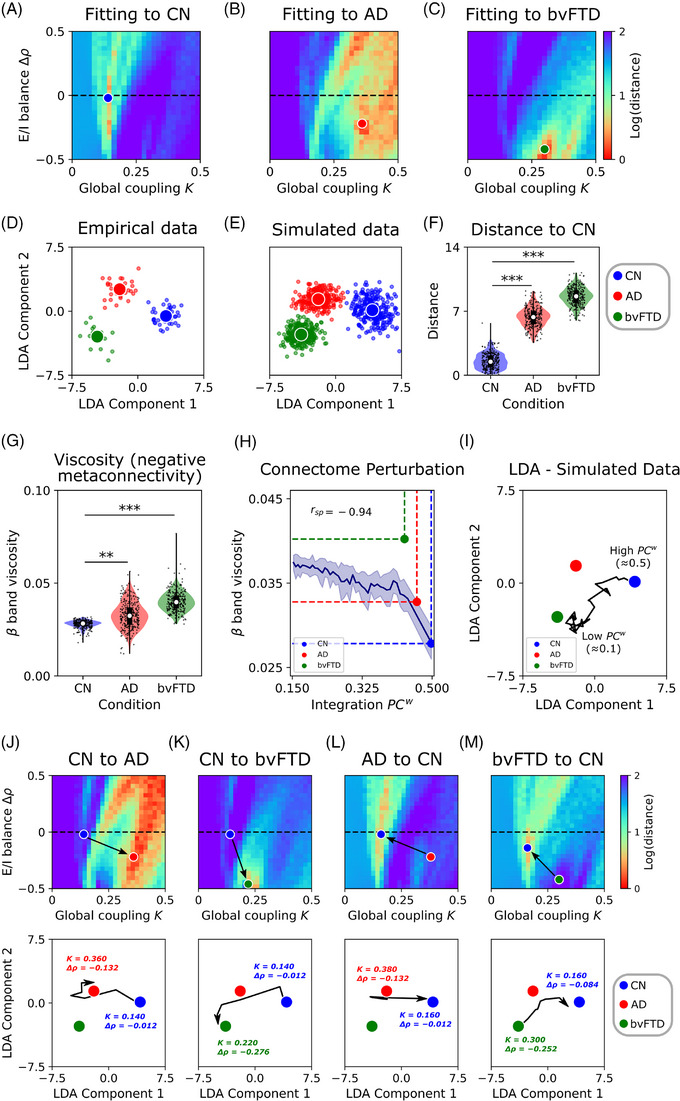
Fitting of the model to empirical metaconnectivity features. A–C, The two parameters of the model (global coupling, $K$, and change in target firing rate, $\mathrm{\Delta }\rho$) were fitted to empirical data using features based on metaconnectivity and LDA. Red values, which indicate a lower distance of the simulated features to the target empirical centroids, are a hallmark of a better fit to empirical data. D, E, Empirical and simulated data (data augmentation up to 300 models’ realizations) projected using LDA. F, Distance from each simulated data point to the CN centroid. G, The simulated data showed an increment of $\beta$ band dynamics viscosity in AD and bvFTD, similar to the empirical results. H, Modeling of structural alterations in neurodegeneration. Healthy connectome disintegration (reducing structural integration), from right to left, is related to more viscous brain dynamics. Colored dots corresponded to the measurements of each group (simulated data). I, Trajectories from the healthy state (CN, high $P{C}^w$) to pathological conditions. Each point in the trajectory corresponds to simulations where the connectome was sequentially perturbed decreasing its $P{C}^w$. J, K, The transition from the healthy condition (CN) to the pathological ones (AD or bvFTD) involved an increment of global coupling, $K$, and a negative change in firing rates, $\mathrm{\Delta }\rho$, which moves the model toward hypoexcitation. In the second row, the trajectories in the LDA space corresponded to the paths marked by the black arrows in the ($K,\mathrm{\Delta }\rho$) parameter space. The initial and final combination of parameters were drawn near their respective centroids. The opposite transition in (L, M) involved a decrease in $K$ and an increase in $\mathrm{\Delta }\rho$. *|D| > 0.5, **|D| > 0.8, ***|D| > 1.2. Data points in violin plots correspond to different model realizations (random seeds). Box plots were built using the first and third quartiles, the median, and the maximum and minimum values of distributions. Confidence intervals were built using the mean ± standard deviation. Correlations were computed using Spearman's $r_{sp}$. AD, Alzheimer's disease; bvFTD, behavioral variant frontotemporal dementia; CN, healthy control; E/I, excitatory/inhibitory; LDA, linear discriminant analysis.

Based on the empirical results shown in Figure 1F, simulated data indicated an increase in $\beta$ band viscosity as illustrated in Figure 4G. The altered viscosity and metaconnectivity can be explained by two mechanisms: structural disintegration and/or E/I balance disturbances. The patients’ $P{C}^w$ was reduced, with bvFTD exhibiting lower values, as represented by the color dots in Figure 4H. To establish a robust link between the structural integration and the functional features of the data (viscosity and LDA measures of metaconnectivity), we used the model that was fitted to the CN and performed simulations with perturbed versions of the connectome. The perturbations involved iteratively reducing the healthy connectome $P{C}^w$ (integration), as illustrated in Figure 4H. When $P{C}^w$ was reduced, viscosity increased and a negative correlation between $P{C}^w$ and viscosity was found (Spearman $r_{sp}=-0.94,p<0.00001$). Surprisingly, the measurements for CN and AD were close to the curve. Therefore, these results suggested that structural disintegration (reduced integration) may be responsible for the increase in viscosity in AD and, to some extent, in bvFTD. The distance between the bvFTD point and the curve might indicate that both structural disintegration and hypoexcitation contribute to the increase in dynamic viscosity in this condition.

In the simulations with the perturbed connectomes, we projected the data using LDA with the same coefficients as empirical data. In Figure 4I, a trajectory from the CN centroid is observed that diverges from the healthy brain state as the $P{C}^w$ is sequentially reduced. Moving in the direction of the trajectory reduces the distance from the original position (CN centroid) to both AD and bvFTD. Thus, the perturbed connectome moves the model, in the low dimensional space toward brain dynamics resembling the states in AD and bvFTD. As shown in Figure S10 in supporting information, we repeated the fitting procedure using functional connectivity matrices instead of metaconnectivity. Adequate fitting to empirical connectivity matrices (SSIM values > 0.6 for CN, AD, and bvFTD) reproduced the increase in dynamic viscosity in both AD and bvFTD compared to CN. When perturbating the healthy connectome, we obtained comparable results to the original ones using metaconnectivity for model fitting (Figure S10). However, compared to metaconnectivity, the model fitted using functional connectivity was not capable of reproducing the specific features extracted from empirical data.

Different pathophysiological pathways can be involved in brain disorders ¹⁰¹ affecting both structural connectivity ⁵⁴ , ⁵⁵ , ⁵⁶ , ¹⁰² , ¹⁰³ , ¹⁰⁴ and E/I balance. ⁵⁷ , ⁵⁸ , ⁵⁹ , ⁶⁰ In our model, the inclusion of inhibitory synaptic plasticity (Figure 2A) allows us to directly control the firing rates of pyramidal neurons in simulations, moving the model toward excitation‐ or inhibition‐dominated regimes of activity. This model enabled us to test the hypothesis that alterations in E/I balance produce transitions between healthy and pathological states and vice versa. We fitted the model to the CN condition to analyze what combinations of $K$ and $\mathrm{\Delta }\rho$ parameters increased the goodness of fit to the AD and bvFTD groups. Results showed that an increase in $K$ alongside a decrease in $\mathrm{\Delta }\rho$ better reproduces the brain dynamics in AD and bvFTD (Figure 4J,K), using the healthy participant's connectome from CN parameters. In the last row of Figure 4, trajectories from the centroids in the LDA space are drawn, in addition to the initial (CN) and final (AD or bvFTD) parameters. The opposite transitions from AD or bvFTD to CN (Figure 4L,M), require decreasing $K$ and increasing $\mathrm{\Delta }\rho$. Thus, for moving the brain dynamics to the ones observed in AD and bvFTD from CN, the model must be pushed toward hypoexcitation, and vice versa for the opposite transition (from hypoexcitation to balanced E/I).

3.4. Perturbational landscapes identify the transitions to healthy and pathological states

Perturbational landscapes, that is, the models’ trajectories during perturbations in the LDA‐reduced dimensional space, reveal potential therapeutic targets for healthy and pathological brain states. As whole‐brain models have the potential to inspire novel therapies, ¹³ , ³⁶ , ³⁷ we explored in silico perturbations of homotopic brain regions ⁹⁷ with excitatory and inhibitory protocols (Figure 5) to identify potential therapeutic targets. In Figure 5A,B, we perturbated single pairs of brain regions, with the magnitude of the perturbation defining the observed trajectories in the reduced dimensional space. For bvFTD, inhibitory perturbations led to transitions from pathological to healthy states, while excitatory perturbations led to the opposite transitions. To summarize the results, we presented the distance between the best trajectories and the target centroids in Figure 5C. The results for in silico perturbation in bvFTD were consistent with previous sections, in which a shift toward hypoexcitation (inhibitory perturbation) was required to drive the dynamics from the healthy to pathological states, and vice versa. In contrast, for AD both inhibitory and excitatory protocols led to transitions from CN to AD state, although the brain regions involved differed. We included a null case that represented the distance from the initial to the target centroid. All perturbation protocols were efficient in deviating the model from the null case (|D| > 1.2, Figure 5C), but only for the CN $\to$ bvFTD transition (and vice versa) did the perturbation protocol influence the distance to the target centroid (|D| > 1.2, Figure 5C). These findings suggest that targeted excitatory and inhibitory perturbations of specific brain regions may have therapeutic potential for the treatment of neurodegenerative diseases.

FIGURE 5.

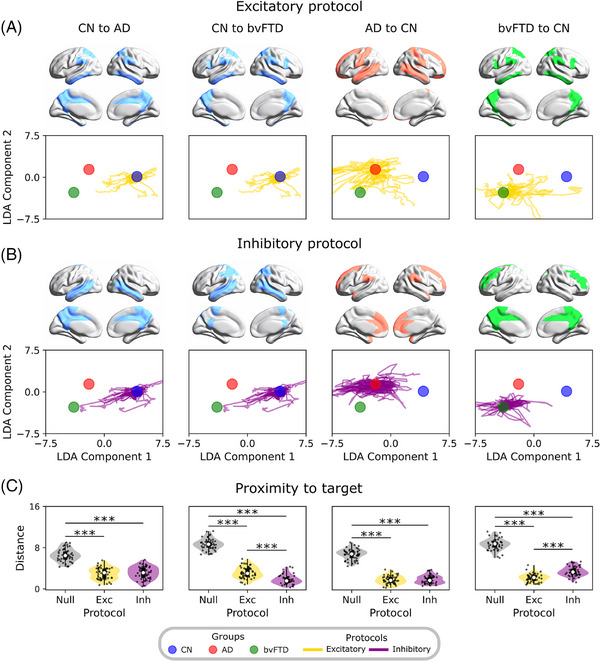
Perturbational approach mediating the transitions between states. A, B, The excitatory and inhibitory perturbation protocols were used to produce transitions from AD or bvFTD to CN and vice versa. These consisted of perturbating single pairs of homotopic regions, producing trajectories that corresponded to different perturbation magnitudes. C, Evaluation of protocols’ performance by measuring the distance from the best point on the trajectories to the target centroid. Lower distance values indicate a better performance. *|D| > 0.5, **|D| > 0.8, ***|D| > 1.2. Data points in violin plots correspond to different model realizations (random seeds). Box plots were built using the first and third quartiles, the median, and the maximum and minimum values of distributions. The colored areas on the brains’ surface represent the best perturbation targets to drive the transitions, for each perturbation protocol. AD, Alzheimer's disease; bvFTD, behavioral variant frontotemporal dementia; CN, healthy control; LDA, linear discriminant analysis.

Finally, we identified the top five pairs of homotopic brain regions, which are associated with the trajectories that most reduce the distance to the target condition, in mediating the different transitions (Figure 5 and Table S11 in supporting information). In the case of AD, we identified a subnetwork of frontoparietal and temporal brain regions, using both protocols, including the superior frontal gyrus, the superior and middle temporal gyrus, and the precuneus. For bvFTD, the characterized network consisted of several frontotemporal brain areas, such as the middle temporal gyrus, frontal gyrus (middle and inferior), and the precuneus. Overall, our in silico brain perturbation approach allows us to identify key brain regions involved in the pathological trajectories, which can be proposed as therapeutic targets for real‐life perturbation protocols (e.g., transcranial magnetic stimulation, and deep brain stimulation).

3.5. Out‐of‐sample validation of metaconnectivity and mechanisms

We conducted an out‐of‐sample validation to evaluate the robustness of our approach and its generalizability to more heterogeneous contexts. To achieve this, we used a second subsample of participants (CN = 101, AD = 110, bvFTD = 26) and replicated key analyses from our original dataset. These analyses included altered metaconnectivity and increased viscosity in neurodegeneration, model fitting by manipulating global coupling and E/I balance, and connectome disintegration, which are all associated with the model's mechanisms for simulating altered metaconnectivity in AD and bvFTD. For validation purposes, we first used the same metaconnectivity‐based features (normalized to match the range of the first dataset) as inputs for the machine learning classifier. Then, we projected the data using the LDA trained with the original dataset. Next we conducted model fitting by sweeping the global coupling and target firing rate parameters while comparing the model's output to the new features in the reduced‐dimensional space through LDA. Last, we replicated the connectome perturbation analysis using the model fitted to the CN group of the validation dataset to explore the relationship between viscosity and structural disintegration.

Using the same classifier, we found good discrimination values between AD (AUC = 0.883) and bvFTD (AUC = 0.957) patients and healthy controls (Figure 6A,B). These results demonstrate the robustness of metaconnectivity as a biomarker for dementias, with better performance than pairwise functional connectivity in previous findings (Figure 3). In the new dataset, we again found a similar pattern of increased $\beta$ band viscosity in AD (P = 0.00011, t = 3.94, D = 0.55) and bvFTD (P < 0.00001, t = 6.07, D = 1.36), suggesting again a shift to a more uncoordinated or viscous brain dynamics in patients (Figure 6C). The data were then projected into a two‐dimensional space using LDA (Figure 6D), and while the overlap between groups was slightly higher than in previous results (Figure 4E), metaconnectivity still achieved good discrimination of CN from AD (P < 0.00001, t = 12.13, D = 1.68) and bvFTD (P < 0.00001, t = 10.00, D = 2.22) using LDA (Figure 6E).

FIGURE 6.

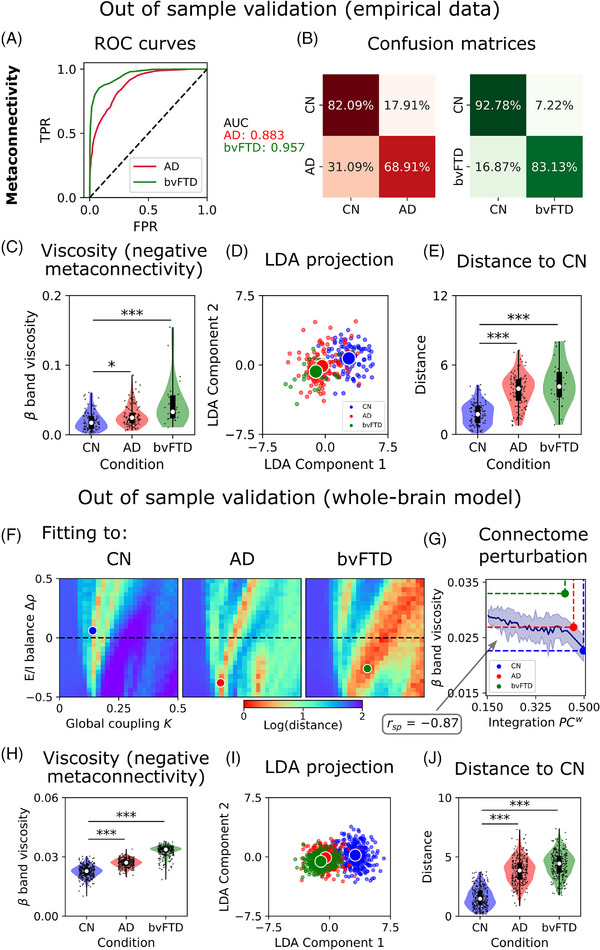
Out‐of‐sample validation of whole‐brain metaconnectivity and mechanisms. A, ROC curves and AUC values for AD and bvFTD. B, Confusion matrices. C, Dynamic viscosity is defined as the absolute sum of the negative values within the metaconnectivity matrices. $\beta$ band viscosity was higher in AD and bvFTD with respect to CN. D, Empirical data projected using LDA. E, Distance from each empirical data point to the CN centroid. F, Two parameters fitting (global coupling, $K$, and change in target firing rate, $\mathrm{\Delta }\rho$) of the model to empirical data using features based on metaconnectivity and LDA. Red values, which indicate a lower distance of the simulated features to the target empirical centroids, are a hallmark of a better fit to empirical data. G, Healthy connectome disintegration (reducing structural integration) from right to left is related to more viscous brain dynamics. Colored dots corresponded to the measurements of each group (simulated data). H, The simulated data showed an increment of $\beta$ band dynamics viscosity in AD and bvFTD, similar to the empirical results. I, Simulated data (data augmentation up to 300 models’ realizations) projected using LDA. J, Distance from each simulated data point to the CN centroid. *|D| > 0.5, **|D| > 0.8, ***|D| > 1.2. Data points in violin plots correspond to different model realizations (random seeds) and subjects. Box plots were built using the first and third quartiles, the median, and the maximum and minimum values of distributions. Confidence intervals were built using the mean ± standard deviation. Correlations were computed using Spearman $r_{sp}$. AD, Alzheimer's disease; bvFTD, behavioral variant frontotemporal dementia; CN, healthy control; LDA, linear discriminant analysis; ROC, receiver operating characteristic.

The whole‐brain model was re‐fitted using the new data projected using LDA. Although the parameters were different from the original ones (Figure 4A‐C), we observed the same original pattern: fitting the model to AD and bvFTD conditions required a higher global coupling and a shift to hypoexcitation, compared to CN (Figure 6F). The simulated data showed a similar pattern of increased $\beta$ band viscosity in AD (D = 1.63) and bvFTD (D = 3.58) with respect to CN (Figure 6H). Using data projection with LDA (Figure 6I), the model showed good discrimination between AD (D = 2.34) and bvFTD (D = 2.89) from CN (Figure 6J). Finally, using the same perturbational procedure of connectome disintegration, we found again a link between structural integration and dynamic viscosity (Spearman $r_{sp}=-0.87,P<0.00001$; Figure 6G). Thus, by using an external dataset with large heterogenous sources, we validated and generalized the whole‐brain metaconnectivity mechanisms (structural disintegration and hypoexcitability) in neurodegeneration.

4. DISCUSSION

We applied whole‐brain semi‐empirical modeling to brain data and causal mechanistic explanations for the transition from brain health to disease (and vice versa) in neurodegeneration. Results showed increased dynamic viscosity in AD and bvFTD compared to healthy controls, along with altered metaconnectivity across all frequency bands. The metaconnectivity‐based features outperformed pairwise interactions, and partially predicted disease severity. These high‐order interactions also discriminated between patient groups. The computational modeling reproduced the metaconnectivity‐based features extracted from empirical data and identified the mechanisms explaining the viscosity/metaconnectivity patterns in patients, supporting the hypothesis of reduced structural integration ²⁷ , ¹⁰⁵ , ¹⁰⁶ and alterations in E/I balance ⁵⁷ , ⁵⁸ , ⁵⁹ , ⁶⁰ linked to AD and bvFTD. We also identified key brain regions using a perturbational approach that mediates the transitions from pathological states to the healthy state and vice versa. Overall, our work provides novel and theoretically supported EEG‐based biomarkers for characterizing dementias in underrepresented, diverse, and non‐stereotypical populations.

Our study shows that metaconnectivity outperformed pairwise functional connectivity as a biomarker for dementia classification. Results resemble previous works of our team, ⁴⁹ using a different approach to high‐order interactions in AD and bvFTD. The altered metaconnectivity patterns observed in our study overlapped with previously identified brain regions affected in both AD ¹⁰⁷ and bvFTD ¹⁵ , ¹⁰⁸ , ¹⁰⁹ including frontoparietal, temporal, and frontotemporal brain regions. We found that while patterns of increased and decreased metaconnectivity were observed in all frequency bands, ⁴⁹ reduced metaconnectivity was mainly associated with faster oscillatory regimes such as beta and gamma, which is consistent with the widely supported slowing of EEG rhythms reported in dementia, ²⁴ , ²⁷ , ²⁸ , ¹⁰⁵ , ¹¹⁰ , ¹¹¹ and previous results using information theory. ⁴⁹ Our results also demonstrated that these metaconnectivity features predicted severity and disease presentation, especially in bvFTD. However, weaker correlations were observed between metaconnectivity and disease severity in AD, possibly due to the more advanced stage of the pathology in terms of years with the disease, lower MoCA scores, and advanced atrophy. As brain damage is widespread at these stages, functional measurements are less powered to predict the disease stage. Our findings highlight the robustness of high‐order interactions beyond pairwise functional connectivity ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ , ⁴⁹ , ¹¹² and support the growing body of evidence suggesting that complex brain dynamics should be better characterized by simultaneous interactions, ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ , ¹¹² dementia included among them.

We enhanced our empirical analysis by incorporating computational semi‐empirical modeling, which provided causal mechanisms linking altered viscosity and metaconnectivity patterns. Our findings showed that disrupting the structural brain hubs (connectome disintegration) led to increased viscosity in AD and bvFTD. Considering that (1) higher viscosity is a signature of an uncoordinated (less integrated) brain dynamics, ⁵⁰ , ⁵¹ , ⁵² and (2) brain hubs are essential for orchestrating brain activity ¹⁰⁴ and promoting integrated brain states, ¹¹³ , ¹¹⁴ , ¹¹⁵ , ¹¹⁶ compromising the brain's structural hubs would impair functional integration (increasing viscosity) in patients with dementia. These hubs are very susceptible to excitotoxicity and damage, ¹¹⁴ and are compromised in neurogenerative diseases. ⁵⁴ Our model suggests that disrupting the rich‐club organization of the human connectome may be a possible pathway to generate AD‐ and bvFTD‐like brain dynamics. We explored a second mechanism in the model based on E/I balance. Specifically, a shift toward hypoexcitation was necessary to recover the metaconnectivity observed in empirical data and to produce a transition from healthy to pathological states. Overall, our results are in line with the dual profile of E/I balance in neurodegenerative diseases. ⁵⁷ Both human and animal studies suggest that in preclinical stages, dementia is characterized by hyperexcitation, due to the accumulation of Aβ and tau aggregates. ⁵⁷ , ⁵⁸ , ⁵⁹ As the disease progresses, hyperexcitability leads to neuronal loss, producing a shift toward hypoexcitation, hypometabolism, and the slowing of EEG rhythms. ²⁴ , ²⁷ , ⁵⁷ , ⁵⁸ , ⁵⁹ , ¹⁰⁵ , ¹¹⁰ , ¹¹⁷ , ¹¹⁸ , ¹¹⁹ , ¹²⁰ , ¹²¹ , ¹²² Thus, our results provide the first semi‐empirical modeling support for two different but complementary pathways triggering the functional disturbances in neurodegenerative diseases.

The perturbational approach identified key brain regions that could be targeted for stimulation in therapies such as transcranial magnetic stimulation or deep brain stimulation. ¹²³ , ¹²⁴ , ¹²⁵ Data‐driven approaches suggested that the precuneus, compromised in AD ¹²⁶ and proposed as a therapeutic target for stimulation ¹²⁶ ; and the frontal gyrus (superior, and middle) and temporal poles, structures impaired in bvFTD, ¹⁰⁸ , ¹⁰⁹ , ¹²⁷ could be effective targets. Similar results were found in a previous functional MRI study from our team, ³³ in which the best stimulation targets were posterior (AD) and frontotemporal (bvFTD) brain regions. Interestingly, in our work, the best protocol for producing the transition from bvFTD to CN corresponded to the excitatory protocol, which is consistent with our previous results in which increasing the model's excitability mediates the transition from bvFTD to a brain state that most resembles healthy controls. Another avenue for future research involves simulating in silico pharmacological therapies to restore healthy brain function. ¹³ , ³⁵ , ³⁹ Based on our results indicating hypoexcitation, whole‐brain models informed with neurotransmitters and neuromodulator receptor expression could be used to test pharmacological interventions that may restore a healthy E/I balance in patients. Possible candidates include cholinergic drugs ¹⁰⁷ , ¹²⁸ and psychedelics, ¹²⁹ which have been found to restore normal brain function in other disorders. ¹³⁰

From a more methodological perspective, our work provides valuable computational tools for studying whole‐brain dynamics in both health and disease, ¹¹ and we have made these tools publicly available alongside this publication. Compared to other biophysical or purely phenomenological computational works, ³⁵ , ¹³¹ our model can reproduce functional connectivity in a wide range of the EEG spectrum. As a biophysical‐inspired model, it can answer more specific questions directly, for example, how E/I balance, neuromodulators, and local connectivity impact whole‐brain activity. Other brain models suggested a shift toward hyperexcitation for explaining the slowing of the EEG rhythms in AD, ³² , ³⁵ which may seem contradictory to our findings. However, that is more likely to occur in the preclinical and early stages of dementia, during which a shift toward brain hypometabolism predominates in the middle and advanced stages. ⁵⁷ , ¹¹⁸ , ¹¹⁹ , ¹²⁰ , ¹²¹ Moreover, both hyperxcitation and hypoexcitation can coexist in AD, with some brain regions exhibiting increased or decreased excitability. ³² , ³⁴ Further, our work is unique in combining metaconnectivity with whole‐brain modeling, which differs from other modeling studies that have reproduced empirical observables using theoretical models without previously addressing how well these features characterize neurodegenerative diseases.

Our approach was effectively generalized through out‐of‐sample validation, which incorporated more heterogeneous, diverse, and non‐harmonized datasets. Using data from various countries, EEG configurations, channel quantities, and diverse demographics, we successfully replicated previous findings based on harmonized data. In the second subsample, metaconnectivity continued to demonstrate its robustness in distinguishing patients from healthy controls. Notably, the impaired metaconnectivity dynamics (viscosity) were observed in both AD and bvFTD groups even with comparable effect sizes and directionality (bvFTD > AD > controls). The compromised mechanisms identified by the model also accounted for the empirical dynamics in the out‐of‐sample validation. These findings support the generalization of both metaconnectivity alterations and biophysical mechanisms attributed to these deficits. Expanding model generalization to underrepresented, non‐stereotypical, and diverse samples is crucial for understanding brain‐phenotype associations. ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁶³ While future research should consider validations using harmonized datasets, our findings underscore the strength of our results when applied to complex and variable data sources.

There are important limitations that should be addressed in future work. First, although comparable or larger than similar studies, ³² , ³⁴ , ¹¹⁷ our results should be confirmed with more participants from the Global North and South. Still, the theoretical framework based on biophysical modeling may allow us to make better use of small datasets and improve the understanding of brain function by linking empirical features with biophysical mechanisms. ³⁰ We have validated our results with diverse samples from the Global South, which are crucial for better representation in global research. ¹ , ¹² Nevertheless, future works should compare stereotypical versus non‐stereotypical patients to test the generalizability and specificity of our findings and should account for the differences between the Global North and South. More specifically, we suggest including differences such as structural inequalities ⁶ , ⁷ , ¹³² such as the Gini coefficient, socioeconomic disparities (social determinants of health, socioeconomic status), educational differences, and varied genetic admixtures, with a higher degree in Latin America. Environmental factors like pollution levels also distinguish these regions. Incorporating these elements as parameters in generative models ¹¹ could significantly enhance region‐specific analyses. Second, we used averaged empirical priors for model fitting, while personalized whole‐brain models are gaining acceptance for characterizing brain dynamics in many brain conditions and disorders. ¹³³ Such personalized models could lead to individualized therapies for restoring healthy brain function, ³² , ¹³⁴ which is particularly relevant given the high heterogeneity among dementia patients. ¹³⁵ Further, the current group‐level atrophy assessments should be expanded to individualized approaches using weighted matrices and functional connectivity metrics, offering more personalized brain analysis. Therefore, we plan to expand our model to perform single‐subject characterization in future work. Finally, the model could be further improved by incorporating other empirical priors, ³² , ³³ , ³⁵ , ³⁹ , ¹⁰¹ , ¹³⁶ such as metabolic Aβ and tau brain aggregates, and neurogenetic maps, among others. ¹¹ This could improve the precision of our model in reproducing AD‐ and bvFTD‐like phenotypes.

Our results provide a well‐rounded characterization of AD and bvFTD brain phenotypes using a novel whole‐brain semi‐empirical modeling framework. The findings establish a comprehensive computational framework and a multilevel research roadmap for advancing dementia characterization, encompassing early stages, longitudinal investigations, diverse dementia subtypes, and individualized trajectory evaluations in clinical trials.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest. Author disclosures are available in the supporting information.

Supporting information

Supporting Information

Supporting Information

Coronel‐Oliveros C, Gómez RG, Ranasinghe K, et al. Viscous dynamics associated with hypoexcitation and structural disintegration in neurodegeneration via generative whole‐brain modeling. Alzheimer's Dement. 2024;20:3228–3250. 10.1002/alz.13788