Mechanics of colloidal supraparticles under compression

The structure of a spherical colloidal particle agglomerate predicts its fracture and deformation resistance.

Abstract

Colloidal supraparticles are finite, spherical assemblies of many primary particles. To take advantage of their emergent functionalities, such supraparticles must retain their structural integrity. Here, we investigate their size-dependent mechanical properties via nanoindentation. We find that the deformation resistance inversely scales with the primary particle diameter, while the work of deformation is dependent on the supraparticle diameter. We adopt the Griffith theory to such particulate systems to provide a predictive scaling to relate the fracture stress to the geometry of supraparticles. The interplay between primary particle material and cohesive interparticle forces dictates the mechanical properties of supraparticles. We find that enhanced stability, associated with ductile fracture, can be achieved if supraparticles are engineered to dissipate more energy via deformation of primary particles than breaking of interparticle bonds. Our work provides a coherent framework to analyze, predict, and design the mechanical properties of colloidal supraparticles.

INTRODUCTION

Colloidal supraparticles (SPs), consisting of spherical assemblies of a large number of colloidal particles, have recently emerged as a promising material system (1–3). Such SPs are structural entities that bridge the micro- and mesoscale. They not only exhibit emergent ensemble properties found in individual colloidal particles but also display discrete features that are distinct from bulk colloidal assemblies. SPs are typically fabricated via evaporation of droplets of aqueous colloid dispersions in emulsions (4–6), in air (7, 8), or on superhydrophobic substrates (9–11).

Besides providing insights into fundamental questions on the thermodynamics and kinetics of confined self-assembly processes (12–16), SPs offer a wide range of attractive properties. One of their key characteristics is the vast structural diversity. The composition, size, materials, and even the shape of the SPs can be easily and precisely tuned via the constituent colloidal building blocks (17–19), the size of the confining droplet, and the kinetics of the consolidation process (4, 7, 11, 15, 20, 21). As mesoscopic objects, they exhibit emergent properties arising from the defined internal arrangement of the constituent particles. For example, SPs consisting of primary particles (PPs) with dimensions in the range of visible light can display vivid structural color (5, 22). The coloration of such SPs can be controlled via the internal structure (5, 22, 23). Last, SPs themselves can be used as finite-size building blocks, ready to form macroscopic structures with a high level of hierarchy (24). Structures with multiple levels of hierarchies are common motifs in nature (25), through which exceptional properties are achieved from the limited and usually underperforming material choices in biological systems (25), as evidenced, e.g., by nacre (26) and sea sponges (27). As an emerging field, colloidal SPs have already found applications in optical pigments (28), lasers (29), sensors (30, 31), tissue engineering (32, 33), drug delivery (34), anti-counterfeiting (35), and additive manufacturing (8).

One prerequisite for any meaningful application involving colloidal SPs is that they must be mechanically robust. Because their properties arise from well-defined internal structures, colloidal SPs must maintain structural integrity throughout the fabrication, handling, and in the application environment. The material may fail, gradually or catastrophically, for example, by impact shock from the solid substrates, shearing from the suspended liquid, stretching of the surrounding matrix, or compression from external forces during application.

However, the mechanical response of SPs is complex, as it involves hierarchical levels of deformation. At the individual PP level, the mechanical properties are determined by the material, potentially modified by size effects, which can be probed by nanoindentation on single colloidal particles (36). At this single-particle level, theoretical models are needed to evaluate the data and extract relevant mechanical parameters, such as Young’s modulus, which are usually defined from the uniaxial deformation of flat specimens rather than spherical objects. As an example, the Hertz model has often been used to obtain the elastic modulus of a single silica sphere of a few hundred nanometers from the load and displacement data during compression (37, 38). Attractive forces act between the individual PPs in contact, especially van der Waals forces at particle contact, capillary forces from liquid bridges at the neck of contact caused, e.g., by water condensation (39, 40), and potential solid bridges from impurities in the drying dispersion (41). Static and dynamic friction (42) between the particles may further change the resulting mechanical properties. At the assembly level, the force network of the interacting PPs determines the distribution of the external pressure, and the arrangement of particles may thus influence crack propagation or dislocation movement (43–45). All of these individual contributions are coupled dynamically to the structure of the SP during its mechanical response to external forces.

There have been continuous theoretical and experimental efforts to address the mechanics of particle assemblies (46, 47). The most relevant model for SPs was proposed by Rumpf (48), which reasons that the fracture of agglomerates under load is caused by tensile stress within the structure and predicts the critical fracture stress by summing all adhesive forces between interparticle bonds in a fracture plane. This model provides important rule of thumb predictions on agglomerate stability, as it can involve important parameters such as van der Waals and capillary forces, solid bridges, particle interlocking, binders, and the packing fraction of the agglomerate. However, it assumes a clear fracture plane that disintegrates the whole agglomerate into two pieces, which is usually not the case in ductile deformation or when fracture occurs gradually within the structure (46, 47). In addition, the size of the agglomerate does not play a role in the model. From the experimental side, the nanomechanical behavior of granular materials in bulk or in specifically shaped specimens has received growing attention (45, 49–54). Pioneering micromechanical studies have focused on failure and fracture of spherical granulates or agglomerates under compression (10, 55–59). Modeling studies are based mostly on the discrete element method incorporating elastic and inelastic contact models (60–62). However, a common obstacle is the lack of control in the geometric features in such assemblies, in terms of both PP size and agglomerate size, which can hinder interpretation of data. A detailed understanding of the mechanical response, especially tailored for colloidal SPs, is largely missing to date.

Here, we fabricate colloidal SPs with uniform, well-defined geometric features using droplet-based microfluidics (23). The method creates uniform droplets of a colloidal dispersion in a continuous oil phase. The diameters of these droplets can be accurately controlled (63), which enables precise, independent control of PP size, material, and the subsequent SP sizes. We use this ideal model system to investigate the mechanical stability of SPs under compression using a nanoindenter and observe the deformation both in situ and post-measurement in a scanning electron microscope (SEM). We find that the prepared colloidal SPs are very stable and show ductile deformation in ambient humidity. We provide a scaling relationship between the fracture stress and the geometric features of the SP, rationalized by Griffith’s theory. We further demonstrate the change of fracture mode from ductile to brittle by varying the contributions to the adhesive forces within the SP. Last, we provide a general understanding into the deformation and fracture of colloidal SPs involving multiple levels of forces.

RESULTS

The fracture of colloidal SPs under compression

We fabricate colloidal SPs using emulsion droplets that encapsulate PPs. The droplets are produced in a cross-junction polydimethylsiloxane (PDMS) microfluidic device (Fig. 1A), where an aqueous dispersion of polystyrene (PS) PPs is emulsified into monodispersed droplets in a perfluorinated oil continuous phase, stabilized by a nonionic fluorosurfactant (64). The drying process is driven by water diffusion into the oil phase, eventually consolidating the dispersed colloidal particles into compact SPs (5, 15). All relevant geometric features of the SP—final diameter and PP diameter—can be independently controlled by changing the droplet size or the colloidal dispersion of PPs, which provides ideal model systems to study structure-property relations of colloidal SPs. Figure 1B shows an optical microscopy image of PS SPs underlying the high uniformity (PP = 230 nm). All SPs exhibit the characteristic structural color signature of a consolidated, spherical symmetry with defined, onion-like {111} layers and an amorphous core (3, 5), indicating that the internal structure of the particles is similar and uniform. The inset shows a SEM image revealing the ordered surface structure of the SPs.

Fig. 1. Uniform SPs prepared from droplet-based microfluidics used as model systems.

(A) Emulsion droplets of an aqueous colloid dispersion in oil fabricated by microfluidics. (B) Optical microscope image of colloidal SPs exhibiting structural color. The SEM image in the inset reveals the ordered surface of the SPs and their constituent PPs. (C) Side view of a colloidal SP on a substrate under the flat indentation tip. The force and displacement of the tip are recorded during compression to study the mechanical properties at a single particle level.

We deposit SPs on flat silicon substrates and use a diamond flat punch indenter to investigate the mechanical stability of SPs under compression (Fig. 1C). The large tip diameter (90 μm) ensures that the entire SP is always compressed between two parallel walls. The mechanical response of the SPs, especially the deformation resistance and fracture, is reflected by the force and displacement recorded at the indentation tip.

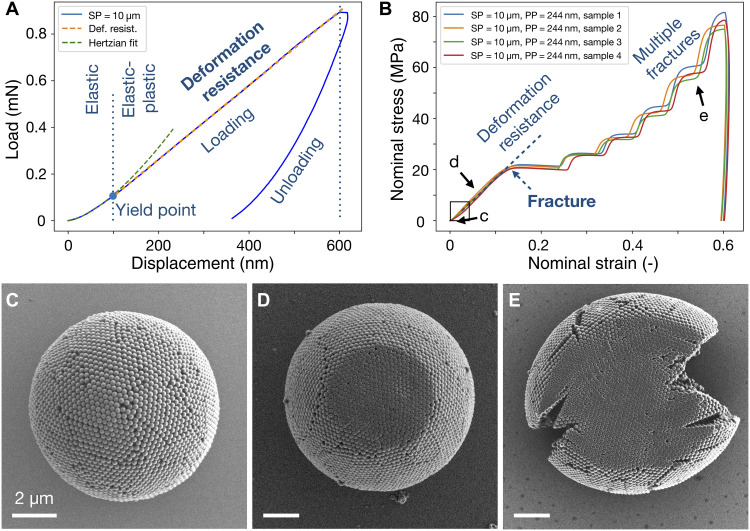
A typical force-displacement curve during the compression of colloidal SPs is shown in Fig. 2A (SP = 10 μm, PP = 244 nm). The nanocompression is performed in ambient condition at 50% humidity in speed control mode at 50 nm/s followed by a cleaning protocol to ensure the compression process (fig. S1). Shortly after the tip contacts the SP (displacement less than about 100 nm), the SP deforms elastically. Although the SP is a porous assembly of individual spherical PPs, its mechanical response can be fitted by the Hertzian model, which assumes a continuum solid sphere (green dashed curve) (38), agreeing to previous observations in spherical granulate materials with inhomogeneous PP sizes (61, 62). After the yield point, the SP enters the elastic plastic deformation regime. The slope of the linear region in the loading curve indicates the magnitude of resistance against deformation of the SP under compression. The force applied to the indenter tip is stopped after the tip advances 600 nm into the SP, but the SP continues to deform slightly, indicating creep behavior typical of viscoelastic polymeric material (65). When the indenter tip retracts from the SP, the elastically stored energy is recovered, as shown in the unloading curve. The elastic plastic loading (EPL) index (66) can be calculated by the area underneath the unloading and loading curve, which represents, respectively, the energy stored in the reversible elastic deformation and the total energy including the additional irreversible plastic deformation. A completely elastic material has an EPL of 0 and a completely plastic material of 1. The colloidal SP measured here has an EPL of 0.72 at 5% nominal strain, suggesting a strong plastic deformation. We measured that the pure elastic deformation regime of SP is limited to 100-nm displacement, which is half the PP diameter. This length scale is very small compared to the SP diameter. We therefore focus on the inelastic mechanical behavior of SPs at larger deformation, which is more application relevant.

Fig. 2. Mechanical properties of PS colloidal SPs under compression in 50% ambient humidity.

(A) Load-displacement curve of a typical colloidal SP consisting of 244-nm primary PS particles during loading and unloading. After initial elastic deformation, the SP undergoes a linear region of elastic-plastic deformation, the slope of which represents the resistance against deformation under compression. The area under loading and unloading curve indicates toughness and the stored elastic energy during deformation. (B) Nominal stress-strain curves for four individual SPs, highlighting the reproducible compression behavior. (C to E) SEM images at different stages of the compression experiment. The SP (C) first deforms elastic-plastically at the beginning of compression (D) and then undergoes multiple fracturing indicated by pop-ins (plateaus) as the material fails (E). The SP is ductile, and individual PPs are heavily deformed.

We first define some key parameters to describe the mechanical behavior of SPs, including stress, strain, Young’s modulus, and yield strength. Figure 2B shows four SPs (SP = 10 μm, PP = 244 nm) under compression at large deformation. During compression, the SP undergoes a continuous change in shape, resulting in a dynamically increasing contact area under the indenter tip (67). Instead of actual stress and strain, we therefore calculated a nominal stress by dividing the force by the cross-sectional area of SP and a nominal strain by dividing displacement by the diameter of the SP before compression. Typically, the slope in the linear region of the stress-strain curve is used to evaluate the mechanical properties, i.e., the Young’s modulus of elastic material. Here, we define the slope in this linear region as deformation resistance (indicated by dashed lines in Fig. 2B), which indicates the resistance of SP against external force during its plastic deformation before fracture. Similarly, we define the fracture stress and strain at the first inflexion point (blue arrow; Fig. 2B), which indicates the first fracture event of an SP, conceptually similar to the yield strength when a material start to fail. The mechanical response of SPs is highly uniform and reproducible, evident in the overlapping nominal stress-strain curves of the four samples (Fig. 2B). The initial pure elastic deformation is not visible, as the SP yields at about 1% (Fig. 2B, arrow c). We examine the SPs after compression in the SEM and find no visible residual deformation in either the individual PP or at SP level in the initial pure elastic regime (Fig. 2C). As compression continues, the deformation is characterized by a linear region until the curve flattens at around 15% nominal strain and 20-MPa nominal stress, indicating a reduction in resistance caused by the fracture. In this regime (Fig. 2B, arrow d), the SP remains spherical at the periphery, while individual PPs are visibly deformed in the contact area (Fig. 2D). Further compression results in multiple plateaus in the nominal stress-strain curve, presumably caused by the formation of consecutive cracks, which extend from the periphery to the center, as indicated by the SEM image (Fig. 2E). The deformation of the SP is ductile, and the fractured SP remains as one piece. The slope after each plateau becomes steeper, indicating that the SP becomes more resistant to external forces as it deforms, probably due to the enlarged contact area, which is also observed in consecutive loading-unloading compression cycles (fig. S2). After compression, the individual PPs are heavily deformed without positional rearrangement, evident in the flattened SP surface (Fig. 2E and fig. S3). The almost vertical unloading curve indicates little stored elastic energy and heavy plastic deformation of the SP. Both the shape of the stress-strain curve and the multiple fracture pattern of the PS SP, a material composed (of a discrete) particulate assembly, shows similarities to individual micrometer-sized amorphous silica or titania particles (37, 68), although the measurements were performed under different environmental conditions. These similarities may suggest a universality of plasticity in particulate matter, covering length scales down to the atomic realm (53, 69). We note that the cooperative mechanical response of SPs is additive (fig. S4A), which allows estimation of mechanical stability of assemblies of SPs such as monolayer (Fig. 1B) or even superlattices at higher hierarchies.

The scaling between fracture and SP geometry

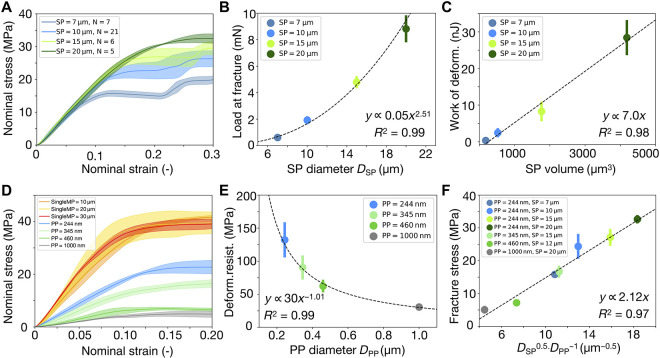
Given the well-defined structure of our SPs, we next set out to derive scaling relationships connecting the key mechanical properties described in Fig. 2B to the relevant geometrical characteristics of the SPs. First, we investigate the effect of SP size on the deformation resistance against compression. Using colloidal PPs with a size of 244 nm, we fabricate SPs with four different diameters (Fig. 3A). The solid line depicts the averaged nominal stress strain value, and the color band represents the deviation from the averaged value. We select 10-μm SP as a reference (light blue curve) and tested a statistically significant number (N = 21) of samples. The reproducible mechanical behavior of SPs reflects the high uniformity of the fabricated samples. For subsequent samples, we used a smaller number of measurements, which yielded similar experimental deviations in the data (Fig. 3A), thus indicating that these smaller sample sizes also provide reliable data. The slope of the nominal stress-strain curves for all SPs (SP = 7, 10, 15, and 20 μm) overlaps completely, independent of the SP size (Fig. 3A). This indicates that the deformation resistance is an inherent material property of SPs and does not depend on the diameter of the SP. However, the fracture event depends on the SP size. The load at which fracture occurs scales with the SP diameter with a power law exponent of 2.5 (Fig. 3B). The displacement at which fracture occurs scales with the SP diameter with a power law exponent of 1.5 (fig. S5B). This suggests a simple linear relationship between load and displacement at the onset of SP fracture (fig. S5C), which allows predicting the SP mechanical behavior by measuring only a few different samples. Notably, while the fracture stress and strain depend on the SP diameter, our data analysis suggests that the work of deformation, i.e., the energy adsorbed by the SP until fracture, is proportional to the SP volume (Fig. 3C). This scaling suggests that although SPs of different diameters fracture at different strains, fracture occurs after adsorbing a certain amount of energy proportional to the number of particles in the SP. In other words, the energy is shared by all involved PPs, and fracture sets in when this absorbed energy per particle reaches a threshold. Corroborating with this behavior, we found that the EPL index at 5% nominal strain (EPL) decreases with increasing SP size (fig. S5D). This suggests that larger SPs have a higher elastic energy storage capability, as there are more PPs to share the absorbed energy, thus requiring less plastic deformation of each PP to dissipate energy.

Fig. 3. Influence of SP and PP diameter on the mechanical response of SPs under compression.

(A) The deformation resistance, which can be considered the equivalent of a Young’s modulus in the SPs, is independent of SP diameter (PP diameter = 244 nm), indicated by the linear region of nominal stress-strain curves. (B) The fracture load of SP scales with its diameter via a power law with an exponent of 2.5. (C) The work of deformation is linearly proportional to the volume of SPs. (D) The deformation resistance of SPs increases as the PP diameter decreases (gray to green to blue), approaching the value of single large PS particles (yellow, pink, and red). (E) The deformation resistance of SPs scales inversely with the PP diameter. (F) Universal scaling relationship between fracture stress and the diameters of SPs and PPs. SDs are shown as error bars. In some cases, the error is smaller than the data points.

Having established that the deformation resistance is independent of the SP diameter and, by this, the number of PPs in the SP (Fig. 3A), we can conveniently isolate the effect of different PP diameters (Fig. 3D) without having to fix either the SP diameter or the number of constituent PPs. Assuming no inherent size effect of different polymeric PPs used in this study (37, 51) (D_PP = 1000, 345, and 244 nm; gray to green to blue in Fig. 3D), we find that the deformation resistance of SP scales inversely with PP diameter (Fig. 3E). Compared to SPs, micrometer-sized solid PS particles have the highest deformation resistance (abbreviated as singleMP, diameters of 10, 20, and 30 μm; yellow, pink, and red curves), which follows the same trend when one assumes them to be composed of infinitely small PPs. Similar to SPs, the nominal stress-strain curves of these solid PS microparticles also collapse into one, but their fracture stresses are not affected by the different diameter. In addition, multiple fracture events are also observed for solid PS spheres during compression, similar to our SPs (Fig. 2E) and other micrometer-sized particles (37, 68) but without large cracks at the periphery (fig. S4D). These similarities suggest that PS SPs behave similarly to a large porous PS sphere under compression. The deformation resistance can therefore be considered as an inherent material property, depending only on the pore sizes, which is determined by the PP diameter.

To rationalize the scaling, we apply the Griffith fracture mechanics (65, 70) to the SPs with the consideration of their particulate nature. Both the pop-in events in the quantitative load and displacement data and the in situ observations of deformation point out that the failure of the SPs is controlled by the formation and propagation of a crack. According to Griffith criterion of fracture, the initiation of the crack propagation is predicted by

$${\mathrm{\sigma }}_{\mathrm{c}}=\sqrt{\frac{2E\mathrm{\gamma }}{\mathrm{\pi }a}}\bullet f$$

where σ_c is the critical stress at fracture, E is the Young’s modulus of the sample, f is the geometry factor, γ is the surface energy density, and a is the size of the initial defect.

The energy required to create two free surfaces per area is represented by γ, which, in our case, is the energy required to break the bonds between neighboring PPs by overcoming their cohesion forces. Therefore, it scales with the surface energy density of such interparticle bonds

$$\mathrm{\gamma }\propto d_{\text{bonds}}\bullet (F_{\text{capillary}}+F_{\text{vdw}})$$

The bond density d_bonds is the number density of bonds per surface area; therefore, it scales with the number of bonds between PPs at the surface of the SP (N_PP), divided by the SP surface area (A_SP)

$$d_{\text{bonds}}=N_{\mathrm{c}}\frac{N_{\text{PP}}}{A_{\text{SP}}}=N_{\mathrm{c}}\frac{A_{\text{SP}}}{A_{\text{PP}}}\bullet \frac{1}{A_{\text{SP}}}=N_{\mathrm{c}}\frac{{D_{\text{SP}}}^2}{{D_{\text{PP}}}^2}\bullet \frac{1}{{D_{\text{SP}}}^2}=\frac{N_{\mathrm{c}}}{{D_{\text{PP}}}^2}$$

where N_c is a constant representing the coordination number of particles on the SP surface (six in an ideal sphere packing) and D_SP and D_PP are the diameters of the SPs and PPs, respectively. Note that N_PP is calculated by dividing the total surface area of the SP (A_SP) by the area occupied by each PP (A_PP).

The cohesion forces between PPs have two contributions: the capillary force from the meniscus of condensed water in ambient humidity between two PPs, F_capillary, and the van der Waals attraction between two PPs, F_vdw. For spherical particles, it was shown that both the van der Waals and capillary force scale with their radius (71, 72). Therefore, the interparticle cohesion forces scale with the PP diameters

$$F_{\text{capillary}}+F_{\text{vdw}}\propto D_{\text{PP}}$$

It follows that

$$\mathrm{\gamma }\propto (F_{\text{capillary}}+F_{\text{vdw}})\bullet d_{\text{bonds}}\propto \frac{1}{D_{\text{PP}}}$$

The parameter a in the Griffith equation describes the defect size from which a crack is initiated. Recall that the geometric structure of SP consists of concentric spherical shells, and each shell consists of hexagonal close packed PPs. The outermost shell at the SP surface is seen in the SEM images (Fig. 1B). The presence of additional, stacked, concentric shells can be deduced from the structural coloration of the SPs (5). During compression, the SP experiences compressive stress along the direction of indenter tip and tensile stress along the periphery—the closer to the SP surface, the larger the tensile stress. The tensile stress, responsible for the fracture, is distributed via the contacts between neighboring PPs on the surface of the SP. We observe that the crack initiates from the surface of the SP (movie S1), breaking the bonds between neighboring PPs and separating them without causing deformation. Therefore, we assume that the initial defect size in the SP is determined by the contact distance between two PPs, l_contact. This distance may be slightly modulated by surface roughness and the contact region extended by contact deformation depending on the effective elastic and inelastic properties of the PP. However, because the PPs in an SP are in direct contact, l_contact will necessarily be at a molecular length scale (71), therefore independent of the diameter of the PP (D_PP). During compression, tensile stress is concentrated at the circumference of the SP and distributed among all PP contacts in this circumference, whose number scales linearly with SP diameter (D_SP). This implies that the stress required to break an interparticle bond is inversely proportional to D_SP. Thus, the effective initial defect size scales is

$$a\propto \frac{l_{\text{contact}}}{D_{\text{SP}}}\propto \frac{1}{D_{\text{SP}}}$$

This proposed scaling is confirmed in our measurements (Fig. 3, A and B). With the same PP (hence the same the Young’s modulus E and surface energy density γ), the fracture stress σ_c scales with SP diameter D_SP with a power law exponent of 0.5.

For a particulate material such as our SPs, the Young’s modulus (or the Poisson ratio) is unknown a priori. However, our measurements indicate that the slope of the SP nominal stress-strain curve (up to 10% strain; Fig. 3C) follows the trend of the initial elastic region (less than 1% strain before yielding; Fig. 2A), which can approximate SP Young’s modulus. This relation suggests that the modulus is inversely proportional to D_PP (Fig. 3E)

$$E\propto \frac{1}{D_{\text{PP}}}$$

Together, applying Griffith criterion based on these considerations of particular assembly predicts the critical fracture stress based on the SP geometry

$${\mathrm{\sigma }}_{\mathrm{c}}=\sqrt{\frac{2E\mathrm{\gamma }}{\mathrm{\pi }a}}\bullet f\propto \frac{{D_{\text{SP}}}^{0.5}}{D_{\text{PP}}}$$

where D_SP and D_PP are the diameters of the SPs and PPs, respectively. We replot all our data and find that this scaling relationship accurately predicts the fracture stress of all samples with different SP and PP diameters (Fig. 3F). Although Griffith’s theory was originally proposed to account for brittle fracture in elastic continuum materials (70), the surface energy in the model can be replaced by strain energy release rate developed by Irwin (73), where nonlinear inelastic effects observed in our SPs are also considered. Our development of the Griffith criterion for particulate material provides a powerful scaling that accurately predicts the resulting mechanical properties of SPs from the involved PP and SP diameters.

Influence of cohesive forces between primary particles

We estimate the individual contribution of the van der Waals and capillary forces to the adhesive forces in SPs. The contribution of attractive van der Waal forces (71, 72) between neighboring PPs can be expressed by

$$F_{\text{vdw}}=\frac{A{D}_{\text{PP}}}{24d^2}$$

where A is the Hamaker constant and d is the separation between the surface of constituent particles. The attractive capillary forces between neighboring particles (71, 72) is given by

$$F_{\text{capillary}}=2\mathrm{\pi }{\mathrm{\gamma }}_{\mathrm{L}}{D}_{\text{PP}}\text{cos}\mathrm{\theta }$$

where γ_L is the interfacial tension of the liquid and cosθ is the contact angle between liquid and the particle. According to Rumpf’s model, the critical stress for fracture in granular material is

$${\mathrm{\sigma }}_{\text{Rumpf}}=1.1\frac{(1-\mathrm{\epsilon })}{\mathrm{\epsilon }}\frac{F}{{D_{\text{PP}}}^2}$$

where ε is the void fraction in the granular material, which for SPs is determined by the internal arrangement of the PPs. We assume values for the Hamaker constant A of PS to be 7 × 10⁻²⁰ J (72) and the separation between 244-nm particles d to be 0.15 nm (72) and approximate the void fraction ε to be 0.26 by considering the PPs to form a perfect face-centered cubic (fcc) structure. Note that while our SPs exhibit a well-ordered internal structure, evidenced by the structural coloration shown in Fig. 1B (5), the assumption of an perfect fcc packing slightly underestimates the void volume. Using these values, the van der Waals forces between two particles are calculated to be around 30 nN, which contribute to a fracture stress of approximately 2 MPa. Assuming γ_L of water to be 72 mN/m and the contact angle to be 30° (74), the capillary force between two particles is calculated to be around 90 nN, contributing to a fracture stress of approximately 6 MP. Combining both forces, a fracture stress of approximately 8 MPa is expected.

This value is lower than the measured value of 15 to 30 MPa (SP = 7 to 20 μm, PP = 244 nm). The discrepancy may originate from additional effects occurring at the interparticle bonds that are not captured in the models. On the PP level, both van der Waals and capillary forces are known to deform nanometer-sized PS particles and may enhance the adhesion due to enlarged contact area (75–77). During compression, the contact area increases substantially due to deformation of PS particles, which further increases the adhesive forces. In addition, surfactants may deposit in the interstitial sites of the SP upon drying and additionally strengthen the interparticle bonds. On the SP level, the Rumpf model assumes brittle fracture along a fracture plane that disintegrates the granular material. Our experiment shows a ductile deformation, and the SP remains in one piece after fracture, which allows notably more energy dissipation by deformation of PPs, and hence higher fracture stress than predicted from Rumpf’s theory. We estimate that the contact area between PPs (244 nm in diameter) needs to have a diameter of about 70 nm during compression to account for a measured value of 15 MPa in the fracture stress, which is likely given the increasing deformation of the PPs as seen in Fig. 2D. This already implies that PPs with higher compressive strength, such as silica, may result in lower fracture stress of SPs due to smaller contact area. However, we note that the clear size dependency of the fracture stress cannot be rationalized in the framework of the Rumpf model but is accounted for in the scaling analysis that we derived above.

The state of the capillary meniscus between PPs depends on the amount of water content in the SPs and hence the surrounding humidity (47, 78). A reduced humidity should therefore reduce the mechanical stability of SPs. Because our nanoindenter cannot control humidity during measurement, we resort to measure the same SP samples in summer and winter when the humidity drops from around 50 to 20% and accurately record the ambient humidity at the time of the measurement. In less humid environment, the deformation resistance of SPs reduces by more than half, and the fracture pressure drops from around 20 to 8 MPa (fig. S6A). In addition, the fracture mode changed from ductile to brittle. However, our previous findings (Fig. 3F) still hold true at reduced humidity—the deformation resistance is independent of SP size (fig. S6B) and approaches the value of solid PS microparticles with decreasing PP size (fig. S6C).

To exclude capillary forces completely, we perform nanocompression on SPs in the ultrahigh vacuum inside an SEM chamber (79). We equilibrate the sample under vacuum (~10⁻⁶ mbar) inside the SEM chamber for more than 24 hours. We verify that both devices (in ambient condition and inside the SEM) give quantitatively comparable results by compressing large solid PS microparticles (20 μm) as reference (fig. S7A). This implies that the mechanical properties of individual PS microparticles are not influenced by humidity—any changes in the SPs measured in vacuum must therefore be related to their internal structure or the forces acting between the PPs.

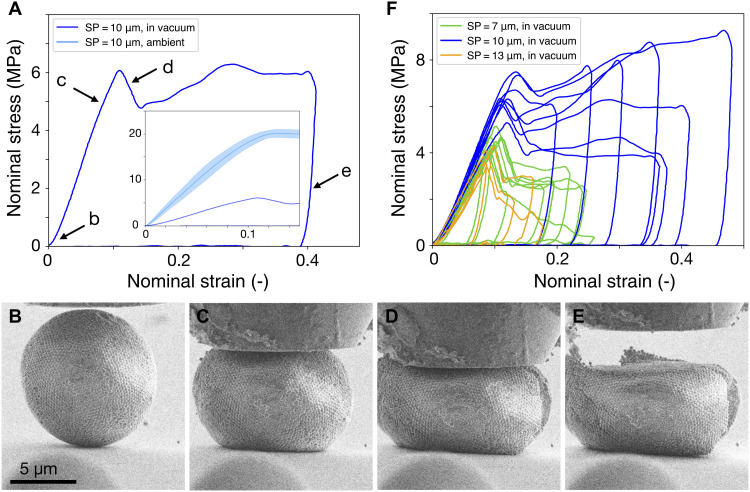
A typical nominal stress-strain curve of SP (SP = 10 μm, PP = 244 nm) compressed in the high vacuum of the SEM is shown in Fig. 4A (dark blue curve). The inset shows the same sample under ambient conditions for comparison (light blue curve, taken from Fig. 2C). From our previous estimation, the van der Waals forces contribute approximately 25% to the total adhesive forces between PPs and the capillary forces contribute approximately 75%. Complete removal of water content should therefore cause a fourfold reduction in the critical fracture stress. The stress at fracture drops from 20 MPa in humid condition (50%) to about 6 MPa in vacuum. Note that the value does not decrease linearly with decreasing humidity (from 20, 8, to 6 MPa at 50, 20, and 0% humidity in Fig. 3A, fig. S6A, and Fig. 4A, respectively), a known phenomenon in wet granular matter because the distribution of water and the state of capillary bridges are complex functions of the water content (44, 71, 80). Our customized setup enables in situ observation of the deformation process (movie S1). We verify that the electron beam does not affect the mechanical properties (fig. S7B). Figure 4 (B to E) shows SEM images taken during different stages of compression (indicated in Fig. 4A, taken from movie S1). In the initial states of compression, where the nominal stress-strain curve enters the linear region, the contact area increased, and the SP bulged outward at its equator (Fig. 4C). At fracture, a crack initiated from the SP periphery (Fig. 4D), which causes a drop in the force measured at the indenter tip (Fig. 4A, arrow d). While some particle rearrangement occurred in the contact area with the indenter and particularly close to the crack (Fig. 4D), no PP rearrangement in other regions was observed (fig. S7, C and D), supporting our scaling analysis. The compression continued until 40% nominal strain. The unloading revealed little elastic energy stored in the deformation process (Fig. 4A, arrow e), as the deformed SP recovers only slightly after indenter tip retreats (Fig. 4E).

Fig. 4. Mechanical properties of SPs in vacuum.

(A) Nominal stress–nominal strain curve of PS SPs (PP diameter = 244 nm) measured in high vacuum inside an SEM chamber. The absence of humidity substantially reduces the deformation resistance (humid conditions shown in inset). (B to E) In situ SEM characterization of the SP upon deformation. The SP (B) deforms at the contact with the nanoindenter tip and the substrate (C), followed by fracture from the surface (D), and barely resumes shape after unloading due to mostly plastic deformation (E). (F) The deformation resistance is independent of SP diameter in vacuum. Curves of individual measurements are shown.

For small PPs (PP = 244 nm), the deformation resistance is independent of SP diameter (Fig. 4F), similar to the case in ambient conditions (Fig. 3A and fig. S6B), although the fracture stress is reduced. We increase the PP diameter from 244 to 500 nm and observe a reduced deformation resistance and lowered stress and strain at fracture (fig. S7F). The recorded data scattered notably, and the curves were no longer uniform. This scattering suggests a brittle fracture behavior with catastrophic failure, resulting from a relatively weakened interparticle adhesion for large PPs when water capillaries are removed in vacuum.

Influence of PP material

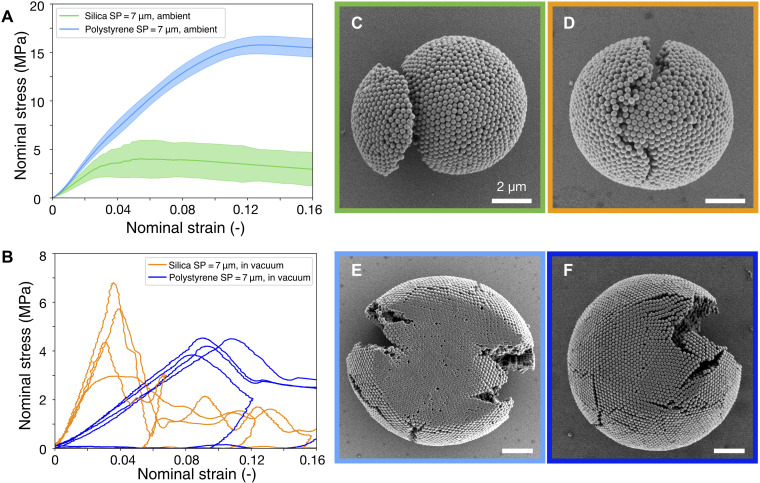
Intuitively, it may be anticipated that the mechanical stability of SPs can be improved by using PPs of stronger material. We use silica particles, whose toughness, elastic, and compressive modulus are magnitudes higher than those of PS particles (65). In addition, higher capillary forces between silica particles are expected due to their more hydrophilic surface than PS particles. However, as shown in Fig. 5, in humid ambient conditions (50%), silica SPs (SP = 7 μm, PP = 230 nm, N = 21) showed a lower deformation resistance compared to PS SPs (SP = 7 μm, PP = 244 nm; identical as in Fig. 2C). With similar SP internal structure, the nominal fracture stress dropped from about 15 MPa (PS SPs) to about 4 MPa (Silica SPs) and the strain from about 12% to 5%. In contrast to PS particles, the mechanical properties of silica SPs remained largely unaffected by humidity, for both deformation resistance and fracture stress (fig. S8). In vacuum, the fracture stress for both silica and PS SPs is similar (Fig. 4B). This is reasonable, as in the absence of humidity, the only contribution to the interparticle adhesion is van der Waals forces, which are comparable for both materials because they have similar Hamaker constants of about 7 × 10⁻²⁰ J (72). This similarity in fracture stress also implies that contact deformation of PS particles is largely suppressed in vacuum, in contrast to the ambient conditions.

Fig. 5. Comparison of PS and silica SPs.

(A) Silica SPs fracture at much lower strain and stress than PS SPs in humid condition. Blue and green lines show the averaged stress-strain data, and the colored band indicates the SD. The larger SD for silica particles indicates a brittle fracture behavior. (B) Vacuum does not influence the deformation resistance of silica SPs but reduces the deformation resistance for PS SPs. In vacuum, silica and PS SPs fracture at similar stress. (C to E) SEM images of the different SPs after compression (box color-coded to match the curve colors in A, B). Brittle silica SPs break into two pieces in both humid condition (C) and in vacuum (D), and their primary silica particles are not deformed at the individual particle level. In contrast to the large deformation in humid condition (E), PS particles show little deformation in vacuum (F).

We notice that silica SP exhibits brittle fracture under compression, splitting into several pieces, both in ambient condition (Fig. 5C) and in vacuum (Fig. 5D and fig. S9), contrasting with the ductile deformation of PS SPs (Fig. 2G). Corroborating this difference in fracture mode, we find that the individual silica PPs do not show any deformation after the SP is fractured in ambient condition (Fig. 5C) and in vacuum (Fig. 5D and fig. S9). In contrast, PS PPs deform heavily after compression in ambient condition (Fig. 5E and fig. S3) but much less in vacuum (Fig. 5F and fig. S7D).

DISCUSSION

We now aim to provide a general picture of the mechanical properties of SPs under compression. The external compressive energy must be dissipated within the SP structure. In extreme cases, the energy can dissipate either completely via deformation of individual PPs, in which case no fracture occurs, or completely via breakage of interparticle bonds, in which case no PP deformation occurs. In reality, both mechanisms are at play. However, the weaker component, either the individual PPs or the interparticle bond, dominates the deformation process and determines the fracture. If the PPs are sufficiently soft, they yield and deform before an interparticle bond is broken, giving rise to high stability and ductility; if the PPs are sufficiently hard, the interparticle bond will break first in a brittle manner with low stability.

Capillary bridges between PPs significantly strengthen the interparticle bonds. Silica particles have a much higher hardness than PS particles (65, 81), hence are more difficult to be deformed at the individual particle level. Therefore, the compressive energy is predominantly dissipated by breaking the interparticle bonds in silica SPs, instead of deforming the silica PPs. This bond breaking causes particle rearrangement and hence catastrophic brittle fracture. For PS SPs, the energy is primarily dissipated by deformation of the PPs. This mechanism toughens the SPs, which remain longer as one piece. The higher fracture stress compared to silica PPs is also accounted for by the fact that the deformation of PS PP further increases the contact area and total adhesive forces. PPs with large diameter require more energy to be deformed than smaller ones, and their interparticle bonds become comparatively weaker. As a result, with large PPs, the compressive loading more likely results in breaking interparticle bonds, which yields a smaller fracture stress and a more brittle behavior of the SPs (Fig. 4C and fig. S6C). Note that, in addition to the size and material of the PPs, their surface roughness may further affect capillary effects and may be used to tailor the mechanical properties.

Reducing humidity also reduces the interparticle adhesion and hence facilitates breakage of the interparticle bonds. In this case, PS SPs fracture at lower stress (Fig. 4F and fig. S7B) and in a brittle mode without observable deformation of the PPs (Fig. 5E and fig. S7D). We note that the surfactant stabilizing the water in oil droplet during SP fabrication may play a role in the mechanical properties, which is not included in our discussion. The surfactant used in our system is an amphiphilic poly(perfluoropropylene glycol)–poly(ethylene glycol) block–poly(propylene glycol) block–poly(ethylene glycol)–poly(perfluoropropylene glycol) (PFPE-PEG-PFPE) triblock copolymer (64). It has two blocks that are industrial fluorinated lubricant and (a) middle (block) a block that is hygroscopic, which may facilitate water condensation. In addition, the polypropylene block is known to show a preferable adsorption to hydrophobic surfaces such as PS instead of hydrophilic surfaces such silica (82). This may be related to the unexpected persistence of the mechanical properties of silica SP stability in the absence of humidity. The effect of the surfactant, its interaction with the particles, and its distribution through the SP merits a detailed, separate analysis. To simplify the discussion, we resorted to the use of the minimal amount of surfactant required to stabilize the emulsion and neglected its contribution to the mechanical properties.

While it is well known in the atomic world that a decrease in size of nanostructures or nanoparticles enhances mechanical properties (83) such as Young’s modulus (84) or strength (85) due to a lower number of defects in a smaller volume, this is not the case for colloidal SPs. Our measurements show that the deformation resistance of SP is independent of the system size and that the fracture stress increases with increasing SP size. This difference is likely caused by comparably weak interactions between PPs in SPs compared to the bonds between atoms in a nanocrystal. In addition, while the number of defects increases with increasing system size in the atomic system, in our confined self-assembly process, increasing the volume of the confinement actually facilitates crystallization as effects of curvature are reduced (7, 15, 27). Given that the number of PPs in SPs is in a similar scale to the number of atoms in nanoparticles, colloidal SPs can serve as a model system to investigate how microscopic interactions translate to macroscopic properties by tuning the interparticle forces and materials.

To conclude, our analysis shows that the mechanical properties of SPs under compression result from an intricate interplay between interparticle adhesion and the deformation of the material of the PPs. We find that the resistance against compression is inversely proportional to PP size, while fracture stress and strain scale with SP size. Using Griffith’s theory, we provide a scaling analysis that successfully relates the mechanical properties to the sizes of SP and PPs. We further examine the contribution of different adhesive forces to the SPs. Reducing humidity lowers the mechanical stability of PS SPs, with regard to both the deformation resistance and the fracture stress and strain. In addition, we demonstrate that PPs with higher mechanical strength, such as silica, yield less stable SPs, as compressive energy dissipates more efficiently into breaking the much weaker interparticle bonds than deforming PPs. As an important basis for any applications, our study reveals that SPs can exhibit an unexpected mechanical stability if sufficient energy is dissipated via deformation of PPs.

The SP mechanics is a complex yet rewarding field that intimately connects different scientific disciplines and has broad implications for applications. The complexity originates from the interplay of interactions leveraged at different hierarchical levels, from the contact points between the particles, via the chemical nature of the PPs, to the structural arrangement in the SP itself. The great wealth of available materials and precise control of particle shapes of colloidal systems, choices of ligands and/or surfactants, and increasing control of the structural arrangement of the PPs provides a rich playground to manipulate these interactions in great detail. SPs may therefore emerge as a versatile platform to investigate and manipulate structure-property relationship and to create hierarchical material with tailored mechanical properties.

MATERIALS AND METHODS

Particle synthesis and colloidal SP fabrication

Chemicals were purchased from Sigma-Aldrich and used as received, including styrene, acrylic acid, and ammonium peroxodisulfate, tetraethyl orthosilicate, ethanol, and ammonia solution. PS colloidal particles were synthesized by surfactant-free emulsion polymerization using acrylic acid as comonomer and ammonium peroxodisulfate as initiator, following literature protocols (5). Silica colloidal particles are synthesized following the classical Stöber process (86). The synthesized particles all had size distributions below 5%. After synthesis, the particle dispersions were centrifuged by ethanol water mixture (1:1) several times. A range of particles were used, the diameter from 150 to 1000 nm. Large solid PS microparticles were purchased from Polysciences and used as received. PDMS microfluidic devices were produced following typical soft lithography methods as described in literature (5). In short, a silicon wafer was spin-coated with SU-8–negative photoresist, and a pattern mask was used to create microstructures on the coated water surface through ultraviolet light. The microstructures were then hardened and coated with an anti-sticking layer to produce the master wafer. PDMS (Sylgard 184 PDMS from Dow Corning) was mixed with a curing agent at a 10:1 weight ratio and degassed before pouring onto the master wafer for approximately 1 cm thickness. The PDMS was cured at 80°C overnight. The cured PDMS chip was cut and peeled off from the wafer. A biopsy punch (1.0 mm; KAI) was used to make the inlets and outlets in the PDMS chip. A scotch tape was used to remove debris and dust on the PDMS chip surface. The chip was washed with ethanol and water (Milli-Q) and dried with compressed air. After cleaning, the PDMS chip and a clean glass slide were plasma-treated for 30 s in oxygen environment at 30-W power (Diener electronic, Femto). After surface activation, the PDMS chip was bonded to the glass slide and put in oven for 30 min to enhance bonding. Afterward, the microfluidic channels were immediately flushed with 2 weight % fluorosilane dissolved in HFE 7500 oil (3M) by injection through a 1-ml syringe of a flat head suiting needle (diameter slightly larger than 1 mm). After 1 hour, the channels were flushed by compressed gas to remove the liquid and kept in oven to dry. Precision pumps (Harvard Apparatus) were used to insert aqueous colloid dispersion and HFE 7500 oil containing PFPE-PEG-PFPE surfactant (64) into the microfluidic channel to produce monodisperse emulsion droplets. Droplets were collected in a 1.5-ml glass vial. After water evaporation, droplets consolidate into solid colloidal SPs. The solid colloidal SPs stored in the oil phase in the glass vial remain stable. For nanoindentation measurements, 2 μl of oil containing the SP is drop-casted onto silicon wafer substrate. After oil evaporation, the substrate was left at room temperature overnight before transferring to the nanoindenter stage.

Nanocompression in ambient condition and in vacuum

Nanocompression on the colloidal SPs was performed in KLA Nano Indenter G200 with 0.01-nm-depth resolution and 50-nN load resolution (XP head) in displacement control. The flat diamond indenter tip had a diameter of 90 μm (Synton-MDP). The diameter of colloidal SPs was determined in SEM and subsequently deposited onto a piece of silicon wafer directly from the fluorinated oil phase. The silicon wafer was glued to the sample holder with minimum superglue (Ultra gel, Pattex). After fixing the wafer, the samples were left to cure for 24 hours. After mounting the sample holder on the indenter stage, at least 1-hour equilibrium time was allowed after closing the indenter chamber. After calibration of the tip to the built-in microscope, a test indent was performed on bare silicon wafer to position the tip to the substrate. In a measurement, the tip advanced toward the sample at maximum speed until 2 μm above the sample and changed to fixed speed. The loading and unloading speed were fixed at 50 nm/s, the maximum displacement was at 60% nominal strain, defined by normalization by the initial SP diameter, and the peak holding time was 10 s. Different loading rates (50, 100, and 200 nm/s) were tested, and no influence on the mechanical response was observed. A double-sided tape was attached to the sample holder to facilitate cleaning of the indenter tip and remove possible particle residues after every measurement. With our instrument, it was not possible to control humidity. We therefore used a comparably small number of measurements for individual samples (Fig. 3), which could be performed in a short time span of 1 to 2 days during which humidity did not significantly change. We note that the comparison to a larger sample size (10-μm SPs) does not evidence an increase in scatter in the data (Fig. 3A), which suggests that the sample size allows adequate characterization of the mechanical properties. Nanocompression experiments under vacuum condition were performed in the SEM (Zeiss Ultra) using a custom-built micromanipulator (79) with a boron-doped diamond punch. The tip plateau diameter was chosen to be 10 or 90 μm, depending on the colloidal SP diameter. The force-displacement data were recorded with a resolution of 10 μN and 5 nm, respectively. To ensure minimal influence of the electron beam during the compression, the tip displacement rate was set to 200 nm/s in vacuum inside the SEM. To minimize irradiation-related damages during measurements, low-dose imaging conditions (2 kV, 10-μm aperture, beam current <8 pA) were used and the electron beam was blanked during measurement (79). All force-displacement curves were analyzed in a Python code.

Supplementary Materials

This PDF file includes:

Figs. S1 to S9

Other Supplementary Material for this manuscript includes the following:

Movie S1