Abstract
Understanding and harnessing renewable energy potential is imperative for developing nations in the context of climate change. However, the wind potential of Yamoussoukro, Côte d'Ivoire, remains inadequately explored. This study employs a Longitudinal Observational Study design, acquiring data at 1-min intervals to capture the dynamic wind characteristics. The research focuses on refining ground data and estimating wind potential using a DAVIS Pro weather station with a cup anemometer for speed and a wind vane for direction. Wind speed and direction are measured in meters per second and degrees. Two distinct approaches are employed for data analysis: arithmetic and cubic averages provide representative values, and the Two-Parameter Weibull Probability Distribution Functions, determined through the method of moments, offer insights into the wind distribution pattern. The study's findings indicate an 8-h time slot during which the wind potential permits obtaining an annual energy production of 53,38 kW/h/m2, a valuable window of opportunity. The rainy season, particularly May, has the highest average monthly wind speed, while the dry season in December has the lowest. Furthermore, the wind rose analysis reveals that the prevailing winds blow from south to north, further highlighting the region's wind potential. The results affirm that Yamoussoukro harbors a moderate wind potential, aptly harnessed through Vertical Axis Wind Turbines (VAWT). This discovery holds significant implications for sustainable development, highlighting the city's potential to transition towards a greener, more energy-efficient economy. Yamoussoukro is poised to contribute substantially to renewable energy and climate change mitigation efforts by unlocking the untapped wind energy potential.
Keywords: Wind energy potential, Weibull distribution, Cubic mean, Useful time slot
1. Introduction
It's undeniable that today's world is undergoing an energy turnaround. We are witnessing a migration towards renewable energy sources and energy efficiency instead of fossil fuel-based energy production and consumption systems (oil, gas, and coal). This is the energy turnaround [1]. According to Vaclav Smil, energy transition is the shift in the primary energy supply and the transformation from a specific energy model to a new state of the energy system [2]. For developing countries, the challenge is twofold. They must meet the needs of populations still lacking access to essential modern energy services while at the same time participating in a global transition to clean energy systems. Therefore, researchers in these countries must support their governments in establishing policies promoting sustainable development.
To establish this policy, researchers need a set of data that will help them understand the energy profile of the location. For this, they can use wind potential maps such as AREA 5, Wind Atlas, or OpenWind [3], which have been developed for this purpose, but the need for ground-based data remains very important. The need for studies on wind energy potential in CI is worth noting, specifically in Yamoussoukro. Knowing that with accurate data on energy potential, orienting policies becomes a manageable task, several research activities have been undertaken in Asia and Africa to provide decision-makers with guidelines to follow.
In South Asia, the energy demand is high, but the transition to low-carbon sources is slow despite ample wind power potential. This situation is repeated in Central Asia, specifically in Turkmenistan, where fossil fuels dominate renewable energies due to their abundance [3]. To reverse this trend, which is confirmed in many Asian countries, several studies have been carried out to demonstrate the potential for renewable energies [[4], [5], [6], [7], [8], [9], [10]].
As far as Africa is concerned, the continent has the potential to generate almost 180 000 TWh of onshore wind power per year, which is enough to meet the electricity demand of the entire continent 250 times over. Several studies confirm this.
North Africa boasts of Algeria as a country with great potential for Renewable Energy. There are vast areas of 25 377 km2 suitable for wind power plants, 13 485 km2 for construction of solar power plants, and 11 199 km2 for both. The Algerian High Plateaux are ideal for energy systems powered by renewable energies, as they have significant solar and wind power potential. Tunisia likewise has sites with excellent wind resources, with available energy of over 5000 kWh/m2/year [11]. Scholars [12] in Morocco reveal an available energy of 3821.6 kWh/m2/year and 1077.4 kWh/m2/year for the Dakhla and Taza sites, respectively.
In North-West Africa, researchers are also active on the issue. The study by Boudi Ould Bilal et al. [13] identifies the months of April and May as those with the most significant potential, with power densities reaching 116 W/m2 and 113 W/m2, respectively, in Nouakchott, the economic and political capital of Mauritania.
The potential of Southern Africa, and Ethiopia in particular, was revealed long before the '99s. The results of [12] revealed the potential for wind power in some areas of the country. This was confirmed thirteen years later by Getachew Bekele's study [14], where three of four regions had an average wind speed of around 4 m/s and the fourth less than 3 m/s at a height of 10 m.
A study conducted by Soulouknga et al. has uncovered the wind potential of Chad, a Central African country [15]. The study analyzed five sites across the country and found that the average wind speeds were up to 3.25 m/s, resulting in a power density of 20.8 W/m2. According to the results, the Enercom E−82 turbine is suitable for all five sites and can generate up to 146 165 182 kWh of energy in February. These findings are consistent with Didane et al.'s, which reported annual energy density values of 490–677 kWh/m2/year at the height of 10 m above ground level [16].
As far as the countries of West Africa are concerned, several studies reveal the potential for renewable energy [[17], [18], [19]]. In Mali, solar power is recorded at 6.3 kW h/m2 [20]. According to a study [18], the coast of Ghana may be an ideal location for small-scale wind energy projects. As part of a technical, financial, and environmental impact assessment, Asamoah et al. [21] evaluated four sites for a proposed 50 MW wind farm in Ghana. The results indicated the project was financially feasible, as all four sites had positive Net Present Values (NPV) based on economic analyses.
Côte d'Ivoire possesses an abundance of natural renewable energy sources, including solar, wind, hydro, biogas, and biomass, which can significantly contribute to the country's economic growth and sustainability. There are several studies on renewable energy potential [[22], [23], [24], [25]], but few of these studies have focused on wind energy potential. In 2000, Touré and Loualy presented a theoretical analysis of the wind potential of three cities in Côte d'Ivoire: Abidjan, Bouaké, and Korhogo. This study aimed to provide the average power obtainable in these three cities and a dimensioning of a wind generator for water pumping needs in the town of Korhogo. These results were consolidated with those of Traoré, who carried out a theoretical study of a mechanical wind pump with diameter D = 4 m, specific speed lambda indice 0 1.2, and displacement q = 0.5 L for pumping needs in the Korhogo area.
In light of the current shortage of research on the wind energy potential in Yamoussoukro, the political capital of Côte d'Ivoire, this study aims to fill this gap by conducting a comprehensive twelve-month investigation utilizing reliable data collection tools. The novelty of our research lies in exploring, for the first time, the wind energy capabilities of Yamoussoukro, explicitly focusing on the year 2017. This article is dedicated to underscore the significance of this exploration, emphasizing the unique insights it can provide into the untapped wind potential of the region.
2. Data and methods
2.1. Study area description
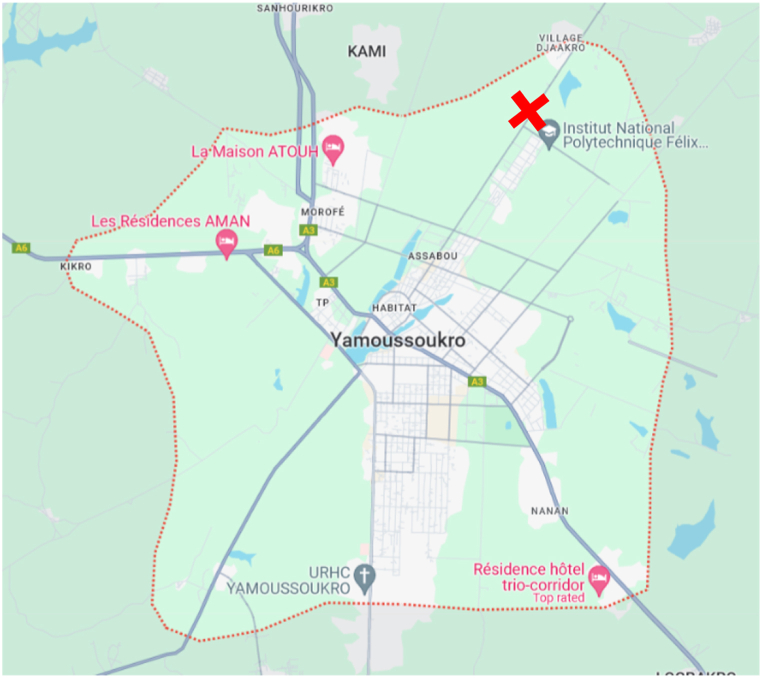
Yamoussoukro is the administrative and political capital of Côte d'Ivoire, located in the heart of the country. It has been serving as the capital since 1983. The city has a unique local authority and is home to around 300 000 people, including indigenous residents and migrants from various regions of Côte d'Ivoire. Yamoussoukro covers an area of 2075 km2 and is home to the Institut National Polytechnique Félix Houphouët Boigny (INPHB). The designated measuring station is located within the INPHB premises, at coordinates 6°52′09.1"N, 5°14′22.6"W (see Fig. 1).
Fig. 1.
Google Map of the studied site.
2.2. Methodology
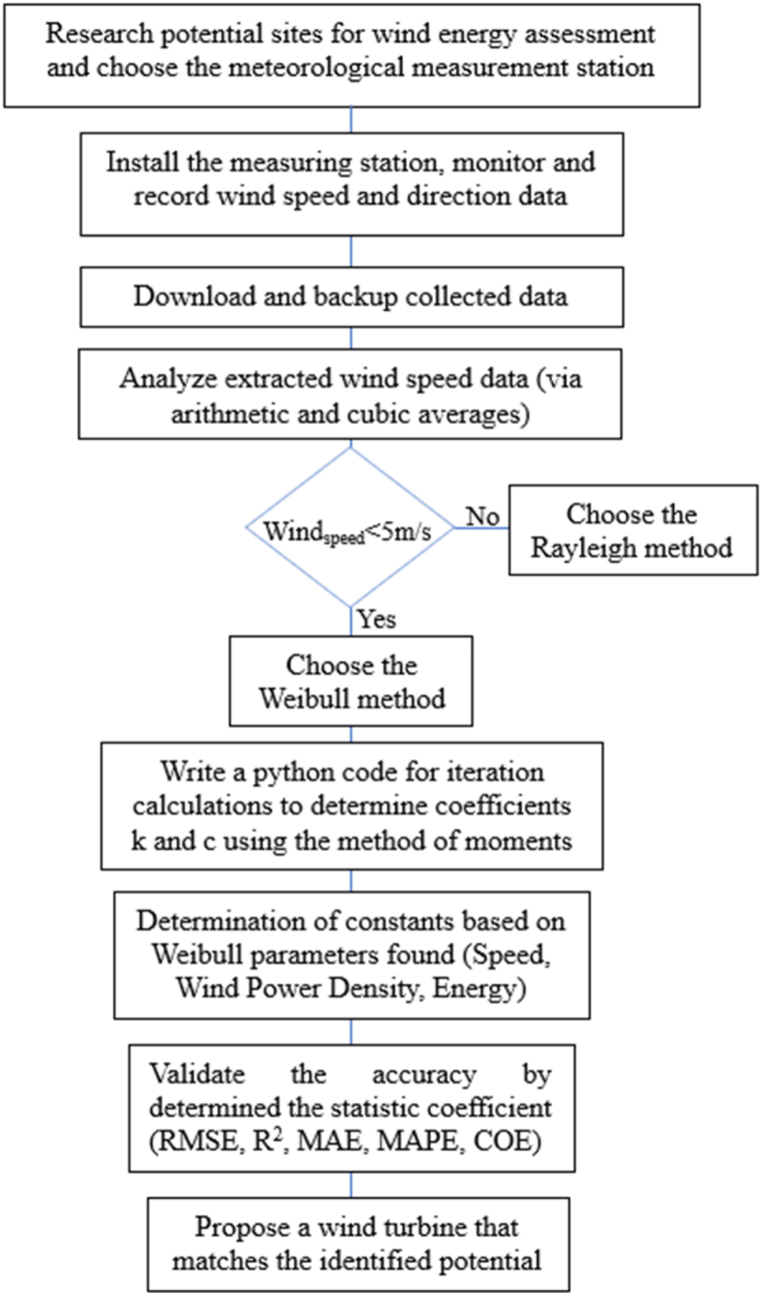
Several sequential steps were undertaken to assess the wind energy potential of the city of Yamoussoukro. Firstly, an appropriate site was carefully selected for wind energy assessment, and a designated measuring station was established to systematically collect wind speed and direction data (Fig. 2).
Fig. 2.
Methodology flowchart.
Subsequently, the collected data underwent processing to extract relevant wind speed and direction information. The wind speed data was then analyzed to determine the most suitable model for further calculations. The Raleigh or Weibull model was chosen depending on average wind speed and stability factors. With the model selected, coefficients k and c were then determined utilizing the method of moments, employing statistical calculations. The velocity and energy derived from the wind were calculated using these coefficients. Lastly, the accuracy of the results was validated by comparing them with statistical velocity and cubic velocity data. This thorough methodology ensured a comprehensive assessment of wind energy potential, providing reliable insights for subsequent analysis and decision-making.
2.3. Data collection instrument
The station used for data collection is the DAVIS Vantage Pro 2 Plus 6163 FR (Fig. 3). In the scientific community, this station is widely used for meteorological data acquisition [5,6,26,27]. The sensors connected to the station are a rain gauge, a temperature sensor, a hygrometer, an anemometer/wind vane, a UV radiation sensor, and a pyranometer.
Fig. 3.
Pictures of the meteorological station.
Two sensors measure wind direction and speed for wind potential data. The wind vane, which measures wind direction, has a resolution of 1° over a measurement range of 0°–360°, with an accuracy of ±3 %. The anemometer, which measures wind speed, has a resolution of 0.1 m/s over a measurement range of 1–80 m/s, with an accuracy of ±5 %. Note that the anemometer provides wind speed and direction every 2.25 s, but we have set the data recording interval to 1 min.
2.4. Setting up the database
Meteorological data are recorded every minute, for 1440 data per day and 525 600 data for the twelve months. We noted 35 093 missing data at the recording time, giving a recovery rate of 93.42 %.
Also, the data shows that wind speeds are high from morning to early evening. We considered the data from 11:00 to 19:59 as belonging to the time slot of our study. However, we will compare the average speed of the data recorded between 11:00 and 19:59 with those recorded throughout the day to appreciate the useful time slot better.
The wind data collection instrument is installed on a mast 2 m above ground level. The power law allows us to extrapolate these data according to the following equation:
| (1) |
and are respectively the velocities taken at 2 m and extrapolated to 10 m above ground. The coefficient ∝, known as roughness coefficient, depends on site-specific conditions. As the measuring station is located in an urban area with dense vegetation, we use [28].
2.5. Wind power potential assessment methods
Determining the wind potential of an area is a crucial task, and it can be done using two main methods: statistical and empirical. The statistical method employs a statistical distribution to estimate the wind potential, while the empirical method involves analyzing data by calculating either the arithmetic mean or cubic mean.
This study aims to compare the results from both the statistical and empirical approaches to obtain a more reliable estimation of the wind potential. By doing so, we will achieve a more confident understanding of the wind potential of Yamoussoukro.
2.5.1. The statistical method
Discrete and random quantitative values are obtained when wind speed data are collected. Several analysis techniques have been proposed to describe this non-linear evolution. These include the Weibull, Rayleigh, Hennessey, and Pearson methods.
The Weibull method will be utilized in this study to estimate wind potential with utmost reliability, as it has proven to be a highly effective approach for approximating wind speeds [12].
The Weibull distribution is a particular case of the gamma distribution and is characterized by the probability density f(V) and the accumulation function of the distribution F(V).
| (2) |
The probability density function is obtained by the derivative of the distribution function:
| (3) |
c: scale parameter in m/s,
k: dimensionless morphological parameter.
The literature lists six main methods for finding the parameters k and c: graphical method, empirical methods of Justus and Lysten, method of moments, maximum likelihood method, empirical method of Lysen, energy model factor.
In this study, we will use the method of moments for its simplicity of implementation and the relevance of its results.
In the method of moments, the shape parameters k and c are determined using the mean velocity.
(Vmean) and standard deviation (σ) obtained from the collected data.
| (4) |
| (5) |
| (6) |
We use Python code to solve the equation to determine the parameters k and c.
2.5.2. The empirical method
The aim is to calculate the arithmetic mean speed and the cubic mean speed directly from the data.
The arithmetic mean speed is calculated using the arithmetic mean of wind speed measurements over a given period.
| (7) |
The cubic mean wind speed method is often used, as it emphasizes higher wind speeds, which have a more significant influence on wind energy production [29,30].
We obtain the cubic mean from the expression of the wind turbine power:
| (8) |
: air density, usually taken as 1.225 kg/m3 [31]
: surface swept by the blades
: Wind speed
: The power coefficient
, and being constants:
Let: .
Average power can be expressed in two ways:
| (9) |
| (10) |
Posing (9) = (10) gives:
| (11) |
3. Results and discussions
3.1. Results based on k and c parameters
Using the method of moments, we found the k and c monthly parameters for 2017 (see Table 1 )
Table 1.
Weibull monthly parameter.
| Months | K | c (m/s) |
|---|---|---|
| January | 1.92 | 2.08 |
| February | 1.30 | 2.30 |
| March | 1.11 | 1.79 |
| April | 1.30 | 2.33 |
| May | 1.40 | 2.63 |
| June | 1.35 | 2.37 |
| July | 1.43 | 2.59 |
| August | 1.48 | 2.52 |
| September | 1.24 | 1.99 |
| October | 1.06 | 1.44 |
| November | 1.18 | 1.8 |
| December | 1.01 | 1.24 |
These parameters provide.
-
•
The Wind Power Density (WPD) formula based on the Weibull probability density function can be expressed in terms of the shape parameter k, the scale parameter c, and the gamma function Γ:
| (12) |
-
•
The Energy Production (EP) that also stands for the Energy Density (ED) over a period of time T and which is the product of the mean power density and the time T [32]:
| (13) |
The Weibull parameters are specific to each month, and by using them to calculate the energy, we obtain a Monthly Production Energy (MEP). The Annual Energy Production (AEP) is the sum of the monthly energy production.
-
•
The Average speed,
| (14) |
The wind speed producing the maximum Energy, which we note as VEmax:
| (15) |
The most probable wind speed, which corresponds to the most frequent wind speed at the site studied, which we denote Vfr:
| (16) |
-
•
The median speed, which divides the wind distribution into two equal parts, is given by Vmed:
| (17) |
The Weibull velocity obtained varied between 1.24 and 2.4 m/s (see Table 2). The highest velocity was observed in May, and the lowest in December. This suggests that May offers favorable wind conditions for wind power generation, as it belongs to the rainy season in tropical climates, when the wind can be more substantial. The most frequent wind speed averages 3.1 m/s, and the highest speed providing maximum energy is 4.9 m/s. These values are crucial for selecting the appropriate wind power equipment and planning energy production. According to the results, April to August is the most favorable period for wind generation. During this time, the wind speeds average less than 3 m/s, which is generally the cut-in speed for Horizontal Axis Wind Turbines (HAWT). However, Yamoussokro's wind potential is better suited to Vertical Axis Wind Turbines (VAWT), specifically Savonius turbines. In recent years, research has been improving this model, which can be used in lighting, street lighting, or gardens [33]. Savonius turbines are still used despite their low efficiency due to several reasons. Firstly, they have a low start-up speed of up to 1.5 m/s, which means they can capture even the slightest wind energy. Secondly, they have a low cut-in wind speed of up to 2 m/s, which means they can start rotating even in low wind conditions. Thirdly, they produce very low noise levels, making them suitable for residential areas. Lastly, they do not require a yaw system, which makes them more straightforward and less expensive to install and maintain [34].
Table 2.
Speed, power and monthly energy.
| Months | (m/s) | (m/s) |
(m/s) |
(m/s) | WPD (w/m2) | EPm (Wh/m2) | Pmax (w/m2) | Emax (Wh/m2) |
|---|---|---|---|---|---|---|---|---|
| January | 1.93 | 2.59 | 3.02 | 1.72 | 7.66 | 2 138,1 | 15.2 | 4243.4 |
| February | 2.13 | 3.57 | 4.71 | 1.73 | 20.16 | 5 079,8 | 57.9 | 14 580.6 |
| March | 1.72 | 3.19 | 4.53 | 1.29 | 14.70 | 4 100,6 | 51.5 | 14 355.6 |
| April | 2.16 | 3.61 | 4.77 | 1.76 | 20.96 | 5 658,4 | 60.2 | 16 241.4 |
| May | 2.40 | 3.87 | 4.96 | 2.02 | 25.53 | 7 121,6 | 67.5 | 18 827.4 |
| June | 2.37 | 3.57 | 4.65 | 1.81 | 20.21 | 5 456,6 | 55.6 | 15 007.6 |
| July | 2.35 | 3.75 | 4.78 | 2.00 | 23.34 | 6 511,6 | 60.3 | 16 834.0 |
| August | 2.28 | 3.57 | 4.49 | 1.97 | 20.10 | 5 608,4 | 50.2 | 13 997.3 |
| September | 1.86 | 3.21 | 4.32 | 1.48 | 14.69 | 3 966,8 | 44.6 | 12 040.9 |
| October | 1.41 | 2.70 | 3.91 | 1.02 | 8.90 | 2 483,8 | 33.2 | 9275.2 |
| November | 1.71 | 3.03 | 4.17 | 1.32 | 12.44 | 3 359,6 | 40.2 | 10 848.1 |
| December | 1.24 | 2.45 | 3.66 | 0.86 | 6.75 | 1 883,6 | 27.1 | 7552.4 |
3.2. Useful time slot
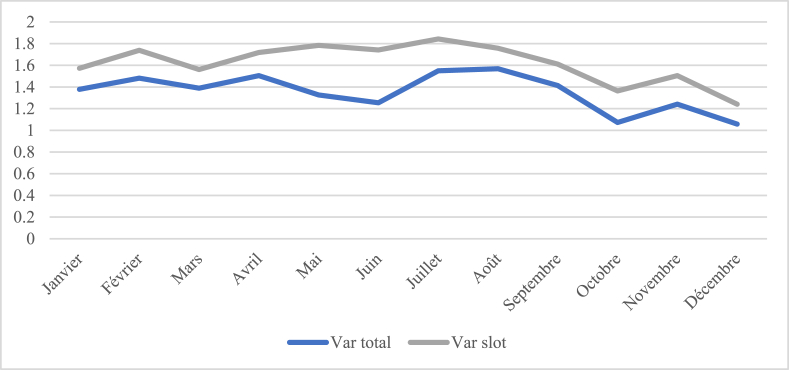
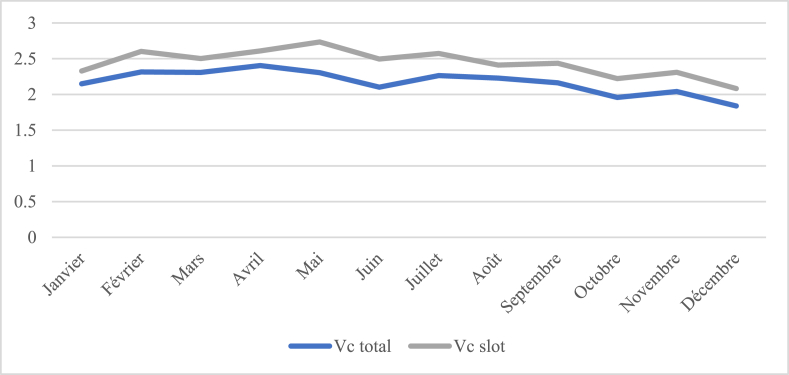
From the findings, it can be deduced that the average speeds (whether cubic or arithmetic) for the useful time slot are higher than that of the entire dataset. This suggests that the wind is typically stronger or more frequent during this specific time frame. This insight holds significant value when assessing the potential for wind energy, as it can affect both the generation of wind power and the operation of turbines. (See Fig. 4, Fig. 5)
Fig. 4.
Comparison between the arithmetic speed of total data (Var total) and the useful time slot (Var slot).
Fig. 5.
Comparison between cubic speed of total (Vc Total) data and cubic speed of useful time slot (Vc slot).
3.3. Comparison of the different methods used to calculate the average speed for the useful time slot
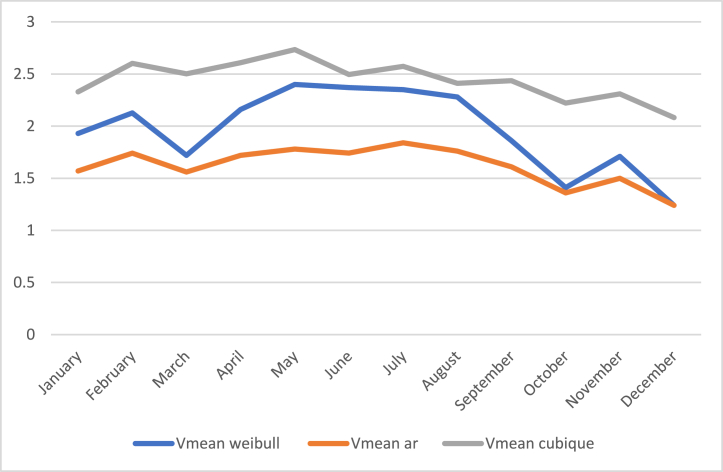
In order to obtain a more reliable estimate of wind potential, we used three methods to calculate the monthly mean speed: the Weibull method , the arithmetic method and the cubic mean method .
The results are shown in the table below (see Table 3).
Table 3.
Average wind speeds obtained by three methods.
| Months | |||
|---|---|---|---|
| January | 1,93 | 1,57 | 2,33 |
| February | 2127 | 1,74 | 2,60 |
| March | 1,72 | 1,56 | 2,50 |
| April | 2,16 | 1,72 | 2,61 |
| May | 2,40 | 1,78 | 2,73 |
| June | 2,37 | 1,25 | 2,10 |
| July | 2,35 | 1,84 | 2,57 |
| August | 2,28 | 1,76 | 2,41 |
| September | 1,86 | 1,61 | 2,44 |
| October | 1,41 | 1,36 | 2,22 |
| November | 1,71 | 1,50 | 2,31 |
| December | 1,24 | 1,24 | 2,08 |
Fig. 6shows that the mean velocity obtained by the Weibull method lies between those obtained by the arithmetic and cubic mean methods (see Fig. 5). It remains higher than the arithmetic mean speed and lower than the cubic mean speed.
Fig. 6.
Comparison of average monthly speed data.
If we compare the average speeds obtained by the Weibull method, the arithmetic method, and the cubic mean method, we can see that the monthly average Weilbull speeds are always bounded at the lower limit by those obtained by the arithmetic method and at the upper limit by those obtained by the cubic mean method. In fact, the empirical arithmetic speed is based on actual data collected, while the empirical cubic speed is calculated from the cubic mean of wind speeds. Weibull velocity, on the other hand, is determined by the distribution parameters obtained from a probabilistic analysis.
Upon evaluating the average speeds derived through the Weibull method, the arithmetic method, and the cubic mean method, it is evident that the monthly average Weibull speeds are consistently confined by the lower limit ascertained by the arithmetic method and the upper limit determined by the cubic mean method. The arithmetic speed is established on factual data, while the cubic speed is determined from the cubic mean of wind speeds. Compared to these empirical methods, Weibull velocity is derived from distribution parameters obtained through a probabilistic analysis.
3.4. Performance analysis
In order to measure the accuracy and the reliability of the estimated data, we can address a series of statistical tests such as:
The root Mean Square error (RMSE) ensuring precise predictions is crucial for any data-driven project. This is where Root Mean Square Error (RMSE) comes into play. By gauging the average size of errors between predicted ( and actual values (), RMSE serves as a valuable tool for evaluating data accuracy. A lower RMSE value indicates a higher level of accuracy in the prediction.
| (18) |
The Coefficient of determination (R2) represents the percentage of variability in the dependent variable that can be explained by the independent variable(s). Higher R2 values indicate a more robust model fit to the data.
| (19) |
The mean absolute error (MAE) refers to the average of the squared differences between the actual and predicted values in a dataset [35]. MAE is calculated as the average difference between a dataset's predicted and actual values. This metric provides insight into the average magnitude of errors, irrespective of their direction. Lower MAE values generally correlate with higher levels of prediction accuracy [36].
| (20) |
The mean absolute percentage error (MAPE) measures the average percentage difference between predicted and actual values. Lower MAPE values indicate greater accuracy.
| (21) |
The coefficient of efficiency (COE) measures how well a regression model explains the dependent variable's variance compared to a baseline model. Higher COE values indicate better efficiency.
| (22) |
The table presented below (Table 4) displays the values of the various coefficients, considering the Weibull Velocity as the predicted one, the Arithmetic Velocity as observed in Case A, and the Cubic Velocity as observed in Case B.
Table 4.
Statistics coefficient.
| Coef | Case A | Case B |
|---|---|---|
| RMSE | 0,48 | 0,54 |
| R2 | 0,64 | 0,56 |
| MAE | 0,39 | 0,49 |
| MAPE | 24,66 | 20,78 |
| COE | 7,34 | 8,53 |
Based on the analysis of the metrics, it can be inferred that Case A has a higher accuracy and data fit than Case B. Case A outperforms Case B in terms of RMSE, R2, MAE, and MAPE, which indicates that Case A provides more precise and well-fitted data. However, it was also observed that Case B has a higher COE value, indicating that Case A is more efficient than Case B.
3.5. Wind rose
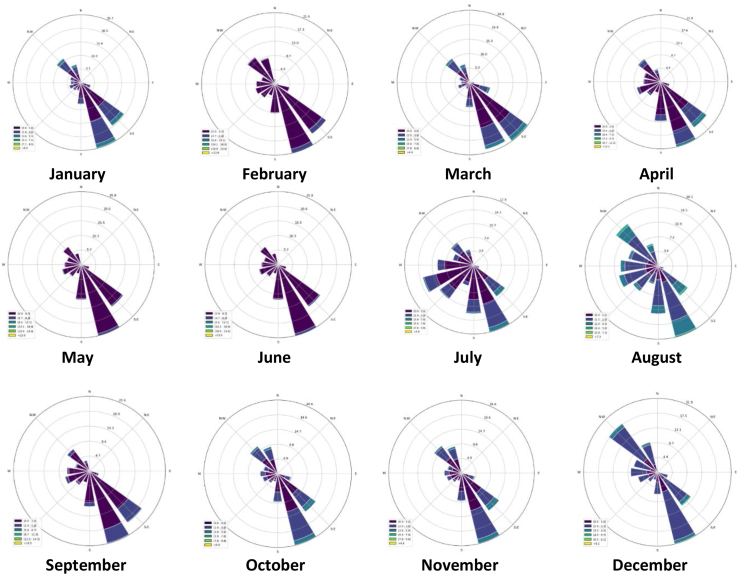
In addition to instantaneous speeds, the data acquired gives us wind direction thanks to the weathervane. These data are processed to produce monthly wind rose diagrams (Fig. 7).
Fig. 7.
Monthly wind rose diagrams.
Based on the wind rose analysis results, it can be determined that the primary wind direction during the useful time slot in Yamoussoukro is from the south. These southerly winds are sea breezes created by the distinct heating rates of water and land. Throughout the day, the land heats up faster than the sea, causing the air above it to warm up and rise, creating a low-pressure area. As a result, the cooler and denser air over the sea moves inland to fill the void, generating a sea-to-land breeze, usually from the south. This phenomenon has a significant effect on air pollution transport and diffusion [37], as well as energy production.
4. Conclusion and perspectives
The findings of the study suggest that the wind potential in the Yamoussoukro area is moderate, with May offering the most favorable wind conditions. Wind speeds fluctuate throughout the year, and the period between April and August is the most conducive for wind power generation. During this time, wind speeds are typically below 3 m/s, which is the cut-in speed for Horizontal Axis Wind Turbines (HAWT). As a result, Vertical Axis Wind Turbines (VAWT) would be more appropriate for this region due to their low cut-in wind speed. Based on the wind potential available in Yamoussoukro, the TURBINA TE 20 turbine seems like a suitable option. It has a cut-in wind speed of 1.5 m/s and starts producing power at 2.5 m/s. The manufacturer claims that the annual energy output at an average wind speed of 2 m/s can range from 10 to 25 kWh (Fig. 8).
Fig. 8.
A vertical axis wind turbines: Turbina Energy [33].
This information is valuable for planning wind projects and estimating wind energy production. However, it's important to compare these estimates with actual production data to obtain a more accurate assessment.
This document provides preliminary information about Yamoussoukro's potential, but some areas still need to be addressed, such as wind shear. Wind shear is one of the best ways to describe the wind profile, and it is determined by measuring wind speeds at different heights. However, most meteorological sites only have anemometers installed at one specific height, making it challenging for researchers to determine the wind shear coefficient accurately [38].
Adrien et al. [39] have developed a model for acquiring data from small wind turbines. This model can be used to observe the fluctuations caused by wind and gain deeper insight into wind potential estimation methods. Comparing real wind turbine data with estimates of cubic velocity, arithmetic velocity, and Weibull velocity is recommended. If the actual data aligns more closely with the Weibull velocity, the Weibull distribution may provide a more accurate estimate of wind potential. However, if the data is more in line with cubic velocity or arithmetic velocity, these methods may be better suited for estimating wind potential in this particular scenario.
Data availability
Data will be made available on request.
Additional information
No additional information is available for this paper.
CRediT authorship contribution statement
Jean-Michel Soumien Kouadio: Data curation, Writing – original draft, Writing – review & editing. Franck Didier Néné: Conceptualization, Software. Moussa Grafouté: Conceptualization, Methodology, Supervision, Validation. Alexandre N'guessan: Supervision, Validation. Siaman Paule Carine Yeboua: Data curation, Formal analysis. N'goran Yao: Funding acquisition, Methodology, Project administration, Supervision.
Declaration of generative AI and AI-assisted technologies in the writing process
During the preparation of this work, Grammarly was used to check the paper's correctness and rephrase it where necessary. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Declaration of competing interest
The research conducted in this article was carried out with the utmost integrity and adhered to ethical principles. I want to declare explicitly that I, as the corresponding author, and all the co-authors have no conflicts of interest to disclose related to this work. The study was conducted without any external influence or financial support that could potentially compromise the objectivity, impartiality, or credibility of the findings presented.
We believe that our research makes a significant contribution to the understanding of renewable energy prospects in the region of Yamoussoukro, Côte d'Ivoire. The findings are based solely on the analysis of wind energy potential and do not involve any personal or financial interests that could influence the results.
We have complied with all ethical guidelines and have obtained all necessary permissions and approvals for data collection and analysis. The work is original and has not been published or submitted elsewhere.
Acknowledgments
We would like to express our sincere gratitude to Mr. Daouda Kone and Mr. Diakaridja Traore from the UFR SSMT, University Felix Houphouët Boigny, Abidjan, Côte d’Ivoire. We would also like to thank Mr. Bernard Kouakou Dje from the Company of Airport, Aeronautical, and Meteorological Operation and Development (SODEXAM), Abidjan, Côte d’Ivoire for their invaluable assistance and guidance throughout the preparation of this article.
Nomenclature
- :
Weibull accumulation function of the distribution
- :
Weibull probability density function
- c:
Scale parameter in m/s
- k:
Dimensionless morphological parameter
- σ:
Standard deviation
- :
Arithmetic mean velocity
- :
The Weibull mean velocity
- :
Air density
- :
Surface swept by the blades
- :
Wind velocity
- :
The power coefficient
- :
The wind power density
- AEP:
Annual energy production
- :
The wind speed producing the maximum Energy
- :
The most probable wind speed
- :
The median speed
- RMSE:
Root Mean Square error
- R2:
Coefficient of determination
- MAE:
The mean absolute error
- MAPE:
Mean absolute percentage error
- COE:
Coefficient of efficiency
References
- 1.Doukas H. 2022 13th International Conference on Information, Intelligence, Systems & Applications (IISA) juill. 2022. Energy transitions, intelligence and big data: towards a prosumer concept with energy autonomy; pp. 1–5. [DOI] [Google Scholar]
- 2.Mazzone A. The Regulation and Policy of Latin American Energy Transitions, L. Noura Guimarães. Elsevier; 2020. Chapter 18 - energy transition in isolated communities of the Brazilian Amazon; pp. 319–330. [DOI] [Google Scholar]
- 3.Bahrami A., Teimourian A., Okoye C.O., Khosravi et N. Assessing the feasibility of wind energy as a power source in Turkmenistan; a major opportunity for Central Asia's energy market. Energy. sept. 2019;183:415–427. doi: 10.1016/j.energy.2019.06.108. [DOI] [Google Scholar]
- 4.Mohamadi H., Saeedi A., Firoozi Z., Sepasi Zangabadi S., et al. Veisi S. Assessment of wind energy potential and economic evaluation of four wind turbine models for the east of Iran. Heliyon. 2021;7(6) doi: 10.1016/j.heliyon.2021.e07234. juin. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Daut I., Zainuddin F., Irwan Y.M., et al. Razliana A.R.N. Analysis of solar irradiance and solar energy in perlis, northern of peninsular Malaysia. Energy Proc. 2012;18:1421–1427. doi: 10.1016/j.egypro.2012.05.158. [DOI] [Google Scholar]
- 6.Daut I., Razliana A.R.N., Irwan Y.M., et al. Farhana Z. A study on the wind as renewable energy in perlis, northern Malaysia. Energy Proc. 2012;18:1428–1433. doi: 10.1016/j.egypro.2012.05.159. [DOI] [Google Scholar]
- 7.Marchenko O.V., et al. Solomin S.V. 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon) oct. 2020. Competitiveness of wind and solar energy use in asian part of Russia and in central Asia; pp. 1–5. [DOI] [Google Scholar]
- 8.Chaurasiya P., Kumar V., Warudkar V., et al. Ahmed S. Evaluation of wind energy potential and estimation of wind turbine characteristics for two different sites. Int. J. Ambient Energy. 2019;42:1–24. doi: 10.1080/01430750.2019.1611634. avr. [DOI] [Google Scholar]
- 9.Balijepalli R., Rajak U., Dasore A., Raj A., et al. Chaurasiya P. 2022. Design and Optimization of NACA 0012, NACA 4412 and NACA 23,012 Aerofoils of Wind Turbine of Solar Updraft Tower Power Plant; pp. 9–18. [DOI] [Google Scholar]
- 10.Verma M., Ghritlahre H., Chaurasiya P., Ahmed S., et al. Bajpai S. Optimization of wind power plant sizing and placement by the application of multi-objective genetic algorithm (GA) in Madhya Pradesh, India. Sustainable Computing: Informatics and Systems. sept. 2021;32 doi: 10.1016/j.suscom.2021.100606. [DOI] [Google Scholar]
- 11.Elamouri M., et al. Ben Amar F. 2010. Evaluation du Potentiel Eolien de Sept Sites Retenus au Nord de la Tunisie », déc. [Google Scholar]
- 12.Mulugetta Y., et al. Drake F. Assessment of solar and wind energy resources in Ethiopia. II. Wind energy. Sol. Energy. 1996;57(4):323–334. doi: 10.1016/S0038-092X(96)00074-6. oct. [DOI] [Google Scholar]
- 13.Ould Bilal B., Kébé C., Sambou V., Ndongo M., et al. Ndiaye P. Etude et modélisation du potentiel éolien du site de Nouakchott. J. Sci. Pour Ingénieur. 2008;9(1):28–34. doi: 10.4314/jspi.v9i1.30056. oct. [DOI] [Google Scholar]
- 14.Bekele G., et al. Palm B. Wind energy potential assessment at four typical locations in Ethiopia. Appl. Energy. 2009;86(3):388–396. doi: 10.1016/j.apenergy.2008.05.012. mars. [DOI] [Google Scholar]
- 15.Soulouknga M.H., Somefun T.E., et al. Doka S.Y. Performance evaluation of wind turbines for sites in Chad. Heliyon. 2022;8(11) doi: 10.1016/j.heliyon.2022.e11565. nov. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Didane D., ab wahab A., Shamsudin S., Rosly N., Fadhli M., et al. Mohd S. « Assessment of wind energy potential in the capital city of Chad, N'Djamena », présenté à. AIP Conf. Proc. 2017 doi: 10.1063/1.4981190. avr. [DOI] [Google Scholar]
- 17.Kansongue N., Njuguna J., et al. Vertigans S. 2018 IEEE PES/IAS PowerAfrica. 2018. Sustainable energy for emerging nations development-A case study on Togo renewable energy; pp. 137–141. juin. [DOI] [Google Scholar]
- 18.Adaramola M.S., Agelin-Chaab M., et al. Paul S.S. Assessment of wind power generation along the coast of Ghana. Energy Convers. Manag. 2014:61–69. [Google Scholar]
- 19.Awanou C.N., Degbey J.M., etE Ahlonsou Estimation of the mean wind energy available in Benin (Ex Dahomey) Renew. Energy. 1991;1(5):845–853. doi: 10.1016/0960-1481(91)90037-P. janv. [DOI] [Google Scholar]
- 20.Diarra D.-C., et al. Akuffo F.O. Solar photovoltaic in Mali: potential and constraints. Energy Convers. Manag. 2002;43(2):151–163. doi: 10.1016/S0196-8904(01)00019-X. janv. [DOI] [Google Scholar]
- 21.Asamoah S.S., Parbey J., Yankey I.K., et al. Awuah, « Techno-economic assessment of a central grid-connected wind farm in Ghana using RETScreen® Expert. Heliyon. 2023;9(1) doi: 10.1016/j.heliyon.2023.e12902. janv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Diallo A., et al. Moussa R. « the effects of solar home system (SHS) on welfare in off-grid areas: evidence from Côte d'Ivoire. Energy. 2019;194 doi: 10.1016/j.energy.2019.116835. déc. [DOI] [Google Scholar]
- 23.Koua B., Zinla D., Koffi P., et al. Gbaha P. Assessment of the energy potential of agricultural crop residues in rural areas of Côte d'Ivoire. Biomass Conversion and Biorefinery. 2022:1–14. doi: 10.1007/s13399-021-02161-x. janv. [DOI] [Google Scholar]
- 24.Zanli B.L., Gbossou K., Tang W., Kamoto M., et al. Chen J. « A review of biochar potential in Cote d'Ivoire in light of the challenges facing Sub-Saharan Africa. Biomass Bioenergy. oct. 2022;165 doi: 10.1016/j.biombioe.2022.106581. [DOI] [Google Scholar]
- 25.Yeboua S.P.C., N'Goran Y., et al. Konan K. Classification of hourly clearness index of solar radiation in the district of Yamoussoukro. EPE. 2019;11(5):220–231. doi: 10.4236/epe.2019.115014. [DOI] [Google Scholar]
- 26.Ugur E., Elma O., Selamogullari U.S., Tanrioven M., et al. Uzunoglu M. 2013 International Conference on Renewable Energy Research and Applications (ICRERA) IEEE; Madrid, Spain: oct. 2013. Financial payback analysis of small wind turbines for a smart home application in Istanbul/Turkey; pp. 686–689. [DOI] [Google Scholar]
- 27.Dunaieva I., et al. Review of automatized meteorological stations use for agricultural purposes. IOP Conf. Ser. Earth Environ. Sci. 2021;937(3) doi: 10.1088/1755-1315/937/3/032097. déc. [DOI] [Google Scholar]
- 28.Ben U.C., Akpan A.E., Mbonu C.C., et al. Ufuafuonye C.H. Integrated technical analysis of wind speed data for wind energy potential assessment in parts of southern and central Nigeria. Cleaner Engineering and Technology. 2021;2 doi: 10.1016/j.clet.2021.100049. juin. [DOI] [Google Scholar]
- 29.Pallabazzer R. « Evaluation of wind-generator potentiality. Sol. Energy. 1995;55(1):49–59. doi: 10.1016/0038-092X(95)00040-X. juill. [DOI] [Google Scholar]
- 30.Jangamshetti S.H., et al. Rau V.G. Site matching of wind turbine generators: a case study. IEEE Trans. Energy Convers. 1999;14(4):1537–1543. doi: 10.1109/60.815102. déc. [DOI] [Google Scholar]
- 31.Ayua T.J., et al. Emetere M.E. Technical analysis of wind energy potentials using a modified Weibull and Raleigh distribution model parameters approach in the Gambia. Heliyon. 2023;9(9) doi: 10.1016/j.heliyon.2023.e20315. sept. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Oyedepo S.O., Adaramola M.S., et al. Paul S.S. Analysis of wind speed data and wind energy potential in three selected locations in south-east Nigeria. Int J Energy Environ Eng. 2012;3(1):7. doi: 10.1186/2251-6832-3-7. mai. [DOI] [Google Scholar]
- 33.Casini M. Small vertical Axis wind turbines for energy efficiency of buildings. JOCET. 2015;4(1):56–65. doi: 10.7763/JOCET.2016.V4.254. [DOI] [Google Scholar]
- 34.Zemamou M., Aggour M., et al. Toumi, « Review of savonius wind turbine design and performance. présenté à Energy Procedia. 2017:383–388. doi: 10.1016/j.egypro.2017.11.047. déc. [DOI] [Google Scholar]
- 35.S. Oswalt Manoj, J. P. Ananth, M. Rohini, B. Dhanka, N. Pooranam, et S Ram Arumugam, « 17 - FWS-dl: forecasting wind speed based on deep learning algorithms », in Artificial Intelligence for Renewable Energy Systems, A. K. Dubey, S. K. Narang, A. L. Srivastav, A. Kumar, et V. García-Díaz, Éd., in Woodhead Publishing Series in Energy. , Woodhead Publishing, 2022, p. 353-374. doi: 10.1016/B978-0-323-90396-7.00007-9.
- 36.Schneider P., et al. Xhafa F. In: Chapter 3 - Anomaly Detection: Concepts and Methods », in Anomaly Detection and Complex Event Processing over IoT Data Streams. Schneider P., et F Xhafa, editors. Academic Press; 2022. pp. 49–66. [DOI] [Google Scholar]
- 37.Pokhrel R., et al. Lee H. Estimation of the effective zone of sea/land breeze in a coastal area. Atmos. Pollut. Res. 2011;2(1):106–115. doi: 10.5094/APR.2011.013. janv. [DOI] [Google Scholar]
- 38.Kutty S.S., Khan M.G.M., Rafiuddin Ahmed M. 1 School of Engineering, The University of the South Pacific, Laucala Campus, Laucala Bay Road, Suva, Fiji, et 2 School of Computing, Information and Mathematical Sciences, The University of the South Pacific, Laucala Campus, Laucala Bay Road, Suva, Fiji, « Estimation of different wind characteristics parameters and accurate wind resource assessment for Kadavu, Fiji. AIMS Energy. 2019;7(6):760–791. doi: 10.3934/energy.2019.6.760. [DOI] [Google Scholar]
- 39.Prévost A., Léchappé V., Brun X., et al. Delpoux R. IEEE 32nd International Symposium on Industrial Electronics (ISIE 2023), Helsinki-Espoo, Finland: IEEE. 2023. An emulator for static and dynamic performance evaluation of small wind turbines.https://hal.science/hal-04099988 juin. Consulté le: 9 février 2024. [En ligne]. Disponible sur: [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.