SUMMARY
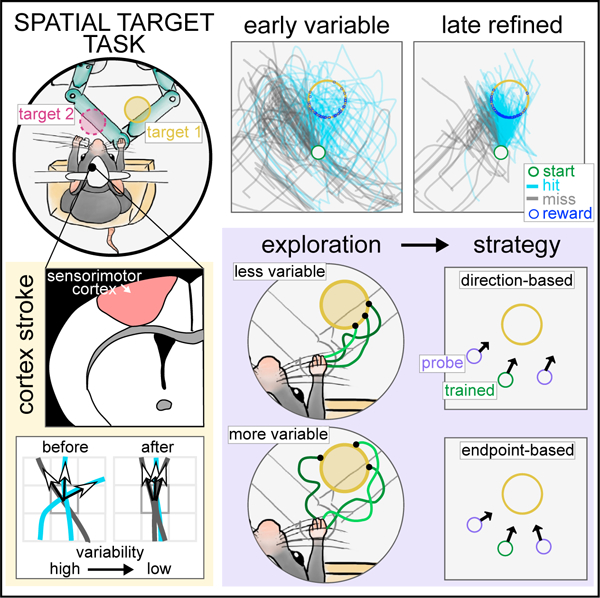
The brain can generate actions, such as reaching to a target, using different movement strategies. We investigate how such strategies are learned in a task where perched head-fixed mice learn to reach to an invisible target area from a set start position using a joystick. This can be achieved by learning to move in a specific direction or to a specific endpoint location. As mice learn to reach the target, they refine their variable joystick trajectories into controlled reaches, which depend on the sensorimotor cortex. We show that individual mice learned strategies biased to either direction- or endpoint-based movements. This endpoint/direction bias correlates with spatial directional variability with which the workspace was explored during training. Model-free reinforcement learning agents can generate both strategies with similar correlation between variability during training and learning bias. These results provide evidence that reinforcement of individual exploratory behavior during training biases the reaching strategies that mice learn.
Graphical abstract
In brief
Mosberger et al. introduce a task where mice refine forelimb reaches to spatial targets through exploration and reinforcement. Variable-targeted reaches require the sensorimotor cortex. A probe test shows that individual mice have direction- or endpoint-learning biases, correlating with how they explore during training. Model-free reinforcement learning recapitulates this learning bias.
INTRODUCTION
To reach for our phones on the nightstand, shift gears, or play drums, we have to precisely reach a covert target in space. In such spatial reaching movements, different movement strategies can be used to get to the target. One strategy is to move in a certain direction for a set distance, as in a learned feedforward movement.1,2 Another is to move so that the hand ends up in the learned target location, using the limb’s sensory state3,4 to move by feedback.5,6 The primary motor cortex is known to be crucial for targeted reaching movements across species.7–13 It has been found to generate activity tightly related to reaching direction14–19 and to integrate sensory feedback into motor commands.20,21 Despite the importance of reaches, in which different strategies can achieve the same outcome,22 it is poorly understood what influences which strategy is learned and how they are controlled by the brain.
It has been proposed that what is learned about an action is determined by the nature of exploration during training,22 because credit is assigned to successful movements from the pool of explored movements.23,24 Specifically, repeated credit assignment allows the brain to gradually converge on what movement aspects were causal to success and reduce their variability in a process called refinement.23,25–29 When primates learn to reach to rewarded target locations, the path length and spatial variance of reach trajectories are refined.30,31 Thus, when different movement strategies can lead to the same outcome, the type of movements explored during training could determine what is assigned credit and bias which strategy is learned. How individual animals explore may depend on their previous experience,32–34 motivation, fatigue, or innate differences. Hence, individuals may learn to use different movement strategies based on what movements they explore during training.
Whereas past work has quantified refinement of relevant movement aspects during learning, this does not resolve what strategy was learned, as assigning credit to either strategy can reduce variability in similar ways. The content of what was learned needs to be specifically probed. One way is to devise a probe test as has been used in the field of learning theory. Probe tests can distinguish egocentric stimulus-response learning35 from allocentric place learning,36–38 for instance, by placing an animal at a new entry of a maze. Similarly, studies in humans and non-human primates have investigated whether reaching movements to visual targets are performed within an intrinsic (goal is a target posture) vs. extrinsic (goal is a target location) reference frame,39–42 by introducing novel start positions or posture changes.43–49
Here, we study reaching movements to an invisible target in space, for which it is poorly understood how different reach strategies are learned, and whether exploration influences what is learned. We developed a forelimb spatial target task (STT), where mice explore a workspace and learn to move a joystick into rewarded target locations, similar to previous experiments in humans.30,50 Mice provide untapped potential to dissect the role of specific circuits in reaching movements.51,52 We positioned mice in a perched posture that enhanced exploration of the workspace, which allowed us to measure refinement of forelimb trajectories, as mice discovered and learned different targets. Using stroke lesions, we show that spatial directional variability and direction control is dependent on the sensorimotor cortex contralateral to the moving limb. By changing the start position in a small number of probe trials, we show that animals displayed direction- or endpoint-learning biases, and that the spatial exploration during training correlated with strategy bias. Finally, we trained reinforcement learning models to perform the task and show that model-free agents have a direction/endpoint-bias that also correlated with the exploratory behavior during training.
RESULTS
Perched mice explore the workspace and learn reaches to covert spatial targets
We implemented the STT with a selective compliance articulated robot arm (SCARA) joystick, providing a homogeneous horizontal workspace,53–55 and used a vertical manipulandum52 that the mice moved unimanually (Figures 1A and 1B). Mice self-initiated movements from a set start position and explored the workspace with complex trajectories (attempts) that were rewarded when they entered the target (hit), or ended after a maximum time (7.5 s) or if the joystick was let go (miss) (Figure 1C). Training started with a short pre-training period during which touching the joystick (phase 1), and then forward movements (phase 2) were rewarded. At the end of pre-training, we defined two target locations for each animal: ±40° from the mean direction of rewarded forward movements (Figure 1D). One of the targets was rewarded for several days until high performance (target training) (Figure 1E). No cues signaled where the target was.
Figure 1. Perched mice explore the workspace and learn reaches to covert spatial targets.
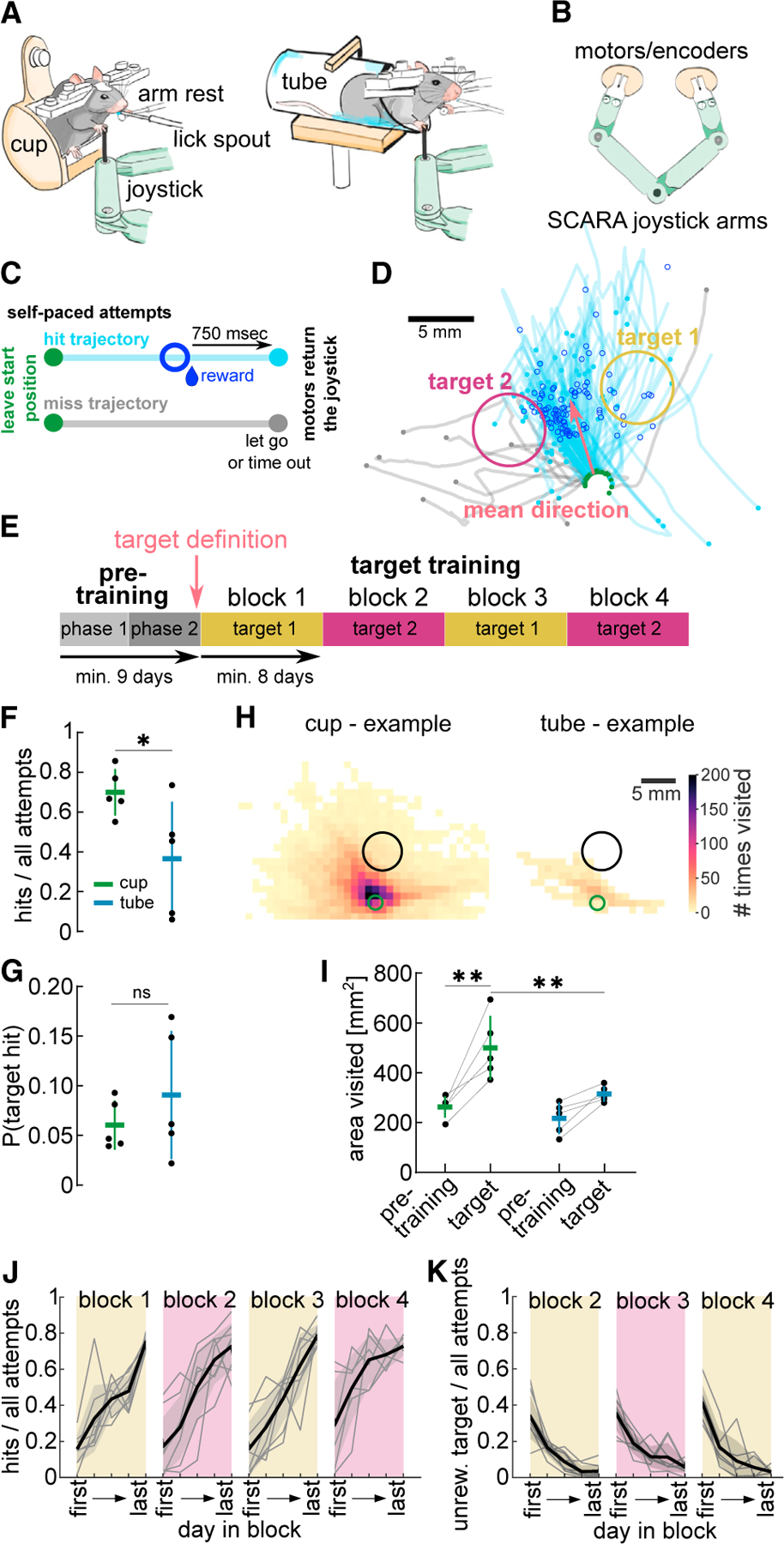
(A) Schematic of head-fixed mice unimanually moving a SCARA joystick. Left: mouse perched in the “cup.” Right: mouse quadrupedal in a “tube.”
(B) Schematic of a top view of SCARA joystick.
(C) Schematic illustrating attempts beginning by moving out of the start position (green dot). Hit trajectory: attempt enters target area, a reward is dispensed (dark blue circle), after 750 ms motors move joystick back to the start. Miss trajectory: target not entered within 7.5 s or joystick is let go, motors move joystick back to the start.
(D) Example trajectories from last pre-training session (hits in blue, misses in gray). Green dots, beginning of the trajectory leaving start position; blue and gray dots, end of hit and miss trajectories, respectively; dark blue circles, position at reward delivery. Targets defined 40° to right and left of mean hit direction.
(E) Experimental design. Pre-training phase 1: touching the joystick rewarded (4 days); phase 2: forward pushes rewarded. Target training: targets rewarded in consecutive blocks of 8 days minimum.
(F) Hit ratio on last session of block 1 for animals in cup and tube.
(G) Baseline probability of entering future target from attempts made on last day of pre-training.
(H) Example heatmaps of visits to 1 mm2 binned workspace for an animal in the cup or tube on first day of target training (green circle, start position; black circle, target).
(I) Total area visited on last day of pre-training and first day of target training for animals in cup or tube.
(J) Hit ratio on 5 equidistant days within each block from first to last day (selected days).
(K) Ratio of attempts that entered the previously rewarded target on selected days of blocks 2–4. (F, G, and I) n = 5 animals per group. (J and K) n = 8 animals. Mean ± SD and single animals. *p < 0.05, **p < 0.01; ns, p > 0.05. See also Figure S1/2/6 and Table S1.
Exploration of the workspace is crucial to discover the target and learn from reinforcement. In contrast to previous studies12,52,56–59 no shaping was used, such that only exploration would lead to target discovery. The movement was also not guided or hindered through force fields or haptic tunnels,59–61 and animals could move at any speed or pause mid-trajectory. To encourage animals to explore the workspace, we tested whether head-fixing mice in a perched posture, as during food handling,62 would increase the forelimb range of motion compared with standard quadrupedal positioning in a horizontal tube.12,51,52,63–65 We developed a cup-shaped holder (cup) that allowed animals to sit on their hindlimbs. Comparing animals trained on a target in the cup or standard tube (Figure 1A), we found that the achieved hit ratio was significantly higher in animals trained in the cup (Figure 1F, unpaired t test: t(8) = 2.42, p < 0.05, Figures S1A and S1B). This difference was not due to a difference in target locations between groups (Figures S1C and S1D). Both groups had a similar baseline chance of hitting the target from their attempts during pre-training (Figure 1G, unpaired t test: t(8) = 0.98, p > 0.05).
To test whether cup animals were better able to explore the workspace, increasing their probability of discovering the target, we analyzed the area visited by all trajectories of a session (Figure 1H, example animals). Cup animals visited more unique spatial bins than tube animals when they had to discover the spatial target (Figure 1I, two-way ANOVA repeated measures, group: F(1,8) = 8.99, p < 0.05, day: F(1,8) = 32.57, p < 0.01, day × group effect: F(1,8) = 5.67, p < 0.05). On the last day of pre-training, when they only had to move the joystick forward, both groups visited a similar area (Figure 1I, Bonferroni correction, pre-training day: t(16) = 0.94, p > 0.05), and achieved the same hit ratio (Figure S1E) with the same number of attempts (Figure S1F). This suggests there was no difference in motivation or ability to learn the task contingency. However, only cup animals increased workspace exploration once the target had to be entered (Figure 1I, Bonferroni correction, cup group, day comparison: t(8) = 5.72, p < 0.01), visiting a larger area than tube animals (Figure 1I, Bonferroni correction, target day, group comparison: t(16) = 3.83, p < 0.01). These results indicate that cup mice were better able to explore the workspace because of their posture. We think it unlikely that there was a difference in motivation or perseverative behavior between groups because both groups received similar total rewards during pre-training (Figure S1G). To further test this, we switched three tube mice to the cup and they all increased the area visited (Figure S1H and S1I), their trajectories became significantly more variable (Figure S1J), and their hit trajectories entered the target from more variable directions (Figure S1K). Taken together, perched mice were able to display a wider, more variable, range of forelimb movements with the joystick, increased their exploration to discover the target, and achieved more target hits.
We used the cup for all other experiments and next tested whether animals could discover and learn different target locations, to allow repeated assessment of learning and refinement. We pre-trained eight mice and defined two target locations for each animal (Figures 1D and S2A), which we rewarded in alternating blocks such that each target was repeated twice (Figure 1E). Each block lasted until the performance criterion was met and all animals progressed through each block within a maximum of 30 days (Figures S2B and S2C). We evaluated the performance on 5 equidistant days (from first to last) within each block, and found a steady increase in hit ratio in each block (first: 0.19 ± 0.07, last: 0.75 ± 0.03) (Figure 1J, mixed-effects model, day in block: F(2.1,14.8) = 54.90, p < 0.01, block: F(2.0,13.8) = 3.08, p > 0.05). In blocks 2–4, animals showed transient perseverative behavior, continuing to enter the previously rewarded target, which decreased as they explored and discovered the new target (Figure 1K, mixed-effects model, day in block: F(2.0,14.2) = 69.64, p < 0.01, block: F(1.5,10.2) = 1.81, p > 0.05). We are confident that animals learned to reach the target through reinforcement of exploratory reaches and did not use external cues, as the task was performed in the dark and performance was unaffected by whisker trimming (Figure S2D).
We next investigated how the target reach trajectories evolved throughout learning (Figure 2A).
Figure 2. Mice explore the workspace with high spatial directional variability and tortuous trajectories.
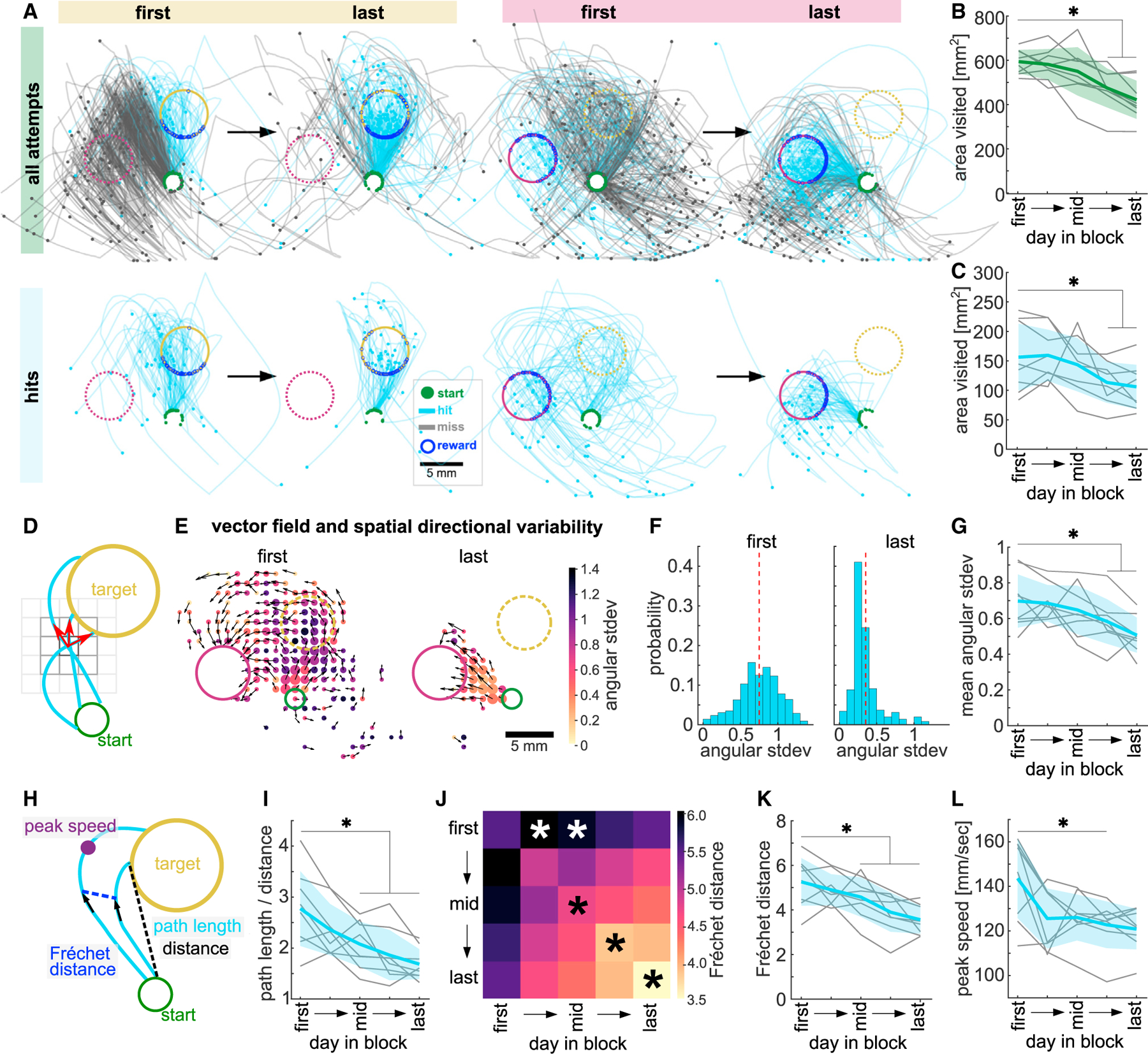
(A) Example miss (gray) and hit (blue) trajectories of first and last days of a target 1 and target 2 block. Top: all attempts. Bottom: 50 subsampled hit trajectories.
(B) Total area explored by all full-length trajectories.
(C) Total area explored by 50 subsampled hit trajectories before target entry.
(D) Schematic of vector field and spatial directional variability.
(E) Example vector fields showing mean vector of all trajectories in a spatial bin (black arrows) and heatmap of directional variability in that bin on first and last day of a target 2 block. Dot size represents number of visits/bin.
(F) Same data as (E), histogram of directional variability weighted by number of visits/bin (dashed line, mean across bins).
(G) Mean spatial directional variability.
(H) Schematics of path length and Euclidean distance from start to target (tortuosity, path length/distance), pairwise Fréchet distance (FD), and peak speed.
(I) Average tortuosity of hits.
(J) Average FD between hit trajectories within and across sessions. Similarity within later sessions is bigger than within the first session (diagonal, black asterisks). Hits in early and middle sessions are dissimilar to those in the first session (top row, white asterisks).
(K) Same as diagonal in (J) showing all animals.
(L) Average peak speed of hits. Data from 5 selected days per block, averaged across all blocks. Green, all full-length trajectories; blue, hit trajectories from start to target entry. One-way ANOVA with repeated measures, Dunnett’s multiple comparisons between the first day and all other days, *p < 0.05. Mean ± SD and single animals (n = 8). See also Figure S2 and Table S2.
Mice explore the workspace with high spatial directional variability and tortuous trajectories
We first asked whether workspace exploration changed with learning by counting the spatial bins visited by all trajectories. We found that, early in each block, a large area of the workspace was explored, which reduced as more hits were performed (Figure 2B, one-way ANOVA, F(3.1,21.6) = 13.95, p < 0.01). However, this could indicate that animals merely stopped producing far-reaching miss trajectories and increased the number of confined hit trajectories. We thus measured the space explored by only hit trajectories subsampling them to the same number for all sessions. Hit trajectories alone occupied a larger area of the workspace at the beginning of the block than at the end, even when we only considered the path from the start to target entry (Figure 2C, one-way ANOVA, F(1.9,13.3) = 6.67, p < 0.05), suggesting that exploratory trajectories that were rewarded at target entry (hits) were refined.
We next investigated how hit trajectories changed with learning and quantified how variable the movement direction was across the workspace (spatial directional variability). We generated a vector field from the hit trajectories per session and quantified the angular standard deviation in each spatial bin (Figures 2D and 2E). This analysis showed that the spatial directional variability was high early in each block and significantly decreased with learning (Figures 2E–2G, one-way ANOVA, F(2.4,16.6) = 7.91, p < 0.01). This decrease was specific to the rewarded segment of the hit trajectories, as the spatial directional variability of all full-length trajectories did not decrease with learning (Figure S2E). We then asked whether a single hit trajectory became less variable, which we quantified using tortuosity (Figure 2H, path length/distance). Hit trajectories were significantly more tortuous at the beginning of the block than at the end (Figure 2I, one-way ANOVA, F(2.7,18.6) = 15.06, p < 0.01), with trajectories becoming straighter with learning.
Having found that target reaches became less variable, we then asked how similar they were to each other in shape and position across a block. We calculated the discrete Fréchet distance (FD)66 between pairwise trajectories (Figure 2H). Hit trajectories within a session became more similar to each other with learning (Figure 2J [diagonal] and Figure 2K, one-way ANOVA, F(2.7,19.0) = 13.82, p < 0.01). Furthermore, hit trajectories on the first day of the block were dissimilar to hit trajectories on other days in the block, particularly to hits in the middle of the block (Figure 2J [top row], one-way ANOVA, F(3.0,21.2) = 5.28, p < 0.01), showing that the overall shape of the hits changed with learning.
Overall, we found that animals initially explored the workspace with hit trajectories that moved in variable directions across the workspace, were tortuous, and dissimilar to each other. These aspects were then refined, reducing variability, and producing straighter trajectories as animals received rewards for entering the target (Video S1). However, this refinement was not accompanied by an increase in movement speed, but rather the peak speed (Figure 2H) achieved per hit decreased with learning (Figure 2L, one-way ANOVA, F(2.1,14.8) = 5.73, p < 0.05), as did its variability (Figure S2F, one-way ANOVA, F(2.2,15.3) = 15.05, p < 0.01), suggesting an increase in control over the peak speed that would allow precise endpoint targeting.
The precision of initial movement direction and targeting accuracy increases with learning
As animals may learn different strategies to move the joystick into the target—moving in a certain direction for a certain distance or moving toward a specific endpoint location from any position—we specifically measured refinement in these aspects.
First, we measured refinement of movement direction by analyzing the direction of the initial segment of hit trajectories and comparing them with the optimal direction straight to the target (Figure 3A). As animals learned, their initial direction significantly approached the target direction (Figure 3B, one-way ANOVA, F(1.5,10.7) = 6.61, p < 0.05, last day ). Importantly, they also significantly decreased the variability of their initial direction (Figure 3C, one-way ANOVA, F(2.2,15.7) = 8.96, p < 0.01).
Figure 3. The precision of initial movement direction and targeting accuracy increases with learning.
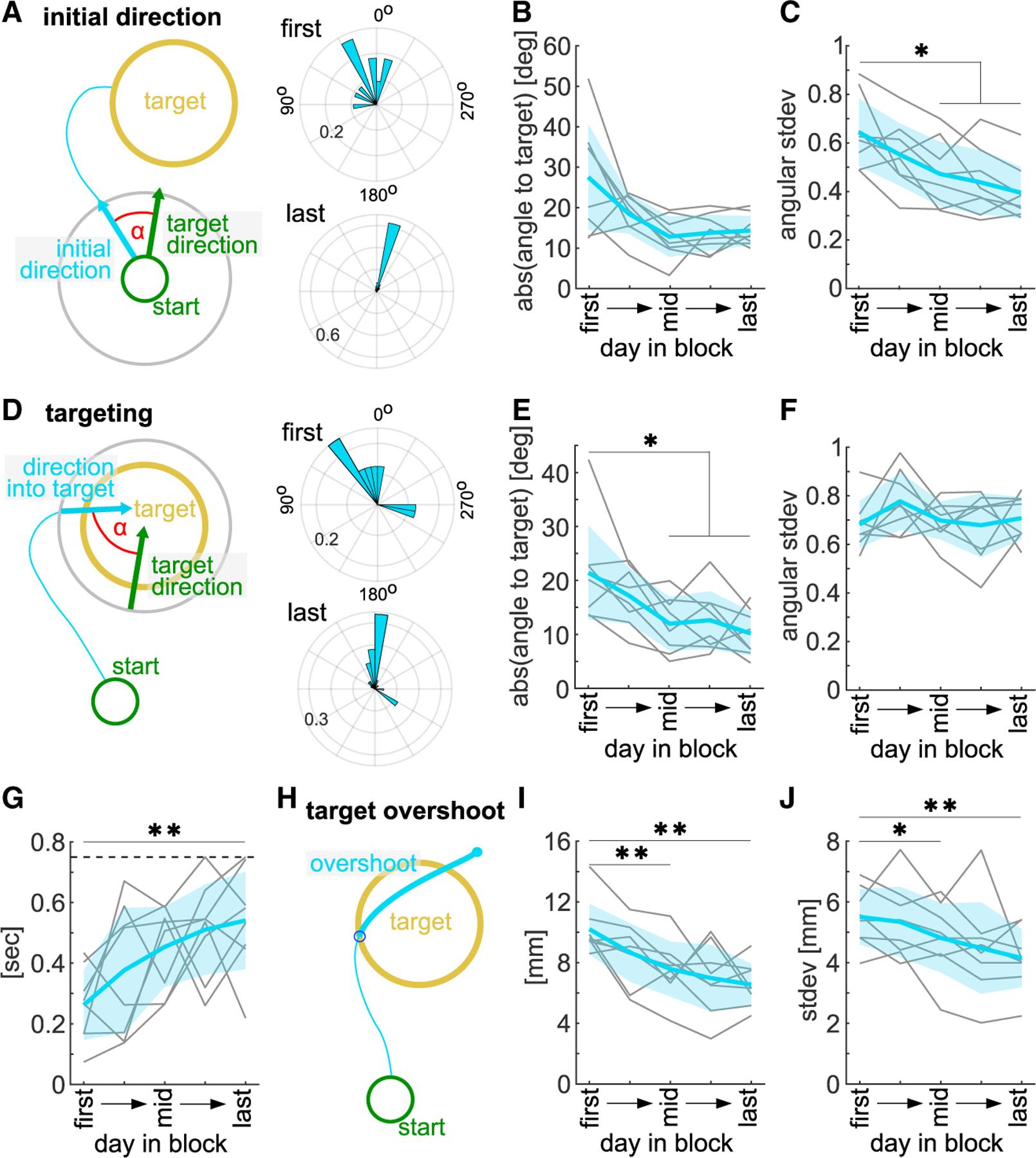
(A) Left: schematic of initial direction. Right: example polar histogram of initial hit direction on first and last day of a block (probability).
(B) Mean absolute initial direction difference to straight target direction (0°).
(C) Variability of initial direction.
(D) Left: schematic of target entry direction. Right: example polar histogram of target entry direction on first and last day of a block (probability).
(E) Mean absolute target entry direction difference to straight target direction (0°).
(F) Variability of target entry direction.
(G) Time spent in and closely around target after target entry until end of attempt (max. 750 ms, dashed line).
(H) Schematic of target overshoot length.
(I) Mean target overshoot.
(J) Overshoot variability. Hit trajectories on 5 selected days, averaged across all blocks. One-way ANOVA with repeated measures, Dunnett’s multiple comparisons between the first day and all other days, *p < 0.05, **p < 0.01. Mean ± SD and single animals (n = 8).
To investigate targeting, we analyzed the final segment of the hit trajectory into the target and measured its direction in relation to the straight target direction (Figure 3D). We found that over learning the mean difference to the straight target direction reduced significantly (Figure 3E, one-way ANOVA, F(2.8,19.4) = 7.36, p < 0.01, last day ), but animals did not decrease the variability of target entry direction, even at high performance (Figure 3F, one-way ANOVA, F(1.9,13.0) = 1.23, p > 0.05). However, with learning, they dwelled significantly longer in and around the target area after target entry (Figure 3G, one-way ANOVA, F(3.2,22.1) = 5.04, p < 0.01) and the trajectory path that overshot the target entry point (Figures 3H and 3I, one-way ANOVA, F(1.8,12.8) = 9.96, p < 0.01) as well as its variability (Figure 3J, one-way ANOVA, F(1.8,12.7) = 5.48, p < 0.05) decreased.
These findings provide evidence that animals refined their reach in a precise direction toward the target, but also show features of endpoint-based movements with variable entry directions into the target. Furthermore, the dwelling in the target location during reward consumption would allow for credit assignment to the target location in space. We next tested if any of these aspects of forelimb reaches were dependent on sensorimotor cortex in the mouse.
A sensorimotor cortex stroke impairs movement direction and spatial directional variability
Learning and performance of forelimb reaching movements have been shown to be dependent on the sensorimotor cortex,8,11,67 but studies of rodents interacting with one-dimensional levers have found no impairment of learned skills upon motor cortex lesion.68 To test whether the mouse sensorimotor cortex controls distinct aspects of spatial forelimb reaches, we performed confined sensorimotor cortex photothrombotic stroke69 lesions in expert animals (target 1). We induced the lesion through a cranial window that had been implanted over the left caudal forelimb primary motor cortex before training. To confirm the lesion location, we registered coronal brain tissue sections into a 3D volume and aligned it to the Allen Reference Brain Atlas using BrainJ70 (Figures S3A and S3B). The unilateral lesions encompassed a total volume of 9.9 ± 3.4 mm3 (Figure 4A), with the largest proportion located in the primary (35% ± 6%) and the secondary (26% ± 5%) motor cortices (Figure 4B). The lateral 16% and 10% of stroke volume affected the primary somatosensory cortices of the forelimb and hindlimb, respectively (Figure 4B). These strokes unilaterally lesioned 59% ± 7% of the total primary motor cortex, 40% ± 19% of the secondary motor cortex, as well as large parts of the primary somatosensory cortices of the forelimb (82% ± 11%) and hindlimb (77% ± 7%) (Figure 4C). Other sensory cortical areas were affected by the stroke to a lesser extent, and in two animals the lesion partially affected the subcortical white matter (Figures S3C and S3D).
Figure 4. A sensorimotor cortex stroke impairs movement direction and spatial directional variability.
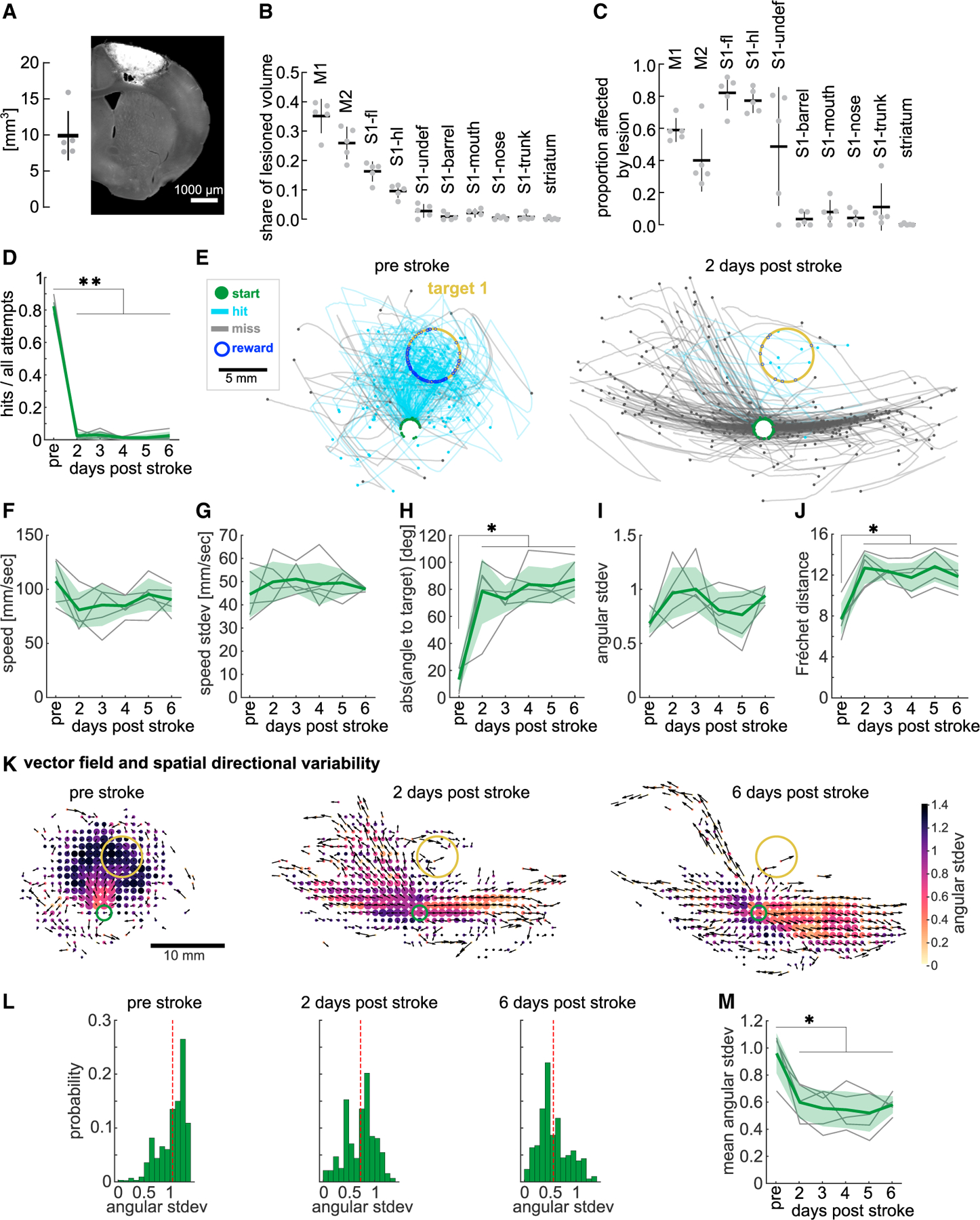
(A) Left: stroke lesion volume. Right: example histological coronal section showing lesion in auto-fluorescence. Scale bar, 1,000 μm.
(B) Share of lesion volume affecting ABA areas (sensorimotor cortex and striatum).
(C) Proportion of ABA areas affected by lesion.
(D) Hit ratio before and after cortex stroke.
(E) Example animal trajectories before and 2 days post-stroke.
(F) Mean peak speed before and after stroke.
(G) Variability of peak speed.
(H) Mean absolute initial direction difference to target direction (0°).
(I) Variability of initial direction.
(J) Post-stroke FD to pre-stroke trajectories.
(K) Example vector fields showing mean direction of all trajectories per spatial bin (black arrows) and heatmap of the spatial directional variability in that bin, pre-stroke, 2, and 6 days post-stroke. Dot size, number of visits/bin.
(L) Histogram of data in (K), directional variability weighted by number of visits/bin (dashed line, mean across bins).
(M) Mean spatial directional variability before and after stroke. Trajectories from all attempts used. One-way ANOVA with repeated measures, Dunnett’s multiple comparisons between the pre-stroke day and post-stroke days, *p < 0.05, **p < 0.01. Mean ± SD and single animals (n = 5). (B and C) ABA, Allen Reference Brain Atlas; M1, primary motor cortex; M2, secondary motor cortex; S1-fl, primary sensory cortex – forelimb; S1-hl, primary sensory cortex – hindlimb; S1-undef, primary sensory cortex – undefined; S1-“others”, primary sensory cortex – other body parts. See also Figures S3 and S4.
Animals were given a day to recover from the non-invasive photothrombotic stroke and placed in the STT on days 2 through 6 post-stroke with the same target as before the lesion. The hit ratio after the stroke was strongly impaired with animals achieving almost no target hits (Figure 4D, one-way ANOVA, F(1.6,6.4) = 614.7, p < 0.01). This was not due to a lack of task engagement as animals readily performed movements with the joystick (Figures 4E and S4A). We investigated how mice manipulated the joystick after the lesion using markerless pose estimation from videos tracking the joystick base and the wrist71 (Figures S4B and S4C; Video S2). As mice moved the joystick, their wrist to joystick distance did not change significantly post-stroke (Figures S4D and S4E), but it became more variable (Figures S4D and S4F). Despite this deficit, the total number of attempts was not affected (Figure S4G). However, as lesioned animals did not finish the session by reaching the maximum number of rewards, their sessions lasted longer and time between attempts (ITI) showed a tendency to be longer as well (Figure S4H).
Next, we investigated what aspects of the reach were impaired. Given the few hits achieved by post-stroke animals, we performed trajectory analyses using all attempts (hits and misses). Trajectories after the cortex lesion still reached a largely similar average peak speed (Figure 4F, one-way ANOVA, F(1.9,7.5) = 2.25, p > 0.05), and peak-speed variability (Figure 4G, one-way ANOVA, F(2.2,8.7) = 0.51, p > 0.05). However, the initial reach direction was significantly deviated after stroke (Figures 4E and 4H, one-way ANOVA, F(2.4,9.7) = 17.71, p < 0.01). Animals either moved too medial or too lateral (Figures S4A and S4I), seemingly unable to push the joystick accurately forward into the target, while the variability of the initial direction was not affected (Figure 4I, one-way ANOVA, F(1.8,7.3) = 2.19, p > 0.05). To further investigate how similar the movements were before and after the lesion, we again used the FD. To focus the analysis on the aimed movement into the target area, we only included the segment of the hits to the target entry and excluded movements made during reward consumption. This analysis showed that trajectories produced after the lesion were very dissimilar to those before the lesion (Figure 4J, one-way ANOVA, F(2.1,8.5) = 18.78, p < 0.01). However, trajectories post-stroke, while initially more widespread, did not consistently occupy a larger area of the workspace (Figure S4J), nor was their tortuosity significantly different (Figure S4K). Applying our vector field analysis on all full-length trajectories before and after stroke revealed a strong decrease in spatial directional variability, which persisted across all post-stroke days (Figures 4K–4M, one-way ANOVA, F(2.4,9.6) = 15.20, p < 0.01). Together, these results show that sensorimotor cortex lesions strongly impaired target reaches, causing reaches with less spatial directional variability, and an inability to reach accurately toward the target.
A probe test reveals that individual animals learned to reach the target using different strategies
To dissociate whether, and to what degree, animals had learned a strategy of moving in a specific direction, or guiding the hand to a specific endpoint location, we devised a probe experiment that challenged expert animals with new start positions. During this session, after a target 1 block, the joystick returned to novel start positions, left or right of the original start position, in a small number of probe trials (Figure 5A). During each probe trial, the animal performed attempts from the new start until the target was hit (or a maximum of 5 min), to limit learning from reinforcement during the probe trial. We confirmed that there was no significant learning during the probe session by analyzing the hit ratio across probe trials (Figure S5A, mixed-effects model, probe trial: F(18,126) = 1.31, p > 0.05).
Figure 5. A probe test reveals that individual animals learned to reach the target using different strategies.
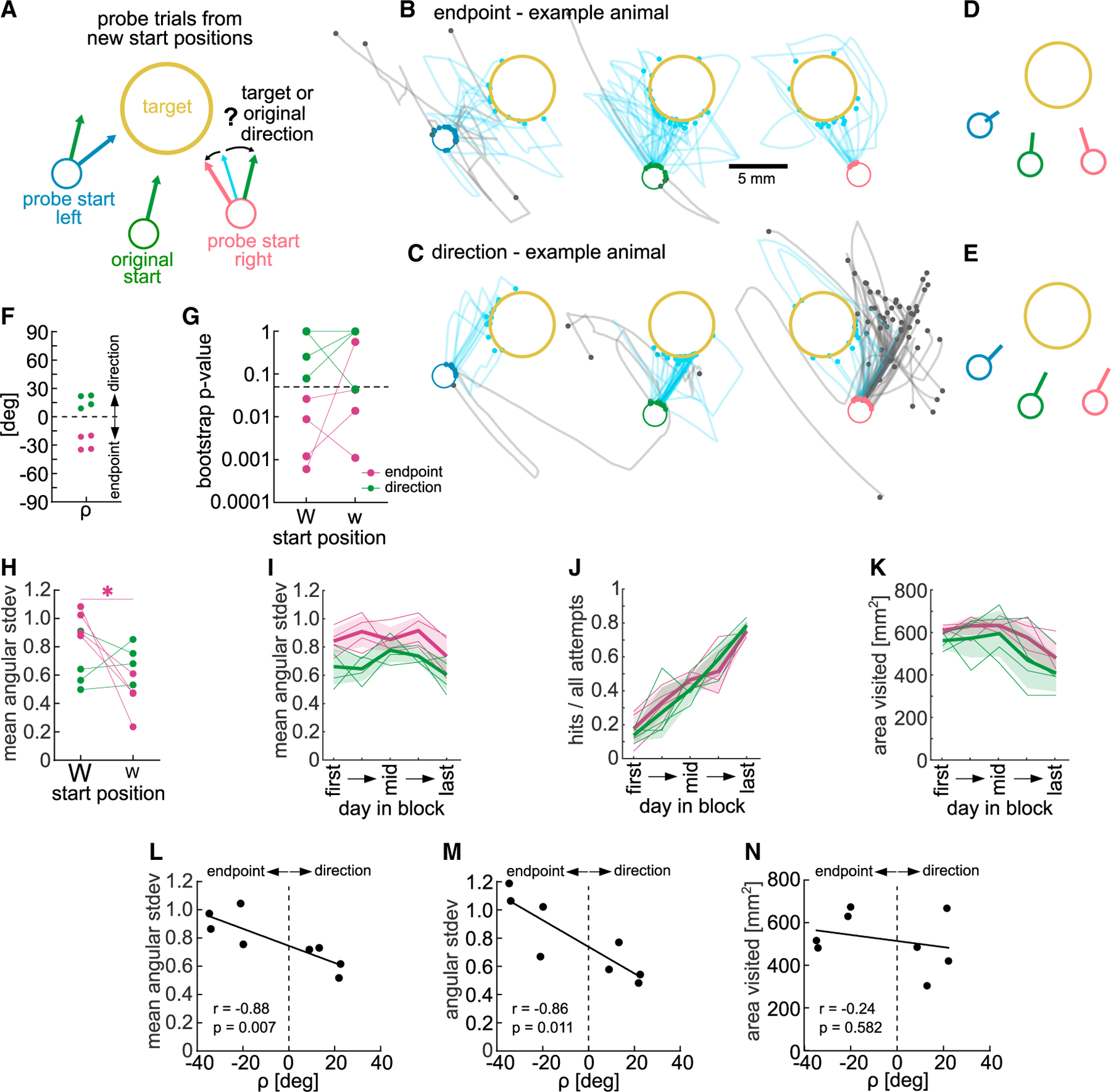
(A) Schematic of probe test showing new start positions to the left and right of original start position.
(B) Example endpoint-biased animal. All trajectories from new start positions and 40 subsampled trajectories from original start position. Hits shown from the start to target entry.
(C) Same as (B) but for direction-biased animal.
(D) Mean initial direction vectors for animal in (B).
(E) Mean initial direction vectors for animal in (C).
(F) angle for all animals. Positive , mean initial direction closer to original direction (direction learner, green); negative , mean initial direction closer to target direction (endpoint learner, maroon).
(G) p values from bootstrapped distributions of mean directions from probe starts, split by weight (p < 0.05, significantly different from mean original direction distribution).
(H) Spatial directional variability during probe trials, split by weight.
(I) Spatial directional variability of endpoint and direction learners during target training (average of blocks 1 and 3, target 1).
(J) Hit ratio of endpoint and direction learners during same blocks.
(K) Total area visited by endpoint and direction learners during same blocks.
(L) Same as (I) showing variability in early sessions (selected day 2) and correlation to .
(M) Variability of target entry direction of early sessions (selected day 2) and correlation to .
(N) Same as (K) showing area visited in late sessions (selected day 4) and correlation to . Trajectories from all attempts. Two-way ANOVA with repeated measures or t tests. Dunnett’s or Bonferroni’s multiple comparisons, *p < 0.05. Mean ± SD and single animals (n = 8 or n = 4). See also Figure S5.
The probe test revealed that indeed some animals moved the joystick toward the target from the new start positions, adjusting their reach direction (Figure 5B, example animal), while others moved in the same direction from all start positions (Figure 5C, example animal). To quantify the degree to which an animal had learned such an endpoint-based or a direction-based strategy, we calculated the mean initial trajectory direction from each start position (Figures 5D and 5E), and determined whether the mean initial direction from the probe start was closer to the mean direction from the original start or to the optimal target direction (Figure S5B). This analysis also took into consideration how much the animal had to adjust its trained original direction to hit the target from the probe start by weighting a larger adjustment more (weights, Figures S5B and S5C). In brief, for each probestartposition we subtractedthe absolute difference between the initial reach direction and the target direction from the absolute difference between the initial reach direction and the original direction (Figure S5B) and multiplied it by the weight. This resulted in a signed angle beta for each start, <0 if the reach direction was closer to the target direction, and >0 if it was closer to the original direction (Figures S5B and S5D). We calculated an endpoint-direction learner bias for each animal as average of both signed values (rho , Figure S5B). From the 8 animals that underwent the probe test, we found for 4, biasedtoward a direction, and for the other 4, biased toward an endpoint strategy (Figure 5F).
We further tested whether endpoint-biased animals significantly adjusted their reach direction away from the original direction toward the target direction. For each animal and start position, we bootstrapped the initial direction from all attempts to get a distribution of the mean direction (Figures S5E and S5F). Then we calculated the 95% confidence interval of the mean direction distribution from the original start and determined what part of the distributions from the probe starts was within the upper/lower bounds of that confidence interval, resulting in a p value for each new start position. The four animals classified as endpoint-biased by their angle also had p values <0.05 for their more difficult start position (large weight) (Figure 5G), indicating that their probe reach direction was significantly different from the original direction. To provide additional evidence that movement adjustments were tailored to the probe start position, we calculated whether reaches from the probe start would have been less successful if they were performed from the original start. Translating trajectories from probe starts to the original start yielded significantly lower hit ratios than original start reaches, particularly in endpoint learners (Figure S5G, two-way ANOVA repeated measures, start position: F(2,12) = 22.49, p < 0.01, learner: F(1,6) = 12.68, p < 0.05, start × learner: F(2,12) = 6.95, p = 0.01). For the easier start, only endpoint learners adjusted the trajectories enough to lead to a significant hit ratio decrease.
We then focused our analysis on how animals adjusted their movements from the probe starts and measured the spatial directional variability. We again found a significant interaction between start position and learner bias, with endpoint learners showing a higher spatial directional variability from the difficult start than the easier start, whereas direction learners displayed the same variability from both (Figure 5H, two-way ANOVA repeated measures, start position: F(1,6) = 9.71, p < 0.05, learner: F(1,6) = 0.19, p > 0.05, start × learner: F(1,6) = 14.32, p < 0.01). These results suggest that reaches of endpoint learners were dependent on the location in space allowing them to increase spatial variability from the difficult start position. Taken together, our findings indicate that endpoint-biased animals had learned to move to the target position in space rather than a specific direction and could adjust their movement depending on difficulty.
Strategy bias is correlated with early spatial exploration
The endpoint and direction learning bias of different animals could be the result of reinforcement of different movements during training. We investigated whether animals that showed different strategies during the probe test had explored the workspace differently during training, biasing what they learned. We found that spatial directional variability across all attempts when target 1 was rewarded (blocks 1 and 3) was significantly higher in endpoint learners compared with direction learners (Figure 5I, two-way ANOVA repeated measures, day in block: F(4,24) = 3.00, p < 0.05, learner: F(1,6) = 11.06, p < 0.05). This difference did not reflect a difference in performance (Figure 5J, two-way ANOVA repeated measures, day in block: F(4,24) = 45.27, p < 0.01, learner: F(1,6) = 0.11, p > 0.05). Furthermore, endpoint-biased animals did not explore a larger area (Figure 5K, two-way ANOVA repeated measures, day in block: F(4,24) = 7.47, p < 0.01, learner: F(1,6) = 2.1, p > 0.05), which would give them more experience with different positions in the space. Instead, the way they explored the space was more variable. Specifically, the spatial directional variability early in learning (day 2 of the 5 selected days) significantly correlated with the degree to which animals were biased toward a direction or endpoint strategy (value of ) (Figure 5L, Spearman correlation, r = −0.88, p < 0.01). In addition, we found that animals that entered the target from more variable directions early in learning also showed a stronger bias of endpoint learning (Figure 5M, Spearman correlation r = −0.86, p < 0.05). When we performed the same correlation analysis on the area explored, where the largest difference between groups during learning was on a late day in the block (day 4), we found no significant correlation with endpoint learning bias (Figure 5N, Spearman correlation, r = −0.24, p > 0.05).
Taken together, animals that explored with more spatial directional variability and entered the target from variable directions, showed an endpoint bias in the probe test. This could indicate that the reinforcement of variable trajectories led to the learning of an endpoint state because the common feature between rewarded trajectories was not a specific movement direction but an endpoint location. Conversely, for direction learners, less variable trajectories could have allowed the reinforcement of a specific direction.
Exploration biases strategy in model-free reinforcement learning agents
To investigate whether reinforcement of different behavior during training is sufficient to bias what is learned, we trained model-free reinforcement learning agents in a similar STT, and confronted them with a probe test.
A point-mass agent was trained to move through a continuous space from a start position to a covert target area to obtain a reward (Figure 6A). The agent was trained such that, given its state at each timestep, an action was chosen that maximizes the sum of future rewards. The state consisted of the agent’s Cartesian position, velocity, and a “Go” signal, which modeled an internal signal to initiate movement. The learned action was a force which influenced the agent’s velocity. Over many trials, the agents increased their reward and decreased the number of timesteps to reach the target (Figure 6B), refining their trajectories from early variable trials to precise later trials (Figure 6C). Once agents were trained, we probed them for endpoint or direction learning bias by moving the start position and found that, as the mice, agents exhibited endpoint (Figure 6D) and direction learner (Figure 6E) behavior.
Figure 6. Exploration biases strategy in model-free reinforcement learning agents.
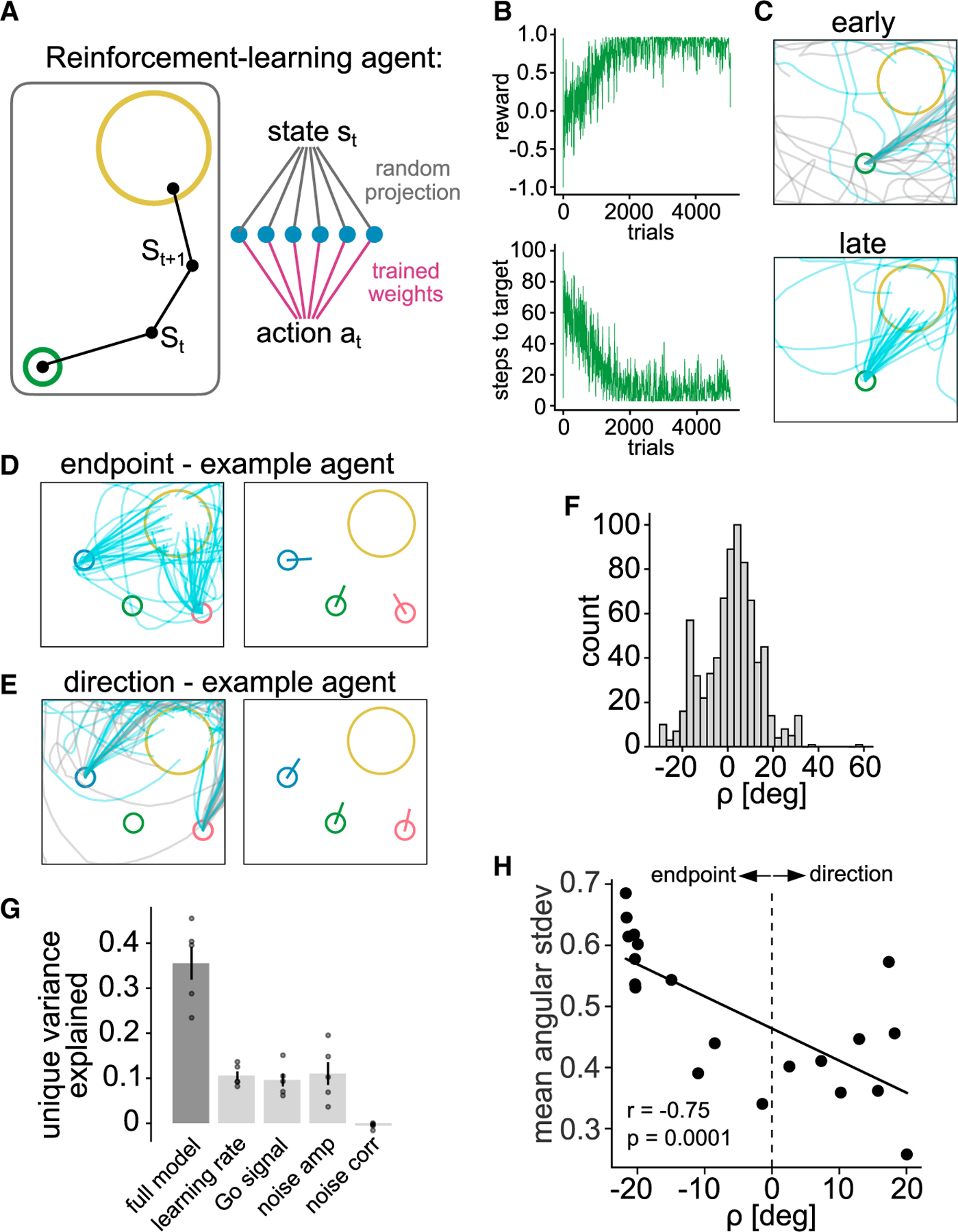
(A) Schematic of single-layer network trained to produce forces that move a point-mass to a target.
(B) Reward per trial (top) and number of steps to reach target (bottom) for an example agent throughout training.
(C) Trajectories for same example agent, early (top) and late (bottom) in training.
(D) Trajectories and mean initial direction during probe test of example agent that produced endpoint learner behavior.
(E) Same as (D) but for agent that produced direction learner behavior.
(F) Distribution of in an ensemble of agents trained with randomly chosen hyperparameters.
(G) Fraction of variance in explained by a multivariate ridge regression model including all randomly chosen hyperparameters as regressors (full model), as well as reduction in variance explained when leaving each of the hyperparameters out of the model (mean ± SEM; points, different cross-validation splits of the data).
(H) Weighted spatial directional variability over training of n = 20 agents trained with identical hyperparameters but distinct initializations correlated to value.
Next, we asked which model hyperparameters most strongly predict this bias. We randomly sampled the hyperparameters (learning rate, Go signal amplitude, exploratory action noise amplitude, and correlation time of exploratory action noise) for each agent. This led to a mix of direction learner ( ) and endpoint learner ( ) agents (Figure 6F). We then performed multivariate regression to predict using the values of these hyperparameters. A regression model trained using all hyperparameters explained less than half of the total variance in (Figure 6G). To quantify the unique contribution of each hyperparameter, we repeated the fit using models in which one regressor was left out. This revealed that the learning rate, Go signal amplitude, and exploratory noise amplitude all accounted for roughly equal and mutually independent contributions, whereas the timescale of noise correlations accounted for essentially none of the variance in (Figure 6G). Hence, most of the variance in was not explained by the hyperparameters of the model and remained unaccounted for in these fits.
However, even agents with identical hyperparameters differed from one another in two respects: the randomly initialized weights (initial condition) and the random actions chosen at each timestep, which could affect strategy bias. We thus trained agents with identical hyperparameters to perform the task and found that the observed range of across agents was similar to that across agents with heterogeneous hyperparameters (Figures 6H vs. 6F), confirming that these agents still showed different strategies. When we analyzed the spatial directional variability of their trajectories, we found that spatial directional variability during training correlated with endpoint-direction bias as in the mice (Figure 6H, n = 20, Spearman correlation, r = −0.75, p < 0.01). Together, these results provide evidence that model-free reinforcement learning models are sufficient to generate endpoint and direction-biased behavior, which is partially explained by spatial directional variability during training.
DISCUSSION
Our task shares features with previous tasks for mice51,52,56,58–61,63,72 that used SCARA joysticks52,59–61,72,73 or spatial reward zones,52,56,59,63 and expands on these studies in key aspects: (1) The perched posture in the cup allowed animals to increase workspace exploration. (2) Continuous movements with the joystick were not guided by motors or spring forces. (3) Reward contingency did not change within a block and movements refined without shaping. (4) Probe trials dissociated what had been learned by individual mice.
Here, we provide evidence that, in an ambiguous reaching task, spatial exploration during learning biases the reach strategy learned by individual animals. These observations are consistent with studies suggesting that exploration during training is related to performance.22,30,74 Our findings expand results from a human study where participants learned to move a virtual object to a target on a tablet and were then challenged with obstacles during transfer tests.75 The study found that exploration during practice correlated with performance on the transfer tests and allowed participants to generalize to a new task-space. As in our mice, the correlation was not with the overall area visited but the trial-to-trial pattern of search.75 Our modeling showed that purely model-free reinforcement learning agents trained in a simple target task show endpoint and direction learning biases as well. Even when we fixed the hyperparameters, agents still showed these biases, which also correlated with the spatial directional variability during training, suggesting that reinforcement of different actions during training affects what is learned.
Reinforcement of spatially variable trajectories, which entered the target from different directions, would have biased endpoint learner mice to assign credit to the target location in space and adopt a movement strategy that is more sensory feedback based (reducing error to a desired endpoint).43,76 In direction learners, reinforcement of less variable trajectories that entered the target from the same direction could have led to learning of feedforward movement, relying less on moment-to-moment feedback.2,6 As endpoint-biased mice learned the task, sensory error-based learning,77–80 which has been shown to exist in mice,51,72 may also have contributed to the refinement81,82 in addition to learning from reinforcement. Endpoint learner animals may thus have improved error sensitivity as it has been reported that the movements made as corrections to sensory feedback errors can be a strong teaching signal that allows learning.83 Accordingly, in endpoint learner mice, the spatial directional variability was increased specifically in the more difficult probe start, suggesting that they increased variability to achieve the larger adjustment to the target.84,85
We considered that the bias of showing direction and not endpoint responses during the probe test could have been confounded by insensitivity to the new start positions, as detected through proprioception. However, mice have been shown to reliably discriminate passive forelimb deviations of only 2 mm,73 and our probe start positions were ~5.5 mm away from the original start. We are confident that animals rely on proprioception in our task because animals performed the task in the dark and performance was unchanged without whiskers. Furthermore, there were no olfactory cues that instructed where the target or start position was.11,86 Yet, we did see attempts by direction learners during which the movement direction was adjusted toward the target eventually, which could indicate that they used sensory feedback only once they were moving, and had learned not to rely on it for the initial reach direction.
Variability of the joystick trajectories during training may have other causes than exploration.74,87,88 Variability can be due to noise in the sensorimotor system,89 and can impair learning.90 The remaining variability in joystick trajectories at high performance could be due to noise. However, we saw an increase in variability of several movement aspects when animals had to discover a target at the beginning of the block, indicating that variability was increased to explore. Similarly, the workspace area visited only increased once perched mice had to search for the rewarded target.
Our results showed that spatial target reaches, particularly their spatial directional variability, depends on the sensorimotor cortex in mice. The sensorimotor cortex has been well established as a crucial structure for learning of forelimb movements in rodents,91–93 particularly reach and grasp movements.8,11,13,94 But its role in the performance of forelimb movements has been challenged after a study in rats reported no effect of motor cortex lesions on a forelimb skill that required high temporal but less spatial precision.68 Beside an increase in variability of the prehension of the joystick manipulandum post-stroke, in line with an impairment of digit control, we found specific deficits in spatial directional variability and initial direction of reaches, whereas movement speed was not affected. These findings suggest a role for the motor cortex in spatial target reaches7,10 but not in temporal control of movements,68,95 as has been reported in primates.96
In summary, our findings suggest that, in a spatial forelimb task in which a target location is reinforced, the spatial directional exploration of the task-space during learning affects what is assigned with credit and what strategy is learned. This behavior in mice provides a research opportunity to dissect the neural circuit mechanisms underlying exploration and the learning of directions or endpoints in forelimb reaches.
Limitations of the study
Head fixation allowed us to investigate reach strategies by maintaining a stable reference frame, but imposes constraints on the animal’s interaction with the joystick compared with freely moving tasks,56 which may be a disadvantage for certain research questions. All animals moved the joystick with their right hand, and their handedness may have affected their behavior. In other cohorts of mice, we have assessed handedness in a cylinder test and found no significant relationship between handedness and learner bias. To make the task equally difficult for different animals, we defined targets individually based on baseline reach direction.
The task design (small target size, high performance criterion, several blocks) required several weeks of training but ensured that skill learning was required in each block, allowing to measure the gradual refinement of reaches across days. This difficulty level can be reduced by changing various task parameters to suit other studies.
We assessed the role of the sensorimotor cortex by inducing stroke lesions because of its clinical relevance, but these lesions also affect fibers of passage. As our stroke lesions affected sensorimotor areas similarly in all animals, including cortical layers, we cannot draw any conclusions about the role of specific cortical areas, or layers, in the reaching movements.
Although we classified animals into endpoint and direction learners, we view these strategies as existing on a gradient, with animals biased toward one or the other strategy to different degrees. We restrict our conclusions to the average response, or bias, of an individual, but note that an animal may show direction or endpoint behavior in single attempts or even switch strategies within an attempt in some cases. Similarly, in humans, reaches to visible targets use direction-based control to quickly move close to the target and slow down to home in on it with endpoint-based control.76,97
Finally, our reinforcement learning models were purposefully kept simple to test whether model-free agents show endpoint- and direction-learning biases. More complex models and models using model-based reinforcement learning may be able to capture more aspects of the mouse behavior. And models using biomechanical actuators instead of a point mass in space may produce trajectories more like those of mice.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Alice C. Mosberger (acm2246@columbia.edu).
Materials availability
This study did not generate new unique reagents.
Headbar design for head-fixation will be made available upon request. TeenScience control board design is available on github. com/Columbia-University-ZMBBI-AIC/Teenscience and has been deposited at https://doi.org/10.5281/zenodo.10685557. SCARA joystick hardware design and 3D printing design of the head-fixation cup (https://innovation.columbia.edu/technologies/CU21353) have been deposited at https://doi.org/10.5281/zenodo.10685557. All DOIs are listed in the key resources table.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Bacterial and virus strains | ||
|
| ||
| AAVretro(SL1)_Syn_GCamp6f | Janelia, custom prep AAVrg (Chen et al.)98 | Addgene Cat# 100837 plasmid; RRID:Addgene_100837 |
| AAVretro_Syn_GCamp7f | (Dana et al.)99 | Addgene Cat#104488-AAVrg; RRID:Addgene_104488 |
|
| ||
| Chemicals, peptides, and recombinant proteins | ||
|
| ||
| NeuroTrace™ 640/660 Deep-Red Fluorescent Nissl Stain | ThermoFisher Scientific | Cat#N21483 |
| Rose Bengal | Sigma Aldrich | 330000; CAS: 632-69-9 |
| D-Sucrose | Fisher Scientific | BP220-1; CAS: 57-50-1 |
| Dental Cement, C&B Metabond Quick Adhesive | Parkell | N/A |
| Super glue, Loctite Superglue Gel | Loctiteproducts.com | N/A |
| Accelerant, Zip Kicker | Robart.com | N/A |
| Optical glue, Norland Optical Adhesive 63 | Norlandprod.com | N/A |
|
| ||
| Deposited data | ||
|
| ||
| Data used to produce figures, behavior data, and metadata | This paper | zenodo: https://doi.org/10.5281/zenodo.10685557 |
|
| ||
| Experimental models: Organisms/strains | ||
|
| ||
| C57BL/6J mice | The Jackson Laboratory | RRID:IMSR_JAX:000664 |
|
| ||
| Software and algorithms | ||
|
| ||
| Spatial Target Task code | This paper | zenodo: https://doi.org/10.5281/zenodo.10685557 |
| Analysis code | This paper | zenodo: https://doi.org/10.5281/zenodo.10685557 |
| Reinforcement learning model code | This paper | zenodo: https://doi.org/10.5281/zenodo.10685557 |
| BrainJ | (Botta et al.)70 | https://github.com/lahammond/BrainJ |
| Imaris 9 | Oxford Instruments | http://www.bitplane.com/imaris/imaris; RRID: SCR_007370 |
| Lightning Pose | (Biderman et al.)71 | https://github.com/danbider/lightning-pose |
| NeuroCAAS | (Abe et al.)100 | https://www.neurocaas.org/ |
| Grid.ai | https://www.grid.ai/ | N/A |
| Bonsai | https://open-ephys.org/bonsai | https://github.com/bonsai-rx/bonsai |
| MATLAB | Mathworks, Inc. | R2019b/R2020a |
| CircStat for MATLAB | (Berens et al.)101 | https://github.com/circstat/circstat-matlab |
| Python | Python.org | 3.7.8 |
| Scikit-learn | https://scikit-learn.org/stable/ | N/A |
| Datajoint | (Yatsenko et al.)102 | 0.13.0 |
| GraphPad Prism | www.graphpad.com | 9.5.1/10.1.0 |
|
| ||
| Other | ||
|
| ||
| Cup for head-fixation 3D printing file | http://innovation.columbia.edu/technologies/CU21353 | zenodo: https://doi.org/10.5281/zenodo.10685557 |
| SCARA joystick 3D printing files and machining files | This paper | zenodo: https://doi.org/10.5281/zenodo.10685557 |
| DC-motors/encoders | Maxon Motors, Inc. | DC-MAX26S GB KL 24V, ENX16 EASY 1024IMP |
| TeenScience, Arduino Teensy 3.6 breakout board | https://github.com/Columbia-University-ZMBBI-AIC/Teenscience | zenodo: https://doi.org/10.5281/zenodo.10685557 |
| Teensy 3.6 | https://www.pjrc.com/store/teensy36.html | N/A |
| Solenoid | The Lee Company | LFVA1220310H |
| USB Camera, ELP USB Camera 1080p | Webcamerausb.com | N/A |
| Lens, Xenocam 3.6mm, 1/2.7″ lens | Amazon.com | N/A |
Data and code availability
Histological raw data of coronal brain sections and processed ‘BrainJ’ output data will be shared by the lead contact upon request. Raw video and tracked key point data will be shared by the lead contact upon request. Metadata, behavior data, and data used to produce figures have been deposited at https://doi.org/10.5281/zenodo.10685557.
Original task code has been deposited at https://doi.org/10.5281/zenodo.10685557. Code implementing reinforcement learning models has been deposited at https://github.com/murray-lab/RL_Reacher and https://doi.org/10.5281/zenodo.10685557. Original data analysis code has been deposited at https://doi.org/10.5281/zenodo.10685557.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
EXPERIMENTAL MODEL AND STUDY PARTICIPANT DETAILS
All experiments and procedures were performed as approved by the Institutional Animal Care and Use Committee of Columbia University. Data of 21 male C57BL/6J wild type mice is shown. All animals were 3–4.5 months old at the beginning of behavior training and maximum 8 months old at the conclusion of the experiment. All animals were single-housed after headbar implantation surgery and during the whole period of the behavior training. 10 animals were used to compare performance in the cup or tube (n = 5 per group). 8 animals were used in the main target training experiment with 6 animals being trained in 4 blocks, and 2 animals in 3 blocks. Cortex stroke lesions were performed in 5 of those animals. Data from an additional 3 animals is shown where we compare the performance before and after whisker trimming. These animals and the 8 animals used in the main target training experiment were also injected with retrograde adeno-associated virus (AAV) and implanted with cranial windows over the left forelimb motor cortex for use in a 2-photon imaging study. However, the main 8 animals were not used for 2-photon imaging because of insufficient viral expression or bone regrowth under the window and were instead used for behavior experiments according to 3R Animal Use Alternatives guidelines (USDA) to reduce the number of animals used in research. No difference in task performance was found between animals that were injected in different areas (Figures S6A and S6B). As only male mice were used, we cannot draw any conclusions on the effect of sex on the results, which is a limitation of the study.
METHOD DETAILS
General surgical procedures and headbar implantation
Surgeries were performed under aseptic conditions. All tools were autoclaved and sterile surgical gloves were used during all procedures. Animals were anesthetized with Isoflurane (2% in oxygen). Buprenorphine SR was administered (1 mg/kg) before the surgery subcutaneously. The scalp was shaved using clippers and animals placed in a stereotaxic frame with cheek bars. Eye cream was applied and the skin cleaned with ethanol and Iodine ointment (BetadineⓇ) swabs. The scalp was removed using spring scissors and the skull cleaned and dried by applying 3% hydrogen peroxide and scraped with a scalpel blade. Dental cement (C&B Metabond Quick Adhesive) was applied to the exposed skull to build a cement cap and the metal headbar was implanted securely into the dental cement. Once the cement was dry the mouse was removed from the stereotaxic frame and placed into a clean cage on a heat mat and monitored until fully ambulating. A custom headbar design was used with small U-shaped ends on either side of the straight bar that allowed easy securing of the mouse’s head in the head-fixation holders by tightening a screw through the U-shaped ends. The headbar implantation was combined with the cranial window surgery for animals that had windows implanted.
AAV INJECTIONS
Animals were injected with AAVretro(SL1)_Syn_GCamp6f98 (1.3e13 GC/ml, Janelia) or AAVretro_Syn_GCamp7f99 (1.0e13 GC/ml, lot #21720; 1.2e12 GC/ml, lot #v52598, Addgene 104488-AAVrg) in the right dorsolateral striatum (DLS) (0.75 mm anterior, 2.55 mm lateral, 3.2 mm ventral of bregma, 100 nL), or the right cervical spinal cord (segments C4-C7/8, 0.5 mm lateral of central blood vessel, −0.9 to −0.5 ventral of surface, 60–75 nL per segment) (Table S1). All injections were made in a stereotaxic surgery through blunt glass pipettes mounted to a Nanoject (Nanoject III, Drummond). Injections in the DLS were made through a small craniotomy at the time of the cranial window implantation and the craniotomy sealed using superglue (Loctite Superglue Gel) and accelerant (Zip Kicker). Injections in the cervical spinal cord were performed in a separate surgery one week before the cranial window implantation. The animal was placed in a stereotaxic frame. A 1.5 cm skin incision was made from the back of the skull to the shoulder blades using a spring scissors. The acromiotrapezius muscle was cut sagittally along the midline for a few millimeters and the muscle retracted. The spinalis muscles were blunt dissected to gain access to the cervical vertebrae and the T2 thoracic process which was clamped to stabilize the spinal cord. The ligaments between the laminae were removed using forceps and the spinal segments injected through the intra-laminar space. The acromiotrapezius muscle was sutured using absorbable sutures (5/0) and the skin sutured with silk (5/0) sutures.
Cranial window implantation
A 3 mm diameter biopsy puncher was used to mark a circle centered on 1.5 mm lateral/0.6 mm anterior of bregma over the left hemisphere. The circle was carefully drilled and the bone removed using forceps. The craniotomy was cleaned with sterile saline and a glass window (2 circular coverslips 5 mm and 3 mm radius glued together using optical glue (Norland Optical Adhesive 63, Lot 201) was placed over the craniotomy and glued to the skull using superglue and accelerator. Dexamethasone (1 mg/kg) was administered after the surgery to prevent brain swelling.
Sensorimotor cortex photothrombotic lesion
Rose bengal (Sigma Aldrich (330000)) was freshly diluted in sterile saline (10 mg/mL) and kept on ice and in the dark. Animals were anesthetized with Isoflurane and placed in a stereotaxic frame using cheek bars. The cranial window was cleaned with water and ethanol using q-tips and an opaque foil template with a circular hole of 3 mm diameter was placed over the cranial window. A cool light source (Schott KL 1600 LED) was attached to the arm of the stereotaxic frame and lowered on top of the cranial window. An intraperitoneal injection of 35 mg/kg Rose Bengal was performed and 6 min later the light source was turned on for 2–3 min at 3 Watt at 400 nm. After the light exposure the animal was removed from the stereotaxic frame and placed in a fresh cage. Rose bengal bioavailability was confirmed by inspecting the animals’ feces for a red tint the next day.
Stroke histology and reconstruction
Animals were anesthetized deeply with Isoflurane and transcardially perfused with 0.1M PBS and 4% Paraformaldehyde (PFA). Brains were extracted and post-fixed for 24 h in 4% PFA and then cut in coronal sections of 75 μm thickness on a vibratome. Sections were counterstained on slide using NeuroTrace 640 (ThermoFisher Scientific (N21483)) according to the manufacturer’s protocol, and then coverslipped in Mowiol. Brain sections were imaged on a Nikon AZ100 Multizoom slide scanner (Zuckerman Institute’s Cellular Imaging platform) at 1 μm/pixel resolution using a 4x objective. Images of full brain sections from the slide scanner were registered and transformed into a 3D volume which was aligned to the Allen Reference Brain Atlas (ABA) using BrainJ.70 This maps the histological sections onto the ABA. The aligned sections were imported to Imaris 9 (Oxford Instruments) and the green autofluorescence, that was acquired at 488/515 nm excitation/emission, was used to manually delineate the lesioned area and render the total lesion volume. The lesion volume was mapped back to the ABA and custom MATLAB (R2020a, Mathworks, Inc.) code was used to calculate the proportion of the areas of the ABA affected by the lesions.
Video analysis of hand/joystick interactions after stroke
Videos of animals before and after the cortex stroke lesion were used to train a pose estimation model (lightning pose71) to track 2 key points: the base of the joystick, and the wrist of the mouse’s right hand. The joystick key point was chosen at the bottom left corner of the joystick spacer which had good contrast for high-fidelity tracking. We labeled 1132 frames (1077 frames from prior cohorts and 55 frames from experiments reported here) across 51 sessions (44 sessions from 10 animals in prior cohorts and 7 sessions from 5 animals that received strokes in experiments reported here) using a custom labeler tool through amazon web service via Neuroscience Cloud Analysis As a Service (NeuroCAAS100), and trained a supervised model on Grid.ai.
Key point coordinates were analyzed by first removing all low-fidelity points with a likelihood of less than 0.99. Periods of active joystick movements in the x-dimension of the video frame were analyzed and the distance in x between the wrist and the joystick key points calculated for each animal and session. The pixel dimension was converted to mm for each video using a known distance in the frame close to the mouse’s hand (the front dimension of the cup). The calibrated average distance between the wrist and the joystick and its standard deviation was calculated for all animals and sessions. Since the wrist coordinate was subtracted from the joystick coordinate, positive distance values indicate that the wrist was located behind the joystick (closer to the mouse’s body), and negative values indicate the wrist was located in front of the joystick (further away from the mouse’s body).
Joystick hardware and spatial target task controls
The SCARA (Selective Compliance Articulated Robot Arm) joystick setup was built from commercial Thorlabs parts and custommade acrylic or 3D printed pieces. Animals were head-fixed in either an acrylic tube (40 mm diameter, with a 45° angled opening at the front) or in a custom-designed 3D printed cup (copyright IR CU21353), and their headbar was positioned 23 mm above the tip of the joystick, offset slightly to the left and back for comfortable interaction of the right limb with the joystick. A metal screw was placed horizontally to the left of the joystick to be used as arm rest for the left limb. A lick spout (16 Gauge blunt needle) was placed in front of the mouth of the animal, connected through tubing to a solenoid (The Lee Company, LFVA1220310H) to dispense the reward. The solenoid also made an audible click sound upon opening acting as a reward signal. Animals were filmed from the right side at 30 Hz under infra-red light (USB Camera, 2.0 Megapixel, with a Xenocam 3.6mm, 1/2.7″ lens). The SCARA joystick arms were 3D printed (Formlabs Form 2 resin) and manually assembled with shielded stainless steel ball bearings (McMaster-Carr, 7804K119) and shafts. The arms were linked at the front through a threaded shaft to which a metal M2 screw was mounted using a female spacer. The head of the screw served as the manipulandum for the mouse to hold and move the joystick with its hand. The 3D printed SCARA arms were attached to custom designed metal hinges that were mounted onto the shaft of the DC-motors which had integrated encoders (DC-MAX26S GB KL 24V, ENX16 EASY 1024IMP, MAXON Motors, Inc.). The motors were mounted on an acrylic platform which was positioned on a Thorlabs breadboard using Thorlabs parts. Dimensions of the SCARA arms were as follows: back arm length = 50 mm, front arm length = 35 mm, distance between motor shafts = 60 mm.
Static friction and effective mass at the end-effector (joystick) were measured under end-effector control at 5000 Hz. End-effector position and force were saved at 1000 Hz for offline analysis. Velocity was calculated offline using a Butterworth Filter with a cut-off frequency of 20 Hz. For static friction, brief force pulses (500 msec) of increasing magnitude (0.25–10 g, 0.25 g increments) were generated at the end-effector across 8 equally-spaced directions, with 10 repeats for each force magnitude and direction. Before each measurement, the end-effector was returned to the start position (within a radius of 1 mm, as in the main experiments). Static friction for each direction was measured as the force magnitude at which the end-effector velocity exceeded 10 mm/s. The values for each direction were then averaged across the 10 repeats. For effective end-effector mass, the SCARA was mounted vertically so that gravity acted downwards on the components of the arm. A stiff spring (10 g/mm) was simulated to hold the end-effector in the start position. Measurements of force were taken across 8 different directions and with 5 values of added weight (0, 5, 13, 22, 35 g). End-effector static friction and effective mass were measured for 4 of the SCARA used in the experiments and for each measure and each SCARA ellipses were fit to the force vectors obtained from the 8 directions (example SCARA, Figures S6C and S6D). Across all directions and the 4 SCARA, the static friction was 4.75 ± 0.43 g and the effective end-effector mass was 14.43 ± 0.43 g. As expected, both measures exhibited a degree of anisotropy. This was relatively low for static friction, as shown by the ratio of the major and minor axes of the ellipses (1.19 ± 0.05) and the small difference in static friction between orthogonal directions (1.20 ± 0.54 g). In contrast, end-effector mass exhibited higher anisotropy (major/minor axes ratio 1.88 ± 0.08), resulting in a larger difference between orthogonal directions (8.94 ± 0.76 g). The method used to measure end-effector mass (with increasing weight added to the end-effector) also allowed us to verify the calibration of force using linear regression (mean gains of 1.10 ± 0.02, R2 values from 0.98 to 1.00, across directions and SCARA).
A capacitive touch sensor was connected to the bottom of the joystick shaft and to the cannula of the lick spout to allow detection of joystick touch and licking. The STT was controlled through a microcontroller board (Teensy 3.6, Arduino) and custom breakout board (TeenScience, github.com/Columbia-University-ZMBBI-AIC/Teenscience). All task designs were written using the Arduino IDE. Touch sensors were read at 40 Hz. The main task loop (2 kHz) recorded the encoder positions, calculated the Cartesian coordinates of the joystick through forward kinematics, and triggered task states depending on the joystick position and touch sensor inputs. Angular positions were measured from the encoders with a resolution of 0.09°. This gave a resolution of 0.06 ± 0.02 mm for joystick position across the workspace (Figure S6E). The joystick was actively moved to the start position and maintained at the start position by a proportional integral derivative (PID) algorithm running via interrupt functions and also operating at 2 kHz. Briefly, to move the joystick to the start position, the angular position of both encoders was compared with the start position (in angle space). Differential values were calculated to produce a driving pulse width modulation signal which was sent to the motors via the H-Bridge power amplifiers included on the TeenScience board. This control signal was calculated and recorded in torque space. To implement an inter-trial-interval (ITI, see below), a maximum force threshold was set in torque space resulting in joystick end-effector force thresholds between 7 and 11g (Figures S6F, S6M and S6N). The mice were required to remain below the force threshold for 100 msec before starting a new attempt. The motors were disengaged and no forces were generated during the active exploration of the workspace by the mice. The joystick position and all task events were recorded via serial output commands through Bonsai (OpenEphys). With all the closed-loop control being performed on the Teensy microcontroller, 4 setups were run on a single standard computer (ASUS, Intel i7 CPU, 16 GB RAM). A total of 13 setups were used across all experiments.
Spatial target task design
Starting on the day before behavior training began, animals were food restricted overnight and then given an individualized amount of chow food after each training session to maintain their body weight at 80% of pre-training baseline. Each session lasted until a maximum number of rewards were achieved. But a maximum time of 150 min was allowed and sessions were ended earlier if the animal stopped making attempts or didn’t consume the reward for an extended period of time, which happened mostly during pre-training. The average duration of a pre-training session was 21 min, and a target training session 33 min. The reward delivered from the lick spout was a 10 μL drop of 7.5% sucrose (D-Sucrose, Fisher Scientific, BP220-1) in water.
Pre-training
Pre-training consisted of 4 days of Phase 1, and 5 or more days of Phase 2 (Figure 1E). For both pre-training and target training, animals could perform movements with the joystick in a self-paced uncued manner. The joystick was initialized at the beginning of the session at a fixed start position (0/65 mm from the motor axis, 1 mm radius). Once head-fixed, the animal could move the joystick out of the start position and explore the workspace without any force generated by the motors for 7.5 s per attempt. In Phase 1 of pre-training, a reward was given independent of the joystick position, upon initial touching of the joystick (with a delay of 500 msec on days 1 and 2 and 1000 msec on days 3 and 4) and at random intervals between 5 and 15 s for continuous touching of the joystick. The session ended after 100 rewards were delivered.
For both Phase 2 and the target training, animals had to move the joystick out of the start position and explore the workspace to receive a reward. If the exploration of the 2D space did not lead to a reward within 7.5 s or if the mouse let go of the joystick for > 200 msec, the attempt ended, the motors engaged, and moved the joystick back to start position (Figure 1C, miss). If the criteria for a reward was met, a reward was delivered and after a 750 msec delay the motors engaged and moved the joystick back to the start position (Figure 1C, hit). In Phase 2 a reward was given for moving the joystick in a forward direction initially within a 100° then a 60° segment for at least 4 mm. The reward was delayed randomly between 15 and 50 msec upon reaching the required radius. The session initially ended after 50 rewards and as performance improved after 100 rewards. The animal progressed to target training if it reached a rewarded attempt ratio of > 0.5 at the 60° segment. Using the rewarded trajectories on the last day of Phase 2, 2 target locations were defined for each animal as follows (Figure 1D). The mean initial direction of all rewarded trajectories was calculated and a target center defined 40° to the left and right of the mean direction at 8 mm distance from the start position. The target radius was set at 2.75 mm. The initial hit probability was not different between the two targets (Figures S6O).
Target training
During any given block in the target training, one of the 2 defined targets was rewarded. If a joystick movement entered the target circle a reward was instantaneously delivered. We did not delay the reward as we found it impaired learning in our mice in pilot experiments. In a similar task in humans, delaying the reward even by a few 100 msec also severely impaired learning.103 Once the joystick was returned to the start at the end of a rewarded (hit) or unrewarded (miss) attempt, an inter-trial-intervaI (ITI) started during which the joystick was continuously held at the start position by the motors until the animal exerted less than 7–11 g (average 8.2 g) force against the joystick in any direction for a minimum of 100 msec (hold period) (Figures S6F, S6M and S6N). Animals were not required to touch the joystick during the hold period, but analysis of the touch sensor showed that they mostly did (Figures S6H, S6K and S6L). At the end of the hold period the motors disengaged and the animal was allowed to initiate a new attempt by moving the joystick out of the start position (post-hold period) (Figures S6G, S6H and S6J). No cue was given that the hold period had ended. The first 2 sessions in each block were completed after 50 target hits were achieved, the next 2 after 100 hits, and the rest after 150 hits. Each movement of the joystick out of the start position was counted as an attempt and task performance was calculated as the number of attempts entering the target circle (hits) divided by all attempts (hit ratio). When an animal reached a 3-day average hit ratio of > 0.65, and had received at least 900 rewards over a minimum of 8 sessions, the target was changed in the next session and a new block began (performance criterion). During the first block, target 1 (lateral to the animal’s body axis) was rewarded in all animals. For the comparison between animals positioned in the cup or the tube, we also defined a termination criterion. If an animal was trained for 10 days on a target without ever exceeding a 3-day average of 0.1 hit ratio, or if an animal did not reach the performance criterion within 21 days, the block was ended. Three animals from the tube group reached the termination criterion and were consecutively switched to be trained in the cup for a within animal comparison (Figures S1H–S1K).
Start change probe test
The probe test was performed after performance criteria was reached on target 1 either in block 3 or in an additional shorter block 5. For each animal, two new start positions were defined by rotating the original start position (0/0 mm) 40° to the left (left start) and right (right start) around the target center, such that the distance between start and target was maintained but the direction to the target was changed. In the probe test session, the original start position was used for the first 10 hits to allow the animal to settle into the session. Then the joystick returned to either the left or right new start position to begin the first probe trial. During the probe trial, the animal could make multiple attempts to hit the target but to prevent learning from reinforcement, the probe trial ended after the target was hit from the new start position and the joystick returned to the original start position for 5–10 hits before the next probe trial. The order of left and right start positions chosen for the probe trials was randomized. If no hit was achieved in a probe trial within 5 min, the probe trial was ended and the joystick returned to the original start position. The probe test was completed when the animal achieved 200 rewards. The number of probe trials across all animals was 14.5 ± 3.2 for the left start and 13.5 ± 2.7 for the right start (Figure S5H). In all probe trials animals performed an average of 32.5 ± 16.5 attempts from the left start and 52.8 ± 82.4 attempts from the right start (Figure S5I), with a median number of attempts from the right of 16.
Additional behavior tests
Three additional animals that were trained in the STT under a 2-photon microscope were used to test the requirement of whiskers for task performance. Animals were trained on a baseline day at expert level on target 1, after the training session animals were briefly anesthetized using Isoflurane and all their whiskers on both sides were cut to a length of about 2–3 mm using scissors. Animals were placed in their home cage to recover from the anesthesia and tested in the task again the next day.
Analysis of joystick data
For the main target training experiment, data of 5 selected days per block is shown. For each block that includes the first and the last day, and 3 equidistant days in between to span the whole block. Data was analyzed for all blocks and a mixed-effects repeated measures model was used to determine if there was a significant effect of the day in the block (p < 0.05), but not of the block itself (Table S2). Only if there was no significant effect of the block itself (p > 0.05), the data was then combined by averaging the selected days across all blocks for each animal. Blocks of target 1 took more days to reach the criterion than blocks of target 2 (Figure S2C). However we found no significant savings effect of target repetition (Mixed-effects model, block: F(1,7) = 4.29/4.32, p > 0.05).
ITI force analysis
End-effector forces of the joystick were calculated from the value of two analog signals recorded from the TeenScience board. These analog voltages were linearly related to the absolute torque generated at each motor. Calibration of the analog Volts to motor torques was performed using a single axis version of the joystick (with a single 35 mm link). The TeenScience board was programmed to simulate a simple un-damped spring, and the analog Volts associated with various weights were recorded (2, 5, 10, 13 g). The conversion factor from Volts to motor torque was obtained from a linear regression. Joystick forces for each data sample were then calculated from the calibrated motor torques using the forward dynamics of the SCARA. The ITI was divided into 3 periods: pre-hold (Figure S6I), hold, and post-hold (Figure S6J). During the pre-hold and hold periods, the joystick was maintained inside the start circle by the motors. The pre-hold period continued until the force was below the 7–11 g threshold. Only pre-hold periods of 10 msec duration or more were analyzed and the average force was calculated across this window (Figures S6F and S6M). If the force on the joystick was below the threshold when the ITI began, the hold period was entered immediately. The hold period was defined as a 100 msec window during which the force on the joystick remained below the threshold. The average force during the hold period was also calculated and was below 1 g on average (Figures S6F and S6N). The post-hold period followed the 100 msec hold period, during which the motors were disengaged. The post-hold period ended when the animal initiated a new attempt, moving the joystick outside the start position. The probability of touch during the ITI was calculated by determining for each time sample whether the touch sensor was active or not and averaging across the entire period (Figures S6H, S6K and S6L).
Preprocessing of trajectories
Trajectories sampled at 500 μsec intervals were downsampled to 6 msec intervals for ease of handling the data.
Trajectories used for quantification
For each attempt a joystick trajectory was recorded. To quantify aspects of refinement of the rewarded attempt, only trajectories that entered the target area (hits) were analyzed. Furthermore, of those hit trajectories, only the path from start to the point of target entry was used in the analysis, as movements performed during reward consummation and voluntary returning to the start position were not considered part of the reinforced movement. For all metrics of variability, 50 trajectories were subsampled for all sessions unless there were less than 50 trajectories available. Analyses on pre- and post-cortex stroke lesion sessions were performed on full length trajectories of all attempts, to assess the overall movement differences, and because the small number of hits post-stroke did not allow analysis of hits only. For trajectory similarity analysis pre- and post-stroke, hit trajectories from start to the point of target entry were used.
Area visited
For the quantification of the area explored, the workspace (40 × 40 mm centered around the start) was divided into 1 × 1 mm bins and for each trajectory the bins visited were calculated using the MATLAB ‘histcount2’ function. Bin counts for all trajectories were summed up and binarized to discount dwell time per bin and multiple visits to each bin. The total number of visited bins is reported as the area visited. In the experiment comparing animals trained in the cup or tube, the analysis was limited to the workspace in the forward direction of the start position 40 × 23 mm as the workspace behind the start position was smaller for animals trained in the tube.
Mean trajectory variability
The full trajectories were downsampled to 200 points each and mean trajectory calculated by averaging along the 200 points across all trajectories. The standard deviation was calculated as the square root of the squared shortest distance to the mean trajectory of all trajectories at each point, divided by the number of trajectories. The average standard deviation along the 200 points was used as metric for the mean trajectory variability.
Tortuosity
For each trajectory the total path length was calculated and divided by the Euclidean distance between the first and the last point of the path. For each session the average tortuosity was calculated.
Vector field analysis
The workspace was divided into 1 × 1 mm bins. For each trajectory the vector going from one bin to the next along the trajectory path was recorded and assigned to the corresponding bin. If the same trajectory passed through a bin more than once, a separate vector was recorded for each pass-through. If the trajectory stopped inside the bin and then continued, the combined vector was recorded. For each bin, the vectors for all trajectories of a session were concatenated and bins with less than 3 vectors (or 2 vectors for pre/post stroke data) were excluded. For the remaining bins, the vector angles were calculated using the ‘atan2’ MATLAB function. The mean vector angle and angular standard deviation (bounded between the interval ) was calculated using the CircStat circular statistics toolbox101 functions ‘circ_mean’ and ‘circ_std’. Mean angles and angular standard deviations were used to plot vector field and heatmap figures. The size of the heatmap dots was scaled according to the number of visits to each bin. The bin-wise angular standard deviation was then weighted by the number of visits to that bin and the mean of these weighted values was calculated as an overall metric for spatial directional variability within a session.
Trajectory similarity
The Fréchet distance (FD) was calculated as a scalar measure of similarity between trajectories. The Fréchet distance can be conceptualized as the shortest leash possible to allow a person to traverse one path while their dog traverses the other. Each can vary their speed but neither can move backwards, thus measuring similarity between the shape of their trajectories while disregarding differences in speed. For each animal, the trajectories for all selected sessions were concatenated and the discrete FD between all pairwise trajectories was calculated using the ‘DiscreteFrechetDist’ MATLAB function.66 The FD is 0 for two trajectories that follow the same exact path even if their speed profile is different. For each animal and session the mean within session FD was calculated and compared across blocks. The FD of trajectories from different sessions within each block was also calculated and averaged across animals to show as heatmaps.
Peak speed
The speed of the downsampled (6 msec interval) trajectory was smoothed using a 30 msec moving average (‘smooth’ function in MATLAB). For analyzed hits, only the trajectory from the start until entering the target was considered. The maximum value of the smoothed speed was calculated for each trajectory and averaged across all trajectories of a session (peak speed) and the standard deviation calculated as well (peak speed stdev).
Time spent at target
Time spent in and 1 mm around the target after the target was entered was measured for each hit and the median per session calculated.
Target overshoot
The target overshoot was calculated as the path length between the point of the trajectory entering the target and the end of the trajectory, when motors engaged (750 msec after entry). For each session the standard deviation of the target overshoot was calculated as a metric of targeting variability.
Initial vector direction
The initial trajectory vector was defined from the point at which the trajectory left the start circle (1 mm radius) to the point of it crossing a circle of 3.75 mm radius from the start position center. The components of all vectors were averaged to calculate the mean vector per session. For each vector and the mean vector the angle was calculated using the ‘atan2’ MATLAB function, subtracted from the angle leading straight to the target center, and the absolute value reported (initial direction). The angular standard deviation across all vectors was calculated using the ‘circ_std’ function (see ‘Vector field analysis’).
Vector of target entry
The direction at which the target was entered was calculated by taking the vector from the point of the trajectory crossing a circle 1 mm bigger than the target itself to it crossing the target border. The angle of this vector was subtracted from the angle leading straight from the start position to the target center and the absolute was reported. The angular standard deviation was calculated as for the initial vector direction.
Quantification of endpoint-direction learner bias
To assess the degree to which animals moved toward the target or in their learned original direction from the probe start positions, we determined the mean initial vector direction from the original start position measured at 3.2 mm radius around the start center (original direction, ). For the left and right probe start positions the angle of the vector pointing to the center of the target was also determined (target direction, ). Depending on the nature of an animal’s original direction, the difference between the and was not the same for the left and right probe start position, requiring different adjustments of the original direction to hit the target from the probe starts. To correct for this we calculated a weighting factor w for each probe start . For all attempts an animal made from a probe start during all probe trials combined, the mean initial vector direction was then determined . was subtracted from and from to determine how close the reach direction during probe trials was to the original direction or the target direction . These were then subtracted from each other and multiplied by the weighting factor, resulting in a final signed angle for each probe start . The sign of indicates whether the probe reach direction was closer to the original or the target direction. The signed from both left and right probe start positions were averaged to calculate in a final angle . If , the attempts from the probe starts were overall closer to the original direction than the target direction, which was considered a ‘direction’ bias. If , the attempts from the probe starts were overall closer to the target direction than the original direction, which was considered an ‘endpoint’ bias. The magnitude of indicated the degree of the bias.
Bootstrapping and calculation of p value for endpoint-direction learner bias
The initial direction angle was calculated for all reaches from each start position, sampled with replacement 10′000 times using MATLAB’s ‘bootstrp’ function, and the mean angle calculated using the ‘circ_mean’ function, resulting in 10′000 mean angles per start. The 95% confidence interval (CI) of the mean angles from the original start position was calculated using the MATLAB function ‘bootci’. To determine whether the distribution of mean angles from the left or right probe start was significantly different from the distribution of mean angles from the original start, we calculated the ratio of the distribution of means that was smaller than the upper CI, or larger than the lower CI, respectively. This ratio was used as the p value.
Reinforcement-learning model
The reinforcement-learning model was implemented in custom Python code. The model consisted of an agent trained with reinforcement learning to map a 5-dimensional state representation onto actions that maximize reward. To create a more useful state representation for the agent, the first 4 components of the state vector (the agent’s position and velocity) were randomly projected via untrained weights onto a set of 99 radial basis functions, and the last component of the state vector, which had amplitude in the first timestep and was zero in subsequent timesteps, was concatenated onto this state representation. The radial basis functions had Gaussian kernels of width (in the spatial dimensions) 1/4 times the width of the arena, and (in the velocity dimensions) 1/16 times the width of the arena (where the timestep size relating position to velocity was ). The 2-dimensional action then consisted of a linear readout from this basis via trained weights, added together with exploratory noise . The noise was correlated from one time-step to the next and was given by , where is the noise amplitude, is the noise correlation time, and .
The action consisted of a force applied to the agent, which influenced the agent’s velocity according to Newtonian dynamics. Specifically, the agent’s position at each timestep was updated as , and the agent’s velocity was updated as . The arena boundaries were impenetrable, such that the agent could move along the boundary but not beyond it. The reward was for each timestep that the target area was not reached, and 1 if the target area was reached. Each trial was completed when the target area was reached or, if the target area was not reached, after timesteps. To prevent the trivial solution in which the agent produces a very large action to reach the target in a single timestep, the agent received a negative reward contribution .
The agent’s weights were trained using actor-critic learning with learning rate to maximize the expected sum of future rewards, with temporal discount factor . The critic learned the value associated with each state via a separate linear readout from the radial basis function representation. To facilitate credit assignment over multiple timesteps, eligibility traces were used in both the actor and critic, with time constants .
In cases where the hyperparameters were chosen randomly, they were sampled uniformly from the range , , , . In cases where the hyperparameters were fixed, they were set to , , , and . Only agents that met a performance criterion of reaching the target in 90% of the last 25% of trials were used for subsequent analysis.
In the multivariate regression model, the four hyperparameters listed above were used as regressors in a leave-one-out ridge regression model using RidgeCV from the Python scikit-learn library. The model was fit on data from 80% of the trained agents and tested on the remaining 20%, and the results shown in Figure 6 illustrate the test performance across the possible data splits.
QUANTIFICATION AND STATISTICAL ANALYSIS
All data was analyzed using custom MATLAB code (MATLAB engine for python R2019b, Mathworks, Inc.) run from a Python analysis pipeline (Python 3.7.8) through a DataJoint database (datajoint 0.13.0)102. One-way ANOVA with repeated measures and Dunnett’s or Bonferroni’s correction for multiple comparison, mixed-effects repeated measures models, simple linear regression, Spearman correlation, and paired and unpaired t-tests were used for statistical analysis and performed in GraphPad Prism (9.5.1/10.1.0). Ridge regression was performed using RidgeCV from the Python scikit-learn library. A p value of less than 0.05 was considered statistically significant, and p values are reported as > 0.05 (not significant, n.s.), < 0.05, and < 0.01. Statistical details of experiments can be found in the results section and figure legends, and in Table S2.
Supplementary Material
Highlights.
Mice explore and refine forelimb reaches to hidden spatial targets
The sensorimotor cortex is required for variable target reaching
Probe trials showed that individual mice have direction or endpoint biases
The degree of variability early in learning correlates with direction/endpoint bias
ACKNOWLEDGMENTS
We thank Luke Hammond and Darcy Peterka from the Zuckerman Institute’s Cellular Imaging platform for guidance with image analysis using Imaris and BrainJ, and for providing the cold light source to induce strokes. We thank Dan Biderman and Matthew Whiteway for their support using lightning pose. We thank Mariana Correia for mouse colony management and Matteo Farinella for help with the design of the graphical abstract. This research was supported by NIH BRAIN Initiative NINDS K99NS126307 (to A.C.M.), NIH NINDS F31NS111853 (to L.J.S.), NIH NINDS K99NS128250 (to V.R.A.), NIH NIMH F32MH118714 (to V.R.A.), NIH NINDS R00NS114194 (to J.M.M.), NIH BRAIN Initiative NINDS U19NS104649 (to R.M.C. and D.M.W.), Swiss National Science Foundation Postdoc fellowship P2EZP3_172128 (to A.C.M.), Swiss National Science Foundation Postdoc fellowship P400PM_183904 (to A.C.M.), and Simons-Emory International Consortium on Motor Control (to R.M.C.). Imaging was performed with support from the Zuckerman Institute’s Cellular Imaging platform. 3D printing and laser cutting were performed with support from the Zuckerman Institute’s Advanced Instrumentation platform.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2024.113958.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- 1.Flash T, and Hogan N (1985). The coordination of arm movements: an experimentally confirmed mathematical model. J. Neurosci. 5, 1688–1703. 10.1523/JNEUROSCI.05-07-01688.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Raichin A, Shkedy Rabani A, and Shmuelof L (2021). Motor skill training without online visual feedback enhances feedforward control. J. Neurophysiol. 126, 1604–1613. 10.1152/jn.00145.2021. [DOI] [PubMed] [Google Scholar]
- 3.Hwang EJ, and Shadmehr R (2005). Internal models of limb dynamics and the encoding of limb state. J. Neural. Eng. 2, S266–S278. 10.1088/1741-2560/2/3/S09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goodale MA, Pelisson D, and Prablanc C (1986). Large adjustments in visually guided reaching do not depend on vision of the hand or perception of target displacement. Nature 320, 748–750. 10.1038/320748a0. [DOI] [PubMed] [Google Scholar]
- 5.Yousif N, and Diedrichsen J (2012). Structural learning in feedforward and feedback control. J. Neurophysiol. 108, 2373–2382. 10.1152/jn.00315.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kasuga S, Telgen S, Ushiba J, Nozaki D, and Diedrichsen J (2015). Learning feedback and feedforward control in a mirror-reversed visual environment. J. Neurophysiol. 114, 2187–2193. 10.1152/jn.00096.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hoogewoud F, Hamadjida A, Wyss AF, Mir A, Schwab ME, Belhaj-Saif A, and Rouiller EM (2013). Comparison of functional recovery of manual dexterity after unilateral spinal cord lesion or motor cortex lesion in adult macaque monkeys. Front. Neurol. 4, 101. 10.3389/fneur.2013.00101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Whishaw IQ (2000). Loss of the innate cortical engram for action patterns used in skilled reaching and the development of behavioral compensation following motor cortex lesions in the rat. Neuropharmacology 39, 788–805. 10.1016/s0028-3908(99)00259-2. [DOI] [PubMed] [Google Scholar]
- 9.Gharbawie OA, Gonzalez CLR, and Whishaw IQ (2005). Skilled reaching impairments from the lateral frontal cortex component of middle cerebral artery stroke: a qualitative and quantitative comparison to focal motor cortex lesions in rats. Behav. Brain Res. 156, 125–137. 10.1016/j.bbr.2004.05.015. [DOI] [PubMed] [Google Scholar]
- 10.Darling WG, Pizzimenti MA, and Morecraft RJ (2011). Functional recovery following motor cortex lesions in non-human primates: experimental implications for human stroke patients. J. Integr. Neurosci. 10, 353–384. 10.1142/S0219635211002737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Guo JZ, Graves AR, Guo WW, Zheng J, Lee A, Rodríguez-González J, Li N, Macklin JJ, Phillips JW, Mensh BD, et al. (2015). Cortex commands the performance of skilled movement. Elife 4, e10774. 10.7554/eLife.10774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Morandell K, and Huber D (2017). The role of forelimb motor cortex areas in goal directed action in mice. Sci. Rep. 7, 15759. 10.1038/s41598-017-15835-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tennant KA, and Jones TA (2009). Sensorimotor behavioral effects of endothelin-1 induced small cortical infarcts in C57BL/6 mice. J. Neurosci. Methods 181, 18–26. 10.1016/j.jneumeth.2009.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Caminiti R, Johnson PB, and Urbano A (1990). Making arm movements within different parts of space: dynamic aspects in the primate motor cortex. J. Neurosci. 10, 2039–2058. 10.1523/JNEUROSCI.10-07-02039.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Georgopoulos AP, Kalaska JF, Caminiti R, and Massey JT (1982). On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J. Neurosci. 2, 1527–1537. 10.1523/JNEUROSCI.02-11-01527.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Georgopoulos AP, Schwartz AB, and Kettner RE (1986). Neuronal population coding of movement direction. Science 233, 1416–1419. 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
- 17.Kalaska JF (2009). From intention to action: motor cortex and the control of reaching movements. Adv. Exp. Med. Biol. 629, 139–178. 10.1007/978-0-387-77064-2_8. [DOI] [PubMed] [Google Scholar]
- 18.Scott SH, and Kalaska JF (1995). Changes in motor cortex activity during reaching movements with similar hand paths but different arm postures. J. Neurophysiol. 73, 2563–2567. 10.1152/jn.1995.73.6.2563. [DOI] [PubMed] [Google Scholar]
- 19.Rickert J, Riehle A, Aertsen A, Rotter S, and Nawrot MP (2009). Dynamic encoding of movement direction in motor cortical neurons. J. Neurosci. 29, 13870–13882. 10.1523/JNEUROSCI.5441-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pruszynski JA, Kurtzer I, Nashed JY, Omrani M, Brouwer B, and Scott SH (2011). Primary motor cortex underlies multi-joint integration for fast feedback control. Nature 478, 387–390. 10.1038/nature10436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Scott SH (2004). Optimal feedback control and the neural basis of volitional motor control. Nat. Rev. Neurosci. 5, 532–546. 10.1038/nrn1427. [DOI] [PubMed] [Google Scholar]
- 22.Pacheco MM, Lafe CW, and Newell KM (2019). Search Strategies in the Perceptual-Motor Workspace and the Acquisition of Coordination, Control, and Skill. Front. Psychol. 10, 1874. 10.3389/fpsyg.2019.01874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Redgrave P, and Gurney K (2006). The short-latency dopamine signal: a role in discovering novel actions? Nat. Rev. Neurosci. 7, 967–975. 10.1038/nrn2022. [DOI] [PubMed] [Google Scholar]
- 24.Fee MS (2014). The role of efference copy in striatal learning. Curr. Opin. Neurobiol. 25, 194–200. 10.1016/j.conb.2014.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shmuelof L, Krakauer JW, and Mazzoni P (2012). How is a motor skill learned? Change and invariance at the levels of task success and trajectory control. J. Neurophysiol. 108, 578–594. 10.1152/jn.00856.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Todorov E, and Jordan MI (2002). Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 5, 1226–1235. 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- 27.Thorndike E (1898). Some Experiments on Animal Intelligence. Science 7, 818–824. 10.1126/science.7.181.818. [DOI] [PubMed] [Google Scholar]
- 28.Santos FJ, Oliveira RF, Jin X, and Costa RM (2015). Corticostriatal dynamics encode the refinement of specific behavioral variability during skill learning. Elife 4, e09423. 10.7554/eLife.09423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fisher SD, Gray JP, Black MJ, Davies JR, Bednark JG, Redgrave P, Franz EA, Abraham WC, and Reynolds JNJ (2014). A behavioral task for investigating action discovery, selection and switching: comparison between types of reinforcer. Front. Behav. Neurosci. 8, 398. 10.3389/fnbeh.2014.00398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stafford T, Thirkettle M, Walton T, Vautrelle N, Hetherington L, Port M, Gurney K, and Redgrave P (2012). A novel task for the investigation of action acquisition. PLoS One 7, e37749. 10.1371/journal.pone.0037749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Georgopoulos AP, Kalaska JF, and Massey JT (1981). Spatial trajectories and reaction times of aimed movements: effects of practice, uncertainty, and change in target location. J. Neurophysiol. 46, 725–743. 10.1152/jn.1981.46.4.725. [DOI] [PubMed] [Google Scholar]
- 32.Dhawale AK, Miyamoto YR, Smith MA, and Ölveczky BP (2019). Adaptive Regulation of Motor Variability. Curr. Biol. 29, 3551–3562.e7. 10.1016/j.cub.2019.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pekny SE, Izawa J, and Shadmehr R (2015). Reward-dependent modulation of movement variability. J. Neurosci. 35, 4015–4024. 10.1523/JNEUROSCI.3244-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wu HG, Miyamoto YR, Gonzalez Castro LN, Ölveczky BP, and Smith MA (2014). Temporal structure of motor variability is dynamically regulated and predicts motor learning ability. Nat. Neurosci. 17, 312–321. 10.1038/nn.3616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hull CL (1943). Principles of Behavior: An Introduction to Behavior Theory (Appleton-Century)). [Google Scholar]
- 36.Tolman EC, Ritchie BF, and Kalish D (1946). Studies in spatial learning: Orientation and the short-cut. J. Exp. Psychol. 36, 13–24. 10.1037/h0053944. [DOI] [PubMed] [Google Scholar]
- 37.Tolman EC, Ritchie BF, and Kalish D (1946). Studies in spatial learning; place learning versus response learning. J. Exp. Psychol. 36, 221–229. 10.1037/h0060262. [DOI] [PubMed] [Google Scholar]
- 38.Morris R (1984). Developments of a water-maze procedure for studying spatial learning in the rat. J. Neurosci. Methods 11, 47–60. 10.1016/0165-0270(84)90007-4. [DOI] [PubMed] [Google Scholar]
- 39.Soechting JF, and Flanders M (1989). Errors in pointing are due to approximations in sensorimotor transformations. J. Neurophysiol. 62, 595–608. 10.1152/jn.1989.62.2.595. [DOI] [PubMed] [Google Scholar]
- 40.Soechting JF, and Flanders M (1989). Sensorimotor representations for pointing to targets in three-dimensional space. J. Neurophysiol. 62, 582–594. 10.1152/jn.1989.62.2.582. [DOI] [PubMed] [Google Scholar]
- 41.Vindras P, and Viviani P (1998). Frames of reference and control parameters in visuomanual pointing. J. Exp. Psychol. Hum. Percept. Perform. 24, 569–591. 10.1037//0096-1523.24.2.569. [DOI] [PubMed] [Google Scholar]
- 42.Bock O, and Arnold K (1993). Error accumulation and error correction in sequential pointing movements. Exp. Brain Res. 95, 111–117. 10.1007/BF00229660. [DOI] [PubMed] [Google Scholar]
- 43.Polit A, and Bizzi E (1979). Characteristics of motor programs underlying arm movements in monkeys. J. Neurophysiol. 42, 183–194. 10.1152/jn.1979.42.1.183. [DOI] [PubMed] [Google Scholar]
- 44.Bizzi E, Accornero N, Chapple W, and Hogan N (1984). Posture control and trajectory formation during arm movement. J. Neurosci. 4, 2738–2744. 10.1523/JNEUROSCI.04-11-02738.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Krakauer JW, Pine ZM, Ghilardi MF, and Ghez C (2000). Learning of visuomotor transformations for vectorial planning of reaching trajectories. J. Neurosci. 20, 8916–8924. 10.1523/JNEUROSCI.20-23-08916.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Malfait N, Shiller DM, and Ostry DJ (2002). Transfer of motor learning across arm configurations. J. Neurosci. 22, 9656–9660. 10.1523/JNEUROSCI.22-22-09656.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Shadmehr R, and Moussavi ZM (2000). Spatial generalization from learning dynamics of reaching movements. J. Neurosci. 20, 7807–7815. 10.1523/JNEUROSCI.20-20-07807.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Shadmehr R, and Mussa-Ivaldi FA (1994). Adaptive representation of dynamics during learning of a motor task. J. Neurosci. 14, 3208–3224. 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Brayanov JB, Press DZ, and Smith MA (2012). Motor memory is encoded as a gain-field combination of intrinsic and extrinsic action representations. J. Neurosci. 32, 14951–14965. 10.1523/JNEUROSCI.1928-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Thirkettle M, Walton T, Shah A, Gurney K, Redgrave P, and Stafford T (2013). The path to learning: action acquisition is impaired when visual reinforcement signals must first access cortex. Behav. Brain Res. 243, 267–272. 10.1016/j.bbr.2013.01.023. [DOI] [PubMed] [Google Scholar]
- 51.Mathis MW, Mathis A, and Uchida N (2017). Somatosensory Cortex Plays an Essential Role in Forelimb Motor Adaptation in Mice. Neuron 93, 1493–1503.e6. 10.1016/j.neuron.2017.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wagner MJ, Savall J, Kim TH, Schnitzer MJ, and Luo L (2020). Skilled reaching tasks for head-fixed mice using a robotic manipulandum. Nat. Protoc. 15, 1237–1254. 10.1038/s41596-019-0286-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lambercy O, Schubring-Giese M, Vigaru B, Gassert R, Luft AR, and Hosp JA (2015). Sub-processes of motor learning revealed by a robotic manipulandum for rodents. Behav. Brain Res. 278, 569–576. 10.1016/j.bbr.2014.10.047. [DOI] [PubMed] [Google Scholar]
- 54.Vigaru B, Lambercy O, Graber L, Fluit R, Wespe P, Schubring-Giese M, Luft A, and Gassert R (2011). A small-scale robotic manipulandum for motor training in stroke rats. IEEE Int. Conf. Rehabil. Robot. 2011, 5975349. 10.1109/ICORR.2011.5975349. [DOI] [PubMed] [Google Scholar]
- 55.Vigaru BC, Lambercy O, Schubring-Giese M, Hosp JA, Schneider M, Osei-Atiemo C, Luft A, and Gassert R (2013). A robotic platform to assess, guide and perturb rat forelimb movements. IEEE Trans. Neural Syst. Rehabil. Eng. 21, 796–805. 10.1109/TNSRE.2013.2240014. [DOI] [PubMed] [Google Scholar]
- 56.Bollu T, Whitehead SC, Prasad N, Walker J, Shyamkumar N, Subramaniam R, Kardon B, Cohen I, and Goldberg JH (2019). Automated home cage training of mice in a hold-still center-out reach task. J. Neurophysiol. 121, 500–512. 10.1152/jn.00667.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Panigrahi B, Martin KA, Li Y, Graves AR, Vollmer A, Olson L, Mensh BD, Karpova AY, and Dudman JT (2015). Dopamine Is Required for the Neural Representation and Control of Movement Vigor. Cell 162, 1418–1430. 10.1016/j.cell.2015.08.014. [DOI] [PubMed] [Google Scholar]
- 58.Park J, Phillips JW, Guo JZ, Martin KA, Hantman AW, and Dudman JT (2022). Motor cortical output for skilled forelimb movement is selectively distributed across projection neuron classes. Sci. Adv. 8, eabj5167. 10.1126/sciadv.abj5167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wagner MJ, Savall J, Hernandez O, Mel G, Inan H, Rumyantsev O, Lecoq J, Kim TH, Li JZ, Ramakrishnan C, et al. (2021). A neural circuit state change underlying skilled movements. Cell 184, 3731–3747.e21. 10.1016/j.cell.2021.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wagner MJ, Kim TH, Kadmon J, Nguyen ND, Ganguli S, Schnitzer MJ, and Luo L (2019). Shared Cortex-Cerebellum Dynamics in the Execution and Learning of a Motor Task. Cell 177, 669–682.e24. 10.1016/j.cell.2019.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wagner MJ, Kim TH, Savall J, Schnitzer MJ, and Luo L (2017). Cerebellar granule cells encode the expectation of reward. Nature 544, 96–100. 10.1038/nature21726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tennant KA, Asay AL, Allred RP, Ozburn AR, Kleim JA, and Jones TA (2010). The vermicelli and capellini handling tests: simple quantitative measures of dexterous forepaw function in rats and mice. J. Vis. Exp. 10.3791/2076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hwang EJ, Dahlen JE, Hu YY, Aguilar K, Yu B, Mukundan M, Mitani A, and Komiyama T (2019). Disengagement of motor cortex from movement control during long-term learning. Sci. Adv. 5, eaay0001. 10.1126/sciadv.aay0001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Guo ZV, Hires SA, Li N, O’Connor DH, Komiyama T, Ophir E, Huber D, Bonardi C, Morandell K, Gutnisky D, et al. (2014). Procedures for behavioral experiments in head-fixed mice. PLoS One 9, e88678. 10.1371/journal.pone.0088678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Peters AJ, Chen SX, and Komiyama T (2014). Emergence of reproducible spatiotemporal activity during motor learning. Nature 510, 263–267. 10.1038/nature13235. [DOI] [PubMed] [Google Scholar]
- 66.Danziger Z (2023). Discrete Frechet Distance. https://www.mathworks.com/matlabcentral/fileexchange/31922-discrete-frechet-distance. [Google Scholar]
- 67.Schubring-Giese M, Molina-Luna K, Hertler B, Buitrago MM, Hanley DF, and Luft AR (2007). Speed of motor re-learning after experimental stroke depends on prior skill. Exp. Brain Res. 181, 359–365. 10.1007/s00221-007-0930-3. [DOI] [PubMed] [Google Scholar]
- 68.Kawai R, Markman T, Poddar R, Ko R, Fantana AL, Dhawale AK, Kampff AR, and Ölveczky BP (2015). Motor cortex is required for learning but not for executing a motor skill. Neuron 86, 800–812. 10.1016/j.neuron.2015.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Labat-gest V, and Tomasi S (2013). Photothrombotic ischemia: a minimally invasive and reproducible photochemical cortical lesion model for mouse stroke studies. J. Vis. Exp. 10.3791/50370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Botta P, Fushiki A, Vicente AM, Hammond LA, Mosberger AC, Gerfen CR, Peterka D, and Costa RM (2020). An Amygdala Circuit Mediates Experience-Dependent Momentary Arrests during Exploration. Cell 183, 605–619.e22. 10.1016/j.cell.2020.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Biderman D, Whiteway MR, Hurwitz C, Greenspan N, Lee RS, Vishnubhotla A, Warren R, Pedraja F, Noone D, Schartner M, et al. (2023). Lightning Pose: improved animal pose estimation via semi-supervised learning, Bayesian ensembling, and cloud-native open-source tools. Preprint at bioRxiv. 10.1101/2023.04.28.538703. [DOI] [PubMed] [Google Scholar]
- 72.Donegan D, Kanzler CM, Büscher J, Viskaitis P, Bracey EF, Lambercy O, and Burdakov D (2022). Hypothalamic Control of Forelimb Motor Adaptation. J. Neurosci. 42, 6243–6257. 10.1523/JNEUROSCI.0705-22.2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Alonso I, Scheer I, Palacio-Manzano M, Frézel-Jacob N, Philippides A, and Prsa M (2023). Peripersonal encoding of forelimb proprioception in the mouse somatosensory cortex. Nat. Commun. 14, 1866. 10.1038/s41467-023-37575-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Dhawale AK, Smith MA, and Ölveczky BP (2017). The Role of Variability in Motor Learning. Annu. Rev. Neurosci. 40, 479–498. 10.1146/annurev-neuro-072116-031548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Pacheco MM, and Newell KM (2015). Transfer as a function of exploration and stabilization in original practice. Hum. Mov. Sci. 44, 258–269. 10.1016/j.humov.2015.09.009. [DOI] [PubMed] [Google Scholar]
- 76.Beggs WD, and Howarth CI (1972). The movement of the hand towards a target. Q. J. Exp. Psychol. 24, 448–453. 10.1080/14640747208400304. [DOI] [PubMed] [Google Scholar]
- 77.Martin TA, Keating JG, Goodkin HP, Bastian AJ, and Thach WT (1996). Throwing while looking through prisms. I. Focal olivocerebellar lesions impair adaptation. Brain 119, 1183–1198. 10.1093/brain/119.4.1183. [DOI] [PubMed] [Google Scholar]
- 78.Wolpert DM, Miall RC, and Kawato M (1998). Internal models in the cerebellum. Trends Cogn. Sci. 2, 338–347. 10.1016/s1364-6613(98)01221-2. [DOI] [PubMed] [Google Scholar]
- 79.Wolpert DM, Ghahramani Z, and Jordan MI (1995). An internal model for sensorimotor integration. Science 269, 1880–1882. 10.1126/science.7569931. [DOI] [PubMed] [Google Scholar]
- 80.Shadmehr R, Smith MA, and Krakauer JW (2010). Error correction, sensory prediction, and adaptation in motor control. Annu. Rev. Neurosci. 33, 89–108. 10.1146/annurev-neuro-060909-153135. [DOI] [PubMed] [Google Scholar]
- 81.Palidis DJ, Cashaback JGA, and Gribble PL (2019). Neural signatures of reward and sensory error feedback processing in motor learning. J. Neurophysiol. 121, 1561–1574. 10.1152/jn.00792.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Izawa J, and Shadmehr R (2011). Learning from sensory and reward prediction errors during motor adaptation. PLoS Comput. Biol. 7, e1002012. 10.1371/journal.pcbi.1002012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Albert ST, and Shadmehr R (2016). The Neural Feedback Response to Error As a Teaching Signal for the Motor Learning System. J. Neurosci. 36, 4832–4845. 10.1523/JNEUROSCI.0159-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Tumer EC, and Brainard MS (2007). Performance variability enables adaptive plasticity of ‘crystallized’ adult birdsong. Nature 450, 1240–1244. 10.1038/nature06390. [DOI] [PubMed] [Google Scholar]
- 85.Kao MH, and Brainard MS (2006). Lesions of an avian basal ganglia circuit prevent context-dependent changes to song variability. J. Neurophysiol. 96, 1441–1455. 10.1152/jn.01138.2005. [DOI] [PubMed] [Google Scholar]
- 86.Galiñanes GL, Bonardi C, and Huber D (2018). Directional Reaching for Water as a Cortex-Dependent Behavioral Framework for Mice. Cell Rep. 22, 2767–2783. 10.1016/j.celrep.2018.02.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Sternad D (2018). It’s Not (Only) the Mean that Matters: Variability, Noise and Exploration in Skill Learning. Curr. Opin. Behav. Sci. 20, 183–195. 10.1016/j.cobeha.2018.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Renart A, and Machens CK (2014). Variability in neural activity and behavior. Curr. Opin. Neurobiol. 25, 211–220. 10.1016/j.conb.2014.02.013. [DOI] [PubMed] [Google Scholar]
- 89.Faisal AA, Selen LPJ, and Wolpert DM (2008). Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303. 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Therrien AS, Wolpert DM, and Bastian AJ (2018). Increasing motor noise impairs reinforcement learning in healthy individuals. eNeuro 5. 10.1523/ENEURO.0050-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Peters AJ, Liu H, and Komiyama T (2017). Learning in the Rodent Motor Cortex. Annu. Rev. Neurosci. 40, 77–97. 10.1146/annurev-neuro-072116-031407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Kleim JA, Barbay S, and Nudo RJ (1998). Functional reorganization of the rat motor cortex following motor skill learning. J. Neurophysiol. 80, 3321–3325. 10.1152/jn.1998.80.6.3321. [DOI] [PubMed] [Google Scholar]
- 93.Luft AR, Buitrago MM, Ringer T, Dichgans J, and Schulz JB (2004). Motor skill learning depends on protein synthesis in motor cortex after training. J. Neurosci. 24, 6515–6520. 10.1523/JNEUROSCI.1034-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Sauerbrei BA, Guo JZ, Cohen JD, Mischiati M, Guo W, Kabra M, Verma N, Mensh B, Branson K, and Hantman AW (2020). Cortical pattern generation during dexterous movement is input-driven. Nature 577, 386–391. 10.1038/s41586-019-1869-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Wolff SBE, Ko R, and Ölveczky BP (2022). Distinct roles for motor cortical and thalamic inputs to striatum during motor skill learning and execution. Sci. Adv. 8, eabk0231. 10.1126/sciadv.abk0231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Golub MD, Yu BM, Schwartz AB, and Chase SM (2014). Motor cortical control of movement speed with implications for brain-machine interface control. J. Neurophysiol. 112, 411–429. 10.1152/jn.00391.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Welford AT, Norris AH, and Shock NW (1969). Speed and accuracy of movement and their changes with age. Acta Psychol. 30, 3–15. 10.1016/0001-6918(69)90034-1. [DOI] [PubMed] [Google Scholar]
- 98.Chen TW, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Dana H, Sun Y, Mohar B, Hulse BK, Kerlin AM, Hasseman JP, Tsegaye G, Tsang A, Wong A, Patel R, et al. (2019). High-performance calcium sensors for imaging activity in neuronal populations and microcompartments. Nat. Methods 16, 649–657. 10.1038/s41592-019-0435-6. [DOI] [PubMed] [Google Scholar]
- 100.Abe T, Kinsella I, Saxena S, Buchanan EK, Couto J, Briggs J, Kitt SL, Glassman R, Zhou J, Paninski L, and Cunningham JP (2022). Neuroscience Cloud Analysis As a Service: An open-source platform for scalable, reproducible data analysis. Neuron 110, 2771–2789.e7. 10.1016/j.neuron.2022.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Berens P (2009). CircStat: A MATLAB Toolbox for Circular Statistics. J. Stat. Softw. 31, 1–21. 10.18637/jss.v031.i10. [DOI] [Google Scholar]
- 102.Yatsenko D, Reimer R, Ecker AS, Walker EY, Sinz F, Berens P, Hoenselaar A, Cotton RJ, Siapas AS, and Tolias AS (2015). Data-Joint: managing big scientific data using MATLAB or Python. BioRxiv. 10.1101/031658. [DOI] [Google Scholar]
- 103.Walton T, Thirkettle M, Redgrave P, Gurney KN, and Stafford T (2013). The discovery of novel actions is affected by very brief reinforcement delays and reinforcement modality. J. Mot. Behav. 45, 351–360. 10.1080/00222895.2013.806108. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Histological raw data of coronal brain sections and processed ‘BrainJ’ output data will be shared by the lead contact upon request. Raw video and tracked key point data will be shared by the lead contact upon request. Metadata, behavior data, and data used to produce figures have been deposited at https://doi.org/10.5281/zenodo.10685557.
Original task code has been deposited at https://doi.org/10.5281/zenodo.10685557. Code implementing reinforcement learning models has been deposited at https://github.com/murray-lab/RL_Reacher and https://doi.org/10.5281/zenodo.10685557. Original data analysis code has been deposited at https://doi.org/10.5281/zenodo.10685557.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.


