Abstract
Predicting cancer drug response using both genomics and drug features has shown some success compared to using genomics features alone. However, there has been limited research done on how best to combine or fuse the two types of features. Using a visible neural network with two deep learning branches for genes and drug features as the base architecture, we experimented with different fusion functions and fusion points. Our experiments show that injecting multiplicative relationships between gene and drug latent features into the original concatenation-based architecture DrugCell significantly improved the overall predictive performance and outperformed other baseline models. We also show that different fusion methods respond differently to different fusion points, indicating that the relationship between drug features and different hierarchical biological level of gene features is optimally captured using different methods. Considering both predictive performance and runtime speed, tensor product partial is the best-performing fusion function to combine late-stage representations of drug and gene features to predict cancer drug response.
Keywords: cancer drug response prediction models, deep learning, visible neural networks, drug embedding, fusion points, fusion function
INTRODUCTION
One of the outstanding biomedical challenges is predicting the response to cancer treatments because of tumors’ heterogeneity [1–5]. Several computational models have been developed to overcome this challenge by improving our understanding of how drugs and genes interact in the human body. For example, the mechanistic models have been developed to investigate the drugs interactions with cells and molecules in the tumors [6, 7], and data mining techniques have been used to find relationships between drugs and genes by representing biological networks through graphs and knowledge-based networks [8]. However, the most common approach is the use of machine learning [9–11] and deep learning [12] in a variety of different ways to predict the treatments’ responses. Particularly, deep learning has become remarkably popular in modeling the complex relationship between genes and drugs to predict cancer treatment responses.
Recent abstractive and purely artificial neural network-based methods have been used to predict drug responses by using complex models called encoder–decoder models. Distinct from fusion models, encoder–decoder models, a subset of which are known as ‘transformers’, operate through a unique data transformation process. Rather than merging information from diverse sources, as is characteristic of fusion models, these models harness the power of data transformation to generate output from input data. Encoder–decoder models process and encode complex patterns in biological and drug representation. Once encoded, the model subsequently decodes this information to predict how a specific drug might interact with a given biological system. Recently, transformers have been proven to be incredibly powerful in a variety of different fields including natural language processing [13], computer vision [14], and even cancer drug response prediction. For instance, DRPreter[15] employs graph neural networks and a type-aware transformer to predict anticancer drug response, while DeepTTA [16] leverages two autoencoders to project drug and cell line features and then predict the sensitivity of the cell lines to drugs. DEERS [17] uses autoencoders and a feed-forward network to predict cell line sensitivity to drugs.
Other types of artificial neural networks (ANN) models such as SWNet [18] and DeepCDR [19] have tried to represent the molecular structures of a drug through graph neural networks (GNN) so that different relationships between different molecules can be found. Drugs are often represented as either molecular fingerprints, text-based representations (SMILES/INCHI), graph-based, or 3D structure & surface. By using the molecular structure of a drug through graphs, one can leverage the structural information to potentially improve drug response predictions. Integrating these graph-based molecular representations along with gene or cell line data can offer a deeper understanding of drug interactions and their effects.
ANN offer valuable insights, but they have limitations when it comes to explaining why a specific drug is effective for some patients but not for others. Due to their complex structure, ANNs are often considered ‘black boxes’ since the rationale behind their predictions remains obscure. Recognizing this drawback, recent research has focused on developing biologically informed neural networks that aim to provide not only predictions but also unravel the biological reasoning behind those predictions. This approach creates a more interpretable and biology-driven framework. One such model, DrugCell [20], has demonstrated outstanding performance in predicting cancer drug response. It combines a 6-layer visible neural network (VNN) for gene embeddings with a 3-hidden-layer ANN for drug embeddings. The VNN branch is built based on the Gene Ontology (GO) hierarchy, utilizing connections between layers that reflect hierarchical relationships between genes and biological processes, referred to as ‘subsystems’.
In addition to DrugCell, other models have leveraged VNN techniques to predict specific outcomes in cancer research. P-Net [22] utilizes genomic profiles to predict prostate cancer, while ParsVNN [21] refines the DrugCell model by removing redundant elements, resulting in a more compact and explainable model. Researchers have also incorporated signal pathways to construct interpretable VNNs, as seen in models like MPVNN [23], which combines pathways and gene mutation data to predict cancer-survival risk. Furthermore, signal pathways have been used with CCLE and GDSC data to forecast anticancer drug responses [29]. Another VNN model, TUGDA [25], employs multi-task learning and domain adaptation to bridge the gap between in vitro findings and the in vivo environment. It interprets predictions using integrated gradients, providing insights into the underlying reasoning behind the model’s decisions.
While VNN models have improved the interpretability of ANN methods the DrugCell model highlights a remaining issue. In DrugCell, a ‘late fusion’ approach is used, where the final-stage representations of genes and drugs are combined and inputted into a network for prediction. However, this approach makes assumptions about gene and drug interactions, as the weights of gene embeddings remain static regardless of the drug target. This static nature limits the model’s ability to consider the potential varied impact of different drugs on identical sets of genes and biological processes. Additionally, the interaction between gene and drug features only occurs at the highest-level subsystem, disregarding nuanced biological information that may be present in lower-level GO subsystems.
Previous researchers have attempted various fusion methods to improve prediction results, but no study has comprehensively compared the performance and speed of different fusion methods used at various fusion points within a deep learning architecture with biologically informed networks. Extended Data Table 1 provides a summary of recent papers focused on drug-gene data for cancer treatment. For instance, PaccMann [24] developed an approach for anticancer compound sensitivity using a multi-modal attention-based neural network. By incorporating the molecular structure of compounds, transcriptomic profiles of cancer cells, and prior knowledge of protein interactions, they outperformed a baseline feed-forward neural network using different encoders. Other research has involved creating abstract representations of gene expression features and drug molecular descriptors using convolutional neural networks, followed by feeding these features into a long and short-term memory neural network for drug response prediction [30]. DREMO [26] utilizes multi-omics data to predict the response of cancer cell lines to therapeutic agents by fusing cell line similarities, drug similarities, and known cell line-drug associations through a multi-layer similarity network, low-dimensional feature vector and machine learning model. Similarly, MOFGCN [28] combines multi-omics data to predict drug sensitivity by integrating cell line similarity, drug similarity, and known cell line-drug associations using graph convolution operators to learn latent features. A recent liver cancer fusion model [27] uses transfer learning to extract deep features from images and PCA to capture local structures of features to evaluate drug responses.
Table 1.
Summary of different approaches in cancer drug response prediction
| Model | Interpretable | Fusion method | Drug representation | Data | Final output | Uses gene expression data | Uses mutation data |
|---|---|---|---|---|---|---|---|
| DrugCell [20] | Yes | Concatenation | Morgan Fingerprint | CTRP,GDSC, & GO | Area Under the Dose-Response Curve | No | Yes |
| ParsVNN [21] | Yes | Concatenation | Morgan Fingerprint | CTRP, GDSC, & GO | Area Under the Dose-Response Curve | No | Yes |
| P-Net [22] | Yes | Concatenation | None | Reactome Pathways, CRPC Dataset | Disease State | Yes | Yes |
| MPVNN [23] | Yes | Concatenation | None | TCGA | Survival Risk | Yes | Yes |
| DEERS [17] | Yes | Autoencoder | Inhibition Profiles | CCLE, GDSC | Drug Response | Yes | Yes |
| PaccMann [24] | Yes | Multi-modal Attention | SMILES | GDSC | IC50 Values | Yes | No |
| DRPreter [15] | Yes | Type-aware Transformer | Graph | CCLE, GDSC2 | IC50 Values | Yes | No |
| TUGDA [25] | No | Feature Fusion | Drug Name | GDSC | Log IC50 Values | Yes | No |
| DREMO [26] | No | Multi-omics Fusion | Unknown | CCLE, GDSC | Drug Response | Yes | Yes |
| Liver Cancer Fusion [27] | No | Late Fusion of Features | None | HepG2 Microscopic Images | HepG2 Cell Drug Response (Classification) | No | No |
| DeepTTA [16] | No | Transformer | SMILES | GDSC2 | IC50 Values | Yes | No |
| MOFGCN [28] | No | Graph Convolution | Morgan Fingerprint | CCLE, GDSC, Omics Data | Log IC50 Values | Yes | Yes |
| SWNet [18] | No | Self-Attention, Dual Convergence | Graph | CCLE, GDSC, PubChem, ChEMB | IC50 Values | Yes | Yes |
| DeepCDR [19] | No | Multi-Modal Fusion | Graph | CCLE, GDSC, TCGA ÍPatient Data | IC50 Values | Yes | Yes |
To fill the gap in comparative studies of different fusion methods used at various fusion points, our research has two primary objectives. Firstly, we aim to devise and evaluate more complex fusion functions that can better capture the higher-order interactions between genes and drugs. Secondly, we intend to investigate the potential benefits of fusing drug embeddings with earlier-stage genotype representations at lower-level GO subsystems, thereby incorporating more specific biological data. Through an extensive review of different fusion methods, we show that an optimal fusion method exists; however, crucially, different fusion methods respond differently to varying fusion points.
METHODS
Visible neural network as base architecture
DrugCell [20] used a modular neural network design that combined a conventional ANN for drug structure embedding and a VNN for genotype embedding. Figure 1 describes the architecture of DrugCell with one branch for gene embeddings and one branch for drug embeddings. The drug structure branch is a fully connected neural network with three layers that takes in a 2048-bit Morgan fingerprint of a drug as its input and then outputs six neurons that depict the drug structure embeddings. The neural network architecture of the Genotype branch mirrors the GO hierarchy of a human cell and takes in the mutation of a gene as input and then outputs six neurons depicting the gene structure embeddings. At the end of the two branches, a function called 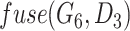 , in which
, in which 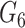 indicates the last layer of gene embeddings and
indicates the last layer of gene embeddings and 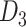 indicates the last layer of drug embeddings, is used to output the fused gene-drug representations. This fused representation is then fed into another hidden layer and then an outcome layer to produce predictions of a cell line’s response to a particular drug. In the original model, concat, short for concatenation, is used as the fuse function:
indicates the last layer of drug embeddings, is used to output the fused gene-drug representations. This fused representation is then fed into another hidden layer and then an outcome layer to produce predictions of a cell line’s response to a particular drug. In the original model, concat, short for concatenation, is used as the fuse function: 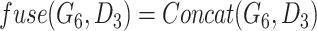 .
.
Figure 1.

Overview of DrugCell Architecture with Variable Fusion Configuration. The model consists of two branches: gene embedding visible neural network with one input layer and five layers (green outlined boxes) and drug embedding artificial neural network with one input layer and three layers (orange outlined boxes). In this paper, we focus on different fusion configuration with respect to fusion function (blue box) and fusion position (blue dotted lines).
Fusion methods
We replaced the baseline fusion function, concatenation, which captures additive interactions between genomics and drug embeddings with new fusion functions designed to capture their multiplicative interactions [31]. Additive fusion, exemplified by concatenation, merges feature sets linearly, keeping their original attributes intact. This approach is ideal in contexts where feature independence is crucial. For example, in an additive framework, a drug’s interaction with genes is viewed in a direct, one-to-one manner, akin to a single drug targeting a specific gene mutation. However, this linear approach might overlook the complexities of genomic interactions in a biological system. Contrastingly, multiplicative fusion introduces a more intricate perspective. Utilizing operations like tensor products, this method does not merely consider individual feature values but also explores their combined effects and complex interrelations. This is particularly important in deciphering the nuanced and often non-linear interplay between genes and drugs. For instance, in our dataset, a drug’s efficacy could be dramatically influenced not just by a single gene mutation but by the interaction of multiple mutations. These complex interactions, which additive models might miss, are crucial for understanding the full biological implication of drug responses. For instance, consider a scenario in our dataset where a drug is observed to be effective in cells with a certain gene mutation. However, when another gene mutation is present, the drug’s efficacy might change. This change could be due to the way these mutations interact – they could amplify or mitigate the drug’s effect, revealing a synergy or antagonism that is only apparent when considering the gene–drug interactions in a multiplicative, high-order framework.
We experimented with two attention-based fusion methods – self-attention and cross-attention [24] – and two variants of tensor-fusion methods [32]. Note, there are various new fusion methods [33], most of them are variants of our chosen fusion methods – concatenation, attention-based fusion and tensor product. We picked these three groups of fusion methods for our study due to two reasons. First, they differ in distinctive ways: concatenation represents additive interaction between gene and drug features; tensor product represents multiplicative interaction and attention-based fusion captures both multiplicative and conditional relationships. Second, they are agnostic to the base model architecture and are flexible with respect to fusion position. This allows us to experiment on and demonstrate the computational phenomenon of interaction effect between fusion function and position.
The first fusion method, self-attention, employed an attention-based encoder for both gene/subsystem and drug embeddings, separately. For each modality, attention weights were generated based on the full context of the modality itself. For example, if done at the last layer of the gene embedding with six hidden units for one root GO subsystem, attention weights for one hidden unit would be computed based on all six hidden units. Then, attention weights would be combined with the input embeddings via dot-product and output the attended input embeddings with the same shape. We then concatenated the two attended embeddings which served as the fused representation of drug and gene embeddings.
The second fusion method, cross-attention, also called contextual attention in Oskooei et al. [24], employed a similar attention-based encoder for both gene/subsystem and drug embeddings but used the other modality as the context to generate attention weights. There were three hyperparameters in this method: gene attention size, drug attention size and activation function used to project the input embeddings into the attention space. We used  as attention size for both gene and drug and used
as attention size for both gene and drug and used 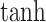 as the activation function. The output of this fusion method was also the concatenated representation of the two cross-attended embeddings.
as the activation function. The output of this fusion method was also the concatenated representation of the two cross-attended embeddings.
The third fusion method, full tensor fusion, produced the fused representation comprised of not only an addition of genomics and drug embeddings but also interactions between the two [32]. The fourth method, partial tensor fusion, is a less memory-intensive version of the former method, only using the first two components of the drug embeddings to fuse with genomics embeddings.
See Extended Data Table 2 for more details about hyperparameters and parameters for the different fusion methods.
Table 2.
Fusion methods and related parameters for combining drug and genomics embeddings
| Fusion method | Formula | Fusion-specific Hyperparameters | Number of fusion parameters |
|---|---|---|---|
| Concatenation |
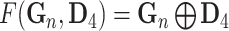
|
N/A |
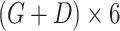
|
| Self-Attention Concatenation |
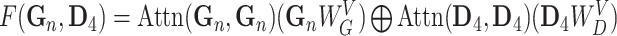
|
Temperature (1.0), Dropout rate (0.0) |
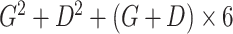
|
| Cross-Attention |
 Note:
Note:  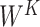 , , 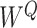 , , 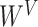 are learnable weights for query, key, and value representations. are learnable weights for query, key, and value representations. |
Temperature (1.0), Dropout rate (0.0), Gene attention size (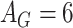 ), Drug attention size ( ), Drug attention size (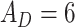 ), Activation Function ( ), Activation Function (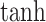 ) ) |
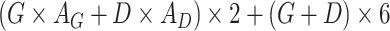
|
| Tensor Product (Full) |
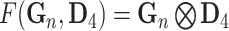
|
N/A |
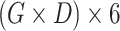
|
| Tensor Product (Partial) |
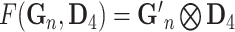 , in which
, in which 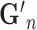 is gene representation reduced to dimension is gene representation reduced to dimension 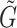 from from 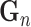
|
Dimension of gene representation to be fused (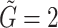 ) ) |
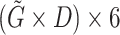
|
Note: Fusion here refers to combining drug and genomics embeddings. 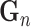 refers to gene embedding after layer
refers to gene embedding after layer 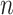 and
and  refers to final drug embedding in the DrugCell model (see Fig. 1).
refers to final drug embedding in the DrugCell model (see Fig. 1). 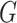 and
and 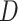 are embedding size of gene and drug embedding respectively.
are embedding size of gene and drug embedding respectively.
Experimental setup
We tested our fusion models on Lung Cancer data using the cancer-specific training samples collected from the Cancer Therapeutics Response Portal (CTRP) v2 [34] and the Genomics of Drug Sensitivity in Cancer (GDSC) database [35]. The gene features used in our analysis were represented in a binary format, indicating the presence or absence of specific mutations. We experimented with non-binary gene expression data but observed no significant difference in conclusions. Therefore, all experimental results reported in this paper used binary gene data. This Lung Cancer data was the most prevalent in the DrugCell paper covering over 684 drugs and 1,235 cell lines. Every drug’s chemical structure was represented by an average of 81 activated bits in the Morgan fingerprint vector. Each bit represented 10 molecular fragments. We used 85% (75 142 samples) of the data for training and 15% (13 260 samples) for testing. We trained the models to associate genotype-drug pairs with a drug response measured by the area under the dose-response curve. We used Pearson correlation as the predictive measurement and run the models 20 times. We then used the Mann-Whitney test U test with significancel level of 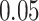 to test the significance of our findings between each of the different models.
to test the significance of our findings between each of the different models.
Note, there is a cross validation (CV) strategy used for evaluating the comboFM, which involves a  nested CV procedure [36]. This means that the data is divided into 10 outer folds, and within each outer fold, a further 5 inner folds are used. Such a nested cross-validation approach is particularly rigorous and is used to optimize model parameters (within the inner folds) while also providing an unbiased evaluation of the model’s predictive performance (across the outer folds). However, because of the computational intensity and resource constraints associated with such a validation procedure, we have adopted a 10-fold CV strategy across various cancer categories, focusing on those with a sample count exceeding 20 000. This was achieved by refining the comprehensive Drugcell cancer dataset to specifically include categories such as blood, which has a total of 93 072 samples; lung, with 88 402 samples; skin, with 30 604 samples; central nervous system, with 29 240 samples; large intestine, which encompasses 27 745 samples; breast, with a total of 24 928 samples, ovary with 23 159 samples and pancreas with 22 101. This selective filtering process enables a more focused and efficient analysis within these high-sample-volume categories.
nested CV procedure [36]. This means that the data is divided into 10 outer folds, and within each outer fold, a further 5 inner folds are used. Such a nested cross-validation approach is particularly rigorous and is used to optimize model parameters (within the inner folds) while also providing an unbiased evaluation of the model’s predictive performance (across the outer folds). However, because of the computational intensity and resource constraints associated with such a validation procedure, we have adopted a 10-fold CV strategy across various cancer categories, focusing on those with a sample count exceeding 20 000. This was achieved by refining the comprehensive Drugcell cancer dataset to specifically include categories such as blood, which has a total of 93 072 samples; lung, with 88 402 samples; skin, with 30 604 samples; central nervous system, with 29 240 samples; large intestine, which encompasses 27 745 samples; breast, with a total of 24 928 samples, ovary with 23 159 samples and pancreas with 22 101. This selective filtering process enables a more focused and efficient analysis within these high-sample-volume categories.
Baseline models
Table 1 showcases a range of models designed for predicting cancer drug responses, but it is critical to recognize the variations in their input and output configurations. This table reveals that Pars VNN is the sole model using the exact same input and output features as the DrugCell. Notably, Pars VNN uses the exact same model architecture as the DrugCell, implying that findings relevant to the DrugCell model are also applicable to Pars VNN. Since the disparity in input characteristics across the models poses challenges for conducting standardized experiments, we have included a set of well-known regression models to serve as our baseline models: Elastic Net, Random Forest Regression, XGBoost Regressor, a Stochastic Gradient Regressor.
ElasticNet [37] is a popular type of linear regression that uses regularization from two popular penalties, the L1 and the L2 penalty function. The L2 penalty penalizes a model based on the sum of the squared coefficients, minimizing their size and preventing any coefficients from being removed from the model. The L1 penalty minimizes the sum of the absolute coefficient values, and this allowed some coefficients to be minimized to zero, effectively removing them from the model. By leveraging both penalties, better performance could be achieved than either one could on certain problems. The stochastic gradient descent linear model (SGDRegressor) [38] was also used, which utilizes gradient descent to efficiently update the model’s parameters using subsets of the data. This reduced computational cost and memory requirements and converged faster. Random forest regression [39] is an ensemble method that combines predictions from multiple tree regressors and then averages the result out into a single prediction. This is a powerful and accurate method that performs well for a variety of complex and non-linear problems. Extreme gradient boosting or XGBoost [40] is an ensemble learning technique that combines multiple weak models (usually decision trees) to form a stronger and more accurate model. In XGBoost, this was achieved through a process of iteratively adding decision trees to the ensemble, with each subsequent tree being trained to correct the errors made by the previous trees.
For all models except for the DrugCell and our models, the inputs are the concatenation of gene and drug features. In the DrugCell and our models, gene features and drug features were passed separately to two different neural network branches as demonstrated in Figure 1.
We leveraged the GridSearchCV function from the Scikit-learn [41] library to systematically explore the hyperparameter space and evaluate performance using cross-validation for each of the Scikit-learn models. We used Spearman’s rank correlation coefficient, Pearson’s correlation coefficient and the mean squared error (MSE) to assess the performance of the optimized model and to determine the optimal hyperparameters. For the hyperparameters of DrugCell and the variations of the architecture, we used the hyperparameters configured from DrugCell: six hidden units for each GO subsystem in the gene embedding branch, and 100-50-6 hidden units for the drug embedding branch. See Extended Data Table 3 for more details.
Table 3.
Hyperparameters used in the experimental setup for different machine learning models
| Model | Parameter | Description | Values |
|---|---|---|---|
| DrugCell | final_gene_embedding_size | Gene Embedding Size | 6 |
| num_gene_visble_layers | Number of Gene Visible Layers | 5 | |
| final_drug_embedding_size | Drug Embedding Size | 6 | |
| num_drug_hidden_layers | Number of Drug Hidden Layers | 3 | |
| drug_hidden_units | Drug Hidden Units | [100, 50, 6] | |
| XGBoost | max_depth | Maximum tree depth | [4, 6, 8] |
| eta | Learning rate | [0.3, 0.2, 0.1] | |
| colsample_bytree | Fraction of columns sampled | [0.25, 0.5, 1] | |
| reg_alpha | L1 regularization term | [0.0, 0.5] | |
| reg_lambda | L2 regularization term | [0.5, 1] | |
| Random Forest | n_estimators | Number of trees in the forest | [100, 200, 400] |
| max_depth | Maximum tree depth | [20, None] | |
| min_samples_split | Minimum number of samples to split | [1, 2, 3] | |
| min_samples_leaf | Minimum number of samples at a leaf node | [1, 2, 4] | |
| max_features | Number of features to consider | [‘sqrt’, ‘log2’] | |
| SGD | loss | Loss function | [‘squared_error’, ‘huber’] |
| penalty | Regularization term | [‘l1’, ‘l2’, ‘elasticnet’] | |
| alpha | Regularization strength | [0.00001, 0.00005, 0.0001, 0.001, 0.01] | |
| learning_rate | Learning rate schedule | [‘invscaling’] | |
| eta0 | Initial learning rate | [0.01, 0.001,.005] | |
| Elastic Net | alpha | Regularization strength | [0.001, 0.01, 1] |
| l1_ratio | L1 regularization weight | [0.2, 0.3, 0.4] | |
| max_iter | Maximum number of iterations | [250, 500, 1000] | |
| precompute | Whether to use precomputed Gram matrix | [True, False] | |
| selection | Algorithm for choosing coefficients | [‘cyclic’, ‘random’] |
RESULTS
Comparison of baseline models with fusion functions
We first conducted an experiment to examine which of the fusion methods discussed under the methods provides better cancer drug response predictions for the three cancer types with the highest number of samples. The genotype and drug embeddings are fused at the final stage of their corresponding branch (drugs at layer 4 and genes at layer 6, counting the input layer as layer 1) in the DrugCell architectural framework. We followed the evaluation protocol indicated in the DrugCell code base (https://github.com/idekerlab/DrugCell/tree/public) and used MSE as the training objective and Pearson Correlation as the evaluation metric (We noted that the DrugCell paper reported Spearman Correlation but their code base used Pearson Correlation.). For each method, we ran the model training 20 times and the Mann-Whitney test to check whether the difference in performance was statistically significant.
Figure 2 shows that all methods that attempted to account for multiplicative interactions between genotype and drug features (cross attention, tensor product fusion full, and tensor product partial) performed better than the method that merely accounted for additive interactions (concatenation) for lung cancer. Among all five fusion methods, tensor product fusion full achieved the best predictive performance. However, tensor product fusion partial not only reduced memory footprint (by using only 2 out of 6 neurons of the drug embeddings, it used 3 times less memory footprint per fusion pair) but also had lower variability. All the fusion methods explored using the DrugCell architecture exhibited significantly higher test accuracy compared to the baseline models (random forest, elastic net, xgboost, and stochastic gradient descent).
Figure 2.
Comparison of different fusion methods and baseline models. Sub-figure A indicate the comparison among differnt Fusion methods, while sub-figure B shows the comparision among baaseline models. The boxplots represent the distribution of the performance of the methods evaluated using the Pearson correlation between the predicted AUC and actual AUC. P-value annotations: ns for 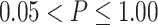 , * for
, * for 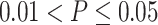 , ** for
, ** for 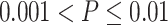 , *** for
, *** for 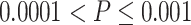 and **** for
and **** for 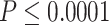 .
.
During our investigation, we also examined the impact of different late-fusion methods and baseline methods in relation to sample size for lung cancer using train, validation, and test split as provided by ParsVNN/DrugCell. We observed that the model performance did not exhibit significant improvement as the drug sample size increased, irrespective of the fusion method employed (see Figure 3.) This finding suggests that all studied fusion methods are similarly robust to sample size.
Figure 3.
Predictive performance and drug sample size. The plot shows the predictive performance of different fusion methods and elastic net over different drug sample sizes. The predictive performance is measured as an average of Pearson correlation of all drugs with the corresponding sample size. Performance does not exhibit significant improvement as the drug sample size increases. This may indicate that other factors beyond sample size might play a more influential role in determining model performance and accuracy.
Analysis of varying fusion points between genomics and drugs
Since the gene embedding deep learning branch follows an actual biological hierarchy, and previous studies have shown how particular drugs affect certain subsystems, we hypothesized that fusing the final-stage drug embeddings with lower-level GO subsystem embeddings might yield better predictive performance. Furthermore, we are interested in seeing how different fusion methods react to the change in fusion points. To test this hypothesis, we trained the DrugCell models 10 times using 10-fold CV with three different fusion points of the genotype embedding branch (layer 1 for early fusion, layer 3 for mid fusion, and layer 6 for late fusion). For this experiment, we used three representative methods - concatenation (original DrugCell model), cross attention, and tensor product partial (tensor product full requires a higher memory footprint so cannot be conducted at earlier fusion points with our available hardware). The results are shown in Figure 4.
Figure 4.
Comparative Analysis of Cancer Types — The plot shows the test performance (mean and standard error of 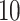 CV runs) of the different fusion methods when final-stage drug embeddings are fused with different stages of genotype embedding using different fusion functions.
CV runs) of the different fusion methods when final-stage drug embeddings are fused with different stages of genotype embedding using different fusion functions.
As shown in Figure 4, our analysis demonstrates that the partial tensor fusion technique consistently outperforms both concatenation and cross-attention methods in predicting drug responses for blood, lung, and skin cancers, irrespective of the fusion point within the model architecture. Specifically, for cancers with the largest datasets—including blood, lung, skin, and large intestine—the most effective model leverages partial tensor fusion at a mid-level integration point. Conversely, for cancers with slightly smaller datasets, such as breast, ovarian, and pancreas cancers, the optimal approach involves implementing partial tensor fusion earlier in the model architecture. This pattern is not attributed to sample sizes of the respective cancer types, as our initial experiments with lung cancer data indicated that the fusion methods demonstrate similar robustness to variations in sample size.
Furthermore, our findings indicate a notable trend across almost all cancer types studied, with the exception of the aggregate cancer dataset and lung cancer specifically. When the drug information is fused with the final-layer genotype embeddings, there is a statistically significant decline in predictive performance of all fusion methods. This pattern underscores the importance of the fusion point within the model structure for maximizing predictive accuracy in cancer drug response prediction. Particularly, the predictive models may benefit from capturing gene–drug interactions at the earlier stages rather than the final stage.
Runtime performance
We used 1 GPU node with 12GB VRAM (NVIDIA RTX 2080ti) to run our experiments. Figure 5 shows the training time performance using different fusion methods at late stage (gene layer 6). All fusion methods used the same batch size ( ) and learning rate (
) and learning rate (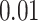 ). Though there is not much difference in training time for 100 epochs, tensor product methods (both full and partial versions) converged twice as fast compared to the baseline concatenation method. Importantly, all models converge before it reaches
). Though there is not much difference in training time for 100 epochs, tensor product methods (both full and partial versions) converged twice as fast compared to the baseline concatenation method. Importantly, all models converge before it reaches  epochs. Therefore, in the runtime result (Figure 5), we compared the runtime to convergence.
epochs. Therefore, in the runtime result (Figure 5), we compared the runtime to convergence.
Figure 5.

Runtime performance of different fusion methods at late fusion stage. All fusion methods have comparable single-epoch run time. However, tensor fusion partial converges faster compared to other fusion methods, which reduces overall training time.
DISCUSSION
The heterogeneity of tumor cells poses a fundamental challenge for predicting clinical response to therapeutic agents [42]. Predicting the sensitivity of tumors to specific anticancer treatments is a challenge of paramount importance for precision medicine. Deep learning models can be used to model the complexity of cancer mutations to be able to predict the response of cancer cell lines and patients to novel drugs or drug combinations. Deep learning models hold immense promise for better drug response predictions, but most of them cannot provide biological and clinical interpretability. Interpretability of predictive models is critical as it may provide a better understanding of specific features of the cancer which would inform patient care as well as provide vital insights in the development of new therapeutic agents. This then calls for the need to develop models that provide better interpretability while maintaining good prediction accuracy.
DrugCell tackled the issue of model interpretability by employing a neural network structure that mirrors biological processes. They provide clinical and biological explanations for cancer drug response by their model. This approach enhances the model’s transparency. However, the DrugCell design presupposes that drug–gene interactions are purely additive and occur exclusively at the top-level GO subsystem.
It’s crucial to consider that a patient’s genomic characteristics can influence their response to specific drugs. Moreover, drug features can intertwine with genomic features, which in turn, affects the drug’s efficacy. To better account for these intricate interactions between drugs and gene features, we delved into state-of-the-art fusion methods without providing any new interpretability approach. However, the clinical and biological explanations for cancer drug response by Drug Cell model can be adopted for these new fusion functions.
In our pursuit to enhance predictive performance, we considered the potential benefits of integrating interactions between lower-level GO subsystems and drug features. We executed an experiment, varying fusion points across several fusion methods – namely, concatenation, cross-attention, and tensor product (partial) fusion. Unfortunately, due to memory limitations, we could not extend this to the tensor product full method.
Our findings reveal that the efficacy of the chosen fusion method can influence outcomes. Specifically, the additive-only fusion method of concatenation didn’t display significant variation across different fusion points for lung and ovarian cancers as well as the full cancer data. However, multiplicative fusion methods of cross-attention and tensor product, exhibited varied performances depending on the fusion points for all individual cancer types. The tensor product method’s predictive capacity enhanced when it factored in interactions between drugs and genes at preliminary fusion points – essentially, at the lower-level GO subsystems. This disparity underscores a distinct characteristic between additive-only and multiplicative interaction fusion methods. It’s conceivable that the embeddings from lower-level GO subsystems more profoundly influence how drug embeddings determine drug outcomes.
We observed that tensor product fusion outperformed cross-attention with an early or mid fusion points for all cancer types in the given task. One possible hypothesis to explain this phenomenon is that the task at hand necessitates the modeling of higher-order interactions between input elements, which are effectively captured by tensor product fusion. This contrasts with cross-attention, which primarily focuses on pairwise relationships. While cross-attention is a learnable mechanism, its parameters, such as attention weights, are updated during the training process to better adapt the attention mechanism to focus on relevant parts of the input when generating output.
The findings for entire cancer data set, blood, lung, skin, central nervous system and large intestine, breast, ovarian and pancreatic cancers show that the mid fusion of tensor product performs the best. However, there is a different pattern for breast, ovarian and pancreas cancers; cross-attention and tensor fusion methods exhibit a consistent downward performance trend when the fusion point increases. This suggests that the fusion point’s impact is not uniform across different cancer types, emphasizing the importance of customizing the fusion strategy for each specific dataset. Early fusion points markedly improved prediction accuracy for some cancer types. This suggests that for these cancers, capturing the nuances of gene-drug interactions at the initial stages may be more critical. The early-stage genes’ interactions, perhaps due to their proximity to the fundamental biological processes, seem to carry substantial predictive weight. These early interactions are likely more reflective of the underlying biological mechanisms that govern drug responses in these cancer types.
We hypothesize that the different performances of tensor fusion and cross-attention at varying fusion points may be attributed to the unique characteristics of these methods. Tensor fusion, which captures complex, high-order interactions between features through a multidimensional array, may excel at earlier stages by encapsulating intricate interactions between raw, high-dimensional gene and drug features. This early capture of complex, potentially non-linear interactions could lead to a more accurate data representation, thereby enhancing performance. The observed performance of cross-attention is notably less effective than tensor fusion and only slightly outperforms concatenation in early stages for some of the cancer types. One potential explanation for this could be the inherent complexity and variability of genes’ interactions. In the early stages, the raw data might present distinct, high-signal features that cross-attention mechanisms can effectively latch onto, leading to improved performance for some of the cancer types such as central nervous system cancer. However, as the model progresses and the data undergoes multiple transformations, these distinct features may become abstracted into higher-level representations that are less amenable to the focused approach of cross-attention. Future research would be needed to fully understand these differences.
During the analysis of run-time performance for various fusion methods, it was observed that while there was no significant difference in training time, the tensor product methods (both full and partial versions) exhibited faster convergence compared to the baseline concatenation method. Notably, the partial tensor product method demonstrated, particularly accelerated convergence. It is important to note that the tensor product full method requires a higher memory footprint, which can limit its practical applicability. Therefore, to strike a balance between performance and memory requirements, adopting the partial tensor product method with an early fusion point would be a favorable choice. This approach enables enhanced predictive capabilities while optimizing memory usage, improving the DrugCell model’s efficiency and effectiveness. We experimented with different numbers of components used in partial tensor fusion (out of six components representing drug embeddings). Using one component shows degraded predictive performance, and using two components showed only slightly lower performance compared to full tensor fusion yet significantly lower memory footprint.
Indeed, extending the experiment to investigate the differences between multiplicative latent features and attended latent features would be a valuable step. By delving deeper into these two approaches, we can gain a more comprehensive understanding of why the multiplicative approach yields superior drug-response predictions. Analyzing the distinctions between these types of latent features can provide insights into the underlying mechanisms and factors that contribute to improved predictive performance. Moreover, it would be important to explore how the multiplicative relationship between drug and gene embeddings can be used to help prune the graph and build more sparse visible neural networks for specific cancer drug-response predictions.
Key Points
This study extends the base model, DrugCell, showing that capturing a multiplicative interaction between genomics and drug features significantly outperforms using additive relationships in predictive accuracy while still maintaining interpretability.
The choice of fusion method significantly impacts predictive outcomes, with early integration of drug–gene interactions in multiplicative methods like tensor product enhancing accuracy.
Out of the fusion methods tested: self-attention, cross-attention, tensor product and tensor product partial, the tensor product partial method strikes the best balance between high predictive performance and reduced runtime on Lung Cancer data sourced from CTRP and GDSC databases. We recommend that both predictive performance and runtime performance should be considered as critical factors in model selection.
Our findings highlight that an interaction between fusion methods and fusion points plays a critical role in performance outcomes.
Author Biographies
Trang Nguyen is a MS/PhD student in Department of Computer Science at the University of Massachusetts Amherst. Her main research area is multimodal machine learning.
Anthony Campbell received an MS Computer Science degree from the University of Massachusetts Amherst.
Ankit Kumar is a PhD student in Department of Mathematics and Statistics at the University of Massachusetts Amherst. His main research area is statistics and computational biology.
Edwin Amponsah received an MS statistics degree from the University of Massachusetts Amherst. He is currently an actuarial analyst at New York Life.
Madalina Fiterau received her PhD degree in machine learning from Carnegie Mellon University. Dr. Fiterau has completed a Postdoctoral Fellowship in Computer Science and Biomedical Engineering at Stanford University. Dr. Fiterau is currently an assistant professor in the College of Information and Computer Sicneces at the University of Massachusetts Amherst.
Leili Shahriyari received her PhD degree in mathematics and MSE degree in computer science from Johns Hopkins University. Dr. Shahriyari is currently an associate professor in the Department of Mathematics and Statistics at the University of Massachusetts Amherst.
Contributor Information
Trang Nguyen, Department of Computer Science, University of Massachusetts Amherst, Amherst 01002, MA, United States.
Anthony Campbell, Department of Computer Science, University of Massachusetts Amherst, Amherst 01002, MA, United States.
Ankit Kumar, Department of Mathematics and Statistics, University of Massachusetts Amherst, Amherst 01002, MA, United States.
Edwin Amponsah, Department of Mathematics and Statistics, University of Massachusetts Amherst, Amherst 01002, MA, United States.
Madalina Fiterau, Department of Computer Science, University of Massachusetts Amherst, Amherst 01002, MA, United States.
Leili Shahriyari, Department of Mathematics and Statistics, University of Massachusetts Amherst, Amherst 01002, MA, United States.
AUTHOR CONTRIBUTIONS
T.N. designed and implemented the code for different fusion functions and varying fusion points. The author contributed to writing the paper. A.C. implemented the code for the baseline models and helped visualize the results. The author contributed to writing the paper. A.K. ran the models for different cancer types and helped visualize the results. E.A. participated in designing varying fusion points experiments and implemented the code to analyze and visualize experimental results. The author contributed to writing the paper. M.F. and L.S. supervised the project. All authors read and approved the final manuscript.
FUNDING
This work received no external funding.
CODE AVAILABILITY
Custom code was developed as part of the analysis reported here, and has been deposited on GitHub: https://github.com/nguyentr17/drug-cell-fusion . The library names and versions used in the implementation are provided in: https://github.com/nguyentr17/drug-cell-fusion/requirements.txt.
DATA AVAILABILITY
All data used and generated from this study are deposited in https://github.com/nguyentr17/drug-cell-fusion. The data used were found here https://github.com/idekerlab/DrugCell/tree/public/data.
References
- 1. Dagogo-Jack I, Shaw AT. Tumour heterogeneity and resistance to cancer therapies. Nat Rev Clin Oncol 2018;15(2):81–94. [DOI] [PubMed] [Google Scholar]
- 2. Lim Z-F, Patrick CM. Emerging insights of tumor heterogeneity and drug resistance mechanisms in lung cancer targeted therapy. J Hematol Oncol 2019;12(1):134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Meacham CE, Morrison SJ. Tumour heterogeneity and cancer cell plasticity. Nature 2013;501(7467):328–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Bedard PL, Hansen AR, Ratain MJ, Siu LL. Tumour heterogeneity in the clinic. Nature 2013;501(7467):355–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Felipe De Sousa E, Melo LV, Fessler E, Medema JP. Cancer heterogeneity–a multifaceted view. EMBO Rep 2013;14(8):686–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Le T, Sumeyye S, Shahriyari L. Investigating optimal chemotherapy options for osteosarcoma patients through a mathematical model. Cells 2021;10(8):2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Budithi A, Sumeyye S, Kirshtein A, Shahriyari L. Data driven mathematical model of FOLFIRI treatment for colon cancer. Cancer 2021;13(11):2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Rintala TJ, Ghosh A, Fortino V. Network approaches for modeling the effect of drugs and diseases. Brief Bioinform 2022;23(4):bbac229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Adam G, Rampášek L, Safikhani Z, et al. Machine learning approaches to drug response prediction: challenges and recent progress. npj Precision Oncology 2020;4(1):19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Paltun BG, Mamitsuka H, Kaski S. Improving drug response prediction by integrating multiple data sources: matrix factorization, kernel and network-based approaches. Brief Bioinform 2019;22(1):346–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Gerdes H, Casado P, Dokal A, et al. Drug ranking using machine learning systematically predicts the efficacy of anti-cancer drugs. Nat Commun 2021;12(1):1850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Rintala TJ, Ghosh A, Fortino V. Network approaches for modeling the effect of drugs and diseases. Brief Bioinform 2022;23(4):06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Wolf T, Debut L, Sanh V, et al. Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, 38–45, Online, October 2020. Association for Computational Linguistics.
- 14. Yifan X, Wei H, Lin M, et al. Transformers in computational visual media: a survey. Computational Visual Media 2022;8(1):33–62. [Google Scholar]
- 15. Shin J, Piao Y, Bang D, et al. Drpreter: interpretable anticancer drug response prediction using knowledge-guided graph neural networks and transformer. Int J Mol Sci 2022;23(22). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Jiang L, Jiang C, Yu X, et al. DeepTTA: a transformer-based model for predicting cancer drug response. Brief Bioinform 23(3):bbac100. [DOI] [PubMed] [Google Scholar]
- 17. Koras K, Kizling E, Juraeva D, et al. Interpretable deep recommender system model for prediction of kinase inhibitor efficacy across cancer cell lines. Sci Rep 2021;11(1):15993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zuo Z, Wang P, Chen X, et al. Swnet: a deep learning model for drug response prediction from cancer genomic signatures and compound chemical structures. BMC Bioinformatics 2021;22(1):434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Liu Q, Zhiqiang H, Jiang R, Zhou M. Deepcdr: a hybrid graph convolutional network for predicting cancer drug response. Bioinformatics 2020;36(Suppl_2):i911–8. [DOI] [PubMed] [Google Scholar]
- 20. Kuenzi BM, Park J, Fong SH, et al. Predicting drug response and synergy using a deep learning model of human cancer cells. Cancer Cell 2020;38(5):672–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kuenzi BM, Park J, Fong SH, et al. Predicting drug response and synergy using a deep learning model of human cancer cells. Cancer Cell 2020;38(5):672–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Elmarakeby HA, Hwang J, Arafeh R, et al. Biologically informed deep neural network for prostate cancer discovery. Nature 2021;598(7880):348–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Roy GG, Geard N, Verspoor K, He S. MPVNN: mutated pathway visible neural network architecture for interpretable prediction of cancer-specific survival risk. Bioinformatics 2022;38(22):5026–32. [DOI] [PubMed] [Google Scholar]
- 24. Oskooei A, Born J, Manica M, et al. PaccMann: prediction of anticancer compound sensitivity with multi-modal attention-based neural networks arXiv e-prints, arXiv:1811.06802. November2018.
- 25. da Silva RP, Suphavilai C, Nagarajan N. TUGDA: task uncertainty guided domain adaptation for robust generalization of cancer drug response prediction from in vitro to in vivo settings. Bioinformatics 2021;37(Supplement_1):i76–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Yu L, Zhou D, Gao L, Zha Y. Prediction of drug response in multilayer networks based on fusion of multiomics data. Methods 2021;192:85–92.Deep networks and network representation in bioinformatics. [DOI] [PubMed] [Google Scholar]
- 27. Hassan M, Ali S, Alquhayz H, et al. Developing liver cancer drug response prediction system using late fusion of reduced deep features. J King Saud Univ - Computer Inform Sci 2022;34(10, Part A):8122–35. [Google Scholar]
- 28. Peng W, Chen T, Dai W. Predicting drug response based on multi-omics fusion and graph convolution. IEEE J Biomed Health Inform 2022;26(3):1384–93. [DOI] [PubMed] [Google Scholar]
- 29. Zhang H, Chen Y, Li F. Predicting anticancer drug response with deep learning constrained by signaling pathways. Front Bioinformatics 2021;1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Li Q, Huang J, Zhu HM, Liu Q. Prediction of cancer drug effectiveness based on multi-fusion deep learning model. In 2020 10th Annual Computing and Communication Workshop and Conference (CCWC), 0634–9, 2020.
- 31. Jayakumar SM, Czarnecki WM, Menick J, et al. Multiplicative interactions and where to find them. 2020.
- 32. Zadeh A, Chen M, Poria S, et al. Tensor fusion network for multimodal sentiment analysis.
- 33. Shaik T, Tao X, Li L, et al. A survey of multimodal information fusion for smart healthcare: mapping the journey from data to wisdom. Information Fusion 2024;102:102040. [Google Scholar]
- 34. Seashore-Ludlow B, Rees MG, Cheah JH, et al. Harnessing connectivity in a large-scale small-molecule sensitivity dataset. Cancer. Discovery 2015;5(11, 11):1210–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Yang W, Soares J, Greninger P, et al. Genomics of drug sensitivity in cancer (GDSC): a resource for therapeutic biomarker discovery in cancer cells. Nucleic Acids Res 2012;41(D1):D955–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Julkunen H, Cichonska A, Gautam P, et al. Leveraging multi-way interactions for systematic prediction of pre-clinical drug combination effects. Nat Commun 2020;11(1):6136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Series B Stat Methodology 2005;67(2): 301–20. [Google Scholar]
- 38. Zhang T. Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the Twenty-First International Conference on Machine Learning, 116, 2004. [Google Scholar]
- 39. Breiman L. Random forests. Machine Learning 2001;45:5–32. [Google Scholar]
- 40. Chen T, Guestrin C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785–94, 2016.
- 41. Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: machine learning in python. J Mach Learn Res 2011;12:2825–30. [Google Scholar]
- 42. Fisher R, Pusztai L, Swanton C. Cancer heterogeneity: implications for targeted therapeutics. Br J Cancer 2013;108(3):479–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data used and generated from this study are deposited in https://github.com/nguyentr17/drug-cell-fusion. The data used were found here https://github.com/idekerlab/DrugCell/tree/public/data.





