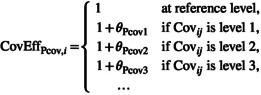Abstract
Modeling the relationships between covariates and pharmacometric model parameters is a central feature of pharmacometric analyses. The information obtained from covariate modeling may be used for dose selection, dose individualization, or the planning of clinical studies in different population subgroups. The pharmacometric literature has amassed a diverse, complex, and evolving collection of methodologies and interpretive guidance related to covariate modeling. With the number and complexity of technologies increasing, a need for an overview of the state of the art has emerged. In this article the International Society of Pharmacometrics (ISoP) Standards and Best Practices Committee presents perspectives on best practices for planning, executing, reporting, and interpreting covariate analyses to guide pharmacometrics decision making in academic, industry, and regulatory settings.
BACKGROUND
Covariates, or predictor variables, are commonly used in pharmacometric models to identify and describe predictable sources of variability and thereby improve the model fit and/or model‐based predictions. Both intrinsic and extrinsic patient variables are typically used as covariates to understand between‐subject variability in model parameters, such as clearance (CL) and volume of distribution (V) in pharmacokinetic (PK) models, and occasionally within‐subject and residual variability. 1 The presence of a parameter‐covariate association by itself does not necessarily imply a causal relationship between the covariates and the parameters, but such associations may be used to generate causal hypotheses and may corroborate or refute prior causal hypotheses. External knowledge is typically required to determine the extent to which a relationship can be assigned a causal 2 , 3 or mechanistic interpretation.
Depending on the domain of application, certain well‐established covariates merit routine consideration. In PK applications, common predictors include body size and composition, 4 , 5 maturation of organ function, 6 , 7 markers of hepatic 8 and renal function, 9 and differences in metabolic pathways related to genotype and concomitant medication. 10 , 11 Table 1 provides a list of covariates that are commonly relevant in assessing the need for dose adjustment in humans.
TABLE 1.
Common covariates for prediction of dose in humans.
| Covariate type | Covariate distribution range | Fold change associated with covariate range (Parameter) | Comment |
|---|---|---|---|
| Size 5 | 0.5–250 kg total body weight |
100 (clearance) 500 (volume) |
Theory based allometric scaling of mass to allometric size |
| Maturation 28 | 22 to 196 post menstrual weeks (up to 3 y post‐natal age) | 10 (clearance) | Empirical sigmoid power function |
| Organ function 9 | 10–150 mL/min (creatinine clearance) | 10 (clearance) | Only part of total clearance predicted by linear function of creatinine clearance |
| Genotype 81 | Homozygous recessive – homozygous dominant | 10 (6‐MP) | Genotype effects usually much smaller (e.g., 2‐fold) than 6‐MP example |
| Concomitant medications 82 | Without – with concomitant medication (sometimes dose and time related) | 2 | Amiodarone inhibition of warfarin clearance, rifampicin induction of clearance for many drugs |
Note: The inclusion of covariates mentioned in this table account for a large part of interpatient variability. After accounting for the influence of the covariates the influence of other covariates, such as sex or race is negligible or nonexistent.
Abbreviation: 6‐MP, 6‐mercaptopurine.
In some cases, specific covariates may be particularly important within a particular therapeutic area. In oncology, for example, higher clearance of therapeutic monoclonal antibodies has been found to be associated with markers of disease severity, such as poor performance status at baseline and lower baseline albumin, and the reversal of disease severity by an effective treatment has been shown to be associated with a decrease in clearance over time. 12 , 13 , 14 In regard to pharmacodynamic (PD) parameters, covariate relationships are frequently associated with particular parameters of a sigmoid exposure‐response curve, such as maximum effect (E max) and concentration at 50% maximal effect (C 50), 15 , 16 and the specific choice of covariates to consider as predictors of these parameters depends on the therapeutic area, mechanism of action, and the outcome to be modeled.
For the purposes of this article, covariate predictors may be classified as being continuous or categorical. Continuous variables (including durations of time) are numeric and can take a theoretically infinite number of values between upper and lower bounds. Examples of continuous covariates commonly of interest in PK analyses include weight, age, albumin concentration, and creatinine clearance (CLcr; time is another, but it is a special case). Categorical variables, conversely, contain finite numbers of categories or distinct groups, with or without a logical order. Sex and race are common examples.
OBJECTIVES
Methodologies related to covariate selection, modeling, presentation, and interpretation continue to evolve. As the number and complexity of these methods increase, the need has emerged to summarize the state of the art and organize a clear set of points for consideration. The intent of this article is to provide such a summary, covering topics related to the planning, conducting, and interpreting covariate analyses in pharmacometrics. This summary provides comparisons and contrasts necessary for modelers to make informed and context‐aware decisions with respect to methodologies, and to foster valid interpretations of results. These considerations of best practices are necessarily generic in nature, and it should be emphasized that for a specific analysis, prior knowledge or mechanistic understanding should always be considered along with the research question at hand. Throughout the article, we present examples discussed in Supplementary Material S1 using the theophylline PD dataset investigated with several different software tools, to illustrate the concepts we discuss. 17 , 18 , 19
PLANNING COVARIATE ANALYSES
Planning of covariate analyses serves at least two purposes. Primarily, as with any activity, adequate planning increases the likelihood of proceeding rationally and efficiently towards one's objectives. Secondarily, the regulatory context that attends many pharmacometric analysis entails a need for transparency in decision making. It is acknowledged that a full prespecification may not be possible, however, the degree of prespecification is a crucial determinant in assessing the strength of evidence of a given finding and may serve as a surrogate for objectivity and guard against potential bias.
The following section describes the different aspects of planning covariate analysis and thereby offers guidance for the prespecification of covariate analyses.
Study design
Where possible, consideration should be given to ensuring multiple design factors, such as adequate sample size, data collection time, and adequate dispersion of the covariates to detect and describe important covariate effects when designing a clinical study. Sample size is particularly important as it can severely affect power to identify an effect, especially if it is subtle or variable. 20 Often, these design factors are governed by the phase of drug development, population studied, and inclusion and exclusion criteria of the study. For instance, to evaluate the effect of renal impairment on drug elimination, subjects covering the full dispersion of renal function in the population of interest should be enrolled in a study. In the context of evaluating drug–drug interactions, design factors, such as timing of co‐administration and selection of appropriate drug sample collection times, are essential in order to observe and quantify any effects. 21 Clinical trial simulation can be used to determine sufficient sample sizes when complex outcomes and models are involved. 22 , 23
Covariate scope
The term “covariate scope” is used in this paper to refer to the set of all candidate covariate‐parameter relationships that are identified as being of interest at the planning stage. As such, scope may be formalized as a list of candidate covariates and functional forms to be considered on each type of model parameter. A large number of potential covariates may be available for analysis, and judicious narrowing of covariate scope is encouraged in order to avoid problems in parameter estimation (such as imprecise estimates of covariate parameters), implementation (such as excessive run times), statistical or mechanistic interpretation (such as large numbers of implausible covariate relationships leading to issues with statistical multiplicity and/or selection bias), and reporting (such as tabulation of covariate effect estimates that are not of primary interest, arguably an unnecessary distraction). Accordingly, we describe some of the key considerations that should be considered before the covariate analysis begins, as listed below:
mechanistic plausibility of covariate relationships,
inclusion/exclusion criteria and stratification factors for the studies being modeled,
dispersion of the covariate (continuous covariate), number of subjects with each category (categorical covariate), informing whether data transformation or some other adjustment to the method is needed,
the potential role of the covariates to support decision making,
the ability of the covariates to represent the clinical conditions of interest (such as hepatic or renal impairment).
In addition to the considerations listed above, graphical exploration of random‐effect estimates of parameters versus covariates and generalized additive models 24 are sometimes used in exploratory contexts to limit the covariate scope before formal covariate model development begins, although it is important to note that this approach may be a source of bias by exclusion. Any use of the observed response (such as concentration in a PK model) to refine the covariate scope may contribute to overall selection bias and multiplicity and, for this reason, should be avoided. The probability of a false positive covariate relationship increases as the number of covariates included in a priori screening increases. In the event that consumers of the analyses are not aware of the extent of screening, this may have the effect of hiding the true risk of false positives. Moreover, the subjective nature of graphical screening entails a less transparent decision path, potentially elevating concerns with “cherry‐picking” in order to obtain a covariate model that supports a desired conclusion. As such, prior exclusion of covariates based on graphical and/or generalized additive model (GAM)‐based screening is generally not suitable in the context of a confirmatory analysis. Additionally, these methods have limitations where empirical Bayes estimates of model parameters may be biased and shrunk toward the population mean when data are not rich to estimate that parameter and thereby warrants caution when using these methods. 25
Correlations between covariates
Once an initial covariate scope has been established, consideration should be given to correlations between covariates. Full investigation of covariate correlations is only possible after data acquisition and as such is not a planning activity in the strict sense. Reduction of covariate scope based on covariate correlations, however – insofar as it is carried out without regard to the observed values of the response variable – maintains the spirit of prespecification and is appropriate even in confirmatory contexts. 26 Consideration of well‐established causal relationships may provide a basis for informing the covariate scope. For example, renal function has an obvious direct causal effect on any renally cleared drug, and the effects of body size and body composition on PK parameters also have a strong biological and experimental basis. 5 , 27 Age, by contrast, is just a marker for the passage of time and thus cannot have a direct causal effect on body structure and function, even though it might be correlated with these. Thus, it is often reasonable to assume that the effect of age is mediated by the more clearly mechanistic causal effects of body size, body composition, and renal function. In such cases, it will often be reasonable in adults to exclude age from the covariate scope. The use of postmenstrual age and postnatal age are important covariates that are not explained by body size, body composition, and renal function in neonates and infants. 28 It should also be noted that the inclusion of covariates, such as age and sex, in the calculation of CLcr does not mean that other covariate effects involving age and sex (such as fat‐free mass) should be considered confounded with CLcr and thus excluded from the covariate scope. This is because the influence of renal function and body composition on a parameter, such as clearance, are mechanistically quite different. It is important to note that potentially misleading associations with increasing age may arise when other mechanistically based covariates that are correlated with age, such as plasma protein binding, are not accounted for.
The inclusion of correlated covariates can result in problems of both bias and imprecision for parameter estimation. In a scenario in which one of two correlated covariates can be considered more mechanistically appropriate, the likelihood of selecting the covariate with the more mechanistic effect decreases with increasing the correlation of the covariates when both are tested on the same parameter in the context of stepwise covariate modeling. 20 In the same vein, in a scenario in which two correlated covariates are both included on the same parameter, increasing correlation between the covariates will lead to increasing correlation between the estimates of the two covariate coefficients, resulting in increased estimation uncertainty in both. 26 When prior information is not sufficient to identify the more mechanistic (explanatory) of two covariates, data‐driven selection may be better, provided there is enough information in the data for this purpose; both candidate covariates could be included in the covariate scope in this instance. 29 Finally, although not a matter of covariate correlation, per se, an additional concern with the “masking” of covariate effects arises in the context of nonlinear mixed effects modeling when substantial shrinkage is present. For example, if PK data have been collected at sparse and/or suboptimal sampling times, population estimates of KA and V parameters may be highly correlated; similarly, if too narrow a range of doses is studied to inform the PD component of a model, population estimates of E max and C 50 may also be highly correlated. In such cases, the risk of selecting the right covariate on the wrong parameter is elevated. Allowing the covariate effect to be estimated on both of the correlated parameters may mitigate the problem, albeit at a cost to model complexity and parameter imprecision. 30
Problems associated with correlated covariates may be less relevant when the objectives are purely predictive and parameter interpretation is not required. Inclusion of correlated predictors will not generally result in biased predictions as long as the correlation between the covariates is maintained in future data, and increased parameter uncertainty does not necessarily result in increased prediction uncertainty (although the inclusion of truly superfluous predictors will always be detrimental with respect to the trade‐off between bias and variance). This predictive justification should be adopted with care, however, because a model built on a sample population (such as a adults or healthy volunteer population) may not be representative of a future population (such as a patient population) owing to the assumption that correlations will be preserved in future data. 5 , 27
Covariate correlations can be explored graphically, or numerically, by calculating pairwise correlation coefficients for continuous and binary covariates (Supplementary Material S1, section 2.2).
Missing covariate data
Missing covariate data are often encountered in the analysis of clinical data. Handling missing covariate values in an appropriate manner is important to avoid bias and imprecision of parameter estimates. Over the past several years, methods to handle missing covariate data, such as substitution with the median or the most common values in the population, single or multiple imputation, complete case analysis or list‐wise deletion, and maximum likelihood modeling, have been proposed for nonlinear mixed effect models. 31 , 32 , 33 Similarly, methods for handling missing categorical covariates (such as complete case analysis, estimation of an additional covariate, and several mixture model approaches) have been proposed based on the underlying reasons for missingness. 34 Methods such as the Fixed Random Effects Model (FREM), have been successful in partially or completely offsetting issues presented by incomplete covariate data. 35 In recent years, machine learning methods, such artificial neural networks and random forests, have also been implemented for imputation of missing covariates. 36 , 37 Regardless of which methodology is selected, it is important from a transparency perspective that the general methodological approach be established prior to consideration of the analysis.
Functional forms of covariate‐parameter relations
At the analysis planning stage, one often lacks a sufficient basis to fully prespecify the functional forms of all parameter‐covariate relationships with complete confidence, even in so‐called “confirmatory” settings. Nonetheless, transparency in model‐building and associated decision making is enhanced to the extent that one documents prior preference for particular functional forms, pending diagnostics that may or may not support that prior preference. Prior preference in many cases is a simple matter of convention and/or mathematical convenience. For example, linear functional forms have the desirable property that a change in the value of the covariate produces a proportional increase or decrease in the associated parameter. Certain functional forms are justifiable in advance, such as the application of allometric theory to describe the relationship between CL and V parameters and body weight.
When dealing with categorical covariates, low‐frequency categories are often encountered. Most often, this is handled by combining with other categories (commonly the reference category). Careful consideration is required when doing this, however, because it may lead to biased estimates of covariate effects or even a failure to identify rare effects. 38 Scientific and clinical judgment and prior knowledge are again essential in such situations. Mathematical specification of a variety of functional forms is provided in the next section.
COVARIATE MODELING
General considerations for continuous covariates
For continuous covariates, such as age and body weight, linear, exponential, or power functions may be used to describe the relationship between the covariate and PK and PD parameters. The choice of the functional form is influenced by several factors, such as the qualitative shape of the relationship between the parameter and the continuous covariate (e.g., linear, concave, convex, and sigmoidal), 39 and the distribution of the covariate itself (if the covariate can include negative values, the use of a power model is not appropriate, for example).
The linear functional form is easier to interpret but may require that the parameter space for the covariate parameter be appropriately bounded in order to avoid physiologically implausible results (such as negative values for parameters). 40 For parameters that have lognormal random‐effect distributions (most PK and PD parameters), covariate relationships described by exponential functions assure that the resulting PK or PD parameters respect appropriate boundaries regardless of covariate values. For power relations, the same is true as long as covariate values are larger than zero. Regardless of the functional form, caution should always be applied when considering extrapolation beyond the range of the observed data. In other cases, well‐established empirical relationships exist, such as those describing maturation effects on CL over the first 2 years of postnatal age. 6 , 28 The particular sigmoid E max function that is typically used for this purpose does not have a mechanistic justification, but it does generate biologically plausible values when extrapolated between age at conception (value = 0) and maturation as an adult (value = 1). 28 Continuous models of this kind offer advantages over more empirical models such as those applying linear splines or breakpoints (an example of which is the so‐called “hockey stick” model) in circumstances in which covariate relationships are nonlinear. Table 2 provides the mathematical equations and summarizes considerations for choosing the most appropriate functional form for a relationship.
TABLE 2.
Summary of functional forms for continuous and categorical covariate models.
| Functional form | Mathematical form | Interpretation | Considerations | |
|---|---|---|---|---|
| Continuous | ||||
| Linear |
|
The linear form is easy to interpret. The represents the relative change in () per unit change in covariate . As with the other continuous functions listed in this table, the shape of this relationship describes monotonic increase or decrease depending on the estimate of . | May require that the parameter space for the covariate coefficient to be appropriately bounded in order to avoid physiologically implausible parameter values (such as negative values) 22 | |
| Exponential |
|
The represents the unit change in log () per unit change in covariate . The shape of this relationship describes monotonic increase or decrease depending on the estimate of . | Use when the relationship between parameter and covariate is non‐linear. Useful for biological parameters where negative values are implausible. However, similar to linear models, biological responses are generally capacity limited and may not indefinitely increase or decrease with change in parameter and therefore may need covariate coefficients to be upper bounded in estimation. | |
| Power |
|
The represents the unit change in log () per unit change in . |
Use when the relationship between parameter and covariate is nonlinear. Not allowed in case both negative and positive covariate values exist. A covariate value of zero will force the parameter to zero. Useful for biological parameters where negative values are meaningless. However, similar to linear models, biological responses are generally capacity limited and may not indefinitely increase or decrease with change in parameter and therefore may need covariate coefficients to be upper bounded in estimation. |
|
| Categorical | ||||
| Linear for nominal |
|
The represents the relative change in the () when the covariate is at the non‐reference level N. | Use for nominal categorical covariate that has binary or polychotomous levels | |
| Linear for ordinal |
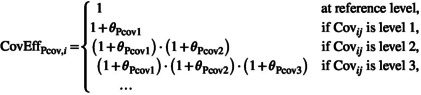
|
The represents the relative change (in relation to to level N‐1) for (), when the covariate is at the non‐reference level N. |
Use when it is important to preserve an ordinal relationship (i.e. for ordered categorical variables) Ordered categorical covariate relationships may be restricted to be either strictly increasing or strictly decreasing, as appropriate |
|
Continuous covariates may be transformed, or binned, into categorical form. Median, tertile, or quartile boundaries are commonly used for this. However, a major disadvantage of this approach is the loss of information that occurs with this kind of coarsening and is not generally preferred. For instance, the US Food and Drug Administration recommends use of a regression approach to better estimate the effect of renal function on PK parameters instead of utilizing categorical variables that correspond to normal, mild, moderate, and severe renal impairment. 41 Categorization may be performed at the simulation stage after a model containing the full continuous covariate has been developed in order to understand the loss of information arising from this transformation.
Remarkably high or low values of covariates – outliers – are not unusual, nor are distributions of values that are non‐normal (most often, heavy‐tailed and/or skewed). In such circumstances, extremely high or low values may inappropriately influence or distort estimates of covariate effects. A common technique applied to offset this problem is to “cap” covariate values over a certain cutoff at the value of the cutoff or to transform the distribution so that it is more “normal” (logarithmic transformation is the most commonly used). 21 Graphical exploration of covariate distributions is a useful way to determine whether this is necessary.
Functional forms for continuous relationships are usually applied after centering (by subtraction) or scaling (by division) the covariate by a reference value so that population parameter estimates will correspond to these reference covariate settings. The reference value used for scaling or centering can be either a centered value of a covariate dispersion, such as a median, or it could be a standard (commonly accepted) reference, such as a weight of 70 kg. 42 However, if the reference covariate value is selected outside the middle of the covariate distribution (e.g., when fitting pediatric data), this may result in inflated parameter imprecision of the structural parameter at the reference value and model instability 43 leading to estimation issues and difficulties in convergence. On the other hand, using a centered reference value can help improve model stability, but can hamper the ease of between‐study comparisons. The choice of using standard or centered reference values therefore depends on one's objective. It should be noted that regardless of the choice, a stable model should converge to the same estimates of the covariate effects and minimum value of the objective function because the likelihood is invariant to the centering/scaling of the parameters. Standard reference values, if widely accepted, can be used when within the covariate range and may be used with caution when extrapolating beyond the covariate range provided the model is stable (e.g., fit the model with both standard and centered reference values and confirm that they converge to the same set of estimates of the covariate effects and objective function value [OFV]). Standard reference values can also be used when applying the same model to an updated dataset, which can help to make comparisons easier. In other situations, a centered value may be used for estimation purposes, but when reporting, parameter values with any covariate reference of interest may be calculated for purposes of comparison. Centering and scaling approaches provide better interpretation of the population parameter at the reference value, and, in addition, reduce correlation between fixed effect estimates for the reference value of the population parameter and covariate effect leading to more stable estimation.
General considerations for categorical covariates
Categorical covariates can be binary (2 categories) or polychotomous (3 or more categories) and can be ordered (ordinal scale) or non‐ordered (nominal scale). An example of nominal categories is geographic region, whereas the Eastern Cooperative Oncology Group function score is an example of an ordinal categorical variable, in which values of 0, 1, or 2, ordered as 0 less than 1 less than 2, represent the degree of functional performance of an individual. In such a case, treating them as ordered is more appropriate than testing them as nominal categories, or combining them. Table 2 presents the typical mathematical forms that are commonly used for either nominal or ordinal categorical covariates. Table 2 also presents some interpretations and considerations for each of these forms.
Modeling the combined effects of multiple covariates on a parameter
The effects of more than one covariate on a specific parameter are often combined using either multiplicative or additive form as shown in Equations 1 and 2 respectively. 44
Multiplicative form
| (1) |
where is the multiplicative change in parameter P due to the covariate (cov) in individual i. is the population reference value of the parameter P in the population. is the typical value of the parameter for individual i with all covariate effects included.
Additive form
| (2) |
Multiplicative specification may be more practical (and sometimes also more plausible and/or mechanistic) than the additive, if the (structural) parameter is restricted to positive values. If, on the other hand, parameters may take positive or negative values, such as a logit probability, log‐hazard, or a difference parameter (such as a mean orthostatic change in blood pressure), the multiplicative formulation is likely to have problems of interpretation and an additive parameterization may be preferred. In Supplementary Material S2, an example of covariate models combined by multiplication of individual covariate effects is presented. In the illustrative example in Supplementary Material S1, section 3.4, equations and demonstrations of fits of different functional forms are demonstrated.
General considerations for time‐varying covariates
The covariates described above may vary with time, such as body weight, the use of concomitant medication, and organ maturation in neonates and infants. Time‐varying covariates present several challenges and complexities: for instance, covariates may be impacted by treatment, as is the case for changes in renal function caused by renally eliminated antibiotics, such as vancomycin, 45 or changes in the performance status of a patient over time, such as in cancer 13 or organ transplantation. 46 Accounting for time‐related changes in covariate effects is often important for ensuring appropriate dosing and exposure, as well as for assessing PD effects without bias. 13 , 14 Baseline values are commonly used, but often this approach may not adequately explain intrasubject variability. As an example, clearance of ipilimumab was observed to decrease over time in some patients and was considered a marker for improvement in clinical condition. Evaluating the effects of time‐varying markers for cancer‐related cachexia, such as albumin, body‐weight, and LDH, helped to further elucidate possible mechanisms of time‐varying CL. 47 Models to implement extensions to the covariate model for time‐varying covariates have been described by Wälbhy et al. in which the covariate effect is either split into the baseline and difference from baseline, and/or an interindividual variability parameter is estimated in the covariate effect. 48 The complexity of time‐varying covariates warrants a broader discussion than we have space for in this article, but it is important that it not be overlooked.
COVARIATE MODEL BUILDING METHODS
The selection of a covariate model‐building approach is generally driven by the objective and context of the analysis (exploratory or confirmatory, for example) and the amount of available information. The covariate model building methods most commonly used are classified into two categories: screening methods and prespecification methods. Within the screening methods, the selection of covariates is driven by the analysis dataset, often with a selection of putative relationships suggested by prior knowledge. With sufficient information, screening approaches may be appropriate and practical for developing models that merely need to be predictive (for use in the simulation of clinical trials, for instance). Screening methods, when applied to external /prior data, can also serve as a guide for the prespecification methods. In contrast, prespecification methods are often useful for confirmatory analyses where justification of dose adjustment (or lack thereof) is the major goal; in this context, demonstrating the practical absence of a covariate effect (such as those related to primary demographic characteristics, such as age, weight, sex, and race, as well as common conditions, such as renal and hepatic impairment) is often just as important as detecting covariate effects that are actually present. In the best application of this approach, even the functional forms of the covariate relationships would be prespecified, either based on prior knowledge or else based on prior application of screening methods, such as graphical exploration or GAM (applied to external/prior data).
A mixture of both approaches that utilizes prior knowledge about common covariates (Table 1) and established covariate models and parameters to build a “base” model, that can then be used as the base for further covariate model building using screening methods, has been used as well. This approach builds on well‐established science (for example, by assuming that PK parameters vary with size, babies mature into adults, and renally eliminated drug clearance is predictable from CLcr) and can then lead to more finely tuned exploration of other covariates that are otherwise lost in the random effect noise. 22 Evaluating covariates based on their mechanistic relevance or exploratory nature has also been implemented in stepwise covariate model (SCM+) building methods described in the sections below. 49
Screening methods
Stepwise generalized additive modeling
This method uses regression of individual post hoc estimates with covariates using generalized additive models. 50 A stepwise addition or deletion is then used to select covariate relationships using a selection criterion, usually the Akaike information criterion (AIC). 51 This approach may be problematic in case of high shrinkage 25 or if not all model parameters of interest include random effects. We refer the reader to section 4.2 in the Supplementary Material S1 for an illustrative example, although this approach is not often used in practice.
Wald approximation method
Kowalski and Hutmacher proposed a covariate model building method based on Wald's approximation method (WAM). 52 The WAM provides a quadratic approximation of the likelihood ratio, based on the covariance matrix of the estimates from a full model. The selection of covariates for WAM consists of obtaining a convergence of the full model (a model including all covariates) and uses the ranked Schwarz information criterion for model selection. The WAM generally requires fewer model runs than stepwise procedures to identify a final reduced model and provides a set of competing parsimonious models. However, the WAM requires that all full models, including all covariate‐parameter relations to be investigated, can be estimated without convergence problems and with a successful covariance step, which can be challenging. We refer the reader to section 4.3 in Supplementary Material S1 for illustrative example and technical details. Again, this method is not in common use.
Stepwise covariate model building and advances
Stepwise covariate modeling (SCM) consists of sequential application of predefined rules to add (forward selection) or remove (backward elimination) covariates depending on the value of a statistic, such as a p value or a model selection criterion, such as AIC or Bayesian Information Criteria, and is one of the most popular methodologies in current use for the systematic selection of covariates. 53 We refer the reader to section 4.4 in Supplementary Material S1 for illustrative example and technical details. Extensions to the standard approach, such as bootstrap SCM, allow the evaluation of selection bias during SCM, identification of correlations between included covariates, and assessment of the type I error rate for covariate inclusion (false positive covariates). 54 First‐ and second‐order linearized SCM can identify parameter‐covariate relationships from a large pool of parameter‐covariate relations in a fraction of computational time compared to traditional SCM and is useful if SCM run times are very long. 55 A novel method, Conditional Sampling used for Stepwise Approach based on Correlation (COSSAC), is based on a statistical test between individual parameters sampled from conditional distribution and covariates has been recently introduced. It has been demonstrated to speed up the SCM process. 56 Additional sophisticated techniques within the SCM toolkit, such as SCM+, which uses the “adaptive scope reduction” and SCM+ with “stage‐wise filtering” that categorizes covariates based on its importance, such as mechanistic, structural, or exploratory have been shown to perform better choosing relevant covariates than traditional SCM methods. 49 Tools such as Perl‐speaks‐NONMEM (PsN) have been developed to automate the process, allowing many covariate relationships and functional forms to be tested in sequence and in parallel. Stochastic Approximation for Model Building Algorithm (SAMBA) is another novel approach that is an iterative procedure that aims to accelerate and optimize the model‐building process by identifying the best way to improve the model components at each step. 57 As with other fields of medicine, machine learning algorithms are also being explored for covariate screening. Machine learning methods, such as random forest, neural networks, and support vector regression were compared to traditional screening methods and were found to be more efficient in case of large datasets or complex models with long run times. Although these advances are promising, experience with these novel methods is relatively limited at the time of writing.
The least absolute shrinkage and selection operator
The least absolute shrinkage and selection operator (LASSO) is a method that aims at optimizing the covariate model for good predictive performance (including covariate relations to the degree they are expected to improve the predictive performance, given the available data for analysis). 58 , 59 Although it may not be a commonly used method, this has been shown to be useful in situations where the SCM is difficult when selecting covariates from small datasets (few subjects, or investigating small subgroups, such as rare genotypes). 58 , 60 Using cross‐validation, the implementation of the LASSO method provides an evaluation of the covariate model and does not require the user to specify a p value for selection. We refer the reader to section 4.5 in Supplementary Material S1 for illustrative example and technical details. The LASSO algorithm has been extended to HyperLasso 60 (which proposes applying a slightly more generalizable penalty function) and the adjusted adaptive Lasso 61 (which may perform better in small datasets).
Prespecification methods
Full fixed effect model
The full fixed effect model (FFEM) has become a popular prespecification approach for evaluating covariate effects. Within FFEM, all the parameter‐covariate relations of interest are estimated simultaneously, in contrast with covariate selection algorithms that evaluate multiple models within the model space for various combinations of presence or absence of individual covariate effects with the goal of finding a parsimonious model (one with fewer covariate parameters) that adequately fits the data. 62 Such parsimonious models may have reduced prediction error relative to a full model, because a full model may have some covariate parameter estimates that are essentially contributing noise to the predictions. In contrast, full model methods (assuming the full model is stable) are better for making inferences about individual covariate effects because they establish a fixed baseline for inference (a single full model is fitted), whereas data‐driven covariate selection methods result in final models in which numerous covariate relationships from the full model have been removed, suggesting more is known about the data than is truly the case and resulting in downwardly biased estimates of standard errors. Whereas the term “full model” is generally understood to refer to a model that includes all relationships that have prior plausibility, the term “saturated model” may be used to refer to a model in which the relationships of all covariates in scope with all parameters are estimated regardless of plausibility. The use of saturated models mitigates the risk of parameter bias due to model misspecification but is not always practical because of the number of parameters to be estimated. The full model approach also considers a data reduction step with regard to avoiding the addition of correlated covariates, such as weight and body mass index, on the same parameter, such as CL, and thereby avoid issues with model instability, as discussed in earlier sections of this review. 62 Another potential caveat in use of FFEM approach, however, may also occur in a situation in which two model parameters are highly correlated – in this instance, the same covariate would be relevant for both, but the coefficients and the precision of the estimate or estimates would be quite different depending on whether the covariate effect was applied to one of the two, or both. In this case, it would probably be most appropriate to apply the effect on only one, with the choice being driven by scientific plausibility and the purpose of the model. We refer the reader to section 3.3 of Supplementary Material S1 for FFEM model fit.
Full random effect model
In the FREM, all covariates are treated as components of a multivariate response. The relationships between all covariates and all parameters of interest are estimated simultaneously as covariances within a multivariate random effects distribution. 63 , 64
There is a benefit in estimating all parameter‐covariate relationships and the computational cost is typically small compared to data‐driven approaches. As implemented in software, such as PsN, all covariates are estimated on all model parameters. For example, if a food effect on absorption rate is included as part of the FREM it will also be included on all other parameters, such as distribution volumes, regardless of whether they are mechanistically plausible, in order to minimize the likelihood of bias introduced by model misspecification. The FREM model may be converted to the FFEM model for diagnostics, goodness‐of‐fit, and for simulations and predictions necessary for communication. We refer the reader to section 4.6 of Supplementary Material S1 for an application example using the PsN implementation.
An overview of the most used covariate model building methods is presented with the advantages and challenges of each method in Table 3.
TABLE 3.
Key characteristics of covariate model building methods.
| Method | Key characteristics |
|---|---|
| Build on established knowledge |
|
| Graphical exploration method |
|
| Stepwise GAM |
|
| SCM |
|
| LASSO |
|
| WAM |
|
| Prespecification methods | |
| FFEM |
|
| FREM |
|
Abbreviations: CL, clearance; EBE, empirical Bayes estimate; FFEM, full fixed effect model; FREM, full random effect model; GAM, generalized additive model; LASSO, least absolute shrinkage and selection operator; PsN, Perl‐speaks‐NONMEM; SCM, stepwise covariate model; V, volume of distribution; WAM, Wald approximation method.
MODEL DIAGNOSTICS FOR COVARIATE EFFECTS
It is important to assess whether covariate‐parameter relationships present in the data are adequately characterized by the functional forms represented in the final model. This can be done by plotting the random effects against the covariates; the plots should demonstrate the removal of trends. In the theophylline example described in Supplementary Material S1, weight and age showed trends when plotted against empirical Bayes estimates (EBEs) of the base model without covariates, whereas the trends were removed after inclusion in the full model with covariates. Such diagnostics should be evaluated with an awareness that ή parameter shrinkage toward the mean has the potential to mask covariate relationships in such displays, 65 although advances in algorithms can correct the bias of EBEs in both estimation of effect size and test statistics. 66
Visual predictive checks (VPCs) stratified by covariates of interest are also useful for illustrating how covariates have influenced model fit. 27 , 67 For continuous covariates, VPCs depicting a continuous covariate as the independent variable can provide a useful method to evaluate the appropriateness of the model at different covariate values. 68 Model diagnostics for covariate effects should be provided to the extent necessary for a reader to develop an appropriate level of confidence in the model's characterization of those relationships. For ease of exposition for nonspecialist readers, diagnostics that are primarily of interest to specialists may be relegated to an appendix or supplementary material. Section 5 in Supplementary Material S1 provides examples of VPCs for the purpose of model diagnostics.
COVARIATE EFFECT SUMMARY AND REPORTING
General principles for reporting
Reporting of covariate results constitutes the crucial hinge by which the insights gleaned from modeling may open or close the door to strategic decisions in the development, approval, and clinical use for dose individualization. Reporting should therefore be carried out in a manner that facilitates comprehension for decision makers, many of whom will be nonspecialists with respect to modeling, whereas at the same time providing sufficient detail to satisfy modeling specialists who may wish to confirm or leverage certain findings in the future models or analyses of their own.
When reporting, model parameters should be summarized in a table that (at a minimum) provides parameter estimates and associated measures of uncertainty (Supplementary Material S1, section 6). Typically, covariate effect parameters and primary parameters (such as bioavailability, clearance, and volume of distribution, in the context of a PK model) can all be described in a single table. One should ideally include a column with brief text in each entry to explain the interpretation (an example would be the change in a parameter per year increase in age). It will frequently be the case that some transformation of a parameter estimate (commonly its exponentiated value) will be more readily interpretable than the parameter itself. Reporting on the transformed (more interpretable) scale tends to be more amenable to supporting the discussion and conclusions in a report, whereas reporting on the scale used for likelihood optimization (or posterior sampling, in a Bayesian framework) is likely to facilitate future use of the model by pharmacometricians who may not have access to the data and/or model output. In many cases, the use of the model by other pharmacometricians can be enabled and facilitated with supplementary material; reporting on the transformed scale may be preferable in the body of a report. The functional form of parameter transformations should be provided for covariate effect parameters that are tabulated on a transformed (e.g., exponentiated) scale. Parameter scales should also be carefully chosen when reporting numerical values. For example, a reported fold odds adjustment of 1.001 per ng/mL concentration creates the impression that the effect of drug concentration is negligible, but if interventions differing on the μg/mL scale are considered, one should note that 1.001^1000 = 2.7, corresponding to a 2.7‐fold change in odds of event for every μg/mL increase.
Discussion of explained parameter variability (EPV), the part of parameter variability explained by inclusion of covariate effect, may facilitate understanding of the importance of a given covariate‐parameter relationship. It is expected that covariate inclusion on a specific parameter will explain part of the parameter variability between subjects leading to increased predictability in response. Hence, it is expected that EPV will increase and the unexplained PV will decrease. 69
Statistical significance in model development and inference
In the context of covariate modeling, statistical significance may arise in two distinguishable ways:
In reference to a prespecified model including a given parameter‐covariate relationship, hypothesis tests provide one framework for valid statistical inference about that relationship. As has been emphasized in the statistical community, 70 inferential frameworks based on confidence intervals (or credible intervals, in the Bayesian context) are typically more informative and less subject to misinterpretation than are p values or assessments of statistical significance. Nonetheless, null hypothesis significance tests may provide a valid means of inferring the direction of covariate effects, when used appropriately in reference to a prespecified model.
As a technique for covariate model development (in stepwise covariate modeling, for example), hypothesis tests (such as the likelihood ratio test [LRT]) merely provide a reasonable heuristically motivated algorithm for including or excluding covariates but do not provide a basis for valid statistical inference. The LRT is based on the difference in minimum OFV between models with and without the covariate relationship. The first and second order approximations of the models as implemented in commonly used software tools such as NONMEM result in OFVs that are approximately proportional to minus twice the logarithm of the likelihood of the data given the model (−2LL). Under the null hypothesis we assume that the simpler covariate model is correct, the difference in OFV (the likelihood ratio [∆OFV]) between two nested models is approximately χ 2‐distributed. Because the simpler model may exclude a number of other important covariates (in addition to other potential model misspecifications and deficiencies in asymptotic approximations), the actual significance levels achieved by the use of the likelihood ratio test will often be different from nominal levels. 71 Indeed, it has been noted that the actual significance level of the likelihood ratio test is upwardly biased. 72 , 73 As discussed in the preceding sections, all screening covariate model building techniques are subject to selection bias, which reduces the evidential value of “statistically significant” results in comparison to the evidential value that statistical significance has in a confirmatory context. Selection bias is often less important with higher‐power covariates (that exert stronger effects) but should be borne in mind where effects are smaller or less precisely estimated.
Statistical significance and clinical relevance
Neither of the above applications of significance testing provides any basis for inferring that a covariate “has no effect.” A lack of significance is rightly interpreted as an “absence of evidence,” but not as “evidence of absence.” Evidence of the (practical) absence of a covariate effect is most convincingly demonstrated by including the covariate effect in the model and assessing (usually by means of a confidence interval) whether non‐negligible values of the covariate effect can be ruled out, as discussed below.
Hypothesis tests of the null hypothesis of “no effect” and associated p values do not provide information about the magnitude of a covariate effect, and so are insufficient to address questions about clinical relevance. 70 It should be noted, however, that this concern relates specifically to hypothesis tests of “no effect.” The concepts of statistical significance and clinical relevance are distinct but need not be applied disjointly. For example, when a clinically relevant threshold * can be established, a statistical test of H0: ≥ * versus H0: < * can result in a valid statistical inference that “the magnitude of the effect is statistically significantly less than any effect that would be clinically relevant” (if the null is rejected) or that, “effects in the clinically relevant range cannot be ruled out” (if the null is not rejected). Whereas this hypothesis testing formulation is rarely explicitly used in pharmacometric covariate analyses, it is often used implicitly by juxtaposing confidence intervals with reference lines that provide working demarcations between clinically relevant and clinically irrelevant values. (This constitutes an implicit use of hypothesis testing because a confidence interval can be inverted to provide a hypothesis test of every parameter in the parameter space. 74 )
The clinical relevance of covariates is usually determined in the context of the need to modify the dosing regimen in accordance with the covariate. A value of 20% difference in exposure has been widely cited as a clinically irrelevant change that does not require dosing adjustment. 75 , 76 This convention has been borrowed from the bioequivalence context, but alternative heuristics have been proposed for establishing regions of practical equivalence that are appropriate to a given context. 77 Once such a region is defined, three scenarios come into play:
If the entire 95% confidence interval (or credible interval) for the covariate effect lies within the clinically relevant region, the covariate relationship is clinically relevant. Such a covariate relationship will be always statistically significantly different from the null (“no effect”) value.
If the entire 95% confidence interval (or credible interval) for the covariate effect lies within the clinically irrelevant region, the covariate relationship is not clinically relevant. Such a covariate relationship may or may not be statically significantly different from the null (“no effect”) value. It may be important in combination with other relationships.
If the 95% confidence interval (or credible interval) for the covariate effect spans both clinically relevant and irrelevant regions, there is insufficient information for the clinical relevance of the relationship to be unambiguously determined. Such a covariate relationship may or may not be statistically significantly different from the null (“no effect”) value. In the event that the null value is excluded, one may confidently infer the direction of the effect, even though the magnitude cannot be established with sufficient resolution.
Predictive summary
Whereas regression coefficients have fairly direct and straightforward interpretations for linear models with normally distributed errors, this is not the case for nonlinear mixed effects models, nor is it the case for generalized linear models. 78 In cases where the covariate is applied to a physiologically interpretable parameter, such as CL, predicted values of that parameter at a variety of covariate settings will facilitate interpretation. Supplementary Material S1, section 6 provides examples of forest plots describing covariate effects. Additionally (and especially when covariate's effect on a parameter has less obvious physiological meaning), interpretation is enhanced by providing a similar plot for the predicted value of an exposure metric, such as the area under the curve from zero to infinity. Predicted values of the dependent variable itself (such as drug concentration or PD effect) may also be shown in a variety of covariate settings (by plotting the expected value against time with uncertainty, using faceting 79 to represent conditioning on values of the covariate, for example).
For categorical covariates, the predicted response can often be shown at each level of the covariate. For continuous covariates, percentiles of the covariate distribution will typically provide helpful reference points at which to assess the model‐predicted values.
When generating predictions across multiple values of a single covariate, it is not always clear how the other covariates and random effects should factor into the predictions. A common practice is to present a predicted value (with confidence interval) for a “reference subject” alongside predicted values (and confidence intervals) for what might be called “perturbed reference subjects,” those with the same covariate, except for one covariate that has been changed to another level. This methodology has been proposed as a reasonable analog to partial regression coefficients, 78 , 80 at least in the sense that the covariate's effect is being evaluated “after adjusting for all other covariates.” Although such partial effects have the merit of essentially re‐expressing regression coefficients on a more interpretable scale, one should consider whether predictions derived in that manner adequately address the research questions of interest. Whereas the ceteris paribus (“other things equal”) approach may be reasonable for answering questions about exogenous interventions (such as “What would happen if we held everything else equal and changed exposure only?”), it may be quite unreasonable to answer questions about the predictive associations of endogenous risk factors (such as “What would happen to the exposure level if we held bodyweight constant at 70 kg, but the patient was 4 years old rather than 65?”). For this reason, it will generally be desirable to complement ceteris paribus simulations with mean or quantile predictions for a population with varying covariate values. For instance, a plot of predicted parameters or exposures could be generated to compare predictions between elderly (age ≥ 65) and non‐elderly (age < 65) in which appropriate values of other covariates for each age category are used.
FREM provides one means by which this may be accomplished, averaging the conditional distribution of other covariates conditional on the covariate under investigation.
USE OF COVARIATE MODELS: REGULATORY AND PATIENT PERSPECTIVES
Covariate analyses have been successfully used to support the recommended dose proposals in regulatory submissions, with the most common covariates that may/may not require a dosage adjustment presented in Table 1. For example, weight‐based dosing is supported by a positive allometric relationship of CL and body weight, whereas “flat” dose proposals (a single dose for all subjects) can be justified by the absence of such a relationship in a suitably designed study with adequate power. Identified covariate relationships have also been used in PK/PD analysis to provide information about the balance between effectiveness and safety. Covariate relationships for PK and PK/PD analyses are also used to guide contraindications, recommendations for situations where drug–drug interactions may occur and for extrapolation. An example of how covariate relationships are used in extrapolation can be found where adult PK data are used to predict dose or exposure in pediatric populations. Extrapolation is particularly useful during PK/PD dose ranging or dose finding studies in one or several pediatric age ranges.
To date, published regulatory guidance on covariate adjustment has focused particularly on the use of covariates in randomized comparisons (https://www.fda.gov/media/123801/download). In that context, covariate adjustment is primarily a matter of statistical efficiency, because randomization itself can be expected to remove most covariate imbalances between treatment groups. As such, randomized comparisons inherently reflect the causal effects of treatment rather than artifacts of causal confounding (except in cases where the randomization is invalidated by intercurrent events occurring between randomization and outcome; see https://www.fda.gov/media/108698/downloadg). By contrast, the associations of interest in pharmacometric analyses typically correspond to non‐randomized comparisons (e.g., high exposure vs. low exposure and normal renal function vs. impaired renal function). In the pharmacometric context, therefore, covariate adjustment does not merely offer optional gains in statistical efficiency but is fundamentally required in order to mitigate the risks of confounding that attend observational (nonrandomized) data. Even more important to patients and clinicians is the use of covariate‐guided dosing when initiating therapy and during follow‐up when response measures may also be available.
In general, trust in the results of a covariate analysis arises from the transparent use of appropriate methodology as described in the previous section on Planning Covariate Analyses and Covariate Modeling. In particular, it is essential for regulators and clinicians to understand which covariates have been evaluated on which parameters in order to correctly assess the strength of evidence. Scientifically plausible relationships between parameters and covariates are needed to make label claims, which puts a strong emphasis on clinically relevant covariate relationships.
With respect to covariate scope, a particular point of clinical and regulatory interest is the degree to which a given covariate accurately represents a clinical condition (such as hepatic or renal impairment). It should be considered whether the covariate effect is scientifically plausible and whether it may be a surrogate for another covariate. For example, estimated CLcr using the Cockcroft‐Gault equation or estimated GFR using the modification of diet in renal disease equation are commonly used to define renal function. However, in some situations, such as in patients who are undergoing kidney replacement therapy, acute renal failure, extremes of age, body size, or muscle mass, conditions of severe malnutrition or obesity, disease of skeletal muscle, or on a vegetarian diet, the use of these equations may not be accurate to reflect the degree of renal impairment. In these situations, CLcr calculated using timed urine collection (e.g., 24 h) or measurement of clearance of an exogenous filtration maker will be more reflective of glomerular filtration. Moreover, modeling renal function as a covariate on a continuous scale is typically encouraged rather than categorizing the renal function into normal renal function or mild, moderate, and severe renal impairment.
Regulators understand that in many cases the different functional forms for covariate relationships may yield similar predictions because the covariate variability range is limited and does not allow such discrimination. In such cases, sensitivity analyses may be conducted to verify that the effect of different forms does not affect the estimate. Regulatory assessment of detected covariate relationships will also pay attention to whether a small number of influential subjects are driving the detected relationship. Fixed values can be accepted for some covariate effect parameters (for example, fixed theory‐based allometric exponents for weight effect on clearance and volume parameters of 3/4 and 1.0, respectively) but the justification for the fixed value should be provided.
Regulatory and patient perspectives require trust in both positive claims (as when an effect for a given covariate has been detected and quantified) and negative claims (as when it is asserted that no dosage modification is required for a given population). Considerations related to practical equivalence, as discussed above in the Reporting section, are therefore especially relevant. It is unlikely that decision makers will accept claims of no relevant clinically significant effect unless the relationship was actually tested. For detected parameter‐covariate relationships, decision makers are interested in knowing how precisely the effect has been estimated and the magnitude of the estimated effect so that appropriate recommendations can be made to the prescriber. It needs to be established whether or not the estimated effect size magnitude warrants a dosage modification. From a regulatory perspective, a two‐fold difference in PK exposure is a commonly used magnitude to justify dose adjustment based on PK data alone. However, the influence of magnitude of covariate effect on PK parameters can be better evaluated if a PK/PD relationship has been characterized and which allows the magnitude of the covariate effect to be put into perspective with regard to effectiveness or safety parameters, as appropriate.
Regulatory agencies are often open to all methods and innovations for covariate analyses, as long as the methods are scientifically sound and appropriately described.
SUMMARY AND RECOMMENDATIONS
It is difficult to recommend a “one‐size‐fits‐all strategy” for covariate model development, given the very wide spectrum of techniques, approaches, and tools that are applied, and the wide diversity in datasets and populations that come into play. Covariate analysis is typically performed, and results are reported, based on the purpose of the analysis and the anticipated audience. Failure to use a standard for reporting parameters 42 has made it difficult to find common features of models and use covariate analysis in a consistent way in order to discover new knowledge.
There are, however, several aspects of covariate analysis that are common to (nearly) all approaches.
Clearly document those aspects of the analysis that were prespecified and those that were decided upon based on the observed response data, so that consumers of the analysis may better assess the strength of evidence associated with the results. Ensure that technical aspects of the analysis (data encoding, functional forms, interpretation, and inference) are fully justified, documented, and subjected to quality control.
Be transparent when departing from prespecified methods and provide a rationale for such departures. A prespecified pharmacometrics analysis plan (PMAP) that prespecifies covariates, covariate selection algorithm, and criteria, etc., can go a long way toward ensuring such transparency. Then, when preparing the report PMAP may be referred for the extent to which the prespecified methods were followed and any departures and the rationale for those departures from the PMAP could be documented in a separate section in the report.
Use prior knowledge, scientific judgment, and mechanism‐based models to overcome challenges arising from inevitable correlations of covariates, such as size, age, and organ function. In the presence of highly correlated covariates, dimensionality may be reduced by focusing on mechanistically plausible relationships. Where no clear mechanistic advantage exists, sensitivity analyses using models with each of the two competing covariates may be performed to investigate the impact on predictions.
Ensure the base model is stable (parameters reliably and consistently estimated, with acceptable precision). Sometimes this may require adding covariate effects (such as allometric scaling of body weight) a priori.
Screening (data‐driven) approaches may be satisfactory when prediction is the primary goal.
If the model is to be used for identifying covariate relations that may be important in dosing or for other descriptive purposes, a prespecification approach will generally be the most appropriate.
Use sensitivity analyses as necessary to ensure that the covariate model is not unduly affected by parametric assumptions or high or low outliers. Complement model‐based analyses with exploratory (non‐model‐based) data analyses.
Facilitate the proper interpretation of negative findings by providing confidence intervals where possible and, in the event that one or more covariates have been excluded from the model entirely based on a screening method, by alerting consumers of the analysis to the possibility that exclusion may simply represent insufficient data to detect the effect in question (“absence of evidence is not evidence of absence”).
We hope that what we have presented in this article will provide a useful basis for analysts to choose the most appropriate approach for their specific sets of circumstances. The goals of the analysis should typically inform the methodology used – no approach is perfect, but some are better suited to certain tasks than others.
FUNDING INFORMATION
None.
CONFLICT OF INTEREST STATEMENT
The authors declared no competing interests for this work.
DISCLOSURE
The opinions expressed in this manuscript are those of the authors and should not be interpreted as the position of the US Food and Drug Administration.
Supporting information
Data S1.
Data S2.
Sanghavi K, Ribbing J, Rogers JA, et al. Covariate modeling in pharmacometrics: General points for consideration. CPT Pharmacometrics Syst Pharmacol. 2024;13:710‐728. doi: 10.1002/psp4.13115
REFERENCES
- 1. Hutmacher MM, Kowalski KG. Covariate selection in pharmacometric analyses: a review of methods. Br J Clin Pharmacol. 2015;79(1):132‐147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Glymour C, Zhang K, Spirtes P. Review of causal discovery methods based on graphical models. Front Genet. 2019;10:524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Rogers JA, Maas H, Pitarch AP. An introduction to causal inference for pharmacometricians. CPT: Pharm Syst Pharmacol. 2023;12(1):27‐40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Germovsek E, Barker CIS, Sharland M, Standing JF. Scaling clearance in paediatric pharmacokinetics: all models are wrong, which are useful? Br J Clin Pharmacol. 2017;83(4):777‐790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Holford NH, Anderson BJ. Allometric size: the scientific theory and extension to normal fat mass. Eur J Pharm Sci. 2017;109:S59‐S64. [DOI] [PubMed] [Google Scholar]
- 6. Anderson BJ, Holford NH. Understanding dosing: children are small adults, neonates are immature children. Arch Dis Child. 2013;98(9):737‐744. [DOI] [PubMed] [Google Scholar]
- 7. Rhodin MM, Anderson BJ, Peters AM, et al. Human renal function maturation: a quantitative description using weight and postmenstrual age. Pediatr Nephrol. 2009;24(1):67‐76. [DOI] [PubMed] [Google Scholar]
- 8. Bosilkovska M, Walder B, Besson M, Daali Y, Desmeules J. Analgesics in patients with hepatic impairment. Drugs. 2012;72(12):1645‐1669. [DOI] [PubMed] [Google Scholar]
- 9. Matthews I, Kirkpatrick C, Holford N. Quantitative justification for target concentration intervention–parameter variability and predictive performance using population pharmacokinetic models for aminoglycosides. Br J Clin Pharmacol. 2004;58(1):8‐19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Fukudo M, Ikemi Y, Togashi Y, et al. Population pharmacokinetics/pharmacodynamics of erlotinib and pharmacogenomic analysis of plasma and cerebrospinal fluid drug concentrations in Japanese patients with non‐small cell lung cancer. Clin Pharmacokinet. 2013;52(7):593‐609. [DOI] [PubMed] [Google Scholar]
- 11. Hesselink DA, van Gelder T, van Schaik RH, et al. Population pharmacokinetics of cyclosporine in kidney and heart transplant recipients and the influence of ethnicity and genetic polymorphisms in the MDR‐1, CYP3A4, and CYP3A5 genes. Clin Pharmacol Ther. 2004;76(6):545‐556. [DOI] [PubMed] [Google Scholar]
- 12. Dai HI, Vugmeyster Y, Mangal N. Characterizing exposure‐response relationship for therapeutic monoclonal antibodies in Immuno‐oncology and beyond: challenges, perspectives, and prospects. Clin Pharmacol Ther. 2020;108(6):1156‐1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Liu C, Yu J, Li H, et al. Association of time‐varying clearance of nivolumab with disease dynamics and its implications on exposure response analysis. Clin Pharmacol Ther. 2017;101(5):657‐666. [DOI] [PubMed] [Google Scholar]
- 14. Wang Y, Booth B, Rahman A, Kim G, Huang SM, Zineh I. Toward greater insights on pharmacokinetics and exposure‐response relationships for therapeutic biologics in oncology drug development. Clin Pharmacol Ther. 2017;101(5):582‐584. [DOI] [PubMed] [Google Scholar]
- 15. Li C, Wang B, Chen SC, et al. Exposure–response analyses of trastuzumab emtansine in patients with HER2‐positive advanced breast cancer previously treated with trastuzumab and a taxane. Cancer Chemother Pharmacol. 2017;80(6):1079‐1090. [DOI] [PubMed] [Google Scholar]
- 16. Verotta D. Covariate modeling in population PK/PD models: an open problem. Adv Pharmacoepidem Drug Safety. 2012;1:006. [Google Scholar]
- 17. Holford N. Population PD Analysis . http://clinpharmacol.fmhs.auckland.ac.nz/teaching/medsci719/workshops/populationpd/
- 18. Holford N, Black P, Couch R, Kennedy J, Briant R. Theophylline target concentration in severe airways obstruction—10 or 20 mg/L? Clin Pharmacokinet. 1993;25(6):495‐505. [DOI] [PubMed] [Google Scholar]
- 19. Holford N, Hashimoto Y, Sheiner LB. Time and theophylline concentration help explain the recovery of peak flow following acute airways obstruction. Clin Pharmacokinet. 1993;25(6):506‐515. [DOI] [PubMed] [Google Scholar]
- 20. Ribbing J, Niclas Jonsson E. Power, selection bias and predictive performance of the population pharmacokinetic covariate model. J Pharmacokinet Pharmacodyn. 2004;31(2):109‐134. [DOI] [PubMed] [Google Scholar]
- 21. Kirkpatrick C, Duffull S, Begg E. Pharmacokinetics of gentamicin in 957 patients with varying renal function dosed once daily. Br J Clin Pharmacol. 1999;47(6):637‐643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. González‐Sales M, Holford N, Bonnefois G, Desrochers J. Wide size dispersion and use of body composition and maturation improves the reliability of allometric exponent estimates. J Pharmacokinet Pharmacodyn. 2022;49(2):151‐165. [DOI] [PubMed] [Google Scholar]
- 23. Holford N, Ma SC, Ploeger BA. Clinical trial simulation: a review. Clin Pharmacol Ther. 2010;88(2):166‐182. [DOI] [PubMed] [Google Scholar]
- 24. Hastie T, Tibshirani R. Generalized additive models. Stat Sci. 1986;1(3):297‐310. [DOI] [PubMed] [Google Scholar]
- 25. Karlsson M, Savic R. Diagnosing model diagnostics. Clin Pharmacol Ther. 2007;82(1):17‐20. [DOI] [PubMed] [Google Scholar]
- 26. Bonate PL. The effect of collinearity on parameter estimates in nonlinear mixed effect models. Pharm Res. 1999;16(5):709‐717. [DOI] [PubMed] [Google Scholar]
- 27. McCune JS, Bemer MJ, Barrett JS, Scott Baker K, Gamis AS, Holford NHG. Busulfan in infant to adult hematopoietic cell transplant recipients: a population pharmacokinetic model for initial and Bayesian dose PersonalizationBusulfan dose prediction in infants to adults. Clin Cancer Res. 2014;20(3):754‐763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Anderson BJ, Holford NH. Mechanism‐based concepts of size and maturity in pharmacokinetics. Annu Rev Pharmacol Toxicol. 2008;48:303‐332. [DOI] [PubMed] [Google Scholar]
- 29. Chasseloup E, Yngman G, Karlsson MO. Comparison of covariate selection methods with correlated covariates: prior information versus data information, or a mixture of both? J Pharmacokinet Pharmacodyn. 2020;47(5):485‐492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Ivaturi VD, Hooker AC, Karlsson MO. Selection Bias in Pre‐Specified Covariate Models. in Poster presented at 2011 .
- 31. Graham JW. Missing data analysis: making it work in the real world. Annu Rev Psychol. 2009;60:549‐576. [DOI] [PubMed] [Google Scholar]
- 32. Johansson ÅM, Karlsson MO. Comparison of methods for handling missing covariate data. AAPS J. 2013;15(4):1232‐1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Schafer JL, Graham JW. Missing data: our view of the state of the art. Psychol Methods. 2002;7(2):147‐177. [PubMed] [Google Scholar]
- 34. Keizer RJ, Zandvliet AS, Beijnen JH, Schellens JHM, Huitema ADR. Performance of methods for handling missing categorical covariate data in population pharmacokinetic analyses. AAPS J. 2012;14(3):601‐611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Nyberg J, Jonsson EN, Karlsson MO, Häggström J. Properties of the full random‐effect modeling approach with missing covariate data. Stat Med. 2023;43(5):817–1082. [DOI] [PubMed] [Google Scholar]
- 36. Bräm DS, Nahum U, Atkinson A, Koch G, Pfister M. Evaluation of machine learning methods for covariate data imputation in pharmacometrics. CPT Pharm Syst Pharmacol. 2022;11(12):1638‐1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Janssen A, Bennis FC, Mathôt RA. Adoption of machine learning in pharmacometrics: an overview of recent implementations and their considerations. Pharmaceutics. 2022;14(9):1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Lagishetty CV, Duffull SB. Evaluation of approaches to deal with low‐frequency nuisance covariates in population pharmacokinetic analyses. AAPS J. 2015;17(6):1388‐1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Bonate PL. Nonlinear mixed effects models: theory. In: Pharmacokinetic‐Pharmacodynamic Model Simulation. 2nd ed. Springer; 2011:233‐301. [Google Scholar]
- 40. Mould DR, Upton RN. Basic concepts in population modeling, simulation, and model‐based drug development—part 2: introduction to pharmacokinetic modeling methods. CPT Pharmacometrics Syst Pharmacol. 2013;2(4):1‐14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Food and Drug Administration guidance for industry, pharmacokinetics in patients with impaired renal function—study design, data analysis, and impact on dosing and labeling, draft, March 2020 .
- 42. Holford N, Heo Y‐A, Anderson B. A pharmacokinetic standard for babies and adults. J Pharm Sci. 2013;102(9):2941‐2952. [DOI] [PubMed] [Google Scholar]
- 43. Montgomery DC, Peck EA. Centering the regressors can remove non‐essential ill‐conditioning thereby reducing variance inflation in the parameter estimates. Introduction to Linear Regression Analysis. Wiley; 1982:341. [Google Scholar]
- 44. Ribbing J. Covariate Model Building in Nonlinear Mixed Effects Models. Acta Universitatis Upsaliensis; 2007. [DOI] [PubMed] [Google Scholar]
- 45. Hirai T, Hanada K, Kanno A, Akashi M, Itoh T. Risk factors for vancomycin nephrotoxicity and time course of renal function during vancomycin treatment. Eur J Clin Pharmacol. 2019;75(6):859‐866. [DOI] [PubMed] [Google Scholar]
- 46. Tornatore KM, Reed KA, Venuto RC. Repeated assessment of methylprednisolone pharmacokinetics during chronic immunosuppression in renal transplant recipients. Ann Pharmacother. 1995;29(2):120‐124. [DOI] [PubMed] [Google Scholar]
- 47. Sanghavi K, Zhang J, Zhao X, et al. Population pharmacokinetics of Ipilimumab in combination with Nivolumab in patients with advanced solid tumors. CPT Pharmacometrics Syst Pharmacol. 2020;9(1):29‐39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Wählby U, Thomson AH, Milligan PA, Karlsson MO. Models for time‐varying covariates in population pharmacokinetic‐pharmacodynamic analysis. Br J Clin Pharmacol. 2004;58(4):367‐377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Svensson RJ, Jonsson EN. Efficient and relevant stepwise covariate model building for pharmacometrics. CPT Pharmacometrics Syst Pharmacol. 2022;11(9):1210‐1222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Mandema JW, Verotta D, Sheiner LB. Building population pharmacokinetic pharmacodynamic models. I. Models for covariate effects. J Pharmacokinet Biopharm. 1992;20(5):511‐528. [DOI] [PubMed] [Google Scholar]
- 51. Wählby U. Methodological Studies on Covariate Model Building in Population Pharmacokinetic‐Pharmacodynamic Analysis. Acta Universitatis Upsaliensis; 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Kowalski KG, Hutmacher MM. Efficient screening of covariates in population models using Wald's approximation to the likelihood ratio test. J Pharmacokinet Pharmacodyn. 2001;28(3):253‐275. [DOI] [PubMed] [Google Scholar]
- 53. Jonsson EN, Karlsson MO. Automated covariate model building within NONMEM. Pharm Res. 1998;15(9):1463‐1468. [DOI] [PubMed] [Google Scholar]
- 54. Keizer RJ, Khandelwal A, Hooker AC, Karlsson MO. The bootstrap of stepwise covariate modeling using linear approximations. Population Analysis Group in Europe; 2011. [Google Scholar]
- 55. Khandelwal A, Harling K, Jonsson EN, Hooker AC, Karlsson MO. A fast method for testing covariates in population PK/PD models. AAPS J. 2011;13(3):464‐472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Ayral G, Si Abdallah JF, Magnard C, Chauvin J. A novel method based on unbiased correlations tests for covariate selection in nonlinear mixed effects models: the COSSAC approach. CPT Pharmacometrics Syst Pharmacol. 2021;10(4):318‐329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Prague M, Lavielle M. SAMBA: a novel method for fast automatic model building in nonlinear mixed‐effects models. CPT Pharmacometrics Syst Pharmacol. 2022;11(2):161‐172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Ribbing J, Nyberg J, Caster O, Jonsson EN. The lasso—a novel method for predictive covariate model building in nonlinear mixed effects models. J Pharmacokinet Pharmacodyn. 2007;34(4):485‐517. [DOI] [PubMed] [Google Scholar]
- 59. Tibshirani R. Regression shrinkage and selection via the lasso: a retrospective. J R Stat Soc Series B Stat Methodology. 2011;73(3):273‐282. [Google Scholar]
- 60. Bertrand J, Balding DJ. Multiple single nucleotide polymorphism analysis using penalized regression in nonlinear mixed‐effect pharmacokinetic models. Pharmacogenet Genomics. 2013;23(3):167‐174. [DOI] [PubMed] [Google Scholar]
- 61. Haem E, Harling K, Ayatollahi SMT, Zare N, Karlsson MO. Adjusted adaptive lasso for covariate model‐building in nonlinear mixed‐effect pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2017;44(1):55‐66. [DOI] [PubMed] [Google Scholar]
- 62. Gastonguay M. Full covariate models as an alternative to methods relying on statistical significance for inferences about covariate effects: a review of methodology and 42 case studies. in Poster presented at 2011 .
- 63. Karlsson MO. A full model approach based on the covariance matrix of parameters and covariates. in Abstr 2455 . 2012.
- 64. Yngman G, Bjugård Nyberg H, Nyberg J, Jonsson EN, Karlsson MO. An introduction to the full random effects model. CPT Pharmacometrics Syst Pharmacol. 2022;11(2):149‐160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Savic RM, Karlsson MO. Importance of shrinkage in empirical bayes estimates for diagnostics: problems and solutions. AAPS J. 2009;11(3):558‐569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Yuan M, Zhu Z, Yang Y, et al. Efficient algorithms for covariate analysis with dynamic data using nonlinear mixed‐effects model. Stat Methods Med Res. 2021;30(1):233‐243. [DOI] [PubMed] [Google Scholar]
- 67. Karlsson MO, Holford N. A tutorial on visual predictive checks. in abstr . 2008.
- 68. Ma G. Quantifying lung function progression in asthma. in Annual Meeting of the Population Approach Group in Europe . 2009.
- 69. Hennig S, Karlsson MO. Concordance between criteria for covariate model building. J Pharmacokinet Pharmacodyn. 2014;41(2):109‐125. [DOI] [PubMed] [Google Scholar]
- 70. Wasserstein RL, Lazar NA. The ASA Statement on p‐values: Context, Process, and Purpose. Taylor & Francis; 2016:129‐133. [Google Scholar]
- 71. Wählby U, Jonsson EN, Karlsson MO. Comparison of stepwise covariate model building strategies in population pharmacokinetic‐pharmacodynamic analysis. AAPS PharmSci. 2002;4(4):68‐79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Sheiner LB, Beal SL. A note on confidence intervals with extended least squares parameter estimates. J Pharmacokinet Biopharm. 1987;15(1):93‐98. [DOI] [PubMed] [Google Scholar]
- 73. White DB, Walawander CA, Liu DY, Grasela TH. Evaluation of hypothesis testing for comparing two populations using NONMEM analysis. J Pharmacokinet Biopharm. 1992;20(3):295‐313. [DOI] [PubMed] [Google Scholar]
- 74. Lehmann EL, Romano JP, Casella G. Testing statistical hypotheses. Vol 3. Springer; 2005. [Google Scholar]
- 75. Duffull SB, Wright DF, Winter HR. Interpreting population pharmacokinetic‐pharmacodynamic analyses–a clinical viewpoint. Br J Clin Pharmacol. 2011;71(6):807‐814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Xu XS, Yuan M, Zhu H, et al. Full covariate modelling approach in population pharmacokinetics: understanding the underlying hypothesis tests and implications of multiplicity. Br J Clin Pharmacol. 2018;84(7):1525‐1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Kruschke JK. Rejecting or accepting parameter values in Bayesian estimation. Adv Methods Pract Psychol Sci. 2018;1(2):270‐280. [Google Scholar]
- 78. Carlin JB, Wolfe R, Brown CH, Gelman A. A case study on the choice, interpretation and checking of multilevel models for longitudinal binary outcomes. Biostatistics. 2001;2(4):397‐416. [DOI] [PubMed] [Google Scholar]
- 79. Wickham H. Data analysis. ggplot2. Springer; 2016:189‐201. [Google Scholar]
- 80. Gelman A, Pardoe I. Average predictive comparisons for models with nonlinearity, interactions, and variance components. Sociol Methodol. 2007;37(1):23‐51. [Google Scholar]
- 81. Relling MV, Gardner EE, Sandborn WJ, et al. Clinical Pharmacogenetics implementation consortium guidelines for thiopurine methyltransferase genotype and thiopurine dosing. Clin Pharmacol Ther. 2011;89(3):387‐391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Xue L, Holford N, Ding XL, et al. Theory‐based pharmacokinetics and pharmacodynamics of S‐ and R‐warfarin and effects on international normalized ratio: influence of body size, composition and genotype in cardiac surgery patients. Br J Clin Pharmacol. 2017;83(4):823‐835. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1.
Data S2.