Abstract
There is growing interest in the use of long‐acting (LA) injectable drugs to improve treatment adherence. However, their long elimination half‐life complicates the conduct of clinical trials. Physiologically‐based pharmacokinetic (PBPK) modeling is a mathematical tool that allows to simulate unknown clinical scenarios for LA formulations. Thus, this work aimed to develop and verify a mechanistic intramuscular PBPK model. The framework describing the release of a LA drug from the depot was developed by including both the physiology of the injection site and the physicochemical properties of the drug. The framework was coded in Matlab® 2020a and implemented in our existing PBPK model for the verification step using clinical data for LA cabotegravir, rilpivirine, and paliperidone. The model was considered verified when the simulations were within twofold of observed data. Furthermore, a local sensitivity analysis was conducted to assess the impact of various factors relevant for the drug release from the depot on pharmacokinetics. The PBPK model was successfully verified since all predictions were within twofold of observed clinical data. Peak concentration, area under the concentration‐time curve, and trough concentration were sensitive to media viscosity, drug solubility, drug density, and diffusion layer thickness. Additionally, inflammation was shown to impact the drug release from the depot. The developed framework correctly described the release and the drug disposition of LA formulations upon intramuscular administration. It can be implemented in PBPK models to address pharmacological questions related to the use of LA formulations.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
Long‐acting (LA) drugs are used for the treatment and prevention of HIV, but also for contraception and schizophrenia. LA drugs create a depot upon intramuscular/subcutaneous injection from which the drug is slowly released to maintain plasma concentrations for days/months with the potential to improve adherence. However, the long elimination half‐life makes the conduct of trials challenging.
WHAT QUESTION DID THIS STUDY ADDRESS?
Physiologically‐based pharmacokinetic (PBPK) modeling allows to simulate unstudied clinical scenarios, however, no mechanistic intramuscular models have yet been developed.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
This study presents a mechanistic framework for PBPK modeling to simulate LA drug disposition considering both the physicochemical drug properties and the physiological characteristics of the injection site.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
This framework allows to simulate unstudied clinical scenarios such as drug–drug interactions or drug disposition in special populations.
INTRODUCTION
Long‐acting (LA) injectables have been initially developed for contraception and schizophrenia. 1 There is currently a growing interest in using LA formulations for the treatment of HIV infection, as indicated by the recent approval of LA cabotegravir, rilpivirine, and lenacapavir. 1 Upon intramuscular or subcutaneous administration, LA formulations form a depot from which the drug is slowly released to keep sustained plasma concentrations for days or months. 2 Patients may benefit from the use of an injectable treatment to reduce confidentiality concerns, avoid pill fatigue, and improve therapy adherence. LA drugs are characterized by a flip‐flop kinetics whereby the rate of absorption is slower than the rate of elimination, thus resulting in a long elimination half‐life. 2 , 3 This makes the conduct of pharmacological studies particularly challenging as long timelines are needed to evaluate the pharmacokinetics or to reach steady‐state.
Physiologically‐based pharmacokinetic (PBPK) modeling is a mathematical technique recognized by regulatory agencies 4 , 5 which allows to investigate unknown clinical scenarios by combining in silico, in vitro, and clinical data to predict drug disposition in a virtual population. 6 PBPK modeling allows to generate a cohort of virtual individuals using physiological data related to body composition, tissues weights, and blood flows for the target population. 7 Available PBPK models for the simulation of drug pharmacokinetics after intramuscular administration do not include a mechanistic framework for the drug release from the depot which limits their applicability. 8 , 9
To address this gap, we developed a framework to mechanistically describe the release of LA drugs after intramuscular administration which was implemented in our existing whole‐body PBPK model. The predictive performance of the model was subsequently verified against clinical data for drugs formulated as nanosuspension.
METHODS
We took three steps to develop and verify the intramuscular PBPK model. First, we developed the framework describing the release of a LA drug after intramuscular administration by including the physiological characteristics of the injection site and the physicochemical properties of the drug. Second, the framework was implemented in Matlab® 2020a in our existing PBPK model. 6 Third, we verified the predictive performance of the model against clinical data for LA drugs formulated as nanosuspension and administered intramuscularly. 10 We also simulated drug–drug interaction (DDI) scenarios with strong inducer (e.g., rifampicin) and inhibitor (e.g., ketoconazole) to verify the ability of the drug models to correctly capture the fraction metabolized by each enzyme. The subsequent sections provide further details for the development and verification of the intramuscular PBPK model.
PBPK model structure
Our whole‐body PBPK model, previously developed in Matlab® 2020a, consists of 17 perfusion‐limited compartments which are divided into vascular, interstitial, and intracellular spaces to take into consideration the lymphatic component in drug disposition. 6 The original model was implemented with a compartment for the intramuscular injection site (i.e., ventrogluteal area) of similar composition than the total skeletal muscle but with a different blood flow and volume. In agreement with Cho et al., 11 we assumed that the drug is injected into the interstitial space of the muscle. Thus, we created an additional compartment within the interstitial space to represent the drug depot from where the drug is slowly released after injection (Figure 1).
FIGURE 1.
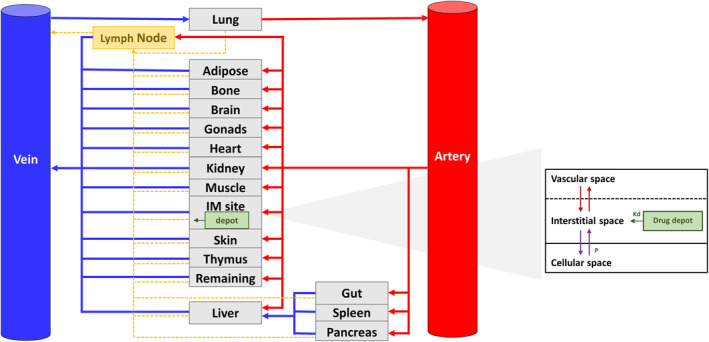
Physiologically‐based pharmacokinetic (PBPK) model structure. Kd, release constant; Kp, partition coefficient; P, passive diffusion clearance.
Physiology of the ventrogluteal injection site
The newly approved LA antiretrovirals (i.e., cabotegravir and rilpivirine) are injected in the ventrogluteal area 12 , 13 which comprises the gluteus medius and minimus. 14 The equations describing the physiology of this injection site, including the gluteal weights and blood flows, were implemented in our previously developed virtual healthy population. 7 The weights of the gluteus medius and minimus relative to the weight of the total skeletal muscle (1.34% and 0.37%, respectively) were obtained from a clinical study (mean age of the population: 57 years, proportion of women: 68%). 15 , 16 , 17 The relative percentages were then used, assuming their validity across age and sex (Figure S1), in combination with our previously developed total skeletal muscle weight equation (Equation 1) 7 to calculate the weight of the gluteus medius (Equation 2) and minimus (Equation 3).
| (1) |
| (2) |
| (3) |
Instead, the gluteal blood flow was found to be 9.6 mL/min/100 g based on published data in healthy young men aged 21–30 years. 18 This value was scaled to total gluteal blood flow using the gluteal weights derived from Equations 2 and 3. The blood flows of the gluteus medius and minimus relative to the blood flow of the total skeletal muscle were calculated (3.68% and 1.03%, respectively). The relative percentages were then used, assuming their validity across age and sex (Figure S1), in combination with our previously developed total skeletal muscle blood flow equation (Equation 4) 7 to derive the blood flow of the gluteus medius (Equation 5) and minimus (Equation 6) expressed as the percentage of the cardiac output (CO).
| (4) |
| (5) |
| (6) |
In order to include the contribution of the lymphatic flow in the drug disposition, we assumed that only a portion of the total skeletal muscle lymph flow (i.e., 16% 19 ) reaches the gluteal muscles and is proportional to the muscle weights (Equation 7).
| (7) |
Mathematical description of the drug release from the depot
The physicochemical properties of the injected drug and the physiological factors of the injection site are considered to be the main drivers of the drug release from the depot; alongside other critical factors including the depot shape and size, the inflammation response after injection, and the diffusion thickness layer. 20 , 21 The implementation of these parameters in the model is detailed thereafter.
By performing magnetic resonance imaging at days 1, 3, and 8 post intramuscular injection of LA cabotegravir, Jucker et al. showed that the shape of the depot is irregular and presents a greater surface area by volume ratio compared to a spherical drug deposition. 21 A similar observation was made by Kalicharan et al. who analyzed the shape of an oil depot after intramuscular injection in the upper arm. 22 Thus, based on these findings, we assumed that the shape of the depot is cylindrical and constituted of spherical particles surrounded by an aqueous liquid vehicle. Conversely to the gastrointestinal tract, the amount of fluids is limited in the muscles with no peristalsis allowing to maintain the drug particles separated from each other. Thus, the spherical particles inside the depot could agglomerate over time into bigger spherical particles which may reduce the depot surface area and consequently the drug release rate. 23
For our simulations, the diffusion coefficient was calculated using the Stokes‐Einstein equation (Equation 8) 24 and was considered constant over time and depending only on the molecular weight and on the density of a given drug.
| (8) |
where k = Boltzmann constant [cm2 × kg/h2 × K]; T = body temperature [K]; ƞ = media viscosity [kg/h × cm]; MW = drug molecular weight [g/mol]; N = Avogadro number [1/mol]; ρ = drug density [g/cm3]. Because the depot was assumed to be injected in the interstitial space and because no data were available for the viscosity of the muscle interstitial space, we assumed that the media viscosity was similar to the viscosity of the water measured at 37°C. 25
The Wang‐Flanagan equation was considered in the model. 26 This equation allows to describe the dissolution kinetics of spherical powder in sink (non‐saturable) and non‐sink (saturable) conditions. Sink conditions are generally difficult to reach for drugs with a low solubility, 26 such as LA cabotegravir, rilpivirine, or paliperidone. 1 , 27 , 28 Thus, the simulations were done assuming non‐sink conditions in agreement with the recommendations by the Center for Drug Evaluation and Research (CDER) of the US Food and Drug Administration (FDA). 23
The release of LA drugs from the depot can also be impacted by the inflammatory response occurring after the injection of the drug. 29 , 30 , 31 Thus, we added an inflammation factor in the equation in order to take into account this physiological response. Given that the inflammatory response lasts for a limited duration, the inflammation factor was integrated in the simulation only up to 15 days post‐injection.
The last factor that can impact the drug release from the depot is the diffusion thickness layer. This parameter was assumed to be constant over time. Based on available data in the literature, the maximal reported value for the diffusion thickness layer is 30 μm for particles with a radius greater than 30 μm. 32 We used this value by default; however, it was optimized as the size of the agglomerate or the diffusion layer are unknown. Furthermore, macrophages may create an additional layer around the drug depot. 29 , 30
The aforementioned assumptions were integrated in Equation 9 which describes the release of the LA drug from the depot after each injection. As mentioned above, Equation 9 is multiplied by the inflammation factor only up to 15 days upon injection.
| (9) |
where dp = depot; N dp = number of depot defined in the study design; Dif = diffusion coefficient [cm2/h]; ρ = drug density [g/cm3]; MW = molecular weight [g/μmol]; C dp = concentration in the depot [μM]; V f = formulation volume [L]; h = diffusion thickness layer [cm]; Sol = solubility [μM]; C msi = concentration in the interstitial space of the muscle injection site [μM]; IF = inflammation factor.
Equation 9 was integrated in the ordinary differential equation representing the interstitial space of the injection site.
Verification of the intramuscular PBPK model
A literature search was performed to identify LA drugs formulated as nanosuspension for the verification of the intramuscular PBPK model. The drugs fulfilling this criterion were cabotegravir, rilpivirine, paliperidone palmitate, and ziprasidone. 10 We did not retain ziprasidone for the validation because the available clinical data were obtained after intramuscular injection into the non‐dominant arm and therefore were not reflective of the gluteal area. 33 For each of the remaining compounds, a drug model was developed using in silico, in vitro, and in vivo data describing the physicochemical and pharmacokinetic properties of the drug of interest. The data used to develop the model are summarized in Table S1. In order to verify the drug models, we used available clinical data obtained after intravenous (if available) and oral administration or injection in the gluteal area (i.e., gluteus medius), as well as concentration‐time profiles measured in the presence of strong or moderate inducers. The modeling strategies are represented in Figure S2; additionally, all the studies for model verification are presented in Table S2 together with their respective demographic parameters. The drug models were considered verified when the predictions were within twofold of clinical observed data. 34 , 35 The cabotegravir and rilpivirine models have also been verified in the framework of a project aiming at simulating DDIs with moderate and strong inducers. 36 Specifically, the predictive performance of the models in presence of a strong cytochrome (CYP) 3A4 and uridine diphosphate glycosyltransferase (UGT) 1A1 inducer (i.e., rifampicin) and CYP3A4 inhibitor (i.e., ketoconazole) were evaluated considering the criteria proposed by Guest et al. 37 Due to the challenges related to the LA drugs, clinical DDI data were available only for oral cabotegravir (30 mg) and rilpivirine (150 mg) Table S2. For paliperidone, no observed clinical DDI data were available in the literature. The parameters used for the model development of rifampicin and ketoconazole are summarized in Table S3.
We made the following assumptions when developing the drug models. First, we optimized the previously reported maximal thickness value of the diffusion layer (i.e., 30 μm) 32 for cabotegravir and rilpivirine in order to have better visual simulations. Second, paliperidone is administered as the prodrug paliperidone palmitate (156 mg paliperidone corresponds to 100 mg paliperidone 38 ). Therefore, we assumed the prodrug to be rapidly converted into the active moiety by the esterase immediately after the release from the depot. 39 Thus, the parameters describing the depot (i.e., diffusion coefficient) related only to the prodrug paliperidone palmitate.
Local sensitivity analysis
We performed a local sensitivity analysis to assess the impact of factors relevant for the drug release from the depot on various pharmacokinetic parameters (i.e., peak concentration [C max], area under the concentration‐time curve [AUC], and trough concentration [C τ]). The value of each individual factors (i.e., viscosity, inflammation, drug solubility, drug density, diffusion thickness layer, and blood flow in the muscle) was increased by 1% and the sensitivity coefficient (SC) was derived using Equation 10, 40 , 41 :
| (10) |
where r is the model predicted dose metric of interest (i.e., C max, AUC, and C τ) with the original parameter value; dr is the difference between the model predicted dose metric of interest with a 1% increase in parameter value and the model predicted dose metric of interest with the original parameter value; p is the original parameter value (i.e., viscosity, inflammation, drug solubility, drug density, diffusion thickness layer, and blood flow in the muscle); dp is the difference between the parameter value changed of 1% and the original parameter value. Based on the criteria defined by Teeguarden et al., parameters with an SC between 0.1 and 0.15 have a low impact on the dose metrics; parameters with an SC between 0.15 and 0.5 have a medium impact, whereas SCs greater or equal to 0.5 have a high impact on the dose metric of interest. 41 Negative coefficients indicate an inverse relationship between the parameter and the dosing metric of interest (i.e., C max, AUC, and C τ). 41
The local sensitivity analyses were performed by simulating a single intramuscular administration of cabotegravir 800 mg injected in the gluteus medius as a split dose (i.e., 2 doses of 400 mg/mL) in a single male individual aged 35 years old with a body mass index of 25 kg/m2.
RESULTS
Model verification
The intramuscular PBPK model was successfully verified as 73% of simulations were within 1.25‐fold, 83% were within 1.5‐fold, and 100% were within twofold of clinically observed data (Table 1).
TABLE 1.
Predicted versus observed data for cabotegravir, rilpivirine, and paliperidone after oral and intramuscular administration.
| Observed | Predicted | Ratio P/O | |
|---|---|---|---|
| Cabotegravir 30 mg single dose oral | |||
| C max, ng/mL | 3344 (24) | 2679 (18) | 0.80 |
| C τ, ng/mL | 1567 (28) | 1763 (27) | 1.13 |
| AUC0–∞, ng h/mL | 132,751 (29) | 162,897 (64) | 1.23 |
| Cabotegravir 30 mg steady‐state oral | |||
| C max, ng/mL | 7631 (22) | 8133 (45) | 1.07 |
| C τ, ng/mL | 4472 (30) | 5426 (62) | 1.21 |
| AUC0–τ, ng h/mL | 133,872 (25) | 163,233 (53) | 1.22 |
| Cabotegravir 400 mg single dose intramuscular | |||
| C max, ng/mL | 700 (55) | 731 (66) | 1.04 |
| C4week, ng/mL | 400 (55) | 672 (70) | 1.68 |
| AUC0–4week, ng h/mL | 290,000 (46) | 439,587 (59) | 1.52 |
| Cabotegravir 800 mg single dose intramuscular | |||
| C max, ng/mL | 3300 (75) | 3772 (44) | 1.14 |
| C4week, ng/mL | 2000 (77) | 1772 (56) | 0.89 |
| AUC0–4week, ng h/mL | 1,497,000 (79) | 1,693,649 (47) | 1.13 |
| Cabotegravir 800 mg single dose/ 400 mg multiple doses intramuscular | |||
| C max, ng/mL | 4400 (31) | 3526 (53) | 0.80 |
| C4week, ng/mL | 3270 (27) | 2818 (59) | 0.86 |
| AUC0–4week, ng h/mL | 5,666,730 a | 4,734,936 (60) | 0.84 |
| Cabotegravir 30 mg steady‐state oral + 600 mg loading dose intramuscular + 600 mg maintenance dose intramuscular | |||
| C max, ng/mL | 3718 | 3514 (55) | 0.95 |
| C τ, ng/mL | 1904 | 1714 (68) | 0.90 |
| AUC0–τ, ng h/mL | 3,986,534 | 3,152,548 (62) | 0.79 |
| Rilpivirine 75 mg single dose oral | |||
| C max, ng/mL | 296 ± 118 | 327 ± 58 | 1.10 |
| C τ, ng/mL | – | 112 ± 36 | – |
| AUC0–∞, ng h/mL | 11,450 ± 4431 | 11,027 ± 4518 | 0.96 |
| Rilpivirine 25 mg single dose oral | |||
| C max, ng/mL | 100 ± 28 | 103 ± 18 | 1.03 |
| C τ, ng/mL | – | 36 ± 11 | – |
| AUC0–τ, ng h/mL | 1095 ± 327 | 1422 ± 279 | 1.30 |
| Rilpivirine 25 mg steady‐state oral | |||
| C max, ng/mL | 160 (31) | 184 (26) | 1.16 |
| C τ, ng/mL | 75 (38) | 91 (39) | 1.21 |
| AUC0–τ, ng h/mL | 2333 (30) | 2973 (31) | 1.27 |
| Rilpivirine 600 mg single dose intramuscular | |||
| C max, ng/mL | 82 (43) | 51 (27) | 0.62 |
| C4week, ng/mL | 44 (65) | 27 (33) | 0.62 |
| AUC0–84days, ng h/mL | 70,416 (34) | 55,020 (31) | 0.78 |
| Rilpivirine 1200 mg single dose intramuscular | |||
| C max, ng/mL | 160 (39) | 191 (30) | 1.20 |
| C4week, ng/mL | 83 (53) | 71 (51) | 0.86 |
| AUC0–84days, ng h/mL | 143,568 (38) | 151,872 (44) | 1.06 |
| Rilpivirine 25 mg steady‐state oral + 600 mg multiple doses intramuscular Q4W | |||
| C max, ng/mL | – | 118 ± 36 | – |
| C8week, ng/mL | 51 ± 20 | 55 ± 19 | 1.07 |
| AUC0–τ, ng h/mL | – | 53,031 ± 17,512 | – |
| Rilpivirine 25 mg steady‐state oral + 900 mg multiple doses intramuscular Q8W | |||
| C max, ng/mL | – | 232 (28) | – |
| C48week, ng/mL | 64 (39) | 63 (35) | 0.98 |
| AUC0–τ, ng h/mL | – | 140,416 (33) | – |
| Paliperidone 1 mg single dose intravenous | |||
| C max, ng/mL | – | – | – |
| t 1/2, h | 23 a | 24 (21) | 1.03 |
| AUC0–∞, ng h/mL | 223 a | 240 (19) | 1.08 |
| Paliperidone 3 mg single dose oral | |||
| C max, ng/mL | 5 ± 2 | 3 ± 0.4 | 0.51 |
| t 1/2, h | 22 ± 4 | 25 ± 4 | 1.13 |
| AUC0–τ, ng h/mL | 185 ± 73 | 155 ± 27 | 0.84 |
| Paliperidone 6 mg single dose oral | |||
| C max, ng/mL | 10 ± 3 | 5 ± 1 | 0.54 |
| t 1/2, h | 27 ± 5 | 25 ± 5 | 0.94 |
| AUC0–τ, ng h/mL | 348 ± 119 | 314 ± 63 | 0.90 |
| Paliperidone 50 mg eq. single dose intramuscular | |||
| C max, ng/mL | 6.9 (2.6–14.8) | 6.5 (4–9.6) | 0.94 |
| C τ, ng/mL | – | – | – |
| AUC0–∞, ng h/mL | 10,088 (8018 – 14,338) | 10,892 (6733 – 16,109) | 1.08 |
| Paliperidone 150 mg eq. single dose intramuscular | |||
| C max, ng/mL | 15.2 (8.6–44.7) | 10.8 (7.2–18.8) | 0.71 |
| C τ, ng/mL | – | – | – |
| AUC0–∞, ng h/mL | 31,344 (17,117 – 53,906) | 32,106 (21,266 – 36,205) | 1.02 |
| Paliperidone 50 mg eq. multiple doses intramuscular | |||
| C max, ng/mL | – | – | – |
| C92days, ng/mL | 8.8 (NA) | 10 (6.5–16.9) | 1.14 |
| AUC0–τ, ng h/mL | – | – | – |
| Paliperidone 100 mg eq. multiple doses intramuscular | |||
| C max, ng/mL | 23 ± 11 | 37 ± 7 | 1.65 |
| C τ, ng/mL | – | – | – |
| AUC0–τ, ng h/mL | 11,928 ± 5947 | 21,474 ± 3953 | 1.80 |
Note: The data are represented as geometric mean (CV) unless otherwise specified as mean ± SD or median (range).
Abbreviations: AUC0–∞, area under the curve from 0 to infinity AUC0–τ, area under the curve from 0 to the end of the dosing interval; AUC0–4week, area under the curve from 0 to 4 weeks after the administration; AUC0–12week, area under the curve from 0 to 12 weeks after the administration; C max, peak concentration; C τ, trough concentration; C 4week, concentration measured 4 weeks after administration; C 8week, concentration measured 8 weeks after administration; C 48week, concentration measured 48 weeks after administration; C 92days, concentration measured 92 days after administration O, observed data; P, predicted data; t1/2, terminal half‐life.
Calculated using Non‐Compartmental Analysis performed in MatLab2020.
Cabotegravir
The HIV integrase inhibitor cabotegravir is metabolized by UGT1A1 and UGT1A9. 42 The model was verified against clinically observed data after the administration of single and multiple oral and intramuscular doses. For the single oral dose (30 mg), the observed: predicted ratios for C max, C τ, and AUC were 0.80, 1.13, and 1.23, respectively (Figure S3, Table 1). After administering multiple oral doses, the observed:predicted ratios for C max, C τ, and AUC were 1.07, 1.21, and 1.22, respectively (Figure S3, Table 1). For the single intramuscular dose administration in the gluteal area, two different doses were evaluated: 400 and 800 mg. For each dose, the clinically observed data were in agreement with the simulations as the observed:predicted ratios for C max, C τ, and AUC for cabotegravir 400 mg were 1.04, 1.68, and 1.52, respectively, and for cabotegravir 800 mg were 1.14, 0.89, and 1.13, respectively (Figure 2a,b, Table 1). Similarly, for the multiple intramuscular injections of cabotegravir (800 mg single dose and 400 mg multiple doses), the simulations were in agreement with the clinically observed data and the predictions were within twofold for C max, C τ, and AUC (Figure 2c, Table 1). Further clinical studies used an oral lead‐in dose of 30 mg administered daily for 1 month followed by the intramuscular injection of cabotegravir. Our model successfully reproduced this scenario as the predictions were within twofold of clinical observed data for C max, C τ, and AUC (Figure 2d, Table 1). For the DDI scenarios, the correlation between observed versus predicted clinical data was evaluated only for C max and AUC. For C max, the correlation resulted to be borderline between the upper and the lower limits defined by Guest et al. 37 ; whereas the correlation between observed and predicted AUC was within the two defined limits (Figure S6).
FIGURE 2.
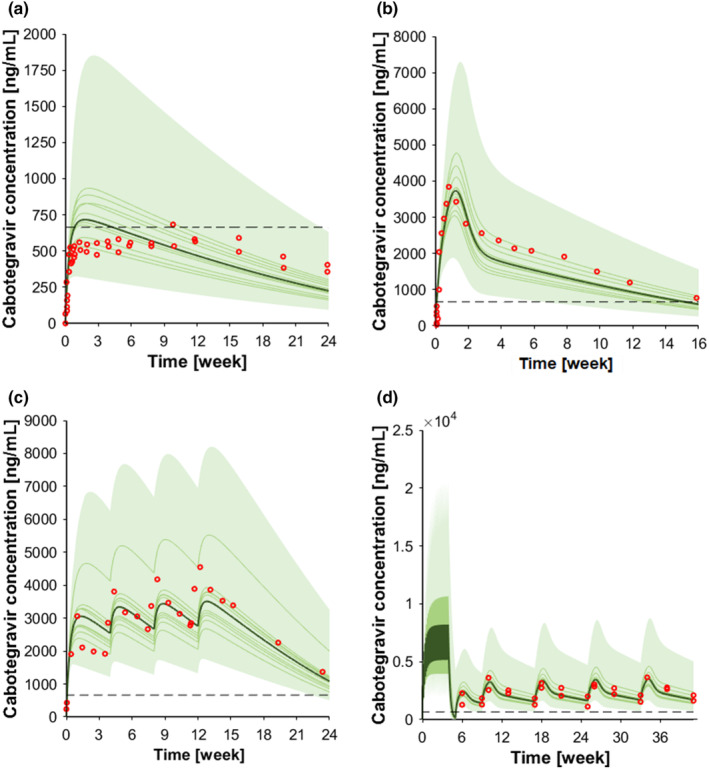
Concentration‐time profile of intramuscular cabotegravir. (a) Cabotegravir 400 mg single dose intramuscular; (b) cabotegravir 800 mg single dose intramuscular; (c) cabotegravir 800 mg single dose intramuscular followed by three 400 mg intramuscular injections, and (d) cabotegravir 30 mg oral at steady‐state followed by 600 mg intramuscular loading dose and by 600 mg intramuscular maintenance doses every other month. The red markers represent clinically observed data for the control scenario. The solid lines, the solid bold line, the shaded area, and the dotted line represent the geometric mean of each virtual trial, the geometric mean of all trials, the 90% normal range of all virtual individuals, and the fourfold protein‐adjusted concentration required for 90% viral inhibition for cabotegravir (664 ng/mL). 56
Rilpivirine
The non‐nucleoside reverse transcriptase inhibitors rilpivirine is mainly metabolized by CYP3A4. 42 For single oral dose administration, two different doses were simulated: 75 mg for which the observed:predicted ratios for C max and AUC were 1.10 and 0.96, respectively, and 25 mg for which the respective ratios were 1.03 and 1.30 (Figure S4, Table 1). After simulating multiple oral doses for rilpivirine 25 mg, the observed: predicted ratios for C max, C τ, and AUC were 1.16, 1.21, and 1.27, respectively (Figure S4, Table 1). Two different doses (600 and 1200 mg) were simulated for the single intramuscular administration in the gluteal area. The clinically observed data were in agreement with the simulations as the observed:predicted ratios for C max, C τ, and AUC for rilpivirine 600 mg were 0.62, 0.62, and 0.78, respectively (Figure 3a); for rilpivirine 1200 mg, the ratios were 1.20, 0.86, and 1.06, respectively (Figure 3b, Table 1). Additional clinical studies used an oral lead‐in dose of 25 mg administered for 1 month prior to the injection of rilpivirine to assess the tolerability. Similarly, to cabotegravir, the model successfully reproduced these clinical scenarios, as in all cases the simulated C τ were within twofold of the observed data (Figure 3c,d, Table 1). For the DDI scenarios, the correlation between observed versus predicted clinical data for C max, AUC, and C τ resulted to be just outside the upper limit defined by Guest et al. 37 (Figure S6). However, the correlations were still within the twofold error; additionally, rilpivirine is considered as a large therapeutic index drug and its co‐administration with rifampicin is contraindicated, thus we consider the model verified. On the other hand, in presence of ketoconazole, the correlation for C max, AUC, and C τ resulted to be within the limits defined by Guest et al. 37 (Figure S6).
FIGURE 3.
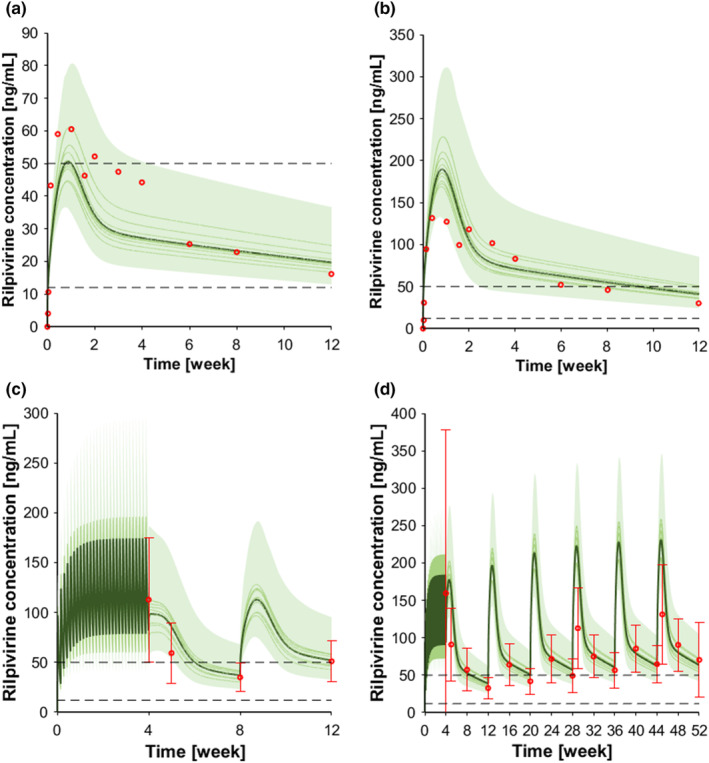
Concentration‐time profile intramuscular rilpivirine. (a) Rilpivirine 600 mg single dose intramuscular; (b) rilpivirine 1200 mg single dose intramuscular; (c) rilpivirine 25 mg oral at steady state follow by two 600 mg intramuscular dose injection every month, and (d) rilpivirine 25 mg oral at steady‐state follow by six 900 mg intramuscular dose injection every other month. The red markers represent clinically observed data for the control scenario. The solid lines, the solid bold line, the shaded area, and the dotted lines represent the geometric mean of each virtual trial, the geometric mean of all trials, the 90% normal range of all virtual individuals, and the fourfold protein adjusted concentration required for 90% viral inhibition for rilpivirine (12 ng/mL), and the minimal concentration for therapeutic response (50 ng/mL). 57
Paliperidone
Paliperidone is indicated for the treatment of schizophrenia and does not have a significant hepatic metabolism. 43 For the intravenous administration (1 mg), the observed:predicted ratios for the terminal half‐life (t1/2) and the AUC were 1.03 and 1.08, respectively (Figure S5, Table 1). For the single oral dose administration, two doses were simulated (3 and 6 mg). For the 3 mg dose, the observed:predicted ratios for C max, t 1/2, and AUC were 0.51, 1.13, and 0.89, respectively, and for the 6 mg dose, the respective ratios were 0.54, 0.94, 0.90 (Figure S5, Table 1). Paliperidone C max was underpredicted in both scenarios, and this is possibly related to the formulation effect which was not implemented in our model. For the single intramuscular dose administration, two doses were simulated: 50 mg eq. for which the observed:predicted ratios for C max and AUC were 0.94 and 1.08, respectively, and 150 mg eq. for which the corresponding ratios were 0.71 and 1.02, respectively (Figure 4a,b, Table 1). For the intramuscular administration of multiple doses (50 and 100 mg eq.), the predictions were always within twofold of clinical observed data (Figure 4c,d, Table 1).
FIGURE 4.
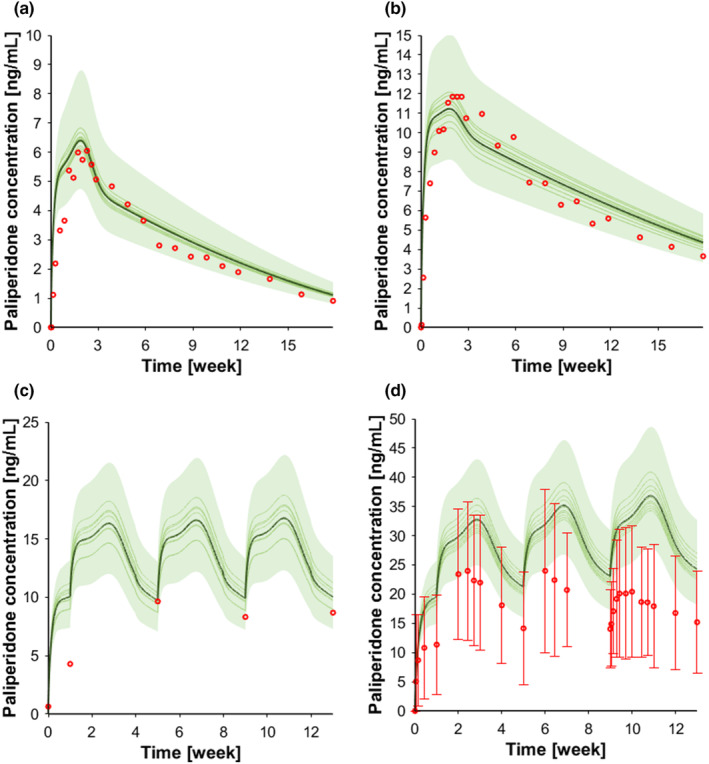
Concentration‐time profile intramuscular paliperidone. (a) Paliperidone 50 mg eq. single dose intramuscular; (b) paliperidone 150 mg eq. single dose intramuscular; (c) paliperidone 50 mg eq. intramuscular dose injection every month, and (d) paliperidone 100 mg eq. intramuscular dose injection every month. The red markers represent clinically observed data for the control scenario. The solid lines, the solid bold line, and the shaded area represent the geometric mean of each virtual trial, the geometric mean of all trials, and the 90% normal range of all virtual individuals.
Local sensitivity analysis
The results of the local sensitivity analysis, aiming at investigating the effect of key parameters for the drug release from the depot on the drug pharmacokinetics, are summarized in Figure 5. The SC derived after changing media viscosity, drug density, and diffusion thickness layer were negative for C max, AUC, and C τ indicating an inverse relationship. On the other hand, drug solubility shows a positive relationship for C max, AUC, and C τ; whereas the inflammation factor shows to have a positive relationship for C max, AUC, and negative relationship for C τ. However, based on the criteria defined by Teeguarden et al., 41 media viscosity, drug solubility, and diffusion thickness layer are the parameters that have a higher impact on the dose metrics.
FIGURE 5.
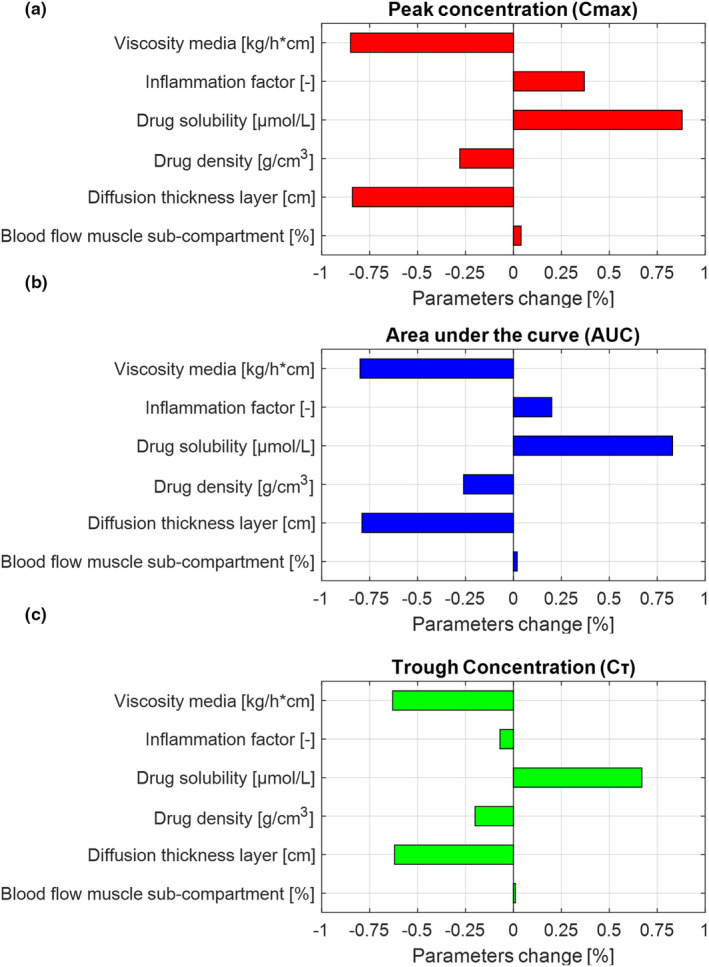
Local sensitivity analysis (LSA) results. (a) LSA effect on peak concentration (C max), (b) LSA effect on area under the curve (AUC), and (c) LSA effect on trough concentration (C τ).
DISCUSSION
The predictive performance of PBPK modeling relies on the ability to mathematically describe each step relevant to drug disposition. The PBPK models currently available in literature do not provide a mechanistic description of the drug release from a depot upon intramuscular administration; therefore, their extrapolation capability is limited. To our knowledge, we present the first mechanistic PBPK model describing the release of a LA drug after intramuscular administration in the ventrogluteal area.
The intramuscular PBPK model was successfully verified against clinically observed data for LA cabotegravir, rilpivirine, and paliperidone formulated as nanosuspension. 10 The predictions were within twofold of the observed clinical data; however, the population variability was underpredicted by the model as it assumes that the drug always reaches the muscle. The real‐world studies, including controlled clinical trials, have shown a large interindividual variability in drug concentrations. 21 , 44 This variability relates to factors that were not included in the model, such as the ventrogluteal injection site (i.e., in real‐world practice, the injected drug does not always reach the muscle but can be deposited in the subcutaneous tissue), injection technique (i.e., a longer needle length needs to be used in obese individuals which is not always done in practice), and split injections (i.e., splitting the injected dose was shown to increase the drug absorption). 45 , 46
The sensitivity analysis demonstrated that the drug release from the depot is influenced by the physicochemical properties of the drug and by the physiology of the injection site. 21 , 47 The main drivers for the drug release from the depot were the drug solubility, the media viscosity, the diffusion layer thickness, and drug density. The inflammation (caused by the administration of the active substance) and the particle size distribution were shown to also have an effect on the pharmacokinetics of LA injectable drugs. 29 , 48 Our findings are consistent with data in the literature showing that a high drug solubility is associated with an increased dissolution rate and consequently with an increased absorption rate.
The current model has several limitations which should be acknowledged. Because there are no dissolution equations to describe the release of the drug after intramuscular administration, we used the Wang‐Flanagan equation, which is generally applied to describe the drug dissolution process occurring in the gastrointestinal tract. Furthermore, there are no data related to the measurement of the diffusion thickness layer. However, there is ongoing research aiming at developing new in vitro methods to test drug dissolution after intramuscular administration, which will allow to address the knowledge gap between in vitro and in vivo drug dissolution. 23 , 49 , 50 Our model did not include drug metabolizing enzymes expressed in the muscle due to the paucity of data in literature. 1 Additionally, the depot has been reported to have an irregular shape 21 which would have required additional assumptions. Therefore, we decided to simplify the shape and assume that the depot had a cylindrical shape and was constituted of spherical drug particles in a liquid aqueous vehicle. The model does not reflect clinical conditions that could impact the physical activity (e.g., osteoarthritis and sarcopenia) and consequently the release of the drug from the depot. Last, the inflammation is considered to be an important contributor in the release from the depot and consequently in the pharmacokinetics. The inflammation cascade occurring after the administration of a LA injectable drug was initially reported in preclinical species 29 , 30 , 48 and was subsequently confirmed in several clinical studies after the intramuscular administration of LA cabotegravir, rilpivirine, and paliperidone. 21 , 51 , 52 The mechanistic description of the inflammation process is complex due to multiple reactions involved in this process. These comprise notably the formation of a layer of immune cells and collagen around the depot and the phagocytic activity of the macrophages. 48 Thus, we decided to use an inflammation factor rather than describe mechanistically the inflammatory processes given that our research questions focus on the drug elimination phase and C τ.
In conclusion, the developed equations allow to simulate the release of LA drugs from the depot after intramuscular administration in the ventrogluteal area by considering the drug physicochemical properties and physiology of the injection site. The equations can be implemented in PBPK models during drug development to address unstudied clinical scenarios related, for instance, to the management of DDIs 36 , 53 and evaluation of the pharmacokinetics in special populations in order to guide clinical decisions. 54 , 55
AUTHOR CONTRIBUTIONS
All authors wrote the manuscript. S.B. and C.M. designed the research. S.B. performed the research. S.B. and M.Be. analyzed the data.
FUNDING INFORMATION
This study was supported by the Swiss National Science Foundation (Grant number: 188504).
CONFLICT OF INTEREST STATEMENT
The authors declared no competing interests for this work.
Supporting information
Table S1.
Table S2.
Table S3.
Figure S1.
Bettonte S, Berton M, Battegay M, Stader F, Marzolini C. Development of a physiologically‐based pharmacokinetic model to simulate the pharmacokinetics of intramuscular antiretroviral drugs. CPT Pharmacometrics Syst Pharmacol. 2024;13:781‐794. doi: 10.1002/psp4.13118
Contributor Information
Sara Bettonte, Email: sara.bettonte@unibas.ch.
Catia Marzolini, Email: catia.marzolini@usb.ch.
REFERENCES
- 1. Owen A, Rannard S. Strengths, weaknesses, opportunities and challenges for long acting injectable therapies: insights for applications in HIV therapy. Adv Drug Deliv Rev. 2016;103:144‐156. doi: 10.1016/j.addr.2016.02.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Sharan S, Fang L, Lukacova V, Chen X, Hooker AC, Karlsson MO. Model‐informed drug development for long‐acting injectable products: summary of american college of clinical pharmacology symposium. Clin Pharmacol Drug Dev. 2021;10:220‐228. doi: 10.1002/cpdd.928 [DOI] [PubMed] [Google Scholar]
- 3. Bettonte S, Berton M, Marzolini C. What is the significance of the pharmacokinetic profile and potential drug‐drug interactions of long‐acting intramuscular cabotegravir and rilpivirine? Expert Opin Drug Metab Toxicol. 2023;1‐5:243‐247. doi: 10.1080/17425255.2023.2223961 [DOI] [PubMed] [Google Scholar]
- 4. U.S. Food and Drug Administration . Physiologically based pharmacokinetic analyses: guidance for industry. https://www.fda.gov/files/drugs/published/Physiologically‐Based‐Pharmacokinetic‐Analyses‐%E2%80%94‐Format‐and‐Content‐Guidance‐for‐Industry.pdf. Accessed August 2023. 2018.
- 5. European Medicines Agency . Guideline on the reporting of physiologically based pharmacokinetic (PBPK) modelling and simulation. https://www.ema.europa.eu/en/documents/scientific‐guideline/guideline‐reporting‐physiologically‐based‐pharmacokinetic‐pbpk‐modelling‐simulation_en.pdf. Accessed August 2023. 2018.
- 6. Stader F, Penny MA, Siccardi M, Marzolini C. A comprehensive framework for physiologically based pharmacokinetic modelling in Matlab((R)). CPT Pharmacometrics Syst Pharmacol. 2019;8:444‐459. doi: 10.1002/psp4.12399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Stader F, Siccardi M, Battegay M, Kinvig H, Penny MA, Marzolini C. Repository describing an aging population to inform physiologically based pharmacokinetic models considering anatomical, physiological, and biological age‐dependent changes. Clin Pharmacokinet. 2019;58:483‐501. doi: 10.1007/s40262-018-0709-7 [DOI] [PubMed] [Google Scholar]
- 8. Lin Z, Li M, Gehring R, Riviere JE. Development and application of a multiroute physiologically based pharmacokinetic model for oxytetracycline in dogs and humans. J Pharm Sci. 2015;104:233‐243. doi: 10.1002/jps.24244 [DOI] [PubMed] [Google Scholar]
- 9. Rajoli RK, Back DJ, Rannard S, et al. Physiologically based pharmacokinetic modelling to inform development of intramuscular long‐acting nanoformulations for HIV. Clin Pharmacokinet. 2015;54:639‐650. doi: 10.1007/s40262-014-0227-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Shah JC, Hong J. Model for long acting injectables (depot formulation) based on pharmacokinetics and physical chemical properties. AAPS J. 2022;24:44. doi: 10.1208/s12248-022-00695-0 [DOI] [PubMed] [Google Scholar]
- 11. Chow TW, Wright MR, Hop C, Wong H. Evaluation of the predictive performance of physiologically based pharmacokinetic models for intramuscular injections of therapeutic proteins. Xenobiotica. 2019;49:1423‐1433. doi: 10.1080/00498254.2019.1571651 [DOI] [PubMed] [Google Scholar]
- 12. U.S. Food and Drug Administration . Cabenuva product label. https://www.accessdata.fda.gov/drugsatfda_docs/label/2022/212888s005s006lbl.pdf. Accessed August 2023. (2021).
- 13. U.S. Food and Drug Administration . Apretude product label. https://www.accessdata.fda.gov/drugsatfda_docs/label/2021/215499s000lbl.pdf. Accessed August 2023.
- 14. Cocoman A, Murray J. Intramuscular injections: a review of best practice for mental health nurses. J Psychiatr Ment Health Nurs. 2008;15:424‐434. doi: 10.1111/j.1365-2850.2007.01236.x [DOI] [PubMed] [Google Scholar]
- 15. Grimaldi A, Richardson C, Stanton W, Durbridge G, Donnelly W, Hides J. The association between degenerative hip joint pathology and size of the gluteus medius, gluteus minimus and piriformis muscles. Man Ther. 2009;14:605‐610. doi: 10.1016/j.math.2009.07.004 [DOI] [PubMed] [Google Scholar]
- 16. Zacharias A, Pizzari T, English DJ, Kapakoulakis T, Green RA. Hip abductor muscle volume in hip osteoarthritis and matched controls. Osteoarthr Cartil. 2016;24:1727‐1735. doi: 10.1016/j.joca.2016.05.002 [DOI] [PubMed] [Google Scholar]
- 17. Cowan RM, Semciw AI, Pizzari T, et al. Muscle size and quality of the gluteal muscles and tensor fasciae latae in women with greater trochanteric pain syndrome. Clin Anat. 2020;33:1082‐1090. doi: 10.1002/ca.23510 [DOI] [PubMed] [Google Scholar]
- 18. Evans EF, Proctor JD, Fratkin MJ, Velandia J, Wasserman AJ. Blood flow in muscle groups and drug absorption. Clin Pharmacol Ther. 1975;17:44‐47. doi: 10.1002/cpt197517144 [DOI] [PubMed] [Google Scholar]
- 19. Gill KL, Gardner I, Li L, Jamei M. A bottom‐up whole‐body physiologically based pharmacokinetic model to mechanistically predict tissue distribution and the rate of subcutaneous absorption of therapeutic proteins. AAPS J. 2016;18:156‐170. doi: 10.1208/s12248-015-9819-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Larsen C, Larsen SW, Jensen H, Yaghmur A, Ostergaard J. Role of in vitro release models in formulation development and quality control of parenteral depots. Expert Opin Drug Deliv. 2009;6:1283‐1295. doi: 10.1517/17425240903307431 [DOI] [PubMed] [Google Scholar]
- 21. Jucker BM, Fuchs EJ, Lee S, et al. Multiparametric magnetic resonance imaging to characterize cabotegravir long‐acting formulation depot kinetics in healthy adult volunteers. Br J Clin Pharmacol. 2022;88:1655‐1666. doi: 10.1111/bcp.14977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Kalicharan RW, Baron P, Oussoren C, Bartels LW, Vromans H. Spatial distribution of oil depots monitored in human muscle using MRI. Int J Pharm. 2016;505:52‐60. doi: 10.1016/j.ijpharm.2016.03.064 [DOI] [PubMed] [Google Scholar]
- 23. U.S. Food and Drug Administration . New in vitro methods to understand and mitigate clinical variability associated with injectable suspensions. https://www.fda.gov/drugs/regulatory‐science‐action/new‐in‐vitro‐methods‐understand‐and‐mitigate‐clinical‐variability‐associated‐injectable‐suspensions. Accessed August 2023. 2021.
- 24. Smith BT. Chapter 3: Solubility and dissolution. Remington Education: Physical Pharmacy. Vol 1. 1st ed. Pharmaceutical Press; 2015:192. [Google Scholar]
- 25. D'Arcy DM, Persoons T. Understanding the potential for dissolution simulation to explore the effects of medium viscosity on particulate dissolution. AAPS PharmSciTech. 2019;20:47. doi: 10.1208/s12249-018-1260-4 [DOI] [PubMed] [Google Scholar]
- 26. Wang J, Flanagan DR. General solution for diffusion‐controlled dissolution of spherical particles. 1. Theory. J Pharm Sci. 1999;88:731‐738. doi: 10.1021/js980236p [DOI] [PubMed] [Google Scholar]
- 27. Spreen WR, Margolis DA, Pottage JC Jr. Long‐acting injectable antiretrovirals for HIV treatment and prevention. Curr Opin HIV AIDS. 2013;8:565‐571. doi: 10.1097/COH.0000000000000002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Trezza C, Ford SL, Spreen W, Pan R, Piscitelli S. Formulation and pharmacology of long‐acting cabotegravir. Curr Opin HIV AIDS. 2015;10:239‐245. doi: 10.1097/COH.0000000000000168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Jucker BM, Alsaid H, Rambo M, et al. Multimodal imaging approach to examine biodistribution kinetics of cabotegravir (GSK1265744) long acting parenteral formulation in rat. J Control Release. 2017;268:102‐112. doi: 10.1016/j.jconrel.2017.10.017 [DOI] [PubMed] [Google Scholar]
- 30. Darville N, van Heerden M, Erkens T, et al. Modeling the time course of the tissue sesponses to intramuscular long‐acting paliperidone palmitate nano−/microcrystals and polystyrene microspheres in the rat. Toxicol Pathol. 2016;44:189‐210. doi: 10.1177/0192623315618291 [DOI] [PubMed] [Google Scholar]
- 31. Groseclose MR, Castellino S. Intramuscular and subcutaneous drug depot characterization of a long‐acting cabotegravir nanoformulation by MALDI IMS. Int J Mass Spectrom. 2019;437:92‐98. doi: 10.1016/j.ijms.2018.05.006 [DOI] [Google Scholar]
- 32. Lu AT, Frisella ME, Johnson KC. Dissolution modeling: factors affecting the dissolution rates of polydisperse powders. Pharm Res. 1993;10:1308‐1314. doi: 10.1023/a:1018917729477 [DOI] [PubMed] [Google Scholar]
- 33. Miceli JJ, Wilner KD, Swan SK, Tensfeldt TG. Pharmacokinetics, safety, and tolerability of intramuscular ziprasidone in healthy volunteers. J Clin Pharmacol. 2005;45:620‐630. doi: 10.1177/0091270005276485 [DOI] [PubMed] [Google Scholar]
- 34. Shebley M, Sandhu P, Emami Riedmaier A, et al. Physiologically based pharmacokinetic model qualification and reporting procedures for regulatory submissions: a consortium perspective. Clin Pharmacol Ther. 2018;104:88‐110. doi: 10.1002/cpt.1013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Abduljalil K, Cain T, Humphries H, Rostami‐Hodjegan A. Deciding on success criteria for predictability of pharmacokinetic parameters from in vitro studies: an analysis based on in vivo observations. Drug Metab Dispos. 2014;42:1478‐1484. doi: 10.1124/dmd.114.058099 [DOI] [PubMed] [Google Scholar]
- 36. Bettonte S, Berton M, Stader F, Battegay M, Marzolini C. Management of drug‐drug interactions between long‐acting cabotegravir and rilpivirine and comedications with inducing properties: a modelling study. Clin Infect Dis. 2023;76:1225‐1236. doi: 10.1093/cid/ciac901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Guest EJ, Aarons L, Houston JB, Rostami‐Hodjegan A, Galetin A. Critique of the two‐fold measure of prediction success for ratios: application for the assessment of drug‐drug interactions. Drug Metab Dispos. 2011;39:170‐173. doi: 10.1124/dmd.110.036103 [DOI] [PubMed] [Google Scholar]
- 38. Samtani MN, Vermeulen A, Stuyckens K. Population pharmacokinetics of intramuscular paliperidone palmitate in patients with schizophrenia: a novel once‐monthly, long‐acting formulation of an atypical antipsychotic. Clin Pharmacokinet. 2009;48:585‐600. doi: 10.2165/11316870-000000000-00000 [DOI] [PubMed] [Google Scholar]
- 39. Rossenu S, Cleton A, Hough D, et al. Pharmacokinetic profile after multiple deltoid or gluteal intramuscular injections of paliperidone palmitate in patients with schizophrenia. Clin Pharmacol Drug Dev. 2015;4:270‐278. doi: 10.1002/cpdd.144 [DOI] [PubMed] [Google Scholar]
- 40. Lin Z, Monteiro‐Riviere NA, Riviere JE. A physiologically based pharmacokinetic model for polyethylene glycol‐coated gold nanoparticles of different sizes in adult mice. Nanotoxicology. 2016;10:162‐172. doi: 10.3109/17435390.2015.1027314 [DOI] [PubMed] [Google Scholar]
- 41. Teeguarden JG, Deisinger PJ, Poet TS, et al. Derivation of a human equivalent concentration for n‐butanol using a physiologically based pharmacokinetic model for n‐butyl acetate and metabolites n‐butanol and n‐butyric acid. Toxicol Sci. 2005;85:429‐446. doi: 10.1093/toxsci/kfi103 [DOI] [PubMed] [Google Scholar]
- 42. Hodge D, Back DJ, Gibbons S, Khoo SH, Marzolini C. Pharmacokinetics and drug‐drug interactions of long‐acting intramuscular cabotegravir and rilpivirine. Clin Pharmacokinet. 2021;60:835‐853. doi: 10.1007/s40262-021-01005-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Paulzen M, Orfanos S, Grunder G. Remission of drug‐induced hepatitis after switching from risperidone to paliperidone. Am J Psychiatry. 2010;167:351‐352. doi: 10.1176/appi.ajp.2009.09081243 [DOI] [PubMed] [Google Scholar]
- 44. Castillo‐Mancilla JR, Anderson PL. Long‐acting injectable cabotegravir: how drug concentrations could help guide patient management. Br J Clin Pharmacol. 2022;88:4384‐4386. doi: 10.1111/bcp.15410 [DOI] [PubMed] [Google Scholar]
- 45. Yu Y, Bigos KL, Marzinke MA, et al. A population pharmacokinetic model based on HPTN 077 of long‐acting injectable cabotegravir for HIV PrEP. Br J Clin Pharmacol. 2022;88:4623‐4632. doi: 10.1111/bcp.15477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Han K, Baker M, Lovern M, et al. Population pharmacokinetics of cabotegravir following administration of oral tablet and long‐acting intramuscular injection in adult HIV‐1‐infected and uninfected subjects. Br J Clin Pharmacol. 2022;88:4607‐4622. doi: 10.1111/bcp.15439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Weng Larsen S, Larsen C. Critical factors influencing the in vivo performance of long‐acting lipophilic solutions – impact on in vitro release method design. AAPS J. 2009;11:762‐770. doi: 10.1208/s12248-009-9153-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Darville N, van Heerden M, Vynckier A, et al. Intramuscular administration of paliperidone palmitate extended‐release injectable microsuspension induces a subclinical inflammatory reaction modulating the pharmacokinetics in rats. J Pharm Sci. 2014;103:2072‐2087. doi: 10.1002/jps.24014 [DOI] [PubMed] [Google Scholar]
- 49. Gholobova D, Gerard M, Decroix L, et al. Human tissue‐engineered skeletal muscle: a novel 3D in vitro model for drug disposition and toxicity after intramuscular injection. Sci Rep. 2018;8:12206. doi: 10.1038/s41598-018-30123-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. McCartan A, Mackay J, Curran D, Mrsny RJ. Modelling intramuscular drug fate in vitro with tissue‐relevant biomimetic hydrogels. Int J Pharm X. 2022;4:100125. doi: 10.1016/j.ijpx.2022.100125 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Jackson AG, Else LJ, Mesquita PM, et al. A compartmental pharmacokinetic evaluation of long‐acting rilpivirine in HIV‐negative volunteers for pre‐exposure prophylaxis. Clin Pharmacol Ther. 2014;96:314‐323. doi: 10.1038/clpt.2014.118 [DOI] [PubMed] [Google Scholar]
- 52. Cleton A, Rossenu S, Crauwels H, et al. A single‐dose, open‐label, parallel, randomized, dose‐proportionality study of paliperidone after intramuscular injections of paliperidone palmitate in the deltoid or gluteal muscle in patients with schizophrenia. J Clin Pharmacol. 2014;54:1048‐1057. doi: 10.1002/jcph.295 [DOI] [PubMed] [Google Scholar]
- 53. Bettonte S, Berton M, Stader F, Battegay M, Marzolini C. Intramuscular cabotegravir and rilpivirine concentrations after switching from efavirenz‐containing regimen. Br J Clin Pharmacol. 2023;89:3618‐3628. doi: 10.1111/bcp.15867 [DOI] [PubMed] [Google Scholar]
- 54. Sunagawa SW, Havens JP, Podany A, Walker B, Scarsi KK, Bares SH. Long‐acting cabotegravir/rilpivirine concentrations in combination with intravenous rifampin: a case report. Open Forum Infect Dis. 2023;10:ofad604. doi: 10.1093/ofid/ofad604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Senkoro E, Bracchi M, Heskin J, et al. Direct switch from an efavirenz‐based regimen to intramuscular long‐acting cabotegravir plus rilpivirine: a case report. Int J STD AIDS. 2023;9564624231217323:1‐3. doi: 10.1177/09564624231217323 [DOI] [PubMed] [Google Scholar]
- 56. Landovitz RJ, Li S, Eron JJ Jr, et al. Tail‐phase safety, tolerability, and pharmacokinetics of long‐acting injectable cabotegravir in HIV‐uninfected adults: a secondary analysis of the HPTN 077 trial. Lancet HIV. 2020;7:e472‐e481. doi: 10.1016/S2352-3018(20)30106-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Aouri M, Barcelo C, Guidi M, et al. Population pharmacokinetics and pharmacogenetics analysis of rilpivirine in HIV‐1‐infected individuals. Antimicrob Agents Chemother. 2017;61:e00899‐16. doi: 10.1128/aac.00899-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1.
Table S2.
Table S3.
Figure S1.


