On the integration of decision trees with mixture cure model

Abstract

The mixture cure model is widely used to analyze survival data in the presence of a cured subgroup. Standard logistic regression-based approaches to model the incidence may lead to poor predictive accuracy of cure, specifically when the covariate effect is non-linear. Supervised machine learning techniques can be used as a better classifier than the logistic regression due to their ability to capture non-linear patterns in the data. However, the problem of interpret-ability hangs in the balance due to the trade-off between interpret-ability and predictive accuracy. We propose a new mixture cure model where the incidence part is modeled using a decision trees-based classifier and the proportional hazards structure for the latency part is preserved. The proposed model is very easy to interpret, closely mimics the human decision-making process, and provides flexibility to gauge both linear and non-linear covariate effects. For the estimation of model parameters, we develop an expectation maximization algorithm. A detailed simulation study shows that the proposed model outperforms the logistic regression-based and spline regression-based mixture cure models, both in terms of model fitting and evaluating predictive accuracy. An illustrative example with data from a leukemia study is presented to further support our conclusion.

1. Introduction

Survival analysis is a branch of statistics that has gained much popularity in the field of biomedical science, specifically in cancer clinical trials. In standard survival analyses, such as the Cox proportional hazards (PH) model, the proportional odds (PO) model, and the accelerated failure time (AFT) model, researchers study and model censored time-to-event data by primarily assuming that all patients in the study will eventually experience the event of interest within a time period of clinical relevance. Here, the event of interest could be recurrence of a disease, death from a disease, or relapse of a particular type of cancer. Now, in clinical trials with good overall prognoses, it is quite possible that a significant proportion of patients would reach a stage where the disease can no more be detected and is harmless. As such, this group of patients would never experience the event of interest even if the follow-up is extended for a sufficiently long period of time. Such a group is called the “long-term survivors” or “cured”. The remaining group of patients who remain susceptible to the event of interest is called the “susceptible” or “non-cured”. As a result, the overall patient population can be regarded as a mixture of these two groups of patients. In such a case, the Kaplan-Meier survival curve shows a long plateau that levels off to a non-zero value, indicating the presence of a cured subgroup.^1–5

To capture the mixture patient population, mixture cure model (MCM) and associated estimation methods have been proposed as extensions to the standard survival models; see the recent monograph by Peng and Yu for a book-length account on MCM.⁶ The cured statuses of patients or their survival probabilities are often the primary parameters of interest in predictions and prognoses. However, from a given survival data, it is impossible to identify whether a right censored observation can be considered as cured. This is because even if a patient survives the end of a study period (and hence becomes right censored), the patient may still be susceptible to the event of interest. This makes the cured status a latent variable, and hence poses a big challenge to unbiased estimation of a treatment-specific cure rate. MCM allows for such estimation of the cure probabilities (or cure rates) as well as the survival probabilities of the uncured group of patients. It is also of primary interest to assess the effects of prognostic factors or covariates on both cure probability and survival distribution of the uncured patients.

Let $U$ denote the latent cured status variable, where $U=0$ indicates that a patient is cured with respect to the event and $U=1$ indicates that a patient is susceptible to the event. Furthermore, let $T_1$ denote the time-to-event (or lifetime) for a susceptible patient and $T_0$ denote the same for a cured patient. Here, $T_0$ is such that $P\left[T_0=\infty \right]=1$. Then, if $T$ denotes the time-to-event for any patient in the mixture population, the MCM is defined through the survival function of $T$, which is known as the population or long-term survival function, and is expressed as

$$S_p(t;\mathit{x},\mathit{z})=P[T>t;\mathit{x},\mathit{z}]=1-\pi \left(\mathit{z}\right)+\pi \left(\mathit{z}\right)S_u(t;\mathit{x}),$$ (1)

where $S_u(t;\mathit{x})=P\left[T_1>t\right]$ is the susceptible survival function and $\pi \left(\mathit{z}\right)=P[U=1]$ with $\mathit{z}={\left(z_1,z_2,\dots ,z_p\right)}^{\prime }$ and $\mathit{x}={\left(x_1,x_2,\dots ,x_q\right)}^{\prime }$ denoting the vectors of covariates affecting the incidence (i.e., $\pi \left(\mathit{z}\right)$ or $1-\pi \left(\mathit{z}\right)$) and the latency (i.e., $S_u(t;\mathit{x})$), respectively. Predominantly, most studies on MCM have considered the sigmoid or logistic link function, defined as $\pi \left(\mathit{z}\right)=\frac{\text{exp}\left(z^{\prime }\gamma \right)}{1+\text{exp}\left(z^{\prime }\gamma \right)}$, to model the effect of covariates on the incidence part of MCM, where $\gamma$ is the vector of regression coefficients (including the intercept term) corresponding to $\mathit{z}$.^7–9 The probit link function, defined as ${\mathbf{\Phi }}^{-1}\left(\pi \right(\mathit{z}\left)\right)={\mathit{z}}^{\prime }\gamma$ with $\Phi (\cdot )$ denoting the cumulative distribution function of the standard normal distribution, and the complementary log-log link function, defined as $\text{log}\{-\text{log}(1-\pi \left(\mathit{z}\right)\left)\right\}={\mathit{z}}^{\prime }\mathit{\gamma }$, have also been used in some studies as alternatives to the logistic link function.^10,11 A major issue with the aforementioned parametric link functions is that they can only capture linear effects of $\mathit{z}$ on the incidence; meaning they implicitly assume the boundary separating the cured and non-cured patients to be linear. Since the cured statuses remain unknown for all patients whose lifetimes are censored, the validity of a linear classification boundary cannot be checked. As such, the assumption of a logistic link function (or the alternatives stated above) may result in impreciseness when it comes to estimation and prediction of the incidence, specifically when the true classification boundary is complex and non-linear. Few non-parametric strategies were also proposed to model the incidence, however, their performances were only validated in the presence of a single covariate.^12,13 Another approach, based on the generalized additive models for location, scale and shape with smooth effects of covariates, was proposed to capture non-linear effects of covariates on the incidence, but the effects still turned out to act on the incidence through the logistic function¹⁴. Other competing approaches to non-parametrically model the incidence include the spline-based method that may not be efficient when the true non-parametric form contains several interaction terms.^15,16 More recently, a non-parametric single-index model was proposed to model the uncure probability in a mixture cure model.¹⁷ Thus, there is a big room for improvement as far as modeling the incidence part of MCM is concerned with an objective to capture more complex (non-linear) effects of covariates on the incidence. This naturally calls for the need to identify a suitable classification function which can model the incidence part more accurately by effectively capturing complex separating boundaries (with respect to the covariates) between the cured and non-cured patients.

To this end, we can think of integrating a suitable machine learning technique with MCM, given that machine learning techniques are well known to capture non-linearity in data.¹⁸ In particular, decision trees (DT)-based classifiers have been proved to be more robust and flexible than the logistic (or the probit) classifier and has become very popular with the growth of data mining.¹⁹ The main advantages of DT are the fact that they are better for categorical data, easy to interpret and can deal co-linearity better than other classification models such as the support vector machine (SVM).²⁰ In addition, DT is expected to be computationally much less expensive when compared to random forests and neural networks. Motivated by this, we propose a novel decision trees (DT)-based mixture cure model, where we model the incidence using the DT classifier and the latency using a semi-parametric proportional hazards structure with an unspecified baseline hazard function.²¹ To the best of our knowledge, this is the first work that employs DT to capture non-linearity in the incidence part of MCM. We call our proposed model as MCM-DT. To estimate the model parameters we develop an estimation method based on the expectation maximization (EM) algorithm. We show that our proposed model outperforms both logistic regression-based MCM (MCM-Logit) and spline regression-based MCM (MCM-Spline) models, noting that MCM-Spline can also capture non-linearity in the data.

The rest of this paper is organized as follows. In Section 2, we discuss the formulation of the MCM-DT model. In Section 3, we discuss the development of the EM algorithm. In Section 4, a detailed simulation study is carried out to demonstrate the performance and superiority of our proposed model. In Section 5, we illustrate the applicability of our proposed model and the estimation algorithm using a data on leukemia patients who went through bone marrow transplantation. Finally, in Section 6, we make some concluding remarks and discuss few potential future research problems.

2. Decision trees-based mixture cure model

2.1. Censoring mechanism, latency modeling, and likelihood structure

We consider a practical scenario where the observed data is subject to right censoring and the censoring mechanism is non-informative. If $Y$ denotes the true lifetime and $C$ denotes the right censoring time, then, the observed lifetime, denoted by $T$, is given by $T=\text{min}\{Y,C\}$. Furthermore, let $\delta$ denote the censoring indicator, i.e., $\delta =1$ if the true lifetime is observed (i.e., $T=Y$) and $\delta =0$ if the true lifetime is right censored (i.e., $T=C$). If $n$ denotes the number of patients in the study, the observed data is defined as: $D_O=\left\{\left(t_i,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i\right),i=\mathrm{1,2},\cdots ,n\right\}$. Now, we define the set of observed and censored lifetimes as: ${\Delta }_1=\left\{i:{\delta }_i=1\right\}$ and ${\Delta }_0=\left\{i:{\delta }_i=0\right\}$, respectively. Note that the cured status $U_i$ is known to take the value 1 if $i\in {\Delta }_1$. However, if $i\in {\Delta }_0,U_i$ can be either 0 or 1 (i.e., unknown).

Next, we turn our attention to modeling the effect of covariates on the latency. For this purpose, we assume the lifetime distribution of the uncured or susceptible patients to follow a proportional hazards structure without assuming any particular form for the baseline hazard function. Thus, we express the hazard function of the uncured patients as:

$$h_u\left(t;\mathit{x}\right)=h_{u0}\left(t\right)\text{exp}\left({\mathit{x}}^{\prime }\mathit{\beta }\right),$$ (2)

where $\mathit{\beta }$ is the associated vector of regression coefficients (without the intercept term) and $h_{u0}(\cdot )$ is an unspecified baseline hazard function that does not involve $\mathit{x}$. The MCM in eqn.(1) can then be rewritten as

$$S_p\left(t;\mathit{x},\mathit{z}\right)=1-\pi \left(\mathit{z}\right)+\pi \left(\mathit{z}\right){\left\{S_{u0}\left(t\right)\right\}}^{\text{exp}\left({\mathit{x}}^{\prime }\mathit{\beta }\right)},$$ (3)

where $S_{u0}\left(t\right)=\text{exp}\left\{-{\int }_0^t{h}_{u0}\left(u\right)du\right\}$ is the baseline survival function. One is of course free to use any other modeling approaches for the susceptible lifetime such as the piecewise linear model²² or the accelerated failure time model¹¹ or a completely parametric model.^23–25

Now, considering the unobserved $U_i$’s to be the missing data, the complete data can be defined as: $D_C=\left\{\left(t_i,{\delta }_i,U_i,{\mathit{x}}_i,{\mathit{z}}_i\right),i=\mathrm{1,2},\cdots ,n\right\}$. Hence, the complete data likelihood function can be expressed as:

$$L_c=\prod _{i=1}^n{\left[{\left\{\pi \left({\mathit{z}}_i\right)f_u\left(t_i;{\mathit{x}}_i\right)\right\}}^{U_i}\right]}^{{\delta }_i}{\left[{\left\{1-\pi \left({\mathit{z}}_i\right)\right\}}^{1-U_i}{\left\{\pi \left({\mathit{z}}_i\right)S_u\left(t_i;{\mathit{x}}_i\right)\right\}}^{U_i}\right]}^{1-{\delta }_i},$$ (4)

where $S_u\left(t_i;{\mathit{x}}_i\right)={\left\{S_{u0}\left(t_i\right)\right\}}^{\text{exp}\left({\mathit{x}}_i^{\prime }\mathit{\beta }\right)}$ and $f_u\left(t_i;{\mathit{x}}_i\right)$ is the density function corresponding to $S_u\left(t_i;{\mathit{x}}_i\right)$. From eqn.(4), the corresponding log-likelihood function can be expressed as:

$$l_c=l_{c1}+l_{c2},$$ (5)

where

$$l_{c1}=\sum _{i=1}^n\left[U_i\text{\hspace{0.17em}log\hspace{0.17em}}\pi \left(z_i\right)+\left(1-U_i\right)\text{\hspace{0.17em}log}\left(1-\pi \left(z_i\right)\right)\right]$$ (6)

and

$$l_{c2}=\sum _{i=1}^n\left[U_i\text{\hspace{0.17em}log\hspace{0.17em}}{S}_u\left(t_i;x_i\right)+{\delta }_i\text{\hspace{0.17em}log\hspace{0.17em}}{h}_u\left(t_i;x_i\right)\right]$$ (7)

with $h_u\left(t_i;{\mathit{x}}_i\right)$ being as in eqn.(2). It is interesting to note that $l_{c1}$ involves parameters related to the incidence part only and $l_{c2}$ involves parameters related to the latency part only. Furthermore, note that $U_i$’s are linear in both $l_{c1}$ and $l_{c2}$. These simplify the development of the EM algorithm which is described in Section 3.

2.2. Incidence modeling using decision trees

To help develop our theory, let us assume that $U_i(i=\mathrm{1,2},\cdots ,n)$ is known through some mechanism (see Section 3). Then, the DT algorithm seeks to build the optimal decision boundary between the two distinguishing classes (cured and uncured) by automatically and recursively partitioning the predictor space into a series of hierarchical non-overlapping regions such that the final tree is made up of internal and terminal nodes. The terminal nodes are the predicted values of the tree.¹⁹ Let $\left({\mathit{z}}_i,U_i\right)$, for $i=\mathrm{1,2},\cdots ,n$, with ${\mathit{z}}_i=\left(z_{i1},z_{i2},\cdots ,z_{ip}\right)$ be the observed data consisting of $p$ inputs (covariates) and a binary response variable $U_i$ (cured status, which takes the value 0 if cured and 1 if uncured). Suppose we have a partition into $M$ regions, $R_1,R_2,\cdots ,R_M$, and we can model the response as binary in each region by letting $m$ denoting the index for terminal node, then, in node $m$, which represents region $R_m$ with $n_m$ observations, define

$${\widehat{P}}_{mk}=P_{mk}\left(U=k\mid z\right)=\frac{1}{n_m}\sum _{z_i\in R_m}I\left(U_i=k\right)$$ (8)

as the proportion of class $k$ (where $k$ takes a value of 0 if cured and 1 if uncured) observations in node $m$. Observations in node $m$ are classified to the class $k$ with the majority points, that is, $k\left(m\right)={\text{argMax}}_k{\hat{P}}_{mk}$.¹⁸ For classification problems, although different measures of node impurity can be considered, in this paper, we decided to use the Gini index, $G_{mk}$, defined as:

$$G_{mk}=\sum _{k\ne k^{\prime }}{\widehat{P}}_{mk}{\widehat{P}}_{m{k}^{\prime }}=\sum _{k=1}^K{\widehat{P}}_{mk}\left(1-{\widehat{P}}_{mk}\right),$$ (9)

where $K$ is the number of classes, which in the given context is 2. The size of the tree is a tuning parameter that controls the complexity of the DT model. The recursive binary splitting technique results in growing a very large tree for classification problems. However, large trees are too flexible and tend to over-fit the data. To mitigate this, the cost-complexity pruning or weakest link pruning is used in this paper to prune the full tree to help narrow down to a number of sub-trees for comparisons. Let $T_0$ denote the full tree, $T^{*}\subset T_0$ denote a sub-tree obtained by pruning $T_0$, and $\left|T^{*}\right|$ denote the number of terminal nodes in $T^{*}$. Then, we define the cost-complexity criterion as

$$C_{\alpha }\left(T^{\text{*}}\right)=\frac{1}{n}\sum _{m=1}^{\left|T^{\text{*}}\right|}{n}_m{G}_{mk}+\alpha \left|T^{\text{*}}\right|\text{ such that }{n}_m\ge n_{\mathit{\text{min}}},$$ (10)

where $\alpha$ is the cost complexity tuning parameter (cp), $n_{\text{m}}$ is the minimum number of observations that must exist in a node in order for a split to be attempted (minsplit) and $n_{\mathit{\text{min}}}$ is the minimum number of observations in any terminal or leaf node (minbucket). The goal is to find the sub-tree that minimizes eqn.(10) for each $\alpha$. Observe that $\alpha$ controls the trade-off between the size of the tree and its flexibility of fit to the data. This means that as $\alpha$ increases, the number of terminal nodes in the sub-tree decreases and vice versa. Specifically, when $\alpha =0$, there’s no penalty and the best sub-tree is $T_0$, created through recursive binary splitting.²⁶ Detailed discussions on obtaining the hyper-parameters($\alpha ,n_{\text{m}}$, and $n_{\mathit{\text{min}}}$) are presented in the next subsection.

2.3. Tuning decision trees

To avoid over-fitting and unwanted bias associated with the estimates of the uncured probabilities, we split the data into two sets, i.e., a training set and a validation or testing set. The training set is used to train the MCM-DT model and the testing set is used to validate the performance of the MCM-DT model. Since decision trees can easily over-fit the training data, a two-way modeling approach is further adopted to prevent over-fitting the MCM-DT model. Firstly, the grid-search ten-fold cross-validation technique is performed on the training set to obtain the optimal hyper-parameters of the model, i.e., $\alpha$ and $n_{\text{m}}$. Three different possible values are specified for each hyper-parameter; $n_{\text{m}}$ is specified as (11, 20, 25) and $\alpha$ is specified as (0.001, 0.005, 0.01). On the other hand, $n_{\mathit{\text{min}}}$ is set as $\frac{n_m}{3}$. The best hyper-parameters obtained through this search are then used to grow the first tree in the first approach. Secondly, we perform cost-complexity pruning on the first tree obtained in the first approach. The cost-complexity pruning parameter, $c{p}_{\mathit{\text{min}}}$, is also obtained using cross-validation. The $c{p}_{\mathit{\text{min}}}$ corresponding to the lowest cross-validation error is used to prune the tree grown in the first approach. The pruned tree obtain in the second approach is very simple and easy to interpret, and, therefore, will be considered as the final optimal MCM-DT model for predictions on unseen data. Furthermore, we validate the performance of the final optimal MCM-DT model using the test set. Model performance evaluation criteria such as the graphical receiver operating characteristic (ROC) curve and it’s area under the curve (AUC) are used to assess the performance of the final model.

2.4. Platt scaling on decision trees output

We apply the Platt scaling technique to transform the predictions of the DT model into well-defined calibrated posterior probabilities of uncured by passing the predictions through a sigmoid function.²⁷ Suppose we let $g\left(\mathit{z}\right)$ denote the output of the DT model. Such an output is treated as raw or uncalibrated predictions defined on [0, 1] for classification. To obtain the calibrated posterior probabilities, we pass these outputs through the following function:

$$\pi \left(\mathit{z}\right)=P\left(U=1∣g\left(\mathit{z}\right)\right)=\frac{1}{1+\text{exp}\left\{Ag\left(\mathit{z}\right)+B\right\}},$$ (11)

where A and B are unknown parameters to be estimated. The parameters A and B are the solutions to the following minimization problem, which can be solved using the gradient descent technique:

$${\text{argmin}}_{A,B}\left[-\sum _{i=1}^n{U}_i\text{\hspace{0.17em}log\hspace{0.17em}}p\left(z_i\right)+\left(1-U_i\right)\text{log}\left(1-p\left(z_i\right)\right)\right],$$ (12)

where

$$p\left({\mathit{z}}_i\right)=\frac{1}{1+\text{exp}\left(Ag\left({\mathit{z}}_i\right)+B\right)}.$$ (13)

Now, using the same data to train the DT model and the sigmoid can cause unwanted bias in the sigmoid training set, which can lead to poor fitted results. To resolve this, we use $k$-fold cross validation to allow the DT model and the sigmoid to be trained on the full training set. For the $k$-fold cross validation method, the data is split into $k$-folds in which at each iteration, one fold is set aside as an independent validation or testing set whereas $k-1$ folds are used to train the model. The $k$ validation sets are then used to estimate the sigmoid parameters. We apply a 3-fold cross-validation in this paper.²⁷ Unlike the splitting method, cross validation produces larger sigmoid training set and thus gives lower variance estimates for the parameters $A$ and $B$. Furthermore, to avoid over-fitting to the training set, we use the out-of-sample model by letting $N_{+}$ and $N_{-}$ respectively denote the number of uncured and cured subjects in the training set, and for each subject, Platt calibration uses outcome values $U_{+}$ and $U_{-}$ instead of 1 and 0, respectively, where

$$U_{+}=\frac{N_{+}+1}{N_{+}+2}\text{ and }{U}_{-}=\frac{1}{N_{-}+2}.$$ (14)

Observe that the out-of-sample target values $U_{+}$ and $U_{-}$ are non-binary but only converges to 1 and 0, respectively, when the training size approaches infinity.

3. Estimation method: EM algorithm

As discussed earlier, the cured status $U_i$ remains unknown (missing) for all patients whose lifetimes are right censored. To handle these missing observations ingrained to the problem set-up and the model structure, we propose to develop the EM algorithm to estimate the unknown parameters of the proposed DT-based MCM.^9,28 For this purpose, we compute the conditional expectation of the complete data log-likelihood function given the observed data and current values of the parameters. This reduces to computing the conditional expectation of the cured status variable $U_i$. Such a conditional expectation at the $k$-th iteration step is given by

$$w_i^{\left(k\right)}={\delta }_i+\left(1-{\delta }_i\right)\frac{{\pi }^{(k-1)}\left({\mathit{z}}_i\right)S_u^{(k-1)}\left(t_i;{\mathit{x}}_i\right)}{1-{\pi }^{(k-1)}\left({\mathit{z}}_i\right)+{\pi }^{(k-1)}\left({\mathit{z}}_i\right)S_u^{(k-1)}\left(t_i;{\mathit{x}}_i\right)},i=1,\cdots ,n,$$ (15)

where $S_u^{(k-1)}\left(t_i;{\mathit{x}}_i\right)={\left\{S_{u0}^{(k-1)}\left(t_i\right)\right\}}^{\text{exp}\left({\mathit{x}}_i^{\prime }{\mathit{\beta }}^{(k-1)}\right)}$. Note that $w_i^{\left(k\right)}$ is interpreted as the conditional probability of $U_i$ taking the value 1. Once we obtain $w_i^{\left(k\right)}$’s, we replace $U_i$’s in eqns.(6) and (7) with $w_i^{\left(k\right)}$’s, for $i=1,\cdots ,n$. Thus, the expectation step (E-step) of the EM algorithm replaces $l_{c1}$ and $l_{c2}$ by

$$Q_1=\sum _{i=1}^n\left[w_i^{\left(k\right)}\text{\hspace{0.17em}log\hspace{0.17em}}\pi \left(z_i\right)+\left(1-w_i^{\left(k\right)}\right)\text{\hspace{0.17em}log}\left(1-\pi \left(z_i\right)\right)\right]$$ (16)

and

$$Q_2=\sum _{i=1}^n\left[w_i^{\left(k\right)}\text{\hspace{0.17em}log\hspace{0.17em}}{S}_u\left(t_i;x_i\right)+{\delta }_i\text{\hspace{0.17em}log}\left\{w_i^{\left(k\right)}{h}_u\left(t_i;x_i\right)\right\}\right],$$ (17)

respectively, after noting that ${\delta }_i\text{log}{w}_i^{\left(k\right)}=0$ and ${\delta }_i{w}_i^{\left(k\right)}={\delta }_i$.

In the maximization step (M-step) of the EM algorithm, the standard approach in the context of MCM is to carry out two maximization problems independently. The first one is with respect to the function $Q_1$ to obtain estimates of $\pi \left({\mathit{z}}_i\right)$, i.e., the incidence, and the second one is with respect to the function $Q_2$ to obtain estimates of $\left(\mathit{\beta },S_{u0}(\cdot )\right)$, i.e., the latency. However, in this work, we do not maximize $Q_1$ to estimate $\pi \left({\mathit{z}}_i\right)$. Instead, we use the DT, as discussed in Section 2.2, to obtain $\widehat{\pi \left({\mathit{z}}_i\right)}$. Now, to employ the DT, note that we mentioned earlier that the values of $U_i$’s should be known for all $i=\mathrm{1,2},\cdots ,n$. However, $U_i$’s are unknown for $i\in {\Delta }_0$. To circumvent this issue, we propose to impute the values of missing $U_i$’s and use a multiple imputation-based technique to estimate $\pi \left({\mathit{z}}_i\right)$. At the $k$-th iteration step of the EM algorithm, the multiple imputation technique is described as follows: for a chosen positive integer $N$, generate $\left\{U_i^{\left(r\right)},i=1,\cdots ,n;r=1,\cdots ,N\right\}$ from a Bernoulli distribution with probability of success $w_i^{\left(k\right)}$. Given the generated $\left\{U_i^{\left(r\right)},i=1,\cdots ,n\right\}$ for each $r=1,\cdots ,N$, estimate $\pi \left({\mathit{z}}_i\right)$ by using the DT followed by the Platt scaling method. Let us denote these estimates by $\widehat{{\pi }^{\left(r\right)}\left({\mathit{z}}_i\right)}$. Calculate the final estimate of $\pi \left({\mathit{z}}_i\right)$ as $\widehat{\pi \left({\mathit{z}}_i\right)}=\frac{1}{N}{\sum }_{r=1}^N\widehat{{\pi }^{\left(r\right)}\left({\mathit{z}}_i\right)}$. For all practical purposes, the number of imputations $N$ can be chosen as 5, which is consistent with the existing works.^20,29

As far as the maximization of $Q_2$ is concerned, the estimating eqn.(17) can be approximated by the partial log-likelihood function⁹

$$\sum _{j=1}^{n_k}\text{\hspace{0.17em}log}\frac{\text{exp}\left(s_j^{\prime }\beta \right)}{{\left[{\sum }_{i^{\prime }\in R_j}{w}_{i^{\prime }}^{\left(k\right)}\text{ exp}\left(x_{i^{\prime }}^{\prime }\beta \right)\right]}^{d_j}},$$ (18)

where ${\tau }_1<{\tau }_2<\cdots <{\tau }_{n_k}$ are $n_k$ distinct ordered uncensored failure times, $d_j$ denotes number of uncensored failure times equal to ${\tau }_j$, $R_j$ denotes the risk set at ${\tau }_j$, and ${\mathit{s}}_j={\sum }_{\left\{i:t_i={\tau }_j\right\}}{\mathit{x}}_i$, for $1\le j\le n_k$. Noting that eqn.(18) is independent of any baseline functions, we use the “coxph()” function in R software to estimate $\mathit{\beta }$ where we treat $\text{log}{w}_i^{\left(k\right)}$ as an offset term. Once the estimate of $\mathit{\beta }$ is obtained, the baseline survival function $S_{u0}(\cdot )$, which is needed to update the E-step in eqn.(15), can be estimated by a Breslow-type estimator. The E- and M-steps are finally repeated until some convergence criterion is achieved such as

$${∥{\mathit{\theta }}^{\left(k\right)}-{\mathit{\theta }}^{(k-1)}∥}_2^2<ϵ,$$ (19)

where $\mathit{\theta }$ denotes the vector of unknown model parameters, i.e., $\mathit{\theta }=\left(\pi \left({\mathit{z}}_i\right),\mathit{\beta },S_{u0}(\cdot )\right),i=\mathrm{1,2},\cdots ,n,ϵ>0$ is a chosen tolerance (e.g., 10⁻³) and $\parallel \cdot {\parallel }_2$ is the $L_2$-norm.

Due to the complexity of the proposed EM algorithm, the standard errors of the estimators are not easily available. We propose to use a bootstrap technique.^9,20 For this purpose, we first fix the number of bootstrap samples, say $R$. Each bootstrap sample is obtained by re-sampling with replacement from the original data, noting that the size of the bootstrap sample is the same as the size of the original data. Then, for each bootstrap sample, we estimate the model parameters by employing the EM algorithm. This gives us $R$ estimates for each model parameter. For a given parameter, the standard deviation of these estimates gives us the estimated standard error of the parameter’s estimator. The steps involved in the development of the EM algorithm can be summarized as follows:

Step 1: Use the censoring indicator ${\delta }_i$ to initiate the value of $w_i$. That is, take the initial value of $w_i$ as $w_i=1$ if ${\delta }_i=1$ and $w_i=0$ if ${\delta }_i=0$, for $i=1,\cdots ,n$.

Step 2: Use the initial value of $w_i$ to impute the values of $U_i$, for $i=1,\cdots ,n$, and then apply the DT together with the Platt scaling method to estimate $\pi \left({\mathit{z}}_i\right)$. The final estimate of $\pi \left({\mathit{z}}_i\right)$ is calculated as the average of $\widehat{\pi \left({\mathit{z}}_i\right)}$’s from multiple imputation.

Step 3: From eqn.(18), use the “coxph” function in R to obtain $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$ and then calculate $\widehat{S_{u0}}\left(t_i\right)$ and, finally, $\widehat{S_u}\left(t_i;{\mathit{x}}_i\right)$.

Step 4: Use the estimates of $\pi \left({\mathit{z}}_i\right)$ and $S_u\left(t_i;{\mathit{x}}_i\right)$ to update $w_i$ using eqn.(15).

Step 5: Repeat steps (2)-(4) above until convergence is achieved.

Step 6: Use the bootstrap method to calculate the standard errors of the estimators.

4. Simulation study

4.1. Data generation

In this section, we assess the performance of the proposed MCM-DT model and the EM-based estimation algorithm through a detailed Monte Carlo simulation study. We also compare the performance of MCM-DT with the MCM-Logit and MCM-Spline models. In addition, we compare the MCM-DT with two other recently proposed machine learning-based mixture cure models, namely the neural network (NN)-based mixture cure model (MCM-NN) and the random forests (RF)-based mixture cure model (MCM-RF).^30,31 The comparisons are done through the calculated bias and mean square error (MSE) of different quantities of interest, and also through the predictive accuracy of cure. For the simulation study, we consider different sample sizes as $n=300,600$, and 900. For any considered model, two-third of the data is used to train the model and the remaining one-third of the data is used to test the model. Furthermore, we consider the following four scenarios to generate the true uncured probabilities:

• Scenario 1: $\pi \left(\mathit{z}\right)=\frac{\text{exp}\left(0.3-5z_1-3z_2\right)}{1+\text{exp}\left(0.3-5z_1-3z_2\right)},$

• Scenario 2: $\pi \left(\mathit{z}\right)=\frac{\text{exp}\left(0.3-5z_1{z}_2-3z_1{z}_2\right)}{1+\text{exp}\left(0.3-5z_1{z}_2-3z_1{z}_2\right)},$

• Scenario 3: $\pi \left(\mathit{z}\right)=\text{exp}\left(-\text{exp}\left(0.3-\left(5z_1{z}_2\right)-\left(3\text{cos}\left(z_2\right)\right)\right)\right)\text{, }$

• Scenario 4: $\pi \left(\mathit{z}\right)=\text{exp}\left(-\text{exp}\left(0.3-5z_1{z}_4+3\text{tanh}\left(z_2{z}_3\right)\right.\right.\left.\left.-8z_3{z}_4{z}_5\left(4-2z_4{z}_5\right)\left(3-1.4z_3{z}_5\right)+\text{log}\left(\text{abs}\left(z_1+z_5\right)\right)\right)\right).$

In scenarios 1, 2 and 3, $z_1$ and $z_2$ are generated from the standard normal distribution. In scenario 4, $z_1$ and $z_2$ are generated from the Bernoulli distribution with success probabilities 0.6 and 0.3, respectively, whereas $z_3$, $z_4$, and $z_5$ are generated from the standard normal distribution. In all scenarios, we consider $\mathit{z}=\mathit{x}$, i.e., we use the same set of covariates in the incidence and latency parts. It is clear that Scenario 1 is the traditional logistic function which implies that the cured and uncured subjects can be linearly separated with respect to the covariates. Scenario 2 is a logistic-type function, however, it has interaction terms, which implies that the cured and uncured subjects cannot be linearly separated. Scenarios 3 and 4 represent non-logistic functions that can produce complex classification boundaries with Scenario 4 having several covariates and complicated interaction terms.

For the latency, we consider the hazard function of the uncured subjects to be of the following form: $h_u(t;\mathit{x})=\alpha t^{\alpha -1}\text{exp}\left({\mathit{x}}^{\prime }\mathit{\beta }\right)$. We select the true values of $\left(\alpha ,{\beta }_1,{\beta }_2\right)$ for scenarios 1, 2 and 3 as (0.5,1,0.5), whereas we select the true values of $\left(\alpha ,{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4,{\beta }_5\right)$ for scenario 4 as (0.9,0.8,1.2,0.5,1.1,−0.6). To generate the observed lifetime data corresponding to the $i$-th subject $(i=\mathrm{1,2},\cdots ,n)$, we generate a random variable $V_i$ from Uniform(0,1) distribution and a right censoring time $C_i$ from Uniform(0,20) distribution. If $V_i\le 1-\pi \left({\mathit{z}}_i\right)$, we set the observed lifetime $T_i$ to $C_i$, i.e., $T_i=C_i$. On the other hand, if $V_i>1-\pi \left({\mathit{z}}_i\right)$, first, we generate a true lifetime $Y_i$ from the considered hazard function $h_u(y;\mathit{x})=\alpha y^{\alpha -1}\text{exp}\left({\mathit{x}}^{\prime }\mathit{\beta }\right)$, which is equivalent to generating the true lifetime from a Weibull distribution with shape parameter $\alpha$ and scale parameter ${\left\{\text{exp}\left({\mathit{x}}^{\prime }\mathit{\beta }\right)\right\}}^{-\frac{1}{\alpha }}$. Then, we set $T_i=\text{min}\left\{Y_i,C_i\right\}$. In all cases, if $T_i=C_i$, we set the censoring indicator ${\delta }_i=0$; otherwise, we set ${\delta }_i=1$. With these, the true cure probability corresponding to scenario 1 is roughly 0.40, whereas the true cure probability for scenarios 2 and 4 are roughly 0.50. The censoring proportion is roughly 0.60 in all these cases, which ensures enough observed events (effective sample size). On the other hand, the true cure probability for scenario 3 is around 0.30 with the censoring proportion being 0.40. Thus, the above four scenarios allow us to study the performance of our model for varying cure rates and censoring proportions.

4.2. Simulation results

All simulation results are based on $M=500$ Monte Carlo runs. For the MCM-DT model, the number of multiple imputations is chosen as 5 which is along the lines of Li et al.²⁰ In Table 1, we present the biases and MSEs of the estimates of $\pi \left(\mathit{z}\right)$ obtained from the proposed MCM-DT model and compare these with the ones obtained from the MCM-Spline and MCM-Logit models. For the MCM-Spline model, we fit a non-parametric additive model using a thin plate spline and use the “gam” function of R package “mgcv”. This allows the effective degrees of freedom of each covariate function to be automatically selected. We use the following formulae to calculate the bias and MSE of the estimate of $\pi \left(\mathit{z}\right)$, denoted by $\hat{\pi }\left(\mathit{z}\right)$:

$$\text{Bias}\left(\widehat{\pi }\left(z\right)\right)=\frac{1}{M}\sum _{r=1}^M\left[\frac{1}{n}\sum _{i=1}^n\left|\left\{\widehat{{\pi }^{\left(r\right)}}\left(z_i\right)-{\pi }^{\left(r\right)}\left(z_i\right)\right\}\right|\right]$$ (20)

and

$$\text{MSE}\left(\widehat{\pi }\left(z\right)\right)=\frac{1}{M}\sum _{r=1}^M\left[\frac{1}{n}\sum _{i=1}^n{\left\{\widehat{{\pi }^{\left(r\right)}}\left(z_i\right)-{\pi }^{\left(r\right)}\left(z_i\right)\right\}}^2\right].$$ (21)

Table 1:

Comparison of bias and MSE of the uncured probability for different models

		Bias			MSE
Scenario	n	DT	Spline	Logit	DT	Spline	Logit
	300	0.2058	0.1364	0.1307	0.0862	0.0417	0.0312
1	600	0.1884	0.1183	0.1083	0.0734	0.0328	0.0222
	900	0.1815	0.1094	0.0978	0.0675	0.0281	0.0180
	300	0.1572	0.3486	0.3552	0.0499	0.1614	0.1656
2	600	0.1452	0.3517	0.3565	0.0391	0.1639	0.1671
	900	0.1420	0.3504	0.3558	0.0357	0.1679	0.1712
	300	0.1963	0.2993	0.3661	0.0894	0.1461	0.1797
3	600	0.1764	0.2980	0.3529	0.0738	0.1461	0.1760
	900	0.1650	0.2961	0.3517	0.0651	0.1453	0.1752
	300	0.2426	0.4431	0.4517	0.1024	0.2162	0.2214
4	600	0.1799	0.4533	0.4579	0.0716	0.2210	0.2236
	900	0.1592	0.4566	0.4598	0.0620	0.2225	0.2242

In eqns.(20) and (21), ${\pi }^{\left(r\right)}\left({\mathit{z}}_i\right)$ and $\widehat{{\pi }^{\left(r\right)}}\left({\mathit{z}}_i\right)$ denotes respectively the true and estimated non-cured probabilities corresponding to the $i$-th subject and $r$-th Monte Carlo run $(i=1,\cdots ,n;r=1,\cdots ,M)$. From Table 1, it is clear that when the cured and uncured subjects are linearly separable (i.e., under scenario 1), MCM-Logit performs better both in terms of bias and MSE. This is not surprising since logistic regression-based models are expected to capture linear patterns in the data better than other models. However, when the cured and uncured subjects are not linearly separable (i.e., scenarios 2–4), MCM-DT outperforms both MCM-Spline and MCM-Logit models. This implies that the proposed DT-based classifier to model the incidence performs better in capturing complex relationships between the covariates and uncured probabilities when compared to the existing spline-based and logistic regression-based techniques to model the incidence. Intuitively, this should also improve the predictive accuracy of cure. We confirm this with the ROC curves, presented in Figure A3.1 of the supplemental material, and the corresponding AUC values, reported in Table 2. It is clear that for scenarios 2–4, and for all considered sample sizes, the proposed MCM-DT model results in the highest predictive accuracy. In particular, when compared to the MCM-Spline model, which is also known to capture complex relationships, note the gain in predictive accuracy that our proposed model provides under scenarios 2–4. Furthermore, the closeness of the training and testing AUC values, specifically for larger sample size in scenarios 2–4, clearly demonstrates that there is no issue with over-fitting.

Table 2:

Comparison of AUC values for different models and scenarios

Scenario	n	Training AUC			Testing AUC
		DT	Spline	Logit	DT	Spline	Logit
	300	0.9226	0.9550	0.9715	0.8681	0.9482	0.9695
1	600	0.9359	0.9592	0.9725	0.8938	0.9539	0.9711
	900	0.9386	0.9611	0.9729	0.9031	0.9581	0.9722
	300	0.9268	0.5652	0.5335	0.8541	0.5510	0.5444
2	600	0.9235	0.5463	0.5225	0.8775	0.5432	0.5322
	900	0.9185	0.5352	0.5198	0.8835	0.5285	0.5250
	300	0.8955	0.7411	0.5357	0.8280	0.6955	0.5369
3	600	0.9132	0.7338	0.5254	0.8624	0.7129	0.5305
	900	0.9148	0.7345	0.5207	0.8716	0.7164	0.5235
	300	0.9262	0.6230	0.5905	0.7150	0.5446	0.5476
4	600	0.9589	0.5920	0.5720	0.8366	0.5380	0.5386
	900	0.9654	0.5810	0.5656	0.8763	0.5352	0.5362

In Table 3, we present the biases and MSEs of the estimates of the overall survival probabilities obtained from the proposed MCM-DT model and compare these with the ones obtained from the MCM-Spline and MCM-Logit models. The formulae used to calculate the biases and MSEs of the overall survival probability are similar to the ones in eqns.(20) and (21) with the non-cured probability being replaced by the overall survival probability. Noting that the overall survival probability is a function of both incidence and latency parameters, we can easily see that the proposed MCM-DT model also results in the smallest bias and MSE of the overall survival probability under scenarios 2–4. Thus, improving the incidence part with the proposed DT-based approach also improves the estimation results corresponding to the overall survival probability, which is an interesting finding. For the susceptible survival probability, which is a pure function of only the latency parameters, the biases and MSEs obtained from different models are comparable (see Table 4). For interested readers, we present the biases and MSEs of the estimates of the baseline survival function in Table A4.1 of the supplemental material for $n=600$. Once again, the results are comparable for different models.

Table 3:

Bias and MSE of the overall survival probability for different models

		Overall Survival Probability (${\mathit{S}}_{\mathit{p}}(\mathit{t};\mathit{x},\mathit{z})$)
Scenario	n	Bias			MSE
		DT	Spline	Logit	DT	Spline	Logit
	300	0.1073	0.0776	0.0871	0.0263	0.0139	0.0163
1	600	0.0910	0.0654	0.0713	0.0199	0.0105	0.0118
	900	0.0830	0.0606	0.0642	0.0167	0.0092	0.0099
	300	0.1055	0.2125	0.2170	0.0241	0.0722	0.0753
2	600	0.0923	0.2107	0.2148	0.0176	0.0710	0.0737
	900	0.0881	0.2046	0.2099	0.0158	0.0672	0.0704
	300	0.1120	0.1644	0.2102	0.0297	0.0521	0.0825
3	600	0.0921	0.1616	0.2007	0.0214	0.0509	0.0771
	900	0.0821	0.1600	0.1996	0.0174	0.0501	0.0771
	300	0.1751	0.3119	0.3186	0.0601	0.1302	0.1340
4	600	0.1294	0.3194	0.3235	0.0412	0.1329	0.1353
	900	0.1130	0.3214	0.3245	0.0350	0.1334	0.1353

Table 4:

Bias and MSE of the susceptible survival probability for different models

		Susceptible Survival Probability (${\mathit{S}}_{\mathit{u}}(\mathit{t};\mathit{x})$)
Scenario	n	Bias			MSE
		DT	Spline	Logit	DT	Spline	Logit
	300	0.0865	0.0650	0.0596	0.0226	0.0150	0.0133
1	600	0.0767	0.0526	0.0472	0.0185	0.0106	0.0091
	900	0.0737	0.0457	0.0407	0.0172	0.0084	0.0072
	300	0.0814	0.0792	0.0803	0.0215	0.0210	0.0214
2	600	0.0690	0.0648	0.0660	0.0167	0.0158	0.0161
	900	0.0610	0.0613	0.0627	0.0136	0.0139	0.0142
	300	0.0884	0.0883	0.0989	0.0201	0.0202	0.0247
3	600	0.0764	0.0772	0.0950	0.0154	0.0158	0.0231
	900	0.0742	0.0749	0.0947	0.0144	0.0148	0.0225
	300	0.0452	0.0456	0.0459	0.0073	0.0074	0.0074
4	600	0.0330	0.0326	0.0326	0.0042	0.0042	0.0042
	900	0.0278	0.0271	0.0269	0.0033	0.0032	0.0031

In Table 5, we present the computation time (in seconds) to produce the incidence and latency estimates along with the standard errors (obtained using a bootstrap sample of size 100) for one Monte Carlo run (i.e., $M=1$) and for different sample sizes. Noting that the MCM-DT model requires multiple imputation to produce the incidence estimates unlike the MCM-Logit and MCM-Spline models, we can say from Table 5 that the MCM-DT model produces results in a very reasonable amount of time. This is specifically true for non-linear classification boundaries, i.e., scenarios 2–4. In Table A4.2 of the supplemental material, we present the estimates and standard errors (using a bootstrap sample of size 100) of individual latency parameters for $n=900$. For other sample sizes, the observations are similar and hence not reported for the sake of brevity. From Table A4.2, we note that when the true classification boundary in non-linear (i.e., under scenarios 2–4) the overall performance of MCM-DT is better than MCM-Spline and MCM-Logit models in the sense that MCM-DT results in more accurate estimates of the latency parameters and smaller standard errors.

Table 5:

Computation times for different models under varying scenarios and sample sizes

Scenario	Model	Computation Time (in seconds)
		$\mathit{n}=300$	$\mathit{n}=600$	$\mathit{n}=900$
	Logit	3.037	4.907	7.434
1	Spline	93.87	127.729	237.701
	DT	374.496	392.608	402.533
	Logit	2.333	3.805	10.394
2	Spline	55.078	87.355	172.660
	DT	115.2	130.879	158.346
	Logit	3.88	9.675	10.755
3	Spline	81.399	109.027	101.891
	DT	121.257	153.558	178.288
	Logit	2.894	3.398	6.284
4	Spline	99.355	117.53	174.155
	DT	156.74	202.758	272.711

In Table 6, we present the biases and MSEs of different quantities of interest when we compare the MCM-DT with MCM-NN and MCM-RF. In Table 7, we present the AUC values and the computation times. For this purpose, we use $n=900$ and $M=200$. For other sample sizes $\left(n\right)$, the observations are similar and are not reported for the sake of brevity. For the MCM-NN, we fit a two hidden layers network with (12, 24) number of neurons respectively in the first and second layers. The sigmoid activation function is considered to fit the fully connected neural network. For the MCM-RF on the other hand, we consider a random forests model with the number trees used in aggregation set to a fixed value (ntree = 200). However, the hyper-parameter, mtry (the number of covariates to randomly sample as candidates at each split), of the random forests model is obtained using the grid-search cross-validation technique. We consider the repeated cross-validation method in fitting the random forests model. The number of resampling iterations and the number of complete sets of folds to compute are specified as 7 and 5, respectively. From Table 6, we note that when the true classification boundary is linear (i.e., under scenario 1) MCM-DT performs better than MCM-NN, however, MCM-RF performs better than both MCM-DT and MCM-NN. On the other hand, when the true classification boundary is non-linear (i.e., under scenarios 2–4) MCM-DT performs better than both MCM-NN and MCM-RF under scenario 2. Under scenario 3, MCM-DT performs better than both MCM-NN and MCM-RF in the estimation of the uncured probability. In this scenario, MCM-DT once again performs better than the MCM-NN and MCM-RF models in the estimation of the overall and susceptible survival probabilities except in three cases. Finally, under scenario 4 MCM-DT performs better than MCM-RF in all cases. In this scenario, MCM-DT performs better than MCM-NN only in the estimation of the susceptible survival probability. A similar conclusion can be drawn from the AUC values reported in Table 7, noting the similarity in the testing AUC values from all models under scenarios 2 and 3. Now, it is worth mentioning that even in cases where the MCM-NN or MCM-RF performed better than MCM-DT we must pay attention to the computing times. In some cases (as in scenario 4) the computing times for MCM-RF and MCM-NN can be respectively 178 times and 133 times that of MCM-DT. Given these heavy computing times for both MCM-RF and MCM-NN and coupled with the fact that both MCM-RF and MCM-NN are difficult to explain to medical professionals, we may prefer to use the proposed MCM-DT model even in cases where the performance of MCM-RF or MCM-NN is slightly better than MCM-DT. Finally, in Table A4.3 of the supplemental material, we present the estimation results (estimates and standard errors) corresponding to the individual latency parameters.

Table 6:

Comparison of DT, NN, and RF models through the biases and MSEs of different quantities of interest for $n=900$

Scenario	Model	$\mathit{\pi }\left(\mathit{z}\right)$		${\mathit{S}}_{\mathit{p}}(\mathit{t};\mathit{x},\mathit{z})$		${\mathit{S}}_{\mathit{u}}(\mathit{t};\mathit{x})$
		Bias	MSE	Bias	MSE	Bias	MSE
	DT	0.1765	0.0618	0.0808	0.0156	0.0719	0.0166
	NN	0.2280	0.1389	0.1412	0.0473	0.0939	0.0257
1	RF	0.1418	0.0341	0.0684	0.0107	0.0584	0.0119
	DT	0.1134	0.0223	0.0744	0.0113	0.0677	0.0135
	NN	0.1659	0.0729	0.1221	0.0365	0.0982	0.0232
2	RF	0.1485	0.0352	0.0871	0.0440	0.0687	0.0138
	DT	0.1650	0.0651	0.0821	0.0174	0.0742	0.0144
	NN	0.1946	0.1170	0.1283	0.0445	0.0880	0.0181
3	RF	0.2001	0.0709	0.0850	0.0140	0.0701	0.0132
	DT	0.1687	0.0653	0.1178	0.0372	0.0255	0.0028
	NN	0.0831	0.0477	0.0697	0.0252	0.0312	0.0037
4	RF	0.4059	0.1812	0.2887	0.1115	0.0281	0.0032

Table 7:

Comparison of DT, NN, and RF models through the AUC values and computation times for $n=900$

Scenario	Model	Training AUC	Testing AUC	Computation Time (in seconds)
	DT	0.9372	0.9041	402.533
1	NN	0.9645	0.8827	15218.178
	RF	0.9533	0.9491	20642.211
	DT	0.9386	0.8951	158.346
2	NN	0.9727	0.8759	18205.223
	RF	0.9127	0.9053	23148.207
	DT	0.9148	0.8716	178.288
3	NN	0.9706	0.8949	10698.232
	RF	0.9158	0.9001	16978.322
	DT	0.9667	0.8916	272.711
4	NN	0.9842	0.9152	36372.963
	RF	0.7991	0.7102	48499.398

5. Application to leukemia data

In this section, we present an application of the proposed MCM-DT model and the EM-based estimation algorithm to a data from a study on leukemia patients who went through bone marrow transplantation.³² A total of 137 leukemia patients were registered in the study. These patients were followed up to 2640 days and a total of 54 patients, representing 39.4% of total patients, were right censored (i.e., disease free survival) at the end of the study. The event of interest is the relapse or death due to leukemia following bone marrow transplantation. The covariate information available in this data includes the following: patient’s age (in years), donor’s age (in years), donor’s sex (1-Male, 2-Female), methotrexate (MTX) used as a graft-versus-host-prophylactic (1-Yes, 0-No), patient’s and donor’s cytomegalovirus (CMV) immune status (1-CMV positive, 0-CMV negative) which was determined based on a serologic study, and waiting time from diagnosis to transplantation (in days).

The complete data set is readily available for downloads in the R package “KMsurv”. In Figure A3.2 of the supplemental material, we present a plot of the Kaplan-Meier estimates of the survival probabilities. The observed long plateau that levels off to non-zero survival probabilities indicates the presence of a cured subgroup. This suggests that the proposed MCM-DT model is suitable for this data set. For the purpose of comparison, along with the MCM-DT model, we also fit the MCM-Logit and MCM-Spline models. To resolve the issue with over-fitting and given the moderate sample size for the leukemia data, we apply a 10-fold cross-validation technique that allows us to train both DT and sigmoid models on the full data, which is along the lines of Hastie et al.¹⁸ The number of multiple imputations is chosen as 5 and we use 100 bootstrap samples to estimate the standard errors of the estimated parameters.²⁰

First, we consider a simple case where we study the effects of two covariates, patient’s age and donor’s age, on both incidence and latency parts of the MCM-DT model (i.e., $p=q=2$). Focusing on the incidence part first, in Figure 1, we present a plot of the estimates of the non-cured probabilities along with their 95% confidence bounds. Clearly, the MCM-DT and MCM-Spline models capture the complex age effects on the uncured probabilities unlike the MCM-Logit model. Under all models, non-cured probabilities tends to reach a local minimum when donor’s age is between 20 and 40 and patient’s age is between 10 and 30. Unlike the MCM-Logit model, the non-cured probabilities for MCM-DT and MCM-Spline are not monotonic functions of patient’s and donor’s ages and tends to rise slowly as patient’s age and donor’s age increases Now, it is of utmost importance to understand whether capturing this complex pattern can result in better predictive accuracy. For this purpose, we compute the AUC values based on the ROC curves. In this regard, Amico et al. proposed estimators of ROC and AUC based on the mixture cure model.³³ However, their formulation heavily depends on the assumption of existence of a known “cured time” beyond which all censored observations are considered as cured. We propose a completely different approach to compute the ROC curves which is independent of such assumption and is more practical. To compute the ROC curves, since the cured statuses are unknown for the set of censored observations, first, we propose to impute these unknown cured statuses. To do this, we estimate the conditional probability of uncured for each censored observation using eqn.(15) and use it to generate a Bernoulli random variable that represents the cured/uncured status. We repeat this process 500 times and, in Figure 2, we present the averaged ROC curves. The corresponding AUC values for the MCM-DT, MCM-Spline and MCM-Logit models turn out to be 0.736, 0.678 and 0.609, respectively. Clearly, the proposed MCM-DT model results in the highest predictive accuracy among the competing models, noting that the performance of MCM-Spline is close to MCM-DT. In Figure A3.3 of the supplemental material, we present the predicted overall and susceptible survival probabilities when patient’s age and donor’s age are fixed at their mean values. Next, we increase the complexity by adding more covariates to the model and consider the following scenarios: $p=q=3$ (patient’s age, donor’s age, MTX), $p=q=4$ (patient’s age, donor’s age, MTX, donor’s CMV), and $p=q=7$ (patient’s age, donor’s age, waiting time, donor’s sex, patient’s CMV, donor’s CMV, MTX). In all cases, we see that the predictive accuracy of the MCM-DT model is the highest (see Table 8 for the AUC values and Figure 2 for the ROC curves). Furthermore, we note that as the number of covariates increases, the difference in predictive accuracy between the MCM-DT and MCM-Spline models becomes more prominent. We present the variable importance plots for all scenarios in Figure A3.4 of the supplemental material. It is clear that in all cases donor’s age has the highest relative importance followed by patient’s age. In Figure A3.5 of the supplemental material, we present the decision tree plot for the full model with seven covariates. It is clear that only donor’s age, patient’s age, and waiting time gets selected among the seven covariates, and this observation supports the findings from Figure A3.4. It is interesting to point out that the MCM-DT also performs some form of covariate selection and can easily identify any interaction effect among covariates; as can be seen in Figure A3.5. For readers interested in the results corresponding to the estimation of the latency parameters, we present these in Table A4.4 of the supplementary material. In Table A4.5 of the supplemental material, we present the computing times and the findings are similar to those obtained from the simulation study.

Figure 1:

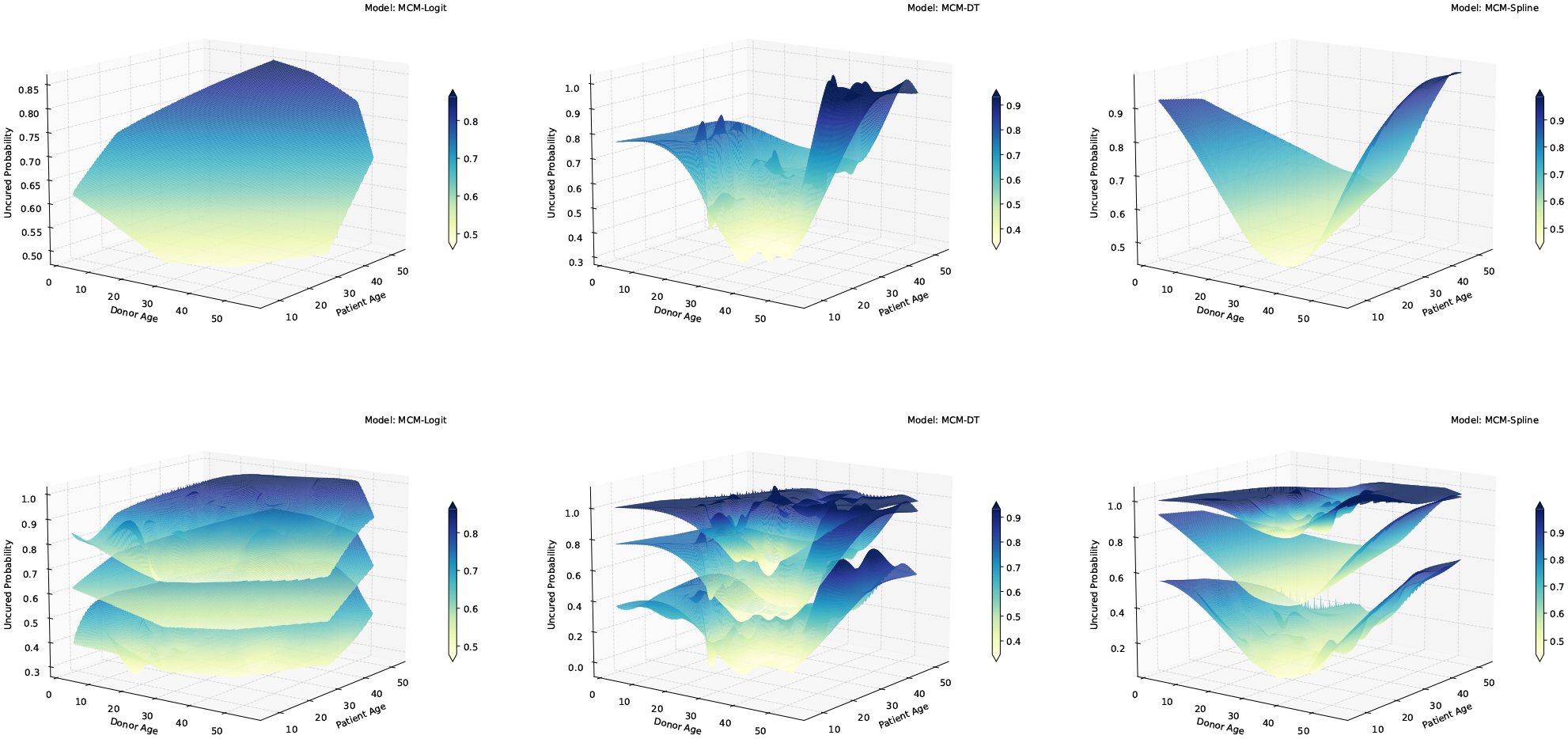
3-dimensional surface plane of uncured probabilities, along with 95% confidence bounds, as a function of patient’s age and donor’s age

Figure 2:

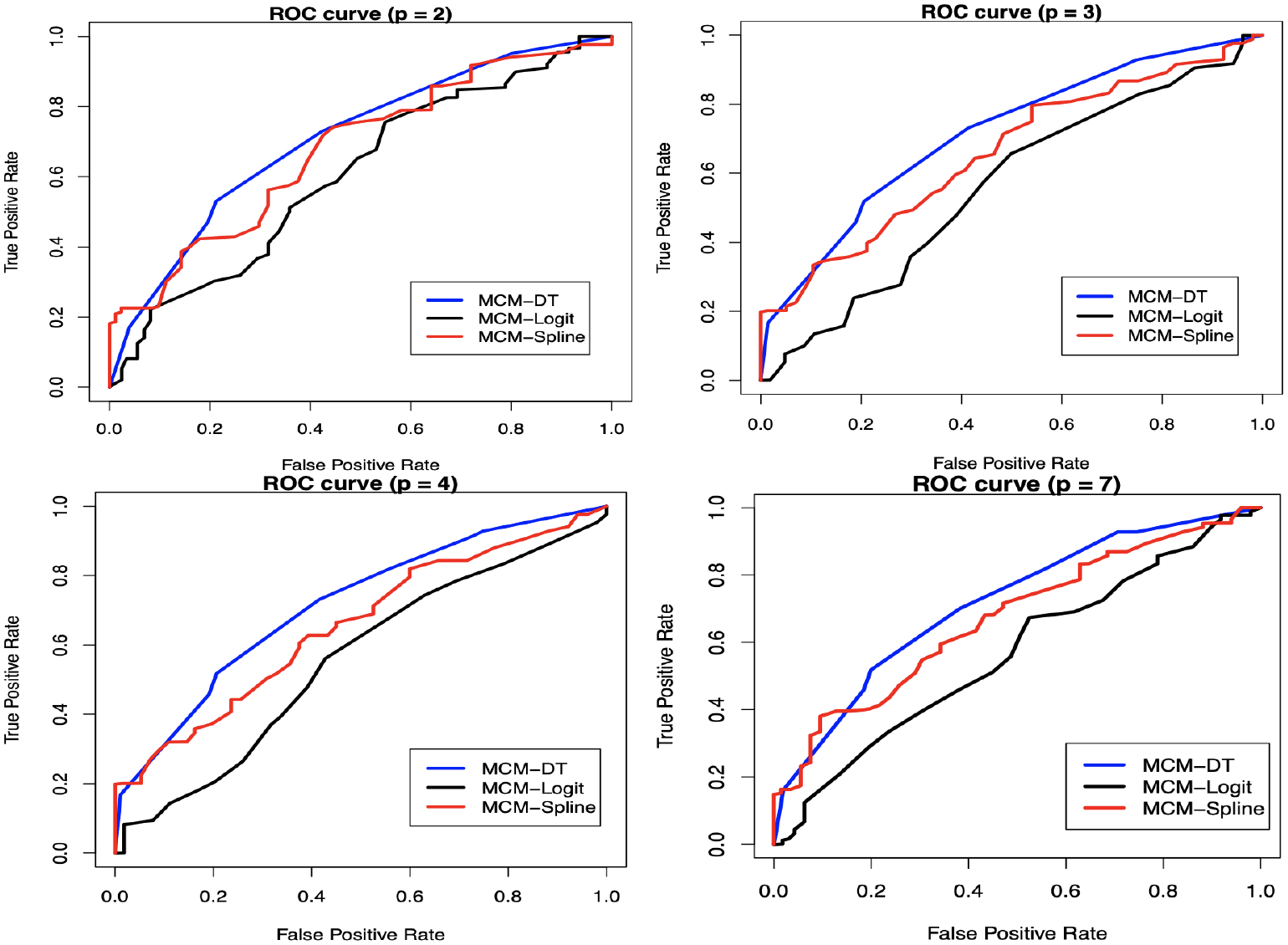
ROC curves for different models corresponding to the leukemia data

Table 8:

Comparison of AUC values under different models

p	AUC values
	MCM-DT	MCM-Spline	MCM-Logit
2	0.736	0.678	0.609
3	0.714	0.657	0.560
4	0.714	0.654	0.557
7	0.723	0.667	0.565

Using the leukemia data, we also compare the MCM-DT with MCM-NN and MCM-RF models. For this purpose, we use the patient’s age and donor’s age as two covariates of interest (i.e., $p=q=2$). This comparison can be easily extended to cases where more covariates are included in the model. In Figure A3.6 of the supplemental material, we present the plots of the estimated non-cured probabilities with respect to the covariates along with their 95% confidence bounds. As expected, it is easy to see that all three models under comparison can capture complex age effects. To find out which of the three machine learning-based models provide the highest predictive accuracy and how much computation cost is associated with it, we also calculated the AUC values and the computing times. The AUC values for the MCM-DT, MCM-NN and MCM-RF models turned out to be 0.736, 0.865 and 0.712, respectively. The corresponding computation times (in seconds) turned out to be 103.100, 640.213 and 8008.150. It is clear that the predictive accuracy of MCM-DT is better than MCM-RF, but not when compared to MCM-NN. Now, given that MCM-DT is easy to interpret and computationally less expensive compared to both MCM-NN and MCM-RF models it is important to ask whether there is any significant difference in the AUC values of 0.736 and 0.865 corresponding to the MCM-DT and MCM-NN models, respectively. We leave this as an interesting future study. For interested readers, we also present the latency parameter estimates along with the estimates of standard errors and p-values in Table A4.6 of the supplementary material.

6. Conclusion

We proposed a new mixture cure rate model by employing the DT algorithm to model the incidence part. We preserved the proportional hazards structure for the latency part because of it’s explanatory ability. To estimate the parameters of this new model, we developed an EM-based estimation procedure. From the simulation study, it is clear that the proposed model can capture complex relationships between the covariates and uncured probabilities better than the existing logistic regression-based and spline regression-based mixture cure models. This results in more accurate (i.e., lower bias) and more precise (i.e., lower MSE) estimates of the uncured probabilities. Furthermore, this also improves the estimation results related to the overall survival probability. In addition, from the real data analysis, we have shown that as the model complexity increases, the difference in predictive accuracy between our proposed model and the existing ones becomes more pronounced, with the predictive accuracy of our proposed model being always the highest. As an immediate future work, it is of great interest to study the performance of the proposed model when the dimension of covariates is high (i.e., the effective sample size is smaller than the covariate dimension). In this regard, it is of interest to develop computationally efficient penalized estimation procedures. Another potential research problem is to extend the current DT-based modeling framework to incorporate competing risks^34–36 and accommodate elimination process of competing risks.^37–44 It will then be of interest to propose flexible modeling for the latent count on competing risks that can accommodate both over-dispersion and under-dispersion.^28,45 Other future research works include integrating machine learning techniques in the context of some recently proposed transformation cure models and studying whether it improves the predictive accuracy of cure.^46,47 We are currently looking at some of these open problems and hope to report the findings in a future manuscript.

Data availability statement

Computational codes for the data generation and DT-based EM algorithm are available in the supplemental material.