A Morphology-Preserving Algorithm for Denoising of EMG-Contaminated ECG Signals

Abstract

Goal: Clinical interpretation of an electrocardiogram (ECG) can be detrimentally affected by noise. Removal of the electromyographic (EMG) noise is particularly challenging due to its spectral overlap with the QRS complex. The existing EMG-denoising algorithms often distort signal morphology, thus obscuring diagnostically relevant information. Methods: Here, a new iterative regeneration method (IRM) for efficient EMG-noise suppression is proposed. The main hypothesis is that the temporary removal of the dominant ECG components enables extraction of the noise with the minimum alteration to the signal. The method is validated on SimEMG database of simultaneously recorded reference and noisy signals, MIT-BIH arrhythmia database and synthesized ECG signals, both with the noise from MIT Noise Stress Test Database. Results: IRM denoising and morphology-preserving performance is superior to the wavelet- and FIR-based benchmark methods. Conclusions: IRM is reliable, computationally non-intensive, fast and applicable to any number of ECG channels recorded by mobile or standard ECG devices.

I. Introduction

In recent years, the number of mobile health devices on the market has been rapidly increasing. Among them, mobile electrocardiographs (ECGs) are the most frequently used devices [1]. These devices are mainly utilized outside the clinical setting, making them highly susceptible to noise. Commonly, ECG signals can be contaminated by different noise sources [2]: (i) baseline wander (BLW) - a low-frequency (<1 Hz) noise component caused by a variety of sources, including perspiration, respiration, body movements, and poor electrode contact; (ii) power-line interference (PLI) – a narrowband component (50/60 Hz) (iii) motion artifact—originating from the change in impedance at the electrode-skin contact, with the spectral content mainly between 1 and 10 Hz; (iv) electromyographic (EMG) noise—a broadband component caused by muscle activity with the spectrum spreading predominantly at higher frequencies (>10 Hz) and overlapping with the spectrum of QRS complex. The latter two are particularly relevant to the mobile ECG signals. The motion artifact can be ameliorated by measurement under stationary conditions. However, the underlying physiology of the EMG noise, resulting from the engagement of fingers during measurement by handheld devices [1], [3], does not allow for an obvious mitigation strategy and must be eliminated in postprocessing.

Success of the EMG noise removal highly depends on the targeted application. Conventional linear filtering methods are sufficient for the diagnoses relying on detection and analysis of R-R intervals, such as atrial fibrillation [3], [4]. However, filter-induced distortions of the QRS complex may render these methods unsuitable for diagnoses requiring the preservation of heartbeat morphology, such as clinical diagnosis of myocardial infarction (MI) and some arrhythmias [5], [6], [7], [8]. Even the advanced filtering methods based on discrete wavelet transformation lead to signal distortion when a significant variation of noise energy is presented [9]. The filters based on adaptive methods require either a reference or generic signal at the input, which is not known a priori [10]. A hybrid method that combines adaptive and wavelet filters shows excellent performance, but retains the problem of signal distortion in the presence of large changes in noise energy [11]. Similarly, the model-based filtering method successfully suppresses noise, compresses and classifies ECG signals, but can introduce heartbeat over-processing thus occluding clinically significant information [12], [13], [14].

Other algorithms suffer from mechanical and practical limitations. For example, the quality of highly-successful ensemble averaging (EA) technique, is proportional to the number of heartbeats included in the averaging process, which may represent a challenge for recordings made with the ECG handheld devices with typical duration below 30 seconds. Furthermore, inter-beat variations of the heartbeat are lost in the averaging procedure [2]. Methods including independent component analysis are powerful; however they require more than one lead for noise signal decomposition, often not present in mobile ECG devices [12]. Finally, over the last decade, denoising methods based on deep learning, such as autoencoders [15] or U-net-like networks [16], have been standard in the literature. The main limitation of these methods is their interpretability and trustworthiness. However, even with these problems surpassed, the necessity for a large amount of data and the result dependence on the quality and dynamics of the training set remain practical limitations of the deep learning method [17], [18].

Therefore, although the problem of EMG filtering of ECG signals has been well-studied in theory and practice, the sweeping solution which would enable exploitation of mobile ECG in cardiovascular diagnostics outside a small number of arrhythmias has not been reached.

In this paper, we present a new Iterative Regeneration Method (IRM) for the suppression of broadband EMG noise. The hypothesis behind the IRM method is that after removing approximations of the dominant components from the ECG signal (primarily QRS and T waves), the remaining cardiac components have a very small frequency overlap with the EMG noise, thus allowing for an easy removal of the EMG noise. It has been found that the EMG noise occurs mainly at frequencies above 10 Hz, T and P waves at frequencies below 10 Hz, while the dominant QRS frequency content is below 50 Hz [19]. We justified the hypothesis by a posterior analysis of the EMG-ECG spectral overlap. Namely, we found that in the frequency region below 10 Hz, in which the spectra of the T and P waves overlap with that of the EMG noise, the spectral power of the EMG noise carries less than 1% of the total EMG spectral power.

Comparison with other techniques on the standard databases shows excellent performance of our method in terms of signal morphology preservation. The algorithm performance shows good potential for telemedical ECG monitoring.

The paper is structured as follows: in Section II, we present the new filtering method and describe the three databases used for IRM validation and comparison with other denosing methods. Results are presented in Section III and discussed in Section IV. Concluding remarks and future steps are presented in Section V.

II. Materials and Methods

A. IRM Method

The IRM method is an iterative process that aims to remove EMG noise from the ECG signal. The main idea behind the method is to free the noisy signal from the dominant ECG components, QRS complex and T wave, upon which the EMG noise can be easily extracted and removed. This is implemented in 3 stages (Fig. 1):

• –Preprocessing stage, in which the frequency components which can affect the IRM stage performance or are content insignificant are spectrally filtered out and the QRS segments are detected;
• –IRM stage, in which the EMG noise is extracted and removed from the signal; and
• –Postprocessing stage, in which the low-frequency signal components filtered out in preprocessing stage are returned to the denoised signal.

Fig. 1.

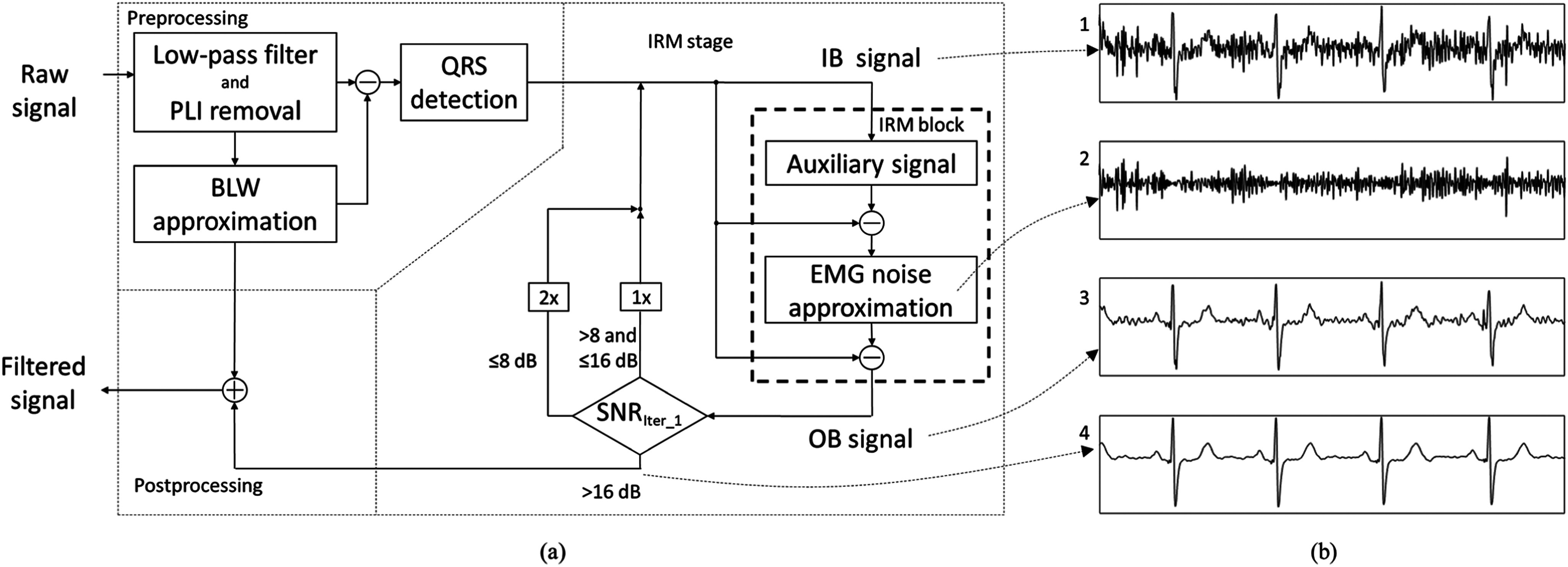
(a) Block diagram of the 3-stage IRM method. IB stands for the signal at the input of the IRM block, OB for the signal at the output of the IRM block. The SN_{Riter_1} stands for the SNR after first iteration. (b) Signals at different steps of the IRM stage: (1) IB signal in 1st iteration, (2) EMG noise approximation, (3) OB signal after 1st iteration, (4) signal at the end of the processing stage (3 iterations). Presented is the signal with SNR_{iter_1}=4.5 dB.

In the preprocessing stage, the following filters are applied:

• –Low-pass 2nd–order Butterworth filter with a cutoff frequency of 100 Hz for removal of the high-frequency components of the EMG noise that do not spectrally overlap with QRS complexes.
• –The 2nd-order IIR notch filter with the frequency of 50 Hz in both forward and reverse directions for removal of PLI;
• –High-pass 5th–order Butterworth filter with a cutoff frequency of 2 Hz to obtain higher similarity between heartbeats. As this filter changes the heartbeats’ morphology, we restore the low-frequency signal component in the postprocessing stage.

All filters were applied in both forward and reverse directions to ensure zero-phase filtering.

Finally, Pan-Tompkins algorithm is applied to detect QRS complexes and heartbeats [20], [21]. Here, heartbeats are related to the R points. The start and the end of the i^th heartbeat are defined as:

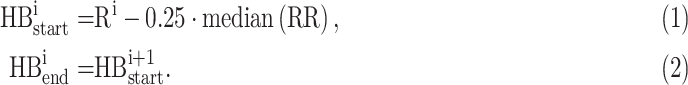In (1), RR is a vector of intervals between consecutive QRS complexes. Note that this definition maintains the heartbeat length.

IRM stage comprises a 2-step IRM block:

• –Step 1: Beat-by-beat generation of auxiliary signal (AS) using EA technique and its subtraction from the input signal. EA evaluates the standard arithmetic mean of the beats included in averaging,
• –Step 2: Extraction of the EMG noise (Fig. 1(b-2)) and its removal from the input signal (Fig. 1(b-3)), and a decision on the number of iterations which is applied only in the first filtering iteration.

We denoted the signal at the input of the IRM block as IB and the signal at the output of the IRM block as OB. We now describe the IRM steps in detail.

In Step 1, IB signal is processed beat-by-beat to obtain the AS in which each heartbeat is replaced by its denoised heartbeat approximation – an auxiliary heartbeat (AHB). The AHB is obtained by EA of all beats morphologically similar to a beat at hand and filtering. Two beats are considered similar if their correlation is greater than the correlation threshold xcorr_thr. As the quality of noise reduction depends on the number of heartbeats included in the averaging procedure, nHB, and their morphological similarity, xcorr, we optimize AHB calculation by the adaptive procedure described in detail in Appendix A.

Upon applying AHB calculation to all heartbeats of the signal, AS is obtained. The AS represents an approximation of a noise-free signal without inter-beat variation. Hence, after subtracting the AS signal from the IB signal, the difference signal comprises the EMG noise and inter-beat variation.

In Step 2, the EMG noise is obtained by applying Butterworth high-pass filter with a cutoff frequency of 10 Hz to the difference signal. The cutoff frequency is chosen based on the spectrum strength of the EMG signal, which is negligible under 10 Hz [19], [22]. At the end of the IRM block, the tentative EMG noise approximation (Fig. 1(b-2)) is removed from the IB signal (Fig. 1(b-3)), creating an OB signal.

The number of times the signal will pass through the IRM block is determined based on the estimated Signal-to-Noise Ratio (SNR) after the first pass through the IRM block, SNR_{iter_1}, calculated as the ratio between the OB signal and a tentative EMG noise approximation, following the rule:

• –If SNRiter_1 > 16 dB, the signal is filtered once,
• –If 8 dB < SNRiter_1 ≤16 dB, the signal is filtered twice,
• –If SNRiter_1 ≤ 8 dB, the signal is filtered three times.

These thresholds are obtained empirically and fixed for all tests.

Postprocessing stage: At the end of the IRM stage, we obtained a signal with reduced EMG noise but with morphological differences compared to the raw signal. The difference stems from the high-pass filter applied in the preprocessing stage. Hence, in the postprocessing stage, the low-frequency content is returned to the signal to obtain the EMG-noise-free ECG signal with minimal morphological alterations.

The algorithm was implemented in MATLAB (MathWorks Inc.).

B. Databases

Three different databases were used to study the performance of the proposed IRM method. Here they are described briefly, while a more detailed description is given in the Appendix B.

• 1)SimEMG database is a unique resource that provides back-to-back recorded ECG signals with and without EMG noise [23]. It contains 37 noise-free and 110 noise-contaminated single-lead recordings generated from 14 healthy subjects (9 females and 5 males aged 40 ± 13). The average SNR_IN of the noise-contaminated signals is 8.53 ± 5.5 dB.
• 2)In MIT-BIH-EMG database, the noise-free signals originate from the MIT-BIH arrhythmia database [24], [25]. Noise-contaminated signals were created by addition of the genuine muscle artifact recordings taken from the MIT Noise Stress Test [26]. The total number of recordings in MIT-BIH-EMG is 228, out of which 51 are reference recordings and 171 are noise-contaminated with the average SNR_IN of 11.90 ± 3.25 dB. Over 25% of recordings are with arrhythmias.
• 3)Synth-EMG database was constructed by adding the EMG noise originated from the MIT Noise Stress Test Database [26] to the noise-free ECG signals obtained by the ECG signal generator described in [27]. The total number of signals in Synth-EMG is 200, out of which 50 are reference signals and 150 are noise-contaminated signals with the average SNR_IN of 6.22 ± 3.11 dB.

C. Benchmark Method

In order to compare the performance of the proposed methods with conventional techniques for noise elimination in ECG signals, we included the Adaptive Wavelet Wiener Filter (AWWF) [11], Wavelet Transform (WT) [9], and Finite Impulse Response (FIR) Low-Pass Filter [14] in the analysis. The principles behind these methods are described in Appendix C.

D. Performance Metric

Upon applying a method for denoising ECG signals, it is necessary to establish a quantitative criterion for success of the filtering process. We assess the noise extraction quality via improvement in SNR and the preservation of the signal morphology via cross-correlation and Pearson coefficients.

The SNR improvement (SNR_IMP) is defined by:

where the SNR of the filtered signal (SNR_OUT) is calculated as a ratio of the noise-free signal and the noise obtained as the difference between the filtered and noise-free signal. Given the same noise-free signal in both terms on the right-hand side, this measure practically assesses the ratio of the original and extracted noise. The higher it is, the better is filter performance.

To estimate the morphology preservation after applying filtering procedure, we calculated correlation coefficient of the whole filtered signal (A) and the whole noise-free signal (B) as:

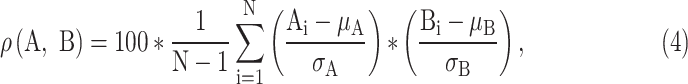where µ_A and σ_A are the mean and standard deviation of the noise-free signal, respectively, and μ_B and σ_B are the mean and standard deviation of filtered signal, respectively. We further assessed the morphology preservation in the fiducial points (P, R, J and T_max) by calculating Pearson coefficients applying (4). Here, µ_A and σ_A are the mean and standard deviation of the noise-free signal amplitude at a given fiducial point, respectively, and μ_B and σ_B are the mean and standard deviation of the filtered signal amplitude at the same point, respectively. Fiducial points were determined manually and verified by a cardiologist.

III. Results

The performance of the IRM filter method on different databases is shown in Table I. The values are averaged for different SNR_IN ranges. The Num stands for number of recordings for specific SNR_IN range; the third column shows the SNR_IMP value of the IRM algorithm with the number of iterations determined based on SNR_{iter_1}. For a more detailed analysis of the IRM method, we let all signals pass 3 times through the IRM block and show the SNR_IMP values after each iteration - columns SNR_IMP 1-3 for the first, second, and third filtering iteration, respectively. Gray values represent the optimum number of iterations for specific SNR_IN range.

TABLE I. SNR_IMP Values Obtained by IRM on SimEMG, MIT-BIH-EMG and Synth Databases.

	SNRIN [dB]	Num	SNRIMP [dB]	SNRIMP 1 [dB]	SNRIMP 2 [dB]	SNRIMP 3 [dB]
SimEMG	<4	33	10.31	6.61	9.29	10.31
	4-8	19	10	7.83	9.84	10.06
	8-12	23	7	6.61	7	6.93
	12-16	28	5.17	5.24	5.17	4.95
	16-20	6	3.36	3.63	3.36	3.12
	>20	1	1.32	1.85	1.32	1.02
	total	110	7.8	6.27	7.46	7.72
MIT-BIH-EMG	<4	0	-	-	-	-
	4-8	15	7.56	4.82	7.37	8.3
	8-12	84	8.07	5.69	8.07	8.11
	12-16	55	7.41	6.7	7.41	6.86
	16-20	15	4.86	5.45	4.73	3.89
	>20	2	1.83	1.83	-0.73	-2.02
	total	171	7.46	5.87	7.4	7.23
Synth	<4	31	7.38	4.65	6.32	7.38
	4-8	89	8.81	5.19	8.25	9.96
	8-12	24	8.93	5.58	8.93	10.25
	12-16	4	9.56	5.64	9.56	10.24
	16-20	2	8.15	8.15	11.23	11.54
	>20	0	0	-	-	-
	total	150	8.54	5.19	8.04	9.5

SNR_IN - SNR of input signals; Num - number of recordings in specific SNR_IN range; SNR_IMP - SNR improvement at the end of the IRM algorithm; SNR_IMP 1-3 - SNR_IMP after 1st, 2nd and 3^rd iteration, respectively. Gray values represent the optimum number of iterations for specific SNR_IN range.

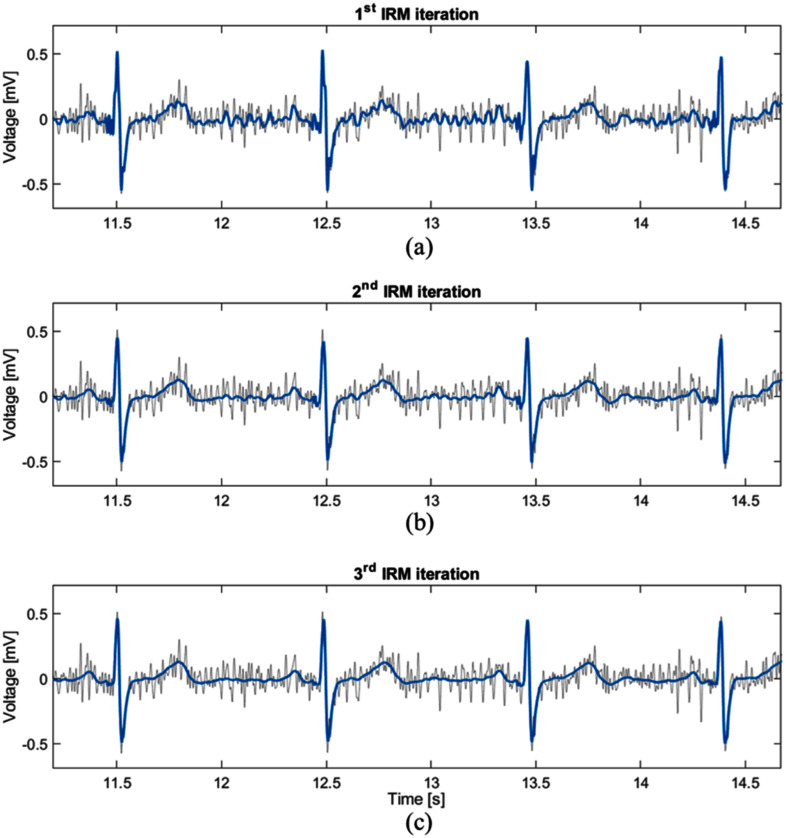
Based on the results from Table I, we can conclude that multiple passes through the IRM block improve the filter performance when the SNR_IN values are < 12 dB. The first pass through the IRM block reduces the noise, while some noise components remain in the filtered signal (Fig. 2(a)). At the second pass through the filtering block, more heartbeats are included in creating the AHB due to the cleaner signal, which leads to better noise suppression (Fig. 2(b)). The same effect appears in the third pass (Fig. 2(c)) when the best noise suppression is achieved. For SNR_IN > 16 dB, we obtained the best performance for a single pass through the IRM block. This indicates that multiple passes can lead to “over-processing” of signals with low noise level.

Fig. 2.

Example signal after passing through the IRM block (a) one, (b) two and (c) three times (blue lines). Gray line represents the original noise-contaminated signal, SNR_IN= 6.72 dB.

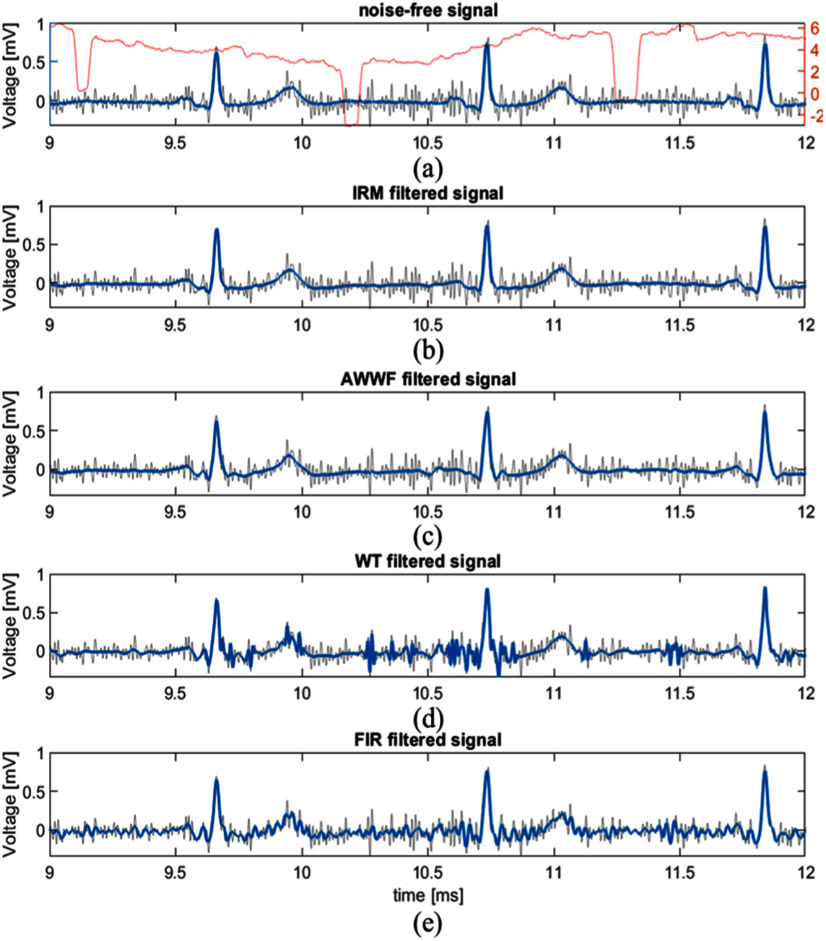
Table II compares SNR_IMP achieved by IRM, AWWF, WT, and FIR methods when applied to SimEMG, MIT-BIH-EMG, and Synth-EMG databases, respectively. The best-performance values are shown in grey. We conclude that on the whole ECG signals, IRM and AWWF have excellent performance, while the SNR improvement by WT and FIR is not guaranteed. This is illustrated by example signals in Fig. 3. The IRM algorithm outperforms AWWF across most SNR ranges and databases. Exceptions are the signals with extremely low signal or high level of noise (SNR < 4 dB) in the Synth-EMG database, and low-noise level (SNR > 20 dB) signals. Importantly, the IRM also works efficiently when the noise level changes within the same recording. For example, it successfully removes lower-level noise around the 1st beat in Fig. 3, higher-level noise around the subsequent beat, as well as the noise of the varying level between the two beats.

TABLE II. SNR_IMP Values Obtained by Different Filtering Methods on SimEMG, MIT-BIH-EMG and Synth Databases.

	SNRIN	SNRIMP/std IRM [dB]	SNRIMP/std AWWF [dB]	SNRIMP/std WT [dB]	SNRIMP/std FIR [dB]
SimEMG	<4	10.31/ 2.6	9.23/ 2.1	4.59/ 1.1	4.19/ 0.7
	4-8	10/ 3	8.57/ 2.4	3.84/ 1.1	3.83/ 1.1
	8-12	7/ 2	6.27/ 1.8	2.15/ 1.5	3.18/ 0.8
	12-16	5.17/ 2.9	4.57/ 2.1	-1.41/ 2.6	2.17/ 1.1
	16-20	3.36/ 1.6	3.26/ 1.3	-2.38/ 2.1	1.45/ 0.8
	>20	1.32/ 0	2.14/ 0	-7.18/ 0	0.22/ 0
	average	7.8/ 3.6	6.92/ 3	1.94/ 3.2	3.22/ 1.3
MIT-BIH-EMG	<4	-	-	-	-
	4-8	7.56/ 1.2	7.03/ 1	1.41/ 0.9	0.67/ 0.1
	8-12	8.07/ 1.4	5.8/ 0.9	0.59/ 0.9	0.47/ 0.2
	12-16	7.41/ 1.9	5.52/ 0.8	-0.08/ 1.7	0.43/ 0.2
	16-20	4.86/ 2.3	4.7/ 1.2	-0.39/ 1.5	0.23/ 0.5
	>20	1.83/ 1.5	2.7/ 0.8	-0.71/ 0.1	0.22/ 0.1
	average	7.46/ 2	5.69/ 1.1	0.35/ 1.4	0.45/ 0.3
Synth	<4	7.38/ 1.4	8.39/ 1	1.22/ 0.9	1.07/ 0.1
	4-8	8.81/ 1.7	7.93/ 0.8	1.17/ 0.7	1.06/ 0.1
	8-12	8.93/ 1.8	6.85/ 0.8	0.82/ 0.5	1.02/ 0.1
	12-16	9.56/ 1.9	5.84/ 1.2	0.8/ 0.3	0.98/ 0.1
	16-20	8.15/ 1.5	4.48/ 0.4	1.16/ 0.1	0.98/ 0
	>20
	average	8.54/ 1.8	7.75/ 1.1	1.11/ 0.7	1.05/ 0.1

SNR_IN - SNR of input signals; SNR_IMP - SNR improvements for different denoising algorithms. Gray values represent highest SNR_IMP for specific SNR_IN range. Bolded values indicate that there is statistical significance between the IRM and AWWF methods.

Fig. 3.

Example of different filtering methods applied on a typical signal from the SimEMG database. Each frame shows the original noise-contaminated signal (gray line). The red line in (a) shows SNR of the input signal (SNR_IN) for 1-second window. SNR_IN averages at 3.71 dB. The blue lines represent: (a) Recorded noise-free signal, (b) IRM-filtered signal, (c) AWWF-filtered signal, (d) WT-filtered signal, (e) FIR-filtered signal.

The excellent filtering performance of IRM and AWWF algorithms is achieved at the expense of extending their runtime. Table I in Supplementary material shows comparison of the algorithm runtimes on SimEMG database. The IRM is for one and two orders of magnitude slower than WT and FIR, respectively. However, it is 2.5 times faster than the AWWF with the comparably high performance parameters.

Table III shows the morphology-similarity assessment based on the whole-signal cross correlation and Pearson coefficients calculated at fiducial points. Since the SNR analysis identified AWWF as the main competing method, IRM is compared back-to-back with it.

TABLE III. Crosscorrelation and Pearson Coefficients in Different Points of Interest Calculated on SimEMG, MIT-BIH-EMG and Synth Databases.

	SNRIN	XCORR/std		Pearson coefficient in P point		Pearson coefficient in R point		Pearson coefficient in J point		Pearson coefficient in T point
	[dB]	IRM	AWWF	IRM	AWWF	IRM	AWWF	IRM	AWWF	IRM	AWWF
SimEMG	<4	96.6/ 3	95.6/ 3.2	0.47/ 0.2	0.36/ 0.2	0.53/ 0.2	0.5/ 0.2	0.11/ 0.3	0.11/ 0.2	0.17/ 0.2	0.12/ 0.2
	4-8	98.6/ 1	98.2/ 1	0.27/ 0.5	0.26/ 0.4	0.68/ 0.2	0.5/ 0.2	0.28/ 0.3	0.26/ 0.3	0.34/ 0.2	0.33/ 0.3
	8-12	98.9/ 0.9	98.7/ 0.9	0.44/ 0.4	0.32/ 0.4	0.72/ 0.2	0.7/ 0.1	0.26/ 0.3	0.19/ 0.3	0.38/ 0.3	0.32/ 0.2
	12-16	99.3/ 0.5	99.3/ 0.4	0.25/ 0.5	0.27/ 0.5	0.79/ 0.1	0.8/ 0.1	0.24/ 0.3	0.26/ 0.2	0.37/ 0.2	0.37/ 0.2
	16-20	99.6/ 0.2	99.6/ 0.2	0.26/ 0.5	0.26/ 0.4	0.84/ 0.1	0.84/ 0.1	0.48/ 0.2	0.35/ 0.2	0.52/ 0.2	0.46/ 0.2
	>20	99.7/ 0	99.8/ 0	0/ 0.3	0/ 0.4	0.91/ 0	0.87/ 0	0.64/ 0	0.36/ 0	0.55/ 0	0.5/ 0
	average	98.3/ 2.1	97.9/ 2.4	0.39/ 0.4	0.32/ 0.4	0.68/ 0.2	0.64/ 0.2	0.23/ 0.3	0.21/ 0.3	0.32/ 0.3	0.28/ 0.2
MIT-BIH-EMG	<4	-	-
	4-8	98/ 0.6	97.8/ 0.4	0.75/ 0.3	0.72/ 0.3	0.9/ 0.1	0.88/ 0.1	0.52/ 0.3	0.42/ 0.4	0.83/ 0.2	0.81/ 0.3
	8-12	99.2/ 0.3	98.7/ 0.4	0.67/ 0.3	0.63/ 0.3	0.8/ 0.2	0.84/ 0.2	0.48/ 0.3	0.39/ 0.3	0.74/ 0.2	0.65/ 0.3
	12-16	99.6/ 0.3	99.4/ 0.2	0.72/ 0.2	0.61/ 0.3	0.71/ 0.3	0.87/ 0.1	0.53/ 0.3	0.41/ 0.3	0.75/ 0.2	0.64/ 0.3
	16-20	99.7/ 0.3	99.7/ 0.1	0.9/ 0.1	0.86/ 0.1	0.88/ 0.2	0.95/ 0.1	0.65/ 0.4	0.63/ 0.3	0.88/ 0.1	0.81/ 0.2
	>20	99.8/ 0	99.9/ 0	0.93/ 0	0.86/ 0.1	0.96/ 0	0.98/ 0	0.86/ 0	0.83/ 0.1	0.87/ 0	0.77/ 0
	average	99.3/ 0.6	99/ 0.6	0.72/ 0.3	0.65/ 0.3	0.79/ 0.2	0.86/ 0.1	0.52/ 0.3	0.42/ 0.3	0.77/ 0.2	0.67/ 0.3
Synth	<4	94.2/ 3	95.6/ 1.6	0.19/ 0.6	0.57/ 0.3	0.53/ 0.3	0.55/ 0.3	0.55/ 0.3	0.55/ 0.3	0.53/ 0.4	0.53/ 0.3
	4-8	98.2/ 0.9	98/ 0.5	0.39/ 0.5	0.6/ 0.3	0.44/ 0.3	0.41/ 0.3	0.5/ 0.3	0.43/ 0.3	0.38/ 0.3	0.37/ 0.3
	8-12	99.2/ 0.4	98.8/ 0.3	0.3/ 0.7	0.63/ 0.3	0.49/ 0.3	0.39/ 0.2	0.56/ 0.3	0.4/ 0.3	0.45/ 0.3	0.36/ 0.3
	12-16	99.7/ 0.1	99.4/ 0.2	0.47/ 0.7	0.75/ 0.3	0.61/ 0.3	0.47/ 0.2	0.76/ 0.2	0.56/ 0.3	0.49/ 0.3	0.17/ 0.3
	16-20	99.9/ 0	99.8/ 0	0.66/ 0.3	0.58/ 0.4	0.97/ 0	0.83/ 0.1	0.86/ 0.1	0.84/ 0.1	0.83/ 0.1	0.77/ 0.1
	>20
	average	97.6/ 2.4	97.7/ 1.4	0.34/ 0.6	0.6/ 0.3	0.48/ 0.3	0.44/ 0.3	0.53/ 0.3	0.46/ 0.3	0.43/ 0.3	0.4/ 0.3

SNR_IN- SNR of input signals; XCORR- crosscorrelation applied between noise-free and filtered signal. Bolded values indicate that there is statistical significance between the IRM and AWWF methods.

It is evident that both methods preserve signal morphology to a high correlation level of above 0.95. The IRM performs better on the noisy signals with SNR<16 dB in both databases with recorded signals, SimEMG and MIT-BIH. AWWF performs better on the recorded signals with SNR > 16 dB (with a minor advantage at the second digit behind the decimal point). Also extremely noisy synthetic signals with SNR < 4 dB are better filtered by AWWF, while for all other noise levels IRM is more successful.

With regard to the diagnostically relevant signal features, the IRM better reproduces signal amplitudes at P, J and T points while AWWF better reproduces R point amplitude on recorded signals. This can be observed in Fig. 3, in which the AWWF distorts the P-wave of the 2nd beat beyond recognition and significantly decreases the P-wave amplitude in the 3^rd beat. On synthetic signals, AWWF loses advantage at R point, but gains advantage at P point. This can be explained by the compliance of the function used in P-wave synthesis with the wavelet used by the AWWF algorithm [11].

Based on all above, we can recommend the IRM for applications with signals with medium-to-high level of noise and for evaluation of the ST elevation interval in the vicinity of J point (from J+10 ms to J+60 ms), highly relevant as the marker of MI [28]. On the other hand, AWWF is recommended for the signals with low-level noise and for precise reproduction of R point.

For a more objective comparison, we calculated statistical significance of performance differences between these two methods. We checked the distribution of data points and found that it was Gaussian. Hence, we applied the Student t-test. It revealed that the statistical difference exists in the MIT-BIH database for SNR range between 8 dB and 16 dB and in the Synth database with SNR range up to 16 dB (shown as bolded values in Tables II and III). Details and results of the Student t-test calculation along with the effect size estimation are shown in Supplementary material.

IV. Discussion

To evaluate the IRM applicability in telemedical monitoring by mobile ECGs, we have checked the algorithm speed and compatibility with lower sample rate recordings typical of these devices. The algorithm needed roughly 0.5 s for a 30 s ECG signal on an average PC, which is sufficient for the immediate presentation of the signal to a doctor on the medical service provider side. In particular, we have downsampled our 500 Hz signals to 300 Hz, as used by KardiaMobile (AliveCor Inc., CA, United States), a mobile handheld device, and performed the cross correlation morphology check. We obtained a negligible difference between the IRM-filtered original and downsampled signals (with a maximum correlation difference of 0.3%), thus confirming applicability of IRM at lower sampling rates.

Furthermore, we assessed the IRM applicability to the measurements in which the significant noise amplitude transition within a single recording is present. Indeed, the minimal signal morphology distortion for SNR_IN > 4 dB (correlation > 0.98) enables successful filtering across signals with transitions. An example is shown in Fig. 3(a)) in which all signal features are preserved despite the SNR excursion of 3 orders of magnitude, from the clear SNR minima generated at T-P intervals to the maxima generated at QRS complexes. Here, the SNR is calculated within 1 second wide moving window.

The performance of the IRM critically depends on the quality of AS, i.e., the quality of each AHB. The EA used in AHB calculation implies that the IRM's performance depends on the signal length - the more heartbeats are included in the process, the more suppressed is the noise in AHB. Therefore, the proposed method has limited performance when filtering very short signals, such as 10-second signals obtained with standard ECG devices or the signals shortened to eliminate extreme motion artefacts. However, we designed the method primarily for filtering signals obtained by mobile ECG devices, which are mostly 30 seconds long [5], [6]. In this setup, we verified by calculations that enough heartbeats can be selected to create a low-noise AHB. Redundant noise was additionally removed by a moving average filter to reach a high-quality AHB. While other filtering methods, such as those based on wavelet or frequency filtering can also be used for this purpose, we have chosen the moving average filtering method as the most straightforward and fastest approach. Likewise, it is possible to completely omit filtering after the EA; however, this would increase the number of IRM iterations to achieve a high-quality AHB.

One drawback of the method is related to the QRS detector- when an R point is omitted, the frequency components of that heartbeat higher than 10 Hz will be marked as the EMG noise and removed from the signal. This detrimentally reduces the information available for that heartbeat.

The number of IRM iterations depends on the SNR level after the first iteration (SNR_{iter_1}). The overall performance of the IRM method showed low sensitivity to changing the thresholds for choosing the number of iterations for ±2 dB. This demonstrates the method's robustness to the threshold selection, along with an excellent performance for a small number of iterations (≤3). We have also tested an automated method for determining the number of iterations that is based on SNR convergence. We processed the signal with the IRM block iteratively until SNR between two consecutive iterations became insignificant (SNR>30 dB). Such automation not only makes the algorithm less supervised, but offers an opportunity for a slight improvement in denoising performance at the cost of computational time.

A discussion in [29] and the references therein suggest that the high frequency content of the ECG signal between 300 Hz and 500 Hz is important. The low-pass filter with the 100 Hz cut-off applied in the preprocessing stage clearly prevents observation of these high-frequency features. We have examined the IRM performance upon removal of the low-pass filter and found out that SNR_IMP improved, which is expected due to the higher noise content. The comparison of IRM and AWWF on the SimEMG database in Table II in Supplementary material is consistent with the comparison in Table II here, with the IRM performing better in all SNR ranges except on the very clean signals with SNR_IN>20dB. Therefore, we showed that IRM can be used without the low-pass filter in the preprocessing stage equally. Considering the current embodiment with the low-pass filter applied, we remind that the “Recommendations for the Standardization and Interpretation of the Electrocardiogram” suggest that most of the diagnostic information carried by the QRS, T and P waves is contained below 100 Hz [30]. Here, the EMG noise is filtered out only upon the removal of the auxiliary signal (AS), which is represented by medians containing the main signal features, such as QRS, T and P waves. Hence, the frequency content of these features, notwithstanding the frequencies above 100 Hz filtered in the preprocessing stage, retains a major part of the clinically relevant information. An intrinsic limit to the capability of the IRM to resolve their high-frequency features is induced by ensemble averaging.

Finally, as various studies utilize different metrics for reporting their results [11], [12], [13], [14], [15], [31], we have tested the key ones and obtained similar results applying RMSE, Noise Reduction Factor (NRF) [13], [31] or Percentage Root Mean Square Difference (PRMS) [15]. Detailed results are given in Supplementary material.

V. Conclusion

In this study, we have introduced a new iterative regeneration method for EMG noise removal from ECG signals suitable for implementation in ECG mobile devices. Essential characteristics of the IRM are the preservation of heartbeat morphology by retaining the low-frequency content and the preservation of inter-beat variation. The morphology preservation is particularly important in segments with small amplitude, such as ST segment crucial for detecting MI and P wave crucial for diagnosis of antrioventricular blocks. The heart beat preservation is mandatory in detection of some arrhythmias, such as premature ventricular contractions. Results of the study show superiority of the IRM compared to the commonly used wavelet and FIR filtering methods, especially when the analysis is performed on signals with significant amount of noise, SNR < 12 dB. The robustness of IRM to the changes in the EMG noise level and the low computational cost make IRM a good candidate for direct application in mobile ECG devices. Moreover, with minor adaptations, concerning mainly the signal preprocessing and adjustment of thresholds, the IRM algorithm can be used for different kinds of noises with the known spectral range, such as baseline wander.

Finally, by analyzing the MIT-BIH database we have implicitly included signals that represent different diagnoses, such as atrial fibrillation, left and right bundle branch block beats, premature ventricular contractions, non-conducted P-wave, etc. Further development of the method will be in the direction of exact compliance with the particular diagnosis accessible by clinical and mobile ECG measurements.

Author Contributions

Conceptualization, V.A. and J.P.; methodology, V.A. and M.I.; software, V.A.; validation, M.M.; formal analysis, V.A., M.I., L.P.M. and J.P.; investigation, V.A. and M.B.; resources, V.A., M.I., M.B. and A.N.; data curation, V.A., and M.B.; writing—original draft preparation, V.A., M.I., J.P.; paper preparation, M.I., J.P., D.P. ; visualization, V.A. J.P., and M.M.; supervision, D.P., J.P. and A.N.; project administration, J.P. and A.N.; funding acquisition, V.A., and A.N. All authors have read and agreed to the published version of the manuscript.

Conflict of Interest

The authors declare no conflict of interest.

Supplementary Materials

Supplementary materials contain detailed results about the IRM and AWWF algorithm runtime, SNR_IMP values obtained on SimEMG by IRM and AWWF without the low-pass filter in preprocessing stage, Student t-test analysis and effect size analysis and comparison of IRM and AWWF using RMSE, normalized RMSE and NRF.

Appendix

A. AHB Calculation

In the proposed method, parameters used for signal filtering are selected in Table IV.

TABLE IV. Tresholds Applied in IRM Method.

IRM algorithm parameters
Preprocessing	HPF cut-off	LPF cut-off	EMG cut-off	Heartbeat start
	2 Hz	100 Hz	10 Hz	Ri - 0.25 RRmedian
IRM stage	xcorrmin	Mov. average window	nHBmin	No. iterrations
	0.91	5 – 15 samples	1	1-3

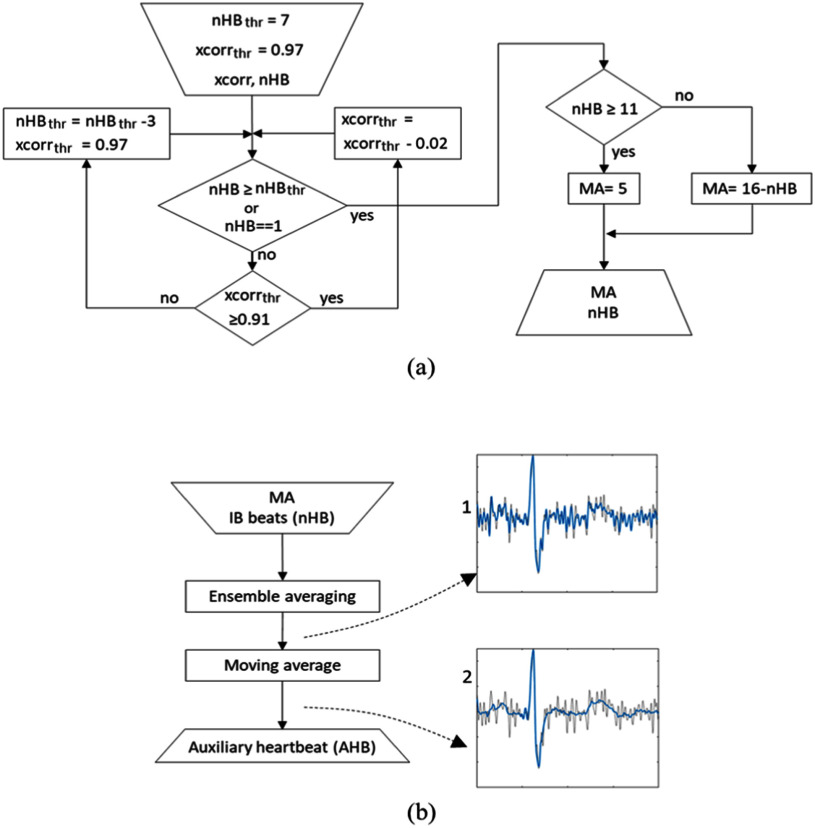
The nHB_thr and xcorr_thr are initially set to 7 and 0.97, respectively. If there are not enough similar heartbeats (nHB<nHB_thr), we reduce xcorr_thr in increments of 0.02 until either nHB ≥ nHB_thr or xcorr_thr = 0.91 is reached. If it is still not possible to have nHB_thr heartbeats, nHB_thr is reduced by 3, while xcorr_thr is restored to its initial value (0.97). This process is repeated until nHB ≥ nHB_thr or nHB = 1 is reached (Fig. 4(a)). The number of similar beats increases with SNR.

Fig. 4.

Block diagram of AHB creation for a single bit. (a) Algorithm that determines the number of beats nHB used in EA procedure and the length of the moving average filter MA. (b) The beat is first averaged with ensemble of all beats from IB that contributed to the nHB count (IB beats (nHB)), and then filtered to obtain AHB. Example signals are shown in b-1 and b-2, where the noise-contaminated heartbeat is given in gray and the filtered signals in blue.

On average, we have detected less than 7 similar beats in signals that have SNR<3 dB, and 7 or more beats in signals with SNR>3 dB (a typical empirical value of noise at which the signal is discernible by bare eye [32]). Hence, by setting the initial nHB_thr to 7, we ensure that the algorithm does not spend excessive time on beats that can be clustered as morphologically similar (xcorr_thr>0.96 [33]) and are efficiently filtered by EA in the first iteration, as well as that it does not corrupt the average by morphologically non-similar signals. The latter is particularly important in noisy signals, the SNR of which dramatically improves after the 1st iteration.

For example, in the SimEMG database, 25% of beats (with average SNR= 2.31 dB) are identified as individual in the 1st iteration, but in the 2nd iteration they were averaged with 9 other beats. We further stress that the algorithm classifies beats solely according to their similarity, with no reference to their diagnosis-relevant normality, and, hence, render a good AHB also for signals in which the abnormal outnumber the normal beats. Nevertheless, it does correctly identify and average all single or multiple heartbeats with a significant morphological difference (e.g., premature ventricular contractions [33]). Fig. 4(b-1) shows an example of the heartbeat after applying ensemble averaging. It is apparent that it contains residual noise. Thus, it was additionally processed by a moving average filter applied to two segments: (i) from the start of a heartbeat to the R-40ms; (ii) from the R+40ms to the end of the heartbeat (Fig. 4(b-2)). The length of the moving average window, MA, was set to approximately neutralize dependence of denoising efficiency on nHB. It ranged from 5 samples when the nHB ≥ 11 to 15 samples when nHB = 1.

B. Databases

Three different databases were used to study the performance of the proposed IRM method.

• 1)
  SimEMG database contains 37 noise-free and 110 noise-contaminated single-lead recordings generated from 14 subjects (9 females and 5 males aged 40 ± 13). All recordings are with duration of 30 seconds. The method relies on a particular placing of ECG electrodes to record signals with and without EMG noise. The noiseless reference measurement was performed with the ECG electrodes placed on the upper arm, which is known to be much less affected by EMG noise than the hands. The noisy measurement was performed with electrodes on fingers, meaning that all signals are equivalent to lead I of the standard ECG. Considering all electrode configurations, the average SNR_IN of the noise-contaminated signals was 8.53 ± 5.5 dB. Here, the SNR_IN is calculated as following:

  

  where s(n) is the reference signal, and z(n) is the EMG noise obtained by subtraction of the reference signal from the simultaneously recorded noisy signal. Here, we defined recorded EMG noise as the difference between the noise-contaminated ECG signal from hands and the reference signal. Most signals obtained from fingers contain a high noise level (SNR_IN < 8 dB), while only seven recordings have SNR_IN beyond 16 dB. The total number of recordings in SimEMG was 147. The SimEMG database is available as open-source at [23].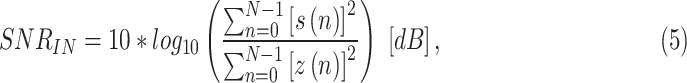
• 2)In the MIT-BIH-EMG database, the 2-lead noise-free signals originate from the MIT-BIH arrhythmia database [24], [25], which comprises 48 30-minute recordings. The first lead of these recordings was cut into 30-second segments and then estimated against the noise rejection criterion defined for the SimEMG database. As a result, 57 recordings obtained from 11 subjects passed the rejection criterion from this database and could be considered noise-free. This subset contains 9 recordings (16%) with atrial fibrillation, 3 with ventricular bigeminy (5%), 4 with ventricular trigeminy, and 1 with nodal (A-V junctional) rhythm. Additionally, the subset comprises normal beats (76.3% of the total number of beats), left bundle branch block beats (10.1%), premature ventricular contractions (8.9%), right bundle branch block beats (1.2%), and other abnormal beats in a smaller percentage. Noise-contaminated signals were created by addition of the genuine muscle artifact (EMG noise) recordings taken from the MIT Noise Stress Test [26] to these signals. The MIT Noise Stress Test database comprises 12 30-minute ECG recordings and 3 30-minute recordings of noise containing predominantly BLW, EMG, and motion artifact noise with different SNR ratios. Since this study focuses on eliminating EMG noise, we have used only the noise recordings that predominately contained this type of noise. To remove BLW, we additionally processed them with a Butterworth high-pass filter with a cutoff frequency of 3 Hz. For every noise-free signal, 3 different randomly selected noise segments are added, resulting in 171 noise-contaminated recordings with an average SNR_IN of 11.90 ± 3.25 dB. The total number of recordings in MIT-BIH-EMG was 228.
• 3)In the Synth-EMG database, the noise-free ECG signals were obtained from the ECG signal generator described in [27], with 5 parameters randomized here. We generated 50 noise-free ECG recordings with duration of 30 seconds. The EMG noise originated from the MIT Noise Stress Test Database. We added 3 different noise segments for every noise-free signal, resulting in 150 recordings with an average SNR_IN of 6.22 ± 3.11 dB. The total number of recordings in Synth-EMG was 200.

C. Benchmark Methods

A detailed description of the AWWF method can be found in [11]. This algorithm uses the dyadic stationary wavelet transform in the Wiener filter. It improves the signal quality by adding the block for noise estimate, which monitors the time dependence of SNR within the signal. It also includes the algorithm for finding suitable parameter values by maximizing the average SNR improvement. We have used a MATLAB implementation of the AWWF algorithm.

WT is the standard method for filtering ECG signals from noise. Here, we applied the algorithm as described in [9]. In addition, we optimized the methods’ parameters (wavelet family, lower and higher thresholds) on the SimEMG dataset. It resulted in sym4 filter banks, a decomposition level of 5, and hard thresholding to manage the cD3 and cD4 coefficients.

Conventional FIR and IIR filters are commonly used to compare different ECG denoising algorithms [11], [14]. Here, we applied a low-pass Butterworth filter with the cut-off frequency set to 40 Hz.

D. Code Availability

As a proprietary code of the HeartBeam, Inc. included in AIMIgo device, the IRM code is not available online. We published our implementation of WT algorithm from reference [9] here https://drive.google.com/file/d/1z-QfXv35dHf65wgX9_vimimJPxaXtPyr/view?usp=drive_link and of FIR here https://drive.google.com/file/d/1xc7KlZablaveLrwHiLno0TGGjUtlI9jI/view?usp=drive_link.

Funding Statement

This work was supported in part by the Ministry of Science, Technological Development and Innovation, INN Vinča under Contract 451-03-47/2023-01/ 200017 and in part by ITS-SASA under Contract 451-03-68/2022-14/ 200175.